Preferential Bayesian optimization improves the efficiency of printing objects with subjective qualities

Abstract

Despite recent advances in closed-loop 3D printing, optimizing subjective and difficult-to-quantify qualities—such as surface finish and clarity of fine detail—remains a significant challenge, often relying on the traditional time-consuming and inefficient trial-and-error process. Preferential Bayesian optimization (PBO) is a machine learning technique that uses human preference judgements to efficiently guide the search for such abstract optimums in a high-dimensional space. We evaluated PBO's ability to identify optimal parameter values in printing profiles of vases and pairs of 3D cones. In semi-autonomous printing campaigns, a human observer ranked triplets of images of these objects with a target object in mind, preferring slender/bulbous vases and cone pairs that were smooth and well-formed. Results show that PBO consistently and quickly identified an optimal parameter combination across repeated testing. Modeling was then used to identify object dimensions responsible for preference judgements and to mimic preference behavior. Findings suggest that PBO is a promising tool for expanding the range of 3D objects that can be printed efficiently.

---

1 Introduction

Advances in artificial intelligence (AI) continue to make transformative changes in all sectors of society, including the practice of science.^1–3 In the past two decades, we have witnessed the development of AI-based closed-loop research systems that autonomously generate scientific hypotheses and experimentally test those hypotheses, all performed by research robots. Such systems are used for experimentation in fields such as microbiology,^4,5 chemistry,^6–9 and materials science.^10–15

One class of these technologies seeks to accelerate research by improving the data collection process. Research depends critically on the ability to collect high-quality data efficiently, thereby minimizing cost (e.g., resources, time) and maximizing their informativeness. Recent advances in machine learning (ML) have yielded approaches to addressing this issue through the development of optimization algorithms that identify experimental designs to achieve a specific objective, making research both efficient and informative.^16,17 The methodology generally involves adapting the experimental design in real time as the experiment progresses. That is, an experiment is run as a sequence of mini-experiments in which the values of designs (e.g., task parameters, compositions of input materials) that are most informative with respect to the objective of interest (e.g., optimizing the growth of carbon nanotubes) are algorithmically chosen for the next mini-experiment based on the data collected in earlier mini-experiments.

Bayesian optimization (BO)^18–20 is one such algorithm that has received much attention due to its success in optimizing unknown and expensive-to-evaluate functions that arise in many real-world setting such as in neuroscience,^21,22 chemistry,^23–27 materials design and discovery,^28–31 and 3D printing.^32–35 Our own labs have demonstrated the effectiveness of the BO algorithm for optimizing experimental designs in the areas of carbon nanotubes synthesis, additive manufacturing (aka 3D printing), and cognitive science.^32,36,37 The present study extends this work in BO-based autonomous experimentation³² to more challenging optimization problems.

Despite the growing popularity of 3D printers, achieving optimal performance remains challenging due to the complex tuning process. Traditionally, this process involves a time-consuming trial-and-error approach where users adjust one or two parameters after each print trial based on a preferential visual assessment of the printed part. However, given that many parameters may require adjustment, and the inter-dependent and conflicting nature of some of the parameters, the traditional tuning process can be time-consuming and frustrating. The challenge of adjusting numerous parameters is particularly evident for extrusion-type systems, such as Direct-Write (DW) and Fused Filament Fabrication (FFF)§ printers, which feature a large number of adjustable parameters. Moreover, the parameters for these printers often need to be re-optimized due to factors such as inconsistencies in feedstock, fluctuating print conditions, and differences between ostensibly identical printers.

In current closed-loop approaches, the challenges associated with tuning system parameters involves employing sensors (optical, electrical, chemical) to acquire data, whose values are fed to an ML algorithm like BO to identify new sets of input parameters for the next experiment.^15,33,37,38 While such systems may work well when objectives are easy to quantify, alone they are likely to be inadequate when holistic and aesthetic evaluation is required to assess elements of part quality, such as surface texture, definition of fine details, or shape (e.g., is the design well balanced or the style of furniture attractive?). Human judgment can be superior to sensor measurements in such cases.

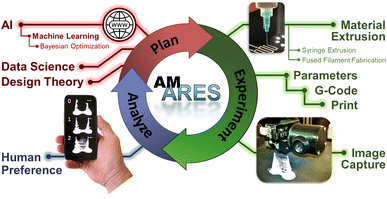
Interest in human-assisted machine learning has grown in recent years and has led to the introduction of multiple algorithms that incorporate human judgment. In what is known collectively as preferential Bayesian optimization (PBO),^39–41 human preference, instead of sensor measurements, serves as a reward function that optimizes an experiment outcome in an otherwise autonomous research system. As such, PBO is a human-in-the-loop machine learning approach.^42–44 The purpose of the present work was to evaluate the suitability of PBO in AM. Since 3D printers are automated systems, they readily lend themselves to PBO integration to optimize a preference-based print objective in a real-world setting. Here we focused the PBO algorithm on parameter optimization for DW and FFF printing.

As a proof-of-concept, we started by printing the profile of a simple 2D vase. Vase proportions can vary greatly, ranging from slender and elongated to wide and rounded, and when viewed from an artistic perspective, their attractiveness is very much a personal preference. Across one set of campaigns, the oracle's (human observer) responses reflected a preference for a slender vase. In a second set of campaigns, the oracle preferred a bulbous vase. For this work, we used our customized closed-loop volumetric extrusion printer with integrated machine vision to deposit modified latex caulk onto a glass build plate. The closed-loop process included capturing images of the printed vases and sending them (in groups of three) to an oracle's cell phone in order to efficiently capture preference responses. It is important to note that while the input parameters for this study were simply geometric (arc intersection coordinates, vase widths) and not tied specifically to 3D printing, it was an invaluable exercise for validating the numerous elements comprising the research pipeline while also assessing the ability of the algorithm to learn preferences (i.e., slender vs. bulbous).

A more challenging test of PBO was undertaken in the second study, in which the printing goal was much more difficult but fully applicable for tuning 3D printers. Here, we employed a customized closed-loop conveyor belt FFF system with integrated machine vision to produce a bonafide 3D specimen; a pair of cones. This specimen was chosen as it embodied several well-known FFF printing challenges as outlined in the methods section. Because FFF printing is notoriously slow due to its serial and layer-by-layer print paradigm, we chose to employ the PBO algorithm toward improving FFF throughput while maximizing part quality. To do this, the system was forced to print at a demanding print speed of 300 mm s⁻¹ while the oracle's responses reflected a desire for cones that were geometrically accurate and had smooth surfaces. The print parameters that were made accessible to the planner were chosen based on their significant influence on the geometric accuracy and visual appeal of the printed specimens without having any appreciable effect on the print time.

The workflow in the two studies is depicted in Fig. 1. In the plan phase, three batches of print parameters were chosen to optimize the search to find the parameters that maximized the print objective. These were passed to the printer (Experiment phase) and the objects were printed in succession. A camera recorded an image of each object, which were then delivered as a group to the oracle's cell phone for preference ranking. The planner, located on a GPU server at Ohio State University, then used the rankings to generate new combinations of print parameters for the next experiment. Three PBO campaigns were run to assess consistency in performance.

Fig. 1 A schematic of workflow in the PBO experiments. See text for a description.

To the extent PBO succeeds in learning the oracle's preference, it should be possible to model this preference from the images and rankings. Such a model would in essence embody, at least partially, the dimensions that define the oracle's preferences. It could possibly be used in place of the oracle to expand the autonomous capabilities of the printer. We explored this idea in the final part of the investigation.

2 Methods

2.1 Preferential Bayesian optimization algorithm

Preferential Bayesian optimization (PBO)^39,40,45,46 is a human-assisted Bayesian optimization (BO) approach in which optimization is driven by human preference decisions on two or more alternatives. BO itself is an active learning algorithm in machine learning⁴⁷ for finding the global optimum of a black-box function that is expensive to evaluate. The algorithm works by adaptively and sequentially sampling candidate points from optimal-potential regions of the function in order to identify the optimum in the fewest possible number of evaluations.^19,48–51 The black-box function is modeled by a Gaussian Process (GP)⁵² which is a flexible nonparametric Bayesian method that can approximate nonlinear functions with minimal assumptions on the functional form. BO combines the GP with what is known as an acquisition function that guides the adaptive search process towards optimal-potential regions. Specifically, for a given experimental design, the acquisition function estimates, through a trade-off between exploration and exploitation, the likelihood of achieving the optimization goal by probing that design. There are multiple commonly employed acquisition functions.^49,53

In PBO, unlike the usual BO, the optimum is an unobservable human preference that is found by executing queries through a series of comparative judgments whose alternatives are chosen by the BO algorithm.⁴⁰ That is, the optimum of the latent (black-box) function is estimated using BO by sampling design points to be compared with one another in an adaptive and efficient manner. The PBO algorithm used in the present work was selected by evaluating the relative performance of eight PBO algorithms, six variants of q Noisy Expected Improvement (qNEI)^41,49 and two variants of Expected Utility of Best Option (EUBO).⁵⁴ They were chosen because of their suitability and performance in past studies. All these algorithms assume GP modeling of a latent utility function.^39,52 Given noisy observations of the outcome function, qNEI selects q (≥2) design choices based on the highest function values by posterior simulation, whereas EUBO directly maximizes the expected utility of the best option and can be applied only to the case of two design choices (i.e., q = 2).

As a prelude to the studies below, we conducted a series of simulations to evaluate and compare performance of the eight algorithms under various experimental conditions that varied in the number of options (q) to choose from and the dimensionality of design space (d), which is defined as the number of parameters in a function to be optimized. The objective was to find the maximum of a simple unimodal function. The results of these simulations (see Suppl†ement) led us to apply what we refer to as the qNEI-UB-woBest algorithm for q = 3. This algorithm selects, on each experimental trial, q – 1 points that jointly maximize expected improvement from the updated best (UB) point, and adds the UB to make q points. It is a compromise between efficiency and task difficulty: The algorithm is reasonably efficient when there are three options (only minor additional improvement was found with more) and ranking of only three options is easier for the oracle than four or more, especially when there are small differences between options.

In the present work we implemented the selected PBO algorithm (i.e., qNEI-UB-woBest) in the following manner. The oracle's preference was first expressed in the form of one rank order among all three choice options. The rank order was then translated into a set of pairwise preference relations. As an example, consider that the oracle gives a rank order among three options as a > b > c, which means that option a is preferred to option b, which itself is preferred to option c. Under the assumption of the transitivity of preference, this rank order is equivalent to three pairwise relations of a > b, b > c, and a > c.¶

2.2 Direct-writing of 2D specimens (vase profile)

In this study, we used our previously developed AM ARES system (Fig. 2a), which is designed for closed-loop autonomous optimization of specimens deposited via volumetric syringe extrusion (Myung et al.,⁵⁵ submitted). The AM ARES system was created by modifying a commercially available Lulzbot TAZ Fused Filament Fabrication (FFF) 3D printer (Aleph Objects Inc., Loveland CO, USA). To dispense fluids with low to moderate viscosity, we replaced the stock FFF print head, which requires commercially produced thermoplastic filament, with a custom-designed volumetric syringe extruder (Fig. 2b). The syringe extruder was specifically engineered to accept disposable 10 mL syringes, which could be equipped with a variety of dispensing tips. For this work, we opted for 0.43 mm (0.017′′) stainless steel dispensing tips (McMaster-Carr, Cat. #75165A684).

Fig. 2 (a) The closed-loop AM ARES syringe-extrusion system, (b) custom syringe extruder (c) custom syringe centrifuge. Commercially available FFF 3D printers were purchased and retro-fitted with custom-designed syringe extrusion print heads (A) with integrated dual camera machine vision systems (E and F). Each camera was fitted with LED light rings were individually addressed by AM-ARES software through an Arduino light controller (C). A peripheral wet sponge cleaning station (B) has been incorporated into the setup to enable dispensing tip cleaning after printing each specimen. The use of disposable polypropylene syringes, which were clamped securely into the extruder (D), reduces cost and encourages exploration of diverse sets of materials.

To provide live visual feedback to the oracle and enable image-based analysis for the planner, a dual-camera machine vision system was incorporated into the print head. One camera, the “process” camera, was mounted at an angle and provided real-time video of the dispensing tip. This camera was essential for “zeroing” the dispensing tip on the surface of the build plate, for precision mapping of the undulations of the build plate, and for monitoring the deposition process. The other camera, the “analysis” camera, was mounted normal to the build plate at a measured offset from the dispensing tip and could be used for asynchronous capture of high quality, top-down images of printed specimens.

To ensure that each experiment began with a clean dispensing tip, a wet sponge reservoir was mounted on one side of the build plate. After each experiment, the dispensing tip was moved to the sponge and an automated cleaning routine was performed where the dispensing tip was wiped against the wet sponge to remove built-up materials. This cleaning process also greatly reduced the risk of nozzle clogging from rapidly drying feedstock.

The feedstock for this study was prepared by combining 20 g of Alex Caulk with 5 g of water in a conical 50 mL centrifuge tube. The mixture was thoroughly blended through a combination of manual stirring and vortex mixing. We transferred 10–12 mL of the mixture to a 10 mL (nom.) polypropylene syringe (Norm-Ject Manuf. #4100.X00V0) which we then subjected to centrifugation in our custom-built syringe centrifuge (Fig. 2c), spinning at 2800 rpm for 25 minutes to remove entrained gases. After spinning, the remaining air was carefully expelled by depressing the plunger and tapping the side of the syringe on a hard surface as needed.

After mounting the syringe in the AM ARES print head, a semi-automated routine to measure the x, y, and z offset between the dispensing tip and the analysis camera was performed. In preparation for a campaign, and as needed after cleaning the build plate, a semi-automated routine to virtually “level” the build plate was performed using the “mesh bed leveling” process. This involved using the process camera to jog the dispensing tip in the z-direction to measure the relative heights of the build plate over a grid of 42 equidistant points. The system's firmware (Marlin) then used these measurements to interpolate an estimated continuous surface. While printing each specimen, the firmware used this virtual surface to keep the distance between the dispensing tip and the build plate relatively constant.

Campaigns were run using a beta version of ARES OS⁵⁶ software. ARES OS manages high-level campaign logistics including termination conditions, parameter planning, build plate partitioning and allocation, analysis routine coordination, tool path generation, and planner communication.

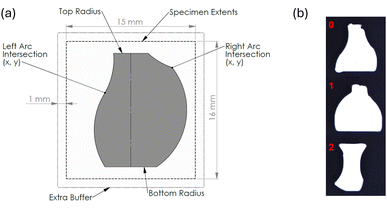
Lower-level AM ARES subroutines were coded in Python.⁵⁷ These included a subroutine to dynamically generate single-layer models of the planner-directed vase designs and another subroutine that employed UltiMaker's CuraEngine⁵⁸ command-line slicer to generate G-code (also known as “the toolpath”) to send to the AM ARES printer. To partition the build plate, ARES OS used the extents extracted from the toolpath to subdivide the area available on the build plate into equal segments for printing specimens (Fig. 3a). Using our AM ARES system, we were able to print a total of 208 specimens (∼69 experiments) before having to clean the build plate in order to continue with the campaign.

Fig. 3 (a) The geometric parameters and print layout for 2D vases. Six parameters employed to verify the functionality of the PBO planner with a closed-loop 3D printer were geometric properties that contributed to aesthetic quality, but had no impact on print quality: Left Arc Intersection X and Y, Right Arc Intersection X and Y, Top Radius, and Bottom Radius. The dotted rectangle denotes the “Specimen Extents,” which ARES OS uses to subdivide the build plate into equal segments for printing specimens. Extra Buffer is set by the user to ensure captured specimen images do not include portions of adjacent specimens. (b) An example of a composite image sent to a user's cell phone for preference ranking.

Three specimens were printed per experiment. After printing each, the analysis camera was used to record a 600 × 600 pixel image of the specimen. The three images were combined into a single composite image and annotated with zero-indexed reference numbers (e.g. “0”, “1”, and “2” might refer to specimens “11”, “12”, and “13”, respectively; Fig. 3b). Next, using Twilio's API for programmatic text messaging and a GitHub repository to host image files, AM ARES sent the 3-specimen image to the oracle's (a member of the research team) mobile phone with instructions to rank their preference. These values were transformed into two-term inequalities before being saved in a JavaScript Object Notation (JSON) file along with corresponding specimen design parameters and maximum and minimum parameter bounds. The JSON file was transmitted to the planner to initiate the next experiment. In each of the three campaigns, a total of 79 experiments were conducted. The parameter values for the first three ‘seed’ experiments (i.e., the first nine designs) were determined using quasi-random number generation within the bounds defined by each parameter.

The design space included six geometric parameters that were selected to influence the aesthetic qualities of the 2D vase profile. These parameters are based in an integral, two-dimensional area of size (100, 100). They were.

(1) Top radius [range = 5–40]: the radius of the top rim of the vase.

(2) Left arc intersection X [range = 10–48]: the x-coordinate of the intersection of the arcs that define the left side of the vase profile.

(3) Left arc intersection Y [range = 15–80]: the y-coordinate of the intersection of the arcs that define the left side of the vase profile.

(4) Right arc intersection X [range = 52–90]: the x-coordinate of the intersection of the arcs that define the right side of the vase profile.

(5) Right arc intersection Y [range = 15–80]: the y-coordinate of the intersection of the arcs that define the right side of the vase profile.

(6) Bottom radius [range = 10–45]: the radius of the base of the vase.

2.3 Fused filament fabrication of 3D specimens (two cones)

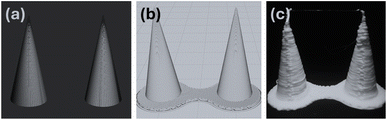
We employed the Autonomous 3D Printing (Auto3DP) system (Inventive Research Solutions LLC, Owatonna MN, USA, Fig. 4) to evaluate PBO against more complex and AM-relevant problems. We down-selected from a collection of well-known 3D printing challenges⁵⁹ and settled on our candidate specimen: a pair of 3D cones 5. The “two-cone” specimen was selected to address the issues known as “blobs”,⁶⁰ “stringing”,⁶¹ and “under-extrusion”.⁶² The Auto3DP system was custom-designed specifically for testing ML algorithms to accelerate and streamline the process of 3D print parameter optimization for FFF printers. To achieve this cost-effectively, the Auto3DP system was constructed by integrating components of two Ender-3 3D printers (Shenzhen Creality 3D Technology Co., Ltd., Shenzhen, China) to produce a unified dual-gantry, closed-loop 3D printing system where one gantry is dedicated to printing (Fig. 4aA) and the other handles imaging (Fig. 4aB). The inclusion of a 5-axis camera (Fig. 4b) provides extensive imaging capabilities, allowing for the capture of multiple images from many perspectives. Additionally, a conveyor belt build surface seamlessly links the two gantries, overcoming the constraints of a finite-area build plate. After printing and imaging, the conveyor belt can be advanced to allow the specimens to detach and fall off into a collection bin.

Fig. 4 (a) The closed-loop Auto3DP FDM system. (b) A close-up view of Auto3DP's 5-axis imaging system.

Before printing each 3D specimen, a print head-mounted touch probe (Creality Ender CR Touch) was deployed to measure the z-height of the conveyor belt surface. Next, a multi-layer (4-8 layers typ.) lattice structure (i.e. a “raft”) was deposited as a foundation for the printed part. The raft enhances adhesion to the conveyor belt and acts to flatten undulations in the surface of the print area. To ensure fairness in comparing specimens, the raft was always printed using the same conditions (a build surface temperature of 60 °C and a tip temperature of 240 °C), regardless of variations in specimen print parameters. Additionally, the raft was deposited using the same material as the specimens which, for this project, was 1.75 mm PLA filament (Duramic 3D PLA Plus). After completing the raft, printing automatically paused while the dispensing tip's temperature adjusted to the desired specimen set-point.

Campaigns were managed using the software developed in tandem with the Auto3DP hardware. The test specimen for the campaign was easily established by selecting and loading an STL file (e.g. “2_cones.stl”, Fig. 5a) into the software. STL files, widely employed in 3D printing, consist of a collection of triangles defining a closed volume. Auto3DP print parameters were adopted from Ultimaker's Cura slicing software and divided into two categories: “fixed parameters” and “campaign parameters”. Users have the ability to set fixed parameter values, which cannot be marked as adjustable by the planner. Campaign parameters can be marked as adjustable, with users designating them as such and setting their upper and lower bounds. Any campaign parameters not designated as adjustable are effectively treated as fixed.

Fig. 5 The transformation of an STL file into a 3D-printed object. (a) A graphical representation of an STL 3D model. An STL (known historically as “STereoLithography” or more contemporarily as “Standard Triangle Language”) uses a collection of triangles to define a closed volume. (b) A simulated 3D representation of the G-code output generated in Cura. A foundational raft structure can be seen below the cones. (c) A photo of an actual pair of 3D-printed cones, which were fabricated based on a combination of inputs including the STL file and the planner-modified parameters.

To generate the G-code for each specimen, Auto3DP employs curaengine.exe, the command-line back-end for Ultimaker's Cura slicing software. Auto3DP aggregates all print parameters and their respective values into a JSON settings file. This file, along with the selected STL file, is then processed by curaengine.exe to generate the corresponding G-code which directs the 3D printing process (Fig. 5b). When the specimen has finished printing, Auto3DP advances the conveyor belt and positions the camera as specified to capture the requisite image(s). For this study, we captured a single image (Fig. 5c). Raw images were fist cropped to remove empty regions (from 2448 × 3264 pixels to 2448 × 2122 pixels) and then resized to 600 × 520 pixels prior to transmission to the oracle.

Campaigns followed the same procedure as in the 2D case. Auto3DP sent a composite image of 3 specimens to the oracle's mobile phone. Ranked preferences were then transmitted back to the planner. Auto3DP then waited for the planner to respond with a new set of 3 specimen designs before initiating the next experiment. Including three ‘seed’ experiments, there were a total of 100 experiments in each of three campaigns.

The six parameters designated as adjustable for this study were chosen based on two criteria: First, we wanted parameters that would have a substantial impact on the quality aspects as outlined above (blobs, stringing, under-extrusion). Second, we selected parameters that would have minimal to no impact on specimen print time. This ensured that the planner could not indirectly undermine our throughput target by, for instance, significantly reducing the acceleration such that the print speed never reached our forced setpoint.

Print parameters:

(1) Retraction distance [range = 0.0001–10.00]: the length of filament (in mm) retracted during a retraction move. Typically, retractions occur prior to beginning a new perimeter layer. A value that is too low can result in material oozing from the nozzle as it travels to start a new perimeter, whereupon the oozed material is deposited as a blob.

(2) Retraction extra prime amount [range = 0.0–0.1]: the opposite of retraction is priming. This value feeds additional filament (in mm³) to the nozzle during priming to account for material lost due to oozing during coasting. A value that is too low can result in under-extrusion at the beginning of a new perimeter.

(3) Outer wall wipe distance [range = 0.0–0.5]: distance (in mm) of a travel move inserted at the end of a perimeter wall print to assist in hiding the z-seam. A value that is too low can result in a blob forming at the end of a perimeter print due to oozing before the filament completes a retraction.

(4) Outer wall flow [range = 50–150]: flow compensation as a percentage of the basal flow rate. A value that is too high can result in excessively wide walls and creation of blobs at the ends and beginnings of perimeters. A value that is too low can result in under-extrusion at high speeds.

(5) Coasting volume [range = 0.0–0.5]: this volume of material (in mm³) corresponds to a calculated distance at the end of a print move. Over this distance, active extrusion is replaced with passive extrusion (i.e. “oozing”). A value that is too high can result in under-extrusion toward the end of a perimeter print. A value that is too low can result in blobs at the end of a perimeter print.

(6) Printing temperature [range = 190 – 260]: the temperature (in °C) of the nozzle. A value that is too low can result in under-extrusion due to the material's viscosity being too high. A value that is too high can result in over-extrusion (blobs) and poor specimen fidelity.

Fixed parameters of note included Retraction Speed, Layer Height, Infill Density, Coasting Speed, Travel Speed, and Print Speed which were set to 300 mm s⁻¹, 0.25 mm, 0%, 100%, 400 mm s⁻¹, and 300 mm s⁻¹, respectively. With these fixed values, print times across all “two cones” specimens (not including overhead such as printing the raft) averaged 222.35 ± 23.03 seconds.

3 Results

The suitability and robustness of PBO were demonstrated in repeated print campaigns of three different test specimens, two 2D vases and one 3D pair of cones.

The performance of PBO is a function of what it learns from the oracle's preference choices from efficient sampling of the print parameter space over a campaign. Learning was measured by examining performance on the final experiment of the campaigns and how the model's preferences changed across experiments. In both cases, model behavior should mirror that of the oracle. That is, if PBO was successful over the given number of experiments in a campaign, then the highest ranked printed specimen in the last experiment should be a good exemplar of what the oracle had in mind when indicating their preferential choices. Further, preferences from the beginning of the campaign can be evaluated relative to this exemplar. We quantified the preference using a well-established measure in decision theory and economics known as latent utility. That is, a latent “utility” function (described in detail below) is devised as a quantitative measure of the strength of preference such that the higher the utility value of a specimen, the stronger the preference for that specimen. Before getting into the details of how this was done, we asked ourselves whether the algorithm worked as expected.

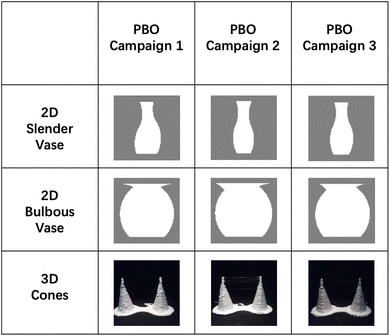
Table 1 provides the most direct evidence that the PBO algorithm successfully learned the oracle's preferences. In the first two rows are drawings of 2D vases made using print parameters extracted from the model on the last experiment of each campaign. They are the vases with the highest utility. For the three PBO campaigns, the vases resemble their respective categories, looking mostly slender when the oracle's preference was slender and bulbous when the preference was bulbous. Some variation among vases is to be expected because what constitutes a slender vase is likely not fixed, but a category of acceptable exemplars. Similar consistency is found with the 3D cones, which are photo images of actual pairs of 3D-printed cones using print parameters extracted from the model on the last experiment of each campaign.

Table 1 The model-inferred vase/cones of the last experiment from each campaigns. The first two rows are drawings of 2D vases made using print parameters extracted from the model on the last experiment of each campaign. The third row shows images of the 3D-printed cones using print parameters extracted from the last experiment of each campaign

---

3.1 Utility analysis

We define the desired utility function as the posterior mean function of a Gaussian Process (GP) estimated at the end of a campaign. Using technical language, suppose that a campaign has finished after N experiments, and in each experiment k (=1, 2, …, N) the oracle indicated their preference among a set of three printed specimens (vases or cones) denoted by x_k = (x_1,k, x_2,k, x_3,k) where x_j,k (j = 1, 2, 3) is a six-dimensional vector. Let us denote the posterior mean function estimated after N experiments by μ_N(x). In terms of this function we calculate a utility value for the j-th specimen presented in experiment k as μ_N(x_j,k). The utility of the specimens generated by PBO can also be calculated and compared with the oracle's. The model's most preferred specimen was defined as the highest mean of the Gaussian Process in each experiment. Given the oracle's rankings and the input parameters chosen thus far in the campaign, it represents the model's best estimate of the oracle's preference; we refer to it as the model-inferred preference. Note that this is not actually shown to the oracle, but instead is statistically inferred by the GP model. Formally, the “model-inferred” specimen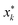 is defined as 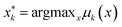, where μ_k(x) is the posterior mean function estimated after k experiments.

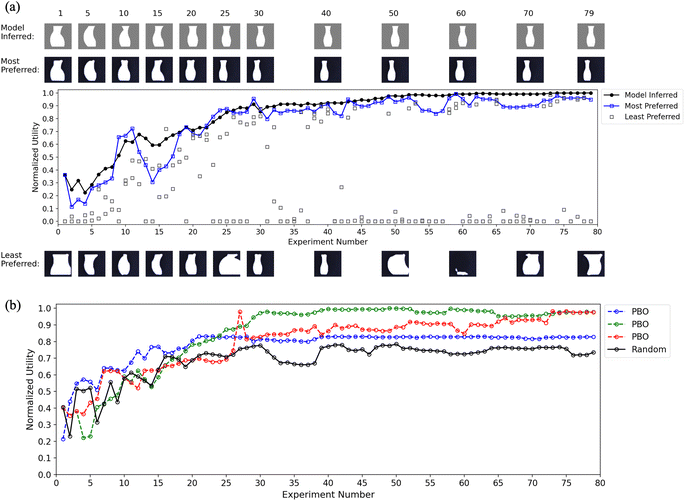
We examined utility across the campaign for both the oracle and the model, beginning with the vase data. Shown in Fig. 6a are the data from one campaign (N = 79 experiments) when the oracle expressed a preference for a slender vase (utility values are normalized on the scale of 0 to 1). The three open squares represent the utility values {μ_N(x_1,k), μ_N(x_2,k), μ_N(x_3,k)} of three vases, with the most-preferred (blue square) and least-preferred (black square) in each experiment. The filled black circles represent the model-inferred utility curve 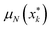for 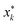(defined above) as a function of experiment number k. Images of vases from a subset of experiments are shown above and below the graph.

Fig. 6 (a) Normalized utility graph of the model-inferred slender vases and the three specimens from a representative PBO campaign. Images of vases from a subset of experiments are shown above and below the graph. The model-inferred vases are drawings made using print parameters extracted from the model, and the most- and least-preferred vases are actual printed specimens shown to the oracle. (b) Normalized utility graph of the model-inferred slender vases from the three PBO campaigns and a single random campaign.

Focusing first on the oracle's responses (open squares), it took 50 experiments to reach a utility value of 1, identifying a parameter configuration that yielded an ideal slender vase in the eyes of the oracle. The utility of the least-preferred vase varies widely across the campaign, reflecting PBO's continuous search to find an even greater optimal parameter configuration. The model-inferred utility function (filled black circles) tracks the most-preferred function, a clear sign that it learned the oracle's preferences from the rankings of a wide variety of vases over experiments. Some of this variety can be seen in the least-preferred images. The most-preferred images transition toward a slender vase over experiments, as they should if the algorithm is learning the oracle's preference.

Comparison of the most-preferred and model-inferred utility functions reveals two other aspects of PBO performance. The dip in the most-preferred function between experiments 12 and 19 can seem like a lapse in the oracle's judgment or errors in ranking. Although this can occur, these dips are most often due to the three options being far from the oracle's ideal of a slender vase, as seen in the images on trial 15. Note that the most- and least-preferred vases are somewhat oddly shaped. The oracle must nevertheless rank the options; their low utility emerges when compared with the reference vase. This is normal behavior of a global optimization algorithm whose search strategy includes significant exploration. Also, once the model has identified an optimum (e.g., experiment 50) it is robust to slight fluctuations in the utility of the most-preferred option. At this point in the campaign, slight changes in the print parameters of the most-preferred vase generate equally good vases (or may not be detectable).

Fig. 6b contains the model-inferred utility functions from the three PBO campaigns and one random campaign (discussed later). To compare these campaigns, the four utility curves were created using a single posterior mean function μ_N(x) that was estimated by combining the data (N = 316) from all four campaigns. Focusing only in the three PBO campaigns, there is reasonable consistency among them. The red and green PBO campaigns follow a similar path, suggesting that the model's rate of preference learning was similar. The blue PBO campaign displays a similar trajectory initially, but asymptotes at a lower utility value, suggesting the final vase is further from the oracle's aggregate (i.e., across three campaigns) ideal; inspection of the drawings in Table 1 confirm this. A likely reason for this outcome is that the algorithm struggled to identify a global optimum because of excessive exploration in dis-preferred regions of the parameter space. Seventy-nine trials may have been insufficient for the model to extract itself from a local minimum to find a parameter set that yielded higher utility.

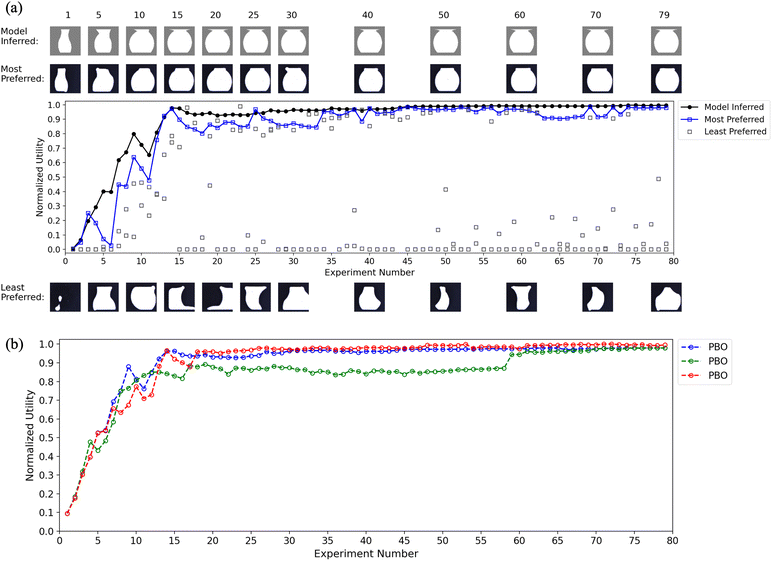
Fig. 7 contains corresponding graphs of the data when the oracle's preference was a bulbous vase. The results are similar to those in Fig. 6. By experiment 16, the model has internalized the combination of print parameters that generate an ideal bulbous vase, with only a modest amount of learning occurring in the reminder of the campaign. Again, the model-inferred utility function parallels that of the most-preferred vase while widely sampling the parameter space, as shown by the utility values and images of least-preferred vases. The combined model-inferred functions in Fig. 7b demonstrate the consistency of the algorithm. Note that these three campaigns were purposefully seeded with parameter settings that generated slender vases (note the first most-preferred image in panel a) to increase learning difficulty. This change in procedure is the reason why the utility value in experiment 1 (mean = 0.09) is consistently lower than that in the slender campaigns (mean = 0.36).

Fig. 7 (a) Normalized utility graph of the model-inferred bulbous vases and the three specimens from a representative PBO campaign. Images of vases from a subset of experiments are shown above and below the graph. The model-inferred vases are drawings made using print parameters extracted from the model, and the most- and least-preferred vases are actual printed specimens shown to the oracle. (b) Normalized utility graph of the model-inferred bulbous vases from the three PBO campaigns.

Taken together, the results of these two sets of 2D vase campaigns demonstrate that the PBO algorithm successfully learned, based solely on a series of preference judgments, to infer the internalized, ideal vase in the oracle's mind. Comparison of slopes of the utility functions in Fig. 6b and 7b shows the former taking about twice as many experiments to asymptote (30 vs. 16) as the latter, suggesting that a slender-vase preference was more difficult to learn. The extended neck of the slender vase may require greater adjustments of symmetry and proportionality between the top half and the bottom half.

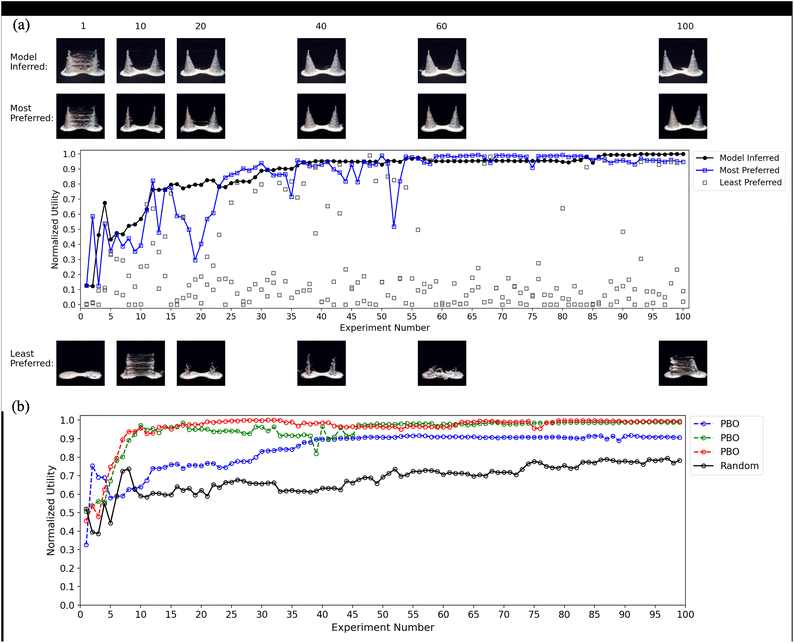
Fig. 8 contains the corresponding graphs for the 3D cones study. Despite the greater difficulty of the print goal, PBO succeeded in finding a good exemplar in each campaign. The data from a single campaign in the top graph show the model-inferred function peaking at experiment 35. Like in the vase campaigns, it follows the oracle's most preferred function, with learning perhaps slowing somewhat when a string of experiments (trials 16–24) include specimens that are not close to the oracle's ideal.

Fig. 8 (a) Normalized utility of the model-inferred 3D cones and the three specimens from a representative PBO campaign. Images of cones from a subset of experiments are shown above and below the graph. The model-inferred cones are photo images of actual 3D-printed specimens using print parameters extracted from the model, and the most- and least-preferred cones are photo images of actual 3D-printed specimens shown to the oracle. (b) Normalized utility of the model-inferred 3D cones from the three PBO campaigns and single random campaign.

The model-inferred functions in the bottom graph (Fig. 8b) again show the efficiency of PBO search and the consistency of PBO in finding an optimum. Within 15 experiments, PBO identified the neighborhood of the optimal parameter configuration in the red and green campaigns. Learning was much slower in the blue campaign, which comes close to but does not reach the same optimum.

Readers might wonder how efficiently the optimum would be found if the PBO algorithm were turned off and parameter combinations were instead sampled randomly in each experiment. We included such a baseline condition in the simulation study (see ESI†), where we could perform many runs to obtain an accurate estimate of the performance benefit. Random was consistently inferior and by a sizable amount. For completeness and as a sanity check in a real print environment, we ran a single random campaign in the slender and cone studies (black lines in Fig. 6 and 8). Performance is below that of the PBO campaigns, but much more so in the cones graph than in the slender-vase graph. Keep in mind that with only a single random campaign, it is impossible to measure accurately the magnitude of the PBO benefit (a single campaign can be exceedingly lucky or unlucky). For this reason, the simulation data, where there were 100 campaigns per algorithm, are most trustworthy in estimating the benefit of PBO.

3.2 Modeling the oracle

The GP model underlying search in PBO finds the most-preferred object. Because the search included significant exploration, the data generated en route to this objective contain a great deal of information about the oracle's likes and dislikes (over 230 images and rankings in each campaign), information which could be used to build a model of the oracle's preferences. If it learned some of the dimensions that determine preference, the model could function as a sort of surrogate oracle, the quality of which could be evaluated by testing its preference behavior (i.e., predictive ability).

We divided this problem into two steps, creating a machine learning model that would extract a feature space of the trained objects, and then building a predictive model using this space to assess how well it mimics the oracle's choices. In the first step, we used a Beta Variational Autoencoder (Beta-VAE).^63,64 Beta-VAE, as a generative variant of the autoencoder,⁶⁵ is an unsupervised deep neural network that is well suited for learning images. An adjustable regularization term ‘Beta (β)’ trades off encoding efficiency (degree of dimensionality reduction or data compression) with reconstruction quality (fidelity of the generated image). The second step involved training a multilayer perceptron (MLP)⁶⁶ to model the oracle's preference judgments using the Beta-VAE's solution space. Would the VAE model learn a feature space from the images that is predictive of the oracle's choice performance? If so, the dimensions of that space should be identifiable.

The Beta-VAE⁶⁴ was trained on printed images (≈1500) of 2D slender and bulbous vases from the six PBO campaigns. The input images to this five-layer neural network were resized to 64 × 64 pixels. Our goal was to extract a low-dimensional feature space that was interpretable and whose predictive performance could be assessed. Through some trial and error, we settled on a 8-dimensional latent space solution of the Beta-VAE with β = 8.

The MLP was then created to model preference judgments by the oracle and was trained on pairwise choices (≈1000) from four campaigns, two slender vase campaigns and two bulbous campaigns. Among the six independently run campaigns, we randomly chose and assigned four campaigns for training the model and set aside the other two campaigns for testing it. The MLP model comprised two distinct two-layer neural networks, one for slender vase data and another for bulbous vase data. The output from the Beta-VAE was fed to each MLP depending upon the shape of the vase being modeled. Generalization performance of the MLP was evaluated by its out-of-sample predictions on preference judgments (≈500 pairwise choices) from two set-aside campaigns, one slender vase and another bulbous vase.

The preceding steps were repeated using the data from the 3D cones campaigns. Specifically, the Beta-VAE was trained on ≈300 images from the three PBO campaigns. Images were resized to 128 × 128 pixels, resulting in loss of some detail regarding smoothness. We again set β = 8. Predictive modeling followed the steps above, using the preference judgements from two PBO campaigns for training and one for testing.

Predictive accuracy of the MLPs was good for both data sets. The model successfully predicted 82.5% and 87.9% of the oracle's choices in the slender vase and bulbous vase campaigns, respectively, and 82% in the cone campaign, all well above chance (50%). These may be slight underestimates of classification performance because as mentioned above, in some experiments all of the objects presented were far from the oracle's ideal (e.g., looking nothing like two cones), but the oracle still had to rank them. These data demonstrate that the VAE learned some of the features of the objects responsible for the oracle's preference judgments. We next analyzed the latent feature space of the vase and cone VAE's to identify dimensions that explain this performance.

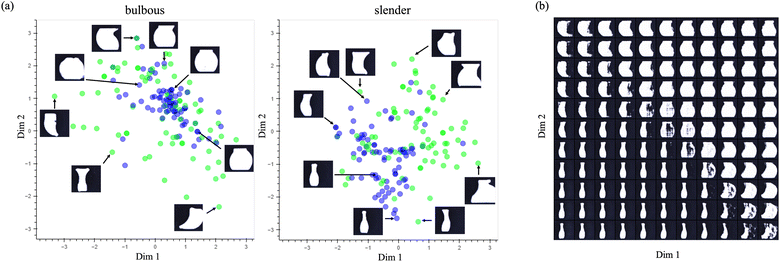
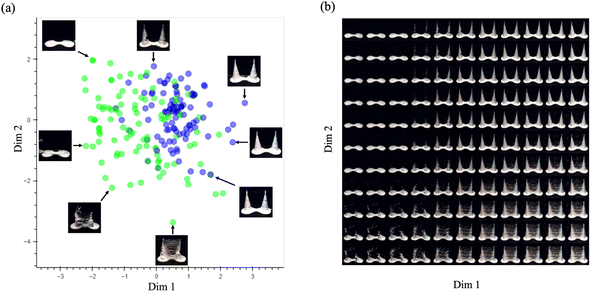
Shown in Fig. 9a are randomly selected preference choices from the oracle projected onto two select dimensions of the 8-dimensional latent feature space of the vase VAE, chosen because of their informativeness about feature encoding. Vases preferred by the oracle are denoted in purple circles; green circles denote dis-preferred vases (79 of each). The left graph displays choices from the bulbous campaign and the right graph choices from the slender campaign. In both graphs, preferences tend to cluster in a region in the feature space while dis-preferred choices are more dispersed. The image insets, which show synthetic vases generated by the VAE at a handful of points, confirm that vases at purple points correspond more closely to the ideal bulbous (or slender) vases than vases at green points, which vary widely in shape. These observations suggest that the VAE's feature space aligns with that of the oracle's (i.e., the VAE learned the categories). If it did not, purple points would likely be more scattered, exhibiting no clustering, and show no association between preference and the vase shape synthesized at those locations in feature space.

Fig. 9 Feature analysis of the vase VAE. (a) The location of preferred (purple) and dis-preferred (green) vases in a two-dimensional projection of the 8-dimensional feature space. Vases corresponding to bulbous preference judgements are plotted on the left, slender on the right. Image insets are VAE-generated synthetic vases at the indicated locations. (b) The same 2D projection as in (a), but filled with VAE-generated synthetic vases to clarify the features visible in this condensed view of the feature space.

A more detailed depiction of the range of vases generated by the VAE within this two-dimensional projection identifies some of the features the VAE encoded (Fig. 9b). Vases change in multiple ways along each dimension. Features learned include the presence of a lip at the opening, symmetry, roundedness, and length of the neck. As is suggested by the relative location of the preferred responses in panel a, preferred slender vases are not too distant from preferred bulbous vases in this 2D projection.

Results from analysis of the cone VAE are shown in Fig. 10. Inspection of the two-dimensional projection and the image insets shows a concentration of preferred choices in the middle-right part of the graph where the insets that show well-formed cone pairs are located. Dis-preferred choices (green) differ markedly from the ideal pairs. The figure of VAE-generated images on the right clarifies the features visible in cones generated in this projection. Good-quality cone pairs are in the upper-right quadrant. Those in the other quadrants exhibit stringing and misshapen cones, or none at all.

Fig. 10 Feature analysis of the cone VAE. (a) The location of preferred (purple) and dis-preferred (green) vases in a two-dimensional projection of the 8-dimensional feature space. Image insets are VAE-generated synthetic cones at the indicated locations. (b) The same 2D projection as in (a), but filled with VAE-generated synthetic cones to clarify the features visible in this condensed view of the feature space.

In both VAE analyses, we had hoped that at least some of the eight dimensions would correspond to readily interpretable object dimensions that the oracle used to evaluate the vases (e.g., width, roundness, proportionality of top and bottom sections). As the 2D projections in Fig. 9 and 10 show, the model's solution space was not cleanly decomposable, but rather combines multiple features together along a few dimensions, at least when viewed in a 2D projection. These two figures are the most interpretable 2D projections, with others being somewhat redundant with these or much less interpretable. Formation of the model's feature space was not constrained to yield such clearly interpretable dimensions, but rather to be as veridical as possible in generating the variety of objects in the training set.

These modeling results suggest that preference data combined with the images of the judged objects can be used to create a model that mimics the oracle's choice behavior to a first approximation. Analysis of the model's feature space suggests that it internalized object features and preferences, and could respond in a similar manner were the oracle replaced by the model. The potential for oracle “surrogates” embedded in a closed-loop printing system is ripe for further exploration.

4 Discussion

Despite the rapid evolution of additive manufacturing technologies, there still remain challenges with optimizing process conditions in order to achieve high quality parts in as little time as possible. This is particularly true for FFF where a large number of sometimes conflicting parameters frequently require recalibration. Traditionally, calibration involves a long and iterative process where the user adjusts one or two parameters per iteration based on a brief visual inspection of a printed object until the desired part quality is achieved. This cumbersome approach acts as a significant barrier to the field of AM, particularly when considering that each change in design or print material could require the re-tuning of as many as 10 parameters to achieve the desired printed product.

The current study is part of a growing effort to integrate advanced sensing technologies to facilitate closed-loop feedback and automate parameter optimization into FFF systems,⁶⁷ including laser profilometry, acoustic emission sensors, and thermal cameras. However, some of these technologies can be cost-prohibitive, while others are restricted to monitoring specific characteristics of the printed parts (e.g., surface roughness, geometric accuracy). An economical and versatile approach to closed-loop feedback for FFF can be achieved by incorporating a basic camera into the system. The literature contains numerous examples where machine vision is used as feedback to optimize FFF parameters through machine learning. Ganitano et al. employed a simulated annealing algorithm to minimize the cost of matching between a single captured image of a FFF-printed object and the corresponding model-generated synthetic image.³⁸ Jin et al. combined deep learning and machine vision to adjust the printer's flow rate to correct for under- or over-extrusion.⁶⁸ Saluja et al. developed an autonomous monitoring system that uses a CNN to detect warping defects in FFF-printed specimens by capturing and analyzing images after each layer of the print is completed.⁶⁹

While these approaches are crucial to advancing AM, they primarily rely on machine-interpreted quantitative metrics. Our work expands on them by leveraging human preference for rapid and comprehensive assessment of the overall quality of a printed part. We focused on improving the efficiency of printing objects that are not easy to automate with sensors alone. A Bayesian optimization algorithm was guided by human feedback to find the combination of parameter values to achieve the oracle's printing goal. In 2D and 3D printing problems, preferential Bayesian optimization performed well, often learning the oracle's preference quickly through its efficient search of the parameter space. Follow-up work demonstrated that the oracle's preferences could be predicted with reasonably accuracy using a model trained on the images and rankings.

The results of this investigation validate PBO in two real-world settings, involving six print parameters, and in the case of the 3D cones, constraints that increased the difficulty of finding an optimal solution. Our choice of algorithm was based on extensive preliminary work in which we evaluated the efficiency of many PBO algorithms and alternative methods for collecting human preference judgments. Use of the qNEI-UB-woBest algorithm combined with the oracle providing three rankings in each experiment yielded efficient performance, reaching an optimum or its neighborhood in as few as 15 experiments (45 printings). Such results were shown to replicate across campaigns, providing a measure of the reliability of PBO, and importantly, the reliability of the oracle in making preference judgments over extended periods of time (one campaign could extend over 40 hours). Both of these are a potentially concerning form of selection bias, which replication addresses. Although preference for an idealized object may well vary over time depending on the objective and from exposure in a campaign, the consistency in the optimum across campaigns is encouraging.

That a few campaigns (blue in Fig. 6b and 8b) failed to reach the target optimum found in the companion campaigns points to further work in understanding and developing PBO algorithms. As suggested earlier, the degree of exploration early in a campaign, which occurred in these two cases, may have constrained what the GP model could learn over the remainder of the campaign, which is why it could only approximate the optimum, not reach it. Finer tuning of the current algorithm might prevent such behavior or the algorithm itself might be in need of further improvements. Nevertheless, the overall success of PBO in this investigation demonstrates its promise as a new printing tool.

Integration of PBO into a printing workflow yields a semi-autonomous system that requires brief interventions by the oracle to rapidly print the desired object. For some applications, the optimum might not be of interest or obtainable. It might be sufficient for PBO to identify only a region of parameter values, after which the user would fine-tune them by hand. For example, a user printing cones might discover that only a degree of surface smoothness is preferable, and that adjusting parameters by hand allows the user to explore a range of possible textures before deciding on one. PBO's focus is preference optimization, not exploring and comparing alternatives.

Although PBO can efficiently learn an oracle's preference, there are limits to PBO and what can be learned. If a great deal of learning is required to achieve the objective, such as simultaneously optimizing many subjective qualities (smoothness, symmetry, right angles, etc.), learning will be slow and could take an unreasonably large number of experiments. Further, to print such objects, it might be necessary to manipulate many parameters. Bayesian optimization struggles beyond 20 dimensions⁵³, even fewer depending on the complexity of the parameter space. This curse of dimensionality⁷⁰ makes it exceedingly difficult to find a global optimum. In these situations, PBO might be most suitable for pointing the user in a promising direction.

When preferences are particularly challenging to optimize, as in the situations discussed in the preceding paragraph, it might be preferable to explore optimization in a virtual environment. In situ autonomous PBO campaigns are resource hungry, requiring extensive equipment (printer, cameras, filament), preparation, and power. Further, a degree of vigilance is required of the oracle, who must wait for the experiment to finish (at least a few minutes) before ranking images of the objects. A 100-experiment campaign can take over eight hours. A simulation environment, in which the objects are rendered in software, has the potential to achieve similar ends faster and with many fewer resources. Indeed, we took this approach when evaluating the PBO algorithms discussed in the Supplement specifically to expedite the project. The algorithm had to learn to position the parts of a face (eyes, eye brows, nose, mouth) on a blank male or female face such that it yielded the most natural face according to the oracle. As in the current study, the oracle ranked three faces in each experiment. A campaign of 40 experiments, usually sufficient to find an optimum, took no more than a few minutes. A virtual printing environment can be a wise starting point, the results from which could then be ported to a 3D printer.

When PBO succeeds in finding an optimum, the oracle's preference has the potential to be modeled given enough campaign data, providing another means of aiding printing. Such a model, even if it does not mimic the oracle perfectly, could replace the oracle in the research loop (Fig. 1), thereby fully automating the print process. In doing so, it adds an important degree of reproducibility across printing setups, making it possible to print the same object regardless of changes in filament, equipment, environment, or software. The printed object should be the same because the model is independent of such changes. As long as the parameter space includes the configuration that will print the preferred object, the model should find it, or at least find its neighborhood. The good performance of the Beta-VAEs suggest that this is a promising avenue for future work.

We end this section by considering some of the limitations of our approach. PBO is being used as a general-purpose method to facilitate printing complex qualities with the help of an oracle. If the oracle has eclectic preferences (likes lopsided vases), the algorithm might not identify a parameter combination that yields something close to the desired object. For example, in the vase campaigns, if we assumed symmetry along the vertical axis, making the left and right sides reflections, the parameter set that generates a lopsided vase would not exist in the search space. Researchers should do what they can to ensure print parameters and their ranges will contain an optimal solution, although admittedly this itself could challenging. Similarly, if the oracle does not have a clear optimum in mind or extensive learning (exploration) is required to determine what is optimal, there will be inconsistencies across campaigns. Finally, if the desired print quality can be described or produced through other means, such as sketching it in software or even via prompt engineering, the oracle is no longer needed during the search campaign because their input has been provided beforehand. The problem simplifies to one of closed-loop BO in which the print target is known and the goal is to find the optimal parameters that print the target via some print-quality measure (e.g., similarity score). We have recently demonstrated the efficiencies of BO in such a setup.^32,55

5 Conclusion

This paper introduces a human-assisted active learning approach to improve the efficiency of autonomous printing. Using readily accessible equipment, we demonstrate the printing efficiencies from using an optimization algorithm that is guided by human preference rankings. PBO rapidly learned the oracle's preferences, with the printer producing the sought-after vase or cone pair in anywhere from 12 to 40 experiments. We also developed a predictive model that mimics the oracle's preferences by learning them from the image and ranking data, thereby making it possible to implement these preferences, and their accompanying efficiencies, in a printer.

Data availability

Data and modeling code from this study are archived at https://osf.io/fqp96/.

Author contributions

M. Pitt and J. Myung: project administration, conceptualization, supervision, writing – original draft. J. Deneault: experimental set-up and design, data curation, writing. Woojae Kim: algorithm development and implementation, data analysis, writing – supplement. Jiseob Kim: algorithm development and VAE modeling. Yuzhe Gu: Data analysis. Jorge Chang: Algorithm development and implementation. B. Maruyama: printer and review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was supported by grant FA9550-21-1-0176 from the Air Force Office of Scientific Research (AFOSR) to MAP and JIM. The authors thank Dr Inhan Kang for technical assistance in an early stage of the research.

Notes and references

1. H. Kitano, AI Magazine, Spring, 2016, pp. 39–49.
2. H. Wang, T. Fu, Y. Du, W. Gao, Y. Bengio and M. Zitnik, et al., Nature, 2023, 620, 47–60.
3. G. Tom, S. P. Schmid, S. G. Baird, Y. Cao, K. Darvish, F. Strieth-Kalthof, M. Seifrid and A. Aspuru-Guzik, et al., Chem. Rev., 2024, 124, 9633–9732.
4. R. D. King, K. Whathen, F. Jones, P. Reiser, C. Bryant, S. M. S, D. Kell and S. Oliver, Nature, 2004, 427, 247–252.
5. R. D. King, J. Rowland, S. G. Oliver, M. Young, W. Aubrey, E. Byrne, M. Liakata, M. Markham, P. Pir, L. N. Soldatova, A. Sparkes, K. E. Whelan and A. Clare, Science, 2009, 324, 85–89.
6. C. W. Coley, D. A. T. III, J. A. M. Lummiss, T. F. Jamison and K. F. Jensen, et al., Science, 2019, 365, 1–9.
7. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, R. S. Sprick and A. I. Cooper, et al., Nature, 2023, 583, 237–241.
8. K. Terayama, M. Sumita, R. Tamura and K. Tsuda, Accounts Chem. Res., 2021, 54, 1334–1346.
9. L. Kavalsky, V. I. Hegde, B. Meredig and V. Viswanathan, Digital Discovery, 2024, 1–12.
10. P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker, M. Krein, J. Poleski, R. Barto and B. Maruyama, npj Comput. Mater., 2016, 2, 16031.
11. D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberia, J. H. Montoya, S. Dwaraknath, M. Aykol and A. Aspuru-Guzik, Nat. Rev. Mater., 2018, 3, 5–20.
12. E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier and B. Maruyama, Matter, 2021, 4, 2702–2726.
13. B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott and C. P. Berlinguette, Nat. Commun., 2022, 13(995), 1–10.
14. N. J. Szymanski, B. Rendy, Y. Fei, R. E. Kumar, Y. Zeng and G. Ceder, et al., Nature, 2023, 624, 86–91.
15. Y. Kim and S. H. Park, Adv. Intell. Syst., 2023, 5, 2200462.
16. A. Atkinson and A. Donev, Optimum Experimental Designs, Oxford University Press, 1992.
17. D. Cohn, Z. Ghahramani and M. Jordan, J. Artif. Intell. Res., 1996, 4, 129–145.
18. B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and A. de Freitas, Proc. IEEE, 2016, 104, 148–175.
19. S. Greenhill, S. Rana, S. Gupta, P. Vellanki and S. Venkatesh, IEEE Access, 2020, 8, 13937–13948.
20. R. Garnett, Bayesian Optimization, Cambridge University Press, 2023.
21. R. Lorenz, R. Pio-Monti, I. R. Violante, C. Anagnostopoulos, A. A. Faisal, G. Montana and R. Leech, Neuroimage, 2016, 129, 320–334.
22. R. Lorenz, M. Johal and F. Geranmaueh, et al., Brain, 2021, 144, 2120–2134.
23. F. Hase, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 1134–1145.
24. J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, ACS Cent. Sci., 2020, 6, 513–524.
25. J. A. Garrido-Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 19999–20007.
26. N. H. Angello, V. Rathore, W. Beker, A. Wotos, B. A. Grzybowski and M. D. Burke, et al., Science, 2022, 378, 399–405.
27. Y. Fukui, K. Minami, K. Shiba, G. Yoshikawa, K. Tsuda and R. Tamura, Digital Discovery, 2024, 1–8.
28. C. Li, D. R. de Celis Leal and S. Venkatech, et al., Sci. Rep., 2017, 7, 1–10.
29. A. M. Gopakumar, P. V. Balachandran, D. Xue, J. E. Gubernatis and T. Lookman, Sci. Rep., 2018, 8, 1–12.
30. Y. Zhang, D. W. Apley and W. Chen, Sci. Rep., 2020, 10(4924), 1–12.
31. A. K. Y. Low, F. Mekki-Berrada, A. Gupta, A. Ostudin, J. Xie, E. Vissol-Gaudin, Y.-F. Lim, Q. Li, Y. S. Ong, S. A. Khan and K. Hippalgaonkar, npj Comput. Mater., 2024, 10(104), 11–14.
32. R. Deneault, J. Chang-Cheng, J. I. Myung, D. Hooper, A. Armstrong, M. A. Pitt and B. Maruyama, MRS Bull., 2021, 46, 566–575.
33. J. Kim, J. Yun, S. I. Kim and W. Ryu, Virtual Phys. Prototyp., 2022, 18, 1–15.
34. E. S. Chen, A. Ahmadianshalchi, S. S. Sparks, C. Chen, A. Deshwal, J. R. Doppa and K. Qiu, Adv. Mater. Technol., 2024, 2400037.
35. M. Hassan, M. Misra, G. W. Taylor and A. K. Mohanty, Compos., Part C: Open Access, 2024, 15, 100513.
36. J. Chang, J. Kim, B.-T. Zhang, M. A. Pitt and J. I. Myung, Proceedings of the 41st Annual Conference of the Cognitive, Science Society, Montreal, QB, 2019, pp. 1479–1485.
37. J. Chang, P. Nikolaev, J. Carpena-Nunez, R. Rao, K. Decker, A. E. Islam, J. Kim, M. A. Pitt, J. I. Myung and B. Maruyama, Sci. Rep., 2020, 10, 1–9.
38. G. S. Ganitano, S. G. Wallace, B. Maruyama and G. L. Peterson, Prog. Addit. Manuf., 2023, 9, 767–777.
39. W. Chu and Z. Ghahramani, Proceedings of the Twenty-second International Conference on Machine Learning (ICML), Bonn, Germany, 2005, pp. 137–144.
40. J. Gonzalez, Z. Dai, A. Damianou and N. D. Lawrence, Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 2017, pp. 1282–1291.
41. E. Siivola, A. K. Dhaka, M. R. Andersen, J. Gonzalez, P. G. Moreno and A. Vehtari, IEEE International Workshop On Machine Learning For Signal Processing, Gold Cost, Australia, 2021, pp. 1–6.
42. R. Monarch, Human-in-the-Loop Machine Learning: Active Learning and Annotation for Human-Centered AI, Manning, 2022.
43. E. Mosqueira-Rey, E. Hernández-Pereira, D. Alonso-Ríos, J. Bobes-Bascarán and Á. Fernández-Leal, Artif. Intell. Rev., 2022, 56, 3005–3054.
44. P. Slade, C. Atkeson, J. M. Donelan, H. Houdijk, K. A. Ingraham, M. Kim, K. Kong, K. L. Poggensee, R. Riener, M. Steinert, J. Zhang and S. H. Collins, Nature, 2024, 633, 779–788.
45. M. Abdolshah, A. Shilton, S. Rana, S. Gupta and S. Venkatesh, Multi-objective Bayesian optimisation with preferences over objectives, Advances in Neural Information Processing Systems, 2019, vol. 32.
46. P. Mikkola, M. Todorovic, J. Jarvi, P. Rinke and S. Kaski, Proceedings of the Thirty-seventh International Conference on Machine Learning (ICML), 2020, pp. 4050–4058.
47. B. Settles, Synthesis Lectures on Artificial Intelligence and Machine Learning, 2012, vol. 6, pp. 1–114.
48. J. Mockus, J. Global Optim., 1994, 4, 347–365.
49. E. Brochu, V. M. Cora and N. De Freitas, arXiv, 2010, preprint, arXiv:1012.2599, 1–49,  DOI:10.48550/arXiv.1012.2599.
50. P. I. Frazier and J. Wang, Information Science for Materials Discovery and Design, Springer International Publishing Switzerland, 2016, ch. 3, pp. 35–75.
51. C. Hvarfner, E. O. Hellsten and L. Nardi, arXiv, 2024, preprint, arXiv:2402.02229v3, 1–22,  DOI:10.48550/arXiv.2402.02229.
52. C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, Cambridge, MA, 2006.
53. P. I. Frazier, arXiv, 2018, preprint, arXiv:1807.02811v1, 1–21,  DOI:10.48550/arXiv.1807.02811.
54. Z. J. Lin, R. Astudillo, P. I. Frazier and E. Bakshy, Proceedings of The 25th International Conference on Artificial Intelligence and Statistics, 2022, pp. 4235–4258.
55. J. I. Myung, J. R. Deneault, J. Chang, I. Kang, B. Maruyama and M. A. Pitt, Digital Discovery, 2025 10.1039/d4dd00281d.
56. D. Hooper, ARES OS, 2021, https://github.com/AFRL-ARES/ARES_OS.
57. Python, 2023, https://www.python.org/.
58. B. V. Ultimaker, Ultimaker, 2023, https://ultimaker.com/.
59. Print Quality Troubleshooting Guide, 2023, https://www.simplify3d.com/resources/print-quality-troubleshooting/.
60. J. O'Connell, 3D Print Zits & Blobs: 6 Tips to Prevent Them, 2023, https://all3dp.com/2/3d-print-zits-tips-tricks-to-avoid-blobs/.
61. B. Obudho, 3D Printer Stringing: 5 Simple Solutions, 2024, https://all3dp.com/2/3d-print-stringing-easy-ways-to-prevent-it/.
62. T. Hullette, 3D Printer Under-Extrusion: 8 Simple Solutions, 2023, https://all3dp.com/2/under-extrusion-3d-printing-all-you-need-to-know/.
63. I. Higgins, L. Matthey, A. Pal, C. Burgess, X. Glorot, M. Botvinick, S. Mohamed and A. Lerchner, International Conference on Learning Representations, 2017.
64. D. P. Kingma and M. Welling, arXiv, 2013, preprint, arXiv:1312.6114,  DOI:10.48550/arXiv.1312.6114.
65. G. E. Hinton and R. R. Salakhutdinov, Science, 2006, 313, 504–507.
66. D. E. Rumelhart, G. E. Hinton and R. J. Williams, Nature, 1986, 323, 533–536.
67. Y. Fu, A. Downey, L. Yuan, A. Pratt and Y. Balogun, Addit. Manuf., 2021, 38, 101749.
68. Z. Jin, Z. Zhang and G. X. Gu, Manuf. Lett., 2019, 22, 11–15.
69. A. Saluja, J. Xie and K. Fayazbakhsh, J. Manuf. Process., 2020, 58, 407–415.
70. W. B. Powell, Approximate Dynamic Programming: Solving the Curses of Dimensionality, John Wiley & Sons, Hoboken, New Jergey, 2007.

---

Footnotes

† Data and code from this study are archived at https://osf.io/fqp96/.

‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00320a

§ Fused Filament Fabrication is a generalised synonym of the more popular but trademarked term Fused Deposition Modeling (FDM).

¶ The equivalence relationship between a rank order and a set of pairwise preference relations requires the assumption of transitivity. As a counterexample, consider the following set of pairwise preferences among three options: a > b, b > c, and c > a. This set clearly violates the transitivity assumption, and therefore, there is no equivalent rank order that is consistent with such preference relations.

---