Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Digital workflow optimization of van der Waals methods for improved halide perovskite solar materials†
Celso R. C.
Rêgo
 *a,
Wolfgang
Wenzel
*a,
Wolfgang
Wenzel
 a,
Maurício J.
Piotrowski
a,
Maurício J.
Piotrowski
 b,
Alexandre C.
Dias
b,
Alexandre C.
Dias
 c,
Carlos
Maciel de Oliveira Bastos
c,
Carlos
Maciel de Oliveira Bastos
 c,
Luis O.
de Araujo
d and
Diego
Guedes-Sobrinho
c,
Luis O.
de Araujo
d and
Diego
Guedes-Sobrinho
 d
d
aKarlsruhe Institute of Technology (KIT), Institute of Nanotechnology (INT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: celso.rego@kit.edu
bDepartment of Physics, Federal University of Pelotas, PO Box 354, Pelotas, RS 96010-900, Brazil
cInstitute of Physics and International Center of Physics, University of Brasília, Brasília 70919-970 Distrito Federal, Brazil
dChemistry Department, Federal University of Paraná, Curitiba, PR 81531-980, Brazil
First published on 18th February 2025
Abstract
Hybrid organic–inorganic metal halide perovskites are low-cost and highly efficient materials used in solar cell devices. However, the intricacies of perovskites that merge organic cations with inorganic frameworks necessitate further elucidation, particularly from the long-range van der Waals perspective. Here, we scrutinize the van der Waals (vdW) methods by conceptualizing organic cations for XH4PbI3 and CH3XH3PbI3 prototype perovskites (X = N, P, As, and Sb), to investigate the thermodynamic stability. To handle the enormous amount of raw data generated from DFT + vdW + SOC with DFT-1/2 (quasi-particle correction method), we have used the SimStack workflow framework, which enhanced the efficiency, reproducibility, and data transferability. The results reveal the critical role of the organic cations, inferred from ionic radius estimates and documented electronegativity, in elucidating the accommodation of symmetric XH4+ or asymmetric CH3XH3+ cations within the limited volumes of cuboctahedral cavities. The discrepancy in the ionic size within the XH4PbI3 (CH3XH3PbI3) group positions NH4PbI3 (CH3NH3PbI3) outside (within) the stable perovskite region suggests the theoretical viability of perovskites containing phosphonium, arsonium, and stibonium beyond CH3NH3PbI3. As we move from N to Sb, the organic cation's properties, such as ionic radius and electronegativity, affect the thermodynamic stability and local geometry of octahedra, directly influencing the band gaps.
1 Introduction
Metal halide perovskites (MHPs) have received unparalleled attention today, especially by the emergence of hybrid (organic–inorganic) MHPs,1,2 since they constitute the most promising candidates for application in the third generation of photovoltaic solar cells, where their power conversion efficiency evolved from 3.8%1 up to amounts exceeding 21% in less than a decade-and-a-half of study,3–5 for instance, in the case of FAPbI3, it surpassed 26% when applied in single-junction devices.6 Concomitantly, the interest in hybrid MHPs for use as a solar cell absorber has been boosted rapidly because of their unique physical and chemical properties, the wide possibility of compositional modification, and production feasibility through simple benchtop chemistry.7–9 However, the complexity arising from the addition of organic cations within an inorganic template leads to a high degree of difficulty faced by theoreticians and experimentalists, even more so in the attempt to correlate the acquired understanding at electronic and atomistic levels with empirical verified physico-chemical properties,10,11 such as in contexts of tunable band gaps12 and long carrier lifetimes.13,14Among the possible organic–inorganic MHPs, methylammonium lead triiodide (CH3NH3PbI3) has been the flagship of research, with a lower proportion of acclaim directed to other molecular cations (e.g., formamidinium or acetamidinium).7–9 In general, the attention is focused on the compositional engineering of the divalent-metal cation (Pb2+) substitution by alternative species (e.g., Ge2+ and Sn2+),15,16 or by the exchange of the halide anion (e.g., I− by Cl− or Br−),1,17 or even by compositional alloys.18–20 However, few studies have focused on the automatic design of the MHP composition in the sense of improving solar cell efficiencies and tuning absorption energy.21,22 Given the flexibility of the organic cation choice, it is possible to consider a variety of organic molecules with different sizes, symmetries, and chemical features, which can directly influence the octahedral framework from distortions and reorientations until charge balance, energy stabilization, and dimensionality changes in MHPs, leading to profound effects on the electronic structure.8,9 Consequently, in principle, one could model the strength of organic–inorganic interactions by designing organic cations. This fact would imply the possibility of moving between structures with a minimal octahedral tilt, implying low-gap perovskites (optimum photovoltaic efficiency), or structures with a maximum tilt, implying large-gap perovskites (application in visible spectrum light-emitting diodes).21
In addition to the direct motivation of molecular cation design/substitution to tune optoelectronic properties,21–24 there is a genuine motivation that resides in altering the cations, varying their constitutional chemical nature to increase the stability of the system as a whole without compromising the desirable range of band gaps for solar cell applications.25 Even excluding any significant contribution of organic cations to the electronic structure (specifically around the band edges) and confirming their role in structural electrostatic stabilization,26,27 we should consider the indirect role that organic cations (and their tuning) can play in electronic properties by inducing structural changes in inorganic octahedra through electronic coupling, hydrogen-bonding, and van der Waals (vdW) interactions.25,28,29 For instance, it is shown that in the theoretical treatment of hybrid MHPs, based on density functional theory (DFT), the vdW correction inclusion changes the CH3NH3+ spatial orientation, distorting the PbI6 octahedra, leading to a direct–indirect band gap transition.28 Thus, similar to the experimental situation in which hybrid MHPs are sensitive to processing conditions, computational modeling approaches to treat hybrid MHPs are also sensitive to the theoretical level. Hence, for hybrid MHPs, only a thorough study considering vdW corrections can achieve good agreement with experimental data, as reported by the first study combining dispersive interactions and spin–orbit coupling (SOC) treatments.30
Despite the well-established DFT success as an investigative/predictive tool,31–34 being considered a workhorse in computational materials science, its proper application through standard (plain) DFT calculations based only on local, semilocal, and hybrid exchange–correlation functionals needs care,31 since it misdescribes (or does not describe) long-range electronic correlation effects, for example, which means not counting the London dispersion interactions.35–38 In the last few decades, there have been enormous efforts to improve the description of the vdW interactions through nonlocal vdW-DF functionals39–41 and a posteriori approaches within the DFT framework, which have resulted in a variety of a posteriori methods, which we will focus from now on.35,36,42–45 These corrections are based on the atom-pairwise potential interactions, where the vdW dispersion energy correction, Edisp, is added to the DFT total energy: Etot = EDFT + Edisp,46–48 and they can be divided in (i) empirical approaches, having as main representatives D2, D3, and D3BJ frameworks proposed by Grimme,42,43,49 where D2 (ref. 42) does not take into account environmental effects, which were subsequently introduced in the D3 (ref. 43) and D3BJ49 frameworks through the addition of the coordination number dependence from the dispersion energy contributions in nth-order terms. The use of higher nth-order terms has presented an overestimation of lattice parameters for weakly bound bulk systems, so D3 has been recommended.43,50 At the same time, for D3BJ, replacing the damping function with the Becke–Johnson (BJ) model provided better results for molecular systems involving non-bonded distances.49
On the other hand, we have (ii) the semi-empirical approaches, with (ii.1) TS, TSSCS, and MBD proposals by Tkatchenko and Scheffler,35,36,51 where the vdW correction is determined from the ground-state electron density of the system, which allows capturing hybridization effects, as well as the environmental effects, by accounting for polarizability through the Hirshfeld volume.35,36,52 TS does not include interactions beyond the local environment, disregarding the fluctuating dipole interaction effects. In contrast, TSSCS includes the self-consistent screening (SCS) effects, where the dipole long-range fluctuations are considered to have polarizability.36 The many-body dispersion (MBD)51 method is based on the random phase expression of the correlation energy and the dynamic response is approximated by that of dipole-coupled quantum harmonic oscillators, representing a more general approach that goes beyond the pairwise-additive treatment of dispersion. To complement (ii.2) the dDsC proposed by Steinmann and Corminboeuf44,45 with similarities to the D2 method, except by the dispersion coefficients and damping function, which are charge-density-dependent. Therefore, to obtain the adequate refinement level, in addition to theoretical treatments that advance the DFT, one must consider the role played by vdW corrections.
Thus, herein, considering the standard DFT calculations and the main empirical (D2, D3, and D3BJ) and semi-empirical (TS, TSSCS, MBD, and dDsC) vdW corrections, within extrarelativistic corrections (SOC and quasiparticle DFT-1/2 (ref. 53)), we have accomplished a systematic investigation to assess the properties of the two archetypal hybrid MHPs. The chosen structural sets are based on a polar methylammonium cation (CH3NH3+)54 and its smaller nonpolar analog ammonium cation (NH4+),23,26,55 combined with the lead iodide (PbI3−) inorganic part. For this, there is an experimental relationship between transformation56 and reverse transformation57 of NH4PbI3 to CH3NH3PbI3 perovskites. For this purpose, we considered the family generated from ammonium – NH4+ (methylammonium – CH3NH3+) by descending the pnictogen column in the periodic table, i.e., including the hypothetical compounds formed by phosphonium – PH4+ (methylphosphonium – CH3PH3+), arsonium – AsH4+ (methylarsonium – CH3AsH3+), and stibonium – SbH4+ (methylstibonium – CH3SbH3+), constituting the XH4PbI3 and CH3XH3PbI3 (X = N, P, As, and Sb) set of MHPs. Consequently, we intend to obtain a complete overview of the effects of different vdW flavors in characterizing archetypal MHP structures, considering the complete picture that permeates among thermodynamic stability, structural feasibility, and maintenance of the band gap within a viable range for application in solar cells.
In our detailed investigation of metal halide perovskites (MHPs), we focused on the complex interactions between organic and inorganic components within hybrid systems. We examined the dynamic interplay involving non-symmetrical, polar, and symmetrical, and non-polar organic molecular families central to the perovskite structure. This study revealed opportunities for manipulating orientational disorder and polarization through the custom design of organic cations by altering their chemical properties, directly impacting the structural motifs of the inorganic components and indirectly influencing the electronic structure. However, selecting the most compelling theoretical approach to address dispersive interactions within this organic–inorganic nexus remains a significant challenge due to the structural complexity of hybrid perovskites.
We integrated all simulation protocols into the SimStack modules called Workflow Active Nodes (WaNos) to manage this complexity.58 Implementing scientific workflows contributes to making their data FAIR (Findable, Accessible, Interoperable, and Reusable) by automating and standardizing the execution of complex computational protocols. Workflow frameworks, such as SimStack,58 AiiDA,59 Pyiron,60 and others, ensure that the entire simulation process is well-documented, reproducible,61–63 and enriched with metadata. These workflows capture data provenance, detailing the parameters, software, and computational environments used at every step, which is critical for ensuring traceability and reproducibility. Furthermore, by integrating high-throughput and multiscale modeling, workflows streamline the generation and management of large datasets, which can then be stored in repositories such as GitHub, Materials Cloud, or NOMAD. This approach promotes data reuse and reduces non-expert users' barriers to leveraging advanced computational methods, ensuring broader accessibility and improved scientific collaboration. The user-friendly interface and versatile capabilities of SimStack facilitated the execution of complex computational workflows, aligning our research with the FAIR (Findable, Accessible, Interoperable, and Reusable) and TRUE (Transparent, Reproducible, Usable by others, and Extensible) principles,61,64–69 thereby enhancing the scientific rigor of our study. Using SimStack, we systematically explored the effects of different van der Waals corrections on the properties of typical hybrid MHPs with unprecedented precision and efficiency, paving the way for further theoretical investigations into this intriguing class of materials.
2 Theoretical approach, computational details, and workflow
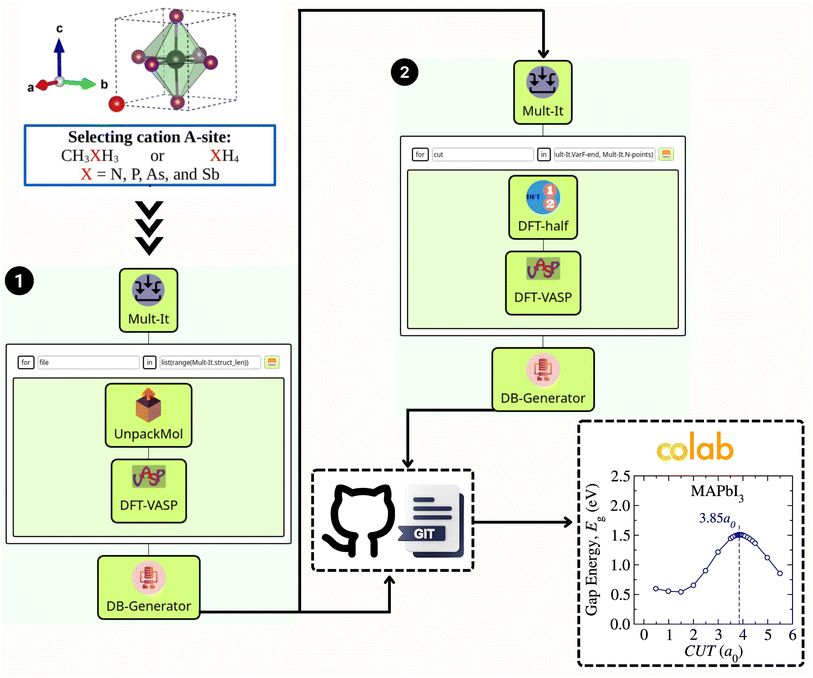
Fig. 1 illustrates the workflow built within the SimStack58 framework, designed to streamline the virtual screening process for van der Waals (vdW) methods within the exploration of various metal halide perovskite (MHP) cation compositions. This strategic approach facilitates a systematic investigation of stability, structural, and electronic characterization, thereby enabling the rapid prototyping of many vdW corrections. Such simulations are interconnected through multimodule workflows, significantly enhancing the efficiency of raw data production. The first segment, Fig. 1, part (1), engages in geometry optimization using a chosen vdW approach. It begins by selecting an A-site cation, which can be either CH3XH3 or XH4, where X symbolizes elements such as N, P, As, or Sb. The process continues through Mult-It WaNo, which iteratively processes the molecular geometry with UnpackMol. Following this, DFT-VASP performs the geometry optimization, with the DB-Generator compiling the outcomes into a structured dataset.The second segment, Fig. 1, part (2), of the workflow, illustrated on the right side of Fig. 1, utilizes the optimized structure from the first part. Herein, Mult-It embarks on iterative calculations to determine the band gap employing the DFT-1/2 method, complemented by a single-shot calculation via DFT-VASP. The results are then channeled into the DB-Generator. The automated flow of information is critical; the two .yml dataset files produced by the DB-Generator WaNo are pushed to a GitHub repository. From there, a Colab notebook can readily fetch the data for further analysis, such as estimating the bandgap energy and plotting the corresponding figure, as showcased for the MAPbI3 case.
The project's documentation is available to the public via the GitHub repository at https://github.com/KIT-Workflows/Halide-Perovskites. This repository provides all the Workflow Active Nodes (WaNos) used in this project. In addition, the SimStack framework – a free and open-source workflow engine – is documented with a detailed guide and tutorials are hosted at https://simstack.readthedocs.io. This documentation offers a straightforward step-by-step walkthrough, encapsulates best practices, and provides comprehensive operational details, ensuring that the framework's full potential can be harnessed for advanced materials science research and development.
2.1 Total energy calculations
We carried out DFT-based70,71 total energy calculations and structural optimizations within the semilocal exchange–correlation (xc) functional from the generalized gradient approximation72 formulated by Perdew, Burke, and Ernzerhof73 (PBE) as implemented in the Vienna Ab initio Simulation Package (VASP), version 5.4.1.74,75 As previously highlighted, the semilocal xc functionals cannot provide a correct description of the nonlocal long range vdW interactions; consequently, several vdW energy corrections based on pairwise interactions have been proposed considering the dispersion energy (Edisp) in the energetic context of the plain DFT, Etot = EDFT + Edisp.46–48 As a result, we have considered the most important (i) empirical approaches, i.e., D2 and D3 corrections proposed by Grimme42,43 and the D3 correction including the Becke–Johnson (BJ) damping function (D3BJ), which is developed to improve the non-bonded distances.49 In addition to the most relevant (ii) semi-empirical approaches, such as (ii.1) the Tkatchenko and Scheffler methods,35,36,51 including Tkatchenko–Scheffler correction (TS), Tkatchenko–Scheffler with self-consistent screening (TSSCS), and many-body dispersion (MBD), where the term Edisp is based on ground state electron density of the system, and (ii.2) the Steinmann and Corminboeuf approach (dDsC),44,45 which is very similar to the D2 method, except that the dispersion coefficients and damping function are charge-density-dependent. Thus, we have performed a benchmarking considering D2, D3, D3BJ, TS, TSSCS, MBD, and dDsC vdW corrections, as implemented by Bučko et al. in VASP.33,34,76,77To solve the Kohn–Sham (KS) equations, we employed the all-electron projector augmented wave method,78,79 as implemented in VASP,74,75,80 where the KS orbitals are expanded in plane waves up to a specific cutoff energy. By default, our plain DFT calculations are performed considering the scalar-relativistic approximation,81,82 in which a fully relativistic calculation, including spin–orbit coupling (SOC), is taken into account for the core states. However, since SOC can play an essential role for Pb-based perovskites,83–85 especially in non-spherical atomic orbitals affecting the directionality of metallic bonds,8 we have also included SOC for the valence states. We employed a plane-wave cutoff energy of 500 eV for the total energy calculations. At the same time, a stress tensor and atomic force optimization were performed to obtain the equilibrium bulk structures. A total energy convergence criterion of 1.0 × 10−5 eV was adopted in the KS self-consistent field cycle, while the equilibrium of Hellmann–Feynman forces was obtained once the atomic forces (on every atom) were smaller than 0.010 eV A−1. For the Brillouin zone integration, a Monkhorst–Pack k-mesh of 4 × 4 × 4 was employed, while a Gaussian smearing parameter of 50 meV was employed for all calculations. In addition to calculating the gap energies via plain DFT and DFT + SOC, we also used the relativistic quasiparticle correction (DFT-1/2)53 combined with SOC since it provides results with high precision, comparable to hybrid functionals such as HSE06 and the GW approach, requiring a low computational cost, which is similar to plain DFT. To verify the efficiency of this approach and obtain more details, please check our previous work.16,86,87
2.2 Atomic configurations
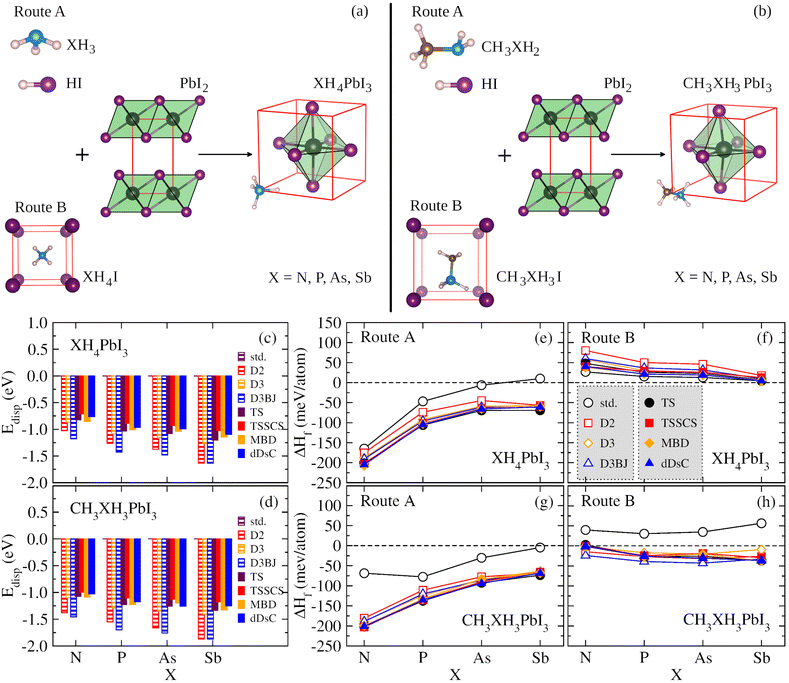
We have used a cubic structure based on the cubic unit cell (1 × 1 × 1) to model XH4PbI3 and CH3XH3PbI3 (X = N, P, As, Sb), where the atomic configurations are presented in Fig. 2(a) and (b) as a result of two possible route paths for each case, respectively. The mechanisms for XH4PbI3(s) formation (Fig. 2(a)) can be based on XH3(g) and HI(g) precursors in the gas phase (named Route A),| XH3(g) + HI(g) + PbI2(s) → XH4PbI3(s), | (1) |
| XH4I(s) + PbI2(s) → XH4PbI3(s). | (2) |
| CH3XH2(g) + HI(g) + PbI2(s) → CH3XH3PbI3(s), | (3) |
| CH3XH3I(s) + PbI2(s) → CH3XH3PbI3(s). | (4) |
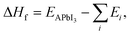 | (5) |
Thus, our XH4PbI3 and CH3XH3PbI3 archetypes are perovskite models with the inorganic lead iodide components forming a network of corner-sharing octahedra, where the diagonal and its perpendicular edges define, respectively, the apical and equatorial directions in the octahedron's frame, with the XH4+ and CH3XH3+ cations located in the center of the inorganic cuboctahedral cavity. Concerning the orientation of the organic molecules in the inorganic cuboctahedral cavity, the initial setup of the molecular cations are free to rotate during the full geometry optimizations, i.e., there are no constraints. For XH4PbI3, there is no significant orientation dependence of XH4+ due to its approximately spherical topology and nonpolar nature, as reported in the context of the ammonium ion.55 For CH3XH3PbI3, the orientational behavior of CH3XH3+ is a little more intricate owing to its polar nature (molecular dipole) and non-spherical topology. However, as reported in ref. 28, the potential energy surface (energy landscape) is shallow for different possible orientations of organic cations. There is the possibility, for example, of (001)-, (111)-, or (011)-oriented molecules constituting flat local minima (almost equivalent), with energy differences of tens of meV.23,28,55 As this energetic order represents values smaller than kBT, we have that at 300 K the XH4+ and CH3XH3+ are free to rotate, as evidenced experimentally for the methylammonium case.88 Notwithstanding this, the organic–inorganic interactions have a relevant role in the results that will be presented, making it clear that the dispersive forces are critical for the internal geometry optimization of the studied systems.
3 Results
3.1 vdW energy contributions
To verify the contributions of various types of vdW energy corrections based on pairwise interactions, we calculated the Edisp term, from the Etot = EDFT + Edisp context, taking into account the empirical (D2, D3, and D3BJ) and semi-empirical (TS, TSSCS, MBD, and dDsC) approaches, and the standard (std) DFT calculation (without vdW correction), for the XH4PbI3 and CH3XH3PbI3 MHPs, considering different pnictogens, i.e., X = N, P, As, and Sb, as shown in Fig. 2(c) and (d), respectively. We noticed that the vdW corrections contribute towards reducing the total energies to the calculation without vdW, i.e., one improves the energy stabilization of the studied systems, given the improvement in the description of organic cations, inorganic framework, as well as their interactions (organic–inorganic). The Edisp accounting for the total energy ranges from 0 eV (std) to about 1.63 eV for XH4PbI3 and 1.87 eV for CH3XH3Pb3 in the case of empirical corrections involving Grimme's family, which are larger (more pronounced) compared to semi-empirical corrections (maximum contributions of 1.20 eV for XH4PbI3 and 1.34 eV for CH3XH3Pb3).For both XH4PbI3 and CH3XH3PbI3 sets, we observed the same trend of vdW flavors as a function of the X element, with some main characteristics, and the Edisp average magnitude range increases through different elements of the nitrogen family, i.e., it increases from N to Sb, which is expected since the vdW corrections more pronouncedly assess the non-covalent inter- and intramolecular interactions. Furthermore, the magnitude of vdW corrections is larger for CH3XH3PbI3 than for XH4PbI3, which is explained by the molecular nature of the organic cation itself, i.e., CH3XH3+ has a larger (lower) cation size (symmetry) than XH4+. Consequently, CH3XH3+ undergoes further improvements to describe the electrostatic interactions (and beyond) between fluctuations in electronic charge density than XH4+, added to the higher interactions within the inorganic cuboctahedral cavity, which causes a larger distortion of the (inorganic) PbI6 octahedra due to the accommodation of (organic) cations.
3.2 Formation enthalpies
Once the Edisp contributions have been identified, we need to explore the nature and influence of dispersion forces on the thermodynamic feasibility of the MHPs studied here. The formation enthalpy (ΔHf) was considered from two possible formation routes (A and B) for XH4PbI3 and CH3XH3PbI3, whose ΔHf values are depicted in Fig. 2(e)–(h) as a function of group 15 elements. In general, the ΔHf versus X trends in both routes are similar across the XH4PbI3 and CH3XH3PbI3 sets for all vdW corrections, i.e., on the one hand, we have the (almost completely exothermic) Route A that combines the molecular precursors in the gas phase with PbI2(s) and presents the compound with X = N as the most thermodynamically favorable, in accordance with what was observed experimentally for CH3NH3PbI3,89 with the ΔHf magnitude decreasing with increasing atomic number X. On the other hand, we have the (endothermic, greatly for std) Route B, with precursors in the solid phase, with a reduced tendency for compound formation that is practically unalterable concerning the X exchange.In addition to Route A being energetically favorable to Route B for all X elements and considering all vdW corrections, the thermodynamic stability trend for the XH4PbI3 exothermic (endothermic) process as a function of X is similar for calculations with and without vdW corrections, with additive (diminutive) contributions in the XH4+ description by different vdW flavors that shift down (up) the negative (positive) ΔHf values on Route A (Route B), with a significant emphasis on the SbH4PbI3 ΔHf value, which is corrected from positive (std) to negative (all vdW flavors) in Route A. In the CH3XH3PbI3 case, we also observed the higher thermodynamic stability of Route A compared to Route B, so that the vdW approaches correct for a more exothermic trend (downward shift in) the ΔHfversus X behavior without vdW (std). This highlights the correction of the underestimated ΔHf magnitude in Route A to CH3NH3PbI3 and the complete change from endothermic (std) to exothermic (all vdW flavors) in the Route B formation mechanism.
Thus, considering the vdW corrections, the XH4PbI3 and CH3XH3PbI3 compounds proved likely for the formation Route A considered here, where the ΔHf magnitude obtained by semi-empirical vdW flavors is larger than those obtained by empirical vdW corrections, with both approaches describing the thermodynamic stability order: NH4PbI3 < PH4PbI3 < AsH4PbI3 ≤ SbH4PbI3 and CH3NH3PbI3 < CH3PH3PbI3 < CH3AsH3PbI3 < CH3SbH3PbI3. Therefore, it is verified that the thermodynamic feasibility decreases with the change of X (from N up to Sb) in the organic cation composition within the MHP archetypes. To understand this stability variation with the molecular cation design used here (X variation) and how the different vdW type corrections can influence, we need to discuss (i) the nature of the organic cations, initially going through the feasibility of building XH4PbI3 and CH3XH3PbI3 MHPs, through different ionic sizes and electronegativities (see Tables S1 and S2†); (ii) the structural analysis considering the lattice parameters and volume of the XH4PbI3 and CH3XH3PbI3 bulks systems, with the changes arising in the inorganic counterpart (PbI6 octahedra); (iii) the electronic behavior (through the energy gaps) for possible technological applications.
3.3 The nature of the organic cations
To complement the understanding of the stability trend obtained via molecular cation design and to expand the discussion about the contribution of different vdW corrections, it is necessary to infer the nature of the organic cations. Before that, it is essential to analyze the organic–inorganic configuration in cubic-motif perovskite, where all ions are treated as rigid spheres. For the inorganic framework, we have the halogen anion (I−) occupying the vertices of regular PBI6 octahedra, with the divalent metal cations (Pb2+) in the center of the octahedra, where the volume enclosed by the neighboring octahedra defines the cuboctahedral cavity, which hosts the monovalent organic cation (XH4+ or CH3XH3+). Thus, considering the ionic radii,90,91rion (see Table S1†), our MHP model structures are contained within the minimum radius ratio for the stability of the octahedron (geometric factor of octahedron formation, 0.414),90i.e., the octahedral factor considered here, given by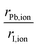 , is equal to 0.54. Therefore, as evidenced by the relatively low octahedral distortion shown in Fig. S2,† the stability of the perovskite octahedra implies that the cuboctahedral cavities provide only a limited volume for the organic cations.16,87 Consequently, accurately determining the size of these molecular cations is essential to elucidate the interplay between the inorganic framework and the organic moieties in hybrid perovskites.
, is equal to 0.54. Therefore, as evidenced by the relatively low octahedral distortion shown in Fig. S2,† the stability of the perovskite octahedra implies that the cuboctahedral cavities provide only a limited volume for the organic cations.16,87 Consequently, accurately determining the size of these molecular cations is essential to elucidate the interplay between the inorganic framework and the organic moieties in hybrid perovskites.
The ionic radius determination is a challenge, even for symmetrical cations (such as XH4+) and even more for nonspherically symmetric cations (such as CH3XH3+), since we are dealing with molecular cations free to rotate about its center of mass, with bond lengths that can vary due to hydrogen-bonding interactions with the anionic counterparts. Therefore, to estimate the ionic radius of XH4+, rXH4, we have considered the X–H average bond lengths, dav,X–H, in the context of 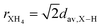 ; while for the CH3XH3+ ionic radius, rCH3XH3, we have considered two ways of estimating (i) based on the C–X bond lengths, dC–X, and the rion of X elements, through rCH3XH3 = 0.5dC−X + rX,ion, and (ii) from the distance between the center of mass (CM) of the organic cation and the atom with the largest distance to CM (except for the H atoms), dCM, being estimated from rCH3XH3 = dCM + rX,ion. Thus, the ionic radii for the organic cations have the dav,X–H, dC–X, and dCM quantities calculated for X within empirical, semi-empirical, and without (std) vdW corrections (see Table S3†), presenting a variation of values smaller than 1.16% among the different approaches. As an inherited result, the rXH4 and rCH3XH3 values also showed a small variation (<0.69%) with different vdW corrections.
; while for the CH3XH3+ ionic radius, rCH3XH3, we have considered two ways of estimating (i) based on the C–X bond lengths, dC–X, and the rion of X elements, through rCH3XH3 = 0.5dC−X + rX,ion, and (ii) from the distance between the center of mass (CM) of the organic cation and the atom with the largest distance to CM (except for the H atoms), dCM, being estimated from rCH3XH3 = dCM + rX,ion. Thus, the ionic radii for the organic cations have the dav,X–H, dC–X, and dCM quantities calculated for X within empirical, semi-empirical, and without (std) vdW corrections (see Table S3†), presenting a variation of values smaller than 1.16% among the different approaches. As an inherited result, the rXH4 and rCH3XH3 values also showed a small variation (<0.69%) with different vdW corrections.
The ionic radius values follow the atomic size increase of pnictogens, i.e., rNH4 < rPH4 < rAsH4 < rSbH4 and rCH3NH3 < rCH3PH3 < rCH3AsH3 < rCH3SbH3 (by (i)), in good agreement with the relative difference for ionic sizes concerning N, wherein P, As, and Sb are 45.21%, 52.05%, and 67.81%, respectively, larger than that of N.90,91 Our rXH4 and rCH3XH3 results are in agreement with previous theoretical work21 in the context of steric radii (within LDA), while our specific results for rNH4 (146.79 pm) and rCH3NH3 (220.43 pm by (i) and 224.53 pm by (ii)), using dDsC, are the closest to the effective radius values of 146 pm and 217 pm, respectively, taken as a reference.9,92
Once the ionic radii for the organic cations are estimated, we can verify the feasibility of perovskite formation through the archetypal models studied here, using the Goldschmidt tolerance criterion, 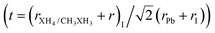 , 0.8 ≤ t ≤ 1.0,8,9,93 which assesses whether the organic cation site can fit within the cavities of the inorganic structure. Consequently, from t, it is possible to evaluate the ionic size mismatches to indicate the different structural types, where a perfectly packed structure is obtained for t ≈ 1, with mostly cubic structures for 0.9 < t < 1 and distorted structures for 0.8 < t < 0.89, whereas t < 0.8 (too small cation) and t > 1 (too large cation) refer to the formation of other structural motifs, e.g., tetragonal and hexagonal, respectively.7,8,92,94 It is important to note that obtaining a positive ascension for the formability criterion does not imply that the perovskite is the only stable phase for a given compound since perovskite has a propensity to undergo a series of phase transitions that can be modulated by chemical factors, temperature, and pressure.8,9
, 0.8 ≤ t ≤ 1.0,8,9,93 which assesses whether the organic cation site can fit within the cavities of the inorganic structure. Consequently, from t, it is possible to evaluate the ionic size mismatches to indicate the different structural types, where a perfectly packed structure is obtained for t ≈ 1, with mostly cubic structures for 0.9 < t < 1 and distorted structures for 0.8 < t < 0.89, whereas t < 0.8 (too small cation) and t > 1 (too large cation) refer to the formation of other structural motifs, e.g., tetragonal and hexagonal, respectively.7,8,92,94 It is important to note that obtaining a positive ascension for the formability criterion does not imply that the perovskite is the only stable phase for a given compound since perovskite has a propensity to undergo a series of phase transitions that can be modulated by chemical factors, temperature, and pressure.8,9
Our results for t as function of rXH4 or rCH3XH3 are depicted in Fig. 3 (numerical values in Table S3†) considering the different vdW corrections. The first finding is related to the small variation in t values from different vdW flavors, ≤0.37%, corresponding to average t values of 0.766 for NH4PbI3, 0.878 for PH4PbI3, 0.907 for AsH4PbI3, 0.960 for SbH4PbI3, 0.919 (0.928) for CH3NH3PbI3, 1.088 (1.135) for CH3PH3PbI3, 1.123 (1.136) for CH3AsH3PbI3, and 1.265 (1.116) for CH3SbH3PbI3, where the values in parentheses are obtained through dCM. The t values for NH4PbI3 and CH3NH3PbI3 are in good agreement with the respective values (tNH4 = 0.763 and tCH3NH3 = 0.912) obtained from the ionic radii reported in the literature.91,92 Contrary to the other archetypes of the XH4PbI3 (CH3XH3PbI3) group, NH4PbI3 (CH3NH3PbI3) lies outside (inside) the stable region for perovskites. Thus, the cuboctahedral cavity has a size limitation concerning the organic cation size, i.e., small organic cations are expected to fit better into the structure (except for NH4PbI3). In addition to CH3NH3PbI3, some hypothetical perovskites with phosphonium, arsonium, and stibonium are predicted, in agreement with previous work.21
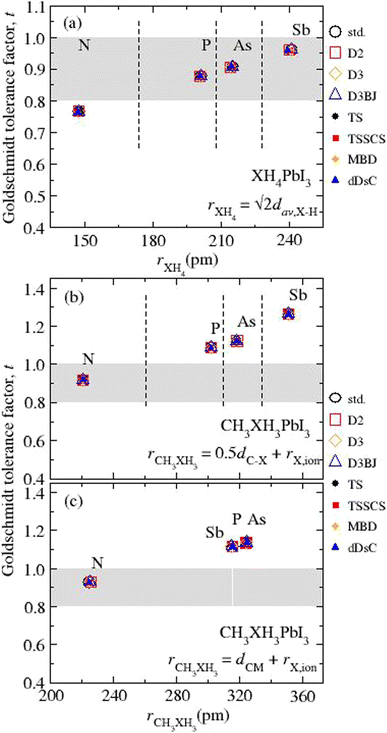 | ||
| Fig. 3 Calculated Goldschmidt tolerance factors (t) concerning the ionic radius for the organic cations (rXH4 and rCH3XH3) for all the (a) XH4PbI3 and CH3XH3PbI3 calculated from (b) rCH3XH3 = 0.5dC–X + rX,ion and (c) rCH3XH3 = 0.5dCM + rX,ion, where X = N, P, As, and Sb. The mathematical expressions used to estimate the ionic radii of molecular cations are indicated inside each graphical part, while the ionic radii of the elements90,91 can be found in Table S1.† The grey area corresponds to the geometric criterion for the Goldschmidt tolerance factor.93 | ||
In general, it is observed that the interaction between the organic cations and the inorganic framework, which translates into the molecular cation confinement in the inorganic cavity, results in only slight structural changes of XH4 and CH3XH3, even using different vdW flavors, as evidenced by the dav,X–H, dC–X, and dCM results and their respective small variations concerning the std calculations (without vdW). Thus, the main influence inflicted on the organic part by coupling with the inorganic counterpart is related to the conformation of the organic component, with the bond formation between the I and H atoms. On the other hand, the inorganic framework undergoes larger structural changes due to the influence of organic cations, as we will discuss in the next subsection. Finally, through the t results, it is evident that the increases in the X ionic radius in group 15 elements for the CH3XH3PbI3 set, previously associated with a decrease in thermodynamic stability (Route A), result in structural destabilization (t > 1 for X = P, As, and Sb). In the case of XH4PbI3 set, we also have the thermodynamic destabilization with the increase in the ionic size. However, t remains within the structural stability (cubic) limit (0.9 ≲ t < 1), so, we need to add to the discussion the electronegativity of the X elements involved in the formation of the XH4+ cations.
Considering the Pauling electronegativity scale (see Table S2†) for the chemical elements of XH4PbI3 and CH3XH3PbI3 sets, it is evident that altering the pnictogen changes the nature of the organic cations not only in terms of ionic radius but also in terms of electronegativity, as follows: N (3.04) > P (2.19) > As (2.18) > Sb (2.05).95 Starting from the NH4+ cation, more commonly used in the XH4PbI3 compounds,23,26,55 we have in its composition a strongly electronegative atom of N which compared to the electronegativity of I (2.66) will keep the H atoms tightly bonded in the organic cation, minimizing the interaction with the inorganic octahedron. Similarly, the CH3NH3+ cation, most commonly employed in the CH3XH3PbI3 set,54 is composed of the strong electronegative atom of N and the moderate electronegative atom of C (2.55), so taking into account the I electronegativity, the H atoms will remain strongly bonded in CH3NH3+, also resulting in a small organic–inorganic interaction. However, when the organic cations are modified, exchanging N for other less electronegative pnictogens, there will be a reduction in the X–H binding strength, which is evidenced, for example, by the increase in the dav,X–H values with the atomic number increasing from N to Sb (see Table S3†), causing an increase in interaction with the PbI6 octahedron.
Thus, we verified the design of the organic cations by considering their ionic radius, and electronegativity provides the premises for understanding the thermodynamic stability trend of the XH4PbI3 and CH3XH3PbI3 compounds via Route A. The ionic radius increases and the electronegativity decrease (from N up to Sb) in the organic cation composition leads to a decrease in thermodynamic stability, which are directly evidenced by the structural (cubic) destabilization for the CH3XH3PbI3 set (when t > 1 for X ≠ N) and by the employment of less electronegative elements than N for the XH4PbI3 set (since the whole set still maintains the t < 1 condition). Both bring up the intensification of the ionic electrostatic interaction with the inorganic framework, resulting in the increase in its structural distortions and consequent stability decrease. To demonstrate and prove the trends that can be obtained from the electronegativity difference between two atoms, which can reflect from the polarity measure to the ionic character of the bond between them, we have calculated the charge population through the density-derived electrostatic and chemical (DDEC6)96 method for the partial charge mapping of XH4PbI3 and CH3XH3PbI3 MHPs, considering the atoms (of the organic cations) and ions individually, as can be found in Fig. S1.†
3.4 Structural analysis
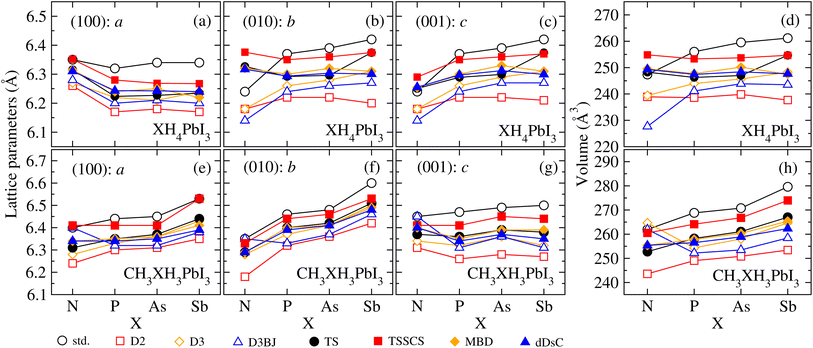
To understand the structural changes of our perovskite models that arise from the design of organic cations, XH4+ and CH3XH3+, as well as the influence of different vdW corrections, we have verified the a, b, and c lattice parameters along the (100), (010), and (001) directions, respectively, and the volume for all XH4PbI3 and CH3XH3PbI3 MHPs as a function of X. The lattice parameters and volume results are shown in Fig. 4, where it is possible to verify the slight (average) increase in the structural volume that results from the modification of the organic cation by replacement of the smaller ionic radius pnictogen by a larger one in both sets, i.e., increasing the atomic number in group 15 elements of the periodic table increases (on average) the volume. However, we observe that the volumetric increase due to X substitution (from N up to Sb) does not necessarily mean an increase of all lattice parameters (e.g., see (100): a for XH4PbI3) and also does not necessarily imply a similar increase along all directions (e.g., compare (010): b and (001): c for CH3XH3PbI3).In terms of vdW corrections, it is noticeable that the lattice parameter values are decreased in relation to the std values, with few exceptions. The most significant decreases (maximum contractions) on average occur for empirical vdW corrections, with D2 presenting the most underestimated structural parameters, while semi-empirical corrections have an intermediate behavior (between the Grimme family corrections and calculations without vdW). The small leakages from a well-behaved trend of the lattice parameters and volume can be attributed to the different possible orientations of the organic cations within cuboctahedral cavities, which are a direct result of a full structural optimization – free of constraints. In addition, larger or smaller cations, in the context of t ≈ 1, can lead to significant changes in the inorganic part (which we will discuss soon) because of the interaction strength variation between the organic and inorganic parts, governed by the electronegativity difference between interacting ions, which is reflected in the octahedral distortions.
From the structural parameters, we found that, regardless of whether or not there are vdW corrections, all the CH3XH3PbI3 structures adopt a pseudo-cubic motif, where a ≠ b ≠ c; while all the XH4PbI3 structures adopt a tetragonal motif, where a ≠ b = c. For both, the lattice constant values and volume (on average) correlate with the atomic sizes of the pnictogens, i.e., NH4PbI3(CH3NH3PbI3) < PH4PbI3(CH3PH3PbI3) < AsH4PbI3(CH3AsH3PbI3) < SbH4PbI3(CH3SbH3PbI3). Moving on to considering vdW corrections, the structural description is improved, correcting the calculated lattice constants, and the indirect impact of vdW interactions is mainly correlated with the unit cell volume, which is decreased (contracted) concerning the value obtained via std calculations.
Our lattice constants for CH3NH3PbI3 (where c > a > b) vary between 6.35 and 6.45 Å for std calculation, improving with the best vdW correction (D3) for values between 6.28 and 6.34 Å, which represent deviations between −0.63% and 0.32% in comparison with experimental report (6.32 Å).97 The calculated lattice parameters for CH3NH3PbI3 are also in good agreement with another experimental study based on powder and single crystal X-ray diffraction measurements: 6.26 Å (ref. 54) and 6.31 Å,98 as well as the lattice parameters for CH3NH3PbI3 and NH4PbI3 are found to be in good agreement with theoretical approaches.26,55 It is important to note that DFT-based calculations are performed at 0 K, while experimental lattice constant values are measured at room temperature or above;98 consequently, the reported experimental values may be influenced by thermal expansion.
Despite the initial orientational freedom for the organic cations within the cuboctahedral cavity, our results suggest that the relaxed structures are the result of the interactions (i.e., the complementation) between the molecular cation and the inorganic framework, which are governed by the low symmetry of the organic cations, the inorganic framework deformations, and the symmetry reduction of the octahedra, all of them aiding the perovskite stabilization. Consequently, it is crucial to include vdW interaction in MHP simulations since they indirectly affect structural stability. When they comprise, the reduction of the unit cell volume influences the organic–inorganic interaction. As a result, it is necessary to verify two complementary structural aspects: the octahedral distortions from the strain that the organic cations exert on the inorganic part and the possible formation of hydrogen bonds between the organic and inorganic parts.
Specifically, to treat the structural distortions of the inorganic part, one can dose them by variations with the Platonic model21,54 and its values of the Pb–I bond lengths and the Pb–I–Pb angles. Both properties are given regarding the plane formed by the ac-lattice parameter, named equatorial direction, and relative to the b-axis, named apical direction. From the X-ray diffraction data,54 the Pb–I average bond length value is equal to 3.18 Å (or 3.16 Å98) with the largest relative deviations of 0.1%, which implies extremely regular bond distances. In addition, the Platonic model has collinear Pb–I–Pb bonds, which present a Pb–I–Pb angle of 180°. Consequently, the two diagonals of PbI6 are practically perpendicular (maximum angular deviation of 4°).54 However, contrary to the Platonic model, our results for equatorial and apical Pb–I bonds and Pb–I–Pb angles, as local structure parameters (see Tables S4 and S5†) show large deviations for XH4PbI3 and CH3XH3PbI3, which reflect on the distortions suffered by the inorganic framework, given the interaction and accommodation of different organic cations.
The design of XH4+ and CH3XH3+ cations by changing the nature of these organic cations through the ionic radius (electronegativity) increase (decrease) of X from N up to Sb reflects the (slight) increase of the lattice constants and volume. As a consequence, their octahedra are locally more distorted, as can be seen through the differences between the smallest and largest Pb–I distance values and Pb–I–Pb angles, both on equatorial and apical directions (Tables S4 and S5†). The angles between the lattice constants, α, β, and γ, reveal negligible (appreciable) deviations in relation to the 90° – Platonic case – for our archetypes with t < 1 (t > 1).
Similar to the lattice parameter results, the different vdW corrections reduce the equatorial and apical Pb–I bond values compared to the calculation without vdW. These reductions reach maximum values of 4.1% (8.7%) for XH4PbI3 (CH3XH3PbI3) with the D2 correction. Thus, despite having the same inorganic framework for all archetypes here, we observed that all structures comprise distortions in Pb–I bonds concerning what would be expected from the Platonic case, with the closest proximity to the std values. The appearance of octahedral deformations is also reflected in the equatorial and apical Pb–I–Pb angles, with the largest leakages from the Platonic model appearing for systems with smaller organic cations (e.g., NH4PbI3) and with the use of empirical vdW corrections or std calculations. On the other hand, we observed that the use of larger organic cations (e.g., CH3AsH3PbI3) leads to equatorial and apical angles closer to 180° since the bonds and bond angles of the inorganic part define the cuboctahedral cavity volume.
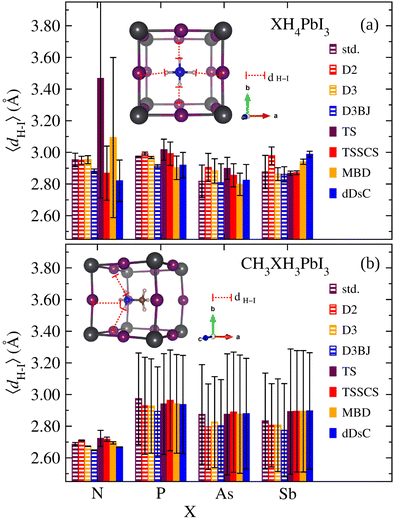
In general, the nature of organic cations, tuned by the ionic size and electronegativity of the X species, influences the inorganic framework reorientations. Added to the fact that the electronic properties are highly sensitive to the Pb–I modifications,16,87 it is verified that in addition to the organic cation size, the effect of electronegativity differences between the ionic constituents is also relevant since they are associated with partial charges and polarizability. Consequently, one of the mechanisms that permeates the organic–inorganic interaction and that can reflect the connection between the nature of organic cations and distortion of the PbI6 octahedra reside in the hydrogen bond formation. So, the strength of the hydrogen bonding is reported as an indication of the octahedral tilting.99 Thus, considering the relevant bridging bond between the electron-donating element in the organic cation (X) and H atoms forming a bridge with the I, we present in Fig. 5 the average H–I bond lengths, 〈dH–I〉, for XH4PbI3 and CH3XH3PbI3 as a function of X for calculations without vdW and with empirical or semi-empirical vdW corrections.
Considering the XH4+ tetrahedral symmetry and their non-polar character, one would expect a centrally located geometric conformation in the inorganic cuboctahedral cavity with the four H atoms pointing in the interstitial regions. Although Fig. 5 confirms this situation by presenting an approximately similar general 〈dH–I〉 magnitude for all X, which would reveal a smaller role for the electronegativity in the H–I bond formation, we have to take into account the mean squared deviation (denoted in Fig. 5). We found some outstanding situations in the NH4PbI3 case, the calculations without and with empirical vdW corrections generate 〈dH–I〉 = 2.9–3.0 Å (in fact, smaller values are obtained for D3BJ, ≈2.88 Å), presenting exactly the expected behavior with the molecular centralization due to the higher N electronegativity, while the semi-empirical vdW corrections are more sensitive to the electrostatic interactions between the organic and inorganic parts, which distort the tetrahedral geometry with the molecular displacement from the cavity center to the proximity of the cuboctahedral wall (approaching two H atoms). This trend is greatly exacerbated for NH4PbI3 in the case of TS description. Still, it is repeated, more attenuated for other semi-empirical vdW corrections, with at least one displaced H atom. Similar to NH4PbI3, for PH4PbI3, we observed higher 〈dH–I〉 values and better behavior. However, for AsH4PbI3 and SbH4PbI3, all approximations are unanimous in describing the molecule as slightly displaced bilaterally with half of the H atoms being further away from the cuboctahedral wall and the remaining closer.
For the CH3XH3PbI3 case, we observed a situation with an increased influence of the X electronegativity since we are dealing with a non-symmetrical and polar organic cation. Unlike the highest values presented for the smallest H–I distances for XH4PbI3, in the case of CH3XH3PbI3 set, we observe that the minimum H–I bond values (considering the mean squared deviation) are around 2.57–2.69 Å, which characterizes hydrogen bonds, with the exception that the bonds are barely stretched for the case of high electronegativity of the N atom, which keeps the bonded H atoms gripped. In contrast, the X substitution by species with smaller electronegativities has more pronounced H–I bonds. This result is in good agreement with the experimental neutron diffraction97 and with the theoretical distance criterion of H⋯I < 3.0 Å to identify hydrogen bonding interactions of CH3NH3PbI3.100 Thus, with the CH3NH3PbI3 exception, the other systems present the three H atoms (from the N side) arranged with two of them closer to the cavity wall, while the third H atom is further away. The center of CH3XH3+ deviates from the cavity center so that the X end is closer to the vertex, consequently the three H from the CH3XH3+ group are closer to the three halide anions, which significantly favor the development of H(N)⋯I bonds.
3.5 Energy gaps
To fully elucidate our MHP archetypes and the role played by vdW corrections, in addition to aspects of thermodynamic stability and structural changes, it is necessary to access the electronic structure of these systems via energy gap, Eg, calculations. For this purpose, we have taken into account three calculation sets for the XH4PbI3 and CH3XH3PbI3 paragon structures resulting from the structural optimization without vdW correction and including the different empirical and semi-empirical vdW corrections, i.e., calculations based solely on the DFT, including SOC (DFT + SOC), and with the relativistic quasiparticle correction (DFT-1/2) combined with SOC (DFT-1/2+SOC), as shown in Table 1. The vdW corrections indirectly obtain the gap energies since their role is predominant in the structural description, especially of the inorganic part. Consequently, it is necessary to analyze the possibility of band gap tuning via modification of the X species in MHPs; for the same X, the different structural motifs coming from the different vdW corrections must be considered as well.| System | E g (eV) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Std | D2 | D3 | D3BJ | TS | TSSCS | MBD | dDsC | ||
| NH4PbI3 | DFT | 1.87 | 1.69 | 1.69 | 1.81 | 1.38 | 1.43 | 1.43 | 1.43 |
| DFT + SOC | 0.85 | 0.80 | 0.80 | 0.84 | 0.41 | 0.38 | 0.41 | 0.41 | |
| DFT-1/2 + SOC | 2.00 | 1.80 | 1.81 | 1.93 | 1.17 | 1.44 | 1.42 | 1.41 | |
| PH4PbI3 | DFT | 1.42 | 1.15 | 1.22 | 1.22 | 1.26 | 1.36 | 1.34 | 1.32 |
| DFT + SOC | 0.31 | 0.41 | 0.13 | 0.12 | 0.14 | 0.26 | 0.25 | 0.23 | |
| DFT-1/2 + SOC | 1.41 | 1.09 | 1.19 | 1.17 | 1.22 | 1.35 | 1.32 | 1.30 | |
| AsH4PbI3 | DFT | 1.51 | 1.17 | 1.25 | 1.26 | 1.27 | 1.38 | 1.37 | 1.34 |
| DFT + SOC | 0.45 | 0.13 | 0.15 | 0.19 | 0.16 | 0.30 | 0.30 | 0.27 | |
| DFT-1/2 + SOC | 1.54 | 1.12 | 1.22 | 1.24 | 1.24 | 1.39 | 1.37 | 1.32 | |
| SbH4PbI3 | DFT | 1.44 | 1.32 | 1.31 | 1.26 | 1.31 | 1.36 | 1.34 | 1.39 |
| DFT + SOC | 0.32 | 0.30 | 0.21 | 0.18 | 0.22 | 0.26 | 0.28 | 0.34 | |
| DFT-1/2 + SOC | 1.44 | 1.28 | 1.28 | 1.23 | 1.29 | 1.36 | 1.33 | 1.38 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Std | D2 | D3 | D3BJ | TS | TSSCS | MBD | dDsC | ||
| CH3NH3PbI3 | DFT | 1.63 | 1.66 | 1.51 | 1.47 | 1.46 | 1.50 | 1.51 | 1.55 |
| DFT + SOC | 0.62 | 0.80 | 0.50 | 0.48 | 0.43 | 0.46 | 0.55 | 0.54 | |
| DFT-1/2 + SOC | 1.50 | 1.57 | 1.33 | 1.28 | 1.36 | 1.42 | 1.47 | 1.37 | |
| CH3PH3PbI3 | DFT | 1.55 | 1.32 | 1.39 | 1.37 | 1.44 | 1.51 | 1.44 | 1.43 |
| DFT + SOC | 0.40 | 0.21 | 0.28 | 0.24 | 0.31 | 0.36 | 0.31 | 0.29 | |
| DFT-1/2 + SOC | 1.53 | 1.29 | 1.38 | 1.33 | 1.42 | 1.43 | 1.43 | 1.48 | |
| CH3AsH3PbI3 | DFT | 1.59 | 1.37 | 1.45 | 1.41 | 1.47 | 1.53 | 1.48 | 1.47 |
| DFT + SOC | 0.40 | 0.22 | 0.28 | 0.24 | 0.35 | 0.39 | 0.34 | 0.33 | |
| DFT-1/2 + SOC | 1.59 | 1.34 | 1.44 | 1.38 | 1.48 | 1.56 | 1.51 | 1.49 | |
| CH3SbH3PbI3 | DFT | 1.63 | 1.55 | 1.52 | 1.47 | 1.57 | 1.67 | 1.59 | 1.62 |
| DFT + SOC | 0.51 | 0.66 | 0.45 | 0.41 | 0.51 | 0.52 | 0.53 | 0.65 | |
| DFT-1/2 + SOC | 1.65 | 1.64 | 1.56 | 1.50 | 1.61 | 1.61 | 1.61 | 1.68 | |
From our energy gap results, we find that the standard DFT-based methods (here, using PBE), despite the unphysical self-coulombic repulsion,101 lead to a reasonable description of the MHP band gaps, however, as an artificial effect from cancellation of errors, which can occur for materials formed by Pb2+ cations.102 When SOC is included, the gap energy is strongly underestimated, in agreement with literature results for CH3NH3PbI3 systems.27,84 With excellent cost-benefit, outstanding band gap results are obtained for MHPs when the DFT-1/2 approach is combined with SOC.16,87 Specifically, in the case of CH3NH3PbI3 perovskite, for which we can compare our DFT-1/2 + SOC results with the experimental results (Eg = 1.48–1.68 eV),103–107 we have excellent agreement with the magnitude of deviations between 1.30 and 14.67%. Thus, from now on, we will focus our discussion on the band gap results obtained via DFT-1/2 + SOC.
In general, we observed a direct relationship between the local structural distortions and band gaps in the XH4PbI3 and CH3XH3PbI3 systems, in which the organic cations indirectly contribute to the band gap, since they do not electronically influence the frontier orbitals. However, their nature (ionic size and electronegativity differences) has an additive role in reducing the symmetry of the inorganic framework. Consequently, the more distorted the structural motifs are, as evidenced by the larger differences between the smallest and largest Pb–I bonds and Pb–I–Pb angles in both equatorial and apical directions (Tables S4 and S5†), the larger the energy gaps. This fact is further evidenced by the band gap values obtained from the optimized structures using different vdW corrections. Additionally, as long-range empirical and semi-empirical corrections contribute towards highlighting the organic–inorganic interactions, there is an improvement in the description of distortions, which reflects a band gap reduction concerning the std calculations. This gap energy closing by vdW description agrees with the slight contraction of the lattice parameters (and volume reduction).
Thus, combining thermodynamic stability with the structural modifications resulting from different organic cations, we found some structures that are promising candidates, in particular, PH4PbI3, AsH4PbI3, and SbH4PbI3, all with band gaps ranging between 1.09 and 1.33 eV, which fall in the middle of the range for optimum photovoltaic efficiency. Besides the low gap, our archetype perovskites with large cations have the advantage that the cavity filling should oppose the water incorporation since it can avoid the degradation of perovskite solar cells.18 However, it is worth mentioning the correlation between the increasing size of X in the CH3XH3 cation and a slight opening of band gaps by going from X = N to Sb, which is due to the employment of local distortions on the inorganic sublattice through the use of large organic cations.
4 Conclusion
The SimStack workflows are a testament to efficiency in computational materials science. By automating the intricate sequence of tasks—from cation selection and molecular geometry processing to electronic structure calculation and data compilation—SimStack significantly accelerates raw data production. More notably, the automated data transfer from the ‘DB-Generator’ to GitHub, followed by analysis in a Colab notebook, exemplifies a streamlined, end-to-end process that reduces the time to insight. This seamless integration of simulation, data management, and analysis within the SimStack framework promises to save researchers an enormous amount of time, thereby relieving them of the burden of tedious tasks and expediting innovation and discovery in materials science. By using the above workflows, we assessed the performance of the empirical and semi-empirical vdW corrections in designing organic cations of the XH4PbI3 and CH3XH3PbI3 prototype perovskites via change of the X species (N, P, As, and Sb). In addition to the relativistic PBE-based calculations, we included the D2, D3, D3BJ, TS, TSSCS, MBD, and dDsC vdW approaches to describe the thermodynamic stability, structural properties of the organic and inorganic parts, and energy gaps, the latter using SOC calculations combined with the DFT-1/2 quasiparticle approximation. Our results reveal that the dispersive energy term contributes to improving the energy stabilization of the studied systems. The thermodynamic feasibility was confirmed for both sets through an exothermic formation route based on the molecular precursors in the gas phase combined with PbI2(s), where the formation enthalpy magnitude decreases with X, and the most thermodynamically favorable compounds are obtained for X = N.The stability trend was related to the nature of organic cations in the design process, i.e., the feasibility of building XH4PbI3 and CH3XH3PbI3 through different ionic sizes and electronegativities. As the octahedron stability implies a limited volume of the cuboctahedral cavities to accommodate the organic cations, we estimated the ionic radii for symmetrical (XH4+) and nonspherically symmetric (CH3XH3+) cations, which follow the atomic size increase of pnictogens. Our archetypal models have a Goldschmidt criterion that points to a ionic size mismatch in the XH4PbI3 (CH3XH3PbI3) group, where NH4PbI3 (CH3NH3PbI3) lies outside (inside) the stable region for perovskites. With the expectation that small organic cations fit better into the structure (except NH4PbI3), consequently, in addition to CH3NH3PbI3, some hypothetical perovskites with phosphonium, arsonium, and stibonium are predicted.
We identified a situation of cation confinement in the inorganic cavity, with slight structural changes due to different vdW flavors concerning the standard calculations (without vdW), e.g., it was ≤0.37% for the tolerance factor. However, only including the X electronegativity, it was possible to understand the thermodynamic stability trend, i.e., from N up to Sb, the ionic radius increases and the electronegativity decreases in the organic cation composition, which lead to a decrease in thermodynamic stability (also evidenced by the tolerance factor), since there is an intensification of the ionic electrostatic interaction with the inorganic framework, resulting in larger structural distortions. Therefore, it was possible to verify a slight (average) increase in the structural volume (lattice parameters) with the X atomic number that results from the cavity deformation to accommodate the organic cations.
The empirical vdW corrections (especially D2) showed a more significant contraction of lattice parameters than semi-empirical vdW and standard calculations. Consequently, the vdW corrections indirectly affect the structural stability by improving the treatment of organic–inorganic interactions since the structural motifs showed octahedral distortions and hydrogen bond formation. Despite having the same inorganic framework for all archetypes, the local distortions of the octahedra were evidenced by deformations in equatorial and apical Pb–I bonds and Pb–I–Pb angles concerning the expected well-behaved Platonic case. In connection to that, we have the bridging bond between the electron-donating element in the organic cation (X) and H atoms, forming a bridge with the I, causing the (bilateral) molecular displacement from the cavity center. The organic cations indirectly contribute to the band gap since they induce the local structural distortions, directly affecting the XH4PbI3 and CH3XH3PbI3 band gaps. The more distorted structural motifs showed more significant energy gaps, considering all optimized structures through different vdW approaches. Thus, considering the complete picture, the vdW correction allowed an improved description of hybrid MHPs with some up-and-coming new hypothetical candidates, e.g., PH4PbI3, AsH4PbI3, and SbH4PbI3.
Data availability
The authors confirm that the data supporting this study's findings are available in the article and the ESI† and upon request. The Halide-Perovskite Workflow is also available to the public via the Halide-Perovskite repository at https://github.com/KIT-Workflows/Halide-Perovskites.Author contributions
C. R. C. R. analyzed the data, wrote the first version of the manuscript, and developed the workflows to automate the calculations. W. W. helped develop ideas and provided computational/software resources. M. J. P. wrote the first version of the manuscript and helped develop ideas and data analyses. A. C. D. helped develop ideas and helped with data analysis. C. M. O. B. helped develop ideas and helped with data analysis. L. O. A. helped develop ideas and helped with data analysis. D. G. S. carried out the DFT calculations, analyzed the data, made the graphs, and wrote the first version of the manuscript. All authors performed subsequent revisions of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the National Council for Scientific and Technological Development (CNPq, grant numbers 307345/2021-1, 408144/2022-0, 305174/2023-1, 444431/2024-1 and 444069/2024-0), the Federal District Research Support Foundation (FAPDF, grant numbers 00193-00001817/2023-43 and 00193-00001817/2023-43), the Coordination for Improvement of Higher Level Education (CAPES), and the Rio Grande do Sul Research Foundation (FAPERGS, grant 24/2551-0001551-5) for providing financial support and the German Federal Ministry of Education and Research (BMBF) for funding the Innovation-Platform MaterialDigital (http://www.materialdigital.de) project under project number FKZ 13XP5094A. The authors acknowledge the use of the HoreKa supercomputer, supported by the Ministry of Science, Research and the Arts Baden-Württemberg and the Federal Ministry of Education and Research. We acknowledge support by the KIT Publication Fund of the Karlsruhe Institute of Technology. Additionally, the authors extend their thanks to the “Centro Nacional de Processamento de Alto Desempenho em São Paulo” (CENAPAD-SP, UNICAMP/FINEP – MCTI project) for providing resources for projects 897 and 570 to Lobo Carneiro HPC (NACAD) at the Federal University of Rio de Janeiro (UFRJ), for project 133 to CIMATEC SENAI at Salvador – BA, Brazil, for their partnership and support through the Ogun Supercomputer, and to the “Laboratório Central de Processamento de Alto Desempenho” (LCPAD) financed by FINEP through CT-INFRA/UFPR projects. A. C. D. also acknowledges the PDPG-FAPDF-CAPES Centro-Oeste grant 00193-00000867/2024-94.Notes and references
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J. E. Moser, M. Gratzel and N.-G. Park, Sci. Rep., 2012, 2, 591 CrossRef PubMed.
- M. Grätzel, Nature, 2014, 13, 838–842 CrossRef PubMed.
- Z. Chen, B. Turedi, A. Y. Alsalloum, C. Yang, X. Zheng, I. Gereige, A. AlSaggaf, O. F. Mohammed and O. M. Bakr, ACS Energy Lett., 2019, 4, 1258–1259 CrossRef CAS.
- X. Li, J. Du, H. Duan, H. Wang, L. Fan, Y. Sun, Y. Sui, J. Yang, F. Wang and L. Yang, Nano Res., 2022, 15, 1375–1382 CrossRef CAS.
- J. Park, J. Kim, H.-S. Yun, M. J. Paik, E. Noh, H. J. Mun, M. G. Kim, T. J. Shin and S. I. Seok, Nature, 2023, 616, 724–730 CrossRef CAS PubMed.
- D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12 RSC.
- J. S. Manser, J. A. Christians and P. V. Kamat, Chem. Rev., 2016, 116, 12956–13008 CrossRef CAS PubMed.
- B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558–4596 CrossRef CAS PubMed.
- R. Gottesman, L. Gouda, B. S. Kalanoor, E. Haltzi, S. Tirosh, E. Rosh-Hodesh, Y. Tischler, A. Zaban, C. Quarti, E. Mosconi and F. De Angelis, J. Phys. Chem. Lett., 2015, 6, 2332–2338 CrossRef CAS PubMed.
- A. Kovalsky, L. Wang, G. T. Marek, C. Burda and J. S. Dyck, J. Phys. Chem. C, 2017, 121, 3228–3233 CrossRef CAS.
- F. Hao, C. C. Stoumpos, R. P. H. Chang and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 8094–8099 CrossRef CAS PubMed.
- F. Zheng, L. Z. Tan, S. Liu and A. M. Rappe, Nano Lett., 2016, 16, 7316 CrossRef CAS PubMed.
- T. Etienne, E. Mosconi and F. De Angelis, J. Phys. Chem. Lett., 2016, 7, 1638–1645 CrossRef CAS PubMed.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta, N. Mathews and S. G. Mhaisalkar, J. Mater. Chem. A, 2015, 3, 23829–23832 RSC.
- L. O. de Araujo, F. P. Sabino, C. R. C. Rêgo and D. Guedes-Sobrinho, J. Phys. Chem. Lett., 2021, 12, 7245–7251 CrossRef PubMed.
- I. Borriello, G. Cantele and D. Ninno, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 235214 CrossRef.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS PubMed.
- D. Guedes-Sobrinho, I. Guilhon, M. Marques and L. K. Teles, Sci. Rep., 2019, 9, 11061 CrossRef PubMed.
- L. O. de Araujo, C. R. Rêgo, W. Wenzel, C. M. de Oliveira Bastos, M. J. Piotrowski, A. C. Dias and D. Guedes-Sobrinho, J. Alloys Compd., 2024, 992, 174485 CrossRef.
- M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 5757 CrossRef CAS PubMed.
- M. R. Filip, C. Verdi and F. Giustino, J. Phys. Chem. C, 2015, 119, 25209–25219 CrossRef CAS.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. v. Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, M. K. Nazeeruddin, M. GrÃtzel and F. De Angelis, Nano Lett., 2014, 14, 3608–3616 CrossRef CAS PubMed.
- F. E.-M. E. T. Bentria, S. N. Rashkeev, S. Kais and F. H. Alharbi, Sci. Rep., 2016, 6, 30305 CrossRef.
- F. Brivio, K. T. Butler, A. Walsh and M. van Schilfgaarde, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 155204 CrossRef.
- P. Umari, E. Mosconi and F. De Angelis, Sci. Rep., 2014, 4, 4467 CrossRef PubMed.
- C. Motta, F. El-Mellouhi, S. Kais, N. Tabet, F. Alharbi and S. Sanvito, Nat. Commun., 2015, 6, 7026 CrossRef CAS PubMed.
- F. E.-M. E. T. Bentria, A. Marzouk, S. N. Rashkeev, S. Kais and F. H. Alharbi, npj Comput. Mater., 2016, 2, 16035 CrossRef.
- D. A. Egger and L. Kronik, J. Phys. Chem. Lett., 2014, 5, 2728–2733 CrossRef CAS PubMed.
- K. Lejaeghere, V. V. Speybroeck, G. V. Oost and S. Cottenier, Crit. Rev. Solid State Mater. Sci., 2014, 39, 1–24 CrossRef CAS.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. D. Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. D. Marco, C. Draxl, M. Dulak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Granäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iusan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Kücükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. V. Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351, 1415 CrossRef CAS.
- C. R. C. Rêgo, L. N. Oliveira, P. Tereshchuk and J. L. F. Da Silva, J. Phys.: Condens. Matter, 2015, 27, 415502 CrossRef PubMed.
- C. R. C. Rêgo, L. N. Oliveira, P. Tereshchuk and J. L. F. Da Silva, J. Phys.: Condens. Matter, 2016, 28, 129501 CrossRef.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef.
- A. Tkatchenko, A. Ambrosetti and R. A. DiStasio, J. Chem. Phys., 2013, 138, 074106 CrossRef PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 109902 CrossRef PubMed.
- G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Phys., 2011, 134, 044117 CrossRef.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Theory Comput., 2011, 7, 3567–3577 CrossRef CAS PubMed.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 066501 CrossRef.
- J. Park, B. D. Yu and S. Hong, Curr. Appl. Phys., 2015, 15, 885–891 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- W. Reckien, F. Janetzko, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2012, 33, 2023–2031 CrossRef CAS.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- L. G. Ferreira, M. Marques and L. K. Teles, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 125116 CrossRef.
- T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641 RSC.
- F. Brivio, A. B. Walker and A. Walsh, APL Mater., 2013, 1, 042111 CrossRef.
- Y. Zong, Y. Zhou, M. Ju, H. F. Garces, A. R. Krause, F. Ji, G. Cui, X. C. Zeng, N. P. Padture and S. Pang, Angew. Chem., Int. Ed., 2016, 55, 14723–14727 CrossRef CAS.
- W. Huang, J. S. Manser, S. Sadhu, P. V. Kamat and S. Ptasinska, J. Phys. Chem. Lett., 2016, 7, 5068–5073 CrossRef CAS PubMed.
- C. R. C. Rêgo, J. Schaarschmidt, T. Schlöder, M. Penaloza-Amion, S. Bag, T. Neumann, T. Strunk and W. Wenzel, Front. Mater., 2022, 9, 877597 CrossRef.
- S. P. Huber, S. Zoupanos, M. Uhrin, L. Talirz, L. Kahle, R. Häuselmann, D. Gresch, T. Müller, A. V. Yakutovich, C. W. Andersen, F. F. Ramirez, C. S. Adorf, F. Gargiulo, S. Kumbhar, E. Passaro, C. Johnston, A. Merkys, A. Cepellotti, N. Mounet, N. Marzari, B. Kozinsky and G. Pizzi, Sci. Data, 2020, 7, 300 CrossRef PubMed.
- J. Janssen, S. Surendralal, Y. Lysogorskiy, M. Todorova, T. Hickel, R. Drautz and J. Neugebauer, Comput. Mater. Sci., 2019, 163, 24–36 CrossRef CAS.
- J. Schaarschmidt, J. Yuan, T. Strunk, I. Kondov, S. P. Huber, G. Pizzi, L. Kahle, F. T. Bölle, I. E. Castelli, T. Vegge, F. Hanke, T. Hickel, J. Neugebauer, C. R. C. Rêgo and W. Wenzel, Adv. Energy Mater., 2021, 12, 2102638 CrossRef.
- S. Bekemeier, C. R. Caldeira Rêgo, H. L. Mai, U. Saikia, O. Waseda, M. Apel, F. Arendt, A. Aschemann, B. Bayerlein, R. Courant, G. Dziwis, F. Fuchs, U. Giese, K. Junghanns, M. Kamal, L. Koschmieder, S. Leineweber, M. Luger, M. Lukas, J. Maas, J. Mertens, B. Mieller, L. Overmeyer, N. Pirch, J. Reimann, S. Schröck, P. Schulze, J. Schuster, A. Seidel, O. Shchyglo, M. Sierka, F. Silze, S. Stier, M. Tegeler, J. F. Unger, M. Weber, T. Hickel and J. Schaarschmidt, Adv. Eng. Mater., 2025, 2402149 CrossRef.
- G. R. Da Silva, J. P. Cerqueira Felix, C. R. C. Rêgo, A. C. Dias, C. M. de O. Bastos, M. J. Piotrowski and D. Guedes-Sobrinho, Sci. Rep., 2025, 15, 1939 CrossRef CAS PubMed.
- H. Pecinatto, C. R. C. Rêgo, W. Wenzel, C. A. Frota, B. M. S. Perrone, M. J. Piotrowski, D. Guedes-Sobrinho, A. C. Dias, C. Mota, M. S. S. Gusmão and H. O. Frota, Sci. Rep., 2023, 13, 17157 CrossRef CAS.
- M. Soleymanibrojeni, C. R. Caldeira Rego, M. Esmaeilpour and W. Wenzel, J. Mater. Chem. A, 2024, 12, 2249–2266 RSC.
- B. Mieller, M. Valavi and C. R. Caldeira Rêgo, Adv. Eng. Mater., 2024, 2400872 CrossRef.
- L. O. de Araujo, C. R. C. Rêgo, W. Wenzel, M. J. Piotrowski, A. C. Dias and D. Guedes-Sobrinho, npj Comput. Mater., 2024, 10, 146 CrossRef CAS.
- J. F. Dalmedico, D. N. Silveira, L. O. de Araujo, W. Wenzel, C. R. C. Rêgo, A. C. Dias, D. Guedes-Sobrinho and M. J. Piotrowski, ChemPhysChem, 2024, 25, e202400118 CrossRef CAS.
- M. Mostaghimi, C. R. C. Rêgo, R. Haldar, C. Wöll, W. Wenzel and M. Kozlowska, Front. Mater., 2022, 9, 840644 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B:Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- T. Bučko, S. Lèbegue, J. Hafner and J. G. Ángyán, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 064110 CrossRef.
- T. Bučko, S. Lèbegue, J. Hafner and J. G. Ángyán, J. Chem. Theory Comput., 2013, 9, 4293–4299 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107–3114 CrossRef CAS.
- T. Takeda, Z. Phys. B, 1978, 32, 43–48 CrossRef CAS.
- J. Even, L. Pedesseau, M. Dupertuis, J. Jancu and C. Katan, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 205301 CrossRef.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS.
- J. Even, L. Pedesseau, C. Katan, M. Kepenekian, J. Lauret, D. Sapori and E. Deleporte, J. Phys. Chem. C, 2015, 119, 10161–10177 CrossRef CAS.
- D. Guedes-Sobrinho, I. Guilhon, M. Marques and L. K. Teles, J. Phys. Chem. Lett., 2019, 10, 4245–4251 CrossRef CAS PubMed.
- L. Octavio de Araujo, C. R. C. Rêgo, W. Wenzel, F. P. Sabino and D. Guedes-Sobrinho, J. Phys. Chem. C, 2022, 126, 2131–2140 CrossRef CAS.
- R. E. Wasylishen, O. Knop and J. B. Macdonald, Solid State Commun., 1985, 56, 581–582 CrossRef CAS.
- S. R. Raga, L. K. Ono and Y. Qi, J. Mater. Chem. A, 2016, 4, 2494–2500 RSC.
- L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 1960 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, Taylor & Francis Group, 95th edn, 2014 Search PubMed.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- J.-H. Lee, N. C. Bristowe, J. H. Lee, S.-H. Lee, P. D. Bristowe, A. K. Cheetham and H. M. Jang, Chem. Mater., 2016, 28, 4259–4266 CrossRef CAS.
- J.-H. Lee, N. C. Bristowe, P. D. Bristowe and A. K. Cheetham, Chem. Commun., 2015, 51, 6434–6437 RSC.
- J. P. Perdew and A. Zunger, Phys. Rev. B:Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- S.-H. Wei and A. Zunger, Phys. Rev. B:Condens. Matter Mater. Phys., 1997, 55, 13605 CrossRef CAS.
- S. Singh, C. Li, F. Panzer, K. L. Narasimhan, A. Graeser, T. P. Gujar, A. Köhler, M. Thelakkat, S. Huettner and D. Kabra, J. Phys. Chem. Lett., 2016, 7, 3014–3021 CrossRef CAS PubMed.
- A. M. A. Leguy, P. Azarhoosh, M. I. Alonso, M. Campoy-Quiles, O. J. Weber, J. Yao, D. Bryant, M. T. Weller, J. Nelson, A. Walsh and M. van Schilfgaarde, et al. , Nanoscale, 2016, 8, 6317–6327 RSC.
- L. Q. Phuong, Y. Yamada, M. Nagai, N. Maruyama, A. Wakamiya and Y. Kanemitsu, J. Phys. Chem. Lett., 2016, 7, 2316–2321 CrossRef CAS PubMed.
- L. Jiang, T. Wu, L. Sun, Y.-J. Li, A. Li, R. Lu, K. Zou and W.-Q. Deng, J. Phys. Chem. C, 2017, 121, 24359–24364 CrossRef CAS.
- F. Palazon, D. Pérez-del Rey, B. DÃnekamp, C. Dreessen, M. Sessolo, P. P. Boix and H. J. Bolink, Adv. Mater., 2019, 31, 1902692 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional results of the geometric and electronic property characterization. See DOI: https://doi.org/10.1039/d4dd00312h |
| This journal is © The Royal Society of Chemistry 2025 |