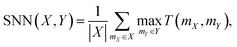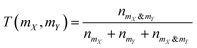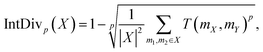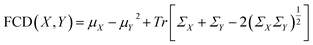Benchmarking study of deep generative models for inverse polymer design

Abstract

Molecular generative models based on deep learning have increasingly gained attention for their ability in de novo polymer design. However, there remains a knowledge gap in the thorough evaluation of these models. This benchmark study explores de novo polymer design using six popular deep generative models: Variational Autoencoder (VAE), Adversarial Autoencoder (AAE), Objective-Reinforced Generative Adversarial Networks (ORGAN), Character-level Recurrent Neural Network (CharRNN), REINVENT, and GraphINVENT. Various metrics highlighted the excellent performance of CharRNN, REINVENT, and GraphINVENT, particularly when applied to the real polymer dataset, while VAE and AAE show more advantages in generating hypothetical polymers. The CharRNN, REINVENT, and GraphINVENT models were successfully further trained on real polymers using reinforcement learning methods, targeting the generation of hypothetical high-temperature polymers for extreme environments. The findings of this study provide critical insights into the capabilities and limitations of each generative model, offering valuable guidance for future endeavors in polymer design and discovery.

---

1 Introduction

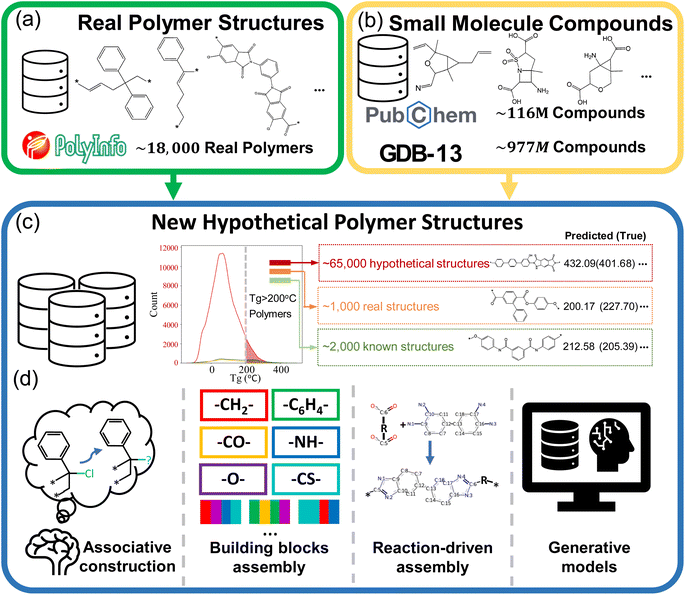
Polymers represent an important class of materials, known for their exceptional versatility in numerous properties, including thermal, mechanical, optical, and dielectric characteristics.^1–5 Plentiful studies are recently dedicated to the molecular design of new polymers endowed with exceptional properties.^6–11 With the recent advancements in deep learning and its application in polymer science and engineering, de novo polymer design has been recognized as a promising method to expedite the design and discovery of new high-performance polymer materials.^7,12–14

A large number of hypothetical polymer structures can provide a vast design space, which is crucial for the success of de novo polymer design strategies. As shown in Fig. 1(a) and (b), the PolyInfo¹⁵ database lists merely 18 697 polymer structures. In comparison, there are around 116 million real small molecule compounds documented in PubChem¹⁶ and GDB-13 (ref. 17) offers us more than 900 million hypothetical small molecule compounds, which provide us with a vast chemical space for drug discovery. Fig. 1(c) illustrates that compared to the real polymer dataset (represented by orange and green lines), the ML-generated PI1M¹⁸ dataset offers researchers a large number of promising high T_g hypothetical candidates, as shown by the red line.¹⁹ Extensive research has been conducted on the de novo design of polymers, with researchers adopting various approaches, especially for proposing new hypothetical polymer structures, as summarized in Fig. 1(d).

Fig. 1 (a) The number of real polymers is very limited in the literature. (b) In contrast, datasets for small molecule compounds contain many real (e.g., PubChem) and hypothetical (e.g., GDB-13) compounds, providing ample opportunities for the development of new small compounds. (c) Due to the limited number of real polymers, hypothetical polymer structures are essential in designing new polymers with exceptional properties. (d) The four primary methods for generating these structures include manual design based on existing structures (associative construction), assembly of building blocks, leveraging existing small molecule compounds and synthetic routes, and employing deep generative models.

For example, Sharma et al. employed a polymer building block approach and high-throughput density functional theory (DFT) to design organic polymers with high energy storage capabilities.²⁰ Initially, repeat units were created using four building blocks within each unit, with each block selected from a pool comprising –CH₂–, –C₆H₄–, –C₄H₂S–, –NH–, –CO–, –O–, and –CS–. These blocks were chosen due to their prevalence in polymer backbones. This was followed by a multi-stage screening process involving quantum mechanics-based searches and molecular dynamics techniques. The final phase included synthesizing and testing the most promising polymers, validating this approach for material selection. Similarly, Li et al. devised novel polysulfates by leveraging their knowledge of known polymer structures and the characteristics of functional groups.²¹ They then confirmed these structures' high glass transition temperature (T_g) and band gap (E_g) values through experimental synthesis and characterizations. The advantages of these two studies are that they allow for control over the structural complexity of the hypothetical polymers and enable the prediction of their overall properties based on the characteristics of functional groups or substructures. However, such a combination method of polymer building blocks becomes quite challenging when there is a desire to obtain a large number of candidates, in particular, on the order of millions.

To obtain candidates on a larger scale, another strategy for generating hypothetical polymer structures is based on existing small molecules and known polymerization reactions (or synthetic routes). As we mentioned earlier, numerous studies have contributed various datasets, including a vast number of small molecule structures. Taking advantage of these existing small molecules, Tao et al. generated an 8 million hypothetical polyimides and uncovered polyimides that possessed a multitude of outstanding thermal and mechanical properties simultaneously.^8,22 Using diamine and dianhydride monomers sourced from PubChem, hypothetical polyimides were generated following a predefined reaction route. To efficiently screen these generated compounds, a machine learning method was employed for high-throughput evaluation. In a similar vein, Wang et al. generated 110 hypothetical polyimides by utilizing diamine and dianhydride monomers, resulting in high-temperature polymer dielectrics.⁶ This approach can provide a large number of candidates, but its chemical space is still limited by the small molecules used.²³

With the rise of deep learning, generative models, and reinforcement learning, an increasing number of researchers are utilizing deep generative methods to expand the chemical space of various materials. This trend is particularly evident in the fields of cheminformatics and drug discovery.^24–47 In polymer informatics, Ma and Luo created the PI1M dataset, comprising 1 million hypothetical polymers generated using an RNN trained on actual polymers sourced from PolyInfo.¹⁸ In their study, they compiled 12 000 homopolymer structures from the PolyInfo database to train an RNN model. This training enabled the generation of 1 million new polymers, collectively referred to as PI1M. It was observed that while PI1M encompasses a chemical space similar to PolyInfo, it also fills in gaps where PolyInfo data is lacking, thereby offering a more comprehensive view of the polymer landscape.

The other researchers have directly generated hypothetical polymers with tailored properties using different deep generative models. For example, Wu et al. introduced Bayesian molecular design to discover polymers with high thermal conductivity.⁷ Gurnani et al. employed graph-to-graph (G2G) translation, called polyG2G, which can discern subtle chemical differences (referred to as translations) leading to significant property variations in polymeric materials.⁴⁸ A latent space searching strategy is employed in this study to generate hypothetical polymers with desired properties. They then used this knowledge to sample and design new polymers with high E_g and electron injection barrier. Batra et al. utilized syntax-directed VAE in conjunction with Gaussian process regression (GPR) models to identify polymers expected to exhibit robustness under extreme conditions, such as high temperatures, high electric fields, and their combination.⁴⁹ Liu et al. employed an invertible graph generative model to generate hypothetical polymers with promising properties, particularly focusing on high-temperature polymer dielectrics.⁵⁰ Kim et al. employed a method of searching and decoding within the latent space offered by a VAE to generate candidates with high polymer log P values^51,52 Huang et al. developed a surrogate deep neural network model to predict thermal conductivity and compiled a library of polymer units consisting of 32 sequences. They utilized two advanced multi-objective optimization algorithms: Unified Non-dominated Sorting Genetic Algorithm III (U-NSGA-III) and Q-Noisy Expected Hypervolume Improvement, for designing sequence-ordered polymers that not only exhibit high thermal conductivity but also possess feasible synthetic potential.⁵³

When researchers intend to employ generative models in de novo polymer design, the initial step involves selecting a suitable model. However, at present, there is no work dedicated to assisting in the selection of generative models for hypothetical polymer structures. In contrast, numerous studies have been conducted to compare the performance of various models on small drug-like molecules, greatly aiding researchers in the field of drug discovery. One notable example of such a benchmarking platform is Molecular Sets (MOSES), which was developed to standardize the training and comparison of generative models for small molecules.²⁶ Zhang et al. conducted a benchmark study with a focus on functional groups and ring systems.⁵⁴ Weng et al. performed a benchmark specifically centered around biological properties.⁵⁵ Recently, Nigam et al. created a set of practical benchmark tasks called “Tartarus”, which relies on physical simulations of molecular systems to emulate real-world challenges in molecular design for materials, drugs, and chemical reactions.⁵⁶

Compared to small molecules, generating polymer structures involves unique complexities that demand specialized approaches and considerations. While small molecules are fully represented by their complete structures in SMILES, polymers typically consist of very large and intricate architectures. Consequently, the representation of polymers—particularly linear homopolymers—relies on identifying their repeating units and using wild cards (e.g., “*”) to denote polymerization points. On the surface, this strategy appears similar to describing small compounds. However, in practice, wild cards like “*” are not simply placeholders for arbitrary bonds. Rather, they capture specific chemical bonding patterns and the connectivity between repeating units. Therefore, models must handle the additional complexity introduced by these wild cards during the generation process. Treating “*” as a generic wild card can lead to inaccuracies in depicting polymer topologies and connectivity, resulting in invalid molecular design. As a result, conclusions drawn from studies on small molecules cannot be directly applied to the generation of hypothetical polymer structures. Therefore, there is a timely need to develop specific benchmarks and methodologies tailored to the unique challenges and requirements of the generative design of polymers.

In this study, we initially used three different polymer datasets: real polymers from PolyInfo,¹⁵ and hypothetical polyimides generated based on GDB-13 (ref. 17) and PubChem,^57,58 to train six different generative models – VAE, AAE, ORGAN, CharRNN, REINVENT, and GraphINVENT. These models were trained on each dataset and generated about 10 million hypothetical polymer structures. We then evaluated these hypothetical polymer structures using the fraction of valid polymer structures f_v, the fraction of unique polymer structures from a sample of 10 000 f_10k, the Nearest Neighbor Similarity (SNN), the Internal Diversity (IntDiv) metric, and the Fréchet ChemNet Distance (FCD). These five metrics are provided by the MOSES platform. Furthermore, the t-distributed Stochastic Neighbor Embedding (t-SNE) method was employed to visualize their chemical space distribution.

We further used reinforcement learning techniques, targeting the T_g, to train CharRNN, REINVENT, and GraphINVENT models to design hypothetical polymer structures with high T_g values. These three models are selected because of their outstanding performance based on the previous evaluation. All these models demonstrated success in generating hypothetical polymers with high T_g values after 1000-generation training. Overall, CharRNN provided us with the most favorable results. On the other hand, the effective hypothetical polymer structures generated by REINVENT show an outstanding distribution in the predicted values but have the lowest efficiency. The results of this study demonstrate the immense potential of generative models in the field of polymer informatics. They also provide valuable insights into the capabilities and limitations of various generative models within the realm of polymer science and engineering. This understanding is crucial for researchers when it comes to selecting the most appropriate generative model for their specific needs.

2 Results and discussion

2.1 Dataset and deep generative models

In this study, we focus on hypothetical linear homopolymer structures. Three datasets were employed, including real homopolymers manually collected from PolyInfo, hypothetical polyimides generated using small molecules (polycondensation between diamine and dianhydride/diisocyanate monomers) from PubChem, and GDB-13, as discussed in our previous study.²² The real polymer dataset includes approximately 13 000 homopolymer structures out of a total of 18 000 polymer structures, while generative models typically require more training data. For example, Polykovskiy et al. utilized approximately 4.5 million samples for their work on MOSES,²⁶ and Zhang et al. used around one million samples for their study.⁵⁴ Therefore, we also utilized two hypothetical polyimides datasets for this purpose. The hypothetical polyimides generated using small molecules from PubChem and GDB-13 include a large number of structures, from which we randomly selected approximately 10 million for model training. There are no shared polymer structures among the three datasets. None of the three datasets were subjected to any preprocessing or cleaning.

Besides the difference in the number of samples in these datasets, these three datasets also vary in molecular weight and the number of types of atoms. It's important to note that the molecular weight values mentioned refer specifically to the repeat unit molecular weight of the polymer. This distinction is crucial because the repeat units serve as the input for analysis and modeling in these studies.

Repeat units of real polymers from the PolyInfo database exhibit an average molecular weight of 443.7 and an average of 34.1 atoms per sample, encompassing 25 different types of atoms. In contrast, repeat units of hypothetical polyimides derived from PubChem show an average molecular weight of 530.4 and an average of 40.7 atoms, but with a limited variety of only 5 types of atoms. Repeat units of hypothetical polyimides created based on the GDB-13 have a higher average molecular weight of 645.8 and an average of 48.5 atoms per sample, featuring 18 different types of atoms. Tables S1–S3 in the ESI† provide a detailed count of each atom type present in these datasets. These factors could significantly impact the training and performance of generative models. Specifically, the average number of atoms directly affects the size of the strings and graphs used for network input, while the variety of atomic types influence the molecular design of polymers by using different deep generative models. Utilizing these three diverse datasets enable us to better explore how different generative models perform in polymer informatics. Polymer-Simplified Molecular Input Line Entry System (p-SMILES) strings are specialized string representations used to depict the chemical structures of polymers. These strings are instrumental in data-driven tasks related to polymer discovery, design, or prediction. The format of a p-SMILES string is based on the standard SMILES syntax as defined by OpenSMILES.⁵⁹ However, p-SMILES introduces a unique feature to represent polymers: it includes two stars ([*] or *) within the string. These stars signify the endpoints of the polymer's repeat unit (for linear homopolymers, there are two endpoints), effectively marking the boundaries of the repeating segment in the polymer chain.

At present, large-scale generative models like Generative Pre-Trained Transformers (GPT)⁶⁰ have attracted widespread attention, but their scale and cost may be daunting for some researchers, particularly those who only wish to obtain some candidates in polymer design research. In these cases, smaller-scale generative models are still a more practical and accessible option. At the same time, due to the inherent differences between polymers and small molecules, such as higher complexity, larger molecular weight, and the use of p-SMILES, not all techniques applicable for generative models of small molecules are suitable for the generation of polymer structures. For example, a structural representation method like SELFIES,⁶¹ specifically designed for small compound generation, cannot represent the repeat unit structures of polymers. Additionally, models like LatentGAN,⁶² developed for small compound generation tasks, are not capable of processing p-SMILES strings. In this study, as shown in Fig. 2, we selected the following six networks: VAE, AAE, ORGAN, CharRNN, REINVENT, and GraphINVENT, which are briefly discussed below.

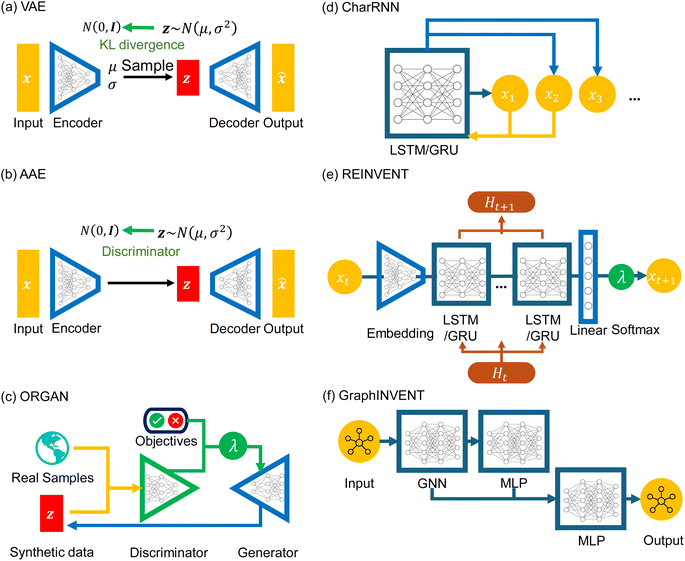Fig. 2 Architectures of six types of deep generative models: (a) VAE, (b) AAE, (c) ORGAN, (d) CharRNN, (e) REINVENT, and (f) GraphINVENT.

2.1.1 VAE. VAE is a class of machine learning models that focuses on data generation and latent space learning. As shown in Fig. 2(a), a VAE consists of two main components: the encoder and the decoder. The input encoder takes data x and maps it to a latent space representation, characterized by a distribution with mean μ and variance σ². The VAE imposes a regularization by encouraging the latent distribution to resemble a standard Gaussian distribution N(0,I), where I is the identity matrix. This is expressed in the objective function as the maximization of the similarity max sim(N(μ,σ²), N(0,I)), which typically involves minimizing the Kullback–Leibler (KL) divergence (D_KL) between the two distributions. From the latent space, a sample z is drawn and passed to the decoder, which attempts to reconstruct the original input, producing x̂. The training process involves minimizing D_KL and the reconstruction error, the loss function can be formulized as L = w_KLD_KL + ‖x̂ − x‖, making the decoded output as close as possible to the original input data. Our VAE model is implemented using the MOSES package and p-SMILES is used as input x and output x̂ representations.

2.1.2 AAE. AAE is a machine learning model that merges the concepts of Autoencoders (AE) and Generative Adversarial Networks (GANs). It can be observed from Fig. 2(b) that in the AAE framework, the input encoder receives raw data x and encodes it into a latent representation z. This latent representation is intended to follow a predefined probability distribution, typically a standard normal distribution. The AAE includes a discriminator, which distinguishes whether the latent representations z generated by the encoder follow the set distribution. The output z from the encoder is then passed to the decoder, whose task is to reconstruct the input x to produce x̂, with the goal of minimizing the reconstruction error min‖x̂ − x‖ and adversarial loss, which ensures the latent space distribution matches the target distribution. During training, the reconstructed output incrementally approaches the original input. We implement the AAE model using the MOSES package as well.

2.1.3 ORGAN. ORGAN is a variant of the traditional GAN that incorporates objective reinforcement for improved generation of complex data. In the ORGAN framework, the generator creates synthetic data (represented by z) which is intended to mimic real data samples. The discriminator, on the other hand, evaluates the synthetic data against real samples. Its goal is to distinguish between the two, effectively learning to tell apart genuine data from the imitations created by the generator. The twist in ORGAN compared to a standard GAN is the inclusion of a reinforcement signal, denoted by λ, which adjusts the generator's objectives beyond merely fooling the discriminator. The final reward function R can be expressed as a linear combination of the discriminator D and domain-specific objectives O: R = λD + (1 − λ)O.³⁴ The ORGAN is implemented with the MOSES package, chemical validity and uniqueness are used as rewards, with λ = 0.7 applied because this is the default value in MOSES.

2.1.4 CharRNN. CharRNN is a type of neural network specifically designed for sequence prediction problems. This architecture is particularly useful for handling tasks where the input and/or output is a sequence of characters, such as text generation or in this case, p-SMILES generation. As shown in Fig. 2(e), a CharRNN utilizes either Long Short-Term Memory (LSTM) or Gated Recurrent Unit (GRU) cells, both of which are variants of RNNs that are capable of learning long-term dependencies. The network depicted here processes the input sequence one character at a time (x₁, x₂, x₃, …), with each character being fed into the LSTM/GRU cell. These cells then produce an output sequence, where each output character is influenced by the previous characters in the sequence of p-SMILES. We use the MOSES package to implement the CharRNN.

2.1.5 REINVENT. REINVENT is a sequence-based generative model that utilizes reinforcement learning for the generation of novel chemical entities, such as drug molecules or polymers. At the beginning of the sequence generation, each token x_t of the encoded p-SMILES string is sequentially fed into an embedding layer, which transforms the discrete chemical symbols into continuous vectors. These vectors are then fed into a series of LSTM or GRU layers. Both LSTM and GRU are types of RNN cells capable of capturing long-term dependencies in sequential data. The recurrent cells process the input sequence, maintaining an internal state H_t that contains information about the sequence processed thus far. This state is updated with each new input symbol and is used to predict the next symbol in the sequence. After the LSTM/GRU layers, a linear layer followed by a softmax activation function produces a probability distribution over possible next symbols λ, from which the next symbol x_t+1 is sampled.²⁸ In this study, the embedding size is set to 256, the number of layers to 3, and each GRU layer has a size of 512.

2.1.6 GraphINVENT. In GraphINVENT, a graph is generated through a structured, step-by-step process that builds molecular structures by iteratively adding atoms (nodes) and bonds (edges). The process begins with an initial molecular fragment or monomer, which is an input into a Graph Neural Network (GNN). The GNN processes this initial structure, capturing essential features and relationships between nodes and edges within the molecular graph. After the GNN processes the input, its output is passed to a Multilayer Perceptron (MLP). This MLP interprets the extracted features and makes predictions about the next steps in the molecule's construction. It determines, based on these features, whether to add a new node (atom), connect existing nodes with an edge (bond), or terminate the graph generation. This iterative decision-making continues until the graph reaches a complete molecular structure. An additional parallel MLP layer may also be employed to process separate features or impose specific constraints, such as ensuring the chemical validity or optimizing certain molecular properties.^63,64

2.2 Evaluation metrics of deep generative models

Once each model was trained, 10 million hypothetical polymers were sampled from each trained model. To demonstrate their effectiveness, we carefully selected five crucial metrics from the MOSES platform to evaluate the performance of these generative models. These metrics include the fraction of valid polymer structures f_v, which measures the percentage of chemically valid structures generated by the model. The chemical validity of the hypothetical polymer structure is determined by using RDKit package and the count of *. The RDKit package attempts to convert the p-SMILES string into a molecular structure to check its validity, while also ensuring that [*] appears exactly twice for p-SMILES of linear homopolymers. We also considered the fraction of unique polymer structures from a sample of 10 000 f_10k, assessing the model's ability to generate diverse chemical structures.

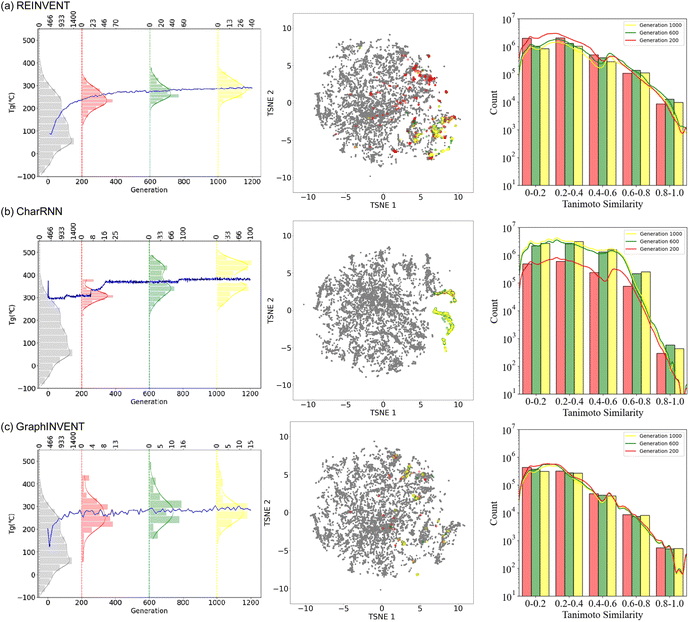
Additionally, the Nearest Neighbor Similarity (SNN) was used to calculate the average similarity of the generated polymers to the closest polymer in the test set, providing an insight into how the generated polymers compared to known structures. SNN represents the average Tanimoto similarity T(m_X, m_Y). This similarity is calculated between the fingerprints of a polymer m_X in the generated set X and its closest neighboring polymer m_Y in the reference dataset Y:

where n_mX is the count of bits “on” in polymer m_X's fingerprint but not in polymer m_Y's fingerprint, n_mY is the count of bits “on” in polymer m_Y's fingerprint but not in polymer m_X's fingerprint, and n_mX&mY is the count of bits “on” both in polymer m_X's fingerprint and in polymer m_Y's fingerprint.

The Internal Diversity (IntDiv) metric, representing the average pairwise similarity among generated polymers, was included to gauge the diversity within the generated polymer structures.⁶⁵ IntDiv assesses the chemical diversity within the generated set of polymers X:

where p = 1 is used in this study.

Lastly, the Fréchet ChemNet Distance (FCD) was employed to quantify the difference in the distribution of the last layer activations of ChemNet,⁶⁶ which is trained to predict bioactivities of about 6000 assays available in three major drug discovery databases (ChEMBL,⁶⁷ ZINC,⁶⁸ PubChem⁵⁷), effectively measuring the disparity between the generated polymer distribution and a reference set.⁶⁹ For two sets of polymers dataset X and dataset Y, FCD is defined as

where μ_X, μ_Y are mean vectors and Σ_X, Σ_Y are full covariance matrices of activations for polymers from sets X and Y, respectively. The reference dataset Y for SNN and FCD calculation is the test set from the training process.

After all, both t-SNE and Tanimoto similarity metrics were employed to assist in comparing differences between various polymer structures. t-SNE, a widely used technique for nonlinear dimensionality reduction and data visualization, effectively maintains nonlinear similarities between data points. It operates by initially determining the similarity between high-dimensional data points using a Gaussian distribution. Subsequently, it assesses the similarity among data points in a reduced, low-dimensional space based on a t-distribution. The goal of t-SNE is to minimize the disparity between these high-dimensional and low-dimensional similarities. These selected metrics will be employed in the initial phase of comparison to sieve out the generative models that demonstrate superior performance.

2.3 Performance and coverage of generative models

Fig. 3 shows the performance of the six generative models when applied to the real polymer dataset from PolyInfo. In terms of f_v, the CharRNN model achieved the highest result, nearly reaching 0.9. Both the GraphINVENT and REINVENT models achieved greater than 0.5. However, the VAE, AAE, and ORGAN models obtained notably lower scores. These outcomes indicate a comparatively lower effectiveness of these models in generating valid polymer structures (or p-SMILES) compared to other models. For the metric f_10k, AAE, ORGAN, REINVENT, and VAE exhibit good performance, with scores around 0.8. CharRNN and GraphINVENT, while not performing as well as the aforementioned models, still achieve results greater than 0.5, which is considered acceptable.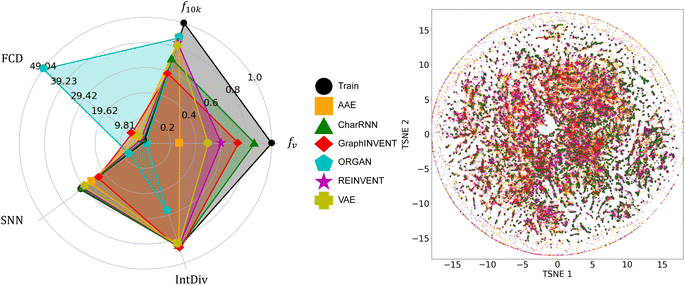

Fig. 3 A comparison of the performance of the six generative models on the real homopolymer dataset collected from the PolyInfo, as well as the chemical space distribution of the generated polymers.

In evaluating the performance of generative models using the SNN and IntDiv metrics, higher values are generally sought after. These metrics provide insights into the models' ability to generate both diverse and chemically relevant polymer structures. It can be observed that all models, except for ORGAN, exhibit results that closely resemble those in the training set.

For the FCD metric, lower values are generally preferred. This metric measures the difference in distributions between the generated polymers and a reference set, with a lower score indicating that the generated polymers are more chemically similar to real polymers. The observations indicate that, similar to the SNN metric, VAE, REINVENT, and CharRNN achieved relatively low FCD scores. AAE and GraphINVENT obtained higher scores, while ORGAN exhibited a significantly higher FCD score.

Considering all the metrics collectively, it appears that CharRNN, REINVENT, and GraphINVENT deliver the best performance, while AAE and VAE follow behind. However, ORGAN's performance leaves much to be desired. This result bears similarity to previous benchmark work based on small molecules. In MOSES, Polykovskiy et al. found that among a wide array of models, CharRNN currently outperforms others in terms of these key metrics.²⁶ In RediscMol, Weng et al. observed that CharRNN, VAE, and REINVENT yield superior results, followed by AAE and ORGAN.⁵⁵ Additionally, in studies considering ring system coverage and functional group coverage, AAE, REINVENT, VAE, CharRNN, and GraphINVENT all exhibit better performance compared to ORGAN.⁵⁴

CharRNN consistently shows remarkable results in these benchmark studies, while the performance of AAE and VAE tends to be less impressive in our result. This could be attributed to the fact that the PolyInfo dataset is significantly smaller than datasets for small molecules. Additionally, the structural differences between real polymers and small molecules also play a role. The ZINC Clean Leads⁷⁰ used in the MOSES project have molecular weights ranging from 250 to 350 Daltons.²⁶ However, the molecular weight (of the repeat unit) in the real polymer dataset varies widely, ranging from 14 to 2202 dalton. This variation is due to the presence of polymers with complex structures as well as those with very simple repeat units. For example, polyethylene, the simplest polymer, has a p-SMILES representation of just ‘*C*’. The t-SNE visualization further corroborates the analysis derived from these metrics, providing a graphical representation of how well each model captures the chemical space of polymers. The individual t-SNE results for each model can be found in the ESI† for better visual comparison.

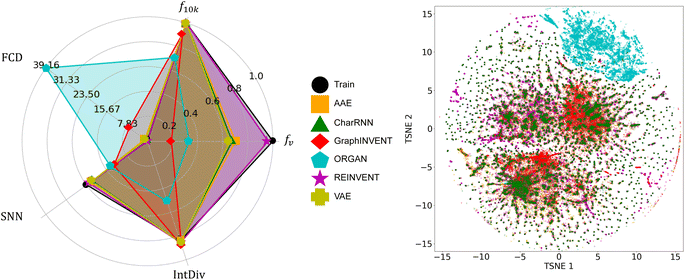
Fig. 4 presents the performance of six different generative networks when applied to the hypothetical polyimide dataset based on GDB-13. For f_v, the REINVENT model achieved the highest result, nearly equal to 1. In comparison, the AAE, VAE, and CharRNN models show a similar performance level, with their values clustered around 0.7. On the other hand, the ORGAN and GraphINVENT models have considerably lower scores, below 0.2.

Fig. 4 A comparison of the performance of the six generative models on the hypothetical polyimide dataset synthesized based on GDB-13, as well as the chemical space distribution of the generated polymers.

In f_10k part, several models exhibited impressive results. REINVENT, AAE, VAE, and CharRNN all achieved a result of 1. It indicates an excellent ability of these models to generate a diverse set of polymer structures, with no duplicates in a sample of 10 000 p-SMILES strings. GraphINVENT, while not reaching a perfect score, still performed commendably, with its value being close to 0.9. However, ORGAN scored below 0.7, indicating less diversity in its generated polymer structures.

For the SNN metric, it was observed that, apart from ORGAN and GraphINVENT, the other four models showed similar performance. Regarding IntDiv, all models except for ORGAN exhibited closely matched performances. These observations suggest that REINVENT, AAE, VAE, CharRNN, and GraphINVENT are capable of producing a wide variety of polymer structures, demonstrating a good internal diversity among the generated hypothetical polymers.

Observations show that, similar to the SNN metric, the models AAE, VAE, REINVENT, and CharRNN achieved relatively low FCD scores. GraphINVENT recorded a somewhat higher FCD score, indicating less chemical similarity between its generated structures and the training dataset. ORGAN exhibited a significantly higher FCD score, implying a larger disparity between its generated structures and the real-world polymers.

Fig. 5 denotes the performance of the same six generative models when applied to the hypothetical polyimide dataset derived from PubChem. It is observed that the performance and comparative results of these six models are almost consistent with those outcomes from training on the hypothetical polyimide based on GDB-13, which means the REINVENT model demonstrated the best performance. However, the performance of the ORGAN model was notably worse, to the point of being considered unacceptable for the task at hand. The specific scores for all these models and datasets are provided in ESI Tables S6–S8.†

Fig. 5 A comparison of the performance of the six generative models on the hypothetical polyimide dataset synthesized based on PubChem, as well as the chemical space distribution of the generated polymers.

Table 1 summarizes the performance of six models under various challenges. All the above results show that the REINVENT model shows the most favorable performance. The AAE, CharRNN, and VAE models follow closely, while GraphINVENT and ORGAN demonstrate a much worse performance. It should be noted that the performance of these six generative models varies across the three datasets, which is related to the characteristics of each dataset. Compared to the real polymer dataset, PolyInfo, the AAE and VAE show significant improvement on the hypothetical polyimide datasets. Despite the larger average atom count per repeat unit in these hypothetical datasets, which implies more complex molecular structures and longer SMILES strings, this improvement suggests that these models require a substantial amount of training data to achieve high-quality generative performance. With abundant data, they can learn more robust latent representations. Additionally, models based on variational techniques perform better on datasets derived from PubChem, which generally have simpler atomic types and lower diversity. These models excel in scenarios with limited atom types, as they likely rely more on capturing global molecular features and latent representations, which can be challenging to learn in datasets with high atomic diversity.

Table 1 Comparison of six generative models across different molecular design scenarios. The number of stars indicates the effectiveness of the model, with more stars signifying better performance. “Low data volume” corresponds to the PolyInfo dataset, “high atomic count” corresponds to two hypothetical polyimide datasets, and “complex types of atoms” corresponds to a hypothetical polyimide dataset synthesized based on GDB-13

Models	Low data volume	High atomic count	Complex types of atoms
AAE	★	★★	★★
CharRNN	★★★	★★★	★★
GraphINVENT	★★★	★	★
ORGAN	★	★	★
REINVENT	★★	★★★	★★★
VAE	★	★★	★★

---

GraphINVENT performs better on the real polymer dataset compared to the other two datasets. This is likely due to the real polymer dataset having a smaller average molecular weight and number of atoms, resulting in smaller and simpler graph data structures. GraphINVENT, which rely on GNNs, are inherently well-suited to handle molecular structures directly as graphs. This gives GraphINVENT an advantage on datasets with simpler graph structures, such as the real polymer dataset, where molecular weights and atomic counts are lower. However, GNN-based models may encounter challenges when dealing with larger or more complex structures, as the molecular graph data scale of the repeat unit increases significantly with the number of atoms it contains. This is also related to the network's parameter settings. For datasets with larger molecular weights, using a larger k-hop neighbor size may improve the network's performance.

As for the two RNN-based generative networks, REINVENT demonstrates outstanding performance on both hypothetical polyimide datasets, proving its ability to handle such tasks when sufficient data is available. CharRNN, however, shows weaker performance on the polyimide dataset based on GDB-13 compared to the other two datasets. RNN-based models process molecules as continuous SMILES strings. When the average number of molecules in the dataset increases, this often results in longer string lengths, and when the diversity of molecular types increases, it means a greater variety of characters in the string. Both of these factors increase the complexity of the task. The polyimide dataset based on GDB-13 has the largest number of atom types and atomic counts, making it the most challenging task for RNN-based models. This explains the performance drop of CharRNN on this dataset, while REINVENT's results demonstrate the effectiveness of its design, which first transforms discrete chemical symbols into continuous vectors before processing them through a series of LSTM or GRU layers.

ORGAN demonstrates weaker performance across most datasets, possibly due to challenges in balancing the generative adversarial training process. GANs are known to be sensitive to training stability, especially with complex and diverse data. ORGAN may be overfitting or struggling to maintain a stable learning process, particularly on the datasets with more atomic diversity or larger molecular sizes.

We also observed that these findings align closely with the results of work of Zhang et al., particularly in their results regarding ring system coverage. In their study, they utilized the GDB-13 dataset as a training set, which happens to be one of the sources we used to generate hypothetical polyimides for our research.⁵⁴

In addition to p-SMILES notation for polymers, new methods for representing polymer structures have been developed as related research progresses. One example is BigSMILES notation, which provides a more robust approach for describing polymeric systems.^71–77 BigSMILES is particularly advantageous for describing network polymer systems, which are challenging for p-SMILES to capture comprehensively. Therefore, we performed benchmark tests on five models—AAE, VAE, ORGAN, CharRNN, and REINVENT—using BigSMILES on a real polymer dataset. The results indicate that using BigSMILES with the ORGAN and AAE models leads to improved outcomes, suggesting that BigSMILES may be more suitable for models that incorporate a discriminator. However, performance declined with the REINVENT and CharRNN models, likely due to the increased complexity of the character set in BigSMILES. Detailed results can be found in ESI Material Table S9.† Since this work primarily focuses on linear homopolymers, BigSMILES does not fully demonstrate its advantages here.

2.4 Deep generative design with reinforcement learning

The introduction of reinforcement learning algorithms empowers generative models with the capability to design hypothetical polymer structures possessing specific properties. This method represents a transformative step towards more efficient and purpose-driven material discovery and design. Fig. 6 illustrates the fundamental architecture of reinforcement learning as applied to these generative models. In this framework, the agent, which is the generative model, initiates the process by generating a set of candidate polymer structures. The evaluation of these candidates follows a specific scoring mechanism.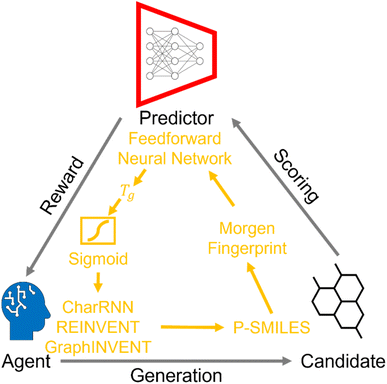

Fig. 6 The core framework of reinforcement learning with deep generative model, and the specific data flow utilized in this study.

Firstly, the generated p-SMILES strings are converted into 1024-bit Morgan Fingerprint (MF). These MFs are then used as input to a Feed-Forward Neural Network (FNN), which is tasked with predicting the T_g values of these candidates. Detailed information about the FNN is available in the ESI.† After obtaining the T_g predictions, a sigmoid function is applied to these values. The output of this sigmoid function is treated as the reward, which is fed back to the agent. The feedback received in the form of rewards is then used by the agent to further train and optimize its performance. Specifically, the reward informs the agent's policy updates, encouraging it to generate structures that yield higher T_g values, thereby refining its sampling strategy over successive iterations (ESI Fig. S6†).

According to the previous results, particularly the comparison of generative models trained on the PolyInfo dataset, we selected REINVENT, CharRNN, and GraphINVENT as our models of choice for generative design of new polymers. Employing reinforcement learning, we used PolyInfo as the training dataset with the goal of training these models to generate hypothetical polymer structures that exhibit high T_g values.

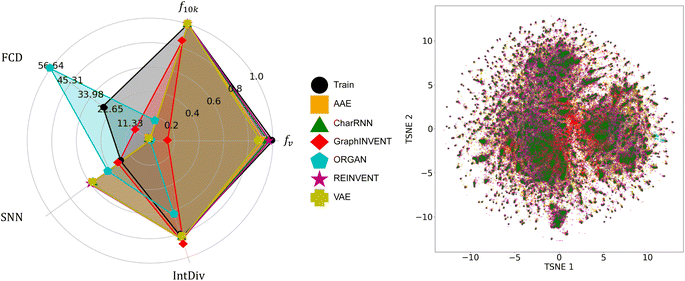
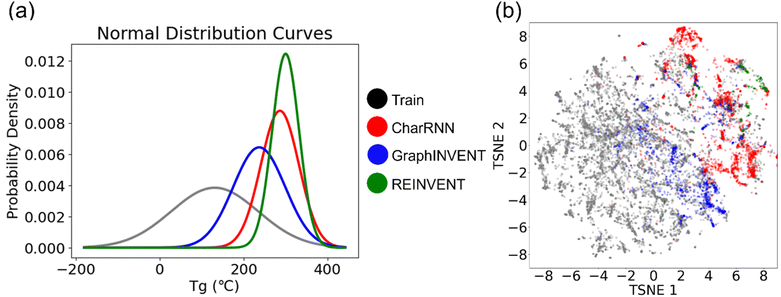
Fig. 7 presents the performance of these three models undergoing reinforcement learning. The leftmost part of the figure shows the change in the predicted average T_g of the generated hypothetical polymer structures across training generations, along with the predicted T_g distribution of polymers generated at the 200th, 600th, and 1000th training steps as well as the training set (0th step). As training iterations increased, it was observed that the predicted T_g values of the hypothetical polymer structures generated by all three generative models showed an upward trend. Notably, CharRNN achieved the highest average predicted T_g value at the 1000th step, while REINVENT and GraphINVENT exhibited similar performance. Additionally, the distribution of the predicted T_g values for all generated hypothetical polymers shifted towards higher values. This outcome demonstrates the capability of reinforcement learning to effectively steer the generative process towards specific target properties, in this case, achieving higher T_g in the hypothetical polymer structures.

Fig. 7 Performance of three generative models, (a) REINVENT, (b) CharRNN, and (c) GraphINVENT, combined with reinforcement learning. (Left) Depiction of how the predicted average T_g of the generated hypothetical polymer structures evolves over various training generations. This includes a detailed view of the T_g distributions for structures produced at the 200th, 600th, and 1000th training steps, as well as those in the training set. (Middle) The central t-SNE plot visualizes the chemical space: the area covered by the training set is shown in grey, while the red, green, and yellow points represent the chemical spaces for structures generated at the 200th, 600th, and 1000th steps, respectively. (Right) The graphs displaying the Tanimoto similarity between the hypothetical polymer structures generated at the 200th, 600th, and 1000th steps and the training set provide critical insights into the dynamics of the training process.

In the middle of Fig. 7, t-SNE plot, illustrates the area covered by the training set in grey. The red, green, and yellow points represent the chemical spaces of structures generated at the 200th, 600th, and 1000th steps, respectively. The chemical space of polymer structures generated over training epochs ranging from 0 to 1200 are detailed in ESI Fig. S7.† This color gradient visually represents the evolution of the generated polymers' chemical space throughout the reinforcement learning process.

For REINVENT and GraphINVENT, it was observed that the chemical space of the newly generated polymers remained within the bounds of the chemical space covered by the original training set. As training progressed, there was a noticeable shift from larger purple-red regions to smaller, more concentrated yellow areas. Similar to REINVENT and GraphINVENT, the CharRNN model also exhibited a gradual concentration of the chemical space of the generated polymer structures during the training process. However, a distinct behavior was observed in CharRNN's approach. Unlike the other two generative models, CharRNN began within the chemical space covered by the original training set and progressively expanded its search into chemical spaces beyond what was covered in the training set. As a result, the hypothetical polymers generated by CharRNN occupied a much larger area in the chemical space.

The right panel of Fig. 7 illustrates the Tanimoto similarity between the hypothetical polymer structures generated at the 200th, 600th, and 1000th training steps and the training set, reveals an important aspect of the training process. This observation suggests that, as the models are trained, the generated polymer structures maintain a certain level of structural resemblance to those found in the initial training set. The absence of a convergence towards zero in the Tanimoto similarity indicates that the models are not diverging significantly from the structural characteristics of real polymers.

This pattern suggests that as the number of training epochs increased, both REINVENT and GraphINVENT models started to focus on generating polymer structures within specific, more defined regions of the chemical space (exploitation). This convergence towards certain areas within the training set's chemical space could indicate that the models are focusing on regions that are more likely to yield polymers with the desired high T_g values. This demonstrates that reinforcement learning strategies are effectively guiding generative models in exploring the polymer chemical space.

Meanwhile, it was observed that the results from the REINVENT and GraphINVENT models remained within the chemical space defined by the training dataset, while CharRNN showed an expansion beyond the initial training set boundaries (exploration). It's important to note that the different chemical space distributions observed do not affect the similarity of the generated hypothetical polymer structures to the training set. This is because the hypothetical polymer structures generated by the CharRNN, REINVENT, and GraphINVENT models exhibit a Tanimoto similarity that is essentially consistent with each other. The REINVENT and GraphINVENT models are particularly adept at controlling the generated structures within the confines of the training set, making them suitable choices for researchers who desire such candidates. As for CharRNN, the expansion beyond the initial training set boundaries suggests that it was exploring more novel regions of the chemical space, potentially leading to the discovery of new polymer structures with higher T_g values. This exploration outside the known chemical space is a key factor in why CharRNN's generated hypothetical polymers had overall higher mean predicted T_g values during the training.

However, as previously discussed, the limited number of polymer structures in the real polymer dataset can lead to decreased effectiveness. Ma et al. utilized RNNs and a reinforcement learning algorithm to generate hypothetical polymer structures with high thermal conductivity. They used a significantly larger training dataset (PI1M), consisting of 1 million samples, which far exceeds the size of the real polymer dataset.¹⁸ A larger dataset provides more comprehensive coverage of the chemical space in their study, allowing models to learn a wider range of patterns and features. This can lead to the generation of more unique and diverse polymer structures, enhancing the potential for discovering novel materials with desirable properties. In their study, the visualization of generated polymers alongside real polymers from PolyInfo using t-SNE showed a pattern similar to that of CharRNN's results here. The newly generated molecules show an expansion beyond the initial boundaries of the training set, indicating exploration into new areas of the chemical space. Additionally, Moret et al. have demonstrated the generation of novel small molecules with bespoke properties and structural diversity using an RNN. The chemical space explored in their research exhibits a pattern similar to what we have observed in other studies, highlighting the RNN's capability to navigate and innovate within the chemical space.⁷⁸

Furthermore, graph-based generative networks for polymers, such as PolyG2G, have also exhibited outstanding performance.⁴⁸ Instead of using reinforcement learning, their network employed a latent space-searching strategy to generate hypothetical polymers with desired properties. The same concept of latent space utilization is also evident in VAEs based on the inclusion of a latent space in these models' architecture.^49,52 Similarly, Liu et al. utilized a graph-based invertible molecular generative model along with a latent space strategy for the design of high-temperature polymer dielectrics.⁵⁰ Observations of these two graph-based generated models employing latent space strategies reveal that the main frameworks of the generated repeat units often bear resemblance to certain structures within the training set. This similarity might be a contributing factor to the close alignment of the chemical space of the generated hypothetical polymers with that of the training set.

The size of the training dataset also significantly impacts the efficiency and uniqueness of the hypothetical polymer structures generated by these models, both of which are critical factors for practical applications. Fig. 8 illustrates the comparison of these two metrics – the efficiency and non-redundancy rates – for the three networks at the 200th, 600th, and 1000th steps, as well as their overall trends throughout the training process.

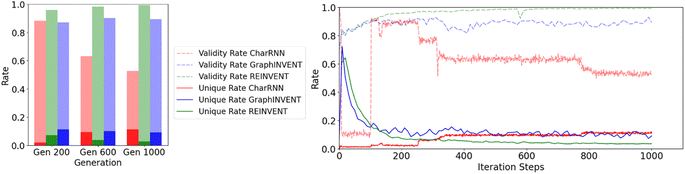Fig. 8 Effect of iteration steps on the validity and redundancy rates of three generative models, CharRNN, GraphINVENT, and REINVENT, during the reinforcement learning process.

Then the 1,000th-training-iteration models are used for 100 000 hypothetical polymers generation. Fig. 9(a) displays the normalized probability density distribution of predicted T_g values of these hypothetical valid unique polymers. When the models are employed to generate a large number of hypothetical polymer structures, there is a slight shift in the mean prediction values. It is evident that the probability distributions of the three generative models are significantly different from the training set, favoring higher T_g values. Generative models based on RNN and GNN architectures have been effectively used to directly create hypothetical polymer structures with desired properties, achieving commendable results. Among them, REINVENT has the highest mean and the smallest variance in its probability density distribution, indicating that it can more stably generate many high T_g hypothetical polymer structures. CharRNN and GraphINVENT are less effective in comparison. However, it is important to note, as shown in Fig. 8, that the unique rate and validity rate of REINVENT model are relatively low. In contrast, CharRNN is considered as the best option.

Fig. 9 (a) Normalized probability density distribution of predicted T_g values (at 1000th training step) and the (b) chemical space distribution of the hypothetical valid unique polymers generated by CharRNN (red), GraphINVENT (blue), REINVENT (green), and the real polymers (grey).

Fig. 9(b) showcases the chemical space distribution of these hypothetical, valid, and unique polymers. The results align with those presented in Fig. 7, showing that among the three generative models, CharRNN generates hypothetical polymers (red points) that are the most distinct from real polymers (grey points) in terms of distance. In contrast, the polymers generated by the other two models are interspersed within the distribution of real polymers.

From these results, it is evident that CharRNN demonstrates a distinct advantage in both efficiency and uniqueness. This superiority is likely connected to its broader exploration of the polymer chemical space. As previously discussed in comparisons and discussions of various generative models, CharRNN has shown the best performance with real polymers collected from PolyInfo and a variety of small molecule tests. While REINVENT exhibits the best normalized probability density distribution, its unique rate should be considered. Hence, REINVENT becomes the optimal choice specifically when there is a requirement to generate a substantial volume of candidates, ranging from hundreds to thousands.

3 Concluding remarks

This study conducts a comprehensive evaluation of generative models within the context of polymer informatics, highlighting both their potential and limitations. Initially, six generative models – AAE, VAE, CharRNN, REINVENT, GraphINVENT, and ORGAN – were tested and trained using datasets of hypothetical polyimides based on PubChem and GDB-13, as well as real polymer datasets collected from PolyInfo. The performance of these generative models was assessed using various metrics: the fraction of valid structures, the fraction of unique structures from a sample of 10 000, SNN, IntDiv, and FCD. It was observed that CharRNN, REINVENT, and GraphINVENT produced superior results when trained with the PolyInfo dataset. Meanwhile, REINVENT demonstrated outstanding performance when trained with the two hypothetical polyimide datasets, with AAE, VAE, and CharRNN also showing commendable outcomes. This difference in performance may be attributed to the more complex structures and larger molecular weights of hypothetical polyimides.

Subsequently, CharRNN, REINVENT, and GraphINVENT were combined with reinforcement learning algorithms using the PolyInfo dataset to generate hypothetical polymer structures with higher T_g values. All three models performed impressively, but with notable differences in their capabilities. CharRNN displayed a unique ability to extend beyond the chemical space of the training set, generating polymers with higher predicted T_g values. After training, REINVENT demonstrates the most outstanding probability distribution in its generated results. However, compared to CharRNN and GraphINVENT, it has a lower unique rate and valid outcomes.

The study underscores the need for specific benchmarks and methodologies tailored to the unique challenges of polymer design. The integration of reinforcement learning proved effective in guiding the generative process toward the desired properties, highlighting the potential of these models in future materials design and discovery. This work also leverages the power of computational modeling and machine learning, paving the way for more targeted and efficient development of new polymeric materials, such as organic photovoltaics, polymer membranes, and dielectrics.

4 Experimental procedures

4.1 Model training

For the PolyInfo dataset, approximately 11 000 homopolymers were randomly selected to constitute the training set, while around 1200 were designated as the test set. Regarding the other two hypothetical polyimide datasets based on PubChem and GDB-13, a subset of 0.8 million polyimides was randomly chosen and utilized as the training set for all the generative models. Furthermore, two additional sets of 0.2 million polyimides were specifically selected to serve as the validation sets. For the implementation of REINVENT and GraphINVENT in this study, the hyperparameters were directly sourced from their respective GitHub repositories. The code of REINVENT model (version 2eeca2d73e197943bc7f704022d30eee14c49cb6) is available at https://github.com/undeadpixel/reinvent-randomized/tree/2eeca2d73e197943bc7f704022d30eee14c49cb6, and the code of GraphINVENT model (version 6ef587ddb983f0c853dc8bc7b418f43cb69420c9) is available at https://github.com/MolecularAI/GraphINVENT/tree/6ef587ddb983f0c853dc8bc7b418f43cb69420c9. In the case of CharRNN, AAE, VAE, and ORGAN, the hyperparameters were adopted from the models' configuration files available in the MOSES GitHub repository (version dd7ed6ab38e23afd3ef5371d67939a1760bd8599): https://github.com/molecularsets/moses/tree/dd7ed6ab38e23afd3ef5371d67939a1760bd8599. All details of the model parameters are provided in the ESI† titled “Details of model parameters.”

The CharRNN model integrated with reinforcement learning was utilized, with its code accessible at the GitHub repository (version b112b811616bee01fb3348e867b7406e4e6a62f4): https://github.com/aspuru-guzik-group/Tartarus/tree/b112b811616bee01fb3348e867b7406e4e6a62f4. The REINVENT model (version 99b8f28c2a76196017eabf23118195ae546f5714), incorporating reinforcement learning, was employed, with its code available at https://github.com/MolecularAI/Reinvent/tree/99b8f28c2a76196017eabf23118195ae546f5714. The GraphINVENT model, integrated with reinforcement learning (version 99b8f28c2a76196017eabf23118195ae546f5714), was utilized in this study. Its code is accessible at https://github.com/olsson-group/RL-GraphINVENT/tree/d4629a3c411c793e1ed1682592d5bf67937564a1. This ongoing process of generation, evaluation, and feedback allows the generative models to progressively improve in its ability to design hypothetical polymer structures that closely match the targeted properties, thus enhancing the efficiency and effectiveness of the materials design process.

4.2 Technical details

The training of generative models from the MOSES platform was conducted using the Docker container “molecular sets/moses”. This training took place on Linux workstations equipped with NVIDIA Quadro RTX 8000 graphics cards, utilizing CUDA 12.1 for computational acceleration. For the GraphINVENT model, the training environment comprised Python 3.6.8 and PyTorch 1.3.1. This model was also trained on Linux workstations, but with NVIDIA Quadro P6000 graphics cards, again leveraging CUDA 12.1 for enhanced processing capabilities. Regarding the REINVENT model, it was trained using Python 3.7.7 and PyTorch 1.7.0. This model's training was performed on Linux workstations equipped with NVIDIA RTX A6000 graphics cards, utilizing the same 12.1 version of CUDA, 12.1, for computational support.

Code availability

The code of this work is available at https://github.com/ytl0410/Polymer-Generative-Models-Benchmark/tree/ccc047eac7e0ec1d298a7142331d7f271f300a63.

Data availability

The real homopolymers dataset used in this study for generative models training can be found at: https://github.com/ytl0410/Polymer-Generative-Models-Benchmark/tree/34f57dc1d87a6828c2c02ecbb0463e924df43fa1/MOSES. The hypothetical polyimides datasets used in this study for generative models training can be found at: https://zenodo.org/records/13821449. The code of this work is available at https://github.com/ytl0410/Polymer-Generative-Models-Benchmark/tree/ccc047eac7e0ec1d298a7142331d7f271f300a63 (DOI: https://doi.org/10.5281/zenodo.14735412). The code of CharRNN, AAE, VAE, and ORGAN models is available at https://github.com/molecularsets/moses/tree/dd7ed6ab38e23afd3ef5371d67939a1760bd8599. The code of REINVENT model is available at https://github.com/undeadpixel/reinvent-randomized/tree/2eeca2d73e197943bc7f704022d30eee14c49cb6. The code of GraphINVENT model is available at https://github.com/MolecularAI/GraphINVENT/tree/6ef587ddb983f0c853dc8bc7b418f43cb69420c9. The code of the CharRNN model integrated with reinforcement learning is available at https://github.com/aspuru-guzik-group/Tartarus/tree/b112b811616bee01fb3348e867b7406e4e6a62f4. The code of the REINVENT model integrated with reinforcement learning is available at https://github.com/MolecularAI/Reinvent/tree/99b8f28c2a76196017eabf23118195ae546f5714. The code of GraphINVENT model, integrated with reinforcement learning is accessible at https://github.com/olsson-group/RL-GraphINVENT/tree/d4629a3c411c793e1ed1682592d5bf67937564a1. The trained models in this work can be found at https://github.com/ytl0410/Polymer-Generative-Models-Benchmark/tree/ccc047eac7e0ec1d298a7142331d7f271f300a63 (DOI: https://doi.org/10.5281/zenodo.14735412) and https://zenodo.org/records/12734266 (only for GraphINVENT, DOI: https://doi.org/10.5281/zenodo.12734266). All generation results can be found at https://zenodo.org/records/12636925 (DOI: https://doi.org/10.5281/zenodo.12636925), and the generation results for reinforcement learning can be accessed at https://zenodo.org/records/12728016 (DOI: https://doi.org/10.5281/zenodo.12728016). This study was carried out using publicly available data from GDB-13 at https://gdb.unibe.ch/downloads/, as well as PubChem at https://pubchem.ncbi.nlm.nih.gov/.

Author contributions

Conceptualization, Y. L. and V. V.; methodology, T. Y., L. T., and Y. L.; software T. Y., L. T.; validation, T. Y.; formal analysis, T. Y., Y. L.; investigation, T. Y., Y. L.; resources, Y. L.; data curation, T. Y., L. T.; writing—original draft, T. Y.; writing—review & editing, T. Y., V. V., and Y. L.; visualization, T. Y., L. T.; supervision, Y. L.; funding acquisition, Y. L.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

We gratefully acknowledge financial support from the Air Force Office of Scientific Research through the Air Force's Young Investigator Research Program (FA9550-20-1-0183; Program Manager: Dr Ming-Jen Pan and Capt Derek Barbee), Air Force Research Laboratory/UES Inc. (FA8650-20-S-5008, PICASSO program), and the National Science Foundation (CMMI-2314424, CMMI-2316200, and CAREER-2323108). Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the U.S. Department of Defense or the National Science Foundation. The authors also acknowledge the National Renewable Energy Laboratory for providing HPC resources that have contributed to the research results reported within this paper. Support for this research was also provided by the University of Wisconsin–Madison, Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation.

References

1. G. Li, R. Zhu and Y. Yang, Polymer solar cells, Nat. Photonics, 2012, 6(3), 153–161.
2. R. Hsissou, R. Seghiri, Z. Benzekri, M. Hilali, M. Rafik and A. Elharfi, Polymer composite materials: A comprehensive review, Compos. Struct., 2021, 262, 113640.
3. S. Diaham, Polyimide in electronics: Applications and processability overview, Polyimide for Electronic and Electrical Engineering Applications, 2021, 2020–2021.
4. I. Gouzman, E. Grossman, R. Verker, N. Atar, A. Bolker and N. Eliaz, Advances in polyimide-based materials for space applications, Adv. Mater., 2019, 31(18), 1807738.
5. A. Anstey, E. Chang, E. S. Kim, A. Rizvi, A. R. Kakroodi, C. B. Park and P. C. Lee, Nanofibrillated polymer systems: Design, application, and current state of the art, Prog. Polym. Sci., 2021, 113, 101346.
6. R. Wang, Y. Zhu, J. Fu, M. Yang, Z. Ran, J. Li, M. Li, J. Hu, J. He and Q. Li, Designing tailored combinations of structural units in polymer dielectrics for high-temperature capacitive energy storage, Nat. Commun., 2023, 14(1), 2406.
7. S. Wu, Y. Kondo, M.-a. Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. Xu and J. Shiomi, et al., Machine-learning-assisted discovery of polymers with high thermal conductivity using a molecular design algorithm, npj Comput. Mater., 2019, 5(1), 66,  DOI:10.1038/s41524-019-0203-2.
8. T. Yue, J. He, L. Tao and Y. Li, High-Throughput Screening and Prediction of High Modulus of Resilience Polymers Using Explainable Machine Learning, J. Chem. Theory Comput., 2023, 19(14), 4641–4653.
9. Z. P. Zhang, M. Z. Rong and M. Q. Zhang, Polymer engineering based on reversible covalent chemistry: A promising innovative pathway towards new materials and new functionalities, Prog. Polym. Sci., 2018, 80, 39–93.
10. J. Chen, Y. Zhou, X. Huang, C. Yu, D. Han, A. Wang, Y. Zhu, K. Shi, Q. Kang and P. Li, Ladderphane copolymers for high-temperature capacitive energy storage, Nature, 2023, 615(7950), 62–66.
11. J. Dong, L. Li, P. Qiu, Y. Pan, Y. Niu, L. Sun, Z. Pan, Y. Liu, L. Tan and X. Xu, Scalable Polyimide-Organosilicate Hybrid Films for High-Temperature Capacitive Energy Storage, Adv. Mater., 2023, 35(20), 2211487.
12. Y. Zhang, J. Zhang, K. Suzuki, M. Sumita, K. Terayama, J. Li, Z. Mao, K. Tsuda and Y. Suzuki, Discovery of polymer electret material via de novo molecule generation and functional group enrichment analysis, Appl. Phys. Lett., 2021, 118(22), 223904.
13. X. Yin, T. Wan, X. Deng, Y. Xie, C. Gao, C. Zhong, Z. Xu, C. Pan, G. Chen and W.-Y. Wong, De novo design of polymers embedded with platinum acetylides towards n-type organic thermoelectrics, Chem. Eng. J., 2021, 405, 126692.
14. D. Mei, L. Yan, X. Liu, L. Zhao, S. Wang, H. Tian, J. Ding and L. Wang, De novo design of single white-emitting polymers based on one chromophore with multi-excited states, Chem. Eng. J., 2022, 446, 137004.
15. S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu, and M. Yamazaki, PoLyInfo: Polymer database for polymeric materials design, in 2011 International Conference on Emerging Intelligent Data and Web Technologies, IEEE, 2011, pp 22–29.
16. S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen and B. Yu, PubChem 2023 update, Nucleic Acids Res., 2023, 51(D1), D1373–D1380.
17. L. C. Blum and J.-L. Reymond, 970 million druglike small molecules for virtual screening in the chemical universe database GDB-13, J. Am. Chem. Soc., 2009, 131(25), 8732–8733.
18. R. Ma and T. Luo, PI1M: a benchmark database for polymer informatics, J. Chem. Inf. Model., 2020, 60(10), 4684–4690.
19. R. Ma, H. Zhang and T. Luo, Exploring high thermal conductivity amorphous polymers using reinforcement learning, ACS Appl. Mater. Interfaces, 2022, 14(13), 15587–15598.
20. V. Sharma, C. Wang, R. G. Lorenzini, R. Ma, Q. Zhu, D. W. Sinkovits, G. Pilania, A. R. Oganov, S. Kumar and G. A. Sotzing, Rational design of all organic polymer dielectrics, Nat. Commun., 2014, 5(1), 4845.
21. H. Li, B. S. Chang, H. Kim, Z. Xie, A. Lainé, L. Ma, T. Xu, C. Yang, J. Kwon and S. W. Shelton, High-performing polysulfate dielectrics for electrostatic energy storage under harsh conditions, Joule, 2023, 7(1), 95–111.
22. L. Tao, J. He, N. E. Munyaneza, V. Varshney, W. Chen, G. Liu and Y. Li, Discovery of multi-functional polyimides through high-throughput screening using explainable machine learning, Chem. Eng. J., 2023, 465, 142949.
23. M. Ohno, Y. Hayashi, Q. Zhang, Y. Kaneko, and R. Yoshida, SMiPoly: Generation of Synthesizable Polymer Virtual Library using Rule-based Polymerization Reactions, 2023.
24. E. J. Bjerrum and R. Threlfall, Molecular generation with recurrent neural networks (RNNs), arXiv, 2017, preprint, arXiv:1705.04612,  DOI:10.48550/arXiv.1705.04612.
25. P.-C. Kotsias, J. Arús-Pous, H. Chen, O. Engkvist, C. Tyrchan and E. J. Bjerrum, Direct steering of de novo molecular generation with descriptor conditional recurrent neural networks, Nat. Mach. Intell., 2020, 2(5), 254–265.
26. D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy and M. Veselov, Molecular sets (MOSES): a benchmarking platform for molecular generation models, Front. Pharmacol., 2020, 11, 565644.
27. O. Prykhodko, S. V. Johansson, P.-C. Kotsias, J. Arús-Pous, E. J. Bjerrum, O. Engkvist and H. Chen, A de novo molecular generation method using latent vector based generative adversarial network, J. Cheminf., 2019, 11(1), 1–13.
28. J. Arús-Pous, S. V. Johansson, O. Prykhodko, E. J. Bjerrum, C. Tyrchan, J.-L. Reymond, H. Chen and O. Engkvist, Randomized SMILES strings improve the quality of molecular generative models, J. Cheminf., 2019, 11(1), 1–13.
29. T. Blaschke, J. Arús-Pous, H. Chen, C. Margreitter, C. Tyrchan, O. Engkvist, K. Papadopoulos and A. Patronov, REINVENT 2.0: an AI tool for de novo drug design, J. Chem. Inf. Model., 2020, 60(12), 5918–5922.
30. S. Kang and K. Cho, Conditional molecular design with deep generative models, J. Chem. Inf. Model., 2018, 59(1), 43–52.
31. J. Wang, C.-Y. Hsieh, M. Wang, X. Wang, Z. Wu, D. Jiang, B. Liao, X. Zhang, B. Yang and Q. He, Multi-constraint molecular generation based on conditional transformer, knowledge distillation and reinforcement learning, Nat. Mach. Intell., 2021, 3(10), 914–922.
32. M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, Molecular de novo design through deep reinforcement learning, J. Cheminf., 2017, 9(1), 1–14.
33. S. R. Krishnan, N. Bung, G. Bulusu and A. Roy, Accelerating de novo drug design against novel proteins using deep learning, J. Chem. Inf. Model., 2021, 61(2), 621–630.
34. G. L. Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. L. C. Farias, and A. Aspuru-Guzik, Objective-reinforced generative adversarial networks (organ) for sequence generation models, arXiv, 2017, preprint, arXiv:1705.10843,  DOI:10.48550/arXiv.1705.10843.
35. C. Shi, M. Xu, Z. Zhu, W. Zhang, M. Zhang, and J. Tang, Graphaf: a flow-based autoregressive model for molecular graph generation, arXiv, 2020, preprint, arXiv:2001.09382,  DOI:10.48550/arXiv.2001.09382.
36. A. Schneuing, Y. Du, C. Harris, A. Jamasb, I. Igashov, W. Du, T. Blundell, P. Lió, C. Gomes, and M. Welling, Structure-based drug design with equivariant diffusion models, arXiv, 2022, preprint, arXiv:2210.13695,  DOI:10.48550/arXiv.2210.13695.
37. I. Igashov, H. Stärk, C. Vignac, V. G. Satorras, P. Frossard, M. Welling, M. Bronstein, and B. Correia, Equivariant 3d-conditional diffusion models for molecular linker design, arXiv, 2022, preprint, arXiv:2210.05274,  DOI:10.48550/arXiv.2210.05274.
38. B. B. Gaines, and J. A. Bi, deep molecular generative model based on multi-resolution graph variational Autoencoders, 2021.
39. A. Button, D. Merk, J. A. Hiss and G. Schneider, Automated de novo molecular design by hybrid machine intelligence and rule-driven chemical synthesis, Nat. Mach. Intell., 2019, 1(7), 307–315.
40. C. Shen, M. Krenn, S. Eppel and A. Aspuru-Guzik, Deep molecular dreaming: Inverse machine learning for de novo molecular design and interpretability with surjective representations, Mach. Learn.: Sci. Technol., 2021, 2(3), 03LT02.
41. T. Gaudin, A. Nigam, and A. Aspuru-Guzik, Exploring the chemical space without bias: data-free molecule generation with DQN and SELFIES, in Second Workshop on Machine Learning and the Physical Sciences NeurIPS, 2019.
42. D. Flam-Shepherd, T. C. Wu and A. Aspuru-Guzik, MPGVAE: improved generation of small organic molecules using message passing neural nets, Mach. Learn.: Sci. Technol., 2021, 2(4), 045010.
43. A. Nigam, R. Pollice and A. Aspuru-Guzik, Parallel tempered genetic algorithm guided by deep neural networks for inverse molecular design, Digital Discovery, 2022, 1(4), 390–404.
44. B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361(6400), 360–365.
45. R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4(2), 268–276.
46. R.-R. Griffiths and J. M. Hernández-Lobato, Constrained Bayesian optimization for automatic chemical design using variational autoencoders, Chem. Sci., 2020, 11(2), 577–586.
47. H. Iwata, T. Nakai, T. Koyama, S. Matsumoto, R. Kojima, and Y. Okuno, VGAE-MCTS: a New Molecular Generative Model combining Variational Graph Auto-Encoder and Monte Carlo Tree Search, 2023.
48. R. Gurnani, D. Kamal, H. Tran, H. Sahu, K. Scharm, U. Ashraf and R. Ramprasad, PolyG2G: A novel machine learning algorithm applied to the generative design of polymer dielectrics, Chem. Mater., 2021, 33(17), 7008–7016.
49. R. Batra, H. Dai, T. D. Huan, L. Chen, C. Kim, W. R. Gutekunst, L. Song and R. Ramprasad, Polymers for extreme conditions designed using syntax-directed variational autoencoders, Chem. Mater., 2020, 32(24), 10489–10500.
50. D.-F. Liu, Y.-X. Zhang, W.-Z. Dong, Q.-K. Feng, S.-L. Zhong and Z.-M. Dang, High-Temperature Polymer Dielectrics Designed Using an Invertible Molecular Graph Generative Model, J. Chem. Inf. Model., 2023, 63(24), 7669–7675.
51. S. A. Wildman and G. M. Crippen, Prediction of physicochemical parameters by atomic contributions, J. Chem. Inf. Comput. Sci., 1999, 39(5), 868–873.
52. S. Kim, C. M. Schroeder and N. E. Jackson, Open Macromolecular Genome: Generative Design of Synthetically Accessible Polymers, ACS Polym. Au, 2023, 3(4), 318–330.
53. X. Huang, C. Y. Zhao, H. Wang and S. Ju, AI-assisted inverse design of sequence-ordered high intrinsic thermal conductivity polymers, Mater. Today Phys., 2024, 44, 101438.
54. J. Zhang, R. Mercado, O. Engkvist and H. Chen, Comparative study of deep generative models on chemical space coverage, J. Chem. Inf. Model., 2021, 61(6), 2572–2581.
55. G. Weng, H. Zhao, D. Nie, H. Zhang, L. Liu, T. Hou and Y. Kang, Rediscmol: Benchmarking molecular generation models in biological properties, J. Med. Chem., 2024, 67(2), 1533–1543.
56. A. Nigam, R. Pollice, G. Tom, K. Jorner, J. Willes, L. A. Thiede, A. Kundaje, and A. Aspuru-Guzik, Tartarus: A benchmarking platform for realistic and practical inverse molecular design, arXiv, 2022, preprint, arXiv:2209.12487,  DOI:10.48550/arXiv.2209.12487.
57. S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen and B. Yu, PubChem 2019 update: improved access to chemical data, Nucleic Acids Res., 2019, 47(D1), D1102–D1109.
58. Y. Wang, J. Xiao, T. O. Suzek, J. Zhang, J. Wang and S. H. Bryant, PubChem: a public information system for analyzing bioactivities of small molecules, Nucleic Acids Res., 2009, 37(suppl_2), W623–W633.
59. F. Eyben, M. Wöllmer, and B. Schuller, Opensmile: the munich versatile and fast open-source audio feature extractor, in Proceedings of the 18th ACM international conference on Multimedia, 2010, pp 1459–1462.
60. A. Radford, K. Narasimhan, T. Salimans, and I. Sutskever, Improving language understanding with unsupervised learning, 2018.
61. M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Self-referencing embedded strings (SELFIES): A 100% robust molecular string representation, Mach. Learn.: Sci. Technol., 2020, 1(4), 045024.
62. O. Prykhodko, S. V. Johansson, P.-C. Kotsias, J. Arús-Pous, E. J. Bjerrum, O. Engkvist and H. Chen, A de novo molecular generation method using latent vector based generative adversarial network, J. Cheminf., 2019, 11, 1–13.
63. R. Mercado, T. Rastemo, E. Lindelöf, G. Klambauer, O. Engkvist, H. Chen and E. J. Bjerrum, Graph networks for molecular design, Mach. Learn.: Sci. Technol., 2021, 2(2), 025023.
64. R. Mercado, T. Rastemo, E. Lindelöf, G. Klambauer, O. Engkvist, H. Chen and E. J. Bjerrum, Practical notes on building molecular graph generative models, Appl. AI lett., 2020, 1(2).
65. M. Benhenda, ChemGAN challenge for drug discovery, can AI reproduce natural chemical diversity?, arXiv, 2017, preprint, arXiv:1708.08227,  DOI:10.48550/arXiv.1708.08227.
66. A. Mayr, G. Klambauer, T. Unterthiner, M. Steijaert, J. K. Wegner, H. Ceulemans, D.-A. Clevert and S. Hochreiter, Large-scale comparison of machine learning methods for drug target prediction on ChEMBL, Chem. Sci., 2018, 9(24), 5441–5451.
67. A. P. Bento, A. Gaulton, A. Hersey, L. J. Bellis, J. Chambers, M. Davies, F. A. Krüger, Y. Light, L. Mak and S. McGlinchey, The ChEMBL bioactivity database: an update, Nucleic Acids Res., 2014, 42(D1), D1083–D1090.
68. J. J. Irwin, T. Sterling, M. M. Mysinger, E. S. Bolstad and R. G. Coleman, ZINC: a free tool to discover chemistry for biology, J. Chem. Inf. Model., 2012, 52(7), 1757–1768.
69. E. Putin, A. Asadulaev, Q. Vanhaelen, Y. Ivanenkov, A. V. Aladinskaya, A. Aliper and A. Zhavoronkov, Adversarial threshold neural computer for molecular de novo design, Mol. Pharmaceutics, 2018, 15(10), 4386–4397.
70. T. Sterling and J. J. Irwin, ZINC 15–ligand discovery for everyone, J. Chem. Inf. Model., 2015, 55(11), 2324–2337.
71. D. Walsh, W. Zou, L. Schneider, R. Mello, M. Deagen, J. Mysona, T.-S. Lin, J. de Pablo, K. Jensen, and D. Audus, CRIPT: A Scalable Polymer Material Data Structure, 2022.
72. W. Zou, A. M. Monterroza, Y. Yao, S. C. Millik, M. M. Cencer, N. J. Rebello, H. K. Beech, M. A. Morris, T.-S. Lin and C. S. Castano, Extending BigSMILES to non-covalent bonds in supramolecular polymer assemblies, Chem. Sci., 2022, 13(41), 12045–12055.
73. L. Schneider, D. Walsh, B. Olsen and J. de Pablo, Generative BigSMILES: an extension for polymer informatics, computer simulations & ML/AI, Digital Discovery, 2024, 3(1), 51–61.
74. T.-S. Lin, C. W. Coley, H. Mochigase, H. K. Beech, W. Wang, Z. Wang, E. Woods, S. L. Craig, J. A. Johnson and J. A. Kalow, BigSMILES: a structurally-based line notation for describing macromolecules, ACS Cent. Sci., 2019, 5(9), 1523–1531.
75. T.-S. Lin, N. J. Rebello, G.-H. Lee, M. A. Morris and B. D. Olsen, Canonicalizing bigsmiles for polymers with defined backbones, ACS Polym. Au, 2022, 2(6), 486–500.
76. N. J. Rebello, T.-S. Lin, H. Nazeer and B. D. Olsen, BigSMARTS: A Topologically Aware Query Language and Substructure Search Algorithm for Polymer Chemical Structures, J. Chem. Inf. Model., 2023, 63(21), 6555–6568.
77. J. Shi, N. J. Rebello, D. Walsh, W. Zou, M. E. Deagen, B. S. Leao, D. J. Audus and B. D. Olsen, Quantifying Pairwise Similarity for Complex Polymers, Macromolecules, 2023, 56(18), 7344–7357.
78. M. Moret, L. Friedrich, F. Grisoni, D. Merk and G. Schneider, Generative molecular design in low data regimes, Nat. Mach. Intell, 2020, 2(3), 171–180.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00395k

---