The structure–property relationship of metallocene-based ethylene oligomerization catalysts using DFT and graph neural networks

Abstract

Ethylene oligomerization catalysts have been extensively studied in both experimental and simulation contexts, yet a molecular-level understanding of structure-property relationship remains far from full understanding. Herein, an applicable strategy for the design of ligands of ethylene oligomerization catalysts is proposed. Density functional theory (DFT) and 3D graph neural networks (3D GNNs) have been combined to establish the relationship between the catalyst structure and its property. A series of titanium-based metallocene catalysts with different ligands were designed and calculated using DFT to establish a dataset. The catalyst prediction model was constructed using 3D GNNs, and a weighted removal approach was used to compare output results and study the impact of different ligand structures on the oligomerization selectivity represented by the energy barrier difference between β-hydrogen transfer and the fourth ethylene insertion. The R² values of the energy barrier difference predictions by four 3D GNNs were 0.93–0.96, indicating good predictive accuracy of the graph network models. Using the graph neural network explanation algorithms, we investigated the influence of different substructures within the ligands on trimerization selectivity. Based on the training and explanation results of the model, an external validation set is designed, and the R² is 0.92, suggesting the generalization ability of the model. This enabled a molecular-level study of the relationship between the structure of the titanocene catalyst and its properties, providing guidance for the design of new catalyst structures.

---

1. Introduction

Linear α-olefins,^1–3 essential organic chemical raw materials for producing plastics, lubricants, synthetic rubber, and various other products, can be synthesized through ethylene oligomerization.^4–6 In this process, the production of high-purity 1-hexene and 1-octene, which are α-olefins with fixed carbon chain lengths, requires selective ethylene oligomerization techniques. The design and development of ethylene oligomerization catalysts have long been a focal point of interest in both academic and industrial sectors within the polyolefin field. Current research^7–9 on selective ethylene oligomerization catalysts primarily focuses on developing novel ligands and corresponding transition metal catalysts. Firstly, it is widely acknowledged that the structural design space for catalysts, especially ligands,^10,11 is vast. Traditional experimental design methods based on experience and trial-and-error, or quantum chemical calculations, are insufficient to meet the demands for the development of new catalysts. With advancements in materials genomics, the integration of high-throughput experimentation/calculation with machine learning can significantly enhance the efficiency of catalyst development.^12–16 Secondly, fundamental yet critical scientific issues persist in oligomerization reactions.¹⁷ Specifically, the structure–activity relationships of oligomerization catalysts and the factors governing the activity and selectivity of specific catalysts remain unclear, leading to an insufficient molecular-level understanding of the catalytic oligomerization process. The design of oligomerization catalysts lacks systematic theoretical guidance, resulting in the development of new systems with an element of unpredictability and inefficiency. However, high-throughput experimentation/calculation provides data support for elucidating the structure–activity relationship of catalysts, while machine learning offers an efficient tool to establish prediction models.^{14,16,18–20}

This paper focuses on the impact of the ligand structure in titanium-based metallocene catalysts on ethylene trimerization selectivity. There are several reasons for choosing titanium-based catalysts.^2,6,21–23 Firstly, compared to other catalysts, they exhibit extremely high activity, allowing potential industrial applications. The oligomerization mechanism is primarily the metallacycle mechanism,²⁴ whereas other metal-based catalysts might involve multiple reaction mechanisms. Additionally, titanium-based catalysts are cost-effective, produce fewer by-products,^4,25 and are more environmentally friendly. However, due to the excellent trimerization selectivity of most titanium-based catalysts, many studies have focused on ethylene trimerization, with less research on its tetramerization and further oligomerization or polymerization. Furthermore, the structural design of metallocene titanium catalysts can be optimized by introducing different ligand substituents and developing novel constrained geometry catalysts. The previous reports^17,26–30 indicate that ligands can modulate the catalyst's steric and electronic characteristics, thereby optimizing the catalyst's activity and selectivity.

Due to the complexity of the micro-mechanisms involved in ethylene oligomerization reactions, quantum chemical calculations have been widely used to elucidate these mechanisms. Quantum chemical calculations, especially density functional theory (DFT) calculations,^12,31 can identify the energies and reaction pathways of different intermediates, as well as the effects of various ligands on the geometry, active centers, and electronic structures of transition metal complexes.^15,32–35 This allows for the prediction of their selectivity and activity in catalytic ethylene oligomerization, leading to the design of new ligands to enhance the activity and selectivity of oligomerization reactions.³⁶ On the other hand, the lack of high-throughput experimental data poses challenges for constructing structure–property relationship prediction models based on big data analysis. Recent research trends indicate that while conducting high-throughput experimentation/calculation, some studies^18,19,37,38 are also attempting to construct structure–property relationship models of catalysts using quantum chemical calculations.

Machine learning models can uncover patterns from complex data,^20,39,40 specifically by establishing a mapping relationship between the catalyst structure and property, thereby providing guidance for designing new structures. However, most machine learning models used in previous catalyst studies are artificial neural networks,^41,42 Gaussian processes,⁴³ random forests,⁴⁴ and others.^45–47 These models typically use sequence data derived from molecular structures as input. On the other hand, 3D graph neural networks (GNNs)^48–51 are capable of efficiently processing and analyzing three-dimensional graphic data. For example, the SchNet⁵² model employs continuous filters to process 3D molecular structures, demonstrating outstanding performance in predicting materials’ electrical and thermal conductivity. The DimeNet⁵³ model further incorporates angular information and has shown excellent performance in molecular docking predictions in drug design, significantly enhancing the efficiency of drug discovery. These examples illustrate the significant advantages of 3D GNNs in understanding the relationship between the material structure and properties. Moreover, trained 3D GNNs can utilize post hoc explanation techniques to explain the influence of a catalyst's three-dimensional molecular structure on selectivity, providing a scientific explanation for catalyst trimerization selectivity. In this paper, we combine DFT and 3D GNNs to study the impact of ligand structures in titanium-based metallocene catalysts on ethylene oligomerization selectivity. Based on the model construction and explanation, the importance of carefully selecting and optimizing the substructure of the labile ligating group (substructure C in Fig. 1a) in catalyst design to achieve desired selectivity has been addressed.

Fig. 1 A schematic diagram of ethylene oligomerization starting from the metallocycle intermediate: (a) the chain termination resulting in the trimerization product and chain propagation for further oligomerization or even polymerization based on the metallocycle intermediate structure, and the three-dimensional schematic diagrams of two types of specific active species M3 shown in (b) and (c), respectively.

2. Methods

2.1. Dataset

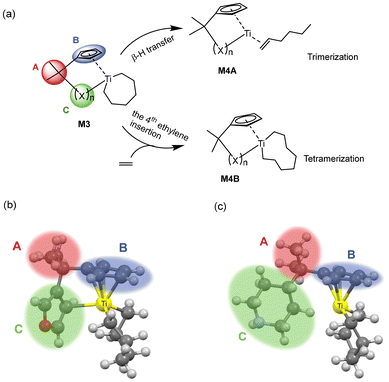
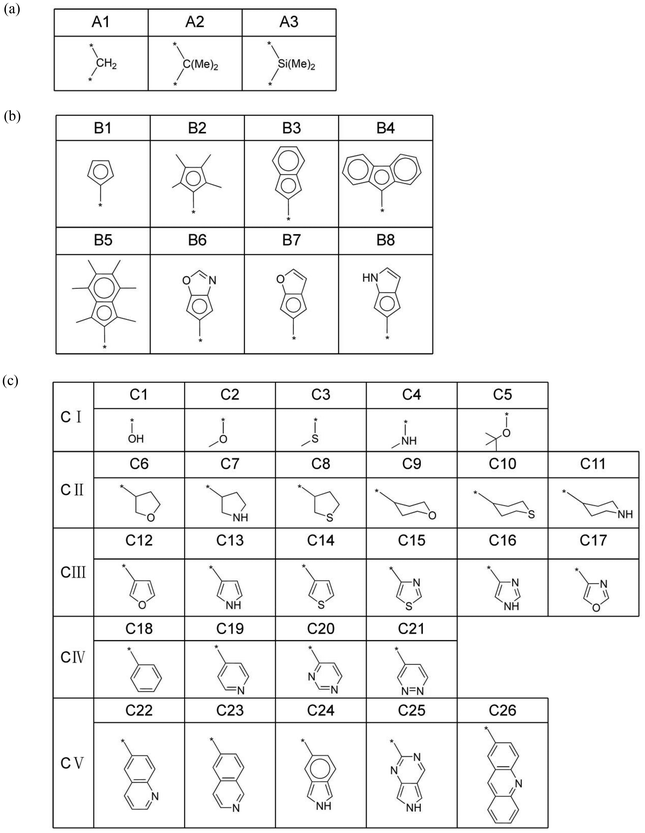
The mechanism of ethylene oligomerization follows a metallacycle pathway, where ethylene monomers initially form cyclic intermediates through oxidative coupling in the presence of a transition metal catalyst, subsequently undergoing continuous ethylene insertion or β-hydrogen transfer reactions to yield oligomers. The key to selectivity between trimerization and further oligomerization or polymerization lies in whether the metallacyclic intermediate (M3 in Fig. 1a) undergoes β-hydrogen transfer to produce 1-hexene or further insertion of the fourth ethylene molecule. The criterion for determining the trimerization or further oligomerization and even polymerization selectivity of a catalyst is based on the relative magnitudes of the β-hydrogen transfer energy barrier (ΔG_{β-H transfer}) and the fourth ethylene insertion energy barrier (ΔG_{ethylene insertion}): if the ΔG_{β-H transfer} is smaller than the ΔG_{ethylene insertion}, the catalyst is selective for trimerization; otherwise, it is selective for producing tetramers and/or heavier oligomers or polymers. Fig. 1(a) illustrates the intermediate structure of the designed catalyst after trimerization and schematically depicts the two pathways of β-hydrogen transfer and the fourth ethylene insertion. The complete ethylene oligomerization process can be referred to in the literature.^{6,14,15,21,26,27} The design of the ligand structures in the catalyst was based on published literature reports.^6,21,26,27 To investigate the selectivity of titanium-based metallocene catalysts for ethylene trimerization and further oligomerization or even polymerization, we designed catalysts with different ligand structures and utilized DFT to simulate the ethylene oligomerization process based on the well-documented metallocycle intermediate (Fig. 1a) involved in the metallocycle mechanism, calculating the ΔG_{β-H transfer} and ΔG_{ethylene insertion}. In Fig. 1(a), the central metal of the catalyst is titanium, with the ancillary ligand and a cyclohexyl group. Fig. 1(b) and (c) show two specific three-dimensional stick-and-ball molecular structure diagrams of M3. As the models of cationic active species, the side-arm (part C) in M3 might coordinate to (Fig. 1b) or dissociate from (Fig. 1c) the titanium center, playing a role of a hemilabile ligating group. To explore how ligands influence the selectivity, this study designed ligands with different structures, including substructures A, B, and C. The specific structures of A, B, and C are shown in Fig. 2. Specifically, part A consists of 3 bridging groups (A1–A3), while part B part includes 8 aromatic cyclic groups (B1–B8), and part C comprises 26 substituents that may coordinate to the metal center in some cases, which is classified into five classes according to its degree of unsaturation (0, 1, 3, 4, and greater than 4, respectively). In subsequent research, these five classes are denoted as CI, CII, CIII, CIV, and CV. The lines ending with a star symbol in the figure represent the connections between different substructures. Note that A is connected to B and C sequentially. B is connected to A, and there is a coordination interaction bond between the aromatic B and titanium center. The substructure C is also similarly linked to A, and has possibility to disconnect to the titanium center, depending on the specific structure. It is noted that this study utilizes machine learning methods to explore the relationship between the ligand structure and selectivity. Given the performance of machine learning, a diverse range of ligand structures included in the constructed dataset will be beneficial for further machine learning studies. Therefore, some catalyst samples were modeled without considering their synthetic feasibility.

Fig. 2 The schematic diagrams of the specific substructures of A, B, and C in the designed catalyst molecules, where * represents a connection to other substructures. Specifically, the * in A represents connections to B and C, and the * in both B and C represents a connection to A.

2.2. DFT calculations

The structure optimizations were performed using the B3P86 functional. The LANL2DZ basis set was applied for titanium, and the 6-31G(d,p) basis set was used for nonmetal (C, H, O, N, F, S, Si, and Cl) atoms. Subsequently, all structures were analyzed using harmonic vibrational frequencies at the same level as the geometry optimizations to characterize each stationary point as a minimum (no imaginary frequency) or transition state (one imaginary frequency), and to obtain the thermodynamic corrections for Gibbs free energy in the gas-phase at a temperature of 298.15 K. The energy barriers ΔG_{β-H transfer} and ΔG_{ethylene insertion} for each designed catalyst structure were obtained from the DFT calculations. To further enhance the accuracy of the energy evaluations, high-level single-point energy calculations were performed on the optimized structures. For these calculations, the M06 functional and the 6-311+G(2d,p) basis set for non-metal atoms and the SDD basis set together with the associated pseudopotential for the Ti atom were utilized. These high-level single-point energies were used to refine the energy barriers, ΔG_{β-H transfer} and ΔG_{ethylene insertion}, ensuring a more reliable description of the catalytic performance. All DFT calculations were carried out using the Gaussian 16 program.⁵⁴ To access the reliability of the calculation method used, the [(η⁵-C₅H₄-CMe₂)(3,5-Me₂-C₆H₃)]Ti(cyc-C₆H₁₂) and (η⁵-C₅H4-CMe₃)Ti(cyc-C₆H₁₂) complex mediated β-H transfer and ethylene insertion have been calculated. It is found that the former favors trimerization (ΔG_{β-H transfer} of 15.4 kcal mol⁻¹ vs. ΔG_{ethylene insertion} of 17.4 kcal mol⁻¹) and the latter favors ethylene insertion (ΔG_{β-H transfer} of 20.9 kcal mol⁻¹ vs. ΔG_{ethylene insertion} of 5.4 kcal mol⁻¹). These calculation results are in line with previous experimental observations²⁶ that the η⁵-C₅H₄-CMe₂(3,5-Me₂-C₆H₃) ligated titanocene produced 97 wt% of trimerization product and the (η⁵-C₅H₄-CMe₃) ligated complex dominantly mediated polyethylene formation.

A total of 624 different catalysts were modeled for the aforementioned DFT calculations. Unfortunately, three of these structures failed in locating the transition states. As a result, a dataset of 621 titanocene-based metallocyclic complexes (M3) and corresponding β-H transfer and ethylene insertion transition states together with their energies were constructed. The raw dataset is available in the ESI,† including .xyz files, electronic energies, energy barriers, and the lowest frequencies for M3 and two transition states for β-H transfer (which tends to form the trimerization product) and continuous ethylene insertion (which tends to form a higher oligomer or polyethylene). It is noteworthy that, thanks to the available X-ray crystal structures of cationic ansa-(η⁵-cyclopentadienyl)(η⁶-arene) titanium complexes,²⁷ the current catalyst samples were modeled based on these analogous crystal structures and therefore were further locally optimized without time-consuming conformer search, which was also adopted in previous works.^26,31 As to the orientation of substructure C containing a heteroatom and/or a ring moiety during the construction of the initial structure, the following rules are adopted. In the case of C1–C5 having a heteroatom at the α-position, the heteroatom is initially modeled to coordinate to the titanium center. In the case of ring-featured C6–C26, if there is a heteroatom at the β-position or an α,β-unsaturated bond, the heteroatom or the unsaturated bond is initially modeled to coordinate to the titanium center, where the heteroatom has a higher priority than the unsaturated bond if they both exist; if the substructure C contains neither a β-heteroatom nor an α,β-unsaturated bond, such as C6–C11, the C moiety features a β-C–H⋯Ti agostic interaction in the initial structure model. As to the construction of the hydrogen transfer transition state leading to a trimerization product, it is based on the optimized intermediate M3 featuring a C–H⋯Ti agostic interaction in the seven membered metallocycle. The H atom in the C–H bond was modeled to be the transferring hydrogen because such a C–H bond is already activated by the agostic interaction (Table S1†). In the case of the subsequent ethylene insertion transition state, we compared two cases, viz., coordination–insertion occurring at the side of agnostic insertion (backside) and its opposite side (frontside), as shown in Table S1.† We tested several samples, and found that the latter case resulted in a lower insertion transition state in energy (Table S1†). In the current database, the subsequent insertion of the fourth ethylene was therefore modeled as the case of frontside insertion. It is noted that this study did not conduct a comprehensive search for conformers, rotamers, and other possible isomers, which is a limitation of the current work. Although the available X-ray structures were applied to construct all the catalyst structures, we recognize that different conformers and isomers may have effects on the model predictions. However, the dataset was constructed based on the same rule as mentioned earlier and the machine learning model shows good predictive performance on an external validation set (vide infra), which allows us to compare the effects of substructures on the trimerization selectivity. In future work, the balance between the computational cost of conformer search and accuracy is still worth considering.

2.3. 3D GNNs

The 3D GNNs can directly extract valuable information from the DFT-optimized structures to construct models for predicting the energy barrier difference (ΔΔG) between ΔG_{β-H transfer} and ΔG_{ethylene insertion}, while also providing the relationship between the ligand structure and selectivity. To construct prediction models for the structure–property relationship between the molecular structure and ΔΔG, 3D GNNs are applied to deal with the 3D graph information in the catalyst dataset. In this paper, four models,⁵⁵ including DimeNet, SchNet, SphereNet, and ComENet, are selected because of their great performance in processing the 3D graph structure data especially molecules. These networks augment the model's proficiency in learning the three-dimensional structure of molecules by refining input features, modifying information transmission mechanisms, and altering network architectures, thereby reducing computational complexity and enhancing the accuracy of molecular property prediction. An individual introduction of each network is provided in the following. DimeNet⁵³ is a deep learning framework designed for the learning of molecular representations. It leverages distance and angle information, in conjunction with inter-atomic interactions, to facilitate the construction of molecular representations. Through the incorporation of bond direction and bond lengths as input features, DimeNet significantly enhances the predictive accuracy for molecular properties. SchNet⁵² employed continuous-filter convolutional layers to model atomic interactions, rendering it highly adept at predicting molecular properties including energy, forces, and vibrational frequencies. SphereNet⁵⁶ utilizes the spherical message passing approach, leveraging inter-atomic distances, angles, and dihedral angles to encapsulate three-dimensional information, thereby achieving a more comprehensive data representation. SphereNet demonstrates superior performance in the handling of three-dimensional molecular graphs, particularly in the prediction of molecular properties such as bond lengths and bond angles. ComENet⁵⁷ (Complete and Efficient Graph Neural Network) constitutes a neural network architecture tailored for 3D molecular graphs. It employs a novel message passing scheme to comprehensively and efficiently integrate 3D information, an approach unprecedented among existing methods. ComENet places particular emphasis on global and local completeness, introducing critical rotational angles to achieve global completeness. Furthermore, ComENet offers a significant improvement in computational efficiency, outpacing previous methods by several orders of magnitude.

DimeNet, SphereNet, SchNet and ComENet are constructed to predict the ΔΔG and we compared Graph Convolutional Networks (GCN), Graph Attention Networks (GAT) and Multilayer Perceptron (MLP) with the 3D GNNs. GCN and GAT are considered two-dimensional graph neural networks (2D GNNs) because they primarily handle graph structures based on the connections between nodes, without directly accounting for the three-dimensional coordinates or geometric information of the nodes in space. GCN performs convolution operations based on the graph's adjacency matrix and node features, allowing each node to aggregate information from its neighboring nodes. In contrast, GAT employs an adaptive attention mechanism to assign different weights to neighboring nodes, dynamically adjusting how information from neighbors is integrated. To maintain consistency with the 3D GNNs, the input of both GCN and GAT is the same as that of the 3D GNNs, consisting solely of the atomic types and coordinates of the catalyst intermediate structures. The MLP consists of multiple fully connected layers and is used to process fingerprints derived from graph-structured data. The dataset constructed by DFT calculations is divided into train and test sets in an 8 : 2 ratio. The test set was employed to assess the prediction performance of the models, with the evaluation metric being the R² score and mean absolute error (MAE). R² is used to measure the goodness of fit between the predicted and true values of the model. Its value ranges from 0 to 1, with R² closer to 1 indicating a better fit. A smaller MAE indicates a more accurate model. The hyperparameters of models, including the network depth, learning rate, and so on, were optimized automatically using Optuna.⁵⁸ The epoch size was set to 200 during the training process.

2.4. Explanation method

To understand the influence of various ligand substructures on the ΔΔG and thereby elucidate the ligand structure's impact on catalyst selectivity, we have devised a molecular structure explanation method inspired by ablation studies. Ablation studies originated from the field of biology, where they were used to investigate the effects of removing a specific organ or function on the overall performance of an organism. In deep learning, ablation studies are a commonly used method for evaluation and optimization. This approach involves systematically removing a component or feature of a model to observe its impact on model performance, thereby understanding the contribution and importance of each component within the model. Applying the concept of ablation studies to investigate the impact of the groups in a molecule on its property, we would remove the substructures from the input based on a pre-trained graph neural network and compare the impact of their absence on the network's predictive results to assess their influence on properties. However, directly removing substructures disrupts the overall molecular structure, resulting in a fundamental alteration of the molecule. This is because graph neural networks rely on the connectivity between atoms for information propagation. Building upon this, we propose a weighted removal graphical explanation algorithm, where the data corresponding to the substructure to be removed is assigned a very small weight, such as 0.1. This approach allows us to investigate the influence of the substructure on the properties without compromising the integrity of the overall molecular structure.

The output variation corresponding to each substructure is represented by the following formula:

Δy = y_G − y_G′, (1)

where Δy denotes the change in output that measures the importance of the substructure, y_G represents the original model output value, and y_G′ represents the model output value after applying the weight. This study predicts the ΔΔG, which is equal to ΔG_{ethylene insertion} minus ΔG_{β-H transfer}. Therefore, if the predicted value decreases after applying the weight to a substructure, i.e., Δy > 0, it indicates that this substructure relatively increases the ΔG_{ethylene insertion} and/or decreases the ΔG_{β-H transfer}, thereby enhancing the trimerization selectivity of the catalyst. In summary, when Δy > 0, it suggests that the corresponding substructure increases the selectivity for trimerization and decreases the selectivity for further oligomerization or polymerization; conversely, when Δy < 0, it indicates that the corresponding substructure is beneficial for the formation of tetramers or higher oligomers even polymers.

3. Results and discussion

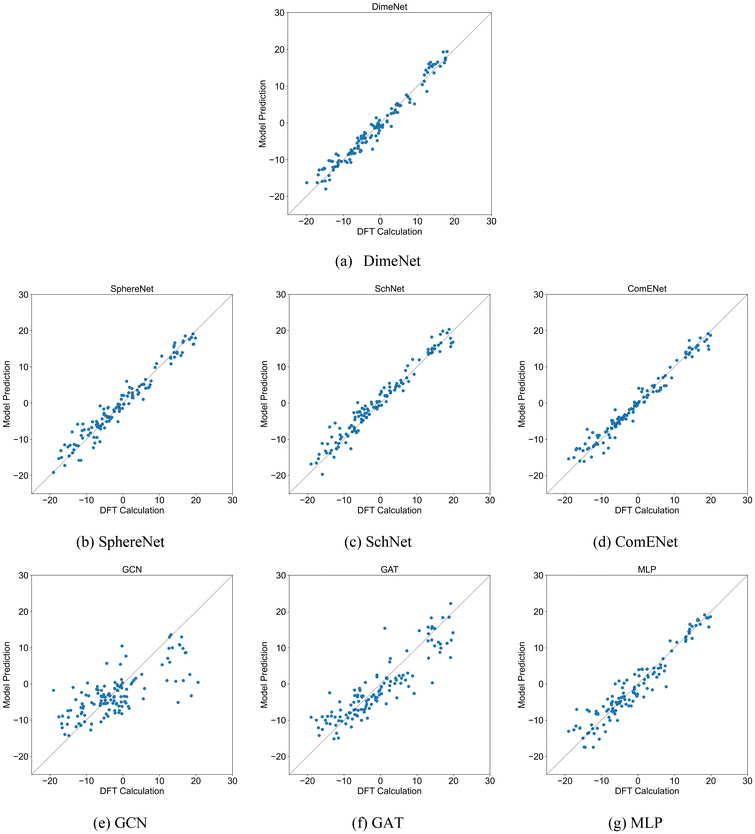
Four 3DGNN models and three comparison methods were trained and tested according to the settings in Section 2.3. To avoid the effect of dataset partitioning on the results, the training and testing process was repeated 5 times, and each time the training and testing sets were re-partitioned randomly. Table 1 presents the R² and MAE values of various models in the test set for predicting ΔΔG. Based on the R² values, the DimeNet model demonstrates the best performance, followed by ComENet. The R² values of other 3D GNN models are also close to 1, indicating their strong fitting capability in predicting ΔΔG, although slightly inferior to that of DimeNet. In contrast, the performance of comparative methods such as GCN, GAT, and MLP is less competitive than that of 3D GNNs. Notably, the R² value of MLP reaches 0.90, suggesting that the molecular structural information derived from two-dimensional features is highly correlated with catalyst selectivity. However, the relatively lower performance of MLP compared to that of 3D GNNs can be attributed to its inability to effectively capture the three-dimensional structural information of catalyst molecules due to its learning mechanism. Scatter plots comparing DFT calculation values and model predictions of test sets are shown in Fig. 3. The closer the scatter points are to the diagonal line in the figures, the closer the model's predictions are to the true values. As shown in Fig. 3, the predictions from the 3D GNN models are close to the DFT calculation values, whereas the distribution of data points in the GCN model is quite wide, while GAT and MLP performed better, but they still lag behind 3D GNNs. In short, the 3D GNN models successfully predict the ΔΔG from the molecular three-dimensional structures, demonstrating that the spatial characteristics of the ligands in the catalyst have a significant impact on the selectivity for trimerization and further oligomerization or polymerization.

Fig. 3 Scatter plots comparing DFT calculation values and model predictions of test sets for models (a) DimeNet, (b) SphereNet, (c) SchNet, (d) ComENet, (e) GCN, (f) GAT and (g) MLP. The X-axis represents the DFT calculation values, while the Y-axis represents the predictions by each model. Each subplot corresponds to a different model.

Table 1 The predictive performance of models for energy barrier difference ΔΔG

Models	DimeNet	SphereNet	SchNet	ComENet	GCN	GAT	MLP
R^2	0.96	0.95	0.93	0.96	0.50	0.73	0.90
MAE (kcal mol^−1)	1.40	1.66	1.85	1.41	4.99	3.82	2.21

---

To investigate the effects of various substructures of ligands on ΔΔG, the explanatory algorithm described in Section 2.4 was employed. This involved applying a small weight to the input sequence of specific substructures within the molecular structure and comparing the resulting changes in the model output. In this study, the weight is set to 0.1, and the pre-trained DimeNet model was utilized. Since the influence of a ligand structure can result from not only its individual structure but also combinations of two or more substructures, the study of the structure–property relationship of ligands concerning ΔΔG was divided into two parts. The first part focuses on individual structures, specifically applying weights to substructures A, B, and C (in Fig. 1(a) M3) separately. The second part examines combinations of substructures, applying weights to combinations AB, AC, and BC.

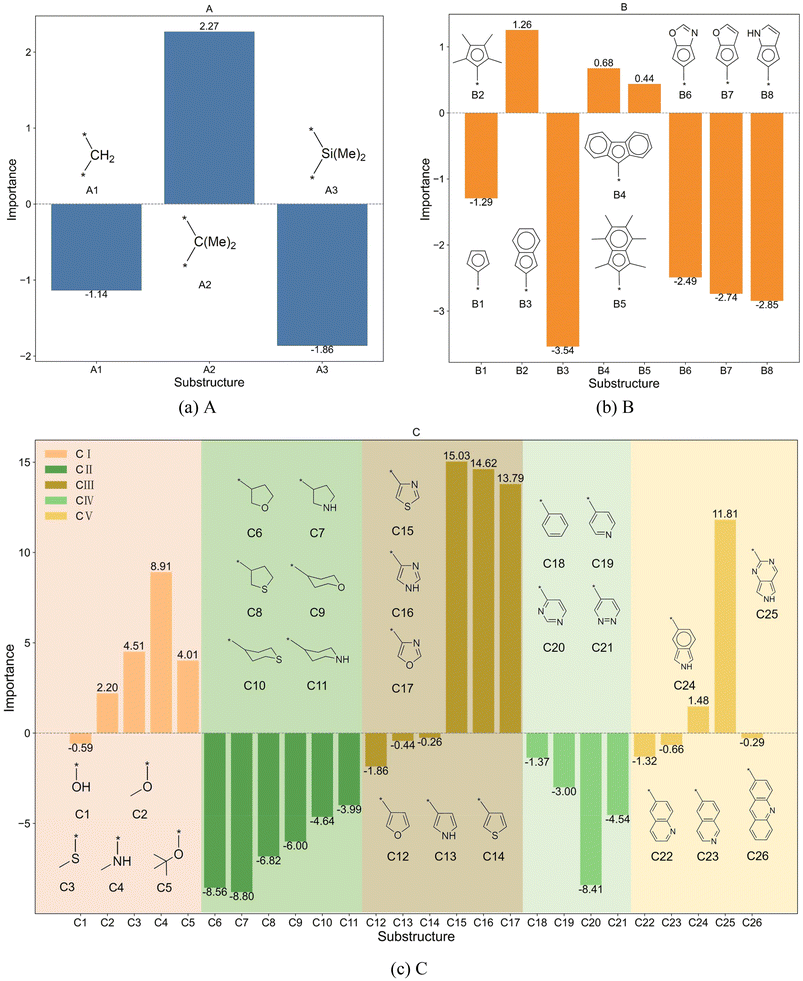
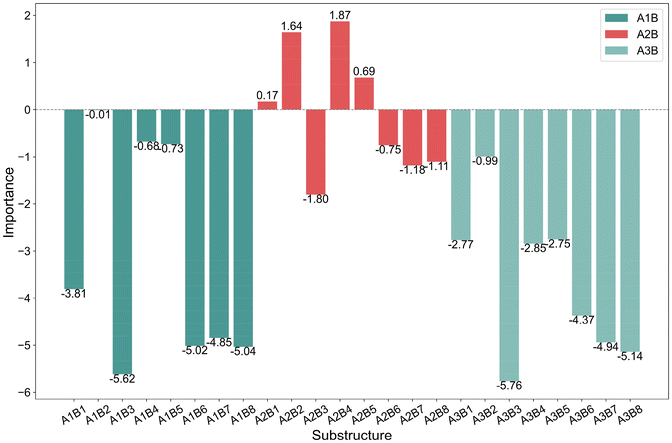
The bar charts in Fig. 4 compare the impact of individual substructures A, B, and C on the output of the predictive model when weighted explanations are applied separately. Firstly, by comparing the y-axis ranges of Fig. 4, it is evident that substructure C has a greater impact on the output than substructures A and B. Secondly, according to the analysis in Section 2.4, importance values greater than 0 indicate that the corresponding structure favors trimerization, while values less than 0 favor further oligomerization or even polymerization. Acting as a bridging structure, substructure A exhibits a relatively minor influence on selectivity: A3 (Si(Me)₂) favors further oligomerization or even polymerization, whereas A2 (C(Me)₂) promotes trimerization. As for the cyclopentadienyl substructure B, B2(pentamethylcyclopentadienyl, Cp*), B4(9-fluorenyl), and B5(2-hemamethylindenyl) contribute more significantly to trimerization compared to other cyclopentadienyl substructures, as they hinder the insertion of the fourth ethylene molecule. Upon examining their structures, it can be observed that B2, B4, and B5 occupy larger spatial volumes compared to other cyclopentadienyl substructures. Thus, the larger steric hindrance of the cyclopentadienyl substructure is associated with enhanced trimerization selectivity, which is consistent with the findings reported in the literature,^26–30 where steric effects were shown to influence the selectivity of ethylene oligomerization. Such consistent results suggest that the methodology used in this work is helpful in elucidating the effects of the substructures. Within the same category, substructure C exhibits similar importance values, suggesting that analogous structural subunits may impart similar catalytic selectivity. Among these, CI, CIII, and CV favor trimerization, while CII and CIV favor tetramerization or further oligomerization or even polymerization. Notably, within the CIII category, the influence of C15(4-thiazoyl), C16(4-imidazoyl), or C17(4-oxazoyl) is significantly greater than that of C12(3-furan), C13(3-pyrrolyl), or C14(3-thiophenyl). Structural analysis reveals that, in C15 to C17, the atom coordinating to the titanium center is an ortho-N atom. Similarly, in the CV category, C25(2-6H-pyrrolo[3,4-d]pyrimidinyl), where the ortho-N atom is coordinated to the titanium center, results in a greater output change compared to other substructures within the same category. A comparable observation is made for C4(dimethylaminyl) in the CI category. Therefore, it can be concluded that the coordination bond between the titanium center and a ortho-N atom in the catalyst structure enhances trimerization selectivity.

Fig. 4 Bar charts showing the importance of (a) A, (b) B, and (c) C substructures individually.

Fig. 5 illustrates the impact of the combination of A and B substructures on the model output. The bar charts reveal that different AB combinations vary in their influence on the predictive results. The A2B4(A2: C(Me)2, B4: 9-fluorenyl) combination exhibits a positive importance value, indicating that it favors trimerization. In contrast, combinations like A1B3(A1: CH2, B3: indenyl) and A3B3 (A3: Si(Me)2, B3: indenyl) show negative importance values with relatively high absolute values, suggesting that these combinations reduce trimerization selectivity. Additionally, details in Fig. 5 highlight that certain specific A or B substructures exhibit consistent behavioral patterns when paired with other substructures. For instance, A1 and A3 tend to produce negative importance values across various B combinations, indicating that these A substructures generally promote further oligomerization or polymerization in the case of such combinations. This analysis offers valuable insights into the significance of AB combinations in catalyst design, guiding the rational selection and optimization of substructure combinations when designing new catalysts.

Fig. 5 A bar chart showing the importance of the combination of A and B substructures.

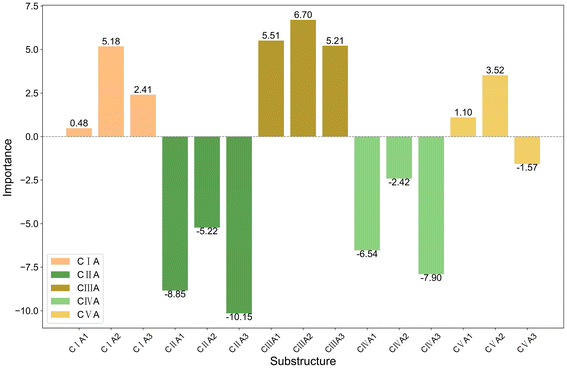
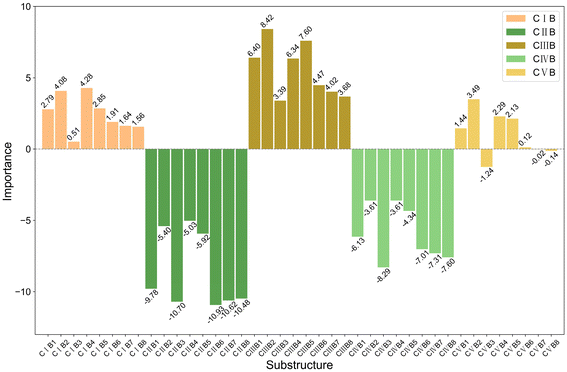
Fig. 6 and 7 show the impact of AC and BC combinations on the model output, with C substructures categorized and presented in bar charts due to their abundance. The figures reveal that regardless of whether C is combined with A or B, it retains the dominant influence, consistent with the above observations that C induces much greater changes than A or B (Fig. 4). This underscores the critical role of C substructures in affecting trimerization selectivity or further oligomerization or even polymerization, emphasizing the importance of carefully selecting and optimizing C substructures in catalyst design to achieve desired selectivity and activity. Furthermore, within the same class of C, the patterns observed for A and B align with the trends identified in Fig. 4 when analyzing their importance individually. This indicates that the combined effect of the substructures is roughly an additive trend of their individual effects, although the numerical influence is somewhat reduced. This reduction is due to the message-passing mechanism in graph neural networks, where weakening a substructure also diminishes the interactions between the substructures. Thus, the individual impact of a substructure inherently includes its interactions with neighboring substructures.

Fig. 6 A bar chart showing the importance of the combination of A and C substructures.

Fig. 7 A bar chart showing the importance of the combination of B and C substructures.

An external validation set was constructed to further evaluate the performance of the trained DimeNet model and verify its generalization ability. The external validation set is independent of the previous datasets and does not participate in the training or testing of the model, but is specifically used to assess the model's performance on unseen data, further ensuring the model's reliability. Based on the previous interpretation of the model regarding the structure–property relationship, the C substructures in the ligands have a significant impact on selectivity. Therefore, 14 new C substructures were designed, as shown in Fig. 8. Among them, C27(ethoxyl) and C28(tert-butyl thiol) may form σ-donation coordination bonds with the titanium center, while unsaturated cyclic groups C31–35 may form π-coordination bonds with the titanium center. C29(cyclohexyl), C30(piperidyl), and the heteroatom-containing bicyclic C36–40 find it hard to coordinate to the titanium center. These C substructures were randomly combined with A and B to form complete ligands. The stable intermediate structures and corresponding energy barriers for the catalysts in the external validation set were obtained using the same DFT method as that used for the previously constructed catalyst dataset. Detailed structures and data can be found in the ESI.† The trained DimeNet model uses the intermediate structures as input to predict the ΔΔG, which are then compared with the DFT calculation ΔΔG to evaluate the model's generalization performance.

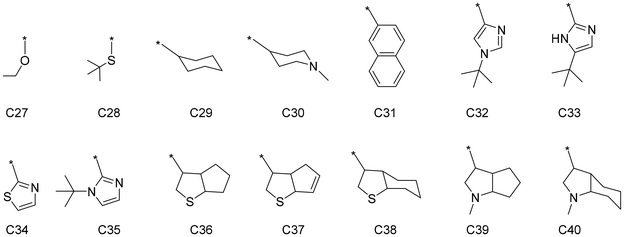Fig. 8 The schematic diagrams of the specific substructures of C in the external validation set, where * represents a connection to A.

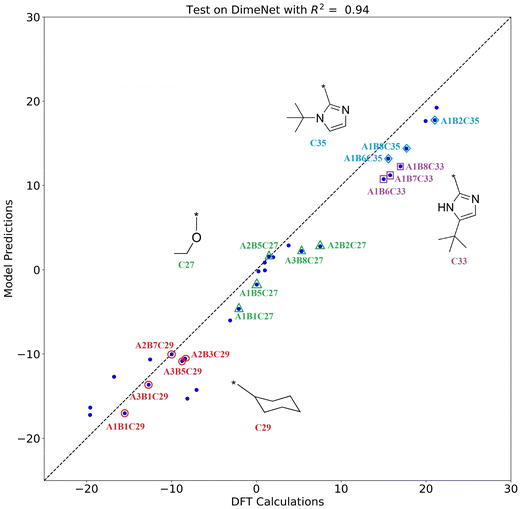
The scatter plot of the model predictions versus DFT calculations is shown in Fig. 9. The horizontal axis represents the DFT calculations, and the vertical axis represents the model predictions. The DFT calculations and model predictions show a strong correlation, with an R² value of 0.94. The closer the scatter points are to the diagonal, the closer the model's predictions are to the DFT calculation values, indicating better generalization performance of the model. The points corresponding to the catalyst structures containing substructures C27 (ethoxyl), C29 (cyclohexyl), C33 (2–5-(tert-butyl)-1H-imidazoyl), and C35 (2–1-(tert-butyl)-1H-imidazoyl) are labeled in Fig. 9. By observing the distribution of the points, it can be seen that the ΔΔG values of catalysts with the same side-arm (substructure C) are very close to each other, which is consistent with the aforementioned results that substructure C has a greater effect on the catalyst selectivity compared to A and B. The substructures and corresponding ΔΔG in the external validation set are detailed in Fig. S1 and Table S3.†

Fig. 9 The scatter plot of DimeNet predictions on the external validation set. The horizontal axis represents the DFT calculations for the external validation set, and the vertical axis represents the predictions by the trained DimeNet model.

4. Conclusions

In this study, we conducted an in-depth investigation into the design of titanium-based metallocene catalyst ligands by combining DFT and 3D GNNs to explore the effects of ligand structures on the selectivity of ethylene oligomerization. Initially, we constructed a dataset for ethylene oligomerization catalysts using DFT calculations. Subsequently, we developed a prediction model for the relationship between the ligand structure and the energy barrier difference ΔΔG for trimerization and further oligomerization or polymerization using 3D GNNs. By applying weighted explanations to ligand structures, we utilized the trained model to elucidate the influence of ligand structures on the selectivity of ethylene oligomerization. Based on the constructed dataset, statistical analysis of the explanation results highlighted the significant role of ligand substructures in the selectivity of ethylene oligomerization, with key findings as follows. The bridging structure C(Me)₂ helps increase the trimerization selectivity of the catalyst; larger cyclopentadienyl structures (substructure B) are beneficial for trimerization selectivity; the potential ligation group within substructure C with similar structural features exhibits similar selectivity; and the coordination bond formed between the side-arm (substructure C) of the ligand and the titanium center has a significant impact on oligomerization selectivity. Specifically, the side-arm (substructure C) with a five-membered ring containing an ortho-N atom has a relatively significant effect on the oligomerization selectivity. These findings clarify how ligand structures influence the selectivity of ethylene oligomerization. The model also demonstrated good predictive performance on the external validation set, providing theoretical support for the design of new catalyst molecular structures.

For instance, the combination analysis of substructures emphasizes the importance of carefully selecting and optimizing side-arm substructures in catalyst design to achieve desired selectivity. As a side note, there is a limitation of the current model since the time-consuming conformer search was not carried out in constructing the database. This research highlights that integrating DFT calculations with machine learning explanations could serve as an efficient methodology for providing theoretical foundations to design titanocene catalysts for ethylene oligomerization.

Data availability

The raw data of the catalyst dataset and the external validation set required to reproduce the above findings are available to download from the ESI as ESI.pdf and ESI.xyz files.†

Conflicts of interest

The authors declare no conflicts of interest.

References

1. F. Speiser, P. Braunstein and L. Saussine, Organometallics, 2004, 23, 2625–2632.
2. P.-A. R. Breuil, L. Magna and H. Olivier-Bourbigou, Catal. Lett., 2015, 145, 173–192.
3. T. Dietel, F. Lukas, W. P. Kretschmer and R. Kempe, Science, 2022, 375, 1021–1024.
4. A. Peng, Z. Huang and G. Li, Catalysts, 2024, 14(4), 268.
5. O. L. Sydora, Organometallics, 2019, 38, 997–1010.
6. D. S. McGuinness, Chem. Rev., 2011, 111, 2321–2341.
7. X. Yang, H. Shao, B. Hao, H. Fan, Y. Wang and T. Jiang, Appl. Organomet. Chem., 2023, 37, e7244.
8. Y. Yang, J. Gurnham, B. Liu, R. Duchateau, S. Gambarotta and I. Korobkov, Organometallics, 2014, 33, 5749–5757.
9. T. Agapie, Coord. Chem. Rev., 2011, 255, 861–880.
10. W. Kong, X. Ma, J. Zuo, X. Zhao and J. Zhang, Organometallics, 2023, 42, 651–659.
11. B. Hao, F. Alam, Y. Jiang, L. Wang, H. Fan, J. Ma, Y. Chen, Y. Wang and T. Jiang, Inorg. Chem. Front., 2023, 10, 2860–2902.
12. H. Fan, X. Yang, J. Ma, B. Hao, F. Alam, X. Huang, A. Wang and T. Jiang, J. Catal., 2023, 418, 121–129.
13. S. Gharajedaghi, Z. Mohamadnia, E. Ahmadi, M. Marefat, G. Pareras, S. Simon, A. Poater and N. Bahri-Laleh, Mol. Catal., 2021, 509, 111636.
14. S. M. Maley, D.-H. Kwon, N. Rollins, J. C. Stanley, O. L. Sydora, S. M. Bischof and D. H. Ess, Chem. Sci., 2020, 11, 9665–9674.
15. F. A. Pasha, J.-M. Basset, H. Toulhoat and T. de Bruin, Organometallics, 2015, 34, 426–431.
16. S. Mace, Y. Xu and B. N. Nguyen, ChemCatChem, 2024, 16, e202301475.
17. G. Tembe, Catal. Rev., 2023, 65, 1412–1467.
18. J. Benavides-Hernández and F. Dumeignil, ACS Catal., 2024, 14, 11749–11779.
19. G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa and A. Fazzio, J. Phys.: Mater., 2019, 2, 032001.
20. G. Tanimu, J. O. Ajadi, Y. Yahaya, H. Alasiri and N. A. Adegoke, ChemCatChem, 2023, 15, e202300598.
21. L. Azimnavahsi and Z. Mohamadnia, Appl. Organomet. Chem., 2019, 33, e4666.
22. F. F. Karbach, J. R. Severn and R. Duchateau, ACS Catal., 2015, 5, 5068–5076.
23. H. Audouin, R. Bellini, L. Magna, N. Mézailles and H. Olivier-Bourbigou, Eur. J. Inorg. Chem., 2015, 2015, 5272–5280.
24. J. R. Briggs, J. Chem. Soc., Chem. Commun., 1989, 674–675.
25. J. A. Suttil and D. S. McGuinness, Organometallics, 2012, 31, 7004–7010.
26. P. J. W. Deckers, B. Hessen and J. H. Teuben, Organometallics, 2002, 21, 5122–5135.
27. E. Otten, A. A. Batinas, A. Meetsma and B. Hessen, J. Am. Chem. Soc., 2009, 131, 5298–5312.
28. K. Vanka, Z. Xu, M. Seth and T. Ziegler, Top. Catal., 2005, 34, 143–164.
29. L. Fan, D. Harrison, T. K. Woo and T. Ziegler, Organometallics, 1995, 14, 2018–2026.
30. Z. Xu, K. Vanka and T. Ziegler, Organometallics, 2004, 23, 104–116.
31. T. de Bruin, P. Raybaud and H. Toulhoat, Organometallics, 2008, 27, 4864–4872.
32. S. Ishii, T. Nakano, K. Kawamura, S. Kinoshita, S. Ichikawa and T. Fujita, Catal. Today, 2018, 303, 263–270.
33. Z.-X. Yu and K. N. Houk, Angew. Chem., 2003, 115, 832–835.
34. D.-H. Kwon, S. M. Maley, J. C. Stanley, O. L. Sydora, S. M. Bischof and D. H. Ess, ACS Catal., 2020, 10, 9674–9683.
35. B. Venderbosch, L. A. Wolzak, J.-P. H. Oudsen, B. De Bruin, T. J. Korstanje and M. Tromp, Catal. Sci. Technol., 2020, 10, 6212–6222.
36. Z. Wang, L. Liu, X. Ma, Y. Liu, P. Mi, Z. Liu and J. Zhang, Catal. Sci. Technol., 2021, 11, 4596–4604.
37. K. McCullough, T. Williams, K. Mingle, P. Jamshidi and J. Lauterbach, Phys. Chem. Chem. Phys., 2020, 22, 11174–11196.
38. X. Liu, B. Liu, J. Ding, Y. Deng, X. Han, C. Zhong and W. Hu, Adv. Funct. Mater., 2022, 32, 2107862.
39. B. Mahesh, Int. J. Sci. Res., 2020, 9, 381–386.
40. M. I. Jordan and T. M. Mitchell, Science, 2015, 349, 255–260.
41. L. Sun and Y. Mu, Asian J. Res. Comput. Sci., 2022, 1–12.
42. H. Fan, Y. Zhang, F. Alam, J. Ma, B. Hao, Y. Chen, Y. Wang, J. Huang and T. Jiang, J. Catal., 2024, 429, 115237.
43. Q. Tang, Y. B. Lau, S. Hu, W. Yan, Y. Yang and T. Chen, Chem. Eng. J., 2010, 156, 423–431.
44. T. Williams, K. McCullough and J. A. Lauterbach, Chem. Mater., 2019, 32, 157–165.
45. G. dos Passos Gomes, R. Pollice and A. Aspuru-Guzik, Trends Chem., 2021, 3, 96–110.
46. G. A. Landrum, J. E. Penzotti and S. Putta, Meas. Sci. Technol., 2004, 16, 270.
47. Z. Luo, J. Peng, Y. Mu, L. Sun, Z. Zhu and Z. Liu, J. Catal., 2023, 428, 115127.
48. W. Shi and R. Rajkumar, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020, pp. 1711–1719.
49. Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang and S. Y. Philip, IEEE Trans. Neural Netw. Learn. Syst., 2020, 32, 4–24.
50. H. Nt and T. Maehara, arXiv preprint arXiv:1905.09550, 2019.
51. J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, AI Open, 2020, 1, 57–81.
52. K. T. Schütt, P.-J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K.-R. Müller, in Proceedings of the 31st International Conference on Neural Information Processing Systems, Curran Associates Inc., Red Hook, NY, USA, 2017, pp. 992–1002.
53. J. Gasteiger, J. Groß and S. Günnemann, in ICLR 2020, 2020.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
55. T. Liyaqat, T. Ahmad and C. Saxena, arXiv preprint arXiv:2408.09461, 2024.
56. Y. Liu, L. Wang, M. Liu, Y. Lin, X. Zhang, B. Oztekin and S. Ji, in Proceedings of the ICLR2022 International Conference on Learning Representations(ICLR2022), 2022.
57. L. Wang, Y. Liu, Y. Lin, H. Liu and S. Ji, arXiv, 2022.
58. T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Association for Computing Machinery, New York, NY, USA, 2019, pp. 2623–2631.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt03065f

‡ These authors contributed equally to this work and should be considered as co-first authors.

---