Six-fold screening unfolds optimized rylene diimides towards organic solar cells: a DFT perspective

Abstract

Harnessing sunlight to produce electricity is the most sustainable form of alternative energy. Apart from commercial silicon solar cells, organic solar cells (OSCs) have great potential due to their flexibility, processability and cost. To improve device performance, broadband absorption, electrical mobility and charge separation are the key components for optimization. Although discrete efforts have been dedicated to comprehending the role of different chemical structures on their power conversion efficiencies (PCE), a systematic screening of multiple structural factors on PCE has not been reported. Herein, we shortlisted rylene diimides as model acceptors in OSCs and demonstrated the role of (a) expanding the rylene core (pyromellitic to bisazulene); (b) changing the ring size (five-member and six-member) and positions (2,3- vs. 1,8/9) of the diimide; (c) changing the diimide sidechain from alkyl to aryl; and (d) twisting core-planarity of rylene (pyrene to corannulene) and the effect on their structural parameters, optical absorption spectra and electron mobilities. Moreover, the combined six-fold screening predicted the candidate with the highest electron mobility in the series. This comprehensive assessment of critical factors on OSC performance paves the way for improved design of acceptor molecules for higher PCE.

---

Introduction

Solar energy harvesting has been touted as the most affordable alternative energy resource with minimal environmental footprint. Commercially deployed silicon-based solar cells have multiple scope for improvements like performance, cost, and flexibility. Organic semiconducting materials have been extensively utilised in energy conversion and electrical applications for over two decades. The power conversion efficiency (PCE) of organic solar cells (OSCs) has experienced a substantial improvement (up to 18%) over the course of its introduction. This progress can be attributed to innovations in device architecture, strategic design of organic semiconductors, and close supervision of the blending and phase separation of these semiconductor components.¹ OSCs offer many perks over conventional technology because of their solution-based nature, ability to function at lower temperatures, and lower production expenses.²

To enhance OSC efficiency, factors such as optical band gap, electron mobility, solution processability, thin film morphology, energy level, and the absorption band require optimisation. In addition, broad differences between the absorption spectra of the acceptor and total solar irradiation, inadequate charge transmission, and instability are the prime reasons for low efficiency in OSC devices.³ In terms of charge mobility, the delocalised electrons in linear conjugated aromatic compounds facilitate intramolecular charge transfer that amplifies the non-linear optical (NLO) response, including polarizability and hyperpolarizability, computed using the CAM-B3LYP functional.⁴ End-capped modifications with functional groups and heterocycles such as thiophenes also result in a decreased band gap and enhanced charge mobility and PCE in OSCs.⁵ Similar modifications in the indandione acceptor with electron withdrawing groups and three thiophene units as the donor component unveiled the structure–property relationship, together with optoelectronic and photovoltaic properties, where the dichloro functionalized acceptor demonstrated an increased red shift, decreased binding energy, and enhanced mobility for holes and electrons in OSCs.⁶

Therefore, one solution for increased OSC efficiency is the construction of bulk-heterojunction (BHJ) polymer solar cells, with the primary layer having a p-type polymer (e.g. polythiophenes) in conjunction with an n-type polymer (e.g. cyanated polyphenylenevinylenes, polybenzothiadiazoles and polycyclic diimides) with dicarbonyl and en-capped modification.⁷ In particular, rylene diimide-modified n-type polymers such as pyromellitic diimides (PMDI), naphthalene diimides (NDI), anthracene diimides (ADI), pyrene diimides (PyDI), perylene diimides (PDI), corannulene diimide (CorDI), and biazulene diimides (BAzDI) are considered to be some of the most effective due to the following reasons: (1) excellent photostability and wide range of optical absorption, spanning from the visible to the near-infrared (NIR) region; (2) swift electron mobilities and suitable electron affinities; (3) well-known synthetic protocol for structural manipulation by the substituents on the imide nitrogen atom, sidechain unit adjustment, and rylene core expansion. However, some fundamental aspects need to be explored to unveil the true potential of diimide systems. For example, (1) can we correlate the rylene core expansion and the band-gap reduction linearly? (2) Does the position (2,3- vs. 1,8/9) and ring size (five-member vs. six-member) of diimide unit play any role? (3) What is the specific role of the diimide sidechain (conjugated vs. non-conjugated) (4) Is ring planarity crucial for higher conductivity? Overall, the simultaneous presence of the above characteristics in a single structure should generate optimal performance for OSCs.

This study addressed the aforementioned questions by examining specific sets of rylene diimides based on (1) expanding the ring number linearly (from pyromellitic to pyrene); (2) changing the ring size (5-member and 6-member) and positions (2,3- vs. 1,8/9) of the diimide; (3) changing diimide sidechain substitution from methyl (non-conjugated) to phenyl (conjugated) and (4) modifying core-planarity of the rylene core, from pyrene to corannulene. Our findings demonstrate that increasing the number of aromatic rings in the rylene core does not affect the planarity of the structures from PMDI to PyDI (benzene ring count from one to four). Such planarity in the structure induces efficient transport of electrons, reduces the electron–hole pair recombination and band gap energy, and boosts the charge carrier mobility. Besides, diimide ring sizes and positions (five-member for 2,3 substitution and six-member for 1,8/1,9 substitution) indicate higher electron mobility for linear diimides rather than transverse geometry (for naphthalene to anthracene). The N-substitution effect by incorporating methyl groups shows better electron mobility than substitution with phenyl groups. Finally, the core planarity distortion from linear to twisted and bowl-shaped affords a steady decrease in electron mobility. The combined outcomes cumulatively predict the highest electron mobility with the perylene core and six-membered linear diimide ring exhibiting methyl substitution (PDI) in the series. Overall, our comprehensive investigation highlights the effect of major structural parameter modulation and their contribution towards OPV device performance. Therefore, we present an unprecedented and timely framework for optimized OPV design.

Methods

The published crystal structures of NDI, PDI, PMDI, ADI, PyDI, CorDI, and BAzDI determined by single-crystal (SCXRD) and powder X-ray diffraction (PXRD) experiments were selected as the reference point of initial estimates. Then, the crystal structures of their derivatives were designed by strategically positioning the optimized individual molecules with specific side chains (methyl and phenyl) to create molecular structures with comparable energy.⁸ The DFT calculations in Gaussian09⁹ were performed to optimise the geometry, calculate the border orbitals and their energies, analyse the absorption spectra, and estimate the reorganization energy of the diimides. The computations were conducted using the 6-311++g(2d,2p) basis set, employing two different functionals: B3LYP¹⁰ and ωB97XD.¹¹ Geometry optimisation, absorption spectra and reorganization energy were calculated using the hybrid B3LYP functional due to its reliable accuracy with low computational cost for organic molecules. A larger fraction of exact exchange is required for accurate computation of the redox potential, which is well handled by the ωB97XD functional.⁵ The absorption spectra of the diimides were computed by Gaussian09's TD-DFT^12–16 function, and absorptivity (ε) was estimated using the oscillator strength (f) and excitation energy of transitions (E_exc). The DOS-PDOS analysis of all structures was performed using GaussSum¹⁷ to support the FMO analysis. The absorption shifts for small molecules in different packing order (monomer, dimer, tetramer and crystal) are minimal when computed with B3LYP in the solid-state calculation. Hence, all the molecular computations were executed in a gaseous isolated state.¹⁸ B3LYP accurately reproduces experimental peaks and captures the subtle effects of packing, such as slight red shifts in stacked dimers and broadening in tetramers, without introducing significant errors. This makes B3LYP a reliable choice for studying the optical properties of small molecules in different packing arrangements.

The redox potential¹⁹ was calculated using eqn (1).

E_ox(red) = E⁺⁽⁻⁾ − E° (1)

where E⁺, E⁻, and E° are the energies of the cation, anion and neutral molecules, respectively. The change in , where 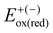and represent the oxidation (reduction) potential of the respective ionic and neutral acceptors. The reorganization energy was calculated using eqn (2).where E°(M°) and E°(M⁺⁽⁻⁾) are the energy of the neutral molecule at its optimized geometry and at the geometry of the ion, respectively; E⁺⁽⁻⁾(M⁺⁽⁻⁾) and E⁺⁽⁻⁾(M°) is the energy of the ion at its optimized geometry and the optimized geometry of the neutral molecule.

Results and discussion

Screening criteria

We imposed six-point screening criteria for rylene diimides (ring number, size, position, geometry, planarity and substitution) to find the optimal OSC candidate. The detailed structures are as follows; N,N′-dimethyl and diphenyl pyromellitic diimides (m-PMDI and p-PMDI, respectively), N,N′-dimethyl and diphenyl naphthalene diimides (m-NDI and p-NDI, respectively), N,N′-dimethyl and diphenyl anthracene diimides (m-ADI and p-ADI, respectively), N,N′-dimethyl and diphenyl pyrene diimides (m-PyDI and p-PyDI, respectively), N,N′-dimethyl and diphenyl perylene diimides (m-PDI and p-PDI, respectively), N,N′-dimethyl and diphenyl corannulene diimide (m-CorDI and p-CorDI, respectively), and N,N′-dimethyl and diphenyl biazulene diimides (m-BAzDI and p-BAzDI, respectively). The molecules under investigation can be easily synthesised by the condensation of corresponding rylene dianhydride and amine.²⁰ The selection of these specific acceptors bears significant influence on the structural, electrical, and optical parameters, as documented in the following sections (Fig. 1).

Fig. 1 Structure of rylene diimides examined in this work.

Pyromellitic diimides (PMDIs) are the simplest rylene derivative, where bay functionalization with aliphatic and aromatic groups improve the hole mobility.²¹ On the other hand, diimide N-substitution with aliphatic/aromatic groups is expected to alter the electronic states, albeit to a lesser extent as opposed to bay functionalization due to the higher proximity from the chromophores. N-Substitution with butylphenyl and phenylpyrrole groups on the two end positions of PMDI improve the hole mobility, whereas pyrazine and pyrazole rings facilitate electron mobility.²² Thus, N-substitutions are expected to alter the reorganization energy, examined vide infra. Herein, both aliphatic (methyl) and aromatic (phenyl) functional groups are introduced in PMDI (m-PMDI and p-PMDI) to comprehend the effect in comparison to the literature values.

Naphthalene diimides (NDI) derivatives are of interest for their appreciable electron affinity, charge mobility, photoluminescence quantum yields and electro-thermochemical stability.^23,24 Notably, two types of NDI derivatives (NDI and NDI2) are taken into consideration, where the diimide group positions are perpendicular to each other. Such modification will allow us to favourably ascertain the best NDI derivative for optoelectronic applications. Interestingly, alkyl/aryl-N substitutions hamper π–π stacking between the NDI monomers, resisting aggregation induced emission (AIE) that is more prominent in extended rylene derivatives as discussed further.^25,26 Interestingly, 2,6 diisopropyl phenyl (iPrP-NDI) and diphenylmethylene (DPM-NDI) substitutions exhibit much higher mobility than state-of-the-art fullerene acceptors, making them potential candidates to replace fullerenes in organic electronics.²⁴ The presence of electron withdrawing diimide units facilitates a reduction process and stabilizes the anion radical.

Similar to NDI, anthracene diimides have two types of derivatives (ADI and ADI2), where diimides are either linear five-membered or transverse six-membered.²⁷ The DFT calculation shows that the six-membered diimide is directly involved in delocalization with the anthracene backbone, increasing the effective conjugation length. This results in a low-lying LUMO energy level and excellent oxidative stability compared to the five-membered anthracene diimide. Thus, six-membered diimides exhibited better electron-accepting properties in OSCs. Such positioning offers direct trend analysis with NDI derivatives to understand the effect of rylene extension, diimide position, ring size and transverse geometry.

Similarly, pyrene derivatives (PyDI1 and PyDI2) can be considered orthogonally extended structures of NDI.²² However, the effect of increasing the π-conjugation of pyrene by attaching aryl substituted imide groups is very rarely reported.²⁸ Two pyrene imide isomers can be obtained, one having transverse imide rings at the nodal-region (PyDI1) and another having centrosymmetric five-membered imide rings (PyDI2). However, such derivatives have not been experimentally observed in the literature. Their characterisation will unveil new avenues for pyrene derived semiconductors. Moreover, the definitive role of aryl substitution can also be established by comparison with the alkyl substituted derivative.

Perylene diimides (PDIs) are the most promising acceptors for OPV applications due to their ease of functionalization, suitable optical absorption range, and strong electron deficiency.²⁹ The strong tendency towards aggregation of PDI can be minimized by two strategies to reduce the strong π-stacking, enhance the processability and form favorable BHJ domains. One is to disrupt the strong π–π interaction by introducing torsion in the PDI backbone, such as twisted PDI dimers connected at the N-position or bay positions (1-, 6-, 7-, and 12-positions). Another is synthesizing A–D–A (Acceptor–Donor–Acceptor) molecules with the donor coupled to PDIs at the bay positions.³⁰

Corannulene and azulene diimides (CorDI and BAzDIs, respectively) deviate from the core planarity of the rylene. They are very rare and assemble into 1D ribbons by face-to-face π–π stacking/hydrophobic interactions, facilitating appreciable electron mobility.^31–34

Geometry

In terms of electrical materials, the geometries play a significant role in molecular packing. Band gaps,³⁵ absorption,³⁶ and the highest occupied molecular orbital (HOMO) and LUMO energy levels³⁷ are crucial variables for electrical applications. Each molecule's geometry is optimised using B3LYP/6-311++g(2d,2p) and ωB97XD/6-311++g(2d,2p). The structures optimised using functional B3LYP exhibit a ground state with reduced energy and minimal alterations in their structure compared to the molecules optimised using ωB97XD. This deviation can be inferred from the approximations. Additionally, frequency calculations were performed to verify the attainment of true minima. The two measurable bond parameters—dihedral angle and bond length—are utilised to assess the influence of substituted acceptors on their attachment sites.³⁸ The bond length is a crucial metric that indicates the presence of effective conjugation in a bond. The dihedral angles connecting the core and end substituents exhibit a high level of concordance with estimates previously reported for similar systems. The bond lengths of all examined molecules fall within the range of 1.40–1.49 Å: the bond lengths of C–C (1.54 Å) and C=C (1.34 Å).³⁹ This highlights the presence of π-conjugation between the acceptor (A) and substituent regions. The phenomenon of conjugation resulting from the dispersion of pi-electrons facilitates the transfer of charges between regions of electron donation and electron acceptance.⁴⁰

NDI, ADI2, PDI, and BAzDI have substituents positioned perpendicular to their core in both functionals. Conversely, the remaining structures align with the core plane, albeit with a slight deviation in the angle. The core of the CorDI has a conventional bowl-shaped form, with a sidechain positioned beneath the plane of the core. The substituent of BAzDI is rotated relative to the plane of the core. Due to the existence of conjugation and planarity, these molecules can effectively facilitate charge transfer, potentially enhancing their efficiency.

Electronic properties

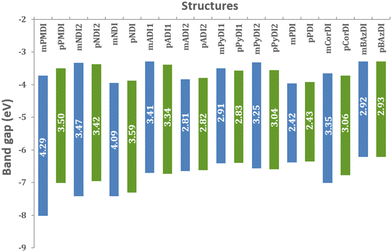
The frontier molecular orbital (FMO) investigation helps to ascertain the HOMO and LUMO energy levels. Fig. 2 shows the fully optimised geometries of designed molecules in their ground state. E_HOMO and E_LUMO levels ranged from −7.99 to −5.93 eV and −3.93 to −3.26 eV, respectively in the energy level diagram of proposed acceptors (Fig. 3).

Fig. 2 Optimised structures of rylene diimides.

Fig. 3 Band gap energy of rylene diimides.

However, the band gap considerably affects charge transport. Table 1 shows the band gap values of all compounds calculated using the following formula:

E_g = E_LUMO − E_HOMO

Table 1 Band gap energy of the frontier orbitals

Structure	Methyl				Phenyl
	state number	E HOMO	E LUMO	E g (eV)	state number	E HOMO	E LUMO	E g (eV)
PMDI	63 → 64	−7.99	−3.70	4.29	95 → 96	−6.98	−3.48	3.50
NDI2	76 → 77	−7.40	−3.31	4.09	108 → 109	−6.93	−3.35	3.57
NDI	76 → 77	−7.39	−3.91	3.47	108 → 109	−7.27	−0.14	3.41
ADI1	89 → 90	−6.67	−3.26	3.41	121 → 122	−6.70	−3.36	3.34
ADI2	89 → 90	−6.62	−3.80	2.81	121 → 122	−6.59	−3.77	2.82
PyDI1	95 → 96	−6.39	−3.47	2.91	127 → 128	−6.37	−3.54	2.83
PyDI2	95 → 96	−6.54	−3.30	3.24	127 → 128	−6.56	−3.52	3.03
PDI	108 → 109	−6.35	−3.93	2.42	140 → 141	−6.33	−3.90	2.43
CorDI	107 → 108	−6.98	−3.63	3.35	139 → 140	−6.75	−3.69	3.05
BAzDI	109 → 110	−6.18	−3.26	2.92	141 → 142	−6.19	−3.26	2.93

---

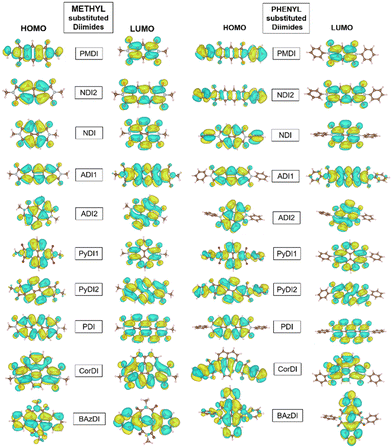
The charge transport characteristics of the molecules are qualitatively represented by the distribution pattern of the HOMO and LUMO. The imide N substitutions generally leave the central moieties unaltered. Thus, LUMO orbital connections are more likely than HOMO orbital connections. This promotes electron transfer over hole transfer. The spatial arrangement of FMOs is delocalized across the molecule for all acceptors (Fig. 4), causing significant optical absorption.

Fig. 4 HOMO and LUMO of rylene diimide structures.

The HOMO and LUMO of methyl substituted diimides are distributed on the core but not on the methyl group. However, phenyl substituted diimides have their HOMO distributed on the core and the end group, except for ADI1, ADI2 and PDI. This exception is due to the differences in conjugation and resonance within the aromatic core and phenyl substituent which lead to variations in the HOMO distribution. The LUMO of methyl and phenyl substituted PMDI is only located on the diimide core whereas the HOMO is distributed on the core and corresponding substituents. NDI and NDI2 have their HOMO and LUMO only distributed on the core of the methyl substituted structure, but the phenyl substitution has its HOMO on the core and the phenyl group. The HOMO and LUMO of the methyl and phenyl substituted ADI1 and ADI2 structures are only located on their aromatic core. PyDI1 and PyDI2 are distributed with LUMO only on the aromatic whereas the phenyl substituted structure has its HOMO also on their substituent.

The HOMO and LUMO of methyl substituted PDI is mostly located on the core but the HOMO is extended to its substituent phenyl group for the phenyl substitution. The HOMO and LUMO of the CorDI structure are spread throughout the core but the phenyl substituted HOMO is extended due to its phenyl substitution. The HOMO of the methyl substituted BAzDI is distributed on the entire molecule in the core and the methyl group whereas the LUMO is only spread linearly along its core. Similarly, the phenyl substituted BAzDI LUMO is only extended along its core, but the HOMO is covered to its entirety (Fig. 4).

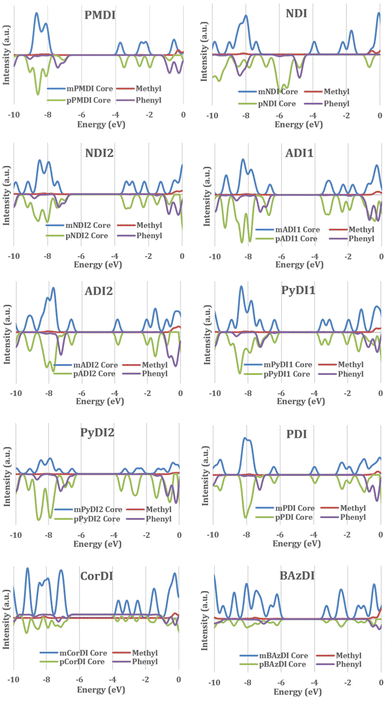
To corroborate the results of the FMO analysis, DOS analysis was conducted of all the structures investigated in this study using GaussSum software. The structures were divided into two parts: the central acceptor core (rylene core) and the terminal substituents (methyl and phenyl) to generate the PDOS curve graphs (Fig. 6).

Fig. 5 Band gap trends of (a) methyl substituted and (b) phenyl substituted rylene diimides. A linear decrease in the bandgap with increasing rylene core is observed with two deviations: increasing band gap of PyDI and CorDI.

Fig. 6 PDOS of rylene diimides. The contribution of mRDI's core and its methyl groups are shown in blue and red lines. The contribution of pRDI's core and its phenyl groups are shown in green and violet lines.

The density distribution of rylene diimide for HOMO and LUMO is analysed through partial density of state calculation with GaussSum software. The substituent's partial density for most of the rylene diimide is positioned at a lower energy than the HOMO and at a higher energy than the LUMO and the rylene core contributes to the HOMO–LUMO orbital.

Optical properties

Optical features of low excitation energy, wider absorption spectrum, and high oscillator strength are crucial for the advancement of next generation OSCs. Table 2 compiles the wavelength at which maximum absorption occurs, the excitation energy, the oscillator strength, and the contribution of the primary electronic transition for the diimide molecules. B3LYP/6311++g(2p,2d) was utilised to compute these parameters, employing the TD-DFT technique. The absorption spectra of all compounds were acquired using Origin.

Table 2 Transitions of rylene diimides

Methyl
Structures	State number	Wavelength (nm)	Oscillator strength (f)	Transition energy (eV)	Major transitions
					Orbitals involved	Contribution (%)
PMDI	14	240.32	0.5113	5.1591	H → L+1	76.20
	19	219.15	0.6527	5.6576	H−6 → L+1	79.22
NDI	39	194.20	1.3123	6.3843	H−8 → L+1	53.85
	3	385.45	0.3044	3.2166	H → L	98.08
PDI	46	225.72	0.8593	5.4928	H−3 → L+3	54.37
	1	536.79	0.6544	2.3097	H → L	99.99
ADI1	9	298.07	1.7138	4.1596	H−1 → L	75.94
	38	213.06	0.5921	5.8191	H → L+7	72.04
ADI2	13	259.83	0.4138	4.7718	H → L+2	45.65
	1	489.86	0.1837	2.5310	H → L	98.87
PyDI1	31	228.69	1.0335	5.4214	H−1 → L+2	40.84
	50	203.99	0.8825	6.0780	H−3 → L+4	88.43
PyDI2	11	281.16	0.6944	4.4098	H−1 → L+1	74.08
	1	427.33	0.2503	2.9014	H → L	86.31
CorDI	41	229.91	0.5909	5.3927	H−3 → L+3	55.11
	10	339.12	0.3560	3.6560	H−3 → L	75.26
BAzDI	14	324.98	1.2752	3.8151	H−1 → L+3	56.96
NDI2	11	269.86	1.0106	4.5944	H−1 → L+1	73.74
	47	181.20	0.3426	6.8424	H → L+8	90.65

---

Phenyl
Structures	State number	Wavelength (nm)	Oscillator Strength (f)	Transition energy (eV)	Major transitions
					Orbitals involved	Contribution (%)
PMDI	12	284.05	0.4841	4.3649	H−6 → L	70.95
	29	224.71	1.3015	5.5175	H−7 → L+1	58.23
NDI	6	383.58	0.3601	3.2323	H−4 → L	73.59
	31	235.12	0.1358	5.2732	H−4 → L+2	86.59
PDI	1	539.40	0.7806	2.2985	H → L	99.91
	27	268.09	0.0776	4.6248	H → L+4	55.61
ADI1	19	289.61	2.2230	4.2811	H−7 → L	71.30
	4	380.08	1.0993	3.2620	H−1 → L	48.40
ADI2	19	259.52	0.4777	4.7775	H → L+2	44.17
	1	491.17	0.2348	2.5243	H → L	98.78
PyDI1	35	247.34	0.6038	5.0127	H → L+5	50.63
	15	317.43	0.5611	3.9059	H → L+2	80.36
PyDI2	25	278.30	0.8508	4.4550	H−5 → L+1	78.76
	10	340.40	0.5671	3.6424	H−2 → L+1	43.01
CorDI	31	273.05	0.4624	4.5407	H → L+3	55.78
	19	327.49	0.2301	3.7859	H−6 → L+1	73.19
BAzDI	16	328.47	0.8485	3.7746	H−1 → L+3	51.03
NDI2	8	341.85	0.8791	3.6268	H−4 → L	54.23
	25	258.67	1.9118	4.7932	H−7 → L+1	77.79

---

Both phenyl-substituted PDI and NDI have the highest λ_max value, indicating that substituted acceptor groups perform better than other compounds. However, methyl substituents (mPDI and mNDI) have the shortest λ_max value. The electron-withdrawing phenyl group in the acceptor component led to a change in λ_max wavelengths towards longer wavelengths. NDI and PMDI show a 40 nm hypsochromic shift with WB97XD. Oscillator strength usually increases the experimental absorption coefficient. The predicted f values are: pADI1 > mADI1 > mNDI > mBAzDI > mPyDI1 > mNDI2 > pNDI2 > mPDI > pPyDI2 > pBAzDI > pPDI > mPyDI1 > mCorDI > mPMDI > pPMDI > pADI2 > pCorDI > mADI2 > pNDI.

An increase in the number of aromatic rings in the methyl substituted diimides shifts the absorption band to longer wavelengths. Electron-donating methyl substituents in the diimides can also lead to a red shift by increasing electron density in the aromatic system, stabilizing the pi electrons and lowering the energy of electronic transitions. mPMDI with one aromatic ring in its core has its major transition at 219 nm whereas mNDI2 with two aromatic rings has its major absorption peak shifted to a longer wavelength of 259 nm. mADI2 with three aromatic rings also lies around the same wavelength since it has a slightly inclined planar structure. mPyDI2 with four non-linear aromatic rings is further red shifted to 281 nm. mADI1 with three aromatic rings but a linear structure is red shifted to 298 nm. However, mBAzDI with a seven-membered ring inclined vertically with the seven-membered diimide is shifted to a longer wavelength of 324 nm. This longer red shift is due the presence of a bulkier seven-membered aromatic ring vertically inclined to a seven-membered diimide structure. However, the remaining methyl substituted diimide derivatives have narrow absorption peaks. The mNDI derivative has a more intense narrow absorption peak at 194 nm. The major absorption peak of mPyDI1 is red shifted to 228 nm due to an increasing number of aromatic rings in the core. Similarly, mCorDI is red shifted to 229 nm in the same region due to the vertical inclined planarity. mPDI has its maximum absorption at 225 nm but it also has a broad peak at around 540 nm due to the presence of five aromatic rings stacked up (Fig. 7).

Fig. 7 (a) Overall absorption spectra of methyl substituted diimide. (b) and (c) Absorption spectra of methylated diimides with similar trends. (d) Overall absorption spectra of phenyl substituted diimide. (e) and (f) Absorption spectra of phenylated diimides with similar trends.

Phenyl substituted diimides also follow the same pattern of λ_max absorption peaks. The pPMDI derivative has its major transition at 224 nm, followed by the red shift from pNDI2 at 258 nm. pADI2 also lies in the same region of 259 nm but with a low intensity absorption peak. This is due to the presence of a twisted phenyl substituent that affects the delocalization of the π-electrons. pPyDI2 with four aromatic rings also has less intensity but is red shifted to 273 nm. The absorption peak of pADI1 with three linear aromatic rings is shifted to the longer wavelength of 289 nm. However, vertically inclined pBAzDI is red shifted to 328 nm due to the presence of twisted phenyl substitution. The remaining compounds have varied absorption peaks with differing intensities. pPyDI1 with four aromatic rings has its major absorption peak at 247 nm. It is followed by pCorDI's absorption peak around 273 nm which is red shifted from pPyDI1 due to increased aromatic rings in the core. The pNDI and pPDI structures have twisted phenyl substitutions, which increases the electron density around the aromatic core. This stabilizes the π-electron system and lowers the energy of electronic transitions, causing a red shift at 383 nm and 539 nm, respectively.

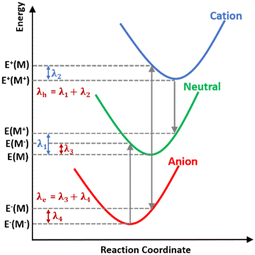
Reorganization energy

Understanding how molecular structure affects charge transport is essential for developing OSC device candidates. Reorganisation energy controls the charge transfer motion. It consists of two contributions: internal (λ_int) and external (λ_ext). The charge transfer mechanism involves λ_int owing to molecular geometric changes and λ_ext due to environmental changes produced by the surrounding medium's polarisation. Considering that λ_ext is substantially smaller than λ_int (approximately 0.01 eV), the external influence is often overlooked.⁴¹ Therefore, this study assumes that λ is equal to λ_int (Fig. 8).

Fig. 8 Schematic energy profile of reorganization energy.

The hole transfer rate negatively correlates with reorganisation energy. Therefore, a higher reorganisation energy leads to poorer hole mobility in the material. Hence, new materials with minimal reorganisation energy serves as a promising foundation for investigating the charge transport characteristics in OSCs.

The order of reorganization energy for holes and electrons are listed below:

Holes: pNDI < pPyDI1 < pPDI < mBAzDI < pADI2 < mADI2 < mPyDI2 < pPyDI2 < mPyDI1 < mNDI2 < mPDI < pADI1 < pBAzDI < mCorDI < mNDI < mPMDI < mADI1 < pCorDI < pPMDI < pNDI2.

Electrons: mPyDI1 < pPyDI1 < mADI1 < mPDI < pADI1 < mCorDI < pPDI < mNDI2 < mNDI < pCorDI < pNDI < pNDI2 < pPyDI2 < pBAzDI < mBAzDI < mPMDI < mPyDI2 < mADI2 < pADI2 < pPMDI.

pNDI and pPyDI1 have higher hole transport energy when calculated using B3LYP, while mPyDI1 and pPyDI1 demonstrate higher electron transfer energy with B3LYP (Fig. 9).

Fig. 9 Reorganization energy of (a) cationic and (b) anionic rylene diimides with methyl (orange) and phenyl (blue) substituents. The hole mobility of ADI1, CorDI and electron mobility of ADI1, PyDI2 are found to deviate from the linear trend of reorganisation energy.

An exhaustive analysis of λ_e and λ_h for diimide derivatives reveals that all compounds can function as hole carrying materials and electron transporters. Furthermore, all the planned acceptors maintained their original configuration in the ionic state, with only minor alterations in the lengths of C–C, C–N, and N–O bonds. This evidence supports the use of studied derivatives that exhibit favourable geometric relaxation characteristics and high charge carrier mobility, leading to a diverse and effective range of acceptors.

Discussion

Based on the obtained results and by comparing the trends from different point of views, the following observations were made:

Rylene core

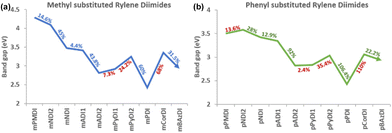
Increasing the number of aromatic rings in the diimide's rylene core does not affect the planarity of the structures from PMDI to PDI (benzene ring count from one to five). Planarity in the diimide structure induces π-electron delocalisation within the extended conjugated system. This promotes efficient transport of electrons, reducing the likelihood of recombination and increasing the overall charge carrier mobility. Also, the potential energy of the diimides shows a linear steady trend from pyromellitic to bisazulene molecules. The extended planarity and overlapping π-orbitals ensure a steady decrease in the energy barrier, resulting in a smaller band gap. A linear decrease in the HOMO–LUMO energy gap is observed from pyromellitic to anthracene diimides but pyrene diimide shows a sudden increase in the band gap due to the bay-substituted arrangement which may introduce some steric effects or alter the specific nature of the π-orbital interactions compared to anthracene (Fig. 5). The increased conjugation in pyrene diimide results in a more stabilized electronic structure, leading to higher energy levels for HOMO and LUMO. However, fused benzene rings arranged in a non-linear, bay-substituted manner in perylene diimide introduces some structural complexity which results in a reduction of the band gap energy. Due to the non-planar nature of corranulene (bowl shaped core) and bisazulene (twisted core), the conjugation and electron distribution is disrupted and the HOMO–LUMO energy gap is notably affected, as discussed in the later sections.

Diimide ring size and position

The change in the diimide ring size from five-membered to six-membered shows varied outcomes in contrasting patterns. Compared with the six-membered diimides, the structures with five-membered diimide rings (PMDI, NDI2, ADI1, PyDI1, and PyDI2) show a linear increase in electron mobility with an increasing number of rylene cores. The five-membered counterpart of naphthalene diimide and anthracene diimide (NDI2 and ADI1) show better electron mobility compared to their six-membered diimide structure (NDI and ADI2). PDI with six-membered diimide exhibits better electron mobility with an increasing rylene core than NDI and ADI as expected. Positioning the diimide rings to the rylene core at their 2,3 position has better electron mobility than the 1,2 position. This is due to the transverse geometry of 1,2-diimide rylene which restricts the linear movement of charges in the crystal lattice, reducing the charge transfer ability. The 2,3-diimide rylenes have linear functionalization with diimides giving a unidirectional flow of charges in their plane of symmetry.

Substitution

The substitution effect and the extension of core conjugation is studied by substituting methyl (electron donating) and phenyl (electron withdrawing) groups at the N position of the diimide. Methyl substituted rylene diimides generally show better electron mobility compared to the phenyl substituted rylene diimides. This is due to disruption of the structure's planarity induced by the twisting of the phenyl ring at an angle of 30° to 90°. Consequently, all the LUMO of the phenyl substituted rylene diimide is centralized along the rylene core, with the least delocalization over the phenyl substitution. This charge distribution deviation of phenyl substituted rylene diimides reduces their electron transport ability, whereas the methyl substituted rylene diimides have favourable charge distribution due to their simple electron donating ability.

Core planarity

PMDI to PDI structures have rylene core expansion from one to five rings in a linear fashion. We observed a non-planar (bowl-shaped) rylene core with five aromatic rings (corannulene) and a non-planar (twisted) core with a seven-membered diimide ring (biazulene). Although the non-planar structures show a steady red shift and reduced band gap along with the planar structures, the reduced electron mobility of the non-planar structures demonstrate the disruption of charge distribution pathways compared to the planar counterparts.

Conclusions

Overall, this manuscript highlights the main structural variations of rylene diimide acceptors with respect to the core and substitution, followed by their effect on optical and electronic parameters. The essential roles of rylene core expansion, diimide ring size, position, substitution as well as core planarity were extensively compared. We observed a steady decrease in band gap and an increase in electron mobility upon linear ring size expansion from one to five, whereas twisted and bowl shaped non-planar counterparts exhibit diminished mobility. Regarding diimide substitution, the five-membered diimide shows better charge transport compared to six-membered counterparts, and 2,3-substituted diimide demonstrates higher conductivity than 1,2 substituted diimide due to transverse geometry and structural symmetry. Finally, the N-substituted methyl group containing diimides show better performance than phenyl containing diimides on account of steric induced twisting and conjugation disruption in phenyl substitution. The wide variation and their effect on the optical and electrical properties of the solar cell acceptor will guide us to design better materials in the future.

For example, bay functionalization and dimer/chain formation may provide additional features such as wide solar spectrum utilization, unidirectional charge transport and reduced recombination. The position of functionalization (e.g., peri, bay or ortho) would induce further changes in the physical property, crystallinity and self-assembly morphology of PDI.³¹ This suggests that structural modification by appropriate substituents exerts influences on PDI in the solid state. The peri-functionalization with alkyl chain tends to affect the solubility and J-aggregation of PDI, influenced by solvent polarity, which may lead to solvatochromism,⁴² which is an ongoing investigation in our laboratory.

Author contributions

SV performed all the calculations and wrote the original manuscript. TK and AP supervised the project, acquired funding, and formatted the draft and graphics.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge the Science and Engineering Research Board (SERB) Start Up Research Grant SRG/2022/002195 for funding. Authors thank High-Performance Computing Centre, SRM Institute of Science and Technology for providing the computational facility.

References

1. A. Wadsworth, Z. Hamid, J. Kosco, N. Gasparini and I. McCulloch, Adv. Mater., 2020, 32, 2001763.
2. S. K. Shah, Nano Express, 2020, 1, 020037.
3. F. Gao, S. Ren and J. Wang, Energy Environ. Sci., 2013, 6, 2020.
4. M. Janjua, J. Iran. Chem. Soc., 2017, 14, 2041–2054.
5. M. Haroon, A. A. Al-Saadi and M. Janjua, J. Phys. Org. Chem., 2022, 35, e4314.
6. M. Y. Mehboob, R. Hussain, M. Adnan, K. Saira, U. Farwa, Z. Irshad and M. Janjua, J. Phys. Chem. Solids, 2022, 162, 110508.
7. J. Yang, B. Xiao, A. Tang, J. Li, X. Wang and E. Zhou, Adv. Mater., 2018, 31, 1804699.
8. A. Pal, L. K. Wen, C. Y. Jun, I. Jeon, Y. Matsuo and S. Manzhos, Phys. Chem. Chem. Phys., 2017, 19, 28330–28343.
9. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16 Rev. A.03, Gaussian, Inc., Wallingford, UK, 2016.
10. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
11. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
12. U. Gross and W. Kohn, Adv. Quantum Chem., 1990, 21, 255–291.
13. E. K. U. Gross and W. Kohn, Phys. Rev. Lett., 1985, 55, 2850–2852.
14. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000.
15. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
16. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
17. N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845.
18. S. T. Ang, A. Pal and S. Manzhos, J. Chem. Phys., 2018, 149, 044116.
19. N. Dardenne, X. Blase, G. Hautier, J.-C. Charlier and G.-M. Rignanese, J. Phys. Chem. C, 2015, 119, 23373–23378.
20. L. Chen, C. Li and K. Müllen, J. Mater. Chem. C, 2014, 2, 1938–1956.
21. Q. Zheng, J. Huang, A. Sarjeant and H. E. Katz, J. Am. Chem. Soc., 2008, 130, 14410–14411.
22. R. Khatua, S. Debata and S. Sahu, New J. Chem., 2020, 44, 8412–8421.
23. S. Amiralaei, D. Uzun and H. Icil, Photochem. Photobiol. Sci., 2008, 7, 936–947.
24. N. Kumari, S. Naqvi, M. Ahuja, K. Bhardwaj and R. Kumar, J. Mater. Sci.: Mater. Electron., 2020, 31, 4310–4322.
25. Y. Chen, J. W. Y. Lam, R. T. K. Kwok, B. Liu and B. Z. Tang, Mater. Horiz., 2019, 6, 428–433.
26. L. Zong, Y. Xie, C. Wang, J. Lǐ and Q. Li, Chem. Commun., 2016, 52, 11496–11499.
27. A. R. Mohebbi, C. Munoz and F. Wudl, Org. Lett., 2011, 13, 2560–2563.
28. L. Zou, X.-Y. Wang, X.-X. Zhang, Y.-Z. Dai, Y.-D. Wu, J.-Y. Wang and J. Pei, Chem. Commun., 2015, 51, 12585–12588.
29. D. Zhao, Q. Wu, Z. Cai, T. Zheng, W. Chen, J. R. Lu and L. Yu, Chem. Mater., 2016, 28, 1139–1146.
30. Q. Yan, Y. Zhou, Y.-Q. Zheng, J. Pei and D. Zhao, Chem. Sci., 2013, 4, 4389.
31. W. Ji, L. Ye, X. Li, C. Xiao, F. Tan, W. Zhao, J. Hou and Z. Wang, Chem. Commun., 2014, 50, 1024–1026.
32. K. Shi, T. Lei, X. Wang, J. Wang and J. Pei, Chem. Sci., 2014, 5, 1041–1045.
33. H. Xin, C. Ge, X. Yang, H. Gao, X. Yang and X. Gao, Chem. Sci., 2016, 7, 6701–6705.
34. X. Fu, Y. Zhen, Z. Ni, Y. Li, H. Dong, J. S. Siegel and W. Hu, Angew. Chem., Int. Ed., 2020, 59, 14024–14028.
35. M. Miar, A. Shiroudi, K. Pourshamsian, A. R. Oliaey and F. Hatamjafari, J. Chem. Res., 2020, 45, 147–158.
36. X. Shang, D. Han, M. Liu and G. Zhang, RSC Adv., 2017, 7, 5055–5062.
37. B. Gi Kim, X. Ma, C. Chen, Y. Ie, E. W. Coir, H. Hashemi, Y. Aso, P. Green, J. Kieffer and D. H. Kim, Adv. Funct. Mater., 2012, 23, 439–445.
38. S. J. Akram, N. M. A. Hadia, J. Iqbal, R. F. Mehmood, S. Iqbal, A. M. Shawky, A. Asif, H. H. Somaily, M. Raheel and R. A. Khera, RSC Adv., 2022, 12, 20792–20806.
39. R. C. Fortenberry, C. M. Novak, T. J. Lee, P. P. Bera and J. E. Rice, ACS Omega, 2018, 3, 16035–16039.
40. Y.-J. Cho, A.-R. Lee, S.-Y. Kim, M. Cho, W.-S. Han, H.-J. Son, D. W. Cho and S. O. Kang, Phys. Chem. Chem. Phys., 2016, 18, 22921–22928.
41. E. F. Oliveira and F. C. Lavarda, Polymer, 2016, 99, 105–111.
42. C. A. Fuller and C. E. Finlayson, Phys. Chem. Chem. Phys., 2017, 19, 31781–31787.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dt00250h

---