Kinetically induced memory effect in Li-ion batteries

Abstract

Effective optimization and control of lithium-ion batteries cannot neglect the relationship between fundamental physicochemical phenomena and performance. In this work, we apply a multi-step charging protocol to commercially relevant electrodes, such as LiNi_0.8Mn_0.1Co_0.1O₂ (NMC811), LiFePO₄ (LFP), LiMn_1.5Ni_0.5O₄ (LMNO), LiMn_0.4Fe_0.6PO₄ (LMFP), Li₄Ti₅O₁₂ (LTO) and Na₃V₂(PO₄)₃ (NVP), to investigate how the initial rate affects their kinetic response. Remarkably, electrodes undergoing phase separation exhibit a pronounced counter-intuitive memory effect under high-rate operating conditions. Using operando microbeam X-ray diffraction, the origin is demonstrated to be embedded in rate-dependent multi-electrode particle dynamics. Developed phase-field electrochemical models capture the collective behaviour of electrode particles underlying the kinetically induced memory effect, establishing how the thermodynamics of the nanoscale (primary particle) level affects the macroscopic electrode response under realistic conditions. Building upon these findings, an analytical model is presented, capable of capturing and predicting these effects. These results challenge established battery management strategies, opening the doors for improved characterization and optimization of fast-charging protocols, crucial in minimizing aging and heat production while enhancing energy efficiency and benefitting a wide range of battery-powered applications.

---

Broader context

Lithium-ion batteries are among the defining technologies of this century, playing an irreplaceable role in grid storage and electric vehicles. These systems are inherently dynamic, requiring the batteries to respond to unpredictable power demands. To maximize their performance, accurately predicting their response to such inputs is essential. Achieving this requires a comprehensive understanding of their chemo-physical behaviour, coupled with advanced computational modelling. This study presents a series of electrochemical experiments conducted on commercial electrode materials, including LFP, LTO, and NMC. The results reveal unexpected behaviours in materials undergoing phase separation, characterized by their thermodynamic tendency to form Li-rich and Li-poor phases. Remarkably, these materials exhibit an “activation” effect during faster (dis)charging pulses, resulting in a kinetic memory effect through an inverse correlation between overpotential and the prior (dis)charge rate. The findings are further supported by a chemo-physical explanation derived from microbeam X-ray diffraction and electrochemical phase-field modelling. These results are directly applicable to practical battery operations and highlight the importance of accounting for phase separation phenomena when designing and operating lithium-ion batteries.

Introduction

The pursuit of a sustainable future has propelled lithium-ion batteries (LIBs) into a pivotal role across diverse technological realms.¹ Initially confined to consumer electronics, LIBs have become indispensable in electric vehicles, renewable energy storage, off-grid power systems, and grid stabilization applications. A comprehensive understanding of their chemo-physical behaviour is essential to unlocking the full potential of LIBs within complex and multi-component systems such as electric vehicles and grid storage.

The concept of ‘memory effect’ in batteries has gained widespread recognition in the case of Ni–Cd and Ni–metal-hydride systems, where traces of prior cycling are retained, distorting the voltage profile.^2–4 Interestingly, while this phenomenon has been assumed not to affect LIBs, a pivotal study by Sasaki et al.⁵ provided the first insights that this may not be true. Researchers⁵ redefined the memory effect found in the study as ‘abnormal changes in working voltage’ and provided compelling evidence of its occurrence in materials that undergo phase separation within LIBs. Specifically, they show that when a LiFePO₄ (LFP) electrode is charged to a designated state of charge (SOC), discharged, and then rapidly recharged, a small voltage peak emerges in its voltage profile. This peak is consistently observed among different experiments, but it is limited in magnitude and short-lived, making it a phenomenon of purely fundamental importance, without strong practical implications. Moreover, path-dependent effects on the voltage of phase-separating materials were also notably described by Katrašnik⁶ and Deng⁷ who focused on the observation of a slight change in open circuit voltage at a given SOC depending on the previous discharge pulse.

The common denominator in the aforementioned studies is the possibility of explaining these phenomena through the lenses of the complex kinetic behaviour of phase-separating active materials. In the active materials that (de)lithiate following a solid-solution path, such as LiCoO₂ (LCO) and LiNi_{xMnyCo1−x−y}O₂ (NMC), Li diffuses inside the particles uniformly such that, when the current is stopped, the concentration inside the particles quickly equilibrates, both on crystal and agglomerate levels. Thus, the system evolves without substantial intra- or inter-particle heterogeneities, relying solely on the particle's size distribution and position with respect to the electrode's depth as a source of heterogeneities. In contrast, LiFePO₄ (LFP) and Li₄Ti₅O₁₂ (LTO) undergo phase separation during the (de)lithiation process due to their physio-mechanical properties. At a given state of charge, even under equilibrium conditions, these particles exhibit coexisting Li-poor and Li-rich phases. This fundamental difference in reaction behaviour, evident in a flat voltage plateau and an equilibrium voltage hysteresis,⁸ is intricately linked to inter-particle heterogeneities.

The literature consistently reveals that the applied current does not uniformly distribute among all particles in the electrode; rather, a subset of active particles carries the bulk of the current while others remain unaffected in terms of (de)lithiation.^9–12 Moreover, the active particle fraction has been established to be proportionate to the applied rate.^9,10 This phenomenon stems from the size-dependent energy barrier for the nucleation of both the lithium-rich and the lithium-poor phases, favouring the reaction in smaller or nucleated primary particles.¹³ Consequently, the reaction dynamics exhibit rate-dependent behaviour, ranging from particle-by-particle lithiation at low rates to collective lithiation at high rates, where the majority of particles are active to sustain the applied current. These dynamic systems can be mathematically described using the regular solution theory,^14–17 and simulated with phase-field modelling, providing a realistic and predictive depiction of the complex dynamics.

Building on this established theory, the acknowledged path dependence of electrode materials,^5,18–21 and previously observed memory effects,^5,7,18 our study reveals the presence and the origin of the strong influence of the initial applied rate on the subsequent cycling performances. Specifically, the discovered phenomenon – hereby addressed as the kinetically induced memory effect – presents an increase of 50% in the fast-charging overpotential when slow charging is applied in the initial step. Furthermore, herein, we demonstrate this to be a general phenomenon in electrodes that exhibit a first-order phase transition upon (dis)charge. Employing operando monitoring of individual electrode crystallites, we reveal the effect of the current on the active particle fraction, while electrochemical phase-field simulations deepen the understanding of the underlying mechanism. Finally, the obtained relationship between C-rates and active particles is included in an analytical model capable of explaining directly the observed results. We conclude by recognizing the pivotal role of preceding applied rates in shaping the voltage profile and suggest its influence on SOC estimation and fast-charging protocol optimization in large-scale erratic systems coupled with LIBs.²²

Results and discussion

Memory effect in commercial battery electrode materials

Real-world battery utilization often results in frequent current changes. So, to better understand the behaviour of commercial battery electrodes in these scenarios, we designed a protocol that is simple enough to allow interpretation and understanding but can reproduce some of the key features of multi-step charging (Fig. 1a). The protocol consists of three distinct steps: the writing step, the resting step, and the reading step. The writing step refers to a partial (dis)charge of the battery to 50% SOC imposed at varying rates, to induce a non-equilibrium state. Subsequently, a 1 h resting step under open circuit conditions is applied to let the system partially relax and ensure that no kinetically induced gradients exist in the electrolytes. Finally, the reading step completes the (dis)charge process at a fixed rate to examine the impact of the previously imposed rate on the dynamic behaviour of the battery. The cell is then slowly cycled towards full charge and discharge before applying the next protocol, bringing the system to an equilibrium state and erasing the effect. Fig. 1a provides a schematic view of the procedure. The results in Fig. 1c–e illustrate typical electrochemical responses recorded from the described writing, relaxation, and reading steps for commonly used electrode materials. Focusing on the voltage curves during the reading steps, a clear distinction emerges between the different electrode materials. As expected, in the case of LiNi_0.8Mn_0.1Co_0.1O₂ (NMC811), in Fig. 1c, when a lower charging rate (0.5C) is applied during the writing step, the reading step shows similar overpotential and marginally higher capacity compared to writing steps performed at 1.0C or 2.0C. In contrast, the protocol on an LFP||Li cell shows a different behaviour (Fig. 1b and Fig. S1†): when the writing step is conducted at 0.2C, the reading step presents a 3.75 V plateau, whereas a writing step at 5.0C yields a plateau voltage of 3.63 V. The inverse proportionality between the applied rate and reading step overpotential is clearly observed in Fig. 1b, which also highlights a saturation current at 3.0C, beyond which no further reduction in the overpotential occurs. Moreover, an additional 4% capacity can be charged in the 5.0C–3.0C cycle compared to the 0.2C–3.0C case. The LFP electrode, despite starting the 3.0C reading step from the same SOC and at the same open circuit voltage, shows a great difference in overpotential and capacity depending on the previously applied rate. This demonstrates that this material displays a kinetically induced memory effect, that is, it is influenced by the previous cycling history. Notably, the LTO||Li cell shows the same unexpected behaviour (Fig. 1e) although no saturation current was observed within the range of C-rates tested (Fig. 1b). The origin of this difference can be found in the different reaction kinetics between LFP and LTO (Fig. S15 and S22†). Moreover, the same behaviour can also be observed when a similar protocol is applied under other conditions: applying different reading rates (Fig. S1†), during discharge of an LFP||graphite full cell (Fig. S2†), and at various resting times (Fig. S3†).

Fig. 1 Demonstration of the kinetically induced memory effects in phase-separating electrode materials. (a) Schematic of the memory effect protocol: the depicted coloured voltage curves relate to the various currents used in the writing step; zero current is applied during the resting step, and a constant selected current is applied during the reading step. (b) Overpotentials in LFP||Li and LTO||Li half-cells, measured 60 seconds into the reading step (voltage plateau) at different writing C-rates. The C-rate refers to the writing step and the equilibrium voltages of LFP and LTO are considered to be 3.42 V and 1.55 V, respectively. (c) Voltage profile of NMC811||Li half-cells with a charging rate of 0.5C/1.0C/2.0C in the writing step, and 2.0C in the reading step (1.0C = 180 mA g⁻¹). (d) Voltage profile of LFP||Li half-cells with a charging rate of 0.2C/1.0C/3.0C/5.0C in the writing step, and 3.0C in the reading step (1.0C = 150 mA g⁻¹). The voltage relaxation during the resting step is also shown. (e) Voltage profile of LTO||Li half-cells with the charging rate of 0.2C/1.0C/5.0C/10.0C in the writing step, and 3.0C in the reading step (1.0C = 175 mA g⁻¹).

The distinguishing factor between LFP, LTO, and NMC is the presence of a first-order phase transition upon (de)lithiation for the first two: materials undergoing a first-order phase separation are susceptible to the kinetically induced memory effect. To confirm this hypothesis, more materials displaying a first-order phase transition, such as LiNi_0.5Mn_1.5O₄ (LMNO), LiMn_0.4Fe_0.6PO₄ (LMFP), and Na₃V₂(PO₄)₃ (NVP) were evaluated using similar protocols, also displaying the same phenomenon (Fig. S4–S6†). This observation aligns with previously documented memory effects on phase-separating materials,^5,6 here demonstrating the great impact on realistic high-rate conditions. Altogether, these results suggest a broad and general phenomenon that highlights the crucial necessity for more extensive investigations into the dynamic response of these materials under diverse operating conditions.

Monitoring the phase transition in individual grains

In order to better describe the kinetically induced memory effect, we investigated the impact of applied rates on the active particle population throughout different stages of the test protocol. Given the extensive knowledge of it and its relevance as a commercial material, LFP was selected as the representative phase-separating material for this study, with the primary objective of quantifying the active particle fraction during variable reading rates. A unique method to monitor the phase transformation of individual crystallites (primary particles) during operando conditions in pouch cells is microbeam X-ray diffraction.^10,11 This technique employs use of an X-ray beam of size comparable to the particle size (∼1 μm) to obtain single-grain reflections instead of powder averages (Fig. 2a). Observing the evolution of their 2θ values it is possible to identify the crystallite's composition (by observing the 2θ angle) and orientation (monitoring the η values), during operando conditions. Approximately 100 reflections, representing an equal amount of LiFePO₄ crystallites, were tracked during the electrochemical protocol with the same methodology applied by van Hulzen.^10,11 From hereon we refer to one crystallite as one particle. The anticipated first-order phase transition between LiFePO₄ (LFP) and FePO₄ (FP) is observed through the disappearance of the LFP reflection and the appearance of the FP reflection at a different 2θ value (Fig. 2d and e). Particle categorization is established on the observed shift of the 2θ reflections at the conclusion of the writing step. As shown in Fig. 2d and e, charged particles are identified based on the exclusive presence of the peak associated with the FP phase during the resting step; partially charged particles exhibit both the FP and LFP peaks, indicating partial delithiation; uncharged particles retain an unaffected LFP phase and are activated only during the subsequent reading step. The sudden shift in the 2θ value indicates fast delithiation, while the presence of two parallel 2θ values at the same η value indicates slow delithiation, occurring through phase separation.

Fig. 2 Microbeam X-ray diffraction analysis. (a) Schematic of the microbeam X-ray diffraction experimental setup. (b) Measured voltage evolution during the microbeam X-ray diffraction operando experiments: 0.2C–3.0C and 5.0C–3.0C cycles, respectively. (c) Fractions of particles uncharged (LiFePO₄, red), charged (FePO₄, blue) and partially charged (Li_xFePO₄, striped) at the end of the resting writing steps of the 0.2C–3.0C and 5.0C–3.0C cycles, respectively. (d) Evolution of the (200) reflection during the 5.0C–3.0C cycle for three different tracked grains. (e) Evolution of the (111) and (020) reflections during the 0.2C–3.0C cycle for three different tracked grains. The left-hand graphs show the evolution of the maximum intensity point for the selected grain reflection along the 2θ and η directions. The heatmaps show the detected grain reflection at different times.

Two different charging protocols were applied to the same battery: a protocol where the writing step was conducted at a high charging rate (5.0C) and one where it was conducted at a low charging rate (0.2C). In both cases, the battery was rested for 30 minutes, and the charging was completed at 3.0C (Fig. 2b). After both protocols a 0.1C memory-erasing discharge was conducted so that the batteries differ only in the charge rate during the writing step. Analysing the microbeam results provides direct insights into the role of the active particle population in the kinetically induced memory effect under operando conditions (Fig. 2d). Specifically, at a charge rate of 0.2C (writing step), a particle-by-particle lithiation mechanism is observed, where few particles are rapidly delithiating at each given time. Focusing on the electrode's state after the completion of the resting step, we found 39% of the particles being charged (full phase transition from LFP to FP) and 27% nucleating the lithium-poor phase without completing the charge (i.e., the coexistence of LFP and FP phases), while the rest remain uncharged (LFP phase). This is in line with the expected mosaic arrangement composed of either lithiated or delithiated crystals. Subsequently, during the 3.0C reading step, the remaining particles (61%) are charged by the imposed current. In contrast, when subjected to a charge rate of 5.0C during the writing step, a lower fraction of particles (26%) achieves full charge during this step, while the majority (47%) enter the resting period partially charged, in a phase-separated state. The subsequent 3.0C current can then be sustained by a higher fraction of particles (74%) being either partially charged or uncharged. These findings, summarized graphically in Fig. 2c, underscore the complex relationship between the charging rates of the active particle population, shedding light on the dynamics of (de)lithiation processes within the electrode.

The kinetically induced memory effect can so be explained by the difference in multi-particle dynamics during the initial step. Specifically, at high applied charge rates, the current is supported by a greater number of particles (increased active population), resulting in a higher fraction of nucleated (phase-separated) particles at 50% SOC. These nucleated particles are more accessible to the system during the subsequent reading step, having already surmounted the nucleation energy barrier. Notably, the phase separation persists during the resting period. Conversely, at low applied writing rates the electrode reaches 50% SOC following particle-by-particle delithiation, so the majority of the particles result in being either uncharged (lithiated) or completely charged (delithiated). In the subsequent reading step, the applied current is sustained by a reduced number of particles, i.e. the particles that are either partially charged or uncharged. Moreover, the uncharged particles need to overcome the nucleation barrier. The combination of these factors leads to the higher overpotentials as shown in Fig. 1b.

Previous work^10,11,23 described the formation of a metastable solid solution phase transition in LFP, such that, during fast (dis)charge, the particle cannot proceed toward phase separation due to the mismatch in characteristic times between reaction and diffusion kinetics. In contrast, no solution phase transition at 5C was observed within this study, which can be attributed to a fundamental distinction in particle shape. Specifically, by leveraging the b crystalline direction for 1D fast diffusion kinetics, platelet-shaped LFP particles demonstrate a reaction-limited behaviour. On the other hand, the spheroidal commercial particles employed in this work (Fig. S7–S9†), characterized by higher defect concentrations and, consequently, quasi-isotropic diffusivity, effectively exhibit diffusion-limited behaviour resulting in more favourable phase separation. Moreover, the presence of the kinetically induced memory effect in a wide set of phase-separating materials (Fig. 1e and Fig. S4–S6†) shows that the presence of a metastable solid solution transition in LFP is not a decisive factor in explaining the observed memory effect.

Electrochemical modelling of the memory effect

To further unravel and quantify the underlying mechanisms responsible for the kinetically induced memory effect, we suggested electrochemical porous electrode models extended to encompass the thermodynamics of phase-separating active particles through phase-field modelling.¹⁴ Traditional models²⁴ consider uniform diffusion and fit the open circuit voltage from experimental data; in contrast, phase-field models account for size-dependent nucleation barriers^25–27 and derive the chemical potential from the free energy landscape.¹⁷ This technique can predict the behaviour of phase-separating active battery materials at both the single-particle and multi-particle levels under various operating conditions.^{7,9,15,17,28–34} The coupling between the phase-field and electrochemical modelling can also fit experimental voltage curves,^30,35 provide an accurate picture of the active particle population,⁹ and generate realistic operando X-ray diffractograms.¹⁷ Considering the capabilities of this modelling technique, we utilize the software MPET¹⁴ to build an LFP electrode model capable of reproducing the experimental results. In particular, we consider spherical diffusion-limited particles that react with the surrounding electrolyte following the couple ion-electron transfer theory,³⁶ and account for electronic transport losses between the particles (see the Methods section and the ESI† for further details).

The simulated results for LFP in Fig. 3 unfold the kinetics of the system during the memory protocol, revealing the effect of a range of writing rates on the reading overpotentials. The voltage curves in Fig. 3b are in good agreement with the experimental results (Fig. S11†), showing the correct voltage at the onset of the reading steps, the kinetically induced capacity losses, and plateauing at high rates. It is noteworthy to specify that the model does not consider the evolution of the charge transfer resistance of the Li metal electrode or self-discharge mechanisms. The simulations, by matching the experiments solely considering the phase separation mechanism, also confirm it to be the main responsibility of the memory effect.

Fig. 3 Electrochemical modelling results. (a) Deconvoluted average overpotentials and active particle population at the onset of the reading step vs. writing rate (see the Methods section for further details). (b) Simulated voltage profiles for the memory protocols of LFP at writing rates varying from 0.1C to 6.0C and a fixed reading rate of 3.0C. (c) Li-ion distribution in a randomly selected set of representative particles of phase-field simulation at 55% SOC during the reading step for the case of 0.2C and 5.0C writing rates. Blue corresponds to the FP phase, and red corresponds to the LFP phase. The transport phenomena considered in the model are also shown. (d) Fraction of particles in the charged (FePO₄), partially charged (Li_xFePO₄), and discharged (LiFePO₄) states at 55% SOC at different writing rates. (e) Evolution of the active particle population during the memory protocols for the simulation presented in (b). A particle is considered active if its average lithiation state is between 15% and 85%.

By analysing the simulation data, the origin of the total overpotential can be separated into its components (Fig. 3a): both the reaction and diffusion overpotentials at the onset of the reading step are inversely proportional to the applied writing rate, whereas the transport overpotential is marginally affected by the writing rate due to the low loading of the tested sample (2 mA h cm⁻²).

Fig. 3e illustrates the complete multi-particle dynamics by showing the evolution of the active particle population during the memory protocol. At low rates, the system maintains a low active particle population during the writing step, following a particle-by-particle lithiation scheme, reaching the reading step with a few particles that are internally phase-separated. The system is then forced to overcome the nucleation barrier with a reduced available reactive area. As the writing rate increases, the system reacts more homogenously, accommodating higher currents towards more particles. Due to the wide difference in particle sizes (Fig. S8 and S9†), the smaller particles will be delithiated faster such that the active particle population starts to decrease before reaching 50% SOC. The kinetics is therefore dominated by larger-sized particles, which are the system's major current drivers. This imposes a limit on the maximum active particle population achievable during (dis)charge and explains the saturation of the kinetically induced memory effect at rates higher than 3.0C. After the resting step, where we observe a small drop in the active particle fraction due to intra-particle Li exchange (Fig. 3e), the available surface area of the phase-separated particles will accommodate the reading step current. Additionally, in the supplementary results, we explore the effect of the resting step on the active particle population (Fig. S20†). It is important to note that while the overpotential saturation occurs at 3.0C for LFP, the LTO electrode does not exhibit saturation even at 10.0C (Fig. S13†). Despite the similar particle size, the maximum active particle population, and its related saturation current, depend on both particle size and exchange current density. The significant difference in reaction kinetics between the two materials accounts for the distinct behaviour (Fig. S22†). This highlights the capability of the memory protocol to provide insights into charge transfer resistance in phase-separating materials. To further clarify this relationship, in the supplementary results, we present the influence of the particle size distribution and exchange current density on active particle population dynamics (Fig. S15†) and saturation current (Fig. S16†).

Fig. 3d depicts the dynamics of the system in the same fashion as described for the microbeam data, i.e. an increase in the writing rate leads to a greater fraction of particles being phase-separated at the onset of the reading step. In particular, the 5.0C writing rate leads to 46% of the particles being phase-separated and only 2% of them being fully delithiated, while the 0.2C writing rate only achieves 5% and 12% of phase-separated and delithiated particles, respectively. Finally, Fig. 3b visually shows the particle concentration at the beginning of the reading step for the two C-rates explored: 0.2C and 5.0C. The former presents a mosaic lithiation scheme where most particles are found either completely uncharged or charged due to the particle-by-particle lithiation dynamics. In particular, smaller particles are completely charged due to their lower energy barrier for nucleation and faster diffusion times, while larger particles are mostly uncharged. The 5.0C case is instead mostly composed of phase-separated particles, with only a minority of smaller particles being completely charged.

The thermodynamic interpretation of the phenomenon also clarifies why solid solution materials cannot experience a kinetically induced memory effect. As the electrochemical model demonstrates (Fig. S14†), the combination of Fickian diffusion and monotonic chemical potential of solid solution materials imposes fast relaxation on the system: the single particle is rapidly homogenized by internal diffusion, and the difference between the surface concentrations, induced by the previous fast kinetics, drives an inter-particle reaction that quickly homogenizes the system. In phase-separating materials, instead, once the particle is nucleated, both phases will be characterized by similar chemical potentials, and the driving force for multi-particle equilibration is strongly reduced. The origin of this kinetic response is also shown to be general and reproducible in other phase-separating materials as shown by the simulation performed with the Li₄Ti₅O₁₂ model¹⁵ (Fig. S13†).

Linking C-rate to overpotential: an analytical approximation

Although a complete description of the phenomenon requires solving a set of partial differential equations, this approach is often impractical. Here, we present an analytical approximation that captures the key trends using simplified relationships. For a uniform particle size distribution, the reactive surface area is proportional to both the fraction of active particles during the reading step (f) and the total reactive area (S). Given the exchange current density at the particle surface (j₀), the reaction overpotential (η_rxn) can be expressed as a function of f and imposed reading current i_R. Assuming Butler–Volmer reaction kinetics we obtain:

In addition to the reaction overpotential, the diffusion overpotential (η_diff) can be approximated using the Nernst relationship η_diff ∼ ln(c_s/c_eq), where c_s and c_eq are the surface and equilibrium concentrations of the delithiated phase, respectively. Approximating the ionic diffusion with a mass transfer coefficient, k_m, we can also obtain a relationship between f and η_diff:

These equations hold under the assumption that the current regime during the reading step activates all remaining particles (see the Methods section of the ESI†). Finally, an empirical relationship, based on a sigmoid function, is used for linking f to the writing C-rate (CR):

where the maximum active particle fraction f_max, the weight w and the bias b, are fitted based on the phase-field results. This relationship is admittedly difficult to obtain analytically since it depends on the particle size distribution, exchange current density and the state of charge.

When plotted (Fig. 4a), the resulting relationships show the significant influence of the active particle population on reaction and diffusion overpotentials. For instance, the diffusion overpotential can increase by a factor of four if the active particle population is reduced. The analytical model is then used to fit the experimental data presented in Fig. 1. By allowing w and b to vary within realistic bounds (informed by the phase-field model), the relationship between the writing C-rate and active particle fraction can be captured accurately.

Fig. 4 Analytical solution for the relationship between the writing C-rate and reaction and diffusion overpotentials. (a) Scaling of the reaction and diffusion overpotentials as a function of active particle fraction. The overpotentials are normalized w.r.t. the values at f = 1. Arbitrary parameters were chosen within reasonable values (close to fitted values). (b) Schematic of different phase arrangements of particles corresponding to varying active particle fractions. (c) Fit of the experimental overpotential for the LiFePO₄||Li half-cell. (d) Fit of the experimental overpotential for the Li₄Ti₅O₁₂||Li half-cell.

The precision in the fitting, of both the LFP and LTO cases (Fig. 4c and d), showcases the use of the derived approximation for predicting and understanding the kinetically induced memory effect. The effective diffusivity of LTO and LFP is comparable, as is their particle size, resulting in similar activation-induced overpotentials. The slower reaction kinetics of LFP is the primary reason for its larger overpotential difference between slow and fast charging. Moreover, the fit also predicts that the relationship between active particle population and C-rate is in good agreement with the phase-field results. This and the possibility to fit these data with the provided analytical model further validate the conclusion that the previously activated particles are responsible for the difference in overpotentials.

Conclusion

This study shows and explains a general phenomenon affecting all phase-separating electrode materials: a strong inverse correlation between the initial applied (dis)charging rate and the resulting overpotential during a subsequent step, thus a kinetically induced memory effect. The origin of this behaviour is herein described from a thermodynamic perspective (Fig. 5).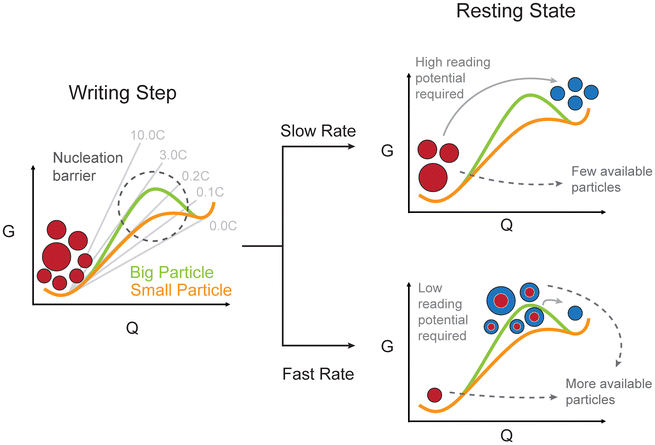

Fig. 5 Schematic summary of the origin of the kinetically induced memory effect. The thermodynamic origin of the memory effect in terms of free energy (G) evolution during slow and fast writing steps is described. The size-dependent energy barriers are considered.²⁶ The common energy tangent is followed at low rates, increasing the rate results in a deviation from the minimum energy path. Lower rates are thus capable of overcoming the energy barrier for small particles, while higher rates allow particles of greater size to reach a metastable higher energy configuration. The resulting difference in the energy landscape is represented with red particles as fully lithiated (low energy), blue particles as fully delithiated (high energy) and bi-coloured particles as phase separated. Energy and capacity (Q) are purely representative and not at scale.

If lower rates are employed during the writing step of the protocol (e.g. 0.2C) the reaction primarily occurs for smaller particles, characterized by faster kinetics and a lower nucleation barrier. The resulting electrode is composed mostly of either fully lithiated or fully delithiated particles. A greater overpotential is required to activate larger-sized particles during the reading step. Higher charging rates (e.g. 5.0C) spread the current to multiple particles, leading to a set of phase-separated metastable particles. The inter-particle lithium exchange is delayed by the coexistence of the same chemical potential of the two phases and, when the reading current is applied, the phase-separated particles are electrochemically more active since the nucleation barrier has vanished. This allows the system to achieve the same reading rate (e.g. 3.0C) with lower overpotentials. From an energy perspective, part of the additional energy supplied to the system during a high-rate writing step is stored within the phase boundaries. Consequently, less additional energy is required to drive the current during the reading step. This nuanced interplay between current rates and phase-separation dynamics sheds light on the crucial role of activation barriers and population dynamics in governing the electrochemical behaviour of these systems.

Multiple studies, primarily focusing on LFP, assessed the non-trivial multi-particle and single-particle reaction path that phase-separating materials follow during (de)intercalation.^37–41 Early descriptions relied on a domino-cascade model, suggesting a particle-by-particle (de)lithiation process.⁴¹ However, subsequent experimental^9,10 and computational^9,15 studies have provided compelling evidence that the active particle population is intricately linked to the applied rate, challenging the initial univocal interpretation. Building on these findings, other works have been focused on the investigation of the metastable solid solution^25,26,28,29 (characteristic of LFP but not universal to all phase-separating materials) and the relaxation behaviour,^7,42,43 providing a foundation for the understanding of current-induced phenomena. Specifically, Deng and coworkers⁷ characterized the unexpected change in overpotential during quasi-equilibrium discharge of LFP following a high-rate current pulse, revealed by the study of Katrašnik et al.,⁶ through X-ray microscopy and phase-field modelling on reaction-limited micro-platelet particles. Notably, whilst offering valuable insights, they did not quantitatively assess the significant consequences of these pulses under the subsequent high-rate operating conditions.

Our protocol, which is closer to those using commercially relevant rates, reveals the impact of these non-equilibrium phenomena on typical battery operations. The thermodynamic interpretation of it (Fig. 5), obtained by combining modelling and operando monitoring of individual particles, opens the doors to improved protocol design for both deeper fundamental understanding and battery management strategies.

Robust indication of multi-particle dynamics can be obtained by combining the multi-step protocol and the developed analytical model (eqn (1)–(3)). By collecting data from a set of writing currents, we use the presented relationships to obtain the active particle population as a function of the C-rate. This offers valuable insights into optimal charging rates able to activate the majority of particles within the electrode.

While this study focuses on half-cell charging for better fundamental understanding, we also prove the described memory effect in commercially relevant LFP||graphite full cells (Fig. S2†). Similarly, the previously applied current influences the subsequent overpotential, but the role of graphite hinders its presence when a higher rate is applied during the reading step. The kinetically induced memory effect in full cells is so dependent on the kinetically limiting electrode and therefore on a wide range of manufacturing parameters. Based on these results, we also speculate the presence of the memory effect in an LTO||NMC cell. In fact, LTO electrodes reliably show the kinetically induced memory effect, while the kinetics of the NMC is not influenced by the previous current rate. The combination of these materials, important in high-power applications, is therefore a candidate process for the exploitation of the discovered phenomenon. Since the discovered effect arises from particle-level heterogeneities, its magnitude can be reduced in high-capacity electrodes, where the ionic or electronic transport along the electrode thickness is the limiting factor (Fig. S19†). In the case of next-generation battery materials, such as LMNO, LMFP and NVP,⁴⁴ the kinetically induced memory effect can instead become a tool for characterizing specific regions of capacity that exhibit phase separation (Fig. S4–S6†).

Moreover, our study underlines the significant implications that may arise from oversimplifying the treatment of phase-separating materials, both computationally and experimentally. Although single-particle models have demonstrated their ability to predict constant current kinetics,⁴⁵ they fall short in capturing behaviours intrinsically linked to the active particle population and phase separation. In fact, the relationship between SOC and kinetic properties is not univocally definable. At the same SOC, the electrode can be composed of different ratios of phase-separated and homogeneous particles depending on the previous applied rate. As shown here, these phenomena have a significant effect on the voltage profile. Thus, its prediction and the subsequent management and optimization of battery operations can be misled by oversimplified models.^24,46–48 It becomes so critical, when modelling phase-separating materials, to account for multi-particle dynamics and phase-separation kinetics to correctly predict voltage and current responses in complex protocols (Fig. S17 and S18†). Thus, this study proves the necessity of phase-field methods for improving state-of-the-art battery management strategies.⁴⁹ We also speculate that SOC estimation algorithms could be misled by these memory effects, if not properly included in the equivalent circuit representation. To apply these findings to fast control-oriented numerical tools, we suggest coupling phase-field models and advanced equivalent resistors. The former would be initially used to capture the relationship between the C-rate, SOC and active particle population (eqn (3)), and the latter can then be modelled based on the analytical equations provided in this work (eqn (1) and (2)). Furthermore, how multi-step protocols can maximize the active particle population has been shown. This can directly translate into the reduction of intra-particle stresses, side reactions, heat generation, and energy consumption. To fully deploy this effect in real-world scenarios, future studies should focus on exploiting this phenomenon via numerical optimization and clarifying its impact at multiple SOCs, temperatures, and rates.

Finally, we showed how the continual pursuit of fundamental knowledge in the field of batteries can have direct implications on current technology, leading to better protocols for battery management systems, improving battery performance, energy efficiency, and lifespan, ultimately contributing to advancing battery technologies and the broader field of energy storage systems.

Materials and methods

Materials

LiFePO₄, composed of single crystal particles, was obtained from Leneng Technology. The cathodes were prepared by mixing the LiFePO₄ material, poly(vinylidene difluoride) (PVDF, MTI) binder and Super P (Alfa Aesar) conductive carbon in a weight ratio of 92 : 4 : 4. The resulting slurry was cast on Al foil and then dried at 60 °C for 6 h, followed by drying overnight at 120 °C in a vacuum oven. The Li₄Ti₅O₁₂ anode and LiNi_0.5Mn_1.5O₄ were purchased from MTI Corporation and used as received. LiNi_0.8Mn_0.1Co_0.1O₂ (NMC811) was synthesized using the coprecipitation method: a certain amount of alkaline aqueous solution (NH₄OH and NaOH) was poured into deionized water (1.5 L) to form the base solution in a tank reactor under continuous stirring. Then, a 2 M solution of NiSO₄·6H₂O, CoSO₄·7H₂O, and MnSO₄·H₂O with a molar ratio of 8 : 1 : 1 and an aqueous solution of 5 M NH₄OH and 10 M NaOH were added into the base solution in the tank reactor at a steady rate of 8 mL min⁻¹. The coprecipitation temperature was controlled at 50 °C, and the pH value was maintained at approximately 11 by NH₄OH with a stirring speed of 500 rpm under a nitrogen atmosphere. The coprecipitated Ni_0.8Mn_0.1Co_0.1(OH)₂ precursor was prepared, which was subsequently washed with deionized water and ethanol four times and dried in a vacuum at 120 °C for 24 h. The apparent and tap density of the Ni_0.8Mn_0.1Co_0.1(OH)₂ precursors were measured at 1.88 g cm⁻³ and 2.06 g cm⁻³, respectively. For the preparation of NMC811 materials, the as-obtained precursor was mixed with LiOH·H₂O at a molar ratio of 1 : 1.03, then heated to 500 °C for 5 h and subsequently calcined at 780 °C for 12 h in an oxygen atmosphere. After cooling naturally, the material was immediately placed in an Ar-filled glovebox to prevent being exposed to moisture. The NMC811 electrodes were prepared by mixing active material, Super P and PVDF binder in a mass ratio of 90 : 5 : 5 in an N-methyl-2-pyrrolidone (NMP) solvent and cast on Al foil and then dried at 60 °C for 6 h, followed by drying in a vacuum oven at 120 °C overnight. The X-ray diffraction pattern demonstrates the pure phase of this prepared NMC811 material. Battery-grade lithium hexafluorophosphate (LiPF₆), ethylene carbonate (EC), diethyl carbonate (DEC), and fluoroethylene carbonate (FEC) were purchased from E-Lyte innovations, and subsequently dehydrated using a 4 Å molecular sieve (Sigma-Aldrich).

Electrochemical measurements

Electrochemical cycling tests of all batteries were based on CR2032 coin cells assembled in an Ar-filled glove box (H₂O < 0.1 ppm, O₂ < 0.1 ppm) with Celgard 2500 separators and tested at room temperature, unless stated otherwise. The electrolyte used consisted of 1 M LiPF₆ in EC/DEC (1 : 1 in volume) with 5% FEC. 70 μL of electrolytes were injected into each coin cell for comparison. All coin cells were tested using multi-channel battery testing systems (Land CT2001A or Lanhe G340A). 15.6 mm diameter lithium metal foil of 250 μm thickness was used as both the working and counter electrodes. The electrochemical cycling performance of the electrodes (12 mm diameter) was tested using an areal capacity of 2 mA h cm⁻² with lithium metal foil as the counter electrode. All the cells underwent a formation cycle comprising two 0.1C (0.2 mA cm⁻²) charge–discharge cycles.

Materials characterization

The morphologies of the electrodes were observed using a cold field scanning electron microscope (SEM, HITACHI-S4800, SU8010). XRD was performed using a Bruker D8 Advance diffractometer equipped with a Cu Kα radiation source (λ₁ = 1.54060 Å and λ₂ = 1.54439 Å at 40 kV and 40 mA). Rietveld refinement of the XRD data was carried out using General Structure Analysis System software with the EXPGUI software interface. TEM experiments were performed using a STEM instrument (JEM-ARM300F, JEOL) operated at 300 kV with a cold field emission gun and Cs double correctors. The microscope was equipped with Gatan OneView and K2 cameras for image recording. STEM images were obtained at an electron dose rate of 50–500 e⁻ Å⁻² s⁻¹ with an exposure time of several seconds for each image, with a built-in drift correction function in GMS3 using the OneView and K2 cameras.

Microbeam diffraction experiments

For the LFP microbeam diffraction experiment, a similar setup was used as described in van Hulzen et al.¹⁰ The LFP||Li half-cells were prepared as pouch cells and fixed in a clamp with a conic opening on both sides to allow the X-ray beam to pass through. A monochromatic X-ray beam with wavelength 0.2852 Å (energy 43.47 keV) and spot size of ∼1 micron was used to register the diffraction patterns on an Eiger2 X CdTe 4M detector with 2068 × 2162 pixels. To increase the number of grains under Bragg conditions the sample was rotated along the z-axis (perpendicular to the beam). For all measurements the total rotation was 5° with a step size of 0.05° and an exposure time of 0.05 seconds, collecting 101 frames in about 6 seconds. To mitigate beam damage, four locations were probed by rotation resulting in a time resolution of about 30 seconds per location. A detailed description of the provided data can be found in ESI section 2.a.† The raw data were analysed following the methodology outlined in the Methods section of van Hulzen et al.¹⁰

Electrochemical phase-field modelling

The physics-based electrochemical model was developed by expanding on the open-source software MPET.¹⁴ The single particle of LFP was simulated by considering a diffusion-limited spherically symmetric one-dimensional particle axis so that the local Li concentration c evolves accordingly to
where D is the concentration-dependent diffusivity and μ is the phase-field chemical potential. The particle's reaction rate R between the particle of concentration c, and the electrolyte of concentration c_Li⁺ is modelled through the coupled ion electron transfer theory,^36,50 specifically the electron-coupled ion transfer approximation:
where k₀ is the exchange current density, η_f is the formal overpotential and λ is the reorganization energy for the electron transfer. The electrode is discretized into sub-volumes, each consisting of 8 particles of varying sizes following the experimental particle size distribution. The electrode-level ionic and electronic losses were modelled employing porous electrode theory.¹⁶ Moreover, wiring losses within the sub-volume are considered, similar to the work of Li et al.⁹ A more detailed description of the model can be found in ESI sections 2.b. Model formulation and 2.c. Model parameters.†

The analysis of the overpotentials was defined as follows: the reaction overpotential of a single particle is the overpotential driving the reaction, and it corresponds to the difference between the surface chemical potential of the particle and the electrolyte chemical potential at a specific electrode depth; the diffusion overpotential is defined as the difference between the surface chemical potential and the equilibrium potential of the material at that average composition; the transport overpotential is the difference between the electrochemical potential of Li ions at the Li-metal–electrolyte interface and the electrochemical potential at the current collector. The total overpotential is the difference between the equilibrium chemical potential of the LFP plateau and the potential at 55% SOC.

Author contributions

M. W. and C. Z. conceived the idea. Q. W. and C. Z. designed the experiments. Q. W. and C. Z. performed the material synthesis, characterization, and electrochemical measurements. Q. W. conducted the microbeam X-ray experiments and analyzed data with P. O. and M. H. P. O. and A. V. developed the electrochemical model and analyzed the data. P. O. developed the analytical approximation and the thermodynamic interpretation. F. W., Z. G., X. H., and B. L. performed the SEM, TEM, and XRD characterization and electrochemical measurements and analyzed the data with Q. W. and C. Z. Q. W., P. O., A. V., C. Z., and M. W. prepared this manuscript with inputs from all other co-authors. Q.W. and P.O. contributed equally to this work.

Data availability

Materials generated in this study will be made available on reasonable request.

Data and code availability: The code necessary to reproduce the simulations, the simulation results, and the Operando Microbeam X-ray diffraction data are available at https://doi.org/10.5281/zenodo.15012305.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the support from Shell Global Solutions International B.V. We also acknowledge the European Synchrotron Radiation Facility for the provision of synchrotron radiation facilities and thank the beamline staff for assistance in using the beamline.

References

1. J. B. Goodenough and K. S. Park, The Li-Ion Rechargeable Battery: A Perspective, J. Am. Chem. Soc., 2013, 135(4), 1167–1176.
2. R. Barnard, G. T. Crickmore, J. A. Lee and F. L. Tye, The cause of residual capacity in nickel oxyhydroxide electrodes, J. Appl. Electrochem., 1980, 10(1), 61–70.
3. R. Huggins,  Mechanism of the memory effect in “Nickel” electrodes, Solid State Ionics, 2006, 177(26–32), 2643–2646.
4. Y. Sato, S. Takeuchi and K. Kobayakawa, Cause of the memory effect observed in alkaline secondary batteries using nickel electrode, J. Power Sources, 2001, 93(1–2), 20–24.
5. T. Sasaki, Y. Ukyo and P. Novák, Memory effect in a lithium-ion battery, Nat. Mater., 2013, 12(6), 569–575.
6. T. Katrašnik, J. Moškon, K. Zelič, I. Mele, F. Ruiz-Zepeda and M. Gaberšček, Entering Voltage Hysteresis in Phase–Separating Materials: Revealing the Electrochemical Signature of the Intraparticle Phase–Separated State, Adv. Mater., 2023, 2210937.
7. H. D. Deng, N. Jin, P. M. Attia, K. Lim, S. D. Kang and N. Kapate, et al., Beyond Constant Current: Origin of Pulse-Induced Activation in Phase-Transforming Battery Electrodes, ACS Nano, 2024, 18(3), 2210–2218.
8. W. Dreyer, J. Jamnik, C. Guhlke, R. Huth, J. Moškon and M. Gaberšček, The thermodynamic origin of hysteresis in insertion batteries, Nat. Mater., 2010, 9(5), 448–453.
9. Y. Li, F. El Gabaly, T. R. Ferguson, R. B. Smith, N. C. Bartelt and J. D. Sugar, et al., Current-induced transition from particle-by-particle to concurrent intercalation in phase-separating battery electrodes, Nat. Mater., 2014, 13(12), 1149–1156.
10. M. van Hulzen, F. G. B. Ooms, J. P. Wright and M. Wagemaker, Revealing Operando Transformation Dynamics in Individual Li-ion Electrode Crystallites Using X-Ray Microbeam Diffraction, Front. Energy Res., 2018, 6, 59.
11. X. Zhang, M. Van Hulzen, D. P. Singh, A. Brownrigg, J. P. Wright and N. H. Van Dijk, et al., Direct view on the phase evolution in individual LiFePO4 nanoparticles during Li-ion battery cycling, Nat. Commun., 2015, 6(1), 8333.
12. P. Bai and G. Tian, Statistical kinetics of phase-transforming nanoparticles in LiFePO4 porous electrodes, Electrochim. Acta, 2013, 89, 644–651.
13. D. A. Cogswell and M. Z. Bazant, Size-dependent phase morphologies in LiFePO4 battery particles, Electrochem. Commun., 2018, 95, 33–37.
14. R. B. Smith and M. Z. Bazant, Multiphase Porous Electrode Theory, J. Electrochem. Soc., 2017, 164(11), E3291–E3310.
15. A. Vasileiadis, N. J. J. de Klerk, R. B. Smith, S. Ganapathy, P. P. R. M. L. Harks and M. Z. Bazant, et al., Toward Optimal Performance and In-Depth Understanding of Spinel Li ₄ Ti ₅ O ₁₂ Electrodes through Phase Field Modeling, Adv. Funct. Mater., 2018, 28(16), 1705992.
16. T. R. Ferguson and M. Z. Bazant, Nonequilibrium Thermodynamics of Porous Electrodes, J. Electrochem. Soc., 2012, 159(12), A1967–A1985.
17. P. Ombrini, M. Z. Bazant, M. Wagemaker and A. Vasileiadis, Thermodynamics of multi-sublattice battery active materials: from an extended regular solution theory to a phase-field model of LiMnyFe1-yPO4, npj Comput. Mater., 2023, 9(1), 148.
18. T. Katrašnik, J. Moškon, K. Zelič, I. Mele, F. Ruiz-Zepeda and M. Gaberšček, Entering Voltage Hysteresis in Phase–Separating Materials: Revealing the Electrochemical Signature of the Intraparticle Phase–Separated State, Adv. Mater., 2023, 35(31), 2210937.
19. X. Guo, B. Song, G. Yu, X. Wu, X. Feng and D. Li, et al., Size-Dependent Memory Effect of the LiFePO ₄ Electrode in Li-Ion Batteries, ACS Appl. Mater. Interfaces, 2018, 10(48), 41407–41414.
20. V. Srinivasan and J. Newman, Existence of Path-Dependence in the LiFePO₄ Electrode.
21. J. Jia, C. Tan, M. Liu, D. Li and Y. Chen, Relaxation-Induced Memory Effect of LiFePO ₄ Electrodes in Li-Ion Batteries, ACS Appl. Mater. Interfaces, 2017, 9(29), 24561–24567.
22. W. Shi, J. Wang, J. Zheng, J. Jiang, V. Viswanathan and J. G. Zhang,  Influence of memory effect on the state-of-charge estimation of large-format Li-ion batteries based on LiFePO4 cathode, J. Power Sources, 2016, 312, 55–59.
23. J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee and P. Bai, et al., Origin and hysteresis of lithium compositional spatiodynamics within battery primary particles, Science, 2016, 353(6299), 566–571.
24. X. Duan, D. Hu, W. Chen, J. Li, L. Wang and S. Sun, et al., Electrochemical Modeling of Fast Charging in Batteries, Adv. Energy Mater., 2024, 2400710.
25. M. Wagemaker, F. M. Mulder and A. Van der Ven, The Role of Surface and Interface Energy on Phase Stability of Nanosized Insertion Compounds, Adv. Mater., 2009, 21(25–26), 2703–2709.
26. M. Wagemaker, D. P. Singh, W. J. H. Borghols, U. Lafont, L. Haverkate and V. K. Peterson, et al., Dynamic Solubility Limits in Nanosized Olivine LiFePO ₄, J. Am. Chem. Soc., 2011, 133(26), 10222–10228.
27. D. A. Cogswell and M. Z. Bazant, Theory of Coherent Nucleation in Phase-Separating Nanoparticles, Nano Lett., 2013, 13(7), 3036–3041.
28. P. Bai, D. A. Cogswell and M. Z. Bazant, Suppression of Phase Separation in LiFePO ₄ Nanoparticles During Battery Discharge, Nano Lett., 2011, 11(11), 4890–4896.
29. D. A. Cogswell and M. Z. Bazant, Coherency Strain and the Kinetics of Phase Separation in LiFePO ₄ Nanoparticles, ACS Nano, 2012, 6(3), 2215–2225.
30. G. Galuppini, M. D. Berliner, D. A. Cogswell, D. Zhuang, M. Z. Bazant and R. D. Braatz,  Nonlinear identifiability analysis of Multiphase Porous Electrode Theory-based battery models: A Lithium Iron Phosphate case study, J. Power Sources, 2023, 573, 233009.
31. B. Koo, J. Chung, J. Kim, D. Fraggedakis, S. Seo and C. Nam, et al., Dynamic surface phases controlling asymmetry of high-rate lithiation and delithiation in phase-separating electrodes, Energy Environ. Sci., 2023, 16, 3302–3313.
32. M. Bazant, H. Zhao, H. Deng, A. Cohen, J. Lim and Y. Li, Learning heterogeneous reaction kinetics from X-ray movies pixel-by-pixel, Nature, 2023, 621(7978), 289–294.
33. T. K. Schwietert, P. Ombrini, L. S. Ootes, L. Oostrum, V. Azizi and D. Cogswell, et al., Phase-Field Computational Framework for Addressing Challenges in Solid-State Batteries, PRX Energy, 2023, 2(3), 033014.
34. P. Karanth, M. Weijers, P. Ombrini, D. Ripepi, F. Ooms and F. M. Mulder, A phase inversion strategy for low-tortuosity and ultrahigh-mass-loading nickel-rich layered oxide electrodes, Cell Rep. Phys. Sci., 2024, 101972.
35. Y. Zhang, T. T. Zuo, J. Popovic, K. Lim, Y. X. Yin and J. Maier, et al., Towards better Li metal anodes: Challenges and strategies, Mater. Today, 2020, 33, 56–74.
36. M. Z. Bazant, Unified quantum theory of electrochemical kinetics by coupled ion-electron transfer, Faraday Discuss., 2023, 246, 60–124.
37. R. Malik, A. Abdellahi and G. Ceder, A Critical Review of the Li Insertion Mechanisms in LiFePO ₄ Electrodes, J. Electrochem. Soc., 2013, 160(5), A3179–A3197.
38. G. Brunetti, D. Robert, P. Bayle-Guillemaud, J. L. Rouvière, E. F. Rauch and J. F. Martin, et al., Confirmation of the Domino-Cascade Model by LiFePO ₄ /FePO ₄ Precession Electron Diffraction, Chem. Mater., 2011, 23(20), 4515–4524.
39. W. C. Chueh, F. El Gabaly, J. D. Sugar, N. C. Bartelt, A. H. McDaniel and K. R. Fenton, et al., Intercalation Pathway in Many-Particle LiFePO ₄ Electrode Revealed by Nanoscale State-of-Charge Mapping, Nano Lett., 2013, 13(3), 866–872.
40. L. Laffont, C. Delacourt, P. Gibot, M. Y. Wu, P. Kooyman and C. Masquelier, et al., Study of the LiFePO ₄ /FePO ₄ Two-Phase System by High-Resolution Electron Energy Loss Spectroscopy, Chem. Mater., 2006, 18(23), 5520–5529.
41. C. Delmas, M. Maccario, L. Croguennec, F. Le Cras and F. Weill, Lithium deintercalation in LiFePO4 nanoparticles via a domino-cascade model, Nat. Mater., 2008, 7(8), 665–671.
42. H. Liu, F. C. Strobridge, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman and P. J. Chupas, et al., Capturing metastable structures during high-rate cycling of LiFePO ₄ nanoparticle electrodes, Science, 2014, 344(6191), 1252817.
43. Y. Li, H. Chen, K. Lim, H. D. Deng, J. Lim and D. Fraggedakis, et al., Fluid-enhanced surface diffusion controls intraparticle phase transformations, Nat. Mater., 2018, 17(10), 915–922.
44. Y. Deng, C. Yang, K. Zou, X. Qin, Z. Zhao and G. Chen, Recent Advances of Mn-Rich LiFe _{1- y}, Mn _y PO ₄ (0.5 ≤ y &lt; 1.0) Cathode Materials for High Energy Density Lithium Ion Batteries, Adv. Energy Mater., 2017, 7(13), 1601958.
45. G. Pozzato, A. Takahashi, X. Li, D. Lee, J. Ko and S. Onori, Core-Shell Enhanced Single Particle Model for lithium iron phosphate Batteries: Model Formulation and Analysis of Numerical Solutions, J. Electrochem. Soc., 2022, 169(6), 063510.
46. V. Azimi, A. Allam and S. Onori, Extending Life of Lithium-Ion Battery Systems by Embracing Heterogeneities via an Optimal Control-Based Active Balancing Strategy, in, IEEE Transactions on Control Systems Technology, 31(3), 1235–1249,  DOI:10.1109/TCST.2022.3215610.
47. G. Galuppini, M. D. Berliner, H. Lian, D. Zhuang, M. Z. Bazant and R. D. Braatz, Efficient Computation of Safe, Fast Charging Protocols for Multiphase Lithium-Ion Batteries: A Lithium Iron Phosphate Case Study, SSRN, 2023. Available from: https://www.ssrn.com/abstract=4392427.
48. J. Rivera-Barrera, N. Muñoz-Galeano and H. Sarmiento-Maldonado, SoC Estimation for Lithium-ion Batteries: Review and Future Challenges, Electronics, 2017, 6(4), 102.
49. A. K. M. A. Habib, M. K. Hasan, G. F. Issa, D. Singh, S. Islam and T. M. Ghazal, Lithium-Ion Battery Management System for Electric Vehicles: Constraints, Challenges, and Recommendations, Batteries, 2023, 9(3), 152.
50. D. Fraggedakis, M. McEldrew, R. B. Smith, Y. Krishnan, Y. Zhang and P. Bai, et al., Theory of coupled ion-electron transfer kinetics, Electrochim. Acta, 2021, 367, 137432.

---

Footnotes

† Electronic supplementary information (ESI) available: Supplementary results, such as electrochemical experiments on other materials, materials characterization, and additional phase-field electrochemical modelling results, in-depth explanations of the microbeam data analysis, and a comprehensive description of the phase-field model and its parameters. See DOI: https://doi.org/10.1039/d5eb00014a

‡ These authors contributed equally to this work.

---