Open Access Article
Open Access ArticleA microstructural electrochemo-mechanical model of high-nickel composite electrodes towards digital twins to bridge the particle and electrode-level characterizations†
Jihun
Song
a,
Royal C.
Ihuaenyi
a,
Jaejin
Lim
b,
Zihan
Wang
c,
Wei
Li
a,
Ruqing
Fang
a,
Amin Kazem
Ghamsari
a,
Hongyi
Xu
c,
Yong Min
Lee
 *b and
Juner
Zhu
*b and
Juner
Zhu
 *a
*a
aDepartment of Mechanical and Industrial Engineering, Northeastern University, Boston, MA 02115, USA. E-mail: j.zhu@northeastern.edu
bDepartment of Chemical and Biomolecular Engineering, Yonsei University, Seoul 03722, Republic of Korea. E-mail: yongmin@yonsei.ac.kr
cDepartment of Mechanical Engineering, University of Connecticut, Storrs, CT 06269, USA
First published on 20th February 2025
Abstract
Cell-level battery models, most of which rely on the successful porous electrode theories, effectively estimate cell performance. However, pinpointing the contributions of individual components of an electrode remains challenging. In contrast, particle-level models based on real microstructures describe active material characteristics but do not accurately reflect performance under cell-level operating conditions. To bridge this modeling gap, we propose a microelectrode modeling framework that considers each component of a composite electrode. This framework enables us to analyze the complex electrochemo-mechanical relationships within the composite electrode. The realistic 3D microstructure of the LiNi0.7Mn0.15Co0.15O2 composite electrode is reconstructed from focused ion beam-scanning electron microscopy images. By applying the intrinsic properties of every component, the composite microelectrode model achieves more than 98% accuracy in terms of the voltage profile compared to the measurement on coin cells. This model allows us to identify three important mechanisms that contribute to the discrepancy between cell and particle levels, i.e., reduced reaction area, increased diffusion length, and insufficient amount of electrolyte. Simulations under excessive electrolyte conditions reveal a significant improvement in rate capability with 94% capacity retention at 4C. In addition, the model considers the role of conductive materials and binders as well as the viscoplasticity of the polymeric binder, enabling the study of degradation mechanisms involving the stability of the binder-particle connection.
Broader contextLithium-ion batteries (LIBs) have been pivotal in advancing electric transportation but still face significant challenges in achieving higher energy densities, faster charging times, and longer cycle life. Addressing these challenges requires a comprehensive analysis of the factors affecting battery performance. To this end, a microelectrode modeling framework is proposed. This framework enables a thorough analysis of the complex electrochemical and mechanical interactions by considering each component within the composite electrode. The model identifies three primary mechanisms that impact battery performance: reduced reaction area, increased diffusion length, and insufficient electrolyte volume. To mitigate these issues, a design incorporating excessive electrolyte is proposed. Simulations indicate that this design not only significantly enhances rate capability but also exhibits excellent mechanical properties. Furthermore, the model provides valuable insights into degradation mechanisms by examining the roles of conductive and binder materials and the viscoplasticity of the polymer binder. |
Introduction
Lithium-ion batteries (LIBs) have been at the forefront of electrifying transportation, yet they confront significant hurdles in achieving higher energy density, faster charging times, and longer lifespan. Addressing these challenges requires a thorough analysis of factors impacting battery performance. LIBs function by transferring electrons from a current collector through conductive materials and active materials, alongside the movement of lithium ions from one active material to the other active material via electrolytes. Therefore, the performance of lithium secondary batteries hinges on the efficient mobility of electrons and lithium ions, a process heavily influenced by the structural characteristics of the composite electrode. An illustrative case of enhancing this mechanism is LiFePO4 (LFP), widely adopted in transportation electrification due to its cost-effectiveness and extended cycle life. Initially, LFP encountered limitations such as low specific capacities (100–110 mA h g−1) owing to its low electrical conductivity and diffusion coefficients.1 However, innovations in particle-level structural design, such as reducing particle size and applying carbon coatings to the particle surface, have enabled its successful commercialization.2,3From this perspective, extensive research has focused on analyzing the electrochemo-mechanical properties of active materials at the particle level. Techniques such as single particle measurement, scanning transmission X-ray microscopy (STXM), Bragg coherent diffractive imaging (BCDI), and nanoindentation have been employed for these investigations.4–7 Moreover, to overcome experimental constraints, modeling approaches for operando electrochemo-mechanical analysis have been developed, including phase field modeling and 3D reconstruction-based modeling that implement a realistic particle.8–11 These models assess the feasibility of fast charging and address critical factors such as cracks, critical factors affecting the degradation of high-nickel particles. However, particle-level studies often overlook the structural attributes of the composite electrode beyond the active material, complicating accurate predictions of overall cell behavior.
In contrast, cell-level modeling can directly measure cell performance but is too large in scale to accurately reflect the characteristics of all components. The battery electrodes are composed of millions to hundreds of billions of particles: a coin cell (∼1 A h) includes millions, a cylindrical cell (∼5 A h) contains tens of billions, and an EV pouch cell (∼100 A h) contains hundreds of billions. Thus, the preferred approach involves pseudo-2-dimensional (P2D) modeling based on the Doyle–Fuller–Newman model,12,13 which visually represents particles. To estimate the temperature effects and behavior of the cell, a P2D model is integrated with a 3D heat transfer modeling framework to develop a thermal-electrochemical model. This model calculates heat generation within the P2D framework and simulates heat transfer throughout the 3D framework.14,15 While these multiphysics models effectively predict cell performance under various scenarios through parameter adjustments, their virtual construction that ignores the microstructure of the electrodes limits the ability to analyze the specific characteristics of each battery component individually.
Binders are a component that is often overlooked in cell-level modeling. It binds the active materials, preventing delamination, and enhances the electrical conductivity of the composite electrode by combining it with conductive materials. During battery operation, binders undergo cyclic mechanical loads due to the continuous volume expansion and contraction of the active materials. These cyclic loads can potentially cause fatigue of the binder materials and the failure of the binder-particle interface, greatly shortening the battery lifespan.
Microelectrode-level modeling allows for the individual implementation of tens to hundreds of particles, conductive and binder materials (CBM), pores, and current collectors, bridging the gap between particle-level and cell-level modeling. Integration of advanced imaging technologies such as focused ion beam-scanning electron microscopy (FIB-SEM), X-ray microscopy (XRM), or nano-computed tomography (nano-CT) enables realistic representations of active materials, CBM, pores, and current collectors. This approach facilitates the analysis of structure-influenced electrochemical properties, including changes in effective exchange current density due to alterations in active surface area and effective diffusivity influenced by particle deformation during cycling.16–18 One of the fundamental challenges of furthering microelectrode-revolved models lies in the complex coupling between electrochemistry and mechanics. Most of the existing successful models are developed for small deformation, limited in simulating the physical contraction and expansion of active materials during cycling. This significantly affects both electrochemical and mechanical properties and reduces prediction accuracy. Also, these models only consider elastic deformation when analyzing CBM mechanical characteristics, neglecting the plastic deformation observed in real cells.
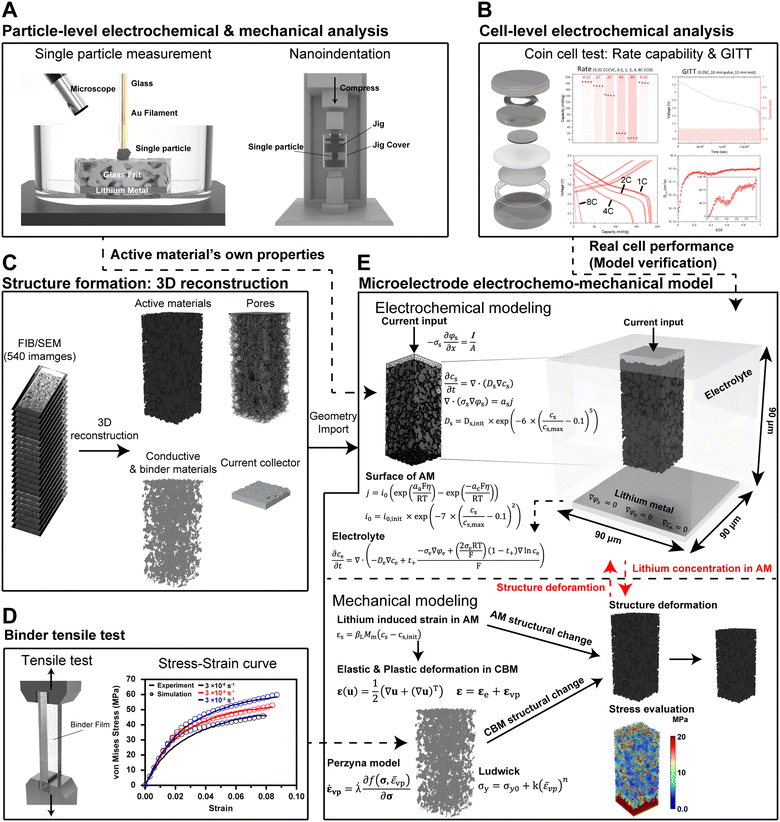
To address these challenges, we acquired hundreds of FIB/SEM images of the LiNi0.7Mn0.15Co0.15O2 (NMC711) composite electrode, capturing the detailed structure of active materials, CBM, pores, and current collectors. Leveraging these reconstructions, we developed an electrochemo-mechanical model at the microelectrode level capable of simulating structural changes within the composite electrode during cycling. Our investigation meticulously examines how these changes impact both electrochemical performance and mechanical characteristics. Furthermore, our model simulates the inelastic deformation within composite electrodes and predicts mechanical degradation in CBM based on viscoplastic deformation.
Results and discussion
Development of a microelectrode-level electrochemo-mechanical model
A composite electrode includes many components: active materials, conductive materials, binders, and a current collector. For an accurate model, it is crucial to assign appropriate electrochemical and mechanical characteristics to each constituent. Cell-level models adopt homogenization, and the effective or equivalent properties are typically applied to each component.19–22 While these homogenized properties may be adequate for simulating the overall trends of cell performance, they can introduce significant errors in models requiring advanced analyses, such as fast charging and cell degradation.23 This discrepancy underscores the necessity of applying individual properties to each component. For this purpose, methods allowing separate experimentation on active materials and CBM must be employed.One of the effective ways to measure the properties of active materials is through particle-level experiments. In this study, we used the reported electrochemical and mechanical parameters of single NMC711 particles, measured through single particle measurements and nanoindentation (Fig. 1A), and applied these properties to the active material structures.9 On the other hand, we manufacture coin cells and directly investigate the electrochemical properties of the whole cell. These measurements can be compared with the model predictions to verify the parameters of each component of the composite electrode. To this end, we fabricated a cathode composite electrode with a weight ratio of NMC711![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PVdF
PVdF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Super-P = 96
Super-P = 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and conducted rate capability evaluations at 1C, 2C, 4C, and 8C rates using a half cell (Fig. 1B). By comparing the rate capabilities at both the particle and cell levels, we aim to understand the factors influencing the performance of the composite electrode.
2 and conducted rate capability evaluations at 1C, 2C, 4C, and 8C rates using a half cell (Fig. 1B). By comparing the rate capabilities at both the particle and cell levels, we aim to understand the factors influencing the performance of the composite electrode.
A critical step in developing a composite microelectrode model is accurately representing the structure of the components. This involves generating the structures of all components, including the active materials, conductive additives, binders, and current collectors, and appropriately applying their electrochemical and mechanical properties. We reconstructed a 3D structure using 540 tomography images taken by FIB/SEM with a resolution of 43 nm (Fig. 1C). In the SEM images, the active materials, current collector, and pores are distinguishable. After image preprocessing, we set a threshold for grey values to form these structures. Nevertheless, due to the limitations of equipment precision and computational resources, it is almost impossible to accurately capture the exact shapes and distribution of conductive materials that range from sub-nano to tens of nanometers. Consequently, we combined the conductive materials and binders in the model and applied electrochemical and mechanical parameters to the combined CBM domain.
The mechanical properties of binder film have only been reported by a few experimental studies.24,25 Our study utilized the reported stress–strain curve at different strain rates (0.00003 s−1–0.003 s−1) to derive Young's modulus of 1.05 GPa and yield strength of 19.36 MPa (Fig. 1D). It is worth noting that these values are measured using dried binder film, so they do not accurately reflect the change in mechanical properties influenced by the electrolyte. Among various electrolyte effects, the most important is probably the binder swelling induced by electrolyte impregnation. We observed this phenomenon during the first tens of hours after cell manufacturing. The essential electrochemical property of CBM for model development is electronic conductivity, as there is no electrochemical reaction but current flow through the CBM. Although some studies have measured the electronic conductivity of CBM, the swelling caused by electrolyte impregnation and structural deformation during cycling alter the electronic conductivity. Due to the lack of additional physical measurements, this effect has not been included in our model. We applied an average measured value for CBM's electronic conductivity.26
Compared with cell-level models, the microstructure-resolved model enhances the accuracy by directly defining the governing equations on each component (Fig. 1E), avoiding homogenization and approximations. Conventional cell-level models commonly approximate porosity, tortuosity, and active surface area using effective values, which hinders the accurate prediction of electrochemo-mechanical properties during cycling. Our model fundamentally eliminates the necessity for these approximations and can account for structural changes that occur during cycling. More detailed information is available in the Modeling methodology section.
Structural, electrochemical, and mechanical analysis by the electrochemo-mechanical model of the microstructure
Active materials undergo expansion and contraction due to lithium intercalation and deintercalation, widely recognized as a major cause of electrode degradation.27–29 The volume changes in the active material result in alterations in both electrochemical and mechanical properties. For example, when the active material expands, the increased active surface area can induce more reactions between the electrolyte and the active material. On the other hand, this expansion can also increase the diffusion length within the active material, resulting in high overpotential. Additionally, the alternating expansion and contraction of the active material during cycles generate stress between active materials, between the active material and the binder, and between the binder and the current collector. This stress can cause particle cracks, particle delamination, and even electrode delamination. Therefore, it is essential to thoroughly analyze the electrochemo-mechanical characteristics resulting from structural changes within the electrode. It is difficult to experimentally analyze these structural characteristics on the nanometer to tens of micrometer scale in real-time. Our microelectrode-resolved electrochemo-mechanical model sheds light on encompassing characteristics from the particle to cell level by virtually implementing the structure of dozens of particles, pores, and CBM using FIB/SEM.Comparison of experimentally measured characteristics at the particle and cell levels and interpretation of the results using structural analysis
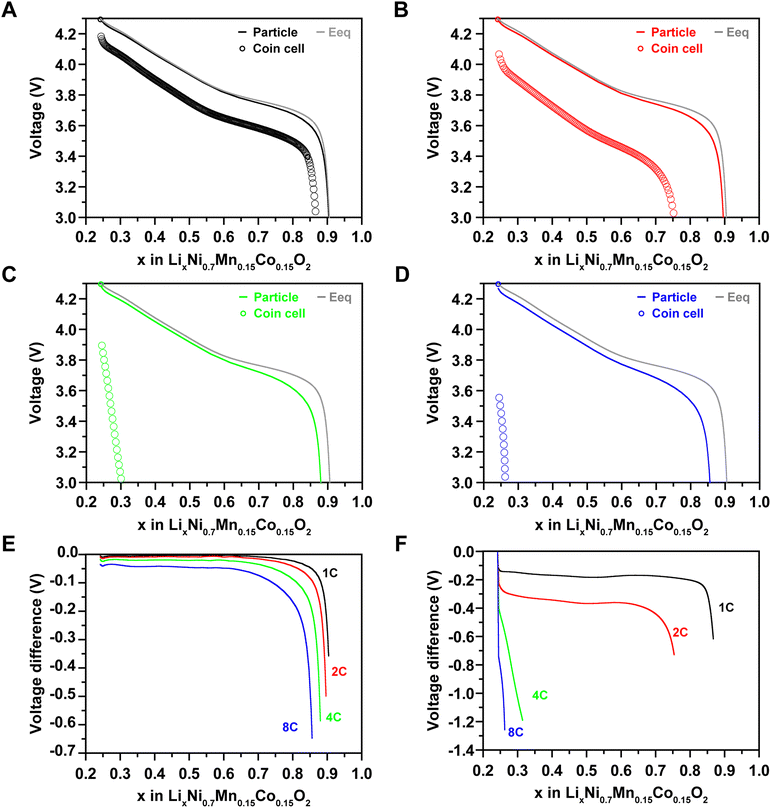
One of the main motivations of our model is to bridge the gap between single-particle and cell-level measurement. To investigate the performance discrepancy between these two levels, we compared the rate capabilities of the coin cell with the single particle measurement results and equilibrium potentials at 1C, 2C, 4C, and 8C rates (Fig. 2A–F).9 At the beginning of discharge (x = 0.24 in LixNi0.7Mn0.15Co0.15O2) at 1C rate (60 minutes), the particles showed an overpotential of only 0.0089 V (equilibrium potential – cell voltage), whereas the coin cells exhibited a 15-fold higher overpotential (0.1383 V). However, the slopes in the voltage profiles of the particle, coin cell, and equilibrium potential were similar until x = 0.8 in LixNi0.7Mn0.15Co0.15O2, indicating that the voltage difference was primarily due to the initially generated overpotential. After reaching the cut-off voltage (3 V), the overpotentials were 0.3577 for the particle and 0.6169 for the coin cell.When the C-rates were increased to 2C (30 minutes), 4C (15 minutes), and 8C (7.5 minutes), the particle showed overpotentials of 0.0142 V, 0.0244 V, and 0.0405 V, respectively, at x = 0.24 in LixNi0.7Mn0.15Co0.15O2, while the coin cell exhibited 18–20 times higher overpotentials of 0.2538 V, 0.4505 V, and 0.8234 V, respectively. The capacities of the coin cell were decreased by 23.89%, 89.23%, and 96.95% compared to the equilibrium potential at 2C, 4C, and 8C, respectively. This demonstrates the difficulty in fully charging within 15 minutes at the cell level, although the particle results indicate the possibility of fast charging. Therefore, to achieve fast charging at the cell level, we need to closely analyze and bridge the gap between particle and cell performance. In coin cells, the overpotentials are significantly affected by both the anode and the cathode. In this study, since lithium metal is used as the anode and its overvoltage is assumed to be constant, the analysis is focused on the cathode.
In this regard, we used microelectrode modeling of the cathode to determine the factors affecting fast charging and conducted an in-depth analysis. From a structural perspective, the higher initial overpotential of the coin cell compared to the particle can be attributed to differences in the electron pathways of the active material and the active surface area which is the contact area between the electrolyte and the active material. The specific active surface areas (surface area/volume) for the particles and the microelectrode are 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476
476![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784 m2 m−3 and 1
784 m2 m−3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720
720![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752 m2 m−3, respectively, a difference of 30.52%.
752 m2 m−3, respectively, a difference of 30.52%.
For the composite electrode of the coin cell, both the CBM and current collector must be considered. Given that CBM contains 12% electrolyte, we assumed that 12% of the interfaces between active materials and CBM are active surface area and the remaining 88% of the interfaces (8.30 × 10−9 m2) are non-reactive. Also, the interfaces of active materials and the current collector (7.71 × 10−10 m2) are non-reactive. By subtracting these non-reactive surface areas from the total area of active materials (7.62 × 10−8 m2), the specific active surface area of the microelectrode is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 538
538![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 m2 m−3, which is only 62.11% of the particle's specific surface area. Additionally, since the active material surfaces positioned at the sides of the composite electrode are not in contact with the electrolyte, the specific active surface area of the microelectrode is 1
340 m2 m−3, which is only 62.11% of the particle's specific surface area. Additionally, since the active material surfaces positioned at the sides of the composite electrode are not in contact with the electrolyte, the specific active surface area of the microelectrode is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 529
529![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 744 m2 m−3, which is 61.76% of the particle's specific active surface area.
744 m2 m−3, which is 61.76% of the particle's specific active surface area.
Since the experiment was conducted under constant current conditions, assuming that the ohmic overpotential remains constant, the increase in overpotential as the discharge progresses can be attributed to concentration overpotential. Although some literature reports that concentration within a particle can be analyzed using experimental methods, these methods have limitations.30 In the following of the paper, we will use our model to investigate this aspect.
Electrochemical analysis of the composite microelectrode
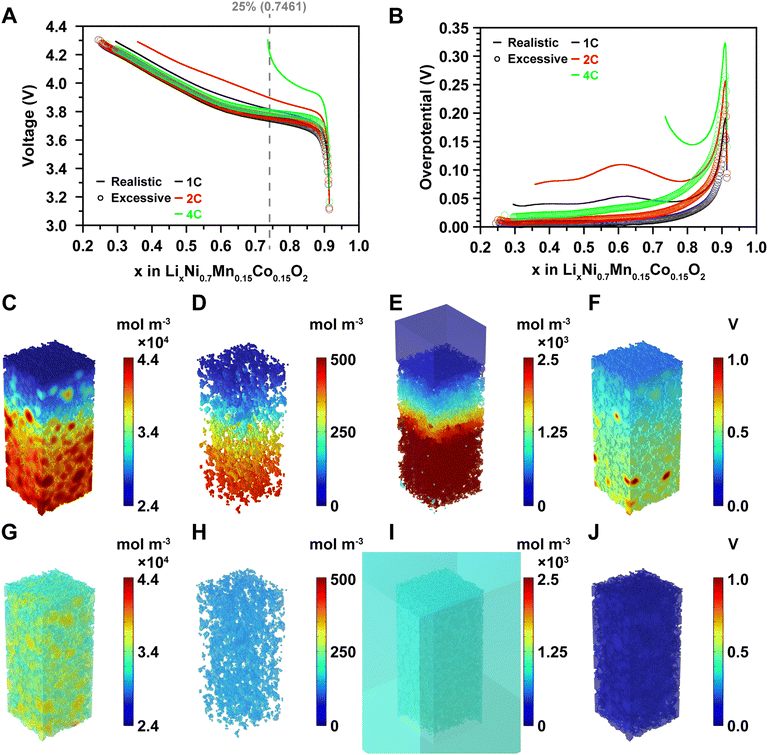
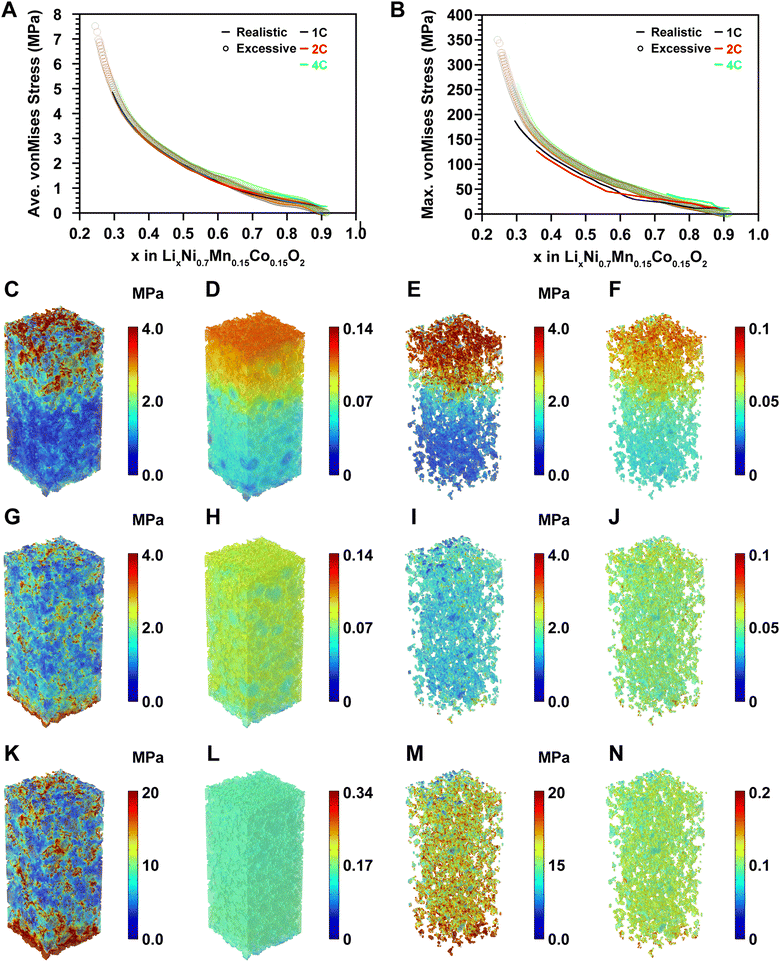
The electrochemical model of the microelectrode was developed based on Fick's law of diffusion, Ohm's law, and the Butler–Volmer equation (see Modeling methodology). The boundary conditions are illustrated in Fig. S1 (ESI†). For model development, we utilized the fitted parameters from particle-level studies for the cathode active materials without additional fitting, while the overpotentials for the anode were measured based on lithium metal three-electrode experiments (Fig. S2, ESI†). The developed model was simulated at 1C, 2C, and 4C rates and validated with an average accuracy of 99.23%, 99.51%, and 98.95%, respectively, compared to the rate capability of the coin cell (Fig. S3A–C, ESI†). The errors for each voltage profile are depicted in Fig. S3D–F (ESI†).At the particle level, all particle surfaces are surrounded by electrolytes, ensuring sufficient reaction sites. However, at the cell level, contact areas between active materials, between active materials and CBM, and between active materials and the current collector reduce the effective active surface area. Insufficient electrolyte further exacerbates the issue, creating a gradient of lithium-ion concentration within the electrolyte, leading to significant overpotential.31 From this perspective, we compared the rate capabilities and overpotentials at 1C, 2C, and 4C under realistic electrode conditions and excessive electrolyte conditions (Fig. 3A and B). The realistic electrode condition is when the electrolyte does not cover the electrode side, and the excessive electrolyte condition is when the electrolyte surrounds the entire electrode as shown in Fig. S1A and D (ESI†). So, the difference between the realistic electrode condition and the excessive electrolyte condition is whether the electrolyte is in contact with the sides. Under excessive electrolyte conditions, capacities were maintained at 100%, 96.72%, and 94.01% at 1C, 2C, and 4C, respectively, despite the relatively higher overpotential at the initial stage of charge compared to the overpotential at the late stage of charge. This was attributed to sufficient reaction sites and electrolytes mitigating the initial overpotential. In contrast, under the realistic electrode condition where sufficient reaction area and electrolyte volume were not ensured, charging capacities dropped significantly to 90.5%, 81.58%, and 26.5% at 1C, 2C, and 4C, respectively, much lower than those under excessive electrolyte conditions. In these realistic electrode conditions, smooth delithiation did not occur due to inadequate reaction area and electrolyte, leading to concentration gradients of lithium ions in both the electrolyte and electrode during charging.
These findings highlight the challenge of achieving high-rate charging above 2C (30 minutes) with currently commercialized batteries, influenced by both cathode and anode rate capabilities. To gain insight into fast charging, we employed our model's advanced analysis technique, 3D operando analysis, which was conducted at 25%, 50%, 75% charge, and cutoff voltages at 1C, 2C, and 4C under both realistic electrode and excessive electrolyte conditions. This analysis included evaluation of lithium-ion concentration in the active materials (Fig. 3C and G, and Fig. S4–S6, ESI†), CBM (Fig. 3D and H, and Fig. S7–S9, ESI†), electrolyte (Fig. 3E and I, and Fig. S10–S12, ESI†), and overpotential of the active material (Fig. 3F and J, and Fig. S13–S15, ESI†).
In the realistic electrode condition at 25% charge at 4C, despite some electrolyte penetrating the electrode and facilitating simultaneous reactions on the electrode surface and within, a larger quantity of lithium ions is deintercalated near the electrode surface compared to near the interface of the active materials and the current collector, creating a significant concentration gradient of lithium ions (Fig. 3C). Analysis of the lithium-ion concentration in the CBM and electrolyte reveals a gradient where concentrations are higher near the current collector and lower near the electrode surface, as lithium ions struggle to diffuse sufficiently into the bulk electrolyte (Fig. 3D and E). Furthermore, due to the migration of lithium ions towards lithium metal, the lithium-ion concentration in the bulk electrolyte is much lower than in the electrolyte impregnated within the electrode pores and CBM, resulting in a pronounced concentration gradient of lithium ions and consequently a high overpotential near the current collector (Fig. 3F).
On the other hand, under the excessive electrolyte condition at 25% charge at 4C, lithium-ion concentration near the electrode surface and current collector remains uniform (Fig. 3G). The surplus electrolyte ensures sufficient lithium ions, resulting in even distribution within the CBM and electrolyte, leading to uniform lithium-ion concentrations (Fig. 3H and I) and low overpotential throughout the electrode (Fig. 3J). These findings suggest the potential for enhanced performance through various patterns etched onto composite electrodes, which increase specific active surface area and promote rapid lithium-ion diffusion from active materials to the reaction surface near the current collector.32–34 Moreover, they indicate the feasibility of supporting charging rates of 4C or higher in a 70 μm-thick composite electrode, albeit with a trade-off between improving rate capability and energy density through patterning.
Particle size is another factor influencing fast charging. Larger particles exhibit slower diffusion between the center and surface, resulting in reduced rate capability due to increased diffusion lengths within the particle. Our results also demonstrate less delithiation in larger particles under both excessive electrolyte and realistic electrode conditions (Fig. 3C and G). Previous literature investigating lithium-ion diffusion in active materials during charging and discharging confirms that particle size significantly impacts rate capability, as effective lithium diffusion across the composite electrode depends on particle size optimization.35–37 However, particle size must balance with mechanical robustness, as smaller particles are more prone to cracking.38 Therefore, achieving optimal rate capability hinges on effectively managing the trade-offs between energy density and mechanical durability.
Structural analysis of the composite microelectrode
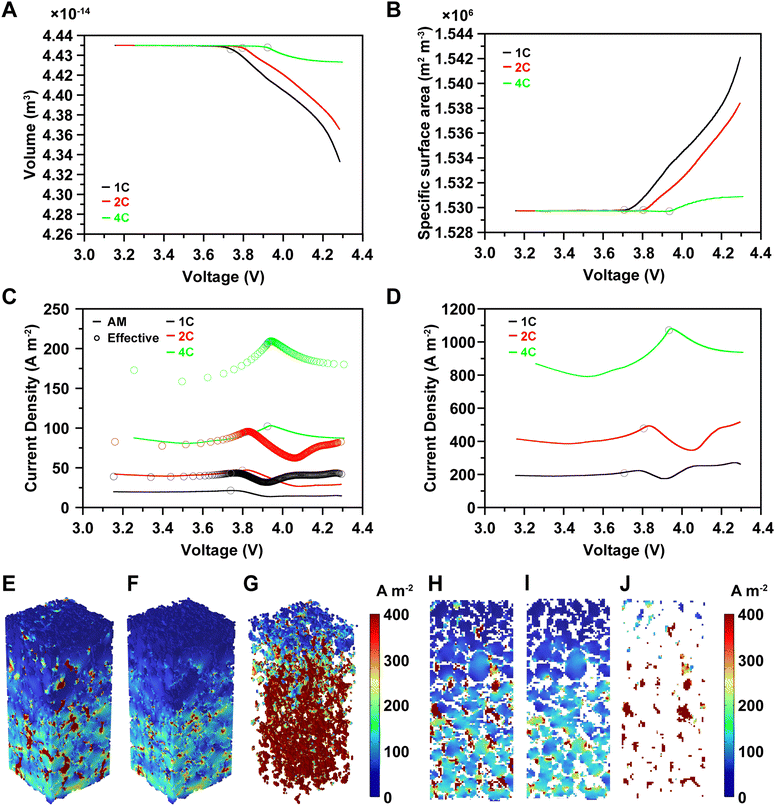
Published literature indicates that the structural characteristics of electrodes significantly influence their electrochemical properties.39,40 However, accurately analyzing structural changes poses a challenge due to the deformation of active materials during cycling. Therefore, our model incorporates a dynamic microstructure that adjusts to reflect active material deformation depending on lithium-ion concentration. We simulated structural deformations that influence the flow of current and modify the reaction surface area, including the viscoplasticity of CBM under realistic electrode conditions at 1C, 2C, and 4C rates (Fig. 4, Fig. S16–S18, and Video S1, ESI†). Initially, there was little deformation observed during charging. However, upon analyzing the structural changes in the cross-section of the composite electrode, we observed numerous deformations inside the electrode (Video S1, ESI†). The deformation increases rapidly between 3.7 V and 3.9 V. The onset voltage of significant volume changes varies with each rate due to differences in overpotential, illustrated by gray circles (Fig. 4A). Upon completion of charging at 4.3 V, volume reductions of 2.37%, 1.71%, and 0.34% were observed, accompanied by respective increases in specific surface area of 0.81%, 0.57%, and 0.08% at 1C, 2C, and 4C (Fig. 4A and B).The volume changes in active materials during cycling can lead to deformation of CBM and potential detachment of the composite electrode from the current collector. However, to achieve high energy density, composite electrodes minimize the fraction of CBM and emphasize uniform distribution for mechanical robustness.41 Less discussed in literature is CBM's impact not only on mechanical strength but also on electronic conductivity within composite electrodes. Specifically, CBM greatly enhances effective electrical conductivity due to its electronic conductivity (3.75 × 106 S cm−1), which is billions of times higher than that of the active material (10−7–10−2 S cm−1).26,42 Therefore, CBM deformation by active material changes can significantly alter current density within the electrode.
We analyzed current densities inside the electrode, revealing averages of 16.29 A m−2, 35.20 A m−2, and 96.60 A m−2 in active materials, and 222.10 A m−2, 431.01 A m−2, and 1012.92 A m−2 in CBM at 1C, 2C, and 4C rates, respectively (Fig. 4C and D). CBM exhibited over 1000% higher current density than active materials, resulting in effective current densities (averages of active material and CBM) of 38.78 A m−2, 78.39 A m−2, and 196.40 A m−2, approximately 200% higher than that of the active material, despite CBM comprising only 4 wt% (Fig. 4C). This indicates that current flow from the current collector to the electrode surface predominantly occurs through CBM rather than active materials. However, the volume change and specific surface area do not proportionally correspond to the current density, as the overpotential increases sharply. Consequently, the current density decreases, as shown in Fig. S15–S17 (ESI†), after the gray circle in Fig. 4. This finding was corroborated by operando analysis, which revealed high current density areas predominantly within CBM dispersed throughout the electrode at 25% charge by 4C in both 3D and 2D views (Fig. 4E–J, and Fig. S16–S18, ESI†).
High current density areas are sporadically observed within CBM, while active materials show high current density only at surfaces in contact with CBM, diminishing towards the particle center (Fig. 4F and I). Within CBM, the current density is high from the current collector to two-thirds of the composite electrode but low near the electrode surface. This is due to binder boiling during electrode drying at 130 °C after slurry production, which creates voids and reduces CBM connectivity near the electrode surface (Fig. 4G and J). Consequently, CBM near the electrode surface exhibits current densities similar to those of active materials, primarily facilitating current flow between particles rather than from the current collector.
Mechanical analysis of the composite microstructure
Analyzing the mechanical integrity of electrode materials, particularly those based on high-nickel compositions, is essential for ensuring long-term electrode stability. The deformation behavior of these materials significantly influences the mechanical integrity of composite electrodes. Therefore, evaluating the volumetric strain in high-nickel active materials involves a detailed analysis of the lattice parameters along the a-axis and c-axis at the unit cell level during the processes of charging and discharging.43 High-nickel active materials exhibit anisotropic deformation due to varying strains along the a-axis and c-axis during lithiation and delithiation. During manufacturing, many NMC primary particles are sintered to form secondary particles. Therefore, the anisotropic expansion/contraction behavior is homogenized. In addition, our computational model consists of a large number of secondary particles, and therefore, it is safe to assume isotropic expansion. To reflect the realistic electrode condition, an initial pressure equivalent to the reported initial pressure at the electrode surface was applied, resulting in greater stress and strain compared to scenarios without initial pressure. Specifically, a constant initial pressure of 20 N generated by the coin cell spring was applied.44,45Using these assumptions, the stress evolution in the electrode was predicted by applying hygroscopic swelling theory for the active materials and large-deformation elasto-viscoplasticity for the CBM. Mechanical properties were evaluated under excessive electrolyte conditions, demonstrating superior characteristics despite higher stress levels (Fig. 5, Fig. S19–S30, and Videos S3 and S4, ESI†). Furthermore, overpotential was lower under excessive electrolyte conditions compared to the realistic electrode condition (Fig. 3F and J), enabling a broader x range in LixNi0.7Mn0.15Co0.15O2 utilization, which resulted in higher average and maximum stresses at the end of charge (Fig. 5A and B). Consequently, superior mechanical integrity was observed under excessive electrolyte conditions when compared at similar x in LixNi0.7Mn0.15Co0.15O2. 3D operando analyses of stress and strain were conducted under both excessive electrolyte and realistic electrode conditions. Under the realistic electrode condition at 25% charge by 4C, stress concentrated near the electrode surface with significant strain in active materials (Fig. 5C and D). Conversely, the excessive electrolyte condition at 25% charge by 4C exhibited relatively uniform deformation throughout the electrode, resulting in uniform stress distribution (Fig. 5G and H). Stress and deformation in CBM were concentrated near the surface in the realistic electrode condition (Fig. 5E and F), while they were evenly distributed in the excessive electrolyte condition (Fig. 5I and J), similar to the behavior observed in active materials. However, in both excessive electrolyte conditions and realistic electrode conditions, significant stress was observed in CBM near the current collector. Upon completion of charging (94% charge) in the excessive electrolyte condition (Fig. 5K–N), the maximum stress near the current collector increased to 314 MPa (Fig. 5B). This high stress in active materials translated to high stress and strain in CBM (Fig. 5M and N), eventually leading to plastic deformation in CBM (Fig. S31, ESI†). Although plastic deformation in CBM may not cause immediate mechanical degradation in composite electrodes within a single cycle, hardening evolution over repeated cycles can lead to mechanical degradation in CBM and potentially result in electrode delamination from the current collector.
Mechanical degradation of conductive and binder materials: cycle simulation
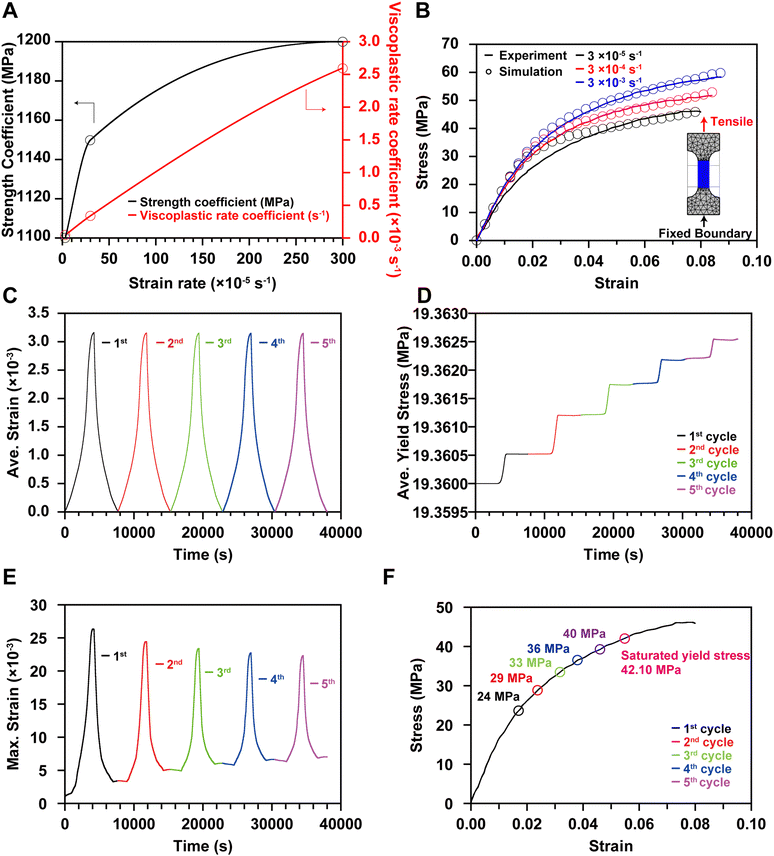
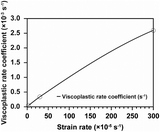
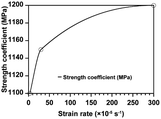
The mechanical degradation and stress–strain evolution in CBM were analyzed using an elastic-viscoplastic framework, as detailed in the Modeling methodology section. A tensile test model, mirroring experimental conditions, was developed to simulate tensile tests at strain rates of 0.00003 s−1, 0.0003 s−1, and 0.003 s−1. The strength and viscoplastic rate coefficients of the Perzyna model were calibrated at these strain rates (Fig. 6A), yielding accuracies of 89.21%, 93.75%, and 97.11%, respectively (Fig. 6B).Using these well-fitted parameters, mechanical degradation was predicted under the assumption that the volume change of the active materials remains constant over cycles. Specifically, the model was run for 5 cycles at 1C in the realistic electrode condition, with the strain evolution quantified at each cycle. The average strain over 5 cycles ranged from 0 to 0.00316, remaining nearly constant within each cycle (Fig. 6C). The average yield strength increased by 0.01% after 5 cycles (Fig. 6D), indicating minimal hardening of CBM. Therefore, the overall strain in CBM is insufficient to induce significant plastic deformation during cycling in the NMC composite electrode containing 2 wt% PVdF. Nevertheless, analyzing the maximum strain is crucial as partial degradation of CBM can lead to a significant decline in cell performance. Literature reports indicate that after hundreds of cycles, particles may detach from the surface of the composite electrode, with these separated particles observed on the separator surface in post-mortem analyses.14,46,47 Furthermore, if the CBM bonded to the current collector degrades, the entire composite electrode may separate, resulting in dramatic deterioration in cell performance.48
To further elucidate the mechanical behavior, we analyzed the maximum strain occurring near the current collector in our microelectrode model (Fig. 6E). Unlike the average strain behavior, the maximum strain decreases with each cycle, indicating plastic deformation in the CBM. This plastic strain drives the increase in the yield stress, reflected in the hardening of the CBM. However, since the maximum strain is insufficient to cause fracture or failure, the increase in yield stress diminishes over cycles and stabilizes at 42 MPa, as calculated by linear extrapolation (Fig. 6F). Given that the fracture strength of PVdF is 45 MPa at a slow loading rate of 0.00003 s−1 (Fig. 6B), it is evident that the PVdF material in the NMC active material composite structure ensures mechanical integrity. This finding underscores the widespread use of PVdF in batteries.
Despite the development of an advanced CBM model, its limitations are evident. This model predicts the mechanical degradation of CBM solely based on the hardening due to plastic deformation. To achieve more accurate simulations of CBM degradation, such as electrode separation from the current collector or particle peeling, a sophisticated fracture model incorporating precise CBM mechanical properties is required.
Conclusions
The motivation for this study stemmed from the observation that the high-rate capability demonstrated at the particle level significantly diminishes when applied at the cell level. Therefore, we aimed to understand the structural, electrochemical, and mechanical complexities when extending from the particle level to the cell level, with a particular focus on fast charging. To achieve this, we compared particle-level electrochemical characteristics with those at the cell level. Our findings revealed that achieving a full charge in less than 15 minutes is challenging for an electrode with a thickness of 70 μm, a loading level of 23.15 mg cm−2, and a density of 3.3 g cm−3, which are conditions similar to those of commercialized electrodes.14To thoroughly analyze and understand the experimental findings, we developed an electrochemo-mechanical model at the microelectrode level using 3D reconstruction that accurately reflects the active materials, pores, and CBM in a domain of tens of micrometers. Our results indicate that the amount of electrolyte, specific surface area, and electrode thickness significantly influence both electrochemical and mechanical characteristics by generating lithium-ion concentration gradients in the active materials, CBM, and electrolyte. Additionally, we analyzed the impact of CBM, which is not considered at the particle level. CBM, being a material through which current predominantly flows inside a composite electrode, significantly affects electrochemical performance by increasing effective electrical conductivity. Uneven binder distribution in the composite electrode interferes with current flow, causing overpotential, and this uneven distribution becomes more frequent as the electrode thickens.
From a mechanical perspective, the degradation of the composite electrode is closely related to the plastic deformation of the CBM. We applied an elastic-viscoplastic model to estimate the large deformation of CBM over cycles. Our results show that PVdF can withstand the stress generated by the deformation from nickel-based active materials during cycling, as the yield stress saturates before reaching the fracture stress. Therefore, PVdF is one of the most stable materials that has been widely used for NMC composite electrodes. At the same time, it is worth noting that due to computational limitations, this model has not considered the long-term degradation effects such as particle fatigue crack, SEI growth, Li plating, and gas generation. In reality, as the cycle number increases, these effects will become prominent, and the plastic deformation of PVdF binder is expected to accumulate.
Despite the development of this advanced analytics platform, several challenges remain to be addressed: (1) during the battery manufacturing stage, it is crucial to account for the expansion of the composite electrode due to electrolyte impregnation, as CBM impregnated with electrolyte exhibits poorer mechanical properties than dried CBM. Therefore, the properties of CBM impregnated with electrolyte must be accurately measured and applied to the model. Although several studies have attempted to analyze the mechanical properties of binders, ensuring their reliability is challenging due to the inconsistency in the reported properties of PVdF.24,25,49 (2) For a more accurate simulation of current flow, the conductive materials and binder materials should be separately reconstructed. However, this presents a significant challenge due to the disparity in scale: conductive materials are only tens of nanometers in size, while particles are several to tens of micrometers. Focusing on the conductive materials and performing 3D reconstruction at high resolution would result in a very heavy simulation, as the entire electrode would need to include tens of billions of voxels. (3) For long cycle estimation, it is crucial to consider electrochemo-mechanical degradation phenomena such as particle cracking, nickel dissolution, and SEI cracking/formation. Additionally, to accurately simulate the separation of electrodes or particles, the general model framework should incorporate a fracture model. (4) Since our model used a separator with a significantly high porosity, the effect of the separator was not considered. However, the influence of the separator cannot be ignored in general batteries. Since the technology for 3D reconstruction of separators using Cryo-FIB-SEM has been developed, it is possible to develop a microstructure model of the separators, reflecting this will enable the development of a more sophisticated model.
Experimental section
Fabrication of the LiNi0.7Mn0.15Co0.15O2 composite electrode
We prepared a mixture consisting of 96 wt% NMC711, 2 wt% polyvinylidene fluoride (PVdF, KF-1300, Mw 350k, Kureha, Japan) binder, and 2 wt% conductive carbon (Super P Li, Imerys, Belgium). The resulting slurry was then coated onto an aluminum current collector (15 μm, Sam-A Aluminum, Korea), dried at 160 °C for 1 hour, and roll-pressed to achieve a thickness of 70 μm and a density of 3.3 g cm−3. Then, coin cells were fabricated using a 20 μm-thick separator (Tonen, Japan) and lithium metal as the counter electrode. For the electrolyte (Enchem, Korea), we used 1 M lithium hexafluorophosphate (LiPF6) in a mixture of ethylene carbonate (EC) and ethyl methyl carbonate (EMC) in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 volume ratio.
7 volume ratio.
Microelectrode structure formation of NMC711 composite electrode
A FIB/SEM system (NB 5000, Hitachi, Japan) was used to cut the NMC711 composite electrode at 65 nm intervals. Tomography was performed 540 times with a pixel size of 43.78 nm at a resolution of 2048 × 1536. The structures of the active materials, CBM, pores, and current collector were formed by performing image synthesis. To obtain a digital representation of the observed structures, we firstly utilized the meta segment anything model (SAM)50 to obtain the total area of active materials, CBM, pores, and current collector, and eliminate the background from the tomography images, where background refer to the space outside the electrodes. SAM is a cutting-edge deep learning-based segmentation tool that allows for precise and automatic segmentation of objects in the image. Its ability to segment “anything” enables accurate background removal without extensive manual annotation. The interfaces between the active materials and the current collector are also identified using SAM. Subsequently, we further segment the image to classify pixels into three phases: active materials, CBM, and pores. Specifically, we applied median filters to remove random noise and differentiate the three phases based on their greyscale values. The obtained 3-phase 2D images were converted to a 3D representation of the electrode structure by stacking them in the third dimension. The 3D representation is formatted as voxel meshes. Considering the computational time required for simulations, the resolution of the synthesized 3D structures was reduced to 600 nm per voxel. Each voxel was then converted to an 8-node solid element (Fig. 1C). The synthesized 3D structures were validated by comparing the volume fraction of each phase in a cropped volume of 30 × 70.8 × 30 μm with the original tomography images in the same domain range, as detailed in Table 1. A good match can be observed between the reconstructed and the true structures.| True structures | Synthesized structures | |
|---|---|---|
| Domain: W × T × D (μm) | 30 × 71 × 30 | 30 × 70.8 × 30 |
| NCM711 fraction in domain | 0.68355 | 0.68351 |
| CBD fraction in domain | 0.08062 | 0.08067 |
| Porosity | 0.23583 | 0.23582 |
| Voxel length (nm) | 43.78 | 600 |
Electrochemo-mechanical parameters of the LiNi0.7Mn0.15Co0.15O2 composite electrode
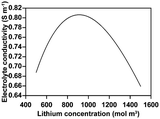
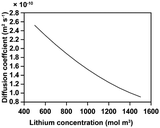
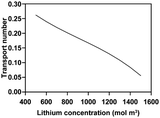
The electrochemo-mechanical parameters applied to the active material were obtained through single particle measurement, nanoindentation, and model fitting9 (Table 2). For conductive materials and binders, since they cannot be isolated separately in the structure, we applied the parameters in CBM level, representing the combination of the conductive materials and binders. The electrochemo-mechanical parameters for the CBM are shown in Table 3. For the electrolytes and current collectors, we used the values provided by COMSOL Multiphysics 6.0 (Tables 4 and 5).| Electronic conductivity (S m−1) | 3.58 × 107 |
| Density (g cm−3) | 2.70 |
| Poisson's ratio | 0.3314 |
| Young's modulus (GPa) | 6.88 |
| Yield strength (MPa) | 276 |
| Isotropic tangent modulus (GPa) | 0.562 |
| Resistivity (Ω m) | 2.79 × 10−8 |
| Young's modulus (GPa) | 2.611 |
Modeling methodology
Mass conservation
Mass conservation in active materials in composite electrode is described by Fick's law of diffusion as follows: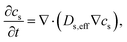 | (1) |
Boundary condition: 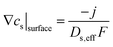 , and cs|center = cs,init.
, and cs|center = cs,init.
D s,eff (m2 s−1) is effective diffusion coefficient in the composite electrode, which determines rate of lithium-ion intercalation or deintercalation. In our model, Ds,eff = Ds can be applied as intrinsic properties that does not changed with cell design because active materials are replicated completely by 3D reconstruction. So, eqn (1) is simplified as follows:
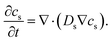 | (2) |
In this way, the realistic structures of each component can contribute to the development of more accurate models by fundamentally removing structural parameters and preventing overfitting. Therefore, we were able to apply the Ds in a way that depends on the lithium-ion concentration as follows:
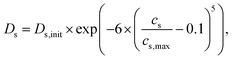 | (3) |
As for the electrolyte, mass conservation equation is as follows:
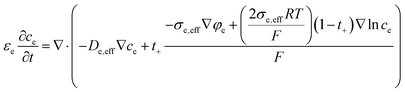 | (4) |
Boundary condition: ce|Electrolyte|CC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) surface = ce,init.
surface = ce,init.
In the electrolyte, we can apply εe = 1, De,eff = De, and σe,eff = σe because realistic structures include all electrolyte structure in the composite electrode. So, eqn (4) is changed as follows:
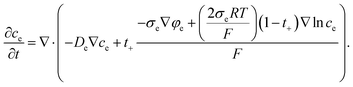 | (5) |
However, in the CBM, εe, De,eff, and σe,eff are determined by the amount of electrolyte that penetrates the CBM. In this paper, PVdF was used for binders, so the εe is 0.16, which is the volume expansion rate of PVdF due to electrolyte penetration24 and with the Bruggeman relation, De,eff = εe1.5De and σe,eff = εe1.5σe are used as effective value. So, eqn (4) can be written for CBM as follows:
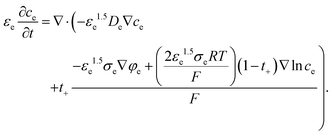 | (6) |
Charge conservation
The charge conservation in active materials and CBM is described by Ohm's law as follows:| ∇·(σs,eff∇φs) = asj, | (7) |
Boundary condition:  , and ∇·(σs,eff∇φs)|AM
, and ∇·(σs,eff∇φs)|AM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) surface = 0.
surface = 0.
In the active materials, the σs,eff = σs was applied thanks to the realistic structures (Fig. 1). Eqn (7) can be written as follows:
| ∇·(σs∇φs) = asj. | (8) |
The charge conservation equation in liquid phases of electrolyte and CBM is as follows:
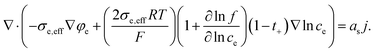 | (9) |
Likewise, in the electrolyte, we can apply σe,eff = σe so, eqn (9) is changed as follows:
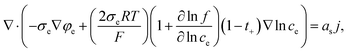 | (10) |
Boundary condition: φe|Electrolyte|CC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) surface = 0.
surface = 0.
However, eqn (10) cannot be applied for CBM because electrolyte is combined with CBM. So σs,eff can be determined by Bruggeman relation as follows:
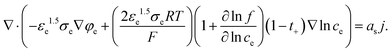 | (11) |
Reaction kinetics
The variables, concentrations and potentials in active materials, electrolyte, and CBM in mass and charge conservation equations, are coupled by the Butler–Volmer equation described as follows: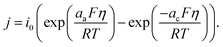 | (12) |
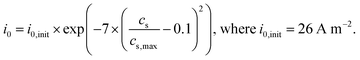 | (13) |
The current density j in eqn (12) is driven by overpotential defined as follows:
| η = φs − φe − Ueq. | (14) |
Mechanical model formulation
The formulation for the mechanical model considers the elastic – hygroscopic response of the NMC711 active material and the elastic – viscoplastic response of the CBM, under the assumption of infinitesimal deformations. Hence, for a deformable domain Ω, the kinematic strain–displacement relationship is expressed as: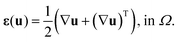 | (15) |
Here, ε and u denote the strain and displacement tensor fields within the domain Ω respectively. Also, a Dirichlet boundary condition is imposed on the displacement field over the domain, expressed as:
| u = û, on Ωu, | (16) |
The conservation of linear momentum gives us the force equilibrium condition:
| ∇·σ + b = 0, in Ω, | (17) |
σ·n = ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) , on Ωt, , on Ωt, | (18) |
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) is the prescribed traction vector on the Neumann boundary. Furthermore, we can express the general form of the constitutive relationship as:
is the prescribed traction vector on the Neumann boundary. Furthermore, we can express the general form of the constitutive relationship as:σ = σ(ε, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) ) ) | (19) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) is the strain rate tensor. Consequently, under the small deformation assumption, the strain tensor is additively decomposed into three parts: the elastic strain εe, the viscoplastic strain εvp, and the hygroscopic strain εs:
is the strain rate tensor. Consequently, under the small deformation assumption, the strain tensor is additively decomposed into three parts: the elastic strain εe, the viscoplastic strain εvp, and the hygroscopic strain εs:| ε = εe + εvp + εs | (20) |
The Cauchy stress is determined by:
σ = ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) :εe, :εe, | (21) |
![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) is the fourth-order elastic modulus tensor.
is the fourth-order elastic modulus tensor.
NMC711 active material has been well documented to show brittle mechanical behavior.51,52 Hence its strain tensor formulation excludes consideration of viscoplastic strains and is limited to elastic and hygroscopic strains.
| ε = εe + εs | (22) |
An isotropic volumetric change is assumed to occur based on the lithium-ion concentration, allowing for the application of hygroscopic theory to simulate the lithium-induced strain as outlined in previous studies:53,54
| εs = βLMm(cs − cs,init), | (23) |
The lithium-induced strain, εs dependent on the lithium-ion concentration are reported in ref. 55 and 56, the molar mass (Mm), and lithium-ion concentration change (cs − cs,init) are calculated (Fig. S32A–C, ESI†). So, we reversely derived the lithium-induced strain coefficient, βL (Fig. S32D, ESI†).
In the CBM, both elastic and viscoplastic deformations are observed, typical of such polymeric materials. These deformations are induced by the deformation of active materials. Thus, eqn (20) reduces to the following formulation:
| ε = εe + εvp. | (24) |
The Perzyna model is used to describe the viscoplastic strain evolution.57 This model, originally formulated for the viscoplastic response of metals at high temperatures has been successfully applied to model the inelastic rate-dependent response of polymeric materials.58,59 The model equation for the viscoplastic strain rate is:
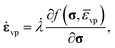 | (25) |
f(σ,![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) vp) = vp) = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) − σy, − σy, | (26) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is the equivalent stress expressed in the form:
is the equivalent stress expressed in the form: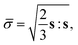 | (27) |
σy = σy0 + k(![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) vp)n, vp)n, | (28) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) vp is the accumulated equivalent viscoplastic strain expressed in the form:
vp is the accumulated equivalent viscoplastic strain expressed in the form: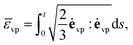 | (29) |
![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) in the associated flow rule (eqn (25)) according to the Perzyna model is expressed as:
in the associated flow rule (eqn (25)) according to the Perzyna model is expressed as: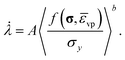 | (30) |
A is the viscoplastic rate coefficient, b is the stress exponent typically set to be unity for Perzyna type models and 〈·〉 is the Macauley bracket,
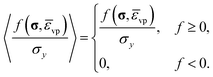 | (31) |
All parameters for the model are described in Tables 2–5 and their descriptions are provided in Table 6.
| D s,eff | Effective diffusion coefficient in active materials, [m2 s−1] |
| c s | Lithium-ion concentration in active materials, [mol m−3] |
| c s,init | Initial lithium-ion concentration in active materials, [mol m−3] |
| j | Current density on the electrode, [A m−2] |
| F | Faraday constant, [96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 C mol−1] 487 C mol−1] |
| D s | Intrinsic diffusion coefficient in active materials, [m2 s−1] |
| D s,init | Initial diffusion coefficient in active materials, [m2 s−1] |
| c s,max | Maximum lithium-ion concentration in active materials, [mol m−3] |
| ε e | Electrolyte volume fraction in porous materials |
| c e | Lithium-ion concentration in the liquid phase, [mol m−3] |
| D e,eff | Effective diffusion coefficient in electrolyte, [m2 s−1] |
| σ e,eff | Effective electronic conductivity of electrolyte [S m−1] |
| R | Gas constant, [8.3143 J mol−1 K−1] |
| T | Temperature, [303.15 K] |
| t + | Transport number |
| D e | Intrinsic diffusion coefficient in electrolyte, [m2 s−1] |
| σ e | Intrinsic electronic conductivity of electrolyte [S m−1] |
| σ s,eff | Effective electronic conductivity of active materials [S m−1] |
| σ s | Intrinsic electronic conductivity of active materials [S m−1] |
| I | Applied current |
| φ s | Potential in the active materials, [V] |
| a s | Specific surface area, [m2 m−3] |
| φ e | Potential in the electrolyte, [V] |
| i 0 | Exchange current density [A m−2] |
| a a | Anodic transfer coefficient |
| a c | Cathodic transfer coefficient |
| i 0,init | Initial exchange current density [A m−2] |
| η | Overpotential [V] |
| U eq | Equilibrium potential [V] |
| ρ | Density, [kg m−3] |
| ε | Strain tensor |
| u | Displacement field, [m] |
| Ω | Domain |
| û | Prescribed displacement |
| Ω u | Dirichlet boundary condition |
| σ | Second order stress tensor [Pa] |
| b | Body force per unit volume [N m−3] |
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif)
|
Prescribed traction vector |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif)
|
Strain rate tensor |
| ε e | Elastic strain |
| ε vp | Viscoplastic strain |
![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) |
Fourth-order elastic modulus tensor |
| Q p | Plastic potential [Pa] |
| ε s | Hygroscopic strain |
| β L | Lithium-induced strain coefficient [m3 kg−1] |
| M m | Molar mass [kg mol−1] |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) vp
vp
|
Viscoplastic strain evolution |
| f | Yield function of the material |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif)
|
Equivalent stress |
| s | Deviatoric stress tensor |
| σ y | Yield stress [Pa] |
| σ y0 | Initial yield stress [Pa] |
| k | Strength coefficient |
| n | Hardening exponent |
| A | Viscoplastic rate coefficient |
| b | Stress exponent |
Tool for developing an electrochemo-mechanical model
The ECM model was developed using COMSOL Multiphysics 6.0 with modules of lithium-ion battery, transport of diluted species, solid mechanics, and deformed geometry. Specifically, the modules of lithium-ion battery and transport of diluted species are used to calculate electrochemical performance and the calculated lithium-ion concentration in active materials is used to calculate the lithium-induced strain in solid mechanics and deformed geometry module. This deformed structure affects the simulation of electrochemical performance in the modules of lithium-ion battery and transport of diluted species.The numerical calculations were performed on a workstation featuring an AMD Ryzen Threadripper PRO 3995WX processor (64 cores, 2.70–4.20 GHz) and 1 TB of SK Hynix PC4-3200AA-L 3200 MHz ECC server RAM (4 × 256 GB). The simulation required approximately two weeks to compute a single discharge curve.
Author contributions
J. S. conceived the idea and methodology, developed the electrochemo-mechanical model, and wrote the final version of the manuscript. R. I. helped develop viscoplastic model and write the manuscript. J. L. measured electrochemical properties. Z. W. performed the 3D reconstruction of the composite electrode. W. L. helped with the mechanical analysis. R. F. helped with the electrochemical analysis. A. K. G. assisted in writing the manuscript. H. X. supervised the 3D reconstruction. Y. M. L. supervised the electrochemical analysis. J. Z. supervised modeling and wrote the final version of the manuscript.Data availability
The published article includes all data generated or analyzed during this study. The authors declare that the experimental data that support the findings of this paper are available within the article and its ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The research team at Northeastern University is supported by the Center for Battery Sustainability financially supported by Hyundai Motor Company, Shell, SES.AI, Saint-Gobain, and Seimens. The UConn team is financially supported by National Science Foundation (CMMI-2142290).References
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS.
- Y. D. Cho, G. T. K. Fey and H. M. Kao, J. Power Sources, 2009, 189, 256–262 CrossRef CAS.
- C. Delacourt, C. Wurm, L. Laffont, J. B. Leriche and C. Masquelier, Solid State Ionics, 2006, 177, 333–341 CrossRef CAS.
- C. X. Tian, Y. H. Xu, D. Nordlund, F. Lin, J. Liu, Z. H. Sun, Y. J. Liu and M. Doeff, Joule, 2018, 2, 464–477 CrossRef CAS.
- J. S. Kim, S. Lim, H. Munakata, S. S. Kim and K. Kanamura, Electrochim. Acta, 2021, 390, 138813 CrossRef CAS.
- C. Zhao, C. W. Wang, X. Liu, I. Hwang, T. Y. Li, X. W. Zhou, J. C. Diao, J. J. Deng, Y. Qin, Z. Z. Yang, G. Y. Wang, W. Q. Xu, C. J. Sun, L. L. Wu, W. Cha, I. Robinson, R. Harder, Y. Jiang, T. Bicer, J. T. Li, W. Q. Lu, L. X. Li, Y. Z. Liu, S. G. Sun, G. L. Xu and K. Amine, Nat. Energy, 2024, 9, 345–356 CrossRef CAS.
- J. H. Song, Y. J. Kim, J. Kim, S. M. Oh and S. Yoon, Bull. Korean Chem. Soc., 2016, 37, 1298–1304 CrossRef CAS.
- M. Klinsmann, D. Rosato, M. Kamlah and R. M. McMeeking, J. Mech. Phys. Solids, 2016, 92, 313–344 CrossRef CAS.
- J. Song, S. H. Lim, K. G. Kim, N. Umirov, H. Y. B. Lee, C. B. Dzakpasu, J. Lim, J. Nam, J. Park, J. N. Lee, H. Munakata, K. Kanamura, S. S. Kim and Y. M. Lee, Adv. Energy Mater., 2023, 13, 2204328 CrossRef CAS.
- J. Song, J. Park, W. A. Appiah, S. S. Kim, H. Munakata, K. Kanamura, M. H. Ryou and Y. M. Lee, Nano Energy, 2019, 62, 810–817 CrossRef CAS.
- A. Singh, J. Song, W. Li, T. Martin, H. Y. Xu, D. P. Finegan and J. E. Zhu, Extreme Mech. Lett., 2024, 69, 102164 CrossRef.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1–10 CrossRef CAS.
- E. Kim, J. Song, C. B. Dzakpasu, D. Kim, J. Lim, D. Kim, S. Park, H. Y. B. Lee, T. S. Kwon and Y. M. Lee, J. Energy Storage, 2023, 72, 108627 CrossRef.
- J. Song, H. Lee, S. Kim, D. Kang, S. Jung, H. Lee, T. S. Kwon and Y. M. Lee, Front. Mater., 2022, 9, 824168 CrossRef.
- N. Abdelmoula, B. Harthong, D. Imbault and P. Dorémus, J. Mech. Phys. Solids, 2017, 109, 142–159 CrossRef.
- X. K. Lu, M. Lagnoni, A. Bertei, S. Das, R. E. Owen, Q. Li, K. O'Regan, A. Wade, D. P. Finegan, E. Kendrick, M. Z. Bazant, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2023, 14, 5127 CrossRef CAS PubMed.
- T. Tancogne-Dejean, M. B. Gorji, J. E. Zhu and D. Mohr, Int. J. Plast., 2021, 146, 103072 CrossRef CAS.
- P. Gupta, I. B. Üçel, P. Gudmundson and E. Olsson, Exp. Mech., 2020, 60, 847–860 CrossRef CAS.
- H. Huang, K. Chen, C. Li, Z. Zhou, W. Wang, B. Deng, S. Liu, C. Qian, M. Yue, Z. Chi, J. Xu and Y. Zhang, Chem. Eng. J., 2024, 481, 148577 CrossRef CAS.
- W. Zeng, W. Shu, J. Zhu, F. Xia, J. Wang, W. Tian, J. Tian, S. Zhang, Y. Zhang, H. Peng, H. Zhao, L. Chen, J. Wu and S. Mu, ACS Energy Lett., 2024, 9, 346–354 CrossRef CAS.
- C. Zhang, J. Xu, L. Cao, Z. N. Wu and S. Santhanagopalan, J. Power Sources, 2017, 357, 126–137 CrossRef CAS.
- H. Lee, S. Yang, S. Kim, J. Song, J. Park, C. H. Doh, Y. C. Ha, T. S. Kwon and Y. M. Lee, Curr. Opin. Electrochem., 2022, 34, 100986 CrossRef CAS.
- S. Byun, Y. Roh, K. M. Kim, M. H. Ryou and Y. M. Lee, Appl. Mater. Today, 2020, 21, 100809 CrossRef.
- A. Santimetaneedol, R. Tripuraneni, S. A. Chester and S. P. V. Nadimpalli, J. Power Sources, 2016, 332, 118–128 CrossRef CAS.
- Y. H. Chen, C. W. Wang, G. Liu, X. Y. Song, V. S. Battaglia and A. M. Sastry, J. Electrochem. Soc., 2007, 154, A978–A986 CrossRef CAS.
- O. Furat, D. P. Finegan, Z. Z. Yang, M. Neumann, S. Kim, T. R. Tanim, P. Weddle, K. Smith and V. Schmidt, Energy Storage Mater., 2024, 64, 103036 CrossRef.
- F. Guo, Y. Chen, Y. Song, Y. Deng, W. Hua, W. Yang, T. Chen, Z. Wu, L. Qiu and X. Guo, Small, 2024, 20, 2310321 CrossRef CAS PubMed.
- J. Liu, X. Hu, S. Qi, Y. Ren, Y. Li and J. Ma, InfoMat, 2024, 6(2), e12507 CrossRef CAS.
- J. R. Lawrence, G. D. W. Swerhone, G. G. Leppard, T. Araki, X. Zhang, M. M. West and A. P. Hitchcock, Appl. Environ. Microbiol., 2003, 69, 5543–5554 CrossRef CAS PubMed.
- F. J. Günter, C. Burgstaller, F. Konwitschny and G. Reinhart, J. Electrochem. Soc., 2019, 166, A1709–A1714 CrossRef.
- J. H. Pikul, H. G. Zhang, J. Cho, P. V. Braun and W. P. King, Nat. Commun., 2013, 4, 1732 CrossRef PubMed.
- D. Kim, C. Bak, N. Kim, J. Park, M. Lee, D. O. Shin, Y. G. Lee and Y. Lee, Mater. Today Sustainability, 2023, 22, 100338 CrossRef.
- A. Izumi, M. Sanada, K. Furuichi, K. Teraki, T. Matsuda, K. Hiramatsu, H. Munakata and K. Kanamura, Electrochim. Acta, 2012, 79, 218–222 CrossRef CAS.
- T. F. Liu, L. Zhao, D. L. Wang, J. S. Zhu, B. Wang and C. F. Guo, RSC Adv., 2014, 4, 10067–10075 RSC.
- J. L. Liu, Z. Z. Wang, G. H. Zhang, Y. Liu and A. S. Yu, Int. J. Electrochem. Sci., 2013, 8, 2378–2387 CrossRef CAS.
- N. Anansuksawat, T. Sangsanit, S. Prempluem, K. Homlamai, W. Tejangkura and M. Sawangphruk, Chem. Sci., 2024, 15, 2026–2036 RSC.
- W.-X. Chen, J. M. Allen, S. Rezaei, O. Furat, V. Schmidt, A. Singh, P. J. Weddle, K. Smith and B.-X. Xu, J. Power Sources, 2024, 596, 234054 CrossRef CAS.
- H. S. Bae, I. Phiri, H. S. Kang, Y. M. Lee and M. H. Ryou, J. Power Sources, 2021, 514, 230553 CrossRef CAS.
- J. Y. Kim, S. Jung, S. H. Kang, J. Park, M. J. Lee, D. Jin, D. O. Shin, Y. G. Lee and Y. M. Lee, Adv. Energy Mater., 2022, 12, 2103108 CrossRef CAS.
- C. Bak, K.-G. Kim, H. Lee, S. Byun, M. Lim, H. An, Y. Roh, J. Lim, C. B. Dzakpasu, D. Kim, J. Lee, H. Lee, H. Lee and Y. M. Lee, Chem. Eng. J., 2024, 483, 148913 CrossRef CAS.
- R. Amin and Y. M. Chiang, J. Electrochem. Soc., 2016, 163, A1512 CrossRef CAS.
- T. Y. Li, X. Z. Yuan, L. Zhang, D. T. Song, K. Y. Shi and C. Bock, Electrochem. Energy Rev., 2020, 3, 43–80 CrossRef.
- J. P. Singer, C. Sämann, T. Gössl and K. P. Birke, Sensors, 2018, 18, 3808 CrossRef PubMed.
- J. H. Sun, J. Y. Peng, T. R. Y. Ring, L. Whittaker-Brooks, J. E. Zhu, D. Fraggedakis, J. Niu, T. Gao and F. Wang, Energy Environ. Sci., 2022, 15, 5284–5299 RSC.
- W. X. Wu, R. X. Ma, J. Z. Liu, M. Liu, W. L. Wang and Q. Wang, Int. J. Heat Mass Transfer, 2021, 170, 121024 CrossRef CAS.
- A. Iturrondobeitia, F. Aguesse, S. Genies, T. Waldmann, M. Kasper, N. Ghanbari, M. Wohlfahrt-Mehrens and E. Bekaert, J. Phys. Chem. C, 2017, 121, 21865–21876 CrossRef CAS.
- C. Lürenbaum, B. Vortmann-Westhoven, M. Evertz, M. Winter and S. Nowak, RSC Adv., 2020, 10, 7083–7091 RSC.
- M. Sang, S. Wang, M. Liu, L. F. Bai, W. Q. Jiang, S. H. Xuan and X. L. Gong, Compos. Sci. Technol., 2018, 165, 31–38 CrossRef CAS.
- A. Kirillov, E. Mintun, N. Ravi, H. Z. Mao, C. Rolland, L. Gustafson, T. T. Xiao, S. Whitehead, A. C. Berg, W. Y. Lo, P. Dolla'r and R. Girshick, IEEE, 2023, 3992–4003, DOI:10.1109/Iccv51070.2023.00371.
- Y. H. Shin, S. Maeng, Y. M. Chung, G. K. Krumdick and S. Min, Small, 2021, 17, 2100040 CrossRef CAS PubMed.
- R. Xu, H. Sun, L. S. de Vasconcelos and K. J. Zhao, J. Electrochem. Soc., 2017, 164, A3333–A3341 CrossRef CAS.
- T. Ikeda, T. Mizutani, K. Miyake and N. Miyazaki, J. Electron. Packag., 2013, 135, 041005 CrossRef.
- M. Masmoudi, Z. Moumni and F. Bidault, J. Electrochem. Soc., 2019, 166, A5445–A5461 CrossRef CAS.
- R. Koerver, W. B. Zhang, L. de Biasi, S. Schweidler, A. O. Kondrakov, S. Kolling, T. Brezesinski, P. Hartmann, W. G. Zeier and J. Janek, Energy Environ. Sci., 2018, 11, 2142–2158 RSC.
- J. Li, J. Harlow, N. Stakheiko, N. Zhang, J. Paulsen and J. Dahn, J. Electrochem. Soc., 2018, 165, A2682–A2695 CrossRef CAS.
- P. Perzyna, in Advances in Applied Mechanics, ed. G. G. Chernyi, H. L. Dryden, P. Germain, L. Howarth, W. Olszak, W. Prager, R. F. Probstein and H. Ziegler, Elsevier, 1966, vol. 9, pp. 243–377 Search PubMed.
- D. Tscharnuter, M. Jerabek, Z. Major and G. Pinter, Mech. Time-Depend. Mater., 2012, 16, 275–286 CrossRef CAS.
- D. Vasiukov, S. Panier and A. Hachemi, Compos. Struct., 2015, 132, 527–535 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee04856c |
| This journal is © The Royal Society of Chemistry 2025 |