Experimental study on the motion characteristics and critical hydraulic parameters of microplastics in a freshwater environment†
Ming
Dou
 *ab,
Zhen
Wang
a,
Yuxuan
Li
b,
Bin
Sun
a,
Yongyong
Zhang
c,
Yuze
Zhou
a and
Ruipeng
Jia
a
*ab,
Zhen
Wang
a,
Yuxuan
Li
b,
Bin
Sun
a,
Yongyong
Zhang
c,
Yuze
Zhou
a and
Ruipeng
Jia
a
aSchool of Water Conservancy and Transportation, Zhengzhou University, No. 100 Kexue Road, Zhengzhou, 450001, Henan, China. E-mail: dou_ming@163.com
bSchool of Ecology and Environment, Zhengzhou University, Zhengzhou, 450001, China
cKey Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing, 100101, China
First published on 13th December 2024
Abstract
The migration behavior of microplastics in water is affected by many factors; in particular, the migration mechanism of microplastics in the terrestrial freshwater environment is more complicated than that in the marine environment. In order to understand the migration behavior of microplastics in the freshwater environment, the hydraulic parameter thresholds of different types of microplastics in water were identified based on hydraulic experiments and force analysis methods. The results show that the motion state of microplastics is affected by their own internal factors and external environmental factors, and the flow rate is the key external factor affecting the change of their motion state. In the vertical direction, the higher the density, the rougher the environment, and the closer the shape to the flake, the greater the critical starting flow velocity and the critical resuspension flow velocity. The settling velocities, critical initiation velocities, and critical resuspension velocities of microplastics range from 0.05 to 0.17 m s−1, 0.03 to 0.44 m s−1, and 0.251 to 0.83 m s−1, respectively. Horizontally, the bottom rolling velocities of microplastics vary significantly. These velocities are positively correlated with water flow velocity but are inversely proportional to the density of the microplastics and the roughness of the substrate. By combining experimental data, mathematical expressions for the critical hydraulic parameters of microplastics were derived, showing improved accuracy compared to traditional methods. This paper explores the trajectory of different types of microplastics after entering the water body and analyzes their migration mechanism in the river. The research results have certain theoretical guiding significance for revealing the migration law of microplastics in the freshwater environment.
Environmental significanceMicroplastics (MPs) can migrate to all corners of the earth under the action of external forces, seriously threatening the safety of humans, animals and plants. The study of the movement characteristics of microplastics in the freshwater environment can not only make up for the lack of research on the migration mechanism of microplastics, but also provide a theoretical reference for the prevention of microplastic pollution. Therefore, the motion trajectory of microplastics in the freshwater environment is explored by using the principle of sediment dynamics to analyze the stress of microplastics and carry out hydrodynamic tests. Combined with the experimental data, the mathematical expression of the critical hydraulic parameters of microplastics was obtained, which improved the fitting effect compared with the traditional method. |
1. Introduction
The widespread use of plastic products, while bringing convenience to human life, has also created significant pollution problems for the ecological environment. Microplastics (MPs), a large number of small plastic particles in the water environment, are threatening human and ecosystem health.1 Because MPs have the characteristics of small particle size, large quantity, strong adsorption and chemical stability,2 they will be transported and migrate in the environment through complex external forces such as wind, runoff and artificial wastewater discharge. MPs are the most widely distributed in the aquatic environment, oceans, and coastlines,3–5 and freshwater waters such as rivers and lakes generally contain a certain number of MPs.6–10Research into the migration mechanisms of MPs has garnered significant attention from scholars, yet studies focusing on the movement principles of microplastic particles within inland water bodies remain limited. The migration of MPs in water is mainly manifested in vertical movement and horizontal migration, including drifting, suspension, sedimentation, resuspension, grounding, refloating and deposition. Usually, these processes may be carried out simultaneously, cyclically, or spontaneously.11 This is not only related to the particle size, density and shape of the MPs, but also to the conditions in the external water environment where the MPs are located.12 Isobe et al.13 studied the migration process of different sizes of plastics along the west coast of SetoNaikai and found that the smaller the particle size of MPs, the farther the distance to the ocean, while large plastics will selectively move to the shore. A critical determinant of microplastic mobility in water bodies is the variability in water current velocities.14 MPs are more likely to settle in regions characterized by slow-moving currents and deeper waters, while those already deposited may be remobilized in areas with faster currents and shallower depths.11 The cause of the motion state of a single microplastic particle is the mixing of various external forces.15 Therefore, different external environmental conditions lead to differences in the motion state of MPs.
Most of the current research on the movement of MPs has focused on marine environmental systems, whereas few studies have focused on freshwater environmental systems.16,17 The trajectory and driving factors of MPs in the freshwater environment are quite different from those in the marine environment (such as more complex water flow patterns and more frequent transitions of MPs). Moreover, the freshwater environment is closely related to the survival and development of human beings and should be the focus of microplastic pollution prevention and control. The complexities of riverine hydrological conditions exacerbate the variability in microplastic movement, with high-density MPs frequently unable to settle in turbulent currents, ultimately depositing at riverbeds' bottoms and ceasing further migration. At the same time, MPs can also migrate between the terrestrial environment, freshwater environment and marine environment. Some of the MPs in the terrestrial environment will be deposited underground under the influence of gravity and biological activities, and others will remain on the surface. Lighter MPs are transported through the air by wind, whereas heavier ones enter the freshwater system via rainwater runoff, agricultural irrigation, and drainage canals, ultimately reaching the marine environment.18,19 In addition, some MPs deposited underground may also enter the freshwater system through underground runoff.20 Therefore, the irregularity of the motion state of MPs in the freshwater environment is more obvious.
The purpose of this study is to explore the movement mechanism of MPs in the freshwater environment and identify the factors affecting the mutual transformation of MPs through the combination of sediment dynamics theory and hydraulic experiments. The specific research objectives are:
(1) Through the hydraulic experiment to observe the trajectory of different shapes and materials of microplastic particles in the water, analysis of the force in the process of movement.
(2) Identify the motion rate coefficients of different types of MPs in water surface drift, water suspension, and underwater movement.
(3) Establish the key factors affecting the motion state of MPs and determine the critical hydrodynamic parameters for the mutual transformation of MPs between different motion states.
2. Materials and methods
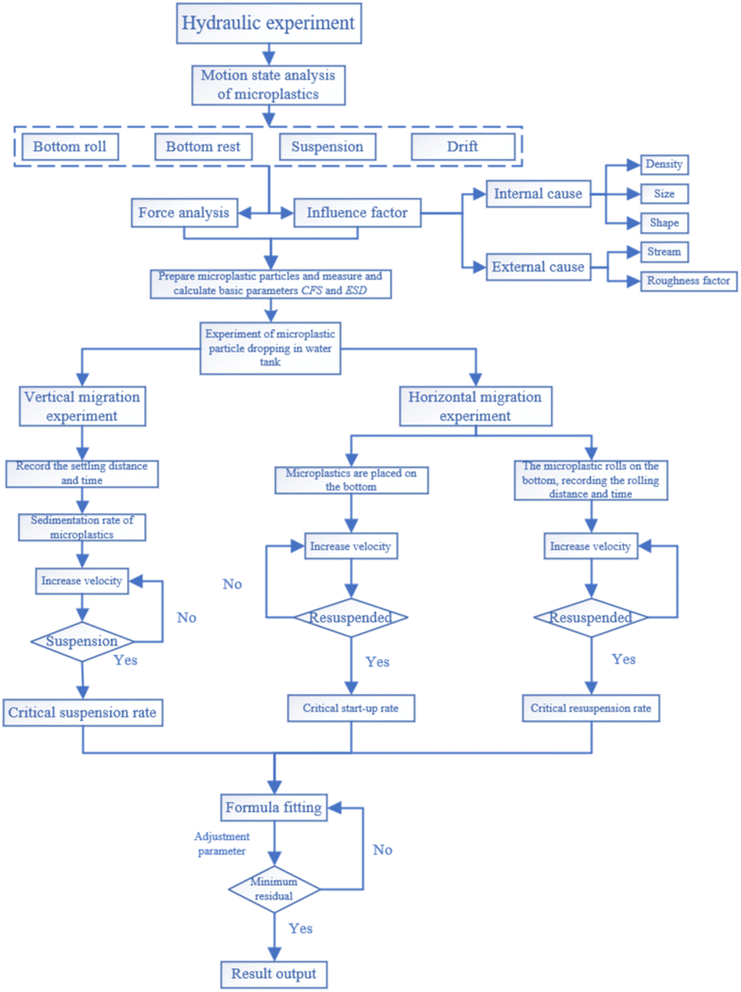
Once the microplastic particles enter the water environment, they will form a mechanical mixing state with the water body. Their behavior patterns are similar to those of viscous particles, sediment, and silt, which can be classified as particle dynamics problems in solid–liquid two-phase flow. Based on the theory of sediment dynamics, in this paper the movement of MPs in water is observed by means of hydraulic experiments, and then the movement mechanism and critical motion state transformation process of MPs in water are elucidated, and the movement mechanism of different types of MPs in water is studied.Generally, the factors influencing the motion state of MPs in water bodies are primarily internal (including microplastic density, particle size, and shape) and external (such as water velocity, turbulence, external wind force, vegetation, and roughness). In terms of internal factors, this study observes the differences in motion of MPs in water by selecting those with different chemical compositions, shapes, and categories. As for external factors, since the primary influences on the motion state of MPs in flume experiments are water flow force (velocity conditions) and channel resistance (roughness), these two factors are given special consideration in the design of external environmental conditions. The main research ideas of this study are as follows: firstly, the hydraulic experiment of microplastic movement is carried out in the experimental flume device, including the vertical delivery experiment of MPs under different water flow conditions, and the horizontal migration experiment of MPs under different roughness conditions. Secondly, starting from the force analysis of a single microplastic particle, the trajectory of MPs under different conditions is observed. Special attention is paid to the transformation of MPs from the static state of settlement to the bottom of the tank to the rolling state, finally reaching the critical flow rate condition in the resuspension state, so as to determine the critical condition threshold that affects the change of MPs' motion state. Finally, based on many experimental data, the critical start-up formula of sediment particles is improved to obtain a formula suitable for the movement of MPs. The technical route is shown in Fig. 1.
2.1 Test samples and devices
In this study, the density difference between plastics and water is primarily used to distinguish the experimental processes, which are divided into surface drift experiments for low-density MPs, suspension experiments for high-density microplastics in the water column, and bed load transport and resuspension experiments at the bottom of the water body. Five of the most commonly found types of plastics were selected for these experiments: polypropylene (PP), polyamide (PA), polystyrene (PS), polyethylene terephthalate (PET), and polyvinyl chloride (PVC). Among these, PP has a density lower than that of natural water, whereas the other four polymers have densities higher than that of natural water. Starting from the original plastic samples purchased, we used a Shanghai Jingxin liquid nitrogen cryogenic grinding machine (JXFSTPRP-II-02) to freeze the plastic samples with liquid nitrogen, and then ground them into irregular microplastics with a particle size of less than 5 mm (Table 1), with a total of 24 samples. Fig. 2 shows some microplastic samples.| Types | Density (kg m−3) | Original particles | Polyhedral particles | Fragment | Fiber |
|---|---|---|---|---|---|
| PP | 900 | White ellipsoid | Obtained by grinding the original particles | Ground from a black plastic tea lid, 0.445 mm thick | |
| PS | 1050 | Black cylindrical | Ground from a black plastic knife, 0.445 mm thick | ||
| PA | 1140 | Black cylindrical | Ground from a black plastic sheet, 0.5 and 1.0 mm thick | Ground from a yellow fishing line, 7 kinds in total, line thickness 0.128–0.405 mm | |
| PET | 1390 | White cylindrical | Ground from a black plastic sheet, 0.3 mm thick | ||
| PVC | 1390 | Black cylindrical | Ground from a black plastic sheet, 0.5 and 1.0 mm thick |
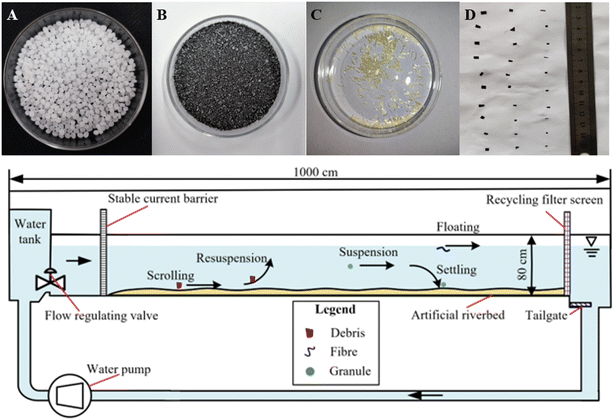 | ||
| Fig. 2 Some MP samples (A, B, C, and D are PP ellipsoids, PS multi-edged particles, PA fibers, and PET fragments, respectively) and schematic diagram of hydraulic experiments. | ||
The three axes (major axis X, central axis Y, and minor axis Z) of each MP were measured using a micrometer with an accuracy of 0.01 mm, and the equivalent diameters, ESD, were calculated using 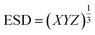 .21 For MP fibers, only the thread thickness and length were measured. To determine the specific shape classification of microplastics, fibrous microplastics are distinguished by observation, while other shaped microplastics are classified by calculating the shape factor CSF
.21 For MP fibers, only the thread thickness and length were measured. To determine the specific shape classification of microplastics, fibrous microplastics are distinguished by observation, while other shaped microplastics are classified by calculating the shape factor CSF 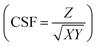 of non-fibrous microplastics. During the experiment, the formula was fitted by recording the CSF of each particle and other corresponding experimental data, and the shape was judged by observation.
of non-fibrous microplastics. During the experiment, the formula was fitted by recording the CSF of each particle and other corresponding experimental data, and the shape was judged by observation.
This experiment is carried out in the self-circulating water tank system, which is composed of a water tank, flow regulating valve, steady flow grid, recovery filter, artificial riverbed, and other devices. The flume sides and bottom were transparent smooth plates 10 m long, 0.4 m wide, and 0.8 m high; they were rectangular in section, with a flat bottom slope and approximately uniform flow conditions (Fig. 2). The flume flow velocity was measured using a portable flow velocity meter (LS300-A). To prevent microplastics from clogging the sink system, microplastics are recycled and reused through a recycling filter at the tail end. In the experiments, the flume flow velocity was adjusted to the range of 0.030–0.910 m s−1 and the water depth was adjusted to the range of 0.065–0.5 m.
After being ground, the MP samples floated above the water surface because of their irregular shape and high surface roughness, even if the density was greater than that of the aqueous solution. Before conducting the formal experiment, each group of MP samples were immersed in the aqueous solution for more than 4 h to allow the aqueous solution to fully infiltrate the MPs and ensure a smooth experimental process.
2.2 Experimental design
This study investigates the trajectories of MPs under different water flow velocities using hydraulic experiments, and the motion rates of different microplastics under drift, suspension and push conditions are analyzed. The critical starting velocity of microplastics from static to rolling at the bottom, the critical resuspension velocity from push motion to suspension motion, and the critical suspension velocity from free settlement motion to suspension motion with water flow are determined. In the horizontal migration experiment, 180 PP plastic particles of different shapes (cylindrical, multi-edged particles, fragments, fibers) were placed into the experimental tank for the water surface drift experiment, 300 PS, PA, PET, and PVC plastic particles of different shapes were selected for the water suspension experiment, and 270 PS, PA, PET, and PVC plastic particles were subjected to underwater push experiments. In order to reflect the influence of the bottom environment of the river on the microplastics, three working conditions of no laying (acrylic plate), thick carpet and artificial turf were set up in the pushing experiment. In the vertical delivery experiment, 300 PS microplastic particles were placed in the experimental flume under six flow rate conditions in the range of 0.068–0.315 m s−1. In the range of 0.071–0.719 m s−1, 680 PA microplastic particles were subjected to seven kinds of flow rate conditions. In the range of 0.086–0.903 m s−1, 400 PET microplastic particles were subjected to six kinds of flow rate conditions. A total of 420 PVC microplastic particles were placed at six flow rates in the range of 0.069–0.813 m s−1. A total of two groups of horizontal migration experiments and vertical delivery experiments were designed. The specific experimental conditions are shown in Table 2.| Experimental materials | Shape | Horizontal migration experiment | Vertical drop experiment | ||
|---|---|---|---|---|---|
| ESD (mm) | Flume flow velocity (m s−1) | ESD (mm) | Flume flow velocity (m s−1) | ||
| PP | Ellipsoid | 2.541–3.534 | 0.167–0.55 | ||
| Polyhedral particles | 1.587–2.860 | ||||
| Fragment | 1.101–1.907 | ||||
| PS | Cylindrical | 1.704–2.959 | 0.036–0.420 | 1.718–3.328 | 0.068–0.315 |
| Polyhedral particles | 1.105–2.621 | 0.934–2.692 | |||
| Fragment | 1.375–2.520 | 1.077–2.339 | |||
| PA | Cylindrical | 1.714–2.996 | 0.062–0.762 | 1.718–3.391 | 0.071–0.718 |
| Polyhedral particles | 1.243–2.904 | 0.912–2.86 | |||
| Fragment (1.0) | 1.260–2.224 | 1.169–2.642 | |||
| Fragment (0.5) | 1.000–1.817 | 0.737–1.982 | |||
| Fiber | 0.405 | 0.128–0.405 | |||
| PET | Cylindrical | 2.088–2.621 | 0.085–0.748 | 2.129–2.617 | 0.086–0.903 |
| Polyhedral particles | 1.587–2.502 | 0.461–2.483 | |||
| Fragment | 0.843–1.466 | 0.433–1.43 | |||
| PVC | Cylindrical | 2.274–3.522 | 0.102–0.769 | 2.39–3.555 | 0.067–0.812 |
| Polyhedral particles | 1.474–3.374 | 1.084–3.291 | |||
| Fragment (1.0) | 1.375–2.924 | 0.993–2.823 | |||
| Fragment (0.5) | 1.026–1.983 | 0.804–1.989 | |||
| Else | Acrylic boards, thick carpets, and artificial turf are laid on the bottom of the flume to simulate different river bottom environments | ||||
This study uses the control variable method to study the role of each influencing factor. In each group of working condition tests, the flow rate and water level of the flume are adjusted to the preset working condition level by controlling the opening of the flow regulating valve and the downstream tailgate. After the water flow is stabilized to form an approximately uniform flow, a portable flow meter is used to measure the flow velocity in the observation section, and then microplastic particles are placed to observe its motion state, and its motion process is recorded with a digital camera. Each experiment is conducted with a single microplastic particle. Since the change of temperature will lead to the change of water viscosity, which will affect the movement process of microplastics,22 the room temperature is maintained at about 25 °C through the air conditioning system throughout the experiment to ensure the stability of water viscosity.
The operation steps of the MP horizontal migration experiment are as follows: (a) the flume flow velocity is adjusted to the minimum, the MP is placed at the bottom of the flume, and the flow velocity is gradually increased to observe MP movement at the bottom. When the MPs begin to move at the bottom, the flow rate is recorded as the critical starting flow rate; (b) the flow rate is increased gradually, and the displacement distance and time of microplastics are recorded at different flow rates until the microplastics move from the bottom to the suspension, and the flow rate is recorded at this time as the critical resuspension flow rate; (c) the MPs are replaced with different materials, shapes and particle sizes, and the above experiments are repeated at least 10 times for each type; (d) in order to simulate the different conditions at the bottom of the natural river, different materials are laid at the bottom of the flume: no matting (acrylic plate), thick carpet and artificial turf, which represent plants such as hard river, sediment and water grass, respectively.
The operation steps of the vertical MP release experiment are as follows: (a) similar to the horizontal migration experiment, the microplastics are released from 5 cm below the water surface to avoid the influence of water surface tension and gradually increase the flow rate. At the same time, the settlement distance and time of microplastics at different flow rates are observed and recorded; (b) when the microplastics no longer settle but begin to move with the water flow, the flow rate at this time is recorded as the critical suspension flow rate; (c) the flow rate is increased gradually, and the suspension distance and time of microplastics are recorded under various flow rate conditions. Each particle is tested 10 times; (d) the experiment is repeated by switching MPs into different materials, shapes, and particle sizes; each shape is tested at least 10 times.
Because of the complexity of the MP movement process in a water environment, the observation process is prone to large errors, and the turbulence of the water body further increases the difficulty of MP observation. Therefore, the effect of each influencing factor on the migration process was studied using the control variable method, in which the movement distance, time, flow rate, and water depth of the MPs were manually recorded, and a camera was used to shoot and record them synchronously. Subsequently, the motion video of the MPs was analyzed by Adobe Premiere Pro 2020 software, and the manually recorded data were checked again to ensure the accuracy of the data observation.
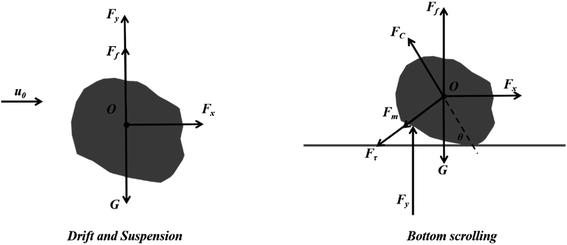
2.3 Force analysis of MPs in water
The main forces exerted on MPs when they move in a water body include the flow drag force Fx, the upward lifting force Fy, gravity G, and buoyancy force Ff. When the sum of the uplift force (Fy) and buoyancy force (Ff) is much larger than gravity (G), the MP remains on the surface of the water body and drifts by the current drag force (Fx) with the water. When the sum of the uplift force (Fy) and buoyancy force (Ff) is equal to gravity (G), MPs are in water and are suspended by water flow drag force (Fx). When the sum of the uplift force (Fy) and buoyancy force (Ff) is much smaller than gravity (G), the MP moves to the bottom of the river and rolls with the current. In addition to the aforementioned four forces, the particle scrolls with an additional mass force, Fm; centrifugal force, FC; and shear stress, Fτ. Among these forces, the uplift force (Fy), centrifugal force (FC), buoyancy force (Ff) and current drag force (Fx) promote the rolling of MPs, and gravity (G), additional mass force (Fm), and shear stress (Fτ) prevent the scrolling of MPs.In the water body, the change of water flow velocity has the greatest influence on the force of microplastics: when the water flow rate changes, the MPs' own gravity (G) and the buoyancy force (Ff) on the particle are basically unaffected by the outside world and cannot be ignored; the drag force (Fx) and uplift force (Fy) of the water flow change directly, which affects the force of microplastics and changes the motion state; the additional mass force (Fm), centrifugal force (FC), and shear stress (Fτ) changes are negligible and do not affect the state of motion of the MP23 (Duan et al., 2019).
When the flow rate is small, the microplastics are at the bottom of the water. At this time, they are still or moved by the combined force of the three forces of effective gravity (W), drag force (Fx) and lift force (Fy). When the flow velocity increases, the effective gravity (W) remains unchanged, while the uplift force (Fy) increases. When the uplift force (Fy) is equal to the effective gravity (W), the microplastics will re-suspend to the water body for suspension movement. In contrast, when the flow rate continues to decrease, the microplastics will also settle down again until they are still. In the vertical direction, it is manifested as the settlement or resuspension of microplastics (Fig. 3).
2.4 Determination of critical hydraulic parameters
There are two main links in the change in MPs from the state of movement in the water body: one is from the stationary state to the rolling state, and the other is from the rolling state to the suspended state (resuspension). During the experiment, the velocity threshold of critical change of microplastics' motion state was determined and recorded by camera recording and actual observation of various external conditions of critical change of microplastics. According to Section 2.3, among the external factors, the flow velocity is the largest factor affecting the motion state of microplastics, and its change affects the flow drag force (Fx) and lift force (Fy) of microplastics. Therefore, the flow velocity threshold that affects the motion state of microplastics is the critical hydraulic parameter.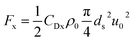 | (1) |
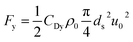 | (2) |
The effective gravity (W) of microplastics in water is the microplastics' own gravity (G) minus buoyancy (Fy), and its expression is as follows:
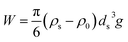 | (3) |
With the center of gravity of the MP as point O, the moments of the three forces are l1, l2, and l3, respectively, where l1 = β1ds, l2 = β2ds, and l3 = β3ds. When the moments are balanced with each other, the MPs are critically activated. Eqn (1), (2), and (3) are introduced into eqn (4), and (6) can be obtained.
| l1Fx + l2Fy = l3W | (4) |
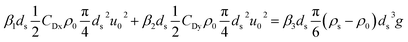 | (5) |
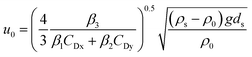 | (6) |
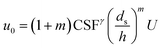 | (7) |
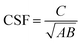 . The other symbols are consistent with the above.
. The other symbols are consistent with the above.
Bringing eqn (7) into eqn (6) gives eqn (8).
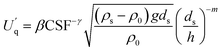 | (8) |
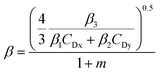 | (9) |
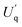 is the critical starting flow rate of MPs, and β, γ, and m are the parameters, which are obtained by fitting the experimental data.
is the critical starting flow rate of MPs, and β, γ, and m are the parameters, which are obtained by fitting the experimental data.
| W = Fy | (10) |
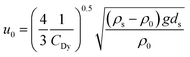 | (11) |
The exponential flow velocity distribution in eqn (7) is also used to convert the point flow velocity into the average cross-sectional flow velocity; thus, eqn (12) is substituted into eqn (13).
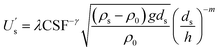 | (12) |
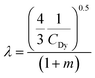 | (13) |
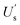 is the critical resuspension flow rate of MPs and λ, γ, and m are the parameters which are obtained by fitting the experimental data.
is the critical resuspension flow rate of MPs and λ, γ, and m are the parameters which are obtained by fitting the experimental data.
The experimental data were statistically analyzed using MATLAB and SPSS software, and the absolute value of the residuals was minimized by nonlinear regression to determine the relationship between the critical flow velocity of the MPs and their influencing factors.
3. Results and discussion
3.1 Analysis of the horizontal movement of MPs
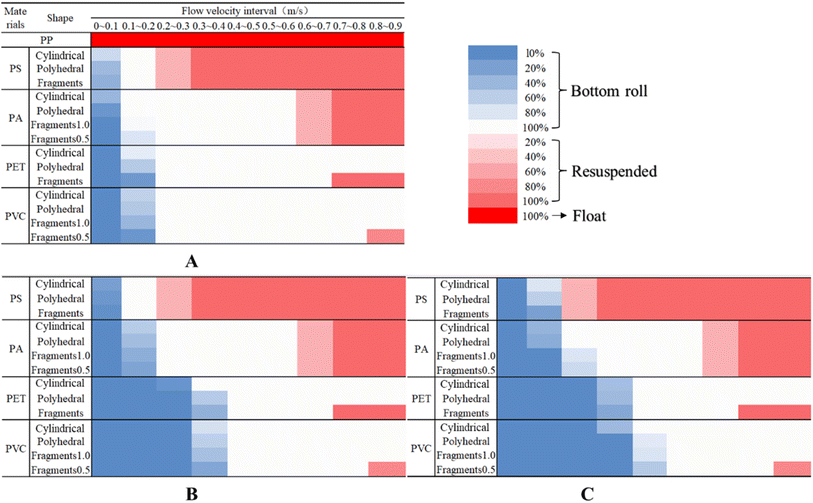
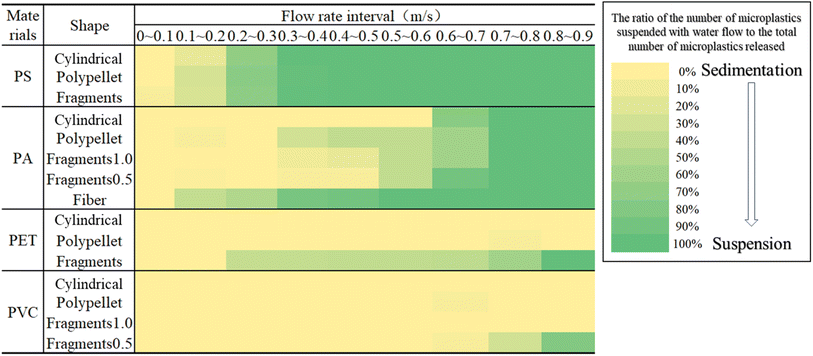
As shown in Fig. 4A, almost all MPs having a density less than that of the water body, such as the various shapes of PP MPs, regardless of the flow rate of the water body, are always floating on the water surface. For MPs having a density greater than that of the water body, at flow velocities of 0–0.1 m s−1, PS MPs in cylindrical form first started to appear, followed by polyhedral particles, and finally the fragment form; the cylindrical and polyhedral PA MPs only rolled. At flow velocities of 0.1–0.2 m s−1, PA, PET, and PVC fragments begin to roll; however, the larger the density and the closer the shape to the sheet, the smaller the probability of the rolling phenomenon, indicating that the rolling phenomenon requires a larger flow rate to drive.
As shown in Fig. 4B, when the bottom working condition changed from a smooth acrylic plate to a rough carpet, only the columnar, polygonal particles and fragments of PS microplastics started to roll at flow velocities of 0–0.1 m s−1, but the required flow rate is greater than that of condition A; at flow velocities of 0.1–0.2 m s−1, the four shapes of the PA MPs began rolling, and the flow rate is also greater than that of working condition A. At flow velocities of 0.2–0.3 m s−1, only the cylindrical shape of the PET MP exhibited rolling. At flow velocities of 0.3–0.4 m s−1, only polyhedral particles, fragment forms of PET, and denser PVCs exhibited rolling.
As shown in Fig. 4C, the flow velocity required for rolling the MPs of the four materials was greater when the bottom was changed to working conditions with the plants. When the flow rates of PS, PA, PET and PVC MPs were 0.2–0.3 m s−1, 0.3–0.4 m s−1, 0.4–0.5 m s−1 and 0.5–0.6 m s−1, respectively, all of them showed the rolling phenomenon. It can be seen from this that the higher the density of the MP, the closer the shape is to flakes, and the rougher the bottom environment, the higher the critical starting flow velocity (Table 3).
| Work conditions | Materials | Shape | |||
|---|---|---|---|---|---|
| Cylindrical | Polyhedral | Fragments 1.0 | Fragments 0.5 | ||
| Acrylic | PS | 0.03 | 0.059 | 0.065 | |
| PA | 0.062 | 0.090 | 0.105 | 0.123 | |
| PET | 0.115 | 0.143 | 0.188 | ||
| PVC | 0.138 | 0.146 | 0.164 | 0.190 | |
| Carpet | PS | 0.081 | 0.088 | 0.095 | |
| PA | 0.142 | 0.155 | 0.169 | 0.177 | |
| PET | 0.290 | 0.343 | 0.365 | ||
| PVC | 0.324 | 0.339 | 0.347 | 0.375 | |
| Turf | PS | 0.120 | 0.140 | 0.181 | |
| PA | 0.163 | 0.169 | 0.22 | 0.23 | |
| PET | 0.355 | 0.359 | 0.374 | ||
| PVC | 0.359 | 0.417 | 0.422 | 0.444 | |
The resuspension of MPs was almost the same regardless of the bottom environmental conditions. When the flow velocity was 0.2–0.3 m s−1, the lower density PS MP shifted from rolling to resuspension, and its critical resuspension flow velocity was 0.250 m s−1; when the flow velocity was 0.6–0.7 m s−1, the PA MP also became resuspended, and its critical resuspension flow velocity was 0.649 m s−1. For the denser PET MP, only fragments appeared to be resuspended at flow velocities of 0.7–0.8 m s−1, and the critical resuspension flow velocity was 0.710 m s−1. When the flow velocity was 0.8–0.9 m s−1, only 0.5 mm thick microplastics of PVC with the highest density exhibit the resuspension phenomenon, and the critical resuspension flow velocity is 0.820 m s−1. The critical resuspension velocity of MPs was not related to the bottom environment. When the flow velocity increased, the Fy of the MP increased until it equaled W, and the motion state of the MP changed from bottom rolling to resuspension. The higher the density, the higher the critical resuspension flow velocity. Additionally, high-density MP fragment shapes have a larger force area in the vertical direction and are therefore more susceptible to resuspension than cylindrical and polyhedral particles.
| vs = ksU | (14) |
| vd = kdU | (15) |
| vsc = kscU | (16) |
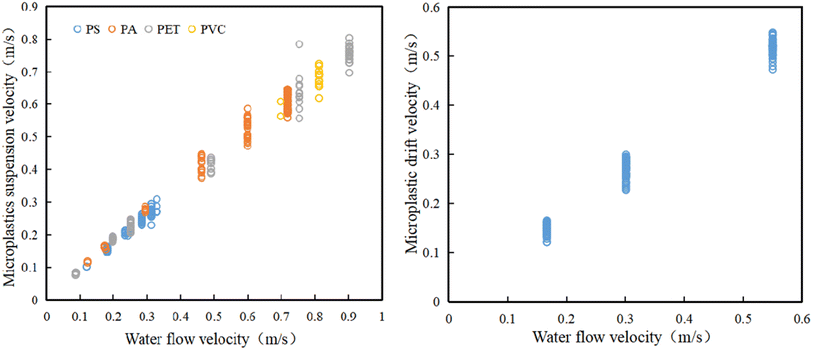
After analyzing the results of the horizontal migration experiment, the experimental results showed that a significant positive correlation was evident between the hovering velocity of MPs and the flow velocity of water, and that the smaller the density of MPs, the greater their relative hovering velocity. In terms of shape, fibrous MPs were clearly different from the other MPs and moved the fastest with the flow of water. The suspension coefficients (ks) of nonfibrous PS, PA, PET, and PVC MPs were 0.86, 0.84, 0.84, and 0.83, respectively; the suspension coefficient of fibrous PA MPs was 0.94; and the drift coefficient (kd) of PP MPs was 0.91. Similarly, the floating velocity of microplastics is also positively correlated with the flow velocity, but the drift velocity of MPs was significantly greater than the suspension velocity in the relative suspension motion because the water resistance of MPs in the water body is greater than that of MPs drifting on the water surface.
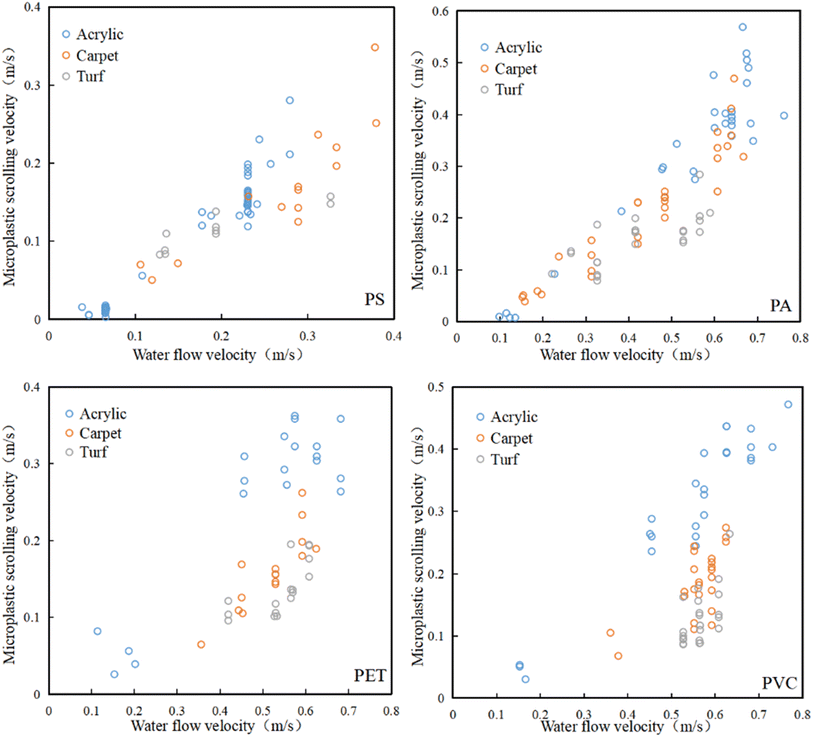
The velocity of lower-density MPs (e.g., PS, PA) is positively correlated with the velocity of water flow, and the velocity decreases slightly in the coarser sediment environment, while the velocity of the denser MPs (e.g., PET, PVC) also shows a positive correlation, but in the sediment with greater roughness, the velocity shows obvious irregularity (Fig. 6). The transition coefficients of different MPs are calculated according to eqn (16), and the results are shown in Table 4. The higher the density of MPs and the rougher the substrate, the smaller their rolling velocity. This phenomenon is because the rougher the bottom environment, the greater the frictional resistance of MPs. Different bottom environments also make the critical start-up speed of microplastics different, and greater resistance makes it more difficult for microplastics to change from a static state to a push state.
| Types | PS | PA | PET | PVC |
|---|---|---|---|---|
| Acrylic | 0.601 | 0.6 | 0.543 | 0.452 |
| Carpet | 0.544 | 0.459 | 0.349 | 0.305 |
| Turf | 0.496 | 0.389 | 0.236 | 0.201 |
3.2 Analysis of the vertical motion law of MPs
As shown in Fig. 7, the smaller the density of microplastics, the smaller the critical suspension velocity from settlement to suspension with water flow. When the suspension rate of MPs is >50%, the flow velocity is the same as the critical suspension flow velocity. When the flow velocity is 0.1–0.2 m s−1, 25% of the PS MPs no longer settle and are suspended in the water flow. When the flow velocity increases to 0.2–0.3 m s−1, almost 80% of the PS MPs do not settle. Therefore, the average critical suspension velocity is calculated by the experimental data in the flow velocity range, and the critical suspension velocity is determined to be 0.251 m s−1. When the flow velocity is greater than 0.3 m s−1, all the microplastics are suspended with the water flow, and there are no microplastics settling to the bottom of the water, so the suspension rate is 100%.
For the PA fibers, the critical suspension flow velocity was much lower than that of the block PA. Thirty percent of PA fibers no longer settle when the flow velocity is 0.1–0.2 m s−1, and almost 70% of PA fibers no longer settle when the flow velocity increases to 0.4–0.5 m s−1. Therefore, the critical suspension flow velocity of the PA fibers was 0.43 m s−1. When the flow velocity increased to 0.6–0.7 m s−1, almost 85% of PA cylindrical, polygonal particles, and fragments no longer settle; their critical suspension flow velocity was 0.649 m s−1.
For denser PET and PVC, when the flow velocity increases to 0.7–0.8 m s−1, nearly 80% of PET fragments no longer settle, and the critical suspension flow velocity is 0.705 m s−1. When the flow velocity is 0.8–0.9 m s−1, nearly 70% of the PVC MPs with 0.5 mm thick fragments no longer settle, and the critical suspension flow velocity is 0.83 m s−1.
This result indicates that the higher the density of MPs, the higher the critical suspension flow velocity. Fragmented microplastics have a large force area and are more prone to suspension in flowing water. From the numerical point of view, the critical suspension flow velocity of MPs was almost the same as the critical resuspension flow velocity, which deviated from the experimental expectation. This phenomenon occurred because as the flow velocity increased to a certain value, the Fy of the MP was almost equal to W; the rolling MP was resuspended, and the settling MP changed from settling to suspended with water flow.
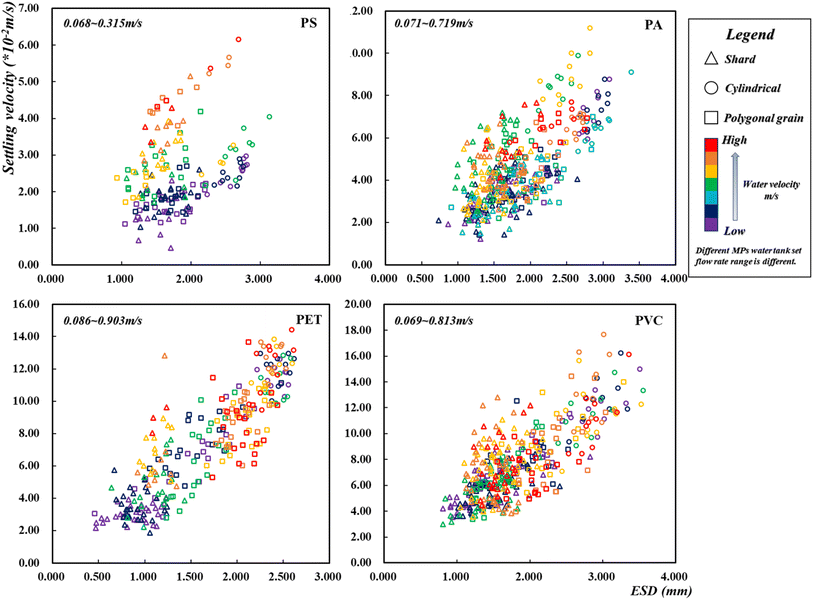 | ||
| Fig. 8 Sedimentation velocity of MPs at different flow rates (circles represent cylindrical particles, squares represent polygonal particles, and triangles represent fragments). | ||
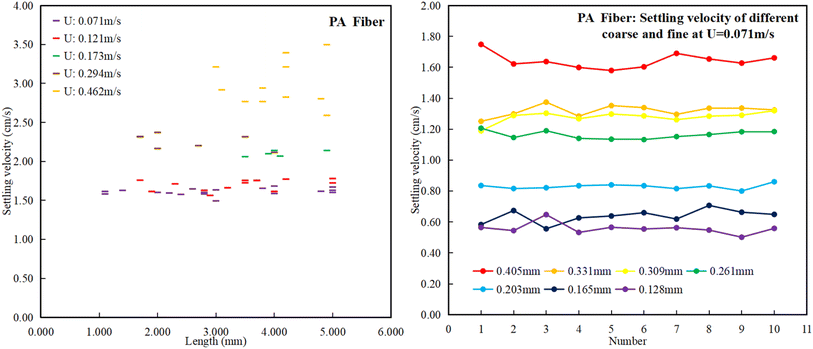
As special MPs, the sedimentation velocity of fibrous MPs is much smaller than that of bulk MPs, and the maximum sedimentation velocity of PA fibers is 3.5 cm s−1, while the sedimentation velocity of PA bulk MPs is much greater. However, the sedimentation rate of PA and PET fibers increased when the flow rate increased, consistent with the performance of PA bulk MPs (Fig. 9). It can be seen from the figure that the sedimentation velocity of microplastics of different lengths of fishing line PA fibers with a roughness of 0.405 mm basically had a horizontal linear distribution under the same water flow conditions. To explore whether microplastics of other materials also follow the same law, the sedimentation velocity of PET fibers with a roughness of 0.3 mm was measured. The experiment shows that the sedimentation velocity at different lengths also has a horizontal linear distribution. When the flow velocity is large, the distribution of PA and PET microplastics goes slightly up and down, but it is still distributed near its horizontal line. Therefore, in order to explore the law of the fiber sedimentation process, this experiment also selected PA fibers with wire thicknesses of 0.331, 0.309, 0.261, 0.203, 0.165, and 0.128 mm for sedimentation experiments at a flow rate of 0.071 m s−1. Ten fibers of each thickness were selected, and their length was distributed between 1.5 and 3.5 mm. Based on the results, the sedimentation rate of fibrous MPs is not related to their length, but to the thickness; the coarser the fiber, the faster its sedimentation rate. This may be because the force of the fiber is not similar to that of other shapes of microplastic particles, the force is not uniform and the center of gravity is not fixed, resulting in its special parameters which are different from those of other shapes of microplastics.
3.3 Determination of critical hydraulic parameter calculations
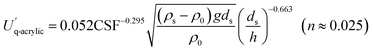 | (17) |
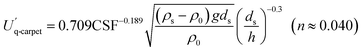 | (18) |
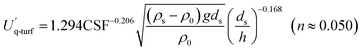 | (19) |
Similarly, after fitting eqn (12), λ = 9.848, γ = 0.063, and m = −0.019; the mean relative error was calculated to be 0.05 and the R2 was 0.93 (Fig. 10B). Therefore, the critical resuspension flow rate of MPs was calculated as follows:
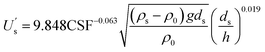 | (20) |
| Equations | Average relative deviation | Sum of squared error | Sum of log deviation | |
|---|---|---|---|---|
a 1 δ is the thickness of the film water, taken to be 0.0001 mm; ε is the porosity, which has a stable value of 0.4; 2 sum of square errors: 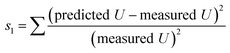 ; 3 sum of logarithmic deviations: ; 3 sum of logarithmic deviations: 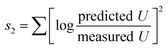 . .
|
||||
| Article predictions | Eqn (17), (18), (19) | 0.008 | 5.195 | 1.196 |
| Meyer-Piedt25 |
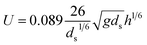
|
3.442 | 2966.285 | 53.321 |
| Goncharov26 |
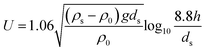
|
0.110 | 43.433 | 5.224 |
| Zhang Ruijin26 |
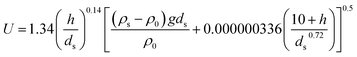
|
0.030 | 31.596 | 5.658 |
| Sha Yuqing26 |
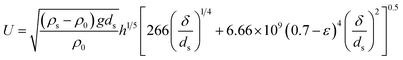
|
0.206 | 56.482 | 5.559 |
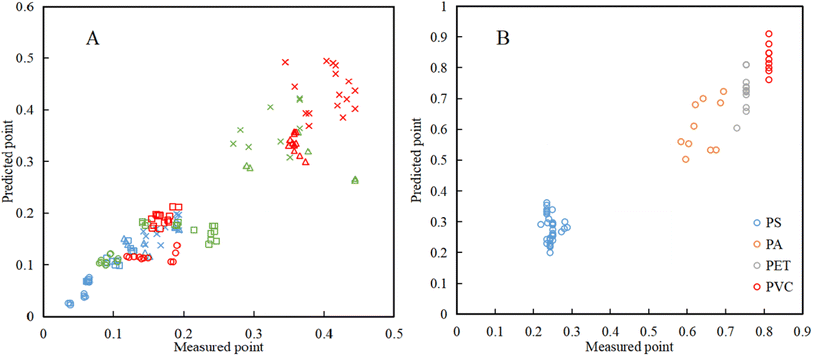
As shown in Table 5, the deviation indices of the MP critical start-up formula predicted in this paper are relatively small, with an average relative error of only 0.008, which is within the ideal range. The influence of particle and water density was not considered in the Meyer-Piedt formula. The error indices are the maximum, and the sum of the square errors was as high as 2966.285, which is a large deviation. The Goncharov formula focuses on the influence of water flow force and particle gravity on the starting flow velocity in the dynamic equilibrium equation, and its deviation is relatively small, with an average relative error of 0.11. Zhang's formula considers the effect of water flow dynamics on the particles, and also considers the influence of the cohesive force of the particles; their calculation results are close to the measured data. However, the formula proposed in this study shows the smallest average relative error of only 0.03. Compared with other formulae, Sha's formula pays more attention to the influence of water depth on the sediment starting flow velocity, closer to that of an actual natural river, and also considers the cohesive force caused by contact; however, the description and expression of the mechanical mechanism is unclear, and it is basically an empirical formula, with a large deviation. Evidently, previous research results demonstrate certain differences, and due to the different physical and chemical properties of sediment particles and MPs, each formula also has many constraints in its application. In summary, the initiation formula of sediment particles has a relatively large deviation and poor applicability when applied to MPs. The fitting formula in this paper is based on experimental results and has high usability. Compared with other critical formulae, the fitting formula in this experiment is closer to the actual situation of microplastics. Compared with other experimental results, the deviation is smaller, and the control of variables is more in place during the experiment. However, due to the limitations of experimental conditions, the formula fitted in this study takes less consideration of working condition variables and uses fewer types of microplastics. More perfect formulae that fit the actual working conditions will be added in subsequent research.
4. Conclusion
Overall, significant efforts have been made in the study of microplastics. Presently, the majority of research primarily revolves around field surveys and simulation analyses, with a noticeable lack of investigation into the mechanisms governing the movement of microplastics. Given the distinct nature of microplastics, they cannot be treated solely as conventional soluble pollutants. This study adopts a particulate state perspective to explore these materials, initiating its approach through an analysis of the forces exerted on microplastics to design hydraulic experiments. Throughout the experimental phase, attention was given to the morphological traits of microplastics, examining their behavior in water while considering two key external variables: flow velocity and surface roughness.The findings from a series of hydraulic experiments reveal that the drift and suspension of microplastics in aquatic systems are independent of their intrinsic attributes but are significantly influenced by water flow velocity. Specifically, as the flow velocity increases, so does the rate of movement of the microplastics. Moreover, the bottom-rolling speed of microplastics is positively associated with water flow velocity but negatively correlates with the density of the microplastics and the roughness of the sediment. It was observed that the critical resuspension velocity required for microplastics to transition from rolling to re-suspension matches the critical velocity needed for them to shift from deposition to suspension, and both are higher than the critical initiation velocity necessary for static microplastics to start rolling. The greater the density, the rougher the environment, and the closer the shape to the sheet, the greater the critical start-up flow rate and the critical resuspension flow rate of microplastics, in which the density of microplastics plays a key role.
The relationship between the critical starting flow velocity and the critical resuspension flow velocity of microplastics with shape, density and particle size is fitted by experimental data. The fitting results are good, and the conversion between the motion trajectory and the motion state of microplastics is well explained. However, the study is not without limitations. In exploring the movement mechanics of microplastics, constraints imposed by research methodologies and time, the conditions and characteristics of external factors are still immature, and other working conditions are not considered. Only the stress analysis under ideal water conditions is considered while the complex water flow conditions in the actual situation are ignored, which will bring additional stress conditions. The consideration of the migration of microplastics in actual rivers is not perfect. Consequently, future research endeavors should integrate actual environmental conditions, incorporate a broader range of external influences, and delve deeper into understanding the migration patterns of microplastics within natural freshwater ecosystems.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Ming Dou: research and investigation, methods, draft revision; Zhen Wang: carried out the experiment, analyzed the data and wrote the manuscript; Yuxuan Li: error checking, draft revision; Bin Sun: provided experimental equipment and carried out research investigation; Yongyong Zhang: revised and refined the draft; Yuze Zhou: experimental conjecture verification, method; Ruipeng Jia: revised and refined the draft.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was supported by the Major Science and Technology Projects of Henan Province [No. 22110032200], the Science and Technology Research Projects of Henan Province [No. 2221023020211], and the Program for key Science & Technology projects in Universities of Henan Province [No. 21A570008].References
- K. L. Law and R. C. Thompson, Microplastics in the seas, Science, 2014, 345(6193), 144–145 CrossRef CAS PubMed.
- D. K. Barnes, F. Galgani and R. C. Thompson, et al., Accumulation and fragmentation of plastic debris in global environments, Philos. Trans. R. Soc., B, 2009, 364(1526), 1985–1998 CrossRef CAS.
- F. Dubaish and G. Liebezeit, Suspended microplastics and black carbon particles in the Jade system, southern North Sea, Water, Air, Soil Pollut., 2013, 224(2), 1–8 CrossRef CAS.
- A. Collignon, J. H. Hecq and F. Galgani, et al., Annual variation in neustonic micro-and meso-plastic particles and zooplankton in the Bay of Calvi (Mediterranean-Corsica), Mar. Pollut. Bull., 2014, 79(1–2), 293–298 CrossRef CAS PubMed.
- W. J. Desforges, M. Galbraith and N. Dangerfield, et al., Widespread distribution of microplastics in subsurface seawater in the NE Pacific Ocean, Mar. Pollut. Bull., 2014, 79(1–2), 94–99 CrossRef.
- R. A. Castañeda, S. Avlijas and M. A. Simard, et al., Microplastic pollution in St. Lawrence River sediments, Can. J. Fish. Aquat. Sci., 2014, 71(12), 1767–1771 CrossRef.
- M. C. Free, P. O. Jensen and A. S. Mason, et al., High-levels of microplastic pollution in a large, remote, mountain lake, Mar. Pollut. Bull., 2014, 85(1), 156–163 CrossRef PubMed.
- S. Lei, Y. Xue and L. Li, et al., Microplastics in Taihu Lake, China, Environ. Pollut., 2016, 216, 711–719 CrossRef PubMed.
- P. J. Anderson, S. Warrack and V. Langen, et al., Microplastic contamination in Lake Winnipeg, Canada, Environ. Pollut., 2017, 225, 223–231 CrossRef CAS.
- R. Z. Miller, A. J. R. Watts and B. O. Winslow, et al., Mountains to the sea: River study of plastic and non-plastic microfiber pollution in the northeast USA, Mar. Pollut. Bull., 2017, 124(1), 245–251 CrossRef CAS.
- Q. Zhou, H. B. Zhang and Y. Li, et al., Progress on Microplastics pollution and its ecological effects in the coastal environment, Chin. Sci. Bull., 2015, 60, 3210–3220 Search PubMed.
- R. Kumar, P. Sharma and A. Verma, et al., Effect of physical characteristics and hydrodynamic conditions on transport and deposition of microplastics in riverine ecosystem, Water, 2021, 13, 2710 CrossRef CAS.
- A. Isobe, K. Kubo and Y. Tamura, et al., Selective transport of microplastics and mesoplastics by drifting in coastal waters, Mar. Pollut. Bull., 2014, 89(1–2), 324–330 CrossRef CAS PubMed.
- K. Critchell and J. Lambrechts, Modelling accumulation of marine plastics in the coastal zone; what are the dominant physical processes?, Estuarine, Coastal Shelf Sci., 2016, 171, 111–122 CrossRef.
- A. Ballent, S. Pando and A. Purser, et al., Modelled transport of benthic marine microplastic pollution in the Nazare Canyon, Biogeosciences, 2013, 10(12), 7957–7970 CrossRef.
- A. Lechner, H. Keckeis and F. Lumesberger-Loisl, et al., The Danube so colourful: A potpourri of plastic litter outnumbers fish larvae in Europe’s second largest river, Environ. Pollut., 2014, 188, 177–181 CrossRef CAS PubMed.
- J. R. Jambeck, R. Geyer and C. Wilcox, et al., Plastic waste inputs from land into the ocean, Science, 2015, 347, 768–771 CrossRef CAS PubMed.
- F. L. Jia, C. Z. Sun and F. Y. Li, et al., Progresses in the studies on oceanic microplastic pollution, Trans. Oceanol. Limnol., 2018, 02, 146–154 Search PubMed.
- S. M. Zhang, J. Zha and W. Meng, et al., A Review of microplastics in Environment and Their Effects on Human Health, China Plast., 2019, 33(4), 81–88 Search PubMed.
- H. B. Zhang, Q. Zhou and Y. Zhou, et al., Raising concern about microplastic pollution in coastal and marine environment and strengthening scientific researches on pollution prevention and management, Bull. Chin. Acad. Sci., 2016, 31(10), 1182–1189 Search PubMed.
- R. G. Kumar, K. B. Strom and A. Keyvani, Floc properties and settling velocity of San Jacinto estuary mud under variable shear and salinity conditions, Cont. Shelf Res., 2010, 30, 2067–2081 CrossRef.
- D. Kaiser, A. Estelmann and N. Kowalski, et al., Sinking velocity of sub-millimeter microplastic, Mar. Pollut. Bull., 2019, 139, 214–220 CrossRef CAS PubMed.
- Z. H. Duan, J. Chen and C. B. Jiang, et al., Experimental study on bedload sediment transport under unsteady flow, Sci. Sin. Tech., 2019, 49, 1372–1382 Search PubMed.
- M. C. Zhao, W. X. Huai and T. R. Li, Study of velocity profile of uniform flow in open channels, Eng. J. Wuhan Univ., 2010, 43(5), 554–557 Search PubMed.
- Y. H. Chen, Bed load movement theoretical model and the movement process calculation, Master's thesis, Tianjin University, 2009.
- H. W. Zhang, Uniform formula for sediment starting flow rate, J. Hydraul. Eng., 2012, 43(12), 1387–1396 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4em00574k |
| This journal is © The Royal Society of Chemistry 2025 |