 Open Access Article
Open Access ArticleEffective measuring campaigns for reliable and informative full-scale WWTP data†
Q. H.
Le
ab,
P.
Carrera
 ab,
M. C. M.
van Loosdrecht
ab,
M. C. M.
van Loosdrecht
 c and
E. I. P.
Volcke
c and
E. I. P.
Volcke
 *ab
*ab
aDepartment of Green Chemistry and Technology, Ghent University, 9000 Ghent, Belgium. E-mail: Eveline.Volcke@UGent.be; Tel: +32 (0) 9 264 61 29
bCentre for Advanced Process Technology for Urban REsource recovery (CAPTURE), Frieda Saeysstraat 1, 9052 Gent, Belgium
cDepartment of Biotechnology, Delft University of Technology, 2600 AA Delft, The Netherlands
First published on 14th January 2025
Abstract
Sensor availability and costs are nowadays no longer limiting data gathering at wastewater treatment plants (WWTPs). However, one should be aware that a higher amount of measured data gathered does not necessarily imply that also more information is obtained. In this light, this contribution assesses the general applicability and the added value of a structured experimental design approach for planning measurement campaigns at WWTPs, in view of mass-balance-based data reconciliation. To this end, the results from full-scale WWTP case studies available in the literature were compared to those obtained with the developed structured experimental design procedure. Planning measurement campaigns comprises the selection of (additional) measurements to meet a pre-set main goal. The need for a structured experimental design procedure replacing past expert judgment approaches became clear from the fact that three out of five case studies available in the literature failed to meet the main goal and/or performed unnecessary additional measurements. Translating the main goal into specific key variables was found essential in this respect. The general applicability of the procedure was proven with three outcomes. First, the procedure, involving well-defined steps, could be applied to different WWTP layouts. Second, it ensured the fulfilment of various main goals. Third, it provided useful outcomes, i.e., optimal measurement campaigns, which reduced the need for additional measurements (40–70% less) compared to expert knowledge approaches, hence more information could be obtained with less analytical data. Overall, the experimental design procedure proved a fast and useful tool ensuring the success of subsequent mass-balance-based data reconciliation.
Water impactNowadays, large amounts of data are generated in wastewater treatment plants (WWTPs) but data-rich does not always mean information-rich. In this light, this contribution assesses the general applicability and the added value of a structured experimental design approach for planning measurement campaigns at WWTPs in view of mass-balance-based data reconciliation for reliable plant data gathering. |
1 Introduction
Measurements provide the main source of information in view of wastewater treatment plant (WWTP) design and optimization, process evaluation, operator training, modelling and simulation, and benchmarking simulation. To verify and improve the quality of collected data, data reconciliation has become a proven technique.1,2 Data reconciliation is directed towards finding better estimates of key process variables, which may be either measured variables or unmeasured variables that are calculated from measured variables. Key variables are process variables, the reconciliation (= identification) of which ensures the fulfilment of the main goal of the study, which is typically stated by the plant operator. The reconciled values are more reliable than the original values in the sense that they satisfy conservation laws (e.g. mass balances) and other constraints. Besides a different (mean) value, the reconciled variables typically also have a higher accuracy, i.e., a lower standard deviation. While data reconciliation has been widely applied in the field of (bio) chemical process engineering,3–5 this concept has received relatively little attention so far in wastewater treatment process engineering (Table A1, Appendix A, ESI†). Nevertheless, published studies so far clearly show the added value of data reconciliation for different purposes such as data validation for modelling and plant assessment,6–8 variable classification and redundancy analysis for sensor placement,9,10 or mass flow analysis of different process variables.11,12In order to guarantee that key variables can be identified through data reconciliation, it is vital that the available measurements satisfy redundancy and steady-state conditions. The data redundancy requirement means that one or more variables in the data set can be calculated from other (measured) variables using the available set of constraints (including mass balances), and are therefore identifiable,5 in the sense that they can be reconciled (identified). In case there are no or not sufficient initially measured data available, additional measurements need to be carried out to ensure the required degree of redundancy and thus the possible identification of key variables. Experimental design involves the determination of sets of (additional) measurements to fulfil this goal. This concept has been proven useful for optimal sensor placement for different applications, including chemical processes13,14 or water networks.15,16 Nevertheless, experimental design formulated as a structured, optimization problem has still limited attention in wastewater treatment processes.17,18 Instead, in available case studies from practice (Table A1, ESI†), providing sufficient redundancy has been interpreted quite intuitively, by ensuring that the number of constraints (independent mass balances) was higher than the number of unknown variables, i.e. aiming at an overdetermined system. In this way, redundancy was considered a ‘global property’ of the system while in reality, it is a property of individual variables.5 It is therefore unclear whether the experimental design approaches followed in the case studies previously reported in the literature guarantee the identifiability of all specified key process variables.17
In order to overcome the shortcomings of previous studies, Le et al.17 presented a more formal, structured experimental design procedure, including a comprehensive redundancy analysis to unambiguously check the identifiability of all key variables. The search for optimal sets of additional measurements is solved as a multi-objective optimisation problem minimising the cost of additional measurements and maximising the accuracy of the improved estimates of key variables. The results are visualized in a Pareto-optimal front, which represents the optimal solutions (= sets of measurements) taking into account the trade-off between their cost and accuracy. This is a valuable outcome for measurement planning, as it allows for compliance with the main goal with an optimal use of resources. However, so far the results obtained with the experimental design procedure of Le et al.17 have not yet been compared with those obtained in previously published studies.
In this work, the added value and general applicability of the structured experimental design procedure of Le et al.17 in view of mass-balance-based data reconciliation were scrutinized by comparing them with previous expert judgment approaches for WWTP measurement campaign planning. In particular, the procedure was assessed in terms of applicability to different layouts and main goals, redundancy and identifiability of key variables, relevance of the mass balances and the number and type of additional measurements. To this end, the experimental design procedure of Le et al.17 was applied to five full-scale WWTP case studies available in the literature dealing with experimental design in view of mass-balance-based data reconciliation.19–22 Going beyond the mere detection of mistakes from the past, this work demonstrates why a rigorous experimental approach is needed for future measurement campaigns and how this can be performed.
2 Materials and methods
The experimental design procedure of Le et al.17 (Appendix B, ESI†) was applied to five available case studies from the literature dealing with experimental design in view of mass-balance-based data reconciliation (Table 1) to evaluate the effectiveness of the proposed measurement campaigns in fulfilling their main goal.| # | WWTP | Type/capacity | Configuration | Main goal of the study | Were key variables specified? | How was the measurement campaign carried out? |
|---|---|---|---|---|---|---|
| a p.e. = population equivalent. b SCADA = supervisory control and data acquisition system. | ||||||
| 1 | WWTP Katwoude,20 average data of one year | Municipal WWTP 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 p.e.a 300 p.e.a |
A2/O process with limited biological phosphorus removal and mainly chemical phosphorus removal | Reliable data for model calibration | Partially | Measurement campaign was not implemented |
| Only total oxygen consumption, and the amount of nitrified nitrogen and denitrified nitrogen were explicitly defined as key variables | Average data of one year from SCADA* and routine lab analysis of the plant was used | |||||
| Variables involved in SRT calculation were not defined as key variables but implied to be so | ||||||
| 2 | WWTP Katwoude,20 8 day measurement campaign | Same as previous | Same as previous | Reliable data for model calibration | Yes | 8 day measurement campaign was carried out with 24 h-composite samples (where available) and grab samples (at peak flow) combined with data from SCADAb and routine lab analyses |
| Seven process flow rates | ||||||
| 3 | WWTP Deventer22 | Municipal WWTP 182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 p.e. 000 p.e. |
Modified UCT-process according to the BCFS-concept | Reliable data for calculating sludge retention time and operational conditions for benchmarking | Partially | Intensive measurement campaign was carried out on three separate days with 24 h-composite samples (where available) and grab samples combined with data from SCADA and routine lab analyses |
| Only total oxygen consumption, and the amount of nitrified nitrogen and denitrified nitrogen were explicitly defined as key variables | ||||||
| Variables involved in SRT calculation were not defined as key variables but implied to be so | ||||||
| 4 | WWTP Houtrust21 | Municipal WWTP 330![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 p.e. 000 p.e. |
A2/O process with primary and secondary sludge fermentation | Reliable data for model validation and calibration | Yes | The plant was monitored for six weeks. Collected comprehensive data set consisting of 24 h-composite samples (where available), grab samples, data from SCADA and routine lab analyses |
| 15 flow variables and six mass flows of COD and total phosphorus | ||||||
| 5 | WWTP Tabriz19 | Petrochemical WWTP 4800 m3 per day | Following steps: oil separation coagulation & flocculation - activated sludge - sand filter | Reliable data for evaluating the performance of individual unit processes | No | Four sampling runs were carried out and combined with data from SCADA and routine lab analyses |
| Only flow measurements were balanced by data reconciliation | ||||||
| Mass flows of COD were reported to be balanced, but they were calculated from balanced flows and measured COD concentrations | ||||||
First of all, experimental design was conducted independently of what was proposed in the previous studies. This involves the translation of the main goal of the measurement campaign into key variables and the determination of optimal sets of additionally measured variables (besides initially available ones) that guarantee the identifiability of these key variables. Typical examples of key variables concern influent and effluent mass flow rates (e.g., total phosphorus, nitrogen) of the activated sludge process or the waste sludge mass flow rate. The oxygen requirements for carbon and nitrogen removal are usually important as well.17 These would be appropriate key variables if one wants to get reliable data for monitoring plant performance or perform model simulations. The sets of additional measurements obtained by solving the multi-objective optimization problem are also referred to as (optimal) solutions and belong to the Pareto optimal front.
The application of the experimental design procedure required three main types of input information: (a) main goal and associated key variables, (b) mass balances and (c) initially measured data set and potential additionally measured variables, with estimated cost and variance of the measured variables. These inputs were obtained from the five case studies.
a. Key variables. The main goal of each case study was translated into key variables, the identification of which ensured that this goal was fulfilled. Key variables can be initially measured or not; their identification means that their value can be calculated from other measured variables through which they are related by mass balances. As a result, the value of this variable can be reconciled by using mass balances. This implies that key variables need to be conservative quantities, i.e., fulfil material conservation laws (mass balances). For the case studies from the literature in which the key variables were not specified explicitly, they were deduced in this study from the given main goal.
b. Mass balances. The mass balances used in this work correspond with the incidence matrices from previous studies. They were represented for each case study in equation form. It can be noted that all the studies used steady-state mass balances and calculated average operating conditions for data reconciliation. For dynamic processes, other approaches such as moving-time window data reconciliation could be used,23 but they were out of the scope of this study.
c. Initially measured data set and potential additionally measured variables, with estimated cost and variance of measured variables. The additionally measured variables were proposed relative to a set of initially available data to ensure the fulfilment of the main goal. From the previous studies, however, it was not always clear which of the presented measured data were initially available and which ones were proposed additionally. For the previous studies in which the initially measured data were not clearly specified, the initially measured data set was assumed. Since the costs of additionally measured variables (flows and concentrations) were not specified in any of the previous studies, the costs of all measured variables were assumed equal. This assumption implies that the cost is proportional to the number of additionally measured variables. The use of measurement-specific costs would not limit the applicability of the procedure but may deliver different optimal solutions in terms of cost. The uncertainty of the measured variables was expressed in terms of their standard deviation, the magnitude of which could be derived from data provided in previous studies.
The set(s) of additionally measured variables proposed by applying the experimental design procedure from Le et al.17 was subsequently compared to those actually carried out in the previous studies. The previous studies defined the experimental design based on expert knowledge, and not explicitly as a multi-objective optimization problem like Le et al.17 Thus, the outcome was a single set of additional measurements. This was compared with the optimal solutions obtained in this study in terms of the number of additionally measured variables and in terms of the accuracy of key process variables. Only additionally measured variables that were used for data reconciliation were considered in the comparison. A detailed analysis of previous approaches was made by answering the following questions:
– Main goal and key variables: Were the key variables defined in previous studies? If yes, to what extent did they reflect the main goal of the measurement campaign?
– Mass balance setup: Were the mass balances relevant?
– Experimental design results: Was the set of (additional) measured variables implemented in the previous study relevant – did it allow the identification of key variables? Are there any alternative sets of additionally measured variables which may be better in terms of the number of required additionally measured variables and/or resulting accuracy of key variables?
3 Results
In what follows, the case studies from literature, in which a WWTP measurement campaign was planned in view of data reconciliation, are analysed one by one. Table 2 summarizes the results. The comparison with respect to the main goal and the key variables was evaluated by analysing the defined and identified key variables (A and B). The relevance of the mass balance setup was assessed by evaluating the number of defined and relevant mass balances (C and D). The experimental design results were assessed by considering the initial dataset, potential additionally measured variables, the additional measurements actually performed and the missing crucial variables (E–I). The sets of optimal solutions, as well as the minimum number of additional variables needed to fulfil the main goal were evaluated as well (J–M).| Number of | Case study 1 (ref. 20) average data of one year | Case study 2 (ref. 20) 8 day data | Case study 3 (ref. 22) | Case study 4 (ref. 21) | Case study 5 (ref. 19) | |
|---|---|---|---|---|---|---|
| a Only considering flows. b As checked in step 3 of the experimental design procedure.17 c No additional measurements were performed in this case study. d M = (G + I − K)/(G + I). Note: in case the additionally measured variables proposed in a previous study (G) were not sufficient for the identification of key variables, the number of missing essential additionally measured variables (I) was added. | ||||||
| Main goal and key variables | ||||||
| A | Key variables (number of which defined in a previous study) | 6 (3) | 7 (7) | 11 (3) | 21 (21) | 9 (0)a |
| B | Key variables identified in a previous study | 3 | 0 | 11 | 17 | 9 |
| Mass balance setup | ||||||
| C | Mass balances set up by previous studies | 8 | 12 | 14 | 20 | 8 |
| D | Relevant mass balances among C | 8 | 6 | 14 | 19 | 8 |
| Experimental design results | ||||||
| E | Initially available measured variables | 20 | 8 | 9 | 11 | 2 |
| F | Potential additionally measured variables, i.e. initially unmeasured variables in mass balances related to key variablesb | 2 | 12 | 25 | 29 | 17 |
| G | Additionally measured variables obtained (measurement campaign) in a previous study | 0c | 21 | 25 | 27 | 17 |
| H | Relevant additionally measured variables obtained in a previous study, i.e. contributing to the identification of key variables | NAc | 4 | 25 | 24 | 17 |
| I | Missing essential additionally measured variable in a previous study, i.e., required for the identification of all key variables | 2 | 2 | 0 | 2 | 0 |
| J | Number of Pareto-optimal solutions found using an experimental design procedure | 1 | 6 | 8 | 12 | 10 |
| K | Minimum number of additionally measured variables needed to identify all key variables (i.e. for the Pareto-optimal solution with minimum number of additionally measured variables) | 2 | 7 | 11 | 18 | 7 |
| L | Additionally measured variables for the most accurate Pareto-optimal solution (i.e. for the optimal solution with a maximum number of additionally measured variables) | 2 | 12 | 25 | 29 | 17 |
| M | Maximum potential reduction of additionally measured variables, compared with a previous study with a Pareto-optimal solution with a minimum number of additionally measured variablesd | NAc | 70% | 56% | 38% | 59% |
3.1 Case study 1: Meijer et al.,20 average data of one year
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 population equivalents (p.e.) and was built according to anaerobic/anoxic/oxic design (A2/O design) with limited biological phosphorus removal and mainly chemical phosphorus removal (Fig. 1). In the first case study by Meijer et al.,20 average data of one year from SCADA and routine lab analysis of the plant (Table C1, Appendix C1, ESI†) were used for data reconciliation. Twenty measured variables were initially available. No additional data were gathered (no measurement campaign).
300 population equivalents (p.e.) and was built according to anaerobic/anoxic/oxic design (A2/O design) with limited biological phosphorus removal and mainly chemical phosphorus removal (Fig. 1). In the first case study by Meijer et al.,20 average data of one year from SCADA and routine lab analysis of the plant (Table C1, Appendix C1, ESI†) were used for data reconciliation. Twenty measured variables were initially available. No additional data were gathered (no measurement campaign).
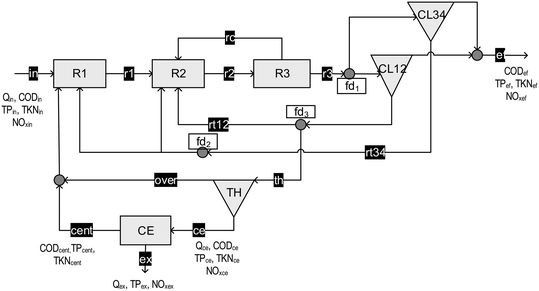 | ||
| Fig. 1 WWTP Katwoude, adapted from Meijer et al.20 Unit processes are indicated in grey: R1 = mixed non-aerated selector, R2 = completely mixed anoxic reactor, R3 = aerated carrousel reactor, CL12, CL34 = four clarifiers were operated in pairs. fd1, fd2, fd3 = flow dividers, TH = sludge thickener and CE = centrifuge. The black boxes refer to the name of the streams. The measured variables are indicated by name at their respective positions. | ||
| # | Unit process | Mass balances | Unit |
|---|---|---|---|
| Q = flow, mTP = total phosphorus mass flow, mTKN = Kjeldahl nitrogen mass flow, mCOD = COD mass flow, mNOx = NO3 mass flow rate. OCnet = net oxygen consumption (kg per day), OCcod = oxygen for COD removal (kg per day), NITR = nitrified nitrogen (kg per day), DENI = denitrified nitrogen (kg per day). | |||
| 1 | WWTP | Q in − Qef − Qex | Flow (m3 per day) |
| 2 | CE | Q ce − Qcent − Qex | |
| 3 | WWTP | m TP in − mTPef − mTPex | Total phosphorus (kg per day) |
| 4 | CE | m TPce − mTPcent − mTPex | |
| 5 | WWTP | m CODin − mCODef − mCODce + mCODcent − OCcod − 2.87·DENI | COD and nitrogen (kg per day) |
| 6 | WWTP | m TKNin − mTKNef − mTKNce + mTKNcent − NITR | |
| 7 | WWTP | DENI − NITR + mNOxef + mNOxin − mNOxex | |
| 8 | WWTP | OC net − OCcod − 4.57·NITR | |
By discarding the effluent flow (Qef) and centrifuge outflow (Qcent) from the set of potential additionally measured variables and by performing again a feasibility evaluation (i.e., checking variable identifiability without Qef and Qcent as additional measurements), it was concluded in this study that they were essential. Qef was required to identify the flow of excess sludge (Qex) and the mass flow of total phosphorus in the influent (mTPin). Qcent was required to identify the amount of denitrified nitrogen (DENI), the amount of nitrified nitrogen (NITR) and the total oxygen consumption (OCnet).
3.2 Case study 2: Meijer et al.,20 data from an 8-day measurement campaign
| Unit process | Mass balance | Unit | ||
|---|---|---|---|---|
| Q = flow, mTP = total phosphorus mass flow, mNH = ammonium mass flow. | ||||
| 1 | R1 | Selector | Q in + Qrt34 + Qover + Qcent − Qr1 | Flow (m3 per day) |
| 2 | R2 | Denitrification reactor | Q r1 + Qrc + Qrt12 − Qr2 | |
| 3 | R3 | Aerated carousel | Q r2 − Qrc − Qr3 | |
| 4 | CL | Clarifiers | Q r3 − Qef − Qrt12 − Qrt34 − Qth | |
| 5 | TH | Thickeners | Q th − Qover − Qce | |
| 6 | CE | Centrifuge | Q ce − Qcent − Qex | |
| 7 | R1 | Selector | m TPin + mTPrt34 + mTPover + mTPcent − mTPr1 | Total phosphorus (kg per day) |
| 8 | R2 | Denitrification reactor | m TPr1 + mTPrc + mTPrt12 − mTPr2 | |
| 9 | R3 | Aerated carousel | m TPr2 − mTPrc − mTPr3 | |
| 10 | CL | Clarifiers | m TPr3 − mTPef − mTPrt12 − mTPrt34 − mTPth | |
| 11 | R1 | Selector | m NHin + mNHrt34 + mNHover + mNHcent − mNHr1 | Ammonium (kg per day) |
| 12 | R2 | Denitrification reactor | m NHr1 + mNHrc + mNHrt12 − mNHr2 | |
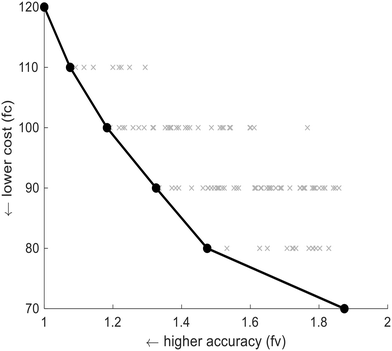 | ||
| Fig. 2 Pareto optimal solutions for the setup of Meijer et al.20 determined by the experimental procedure of Le et al.17 and expressed in terms of accuracy and costs. The line with the filled circles (black) denotes the Pareto-optimal front. ‘x’ = a solution. | ||
For comparison, Meijer et al.20 used 24 measured variables for data reconciliation, 21 of which were measured additionally during an 8-day measurement campaign. The set of additionally measured variables of Meijer et al.20 was not presented in Fig. 2 since it did not satisfy the defined main goal and therefore was not a solution. In fact, our findings suggest that none of the key variables could be identified with the proposed set of additionally measured variables. In order to identify the seven key variables, the proposed set of measured data (Table C2a, Appendix C2, ESI†) should be complemented with the flow from R3 to R2 (Qr2) and the centrifuge output flow (Qcent), making up two additionally measured variables.
From the experimental design procedure, it is clear that only flow measurements can help in identifying flows.17 However, Meijer et al.,20 with the aim of identifying only total flows, included 6 mass balances for total phosphorus (TP) and total Kjeldahl nitrogen (TKN) in the system of mass balances (Table 4) and 17 corresponding concentration measurements of TP and TKN, 15 of which were measured additionally. The measurements of TP and TKN, however, will not contribute to the identification of flow variables as there is no direct relation to total flows in the mass balances. Therefore, setting up total phosphorus and ammonium mass balances and performing 17 concentration measurements of TP and TKN, as proposed by Meijer et al.,20 were irrelevant for the reconciliation of flow rates. The result of the flow balancing would be the same with or without the TP and TKN mass balances and measurements.
In brief, only 6 of the 12 mass balances set in a previous study were relevant. In addition, Meijer et al.20 proposed 21 additionally measured variables, only 4 of which were relevant and still missing 2 essential ones. Using the experimental design procedure from Le et al.,17 the minimum number of additionally measured variables was 7. As a result, the potential reduction in the number of additionally measured variables could be up to 70% (= [21 + 2 − 7]/[21 + 2]) compared to the proposed set of Meijer et al.20
3.3 Case study 3: Puig et al.22
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 p.e. and was built as a modified UCT-process according to the BCFS-concept24 (Fig. 3). The measured data are summarised in Table C3a, Appendix C3, ESI.†
000 p.e. and was built as a modified UCT-process according to the BCFS-concept24 (Fig. 3). The measured data are summarised in Table C3a, Appendix C3, ESI.†
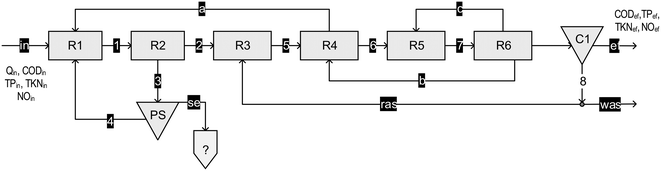 | ||
| Fig. 3 Flow diagram of the Deventer WWTP, The Netherlands (adapted from Puig et al.22). R1 and R2 = two anaerobic reactors, R3 = a contact tank, R4 = an anoxic reactor, R5 = an alternatively aerated reactor, R6 = aerated rector, C1 = six secondary settlers (in parallel) and PS = stripping reactor. Measured variables are indicated. | ||
Four methods for SRT calculation were considered. The first one was the classical SRT calculation obtained as the ratio of the sludge mass TSS in the reactor to the sludge mass TSS flow rate leaving the reactor through the waste sludge stream (‘was’), the secondary settler effluent (‘ef’) and the stripping reactor effluent streams (‘se’) (eqn (1)).
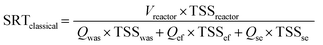 | (1) |
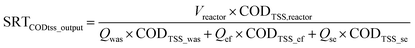 | (2) |
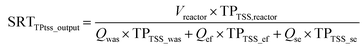 | (3) |
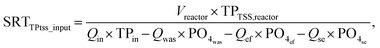 | (4) |
| Unit process | Mass balance | Unit | |
|---|---|---|---|
| Q = flow, mTP = total phosphorus mass flow, mTKN = Kjeldahl nitrogen mass flow, mCOD = COD mass flow, mNOx = NO3 mass flow. OCnet = total oxygen consumption (kg per day), OCcod = oxygen for COD removal (kg per day), NITR = nitrified nitrogen (kg per day), DENI = denitrified nitrogen (kg per day). | |||
| 1 | WWTP | Q in − Qse − Qef − Qwas | Flow (m3 per day) |
| 2 | R1 + R2 | Q in − Qse − Q2 + Qa | |
| 3 | R3 + R4 | Q 2 + Qras − Qa − Q6 + Qb | |
| 4 | R5 | Q 6 − Q7 + Qc | |
| 5 | R6 | Q 7 − Qc − Qb − Q8 | |
| 6 | C1 | −Qras + Q8 − Qef − Qwas | |
| 7 | WWTP | m TP in − mTPse − mTPef − mTPwas | Total phosphorus (kg per day) |
| 8 | R1 + R2 | m TP in − mTPse − mTP2 + mTPa | |
| 9 | R3 + R4 | m TP2 + mTPras − mTPa − mTP6 + mTPb | |
| 10 | C1 | m TP8 − mTPras − mTPef − mTPwas | |
| 11 | WWTP | m TKNin − mTKNse − mTKNef − mTKNwas − NITR | COD and nitrogen (kg per day) |
| 12 | WWTP | NITR − DENI − NOef − NOse − NOwas | |
| 13 | WWTP | m CODin − mCODse − mCODef − mCODwas − 2.78 × DENI − OCcod | |
| 14 | WWTP | −OCcod − 4.57 × NITR + OCnet | |
The key variables corresponding with the defined main goals were not specified by Puig et al.22 but were deduced in this study. Eleven variables related to SRT (eqn (1)–(4)) and operating conditions (NITR, DENI and OCnet in mass balances #11–#14, Table 5) were conservative and therefore defined as key variables, namely: the flow rates and mass flows of total phosphorus in the influent (Qin, mTPin), effluent (Qef, mTPef), excess sludge (Qwas, mTPwas), stripped effluent (Qse, mTPse), amount of nitrified nitrogen (NITR, kg per day), denitrified nitrogen (DENI, kg per day) and total oxygen consumption of WWTP (OCnet, kg per day).
From the SRT calculations (eqn (2)–(4)), it is clear that there are more variables related to the main goal, namely the mass flows of total suspended solids (TSS), orthophosphate (PO), total particulate phosphorus TSS (TPTSS) and particulate COD (CODTSS). They could not, however, be defined as key variables since they are not conservative quantities, which means that no mass balances can be set up for these compounds. As a result, the SRT calculations were based on both the measured and reconciled variables.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 554
554![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 432 possible combinations of additionally measured variables. They were all evaluated in this study through the experimental design procedure of Le et al.,17 resulting in 4944 solutions, 8 of which were Pareto-optimal (Fig. 4, detailed in Table C3b, Appendix C3, ESI†).
432 possible combinations of additionally measured variables. They were all evaluated in this study through the experimental design procedure of Le et al.,17 resulting in 4944 solutions, 8 of which were Pareto-optimal (Fig. 4, detailed in Table C3b, Appendix C3, ESI†).
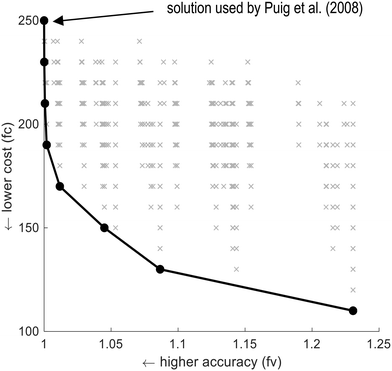 | ||
| Fig. 4 Pareto optimal solutions for the setup of Puig et al.22 determined using the experimental procedure of Le et al.17 and expressed in terms of accuracy and costs. The line with the filled black circles denotes the Pareto-optimal front. ‘x’ = a solution. | ||
The set of measured data used by Puig et al.22 for data reconciliation contained 25 additionally measured variables (indicated in Fig. 4 and detailed in Table C3a, Appendix C3, ESI†). This solution satisfied the main goal and, moreover, belonged to the Pareto-optimal front. More specifically, it was the most accurate but also the most expensive Pareto-optimal solution. In this case study, the minimum number of additionally measured variables was 11. As a result, the potential reduction in the number of additionally measured variables was 56% compared to the proposed set of Puig et al.22 Thus, the set of additional measurements was relevant and allowed the identification of all the key variables. Nevertheless, alternative solutions were found in this study involving fewer measurements and lower cost.
3.4 Case study 4: Meijer et al.21
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 p.e. It consists of an A2/O process configuration with primary and secondary sludge digesters (Fig. 5). The measured data are summarised in Table C4a, Appendix C4, ESI.†
000 p.e. It consists of an A2/O process configuration with primary and secondary sludge digesters (Fig. 5). The measured data are summarised in Table C4a, Appendix C4, ESI.†
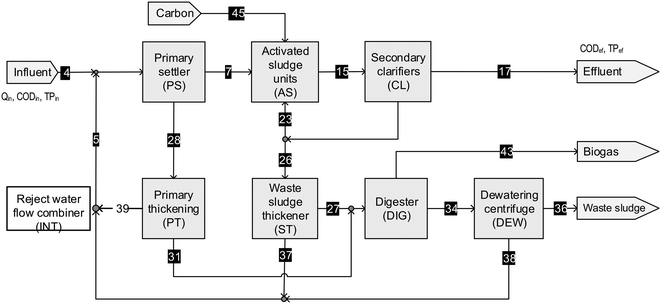 | ||
| Fig. 5 Flow diagram of the Houtrust WWTP, The Netherlands, adapted from Meijer et al.21 Measured variables are indicated. | ||
| Process unit | Mass balance | ||
|---|---|---|---|
| Q = flow, mTP = total phosphorus mass flow, mCOD = COD mass flow, mTSS = mass flow of total suspended solids. | |||
| 1 | WWTP | Q 4 + Q40 − Q17 − Q35 | Total flow (m3 per day) |
| 2 | Water line | Q 7 − Q17 − Q26 | |
| 3 | Sludge line | Q 26 + Q31 − Q35 − Q37 − Q38 | |
| 4 | Rejected water line | Q 5 − Q37 − Q38 − Q39 − Q40 | |
| 5 | Activated sludge units | Q 7 + Q23 − Q15 | |
| 6 | Primary settler | Q 4 + Q5 − Q7 − Q28 | |
| 7 | Primary thickening | Q 28 − Q31 − Q39 | |
| 8 | Secondary clarifier | Q 15 − Q23 − Q26 − Q17 | |
| 9 | Waste sludge thickener | Q 26 − Q27 − Q37 | |
| 10 | Digestor | Q 27 + Q31 − Q34 | |
| 11 | Dewatering | Q 34 − Q35 − Q38 | |
| 12 | WWTP | m TP 4 − mTP17 − mTP35 | Total phosphorus (kg per day) |
| 13 | Water line | m TP 7 − mTP17 − mTP26 | |
| 14 | Secondary clarifier | m TP15 − mTP23 − mTP26 − mTP17 | |
| 15 | Primary settler | m TP 4 + mTP5 − mTP7 − mTP28 | |
| 16 | Sludge line | m TP 26 + mTP28 − mTP5 − mTP35 | |
| 17 | Primary settler | m COD 4 + mCOD5 − mCOD7 − mCOD28 | COD (kg per day) |
| 18 | Sludge line | m COD 26 + mCOD28 − mCOD5 − mCOD35 − mCOD43 | |
| 19 | Digester | m COD27 + mCOD31 − mCOD34 − mCOD43 | |
| 20 | Waste sludge thickener | m TSS26 − mTSS37 + mTSS27 | TSS (kg per day) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870
870![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 possible combinations of additionally measured variables were evaluated with the experimental design procedure, resulting in 4824 solutions. The Pareto-optimal front contains 12 solutions (detailed in Table C4b, Appendix C4, ESI†).
912 possible combinations of additionally measured variables were evaluated with the experimental design procedure, resulting in 4824 solutions. The Pareto-optimal front contains 12 solutions (detailed in Table C4b, Appendix C4, ESI†).
Meijer et al.21 used 34 measured variables for data reconciliation, 27 of which were measured additionally. However, only 24 additionally measured variables actually contributed to the identification of key variables. The TSS mass flow balance around the waste sludge thickener (#20 in Table 6) did not contribute to the identification of any key variables. Therefore, this mass balance and the three associated TSS measurements (TSS26, TSS37 and TSS27) were not necessary in this case study.
Moreover, 4 key variables could not be identified with the measured data from Meijer et al.:21 the total influent flow rate (Q4), the return activated sludge flow rate (Q23), the influent COD mass flow (mCOD4) and the influent mass flow of total phosphorus (mTP4). So, the main goal was not entirely achieved by their measurement campaign. Still, Meijer et al.21 reported that Q4 and Q23 were balanced by data reconciliation – no results were reported for balancing mCOD4 and mTP4.
The set of measured data applied for data reconciliation by Meijer et al.21 missed two crucial additionally measured variables: the settled influent flow rate (Q7) to balance mCOD4 and mTP4 and the inflow rate to the secondary clarifiers (Q15) to balance Q23. These two variables were found essential to identify all the key variables during the redundancy analysis performed in this study. The addition of these two variables (Q7 and Q15) to the measured data set used by Meijer et al.21 would have resulted in a solution (indicated by ‘x’ in Fig. 6 and detailed in Table C4b, Appendix C4, ESI†), i.e., would have allowed the identification of all key variables. However, the latter solution is not a Pareto-optimal solution since it has the same number of additionally measured variables but about 38% lower accuracy than the most expensive Pareto-optimal solution (accuracy fv = 1.38). In this case study, the minimum additionally measured variables were 18. The potential reduction in the number of additionally measured variables could be up to 38% compared to the proposed set of Meijer et al.21
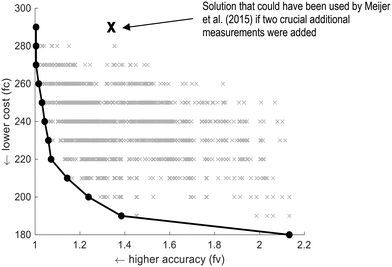 | ||
| Fig. 6 Pareto optimal solutions for the setup of Meijer et al.21 determined using the experimental procedure of Le et al.17 and expressed in terms of accuracy and costs. The line with the filled grey circles denotes the Pareto-optimal front. ‘x’ = a solution. | ||
Overall, 19 of the 20 mass balances set by Meijer et al.21 were considered relevant. However, the set of additional measurements did not allow the identifiability of the key variables. On the one hand, unnecessary measurements were performed. On the other hand, crucial variables were missing.
3.5 Case study 5: Behnami et al.19
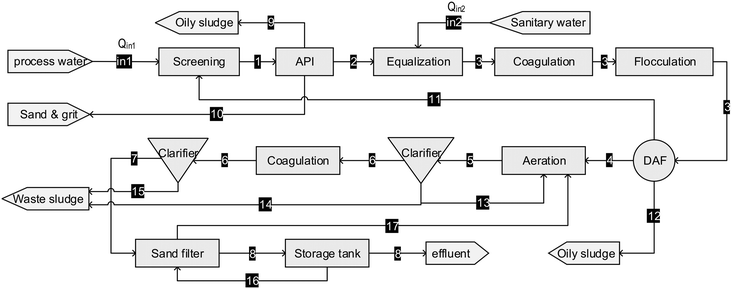 | ||
| Fig. 7 Flow diagram of the Tabriz petrochemical WWTP, Iran.19 Measured variables are presented. | ||
| Process unit | Mass balance | ||
|---|---|---|---|
| Q = total mass flow (density is assumed to be the same for all streams). | |||
| 1 | Screening | Q in1 − Q1 + Q11 | Flow (m3 per day) |
| 2 | API | Q 1 − Q2 − Q9 − Q10 | |
| 3 | Equalization | Q 2 + Qin2 − Q3 | |
| 4 | DAF | Q 3 − Q4 − Q11 − Q12 | |
| 5 | Aeration | Q 4 − Q5 + Q13 + Q17 | |
| 6 | Clarifiers | Q 5 − Q6 − Q13 − Q14 | |
| 7 | Clarifiers | Q 6 − Q7 − Q15 | |
| 8 | Sand filter | Q 7 − Q8 + Q16 − Q17 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 possible combinations of additionally measured variables were analysed and 2612 solutions were found using the experimental design procedure. The result is a Pareto-front with 10 solutions (Fig. 8, detailed in Table C5b, Appendix C5, ESI†).
072 possible combinations of additionally measured variables were analysed and 2612 solutions were found using the experimental design procedure. The result is a Pareto-front with 10 solutions (Fig. 8, detailed in Table C5b, Appendix C5, ESI†).
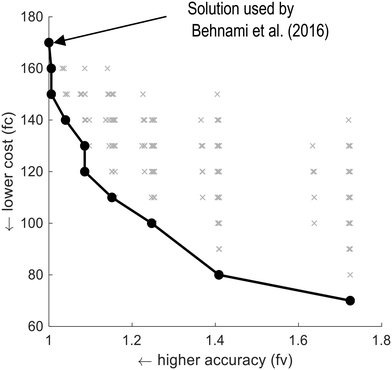 | ||
| Fig. 8 Pareto optimal solutions for the setup of Behnami et al.19 determined using the experimental procedure of Le et al.17 and expressed in terms of accuracy and costs. The line with the filled circles denotes the Pareto-optimal front. ‘x’ = a solution. | ||
Behnami et al.19 used 19 flow measured variables in data reconciliation, 17 of which were considered measured additionally compared to the initially measured flows in the measurement campaign (detailed in Table C5a, Appendix C5, ESI†). This data set satisfied the main goal to identify all key variables. This set also belongs to the Pareto-optimal front obtained using the experimental design procedure. The set of additionally measured variables implemented by Behnami et al.19 provided the highest accuracy (accuracy fv = 1) but with the highest cost (cost fc = 170) (Fig. 8 and detailed in Table C5b, Appendix C5, ESI†). In this case study, the minimum additionally measured variables given by the experimental design procedure would be 7. Therefore, the maximum potential reduction in the number of additionally measured variables could be up to 59%. Overall, a similar conclusion to the case study from Puig et al.22 could be drawn. The set of additional measurements was relevant and allowed the identification of all the key variables, but alternative solutions involving fewer measurements and lower cost were found in this study.
4 Discussion
4.1 Specification of key process variables
Translating the main goal of a study into key variables constitutes the first step in the well-defined, structured experimental design procedure we advocate for Le et al.17 The identification of key variables means that their value can be calculated – by applying data reconciliation – from measured variables through which they are related by mass balances. As a result, two important considerations need to be kept in mind during the key variable selection: the selection of conservative variables and the need for their identifiability.First, only conservative variables can possibly be identified using data reconciliation and therefore qualify as key variables. Some variables related to the main goal cannot appear in the mass balances because they are not expressed in conservative quantities, so they cannot be put forward as key variables. For example, the mass flow of orthophosphate and total suspended solids in case study 3 (ref. 22) and case study 1 (ref. 20) were non-conservative.
A second important requirement to keep in mind during key variable selection is that all key variables must be identifiable for the set of mass balances considered. This is checked through a redundancy analysis of the system of mass balances, which is an integral part (step 4, Fig. B1, Appendix B, ESI†) of the experimental design procedure of Le et al.17 In case one or more key variables are not identifiable, the set of mass balances needs to be reviewed first. In some cases, the problem can be solved by adding mass balances. However, it could also be that some variables related to the main goal, even if they are conservative, cannot be identified because practical constraints make it impossible to close the corresponding mass balances (e.g. measurement of the gas phase components of an open tank with a large surface area).
Redundancy analysis is an essential part of experimental design, as it removes the dependent mass balances and checks the presence of all the key variables in the independent mass balances (detailed mathematical procedure can be found in the study by Le et al.17). This ensures the identifiability of all the key variables. The absence of this analysis might lead to unnecessary mass balances with dependent constraints irrelevant for the identification of the key variables, and associated irrelevant additional measurements. None of the case studies reported in the literature so far performed such redundancy analysis. As a result, irrelevant mass balances were set up in case studies 2 and 4 of Meijer et al.20,21 Subsequently, unnecessary additional measurements were performed.
Besides avoiding the use of mass balances which are irrelevant (not related to key variables) and or redundant (linearly dependent on other mass balances), another point of attention is to take into account the maximum amount available of independent mass balances containing key variables. For instance, in case study 5 of Behnami et al.,19 more mass balances could have been defined and additional associated variables could have been identified. More specifically, in the latter study, only 15 flows were actually reconciled and used for further calculation and process evaluation, while more than 100 variables were additionally measured. These additional measurements were not exploited to their full potential. In case also the mass balances of COD, phosphorus and nitrogen would have been set up, more key variables could have been defined and identified (reconciled) for this case study.
4.2 From more measurements to more information
Increasing the number of measured variables does not always lead to more information in view of data reconciliation. In all case studies, additional measurements and associated mass balances were proposed such that the number of constraints (independent mass balances) was higher than the number of unknown variables, i.e. aiming at an overdetermined system. However, the identifiability of a variable depends on how it appears in the set of mass balances. As a result, aiming at an overdetermined system of mass balances does not guarantee the identifiability of all key process variables.5 It involves the risk of adding measurements without added value (oversized measurement campaigns) while missing out on some critical measurements. For a small number of key variables and mass balances, the identifiability of key variables could be deduced as such. However, for a more extensive set of key variables and mass balances, a clear and straightforward experimental design procedure is essential.In the studies of Puig et al.22 and Behnami et al.,19 additional measurements were collected for all unknown variables that appear in the set of mass balances. The redundant data sets collected in these case studies corresponded with the most expensive (but most accurate) Pareto-optimal solutions identified with the experimental design procedure in this study. The study of Meijer et al.21 involved a relatively complex set of mass balances, which made it challenging to find the right additionally measured variables without a structured experimental design approach. As a consequence, the additional measurements performed in the latter case study missed two crucial additionally measured variables and not all key variables could be identified.
As a side note, it could be mentioned that the measurement accuracy will also influence their usefulness and added value. In the experimental design procedure in this study, the measurement accuracy is taken into account through their variance, which is incorporated in the objective function. Adding redundant sensors for variables which are already observable may lead to improved precision of the reconciled values or to improved sensor fault isolation, as demonstrated by Villez et al.18 through the concept of ‘surplus redundancy’. However, such a procedure was considered beyond the scope of the present study.
Overall, it is clear that more measurements do not necessarily lead to more information. Data gathering should only be done if one knows where to use the data for, i.e. once the main goal and key variables have been defined. Rather than measuring more, one needs to measure the right things. Balancing the number of measurements (costs) and the obtained accuracy of identified variables by staying on the Pareto-optimal front will avoid excess costs for additional measurements that do not add information. Besides the measurement costs as such, also overhead and costs associated with data management cannot be neglected – the costs for sensors are just the tip of the iceberg. Digitalisation of the water industry, a topic which has attracted a lot of interest,25 should therefore never be the goal as such.
4.3 Application of the experimental design procedure to other WWTPs
The potential and general applicability of the experimental design procedure of Le et al.17 was demonstrated in this study through its application to five different case studies. On the one hand, the procedure could be successfully applied to different plant layouts with different main goals. On the other hand, the provided solutions ensured the fulfilment of the main goal (and the identifiability of the key variables). Additionally, the optimal solutions implied fewer additional measurements (about 40–70% less) compared to the previous approaches from the evaluated case studies.The application of the design procedure is straightforward. It consists of seven steps, the first three of which require inputs from the user to organize all the collected information in one preformat input file: to translate the main goal(s) into key variables (step 1), to set up mass balances relating key variables to other, measured variables (step 2) and to inventory initially available data (step 3). Step 4 to step 7 are fully automated and are directed in finding the (optimal) solutions for any problem that can be formulated in the first three steps. For all case studies considered in this contribution, these last four steps took at most 10 seconds. This fast implementation makes one effectively and iteratively rework the set of mass balances and recheck input data and/or the key variable definition in case one or more key variables cannot be balanced/estimated.
The experimental design procedure is very flexible in providing alternative additional measurement sets. For a user-defined set of potential additionally measured variables, the experimental design procedure proposes several alternatives, all of which are Pareto-optimal. The user can then select a solution from the Pareto-front based on the available budget and expected accuracy. Note that additional approaches can be used to define the optimization problem in accordance with the main goal of the study. For instance, Villez et al.18 defined the sensor placement procedure as a trade-off between observability and cost in WWTPs, while other studies in the chemical engineering field also considered objectives such as reliability (= low probability of faults), precision or estimability.26,27 Nevertheless, the Pareto optimal front is considered an excellent option to visualize the solutions.
If problems are expected with the measurement of specific streams, e.g. because of safety issues or difficult access, these can be avoided upfront by discarding them from the set of potential additionally measured variables. Application of the experimental design procedure will then indicate whether the discarded variables are essential (in step 4: feasibility evaluation, see Fig. B1, Appendix B, ESI†) and if not, will propose alternative solutions. For example, in case studies 2 and 3, measuring internal recycling flows, which may be problematic, could be avoided by excluding them from the list of potential additionally measured variables.
While this study deals with measurement campaigns for WWTPs, similar experimental design methodologies for application to water distribution networks and sewer systems could be developed in the future.
5 Conclusions
In the framework of digitalization of the water industry, rather than measuring more, one needs to measure the right things in order to obtain more information. This contribution validates a structured procedure for defining ‘the right things’. More specifically, the general applicability and added value of the experimental design procedure of Le et al.17 for planning measurement campaigns on WWTPs was demonstrated in this study, leading to the following insights:– The application of the experimental design procedure was straightforward and could easily be adapted for different WWTP configurations and different main goals.
– Translating the main goal of a study into key variables is essential to find appropriate additionally measured variable sets. The key variables should be conserved quantities and need to appear in the set of mass balances considered for the system under study, in order to be identifiable during future data reconciliation. In three out of the five case studies from the literature applying expert judgement approaches, the main goal was not translated well into specific key variables and thus they were not well identified with additional measurements.
– A redundancy analysis, to check the identifiability of key variables for the considered set of mass balances, is an essential part of the proposed experimental design procedure. The optimal sets of additionally measured variables proposed using the procedure thus guarantee the identifiability of all the key variables through subsequent data reconciliation. This was not always the case in the literature case studies. This showed that more measurements do not necessarily lead to more information.
– Even though adequate additional measurements were proposed using the expert judgement approach, there were often too many measurements. With the structured experimental design procedure, about 40% to 70% fewer measurements were needed.
Data availability
All the data used for this research have been included in the manuscript and the ESI.†Conflicts of interest
There are no conflicts to declare.References
- C. M. Crowe, Data reconciliation - Progress and challenges, J. Process Control, 1996, 6, 89–98, DOI:10.1016/0959-1524(96)00012-1.
- D. B. Özyurt and R. W. Pike, Theory and practice of simultaneous data reconciliation and gross error detection for chemical processes, Comput. Chem. Eng., 2004, 28, 381–402, DOI:10.1016/j.compchemeng.2003.07.001.
- F. Madron, V. Veverka and V. Vanecek, Statistical-Analysis of Material Balance of a Chemical Reactor, AIChE J., 1977, 23, 482–486, DOI:10.1002/aic.690230412.
- F. Madron and V. Veverka, Optimal selection of measuring points in complex plants by linear models, AIChE J., 1992, 38, 227–236, DOI:10.1002/aic.690380208.
- R. T. J. M. van der Heijden, J. J. Heijnen, C. Hellinga, B. Romein and K. C. A. M. Luyben, Linear Constraint Relations in Biochemical Reaction Systems .1. Classification of the Calculability and the Balanceability of Conversion Rates, Biotechnol. Bioeng., 1994, 43, 3–10, DOI:10.1002/bit.260430103.
- S. Lee, S. Rao, M. J. Kim, I. J. Esfahani and C. K. Yoo, Assessment of environmental data quality and its effect on modelling error of full-scale plants with a closed-loop mass balancing, Environ. Technol., 2015, 36, 3253–3261, DOI:10.1080/09593330.2015.1058859.
- V. Monje, H. Junicke, D. J. Batstone, K. Kjellberg, K. V. Gernaey and X. Flores-Alsina, Prediction of mass and volumetric flows in a full-scale industrial waste treatment plant, Chem. Eng. J., 2022, 445, 136774, DOI:10.1016/j.cej.2022.136774.
- O. Nowak, A. Franz, K. Svardal, V. Muller and V. Kuhn, Parameter estimation for activated sludge models with the help of mass balances, Water Sci. Technol., 1999, 39, 113–120, DOI:10.1016/S0273-1223(99)00065-7.
- A. Spindler, Structural redundancy of data from wastewater treatment systems. Determination of individual balance equations, Water Res., 2014, 57, 193–201, DOI:10.1016/j.watres.2014.03.042.
- K. Villez, P. A. Vanrolleghem and L. Corominas, Optimal flow sensor placement on wastewater treatment plants, Water Res., 2016, 101, 75–83, DOI:10.1016/j.watres.2016.05.068.
- L. Benedetti, G. Dirckx, D. Bixio, C. Thoeye and P. A. Vanrolleghem, Substance flow analysis of the wastewater collection and treatment system, Urban Water J., 2006, 3, 33–42, DOI:10.1080/15730620600578694.
- H. Yoshida, T. H. Christensen, T. Guildal and C. Scheutz, A comprehensive substance flow analysis of a municipal wastewater and sludge treatment plant, Chemosphere, 2015, 138, 874–882, DOI:10.1016/j.chemosphere.2013.09.045.
- M. Carnero, J. L. Hernández and M. Sánchez, Optimal Sensor Location in Chemical Plants Using the Estimation of Distribution Algorithms, Ind. Eng. Chem. Res., 2018, 57, 12149–12164, DOI:10.1021/acs.iecr.8b01680.
- J. Wang, Z. Wang, X. Ma, A. Smith, F. Gu and C. Zhang, et al., Locating Sensors in Large-Scale Engineering Systems for Fault Isolation Based on Fault Feature Reduction, J. Franklin Inst., 2020, 357, 8181–8202, DOI:10.1016/j.jfranklin.2020.05.037.
- A. Soldevila, J. Blesa, S. Tornil-Sin, R. M. Fernandez-Canti and V. Puig, Sensor placement for classifier-based leak localization in water distribution networks using hybrid feature selection, Comput. Chem. Eng., 2018, 108, 152–162, DOI:10.1016/j.compchemeng.2017.09.002.
- C. Winter, V. R. Palleti, D. Worm and R. Kooij, Optimal placement of imperfect water quality sensors in water distribution networks, Comput. Chem. Eng., 2019, 121, 200–211, DOI:10.1016/j.compchemeng.2018.10.021.
- Q. H. Le, P. J. T. Verheijen, M. C. M. van Loosdrecht and E. I. P. Volcke, Experimental design for evaluating WWTP data by linear mass balances, Water Res., 2018, 142, 415–425, DOI:10.1016/j.watres.2018.05.026.
- K. Villez, P. A. Vanrolleghem and L. Corominas, A general-purpose method for Pareto optimal placement of flow rate and concentration sensors in networked systems – With application to wastewater treatment plants, Comput. Chem. Eng., 2020, 139, DOI:10.1016/j.compchemeng.2020.106880.
- A. Behnami, M. Shakerkhatibi, R. Dehghanzadeh, K. Z. Benis, S. Derafshi and E. Fatehifar, The implementation of data reconciliation for evaluating a full-scale petrochemical wastewater treatment plant, Environ. Sci. Pollut. Res., 2016, 23, 22586–22595, DOI:10.1007/s11356-016-7484-5.
- S. C. F. Meijer, H. Van Der Spoel, S. Susanti, J. J. Heijnen and M. C. M. Van Loosdrecht, Error diagnostics and data reconciliation for activated sludge modelling using mass balances, Water Sci. Technol., 2002, 45, 145–156, DOI:10.2166/wst.2002.0102.
- S. C. F. Meijer, R. N. A. van Kempen and K. J. Appeldoorn, Plant upgrade using big-data and reconciliation techniques, in Applications of Activated Sludge Models, ed. D. Brdjanovic, S. C. F. Meijer, C. M. Lopez-Vazquez, C. M. Hooijmans and M. C. M. van Loosdrecht, IWA Publishing, 2015, pp. 357–410 Search PubMed.
- S. Puig, M. C. M. van Loosdrecht, J. Colprim and S. C. F. Meijer, Data evaluation of full-scale wastewater treatment plants by mass balance, Water Res., 2008, 42, 4645–4655, DOI:10.1016/j.watres.2008.08.009.
- Q. H. Le, P. J. T. Verheijen, M. C. M. van Loosdrecht and E. I. P. Volcke, Application of data reconciliation to a dynamically operated wastewater treatment process with off-gas measurements, Environ. Sci., 2022, 8, 2114–2125, 10.1039/d2ew00006g.
- M. C. M. Van Loosdrecht, F. A. Brandse and A. C. De Vries, Upgrading of waste water treatment processes for integrated nutrient removal the BCFS® process, Water Sci. Technol., 1998, 37, 209–217, DOI:10.1016/S0273-1223(98)00290-X.
- S. Vairavamoorthy, The rise of digital water - The Source, 2018 Search PubMed.
- M. Bhushan and R. Rengaswamy, Comprehensive design of a sensor network for chemical plants based on various diagnosability and reliability criteria. 2, Applications, Ind. Eng. Chem. Res., 2002, 41, 1840–1860, DOI:10.1021/ie010437v.
- M. Carnero, J. Hernández and M. Sánchez, A new metaheuristic based approach for the design of sensor networks, Comput. Chem. Eng., 2013, 55, 83–96, DOI:10.1016/j.compchemeng.2013.04.007.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ew00315b |
| This journal is © The Royal Society of Chemistry 2025 |
