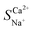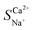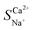Selective removal of Ca2+ from brackish water by electrodialysis desalination: process optimization and application
Received
31st October 2024
, Accepted 17th December 2024
First published on 3rd January 2025
Abstract
Exploration and application of unconventional water sources, particularly brackish water, have emerged as key strategies for addressing freshwater scarcity. Electrodialysis (ED) is utilised in brackish water desalination to eliminate Ca2+ owing to its cost-effectiveness and eco-friendliness. This study integrated electrochemical impedance spectroscopy to examine the effects of voltage, flow rate, and initial concentration on the migration numbers of Na+ and Ca2+ ions as well as the selectivity coefficient for Ca2+ during ED. The experimental results revealed that a lower voltage, flow rate, and initial concentration enhanced the selective removal of Ca2+ compared to Na+, which was linked to variations in the boundary layer thickness near the membrane. The maximum 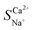 reached 2.48 at an initial concentration of 3.3 mmol L−1, with a voltage of 6 V and an influent flow rate of 36 L h−1. In addition, a 2 month pilot study was conducted using brackish groundwater from northwestern China. This indicates a stable effluent and high efficiency of Ca2+ removal during brackish water treatment via the ED process. The Ca2+ concentration in the effluent remained below 20 mg L−1 with a daily water production efficiency of 90%. This study offers valuable insights into ED technology applicable to the desalination and hardness reduction of brackish water.
reached 2.48 at an initial concentration of 3.3 mmol L−1, with a voltage of 6 V and an influent flow rate of 36 L h−1. In addition, a 2 month pilot study was conducted using brackish groundwater from northwestern China. This indicates a stable effluent and high efficiency of Ca2+ removal during brackish water treatment via the ED process. The Ca2+ concentration in the effluent remained below 20 mg L−1 with a daily water production efficiency of 90%. This study offers valuable insights into ED technology applicable to the desalination and hardness reduction of brackish water.
Water impact
Untreated brackish water often contains higher concentrations of Ca2+, and direct drinking can affect health. Electrodialysis (ED) has become one of the main technologies for Ca2+ removal in brackish water desalination due to its green environmental protection and high ion selectivity. In this study, the electrochemical characteristics of the membrane and its adjacent interfacial layer were analyzed by electrochemical impedance spectrometry, and the effects of voltage, flow rate and initial concentration on the selective removal of Ca2+ in ED were discussed. In addition, this study also conducted a two-month pilot study on underground brackish water from northwest China. This study provides valuable insights into the application of ED in brackish water desalination and selective removal of Ca2+, which could help improve the safety of drinking water.
|
1 Introduction
Based on the salt concentration in water, brine with total dissolved solids (TDS) from 1 g L−1 to 10 g L−1 is generally classified as brackish water.1 Globally, brackish water is primarily found in inland arid areas, deserts, grasslands, and coastal regions.2 The primary forms of brackish water include groundwater and surface water. Its composition is influenced by the geographic location, geological conditions, and the soil and rock through which the water flows, and consistently contains higher levels of soluble solids, fluoride, and heavy metal ions than drinking water sources. Notably, Na+ and Ca2+ are the predominant ionic components of brackish water.3 The Ca2+ content in brackish water is relatively high. Direct utilization of brackish water can result in scaling within water treatment plants, transmission systems, pipelines, and storage tanks,4,5 and consumption can lead to significant health risks, causing various conditions such as gastrointestinal issues, bloating, and urinary tract stones.6,7 Consequently, the Ca2+ concentration in brackish water must be reduced to ensure water safety.
Current technologies for desalinating brackish water and removing Ca2+ primarily include coagulation, ion exchange, and membrane methods.8–11 Ion exchange is infrequently used because of significant drawbacks, such as producing large volumes of waste liquid and requiring long treatment durations. Coagulation entails relatively high operational costs, with ongoing adjustments required for chemical types and dosages. In addition, the environmental impact is significant. In membrane methods such as reverse osmosis and nanofiltration (NF), pressure differentials act as the driving force.12,13 The chemicals used in the pretreatment process may create new pollutants, which negatively impacts the water treatment process, and the water recovery rate is low. NF achieves a retention rate of 90–99% for divalent ions. However, extended operation results in a significant decline in the effectiveness and durability of the NF membrane.14–16 Given that electrodialysis (ED) applies electric field forces directly to charged ions, its driving force for ion transmembrane migration surpasses that of NF, offering high desalination efficiency, straightforward operation, and environmental benefits.17–19 Thus, ED presents distinct advantages for Ca2+ removal from brackish water.
In an ideal mass-transfer process, ion exchange membranes (IEMs) exhibit perfect ion permeability. However, under non-ideal conditions, ion permeability can be affected by IEMs, external solutions, and operating conditions.20 There are currently several aspects to improve the ion selective removal effect of ED, including IEM modification, process optimization, and membrane stack structure innovation. Among them, large-scale IEM modification is complex and expensive, and process optimization is relatively convenient.21–24 Changes in voltage, flow rate, and solution concentration can alter the thickness and concentration of the boundary layer near the membrane, leading to variations in ion removal rates and selectivity.25 Electrochemical impedance spectroscopy (EIS) provides critical insights into the electrochemical properties of the membrane system26 and serves as a powerful tool for examining membrane surface characteristics and ion transport mechanisms. In developing composite IEMs with functional layers, Zhang et al.27 utilized EIS technology to analyse the characteristics of various assembly layers in NaCl and Na2SO4 mixed solutions, enhancing the ion separation efficiency. Zhao et al.28 also studied the fouling of anion exchange membranes (AEMs) by sodium dodecyl sulfate and the impact of membrane cleaning on the fouled AEM performance using EIS. EIS allows for the assessment of membrane resistance under different conditions, as well as ion transfer resistance at the interface (including the diffusion boundary and electrical double layers), thereby deepening our understanding of ion migration mechanisms through the membrane.28
This study explored the selective removal of Ca2+ using ED at different operating voltages, flow rates, and initial concentrations. Combined with EIS, the effects of membrane resistance and interfacial layer resistance on ion migration were analysed. Finally, based on the ion migration mechanism obtained in this study, a guided ED integrated device was designed, and a pilot-scale treatment was conducted to evaluate the feasibility of ED desalination of underground brackish water in northwest China. This study offers critical insights into the application of ED for brackish water desalination and selective Ca2+ removal to enhance drinking water safety.
2 Materials and methods
2.1 Reagents and IEMs
Ultrapure water was sourced from the Milli-Q purification system (resistivity 18.2 MΩ cm) and utilised to prepare experimental solutions (i.e., dilute, concentrated, and electrode solutions). The reagents used in the experiments included CaCl2 (99%), NaCl (99%), anhydrous Na2SO4 (99%), HCl (36.5–38%), and NaOH (99%). All reagents were acquired from Shanghai McLean Biochemical Technology Co., Ltd. (Shanghai, China). The AEMs and cation exchange membranes (CEMs) were sourced from ASTOM Corporation (Tokyo, Japan) and comprised standard commercial membranes without significant selectivity for monovalent and divalent ions. The key performance characteristics of the IEMs are summarised in Table 1.
Table 1 Main performance characteristics of the membranes used in the experiment
| Membranes |
CEM |
AEM |
| CMX |
AM-1 |
| Type |
Strongly acidic cation permeable |
Strongly basic anion permeable |
| Characteristics |
High mechanical, strength (Na+ form) |
Low electric resistance (Cl− form) |
| Exchange capacity (meq g−1) |
2.08 |
1.4–1.7 |
| Electrical area resistance (Ω cm2) |
1.8–3.8 |
1.2–2.0 |
| Burst strength (MPa) |
≥0.40 |
≥0.20 |
| Thickness (mm) |
0.14–0.20 |
0.11–0.16 |
2.2 ED device and experiment
The ED device used in this study is illustrated in Fig. 1a, featuring two graphite electrodes. The membrane stack consisted of 10 membrane pairs, totalling an effective area of 0.0286 m2. Each membrane was spaced apart by a 0.5 mm thick spacer, with rubber gaskets on either side of the electrode plates of the membrane stack to prevent leakage. Three pumps, along with their respective flowmeters, were connected to the concentrate, dilute, and electrode compartments to ensure a constant flow rate through the membrane stack. During the experiments, a variable DC power supply (MP3020D; Maisheng, China) was used to maintain a steady voltage. At the start of each experiment, the initial volume of the concentrated compartment was 2 L, with a volume ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the concentrated, dilute, and electrode compartments, respectively, whereas the electrode compartment contained a 0.1 M Na2SO4 solution.
1 for the concentrated, dilute, and electrode compartments, respectively, whereas the electrode compartment contained a 0.1 M Na2SO4 solution.
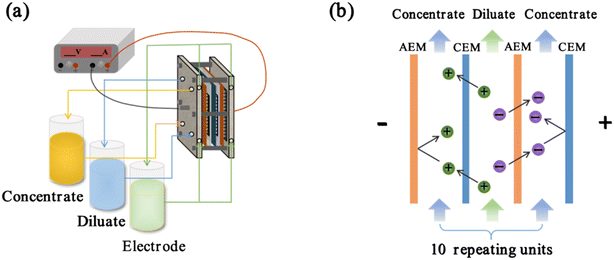 |
| | Fig. 1 (a) Experimental setup of ED and (b) ED schematic. | |
At the beginning of each experimental group, the ED device was operated at a flow rate of 36 L h−1 (unless otherwise noted) for 4 h, followed by a static period without circulation lasting over 10 h. If the solution concentration in each compartment remains stable, the error from selective adsorption at low concentrations is eliminated.25Fig. 1b illustrates the schematic of the ED stack. Initially, the solutions in the dilute and concentrated compartments were identical, each containing 2 L of a mixed NaCl and CaCl2 solution in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Details of the operating conditions, including the voltage, influent flow, and initial concentrations, are listed in Table 2. After each experiment, the membrane was cleaned with 3% NaOH, deionised water, and 3% HCl solution.29
1 ratio. Details of the operating conditions, including the voltage, influent flow, and initial concentrations, are listed in Table 2. After each experiment, the membrane was cleaned with 3% NaOH, deionised water, and 3% HCl solution.29
Table 2 Operational parameters and solution concentrations for ED experiments
| Operating conditions |
S1 |
S2 |
S3 |
S4 |
S5 |
| Operating voltage (V) |
2 |
4 |
6 |
8 |
10 |
| Influent flow (L h−1) |
12 |
24 |
36 |
48 |
60 |
| Initial concentration (mmol L−1) |
3.3 |
6.6 |
13.2 |
26.3 |
39.5 |
2.3 EIS device and experiment
In this study, EIS of the CEM was conducted using a Gamry electrochemical workstation (Interface 1010E, PA, USA) with a four-electrode configuration. Fig. 2a illustrates a schematic of the EIS setup, where the sample cell is made from polymethyl methacrylate and divided by a central partition into two distinct compartments. A pair of platinum foil electrodes served as the working and counter electrodes, and were positioned at opposite ends of the sample cell. A pair of Ag/AgCl electrodes (housed in fine glass tubes containing a saturated KCl solution) functioned as the sensing and reference electrodes located on either side of the CEM.
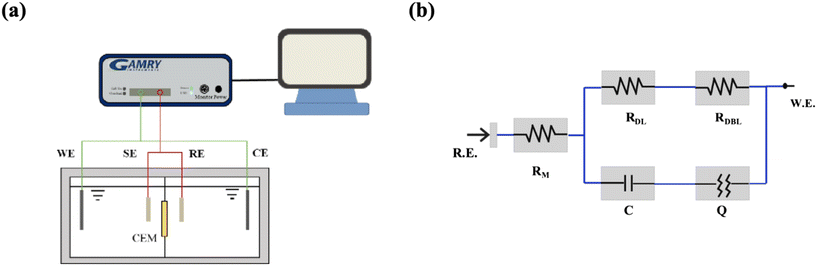 |
| | Fig. 2 (a) Schematic of the EIS device and (b) EIS fitting equivalent circuit. | |
Impedance was measured by applying a small alternating current of known frequency (f) and amplitude (E0 or I0) to the system, and measuring the output amplitude (E(t) or I(t)) and phase shift (φ) between the voltage and current. The impedance is typically represented by a phasor, and its magnitude and phase are given by the following equations:30
| | 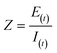 | (1.1) |
Voltage and current are represented by time (t) and angular frequency (ω = 2πf), as follows:
| | E(t) = E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) = E0ejω sin(ωt) = E0ejω | (1.3) |
| | I(t) = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt + φ) = I0ej(ωt+φ) sin(ωt + φ) = I0ej(ωt+φ) | (1.4) |
where
j is an imaginary number,
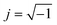
, calculated according to the Euler equation:
| | 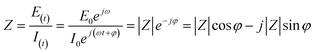 | (1.6) |
where
Z is the impedance modulus, and
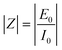
. In general,
Z′ is defined as the real part of the impedance and
Z′′ is the imaginary part of the impedance, calculated using the following equations:
| | Z′ = |Z|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ φ | (1.7) |
| | Z′ = |Z|sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ φ | (1.8) |
Prior to commencing the experiment, the IEM under test was cut into a circular shape with an effective area of 2.835 cm
2. After soaking the IEM in the test solution for 24 h for activation, the solution was placed in a separator. The prepared test solution was poured into the two compartments of a sample box (fully immersed in the IEM). The circuits were connected and the power supply was switched on. After setting the parameters such as the frequency and voltage at the computer end, the test commenced. The experimental data were fitted with the aid of an equivalent circuit diagram (
Fig. 2b) using Gamry Echem Analyst data analysis software. In this study, the frequency range of the EIS experiment is 0.01 Hz to 1000 Hz. Based on previous experiments, it was discovered that when the concentration of the electrolyte solution was too low, the accuracy of the impedance measured by EIS was affected.
31,32 Therefore, the solution concentration in the experiment needed to be appropriately adjusted.
Table 3 presents the experimental design for the EIS tests, including the operating conditions and solution concentrations.
Table 3 Operational parameters and solution concentrations for EIS experiments
| Operating conditions |
S1 |
S2 |
S3 |
S4 |
S5 |
| Voltage (mV) |
50 |
100 |
200 |
300 |
500 |
| Flow rates (r min−1) |
200 |
400 |
600 |
800 |
1000 |
| Solution concentration (mol L−1) |
0.01 |
0.02 |
0.05 |
0.1 |
0.2 |
2.4 Pilot scale ED device
The pilot-scale experiment utilised a guided ED-integrated device with an aluminium alloy shell, as illustrated in Fig. 3a, featuring external dimensions of 427 mm length × 185 mm width × 380 mm height. The power supply was provided by a power adapter (or solar photovoltaic) with a default voltage of 12 V, a current range of 2.5 A to 3 A, and a pump flow rate of 0.5 L min−1. A process flow diagram of the water production is shown in Fig. 3b. Domestic water enters the ED module via the water inlet, effectively removing ions that contribute to scaling, such as Ca2+ and Mg2+. It then undergoes four filtration stages to eliminate minute particles, bacteria, and odours. Finally, it flows into the dilute compartment. The ED equipment operated steadily for two months, with samples taken every 3 days to record the water output, conductivity, and TDS from the dilute chamber. The device can reverse the positive and negative electrodes on both sides of the ED membrane stack, thus keeping the membrane stack clean and ensuring long-term operation. No signs of degradation were observed during the two months of operation of the equipment. In this study, sampling points were randomly selected for water sampling and quality assessment in Gaoling District, Xi'an City, Shaanxi Province, China. The properties of the raw water are summarised in Table 4.
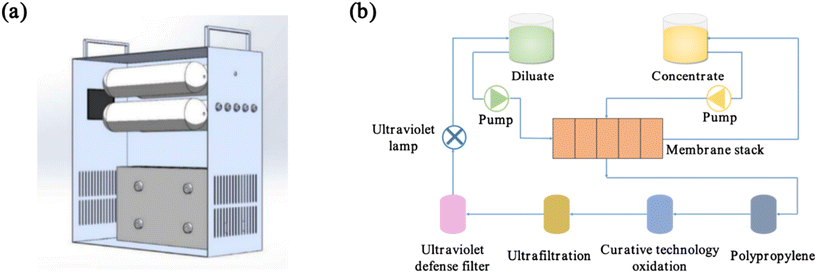 |
| | Fig. 3 (a) Guided ED integrated device and (b) water purification process flowchart. | |
Table 4 Properties of raw water samples in Dongsheng Village
| Analysis index |
Sampling point 1 |
Sampling point 2 |
Sampling point 3 |
| Electrical conductivity (μs cm−1) |
929 |
903 |
915 |
| Total dissolved solids (mg L−1) |
1335 |
867 |
865 |
| Total hardness (mg L−1) |
482 |
504 |
554 |
| Na+ (mg L−1) |
435 |
284 |
270 |
| F− (mg L−1) |
1.15 |
1.34 |
1.36 |
| Cl− (mg L−1) |
274 |
138 |
134 |
| NO3− (mg L−1) |
0.82 |
0.215 |
0.389 |
2.5 Analytical methods and calculations
The electrical conductivity of the solution was measured using a conductivity meter (FE38, METTLER TOLEDO, Shanghai, China) and the ion concentration of the liquid sample was determined using an inductively coupled plasma optical emission spectrometer (ICPE-9820, USA). The injection volume was 10 μL, and the temperature was set at 30 °C. Before injection, the sample was diluted up to a maximum of 500 times. The selective separation coefficient is an important measure for selecting permeability. The method proposed by Bruggen et al.29 was used to characterise the permeability of the membranes to counter ions, which can be calculated as follows:| | 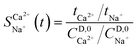 | (1.9) |
where ti represents the migration number of ion i in the membrane and CD,0i represents the initial concentration of ion i in the concentrate chamber, mol L−1. When 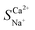 > 1, the target ion (Ca2+) has preferential selective permeability; otherwise, Ca2+ has no preferential selective permeability.
> 1, the target ion (Ca2+) has preferential selective permeability; otherwise, Ca2+ has no preferential selective permeability.
3 Results and discussion
3.1 Effect of voltage on selective removal of Ca2+
In investigating the separation of Ca2+ and Na+, the difference in the charge carried by the ions leads to varying magnitudes of electrostatic forces acting on them.33Fig. 4 illustrates the trends in the ion migration number and selective permeability coefficient as a function of voltage under conditions of a total ion concentration of 13.20 mmol L−1 and an influent flow rate of 36 L h−1. As depicted in Fig. 4a, the migration number and selective permeability coefficient of Ca2+ decrease with increasing voltage. After increasing the voltage from 2 V to 8 V, 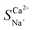 decreased to 0.89, indicating that Ca2+ lost its preferential selective permeability, which hindered the separation of Ca2+ and Na+.
decreased to 0.89, indicating that Ca2+ lost its preferential selective permeability, which hindered the separation of Ca2+ and Na+.
 |
| | Fig. 4 (a) The influence of voltage on 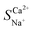 and ion migration number when the initial concentration is 13.20 mmol L−1 and the influent flow rate is 36 L h−1. (b) The influence of voltage on the capacitance and (c) resistance of the NaCl and CaCl2 solution systems when the concentration is 0.1 mol L−1. and ion migration number when the initial concentration is 13.20 mmol L−1 and the influent flow rate is 36 L h−1. (b) The influence of voltage on the capacitance and (c) resistance of the NaCl and CaCl2 solution systems when the concentration is 0.1 mol L−1. | |
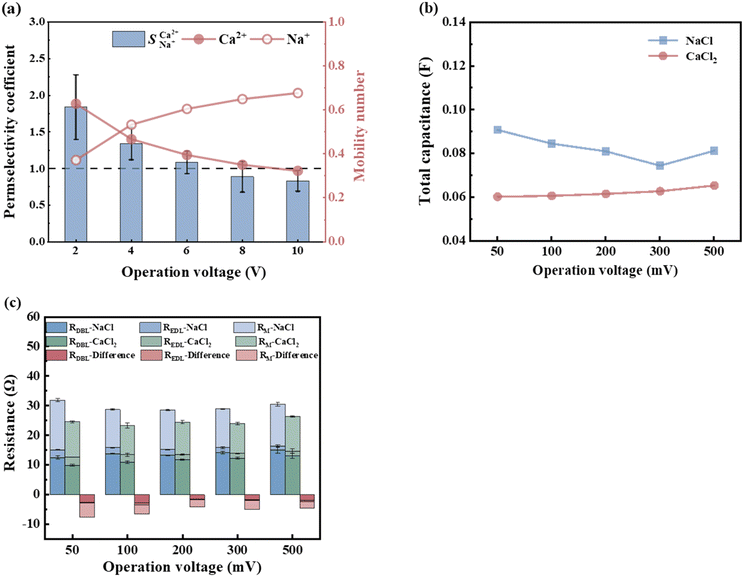
The effect of voltage (50 mV to 500 mV) on the electrochemical characteristics of the membrane and boundary layer during the transmembrane migration of Ca2+ and Na+ at a concentration of 0.1 mol L−1 was investigated through EIS analysis. As shown in Fig. 4b, the overall total capacitance of the NaCl and CaCl2 solution systems remains largely unchanged and fluctuates within 0.001 F. This stability is attributed to the non-uniformity of the interface layer and the constant roughness.34 Resistance reflects the ion mass transfer rate, with differences in resistance between CaCl2 and NaCl solutions indicating relative mass transfer rates. The variations in the pure membrane resistance (RM), electrical double-layer resistance (REDL), and diffusion boundary layer resistance (RDBL) with the solution concentration are presented in Fig. 4c. As the voltage increased to 200 mV, the total resistance of the NaCl solution decreased from 31.88 Ω to 28.61 Ω, accelerating the migration rate of Na+, whereas the total resistance of the CaCl2 solution showed minimal change. Compared to the continuous change in the concentration of the solution, the boundary layer was always in a relatively static environment, and the ions in the boundary layer mainly migrated through diffusion. When the voltage increased, the concentration gradient in the boundary layer increased, and the current transmission in the boundary layer mainly relied on counter ions with a high diffusion rate.35,36 Previous studies have indicated that the boundary layer significantly affects ion transmembrane mass transfer.37 Given the higher self-diffusion coefficient of monovalent ions compared to divalent ions in the boundary layer (Table 5), a higher voltage improves the mass transfer of monovalent ions while diminishing divalent ion migration. Consequently, the migration number and selective permeability of Ca2+ decreased. The total resistance difference between NaCl and CaCl2 solution systems (Table 6) increased with voltage from −7.29 Ω to −4.09 Ω. Therefore, the increase in voltage enhanced Na+ migration while reducing Ca2+ preferential permeability, which hindered selective Ca2+ removal. A lower voltage favours selective Ca2+ removal, with a minimum of 2 V yielding the highest selectivity separation coefficient for Ca2+, reaching 1.84 for 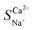 .
.
Table 5 Cation characteristics in aqueous solution at 25 °C (ref. 38)
| Types of cations |
Ionic radius (nm) |
Gibbs hydration energy (kJ mol−1) |
Hydrated ion radius (nm) |
Diffusion coefficient (10−9 m2 s−1) |
| Na+ |
0.098 |
365 |
0.365 (0.276) |
1.33 |
| Ca2+ |
0.100 |
(1306) 1505 |
0.412 |
0.793 |
Table 6 Resistance values at different voltages
| Voltage (mV) |
R
M (Ω) |
R
EDL (Ω) |
R
DBL (Ω) |
R
Total (Ω) |
R
Difference (Ω) |
| NaCl |
CaCl2 |
NaCl |
CaCl2 |
NaCl |
CaCl2 |
NaCl |
CaCl2 |
| 50 |
16.79 |
11.93 |
2.58 |
2.75 |
12.51 |
9.91 |
31.88 |
24.59 |
7.29 |
| 100 |
12.91 |
9.78 |
2.03 |
2.57 |
13.81 |
10.89 |
28.75 |
23.24 |
5.51 |
| 200 |
13.40 |
10.88 |
2.01 |
1.77 |
13.20 |
11.76 |
28.61 |
24.41 |
4.20 |
| 300 |
13.08 |
10.13 |
1.79 |
1.54 |
14.08 |
12.30 |
28.95 |
23.97 |
4.98 |
| 500 |
14.06 |
11.76 |
1.32 |
1.60 |
15.09 |
13.02 |
30.47 |
26.38 |
4.09 |
3.2 Effect of flow rate on selective removal of Ca2+
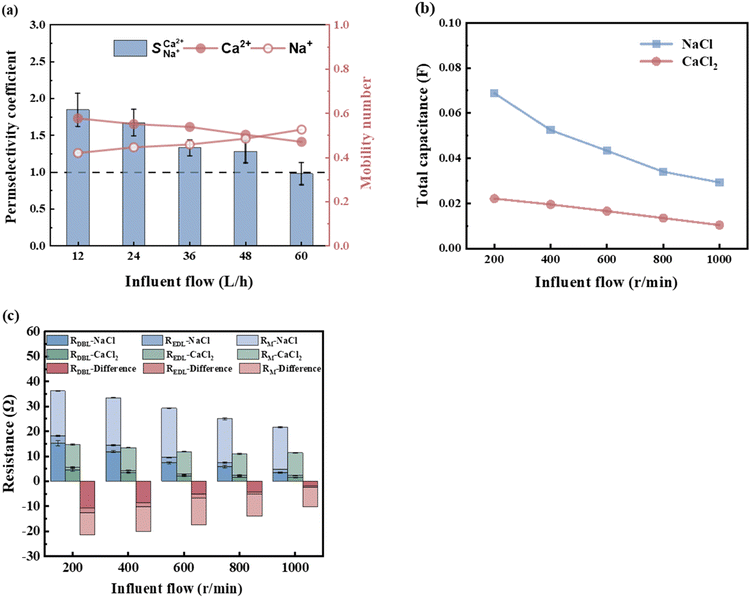
Fig. 5a illustrates the changes in the selective permeability and ion migration number at varying flow rates (from 12 to 60 L h−1). As the flow rate increased, the hydraulic retention time of the concentrated and dilute compartment feed liquids decreased, causing some ions to flow out of the membrane stack without migration, decreasing the number of ion migrations. Therefore, the Ca2+ migration number and the selective permeability coefficient decreased. The selective permeability coefficient decreased from an initial value of 1.85 to 0.99. In this scenario, 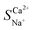 < 1 indicated a lack of preferential permeability.
< 1 indicated a lack of preferential permeability.
 |
| | Fig. 5 (a) The influence of influent flow rate on 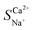 and ion migration number when the initial concentration is 13.20 mmol L−1 and the voltage is 6 V. (b) The influence of influent flow rate on the capacitance and (c) resistance of the NaCl and CaCl2 solution systems when the concentration is 0.1 mol L−1 and voltage is 200 mV. and ion migration number when the initial concentration is 13.20 mmol L−1 and the voltage is 6 V. (b) The influence of influent flow rate on the capacitance and (c) resistance of the NaCl and CaCl2 solution systems when the concentration is 0.1 mol L−1 and voltage is 200 mV. | |
After a current is applied to the membrane stack, counterions with opposing charges migrate through the membrane because of the Donnan exclusion effect. The disparity in the ion transport numbers between the solution and membrane phases results in the formation of a diffusion boundary layer on the membrane surface, which is influenced by the hydraulic characteristics of the solution. EIS was used to further investigate the correlation between the electrochemical properties of the membrane, boundary layer, and influent flow rate. As shown in Fig. 5b, increasing the influent flow rate effectively decreases the total capacitance of the NaCl and CaCl2 solution systems, with the NaCl solution being more significantly affected than the CaCl2 solution. Water molecules form a hydration layer around ions under the influence of electrostatic forces. Ion transport across the membrane entails a balance between the “ion-hydration layer” and “ion-membrane” interactions.38 Na+ has a smaller hydration radius and lower hydration energy compared to Ca2+, making it more susceptible during transmembrane mass transfer.39
As shown in Fig. 5c, the total resistance of the NaCl and CaCl2 solution systems decreases as the flow rate increases. The analysis of the resistance changes at each interface layer revealed that the RM and REDL remained largely unaffected by the flow rate. The double electric layer thickness is at the nanometre scale and is not influenced by turbulence, whereas the diffusion boundary layer typically spans several tens to hundreds of micrometres. An increase in the flow rate enhanced the shear forces between the fluids, compressing and reducing the boundary layer thickness, leading to a notable decrease in the RDBL. The RDBL for the NaCl and CaCl2 solution systems decreased by 77.40% and 66.67%, respectively, as the flow rate increased from 200 to 600 rpm (Table 7). The total resistance difference between the NaCl and CaCl2 solution systems was inversely proportional to the flow rate, reaching a maximum difference of −10.29 Ω. Therefore, a low flow rate favours the improved preferential permeability of Ca2+, with a flow rate of 12 L h−1 yielding a 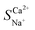 value of 1.85, demonstrating the best selective removal effect for Ca2+.
value of 1.85, demonstrating the best selective removal effect for Ca2+.
Table 7 Resistance values at different flow rates
| Flow rate (r min−1) |
R
M (Ω) |
R
EDL (Ω) |
R
DBL (Ω) |
R
Total (Ω) |
R
Difference (Ω) |
| NaCl |
CaCl2 |
NaCl |
CaCl2 |
NaCl |
CaCl2 |
NaCl |
CaCl2 |
| 200 |
18.00 |
9.10 |
3.00 |
1.00 |
15.13 |
4.50 |
36.13 |
14.60 |
21.53 |
| 400 |
19.00 |
9.18 |
2.60 |
0.85 |
11.78 |
3.30 |
33.38 |
13.33 |
20.05 |
| 600 |
19.78 |
8.95 |
2.10 |
0.74 |
7.34 |
2.10 |
29.22 |
11.79 |
17.43 |
| 800 |
17.50 |
8.49 |
1.60 |
0.77 |
5.80 |
1.60 |
24.9 |
10.86 |
14.04 |
| 1000 |
16.80 |
9.02 |
1.35 |
0.76 |
3.42 |
1.50 |
21.57 |
11.28 |
10.29 |
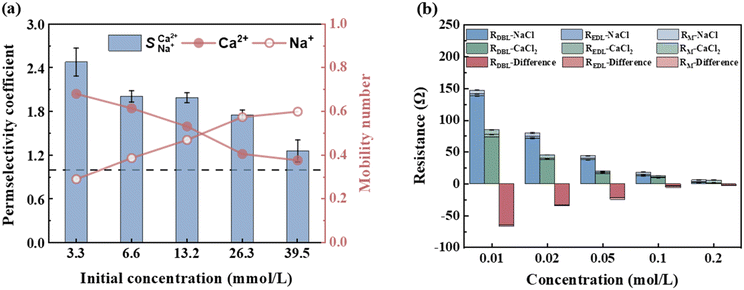
3.3 Effect of initial concentration on selective removal of Ca2+
The variations in the ion migration number and selective permeation coefficient with the initial concentration at a voltage of 6 V and an influent flow rate of 36 L h−1 are illustrated in Fig. 6. The migration number of Ca2+ decreased as the initial concentration increased, whereas that of Na+ showed the opposite trend. At an ion concentration of 39.50 mmol L−1, 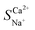 decreased to 1.25 (Fig. 6a). Changes in ion concentration result in alterations in the resistance and thickness of the aqueous phase, membrane phase, and related interface layers, leading to variations in the ion migration number and selective permeation coefficient.30,40 Thus, it is viable to integrate EIS technology to analyse the electrochemical systems of the membrane and boundary layer at varying concentrations. The voltage was set at 200 mV, and different NaCl and CaCl2 solution concentrations (0.01 mol L−1, 0.02 mol L−1, 0.05 mol L−1, 0.10 mol L−1, and 0.20 mol L−1) were selected for the EIS static study.
decreased to 1.25 (Fig. 6a). Changes in ion concentration result in alterations in the resistance and thickness of the aqueous phase, membrane phase, and related interface layers, leading to variations in the ion migration number and selective permeation coefficient.30,40 Thus, it is viable to integrate EIS technology to analyse the electrochemical systems of the membrane and boundary layer at varying concentrations. The voltage was set at 200 mV, and different NaCl and CaCl2 solution concentrations (0.01 mol L−1, 0.02 mol L−1, 0.05 mol L−1, 0.10 mol L−1, and 0.20 mol L−1) were selected for the EIS static study.
 |
| | Fig. 6 (a) The influence of initial concentration on 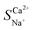 and ion migration number when the voltage is 6 V and the influent flow rate is 36 L h−1. (b) The effect of concentration on the resistance of the NaCl and CaCl2 solution systems at a voltage of 200 mV. and ion migration number when the voltage is 6 V and the influent flow rate is 36 L h−1. (b) The effect of concentration on the resistance of the NaCl and CaCl2 solution systems at a voltage of 200 mV. | |
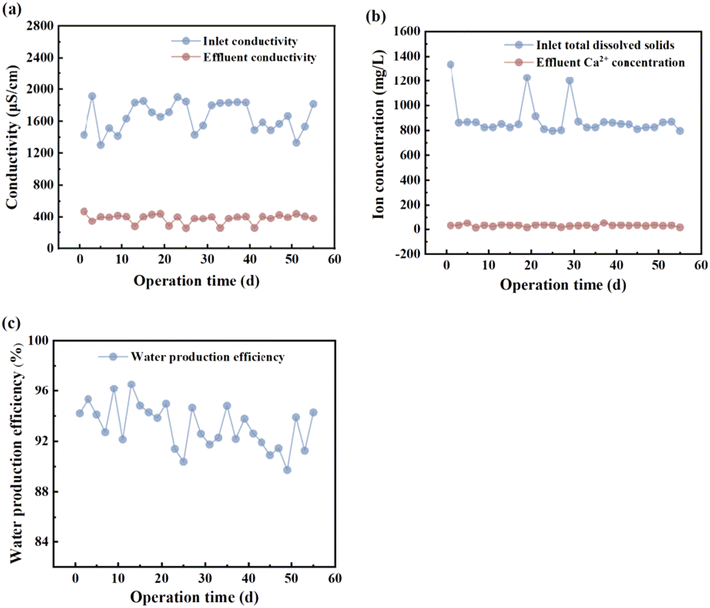
The total resistance is inversely related to the solution concentration. As the concentration increases, the number of conductive ions in the interior and exterior of the membrane increases, thereby lowering the total resistance. Additionally, when the solution concentration was below 0.1 mol L−1, the RDBL of the NaCl and CaCl2 solution systems accounted for >80% of the total resistance, aligning with the trend of the total resistance (Table 8). Thus, in low-concentration solutions (particularly in drinking water), RDBL predominantly influences the total membrane resistance. Consequently, changes in the concentration primarily affect the RDBL, thereby affecting the total resistance. When the solution concentration exceeds 0.1 mol L−1, the total membrane resistance stabilised with RM exceeding 50%, indicating that RM was predominantly affected in high-concentration scenarios. An increased ion concentration resulted in a reduction in the Donnan potential and an increase in the number of ions adsorbed on the IEM, which decreased the RM and compressed the boundary layer thickness, thus lowering the RDBL. The difference in resistance between the CaCl2 and NaCl solution systems increased with increasing concentration (Fig. 6b). As the solution concentration increased from 0.01 to 0.2 mol L−1, the difference shifted from −62.60 to −0.35 Ω, highlighting a significant decrease in the selective permeability of Ca2+, which hampered its selective removal, corroborating findings from ED research. Therefore, the lowest initial concentration yields the most effective selective removal of Ca2+, achieving a maximum value of 2.48 for 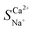 .
.
Table 8 Resistance values at different concentrations
| Concentration (mol L−1) |
R
M (Ω) |
R
EDL (Ω) |
R
DBL (Ω) |
R
Total (Ω) |
R
Difference (Ω) |
| NaCl |
CaCl2 |
NaCl |
CaCl2 |
NaCl |
CaCl2 |
NaCl |
CaCl2 |
| 0.01 |
6.00 |
7.34 |
3.30 |
3.76 |
138.00 |
73.60 |
147.30 |
84.70 |
62.60 |
| 0.02 |
5.10 |
5.19 |
3.00 |
2.12 |
71.50 |
38.21 |
79.60 |
45.52 |
34.08 |
| 0.05 |
4.00 |
1.40 |
2.20 |
1.87 |
38.00 |
16.65 |
44.20 |
19.92 |
24.28 |
| 0.10 |
3.80 |
1.72 |
1.80 |
1.28 |
13.00 |
9.85 |
18.60 |
12.85 |
5.75 |
| 0.20 |
3.05 |
4.00 |
0.67 |
0.74 |
2.60 |
1.23 |
6.32 |
5.97 |
0.35 |
3.4 Pilot-scale treatment to remove Ca2+
To assess the operation and effluent water quality of the guided ED integrated equipment for practical use, the system was operated stably for over two months, and the conductivity, ED water production rate, and Ca2+ ion removal efficiency were measured. Fig. 7a illustrates the variation in the conductivity of raw water before and after treatment with the guided ED-integrated equipment. The conductivity of untreated raw water was notably high, ranging from 1500 μS cm−1 to 2000 μS cm−1, whereas that of the treated effluent water fell between 200 μS cm−1 and 500 μS cm−1. The water quality processed by the guided ED integrated equipment effectively removed over 50% of soluble substances, addressing excessive Ca2+ ion levels in underground brackish water and improving drinking water quality in villages and towns. Fig. 7b shows the TDS of the raw water and the concentration of Ca2+ ions in the produced water post-ED treatment. The long-term operating results indicated that the TDS of the raw water remained at approximately 800 mg L−1, exceeding the total hardness limit of 450 mg L−1 (as CaCO3) set by China's “Hygienic Standards for Drinking Water” (GB 5749-2022), thus failing to meet the specification requirements. Following treatment with the guided ED integrated equipment, the Ca2+ concentration in the produced water remained below 20 mg L−1 and remained stable. As shown in Fig. 7c, the effluent water from the guided ED integrated equipment is stable and complies with drinking water quality standards. The daily water production efficiency of the ED equipment exceeded 90%, facilitating long-term and effective operation.
 |
| | Fig. 7 Long-term operating effects of ED, (a) variations in conductivity of inlet and outlet water, (b) concentration of hardness ions (Ca2+), and (c) changes in water production efficiency. | |
To evaluate the economy of removing high hardness ions of the ED water purification equipment, the cost of removing hardness ions was estimated using the working voltage and current of the ED equipment (calculated at 0.1 $ per kW h). During two months of continuous operation, the ED water treatment cost is approximately 1.2 $ per m3. In a pilot-scale experiment, ED operation does not require phase transitions, chemical reactions, or any chemical substances. This generates desalinated and concentrated water. Consequently, it effectively safeguards a healthy environment from pollution. The concentrated water produced during the ED process typically contains high salt concentrations, which necessitates further treatment. This concentrated water can undergo advanced treatment techniques, such as evaporation crystallisation and membrane concentration, to facilitate resource utilisation or the safe disposal of salt.
4 Conclusion
(1) The simulation experiments utilised commercially available membranes, revealing that a low voltage, flow rate, and initial concentration enhanced the selective removal of Ca2+. At an initial concentration of 3.3 mmol L−1, a voltage of 6 V, and an influent flow rate of 36 L h−1, the selective removal of Ca2+ was maximised, achieving the highest 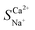 value of 2.48.
value of 2.48.
(2) The results of the EIS study showed that in low-concentration solutions (notably within drinking water limits), RDBL constituted the majority of the total resistance and significantly influenced the Ca2+ migration rates. An increase in the initial concentration and flow rate reduced the total resistance. However, the difference in the resistance between the CaCl2 and NaCl solutions diminished, hindering the selective removal of Ca2+.
(3) Experimental analysis of the pilot ED demonstrated stable operation with a water yield exceeding 90%, compliance with drinking water safety standards, and effective addressing of excessive Ca2+ ion issues in brackish water.
(4) Although ED brackish water desalination technology is relatively mature, further investigation is required. Future research can be conducted from the following aspects: an in-depth exploration of the mass transfer mechanism of ionic membranes, further improving the desalination performance of ionic membranes, reducing the cost of membrane production, and combining ED technology with clean energy power supply technologies, such as solar and wind power, to improve the sustainability of ED technology.
Data availability
Data will be made available on request.
Author contributions
Li Chen: conceptualization, methodology, writing – original draft preparation; Ling Feng: conceptualization, writing – review and editing, supervision; Renliang Zhang: formal analysis and investigation, writing – original draft preparation; Pengyu Liu: funding acquisition, resources; Binghui Tian: supervision, resources, funding acquisition, writing – review and editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research was supported by the Program of China–Sri Lanka Joint Center for Education and Research by the Chinese Academy of Sciences. This study was financially supported by the National Key R&D Program (2022YFC3203005-3).
References
- J. R. Du, X. Zhang, X. S. Feng, Y. Wu, F. Cheng and M. E. A. Ali, Desalination of high salinity brackish water by an NF-RO hybrid system, Desalination, 2020, 491, 114445, DOI:10.1016/j.desal.2020.114445.
- C. C. Liu, J. Wang, P. F. Huang, C. Hu, F. Gao, Y. Liu, Z. Y. Li and B. J. Cui, Response of Soil Microenvironment and Crop Growth to Cyclic Irrigation Using Reclaimed Water and Brackish Water, Plants, 2023, 12(12), 2285, DOI:10.3390/plants12122285.
- Y. Y. Wang, Y. Xiao, J. Puig-Bargués, B. Zhou, Z. Y. Liu, T. Muhammad, H. B. Liang, M. Maitusong, Z. H. Wang and Y. K. Li, Assessment of water quality ions in brackish water on drip irrigation system performance applied in saline areas, Agric. Water Manag., 2023, 289, 108544, DOI:10.1016/j.agwat.2023.108544.
- J. Kim, A. Jain, K. C. Zuo, R. Verduzco, S. Walker, M. Elimelech, Z. H. Zhang, X. H. Zhang and Q. L. Li, Removal of calcium ions from water by selective electrosorption using target-ion specific nanocomposite electrode, Water Res., 2019, 160, 445–453, DOI:10.1016/j.watres.2019.05.016.
- Y. Liu, X. Zhang, M. Chi, H. Matsuyama, Y. Guo, K. Simoens, A. Volodine, R. Dewil, J. Zheng, Z. Dai and B. van der Bruggen, Advancing drinking water safety: Facile fabrication of nanofiltration membrane for enhanced antibiotics removal and efficient water softening, Desalination, 2024, 591, 118024, DOI:10.1016/j.desal.2024.118024.
- R. Devesa and A. M. Dietrich, Guidance for optimizing drinking water taste by adjusting mineralization as measured by total dissolved solids (TDS), Desalination, 2018, 439, 147–154, DOI:10.1016/j.desal.2018.04.017.
- M. Sedighi, M. M. B. Usefi, A. F. Ismail and M. Ghasemi, Environmental sustainability and ions removal through electrodialysis desalination: Operating conditions and process parameters, Desalination, 2023, 549, 116319, DOI:10.1016/j.desal.2022.116319.
- Y. L. Liu and M. Sun, Ion exchange removal and resin regeneration to treat per- and polyfluoroalkyl ether acids and other emerging PFAS in drinking water, Water Res., 2021, 207, 117781, DOI:10.1016/j.watres.2021.117781.
- K. Sara, D. M. Tainah, K. Alessandro, M. Sebastiano, B. Antonio, L. N. Maria, Z. Massimo, B. Letizia, B. Nicoals, I. Artem, C. Matteo, V. T. Alexandr, P. Vincenzo and M. Manuela, Defective graphene nanosheets for drinking water purification: Adsorption mechanism, performance, and recovery, FlatChem, 2021, 29, 100283, DOI:10.1016/j.flatc.2021.100283.
- Y. T. Shi, X. D. Meng, L. Yao and M. Tian, A full-scale study of nanofiltration: Separation and recovery of NaCl and Na2SO4 from coal chemical industry wastewater, Desalination, 2021, 517, 115239, DOI:10.1016/j.desal.2021.115239.
- A. Lhassani, H. Dach and Y. A. Boussouga, Brackish water desalination using nanofiltration membranes in Morocco, Desalin. Water Treat., 2017, 83, 288–293, DOI:10.5004/dwt.2017.21221.
- N. G. Doménech, F. Purcell-Milton and Y. K. Gun'ko, Recent progress and future prospects in development of advanced materials for nanofiltration, Mater. Today Commun., 2020, 23, 100888, DOI:10.1016/j.mtcomm.2019.100888.
- Y. Xu, Q.-B. Chen, J. Wang, P.-F. Li and J. Zhao, Fractionation of monovalent ions from seawater brine via softening nanofiltration and selective electrodialysis: Which is better?, Desalination, 2022, 533, 115717, DOI:10.1016/j.desal.2022.115717.
- M. Qasim, M. Badrelzaman, N. N. Darwish, N. A. Darwish and N. Hilal, Reverse osmosis desalination: A state-of-the-art review, Desalination, 2019, 459, 59–104, DOI:10.1016/j.desal.2019.02.008.
- F. Wang, Y. Wang and C. Jing, Application Overview of Membrane Separation Technology in Coal Mine Water Resources Treatment in Western China, Mine Water Environ., 2021, 40(2), 1–10, DOI:10.1007/s10230-021-00781-3.
- S. Mehdi, B. U. M. Mahdi, I. A. Fauzi and G. Mostafa, Environmental sustainability and ions removal through electrodialysis desalination: Operating conditions and process parameters, Desalination, 2023, 549, 116319, DOI:10.1016/j.desal.2022.116319.
- Y. Xu, Q. Chen, Y. Gao, J. Wang, H. Fan and F. Zhao, Performance comparison of lithium fractionation from magnesium via continuous selective nanofiltration/electrodialysis, Chin. J. Chem. Eng., 2023, 59(7), 42–50, DOI:10.1016/j.cjche.2022.11.013.
- B. Bachiri, H. Ayyoub, M. Tahaikt, M. Hafsi, A. Elmidaoui and M. Taky, Electrodialysis Technology for Water Softening Regarding Water Equilibrium, Arabian J. Sci. Eng., 2024, 49(6), 8021–8030, DOI:10.1007/s13369-023-08624-9.
- H. Wei, L. H. Anne-Claire, A. Susan, B. Tonio, M. P. Ian and G. W. V. Amos, Flexible batch electrodialysis for low-cost solar-powered brackish water desalination, Nat. Water, 2024, 2, 370–379, DOI:10.1038/S44221-024-00213-W.
- H. T. Zhu, B. Yang, C. J. Gao and Y. Q. Wu, Ion transfer modeling based on Nernst-Planck theory for saline water desalination during electrodialysis process, Asia-Pac. J. Chem. Eng., 2020, 15(2), e2410, DOI:10.1002/apj.2410.
- V. Vatanpour, O. Karatas, S. Amiri, H. R. Rajabi, I. Koyuncu and A. Khataee, Different metal-doped ZnS quantum dots photocatalysts for enhancing the permeability and antifouling performances of polysulfone membranes with and without UV irradiation, Chemosphere, 2022, 294, 133705, DOI:10.1016/j.chemosphere.2022.133705.
- K. Hooshyari, S. Heydari, H. Beydaghi and H. R. Rajabi, New nanocomposite membranes based on sulfonated poly (phthalazinone ether ketone) and Fe3O4@SiO2@ resorcinol–aldehyde–SO3H for PEMFCs, Renewable Energy, 2022, 186, 115–125, DOI:10.1016/j.renene.2021.12.074.
- M. R. Ganjali, M. A. Al-Naqshabandi, B. Larijani, A. Badiei, V. Vatanpour, H. R. Rajabi, H. Rezania, S. Paziresh, G. Mahmodi, S. J. Kim and M. R. Saeb, Improvement of dye and protein filtration efficiency using modified PES membrane with 2-mercaptoethanol capped zinc sulfide quantum dots, Chem. Eng. Res. Des., 2021, 168, 109–121, DOI:10.1016/j.cherd.2020.12.026.
- H. Khadijeh, R. Hamidreza, V. Vahid, R. Mohadese and R. H. Reza, New blend nanocomposite membranes based on PBI/sulfonated poly(ether keto imide sulfone) and functionalized quantum dot with improved fuel cell performance at high temperatures, Int. J. Energy Res., 2021, 45(15), 21274–21292, DOI:10.1002/er.7178.
- T. Luo, S. Abdu and M. Wessling, Selectivity of ion exchange membranes: A review, J. Membr. Sci., 2018, 555, 429–454, DOI:10.1016/j.memsci.2018.03.051.
- D. D. Macdonald, Reflections on the history of electrochemical impedance spectroscopy, Electrochim. Acta, 2006, 51, 1376–1388, DOI:10.1016/j.electacta.2005.02.107.
- Y. Zhang, R. Liu, Q. Lang, M. Tan and Y. Zhang, Composite anion exchange membrane made by layer-by-layer method for selective ion separation and water migration control, Sep. Purif. Technol., 2018, 192, 278–286, DOI:10.1016/j.seppur.2017.10.022.
- Z. Zhao, S. Shi, H. Cao and Y. Li, Electrochemical impedance spectroscopy and surface properties characterization of anion exchange membrane fouled by sodium dodecyl sulfate, J. Membr. Sci., 2017, 530, 220–231, DOI:10.1016/j.memsci.2017.02.037.
- B. V. D. Bruggen, A. Koninckx and C. Vandecasteele, Separation of monovalent and divalent ions from aqueous solution by electrodialysis and nanofiltration, Water Res., 2004, 38(5), 1347–1353, DOI:10.1016/j.watres.2003.11.008.
- W. J. Zhang, J. Ma, P. P. Wang, Z. H. Wang, F. M. Shi and H. L. Liu, Investigations on the interfacial capacitance and the diffusion boundary layer thickness of ion exchange membrane using electrochemical impedance spectroscopy, J. Membr. Sci., 2016, 502, 37–47, DOI:10.1016/j.memsci.2015.12.007.
- P. Dlugolecki, P. Ogonowski, S. J. Metz, M. Saakes, K. Nijmeijer and M. Wessling, On the resistances of membrane, diffusion boundary layer and double layer in ion exchange membrane transport, J. Membr. Sci., 2010, 349(1–2), 369–379, DOI:10.1016/j.memsci.2009.11.069.
- F. Roghmans, M. C. Marti-Calatayud, S. Abdu, R. Femmer, R. Tiwari, A. Walther and M. Wessling, Electrochemical impedance spectroscopy fingerprints the ion selectivity of microgel functionalized ion-exchange membranes, Electrochem. Commun., 2016, 72, 113–117, DOI:10.1016/j.elecom.2016.09.009.
- T. Mubita, S. Porada, P. Biesheuvel, A. Van Der Wal and J. Dykstra, Strategies to increase ion selectivity in electrodialysis, Sep. Purif. Technol., 2022, 292, 120944, DOI:10.1016/j.seppur.2022.120944.
- W. J. Zhang, P. P. Wang, J. Ma, Z. H. Wang and H. L. Liu, Investigations on electrochemical properties of membrane systems in ion-exchange membrane transport processes by electrochemical impedance spectroscopy and direct current measurements, Electrochim. Acta, 2016, 216, 110–119, DOI:10.1016/j.electacta.2016.09.018.
- T. Dong, J. Yao, Y. Wang, T. Luo and L. Han, On the permselectivity of di- and mono-valent cations: Influence of applied current density and ionic species concentration, Desalination, 2020, 488, 114521, DOI:10.1016/j.desal.2020.114521.
- V. V. Nikonenko, N. D. Pismenskaya, E. I. Belova, P. Sistat, P. Huguet, G. Pourcelly and C. Larchet, Intensive current transfer in membrane systems: Modelling, mechanisms and application in electrodialysis, Adv. Colloid Interface Sci., 2010, 160, 101–123, DOI:10.1016/j.cis.2010.08.001.
- Y. Kim, W. S. Walker and D. F. Lawler, Competitive separation of di- vs. mono-valent cations in electrodialysis: Effects of the boundary layer properties, Water Res., 2012, 46(7), 2042–2056, DOI:10.1016/j.watres.2012.01.004.
- G. M. Geise, D. R. Paul and B. D. Freeman, Fundamental water and salt transport properties of polymeric materials, Prog. Polym. Sci., 2014, 39(1), 1–42, DOI:10.1016/j.progpolymsci.2013.07.001.
- X. Y. Nie, S. Y. Sun, Z. Sun, X. Song and J. Y. Yu, Ion-fractionation of lithium ions from magnesium ions by electrodialysis using monovalent selective ion-exchange membranes, Desalination, 2017, 403, 128–135, DOI:10.1016/j.desal.2016.05.010.
- B. Sun, M. X. Zhang, S. F. Huang, Z. Cao, L. Lu and X. S. Zhang, Study on mass transfer performance and membrane resistance in concentration of high salinity solutions by electrodialysis, Sep. Purif. Technol., 2022, 281, 119907, DOI:10.1016/j.seppur.2021.119907.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ac,
Renliang
Zhang
ab,
Pengyu
Liu
b and
Binghui
Tian
*ac
*ac,
Renliang
Zhang
ab,
Pengyu
Liu
b and
Binghui
Tian
*ac
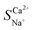 reached 2.48 at an initial concentration of 3.3 mmol L−1, with a voltage of 6 V and an influent flow rate of 36 L h−1. In addition, a 2 month pilot study was conducted using brackish groundwater from northwestern China. This indicates a stable effluent and high efficiency of Ca2+ removal during brackish water treatment via the ED process. The Ca2+ concentration in the effluent remained below 20 mg L−1 with a daily water production efficiency of 90%. This study offers valuable insights into ED technology applicable to the desalination and hardness reduction of brackish water.
reached 2.48 at an initial concentration of 3.3 mmol L−1, with a voltage of 6 V and an influent flow rate of 36 L h−1. In addition, a 2 month pilot study was conducted using brackish groundwater from northwestern China. This indicates a stable effluent and high efficiency of Ca2+ removal during brackish water treatment via the ED process. The Ca2+ concentration in the effluent remained below 20 mg L−1 with a daily water production efficiency of 90%. This study offers valuable insights into ED technology applicable to the desalination and hardness reduction of brackish water.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the concentrated, dilute, and electrode compartments, respectively, whereas the electrode compartment contained a 0.1 M Na2SO4 solution.
1 for the concentrated, dilute, and electrode compartments, respectively, whereas the electrode compartment contained a 0.1 M Na2SO4 solution.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Details of the operating conditions, including the voltage, influent flow, and initial concentrations, are listed in Table 2. After each experiment, the membrane was cleaned with 3% NaOH, deionised water, and 3% HCl solution.29
1 ratio. Details of the operating conditions, including the voltage, influent flow, and initial concentrations, are listed in Table 2. After each experiment, the membrane was cleaned with 3% NaOH, deionised water, and 3% HCl solution.29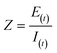
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) = E0ejω
sin(ωt) = E0ejω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt + φ) = I0ej(ωt+φ)
sin(ωt + φ) = I0ej(ωt+φ)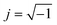 , calculated according to the Euler equation:
, calculated according to the Euler equation:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ + j
φ + j![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ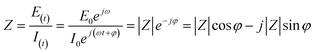
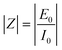 . In general, Z′ is defined as the real part of the impedance and Z′′ is the imaginary part of the impedance, calculated using the following equations:
. In general, Z′ is defined as the real part of the impedance and Z′′ is the imaginary part of the impedance, calculated using the following equations:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ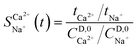
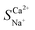 > 1, the target ion (Ca2+) has preferential selective permeability; otherwise, Ca2+ has no preferential selective permeability.
> 1, the target ion (Ca2+) has preferential selective permeability; otherwise, Ca2+ has no preferential selective permeability.
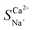 decreased to 0.89, indicating that Ca2+ lost its preferential selective permeability, which hindered the separation of Ca2+ and Na+.
decreased to 0.89, indicating that Ca2+ lost its preferential selective permeability, which hindered the separation of Ca2+ and Na+.
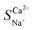 .
.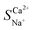 < 1 indicated a lack of preferential permeability.
< 1 indicated a lack of preferential permeability.
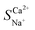 value of 1.85, demonstrating the best selective removal effect for Ca2+.
value of 1.85, demonstrating the best selective removal effect for Ca2+.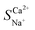 decreased to 1.25 (Fig. 6a). Changes in ion concentration result in alterations in the resistance and thickness of the aqueous phase, membrane phase, and related interface layers, leading to variations in the ion migration number and selective permeation coefficient.30,40 Thus, it is viable to integrate EIS technology to analyse the electrochemical systems of the membrane and boundary layer at varying concentrations. The voltage was set at 200 mV, and different NaCl and CaCl2 solution concentrations (0.01 mol L−1, 0.02 mol L−1, 0.05 mol L−1, 0.10 mol L−1, and 0.20 mol L−1) were selected for the EIS static study.
decreased to 1.25 (Fig. 6a). Changes in ion concentration result in alterations in the resistance and thickness of the aqueous phase, membrane phase, and related interface layers, leading to variations in the ion migration number and selective permeation coefficient.30,40 Thus, it is viable to integrate EIS technology to analyse the electrochemical systems of the membrane and boundary layer at varying concentrations. The voltage was set at 200 mV, and different NaCl and CaCl2 solution concentrations (0.01 mol L−1, 0.02 mol L−1, 0.05 mol L−1, 0.10 mol L−1, and 0.20 mol L−1) were selected for the EIS static study.
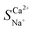 .
.
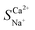 value of 2.48.
value of 2.48.