Unraveling aqueous alcohol freezing: new theoretical tools from graph theory to extract molecular processes in MD simulations

Abstract

Ice clouds in the upper troposphere are crucial for regulating Earth’s climate by affecting stratospheric humidity and the global radiative balance. A key aspect of cloud formation is heterogeneous ice nucleation, influenced by the surface properties of aerosol particles, particularly those with chemical groups capable of hydrogen bonding with water. Short-chained alcohols, such as 1-pentanol and 3-hexanol, which readily accumulate at the liquid–vapor interface, are of particular interest due to their potential impact on ice nucleation, despite their role in freezing processes being underexplored. To address this gap, molecular dynamics (MD) simulations combined with topological graph analysis (GT) were used to investigate the onset of water–alcohol surface freezing at temperatures ranging from 283 K to 192 K. Both macroscopic properties, like surface tension and solubility, and microscopic properties, including the incorporation of alcohols within the 2D-film of surface water, were analyzed. The results indicate that adsorbed films of 1-pentanol and 3-hexanol significantly influence the onset of surface freezing, with 1-pentanol forming more organized and efficiently packed surface layers compared to 3-hexanol, thus reducing surface tension more effectively. The novel application of topological graph analysis based on the representation of intra- and inter-molecular interactions in a graph revealed the insertion of alcohol molecules into the collective hydrogen-bonded 2D network at the water surface, promoting the enhanced formation of six-membered H-bonded rings at lower temperatures. This effect was particularly pronounced with 1-pentanol, which proved more efficient than 3-hexanol in facilitating the creation of ice-like structures—a critical precursor to ice formation. These findings offer valuable insights into the processes governing cloud formation and ice nucleation, with significant implications for understanding climate science and cloud dynamics.

---

1 Introduction

Freezing of supercooled water droplets in the atmosphere affects not only precipitation, but also cloud chemistry, radiative balance, and climate forcing.^1–7 Ice nucleation experiments have measured the rates at which pure water freezes as a function of temperature for bulk samples (millimeter size), through micrometer sized droplets, to nanodroplets and even molecular clusters containing only a few hundreds of molecules.^8–14 In the absence of contaminants or solid surfaces, freezing proceeds via homogeneous nucleation, a process with rates that increase so rapidly as temperatures approach 235 K that lower temperatures can only be reached readily using nanodroplets or molecular clusters. The ice that initially forms in highly supercooled water is stacking default ice, that can then transform to the more stable hexagonal ice given enough time.^15–18 Despite the limitations of current water models, computational studies of pure water freezing have predicted both the overall shape of the rate versus temperature curves, and the nature of the emerging solid phase.^19–25 Although the differences in timescales between MD simulations and experiments are still large, simulations have provided deeper insights into the microscopic molecular mechanisms involved in this complex phase transition.

Atmospheric water droplets are not, however, expected to be pure. In particular, organic matter is ubiquitous in the atmosphere²⁶ and can condense onto existing droplets, many aqueous droplets may have formed by condensing onto aerosol particles rich in organics,²⁷ and other contaminants including soot, mineral dust, biological material can be incorporated into the constantly evolving droplets.^28,29

If the contaminants result in uniform solutions, ice formation is still considered to proceed via homogeneous nucleation but freezing temperatures are generally depressed relative to pure water,^30,31 with some large, soluble biological molecules presenting exceptions.^32,33 When true solids are present, freezing can occur at much higher temperatures and is initiated by the interactions of liquid water with the solid surfaces via heterogeneous nucleation.³⁴ Given the wide range of potential solids, and the distribution of nucleation sites within them, heterogeneous nucleation³⁵ is inherently more complex than homogeneous nucleation and far from fully understood. Some important heterogeneous nuclei present in the atmosphere include mineral dust such as feldspar,^34,36,37 soot³⁸ and certain biological material.³⁹ Recent simulations have contributed insight into important factors beyond simple lattice matching⁴⁰ between the substrate and ice. These include local ordering and decreased density of the liquid water induced by the surface, and reduced variability in the adsorption energy landscape.⁴¹ Less obvious surfaces that can aid water’s liquid–solid phase transition result from the self-assembly of molecules at the air–liquid interface. Experimental work showed that for a series of straight chain alcohols, freezing temperatures increased with the length of the hydrocarbon tail,⁴² an effect that was well matched by molecular simulations.⁴³ A recent study⁴⁴ reported that for long chain alcohols (C₂₀H₄₁OH, C₃₀H₆₁OH, and C₃₁H₆₃OH), ice nucleation is not only influenced by the lattice matching of the alcohol monolayer with the ice underneath but also by geometric features such as the angle between the alcohol C–O bond and the interfacial plane.

The focus of the present simulations is to investigate the effect two short chain alcohols, 1-pentanol (8 mol% or 30 wt%) and 3-hexanol (6 mol% or 25 wt%), may have on freezing in systems with high surface to volume ratios. The concentrations investigated in the simulations are both comparable to the experiments of Sun et al.^45,46 and representative of the concentrations (10–50 wt%) of organic carbon in small aerosol particles.⁴⁷ They are, however, significantly higher than the carbon content typically found in cloud droplets (<100 mg_C L⁻¹).⁴⁸ For these molecules, though their solubility is not negligible, surface enrichment is still significant and, thus, depletion of molecules from the “bulk” cannot be neglected. Our work is motivated by the aqueous–alcohol nanodroplet experiments of Sun et al.^45,46 that examined the effect on freezing of 3 straight chain alcohols (C3, C5, C6) and 2 branched alcohols (C5, C6) at overall concentrations up to 6 mol% alcohol. For straight chain alcohols, freezing was less perturbed by the longer chain alkanes, consistent with higher surface enrichment and lower solubility as chain length increased. The branched alcohols perturbed freezing more readily than the straight chain with the same carbon number, consistent with the increased solubility of the former and their larger molecular area. Solubility, however, is not necessarily the deciding factor since the less soluble (at room temperature) 3-hexanol perturbed freezing more easily than the more soluble (at room temperature) 1-pentanol. Furthermore, the solubility of both alcohols increases with decreasing temperature but measurements are not available in the experimental temperature range.

In this paper, classical Molecular Dynamics (MD) simulations explore the temperature dependent behavior of dilute aqueous solutions of linear and branched alcohol molecules, specifically 1-pentanol and 3-hexanol. One key to understand the onset of freezing processes is to reveal structural properties of the water–alcohol interfaces. The water in contact with the air is known to be organized in a 2-dimensional film made of a highly collective hydrogen-bonded network oriented parallel to the surface,^49,50 of ∼5–10 Å thickness.^49–52 We hence investigate the possible disruption/strengthening caused by alcohol films within this 2D-H-bonded water network at the surface and how this can be correlated with freezing. This is achieved using graph theory (GT) algorithms.^53–59 Graphs encode the topology of molecules and molecular assemblies, through vertices and edges that respectively represent the atoms and their intra- and inter-molecular interactions. With GT, the 3D structures that are explored over the MD trajectories are transformed into a time series of non-isomorphic topological 2D graphs, which are analyzed by graph algorithms in order to extract the time evolution and statistical behaviours of the structures. Our goals include evaluating the comparative effects of alcohol films and pure air–water interfaces on the 2D-H-bonded network of water, as well as examining how temperature influences the dynamics of the network. This represents a critical first step in characterizing freezing processes, even though the actual freezing is not observed within the simulation timescale.

2 Methodology

2.1 Molecular dynamics trajectories

2.1.1 Simulation details. Classical MD simulations were performed using the GROMACS 2020.5 software.⁶⁰ Periodic Boundary Conditions (PBC) were applied across all three dimensions, with bond constraints implemented via the LINCS algorithm.⁶¹ A time-step of 2 fs was used. The TIP4P/2005 water model was employed to describe the water system, known for its accurate representation of surface tension across a wide temperature range and reliable characterization of liquid properties, phase equilibria, and critical properties.^62–67 Numerous theoretical studies have successfully modeled the behavior of alcohols at water surfaces using classical non-polarizable force fields.^68–73 From these, we selected the Transferable Potentials for Phase Equilibria-United Atom (TraPPE-UA) force field to describe the alcohols, which has been previously applied to various alcohols such as methanol⁷⁴ and butanol.⁷⁵ Notably, it has been demonstrated that the combination of the TIP4P/2005 and TraPPE force fields provides the best agreement with experimental data compared to other force field combinations.⁷⁴ Lorentz–Berthelot combination rules^76,77 were utilized to define cross solute–solvent atom interactions. Interactions were truncated at a distance of 12 Å for both short- and long-range interactions. Dispersion correction of the energy due to long-range van der Waals interactions was applied. The Particle Mesh Ewald (PME) algorithm⁷⁸ was employed for evaluating long-range Coulomb interactions, employing fourth-order cubic interpolation and a Fourier spacing parameter of 0.15.⁷⁹ Temperature control was achieved via a Berendsen thermostat with a coupling constant of 0.1 ps,⁸⁰ while pressure was regulated using a Berendsen barostat at 1 bar, employing a semi-isotropic coupling scheme.⁸¹

2.1.2 System setup. Aerosols commonly exist in various forms, including spherical shapes (such as liquid droplets), irregular shapes (like dust and soot), elongated fibers, or aggregates of smaller particles. The curvature of these particles can influence the properties of their surface layers differently than flat surfaces. However, as in the present study, many previous investigations have employed flat surfaces to analyze the structure of aerosol surface droplets.^82–84 A pure water slab was initially generated from a bulk system containing 1000 water molecules within a cubic box measuring 30 Å per side. After energy minimization using the steepest descent algorithm, the bulk system was equilibrated in the isothermal–isobaric (NPT) ensemble at 1 bar for 5 ns. The equilibrated system was then extended along the interface normal (the z-axis) to a length L_z = 120 Å, creating two air–liquid interfaces exposed to vacuum.

The cooling process was initiated with NVT simulations sequentially conducted for 150 ns at five temperatures: 283, 258, 233, 219, 206, and 192 K, guided by the temperatures reported by Sun et al.⁴⁵ Cooling started with the final geometry from the previous higher temperature simulation and initiated the cooling process at the next lower temperature. This methodical approach ensures faster equilibrium, confirming that equilibrium is reached at each reduced temperature before continuing with further cooling.

Based on their respective molecular areas, 45 and 30 molecules of 1-pentanol and 3-hexanol respectively were added on each side of the water slab in order to form a film close to monolayer coverage. Upon addition of the alcohols, the box was further extended to L_z = 180 Å (Fig. 1). Moreover, it was observed that adding the same number of 3-hexanol molecules (45 on each side) as 1-pentanol led to bilayer formation, as already reported for small amphiphilic molecules at higher concentrations.^85–87 Additionally, Sun et al.⁴⁶ suggested that a full monolayer on 60 Å droplets corresponds to an alcohol mole fraction of x₂ ≈ 0.024 for 3-alcohols and x₂ ≈ 0.046 for 1-alcohols. It is consistent with the fact that, to mimic a full monolayer of these two alcohols, the number of 1-pentanol molecules should exceed the one of 3-hexanol.

Fig. 1 Side views of the water–alcohol slab at 233 K after 150 ns: (a) 1-pentanol with 45 molecules on each side and (b) 3-hexanol with 30 molecules on each side. (c and d) Molecular geometries and atom labels for 1-pentanol and 3-hexanol respectively. Atoms are colored according to functional groups: oxygen atoms of alcohol molecules are red, carbon atoms of 1-pentanol or 3-hexanol are orange or magenta respectively, and water molecules are represented in blue.

Among other properties (density profiles, radial distribution functions, binding energy distribution), the surface tension γ (mN m⁻¹) was calculated at 10 ns intervals along the MD trajectories. The cumulative averaged surface tension^88,89 was then computed with its corresponding error.

2.2 Algorithmic graph theory

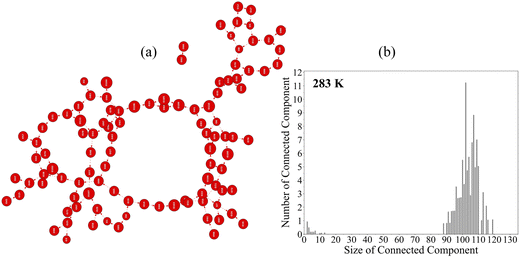
Structural analyses of the water and alcohol films at the water surface were conducted with algorithmic graph theory. We have shown in our previous works the capability of the topological 2D-MolGraphs to capture the H-bond networks in condensed matter molecular systems,^54,55,59 including the air–water interface. In our 2D-MolGraphs, any molecular conformation is defined by a molecular graph where vertices represent the atoms of the molecular system and the edges represent the interactions between these atoms. One crucial step of the algorithm is to set up a model that defines a molecular conformation with the right level of granularity. We chose to define the edges in the graphs in terms of e.g. covalent bonds, hydrogen bonds, electrostatic interactions and organometallic interactions between the atoms (see ref. 54, 57 and 58 for the associated definitions in the 2D-MolGraphs). Each bond or interaction is represented by an (undirected) edge in the graph, except for hydrogen bonds which are represented by directed edges (arcs). We chose not to include hydrogen atoms in the vertices of the 2D-MolGraphs. The only indirect information related to some of the hydrogen atoms that is retained in a 2D-MolGraph is in the edges associated to hydrogen bonds. Edges in the 2D-MolGraphs for H-bonds are indeed directed from the heavy atom donor in the H-bond to the heavy atom accepting the H-bond, as illustrated in Fig. 2. The H atom hence ‘belongs’ to the vertex in the graph associated to the donor atom.

Fig. 2 Schematic representation of an H-bond as a directed edge in a 2D-MolGraph illustrated for a (a) water–water or (b) water–alcohol dimer. In the graphs shown here, the dashed red arrow refers to the H-bond oriented from donor to acceptor while a black line corresponds to a covalent bond. H atoms are not included in the 2D-MolGraph, the alcohol O and C atoms are colored in orange and black respectively.

All details on the definitions used in the construction of the 2D-MolGraphs can be found in ref. 54. The definitions of bonds/interactions are based on geometric criteria (Euclidian distances and angles). For example, the criterion used for the existence of a hydrogen bond is the one from ref. 90: the O–O has to be less than 3.2 Å and the O–H⋯O angle has to be within 180 ± 40°. Note that the use of other H-bond definitions does not change the general conclusions.⁵⁴Fig. 3a shows the 2D-MolGraph of the water–air interface from our MD simulations at 283 K. This interface is made of a highly collective 2D film of hydrogen bonded water, oriented parallel to the surface. The collective network of H-bonds can be easily seen in the 2D-MolGraph by the red vertices (the oxygens of the water molecules located in the interfacial region-BIL^49,91) that are interconnected to each other through the directed red-dashed edges (the H-bonds between the water molecules). One can observe that there are very few vertices (water molecules) that are not part of the collective network. The degree of collectivity of the graph can be measured by the connected components of the graph, as reported in Fig. 3b. One hence observes one dominant peak in the distribution that is centered on ∼95% of the water molecules belonging to the interfacial region, which indeed is the signature of a high degree of inter-connectivity between the water molecules at the water surface.

Fig. 3 (a) Illustration of a 2D-MolGraph for the air–water interface. Vertices of the graph represent the oxygen atoms of the water molecules (red); the dashed red arcs represent the H-bonds between two water molecules oriented from donor to acceptor. (b) Distribution of the connected components of the 2D-MolGraphs for the air–water interface (see text for details).

Once the 2D-MolGraphs are constructed snapshot by snapshot of the MD trajectory, the changes in the molecular conformations being sampled over time are achieved by monitoring the changes in the topologies of the graphs, which can be tracked using the isomorphism algorithm.^54–56,59 Once the ensemble of non-isomorphic 2D-MolGraphs is obtained for the whole trajectory, additional analyses of the graphs can be performed. In this work, we analyze the graphs in terms of the size of the connected components, i.e., the set of subgraphs in which all vertices are connected to each other without interruption (see the above discussion related to Fig. 3b). This will serve to characterize the degree of collectivity in the H-bonded network that can be formed at the interface. This will also serve to characterize the H-bonded network of the aqueous interface, i.e., water–water and water–alcohol H-bonds as well as sizes of H-bonded polygons/chains that can be formed. This latter is obtained by applying the Horton algorithm⁹² that provides a minimum basis of cycles for one given graph.

Once the composition and size of the H-bonded cycles within a graph are known, one can further provide the information on whether alcohol molecule(s) are inserted inside a cycle or are surfing on top of the cycle, as will be discussed in the results section.

All analyses are implemented in the GaTewAY software.⁹³

3 Results

3.1 Alcohol films adsorbed on the water surface

Density probability distributions were computed for water oxygen, the carbon linked to the OH group (C–OH), and the terminal carbons (CT) for 1-pentanol and 3-hexanol at different temperatures (Fig. 4). Both 1-pentanol and 3-hexanol exhibit pronounced surface adsorption tendencies across different temperatures, with the highest density peak observed at the liquid–vapor interface. For 1-pentanol, the CT density is peaked at a larger distance from the film than C–OH, indicating that the alcohol molecules orient themselves at the interface, with their hydrophobic carbon tails directed toward the vapor phase and the hydroxyl groups toward the bulk. Furthermore, the behavior of the CT segments of 3-hexanol reveals that it forms a monolayer with gauche defects directing the long tail toward the vapor phase and the short terminal segment to align along or slightly above the surface, thereby reducing the hydrophobic interactions with the underlying water subphase. The orientation of the alcohols at the interface is influenced by the desolvation of the alkyl chains, the solvation of the hydrophilic head, and enhanced van der Waals interactions between the chains.⁷¹ As shown in the density distribution, the linear alcohol, 1-pentanol, exhibits a straighter and more perpendicular orientation to the surface plane. In contrast, 3-hexanol exhibits a less pronounced orientation, indicating a greater likelihood of staying near the surface plane (see Table S5 in the ESI†). This trend is supported by XPS measurements^72,94 that show a preferred alcohol orientation toward the surface normal as the chain length increased, highlighting also the importance of lateral hydrophobic interactions. Additionally, classical MD simulations showed increased order and packing within the monolayer with higher surface density, particularly pronounced at low temperatures.⁹⁵

Fig. 4 Density distribution profiles along the z axis (perpendicular to the interface) of water oxygen, C–OH group, and terminal carbons (CT) for (left) TIP4P/2005 water slab, (middle) 1-pentanol, and (right) 3-hexanol solutions at different temperatures calculated from the last 10 ns of a 150 ns trajectory. See Fig. 1(c) and (d) for the labels of the atoms. The density was calculated based on the number of molecules per cubic nanometer using 200 slices.

By integrating the density distributions of the C–OH group at the interface and in the bulk phase, we can determine the bulk-to-surface ratios shown in Table 1. The surface, equivalent to the interface, is defined as the region between 10% and 90% of the bulk water density. Despite the data being derived from a limited number of molecules, they consistently show that 1-pentanol is more soluble than 3-hexanol across all temperatures. As the temperature decreases, the solubility of both alcohols approximately doubles. However, no significant increase in solubility is observed below this temperature, although some molecules may diffuse into the subsurface layer or move within the surface layer. Below 233 K, alcohol diffusion slows considerably as the solutions approach freezing and become more viscous. This observation is consistent with neutron diffraction and simulation studies,⁹⁶ which have shown that in binary mixtures of methanol–water and ethanol–water alcohol segregation becomes more pronounced as the temperature drops to 245 K.

Table 1 Bulk-to-surface ratio for 1-pentanol and 3-hexanol at different temperatures. The number of molecules transitioning from one interface to the other over 10 ns (time interval from 140 to 150 ns) is indicated in parentheses

T (K)	1-Pentanol	3-Hexanol
283	0.036 (3)	0.026 (1–2)
258	0.048 (4)	0.032 (2)
233	0.067 (6)	0.058 (3)
219	0.062 (6)	0.055 (3)
206	0.071 (6)	—

---

3.2 Surface tension of water is affected by alcohols

It is widely recognized that accounting for partitioning is crucial for accurately predicting the Cloud Condensation Nuclei (CCN) activity of surface-active aerosols.^97,98 At the molecular level, surface tension is an important parameter that characterises the exchange of matter across the interface. Surfactants and amphiphilic molecules are known to reduce surface tension relative to pure water.^83,97 Although the exact role of surfactants in ice nucleation remains unclear, it is worthwhile to investigate how surface tension changes during freezing and how surfactants influence this process.

As benchmark, the surface tension of pure water was evaluated and compared with previously reported values. At 298 K, our calculated surface tension is 64.3 ± 0.6 mN m⁻¹, which closely aligns with computational values of the TIP4P/2005 water model of 65.4 mN m⁻¹ (without including long-range corrections),⁶⁴ 69.3 ± 0.9 mN m⁻¹ (including long-range corrections)⁶⁴ and 68.4 ± 1.1 mN m⁻¹,⁶⁵ as well as the experimental value of 71.7 mN m⁻¹.⁶⁴ The absence of the tail correction to the surface tension, caused by the truncation of the Lennard-Jones potential, leads to increase the surface tension by at least 2 mN m⁻¹.^64,99 In this study, tail correction has not been applied, surface tension values being compared on a relative basis.

Fig. 5 shows the surface tension values for the pure water slab obtained from the final 50 ns of the simulation, along with their corresponding errors for the various temperatures. The rise in standard deviation as temperature decreases suggests larger fluctuations in surface tension along the dynamics as can be seen in Fig. S1(a) and Table S2 in the ESI.† A standard deviation exceeding 10 mN m⁻¹ indicates that the system has not reached equilibrium at that particular temperature. As a result, data at 192 K will be interpreted with caution.

Fig. 5 Temperature evolution of the surface tension for the pure TIP4P/2005 water, 3-hexanol and 1-pentanol covered slabs. Error bars are derived from the standard deviation at each temperature.

Similarly, the evolution of the surface tension was monitored over time for each temperature in both 1-pentanol and 3-hexanol solutions (Fig. S1(b) and (c) in the ESI†) to check for convergence. Fig. 5 presents the average surface tension values and associated errors for the various alcohol solutions in comparison to pure water across different temperatures. At 283 K, the 3-hexanol solution exhibits an average surface tension of 33.1 ± 1.2 mN m⁻¹, while the 1-pentanol solution has a lower value of 15.9 ± 1.1 mN m⁻¹. Both are significantly below the surface tension of pure water, which is 66.8 ± 0.6 mN m⁻¹. The decrease in surface tension caused by the alcohols is usually attributed to the reduction in water–water hydrogen bonding and to the increase in alcohol–water hydrogen bonding.^100,101 In addition, surface tension is influenced by the molecular arrangement of the alcohols at the interface.⁸⁹

For the 1-pentanol solutions, the surface tension values exhibited significant fluctuations at 192 K, even with a simulation extended to 200 ns, suggesting that equilibrium had not been reached (see Table S3 in the ESI†). Similarly, for the 3-hexanol solutions, considerable fluctuations persisted at 206 K, despite the 200 ns simulation duration (see Table S4 in the ESI†). These fluctuations at very low temperatures are likely caused by water supercooling, which results in a frozen state that hinders the achievement of equilibrium. Moreover, the slab with 1-pentanol films reached equilibrium at lower temperatures compared to the 3-hexanol slab. This may result from the molecular structure of the alcohols: straight-chain alcohols like 1-pentanol form more organized layers at the interface as shown from the density distributions, whereas branched alcohols like 3-hexanol face steric hindrance, leading to less structured films. The reduction in surface tension is also more pronounced with longer alkyl chain lengths. Comparisons between linear and branched isomers show that longer linear alcohols tend to have higher surface excess and smaller surface areas per molecule compared to their branched counterparts. For instance, previous studies^102,103 have shown that as temperature decreases from 308 K to 283 K, surface tension increases, with longer carbon chains resulting in higher surface concentrations and faster adsorption rates. Additionally, 1-propanol, despite having the same bulk concentration as 2-propanol, lowers surface tension more effectively due to its higher surface concentration.¹⁰⁴ This observation aligns with Walz et al.,¹⁰⁵ who found higher surface concentrations for linear alcohols compared to branched ones. These results highlight the link between increased surface concentration and decreased surface tension in aqueous solutions,¹⁰⁶ emphasizing the impact of molecular arrangement at the interface. Thus, accurately characterizing the molecular organization at the surface is crucial.

3.3 Collective 2D-H-bonded-network (2DN) of water at the interface with the air

The water at the interface with the air has been shown to be organized as a 2-dimensional film made of a highly collective H-bonded network in which the water–water H-bonds are formed parallel to the surface, thus the term 2D-H-bonded-network (or 2DN as short notation used hereafter).^{49,50,54,91,107} Such 2D-film was also shown to be present at any hydrophobic aqueous interface,¹⁰⁸ with a thickness of ∼3–6 Å depending on the morphology of the hydrophobic medium in contact with the water and on the possible supplementary interactions between the hydrophobic surface and the water. Very recent innovative SFG-DFG (Sum- and Difference-Frequency Generation) measurements⁵² have confirmed such thickness for the air–water interface. Fig. 3a illustrates the 2D-MolGraph associated with the 2DN for a given snapshot extracted from our classical MD simulations of the neat air–water at 283 K. Following the pathways through the directed edges in the graph (in dotted red lines), one can indeed see how the vertices (i.e. the water molecules) are collectively H-bonded together. This collectivity can be directly measured by the connected components (CCs) of the graph. CCs measure the number of vertices in a graph being connected to each other (here through H-bonds) without interruption.

The distribution of the CCs is reported in Fig. 3 from the statistical graph analysis of the 6 Å thick water interfacial layer over the MD trajectory. One can hence see one main peak in the distribution of CCs centered on average on 103 vertices/water molecules among an average of 108 water located within the interfacial layer. This main CC incorporates ∼95% of the water molecules that belong to the interfacial layer, showing the high degree of collectivity in the 2DN. Note that the size of the largest CC is 119 among a maximum of 121 water molecules that were found located in the interfacial layer over time. Furthermore, there is on average 1.9 number of CCs, i.e. one centered on the main peak of the distribution and one other CC associated to the peak of very small intensity in the distribution that is located below the size value of CC ∼10. This latter peak shows that the very few water molecules that are not incorporated within the 2DN exist as either individual molecules or are part of small clusters/chains at the interface.

3.4 Alcohols are accommodated within the 2DN and strengthen the collectivity of the H-bonded network

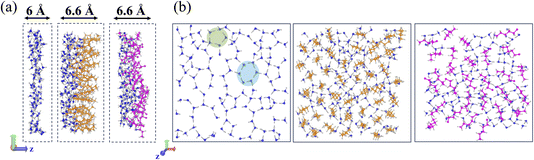
The graph analysis of the interfacial layer is now applied to the simulations of alcohol films adsorbed at the water surface. The Gibbs Dividing Surface (GDS), located at the midpoint of the interface density range, serves as the z-reference for defining the interface (also defined as the BIL – Binding Interfacial Layer⁵⁰) augmented by ±3 Å. Images of the interfacial layers and their thicknesses used in the graph analyses are reported in Fig. 6a, respectively for the air–water, one monolayer film of 1-pentanol and of 3-hexanol adsorbed at the water surface. Fig. 6b illustrates top-views of these interfaces. The increase in the thickness of the water–alcohol BIL is in agreement with e.g. ref. 109 reporting an increase by 0.7 Å of the interface thickness in the presence of alcohols at low ethanol concentrations, that grows with higher alcohol levels. Note that while there are two equivalent interfaces in our simulation boxes, our discussions focus on the upper surface.

Fig. 6 (a) Side view of the interfaces with the selected BIL thickness for the various interfaces: air–water and the alcohol films. (b) Top view of one interface at 219 K for the different systems. Water molecules are represented in blue, 1-pentanol molecules are in orange, and 3-hexanol molecules are in magenta. The dashed blue and green highlighted circles illustrate hexagonal and pentagonal water cycles, respectively.

The graph analyses were conducted on the last 10 ns of the 150 ns MD trajectories, using snapshots recorded every 100 ps. We checked that this sampling allowed achievement of a good compromise between computational time and statistics. It is worth recalling that the 192 K (water slab and 1-pentanol–water slab) and 206 K (3-hexanol–water slab) trajectories have convergence issues for the surface tension calculations, thus data collected from these trajectories should be interpreted with caution.

Fig. 7a (top) reports the evolution with decreasing temperature of the average number of connected components (CCs) in the graphs of the BIL. All three aqueous interfaces clearly experience a continuous decrease in the average number of CCs as temperature is decreasing from 283 K to 210 K, reaching almost 1 CC at the lower temperatures. We remind that one single CC in a graph is the ultimate limit, that in our case represents an organization in the H-bonded network of the BIL where all vertices are interconnected together without any interruption. One can see that this limit is almost reached for both the air–water and the 3-hexanol film–water interfaces at 219 K. At the same temperature, there are still 2 CCs in the 2D-MolGraph for the 1-pentanol–water interface. Note that the rapid decrease from 2 to 1 CCs for 1-pentanol from 219 K to 206 K is presumably more likely due to convergence issues in the MD at this low temperature rather than to a physical reason.

Fig. 7 ((a)-top) Average number of connected components (CCs) in the 2D-MolGraphs, and percentage of water ((a)-middle) or alcohol ((a)-bottom) incorporated in the H-bonded cycles as a function of temperature for pure water (blue lines), 1-pentanol (yellow lines), and 3-hexanol (pink lines) solutions. (b) Distribution of sizes of the H-bonded cycles in the 2D H-bonded network of the water surface (tetragonal, pentagonal, and hexagonal cycles) as a function of decreasing temperatures for the water interface (blue lines), 1-pentanol (yellow lines) and 3-hexanol (pink lines) films adsorbed at the water surface.

Interestingly, at 283 K the adsorbed alcohol films tend to slightly disrupt the connectivity in the water–water H-bonds in the 2DN of the interfacial water, as can be seen by the (small) increase in the average number of CCs in the graphs of the three molecular interfaces in Fig. 7a (top). There are indeed, on average, ∼2 CCs in the 2D-MolGraph of the neat air–water interface, increasing to ∼2.8 (3-hexanol) and ∼4 CCs (1-pentanol) when the alcohol films are adsorbed. As temperature decreases, all three interfaces see the connectivity in the 2DN increasing, as evidenced by the number of CCs in the graphs that continuously decreases. The values in CCs in Fig. 7a are almost identical for the air–water and 3-hexanol film–water interfaces at all temperatures below 283 K, which shows that the collectivity in the 2DN H-bonded network behaves similarly at these two interfaces. The 2D-MolGraphs of the 1-pentanol film–water interfaces always have a higher number of CCs than the two other systems, at all temperatures, showing that there is a tendency for a slightly lower degree of connectivity between the H-bonded water molecules in the 2DN when the 1-pentanol film is adsorbed at the interface.

As was shown by Bougueroua et al.⁵⁴ and Serva et al.¹⁰⁷ the 2DN at the neat water surface is organized through polygons/cycles of H-bonded water molecules. Fig. 7b reports the evolution with decreasing temperature of the distribution of H-bonded tetragons, pentagons and hexagons formed within the 2DN for the neat water surface (blue lines), 1-pentanol–water surface (yellow lines) and 3-hexanol–water surface (pink lines). These three polygons dominate the whole distribution of sizes at all these interfaces. The values shown here at 283 K for the neat water interface are in agreement with ref. 54 and 107 using different set-ups of the MD trajectories at room temperature.

One can see that the percentage of H-bonded tetragons within the 2DN is continuously decreasing as temperature decreases from 283 K to 209 K, for all three aqueous interfaces, while the reverse is observed for pentagons and hexagons. Lower temperatures thus favor larger H-bonded rings in size. Interestingly, the percentage of H-bonded pentagons is predominating at all three aqueous interfaces. While the percentage of pentagons is roughly equal at the water and 1-pentanol–water interfaces, there is an increase by ∼5% in the number of pentagons formed at the 3-hexanol–water interface, at all temperatures. This is reversed for tetragons in the 2DN, for which water and 3-hexanol–water interfaces behave similarly, while 1-pentanol–water has almost twice fewer number of tetragons within the 2DN. More strikingly, it is the presence of the 1-pentanol film adsorbed on water that significantly increases the number of H-bonded hexagons formed within the 2DN, at all temperatures. Also, at the lower temperatures, the percentage in hexagons even becomes comparable to the one of pentagons.

As can now be observed in Fig. 7a (middle), one can further correlate the decrease in the number of connected components (CCs) in the 2D-MolGraphs as temperature of the aqueous interfaces decreases (Fig. 7a (top)) with the increase in the average number of water molecules that are participating in the H-bonded cycles. Hence, the neat water interface sees an evolution from 76% to 92% of the water molecules interconnected within the 2DN in going from 283 K to 209 K. Interestingly, there are already ∼86% of the water molecules located in the BIL that are incorporated within the H-bonded polygons of the 2DN at 283 K when either 1-pentanol or 3-hexanol films are adsorbed on the water surface. The decrease in temperature leads to a further increase in the number of water molecules incorporated in the H-bonded cycles, up to ∼90–92% for both 1-pentanol/3-hexanol films at 219 K, slightly more than at the neat water interface. There is no substantial difference in the plot of Fig. 7a (middle) between 1-pentanol and 3-hexanol aqueous interfaces. Similarly, the fraction of alcohols embedded in the H-bonded cycles in the 2DN increases while temperature drops, from ∼65% of the alcohols at 283 K to ∼80% at 219 K (Fig. 7a (bottom)). There again, there is no substantial difference between 1-pentanol and 3-hexanol films. Greater incorporation of alcohols into the H-bonded cycles formed within the BIL could suggest a segregation of alcohols or water molecules among themselves, which is why it is important to analyze the composition of the cycles and, more specifically, the types of hydrogen bonds that are formed.

3.5 Oxygens of alcohols are integrated in the H-bonded cycles of the collective 2DN network of water

How are the H-bonded tetragons, pentagons and hexagons seen in the previous section, organized? Are they built on water only or do they accommodate the oxygen of the 1-pentanol/3-hexanol alcohols? The 2D-MolGraphs can readily provide that information.

The ESI (Fig. S9 and S10)† contains all the detailed distributions of H-bonded polygons for all systems at all temperatures. Here in Fig. 8, we report data at 283 K, 233 K and 206 K for 1-pentanol aqueous interfaces.

Fig. 8 Distributions of H-bonded cycles present within the 2D H-bonded network of surface water in the presence of the adsorbed 1-pentanol film at 283 K, 233 K and 206 K. The color legends denote the cycle size along with its respective total percentage distribution. The x-axis represents the compositions of the H-bonded cycles (made of water and 1-pentanol molecules, ‘w’ means water, ‘np’ means n pentanol, where n is the number of 1-pentanol molecules) with their contribution to the total percentage for each cycle size reported on the y-axis. The ESI† reports figures at all temperatures for both 1-pentanol and 3-hexanol films.

One can observe that the H-bonded tetragons, pentagons and hexagons that form the collective 2DN can accommodate from 0 to 2 alcohol molecules (1-pentanol or 3-hexanol alike). As discussed above, as temperature decreases the percentage of hexagons become more prevalent in the 2DN, especially for the 1-pentanol film adsorbed on water. These hexagons are more likely accommodating one pentanol oxygen. At all temperatures, there are roughly as many pentagons and hexagons formed that incorporate one pentanol oxygen. For the 3-hexanol film adsorbed within the 2DN (Fig. S10 in the ESI†), there is always ∼5–13% more water-only pentagons than pentagons made of four water and one alcohol. Interestingly the H-bonded hexagons formed in the 2DN at the adsorbed 3-hexanol film show an inverted trend as temperature decreases. While there is indeed ∼3–5% more water-only hexagons than hexagons containing five water and one 3-hexanol formed within the 2DN at the two higher temperatures, water hexagons containing one alcohol start to predominate from 233 K downward.

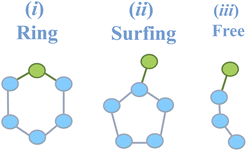
Fig. 9 now analyses whether the inclusion of 1-pentanol/3-hexanol alcohols within the H-bonded rings formed in the 2DN occurs through a complete inclusion in the ring (‘Ring’ label in Fig. 10, violet color bar in Fig. 9), or by surfing on a ring (‘Surfing’ label in Fig. 10, orange color bar in Fig. 9) or by being incorporated in H-bonded chains (‘Free’ label in Fig. 10, pink color bar in Fig. 9). This is analyzed at two extreme temperatures in Fig. 9 for 1-pentanol (top) and 3-hexanol (bottom). One can hence observe that the alcohols prefer to insert in the H-bonded rings (tetragons, pentagons, hexagons) formed by water, rather than to surf above these polygons or even be included in chains. Fig. 9 also reports and compares the percentage of water–water, alcohol–water and alcohol–alcohol interactions within the H-bonded cycles, for the two alcohols at the two extreme temperatures. As temperature drops, one can see that the small decrease in water–water interactions is replaced by water–alcohol interactions. This outcome can be related to the previously discussed evolution of surface tension with temperature.

Fig. 9 Distribution of identified H-bonds depending on the types of interactions in the H-bonded cycles forming the 2DN of surface water on which 1-pentanol (top) and 3-hexanol (bottom) films are adsorbed at two distinct temperatures 283 K and 219 K. Interaction types include water–water (w–w), alcohol–water (p–w for 1-pentanol; h–w for 3-hexanol), and alcohol–alcohol (p–p for 1-pentanol; h–h for 3-hexanol). Alcohol–water interactions can be categorized into ring, surfing, and free configurations as schematized in Fig. 10.

Fig. 10 Possible configurations for the oxygen of the alcohol (green vertex) interacting with the oxygens of the water molecules (blue vertex) within the H-bonded cycles formed at the water surface. As in the 2D-MolGraphs, the graphs in these illustrations are made of the heavy atoms only, here connected together through H-bonds with straight lines.

4 Discussion and conclusion

Our work was focused on the modeling of two water–alcohol films as a function of decreasing temperature. Macro- and micro-scopic properties were extracted from the simulations in order to provide knowledge on the onset of surface freezing. We hence characterized the evolution of the water surface tension with decreasing temperature and the modification of the interface in terms of H-bonded network. The structural analyses done here through topological graphs proved essential in order to obtain a detailed comprehension of the organization within the three aqueous films at various temperatures. The structural knowledge obtained here is almost impossible to gain without such a topological approach. This discussion furthermore tries to connect surface tension measurements with the molecular structures that were revealed.

Our molecular dynamics results align with previous findings,^44,105 that straight-chain alcohols like 1-pentanol form more organized layers at the surface of water, whereas the steric hindrance in branched alcohols results in less structured films, with the C–O bond positioned closer to the surface plane. Consequently, due to its ability to pack more tightly, 1-pentanol is more effective at reducing surface tension of water than 3-hexanol at 283 K, despite its marginal higher solubility over a range of temperatures.

Although the differences in surface tension appear to diminish as the temperature decreases, the molecular arrangement at the interface reveals intriguing properties that could be revealed by graph theory. Interestingly, regardless of the film’s composition, the lower temperatures were found to strengthen the collectivity in the 2D-H-bonded-network (2DN) of the water at the surface. At the lower temperatures, the 2DN is organized as almost one single non-interrupted network of H-bonds even in presence of the alcohols. The similar high degree in the interconnectivity of the H-bonded network at the interface is presumably part of the molecular reason for the surface tension of the three films to increase and to converge to closer values as the temperature drops. However, it is also interesting to observe that, despite the pure water film and the water–3-hexanol film displaying the same values of connected components in the graph of the 2DN, at all temperatures, the absolute value of the surface tension of the water film is roughly twice the one of the water–3-hexanol film at the higher temperatures (283–230 K). The degree of the collectivity in the H-bonded network of the 2DN is not the only molecular ingredient contributing to the value of the surface tension of water.

Beyond the packing of the alcohols at the water surface that differs for 1-pentanol and 3-hexanol (a straight well-organized monolayer of 1-pentanol and a softer and less-packed monolayer of 3-hexanol), the alcohol–water interface is primarily governed by the competitive water–water and alcohol–water hydrogen bonding, as previously observed in other alcohol systems.^105,110 Our analyses demonstrated that both 1-pentanol and 3-hexanol alcohols are integrated within the collective 2D-H-bonded-network of the surface water. The insertion of the alcohol oxygens within the 2DN of the water was quantified with the topological analyses. Hence, one to two alcohols can be found inserted within the H-bonded tetragons, pentagons and hexagons formed by the water in the 2DN. Very few alcohols are found H-bonded to the water rings of the 2DN by surfing above these rings. As temperature decreases, there is an increase in the number of 1-pentanol/3-hexanol alcohols that enter into the composition of the H-bonded tetragons, pentagons and hexagons of the 2DN. There is thus a shift in the percentage of water–water and water–alcohol interactions within the 2DN as temperature decreases, that certainly contributes to the changes in the values of the surface tension.

The insertion of the alcohols in the H-bonded polygons of the water in the 2DN, strengthens the degree of collectivity of the H-bonded network of the 2DN as temperature decreases. Interestingly, at the higher temperature, both alcohols were found to slightly disrupt the collectivity in the 2DN of water, with 1-pentanol films providing more disruption. As temperature drops, the 2DN strengthens, ultimately stabilizing into one single, continuous ensemble of interconnected H-bonded rings/polygons. While this is true for both alcohols, 1-pentanol is still exhibiting a few remarkable differences from 3-hexanol. Hence, the 2DN is slightly less interconnected when 1-pentanol films are adsorbed on water while these films favor the formation and predominance of H-bonded hexagons within the 2DN. There is hence a balance that is reached between the degree of interconnectivity of the 2DN and the formation of hexagon H-bonded cycles at the lower temperatures. 3-Hexanol films adsorbed at the water surface promote far less the formation of hexagons than 1-pentanol films, following closely the behavior observed for the neat water surface, at all temperatures.

If the onset of freezing can be measured by the presence of H-bonded hexagons in the water structures, our results are thus consistent with previous experimental findings on water droplets,⁴⁵ which demonstrated that 3-alcohols disrupt less freezing at lower concentrations compared to their corresponding 1-alcohols. In addition, earlier findings on longer-chain alcohols¹¹¹ demonstrated that certain alcohols might exhibit greater efficiency in ice nucleation. This difference was attributed to the orientation of the OH bond and the increased mobility of the monolayer, which facilitates rearrangement to align more effectively with the emerging ice lattice, as our analysis shows in the case of 1-pentanol compared to 3-hexanol.

Hexagonal cycles become particularly prominent at lower temperatures, in particular for 1-pentanol. We may see these cycles as a foundational framework for the development of “ice-like” structures in the interfacial region. Recognizing these key patterns may help to better understand what sets the stage for surface freezing, even without observing the freezing itself. Essentially, the present study reveals that surface freezing is accompanied by the enhancement of a two-dimensional hydrogen bond network at the interface. Interestingly, although the interfacial hydrogen-bonded network is influenced by the presence of alcohols at room temperature, it adapts during the cooling process to effectively integrate alcohol molecules, specifically incorporating their hydroxyl groups into the polygonal structures formed by water molecules, often in tetragonal or hexagonal arrangements. The strengthening of this hydrogen bond network leads to the formation of well-organized interfacial structures, such as polygons—specifically tetragons and hexagons—formed by the water molecules. However, an important question remains unanswered: how do these interfacial structures propagate into the bulk of the solution? This propagation is crucial to understanding how the two-dimensional order at the interface transitions would affect the bulk properties of the system. Further research is needed to explore how the organized interfacial hydrogen bonding extends beyond the surface and influences the overall phase behavior of the solution.

Data availability

The data supporting this article have been included as part of the supplementary information.† The code for GROMACS can be found at https://www.gromacs.org. The version of the code employed for this study is version 2020.5. The code for GATEWAY can be found at S. Bougueroua, F. Quessette, D. Barth and M.-P. Gaigeot, GaTewAY: Graph Theory-Based Software for Automatic Analysis of Molecular Conformers Generated over Time, ChemRxiv, 2022, DOI: https://doi.org/10.26434/chemrxiv-2022-1d5x8-v2.

Author contributions

R. AbouHaidar: investigation; acquire data; formal analysis of data; performing graph analyses (lead); writing original draft (equal); writing – review & editing (equal). S. Bougueroua: programming, software development on topological graphs; implementation of the computer code and supporting algorithms; conceptualization; performing graph analyses (equal); writing – review & editing. D. Duflot: conceptualization; funding acquisition; writing – review & editing (equal). M. P. Gaigeot: conceptualization; writing original draft (equal); writing – review & editing (equal). B. Wyslouzil: conceptualization; funding acquisition; writing – review & editing. C. Toubin: conceptualization; funding acquisition; writing original draft (lead); writing – review & editing (lead).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. A., D. D. and C. T. acknowledge support from the CaPPA project (Chemical and Physical Properties of the Atmosphere) funded by the French National Research Agency (ANR) through the PIA (Programme d’Investissement d’Avenir) under Contract No. ANR-10-LABX-005, the Région Hauts de France and the Ministère de l’Enseignement Supérieur et de la Recherche (CPER ECRIN) and the European Fund for Regional Economic Development for their financial support. This work was performed using HPC resources from GENCI-TGCC (Grant No. 2024–A0150801859) and the Centre de Ressources Informatiques (CRI) of the Université de Lille. R. A.’s mobility to Ohio State University was partly funded by the ANR SFRI (21-SFRI-0005) GRAEL program of the University of Lille. This work was completed with the financial support of the National Science Foundation under grant number CHE-1900064 (BEW). The calculations reported here were made possible by a generous grant of resources from the Ohio Supercomputer Center.¹¹²

Notes and references

1. B. J. Murray, D. A. Knopf and A. K. Bertram, Nature, 2005, 434, 202–205.
2. M. P. Meyers, P. J. DeMott and W. R. Cotton, J. Appl. Meteorol. Climatol., 1992, 31, 708–721.
3. R. M. Rasmussen, I. Geresdi, G. Thompson, K. Manning and E. Karplus, J. Atmos. Sci., 2002, 59, 837–860.
4. A. Tabazadeh, Y. S. Djikaev and H. Reiss, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15873–15878.
5. A. Gettelman, X. Liu, S. J. Ghan, H. Morrison, S. Park, A. J. Conley, S. A. Klein, J. Boyle, D. L. Mitchell and J.-L. F. Li, J. Geophys. Res.: Atmos., 2010, 115, D18216.
6. U. Lohmann and D. Neubauer, Atmos. Chem. Phys., 2018, 18, 8807–8828.
7. W. Cantrell and J. Heymsfield, Bull. Am. Meteorol. Soc., 2005, 86, 795–807.
8. S. Bauerecker, P. Ulbig, V. Buch, L. Vrbka and P. Jungwirth, J. Phys. Chem. C, 2008, 112, 7631–7636.
9. C. A. Stan, G. F. Schneider, S. S. Shevkoplyas, M. Hashimoto, M. Ibanescu, B. J. Wiley and G. M. Whitesides, Lab Chip, 2009, 9, 2293–2305.
10. B. J. Murray, S. L. Broadley, T. W. Wilson, S. J. Bull, R. H. Wills, H. K. Christenson and E. J. Murray, Phys. Chem. Chem. Phys., 2010, 12, 10380–10387.
11. C. C. Pradzynski, R. M. Forck, T. Zeuch, P. Slavíček and U. Buck, Science, 2012, 337, 1529–1532.
12. A. Manka, H. Pathak, S. Tanimura, J. Wölk, R. Strey and B. E. Wyslouzil, Phys. Chem. Chem. Phys., 2012, 14, 4505–4516.
13. J. A. Sellberg, C. Huang, T. A. McQueen, N. D. Loh, H. Laksmono, D. Schlesinger, R. G. Sierra, D. Nordlund, C. Y. Hampton, D. Starodub, D. P. DePonte, M. Beye, C. Chen, A. V. Martin, A. Barty, K. T. Wikfeldt, T. M. Weiss, C. Caronna, J. Feldkamp, L. B. Skinner, M. M. Seibert, M. Messerschmidt, G. J. Williams, S. Boutet, L. G. M. Pettersson, M. J. Bogan and A. Nilsson, Nature, 2014, 510, 381–384.
14. A. J. Amaya and B. E. Wyslouzil, J. Chem. Phys., 2018, 148, 084501.
15. T. L. Malkin, B. J. Murray, A. V. Brukhno, J. Anwar and C. G. Salzmann, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1041–1045.
16. T. L. Malkin, B. J. Murray, C. G. Salzmann, V. Molinero, S. J. Pickering and T. F. Whale, Phys. Chem. Chem. Phys., 2015, 17, 60–76.
17. A. J. Amaya, H. Pathak, V. P. Modak, H. Laksmono, N. D. Loh, J. A. Sellberg, R. G. Sierra, T. A. McQueen, M. J. Hayes, G. J. Williams, M. Messerschmidt, S. Boutet, M. J. Bogan, A. Nilsson, C. A. Stan and B. E. Wyslouzil, J. Phys. Chem. Lett., 2017, 8, 3216–3222.
18. A. Kalita, M. Mrozek-McCourt, T. F. Kaldawi, P. R. Willmott, N. D. Loh, S. Marte, R. G. Sierra, H. Laksmono, J. E. Koglin, M. J. Hayes, R. H. Paul, S. A. H. Guillet, A. L. Aquila, M. Liang, S. Boutet and C. A. Stan, Nature, 2023, 620, 557–561.
19. T. Li, D. Donadio, G. Russo and G. Galli, Phys. Chem. Chem. Phys., 2011, 13, 19807–19813.
20. A. Haji-Akbari and P. G. Debenedetti, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10582–10588.
21. J. C. Johnston and V. Molinero, J. Am. Chem. Soc., 2012, 134, 6650–6659.
22. J. R. Espinosa, A. Zaragoza, P. Rosales-Pelaez, C. Navarro, C. Valeriani, C. Vega and E. Sanz, Phys. Rev. Lett., 2016, 117, 135702.
23. J. R. Espinosa, C. Vega and E. Sanz, J. Phys. Chem. C, 2018, 122, 22892–22896.
24. M. Fitzner, G. C. Sosso, S. J. Cox and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2009–2014.
25. P. M. Piaggi, J. Weis, A. Z. Panagiotopoulos, P. G. Debenedetti and R. Car, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2207294119.
26. B. Nozière, M. Kalberer, M. Claeys, J. Allan, B. D’Anna, S. Decesari, E. Finessi, M. Glasius, I. Grgić, J. F. Hamilton, T. Hoffmann, Y. Iinuma, M. Jaoui, A. Kahnt, C. J. Kampf, I. Kourtchev, W. Maenhaut, N. Marsden, S. Saarikoski, J. Schnelle-Kreis, J. D. Surratt, S. Szidat, R. Szmigielski and A. Wisthaler, Environ. Sci. Technol., 2007, 41, 1514–1521.
27. M. Liu and H. Matsui, Geophys. Res. Lett., 2022, 49, e2022GL100543.
28. B. Kärcher, C. Marcolli and F. Mahrt, J. Geophys. Res.: Atmos., 2023, 128, e2022JD037881.
29. V. R. Després, J. A. Huffman, S. M. Burrows, C. Hoose, A. S. Safatov, G. Buryak, J. Fröhlich-Nowoisky, W. Elbert, M. O. Andreae, U. Pöschl and R. Jaenicke, Tellus B, 2012, 64, 15598.
30. T. Koop, B. Luo, A. Tsias and T. Peter, Nature, 2000, 406, 611–614.
31. M. C. Barma, Z. Peng, B. Moghtaderi and E. Doroodchi, Sep. Purif. Technol., 2021, 274, 118925.
32. B. G. Pummer, C. Budke, S. Augustin-Bauditz, D. Niedermeier, L. Felgitsch, C. J. Kampf, R. G. Huber, K. R. Liedl, T. Loerting, T. Moschen, M. Schauperl, M. Tollinger, C. E. Morris, H. Wex, H. Grothe, U. Pöschl, T. Koop and J. Fröhlich-Nowoisky, Atmos. Chem. Phys., 2015, 15, 4077–4091.
33. K. Mochizuki, Y. Qiu and V. Molinero, J. Am. Chem. Soc., 2017, 139, 17003–17006.
34. B. J. Murray, D. O’Sullivan, J. D. Atkinson and M. E. Webb, Chem. Soc. Rev., 2012, 41, 6519–6554.
35. B. Wang, A. Laskin, T. Roedel, M. K. Gilles, R. C. Moffet, A. V. Tivanski and D. A. Knopf, J. Geophys. Res.: Atmos., 2012, 117, 2012JD017446.
36. A. Kiselev, F. Bachmann, P. Pedevilla, S. J. Cox, A. Michaelides, D. Gerthsen and T. Leisner, Science, 2017, 355, 367–371.
37. M. Chatziparaschos, N. Daskalakis, S. Myriokefalitakis, N. Kalivitis, A. Nenes, M. Gonçalves Ageitos, M. Costa-Surós, C. Pérez García-Pando, M. Zanoli, M. Vrekoussis and M. Kanakidou, Atmos. Chem. Phys., 2023, 23, 1785–1801.
38. F. Mahrt, C. Marcolli, R. O. David, P. Grönquist, E. J. Barthazy Meier, U. Lohmann and Z. A. Kanji, Atmos. Chem. Phys., 2018, 18, 13363–13392.
39. C. Hoose, J. E. Kristjánsson and S. M. Burrows, Environ. Res. Lett., 2010, 5, 024009.
40. D. Turnbull and B. Vonnegut, Ind. Eng. Chem., 1952, 44, 1292–1298.
41. M. Fitzner, P. Pedevilla and A. Michaelides, Nat. Commun., 2020, 11, 4777.
42. E. Ochshorn and W. Cantrell, J. Chem. Phys., 2006, 124, 054714.
43. Y. Qiu, N. Odendahl, A. Hudait, R. Mason, A. K. Bertram, F. Paesani, P. J. DeMott and V. Molinero, J. Am. Chem. Soc., 2017, 139, 3052–3064.
44. L. Pharoah, A. K. Bertram and G. N. Patey, J. Phys. Chem. A, 2024, 128, 7214–7225.
45. T. Sun, D. Ben-Amotz and B. E. Wyslouzil, Phys. Chem. Chem. Phys., 2021, 23, 9991–10005.
46. T. Sun and B. E. Wyslouzil, J. Phys. Chem. B, 2021, 125, 12329–12343.
47. J. De Gouw and J. L. Jimenez, Environ. Sci. Technol., 2009, 43, 7614–7618.
48. P. Herckes, K. T. Valsaraj and J. L. Collett, Atmos. Res., 2013, 132–133, 434–449.
49. S. Pezzotti, D. R. Galimberti and M.-P. Gaigeot, J. Phys. Chem. Lett., 2017, 8, 3133–3141.
50. S. Pezzotti, A. Serva and M.-P. Gaigeot, J. Chem. Phys., 2018, 148, 174701–174710.
51. F. Tang, T. Ohto, S. Sun, J. R. Rouxel, S. Imoto, E. H. G. Backus, S. Mukamel, M. Bonn and Y. Nagata, Chem. Rev., 2020, 120, 3633–3667.
52. A. P. Fellows, Á. D. Duque, V. Balos, L. Lehmann, R. R. Netz, M. Wolf and M. Thämer, Langmuir, 2024, 40, 18760–18772.
53. L. S. G. Leite, S. Banerjee, Y. Wei, J. Elowitt and A. E. Clark, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2024, 14, e1729.
54. S. Bougueroua, R. Spezia, S. Pezzotti, S. Vial, F. Quessette, D. Barth and M.-P. Gaigeot, J. Chem. Phys., 2018, 149, 184102–184115.
55. S. Bougueroua, Y. Aboulfath, D. Barth and M.-P. Gaigeot, Mol. Phys., 2023, 121, e2162456.
56. S. Bougueroua, M. Bricage, Y. Aboulfath, D. Barth and M.-P. Gaigeot, Molecules, 2023, 28, 2892.
57. A. Hashemi, S. Bougueroua, M.-P. Gaigeot and E. A. Pidko, J. Chem. Inf. Model., 2023, 63, 6081–6094.
58. A. Hashemi, S. Bougueroua, M.-P. Gaigeot and E. A. Pidko, J. Chem. Theory Comput., 2022, 18, 7470–7482.
59. S. Bougueroua, Y. Aboulfath, A. Cimas, A. Hashemi, E. A. Pidko, D. Barth and M.-P. Gaigeot, C. R. Chim., 2024, 27, 1–23.
60. E. Lindahl, M. J. Hess, B. Hess and D. van der Spoel, GROMACS 2020.5 Manual, 2021,  DOI:10.5281/zenodo.4420784.
61. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
62. J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
63. C. Vega, J. L. F. Abascal and I. Nezbeda, J. Chem. Phys., 2006, 125, 034503.
64. C. Vega and E. de Miguel, J. Chem. Phys., 2007, 126, 154707.
65. J. Alejandre and G. A. Chapela, J. Chem. Phys., 2010, 132, 014701.
66. H. Hu and F. Wang, J. Chem. Phys., 2015, 142, 214507.
67. J. W. Biddle, R. S. Singh, E. M. Sparano, F. Ricci, M. A. González, C. Valeriani, J. L. F. Abascal, P. G. Debenedetti, M. A. Anisimov and F. Caupin, J. Chem. Phys., 2017, 146, 034502.
68. C. D. Wick, M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 2000, 104, 8008–8016.
69. B. Chen, J. J. Potoff and J. I. Siepmann, J. Phys. Chem. B, 2001, 105, 3093–3104.
70. Y. Andoh and K. Yasuoka, Langmuir, 2005, 21, 10885–10894.
71. M.-M. Walz, C. Caleman, J. Werner, V. Ekholm, D. Lundberg, N. L. Prisle, G. Öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2015, 17, 14036–14044.
72. V. Ekholm, C. Caleman, J. S. Hub and M. Wohlert, Phys. Chem. Chem. Phys., 2021, 23, 18823–18829.
73. A. Idrissi and P. Jedlovszky, J. Mol. Liq., 2021, 338, 116777.
74. A. Rahbari, R. Hens, S. H. Jamali, M. Ramdin, D. Dubbeldam and T. J. H. Vlugt, Mol. Simul., 2019, 45, 336–350.
75. F. Hrahsheh, Y. S. Wudil and G. Wilemski, Phys. Chem. Chem. Phys., 2017, 19, 26839–26845.
76. D. Berthelot, Compt. Rendus, 1898, 126, 1703–1706.
77. H. A. Lorentz, Ueber Die Anwendung Des Satzes Vom Virial in Der Kinetischen Theorie Der Gase, Ann. Phys., 1881, 248, 127–136.
78. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
79. A. P. dos Santos, M. Girotto and Y. Levin, J. Chem. Phys., 2016, 144, 144103.
80. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
81. M. Bernetti and G. Bussi, J. Chem. Phys., 2020, 153, 114107.
82. S. Takahama and L. M. Russell, J. Geophys. Res.: Atmos., 2011, 116, D02203.
83. O. Ozgurel, D. Duflot, M. Masella, F. Réal and C. Toubin, ACS Earth Space Chem., 2022, 6, 1698–1716.
84. A. C. Stewart, M. J. Paterson and S. J. Greaves, Environ. Sci.: Atmos., 2022, 2, 1516–1525.
85. J. Gao and W. L. Jorgensen, J. Phys. Chem., 1988, 92, 5813–5822.
86. H. Chen, W. Gan, B.-h. Wu, D. Wu, Y. Guo and H.-f. Wang, J. Phys. Chem. B, 2005, 109, 8053–8063.
87. E. Tyrode, C. M. Johnson, S. Baldelli, C. Leygraf and M. W. Rutland, J. Phys. Chem. B, 2005, 109, 329–341.
88. C. M. Phan, T. N. Le, C. V. Nguyen and S.-i. Yusa, Langmuir, 2013, 29, 4743–4749.
89. C. M. Phan, C. V. Nguyen and T. T. T. Pham, J. Phys. Chem. B, 2016, 120, 3914–3919.
90. J. A. White, E. Schwegler, G. Galli and F. Gygi, J. Chem. Phys., 2000, 113, 4668–4673.
91. S. Pezzotti, D. R. Galimberti, Y. R. Shen and M.-P. Gaigeot, Phys. Chem. Chem. Phys., 2018, 20, 5190–5199.
92. J. D. Horton, SIAM J. Comput., 1987, 16, 358–366.
93. S. Bougueroua, F. Quessette, D. Barth and M.-P. Gaigeot, GaTewAY: Graph Theory-Based Software for Automatic Analysis of Molecular Conformers Generated over Time, ChemRxiv, 2022, preprint,  DOI:10.26434/chemrxiv-2022-1d5x8-v2.
94. M.-T. Lee, F. Orlando, L. Artiglia, S. Chen and M. Ammann, J. Phys. Chem. A, 2016, 120, 9749–9758.
95. D. J. Henry, V. I. Dewan, E. L. Prime, G. G. Qiao, D. H. Solomon and I. Yarovsky, J. Phys. Chem. B, 2010, 114, 3869–3878.
96. S. Lenton, N. H. Rhys, J. J. Towey, A. K. Soper and L. Dougan, J. Phys. Chem. B, 2018, 122, 7884–7894.
97. J. J. Lin, T. B. Kristensen, S. M. Calderón, J. Malila and N. L. Prisle, Environ. Sci.: Processes Impacts, 2020, 22, 271–284.
98. M. El Haber, V. Gérard, J. Kleinheins, C. Ferronato and B. Nozière, Chem. Rev., 2024, 124, 10924–10963.
99. J. Alejandre, D. J. Tildesley and G. A. Chapela, J. Chem. Phys., 1995, 102, 4574–4583.
100. M. Tarek, D. J. Tobias and M. L. Klein, Phys. A, 1996, 231, 117–122.
101. T.-M. Chang and L. X. Dang, J. Phys. Chem. B, 2005, 109, 5759–5765.
102. A. Firooz and P. Chen, Langmuir, 2011, 27, 2446–2455.
103. A. Firooz and P. Chen, J. Colloid Interface Sci., 2012, 370, 183–191.
104. D. Ballal and W. G. Chapman, J. Chem. Phys., 2013, 139, 114706.
105. M.-M. Walz, J. Werner, V. Ekholm, N. L. Prisle, G. Öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2016, 18, 6648–6656.
106. J. Werner, J. Julin, M. Dalirian, N. L. Prisle, G. Öhrwall, I. Persson, O. Björneholm and I. Riipinen, Phys. Chem. Chem. Phys., 2014, 16, 21486–21495.
107. A. Serva, S. Pezzotti, S. Bougueroua, D. R. Galimberti and M.-P. Gaigeot, J. Mol. Struct., 2018, 1165, 71–78.
108. S. Pezzotti, A. Serva, F. Sebastiani, F. S. Brigiano, D. R. Galimberti, L. Potier, S. Alfarano, G. Schwaab, M. Havenith and M.-P. Gaigeot, J. Phys. Chem. Lett., 2021, 12, 3827–3836.
109. E. Stewart, R. L. Shields and R. S. Taylor, J. Phys. Chem. B, 2003, 107, 2333–2343.
110. Y. Andoh and K. Yasuoka, J. Phys. Chem. B, 2006, 110, 23264–23273.
111. D. R. Moberg, Q. Li, S. K. Reddy and F. Paesani, J. Chem. Phys., 2019, 150, 034701.
112. Ohio Supercomputer Center, 1987, https://osc.edu/ark:/19495/f5s1ph73.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00165f

---