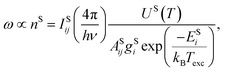Chlorine determination in cement paste samples using laser-induced breakdown spectroscopy and non-matching matrix calibration samples

Abstract

This paper deals with determining the chlorine content in cement matrixes using non-matching calibration samples made from microsilica and potassium chloride. We aimed to make easy-to-prepare calibration samples and determine the chlorine content in cement paste samples. To create proper cement paste samples, it is necessary to allow the concrete to mature for 28 days. Also, this methodology enables faster calibration and higher throughput in routine analysis. To suppress the matrix effect, we tested several strategies of signal normalization and then compared the reference (known) and the predicted chlorine content. Best results were obtained when we normalized the intensity of the chlorine line by a parameter proportional to the particle number density which was a priori determined by the intensity of the hydrogen emission line (H_α) and full width at half-maximum (FWHM). With this parameter, we obtained a high-reliability coefficient for the calibration curve (R² = 0.99) and the best prediction for total chloride content in cement paste, with a sum of mean squares of the prediction error of 0.22 wt%.

---

1 Introduction

It has repeatedly been proven that the detection of chlorine is important in many applications, e.g., civil engineering, specifically chlorine corrosion of reinforcement, pharmacy, air pollution, aqueous solutions, and detection of hazardous organic compounds.¹ The most common methods for determining the chloride content are wet chemistry (potentiometric titration and direct potentiometry) or photometry.² Laser-induced breakdown spectroscopy (LIBS) is an optical emission spectroscopy method. It is a flexible and micro-destructive method that can be used in situ and provides quick analysis, requiring almost no sample preparation. For these benefits, it is used in civil engineering,^3–6 biology,^7–9 forensics,^10–13 polymers,^14,15 and space research.^16,17

For halogens, especially chlorine, detection has typically lower sensitivity in LIBS measurements. Other spectroscopy methods, like atomic absorption spectroscopy (AAS) and inductively coupled optical emission spectroscopy (ICP-OES), provide better chlorine sensitivity. On the other hand, it requires a liquid sample with significant dilution, unlike LIBS, which works with solid samples. X-ray fluorescence (XRF) also works with solid samples, but higher sensitivity applies mainly to higher-Z nonmetallic elements.¹⁸

Thus, many strategies have been developed to improve sensitivity, including the double-pulse (DP) LIBS configuration, for enhancing the emission intensity and lowering the limits of detection. There are two main geometries: collinear and orthogonal. In the orthogonal geometry, one beam is focused on the sample surface, and the second beam is directed parallel to the sample surface. The parallel laser beam can reheat the plasma (re-heating scheme) or it can create an air spark slightly above the sample surface before the ablation of the sample (pre-ablation scheme). In collinear geometry, both laser beams share the same path and are directed at the sample surface.¹⁹ Signal enhancement may be caused by several mechanisms – improved laser material coupling and the resulting ablation rate of the sample material, increased electron density of laser-induced plasma, and higher plasma temperature. Mechanisms of signal enhancement and dynamics of DP LIP are described in detail elsewhere.^20–22

The most common strategy of quantitative analysis in spectroscopy is through regression analysis. This establishes a relationship between a spectral feature (such as the intensity of a selected emission spectral line) and a chosen element content. However, the limitation of this approach lies in a relatively low shot-to-shot stability of LIBS and the resulting emission signal and a strong dependence on the sample matrix. The most prevalent method for augmenting the shot-to-shot signal stability is a normalization utilizing an internal standard. In this approach, the ratio of intensity of the spectral line under investigation to a suitable plasma emission signal is employed. Commonly used internal standards include total plasma emissivity, background emission, and the intensity of a reference spectral line that belongs to the matrix element. An alternative approach is a normalization utilizing an external reference signal of distinct nature, such as acoustic wave signals^23–27 electrical current,²⁸ or ablated mass of the sample.²⁹ Multivariate correlative normalization can also be employed, which enables the simultaneous suppression of multiple causes of signal fluctuations by combining several reference signals. In addition to the aforementioned empirical normalization methods, more rigorous methods that take into account plasma parameters such as electron density and temperature^30–32 have also been proposed. A comprehensive overview of normalization approaches was published by Zorov et al.³³

The physical and mechanical properties of the sample may influence the resulting plasma parameters. This phenomenon is called the matrix effect. In other words, the intensity of the emission line for one element with the same content could be different if we use diverse types of matrices. It is possible to study the matrix effect by comparison of different line intensities for different matrices with similar (or the same) content of the studied element. However, it is impossible to directly utilize the calibration curve based on non-matrix matched samples. On the other hand, if the complex processes beyond laser–matter interaction, material ablation, and laser-induced plasma formation are understood, it is possible to suppress the matrix effect.³⁴

There are several published papers dealing with the matrix effect for metallic samples, but none for non-metals, which include halogens such as chlorine. W. Wang et al.³⁵ studied the matrix effect on laser defocus for metal elements (Cu, Ti, Mn, and Cr) in carbon steel and aluminum alloy. They found that matrix effects have different degrees of influence on the analysis. The lowest matrix effect is observed in the mixed matrix (Al + Fe). Also, the influence of the matrix effect can be reduced by laser defocus. J. M. Anzano et al.³⁶ compared the matrix effect in powder samples of Al₂O₃ and SiO₂ in ores with the same powder samples pressed into tablets. They demonstrated that the matrix effect was less significant in powder samples. A. Hrdlička et al.³⁷ dealt with the determination of sulfur in concrete using SP LIBS and used a simplified calibration series for the quantification, i.e., the standards were not prepared from cement but from synthetic limestone powder and contained a defined addition of sodium sulfate. The same author applied a similar strategy for asphalts³⁸ when detecting the total content of sulfur in asphalts using non-matching calibration samples. They used two different matrices –cellulose and synthetic limestone – with defined weighed amounts of Na₂SO₄·10H₂O.

In this paper, we demonstrate the possibility of using non-matrix-matched calibration samples for chlorine quantification in cement materials. Moreover, the samples were measured under different experimental conditions since the optimal conditions differ due to the matrix effect. Calibration samples are in the form of homogeneous pressed powder tablets made of chloride (KCl) in a pure inorganic matrix (microsilica – SiO₂). Based on this calibration curve, we tried to predict the content of chlorine in homogeneous cement paste with added NaCl. We compared several strategies of normalization and the obtained precision. We normalized the chlorine line intensity to different elemental emission line intensities (such as silicon, hydrogen, and oxygen) presented in both sets of samples. However, the results were insufficient, so we introduced a new coefficient ω which is proportional to the particle number density derived from the H_α line. For each normalization strategy, we observed and compared changes in the reliability coefficient (R²) and a sum of squares of prediction error (PE_err).

2 Materials and methods

2.1. Samples

The first set of calibration samples (henceforth marked as KS) was prepared by grinding silica (SiO₂) in a laboratory agate mortar. Potassium chloride was added to the silica matrix. Both powders are of per analysis purity. The weight of chloride salts was weighed to four decimal places, so it was possible to calculate the exact weight of chlorine in each sample. The powder was homogenized for a couple of minutes in a mortar and then put in a table press for 4 minutes under a pressure of 80 kPa. We kept all samples in Petri dishes in a room with controlled temperature. Also, we tried to study different matrices, such as limestone samples and limestone–microsilica samples, next to the microsilica samples. However, limestone and limestone–microsilica samples were ruined during the measurements.

The second set of samples was made from cement paste (henceforth marked as BAM). Those samples were prepared at the Federal Institute for Materials Research and Testing (Berlin, Germany) and were part of the Round Robin test² organized by the same institute in 2021. To avoid any chemical changes due to contact with moisture, samples were kept in a laboratory desiccator. Samples were prepared by mixing ordinary Portland cement with deionized water and sodium chloride. After 28 days of curing in the atmosphere with humidity, prisms were dried to a constant weight, ground and pressed into pellets. Table 1 presents a list of all used samples and their respective chlorine content.

Table 1 List of KS and BAM calibration samples, their used name, and weight percentage of chlorine in each sample

Used name	Cl [wt%]	Used name	Cl [wt%]	Used name	Cl [wt%]
KS1	0.14	BAM1	0.06	BAM7	0.85
KS2	0.33	BAM2	0.19	BAM8	0.98
KS3	0.53	BAM3	0.32	BAM9	1.15
KS4	1.33	BAM4	0.46	BAM10	1.43
KS5	1.83	BAM5	0.59	BAM11	1.71
KS6	3.90	BAM6	0.72	BAM12	1.95

---

In our experiment, two different chlorides (KCl and NaCl) were used. Research done by S. Millar et al.³⁹ found that different cations do not have a significant influence on chlorine detection.

2.2. LIBS system

For this experiment, the LIBS Discovery (CEITEC BUT, Czech Republic) system was used. The LIBS Discovery consists of a closed interaction chamber and a pulsed Nd:YAG Q-switched laser (532 nm, 8 ns, 20 Hz). For the double-pulse, the second laser was also an Nd:YAG Q-switched laser (1064 nm, 10 ns, 20 Hz). All emissions were brought into the wide-range echelle spectrometer (190–1100 nm) with a gate width of 50 μs. A further description of the system and spectrometer is presented in our former article.⁴⁰ The samples were placed on the motorized and controlled positioning stage. All experiments were done in a helium atmosphere in the interaction chamber under atmospheric pressure. It is possible to detect the chlorine emission line in argon and helium (and air). However, the best signal-to-noise ratio is observed in helium. We are assuming that it is because of the higher ionization energy of helium (24.59 eV) in comparison to argon (15.76 eV), so helium has a greater excitation capacity of plasma.⁴¹ On the other hand, it has a much lower electron density and decays faster than other buffer gases mentioned earlier.⁴² Needless to say, most of the chlorine detection is done in a helium atmosphere. It is proven that this experimental condition shows better results.^43,44

For the KS samples measured with single-pulse (SP) LIBS, the optimal parameters were 64 mJ laser pulse energy and 0.25 μs gate delay. For double-pulse (DP) LIBS, the optimal parameters were 50 mJ and 100 mJ laser pulse energies, 1.5 μs interpulse delay, and 1.0 μs gate delay. For the BAM samples, only DP LIBS was used due to higher sensitivity. The best parameters were 100 mJ, 10 μs and 0.3 μs of laser pulse energies, interpulse delay and gate delay, respectively.

2.3. Data processing

Each sample was represented by 15 LIBS spectra (3 × 5 matrix). For data processing, we used LIBS Analyzer software (CEITEC, Czech Republic) and RStudio (Austria).⁴⁵ First, the background was subtracted from all spectra by moving the minimum algorithm.⁴⁶ Afterward, mean spectra were calculated. Graphs and spectra were prepared in Origin 2020b. Our focus is on a chlorine spectral line, Cl I 837.59 nm, and its peak intensity.

3 Results and discussion

3.1. Optimization

Since our goal was to obtain maximal sensitivity, the experimental parameters were optimized for KS and BAM samples separately. To ensure that Cl line intensity will be above the limits of detection even for non-optimal experimental conditions, we used a specially prepared sample with a Cl content of 7.63 wt%. For the BAM samples, we used the sample BAM12 (1.95 wt%). Our goal was to obtain a maximal signal-to-background ratio (SBR) of Cl I 837.59 nm.

3.1.1. KS sample optimization. For the single-pulse SP LIBS measurement of a KS sample, the laser pulse energy and the gate delay were optimized. In the range of energies given by the laser (max. 100 mJ), we observed an evident trend where higher energy is linearly proportional to SBR. However, the selected energy was a tradeoff between SBR and the sample damage (our goal was to perform at least 15 measurements per sample). In this regard, the best parameters were 64 mJ and 0.25 μs, respectively. For the DP, the first step was to set an optimal interpulse delay. It is worth noting that we did not optimize the energy of the second laser, but we set the energy based on our experiences and on the results of other publications^47,48 in a ratio of 1 : 2, which means that the energy of the first and second laser pulses was 50 mJ and 100 mJ, respectively. The most convenient combination of SBR and signal stability led us to select an interpulse delay of 1.5 μs. The gate delay was set up to 1.0 μs.

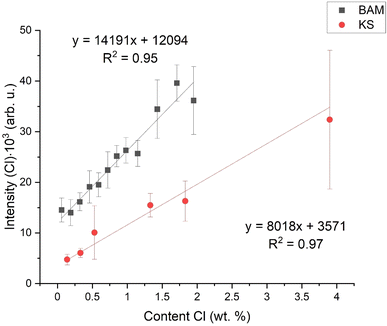
With optimized parameters, we were able to obtain calibration curves for SP and DP for KS samples. The signal enhancement of the chlorine line in comparison to SP and DP LIBS is shown in Fig. 1. As we can see, the slope has increased almost fourteen times.

Fig. 1 Calibration dependence of KS tablets; gray – single-pulse, red – double-pulse, and intensity of the spectral line – Cl I 837.59 nm.

3.1.2. Optimization of BAM samples. Because of the different matrices, the optimization process was done for the pellets made from cement paste. Based on the results of previous optimization, only DP was optimized for BAM samples. Contrary to KS samples, the BAM samples were more solid, and the sample damage was negligible. As a result, we utilized the maximal energy available for both pulses (100 mJ). For these energies, the interpulse delay and gate delay were optimized. The selected interpulse delay and gate delay were 10 μs and 0.3 μs, respectively.

3.2 Quantification

As said in the Introduction, the matrix effect includes the mechanical and physical properties of the sample, such as latent heat. It influences plasma parameters, such as temperature and electron density. The aim of this work is to find a parameter describing these differences and which could suppress the matric effect. As shown in Fig. 2, there is the initial calibration dependence – a simple dependence of Cl I 837.59 nm emission intensity (surface of the spectral line above the background) on the chlorine content in the respective sample. As we can see, even for very similar chlorine contents, the intensities of the chlorine lines differ significantly due to the matrix effect. For the sake of clarity, for both sets of samples (KS and BAM), we add a linear fit. By comparing the intercepts and slopes of both fits, we can briefly estimate the quality of the calibration model.

Fig. 2 Initial calibration dependencies,; intensity of the spectral line – Cl I 837.59 nm.

3.3. Normalization

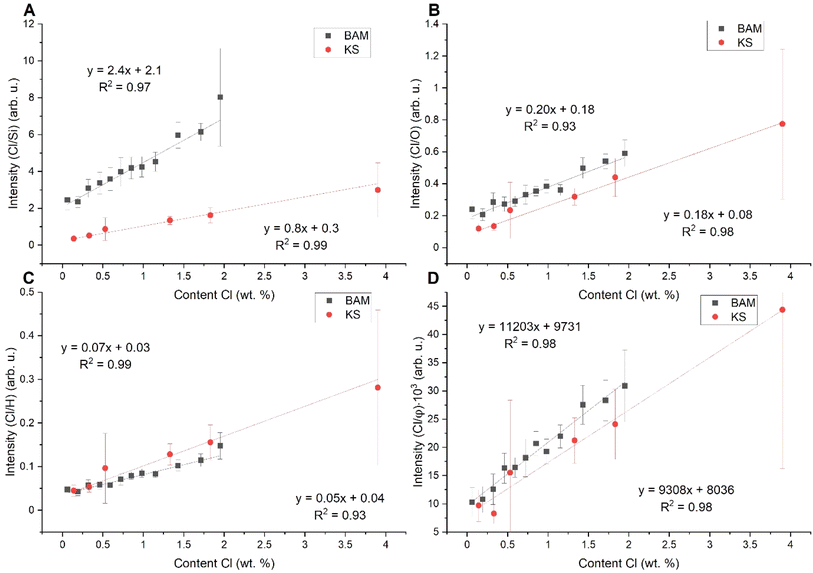
We compare several normalization strategies based on the single matrix calibration curve R² (reliability coefficient) and inter-matrix normalization. In a nutshell, we study the influence of selected normalization on the calibration curve R² (based on KS samples) and the precision of prediction of Cl content in BAM samples based on the KS calibration curve (Fig. 3). The definitions of R² and the procedure for prediction precision determination are discussed in the Appendix (see the ESI).†

Fig. 3 Calibration dependencies normalized to different aspects: (A) normalized to the silicon line Si I 288.16 nm, (B) to the oxygen line O I 777.14 nm, (C) to the hydrogen line H_α 656.28 nm, and (D) to the φ (proportional to the electron density); all intensities are normalized to the intensity of the chlorine spectral line – Cl I 837.59 nm.

We normalized the intensity of the chlorine line to the silicon line (Si I 288.16 nm), see Fig. 3A. Silicon is present in both samples; however, it represents the matrix element in KS samples. Si is also present in cement paste samples because SiO₂ is one of the four major oxides for cement production. However, the Si content in cement paste samples is lower in comparison with KS samples. Fig. 3A shows that the normalization to Si can suppress the shot-to-shot fluctuations and improves the R². However, it does not influence the matrix effect. We normalized the intensity to the oxygen line (O I 777.14 nm), see Fig. 3B. We did the measurements in a helium atmosphere, and we could expect the oxygen to originate from the oxides in the samples. As depicted by the graph in Fig. 3B, the slopes of both linear fits are closer to each other, but there is still a significant difference in the intercept. For normalization, we also utilized the intensity of the hydrogen line (H_α 656.28 nm) and electron density based on the FWHM of H_α, see Fig. 3C and D, respectively. We marked it as a φ, and its value was based on the FWHM of the Lorentz profile of H_α. The FWHM was determined by fitting the H_α by the Voigt analytical function.⁴⁹ The respective partition function was derived from NIST.⁵⁰

It is worth noting that it is not possible to employ the Boltzmann plot or Saha–Boltzmann plot for plasma temperature determination because of a long gate width (50 μs), and also the value derived from H_α will represent only an estimate of the average temperature of a plasma during its lifetime. On the other hand, the goal of this calculation is not to obtain the plasma temperature and particle number density respectively, but only some values describing plasma parameters for different matrices and experimental conditions. We followed the procedure described, e.g., in ref. 51 and an equation:

where Δλ_1/2 is the FWHM in angstrom and α_1/2 is a weak function of electron density and temperature tabulated in ref. 52. As shown in Fig. 3C and D, both approaches improve both the slope and intercept; however, the results are still insufficient for the quantification of chlorine in BAM samples. The primary reason for this insufficiency is that the parameters of the calibration curves do not overlap adequately, which would lead to the precise prediction of the content of BAM samples. The parameter which describes the differences is discussed later and numerically expressed in Table 2.

Table 2 The reliability coefficient (R²) and the sum of mean squares of prediction error (PE_err) for each normalization strategy

Normalization	R ^2 [arb. u.]	PEerr [wt%]	PEerr min [wt% × 10^−3]	PEerr max [wt%]	Figure
None	0.97	48.62	1280.00	10.31	2
Cl/Si	0.99	330.39	7360.00	85.97	3A
Cl/O	0.98	5.08	110.00	0.74	3B
Cl/H	0.99	1.37	0.05	0.31	3C
Cl/φ	0.98	1.85	10.00	0.45	3D
Cl/ω	0.99	0.22	0.93	0.06	4

---

For further calculations, we chose the value proportional to the particle number density derived from the H_α line, so we introduced a new coefficient ω:⁵³

where I^S_ij (eV cm⁻³ s⁻¹) is the intensity of atomic or ionic line of element S, i and j are the indexes of the higher and lower energetic quantum states of the same ionization stage, n^S (cm⁻³) is the total number density of species S, A^S_ij (s⁻¹) is the transition probability of the upper level of species S, g^S_i (dimensionless) is degeneracy of the upper level, E^S_i (eV) is the excitation energy of the upper level, T_exc (K) is the excitation temperature, k_B (eV K⁻¹) is the Boltzmann constant, h (eV s) is the Planck constant and U^S(T) (dimensionless) is the internal partition function of selected species at temperature T_exc (K). The basic idea is described, for example, in ref. 54. The temperature was determined from the Gaussian contribution to the FWHM of H_α:
where Δλ_D is the Gaussian contribution to the FWHM of the Voigt profile of H_α.

As we can see in Table 2, R² is very high (0.99) for this normalization and the PE_err is the lowest. Even though we did the measurements in a helium atmosphere, hydrogen was present in the samples. For BAM samples, the hydrogen was clearly from chemically bound water molecules (crystalline water in the CSH gel). For the KS samples, it was most probably the hydrogen from the air humidity because of the hygroscopic behavior of KCl. Table 2 shows R², the sum of the mean squares of prediction error (PE_err), and the minimum and maximum difference between reference and predicted contents for each applied normalization strategy. In Fig. 4 are the final calibration dependencies.

Fig. 4 Calibration dependence on the normalized intensity of the Cl line (Cl I 837.59 nm).

Conclusion

This study presents the possibility of using non-matching calibration samples to determine chlorine. While earlier studies focused on metallic samples or detected easily excited elements, for our study, we chose cement paste samples and samples made of microsilica, with additional chlorine salts. It simplifies the sample preparation because concrete (and cement paste) samples require time to mature (at least 28 days to receive mostly hydrated cement).

We apply the calculations for spectra to normalize the intensity of the chlorine line and suppress the influence of the matrix effect, which we observed due to the different nature of matrixes. After normalization to spectral line emission intensities of different elements, we chose the best combination of R² and PE_err, which was for the H_α line. The value changed from 0.97 to 0.99 and from 48.62 wt% to 1.37 wt%, respectively. For further data processing, we introduced a new coefficient ω which is proportional to the particle number density. It leads to an improvement in the PE_err to a value of 0.22 wt%. In our case study, only one cement type was used. The presented methodology may not apply to other cement types due to different ratios and chemical composition of components. This methodology has the potential to be used for other elements and matrixes where the calibration standards lack or are hard to establish.

Data availability

Data for this article are available at: https://doi.org/10.5281/zenodo.13885308.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DP gratefully acknowledges the support of TAČR TREND (FW06010042). The authors acknowledge the support of the Faculty of Mechanical Engineering, Brno University of Technology (no. FSI-S-23-8389).

References

1. G. Asimellis, S. Hamilton, A. Giannoudakos and M. Kompitsas, Controlled inert gas environment for enhanced chlorine and fluorine detection in the visible and near-infrared by laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2005, 60(7–8), 1132–1139.
2. T. Völker, G. Wilsch, I. B. Gornushkin, L. Kratochvilová, P. Pořízka and J. Kaiser, et al., Interlaboratory comparison for quantitative chlorine analysis in cement pastes with laser induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2023, 202, 106632.
3. S. Millar, S. Kruschwitz and G. Wilsch, Determination of total chloride content in cement pastes with laser-induced breakdown spectroscopy (LIBS), Cem. Concr. Res., 2019, 117, 16–22.
4. T. A. Labutin, A. M. Popov, S. M. Zaytsev, N. B. Zorov, M. v Belkov and V. v Kiris, et al., Determination of chlorine, sulfur and carbon in reinforced concrete structures by double-pulse laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2014, 99, 94–100.
5. M. A. Gondal, A. Dastageer, M. Maslehuddin, A. J. Alnehmi and O. S. B. Al-Amoudi, Detection of sulfur in the reinforced concrete structures using a dual pulsed LIBS system, Opt Laser. Technol., 2012, 44(3), 566–571.
6. F. Weritz, A. Taffe, D. Schaurich and G. Wilsch, Detailed depth profiles of sulfate ingress into concrete measured with laser induced breakdown spectroscopy, Constr. Build. Mater., 2009, 23(1), 275–283.
7. P. Modlitbová, P. Pořízka and J. Kaiser, Laser-induced breakdown spectroscopy as a promising tool in the elemental bioimaging of plant tissues, TrAC, Trends Anal. Chem., 2020, 122, 115729.
8. A. Šindelářová, P. Pořízka, P. Modlitbová, L. Vrlíková, K. Kiss and M. Kaška, et al., Methodology for the implementation of internal standard to laser-induced breakdown spectroscopy analysis of soft tissues, Sensors, 2021, 21(3), 900.
9. K. Kiss, A. Šindelářová, L. Krbal, V. Stejskal, K. Mrázová and J. Vrábel, et al., Imaging margins of skin tumors using laser-induced breakdown spectroscopy and machine learning, J. Anal. At. Spectrom., 2021, 36(5), 909–916.
10. D. Prochazka, M. Bilík, P. Prochazková, M. Brada, J. Klus and P. Pořízka, et al., Detection of visually unrecognizable braking tracks using laser-induced breakdown spectroscopy, a feasibility study, Spectrochim. Acta, Part B, 2016, 118, 90–97.
11. F. Cicconi, V. Lazic, A. Palucci, A. C. Almeida Assis and F. Saverio Romolo, Forensic analysis of commercial inks by laser-induced breakdown spectroscopy (LIBS), Sensors, 2020, 20(13), 3744.
12. F. F. Hilario, M. L. de Mello and E. R. Pereira-Filho, Forensic analysis of hand-written documents using laser-induced breakdown spectroscopy (LIBS) and chemometrics, Anal. Methods, 2021, 13(2), 232–241.
13. M. Tofanelli, L. Pardini, M. Borrini, F. Bartoli, A. Bacci and A. D'Ulivo, et al., Spectroscopic analysis of bones for forensic studies, Spectrochim. Acta, Part B, 2014, 99, 70–75.
14. I. Chamradová, P. Pořízka and J. Kaiser, Laser-induced breakdown spectroscopy analysis of polymers in three different atmospheres, Polym. Test., 2021, 96, 107079.
15. L. Brunnbauer, S. Larisegger, H. Lohninger, M. Nelhiebel and A. Limbeck, Spatially resolved polymer classification using laser induced breakdown spectroscopy (LIBS) and multivariate statistics, Talanta, 2020, 209, 120572.
16. A. K. Knight, N. L. Scherbarth, D. A. Cremers and M. J. Ferris, Characterization of laser-induced breakdown spectroscopy (LIBS) for application to space exploration, Appl. Spectrosc., 2000, 54(3), 331–340.
17. A. J. Effenberger Jr and J. R. Scott, Effect of atmospheric conditions on LIBS spectra, Sensors, 2010, 10(5), 4907–4925.
18. S. K. H. Shah, J. Iqbal, P. Ahmad, M. U. Khandaker, S. Haq and M. Naeem, Laser induced breakdown spectroscopy methods and applications: A comprehensive review, Radiat. Phys. Chem., 2020, 170, 108666.
19. C. Gautier, P. Fichet, D. Menut, J. L. Lacour, D. L'Hermite and J. Dubessy, Main parameters influencing the double-pulse laser-induced breakdown spectroscopy in the collinear beam geometry, Spectrochim. Acta, Part B, 2005, 60(6), 792–804.
20. E. Tognoni and G. Cristoforetti, Basic mechanisms of signal enhancement in ns double-pulse laser-induced breakdown spectroscopy in a gas environment, J. Anal. At. Spectrom., 2014, 29(8), 1318–1338.
21. D. Prochazka, P. Pořízka, J. Novotný, A. Hrdlička, K. Novotný and P. Šperka, et al., Triple-pulse LIBS: laser-induced breakdown spectroscopy signal enhancement by combination of pre-ablation and re-heating laser pulses, J. Anal. At. Spectrom., 2020, 35(2), 293–300.
22. J. Scaffidi, S. M. Angel and D. A. Cremers, Emission Enhancement Mechanisms in Dual-Pulse LIBS, ACS Publications, 2006.
23. J. Buday, D. Prochazka, A. Záděra, V. Kaňa, P. Pořízka and J. Kaiser, Correlation of characteristic signals of laser-induced plasmas, Spectrochim. Acta, Part B, 2022, 194, 106476.
24. F. Anabitarte García, L. Rodríguez Cobo, J. M. López Higuera and A. Cobo García, Normalization of Laser-Induced Breakdown Spectroscopy Spectra Using a Plastic Optical Fiber Light Collector and Asensor Device, 2012.
25. Y. Cai and N. H. Cheung, Photoacoustic monitoring of the mass removed in pulsed laser ablation, Microchem. J., 2011, 97(2), 109–112.
26. S. Conesa, S. Palanco and J. J. Laserna, Acoustic and optical emission during laser-induced plasma formation, Spectrochim. Acta, Part B, 2004, 59(9), 1395–1401.
27. A. Hrdlička, L. Zaorálková, M. Galiová, T. Čtvrtníčková, V. Kanický and V. Otruba, et al., Correlation of acoustic and optical emission signals produced at 1064 and 532 nm laser-induced breakdown spectroscopy (LIBS) of glazed wall tiles, Spectrochim. Acta, Part B, 2009, 64(1), 74–78.
28. F. Bredice, H. Sobral, M. Villagran-Muniz, H. O. di Rocco, G. Cristoforetti and S. Legnaioli, et al., Real time measurement of the electron density of a laser generated plasma using a RC circuit, Spectrochim. Acta, Part B, 2007, 62(8), 836–840.
29. S. I. Gornushkin, I. B. Gornushkin, J. M. Anzano, B. W. Smith and J. D. Winefordner, Effective normalization technique for correction of matrix effects in laser-induced breakdown spectroscopy detection of magnesium in powdered samples, Appl. Spectrosc., 2002, 56(4), 433–436.
30. L. Li, Z. Wang, T. Yuan, Z. Hou, Z. Li and W. Ni, A simplified spectrum standardization method for laser-induced breakdown spectroscopy measurements, J. Anal. At. Spectrom., 2011, 26(11), 2274–2280.
31. U. Panne, C. Haisch, M. Clara and R. Niessner, Analysis of glass and glass melts during the vitrification process of fly and bottom ashes by laser-induced plasma spectroscopy. Part I: Normalization and plasma diagnostics, Spectrochim. Acta, Part B, 1998, 53(14), 1957–1968.
32. Z. Wang, L. Li, L. West, Z. Li and W. Ni, A spectrum standardization approach for laser-induced breakdown spectroscopy measurements, Spectrochim. Acta, Part B, 2012, 68, 58–64.
33. N. B. Zorov, A. A. Gorbatenko, T. A. Labutin and A. M. Popov, A review of normalization techniques in analytical atomic spectrometry with laser sampling: From single to multivariate correction, Spectrochim. Acta, Part B, 2010, 65(8), 642–657.
34. S. Shabbir, Y. Zhang, C. Sun, Z. Yue, W. Xu and L. Zou, et al., Transfer learning improves the prediction performance of a LIBS model for metals with an irregular surface by effectively correcting the physical matrix effect, J. Anal. At. Spectrom., 2021, 36(7), 1441–1454.
35. W. Wang, L. Sun, P. Zhang, T. Chen, L. Zheng and L. Qi, Study of matrix effects in laser-induced breakdown spectroscopy by laser defocus and temporal resolution, J. Anal. At. Spectrom., 2021, 36(9), 1977–1985.
36. J. M. Anzano, M. A. Villoria, A. Ruíz-Medina and R. J. Lasheras, Laser-induced breakdown spectroscopy for quantitative spectrochemical analysis of geological materials: Effects of the matrix and simultaneous determination, Anal. Chim. Acta, 2006, 575(2), 230–235.
37. A. Hrdlička, J. Hegrová, K. Novotný, V. Kanický, D. Prochazka and J. Novotný, et al., Sulfur determination in concrete samples using laser-induced breakdown spectroscopy and limestone standards, Spectrochim. Acta, Part B, 2018, 142, 8–13.
38. A. Hrdlička, J. Hegrová, E. Havrlová, D. Prochazka, J. Novotný and K. Novotný, et al., Calibration standards for Laser-Induced Breakdown Spectroscopy analysis of asphalts, Spectrochim. Acta, Part B, 2020, 170, 105919.
39. S. Millar, C. Gottlieb, T. Günther, N. Sankat, G. Wilsch and S. Kruschwitz, Chlorine determination in cement-bound materials with Laser-induced Breakdown Spectroscopy (LIBS)–A review and validation, Spectrochim. Acta, Part B, 2018, 147, 1–8.
40. I. Chamradová, P. Pořízka and J. Kaiser, Laser-induced breakdown spectroscopy analysis of polymers in three different atmospheres, Polym. Test., 2021, 96, 107079.
41. J. Mateo, M. C. Quintero, J. M. Fernández, M. C. García and A. Rodero, Application of LIBS technology for determination of Cl concentrations in mortar samples, Constr. Build. Mater., 2019, 204, 716–726.
42. J. A. Aguilera and C. Aragón, A comparison of the temperatures and electron densities of laser-produced plasmas obtained in air, argon, and helium at atmospheric pressure, Appl. Phys. A, 1999, 69, S475–S478.
43. J. Mateo, M. C. Quintero, J. M. Fernández, M. C. García and A. Rodero, Application of LIBS technology for determination of Cl concentrations in mortar samples, Constr. Build. Mater., 2019, 204, 716–726.
44. G. Wilsch, F. Weritz, D. Schaurich and H. Wiggenhauser, Determination of chloride content in concrete structures with laser-induced breakdown spectroscopy, Constr. Build. Mater., 2005, 19(10), 724–730.
45. Team RC, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2016, https://www.r-project.org/.
46. P. Yaroshchyk and J. E. Eberhardt, Automatic correction of continuum background in Laser-induced Breakdown Spectroscopy using a model-free algorithm, Spectrochim. Acta, Part B, 2014, 99, 138–149.
47. R. Ahmed, J. Iqbal and M. A. Baig, Effects of laser wavelengths and pulse energy ratio on the emission enhancement in dual pulse LIBS, Laser Phys. Lett., 2015, 12(6), 066102.
48. P. A. Benedetti, G. Cristoforetti, S. Legnaioli, V. Palleschi, L. Pardini and A. Salvetti, et al., Effect of laser pulse energies in laser induced breakdown spectroscopy in double-pulse configuration, Spectrochim. Acta, Part B, 2005, 60(11), 1392–1401.
49. J. F. Kielkopf, New approximation to the Voigt function with applications to spectral-line profile analysis, J. Opt. Soc. Am., 1973, 63(8), 987–995.
50. A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (ver. 5.3), 2015.
51. J. Ashkenazy, R. Kipper and M. Caner, Spectroscopic measurements of electron density of capillary plasma based on Stark broadening of hydrogen lines, Phys. Rev. A, 1991, 43(10), 5568.
52. H. Griem, Spectral Line Broadening by Plasmas. Elsevier, 2012.
53. D. A. Cremers and L. J. Radziemski, Handbook of Laser-Induced Breakdown Spectroscopy, John Wiley & Sons, 2013.
54. U. Panne, C. Haisch, M. Clara and R. Niessner, Analysis of glass and glass melts during the vitrification process of fly and bottom ashes by laser-induced plasma spectroscopy. Part I: Normalization and plasma diagnostics, Spectrochim. Acta, Part B, 1998, 53(14), 1957–1968.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00370e

---