Open Access Article
Open Access ArticleSparse modeling based Bayesian optimization for experimental design†
Ryuji
Masui
*a,
Unseo
Lee
a,
Ryo
Nakayama
 *b and
Taro
Hitosugi
*b and
Taro
Hitosugi
 b
b
aHACARUS Inc, Kyoto, 604-0835, Japan. E-mail: ryuji@hacarus.com
bDepartment of Chemistry, School of Science, The University of Tokyo, Tokyo, 113-0033, Japan. E-mail: ryo-nakayama@g.ecc.u-tokyo.ac.jp
First published on 20th May 2025
Abstract
The efficient optimization of high-dimensional synthesis parameters using Bayesian optimization (BO) remains challenging in recent materials exploration. Sparse-modeling-based BO is a powerful method for optimizing high-dimensional synthesis parameters. However, previous methods, such as BO using an automatic relevance determination kernel, cannot explore various materials. This study proposes a sparse modeling-based BO using the maximum partial dependence effect (MPDE). The optimization performances of the proposed and conventional BOs are compared using model functions to simulate materials synthesis in a high-dimensional search space. Compared to conventional sparse estimation methods using ARD kernels, Bayesian optimization with MPDE allows the materials researcher to easily set the threshold for sparse estimation, leading to optimization with fewer trials. This is because, in MPDE, the scale of threshold is the same as the materials' properties, allowing an intuitive setting to ignore synthetic parameters that affect, for example, only up to 10% of the target value at most. Therefore, BO using MPDE is expected to facilitate the exploration of materials in a high-dimensional search space and is applicable to automatic and autonomous experiments utilizing robots.
1. Introduction
High-throughput prediction and the synthesis of new materials are paramount for realizing a sustainable society. The combinations of elements include over 1060 possible candidates for new materials, and the synthesis of materials composed of multiple elements is in progress.1–3 Complex experimental procedures and enhanced equipment have increased the number of controllable synthesis parameters. Therefore, the optimization of high-dimensional synthesis parameters in a small number of trials is a formidable challenge because materials synthesis experiments incur significant financial and temporal costs. Thus, there is a strong demand for efficient optimization of high-dimensional synthesis parameters.Bayesian optimization (BO) has recently been applied to materials synthesis to efficiently optimize synthesis parameters.4–11 Moreover, BO has been combined with robotics to realize autonomous materials synthesis, which enhances the efficiency of materials exploration.12–18 In our previous research, we simulated synthesis condition optimization using model functions with one-, two-, and three-dimensional synthesis parameters.19,20 Our results indicated that the number of trials required for optimization tended to grow exponentially with an increase in the dimensionality of the synthesis parameters. The cost of the experiments limited the number of feasible experiments. For instance, in thin-film synthesis using vapor deposition, a single researcher typically synthesizes no more than 50–100 samples per month. Materials researchers have carefully selected important synthesis parameters from several candidate parameters to optimize synthesis conditions based on their knowledge and experience. Although BO can efficiently optimize the parameters, researchers must choose the important ones for BO. Consequently, in such a conventional approach, researchers are constrained by common sense and preconceptions, which limit their exploration to a small fraction of the vast search space. Novel materials such as conductive polymers have been developed using unconventional experimental processes and parameter ranges.21 Therefore, excessive reliance on common sense and preconceptions in material exploration reduces the opportunities to discover high-performance functional materials hidden in unexplored search spaces.
Sparse modeling can facilitate the extraction of only critical synthesis parameters from high-dimensional parameters without human intervention. It is a widely adopted approach in machine learning that assumes that only a few inputs significantly contribute to the output among the numerous input variables.22–24 For instance, in a practical material synthesis, tuning only the critical parameters (e.g., composition, temperature, and pressure) that strongly affect the target variables (e.g., material properties and yield) is expected. Therefore, tuning unimportant parameters that have a negligible impact on the optimization process is undesirable. Sparse modeling can extract important synthesis parameters and facilitate optimization. An automatic relevance determination (ARD) kernel (ARD-BO) can automatically narrow down high-dimensional synthesis parameters by considering sparsity.25 In ARD-BO, by setting a threshold for a hyperparameter of ARD kernel, referred to as a length scale, synthetic parameters that do not affect the target variable are categorized as unimportant, thus facilitating the automated extraction of important parameters. However, materials researchers encounter difficulties in intuitively setting an appropriate threshold value owing to the influence of unimportant synthetic parameters on properties and yields being small but not zero.
This study proposes and demonstrates a sparse modeling-based Bayesian optimization using the maximum partial dependence effect (MPDE), referred to as MPDE-BO. MPDE quantifies the significance of the contribution of each synthesis parameter to the material properties or yield. The synthesis condition optimization is simulated using MPDE-BO with model functions resembling materials synthesis. When one of the four synthesis parameters is an unimportant parameter of the material properties, MPDE-BO successfully reduces the number of trials required for optimization to approximately one-third of that of the general BO with a radial basis function (RBF) kernel (RBF-BO). This result corresponds to the number of trials wherein unimportant parameters are removed in advance. Thus, MPDE-BO can dramatically reduce the number of trials required for optimization when the synthesis parameters have four or more dimensions. Moreover, MPDE-BO can automatically choose synthesis parameters instead of common knowledge or preconceptions, thereby inducing serendipitous materials synthesis.
2. Methods
2.1. Generation of model functions
BO is an optimization method for black-box functions.26,27 The workflow for optimizing synthesis conditions based on BO is as follows. (1) Experiments were conducted to obtain data on explanatory variables (synthesis parameters) and objective variables (physical properties or yield of the obtained material). (2) A prediction model for the objective function was created using techniques such as Gaussian process regression based on experimental data. (3) An acquisition function used to determine the next set of synthesis conditions based on the predicted results from step 2. The synthesis conditions are optimized by sequentially repeating steps 1–3. The details of the BO are provided in the ESI.†The BO requires many trials for optimization as the number of synthetic parameters increases. In certain instances, the synthesis parameters include unimportant parameters that have a minor influence on the properties or yields, particularly in a high-dimensional search space.28 In BO, for conditions of both large predicted mean μ and large variance σ2 (i.e., unexplored synthesis conditions), the search process is conducted to find the global optimum without being trapped in local optima. The RBF-BO method explores synthesis conditions lacking surrounding experimental data, regardless of the influence of synthetic parameters on the properties or yields. Accordingly, when the synthesis parameters include unimportant parameters, RBF-BO tends to choose synthesis conditions that only change the unimportant parameters that have minimal impact on the properties or yields. Therefore, RBF-BO may continue to search around the local optimum by continuously changing only the unimportant parameters, thus failing to reach the global optimum (Fig. 1).
The model functions used in this study include unimportant parameters within the synthesis parameters to evaluate the BO performance (Fig. 1). The model functions based on the multivariate mixture of Gaussian functions satisfied the following criteria. (1) It is a smooth function with multiple local optima. (2) It exhibits finite interactions among explanatory variables (synthesis parameters). (3) Both important and unimportant synthesis parameters are included. (4) It could represent the width of the process window (Pw) during materials synthesis.
In previous studies, we modeled materials synthesis with different Pw values using multivariate mixed Gaussian functions (combining isotropic Gaussian functions).19,20 The background of modeling using isotropic Gaussian functions is explained in the ESI.† Let Pw represents the range of synthesis conditions that yield the desired material properties. For a large Pw, determining the optimal synthesis conditions is easy. Whereas in the case of a small Pw, optimization becomes challenging. We assumed thin-film synthesis using the sputtering method, where the parameters are the oxygen partial pressure and sputtering power, all of which are important parameters influencing the material properties. Based on the literature values, we set Pw for temperature, oxygen partial pressure, and sputtering power at 100 °C, 1.0 × 10−4 Pa, and 10 W, respectively.12,29,30
When considering the number of important synthesis parameters d as d ≥ 1 and the number of unimportant ones as s ≥ 0, the search space x can be defined as x = xd × xs, where xd = [0, M]d, xs = [0, M]s, and M is the resolution of the search space corresponding to the number of grids for each parameter. Assuming that important and unimportant parameters do not have interaction, the model function is defined as follows:
| f(x) = fd(xd) + fs(xs) | (1) |
 for the important parameters xd is defined by a combination of d + 1 Gaussian functions as follows.
for the important parameters xd is defined by a combination of d + 1 Gaussian functions as follows.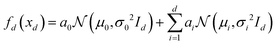 | (2) |
 | (3) |
 represents a gentle variation spreading across the entire xd using a sufficiently small coefficient a0 and a sufficiently large variance σ02. The second term comprises a Gaussian function and introduces multimodality (multiple local optima in the material properties). Eqn (3) is a constraint that sufficiently separates the peaks of each Gaussian function. For the function
represents a gentle variation spreading across the entire xd using a sufficiently small coefficient a0 and a sufficiently large variance σ02. The second term comprises a Gaussian function and introduces multimodality (multiple local optima in the material properties). Eqn (3) is a constraint that sufficiently separates the peaks of each Gaussian function. For the function  for the unimportant parameters xs, a single Gaussian function is used to represent a gentle variation spreading across the entire xs;
for the unimportant parameters xs, a single Gaussian function is used to represent a gentle variation spreading across the entire xs;  , where Is is the s-dimensional identity matrix. When s = 0, fs(xs) = 0, and the model function f(x) = fd(xd). The model function used in this study satisfies the above properties.
, where Is is the s-dimensional identity matrix. When s = 0, fs(xs) = 0, and the model function f(x) = fd(xd). The model function used in this study satisfies the above properties.
2.2. Bayesian optimization based on sparse estimation using the maximum partial dependence (MPDE-BO)
Here, the quantification of the importance of each synthesis parameter and ignoring unimportant parameters can help reduce unnecessary trials around the local optima. One proposed method uses an ARD kernel.31 | (4) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) i for each synthetic parameter (i = 1, …, N). The details of the ARD kernel are provided in the ESI.† By setting a threshold of
i for each synthetic parameter (i = 1, …, N). The details of the ARD kernel are provided in the ESI.† By setting a threshold of ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) i, the synthesis parameters can be classified into important and unimportant parameters. However, in actual materials synthesis, even unimportant synthesis parameters affect the properties or yields, and it is unlikely that they have no impact. In such cases, the intuitive determination of the appropriate threshold for
i, the synthesis parameters can be classified into important and unimportant parameters. However, in actual materials synthesis, even unimportant synthesis parameters affect the properties or yields, and it is unlikely that they have no impact. In such cases, the intuitive determination of the appropriate threshold for ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) i in the ARD kernel is challenging.
i in the ARD kernel is challenging.
We focus on MPDE to quantify the importance of each synthesis parameter. Algorithm 1 presents the pseudocode for MPDE-BO. A simple method for evaluating the importance of explanatory variables involves using a partial dependence plot (PDP); however, PDP is unsuitable for materials synthesis because it cannot correctly evaluate the importance of interactions among explanatory variables.32 The interactions between synthesis parameters are often observed in materials synthesis, and the proposed model can model such cases. For example, during the synthesis of metal oxides, changes in temperature and oxygen partial pressure lead to changes in the thermodynamically most stable phase, oxygen vacancies, crystallite size, and crystal orientation, which in turn affect the material properties. In one of our model functions shown in Fig. 1(a), when the synthesis temperature is 400 °C, an oxygen partial pressure of 9.0 × 10−4 Pa provides a relatively high property value of 0.7. Whereas, for a synthesis temperature of 1000 °C, the property at the oxygen partial pressure of 9.0 × 10−4 Pa is low, and the global maximum value of 1.0 is obtained at 5.0 × 10−4 Pa. The use of an individual conditional expectation (ICE) is effective when interaction exists in explanatory variables.33 MPDE is an indicator obtained from the ICE and shows the maximum change in the target variable (e.g., properties or yields) when only the focused synthesis parameter is varied. Further details on the PDP, ICE, and MPDE are provided in the ESI.†
2.3. Experimental settings
We set the resolution of the search space to M = 50, which corresponds to the number of grids for each synthesis parameter. The number of important explanatory variables (synthesis parameters) was limited to d ≤ 4. The functions of the important synthesis parameters fd(xd) are expressed as eqn (2) where (a0, a1, a2, a3, a4) = (0.3, 1.2, 0.6, 0.7, 0.7), (σ0, σ1, σ2, σ3, σ4) = (20, 5, 5, 6, 6). For example, considering sputter thin-film synthesis with d = 3, the synthesis temperatures, pressures, and sputtering power were limited to 200–1200 °C, 1.0–11 × 10−4 Pa, 100–200 W, respectively, and the width of one grid corresponded to 20 °C, 0.2 × 10−4 Pa, and 2 W, respectively. σ1 represents the Pw for the maximum value peak; Pw = (Pw for temperature, Pw for pressure, and Pw for power) = (100 °C, 1.0 × 10−4 Pa, 10 W). σ2 and σ3 correspond to Pw for local optimum peaks; Pw = (100 °C, 1.0 × 10−4 Pa, 10 W) and (120 °C, 1.2 × 10−4 Pa, 12 W), respectively. The μi = (i = 1, …, d) in eqn (2) for each Gaussian function were obtained by random sampling from the subspace xd = [0, M]d, ensuring that μi satisfied the distance conditions described in eqn (3). Thus, the peak positions of the global and local maxima were random for each model function and were sufficiently separated to avoid overlapping the global and local maxima. The changes in the unimportant synthesis parameters fs(xs) are expressed as eqn (2), where a5 = 0.1, σs = 25, and with the means μs for the Gaussian functions set to for each component. When the unimportant synthesis parameters xs varied, the change in property values across the entire search space was less than 10%.
for each component. When the unimportant synthesis parameters xs varied, the change in property values across the entire search space was less than 10%.
We performed a BO for the model functions using ten initial points selected through random sampling. The number of experiments required to achieve a value of 90% or more of the optimal value  were compared. To minimize the effect of the different μi selected by random sampling, the 90th percentile value of the number of experiments required for optimization was defined over 100 objective functions with distinct μi as N90.19,20 Further, N90 was used as an evaluation metric of the algorithms in this study.
were compared. To minimize the effect of the different μi selected by random sampling, the 90th percentile value of the number of experiments required for optimization was defined over 100 objective functions with distinct μi as N90.19,20 Further, N90 was used as an evaluation metric of the algorithms in this study.
We compared the following three algorithms.
1. RBF-BO: BO using RBF kernel (Algorithm S1).
2. ARD-BO: BO using ARD kernel for sparse estimation (Algorithm S2).
3. MPDE-BO: BO using MPDE for sparse estimation (Algorithm 1).
RBF-BO used the EI as the acquisition function. In ARD-BO and MPDE-BO, xd which maximizes the EI were the values of important parameters in subsequent trials. The values of unimportant parameter xs were selected via random sampling from the search space of each parameter, not by BO, which reduces uncertainty and improves the accuracy of sparse estimation. The threshold of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i for ARD-BO was set to ε
i for ARD-BO was set to ε![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 100, and that of MPDE for MPDE-BO was set to εe = 0.1. Based on our group's previous research, we used 6 and 1 as the initial values for
= 100, and that of MPDE for MPDE-BO was set to εe = 0.1. Based on our group's previous research, we used 6 and 1 as the initial values for ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) i and σARD, respectively, for ARD-BO and MPDE-BO. These values are updated each time by performing gradient-based optimization using GPy's optimization method.
i and σARD, respectively, for ARD-BO and MPDE-BO. These values are updated each time by performing gradient-based optimization using GPy's optimization method.
3. Results
Table 1 presents N90 using RBF-BO, ARD-BO, and MPDE-BO when the search space is fixed in four dimensions. The number of important synthesis parameters (d) and unimportant synthesis parameters (s) are varied as (d,s) = (2,2), (3,1), (4,0). When s = 1, 2, ARD-BO and MPDE-BO successfully reduce N90 compared with RBF-BO. The smaller the N90 values, the higher the performance of the algorithm. For instance, when (d,s) = (2,2), N90 of MPDE-BO (= 36) is approximately half that of RBF-BO (= 104) and less than that of ARD-BO (= 40). Similarly, for (d,s) = (3,1), N90 of MPDE-BO (= 103) is approximately half that of RBF-BO (= 198). These results indicate that with increase in the number of unimportant synthesis parameters (s), MPDE-BO becomes more efficient in the search for optimal synthesis conditions. A plausible reason for the MPDE-BO requiring fewer experimental trials than ARD-BO is as follows. As described in the Methods section, sparse estimation with ARD encounters challenges in quantifying the importance of parameters when unimportant synthesis parameters (s) are varied following the function, fs, where the physical properties gradually change along the xs direction. In contrast, MPDE enhances the accuracy of sparse estimation, further reducing unnecessary experiments. When (d,s) = (4,0), wherein all synthesis parameters are important, all algorithms exhibit approximately the same N90 = ∼300. This result is considered reasonable because the ARD kernel is a generalization of the RBF kernel. Moreover, the only difference between ARD-BO and MPDE-BO is the method of sparse estimation, and MPDE-BO is easier for materials researchers to set the threshold for sparse estimation. Since MPDE has the same scale as the material properties, it allows researchers to set thresholds based on prior experience in materials research—for example, to ignore parameters that cause approximately 5% or 10% changes in the target property. Although the prediction models are essentially identical for ARD-BO and MPDE-BO, the difference in N90 is caused by the threshold setting for sparse estimation. Therefore, MPDE-BO can optimize the synthesis conditions with fewer trials comparable to ARD-BO, where the threshold value was skillfully set by data scientists.| (d,s) | RBF-BO | ARD-BO | MPDE-BO |
|---|---|---|---|
| (2,2) | 104 | 40 | 36 |
| (2,1) | 198 | 124 | 103 |
| (4,0) | 323 | 304 | 297 |
Next, we discuss whether an increase in unimportant parameters results in unnecessary experimental trials. Table 2 presents N90 when (d,s) = (2,0), (2,2) and (3,0), (3,1), where the number of important parameters is fixed to d = 2 and 3, and the number of unimportant parameters (s) is changed. For RBF-BO, as s increases a substantial increase is observed in N90 (N90 for (3,0) = 84 and N90 for (3,1) = 198). In contrast, MPDE-BO exhibits only a modest rise in N90 (N90 for (3,0) = 90, N90 for (3,1) = 103). This result can be attributed to achieving a high-precision sparse estimation with minimal trials. In addition, when comparing RBF-BO and other sparse estimation algorithms (ARD-BO and MPDE-BO) in the case of s = 0, even when the synthesis parameters do not include unimportant parameters, no additional trials are performed for sparse estimation ((d,s) = 4,0) in Table 1, and (d,s) = (2,0), (3,0) in Table 2.
| (d,s) | RBF-BO | ARD-BO | MPDE-BO |
|---|---|---|---|
| (2,0) | 24 | 26 | 26 |
| (2,2) | 104 | 40 | 36 |
| (3,0) | 84 | 90 | 90 |
| (2,1) | 198 | 124 | 103 |
Fig. 2 shows the histograms of the number of experiments for each algorithm when ((d,s) = 3,1). Overall, ARD-BO and MPDE-BO require fewer optimization trials than RBF-BO without sparse estimation. ARD-BO and MPDE-BO avoid the unnecessary trials that only change the unimportant parameters. In this study, MPDE-BO is the most efficient algorithm for optimizing synthesis conditions.
Next, to understand the number of trials required for sparse estimation, we explain the MPDE trace when the search space has four dimensions (Fig. 3). The horizontal and vertical axes represent the number of trials and MPDE values for each synthesis parameter calculated in each trial. The solid and dashed lines represent di and s4−i (i = 2, 3, 4), corresponding to the important and unimportant parameters, respectively. In addition, the threshold for an MPDE of 0.1 is indicated with a dotted line. When (d,s) = (2,2), (3,1), the MPDE values for important parameters tend to increase with an increase in the number of trials (Fig. 3(a) and (b)). The values for unimportant parameters decrease and fall below the threshold of 0.1 after approximately 10 trials. Therefore, MPDE successfully quantifies the importance of synthesis parameters and classifies synthesis parameters into important and unimportant parameters within approximately ten trials. In addition, when all parameters are important ((d,s) = (4,0)), the MPDE values for all synthesis parameters increase significantly, surpassing the threshold of 0.1 by a sufficient margin (Fig. 3(c)). Hence, the MPDE-BO does not mistakenly classify important parameters as unimportant.
4. Discussion
The MPDE-BO proposed in this study reduces the number of trials by automatically narrowing down only the important synthesis parameters, even when all synthesis parameters are considered. MPDE-BO aids in narrowing the synthesis parameters without relying on common sense or preconceptions of researchers. Furthermore, combining the MPDE-BO with autonomous experiments using robots increases the number of feasible experiments and significantly improves the speed at which new materials are synthesized.Compared to ARD-BO, MPDE-BO is superior in terms of threshold setting for sparse estimation. In this study, the MPDE threshold was set at 0.1, which corresponds to about 10% of the change in physical property values (∼1). The range of changes in physical properties that needs to be considered sparse should vary depending on the target material and physical properties. Therefore, setting the threshold for sparse estimation in ARD-BO has been difficult. In contrast, in MPDE-BO, materials scientists can intuitively set the appropriate threshold. Since the MPDE values are calculated for each trial, the threshold value can be flexibly changed by monitoring the trace plot of the MPDE during the experiments.
Furthermore, MPDE-BO is valuable for estimating the number of experiments required for optimization, which aids in the creation of the experimental schedule. If the number of trials needed to optimize the synthesis conditions is predicted, the material inventory, time, and financial costs required to synthesize new materials can be estimated. As the number of important synthesis parameters increases, the number of trials necessary for optimization rises exponentially.20 Therefore, evaluating the number of important synthesis parameters aids in the estimation of the total number of trials. In contrast to conventional BO, the MPDE-BO proposed in this study facilitates a precise estimation of the number of important synthesis parameters with fewer trials by observing the transition of the MPDE during experiments. Thus, MPDE-BO can help estimate the total number of trials required for optimization. Moreover, using MPDE-BO, materials researchers can assess the completion of optimization within a feasible number of experiments during early trials. If optimization is impossible within a viable number of trials, researchers should reconsider the research goal. Setting a proper research goal is essential for effectively utilizing BO in materials research, where the knowledge and experience of materials researchers are still required. Thus, the MPDE-BO can contribute to developing experimental plans that reduce waste in materials inventory, time, and financial costs.
5. Conclusions
This study proposes sparse-modeling-based BO using MPDE to optimize the synthesis conditions of materials. The method successfully reduces the required number of trials to approximately one-half of conventional BO (RBF-BO) when one of the four synthesis parameters exerts a minor influence on the material properties, which is comparable to ARD-BO with a successful threshold setting. The proposed method automatically selects the important synthesis parameters and reduces the number of trials required for optimization when the synthesis parameters have four or more dimensions. Materials researchers can easily set an appropriate threshold of MPDE, which is an advantage over ARD-BO, because the threshold of MPDE corresponds to the maximum change in the properties or yields when only the focused synthesis parameter is varied. Thus, this method paves the way for materials exploration in high-dimensional search spaces.Data availability
The data that supports the findings of this study are available within the article and its ESI.† The Python code developed for this research cannot be released publicly for commercial reasons.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This research was supported by the Japan Science and Technology Agency (JST) Core Research for Evolutional Science and Technology (CREST) (Grant No. JPMJCR20T3), the JST-Mirai Program (Grant No. JPMJMI19G4 and JPMJMI21G2), and the MEXT Program: Data Creation and Utilization-Type Material Research and Development Project Grant Number JPMXP1122712807. R. N. acknowledge funding from JSPS Kakenhi Grant No. 22K14692. We would like to thank Editage (www.editage.jp) for English language editing.References
- P. Kirkpatrick and C. Ellis, Chemical Space, Nature, 2004, 432, 823 CrossRef CAS.
- J.-W. Yeh, S.-K. Chen, S.-J. Lin, J.-Y. Gan, T.-S. Chin, T.-T. Shun, C.-H. Tsau and S.-Y. Chang, Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS.
- Y. Kato, S. Hori, T. Sato, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-power all-solid-state batteries using sulfide superionic conductors., Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- C. Li, D. Rubín de Celis Leal, S. Rana, S. Gupta, A. Sutti, S. Greenhill, T. Slezak, M. Height and S. Venkatesh, Bayesian optimisation for synthesis of short polymer fiber materials, Sci. Rep., 2017, 7, 5683 CrossRef PubMed.
- M. Harada, H. Takeda, S. Suzuki, K. Nakano, N. Tanibata, M. Nakayama, M. Karasuyama and I. Takeuchi, Bayesian optimization-guided experimental search of NASICON-type solid electrolytes for all-solid-state Li-ion batteries, J. Mater. Chem. A, 2020, 8, 15103–15109 RSC.
- N. H. Paulson, J. A. Libera and M. Stan, Frame spray pyrolysis optimization via statistics and machine learning, Mater. Des., 2020, 196, 108972 CrossRef CAS.
- N. H. Paulson, G. A. Yanguas-Gil, O. Y. Abuomar and J. W. Elam, Intelligent agents for the optimization of atomic layer deposition, ACS Appl. Mater. Interfaces, 2021, 13, 17022–17033 CrossRef CAS PubMed.
- Y. K. Wakabayashi, T. Otsuka, Y. Krockenberger, H. Sawada, Y. Taniyasu and H. Yamamoto, Machine-learning-assisted thin-film growth: Bayesian optimization in molecular beam epitaxy of SrRuO3 thin films, APL Mater., 2019, 7, 101114 CrossRef.
- Y. Xie, C. Zhang, H. Deng, B. Zheng, J.-W. Su, K. Shutt and J. Lin, Accelerate synthesis of metal–organic frameworks by a robotic platform and Bayesian optimization, ACS Appl. Mater. Interfaces, 2021, 13, 53485–53491 CrossRef CAS PubMed.
- J. Broucek, D. Khatamsaz, C. Cakirhan, S. H. Zadeh, M. Fan, G. Vazquez, K. C. Atli, X. Qian, R. Arroyave and I. Karaman, Design of high-temperature NiTiCuHf shape memory alloys with minimum thermal hysteresis using Bayesian optimization, Acta Mater., 2025, 286, 120651 CrossRef CAS.
- Y. K. Wakabayashi, T. Otsuka, Y. Krockenberger, H. Sawada, Y. Taniyasu and H. Yamamoto, Bayesian optimization with experimental failure for high-throughput materials growth, npj Comput. Mater., 2022, 8, 180 CrossRef CAS.
- R. Shimizu, S. Kobayashi, Y. Watanabe, Y. Ando and T. Hitosugi, Autonomous materials synthesis by machine learning and robots, APL Mater., 2020, 8, 111110 CrossRef CAS.
- B. P. MacLeod, F. G. L. Parlane, T. D. Morrissey, F. Häse, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. E. Yunker, M. B. Rooney, J. R. Deeth, V. Lai, G. J. Ng, H. Situ, R. H. Zhang, M. S. Elliott, T. H. Haley, D. J. Dvorak, A. Aspuru-Guzik, J. E. Hein and C. P. Berlinguette, Self-driving laboratory for accelerated discovery of thin-film materials, Sci. Adv., 2020, 6, eaaz8867 CrossRef CAS PubMed.
- B. Burger, P. Maffettone, V. Gusev, C. Aitchson, Y. Bai, X. Wang, X. Li, B. M. Alston, R. Clowes, N. Rankin, B. Harris, R. S. Spick and A. I. Cooper, A mobile robotic chemist, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott, T. D. Morrissey, T. H. Haley, O. Proskurin, M. B. Rooney, N. Taherimakhsousi, D. J. Dvorak, H. N. Chiu, C. E. B. Waizenegger, K. Ocean, M. Mokhtari and C. P. Berlinguette, A self-driving laboratory advances the Pareto front for material properties, Nat. Commun., 2022, 13, 995 CrossRef CAS PubMed.
- S. Kobayashi, R. Shimizu, Y. Ando and T. Hitosugi, Autonomous exploration of an unexpected electrode material for lithium batteries, ACS Mater. Lett., 2023, 5, 2711–2717 CrossRef CAS.
- A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, Bayesian optimization of computer-proposed multistep synthetic routes on an automated robotic flow platform, ACS Cent. Sci., 2022, 8, 825–836 CrossRef CAS PubMed.
- A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, A Bayesian experimental autonomous researcher for mechanical design, Sci. Adv., 2022, 6, eaaz1708 CrossRef PubMed.
- R. Nakayama, R. Shimizu, T. Haga, T. Kimura, Y. Ando, S. Kobayashi, M. Sekijma and T. Hitosugi, Tuning of Bayesian optimization for materials synthesis: simulation of the one-dimensional case, STAM Methods, 2022, 2, 119–128 Search PubMed.
- H. Xu, R. Nakayama, R. Shimizu, T. Haga, T. Kimura, Y. Ando, S. Kobayashi, M. Sekijma and T. Hitosugi, Tuning Bayesian optimization for materials synthesis: simulating two- and three-dimensional cases, STAM Methods, 2023, 3, 2210251 Search PubMed.
- C. K. Chiang, C. R. Fincher Jr, Y. W. Park, A. J. Heeger, H. Shirakawa, E. J. Louis, S. C. Gau and A. G. MacDiarmid, Electrical Conductivity in Doped Polyacetylene, Phys. Rev. Lett., 1977, 39, 1098 CrossRef CAS.
- T. Yamamoto, K. Fujimoto, T. Okada, Y. Fushimi, A. F. Stalder, Y. Natsuaki, M. Schmidt and K. Togashi, Time-of-flight magnetic resonance angiography with sparse undersampling and iterative reconstruction: comparison with conventional parallel imaging for accelerated imaging., Invest. Radiol., 2016, 51, 372–378 CrossRef PubMed.
- K. Akiyama, K. Kuramochi, S. Ikeda, V. L. Fish, F. Tazaki, M. Honma, S. S. Doeleman, A. E. Broderick, J. Dexter and M. Mościbrodzka, lmaging the Schwarzschild-radius-scale structure of M87 with the Event Horizon Telescope using sparse modeling, Astrophys. J., 2017, 838, 1 CrossRef.
- H. Numazawa, I. Yasuhiko, S. Kosuke, H. Imai and Y. Oaki, Experiment-oriented materials informatics for efficient exploration of design strategy and new compounds for high-performance organic anode., Adv. Theory Simul., 2019, 2, 1900130 CrossRef CAS.
- Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu, S. Sun, J. R. Deneault, D. Bash, F. Mekki-Berrada and S. A. Khan, et al., Benchmarking the performance of Bayesian optimization across multiple experimental materials science domains, npj Comput. Mater., 2021, 7, 188 CrossRef.
- C. E. Rasmussen and K. I. Williams, Gaussian process for machine learning, MIT Press, 2006 Search PubMed.
- D. R. Jones, M. Schonlau and W. J. Welch, Efficient global optimization of expensive black-box functions, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- Z. Yang, S. Suzuki, N. Tanibata, H. Takeda, M. Nakayama, M. Karasuyama and I. Takeuchi, Efficient experimental search for discovering a fast Li-ion conductor from a perovskite-type LixLa(1−x)/3NbO3 (LLNO) solid-state electrolyte using Bayesian optimization, J. Phys. Chem. C, 2021, 125, 152–160 CrossRef CAS.
- T. Tsuruhama, T. Hitosugi, H. Oki, Y. Hirose and T. Hasegawa, Preparation of layered-rhombohedral LiCoO2 epitaxial thin films using pulsed laser deposition, Appl. Phys. Express, 2009, 2, 085502 CrossRef.
- A. Chaoumead, Y. Sung and D. Kwak, The effects of RF sputtering power and gas pressure on structural and electrical properties of ITiO thin film, Adv. Condens. Matter Phys., 2012, 2012, 651587 Search PubMed.
- B. Chen, R. Castro and A. Krause, Joint optimization and variable selection of high-dimensional Gaussian processes, arXiv, 2012, preprint, arXiv:1206.6396 DOI:10.48550/arXiv.1206.6396.
- J. H. Friedman, Greedy function approximation: a gradient boosting machine, Ann. Stat., 2001, 29, 1189–1232 Search PubMed.
- A. Goldstein, A. Kapelner, J. Bleich and E. Pitkin, Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation, J. Comput. Graph. Stat., 2015, 24, 44–65 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of algorithms and modeling of materials synthesis using isotropic Gaussian functions. See DOI: https://doi.org/10.1039/d5ma00346f |
| This journal is © The Royal Society of Chemistry 2025 |


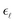


![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif)