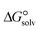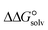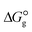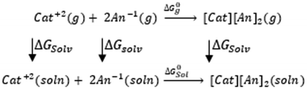View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/D4ME00119B (Paper) Mol. Syst. Des. Eng., 2025, 10, 50-67

The structural, electronic and thermodynamic properties of the designed p-benzoquinone based dicationic ionic liquids: insight from DFT–GD3 and QTAIM†

Hossein Roohi *, Sajedeh Habibipour and Khatereh Ghauri
Department of Applied Chemistry, Faculty of Chemistry, University of Guilan, Rasht, Iran. E-mail: hroohi@guilan.ac.ir; Fax: +981313220066; Tel: +981313243630 35

Received 14th July 2024 , Accepted 8th October 2024

First published on 10th October 2024

Abstract

In this work, the impact of various anions on the physicochemical properties of the designed p-benzoquinone-based dicationic ionic liquids [BTAD][A1–8]2 ([BTAD]2+ = [p-C6O2(N3H2)2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) was investigated at the M06-2X/6-31++G(d,p) level of theory in the gas phase and solvent media. Besides, dispersion-corrected M06-2X-GD3, B2PLYP-GD3 and mPW2PLYP-GD2 functionals were employed to calculate the corrected interaction energies. The thermodynamic interaction energies in gas and solvent media, structural parameters, electrostatic potential maps, natural charge of atoms, charge transfer (CT), electron density properties, potentials of the anodic and cathodic limits (VAL and VCL), electrochemical windows (ECW), acidity (ΔpKa1 and ΔpKa2) and reduced gradient density plots (RGD) were examined. Based on the corrected interaction energies, the stability order of [BTAD][A1–8]2 complexes at all levels of theory is [BTAD][CH3CO2]2 > [BTAD][CF3CO2]2 > [BTAD][N(CN)2]2 > [BTAD][CF3SO3]2 > [BTAD][ClO4]2 > [BTAD][BF4]2 > [BTAD][NTf2]2 > [BTAD][PF6]2. The calculated ECW of [BTAD][A3–8]2 is in the range of 4.5 to 7.5 V, demonstrating that these ILs can be promising candidates for the substitution of currently used electrolyte solutions based on organic molecular solvents in electrochemical devices.


Design, System, Application

In recent years, dicationic ionic liquids (DCILs) have attracted significant attention due to a wide range of applications in both academic and industrial research. Triazolium salts and triazolium-based ILs have been proposed for various applications. Protic ionic liquids (PILs) can transfer a proton and form hydrogen-bonded networks resulting in high conductivities. They exhibit specific characteristics, from fundamental insights into dielectric properties and NMR spectroscopic studies to applications in green chemistry, proton exchange membranes, and fuel cell electrolytes due to the presence of the mobile proton. The 1,2,6,7-tetrahydrobenzo bis(triazole)-4,8-dione ([BTAD]2+ = [p-C6O2(N3H2)2]2+ is a p-benzoquinone based dication which contains a p-benzoquinone (p-BQ) core and four acidic N–H protons in the 1,2,3-triazole units. Combination of the organic acid 1,2,6,7-tetrahydrobenzo bis(triazole)-4,8-dione ([BTAD]2+ with different Brønsted bases affords a novel series of PILs with wide variations in ΔpKa1 and ΔpKa2. In the present work, the physicochemical properties of eight designed DCILs [BTAD][A1–8]2 ([BTAD]2+ = [p-C6O2(N3H2)2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) were explored. To the best of our knowledge, no research has been done on this type of DCIL. Due to the proton donating and accepting abilities of [BTAD]2+ and A−, respectively, these PILs can be used as amphoteric solvents.

1. Introduction

Dicationic ionic liquids (DCILs) are made up of two mono-anions and two cationic units linked by either a rigid or flexible spacer. They possess special structures and more active sites than mono-ionic liquids (MILs).1–3 The thermal stability, surface tension, melting point, density, and viscosity of DCILs are usually greater than the traditional MILs with the same anion. Some of the characteristics that make DCILs excellent for many applications in the fields of solar cells, fuel cells, catalysis, batteries, lubricants, and other branches of their scientific fields are high thermal stability, extensive liquid range, and biological activity.4–6 Furthermore, DCILs serve well as organic solvents7 and find utility in analytical chemistry, particularly as stationary phases in gas chromatography columns.8

Triazolium salts and triazolium-based ILs have been proposed for various applications, such as polymer electrolytes,9–11 solvents,12–15 synthesis of rutaecarpine,16 ion conductors,17–19 extraction,20,21 membranes,22 molecular recognition,23 explosives,24,25 in “click” chemistry,26,27 liquid crystals,28 and capillary electrophoresis.29 In addition, thiazolium-based ILs offer many advantageous properties, such as very good chemical stability under alkaline conditions,30 antimicrobial and antifungal effects31–33 and low cytotoxicity.34 The 1,2,6,7-tetrahydrobenzo bis(triazole)-4,8-dione ([BTAD]2+ = [p-C6O2(N3H2)2]2+) cation is a 1,2,3-triazolium based dication,35–38 containing a p-benzoquinone (p-BQ) core and two acidic N–H protons in the 1,2,3-triazole units.

Protic ionic liquids (PILs)39 are typically prepared by the reaction of a Brønsted base (B) with a Brønsted acid (HA), leading to the formation of a cation and an anion (HA + B → [A]− + [BH]+). PILs can transfer a proton and form hydrogen-bonded networks resulting in high conductivities.40 The properties exhibited by PILs depend largely on their degree of ionization and the degree of proton transfer from acid to base.41–44 They exhibit specific characteristics, from fundamental insights into dielectric properties45 and NMR spectroscopic studies,46 to applications in green chemistry,47 proton exchange membranes,48,49 and fuel cell electrolytes due to the presence of the mobile proton.50,51 Proton transfer reactions can enhance conductivity in PILs by various mechanisms in a multi-component system of charged and neutral species.40

1,2,6,7-Tetrahydrobenzo bis(triazole)-4,8-dione [BTAD]2+ based DCILs are of the subclasses of protic ionic liquids (PILs) composed of a Brønsted acid ([BTAD]2+) and a Brønsted base (anions). The combination of the organic acid [BTAD]2+ with different Brønsted bases affords a novel series of PILs with wide variations in the electronic and thermodynamic properties. The mono-anionic and di-anionic forms of bis(1,2,3-triazole)-p-benzoquinone (C6H2N6O2) (2) were studied by Sato et al.52 The molecular structures of neutral 2, monoanionic 2−, and dianionic 22− were confirmed by single crystal X-ray structural analyses, where the acidic protons in 2 existed in the 2-position of the 1,2,3-triazole unit, whereas one proton in 2− was localized at the 1-position of the 1,2,3-triazole unit. They have demonstrated that the electron-accepting ability of bis(1,2,3-triazole)-p-benzoquinone derivatives decreases in the order 2 > 2− > 22− due to electrostatic repulsive interactions in the anion radical and dianion state. To the best of our knowledge, no investigations have been conducted on [BTAD]2+ based DCILs. In the present work, the structural, electronic and thermodynamic properties of eight [BTAD][A1–8]2 ([BTAD]2+ = [p-C6O2(N3H2)2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) DCILs were explored at the M06–2X/6–31++G(d,p) level of theory in the gas phase and solvent media.

2. Computational details

The geometries of all the structures were optimized at the M06-2X/6-31++G(d,p) level of theory. The suitability of the M06-2X53 density functional method for the study of non-covalent interactions has been confirmed previously.54–57 Dispersion-corrected M06-2X-D3,58 B2PLYP-GD3 (ref. 59 and 60) and mPW2PLYP-GD2 (ref. 61) methods in conjunction with the 6-31++G(d,p) basis set62 were used to calculate the binding energies (BEs). Besides, Goerigk et al. have proved that the double-hybrid functionals63 are the most reliable approaches for thermochemistry and noncovalent interactions.64 The interaction energies are corrected for basis set superposition error (BSSE) using the standard counterpoise correction (CP) method proposed by Boys and Bernardi.65 Vibrational frequency calculations were carried out to obtain thermodynamic properties and to ensure that the optimized structures are global minima.

The solvent effect on the physicochemical properties of DCILs was investigated in three solvents, namely water, methanol and methylcyclohexane by using the polarizable continuum model (PCM)66 in conjunction with the Solvation Model Density (SMD) approach.67 All calculations were carried out using the Gaussian 09 program package.68

To explore the electronic distribution in the cation and anions, the electrostatic potential (ESP) maps69 were analyzed by using Gaussian 09 and GaussView 5.0 (ref. 70) programs at the M06-2X/6-31++G(d,p) level of theory. The natural bond orbital (NBO) analysis71 was carried out by using version 3.1 of the NBO package72 at the M06-2X/6-31++G(d,p) level of theory. To calculate the topological properties of electron charge density, the AIM2000 package73 was utilized at the M06-2X/6-31++G(d,p) level of theory.

3. Results and discussion

3.1. Structural parameters

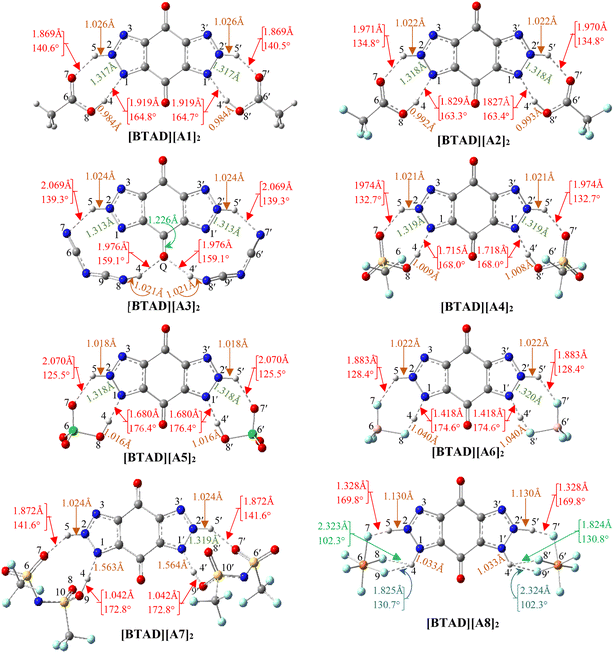
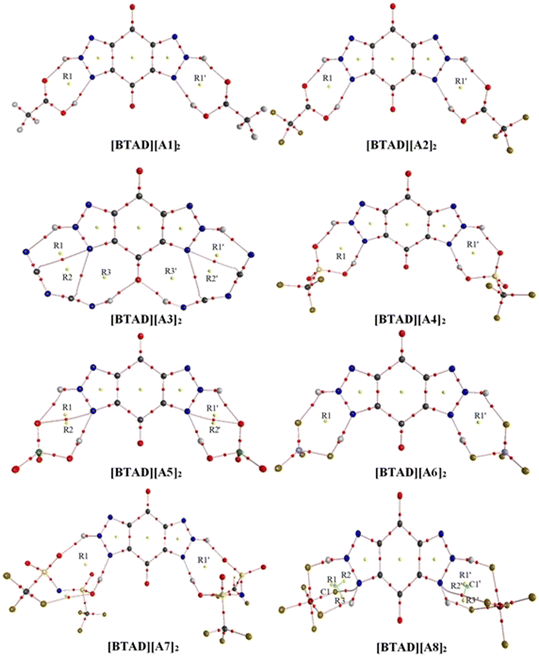
We have searched the various configurations of triple ions by placing the anions in different positions around the cation. The reported structures are the most stable triple ions at the M06-2X/6-31++G(d,p) level. Fig. 1 shows eight most stable complexes of [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−). As can be seen, H-bonding interactions are formed between anions and N–H groups of the cation on both right and left sides of the cation. Since there are two N–H groups, which one is transferred and is it the same for different anions? From MESP profiles, H4 in the N–H4 and H4′ in the N–H4′ have greater positive potential than H5 in the N–H5 and H5′ in the N–H5′, indicating that the acidity of H4 and H4′ is greater than H5 and H5′. Based on this challenge, different configurations were tested for complexes formed from the interaction of anions with the dication. [BTAD][A1–7]2 complexes formed by proton transfer from the N–H4(4′) group of the cation to the anion were energetically more stable than those formed by the transfer of H5(5′). Therefore, optimization of DCIL structures revealed that H4 and H4′ atoms in all [BTAD][A1–7]2 complexes are transferred from the cation to anions. In these complexes, two X–H4(4′)⋯N and two X⋯H5(5′)–N (X = O, N and F) H-bonds are formed between the cation and anions. In contrast, the [BTAD][PF6]2 complex with two X⋯H5(5′)–N and X⋯H4(4′)–N H-bonding interactions is formed without proton transfer.
image file: d4me00119b-f1.tif
Fig. 1 The optimized structures of [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and [A1–8]− = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes in the gas phase at the M06-2X/6-31++G(d,p) level of theory.

The main geometrical parameters (hydrogen bond distances and angles) for the eight studied complexes [BTAD][A1–8]2 (A1–8 = A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) at the M06-2X/6-31++G(d,p) level of theory are given in Fig. 1. The N1–N2 and N1′–N2′ bond lengths in the isolated dication [BTAD]2+ are 1.333 and 1.333 Å which decrease to 1.317(1.317), 1.318(1.318), 1.313(1.313), 1.319(1.319), 1.318(1.318), 1.320(1.320), 1.319(1.319) and 1.323(1.323) Å in [BTAD][A1–8]2, respectively. The N1–H4, N1′–H4′, N2–H5 and N2′–H5′ bonds of the triazole dication are generally involved in interaction with O, F and N atoms of the anions. The N1–H4(N1′–H4′) bond length in the isolated dication is 1.025(1.025) Å which increases to 1.919(1.919) Å, 1.829(1.827) Å, 3.047(3.047) Å, 1.715(1.718) Å, 1.680(1.680) Å, 1.418(1.418) Å, 1.563(1.564) Å and 1.033(1.033) Å in the [BTAD][CH3CO2]2, [BTAD][CF3CO2]2, [BTAD][N(CN)2]2, [BTAD][CF3SO3]2, [BTAD][ClO4]2, [BTAD][BF4]2, [BTAD][NTf2]2 and [BTAD][PF6]2 complexes, respectively. As can be seen, the H4(H4′) atoms are transferred from the dication in [BTAD][A1–7]2 complexes to corresponding anions. The bond length of N2–H5(N2′–H5′) involved in X⋯H5(5′)–N H-bonding interaction in [BTAD][CH3CO2]2, [BTAD][CF3CO2]2, [BTAD][N(CN)2]2, [BTAD][CF3SO3]2, [BTAD][ClO4]2, [BTAD][BF4]2 and [BTAD][NTf2]2 decreases from 1.0263(1.0263) Å in the isolated dication to 1.0262(1.0262), 1.022(1.022), 1.024(1.024), 1.021(1.021), 1.018(1.018), 1.022(1.022) and 1.024(1.024) Å, respectively, while the N2–H5 (N2′–H5′) bond lengths in the [BTAD][PF6]2 DCIL increases to 1.130(1.130 Å) compared with the isolated dication (1.026 Å). As can be seen in Fig. 3, two new C[double bond, length as m-dash]O⋯H4(4′)–N8 H-bonds with a bond distance of 1.976 Å are formed in the [BTAD][N(CN)2]2 DCIL. The average value of X–H4(H4′)⋯N (X = O or N and or F) and X⋯H5(5′)–N H-bonding parameters between the anions and dication in the complexes [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]− is 1.894 Å (152.7°), 1.900 Å (149.1°), 2.023 Å (149.2°), 1.845 Å (150.3°), 1.875 Å (151.0°), 1.650 Å (151.5°), 1.718 Å (157.2°) and 1.701 Å (143.1°), respectively.

As mentioned, the average value of the H-bonding distances in [BTAD][A1–3]2 complexes are 1.894 Å, 1.900 Å and 2.023 Å, and those of H-bonding angles are 152.7°, 149.1° and 149.2°, respectively. Therefore, it is expected that H-bonding interactions in [BTAD][A1]2 are stronger than those in [BTAD][A2–3]2. Therefore, it is expected that [BTAD][A1]2 is more stable than [BTAD][A2–3]2. In the case of the other complexes, there is no direct correlation between H-bonding parameters and the stability of the complexes. The results show that the formation of the complex is accompanied by a significant change in the structure of cations and anions. Therefore, it is impossible to only predict the interaction strength between the anions and cation and, in turn, the stability of the complexes from the structural parameters involved in H-bonding. For example, the optimized structures of [BTAD][A6]2 and [BTAD][A8]2 complexes show that the B–F bond (1.550 Å versus 1.339 Å) involved in the H-bonding in [BTAD][A6]2 and the P–F bond (1.891 Å versus 1.570 Å) involved in the H-bonding in [BTAD][A8]2 are elongated compared to other similar bonds. Therefore, we have found structures F3B⋯F–H⋯N and F5P⋯F–H⋯N in [BTAD][A6]2 and [BTAD][A8]2, respectively. Here, the anion part is effectively divided into two segments, one of which is HF.

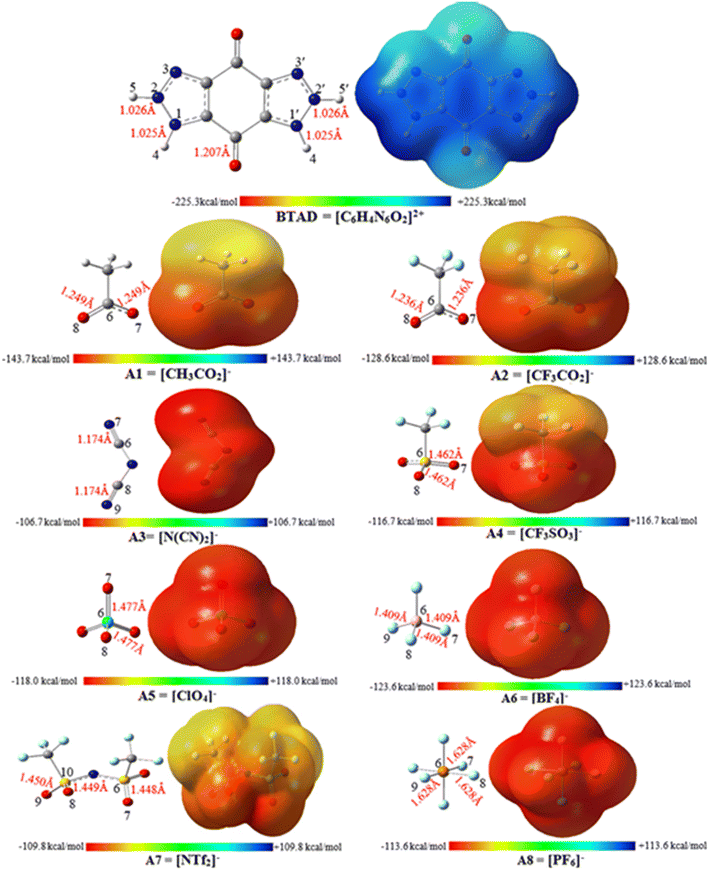
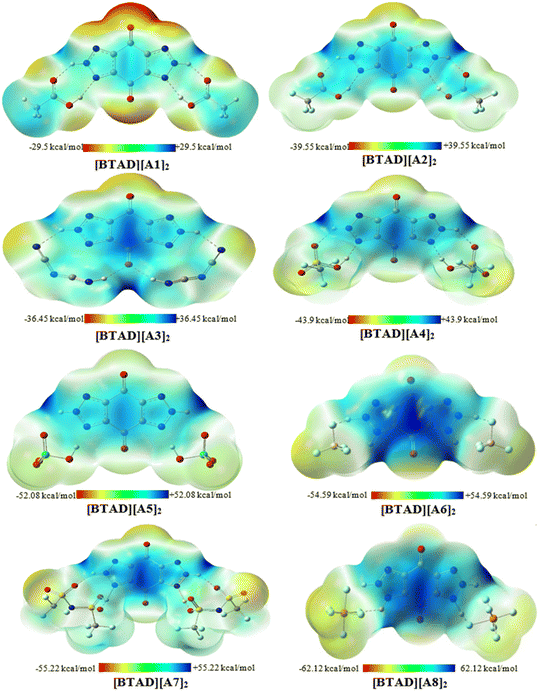
3.2. Molecular electrostatic potential (MESP) maps

MESP analysis has become one of the most effective modern techniques for understanding, interpreting, and predicting the intermolecular interactive behavior of molecules.74 MESP maps serve as a valuable tool for identifying regions of positive and negative potentials on a molecule surface. By analyzing these maps, we can predict the specific locations around a dication where anions are likely to interact. The MESP maps of the optimized isolated anions [A1–8] = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) and [BTAD]2+ dication calculated at the M06-2X/6-31++G(d,p) level of theory in the gas phase are shown in Fig. 2. The colors at the MESP maps display the various values of electrostatic potential energies; a color ranging from red as the minimum electrostatic potential energy value to blue as the maximum. As can be observed in Fig. 2, the H4 (H4′) and H5 (H5′) atoms of the [BTAD]2+ dication have the most positive charge distribution as indicated by the dark blue color. In addition, a negative charge concentration with red color is seen over the nitrogen, oxygen and fluorine atoms in the isolated anions ([A1–8]− = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−). According to MESP maps, the main interactions occur between the O, F and N atoms of anions and positive regions of the dication (H4 (H4′) and H5 (H5′)) atoms. Therefore, H-bonding can be formed between the O, F and N atoms of anions and N–H4(H4′) as well as N–H5(H5′) bonds of the dication. According to electrostatic potential maps given in Fig. 2, eight configurations namely [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes were predicted. Fig. 3 displays the electrostatic potential maps of [BTAD][A1–8]2 complexes.
image file: d4me00119b-f2.tif
Fig. 2 Electrostatic potentials calculated at the M06-2X/6-31++G(d,p) level of theory by the 0.0004 electron density isosurface for free dication BTAD = [C6H4N6O2]2+ and anions [A1–8]− = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−.

image file: d4me00119b-f3.tif
Fig. 3 Electrostatic potential maps calculated at the M06-2X/6-31++G(d,p) level of theory and mapped onto the 0.0004 electron density isosurface for [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and [A1–8]− = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes.

The most commonly used method for theoretically characterizing the influence of the anion type on the distribution of the charge constituent atoms of a cation is the electrostatic minimum potential energy (Vmin) that can be obtained through ESP topographical analysis using software such as the Multiwfn program.75,76Vmin values for N, O, and F atoms involved in H-bonding of both anions in the [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes were computed at the M06-2X/6-31++G(d,p) level of theory. The value of Vmin is a suitable descriptor that shows the shift of electron density from one atom to another in a non-covalent interaction. It is often used to describe the reactivity of a molecule, as the more negative the Vmin, the more likely the molecule is to attract an electrophile. It is predicted that the strength of the interaction is different in the triple ions formed by various anions. The average value of Vmin of heteroatoms in the isolated [A1–8]− anions is −141.58, −127.29, −112.36, − 116.16, −121.61, −130.24, −96.40 and −102.34 kcal mol−1 which changes to −130.5, −123.9, −104.9, −115.8, −117.0, −114.4, −96.7, and −93.4 kcal mol−1 in the [BTAD][A1–8]2 complexes, respectively. The change in 〈Vmin〉 shows that the interaction strength changes due to the type of anion and the shift of electron density occurs from one atom to another in the formation of the complexes. The Δ〈Vmin〉 values obtained for the A (A′) anionic part of [BTAD][A1–2]2 (A1–2 = [CH3CO2]−, [CF3CO2]−) complexes are higher than the other complexes, indicating that the interaction between ions in these complexes is stronger than others.

3.3. Interaction energies

The physical and chemical characteristics of complexes are influenced by various intermolecular interactions including van der Waals forces and hydrogen bonding. The configurations and type of ion present in complexes can have a significant impact on the strength of these interactions, which can affect the physicochemical properties of the complexes.77–85Table 1 displays the interaction energies calculated at the different levels of theory for [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes. As can be observed in Table 1, the range of electronic interaction energy (ΔEelec) for [BTAD][A1–8]2 complexes varies from −288.13 to −432.42 kcal mol−1 at the M06–2X/6–31++G(d,p) level of theory, −289.07 to −433.34 kcal mol−1 at the M06–2X-GD3/6-31++G(d,p) level of theory, 295.63 to −427.87 kcal mol−1 at the B2PLYP-GD3/6-31++G(d,p) level of theory and −293.91 to −429.25 kcal mol−1 at the mPW2PLYP-GD2/6-31++G(d,p) level of theory. The absolute value of dispersion corrected interaction energies for [BTAD]2+ based dicationic ILs (−289.07 to −433.34 kcal mol−1) is greater than those found (−222.67 to −363.97 kcal mol−1) for imidazolium-based dicationic ionic liquids [X][Y1–8]2 (X = [C2(MIM)2]2+ and Y1–8 = CH3CO2−, NO3−, BF4−, ClO4−, NTf2−, PF6−, C(CN)3−, and OH−) (ref. 86) and 1-methyl-4-phenyl 1,2,4 thiazolium-based [PhMTZ][X1–10] ionic liquids (−66.7 to −97.6 kcal mol−1)87 at the M06-2X/6-311++G(d,p) level of theory. This indicates that the interaction energy of anions is significantly influenced by the nature of the cations with which they interact. Based on the interaction energies, the stability order of [BTAD][A1–8]2 complexes at all levels of theory is [BTAD][CH3CO2]2 > [BTAD][CF3CO2]2 > [BTAD][N(CN)2]2 > [BTAD][CF3SO3]2 > [BTAD][ClO4]2 > [BTAD][BF4]2 > [BTAD][NTf2]2 > [BTAD][PF6]2. This indicates that [BTAD][CH3CO2]2 and [BTAD][PF6]2 are the most and least stable complexes, respectively. In addition, the absolute values of electronic interaction energies calculated at the M06-2X/6-31++G(d,p) and dispersion-corrected M06-2X/6-31++G(d,p)-GD3 levels of theory are greater than those calculated by using dispersion-corrected double-hybrid B2PLYP-GD3 and mPW2PLYP-GD2 methods.
Table 1 Electronic interaction energies (kcal mol−1) obtained for the [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) DCILs at various levels of theory
Structures M06-2X/6-31++G(d,p) M06-2X-GD3/6-31++G(d,p) B2PLYP-GD3/6-31++G(d,p) mPW2PLYP-GD2/6-31++G(d,p)
[BTAD][A1] 2 −432.42 −433.34 −427.87 −429.25
[BTAD][A2] 2 −380.17 −381.17 −374.86 −376.09
[BTAD][A3] 2 −354.01 −355.13 −347.88 −349.41
[BTAD][A4] 2 −336.98 −338.24 −329.42 −330.12
[BTAD][A5] 2 −325.57 −325.25 −317.19 −316.76
[BTAD][A6] 2 −311.26 −310.97 −300.64 −301.63
[BTAD][A7] 2 −301.73 −304.19 −295.63 −293.91
[BTAD][A8] 2 −286.43 −286.04 −277.35 −278.38

The electronic interaction energies corrected by BSSE (basis set superposition errors), ZPVE (zero-point vibrational energy) and dispersion ΔEc were calculated. The corrected electronic interaction energies (ΔEc), interaction enthalpy (ΔHc) and Gibbs free interaction energy (ΔGc) for [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes at the M06-2X/6-31++G(d,p) level of theory in the gas phase are reported in Table 2. As can be seen, ΔEc, ΔHc and ΔGc energies are in the range of −285.77 to −426.52, −285.96 to −421.66 and −266.53 to −399.33 kcal mol−1 in [BTAD][A1–8]2 complexes, respectively. The results show that their absolute values are less than uncorrected values. The interaction strength between the anions and dication is affected by van der Waals interaction, which can result in changes to interaction energies when empirical dispersion is included.88 The percentage of the dispersion correction for [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes is 0.21, 0.26, 0.31, 0.37, 0.32, 0.29, 0.81 and 0.40%, respectively. The contribution of dispersion energies captured by using the M06-2X-GD3 method for the DCIL [BTAD][A7]2 with the bulky anion [NTf2]− is greater than the other complexes. Based on the corrected energies, the interaction strength between the dication [BTAD]+2 and anions [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]− decreases in the following order: [BTAD][CH3CO2]2 > [BTAD][CF3CO2]2 > [BTAD][N(CN)2]2 > [BTAD][CF3SO3]2 > [BTAD][ClO4]2 > [BTAD][BF4]2 > [BTAD][NTf2]2 > [BTAD][PF6]2.

Table 2 Interaction energies (kcal mol−1) calculated for [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) DCILs at the M06-2X/6-31++G(d,p) level of theory
Structures ΔZPVE BSSE ΔEelec ΔEdisp ΔEc ΔHc ΔGc E def(DCIL)
[BTAD][A1] 2 4.31 2.51 −432.42 −0.92 −426.52 −421.66 −399.33 203.6
[BTAD][A2] 2 3.47 2.32 −380.17 −1.01 −375.39 −369.93 −352.83 185.5
[BTAD][A3] 2 1.08 2.86 −354.01 −1.12 −351.18 −349.28 −328.27 248.5
[BTAD][A4] 2 1.42 3.30 −336.98 −1.26 −333.52 −331.02 −310.08 170.6
[BTAD][A5] 2 0.70 3.09 −325.57 −1.04 −322.82 −322.04 −298.38 163.2
[BTAD][A6] 2 −0.43 1.89 −311.26 −0.90 −310.70 −311.27 −288.86 106.2
[BTAD][A7] 2 −0.13 4.79 −301.73 −2.46 −299.52 −298.42 −278.47 126.5
[BTAD][A8] 2 −1.05 2.86 −286.43 −1.14 −285.77 −285.96 −266.53 27.2

Since the structure of the cation and anions in the complexes changes with the formation of the DCIL, the deformation energies of the complexes (Edef) are calculated by using eqn (1) and listed in Table 2.

 
Edef = Edication(DCIL) + Eanion(DCIL) + Eanion′(DCIL) − (Edication(isolated) + 2Eanion(isolated))(1)
where the Edication(DCIL) and Eanion(DCIL) or Eanion′(DCIL) are the single point energy of the dication and anions in the optimized structure of the DCIL and Edication(isolated) and Eanion(isolated) are the energy of the isolated optimized dication and anions, respectively. Deformation energy is the energy required to bring monomers from their equilibrium geometry to that in the complex. As can be observed, the energy value in the complexes [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) is 203.6, 185.5, 248.5, 170.6, 163.2, 106.2, 126.5 and 27.20 kcal mol−1, respectively. The deformation energy is always positive because it determines the energy required to reshape monomers from their equilibrium structure to their geometry in the complex. In the studied complexes, except for [BTAD][A1]2 and [BTAD][A2]2, a straightforward correlation was not found between interaction and deformation energies. The highest deformation energy is found for [BTAD][A3]2 because one of the N–H bonds is broken and a new H⋯O bond is formed with the O atom of the C[double bond, length as m-dash]O group. On the other hand, [BTAD][A8]2 has the lowest deformation and interaction energies, that is, H-bonds are weaker, and the deformation energy is smaller.

3.4. Gibbs free interaction energy and solvation energy

In the context of ionic liquids, solvation plays a crucial role in their behavior and properties. The Gibbs free energy of solvation and Gibbs free interaction energy for the complexes [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) in various solvents were calculated by using SMD-PCM approaches at the M06-2X-GD3/6-31++G(d,p) level of theory. 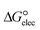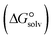Table 3 provides the electrostatic and non-electrostatic contributions (image file: d4me00119b-t1.tif and image file: d4me00119b-t2.tif) to the Gibbs free energy of solvation image file: d4me00119b-t3.tif, the changes in Gibbs free energy of solvation for complex formation 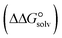image file: d4me00119b-t4.tif, the Gibbs free interaction energy of the complexes in the gas phase 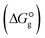image file: d4me00119b-t5.tif and the Gibbs free interaction energy of the complexes in solutions 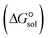image file: d4me00119b-t6.tif. These results indicate that the contribution of the non-electrostatic term in 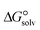image file: d4me00119b-t7.tif for the complexes is less than that of the electrostatic one.
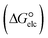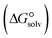Table 3 The electrostatic image file: d4me00119b-t8.tif and non-electrostatic image file: d4me00119b-t9.tif contributions to the Gibbs free energy of solvation image file: d4me00119b-t10.tif, the change in Gibbs free energy of solvation 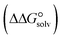image file: d4me00119b-t11.tif of the studied DCILs at the M06-2X/631++G(d,p) level using SMD-PMC approaches in water, methanol and methylcyclohexane solvent media, the Gibbs free interaction energy of the DCILs in the gas phase and solutions, (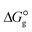image file: d4me00119b-t12.tif and image file: d4me00119b-t13.tif) and solvation energies (ΔEsolv = Eelec(solvent) − Eelec(gas)), calculated at the M06-2X/6-31++G(d,p) level of theory. All energies are in kcal mol−1
Structures Solvent

image file: d4me00119b-t14.tif

image file: d4me00119b-t15.tif

image file: d4me00119b-t16.tif

image file: d4me00119b-t17.tif

image file: d4me00119b-t18.tif

image file: d4me00119b-t19.tif

 ΔEsolv
Water
[BTAD][A1] 2 −29.53 7.93 −21.60 197.82 −405.23 −207.41 −25.26
[BTAD][A2] 2 −30.43 11.16 −19.27 166.01 −357.61 −191.60 −25.60
[BTAD][A3] 2 −27.86 12.26 −15.60 145.50 −331.10 −185.60 −17.72
[BTAD][A4] 2 −31.73 7.14 −24.59 159.69 −313.54 −153.85 −25.91
[BTAD][A5] 2 −49.82 10.41 −31.63 126.27 −301.13 −111.03 −27.53
[BTAD][A6] 2 −37.71 7.97 −29.74 148.10 −289.42 −141.32 −32.11
[BTAD][A7] 2 −32.52 12.23 −20.29 142.99 −280.68 −137.69 −26.91
[BTAD][A8] 2 −33.6 1.97 −39.41 156.17 −267.20 −174.86 −41.72
Methanol
[BTAD][A1] 2 −26.44 8.82 −17.62 190.02 −405.23 −215.21 −23.00
[BTAD][A2] 2 −27.14 10.47 −16.67 159.19 −357.61 −198.42 −23.23
[BTAD][A3] 2 −25.50 6.61 −18.89 139.75 −331.10 −191.35 −16.29
[BTAD][A4] 2 −28.61 10.32 −18.29 149.11 −313.54 −164.43 −23.82
[BTAD][A5] 2 −30.38 11.28 −19.10 146.82 −301.13 −154.31 −25.39
[BTAD][A6] 2 −35.15 6.63 −28.52 142.54 −289.42 −146.88 −30.33
[BTAD][A7] 2 −29.18 13.93 −15.25 133.07 −280.68 −147.61 −24.61
[BTAD][A8] 2 −46.63 6.93 −39.70 121.32 −267.20 −145.88 −39.53
Methylcyclohexane
[BTAD][A1] 2 −5.80 −2.09 −7.89 102.48 −405.23 −302.75 −5.56
[BTAD][A2] 2 −5.48 0.38 −5.10 96.55 −357.61 −261.06 −5.23
[BTAD][A3] 2 −7.12 −6.91 −14.03 96.18 −331.10 −234.92 −2.27
[BTAD][A4] 2 −5.95 −0.61 −6.56 92.71 −313.54 −220.83 −5.56
[BTAD][A5] 2 −6.74 −2.8 −9.54 93.29 −301.13 −207.84 −6.40
[BTAD][A6] 2 −11.4 1.8 −9.60 97.53 −289.42 −191.89 −10.87
[BTAD][A7] 2 −6.20 1.83 −4.37 85.76 −280.68 −194.92 −5.78
[BTAD][A8] 2 −15.17 2.07 −13.10 88.41 −267.20 −178.79 −14.35

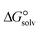image file: d4me00119b-t20.tif is a parameter that reflects the strength of interaction between the solvent and solute. The order of 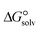image file: d4me00119b-t21.tif values for the complexes is [BTAD][A8]2 > [BTAD][A5]2 > [BTAD][A6]2 > [BTAD][A4]2 > [BTAD][A1]2 > [BTAD][A7]2 > [BTAD][A2]2 > [BTAD][A3]2 in water, [BTAD][A8]2 > [BTAD][A6]2 > [BTAD][A5]2 > [BTAD][A3]2 > [BTAD][A4]2 > [BTAD][A1]2 > [BTAD][A2]2 > [BTAD][A7]2 in methanol and [BTAD][A3]2 > [BTAD][A8]2 > [BTAD][A6]2 > [BTAD][A5]2 > [BTAD][A1]2 > [BTAD][A4]2 > [BTAD][A2]2 > [BTAD][A7]2 in methyl cyclohexane. The dipole moment in water, methanol and methylcyclohexane solvents is 5.16, 5.07 and 4.27 D for [BTAD][A1]2, 0.19, 0.26 and 0.65 D for [BTAD][A2]2, 6.19, 5.91 and 4.03 D for [BTAD][A3]2, 3.29, 3.25 and 2.88 D for [BTAD][A4]2, 4.76, 4.73 and 4.34 D for [BTAD][A5]2, 6.44, 6.46 and 6.43 D for [BTAD][A6]2, 3.98, 3.86 and 3.01 D for [BTAD][A7]2 and 3.04, 3.15 and 3.80 D for [BTAD][A8]2, respectively. When an ionic liquid is dissolved in polar solvents, the dipole moment of the solvent can affect the ionic interactions. For example, a solvent with a large dielectric constant can decrease the attraction between the ions, as the effective dielectric constant increases.

The image file: d4me00119b-t22.tif of the complexes in solvent media is computed using the following thermochemical cycle:

image file: d4me00119b-u1.tif
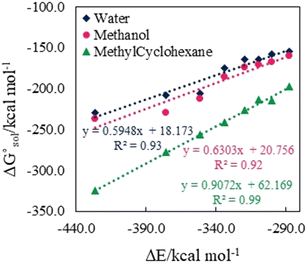
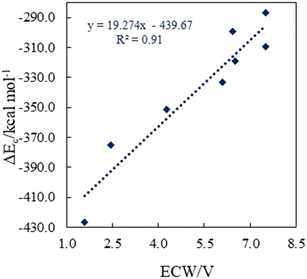
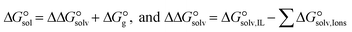where image file: d4me00119b-t23.tif. The results reveal that the Gibbs free interaction energy of the triple complexes decreases significantly with increasing dielectric constant of the solvent (εwater = 78, εmethanol = 32.613 and εmethylcyclohexane = 2.024); for example, from −405.23 kcal mol−1 for [BTAD][A1]2 in the gas phase to −207.41 kcal mol−1 in water. Also, the Gibbs free interaction energy of the triple complexes in the more polar solvent is lower than the less polar one. Fig. 4 shows that there is a good linear relationship between the corrected interaction energy (ΔEc) of the studied complexes in the gas phase with the Gibbs free energy in the solution 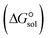image file: d4me00119b-t24.tif, especially in the non-polar solvent methylcyclohexane. It is obvious from Fig. 4 that the increase in the absolute value of ΔEc is accompanied by an increase in image file: d4me00119b-t25.tif of [BTAD][A1–8]2 complexes.


image file: d4me00119b-f4.tif
Fig. 4 Correlation between ΔEc in the gas phase and image file: d4me00119b-t26.tif of [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) in the solutions at the M06-2X/6-31++G(d,p) level of theory.

The strength of intermolecular interactions between the dications and anions of the triple complexes is a key factor in determining their macroscopic properties such as melting point, critical temperature, enthalpy of vaporization and electrical conductivity. The results suggest that a change in the interaction energy leads to a corresponding change in the macroscopic properties of the complexes. Therefore, the interaction energy can be increased or decreased by choosing solvents with different polarities. Table 3 presents the solvation energies of [BTAD][A1–8]2 complexes calculated in solvent media using the equation ΔEsolv = Eelec (solvent) − Eelec (gas). As can be observed, ΔEsolv for the complexes in all the solvents is negative, indicating that the solvation process of the complexes is energetically favorable. The range of ΔEsolv values is from −17.72 (−16.29), and −2.27 to −41.72 (−39.53), and −14.35 kcal mol−1 in water, (methanol), and methylcyclohexane for [BTAD][A1–8]2 triple complexes.

3.5. Proton transfer and ΔpKa

The calculated interaction energies of the complexes [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) are −426.52, −375.39, −351.18, −333.52, −322.82, −310.70, −299.52 and −285.77 kcal mol−1, respectively. It can be found that all of the interaction energies are much larger than the normal hydrogen bond energy, which indicates the existence of strong electrostatic attractions between the dication and the anions. The maximum value of the interaction energy belongs to the [BTAD][CH3CO2]2 complex because the hydrogen atoms H4(H4′) and H5(H5′) in the bonds (N1–H4(N1′–H4′) and N2–H5(N2′–H5′)) possess larger positive charge. Except for the [BTAD][PF6]2 complex, a proton transfer occurs from (N1–H4(N1′–H4′) groups of the cation to [A1–7] anions, which is in good agreement with the large interaction energies obtained for corresponding complexes. As mentioned above, the hydrogen atoms H4(H4′) in the dication [BTAD]+2 have the most positive potential that can facilitate the proton transfer process. In the proton transfer complexes, two hydrogen bonds of N1–H4⋯X and N1′–H4′⋯X are replaced by N1⋯H4–X and N1⋯H4–X′ H-bonds.

The process of proton transfer observed in the triple ions can be expressed as H2B2+ + 2A− → B + 2HA reaction, where H2B2+ and HA are Brønsted acids of B and A− bases, respectively. Due to the proton donating and accepting abilities of H2B2+ and A−, respectively, and based on the above equation, PILs can be used as amphoteric solvents. The free energy of the proton transfer process (ΔGPT(total)) in the solvent water was calculated by using the equation ΔGPT(total) = Gtotal(B) − Gtotal(H2B2+) + 2Gtotal(HA) − 2Gtotal(A−),89 where Gtotal for each solvated species is obtained from the sum of the Gibbs free energy of the gas phase species and its Gibbs free energy of solvation using the COSMO-RS approach at the M06-2X/631++G(d,p) level of theory in water (Gtotal = Ggas + ΔGsolv and ΔGsolv = ΔGnonelec + ΔGelec). The calculated Gibbs free energy of the proton transfer process (ΔGPT(total)) for [BTAD][A1–8]2 (A1–7 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]− and [NTf2]−) is −56.90, −40.76, −31.04, −5.47, 2.79, 22.41, −9.30 and 38.21 kcal mol−1, respectively (see Table 4). The results of ΔGPT(total) in the water solvent show that the proton transfer process in the triple complexes [BTAD][A1–4,7]2 [A1–4,7]− = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]− and [NTf2]− is spontaneous in the water solvent, while for the triple ions [BTAD][A5,6,8]2 [A5,6,8] = [ClO4]−, [BF4]− and [PF6]− it is non-spontaneous. 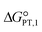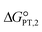From the calculated image file: d4me00119b-t27.tif and image file: d4me00119b-t28.tif, and equation pKeq = ΔpKa = ΔGPT/(2.303 × RT), the pKeq,1 (pKeq,2) of [BTAD]+2 in the water solvent for triple complexes [BTAD][A1–8]2 is −23.8 (−18.0), −17.8 (−12.1), −14.3 (−8.5), −4.9 (0.90), −1.87 (3.9), 5.32 (11.1), −6.30 (−0.5) and 11.12 (16.9), respectively. This indicates that the proton-transfer equilibrium constant Keq,1 for reaction H2B2+ + A− → HB+ + HA is greater than Keq,2 of HB+ + A− → B+2 + HA reaction. Therefore, the first step of proton transfer is thermodynamically more favorable than the second step. In addition, the pKeq of reactions for triple ions [BTAD][A1–3]2 in the water solvent is greater than others. The pKeq = ΔpKa values can be considered as a measure of the tendency of the cation to lose protons. Thus, based on ΔpKa values, it can be predicted that the acidity of the cation in the studied complexes decreases in the following order: [BTAD][CH3CO2]2 > [BTAD][CF3CO2]2 > [BTAD][N(CN)2]2 > [BTAD][NTf2]2 > [BTAD][CF3SO3]2 > [BTAD][ClO4]2 > [BTAD][BF4]2 > [BTAD][PF6]2.

Table 4 The Gibbs free energies of the proton transfer process (ΔGPT1, ΔGPT2 and ΔGPT(total)) and the calculated pKeq,1 for reaction (H2B2+ + A− ⇌ HB+ + HA) and pKeq,2 for reaction (HB+ + A− ⇌ B + HA at the M06-2X/6-31++G(d,p) level in the water solvent
Structures ΔGPT1 ΔGPT2 ΔGPT(total) pKeq,1 (ΔpKa,1a) pKeq,2 (ΔpKa,2a)
a ΔpKa,1 = pKa(cation) − pKa(HA); HA is the conjugate acid of anion A−.
[BTAD][A1]2 −32.40 −24.51 −56.91 −23.75 −17.97
[BTAD][A2]2 −21.62 −13.73 −35.35 −15.85 −10.07
[BTAD][A3]2 −19.47 −11.58 −31.04 −14.27 −8.49
[BTAD][A4]2 −5.98 1.91 −4.06 −4.38 1.40
[BTAD][A5]2 −2.65 8.07 5.42 −1.94 5.92
[BTAD][A6]2 6.27 16.99 22.75 4.59 12.45
[BTAD][A7]2 −8.05 −0.16 −8.20 −5.90 −0.11
[BTAD][A8]2 17.63 25.52 43.15 12.92 18.71

3.6. Vibrational frequency analysis

The change in structural parameters of molecules often leads to alterations in the vibrational frequencies of bonds involved in H-bonding interaction. Due to columbic interactions, this effect in ionic liquids is stronger than in molecular liquids. As can be seen in Table S1 of the ESI,† DCIL formation leads to a considerable change in the vibrational frequency of N–H (N′–H′) bonds of the triazole in the cationic part as well as the N–C, C[double bond, length as m-dash]O, Cl–O, P–F and B–F bonds in the anion part. The results show that the vibrational frequency of N2–H5(N2′–H5′) bonds in the isolated cation and complexes is lower than that of N1–H4(N1′–H′) bonds which is in good agreement with the greater bond length obtained for N2–H5(N2′–H5′) bonds. As mentioned above, N2–H5(N2′–H5′) bonds of the dication are involved in N2–H5⋯X and N2′–H5′⋯X H-bonding in all [BTAD][A1–8]2 complexes. The symmetric stretching vibrational frequencies of N2–H5(N2′–H5′) bonds (νN2–H5 (νN2′–H5′)) show a red-shift of 53.3 cm−1, 10.9 cm−1 and 10.4 cm−1 in [BTAD][A1,3]2, and 9.5 and 1480.5 cm−1 in [BTAD][A7,8]2, respectively. This indicates that the decrease in the frequency of N2–H5(N2′–H5′) bonds upon formation of the [BTAD][PF6]2 DCIL is greater than the others, in good agreement with the greater N2–H5(N2′–H5′) bond lengths found for this DCIL. A blue shift in the vibrational frequency of N2–H5(N2′–H5′) bonds is observed in [BTAD][A2,A4–6]2 by 35.5, 54.2, 76.8 and 32.0 cm−1, respectively, in good agreement with the decrease in N2–H5(N2′–H5′) bond lengths upon complex formation. Only the N1–H4(N1′–H4′) bonds are retained in [BTAD][PF6]2 with a red-shift of 133.1 cm−1, significantly lower than the red-shift observed for N2–H5(N2′–H5′) (1480.4 cm−1). The vibrational frequency of C[double bond, length as m-dash]O, N–C, Cl–O, P–F and B–F bonds of anions ([A]−DCIL) involved in the interaction with the dication increases, compared to the same bonds in free anions ([A]−free), except for [BTAD][A4,5,8]2 complexes.

3.7. AIM analysis

The quantum theory of atoms in molecules (QTAIM) is a valuable tool for elucidating the characteristics of chemical bonds, particularly hydrogen bonds.90–92 The molecular graphs consisting of the ring critical points (RCPs) (yellow balls), bond critical points (BCPs) (red balls), and cage critical points (CCPs) (green balls) for the complexes are given in Fig. 5. Also, Table 5 provides the values of the electron density ρ(r), its corresponding Laplacian ∇2ρ(r), and electronic energy density H(r), at hydrogen bond critical points (HBCPs) of [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes at the M06-2X/6-31++G(d,p) level of theory. The average values of electron densities (〈ρ(r)〉) at N2–H5⋯X (X = O or N or F) and N2′–H5′⋯X′ HBCPs in the [BTAD][A1–8]2 complexes are 0.0298, 0.0241, 0.0225, 0.0229, 0.0182, 0.0254, 0.0259 and 0.1047 a.u., respectively, while that in the non-proton transfer [BTAD][PF6]2 DCIL is higher than the others. The average values of electron densities at X–H4⋯N1 (X = O or N or F) and X′–H4′⋯N1′ of [BTAD][A1–7]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–7 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]− and [NTf2]−) are 0.0293, 0.0366, 0.0258, 0.0483, 0.0528, 0.1029 and 0.0715 a.u., respectively. Also the average value of electron densities at N1–H4⋯F and N1′–H4′⋯F′ HBCPs in the [BTAD][A8]2 complex is 0.0301 a.u.. The results of Table 5 show that the ∇2ρ(r) and H(r) values at N2–H5⋯X (X = O or N or F) and N2′–H5′⋯X′ HBCPs of [BTAD][A1–5,7]2 complexes are positive, indicating the electrostatic nature of these H-bonds.
image file: d4me00119b-f5.tif
Fig. 5 The molecular graphs covering the bond critical points (BCPs) (red spheres), ring critical points (RCPs) (yellow spheres), cage critical points (CCPs) (green spheres), and bond paths for [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes.
Table 5 The electronic density, ρ(r), its corresponding Laplacian, ∇2ρ(r), and electronic energy density, H(r) at hydrogen bond critical points of [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes at the M06-2X/6-31++G(d,p) level of theory
Complexes ρ(r) ∇2ρ(r) H(r) Complexes ρ(r) ∇2ρ(r) H(r)
[BTAD][A1] 2 [BTAD][A5] 2
O8–H4⋯N1 0.0293 0.0822 0.0003 N2–H5⋯O7 0.0182 0.0697 0.0010
O8′–H4′⋯N1′ 0.0293 0.0822 0.0003 N2′–H5′⋯O7′ 0.0182 0.0697 0.0010
H4–O8 0.3347 −2.0352 −0.5726 H4–O8 0.2958 −1.6644 −0.4840
H4′–O8′ 0.3347 −2.0354 −0.5726 H4′–O8′ 0.2958 −1.6644 −0.4840
N2–H5⋯O7 0.0298 0.0991 0.0004 O8–H4⋯N1 0.0528 0.1103 −0.0063
N2′–H5′⋯O7′ 0.0298 0.0991 0.0004 O8′–H4′⋯N1 0.0528 0.1103 −0.0063
[BTAD][A2] 2 [BTAD][A6] 2
O8–H4⋯N1 0.0366 0.0968 −0.0005 H4–F8 0.2335 −0.9419 −0.3378
O8′–H4′⋯N1′ 0.0363 0.0963 −0.0004 H4′–F8′ 0.2335 −0.9419 −0.3378
H4–O8 0.3225 −1.9564 −0.5521 N2–H5⋯F7 0.0254 0.0986 0.0000
H4′–O8′ 0.3228 −1.9597 −0.5529 N2′–H5′⋯F7′ 0.0254 0.0986 0.0000
N2–H5⋯O7 0.0240 0.0806 0.0002 F8–H4⋯N1 0.1029 −0.0160 −0.0629
N2′–H5′⋯O7′ 0.0240 0.0805 0.0002 F8′–H4′⋯N1 0.1029 −0.0160 −0.0629
[BTAD][A3] 2 [BTAD][A7] 2
N8–H4⋯O[double bond, length as m-dash] 0.0258 0.0835 0.0004 O8–H4⋯N1 0.0715 0.0944 −0.0201
N8′–H4′⋯O[double bond, length as m-dash] 0.0258 0.0835 0.0004 O8′–H4′⋯N1′ 0.0715 0.0945 −0.0201
H4–N8 0.3128 −1.7036 −0.4678 H4–O8 0.2646 −1.3221 −0.4039
H4′–N8′ 0.3128 −1.7036 −0.4678 H4′–O8′ 0.2646 −1.3225 −0.4040
N2–H5⋯N7 0.0225 0.0701 0.0007 N2–H5⋯O7 0.0259 0.0990 0.0016
N2′–H5′⋯N7′ 0.0225 0.0701 0.0007 N2′–H5′⋯O7′ 0.0259 0.0990 0.0016
[BTAD][A4] 2 [BTAD][A8] 2
O8–H4⋯N1 0.0483 0.1091 −0.0041 N1–H4⋯F8 0.0301 0.1071 −0.0010
O8′–H4′⋯N1′ 0.0480 0.1088 −0.0040 N1′–H4′⋯F8′ 0.0302 0.1071 −0.0010
H4–O8 0.3004 −1.7244 −0.4982 H5–N2 0.2324 −1.0779 −0.3203
H4′–O8′ 0.3008 −1.7292 −0.4993 H5′–N2′ 0.2324 −1.0787 −0.3204
N2–H5⋯O7 0.0229 0.0812 0.0005 N2–H5⋯F7 0.1047 0.1103 −0.0572
N2′–H5′⋯O7′ 0.0229 0.0812 0.0005 N2′–H5′⋯F7′ 0.1047 0.1106 −0.0570

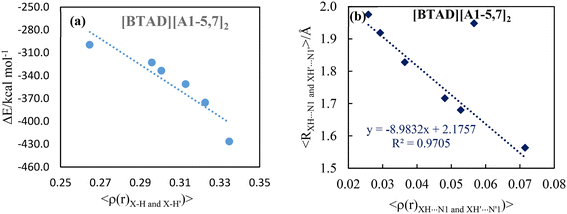
The positive value of ∇2ρ(r) and negative value of H(r) at N2–H5⋯F and N2′–H5′⋯F′ HBCPs of the [BTAD][A6,8]2 complexes implies that the nature of the H-bonds is slightly covalent. Furthermore, the ∇2ρ(r) and H(r) at N1–H4⋯X and N1′–H4′⋯X′ hydrogen bond critical points of [BTAD][A2,4,5,7,8]2 complexes are positive and negative, respectively, implying that the nature of these H-bonds is slightly covalent. The positive values of ∇2ρ(r) and H(r) at N1–H4⋯X and N1′–H4′⋯X′ HBCPs of the [BTAD][A1,3]2 complexes indicate the electrostatic nature of the H-bonds. The negative values of ∇2ρ(r) and H(r) at HBCPs of N1–H4⋯F (N1′–H4′⋯F′) of the [BTAD][A6]2 complex indicate that the nature of these H-bonds is covalent. The correlation between the interaction energy and the average values of the electron densities at X–H (X = O and N) BCPs for proton transfer complexes [BTAD][A1–5,7]2 is shown in Fig. 6a. As can be seen, the greater the electron density, the greater the interaction energy. Besides, the relationship between the average value of the electron densities at XH4⋯N1 (X'H4′⋯N1′) H-bond critical points and the value average of corresponding hydrogen bond distances in [BTAD][A1–5,7]2 is shown in Fig. 6b. This shows that the reduction of the hydrogen bond distance leads to an increase in the electron density of the corresponding HBCP.


image file: d4me00119b-f6.tif
Fig. 6 Correlation between (a) the interaction energy and the average values of the electron densities at X–H (X = O and N) BCPs, and (b) average values of the XH⋯N1 and XH′⋯N1′ hydrogen bond distances and average values of electron density at related HBCPs in the [BTAD][A1–5,7]2 (BTAD = [C6H4N6O2]2+ and A1–5,7 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [NTf2]−) complexes.

3.8. Natural bond orbital (NBO) analysis

The hydrogen bond interactions between the anions and dication in complexes are accompanied by charge transfer between ions.93–95 The charge transfer values can be measured using the natural bond orbital (NBO) method. NBO data containing charge transfer energies (E(2)), natural charge (q) of hydrogen atoms, charge transfer (CT), and occupancy values estimated at the M06-2X/6-31++G(d,p) level of theory for the studied complexes are given in Table 6. The NBO analysis reveals that the donor–acceptor interactions LP(N) → σ*(N–H), LP(O) → σ*(N–H), and LP(F) → σ*(N–H) in the triple ions are the most significant intermolecular interactions between anions and the dication in [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes. The sum of charge transfer energies E(2) corresponding to LP(X) (X = F or O and or N) → σ*(N2–H5) and LP(X) (X = F or O and or N) → σ*(N2′–H5′)) interactions in [BTAD][A1–8]2 complexes is 33.34, 21.85, 16.75, 18.85, 19.26, 99.48 and 25.94 and 210.05 kcal mol−1, respectively, indicating that N2–H5⋯X and N2′–H5′⋯X H-bonding interactions in [BTAD][BF4]2 and [BTAD][PF6]2 complexes are stronger than the other complexes, in good agreement with the greater electron density calculated at N2–H5⋯X and N2′–H5′⋯X HBCPs. In addition, the sum of charge transfer energies of LP(N1) → σ*(X–H4) and LP(N1′) → σ*(X′–H4′) interactions in the proton transfer complexes [BTAD][A1–7]2 is 18.23 (18.21), 26.01 (25.76), 14.35 (21.81), 39.09 (39.48), 44.6 (44.6), 102.28 (102.28) and 67.75 (67.76) kcal mol−1. This indicates that charge transfer energies for [BTAD][A6]2 and [BTAD][A7]2 are greater than [BTAD][A1–5]2 complexes, in good agreement with the greater X(O, N and F)–H bond length found for these complexes. Electron density is transferred from the lone pair to the antibonding orbital of the X–H bond, which causes a weakening and elongation of this bond.
Table 6 NBO data calculated for [BTAD][A1–8]2 (BTAD = [X = C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes and the isolated dication at the M06-2X/631++G(d,p) level of theory
Parameters [X]2+ [X][A1]2 [X][A2]2 [X][A3]2 [X][A4]2 [X][A7]2
q H4/e 0.523 0.543 0.549 0.480 0.553 0.547
q H4′/e 0.523 0.543 0.549 0.480 0.553 0.547
q H5/e 0.523 0.497 0.494 0.494 0.496 0.501
q H5′/e 0.523 0.497 0.494 0.494 0.496 0.501
CT/e 0.907 0.852 1.022 0.782 0.725
Occupancy
σ*(N1–H4) 0.014
σ*(N1′–H4′) 0.014
σ*(N2–H5) 0.014 0.043 0.035 0.041 0.031 0.036
σ*(N2′–H5′) 0.014 0.043 0.035 0.041 0.031 0.036
∑E(2)/kcal mol−1
LP(N7) → σ*(N2–H5) 7.2
LP(N7′) → σ*(N2′–H5′) 9.55
LP(O7) → σ*(N2–H5) 16.67 10.93 9.43 12.97
LP(O7′) → σ*(N2′–H5′) 16.67 10.92 9.42 12.97
Parameters [X][A5]2 [X][A6]2 [X][A8]2
q H4/e 0.540 0.578 0.536
q H4′/e 0.540 0.578 0.536
q H5/e 0.490 0.548 0.532
q H5′/e 0.490 0.507 0.532
CT/e 0.784 0.565 0.341
Occupancy/e
σ*(N1–H4) 0.038
σ*(N1′–H4′) 0.038
σ*(N2–H5) 0.026 0.029 0.138
σ*(N2′–H5′) 0.026 0.029 0.138
∑E(2)/kcal mol−1
LP(O8) → σ*(N1–H4) 5.14
LP(O8′) → σ*(N1′–H4′) 5.14
LP(N2) → σ*(O7–H5) 44.6
LP(N2′) → σ*(O7′–H5′) 44.6
LP(F7) → σ*(N2–H5) 9.63 104.99
LP(F7′) → σ*(N2′–H5′) 9.63 104.99
LP(N1) → σ*(F8–H4) 102.28
LP(N1′) → σ*(F8′–H4′) 102.28
LP(F8) → σ*(N1–H4) 0.97
LP(F8′) → σ*(N1′–H4′) 0.97
LP(F9) → σ*(N2–H5) 0.58
LP(F9′) → σ*(N2′–H5′) 0.58

According to the data shown in Table 6, the occupancy of the anti-bonding orbitals of (σ*(N1–H4), σ*(N1′–H4′), σ*(N2–H5) and σ*(N2′–H5′)) of the dication changes after complex formation. Compared with the free dication, the changes in values of the occupancy of (σ*(N2–H5) and σ*(N2′–H5′)) anti-bonding orbitals in [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes are 0.029, 0.021, 0.027, 0.017, 0.011, 0.015, 0.022 and 0.124 a.u., respectively. The results indicate that the charges of electronic density of σ*(N1–H4)(σ*(N1′–H4′)) or σ*(N2–H5) (σ*(N2′–H5′)) anti-bonding orbitals of the [BTAD]2+ dication in the [BTAD][A8]2 DCIL are higher than [BTAD][A1–5,7]2 complexes with the proton transfer process.

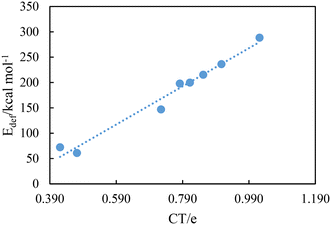
Table 6 shows the computed natural charges of hydrogen atoms in the free dication and the complexes. The positive charge of H4 and H4′ atoms increases after the formation of complexes (except for the [BTAD][A3]2 DCIL). Also, the positive charge of H5 and H5′ atoms involved in N2–H5 and N2′–H5′ bonds decreases after the formation of complexes (except for [BTAD][A6,8]2 complexes). The data of population analysis collected in Table 6 indicate that the charge transfer (CT) takes place from [A1–8]− anions to the [BTAD]2+ dication. The CT is calculated as the difference between the total atomic charges of two anionic components in the complexes and the two isolated anions. The CT values obtained for [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes are 0.907e, 0.852e, 1.022e, 0.782e, 0.784e, 0.565e, 0.725e and 0.341e, respectively, indicating that the negative charge of anions decreases from −2e to corresponding values in complexes. Besides, the CT values of [BTAD][BF4]2 and [BTAD][PF6]2 complexes are the lowest and for the BTAD][N(CN)2]2 complex it is the greatest. The correlation between the deformation energy and CT in the [BTAD][A1–8]2 complexes is shown in Fig. 7. The results prove that the increase in CT is accompanied by the increase in deformation energy.


image file: d4me00119b-f7.tif
Fig. 7 Correlation between CT values and deformation energies for [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes.

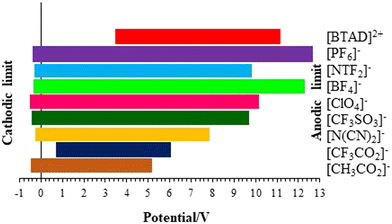
3.9. Electrochemical window (ECW)

The electrochemical window (ECW) of an IL represents the potential range in which the IL remains stable and does not undergo any electrochemical reactions. The ECW is a crucial parameter for the application of ILs in electrochemical devices like batteries, supercapacitors, and electrochemical sensors. It is influenced by factors such as the structural composition of the cation and anion forming the IL, the choice of solvent, and the operating temperature. The ECW of ILs is mainly determined by the cation's resistance to reduction and the anion's resistance to oxidation. The ECW of the complexes can be assessed by quantum chemical computations.96–102 The effect of the anion on the ECW of the complexes is explored at the BVP86/TZVP level of theory. The potentials of cathodic and anodic limits (VCL and VAL), the values of HOMO and LUMO energy levels (EHOMO and ELUMO) and the ECW of [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes calculated by the COSMO-RS technique at the BVP86/TZVP level of theory in the water solvent are given in Table 7.
Table 7 E HOMO, ELUMO, VCL and VAL of ions and ECW of [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) DCILs obtained from the COSMO-RS method at the BVP86/TZVP level of theory in water solvent
[X]2+ [A1]− [A2]− [A3]− [A4]− [A5]− [A6]− [A7]− [A8]−
a [X]2+ = [BTAD]2+. b V AL = −EHOMO/e− = VCPCMAL = min(VCPCMAL,C, VCPCMAL,A). c V CL = −ELUMO/e− = VCPCMCL = max(VCPCMCL,C, VCPCMCL,A). d ECW = VAL − VCL.
E LUMO/eV −3.56 0.58 0.56 0.27 0.52 0.61 0.40 0.37 0.40
E HOMO/eV −11.06 −5.15 −6.01 −7.84 −9.66 −10.06 −12.21 −9.98 −12.65
[X][A1]2 [X][A2]2 [X][A3]2 [X][A4]2 [X][A5]2 [X][A6]2 [X][A7]2 [X][A8]2
V CL/V 3.56 3.56 3.56 3.56 3.56 3.56 3.56 3.56
V AL/V 5.15 6.01 7.84 9.66 10.06 11.06 9.98 11.06
ECW/V 1.59 2.45 4.28 6.10 6.50 7.50 6.42 7.50

For ILs, the potential of cathodic limit (VCL) is determined by the highest value of the cathodic limit of the two ions (the corresponding anion and dication) and anodic limit (VAL) is obtained by the lowest value of their anodic limit. The potentials of the cathodic (VCL) and anodic limits (VAL) of ILs for a one-electron transfer can be characterized by the calculated LUMO and HOMO energy levels, respectively.103 In this method, the ECW is obtained using the following equation:

image file: d4me00119b-t29.tif
As shown in Table 7, the energy of HOMO of [A1–5,7]− anions (−5.15, −6.01, −7.84, −9.66, −0.06 and −9.98 eV) is larger than that of the [BTAD]2+ dication (−11.06 eV), indicating that the anodic stability of these complexes is effectively controlled by corresponding anions. For [A6] and [A8]− anions including the F atoms, the HOMO energy is less than the HOMO energy of the dication (−12.21 and −12.65 eV). Thereby, the anodic stability of the complexes having the [A6] and [A8]− anions is effectively controlled by their dication. The VAL and VCL[BTAD][A1–8]2 complexes are compared graphically in Fig. 8. The anodic stability of the complexes can change as [BTAD][A8]2 = [BTAD][A6]2 > [BTAD][A5]2 > [BTAD][A7]2 > [BTAD][A4]2 > [BTAD][A3]2 > [BTAD][A2]2 > [BTAD][A1]2, demonstrating that the complexes including inorganic anions with atoms of halogen have higher anodic stability than the others. The ECW values are restricted between 1.59 and 7.50 V and decrease in the sequence of [BTAD][A8]2 = [BTAD][A6]2 (7.50 V) > [BTAD][A5]2 (6.50 V) > [BTAD][A7]2 (6.42 V) > [BTAD][A4]2 (6.10 V) > [BTAD][A3]2 (4.28 V) > [BTAD][A2]2 (2.45 V) > [BTAD][A1]2 (1.59 V), indicating that anions with greater anodic stability have a higher ECW. As can be seen, the ECW of [BTAD][A3–8]2 is in the range of 4.5 to 7.5 V, demonstrating that these ILs can be promising candidates for the substitution of currently used electrolyte solutions based on organic molecular solvents in electrochemical devices. As presented in Fig. 9, there is a relationship between the ECW and interaction energy (ΔEc) of [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes. The complexes with the lowest interaction energy have the highest electrochemical stability in the redox reactions.


image file: d4me00119b-f8.tif
Fig. 8 Calculated cathodic and anodic limits for individual ions in [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes using the COSMO-RS method at the BVP86/TZVP level of theory in water solvent.

image file: d4me00119b-f9.tif
Fig. 9 Correlation between the electrochemical window (ECW) and interaction energy (ΔEc) of [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes.

3.10. Frontier molecular orbitals analysis

The frontier molecular orbital analysis (HOMO and LUMO) is a valuable indicator to evaluate the molecular charge distribution. The frontier molecular orbitals of HOMO and LUMO for [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes, LUMO of the dication [BTAD]2+ and HOMO of the anions [A1–8]− at the M06-2X/6-31++G(d,p) level of theory in the gas phase are displayed in Fig. 10. This figure shows that the HOMO of [A1–8]− anions consisting of disfigured p orbitals (EHOMO = −2.81, −4.04, −3.07, −4.73, −4.86, −6.84, −6.01 and −7.75 eV) concentrated on the N, O and F atoms of the anions and the character of the LUMO of the dication [BTAD]2+ is a π* molecular orbital (ELUMO = −11.38 eV) concentrated on the benzene ring and triazole groups. HOMOs of [BTAD][A1,2]2 complexes are distributed on both cationic and anionic parts and the HOMO of the [BTAD][A3]2 DCIL is mostly localized on anionic portions, whereas HOMOs of [BTAD][A4–8]2 complexes are mostly confined on the dication. The character of the LUMO of [BTAD][A1–8]2 complexes is the same and is limited to the cationic portion.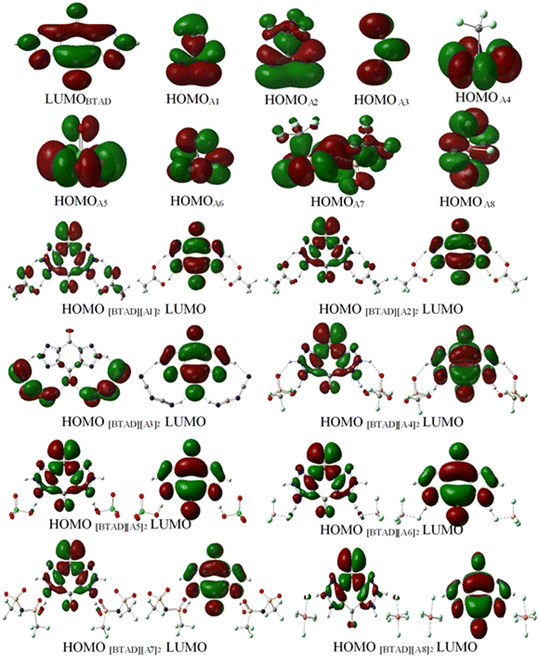
image file: d4me00119b-f10.tif
Fig. 10 Frontier molecular orbital (FMO) for [BTAD]2+ = [C6H4N6O2]2+, A1–A8 anions and [BTAD][A1–8]2 complexes at the M06-2X/6-31++G(d,p) level of theory.

To further understand the influence of different anions on the electronic properties of the complexes, the reactivity descriptors such as ionization potential (I = −EHOMO), electron affinity (A = −ELUMO), electronegativity (χ = (I + A)/2), chemical hardness (η = (I − A)/2), chemical softness (S = 1/2η), electronic chemical potential (μ = −(I + A)/2) and electrophilicity index (ω = μ2/2η)104–106 of [BTAD][A1–8]2 complexes at the M06-2X/6-31++G(d,p) level of theory in the gas phase are collected in Table 8. As can be observed, the HOMO–LUMO energy gap (EGap) values for [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes are 7.49, 7.49, 6.66, 7.49, 7.51, 7.45, 7.44 and 7.11 eV, respectively. The HOMO–LUMO energy gap values are listed in the following order [BTAD][A5]2 > [BTAD][A1]2 ≈ [BTAD][A2]2 ≈[BTAD][A4]2 > [BTAD][A6]2 > [BTAD][A7]2 > [BTAD][A8]2 > [BTAD][A3]2. As given in Table 8, increasing the EGap of [BTAD][A1–8]2 complexes causes an increase in chemical hardness and a decrease in chemical softness. The EGap value of the [BTAD][A3]2 DCIL is lower than the others. So the lowest amount of chemical hardness belongs to the [BTAD][A3]2 complex (3.33 eV). For [BTAD][A1–8]2 complexes, the chemical potential values are −6.20, −6.73, −6.61, −6.96, −7.10, −7.61, −7.04 and −8.55 eV. The chemical potential values of the two complexes [BTAD][A6,8]2 with the greatest ECW are less than the others.

Table 8 The quantum molecular descriptors consist of the HOMO-LUMO energy gap (EGap), ionization potential (I), electron affinity (A), electronegativity (χ), electronic chemical potential (μ), hardness (η), electrophilicity index (ω) (eV) and softness (S/eV−1) of [BTAD][A1–8]2 (BTAD = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes at the M06-2X/631++G(d,p) level of theory in the gas phase
DCILs E HOMO E LUMO E Gap I A χ μ η S ω
[BTAD][A1] 2 −9.94 −2.45 7.49 9.94 2.45 6.20 −6.20 3.75 0.13 5.13
[BTAD][A2] 2 −10.48 −2.98 7.49 10.48 2.98 6.73 −6.73 3.75 0.13 6.05
[BTAD][A3] 2 −9.94 −3.28 6.66 9.94 3.28 6.61 −6.61 3.33 0.15 6.55
[BTAD][A4] 2 −10.71 −3.22 7.49 10.71 3.22 6.96 −6.96 3.75 0.13 6.47
[BTAD][A5] 2 −10.86 −3.35 7.51 10.86 3.35 7.10 −7.10 3.75 0.13 6.72
[BTAD][A6] 2 −11.33 −3.88 7.45 11.33 3.88 7.61 −7.61 3.72 0.13 7.77
[BTAD][A7] 2 −10.76 −3.32 7.44 10.76 3.32 7.04 −7.04 3.72 0.13 6.66
[BTAD][A8] 2 −12.10 −4.99 7.11 12.10 4.99 8.55 −8.55 3.56 0.14 10.27

4. Conclusions

In this work, density functional theory has been used to evaluate the effect of different anions on the electronic and structural properties of new [BTAD][A1–8]2 ([BTAD]2+ = [C6H4N6O2]2+ and A1–8 = [CH3CO2]−, [CF3CO2]−, [N(CN)2]−, [CF3SO3]−, [ClO4]−, [BF4]−, [NTf2]− and [PF6]−) complexes at the M06-2X-GD3/6-31++G(d,p) level of theory. According to the depicted electrostatic potential (ESP) maps of the isolated dication and anions, the most stable configurations of [BTAD][A1–8]2 complexes were determined. The interaction energies were calculated by four functionals, namely M06-2X, M06-2X-GD3, B2PLYP-GD3 and mPW2PLYP-GD2DFT functionals. The Gibbs free energy of [BTAD][A1–8]2 complexes in the gas and solvent (water, methanol and methylcyclohexane) phases was assessed. The optimized structures of the complexes revealed that the proton transfer takes place from the dication to [A1–5,7]− anions which leads to the formation of neutral H-bonded molecular complexes. From the results of this work, it is predicted that only the [BTAD][A8]2 DCIL can be formed. The acidity (ΔpKa1 and ΔpKa2) of the complexes is estimated by determining the change in Gibbs free energy of the proton transfer process in the gas phase and water solvent. The NBO and AIM analyses were employed to quantify charge transfer and characterize the hydrogen bonding interactions, respectively. Also, the electrochemical stability of the complexes was calculated by determining the anodic limit, cathodic limit and ECW in water solvent. The results indicated that the electrochemical stability of the complexes [BTAD][BF4]2 and [BTAD][PF6]2 (about 7.50 V) is higher than the others.

Data availability

All the data required to understand and verify the research presented in their article are available by request.

Author contributions

H. Roohi: conception and theoretical design, data analysis, revision and submission. S. Habibipour: carrying out calculations, extracting the data, and manuscript draft. Khatereh Ghauri: correction of the first draft and checking results.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

No funding was received for conducting this study.

References

  1. F. Pandolfi, M. Bortolami, M. Feroci, A. Fornari, V. Scarano and D. Rocco, Materials, 2022, 15(3), 866 CrossRef CAS.
  2. J. L. Anderson, R. Ding, A. Ellern and D. W. Armstrong, J. Am. Chem. Soc., 2005, 127, 593–604 CrossRef CAS.
  3. A. N. Masri, A. M. Mi and J. M. Leveque, Ind. Eng. Manag., 2016, 5, 197–204 Search PubMed.
  4. L. J. Brennan, S. T. Barwich, A. Satti, A. Faure and Y. K. Gun'ko, J. Mater. Chem. A, 2013, 1(29), 8379–8384 RSC.
  5. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111(5), 3508–3576 CAS.
  6. X. Song, B. S. Vig, P. L. Lorenzi, J. C. Drach, L. B. Townsend and G. L. Amidon, J. Med. Chem., 2005, 48(4), 1274–1277 CAS.
  7. I. Bahadur, P. Singh, S. Kumar, K. Moodley, M. Mabaso and G. Redhi, Sep. Sci. Technol., 2014, 49(12), 1883–1888 CrossRef CAS.
  8. X. Han and D. W. Armstrong, Acc. Chem. Res., 2007, 40(11), 1079–1086 CrossRef CAS PubMed.
  9. S. Martwiset, O. Yavuzcetin, M. Thorn, C. Versek, M. Tuominen and E. B. Coughlin, J. Polym. Sci., Part A: Polym. Chem., 2009, 47(1), 188–196 CrossRef CAS.
  10. U. Akbey, S. Granados-Focil, E. B. Coughlin, R. Graf and H. W. Spiess, J. Phys. Chem. B, 2009, 113(27), 9151–9160 CrossRef CAS PubMed.
  11. M. M. Obadia and E. Drockenmuller, Chem. Commun., 2016, 52(12), 2433–2450 RSC.
  12. M. Brehm, M. Pulst, J. Kressler and D. Sebastiani, J. Phys. Chem. B, 2019, 123(18), 3994–4003 CrossRef CAS PubMed.
  13. S. Sanghi, E. Willett, C. Versek, M. Tuominen and E. B. Coughlin, RSC Adv., 2012, 2(3), 848–853 RSC.
  14. K. Stappert, D. Unal, E. T. Spielberg and A. V. Mudring, Cryst. Growth Des., 2015, 15(2), 752–758 CrossRef CAS.
  15. Z. K. Reeder, A. M. Adler and K. M. Miller, Tetrahedron Lett., 2016, 57(2), 206–209 CrossRef CAS.
  16. M. C. Tseng, H. T. Cheng, M. J. Shen and Y. H. Chu, Org. Lett., 2011, 13(16), 4434–4437 CrossRef CAS PubMed.
  17. B. P. Mudraboyina, M. M. Obadia, I. Allaoua, R. Sood, A. Serghei and E. Drockenmuller, Chem. Mater., 2014, 26(4), 1720–1726 CrossRef CAS.
  18. A. Nguyen, T. C. Rhoades, R. D. Johnson and K. M. Miller, Macromol. Chem. Phys., 2017, 218(21), 1700337 Search PubMed.
  19. M. Pulst, Y. Golitsyn, D. Reichert and J. Kressler, Materials, 2018, 11(9), 1723 Search PubMed.
  20. D. H. Kim, V. Vijayakumar and S. Y. Nam, Alkaline Anion Exchange Membranes for Fuel Cells, 2024, pp. 189–210 Search PubMed.
  21. H. Y. Li, C. Y. Chen, H. T. Cheng and Y. H. Chu, Molecules, 2016, 21(10), 1355 Search PubMed.
  22. S. Sanghi, M. Tuominen and E. B. Coughlin, Solid State Ionics, 2010, 181(25–26), 1183–1188 CAS.
  23. F. Zapata, L. Gonzalez, A. Caballero, I. Alkorta, J. Elguero and P. Molina, Chem. – Eur. J., 2015, 21(27), 9797–9808 Search PubMed.
  24. C. Darwich, T. M. Klapötke and C. M. Sabaté, Chem. – Eur. J., 2008, 14(19), 5756–5771 CAS.
  25. Z. B. Zhang and J. G. Zhang, J. Mol. Struct., 2018, 1158, 88–95 CAS.
  26. B. Schulze and U. S. Schubert, Chem. Soc. Rev., 2014, 43(8), 2522–2571 CAS.
  27. J. M. Aizpurua, R. M. Fratila, Z. Monasterio, N. Pérez-Esnaola, E. Andreieff, A. Irastorza and M. Sagartzazu-Aizpurua, New J. Chem., 2014, 38(2), 474–480 Search PubMed.
  28. A. Riccobono, R. R. Parker, A. C. Whitwood, J. M. Slattery, D. W. Bruce, I. Pibiri and A. Pace, Chem. Commun., 2018, 54(71), 9965–9968 CAS.
  29. J. Li, T. Yu, G. Xu, Y. Du, Z. Liu, Z. Feng, X. Yang, Y. Xi and J. Liu, J. Chromatogr. A, 2018, 1559, 178–185 Search PubMed.
  30. S. Sanghi, E. Willett, C. Versek, M. Tuominen and E. B. Coughlin, RSC Adv., 2012, 2(3), 848–853 RSC.
  31. M. Andersson Trojer, A. Movahedi, H. Blanck and M. Nydén, J. Chem., 2013, 2013(1), 946739 CrossRef.
  32. J. T. Fletcher, J. M. Sobczyk, S. C. Gwazdacz and A. J. Blanck, Bioorg. Med. Chem. Lett., 2018, 28(20), 3320–3323 CrossRef CAS.
  33. W. Tan, Q. Li, F. Dong, J. Zhang, F. Luan, L. Wei, Y. Chen and Z. Guo, Carbohydr. Polym., 2018, 182, 180–187 CrossRef CAS PubMed.
  34. N. Glanzmann, A. M. Carmo, L. M. Antinarelli, E. S. Coimbra, L. A. Costa and A. D. da Silva, J. Mol. Model., 2018, 24, 1–7 CrossRef CAS PubMed.
  35. M. Sato, T. Takeda, N. Hoshino and T. Akutagawa, CrystEngComm, 2017, 19(6), 910–917 RSC.
  36. L. F. Fieser and E. L. Martin, J. Am. Chem. Soc., 1935, 57(10), 1844–1849 CrossRef CAS.
  37. G. Maier, H. P. Reisenauer and K. Rademacher, Chem. – Eur. J., 1998, 4(10), 1957–1963 CrossRef CAS.
  38. X. F. Lu, P. Q. Liao, J. W. Wang, J. X. Wu, X. W. Chen, C. T. He, J. P. Zhang, G. R. Li and X. M. Chen, J. Am. Chem. Soc., 2016, 138(27), 8336–8339 CrossRef CAS.
  39. J. P. Belieres and C. A. Angell, J. Phys. Chem. B, 2007, 111(18), 4926–4937 CrossRef CAS PubMed.
  40. R. Jacobi, F. Joerg, O. Steinhauser and C. Schröder, Phys. Chem. Chem. Phys., 2022, 24(16), 9277–9285 RSC.
  41. M. S. Miran, H. Kinoshita, T. Yasuda, M. A. Susan and M. Watanabe, Phys. Chem. Chem. Phys., 2012, 14(15), 5178–5186 RSC.
  42. J. Stoimenovski, E. I. Izgorodina and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2010, 12(35), 10341–10347 RSC.
  43. M. Yoshizawa, W. Xu and C. Austen Angell, J. Am. Chem. Soc., 2003, 125, 15411–15419 CAS.
  44. X. Sun, B. Cao, X. Zhou, S. Liu, X. Zhu and X. H. Fu, J. Mol. Liq., 2016, 221, 254–261 Search PubMed.
  45. Z. Wojnarowska and M. Paluch, Condens. Matter, 2015, 27(7), 073202 CAS.
  46. V. Overbeck and R. Ludwig, Annu. Rep. NMR Spectrosc., 2018, 95, 147–190 Search PubMed.
  47. J. J. Bailey, E. L. Byrne, P. Goodrich, P. Kavanagh and M. Swadzba-Kwasny, Green Chem., 2024, 26, 1092 RSC.
  48. C. Y. Wong, W. Y. Wong, K. S. Loh and K. L. Lim, React. Funct. Polym., 2022, 171, 105160 CAS.
  49. H. A. Elwan, M. Mamlouk and K. Scott, J. Power Sources, 2021, 484, 229197 Search PubMed.
  50. U. A. Rana, M. Forsyth, D. R. MacFarlane and J. M. Pringle, Electrochim. Acta, 2012, 84, 213–222 CAS.
  51. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7(1), 232–250 RSC.
  52. M. Sato, T. Takeda, N. Hoshino and T. Akutagawa, CrystEngComm, 2017, 19(6), 910–917 RSC.
  53. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120(1–3), 215–241 Search PubMed.
  54. S. Kozuch and J. M. Martin, J. Chem. Theory Comput., 2013, 9(4), 1918–1931 CrossRef CAS PubMed.
  55. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
  56. E. G. Hohenstein, S. T. Chill and C. D. Sherrill, J. Chem. Theory Comput., 2008, 4(12), 1996–2000 CrossRef CAS.
  57. N. Mardirossian and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12(9), 4303–4325 CrossRef CAS.
  58. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104 CrossRef.
  59. S. Grimme, J. Chem. Phys., 2006, 124(3), 034108 CrossRef PubMed.
  60. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397 RSC.
  61. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 4398 RSC.
  62. I. N. Levine, Quantum Chemistry, Pearson, 7th edn, 2013 Search PubMed.
  63. L. Goerigk and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4(6), 576–600 CAS.
  64. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19(48), 32184–32215 RSC.
  65. S. F. Boys and F. J. Bernardi, Mol. Phys., 1970, 19(4), 553–566 CrossRef CAS.
  66. B. Mennucci, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(3), 386–404 CAS.
  67. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS.
  68. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
  69. P. Politzer and D. G. Truhlar, Chemical applications of atomic and molecular electrostatic potentials: reactivity, structure, scattering, and energetics of organic, inorganic, and biological systems, Springer Science & Business Media, 2013 Search PubMed.
  70. R. Dennington, T. Keith and J. Millam, GaussView V, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
  71. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88(6), 899–926 CrossRef CAS.
  72. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. A. Weinhold, NBO, Version 3.1., Department of Chemistry, University of California-Irvine, Irvine, 1995 Search PubMed.
  73. F. Biegler-Konig, J. Schonbohm and D. Bayles, J. Comput. Chem., 2001, 22(5), 545–559 CrossRef.
  74. C. H. Suresh and S. Anila, Acc. Chem. Res., 2023, 56(13), 1884–1895 CrossRef CAS PubMed.
  75. J. Y. Kim, T. H. Kim, D. Y. Kim, N. G. Park and K. D. Ahn, J. Power Sources, 2008, 175(1), 692–697 CrossRef CAS.
  76. S. Kazemiabnavi, Z. Zhang, K. Thornton and S. Banerjee, J. Phys. Chem. B, 2016, 120(25), 5691–5702 CAS.
  77. B. Haddad, A. Paolone, M. Drai, M. Boumediene, D. Villemin, E. Belarbi, M. Rahmouni, S. Bresson and O. Abbas, J. Mol. Struct., 2019, 1175, 175–184 CAS.
  78. Y. S. Ding, M. Zha, J. Zhang and S. S. Wang, Colloids Surf., A, 2007, 298, 201–205 CAS.
  79. Z. X. Zhang, H. Y. Zhou, L. Yang, K. Tachibana and K. Kamijima, Electrochim. Acta, 2008, 53, 4833–4838 CrossRef CAS.
  80. J. C. Chang, W. Y. Ho, I. W. Sun, Y. K. Chou and H. H. Hsieh, Polyhedron, 2010, 29, 2976–2984 CrossRef CAS.
  81. J. C. Chang, W. Y. Ho, I. W. Sun, Y. L. Tung and M. C. Tsui, Tetrahedron Lett., 2010, 66, 6150–6155 CAS.
  82. J. C. Chang, W. Y. Ho, I. W. Sun, Y. K. Chou and H. H. Hsieh, Polyhedron, 2011, 30, 497–507 CrossRef CAS.
  83. H. Shirota, T. Mandai, H. Fukazawa and T. Kato, J. Chem. Eng. Data, 2011, 56, 2453–2459 CrossRef CAS.
  84. Z. Zhang, L. Yang, S. Luo, M. Tian and K. Tachibana, J. Power Sources, 2007, 167, 217–222 CrossRef CAS.
  85. M. Boumediene, B. Haddad, A. Paolone, M. Drai, D. Villemin, M. Rahmouni, S. Bresson and O. Abbas, J. Mol. Struct., 2019, 1186, 68–79 CrossRef CAS.
  86. H. Roohi, S. F. Ghasemi Gildeh, K. Ghauri and P. Fathei, Ionics, 2020, 26, 1963–1988 CrossRef CAS.
  87. H. Roohi and R. Salehi, Ionics, 2018, 24, 483–504 CAS.
  88. L. A. Burns, A. Vázquez-Mayagoitia, B. G. Sumpter and C. D. Sherrill, J. Chem. Phys., 2011, 134, 084107 CrossRef.
  89. J. Stoimenovski, E. I. Izgorodina and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2010, 12(35), 10341–10347 RSC.
  90. U. Koch and P. L. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
  91. P. L. Popelier, J. Phys. Chem. A, 1998, 102, 873–1878 CrossRef.
  92. R. Q. Lü, Z. Qu, H. Yu, F. Wang and S. T. Wang, Comput. Theor. Chem., 2012, 988, 86–91 CrossRef.
  93. P. Hobza, J. Chem. Rev., 2000, 100, 4253–4264 CrossRef CAS.
  94. P. Hobza, V. Spirko, H. L. Selzle and E. W. Schlag, J. Phys. Chem. A, 1998, 102, 2501–2504 CrossRef CAS.
  95. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1998, 88, 899–926 Search PubMed.
  96. V. R. Koch, L. A. Dominey and C. Nanjundiah, J. Electrochem. Soc., 1996, 143, 798–803 CAS.
  97. M. C. Kroon, W. Buijs, C. J. Peters and G. J. Witkamp, Green Chem., 2006, 8, 241–245 CAS.
  98. W. Buijs, G. J. Witkamp and M. C. Kroon, Int. J. Electrochem., 2012, 1–6, 589050 Search PubMed.
  99. P. Wu, R. Chaudret, X. Hu and W. Yang, J. Chem. Theory Comput., 2013, 9(5), 2226–2234 CAS.
  100. W. Buijs, G. J. Witkamp and M. C. Kroon, Int. J. Electrochem., 2012, 2012(1), 589050 Search PubMed.
  101. M. Ue, A. Murakami and S. Nakamurab, J. Electrochem. Soc., 2002, 149(12), 1572–1577 Search PubMed.
  102. M. C. Buzzeo, C. Hardacre Prof and R. G. Compton Prof, ChemPhysChem, 2006, 7(1), 176–180 Search PubMed.
  103. S. P. Ong, O. Andreussi, Y. Wu, N. Marzari and G. Ceder, Chem. Mater., 2011, 23(11), 2979–2986 Search PubMed.
  104. K. K. Hazarika, N. C. Baruah and R. C. Deka, Struct. Chem., 2009, 20, 1079–1085 CAS.
  105. P. K. Chattaraj and D. R. Roy, Chem. Rev., 2007, 107(9), 46–74 Search PubMed.
  106. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105(26), 7512–7516 CAS.

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4me00119b
This journal is © The Royal Society of Chemistry 2025
Click here to see how this site uses Cookies. View our privacy policy here.