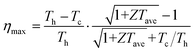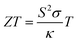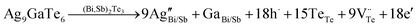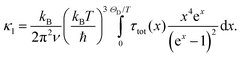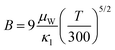High density lath twins lead to high thermoelectric conversion efficiency in Bi₂Te₃ modules

Abstract

Thermoelectric (TE) generators based on bismuth telluride (Bi₂Te₃) are recognized as a credible solution for low-grade heat harvesting. In this study, an combinative doping strategy of both the donor (Ag) and the acceptor (Ga) in Ag₉GaTe₆ as dopants is developed to modulate the microstructure and improve the ZT value of p-type Bi_0.4Sb_1.6Te₃. Specifically, the distribution of Ag and Ga in the matrix synergistically introduces multiple phonon scattering centers including lath twins, triple junction boundaries, and Sb-rich nanoprecipitates, leading to an obviously suppressed lattice thermal conductivity of 0.50 W m⁻¹ K⁻¹ at 300 K. At the same time, such unique microstructures of lath twins synergistically enhance the room-temperature power factor to 48.8 μW cm⁻¹ K⁻² and improve the Vickers hardness to 0.90 GPa. Consequently, a high ZT of 1.40 at 350 K and ZT_ave of 1.24 (300–500 K) are achieved in the Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample. Based on that, a competitive conversion efficiency of 6.5% at ΔT = 200 K is obtained in the constructed 17-couple TE module, which exhibits no significant change in the output property after 30 thermal cycle tests benefiting from the stable microstructure.

---

New concepts

Unlike typical (Bi,Sb)₂Te₃ alloys doped with non-reactive secondary phases such as amorphous B, carbon fibers, or SiC, here, we selected Ag₉GaTe₆ to achieve microstructural modulation characterized by lath twin boundaries through combinative doping. The optimized electronic transport properties, along with the differential scattering of carriers and phonons, reduced the lattice thermal conductivity to 0.50 W m⁻¹ K⁻¹ and increased the power factor to 48.8 μW cm⁻¹ K⁻² at 300 K. Consequently, the optimal Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample exhibited a high average ZT of 1.24 (300–500 K) and a competitive conversion efficiency of 6.5% (ΔT = 200 K). More importantly, the thermoelectric module maintained its output characteristics after 30 thermal cycles, highlighting its significant potential for low-grade waste heat recovery applications.

Introduction

The recovery of low-grade waste heat is conducive to mitigating the global energy demand and reducing the greenhouse gas emission.¹ However, the recovery of the low-grade and distributed thermal heat by using the existing methods is a big challenge.² Thermoelectric (TE) generators, being silent solid-state modules without moving parts and pollution, emerge as a promising solution for low-grade and distributed heat harvesting.³ The energy conversion efficiency η_max of TE generators is described using the following expression:
where T_h and T_c represent the cold-side and hot-side temperatures, respectively, and ZT_ave is the average ZT value within the temperature range. It should be noted that an improved ZT_ave rather than a high ZT_max leads to a substantial enhancement of η_max. The dimensionless figure of merit ZT is defined as:
where S, σ, κ and T represent the electrical conductivity, Seebeck coefficient, total thermal conductivity and absolute temperature, respectively.^4,5 The conception of phonon-glass electron-crystals reveals that successful optimization depends on the ordered crystalline semiconductor structure for robust electronic transport properties and disordered atomic arrangements for low lattice thermal conductivity κ_l. It is challenging to solely enhance the ZT value using one of these mentioned parameters, in view of the intrinsic coupling among S, σ and κ_ele.

As the only commercialized TE material near room temperature, Bi₂Te₃ has been a focal point of both industry and academia for decades.^6–9 Various strategies have been employed to enhance the TE performance of Bi₂Te₃-based materials.^10–12 For example, the effective schemes to improve the ZT values include developing Bi–Sb alloys with different ratios,¹³ co-doping of aliovalent elements to tune the carrier concentration,¹⁴ introducing multiscale defects to suppress lattice thermal conductivity,¹⁵ and so on. Recently, researchers have used stepwise strategies to optimize the carrier concentration and to suppress lattice thermal conductivity.¹⁵ Especially, the introduction of nano-structures to realize differential scattering of carriers and phonons is considered as an effective method for TE enhancement.^16,17 This approach results in a significant decrease in lattice thermal conductivity while having a minimal impact on carrier mobility. For example, high-density twins have been proved to induce highly oriented microstructures and good TE performance in bismuth telluride.¹⁸ As is known, the modulation of Te content can enhance the texture degree and induce gradient twin boundaries in p-type Bi₂Te₃.^13,19,20 Hence, the addition of active telluride provides a promising scheme to improve the ZT for p-type Bi₂Te₃via microstructure design.

Among the various dopants for Bi₂Te₃-based materials, Ag acts as the acceptor while Ga acts as a donor, leading to opposite effects in carrier concentration modulation.²¹ Ag–Ga co-doping is proved to be as effective as the cumulative effect of doping each element individually in modulating the electrical conductivity and suppressing thermal conductivity. That is to say, the superposition effect of Ag–Ga co-doping not only tunes the carrier concentration, but also further reduces lattice thermal conductivity. It is thus practical to carefully control the amount of each dopant to engineer the carrier transport characteristics.²² Based on the improved ZT values of TE materials, the geometric parameters of TE legs (height and the ratio of cross-sectional area) need to be optimized to fit the temperature-dependent heat flow and current density, which determine the TE conversion efficiency and output power of the TE generation module.^23,24 Moreover, it is necessary to study the reliability of TE modules in order to realize practical application.

Motivated by the aforementioned considerations, we used the active telluride Ag₉GaTe₆ as the dopant in the Bi_0.4Sb_1.6Te₃ matrix. By introducing Ag₉GaTe₆, microstructures exemplified by typical lath twin boundaries are designed to balance the TE transport coefficients by effectively enhancing the phonon scattering and reducing the deterioration in carrier transport.²⁰ Subsequently, the room-temperature power factor is synergistically enhanced to 48.8 μW cm⁻¹ K⁻², the corresponding lattice thermal conductivity is suppressed to 0.50 W m⁻¹ K⁻¹, and the Vickers hardness is improved to 0.90 GPa in the x = 0.03 sample. As a result, a high ZT of 1.40 and a ZT_ave of 1.24 (300–500 K) are achieved in the optimal sample, and the fabricated TE module exhibits a competitive conversion efficiency of 6.5% at ΔT = 200 K.

Results and discussion

Strengthened interlayer interaction and high density twin boundaries

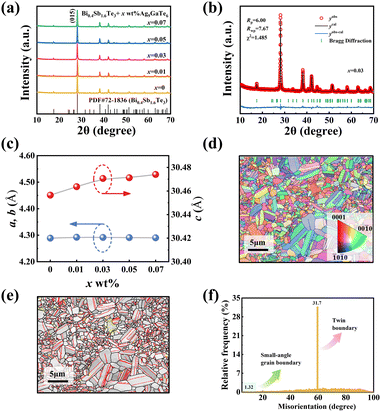
Fig. 1(a) depicts the X-ray powder diffraction (XRD) patterns of the hot-pressed Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ samples. The diffraction peaks of all the samples align with the Bi_0.4Sb_1.6Te₃ standard card (JCPDS# 72-1836), indicating a single-phase structure within the XRD detection limit. The Rietveld refinement patterns of x = 0 and x = 0.03 reveal the consistency of the crystal structure between calculated values and experiment results in Fig. 1(b) and Fig. S1 (ESI†). It is well known that the quintuple layers of Bi₂Te₃ are combined via van der Waals interaction along the c axis direction. With the increasing addition of Ag₉GaTe₆ from 0 to 0.07 wt%, the lattice constant c increases from 30.456 Å to 30.474 Å, while a and b are almost unchanged, as shown in Fig. 1(c). This observation suggests that the additional atoms enter the interstitial positions formed by four Te atoms, thus increasing the distance between the quintuple layers.²⁵

Fig. 1 Microstructure changes induced by Ag₉GaTe₆ doping. (a) The XRD patterns of Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆, Rietveld refined XRD patterns of (b) x = 0.03 at room temperature. (c) Variation of the lattice constants. (d) The inverse pole-figure mapping of the EBSD image for x = 0.03 sample. (e) Kikuchi band contrast map and (f) grain boundary misorientation distribution of x = 0.03 sample.

Fig. 1(d) presents the inverse pole-figure mapping of the electron back scattering diffraction (EBSD) image for the Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample, indicating that the optimized sample orientation of grains is not discernibly preferred. Additionally, Fig. S2 (ESI†) shows the corresponding crystallite size distribution, with the average grain size of approximately 0.93 μm. The distribution of various grain orientations is depicted in Fig. 1(e), with small-angle crystal boundaries (SAGB) and twin boundaries (TB) displayed in yellow and red, respectively. Fig. 1(f) intuitively displays the relative proportion of the LAGBs and TBs, in the Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample, which are 1.3% and 31.7%, respectively. Compared to similar previous results within our group,¹⁵ this work exhibits an increased presence of twins after doping, consistent with the observations of EBSD. Additionally, highly oriented microstructures are provided by lath twins as the transport channel for the anisotropic TE properties.

To gain more insights into the microstructure, transmission electron microscopy (TEM) is carried out on the Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ sample. As can be observed from Fig. 2(a), typical triple junction boundaries and lath boundaries (marked by the white dotted line) emerge in the Bi_0.4Sb_1.6Te₃-based sample after Ag₉GaTe₆ doping, compared to the undoped matrix in Fig. S3 (ESI†). Triple junction boundaries are believed to resist the movement of dislocations like slipping, while the lath boundaries contribute to improving the mechanical properties. Both triple junction boundaries and lath boundaries are crucial for the machinability and stability of Bi_0.4Sb_1.6Te₃-based materials and TE modules. As depicted in Fig. S4 (ESI†), the Vickers hardness of the 0.07wt% Ag₉GaTe₆-doped Bi_0.4Sb_1.6Te₃ is 0.902 GPa, surpassing that of the pristine sample and competitive to that found in other similar work, and is consistent with the increase in triple junction boundaries and lath boundaries. Fig. 2(b) reveals various dislocations and strain fluctuations in the Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample. Focusing on area 1 in Fig. 2(a), the inverse fast Fourier transform (IFFT) is applied to show the high-density dislocations marked as “⊥” inside the grain, with a confirmed d-spacing of 2.077 Å in the IFFT image. The geometric phase analysis (GPA), a semiquantitative lattice image processing tool,^26,27 indicates significant strain fluctuations along different directions in area 1 of Fig. 2(a). Specifically, the generation of dislocations is a local change in the crystal interior initiated by the lattice deformation of the crystal in order to adapt to external stress or internal defects. Conventional high-density dislocations can be attributed to lattice distortion caused by the incorporation of atoms with varying masses, sizes, and valence states. Here, the formation of dislocations can be attributed to the diffusion mechanism. During high-temperature melting, ions released from the active material would diffuse and migrate through lattice vacancies and interstitial sites. The differences in atomic radius and mass prompt the formation of dislocations.

Fig. 2 Analysis of the microscopic morphology of the optimal sample by TEM. Low-resolution TEM images of (a) triple junction boundaries and lath boundaries. (b) Medium-magnification TEM image showing the distinct dislocations. The inverse fast Fourier transformation image and the geometric phase analysis image for the selected area in (a) to indicate the dislocations and stress–strain distribution. (c) Abundant nanoprecipitates, the twin boundaries and the SAED patterns along the [6̄4̄1] zone axis. (d) EDS elemental mapping for the distributions of Bi, Sb, Te, Ag, Ga, and O elements.

Fig. 2(c) presents low-resolution TEM images detecting numerous nanoprecipitates (dark against the bright background), ranging from 5 to 20 nm in diameter and uniformly dispersed within the matrix without agglomeration. These small-size nanoprecipitates have been demonstrated to cover the expected phonon mean free path in Bi₂Te₃-based alloys (1 to 10 nm), which could strengthen the phonon scattering and result in a substantial reduction of κ_l. The lath twin boundaries and the corresponding selected area electron diffraction (SAED) are also depicted in Fig. 2(c), consistent with the EBSD results.²⁸ The lath twin boundaries prevent dislocation from slipping and allow the accumulation and multiplication of dislocation on the lath twin boundaries. The SAED patterns also exhibit a typical symmetry of twin grain structures along the [6̄4̄1] zone axis. The formation of these microstructural features is closely related to the doping of the active telluride Ag₉GaTe₆. Previous studies have shown that telluride deficiency leads to the formation of nanotwins. As an active dopant, Ag₉GaTe₆ enters the lattice and alters the valence state ratios of anions and cations within the lattice. As displayed in the equation below, excessive consumption of telluride relative to its available amount results in a nominal telluride-deficient environment, which promotes the formation of lath twins.

According to previous theoretical analyses,²⁹ the lowest formation energy is associated with the acceptor defect Ag-on-Sb in Sb₂Te, indicating that Ag is likely to substitute for Sb sites and form substitutional point defects. EDS analysis further examined the composition of the aforementioned nanoprecipitates. Elemental mapping shown in Fig. 2(d) and Fig. S5 (ESI†) reveals that the precipitates are slightly enriched in Sb, while Bi, Sb, Te, Ag, and Ga are uniformly distributed. This confirms that Ag₉GaTe₆ has been successfully alloyed into the pristine Bi_0.4Sb_1.6Te₃, consistent with the SEM results shown in Fig. S6 (ESI†). Overall, the addition of trace amounts of Ag₉GaTe₆ introduces multiscale defects—including grain/twin boundaries, dense dislocations, stress–strain clusters, and nanoscale precipitates—into the Bi_0.4Sb_1.6Te₃ matrix efficiently.

Enhancement of electrical transport and high power factor

Fig. 3 summarizes the electronical transport properties of the Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ samples. Due to the typical p-type semiconductor behaviour, the Seebeck coefficient in Fig. 3(a) initially increases with elevating temperature, and then decreases due to the thermal excitation of minority carriers. With the increasing content of Ag₉GaTe₆, the room-temperature Seebeck coefficient slightly decreases. For example, the room-temperature Seebeck coefficient decreases from 211 μV K⁻¹ in the pristine Bi_0.4Sb_1.6Te₃ to 187 μV K⁻¹ in the x = 0.07 sample.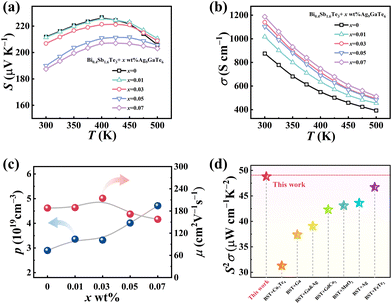

Fig. 3 Significant optimization of electrical transport performance. The temperature-dependent electronic transport coefficients: (a) Seebeck coefficient S, (b) electrical conductivity σ. (c) The carrier concentration p and carrier mobility μ for the samples at room temperature. (d) The comparison of room-temperature values of S²σ in this work and previous reports.^22,30–33

As shown in Fig. 3(b), the electrical conductivity σ of all these samples monotonously decreases with increasing temperature, and roughly exhibits a σ ∝ T^−1.5 relationship, indicating typical degenerate semiconductor behaviour and the dominance of acoustic phonon scattering. At a certain temperature, σ gradually increases with the increasing content of Ag₉GaTe₆. For example, the room-temperature σ obviously increases from 904 S cm⁻¹ in the pristine Bi_0.4Sb_1.6Te₃ sample to 1187 S cm⁻¹ in the x = 0.07 sample.

The room-temperature Hall measurement is obtained to shed light on the variation of S and σ, and the results of hole concentration and carrier mobility of these samples are summarized in Fig. 3(c). As may be seen, the room-temperature hole concentration gradually increases from 2.9 × 10¹⁹ cm⁻³ in the pristine Bi_0.4Sb_1.6Te₃ sample to 4.7 × 10¹⁹ cm⁻³ in the x = 0.07 sample. This increase is attributed to the favorable electronic acceptor properties of Ag in reactive Ag₉GaTe₆. Defect formation energy calculations indicate that Ag tends to substitute for Sb upon dissociation generating additional holes, which enhances the σ while simultaneously reducing the S. Notably, with low levels of Ag₉GaTe₆ doping (x = 0.01 and 0.03), the carrier mobility initially increases with doping concentration, which may be related to atomic intercalation.³⁴ Furthermore, at doping concentrations below 0.03%, the number of point defects remains relatively low, while microstructural features such as lattice twins and small-angle grain boundaries increase. These microstructures can effectively scatter phonons, reducing lattice thermal conductivity. Crucially, they have minimal impact on carrier transport, ensuring the preservation of high carrier mobility. However, with further increases in doping concentration, the number of point defects may rise significantly. The increased concentration of point defects, coupled with carriers themselves intensifying scattering as the hole concentration rises, ultimately would lead to a reduction in the carrier mobility.

With the obviously increased σ and slightly decreased S after Ag₉GaTe₆ doping, the power factor S²σ of the Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ samples are effectively enhanced, as demonstrated in Fig. S7 (ESI†). Especially, the room-temperature S²σ is improved from 40.2 μW cm⁻¹ K⁻² in the pristine Bi_0.4Sb_1.6Te₃ to 48.8 μW cm⁻¹ K⁻² in the x = 0.03 sample. As shown in Fig. 3(d), such a high S²σ obtained in this work is very competitive among the previously reported results about p-type (Bi,Sb)₂Te₃-based materials.^22,30–33 Moreover, the average S²σ between 300 and 500 K of the Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample achieves a value of 35 μW cm⁻¹ K⁻², which could play a significant role in enhancing the output power density in the TE module.

Multiple phonon scattering mechanism and competitive ZT values

Fig. S8(a) (ESI†) illustrates the temperature-dependent thermal conductivity of the Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ samples. At room temperature, the thermal conductivity exhibits a gradual increase with the addition of Ag₉GaTe₆. When the temperature increases, the trend reverses due to the bipolar effect. The value of electronic thermal conductivity κ_e in Fig. S8(b) (ESI†) is calculated according to the Wiedemann–Franz law κ_e = LσT, where the Lorenz number L is estimated by fitting the Seebeck coefficient to the reduced chemical potential, as demonstrated in Fig. S9(a) (ESI†).³⁵ Similar to the σ in Fig. 3(b), the κ_e roughly increases with the addition of Ag₉GaTe₆.

By subtracting the κ_e from the κ_tot value, the value of κ_l + κ_bip is obtained and presented in Fig. 4(a). It is found that the κ_l + κ_bip values are significantly suppressed by the Ag₉GaTe₆ doping. Taking the case at room temperature as an example, the κ_l + κ_bip obviously decreases from 0.72 W m⁻¹ K⁻¹ in the pristine Bi_0.4Sb_1.6Te₃ to 0.50 W m⁻¹ K⁻¹ in the x = 0.03 sample. And the calculated value of κ_l without κ_bip is presented in Fig. 4(b). The depression of κ_l is considered to have a close relationship with the increase of lath twins.

Fig. 4 Collaborative optimization mechanism for thermal transport performance. Temperature dependence of (a) lattice and bipolar thermal conductivity and (b) calculated lattice thermal conductivity. (c) Schematic diagram of the main scattering effects of phonons in the sample. (d) Frequency-dependent κ_s at room temperature for the x = 0.03 sample according to the Debye–Callaway model. (e) The comparison of μ_w and 1/κ_l between this work and previously reported data.^{15,29,36–41} (f) Temperature-dependent ZT values and (g) the comparison of average ZT values (300–500 K) and the peak ZT values for the Ag₉GaTe₆-doped Bi_0.4Sb_1.6Te₃ samples and previous reports.^{8,9,13,15,22,31,37,39–45}

As discussed above, Ag₉GaTe₆ doping induces various phonon scattering centers including junction/lath twin boundaries, high density dislocations, stress–strain clusters, nanoprecipitates, and interstitial Ag and Sb_Ag point defects in the Bi_0.4Sb_1.6Te₃ matrix. These multiscale defects provide enhanced lattice anharmonicity and thereby suppress the κ_l of materials. Using the Debye–Callaway model, the quantitative relationship between κ_l and various defects can be described as follows:⁴⁶

In this expression, the symbols represent the following physical quantities: k_B denotes the Boltzmann constant, ν signifies the in-plane average sound velocity, ħ stands for the reduced Planck constant, ω denotes the phonon frequency, x = hω/k_BT represents the reduced phonon frequency, Θ_D is the Debye temperature, and τ_tot is the phonon relaxation time. The frequency-dependent τ_tot encompasses τ_U (phonon Umklapp process), τ_B (boundary scattering process), τ_PD (point defect scattering process), and τ_D (dislocation and strain scattering process) as per Matthiessen's rule. More details regarding the Debye–Callaway model are available in Table S2 (ESI†). Additionally, the schematic diagram of the main scattering effects of phonons is intuitively illustrated in Fig. 4(c). Focusing on the x = 0.03 sample, we investigate the frequency-dependent κ_s and gain insights into scattering mechanisms. As depicted in Fig. 4(d), the junction/lath twin boundaries and dislocations predominantly scatter low- and mid-frequency phonons, while second-phase nanoprecipitates and point defects mainly scatter high-frequency phonons. In other words, the reduction of κ_l in the 0.03 wt% Ag₉GaTe₆-doped sample is primarily attributed to the introduction of junction/lath twin boundaries and second-phase nanoprecipitates.

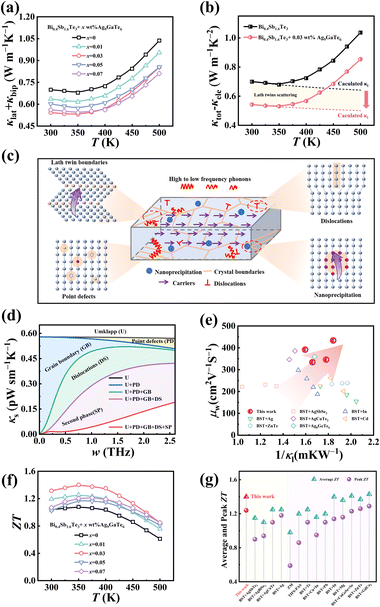
To assess the TE transport properties of the Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ samples, the diagram portraying the weighted mobility (μ_w) and the reciprocal of lattice thermal conductivity (1/κ_l) is constructed in Fig. 4(e), where the weighted mobility μ_W is determined by the equation 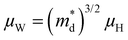.⁴ Superior TE materials typically possess high weighted mobility and low thermal conductivity, and thus occupy the upper right corner of the Fig. 4(e) graph. As illustrated, the Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample in this study is superior to many previously reported (Bi, Sb)₂Te₃-based TE materials.^{15,29,36–41} The quality factor B, serving as an effective assessment of both electronic and phonon transport, can be calculated using the following formula:⁴⁷

As depicted in Fig. S10 (ESI†), the room-temperature value of B displays an increase from 0.32 in the pristine sample to 0.51 in the x = 0.03 sample. As illustrated in Fig. 4(f), the ZT values of these Ag₉GaTe₆-doped samples exhibit significant improvement compared to that of the pristine Bi_0.4Sb_1.6Te₃, showcasing synergistic optimization of both electronic and thermal transport properties. This is attributed to the presence of lath twins in the x = 0.03 sample, which can effectively scatter phonons like random large grain boundaries while remaining transparent to carrier mobility. A peak ZT value of 1.40 at 350 K is achieved in the x = 0.03 sample, and it is 23% higher than that of the pristine sample. Fig. 4(g) summarizes the comparison between the peak ZT_max and average ZT_ave values obtained in this study and those previous research on p-type (Bi, Sb)₂Te₃-based materials. Notably, the ZT_max of 1.40 and ZT_ave of 1.24 (300–500 K) are competitive with those of the previous reports.^{8,9,15,22,31,37,39–44} Additionally, the thermal stability and performance reliability tests for the optimal Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample, as shown in Figs. S11 and S12 (ESI†), further highlight its potential for practical applications.

High conversion efficiency TE module based on simulation design

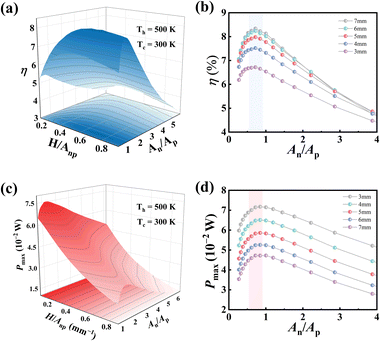
To further verify the benefits of the TE property improvement of the p-type Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ material, the TE module is thus fabricated with it and an n-type zone-melted Bi₂Te_2.7Se_0.3 sample described in our previous work.⁴⁸ Fig. S12 (ESI†) shows the schematic diagram of a home-built TE module test system. Prior to fabrication, we conduct finite element simulations to determine the optimal structural parameters based on experimental data of the Seebeck coefficient, electrical conductivity, and thermal conductivity. Here, A_n,p represents the sum of the cross-sectional areas of the individual p-type and n-type TE legs. As illustrated in Fig. 5(a) and (b), the calculated conversion efficiency (η) initially increases and then decreases upon increasing A_n/A_p with H/A_n,p fixed, where H, A_n, and A_p represent the height of TE legs, and the cross-sectional areas of n-leg, and p-leg, respectively. With a certain A_n/A_p, the η initially increases significantly and then varies less with the increasing H/A_n,p. These results suggest that an A_n/A_p ratio close to 1.0 and a moderate H/A_n,p ratio are beneficial for achieving high η. Fig. 5(c) plots a 3D surface relating the maximum output power P_max with the parameters A_n/A_p and H/A_n,p. As may be seen from Fig. 5(d), the P_max tends to exhibit the highest values with a A_n/A_p ∼ 1.0, and gradually decreases with the increasing H/A_n,p. It can be seen from Fig. 5(b) and (d) that increasing the module height leads to higher efficiency but lower output power. As a consequence, the optimal structural parameters for our Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ TE module are determined to be A_n/A_p = 0.72 and H/A_n,p = 0.55.

Fig. 5 Simulation results for bismuth telluride modules. The simulative results of H/A_n,p and A_n/A_p dependent (a) efficiency η and (c) maximum output power P_max, while (b) and (d) are the respective projection onto A_n/A_p of (a) and (c).

Fig. 6(a) displays the measured V–I curves at several temperature differences, which are performed on a home-built system. The internal resistance (R_i) of the TE module shown in Fig. S13 (ESI†) can be calculated using the slopes of the curves, with the intercept representing the open circuit voltage. It is found that the open circuit voltage of the fabricated TE module is notably high, reaching 2.32 V at a temperature difference of 200 K. Fig. 6(b) demonstrates the current dependent conversion efficiency under different temperature differences, with the highest conversion efficiency obtained in this work being 6.5% at a temperature difference of 200 K (T_h = 500 K and T_c = 300 K). As illustrated in Fig. 6(c), the maximum output power gradually increases from 0.05 W at ΔT = 50 K to 0.77 W at ΔT = 200 K, with the resistance of external load equal to the internal resistance of the TE module. Repeatability was demonstrated by testing two remade modules manufactured in the same process as presented in Fig. 6(d) and Fig. S14 (ESI†). In addition, an aging test is carried out to verify the reliability of this module. We record the efficiency of this module at 200 K temperature differences every 30 minutes. As shown in Fig. 6(e), the efficiency is strictly stable over 30 tests, benefitting from the stable structure of lath twins. The value of 6.5% is significantly higher than that of the commercial Bi₂Te₃-based TE module (∼5.8%),⁴⁹ and is competitive with most of the previous reports, as shown in Fig. 6(f).^{6,13,19,29,38,41,44,50,51} Optical images of the fabricated TE module composed of the p-type Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ and zone-melted n-type Bi₂Te_2.7Se_0.3 are available in Fig. S15 (ESI†).

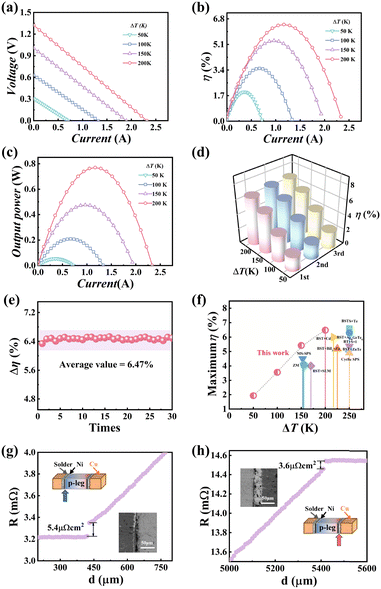Fig. 6 Module efficiency and reliability tests. Current dependence of (a) voltage, (b) conversion efficiency and (c) output power at different temperature differences. (d) Efficiency of three parallel samples at different temperature differences (e). The maximum conversion efficiency as functions of the test number of tests. (f) Comparison of the maximum conversion efficiency η_max.^{6,13,19,29,38,41,44,50,51} The measured contact resistance by the scanning of resistance across the Cu-Bi₂Te₃ interfaces for (g) cold end of the p-leg and (h) hot end of the n-leg, with the inset of SEM images.

At the end of this work, we carry out an analysis of the interfaces of the fabricated TE module. The contact resistance between the TE legs and Cu electrodes is measured using a four-probe method, and the corresponding interfaces are investigated by the SEM-EDS analysis, as depicted in Fig. 6(g), (h) and Fig. S17 (ESI†). The measured values of contact resistance range from 2.6 to 5.4 μΩ cm², showcasing good interface contact in the fabricated TE modules. Furthermore, EDS mapping images of the interface between the Cu electrode and TE also indicate the good interface contact between the TE legs and Cu electrodes, as presented in Fig. S18 and S19 (ESI†).

Experimental section

Sample synthesis

The high-purity Bi (4N), Sb (5N), and Te (5N) elements, and self-synthesized Ag₉GaTe₆ (details provided in the ESI†) were accurately weighed according to the stoichiometry ratio of Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ (x = 0, 0.01, 0.03, 0.05 and 0.07). The mixtures were then sealed into quartz tubes with a vacuum below 0.1 Pa. The sealed tube underwent a melting process at 1023 K for 30 min, followed by a 30 min rocking phase to ensure complete reaction, and subsequently furnace-cooled to room temperature. The resulting ingots were subjected to high-energy ball milling (SPEX-8000 M) for 30 min and further densified into Ø 12.7 cylinders through hot pressing at 693 K for 5 min under 60 MPa.

TE module fabrication

The 20 × 20 mm² TE module incorporates 17 pairs of p–n legs. The p-legs consist of the Bi_0.4Sb_1.6Te₃ + x wt% Ag₉GaTe₆ sample in this study, while the n-legs are composed of the zone-melted Bi₂Te_2.7Se_0.3 sample in a previous report.⁴⁸ More details about the n-type zone-melted Bi₂Te_2.7Se_0.3 are available in Table S3 (ESI†). The dimensions are 2.3 × 2.3 × 5 mm³ for p-legs, and 1.95 × 1.95 × 5 mm³ for n-legs as shown in Fig. S16 (ESI†). Nickel was utilized as the diffusion barrier layer and copper was employed for the electrode, with Pb-based solder for both sides. During the conversion efficiency measurement, the cold-side temperature was maintained at 300 K, while the hot-side temperature increased from 350 to 500 K. The TE conversion efficiency η is calculated by η = P/(Q + P), in which P is the output power and Q is the heat flow from the cold side.

Characterization and measurement

As shown in Fig. S19 (ESI†), the electronic and thermal transport coefficients were measured in the in-plane direction by using the commercial ZEM-3 and LFA-457 equipment, respectively. The thermal conductivity was calculated as κ_tot = ρDC_p, where the sample density ρ was determined using the Archimedes’ method, the thermal diffusivity D was measured by an LFA-457, and the heat capacity C_p was determined by using the Dulong–Petit law as presented in Fig. S9(b) and (c) and Table S1 (ESI†). The XRD (Bruker D8) characterization studies were performed to analyse the phase structure of samples using Cu Kα radiation. The grains were investigated by using the electron backscattering diffraction (EBSD) carried out using SEM. Microstructure analysis was characterized using TEM (Talos F200x). The room-temperature carrier concentration p and carrier mobility μ were evaluated according to the equations p = 1/R_He and μ = σR_H, respectively, based on the Hall coefficient R_H measured on a PPMS-9 system. The Vickers hardness of samples was determined by using a VH-3300 system.

Conclusions

In summary, the TE properties of p-type Bi_0.4Sb_1.6Te₃ are successfully enhanced through Ag₉GaTe₆ doping. A high peak ZT value of 1.40 at 350 K and a notable ZT_ave (300–500 K) of 1.24 are achieved in the Bi_0.4Sb_1.6Te₃ + 0.03 wt% Ag₉GaTe₆ sample. Acting as donor and acceptor impurities simultaneously, Ag₉GaTe₆ effectively tunes the carrier concentration to an optimal range and introduces multiscale defects, including lath twin boundaries, dense dislocations, stress–strain clusters, and Sb-rich nanoprecipitates in the Bi_0.4Sb_1.6Te₃ matrix. These effects synergistically enhance the power factor to 48.8 μW cm⁻¹ K⁻², suppress the lattice thermal conductivity to 0.50 W m⁻¹ K⁻¹, and improve the Vickers hardness to 0.90 GPa in the x = 0.03 sample. Moreover, the fabricated TE module, composed of the prepared p-type 0.03 wt% Ag₉GaTe₆-doped Bi_0.4Sb_1.6Te₃ and n-type zone-melted Bi₂Te_2.7Se_0.3, exhibits low contact resistivity and a reliable conversion efficiency of 6.5% at a temperature difference of 200 K.

Author contributions

Q. S. and G. W. made equal contributions to the present study. The design of this work was orchestrated by Q. S., G. W., X. T., Q. Z., and J. J. Q. S., G. W., Z. G., and Q. P. undertook the synthesis of the samples, conducted measurements related to transport properties, and did the data curation. J. W., G. L., and P. S. contributed to the discussion. Q. S., G. W., Q. Z., and X. T. performed the analysis of experimental data, while Q. S., G. W. and X. T. were responsible for the composition of this manuscript. X. T., Q. Z., P. S., J. W., and J. J. provided the funding support. All authors have given approval to the final version of the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. U21A2079), the Chinese Postdoctoral Science Foundation grant (Grant No. 2024M753342), the Postdoctoral Fellowship Program of CPSF (Grant No. GZB20230786), the Ningbo International Cooperation Project (Grant No. 2023H002), the Ningbo Science & Technology Innovation 2025 Major Project (Grant No. 2022Z187), and the Ningbo Science & Technology Project (Grant No. 2023A-160-B).

References

1. L. E. Bell, Science, 2008, 321, 1457–1461.
2. M. Langan and K. O’Toole, Energy Procedia, 2017, 123, 188–195.
3. C. Forman, I. K. Muritala, R. Pardemann and B. Meyer, Renewable and Sustainable Energy Rev., 2016, 57, 1568–1579.
4. G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149.
5. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
6. Y.-K. Zhu, J. Guo, Y.-X. Zhang, J.-F. Cai, L. Chen, H. Liang, S.-W. Gu, J. Feng and Z.-H. Ge, Acta Mater., 2021, 218, 117230.
7. X. Lu, Q. Zhang, J. Liao, H. Chen, Y. Fan, J. Xing, S. Gu, J. Huang, J. Ma, J. Wang, L. Wang and W. Jiang, Adv. Energy Mater., 2019, 10, 1902986.
8. L. Xie, H. Qin, J. Zhu, L. Yin, D. Qin, F. Guo, W. Cai, Q. Zhang and J. Sui, Adv. Electron. Mater., 2019, 6, 1901178.
9. L. Hu, F. Meng, Y. Zhou, J. Li, A. Benton, J. Li, F. Liu, C. Zhang, H. Xie and J. He, Adv. Funct. Mater., 2020, 30, 2005202.
10. I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904.
11. Q. Wang, Y. Tang, A. Miura, K. Miyazaki, Z. Horita and S. Iikubo, Scr. Mater., 2024, 243, 115991.
12. Y. S. Wang, L. L. Huang, C. Zhu, J. Zhang, D. Li, H. X. Xin, M. H. Danish and X. Y. Qin, Scr. Mater., 2018, 154, 118–122.
13. Y. Pan, Y. Qiu, I. Witting, L. Zhang, C. Fu, J.-W. Li, Y. Huang, F.-H. Sun, J. He, G. J. Snyder, C. Felser and J.-F. Li, Energy Environ. Sci., 2019, 12, 624–630.
14. K. H. Lee, H.-S. Kim, M. Kim, J. W. Roh, J.-H. Lim, W. J. Kim, S.-I. Kim and W. Lee, Acta Mater., 2021, 205, 116578.
15. K. Pang, M. Yuan, Q. Zhang, Y. Li, Y. Zhang, W. Zhou, G. Wu, X. Tan, J. G. Noudem, C. Cui, H. Hu, J. Wu, P. Sun, G. Q. Liu and J. Jiang, Small, 2023, 20, 202306701.
16. H. Liu, P. Zheng, J. Cai, B. Zhu, W. Xu and Y. Zheng, ACS Appl. Mater. Interfaces, 2023 DOI:10.1021/acsaem.3c01807.
17. Q. Zhu, S. Wang, X. Wang, A. Suwardi, M. H. Chua, X. Y. D. Soo and J. Xu, Nano-Micro Lett., 2021, 13, 119.
18. T. Lu, B. Wang, G. Li, J. Yang, X. Zhang, N. Chen, T.-H. Liu, R. Yang, P. Niu, Z. Kan, H. Zhu and H. Zhao, Mater. Today Phys., 2023, 32, 101035.
19. J. Qiu, Y. Yan, H. Xie, T. Luo, F. Xia, L. Yao, M. Zhang, T. Zhu, G. Tan, X. Su, J. Wu, C. Uher, H. Jiang and X. Tang, Sci. China Mater., 2021, 64, 1507–1520.
20. K. Pang, L. Miao, Q. Zhang, Q. Pan, Y. Liu, H. Shi, J. Li, W. Zhou, Z. Zhang, Y. Zhang, G. Wu, X. Tan, J. G. Noudem, J. Wu, P. Sun, H. Hu, G. Q. Liu and J. Jiang, Adv. Funct. Mater., 2024, 34, 2315591.
21. H. S. Kim, S. s Choo, H. j Cho and S. i Kim, Phys. Status Solidi A, 2019, 216, 1900039.
22. K. H. Lee, S.-M. Choi, J. W. Roh, S. Hwang, S. I. Kim, W. H. Shin, H. J. Park, J. H. Lee, S. W. Kim and D. J. Yang, J. Electron. Mater., 2014, 44, 1531–1535.
23. M. Aljaghtham, G. Song, J. García-Cañadas and B. Beltrán-Pitarch, ACS Appl. Electron. Mater., 2023, 5, 3373–3377.
24. W. Li, B. Poudel, R. A. Kishore, A. Nozariasbmarz, N. Liu, Y. Zhang and S. Priya, Adv. Mater., 2023, 35, 2210407.
25. H.-J. Cho, W. H. Shin, S.-S. Choo, J.-I. Kim, J. Yoo and S.-I. Kim, J. Electron. Mater., 2019, 48, 1951–1957.
26. M. J. Hÿtch, J.-L. Putaux and J.-M. Pénisson, Nature, 2003, 423, 270–273.
27. H. Wu, F. Zheng, D. Wu, Z.-H. Ge, X. Liu and J. He, Nano Energy, 2015, 13, 626–650.
28. H. Yao, Y. Liu, X. Sun, Y. Lu, T. Wang and T. Li, Intermetallics, 2021, 133, 107187.
29. Q. Zhang, M. Yuan, K. Pang, Y. Zhang, R. Wang, X. Tan, G. Wu, H. Hu, J. Wu, P. Sun, G. Q. Liu and J. Jiang, Adv. Mater., 2023, 35, 2300338.
30. L. P. Tan, T. Sun, S. Fan, L. Y. Ng, A. Suwardi, Q. Yan and H. H. Hng, Nano Energy, 2013, 2, 4–11.
31. C. Li, S. Ma, W. Cui, X. Sang, P. Wei, W. Zhu, X. Nie, W. Zhao and Q. Zhang, Mater. Today Phys., 2021, 19, 100409.
32. W. H. Shin, J. W. Roh, B. Ryu, H. J. Chang, H. S. Kim, S. Lee, W. S. Seo and K. Ahn, ACS Appl. Mater. Interfaces, 2018, 10, 3689–3698.
33. Y. Sun, H. Wu, X. Dong, L. Xie, Z. Liu, R. Liu, Q. Zhang, W. Cai, F. Guo and J. Sui, Adv. Funct. Mater., 2023, 33, 2301423.
34. L. Li, P. Wei, M. Yang, W. Zhu, X. Nie, W. Zhao and Q. Zhang, Sci. Chin. Mater., 2023, 66, 3651–3658.
35. C. Tan, X. Tan, F. Shi, Y. Yin, G.-Q. Liu, C. Xiong, H. Wang, G. Luo, B. Yu, J. G. Noudem, B. Liang and J. Jiang, Ceram. Int., 2021, 47, 725–731.
36. T. Xing, R. Liu, F. Hao, P. Qiu, D. Ren, X. Shi and L. Chen, J. Mater. Chem. C, 2017, 5, 12619–12628.
37. K.-H. Lee, S. Hwang, B. Ryu, K. Ahn, J. Roh, D. Yang, S.-M. Lee, H. Kim and S.-I. Kim, J. Electron. Mater., 2012, 42, 1617–1621.
38. F. Hao, P. Qiu, Y. Tang, S. Bai, T. Xing, H.-S. Chu, Q. Zhang, P. Lu, T. Zhang, D. Ren, J. Chen, X. Shi and L. Chen, Energy Environ. Sci., 2016, 9, 3120–3127.
39. Q. Zhang, G. Wu, Z. Guo, P. Sun, R. Wang, L. Chen, X. Wang, X. Tan, H. Hu, B. Yu, J. G. Noudem, G. Liu and J. Jiang, ACS Appl. Mater. Interfaces, 2021, 13, 24937–24944.
40. G. Wu, Z. Yan, X. Wang, X. Tan, K. Song, L. Chen, Z. Guo, G.-Q. Liu, Q. Zhang, H. Hu and J. Jiang, ACS Appl. Mater. Interfaces, 2021, 13, 57514–57520.
41. R. Deng, X. Su, S. Hao, Z. Zheng, M. Zhang, H. Xie, W. Liu, Y. Yan, C. Wolverton, C. Uher, M. G. Kanatzidis and X. Tang, Energy Environ. Sci., 2018, 11, 1520–1535.
42. Z. Guo, K. Song, Z. Yan, P. Sun, X. Tan, G. Wu, Q. Zhang, G.-Q. Liu, B. Yu and J. Jiang, Chem. Eng. J., 2021, 426, 131853.
43. F. Shi, H. Wang, Q. Zhang, X. Tan, Y. Yin, H. Hu, Z. Li, J. G. Noudem, G. Liu and J. Jiang, ACS Appl. Mater. Interfaces, 2021, 4, 2944–2950.
44. G. Zheng, X. Su, H. Xie, Y. Shu, T. Liang, X. She, W. Liu, Y. Yan, Q. Zhang, C. Uher, M. G. Kanatzidis and X. Tang, Energy Environ. Sci., 2017, 10, 2638–2652.
45. Z.-Y. Huang, H. Zhang, L. Yang, B. Zhu, K. Zheng, M. Hong, Y. Yu, F.-Q. Zu, J. Zou and Z.-G. Chen, Mater. Today Energy, 2018, 9, 383–390.
46. J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154.
47. H. Wang, Y. Pei, A. D. LaLonde and G. J. Snyder, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9705–9709.
48. W. Huang, X. Tan, J. Cai, S. Zhuang, C. Zhou, J. Wu, G. Liu, B. Liang and J. Jiang, Mater. Today Phys., 2023, 32, 101022.
49. A. Nozariasbmarz, B. Poudel, W. Li, H. B. Kang, H. Zhu and S. Priya, iScience, 2020, 23, 101340.
50. J. Qiu, Y. Yan, T. Luo, K. Tang, L. Yao, J. Zhang, M. Zhang, X. Su, G. Tan, H. Xie, M. G. Kanatzidis, C. Uher and X. Tang, Energy Environ. Sci., 2019, 12, 3106–3117.
51. Y. K. Zhu, Y. Sun, J. Zhu, K. Song, Z. Liu, M. Liu, M. Guo, X. Dong, F. Guo, X. Tan, B. Yu, W. Cai, J. Jiang and J. Sui, Small, 2022, 18, 2201352.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00977k

‡ These authors contributed equally.

---