Highly sensitive strain sensors with ultra-low detection limit based on pre-defined serpentine cracks

Abstract

Flexible and stretchable strain sensors have garnered significant interest due to their potential applications in various fields including human health monitoring and human–machine interfaces. Previous studies have shown that strain sensors based on microcracks can exhibit both high sensitivity and a wide sensing range by manipulating the opening and closing of randomly generated cracks within conductive thin films. However, the uncontrolled nature of microcrack formation can cause a drift in the sensor's performance over time, affecting its accuracy and reliability. In this study, by pre-defining the cracks, we introduce a novel resistive strain sensor with high sensitivity, excellent linearity, an ultra-low detection limit, and robustness against off-axis deformation. The sensor operates on a simple mechanism involving the modulation of ohmic contact within intricately designed conductive serpentine curves, which are encapsulated by pre-stretched thin films. This design facilitates a high gauge factor of 495, exceptional linearity (R² > 0.98), and an ultra-low detection threshold of 0.01% strain. Moreover, it maintains performance integrity during off-axis deformations such as bending and twisting, features that are indispensable for accurately monitoring human motion. To explore practical applications, a driving scenario was simulated where a sensor array was positioned on the driver's neck. The sensor output was analyzed using machine learning algorithms to successfully determine the presence of driver fatigue. This demonstration underlines the potential of our sensor technology in applications ranging from healthcare monitoring to wearable biomechanical systems and human–machine interfaces.

---

New concepts

This study introduces a novel resistive strain sensor that addresses key limitations in existing strain sensor technology, particularly the issue of performance drift due to uncontrolled microcrack formation. Unlike previous designs, this sensor employs pre-defined cracks within conductive serpentine curves, significantly enhancing the sensor's sensitivity, linearity, and robustness. The controlled microcrack formation allows for a high gauge factor of 495, an ultra-low detection limit of 0.01% strain, and reliable performance under off-axis deformations like bending and twisting. This innovative approach not only improves the accuracy and reliability of strain sensors but also expands their potential applications in fields such as healthcare monitoring and human–machine interfaces. The successful application of this sensor in detecting driver fatigue through machine learning further demonstrates its practical utility in real-world scenarios.

Introduction

Flexible sensing technology, characterized by its softness, thinness, and stretchability, has introduced innovative solutions across various application domains, significantly advancing wearable technology,^1–4 medical monitoring,^5–8 robotics,^9–12 and the Internet of Things.^13–16 Among these advancements, resistive flexible strain sensors have attracted considerable attention within these fields due to high sensitivity and ease of data acqusition.^17,18 Previously reported wearable flexible strain sensors have primarily focused on achieving high sensitivity and a broad operating range.^19–22 However, sensors designed to accommodate a wide strain range often display non-linear responses, complicating the data analysis process. In contrast, traditional metal foil or semiconductor strain sensors, while capable of monitoring smaller strain ranges, demonstrate favorable linear response characteristics. Despite this, their low sensitivity (GF < 2) and lack of stretchability limit their suitability for monitoring human motion, thus restricting their use in wearable electronic devices applied directly to the skin. Consequently, there is a compelling need for a flexible strain sensor that can serve as an alternative to conventional rigid strain gauges, one that combines both high sensitivity and excellent linearity to optimize functionality for human motion monitoring.

In recent years, researchers have explored structural designs of sensor's conductive networks to enhance sensitivity and stretchability.²³ Studies have identified microcrack structures as an effective tool for improving sensor sensitivity.^24–28 Inspired by spider webs, Sun et al. developed a strain sensor that utilizes an Au/SWCNT crack structure.²⁹ The rigid Au film undergoes significant resistance changes due to strain-induced cracking, yielding high sensitivity (GF = 7.1 × 10⁴–3.4 × 10⁶). An underlying layer of single-walled carbon nanotubes (SWCNTs) provides additional conductive pathways across cracks, allowing for a wide operational range (⩾100% strain). Furthermore, Sun et al. deposited CNTs and AgNWs on electrospun TPU fiber mats and then applied pre-stretching to create a microcrack structure, which resulted in a sensor that maintained high sensitivity and a broad strain range (0–102% strain, GF = 691; 102–135% strain, GF = 2 × 10⁴; 135–171% strain, GF > 11 × 10⁴).³⁰ While these sensors exhibit high sensitivity and can operate across wide ranges, their performance is hindered by the random formation of microcracks. This results in non-linear strain responses, complicating the accurate interpretation of data. Furthermore, with repeated stretching, sensors with microcrack structures may not return to their original states due to the development of additional cracks. Extreme stretching may worsen this issue, potentially leading to the complete detachment of conductive connections within the crack structures, ultimately causing sensor failure. Addressing these challenges is crucial for enhancing the reliability and durability of the sensors. Researchers have also experimented with pre-defined structural design to develop sensors with serpentine structures, seeking both high sensitivity and robust stretchability.³¹ Zhou et al. used a graphene nanoplatelets/multi-walled CNTs/silicone rubber hybrid conductive network to create a serpentine sensing layer, achieving a sensor with high sensitivity (GF = 6.3–2675.5) and up to 100% strain range.³² Although biomimetic serpentine designs enhance mechanical compliance and improve sensor stretchability, they still exhibit non-linear strain responses across their operative range. To mitigate electrical disturbance from off-axis mechanical loads in tension, Xu et al. designed a serpentine sensor using a composite conductive material (Ag/highly conductive carbon nanoparticles/Au/Ecoflex), resulting in an extensive operating range (>150% strain) but relatively low sensitivity (GF = 1.23–8.67).³³ It is notable that the proposed serpentine geometry effectively mitigates resistance variation due to off-axis deformation. This is achieved by minimizing stress concentration during bending or twisting, as demonstrated by Lin.³⁴ Despite these advances, achieving high sensitivity coupled with high linearity in strain sensors through serpentine structural designs remains a persistent challenge.

Here, we introduce a simple and effective method to prepare highly sensitive strain sensors with an ultra-low detection limit and excellent linearity based on pre-defined cracks. The superior performance of these strain sensors is achieved through the precise opening and closing of pre-formed serpentine cracks within a conductive thin film, which is supported by a pre-stretched elastic encapsulation layer. In particular, our sensors achieve a gauge factor of up to 495 within a 9% strain range. They also offer an ultra-low detection limit of 0.01% strain, making them ideal for monitoring subtle biosignals such as human wrist pulse. Our sensors demonstrate good mechanical robustness, with only 7.9% drift of peak signals observed after 2000 cycles of stretching and releasing at a peak strain of 2%. Importantly, they exhibit minimal sensitivity to off-axis deformations such as bending, ensuring high accuracy for strain sensing under complex deformation conditions. Additionally, the sensors maintain their function under extreme conditions, including resistance to salt spray, ultraviolet radiation, and humid-thermal environments. Furthermore, the potential of these strain sensors in monitoring human activity has been validated through simulations of driving scenarios. A machine learning algorithm was developed to evaluate neck movement in drivers, aiming to identify signs of fatigue. This illustrates a practical application of our sensors in wearable devices to effectively monitor human movement.

Results and discussion

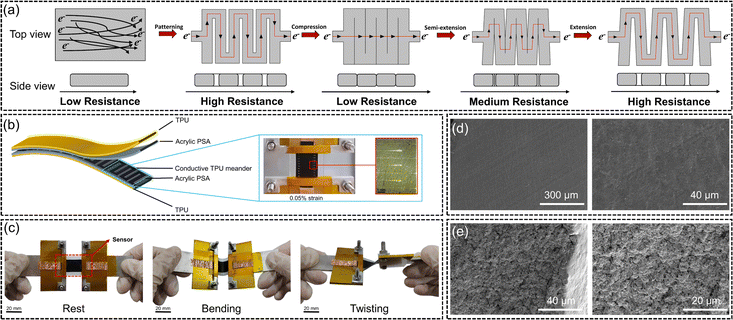
Highly sensitive strain sensors with predefined serpentine cracks were fabricated using a combination of laser cutting and pre-stretching techniques. The fabrication process is illustrated in Fig. 1, with more details provided in the experimental section. Briefly, conductive thin films with a thickness of 500 μm were created using 3D printing with a conductive TPU filament, followed by a subsequent hot press process. These films were then laser cut into serpentine patterns, producing open cracks of varying widths and densities. The patterned films were then transferred onto a pre-stretched elastic TPU film. Upon releasing the pre-stretch, the cracks within the serpentine patterns closed. Copper electrodes were attached at both ends of the conductive thin film, and the resulting strain sensors were ready for characterization.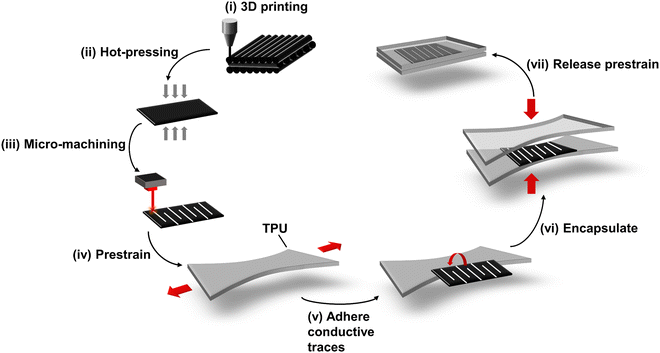

Fig. 1 Schematic illustration of the sensor manufacturing process by transferring the conductive thin film with serpentine cutting patterns onto the pre-stretched TPU substrate.

The resistance change of our strain sensors was precisely controlled through the deliberate manipulation of pre-formed cracks within the conductive thin films. When these cracks were closed, the sensors exhibited a low resistance state because electrons could flow through the contacted and connected conductive pathways between short-circuited conductive serpentine strips. On the other hand, when the cracks were fully opened, the sensors demonstrated a high resistance state as the electrons had to flow through the extended conductive pathways (Fig. 2a). This simple mechanism allows for accurate and repeatable adjustments in resistance, making the sensors highly effective for precise strain measurements. As shown in Fig. 2b, the conductive thin film of TPU was cut into a serpentine pattern and encapsulated within a pre-strained elastic membrane. This design makes the sensors mechanically robust and resistant to environmental interferences, enhancing their durability and reliability under various conditions. It can be seen that by applying a strain as small as 0.05%, the opening of cracks became visible in conductive thin films (Fig. 2b). The strain sensor with its multilayered structure was well bonded and tolerant to various mechanical deformations, such as stretching, bending, and twisting (Fig. 2c). This robust construction ensures reliable performance and durability under different types of mechanical stress. In addition, the microstructure of conductive films based on TPU was extensively characterized using SEM. Fig. 2d shows the SEM image of the top surface of the conductive TPU film, revealing a smooth surface after hot pressing, which effectively eliminated voids and defects in the original 3D-printed film. Fig. 2e displays SEM images of the fractured surface of the conductive TPU film, where the distribution and presence of conductive particles are clearly observable, highlighting the structural integrity and conductive pathways within the material.

Fig. 2 Structure and working principle of the strain sensor. (a) Sketch of the working principle of the strain sensor. After laser cutting, the conductive thin film with a serpentine structure is sandwiched between two pre-stretched TPUs, and the opening and closing of cracks control the resistance changes of the strain sensor. (b) Multilayered structure for the strain sensor. The TPU encapsulation layer is bonded to the serpentine conductive TPU using acrylic adhesive to ensure good mechanical robustness. The opening of cracks is visible by applying a small strain of 0.05% (scale bar, 1 mm). (c) Demonstration of sensor mechanical compliance (scale bar, 20 mm). (d) and (e) Microstructure characterization of the top (d) and fractured surfaces (e) of the TPU conductive film via SEM.

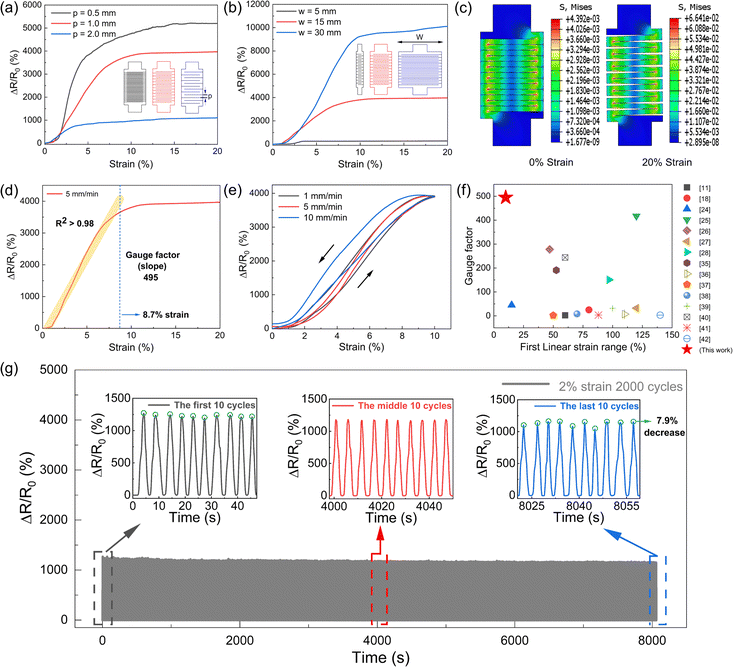
The serpentine patterns of the conductive layer, determined by various cutting parameters, have a direct impact on the sensing performance of our strain sensors. We focus on two main parameters: the pitch length between serpentine curves (p) and the width of these curves (w) to evaluate their effects on sensor performance. Initially, we investigated sensors with the same width (w = 15 mm) but different pitches under stretching through finite element simulation. For simplicity, we modelled four serpentine curves for each of the three parameter sets (p = 0.5, 1 and 2 mm, respectively). We recorded the states of the sensors with different p at different strain levels (Fig. S2, ESI†). Additionally, we measured the contact area of one crack in each sensor (Fig. S3, ESI†) and it indicated that the cracks for the sensor with larger p were separated at smaller strain. The results aligned with the observed trends in electrical resistance response as shown in Fig. 3a. For the strain sensor with p = 2 mm, the sensing range was smaller because the cracks were fully opened at 3.6% strain and no further resistance changes would be observed afterwards. As the p decreased to 0.5 mm, the cracks were fully opened at 14.8% strain. As such, the sensor with p = 0.5 mm showed the largest sensing range of 14.8% strain. Meanwhile, under the same strain level, the strain sensor with smaller p has the higher crack density, which contributes to larger resistance changes and hence higher sensitivity. As a result, the strain sensor with p = 0.5 mm showed the best sensing performance in terms of sensitivity (1154.7) and a sensing range of 14.8%. However, achieving high-quality cutting with p = 0.5 mm was challenging and strain sensors with p = 1 mm were selected for further studies in this work.

Fig. 3 Effect of the serpentine structure with different cutting parameters on sensing performance. (a) Sensor response for various curve pitch lengths (the insets showing three sensor models with different pitch lengths, p). (b) Sensor response for various curve widths (the insets showing three sensor models of different widths, w). (c) Finite element simulation of the stress distribution for the sensor with the parameter of w = 15 mm and p = 1 mm under strains of 0% and 20%, respectively. (d) Linear fitting for the resistance changes as a function of strain for the same sensor. (e) Resistance hysteresis response of the sensor at three different stretching speeds (1, 5, and 10 mm min⁻¹). (f) Gauge factors and linear sensing ranges of our newly developed sensors compared to recent literature reports. (g) Sensor stability study over 2000 cycles at a peak strain of 2%. The insets showing the first 10 cycles, the middle 10 cycles, and the last 10 cycles, respectively.

As for the strain sensors with fixed p = 1 mm, both sensing range and sensitivity increased when the width w increased. As shown in Fig. 3b, by increasing w from 5 to 30 mm, the corresponding sensitivity increased from 179 to 983 and the sensing range increased from 3.5% to 12.5%. To account for these results, we theoretically derived the resistance response trends of sensors with different widths at the same spacing using the formula R = ρL/A, where ρ is the resistivity of the material, L is the length of the sensor, and A is the cross-sectional area of the sensor along its length. The width w was varied among three specific values while maintaining the same length L and thickness for all sensors. A larger w results in a larger cross-sectional area A, thus lowering the resistance R. Consequently, the sensor with a width of w = 30 mm has the largest cross-sectional area, resulting in the smallest initial resistance R₀, which is advantageous for increasing the rate of resistance change. Moreover, a larger crack cross-sectional area also increases the separation area of the sensor under stretching strain, similarly aiding in increasing the rate of resistance change. Combining these two factors, the results align with the actual trends in electrical resistance response, as shown in Fig. 3b, where the configuration with w = 30 mm and p = 1 mm showed the greatest sensitivity, that is, at the same pitch, a larger width results in a greater rate of resistance change.

It is noteworthy that even though the model with parameters w = 15 mm and p = 0.5 mm exhibited the highest strain sensitivity, its linearity was significantly lower compared to the model with parameters w = 15 mm and p = 1 mm. Additionally, considering its suitability for conformal monitoring of movements around fingers, wrists, necks, and other body joints, the sensor with w = 15 mm and p = 1 mm was selected for further performance evaluations. Finite element simulation analysis was performed on the sensor model to capture the opening of serpentine patterns after applying 20% strain.

As depicted in Fig. 3d, the selected sensor with p = 1 mm and w = 15 mm exhibited an excellent linear response up to 8.7% strain, with a high gauge factor of 495. The sensor's linearity, indicated by the coefficient of determination (R²), was derived from a linear regression of resistance data from 0% strain to the saturation point, marked by the yellow line in Fig. 3d. The sensor's sensitivity, defined as (ΔR/R₀)/Δε, was calculated from the slope of the linear fit. During testing, the sensor was stretched at a constant speed of 5 mm min⁻¹ using a universal testing machine, achieving a sensitivity of 495 and an R² value exceeding 0.98 (Fig. 3d). The resistance changes saturated around 10% and did not show any increase even when the applied strain was further increased. This is due to the total separation of the previously contacted conductive serpentine curves, and afterwards, the conductive thin film simply extended without further changes in resistance. Fig. 3f presents a comparison of the gauge factor and the linear sensing range of our newly developed sensors, with those reported in the recent literature^{11,18,25–28,35–42} using other conductive nanocomposites. Table S1 (ESI†) also presents comparisons with previous works in sensing mode.^19,43–50 We further explored the mechanical and resistive hysteresis of the sensor under varying stretching speeds of 1 mm min⁻¹, 5 mm min⁻¹, and 10 mm min⁻¹ and the corresponding results are given in Fig. S4 (ESI†) and Fig. 3e. The average mechanical hysteresis rate was 30.76%, and the average resistive hysteresis rate was 16.43%, both of which are comparable to the values of strain sensors reported in the literature.^51,52 The mechanical robustness of our sensor is demonstrated by its capability to withstand 2000 cycles of 2% strain and 8% strain with a minimal signal drift. As illustrated in Fig. 3g, the average peak value of the final ten cycles was only 7.9% lower than that of the initial ten cycles. Fig. S5 (ESI†) also illustrates that the average peak value of the final ten cycles was only 7.9% lower than that of the initial ten cycles. The sensor was also tested for its ability to maintain resistance under prolonged stretching. Initially, the resistance peaked, then steadily decreased, and stabilized around 4.8 seconds with a 6.8% decrease in the rate of resistance change. Fig. S6 (ESI†) displays the resistance response of the sensor when subjected to a static 8% strain for more than 10 minutes. The excellent static stability is also illustrated by stretching the sensor by 2.5%, 5% and 10% of the strain, with the electrical signals in Fig. S7 (ESI†) showing little overshoot and rapid stabilization. Fig. S8 (ESI†) shows the dynamic stability by applying cyclic 5% strain with the frequency ranging from 0.1–0.5 Hz.

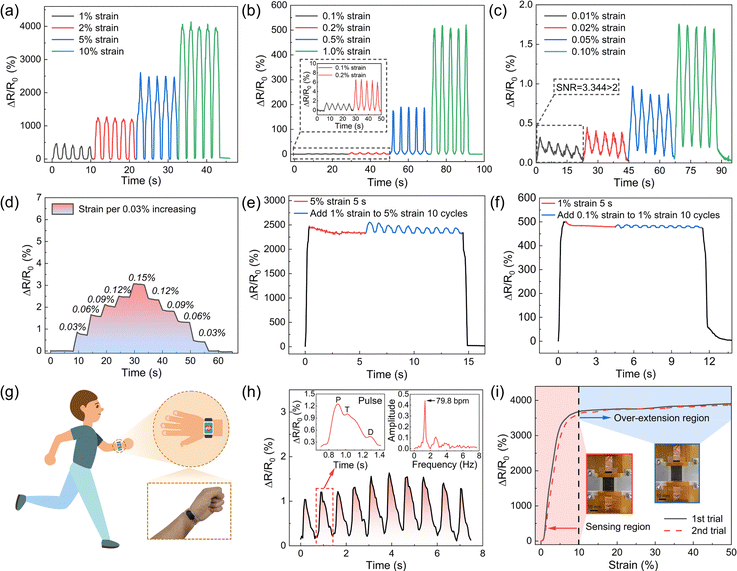
The sensor is capable of distinguishing different levels of strain and has a very low detection limit of 0.01% strain. Fig. 4a–c shows the resistance changes for the strain sensor under different levels of strain, clearly demonstrating that for strains above 0.1%, the resistance change signals are highly recognizable. Even for a very subtle strain of 0.01%, a significant resistance change signal with a signal-to-noise ratio (SNR = 3.344) was validated. This makes the sensors highly potent for monitoring delicate biosignals such as pulse and respiration which are closely related to human health conditions. The ultralow detection limit was also verified by incrementally stretching in steps of 0.03% strain. The resistance changes closely followed the input strain patterns during the stretching-hold process and the subsequent release-hold process (Fig. 4d). When the sensor was pre-stretched to an initial strain of 5%, additional 1% strain cycles were then applied. The sensor demonstrated its high sensitivity by accurately detecting the 1% strain superimposed on the initial deformation, as shown in Fig. 4e. Furthermore, our sensor demonstrated similar detection capability even under a smaller strain regime, where it was pre-stretched to 1% and then ten cycles of 0.1% strain were applied. The sensor was again able to precisely recognize the 0.1% strain fluctuations, as depicted in Fig. 4f. These results clearly demonstrate the sensor's remarkable detection capabilities, even at low strain levels, highlighting its potential for applications requiring fine strain resolution.

Fig. 4 Strain sensor performance and an ultralow detection limit. (a) Sensor recognition of 1–10% tensile strain. (b) Sensor recognition of 0.1–1.0% tensile strain. (c) Sensor recognition of 0.01–0.1% tensile strain. (d) Sensor response to a tensile strain step of 0.03% strain. (e) Recognizing 1% strain with 5% strain applied. (f) Recognizing 0.1% strain with 1% strain applied. (g) Pulse monitoring schematic diagram. (h) Sensor mounted onto the human wrist to monitor the pulse waveform. The inset shows the waveform of a single pulse signal and the corresponding frequency-amplitude curve obtained through FFT analysis of the entire pulse waveform. (i) Sensor response to overstretching, where the strain exceeds the sensing region. The inset shows the photographs of the sensor in the sensing region (red shadow) and the overstretching region (blue shadow) (scale bar, 10 mm).

Due to the sensor's excellent capability of detecting subtle strains, it was utilized to monitor biological signals, specifically the pulse on a healthy male's wrist (Fig. 4g). The sensor was firmly attached to the wrist and it successfully captured the pulse waveform (Fig. 4h). The inset in the upper left corner showed distinct phases of the cardiac cycle: the percussion wave (P wave), tidal wave (T wave), and diastolic wave (D wave). Another inset in the upper right corner displays a frequency-amplitude curve derived through Fast Fourier Transform (FFT) analysis, confirming a pulse rate of 79.8 bpm, consistent with normal heart rate values.

Another important characteristic of this sensor is its tolerance to overstretching beyond its working strain range. As shown in Fig. 4i, the sensor can retain its strain sensing capability even after being stretched over 50%, which is significantly beyond its working range of up to 10% strain. This is attributed to its unique serpentine cutting pattern. As previously discussed, although the contact area of neighboring serpentine conductive strips completely separates after 10% strain, the structure and conductive pathways of the serpentine conductive thin films remain intact even at strains over 50%. After releasing the overstretched strain, the separated serpentine conductive strips make contact again, thereby restoring the sensor's sensing capability. This unusual ability to tolerate high levels of strain significantly enhances the robustness of our sensors. They can maintain their sensing capability even when subjected to overstretching during the mounting or removal processes. This resilience ensures reliable performance and durability, making the sensors suitable for various applications where they might experience mechanical stress beyond their normal operating range.

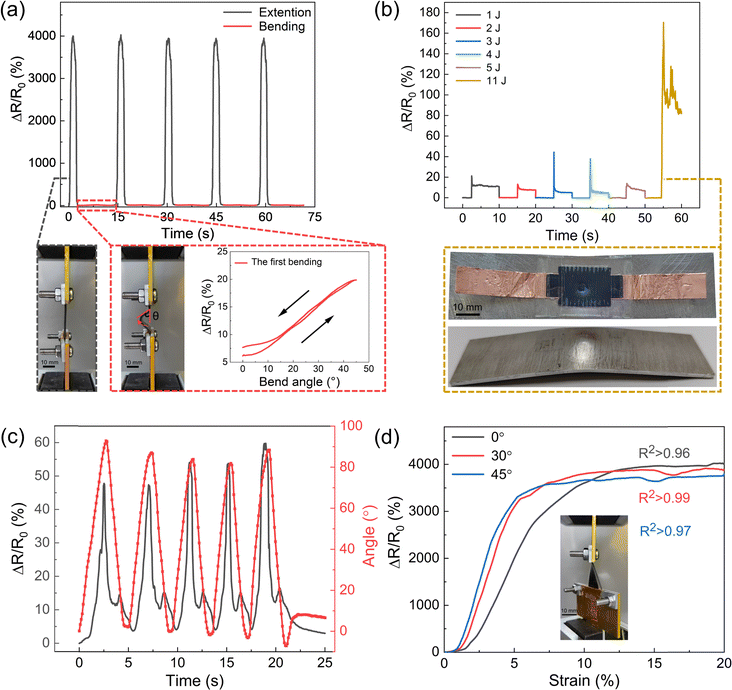
Our strain sensors also demonstrate an impressive capability to maintain a minimal bending response, ensuring that they can deliver highly accurate strain sensing even under complex deformation conditions. This makes them exceptionally reliable for applications requiring precise measurements in environments where traditional sensors might struggle to perform consistently. As shown in Fig. 5a, under cyclic stretching with a 10% strain, our sensors exhibited a substantial resistance change of 4000%. In contrast, during bending tests at a 45-degree angle, the resistance change was only 20%. This indicates that bending generates a negligible signal compared to stretching. These results highlight the sensor's robustness in maintaining accurate strain measurements even under significant deformation conditions, with minimal interference from bending. The sensor demonstrated exceptional resilience to significant impact loads. As illustrated in Fig. 5b, when subjected to impact loads from a drop hammer with energies ranging from 1 to 5 J, the sensor remained undamaged and its initial resistance was restored post-impact. However, at an 11 J impact, the resistance change rate increased to 6.5 times the average rate observed at lower energy impacts, and it did not return to its initial value, indicating structural damage. The inset in Fig. 5b shows resultant surface depressions on the sensor and noticeable deformation on the aluminium plate. Despite this structural damage, the peak damage response was only 4.3% of the peak response observed during linear stretching.

Fig. 5 Effects of off-axis loads and shock loads on strain sensing performance. (a) Sensor response to continuous stretching and bending. The inset shows photographs of the sensor in the stretching configuration (black box) and bending configuration (red box), as well as the sensor's response to bending (red box). (b) Sensor response to different impact energies. The inset shows the sensor and an aluminium alloy shim after an 11 J impact load. (c) Sensor response to continuous torsion from 0° to 90°. (d) Sensor response to strain given a specific initial torsion angle. The inset illustrates the experimental setup.

Our sensor can accurately detect strain even when subjected to combined strain and torsional deformations. Fig. 5c illustrates the sensor's response to continuous torsional motion ranging from 0 to 90 degrees. The average peak response observed over five trials was less than 1.5% of the peak response recorded during tensile stretching at 10% strain. This highlights the sensor's minimal sensitivity to torsional movements. Additionally, in a related set of experiments shown in Fig. 5d, the sensor was initially set to torsion angles of 0°, 30°, and 45° before being subjected to a 20% tensile strain. The results from these experiments indicate a slight decrease in the resistance response as the initial torsion angle increased. Particularly, the resistance change rate at a 45° torsion angle decreased by approximately 6.3% compared to the resistance change rate at a 0° angle. These findings collectively underscore the sensor's limited responsiveness to torsional strains and its exceptional ability to accurately monitor strain information under complex deformation conditions. For joints that experience complex deformation, such as the rotational and bending movements of the wrist, it is crucial to precisely monitor strain information to ensure an accurate assessment of mechanical stresses. These data are essential for understanding the biomechanical behavior of the joint, preventing potential injuries and optimizing the design of assistive devices, such as orthoses or prostheses, to provide better support and enhance overall mobility.

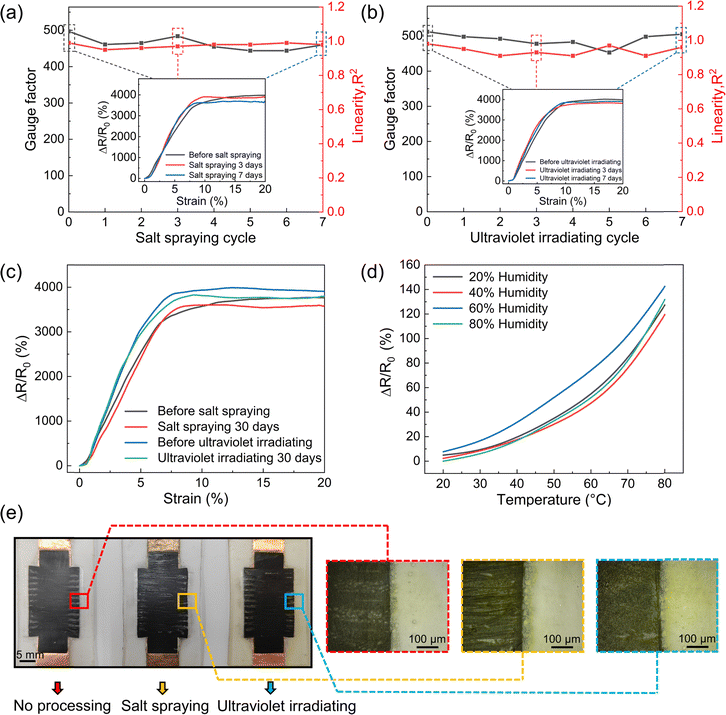
In addition to its minimal interference from bending and torsion, our sensor can maintain its strain sensing capability under various extreme environmental conditions. To investigate the potential effects of human sweat corrosion on the sensor, a salt spray environment test was conducted, as shown in Fig. 6a. Over a period of 7 days, the sensor's sensitivity and linearity in the salt spray environment were assessed. The results indicated that the sensing performance remained unaffected despite prolonged exposure to the corrosive environment. The inset images in Fig. 6a show the strain-resistance change rate curves before the test, as well as at 3 and 7 days post-exposure. These curves demonstrate consistent sensor performance, underscoring its robustness and reliability under conditions that simulate human sweat corrosion. Additionally, the sensor was subjected to intense ultraviolet (UV) light to evaluate its robustness under such conditions. Fig. 6b displays the sensitivity and linearity of the sensor over a week of UV exposure, supplemented by inset images showing the strain-resistance change rate curves before exposure, and after 3 and 7 days. Fig. 6c quantifies these observations, showing a decrease in the resistance change rate at a saturation of 4.8% post salt spray testing and 4.6% post UV exposure after 30 days. This indicates the superior resistance of the sensor to both salt spray and UV aging. Moreover, the sensor was also subjected to humid-heat environmental testing, with results presented in Fig. 6d. This test tracked the resistance change rate as a function of temperature under humidity levels of 20%, 40%, 60%, and 80%. The change in resistance was most significant at 60% humidity, where the resistance response at 80 °C amounted to only 3.6% of the peak value observed during linear stretching. These results demonstrate the sensor's robust performance under humid-heat conditions. Fig. 6e displays the appearances of sensors: an untested sensor (left), a sensor subjected to 30 days of salt spray environmental testing (middle), and a sensor after 30 days of ultraviolet environmental testing (right). Additionally, three dashed boxes on the right side (colored red, yellow, and blue) provide magnified views of each sensor, respectively. The visual comparison reveals minimal changes in appearance after 30 days in the salt spray environment, whereas the sensor demonstrates evident aging and yellowing after the same period under UV light. These findings collectively highlight the sensor's exceptional durability and reliability under various harsh environmental conditions, including salt spray, UV exposure, and humid-heat environments.

Fig. 6 Strain sensor working under various extreme environmental conditions. (a) The impact of salt spray on sensor performance. The inset shows the sensor's response to tensile strain before the salt spray, on the third day, and on the seventh day after spray. (b) The impact of UV irradiation on the sensor. The inset shows the sensor's response to tensile strain before the UV irradiation on the third day, and on the seventh day after UV irradiation. (c) Sensor response to tensile strain after 30 days of salt spray and UV irradiation, respectively. (d) Sensor response to temperature under different humidity levels. (e) Sensor structure and morphology after 30 days of salt spray and UV irradiation, respectively.

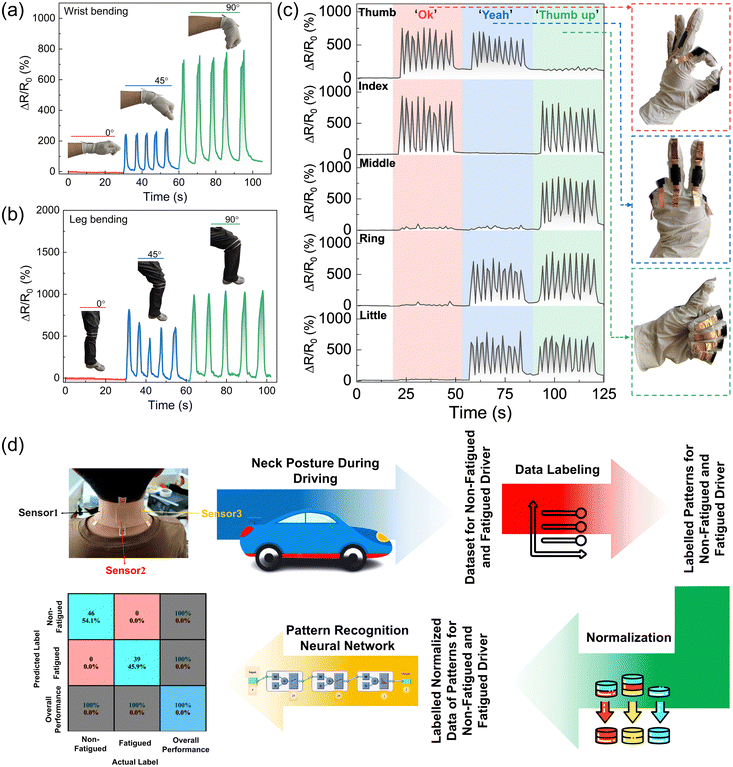
Building on the excellent performance of our sensors, they exhibit significant potential for applications in human health monitoring and human–machine interaction. These sensors were affixed to various locations on the human body to monitor a wide range of physical movements, demonstrating their versatility and effectiveness. Fig. 7a and b show the resistance responses of sensors placed on the wrist and knee at bending angles of 0°, 45°, and 90°. These figures clearly capture the biomechanical dynamics of the wrist and knee joints, making the sensors highly useful for rehabilitation purposes. The results indicate that the sensors can accurately measure and track joint movements, providing valuable insights for developing personalized rehabilitation programs. To further evaluate the sensors’ capability for hand gesture recognition, five strain sensors were individually attached to each finger of a hand. The sensors recorded responses to three distinct gestures: ‘OK,’ ‘Yeah,’ and ‘Thumbs Up.’ Fig. 7c demonstrates that the sensors’ outputs varied distinctly with each gesture, confirming their ability to accurately track and recognize complex hand movements. This functionality is particularly beneficial for facilitating communication among individuals with speaking difficulties, offering them an effective alternative means of expression.

Fig. 7 Sensor application for body joint movement and detection of fatigued driving. (a) Sensor response to 0°, 45°, and 90° bending of the wrist joint. The inset displays the wrist in 0°, 45°, and 90° bending positions. (b) Sensor response to 0°, 45°, and 90° bending of the knee. The inset shows the leg in 0°, 45°, and 90° bending positions. (c) Integration of the five sensors into a glove. The left panel demonstrates the recognition of “OK,” “Yeah,” and “Thumb up” gestures by the integrated glove. The inset on the right shows these three hand gestures. (d) Application of the sensor's output signal combined with machine learning algorithms for the detection of fatigued driving.

Our sensor technology can discover new applications by integrating with emerging technologies such as machine learning. One compelling example we demonstrated is monitoring the driver's status by placing three sensors at the back of the driver's neck. As shown in Fig. 7d, these sensors monitored subtle neck movements in six individuals, collecting a substantial dataset of 859 labeled data points. The data were normalized for two simulated states: normal driving and fatigued driving. This dataset was analyzed using a fully connected feed-forward neural network implemented in MATLAB. The network utilized a logistic sigmoid activation function and a softmax output layer for binary classification, optimized iteratively using a scaled conjugate gradient method. The network architecture included two hidden layers with 25 and 20 neurons each. To enhance efficiency, graphical output was omitted during the model's training phase. The effectiveness of the model was validated using a confusion matrix, which demonstrated its ability to differentiate between non-fatigued and fatigued driving states with 100% accuracy based on the sensor data. This result confirms the robust functionality of the sensors in real-world applications, particularly in safety-critical scenarios such as driver fatigue detection.

Conclusions

In this study, we present a novel resistive strain sensor that features high sensitivity, an ultra-low detection limit, excellent linearity, and robustness against off-axis deformation. This is achieved through a design incorporating conductive serpentine cutting curves encapsulated by pre-stretched thin films. Extensive tests were conducted to evaluate the effects of the serpentine curve's pitch and width on sensor performance, identifying the optimal parameters to ensure the desired sensitivity and strain sensing range. Our innovative design achieves a high gauge factor of 495, exceptional linearity (R² > 0.98), and an ultra-low detection threshold of 0.01% strain. Additionally, the sensor maintains performance integrity during off-axis deformations such as bending and twisting, which is crucial for accurately monitoring human motion. The sensor also demonstrates robustness against environmental challenges such as salt spray, UV exposure, and varying humidity and temperature conditions. This strain sensor is effective for monitoring a range of biosignals, including wrist pulse and joint movements. By integrating our sensors with emerging machine learning technology, we conducted an experiment where sensors were placed on a driver's neck to monitor movements indicative of fatigue. The sensor output was analyzed using machine learning algorithms, successfully identifying signs of driver fatigue. It underscores the sensor's great potential in diverse fields, including personal health monitoring, human-machine interface design, and robotic sensing systems. Our sensor technology not only provides high-performance monitoring but also offers significant improvements in reliability and versatility for real-world applications.

Experimental section

Materials

The thermoplastic polyurethane (TPU) tape was supplied by Kangkejian Biotechnology Co., Ltd, based in Guangzhou, China. The conductive TPU 3D printing filament was obtained from Yousu 3D Technology Co., Ltd, also located in Guangzhou, China. The 3M 1181 conductive copper foil tape was provided by Bagui Construction Engineering Co., Ltd, situated in Jiangsu, China. Additionally, the conductive silver paste was procured from Weixiao Electronics Trading Co., Ltd, Shenzhen, China.

Preparation of sensors

This study utilized 3D printing and thermoforming techniques to produce conductive thermoplastic polyurethane films. These films were subsequently laser-cut into serpentine patterns using a pre-cracking approach. Lastly, the serpentine conductive TPU patterns were encapsulated within pre-stretched TPU films. Initially, the conductive TPU films were fabricated through 3D printing, incorporating carbon black as a conductive filler within the printing filament. These pre-fabricated films were designed to meet specific dimensional criteria, with detailed information provided in Fig. S1 (ESI†). Following 3D printing, the films underwent a hot-pressing process using a flat vulcanizing machine set to a temperature of 210 °C for both the upper and lower plates. The resulting conductive TPU thin films with a thickness of 200 μm were then cut into serpentine patterns using a laser cutter, which was operated under 18% power, 50 mm s⁻¹ speed, and a 100 μm head processing width. The cutting file, generated via CAD software, represented adjacent traces in the curved sections with a single line to minimize the distance between them. The specifications for the serpentine curves were as follows: under the same width w = 15 mm, pitches of 0.5 mm, 1 mm, 2 mm, and a total length of 25 mm, under the same pitch p = 1 mm, widths of 5 mm, 15 mm, 30 mm, and a total length of 25 mm. The designs included rectangular contact electrodes at both ends, each measuring 9 mm by 5 mm, intended for electrical connections using conductive copper foil. More details for the serpentine patterns are given in the ESI.† Post cutting, the serpentine curves were thoroughly cleaned to remove dust and impurities through ultrasonic cleaning, followed by drying. These prepared curves were placed onto a 20 mm wide, 200 μm thick TPU film, which was pre-stretched by 21.5% for the serpentine curve with p = 0.5 mm, 19.8% for p = 1 mm, and 16.3% for p = 2 mm. This assembly was secured using mechanical clamping and connected using acrylic pressure-sensitive adhesive. Conductive silver paste was applied to the contact electrodes, and conductive copper foil was then attached. A second TPU film, matching the first in pre-strain and adhesive application, covered the curves to complete the encapsulation. The pre-strain was released to facilitate electrical connectivity across the serpentine patterns. Finally, the sensor was placed in an oven at 80 °C to cure the conductive silver paste. Aluminium plates were used to clamp both sides of the sensor, ensuring it remained flat and did not bend or deform during the heating process.

Characterization

The samples were stretched utilizing a universal testing machine (SL-018MD, Shenyang Sihongda Technology Co., Ltd) under ambient conditions. The resistance of the sensor was measured using an LCR digital bridge (TH2829, Changzhou Tonghui Electronics Co., Ltd) in conjunction with a FLUKE 2638A data acquisition system. A humidity chamber with temperature control (MW3030, Guangzhou Gaohua Instrument Equipment Co., Ltd) was employed for the humidity testing of strain sensors under different temperature conditions. Ultraviolet exposure testing was performed in an ultraviolet test chamber (JY-UV-225L, Dongguan Huatai Machinery Co., Ltd), and a salt spray test chamber (HT-Y-60, Dongguan Huatai Machinery Co., Ltd) was used for the salt spray tests. The ultraviolet test chamber has six 40 W ultraviolet lamps, and the sensor is placed 0.5 m away from the center of the lamp. Salt spray test was performed at 20 °C using a 5% NaCl solution. The pH was maintained between 6.5 and 7.2, and salt spray was intermittently deposited at a rate of 1–3 mL 80 cm⁻² h. The hot-press moulding process was conducted using a flat vulcanization press (YF-8017, Yangzhou Yuanfeng Testing Equipment Co., Ltd), and laser cutting was carried out using a laser cutting machine (SF960, Jinan Senfeng Technology Co., Ltd).

Ethical statement

All subjects gave their informed consent for inclusion before they participated in the study. The study was conducted in accordance with the Declaration of Helsinki and ethical approval was not sought as the experiments involved low-risk procedures and did not involve any personal information.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (52173077), the Liaoning Provincial Department of Education Series Project (LJKZ0187), the Natural Science Foundation of Liaoning Province (2023-MS-239), and the Liaoning Bai Qian Wan Talents Program (2021921081).

References

1. W. Gao, H. Ota, D. Kiriya, K. Takei and A. Javey, Acc. Chem. Res., 2019, 52, 523–533.
2. S. Chen, J. Qi, S. Fan, Z. Qiao, J. C. Yeo and C. T. Lim, Adv. Healthcare Mater., 2021, 10, 2100116.
3. K. Xu, Y. Lu and K. Takei, Adv. Mater. Technol., 2019, 4, 1800628.
4. Y. H. Kwak, W. Kim, K. B. Park, K. Kim and S. Seo, Biosens. Bioelectron., 2017, 94, 250–255.
5. Y. Yuan, B. Liu, H. Li, M. Li, Y. Song, R. Wang, T. Wang and H. Zhang, Biosensors, 2022, 12, 1069.
6. Y. Khan, A. E. Ostfeld, C. M. Lochner, A. Pierre and A. C. Arias, Adv. Mater., 2016, 28, 4373–4395.
7. Y. Yamamoto, S. Harada, D. Yamamoto, W. Honda, T. Arie, S. Akita and K. Takei, Sci. Adv., 2016, 2, 1601473.
8. K. Takei, W. Honda, S. Harada, T. Arie and S. Akita, Adv. Healthcare Mater., 2014, 4, 487–500.
9. L. Han, J. Ding, S. Wang, J. Xu, N. Yuan, G. Cheng and Z. Liu, Sci. China: Technol. Sci., 2018, 61, 1137–1143.
10. S. Li, H. Zhao and R. F. Shepherd, MRS Bull., 2017, 42, 138–142.
11. Y. Zhang, J. Yang, X. Hou, G. Li, L. Wang, N. Bai, M. Cai, L. Zhao, Y. Wang, J. Zhang, K. Chen, X. Wu, C. Yang, Y. Dai, Z. Zhang and C. F. Guo, Nat. Commun., 2022, 13, 1317.
12. L.-Y. Zhou, Q. Gao, J.-F. Zhan, C.-Q. Xie, J.-Z. Fu and Y. He, ACS Appl. Mater. Interfaces, 2018, 10, 23208–23217.
13. G. A. Salvatore, J. Sülzle, F. Dalla Valle, G. Cantarella, F. Robotti, P. Jokic, S. Knobelspies, A. Daus, L. Büthe, L. Petti, N. Kirchgessner, R. Hopf, M. Magno and G. Tröster, Adv. Funct. Mater., 2017, 27, 1702390.
14. J. Mao, P. Zhou, X. Wang, H. Yao, L. Liang, Y. Zhao, J. Zhang, D. Ban and H. Zheng, Nano Energy, 2023, 118, 108984.
15. Q. Shi, B. Dong, T. He, Z. Sun, J. Zhu, Z. Zhang and C. Lee, InfoMat, 2020, 2, 1131–1162.
16. Y. Yang, X. Guo, M. Zhu, Z. Sun, Z. Zhang, T. He and C. Lee, Adv. Energy Mater., 2022, 13, 2203040.
17. L. Duan, D. R. D'Hooge and L. Cardon, Prog. Mater. Sci., 2020, 114, 100617.
18. M. Zhang, C. Wang, H. Wang, M. Jian, X. Hao and Y. Zhang, Adv. Funct. Mater., 2016, 27, 1604795.
19. J. Chen, J. Zhang, Z. Luo, J. Zhang, L. Li, Y. Su, X. Gao, Y. Li, W. Tang, C. Cao, Q. Liu, L. Wang and H. Li, ACS Appl. Mater. Interfaces, 2020, 12, 22200–22211.
20. T. Yamada, Y. Hayamizu, Y. Yamamoto, Y. Yomogida, A. Izadi-Najafabadi, D. N. Futaba and K. Hata, Nat. Nanotechnol., 2011, 6, 296–301.
21. Y. Mengüç, Y.-L. Park, H. Pei, D. Vogt, P. M. Aubin, E. Winchell, L. Fluke, L. Stirling, R. J. Wood and C. J. Walsh, Int. J. Robot. Res., 2014, 33, 1748–1764.
22. S. Seyedin, P. Zhang, M. Naebe, S. Qin, J. Chen, X. Wang and J. M. Razal, Mater. Horiz., 2019, 6, 219–249.
23. S. Wu, K. Moody, A. Kollipara and Y. Zhu, ACS Appl. Mater. Interfaces, 2022, 15, 1798–1807.
24. D. Wang, X. Li, H. Tian, X. Chen, B. Nie, Y. Luo and J. Shao, Appl. Mater. Today, 2021, 25, 101247.
25. S. Peng, S. Wu, Y. Yu, Z. Sha, G. Li, T. T. Hoang, M. T. Thai, T. N. Do, D. Chu and C. H. Wang, J. Mater. Chem. A, 2021, 9, 26788–26799.
26. S. Peng, S. Wu, Y. Yu, P. Blanloeuil and C. H. Wang, J. Mater. Chem. A, 2020, 8, 20531–20542.
27. S. Wu, S. Peng, Z. J. Han, H. Zhu and C. H. Wang, ACS Appl. Mater. Interfaces, 2018, 10, 36312–36322.
28. S. Mousavi, M. T. Thai, M. Amjadi, D. Howard, S. Peng, T. N. Do and C. H. Wang, J. Mater. Chem. A, 2022, 10, 13673–13684.
29. Z. Sun, S. Yang, P. Zhao, J. Zhang, Y. Yang, X. Ye, X. Zhao, N. Cui, Y. Tong, Y. Liu, X. Chen and Q. Tang, ACS Appl. Mater. Interfaces, 2020, 12, 13287–13295.
30. H. Sun, X. Fang, Z. Fang, L. Zhao, B. Tian, P. Verma, R. Maeda and Z. Jiang, Microsyst. Nanoeng., 2022, 8, 111.
31. S. Li, G. Liu, R. Li, Q. Li, Y. Zhao, M. Huang, M. Zhang, S. Yin, Y. Zhou, H. Tang, L. Wang, G. Fang and Y. Su, ACS Nano, 2021, 16, 541–553.
32. J. Zhou, X. Guo, Z. Xu, Q. Wu, J. Chen, J. Wu, Y. Dai, L. Qu and Z. Huang, Compos. Sci. Technol., 2020, 197, 108215.
33. H. Xu, W. Zheng, Y. Wang, D. Xu, N. Zhao, Y. Qin, Y. Yuan, Z. Fan, X. Nan, Q. Duan, W. Wang, Y. Lu and L. Gao, Nano Energy, 2022, 99, 107384.
34. Z. Yan, T. Pan, D. Wang, J. Li, L. Jin, L. Huang, J. Jiang, Z. Qi, H. Zhang, M. Gao, W. Yang and Y. Lin, ACS Appl. Mater. Interfaces, 2019, 11, 12261–12271.
35. Y. Yang, Z. Cao, P. He, L. Shi, G. Ding, R. Wang and J. Sun, Nano Energy, 2019, 66, 104134.
36. R. Li, X. Gou, C. H. Lee, H. Ruan, X. Wang, Z. Zhou, X. Huang, Z. Liu and P.-A. Yang, Sens. Actuators, A, 2023, 353, 114211.
37. X. Guo, Y. Zhao, X. Xu, D. Chen, X. Zhang, G. Yang, W. Qiao, R. Feng, X. Zhang, J. Wu, Z. Duan, H. Zhang, L. Huang, C. Xu and L. Qu, Compos. Sci. Technol., 2021, 213, 108908.
38. Q. Xia, S. Wang, W. Zhai, C. Shao, L. Xu, D. Yan, N. Yang, K. Dai, C. Liu and C. Shen, Compos. Commun., 2021, 26, 100809.
39. H.-J. Kim, A. Thukral and C. Yu, ACS Appl. Mater. Interfaces, 2018, 10, 5000–5006.
40. T. Wang, Z. Qiu, H. Li, H. Lu, Y. Gu, S. Zhu, G. S. Liu and B. R. Yang, Small, 2023, 19, 2304033.
41. Z. Li, X. Qi, L. Xu, H. Lu, W. Wang, X. Jin, Z. I. Md, Y. Zhu, Y. Fu, Q. Ni and Y. Dong, ACS Appl. Mater. Interfaces, 2020, 12, 42179–42192.
42. R. Nur, N. Matsuhisa, Z. Jiang, M. O. G. Nayeem, T. Yokota and T. Someya, Nano Lett., 2018, 18, 5610–5617.
43. J. Oh, J. C. Yang, J.-O. Kim, H. Park, S. Y. Kwon, S. Lee, J. Y. Sim, H. W. Oh, J. Kim and S. Park, ACS Nano, 2018, 12, 7546–7553.
44. C. Yan, J. Wang, W. Kang, M. Cui, X. Wang, C. Y. Foo, K. J. Chee and P. S. Lee, Adv. Mater., 2013, 26, 2022–2027.
45. G. Lee, G. Y. Bae, J. H. Son, S. Lee, S. W. Kim, D. Kim, S. G. Lee and K. Cho, Adv. Sci., 2020, 7, 2001184.
46. Z. Liu, Y. Zheng, L. Jin, K. Chen, H. Zhai, Q. Huang, Z. Chen, Y. Yi, M. Umar, L. Xu, G. Li, Q. Song, P. Yue, Y. Li and Z. Zheng, Adv. Funct. Mater., 2021, 31, 2007622.
47. Y. Wang, F. Wang, S. Yazigi, D. Zhang, X. Gui, Y. Qi, J. Zhong and L. Sun, Carbon, 2021, 173, 849–856.
48. H. Wei, D. Kong, T. Li, Q. Xue, S. Wang, D. Cui, Y. Huang, L. Wang, S. Hu, T. Wan and G. Yang, ACS Sens., 2021, 6, 2938–2951.
49. J. Wang, C. Zhang, D. Chen, M. Sun, N. Liang, Q. Cheng, Y. Ji, H. Gao, Z. Guo, Y. Li, D. Sun, Q. Li and H. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 51854–51863.
50. J. Zhao, C. He, R. Yang, Z. Shi, M. Cheng, W. Yang, G. Xie, D. Wang, D. Shi and G. Zhang, Appl. Phys. Lett., 2012, 101, 063112.
51. X. Wang, X. Liu and D. W. Schubert, Nano-Micro Lett., 2021, 13, 64.
52. I. Bozyel, Y. I. Keser and D. Gokcen, Sens. Actuators, A, 2021, 332, 113056.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01136h

‡ These authors contributed equally to this work.

---