Demonstration of a novel majority logic in a memristive crossbar array for in-memory parallel computing

Abstract

A memristive crossbar array can execute Boolean logic operations directly within the memory, which is highly noteworthy as it addresses the data bottleneck issue in traditional von Neumann computing. Although its potential has been widely demonstrated, achieving practical levels of operational reliability and computational efficiency remains a challenge. Here, we introduce a three-input majority logic gate supported by near-memory operations, serving as a universal gate and achieving both robust reliability and high efficiency in versatile logic operations. We fabricated a highly reliable HfO_x-based memristive array, incorporating a series resistor to increase the reset voltage of the memristor, thereby increasing the operational voltage margin of the gate operation. This ensured reliable operation of the majority gate, resulting in successful experimental proof of combined 1-bit full adder and subtractor operations performed in 5 steps using 7 cells. Additionally, we propose that an N-bit parallel prefix adder (PPA) operation is possible in O(log₂ N) steps, by taking advantage of the parallel operation capability of the majority gate. This achieves 8.5× higher spatiotemporal efficiency than the previously reported NOR-based logic system in 64-bit adder operation. Moreover, as N increases, the spatiotemporal efficiency further improves, which significantly enhances the applicability of memristive logic-in-memory.

---

New concepts

The practical implementation of memristive logic-in memory (LIM) technology in a crossbar array (CBA) is still challenging since there is no optimal solution that can achieve the highest computational efficiency while overcoming the memristor's intrinsic switching voltage variations. In this study, we present a comprehensive understanding of the conditions under which a logic gate can be both reliable and efficient at the same time, which has not been studied before. We fabricated a reset voltage-modulated memristor to ensure sufficient voltage margin, achieving the reliability of logic operation. Then, we designed a 3-input majority (MAJ) logic with a near-memory approach. The spatiotemporal efficiency was increased 4.5 times in a 1-bit full adder and 8.5 times in a 64-bit parallel prefix adder compared to the 2-input NOR logic system. The results highlight the capability of parallel operation of our MAJ logic and the strength of effective utilization of near memory circuits. This study proposes a completely new approach and overcomes the limitations of conventional LIM techniques. It is expected that our approach will generate further new ideas and studies in the future.

Introduction

The demand for low-power and energy-efficient Boolean logic-in-memory (LIM) computing continues to rise, aiming to overcome the data bottleneck challenges associated with traditional von Neumann computing architecture.^1–3 A fundamental solution to the data bottleneck problem lies in performing computations directly within the memory.^4–6 In this regard, a two-terminal memristive crossbar array (CBA) is noticeable.⁷ In the CBA, memory cells directly share bit lines (BLs) or word lines (WLs). Therefore, when multiple memory cells are accessed simultaneously and voltage is applied to the BLs and WLs of the cells, the voltage distribution varies depending on the state of the memory cells through a voltage divider effect. By utilizing this, the switching of one or more memory cells can conditionally occur based on the state of other memory cells and applied voltage combinations, enabling the execution of various gate operations between the memory cells (i.e., LIM).^8–23 In this approach, the output of the logic operation is directly stored in the memory cell, which is referred to as the stateful logic.

Since the first stateful logic via material implication was proposed in 2010 by Borghetti et al.,¹¹ many studies have demonstrated various methods to implement various logic gates, highlighting the importance of LIM in the CBA and its widespread interest. In the early stages of studies, the focus was on finding ‘effective’ new gates leading to improved computational efficiency. Notably, Sun et al. reached a pinnacle by proposing the Carry gate (utilizing three input cells and one output cell) and the Sum gate (utilizing four input cells and one output cell).¹⁵ However, these seemingly effective gates assumed constant switching voltages, i.e., ideal operation of memristors, leading to consensus on their limitations in practical applications, where the switching voltage variations are inevitable. As a result, subsequent research on memristive LIM has primarily focused on ensuring operational reliability while satisfying improved computational efficiency.

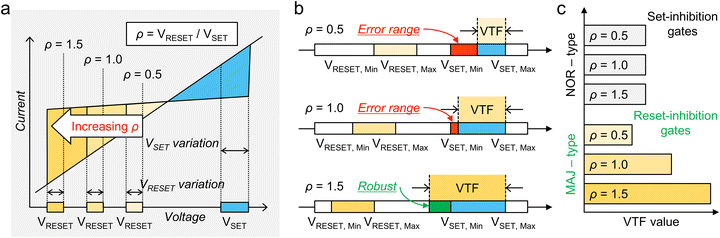
The operational reliability of the given logic gate can be quantified by the variation tolerance factor (VTF).¹⁴ This refers to the acceptable maximum switching voltage variation, which always guarantees a correct gate operation. Most logic operations have been implemented through conditional set switching; therefore, the VTF can refer to an acceptable set voltage (V_SET) variation. The VTF strongly depends on the ratio of the maximum set voltage and the maximum reset voltage (ρ = |V_RESET,Max/V_SET,Max|); the higher the ρ value, the higher the VTF. Meanwhile, the set voltage variation (Δ_SET) is defined as (V_SET,Max − V_SET,Min)/V_SET,Max. In this context, variation-tolerant gate operation means that VTF is larger than Δ_SET. Therefore, decreasing V_RESET,Max is an effective method for achieving a high VTF and variation-tolerant gate operation. The detailed explanation and calculation process of the VTF value of various logic gates can be found in Supplementary Note 1 in the ESI.†

Meanwhile, logic gates can be classified into two types: set-inhibition gates and reset-inhibition gates. The set-inhibition gates, including NOR and NOT gates, require inhibition cells to suppress set switching as they are subjected to experience a high voltage drop during gate operation. These gates have a constant VTF regardless of the reset switching behavior. In this context, it is worth emphasizing the study previously published by Kim et al.¹⁴ In the study, the authors suggested that NOR, NOT, and BUFFER gates (namely, NOR-based logic systems) theoretically have the highest VTF of 0.333, enabling the implementation of the most robust LIM. Using these gates, a 1-bit full adder operation could be executed in 12 steps over 13 cells only using those gates. This can serve as a benchmark, and further research is required to explore more efficient methods.

Unlike set-inhibition gates, reset-inhibition gates, such as the AND gate, have the VTF that depends on the reset switching voltages; as the reset voltage (V_RESET) increases, the VTF increases. Fig. 1a represents three examples of typical bipolar resistive switching curves with a V_RESET to V_SET ratio (ρ) of 0.5, 1.0, and 1.5. The set and reset voltage ranges are indicated as blue and yellow boxes, respectively. Fig. 1b conceptually illustrates the VTF for the three cases. In the reset-inhibition gates, as ρ increases (i.e., as V_RESET decreases), the VTF increases. When ρ = 0.5 or 1.0, the VTF is not enough to cover the full range of the V_SET distribution, meaning that there is a chance of gate operation error. Whereas when ρ = 1.5, error-free gate operation is guaranteed.

Fig. 1 The robustness of stateful logic operations with increasing reset voltage. (a) A representation of typical bipolar I–V curves with three different reset voltage to set voltage ratios (ρ). The variations in set and reset voltages are indicated as blue and yellow boxes, respectively. (b) An illustration of robustness (VTF) dependency for the three ρ cases. (c) The VTF change tendency of set-inhibition and reset-inhibition gates with three different ρ values.

Fig. 1c compares the VTF dependency between set-inhibition and reset-inhibition gates with respect to ρ. Here, when ρ increases, the reset-inhibition gates can be more practically viable, as the VTF is higher than the V_SET ranges. (A comparison of the VTF value of other logic gates with different ρ values is summarized in Fig. S1 in the ESI.†) Consequently, reset-inhibition gates can achieve higher robustness as ρ is tuned to higher levels. However, few studies have demonstrated this approach of concurrently tuning the memristive device and developing the gating strategy.

In this study, we propose a memristive majority (MAJ) gate for the first time, which achieves the highest computational efficiency among the memristive LIM technologies under the robustness-ensured condition. The proposed MAJ gate is a three-input logic gate whose output is identical to the carry-out bit, generating output ‘1’ only if more than two inputs are ‘1’.^24,25 The MAJ gate requires near-memory circuits to supply one input in the form of a voltage. While this requires some additional cost, it may offer a more effective way than the cost, which will be systematically demonstrated later.²⁰ The MAJ gate falls into the reset-inhibition gates. Therefore, to experimentally validate the efficiency of the MAJ gate, we developed a HfO_x-based memristor array with an increased V_RESET (giving V_RESET/V_SET = 1.21), which achieved the VTF of 0.4, which is the highest VTF ever reported. More discussion on the superiority of the HfO_x-based memristor compared to other memristors can be found in Supplementary Note 2 in the ESI.† Moreover, the MAJ gate allowed us to execute a combined 1-bit full adder and full subtractor using 7 memristors in 5 steps, resulting in a 4.5× increase in spatiotemporal efficiency compared to the benchmarking NOR-based logic system. Furthermore, we applied our MAJ-based logic system to the N-bit parallel-prefix adder (PPA) and demonstrated the required number of steps of O(log₂ N), achieving 8.5× the spatiotemporal efficiency in 64-bit adder addition compared to the benchmarking. This remarkably increased efficiency can be explained by extremely low data manipulation steps and parallel operation of the MAJ gate, which will be further discussed later. The efficiency increases as the bit size increases, highlighting its strong potential for large-scale and energy-efficient Boolean computing.

Results and discussion

Majority gate demonstration in a reset voltage-modulated HfO_x-based memristor array

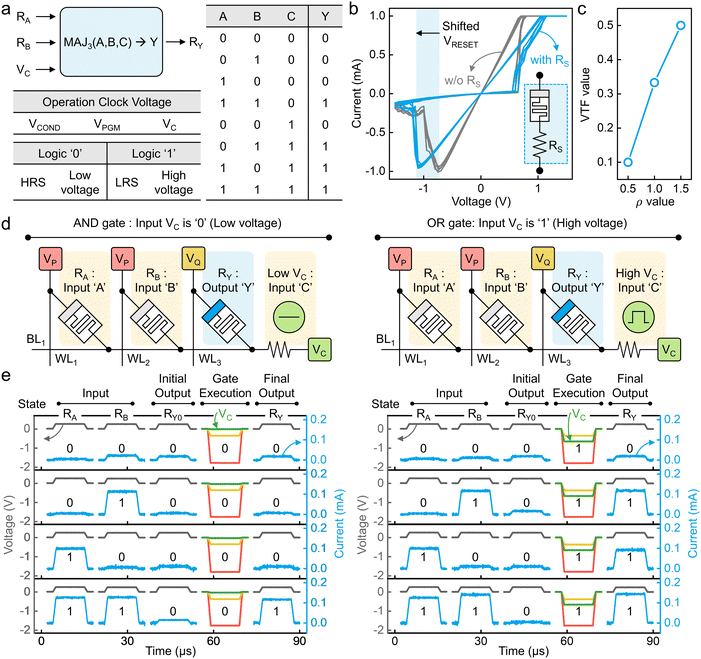
Here, we demonstrate the majority (MAJ) gate operation in a memristive CBA. The MAJ gate is a three-input gate, where two inputs are in the form of resistance states, and the third input is in the form of an input voltage. Therefore, the MAJ gate falls under the near-memory computing category, as near-memory circuitry is required to apply the third input as a voltage. Despite the near-memory circuitry burdens, it offers significant performance advantages enough to outweigh them. Fig. 2a shows a schematic expression of the MAJ gate and its truth table. We denote the MAJ operation as MAJ₃(a, b, c) → y, where a, b, and c are inputs, and y is an output which is logically defined as ab + bc + ca. Here, the two inputs a and b are provided in the form of resistance states, so the two inputs can be denoted as R_A and R_B, where the A and B are two input cells. In them, the HRS (high resistance state) and the LRS (low resistance state) define a logical value of ‘0’ and ‘1’, respectively. Similarly, the third input c is in a voltage form, so it can be denoted as V_C, where a high voltage defines ‘1’ while a ground voltage defines ‘0’. Also, the output is programmed to y as a resistance state, so the output is denoted as R_Y. This gives a logical expression, MAJ₃(R_A, R_B, V_C) → R_Y. The operation clock voltages of the MAJ gate are V_COND (a voltage lower than the set switching voltage but high enough to influence the bit line potential) to the two input WLs, V_PGM (a voltage higher than the set switching voltage) to the output WL, and V_C to the shared BL. The values of them are related to the device's behavior, so they will be discussed later after the device is shown.

Fig. 2 Experimental demonstration of the majority (MAJ) logic gate with an intrinsic series resistor integrated memristors. (a) A schematic of the MAJ gate and its truth table. Logic input ‘0’ is defined as HRS or low voltage, and logic ‘1’ is defined as LRS or high voltage. (b) Comparison of I–V curves between a device with R_S (blue lines) and without R_S (gray lines). (c) The VTF values of the MAJ gate under different ρ values. (d) Schematic circuit configurations of a 3 × 1 array and the operation voltages (V_P, V_Q, and V_C) are represented. The MAJ gate can be divided into two gates, AND (left panel) when C = 0 (i.e., V_C = low voltage) and OR gate (right panel), when C = 1 (i.e., V_C = high voltage) depending on the value of V_C. (e) Experimental demonstration results of the MAJ gate. The left panels correspond to AND C = 0 so V_C = 0 V and the right panels to OR gate when C = 1 so V_C = −0.65 V. Initial (R_A, R_B, and R_Y0) and final (R_Y) states are read before and after the gate operation. At the gate execution phase, the red and yellow pulses represent V_P and V_Q, respectively, and the green pulse represents the third input, V_C.

We demonstrated the MAJ gate operation on a memristive CBA. Here, we designed a series resistor (R_S) incorporated CBA. The incorporated R_S plays a crucial role for two key reasons. Firstly, it ensures the switching endurance of memristor cells. The R_S establishes a self-limited switching configuration during set switching, thereby reducing the chance of over-setting and enhancing cyclic reliability.^26,27 Additionally, the R_S acts as a voltage divider in the LRS, decreasing the V_RESET while not affecting the V_SET.²⁸ This decreased V_RESET reduces the probability of unintended reset switching during logic operations, thereby ensuring a sufficient operational voltage margin.

To harness these advantages, we fabricated a Ta/HfO₂/Pt memristor array in which the R_S was carefully controlled. An optical microscope image of the R_S-controlled array and a TEM image of the HfO_x memristor can be found in Fig. S2 in the ESI.† The array was designed to precisely control the line resistance working as the R_S. In the array, the wire part of the top Ta electrode had a resistance of ∼200 Ω. The bottom Pt electrode was designed with a diamond-shaped bridge structure to minimize the wire resistance. As a result, the Pt wire resistance was ∼50 Ω for the cell closest to the contact pad and ∼150 Ω for the cell farthest from the pad. Consequently, the cells in the array had the R_S in the range of 250 to 350 Ω. Note that this level of the R_S variation does not significantly affect the switching characteristics of the device (see Supplementary Note 3 in the ESI,† for a more detailed discussion on the R_S variation on the gate operation). The HfO₂-based memristor has been widely investigated for its high endurance and stable retention properties.^29–31 More detailed device fabrication procedures can be found in the Experimental section.

Fig. 2b shows the comparison of I–V curves of two devices, one with 300 Ω of R_S (blue lines) and the other one without the R_S (gray lines), for comparing the V_RESET change by the R_S. After including the R_S due to the voltage divider effect, the average value of V_RESET was changed from −0.85 V to −1.2 V, while V_SET was unchanged, resulting in an increase in their ratio (ρ = |V_RESET,Max/V_SET,Max|) from 0.9 to 1.21 (see Supplementary Note 4 in the ESI,† for a more detailed explanation regarding the difference in the voltage divider effect during set and reset switching). The coefficient of variation (σ/μ) was 7.8% for V_SET and 3.6% for V_RESET. (The raw I–V curves for 50 switching cycles, and their V_SET and V_RESET distribution, can be found in Fig. S3 in the ESI.†) Notably, the device exhibited a self-limited switching behavior, where set-switching no longer progresses beyond a certain current level. This occurs due to the presence of a series resistance component, even without applying compliance current, ensuring the device's endurance and retention reliability.²⁶ Consequently, the device shows robust endurance up to 10⁶ cycles (data shown in Fig. S4 in the ESI†), stable results up to 10⁴ seconds at room temperature (data shown in Fig. S5 in the ESI†), and excellent device-to-device uniformity in the array (uniformity results shown in Fig. S6 in the ESI†). The main reason for incorporating the R_S is to increase the VTF. The VTF is defined as an allowable maximum Δ_SET, where Δ_SET = (V_SET,Max − V_SET,Min)/V_SET,Max. Fig. 2c shows the VTF of the MAJ under different ρ values. After incorporating the R_S, the ρ was increased from 0.9 to 1.21, and consequently, the VTF was increased from 0.3 to 0.4. Considering the Δ_SET in our device was 0.28, measured from Fig. S3 in the ESI,† the MAJ gate operation can be error-free with more room for accepting additional variations, such as those that may originate from device-to-device differences.

Fig. 2d shows the basic unit of the MAJ gate, comprising a 3 × 1 array configuration. Note that our MAJ gate operation can be divided into AND gate (when the input C = 0) and OR gate (when the input C = 1) depending on the value of V_C. The optimum MAJ gate operation voltages are V_COND = −1.8 V, V_PGM = −0.35 V, and V_C = −0.65 V (for C = 1) or 0 V (for C = 0). Here, we denoted the V_COND and V_PGM as V_P and V_Q, respectively. (A detailed operating voltage calculation process for the BUFFER, NOT, and MAJ gates can be found in Fig. S7–S9 in the ESI.†) Fig. 2e shows the successfully demonstrated MAJ gate operation results from the prepared array for all of the eight (3-bit) input conditions. The left panel shows the results for four input conditions when C = 0 so V_C = 0 V, which is identical to the AND gate. The right panel shows the results for another four input conditions when C = 1 so V_C = −0.65 V, identical to the OR gate. Here, the initial states of R_A, R_B, and R_Y0 and the final state of R_Y (blue line) were read at 0.25 V (gray line). The final states of R_A and R_B are not shown but their values remain unchanged after the gate execution. After reading the initial states, MAJ gate operations were executed by applying the operating voltages of V_C (0 V when C = 0 and −0.65 V when C = 1, green line), V_P (−1.8 V, red line), and V_Q (−0.35 V, yellow line). The pulse rising time, width, and falling time were 1 μs, 10 μs, and 1 μs, respectively.

The MAJ gate by itself is not functionally complete, meaning its cascading cannot produce all Boolean logic. But it can be completed with a NOT gate.³² In addition, we demonstrated the BUFFER gate to manipulate data location. (Experimental demonstration of the NOT gate can be found in Fig. S10 in the ESI,† and the BUFFER gate in Fig. S11 in the ESI.†) The VTF of NOT and BUFFER gates are 0.333 and 0.877, respectively, which are larger than the value of 0.28 for the Δ_SET. Therefore, they are also practically viable gates with our device.

Experimental demonstration of a combined 1-bit full adder and full subtractor

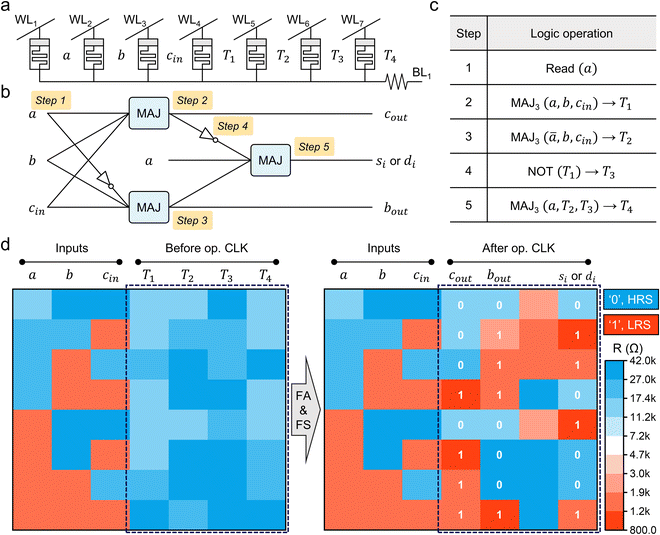
The arithmetic logic unit (ALU) is a core component of the central processing unit (CPU). The ALU includes multiple arithmetic logic gates and selectively performs one of them per the request of the control unit. To achieve its functionality, the ALU inevitably comprises complex circuitry. However, in the memristive logic system, various operations can be implemented through controlling voltage sequences, enabling the replication of ALU operations in a much simpler structure. The MAJ gate system is highly effective in constructing the memristive ALU as it allows for simultaneous generation of carry-out (c_out) and borrow-out (b_out) bits, which are essential for adder and subtractor operations. Fig. 3a shows the circuit configuration comprising 7 memristors sharing the BL used to experimentally demonstrate a combined 1-bit full adder (FA) and full subtractor (FS) (see Fig. S12 in the ESI,† for their truth tables).³³ We used the integrated device (shown in Fig. S2 in the ESI†) for this demonstration. Fig. 3b shows the logic diagram of the operation. Fig. 3c shows a detailed operation procedure. Before starting the operation, we assumed that a, b, and c_in cells store the three inputs, and T₁ to T₄ cells are initialized to 0 (HRS).

Fig. 3 Experimental demonstration of a combined 1-bit full adder (FA) and full subtractor (FS). A circuit configuration of 7 × 1 array (a) and logic diagram (b) of a combined 1-bit FA and FS. (c) 5-steps of the operation procedure. (d) Experimental demonstration of a combined 1-bit FA and FS operation for all input conditions. The first three cells from the left are input cells, and the other four are output cells. Carry-out and borrow-out are stored in the fourth and fifth cells, respectively. The sum (or difference) bit is stored in the seventh cell.

Additionally, a resistance-to-voltage converter (RVC) circuit is required in the peripheral area. This RVC circuit, consisting of a comparator, D flip-flop, inverter, and transistors, functions to read the data from the memristor cell, temporarily store it, and then generate a voltage signal corresponding to the read data. (The RVC's full circuit design and timing diagram can be found in Fig. S13 in the ESI.† A feasible array and circuitry architecture are shown in Fig. S14 in the ESI.†) The RVC consumes negligible energy, suggesting that using the RVC does not harm the performance in terms of energy consumption (a comparison of energy consumption between the RVC circuit and the memristor is calculated in Fig. S15 in the ESI.†) More efficient use of the RVC will be discussed in the next section.

In this standby state, the first step of the logic operation is to fetch the data of a using the RVC. The RVC stores the data temporarily in its D flip-flop, which can be used multiple times during the operation. Moreover, we can use the opposite value of a (i.e., ā) from the negative output of the D flip-flop. The second step is executing the MAJ gate for calculating c_out using R_b, R_c, and V_a as inputs and T₁ as the output, giving a logical equation of MAJ₃(a, b, c_in) → T₁. The third step is executing the MAJ gate again for calculating b_out using R_b, R_c and 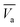as inputs and T₂ as output, giving MAJ₃(ā, b, c_in) → T₂. The fourth step is, inverting c_out using the NOT gate, NOT (T₁) → T₃. The last step is executing the MAJ gate using T₂, T₃, and V_a as inputs and T₄ as the output. MAJ₃(a, T₂, T₃) → T₄, which results in sum (= difference bit) (more detailed logical expressions for this calculation process can be found in Note 5 in the ESI†).

Fig. 3d shows the experimental results of the combined 1-bit FA and FS for all of the eight input conditions. The HRS (logical ‘0’) and LRS (logical ‘1’) are shown in blue and red colors, respectively. The first three columns (a, b, c_in) are input cells for the eight input cases, and the other four columns (T₁, T₂, T₃, and T₄) are output cells during the logic operation. In summary, both 1-bit FA and FS could be achieved in 5 steps with 7 cells, giving a spatiotemporal cost (STC) of 35. (The STC is a measure of the computational efficiency of the memristive LIM, which can be calculated by multiplying the number of required steps by the number of used cells.) Our proposed method is 4.5× more efficient than the NOR-based 1-bit FA, whose STC is 156.¹⁴ (A comprehensive specification comparison of 1-bit full adder is summarized in Table S1 in the ESI.†) Furthermore, outputs of the FS can be obtained simultaneously, which was not possible in the NOR-based logic system, making our system more feasible for the ALU.

Array-level parallel majority gate operation

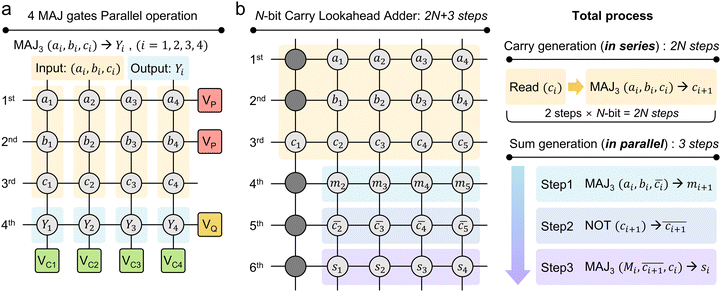
Another crucial and noticeable characteristic of the MAJ gate is its ability to perform parallel operations. This allows multiple rows to operate the gate operation simultaneously, drastically increasing temporal efficiency. Fig. 4a illustrates an example of the parallel operation in a 4 × 4 array, assigning the top three rows (1st, 2nd, and 3rd) for inputs and the fourth row (4th) for the output. In this configuration, each column represents the MAJ gate unit. The top two rows correspond to two input cells (R_A and R_B in Fig. 2d), while the third row is the third input cell whose data will be converted to the input voltage (V_C in Fig. 2d) of the corresponding BL via the RVC. So, it requires four RVC units. For the operation, first, the third row's data are fetched by the RVCs, and corresponding input voltages are applied on each BL as V_C, and the gate operation voltages, V_P and V_Q, are applied to the shared WLs of the top two rows and the fourth WL, respectively. This parallel operation is possible because the input voltage is biased only on either WL or BL, not both lines. In this way, four MAJ gate operations can be performed simultaneously in parallel across the four columns.

Fig. 4 Demonstration of array-level MAJ gate operation. (a) A block diagram of parallel operation of 4 MAJ gates. The resistance state of the c_i is converted to a voltage signal and directly applied to the bit line. 4 outputs are calculated in a single step simultaneously. (b) A block diagram of 4-bit CLA. Carry generation process operates in series, while subsequent sum generation operates in parallel. The sum generation process requires only 3 steps regardless of the number of bits (N) of an adder.

Such parallel operations can be effectively used in multi-bit adder operations. While there are various methods to implement the multi-bit adder,^34–38 we have chosen to demonstrate the carry lookahead adder (CLA) operation, which significantly utilizes parallel operations and therefore maximizes the feasibility of the MAJ gate. Fig. 4b shows the initial data map for the 4-bit CLA operation. Here, the diagram shows that four c_out bits (MAJ₃(a_i, b_i, c_i) → c_i+1, where i = 1, 2, 3, 4) are sequentially obtained via the MAJ gate. Notably, even though c_i is not aligned with a_i and b_i, the logic operation is possible without data copy operation, because the RVC can fetch the c_i from any location. Consequently, only 2 steps (data fetching and MAJ gate execution) are required to obtain a single c_out, therefore, 2N steps are required for all c_out generation during an N-bit CLA. After all of c_out are generated in series, all sum bits can be calculated in parallel using MAJ and NOT gates through the approach of Fig. 4a. It requires only three steps (step 1: MAJ₃(a_i, b_i, c_i) → m_i+1, step 2: 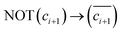, step 3: 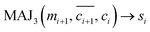) regardless of the number of bits (N), thanks to the advantage of the parallel operation. The data m_i is logically the same with the borrow-out bit (b_i) in FS operation, however, we denoted it as m_i to prevent any confusion (more detailed logic calculation process can be found in Supplementary Note 5, ESI†). In summary, with our proposed logic system, an N-bit adder operation can be achieved in 2N + 3 steps. (The entire step-by-step operation procedure of 4-bit CLA can be found in Fig. S16 in the ESI.†)

Demonstration of the parallel prefix adder

The critical limitation of the memristive stateful logic is its limited operational flexibility; the logic operation is executable only when the input data are located in the same WLs or BLs. This limitation causes a significant number of additional data copy operations, thus increasing the complexity of the total process. In the conventional LIM, this problem becomes more severe as the number of bit sizes increases. However, our MAJ gate stores part of the data externally, which significantly reduces data relocation steps and can enhance computational efficiency. Here, we demonstrate the parallel prefix adder (PPA) to showcase this advantage of the MAJ gate system.

PPA is well-known for high parallelism during its operation, calculating both c_out and sum bits in parallel.^32,39–41 In conventional N-bit adders, such as CLA, c_out are obtained sequentially (in series) so that it is the bottleneck of the entire process. However, PPA executes all operations in parallel, giving the number of required steps to follow a logarithmic function (∼log₂ N). This makes it highly efficient, particularly as the number of bits increases, compared to other conventional adders, whose number of required steps follows a linear function (∼N). In 2017, Pudi et al. proposed the circuit design of the PPA using the MAJ gate, where a recursive majority logic formula was used to maximize parallelism.⁴¹

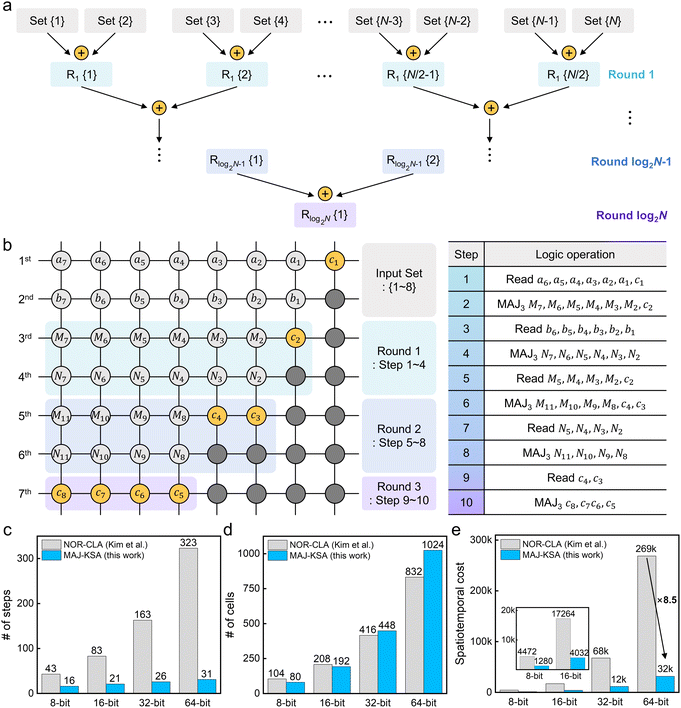
Fig. 5a illustrates the overall schematic of the c_out generation of N-bit PPA. All of the input sets are computed simultaneously in each logic round. Therefore, PPA circuits require O(log₂ N) rounds to add N-bits. While the logic steps required for each round differ in several types of PPA such as Ladner–Fischer adder (LFA),³² Kogge–Stone adder (KSA),³⁹ and Sklansky tree adder (STA),⁴⁰ the fastest one is the KSA due to greater utilization of parallel operations. This characteristic, specialized for parallel operations, makes it optimal for utilizing the MAJ gate, while the KSA has yet to be evaluated in stateful logic. The circuit diagram of the 8-bit KSA constructed solely using MAJ gates can be found in Fig. S17 in the ESI.† ⁴¹ It comprises three levels to obtain all c_out. Fig. 5b shows a data map in the array (left) and a logic operation procedure (right) for 8-bit c_out generation. In the KSA, logic operations are conducted at the round unit, where each round includes a set of parallel MAJ gate operations, and at the k-th level, 2^k−1 of c_out are obtained. Consequently, the N-bit KSA log₂ N logic rounds (i.e., 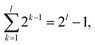where l is the final round) are used to calculate all c_out. In our logic system, 4 steps are required at each logic round except for the final round (2 steps), as shown in Fig. 5b. As a result, calculating all c_out for an N-bit KSA using the MAJ gate requires 4 log₂ N − 2 steps.

Fig. 5 Demonstration of 8-bit Kogge-Stone adder (KSA). (a) An illustration of a parallel prefix adder (PPA). PPA requires log₂N rounds to calculate all carry-out bits. (b) A block diagram and logic operation procedures of 8-bit KSA. Comparison of the required steps (c), cells (d), and spatiotemporal cost (e) for N-bit adders between CLA using the NOR gate and KSA using the MAJ gate in this work.

The next process is to relocate all c_out into a one-dimensional line to calculate sum bits in parallel, where the previously obtained c_out are stored in various rows, as shown in Fig. 5b (c₂ at the 3rd row, c₃ and c₄ at the 5th, and c₅, c₆, c₇, and c₈ at the 7th). This relocation process utilizes the BUFFER gate, which is also viable for parallel operation, and thus it requires log₂ N − 1 steps for moving the c_out from round 1 to round l − 1 to the final row. (Fig. S18 in the ESI,† shows schematically the c_out generation and relocation process of KSA.) Lastly, all sum bits are calculated in parallel within 4 steps, which is the same process as the CLA in Fig. 4b. (Fig. S19 in the ESI,† shows a step-by-step sum calculation procedure.) As a result, the total required step for an N-bit KSA operation is 5 log₂ N + 1 (i.e., 4 log₂ N − 2 + log₂ N − 1 + 4). (An 8-bit and 16-bit KSA block diagram is shown in Fig. S20 and S21 in the ESI,† respectively.)

Fig. 5c and d compare the required steps and cells, respectively, for the N-bit KSA using the MAJ gate proposed in this study and for the N-bit CLA using the NOR gate for ref. 14. Although the MAJ-based operation requires more cells as N increases, the number of steps decreases drastically, making it much more efficient. For the 64-bit adder computation, the number of required cells is 1024, which is 23% more than for the NOR-based operation, but the total required steps are 31, which is 90% less. As a result, as shown in Fig. 5e, the STC of the 64-bit adder operation using the MAJ gate is only 12% of the NOR-based one, which is an 8.5× higher spatiotemporal efficiency, suggesting its high feasibility for use in large-scale computation. Table 1 represents a comprehensive benchmarking of various memristive logic approaches for implementing N-bit adders. Meanwhile, the energy consumption using the MAJ gate is about 10% higher than using NOR-based logic. A comparison of energy consumption in 64-bit adder between the NOR-based and MAJ-based logic system can be found in Fig. S22 in the ESI.† The MAJ-based logic requires slightly more switching events compared to the NOR-based systems because it only utilizes set switching, whereas NOR-based systems use both set and reset switching to perform the same tasks. However, this difference is minor, and in logic applications that demand fast operation, the advantage of MAJ-based logic in terms of higher spatiotemporal efficiency should be emphasized.

Table 1 A comprehensive benchmarking of an N-bit adder

	Adder type	Logic state variable	Reliability ensured?	Steps (X)	Cells (Y)	8-bit adder STC (= X × Y, N = 8)
Kim et al.^14	CLA	Resistance	Yes	5N + 3	13N	4472
Cheng et al.^12	CLA	Resistance	No	6N	11N − 11	3696
Song et al.^18	CLA	Resistance & voltage	No	3N	9N − 9	1512
Ruben et al.^32	PPA (LFA)	Resistance & voltage	No	4 log2 N + 6	48N + 96	8640
This work	PPA (KSA)	Resistance & voltage	Yes	5 log2 N + 1	2N log2 N + 4N	1280

---

Conclusions

This study experimentally demonstrated a fast, robust, and energy-efficient memristive MAJ-based logic system using a novel and unique voltage bias scheme. We fabricated a reset voltage-modulated highly reliable HfO_x-based memristor array and proposed a switching voltage variation-tolerant memristive MAJ gate. The MAJ gate can operate in parallel, which can significantly enhance the spatiotemporal efficiency. We demonstrated the PPA operation and suggested it could increase computation efficiency by up to 8.5 times compared to existing technologies, based on a 64-bit adder benchmark. We have demonstrated that the utilization of near-memory circuitry, previously not considered in conventional stateful logic techniques, can be a method to overcome the limitations of existing stateful logic despite the associated increase in complexity. In this regard, this study holds significance in proposing a new approach to conventional stateful logic, and it is anticipated that new ideas will be generated in the future through such an approach.

Experimental section

Device fabrication

The Pt/Ta/HfO₂/Pt device was fabricated using the following procedure. A 100-nm Pt bottom electrode was deposited onto a 5-nm Ti (adhesion layer)/SiO₂/Si substrate by e-beam evaporation and patterned by a lift-off process. Then, a 5-nm HfO₂ resistive switching layer was deposited by thermal atomic layer deposition (ALD) using a TEMAHf precursor and O₃ as the oxidant. Finally, a 50-nm Ta top electrode followed by a 15-nm Pt contact electrode was deposited by sputtering and e-beam evaporation, respectively, and patterned by a lift-off process.

Material characterization

The cross-section image of Pt/Ta/HfO₂/Pt was acquired using a 200 kV multi EDS field emission TEM (Talos F200X G2, Thermo Fisher). The specimen was prepared using an ultra high-resolution focused ion beam (Helios G4, FEI).

Electrical characterization

All electrical measurements were performed using a semiconductor parameter analyzer (Keithley 4200A-SCS) and a probe station. The I–V characteristics were measured by a source measurement unit (SMU) in a DC sweep mode. The top electrode was biased, while the bottom electrode was ground. For the logic operation demonstrations, voltage pulses were applied and measured by a Keithley 4225-PMU (pulse measurement unit) and 4225-RPM (remote preamplifier/switch module).

Circuit simulation

The circuit simulation was performed by LTSPICE using a LM393LV model for the comparator and embedded D flip-flop and transistor models.

Author contributions

Moon Gu Choi: conceptualization, investigation, methodology, project administration, software, visualization, and writing – original draft. Jae Hyun In: software and methodology. Hanchan Song: software and methodology. Gwangmin Kim: methodology. Hakseung Rhee: methodology and visualization. Woojoon Park: visualization. Kyung Min Kim: funding acquisition, supervision, and writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the National Research Foundation of Korea (NRF) (Grant numbers: RS-2023-00216619, RS-2023-00216992, 2022M3F3A2A01076569, 2022M3I7A4085484, and 2023R1A2C2005159), and NNFC (Grant number:1711160154).

Notes and references

1. P. A. Merolla, J. V. Arthur, R. Alvarez-Icaza, A. S. Cassidy, J. Sawada, F. Akopyan, B. L. Jackson, N. Imam, C. Guo, Y. Nakamura, B. Brezzo, I. Vo, S. K. Esser, R. Appuswamy, B. Taba, A. Amir, M. D. Flickner, W. P. Risk, R. Manohar and D. S. Modha, Science, 2014, 345, 668.
2. M. M. Waldrop, Nat. News, 2016, 530, 144.
3. A. Mehonic and A. J. Kenyon, Nature, 2022, 604, 255.
4. D. Ielmini and H.-S. P. Wong, Nat. Electron, 2018, 1, 333.
5. D. S. Jeong, K. M. Kim, S. Kim, B. J. Choi and C. S. Hwang, Adv. Electron. Mater., 2016, 2, 1600090.
6. M. A. Zidan, J. P. Strachan and W. D. Lu, Nat. Electron., 2018, 1, 22.
7. D. B. Strukov, G. S. Snider, D. R. Stewart and R. S. Williams, Nature, 2008, 453, 80.
8. E. Linn, R. Rosezin, S. Tappertzhofen, U. Bottger and R. Waser, Nanotechnology, 2012, 23, 305205.
9. A. Siemon, T. Breuer, N. Aslam, S. Ferch, W. Kim, J. Van Den Hurk, V. Rana, S. Hoffmann-Eifert, R. Waser and S. Menzel, Adv. Funct. Mater., 2015, 25, 6414.
10. K. M. Kim and R. S. Williams, IEEE Trans. Circuits Syst. I: Regul. Pap, 2019, 66, 4348.
11. J. Borghetti, G. S. Snider, P. J. Kuekes, J. J. Yang, D. R. Stewart and R. S. Williams, Nature, 2010, 464, 873.
12. L. Cheng, Y. Li, K. S. Yin, S. Y. Hu, Y. T. Su, M. M. Jin, Z. R. Wang, T. C. Chang and X. S. Miao, Adv. Funct. Mater., 2019, 29, 1905660.
13. P. Huang, J. Kang, Y. Zhao, S. Chen, R. Han, Z. Zhou, Z. Chen, W. Ma, M. Li, L. Liu and X. Liu, Adv. Mater., 2016, 28, 9758.
14. Y. S. Kim, M. W. Son, H. Song, J. Park, J. An, J. B. Jeon, G. Y. Kim, S. Son and K. M. Kim, Adv. Intell. Syst., 2020, 2, 1900156.
15. Z. Sun, E. Ambrosi, A. Bricalli and D. Ielmini, Adv. Mater., 2018, 30, 1802554.
16. N. Xu, K. J. Yoon, K. M. Kim, L. Fang and C. S. Hwang, Adv. Electron. Mater., 2018, 4, 1800189.
17. Y. S. Kim, J. An, J. B. Jeon, M. W. Son, S. Son, W. Park, Y. Lee, J. Park, G. Y. Kim, G. Kim, H. Song and K. M. Kim, Adv. Sci., 2022, 9, 2104107.
18. Y. Song, X. Wang, Q. Wu, F. Yang, C. Wang, M. Wang and X. Miao, Adv. Sci., 2022, 9, 2200036.
19. T. Park, Y. R. Kim, J. Kim, J. Lee and C. S. Hwang, Adv. Intell. Syst., 2022, 4, 2100267.
20. J. H. In, Y. S. Kim, H. Song, G. Kim, J. An, J. B. Jeon and K. M. Kim, Adv. Intell. Syst., 2020, 2, 2000081.
21. S. Kvatinsky, G. Satat, N. Wald, E. G. Friedman, A. Kolodny and U. C. Weiser, IEEE Trans. Very Large Scale Integr. (VLSI) Syst., 2013, 22, 2054.
22. S. G. Rohani and N. TaheriNejad, presented at IEEE 30th Canadian Conf. on Electrical and Computer Engineering, Canada, 2017, pp. 1–4.
23. G. C. Adam, B. D. Hoskins, M. Prezioso and D. B. Strukov, Nano Res., 2016, 9, 3914.
24. L. Amaru, P.-E. Gaillardon and G. De Micheli, IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst., 2016, 35, 806.
25. F. Miyata, IEEE Trans. Electron. Comput., 1963, EC-12(3), 183.
26. K. M. Kim, S. R. Lee, S. Kim, M. Chang and C. S. Hwang, Adv. Funct. Mater., 2015, 25, 1527.
27. K. M. Kim, J. J. Yang, E. Merced, C. Graves, S. Lam, N. Davila, M. Hu, N. Ge, Z. Li, R. S. Williams and C. S. Hwang, Adv. Electron. Mater., 2015, 1, 1500095.
28. K. M. Kim, J. J. Yang, J. P. Strachan, E. M. Grafals, N. Ge, N. D. Melendez, Z. Li and R. S. Williams, Sci. Rep., 2016, 6, 20085.
29. H. Jiang, L. Han, P. Lin, Z. Wang, M. H. Jang, Q. Wu, M. Barnell, J. J. Yang, H. L. Xin and Q. Xia, Sci. Rep., 2016, 6, 28525.
30. S. Yu, H.-Y. Chen, B. Gao, J. Kang and H.-S. P. Wong, ACS Nano, 2013, 7, 2320.
31. G. H. Kim, H. Ju, M. K. Yang, D. K. Lee, J. W. Choi, J. H. Jang, S. G. Lee, I. S. Cha, B. K. Park and J. H. Han, Small, 2017, 13, 1701781.
32. J. Reuben and S. Pechmann, IEEE Trans. Very Large Scale Integr. (VLSI) Syst., 2021, 29, 1108.
33. M. Sadeghi, K. Navi and M. Dolatshahi, J. Supercomput., 2019, 76, 2191.
34. C. Efstathiou, Z. Owda and Y. Tsiatouhas, IEEE Trans. Circuits Syst. II: Express Br, 2013, 60, 667.
35. A. Weinberger and J. Smith, Nat. Bur. Stand. Circ., 1958, 591, 3.
36. R. E. Ladner and M. J. Fischer, J. Assoc. Comput. Mach., 1980, 27, 831.
37. K. Brent, IEEE Trans. Comput., 1982, 100, 260.
38. J. Reuben, J. Low Power Electron. Appl., 2021, 11, 45.
39. D. Bhattacharjee, A. Siemon, E. Linn, S. Menzel and A. Chattopadhyay, ACM J. Emerg. Technol. Comput. Syst., 2018, 14, 1.
40. A. Siemon, S. Menzel, D. Bhattacharjee, R. Waser, A. Chattopadhyay and E. Linn, Eur. Phys. J.-Spec. Top., 2019, 228, 2269.
41. V. Pudi, K. Sridharan and F. Lombardi, IEEE Trans. Comput., 2017, 66, 1824.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01196a

---