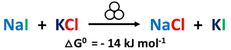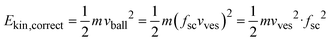Pressure as the driving force for mechanochemical reactions on the example of ion metathesis of alkali halides upon ball milling

Abstract

We report an in situ X-ray diffraction study of the mechanochemical ion metathesis between sodium iodide (NaI) and potassium chloride (KCl) to form sodium chloride (NaCl) and potassium iodide (KI) upon ball milling in a shaker mill. The data permit insights into the fundamental processes occurring during mechanochemistry. The reaction proceeds in incremental steps upon ball impact and consequently follows pseudo-zero order kinetics after an induction period needed for mixing and reduction of the sizes of the salt crystals. The total energy input required for full conversion is a constant value irrespective of the shaking frequency. Different shaking frequencies imply different average kinetic energies of the milling balls and thus different energy transfer per impact. The time for the total energy transfer to the powder thus varies as a function of the kinetic energy of the balls and number of impacts. At lower shaking frequency, i.e., at lower kinetic energy of the balls and a lower impact rate, the time required for full conversion is simply longer. The data reported provide strong evidence that pressure generated by the impact of milling balls is the driving force for the metathesis reaction rather than a temperature increase. The observed pseudo-zero order kinetics complies well with periodic pressure pulses driving the salt metathesis reaction.

---

Introduction

Mechanochemistry has developed into an intensively researched field over the last decades, both in academia and in industry. The reactions proceed either during reactive extrusion or during reactive ball milling. Despite intensive research and use of respective systems, the understanding of the underlying principles governing mechanochemical transformations is still in its infancy. The reason for this lies in the difficulty of studying processes within extruders or ball milling devices during operation. In situ or operando studies are commonly implemented for thermally, light, or electrically activated reactions. In each of these cases, and in contrast to mechanochemical reactions, a certain volume fraction of the activated reaction medium can be irradiated and analyzed by spectroscopic or diffraction techniques.^1,2 Mechanochemistry holds tremendous potential for the design of energy-efficient, atom economical, and environmentally benign reactions. The working principle permits direct energy transfer to molecules or particles, which are brought into intimate contact in the absence of solvent molecules. Specifically, these transient activation effects induce mechanochemical reactions.³

Mechanical activation still lacks fundamental insights, which has allowed thermal, light and electrically induced reactions to move on from interesting peculiarity to industrial processes. Initial efforts have been made to improve the understanding of milling reactions at a more fundamental level by designing milling equipment allowing for in situ analysis of ongoing processes with high energy X-rays or lasers.^4–21 Such in situ milling vessels are often completely constructed of polymers (PMMA or Plexiglas™) to allow for transmission of radiation. They are transparent to high energy X-rays and lasers and thus enable in situ powder diffraction and Raman spectroscopic studies. These hardware developments have triggered significant improvements in understanding the transient activation phenomena and even revealed previously unknown metal organic framework materials (MOFs).⁹ Despite all these benefits, currently the available hardware for in situ analysis is limited to solid–solid or liquid-assisted solid reactions requiring moderate kinetic energies.

However, besides these applications with moderate kinetic energies at work, several other reactions and processes have recently emerged that require harsher conditions and cannot be analyzed within the previously mentioned PMMA milling vessels but require steel body milling vessels.^17,18

Considering the obvious benefits of solvent-free processing and direct energy transfer, which often lead to surprisingly fast reaction kinetics, the knowledge of mechanochemistry was transferred into the development of heterogeneous mechano-catalysis for converting gases by passing them over a solid catalyst during ball-milling.^22–27 The activation of a solid catalyst surface is induced by the impact of the milling ball on the vessel walls covered by the solid catalyst powder. It can be assumed that the energy state of the particles in the powder increases after impact (e.g. generation of local defects, stacking faults, etc.) and decreases again after reaction of the catalyst with molecules from the gas phase. The molecules are transformed into the desired gaseous product by this process.

Another such high energy mechanochemical process that has been under investigation for many years at our laboratory is the mechanochemically activated synthesis of hydrides for hydrogen storage applications under relatively mild conditions (100–200 bar H₂, at 25–100 °C).^28–31

As the described reactions require gas-tight milling vessels and/or must allow for elevated pressures, the respective experiments needed to be performed in steel milling vessels with gas in- and outlets.

For in situ studies of mechanocatalytic systems and hydrogen storage materials, milling vessels consisting of a gas-tight steel bodies with pressure-tight and temperature-resistant polymer windows were constructed. They can be heated up to 150 °C and they are resistant to high mechanical stress.¹⁸ Instead of a whole body polymer vessel, polymer windows in the steel vessels allow monitoring of mechanochemical experiments by X-ray diffraction during high energy ball milling. For testing the usability of the respective steel body milling vessels for in situ studies at the PETRA III synchrotron facility, we used a simple-to-follow ion metathesis reaction (see Scheme 1). A first inspection of the in situ XRD data then indicated that thorough kinetic evaluation might provide valuable insights into the ball milling process as such.

Scheme 1 Standard test reaction investigated here.

Therefore, we performed a systematic study on the said mechanochemical model reaction (Scheme 1), namely the ion metathesis between sodium iodide (NaI) and potassium chloride (KCl) which was shown to form sodium chloride (NaCl) and potassium iodide (KI) under mechanochemical activation.

Experimental

In situ XRD experiments during high energy ball milling

For investigating solid state reactions under realistic reaction conditions, in situ reaction vessels (Fig. 1 and S1†) have been developed. They consist of stainless steel milling vessels with X-ray-transparent polymer windows for monitoring the mechanochemically induced phase transformations during high energy ball milling. As we had started our study using the steel milling vessels, we continued the follow-up work with the same setup even though the ion metathesis reaction studied here would likely also proceed in polymer vessels.²⁰ The milling vessels were mounted on a modified MM400 Retsch ball mill. In situ ball milling experiments were conducted at the P02.1 beamline at the PETRA III synchrotron source (DESY Hamburg, λ = 0.20741 Å). The sample holder of the mill was custom-modified to enable access to the incident X-ray beam using extension arms that place the milling vessels above the housing of the mill, thus allowing the X-ray to pass through the polymer windows of the milling vessels.¹⁸

Fig. 1 Milling vessel and 15 mm steel balls used for the in situ XRD experiments. The milling vessel comprises a stainless steel body, equipped with X-ray transparent PMMA windows (shown to the right of the vessel) covering the cut-outs in the steel body.

For the experiments, the 25 mL stainless steel milling vessels were filled with equimolar amounts of NaI (0.666 g) and KCl (0.334 g), and mechanochemical salt metathesis reactions were conducted using either one or two stainless-steel balls with 15 mm diameter (weight 13.7 g). As no gas flow was applied, the gas inlet and outlet as well as the thermocouple inlet were sealed with screw plugs. The milling experiments were performed at room temperature with different shaking frequencies. Two types of extension arms were used for the experiments (see Fig. S1†).¹⁸ They differ in the radii (95 mm and 134 mm) of the orbital trajectories of the milling vessels. The smaller radius is shorter by a factor of 0.71 compared to the larger one, resulting in a nominal reduction of the kinetic energy of the balls of 50% when the extension arms with a smaller radius are used (see the ESI†). We will refer to these two setups as ‘low energy extension’ and ‘high energy extension’. The high energy extension was used for the experiments with one ball and the low energy extension was used for the experiments with two balls.

Thermal ion metathesis

Thermal transformation of the salt mixture was monitored via in-house in situ diffraction experiments. Ex situ X-ray diffraction data were collected in the 2θ range of 5–50° with a step width of 0.015° on heat-treated samples with a Stoe STADI P transmission diffractometer in Debye–Scherrer geometry (Mo Kα₁, λ = 0.7093 Å) with a primary monochromator (curved germanium (111)) and a Mythen1K position-sensitive detector. Borosilicate glass capillaries (ϕ 0.5 mm) were used for the measurements.

The effect of water vapor on the thermal ion metathesis was studied with a PANalytical X'Pert Pro diffractometer in Bragg–Brentano geometry using Cu Kα_1/2 radiation (λ = 1.5406 Å). Data collection was accomplished with a real-time multi-strip position sensitive detector (X'Celerator), Cu Kβ radiation was eliminated by using a nickel filter. The anti-scatter slit opening was 1°, the divergence slit was set to 0.5°, the soller slits were set to 0.04 rad and the mask was set to 5 mm. For in situ XRD experiments, a reaction chamber (Anton Paar XRK900) was mounted on a PANalytical X'Pert3 Pro Bragg–Brentano diffractometer working with Cu Kα_1,2 radiation (λ = 1.5406 Å). All samples have been prepared in defined weights on a ceramic MACOR© sieve plate as the sample holder allowed the gases to flow through the entire sample volume. The reaction chamber was attached to a gas supply system allowing for defined gas flows. The samples were then heated from room temperature to defined temperatures under varying water contents of the gas atmosphere.

Pressure-induced ion metathesis

NaI and KCl were separately ground to very fine powders. Then equimolar amounts of the salts (0.666 g NaI and 0.333 g KCl) were mixed by shaking them in glass vials (without using a milling ball). The premixed salts were then transferred into the pellet die of a hydraulic press (PW 10, Paul-Otto Weber) and immediately exposed to given pressures (radius of the die and punch were 20.84 mm). After defined times, the pressure was released and the pellets were measured immediately on a Stoe STADI P theta–theta diffractometer, equipped with a PIN diode detector, in Bragg–Brentano geometry using Cu K_α1/2 radiation.

Alternatively, equimolar amounts of the salts (0.666 g NaI and 0.333 g KCl) were dried at 120 °C for 2 hours and then mixed by shaking them in sealed glass vials. The dry salt mixtures were then poured into the pellet die of the hydraulic press and immediately exposed to given pressures. After defined times, the pressure was released and the pellets were measured on a Rigaku HyPix-3000 diffractometer in Bragg–Brentano geometry using Cu Kα_1,2 radiation.

Rietveld refinements

Quantitative Rietveld refinements were performed for data obtained from in situ X-ray diffraction measurements during the mechanochemical reactions and from thermal in situ measurements. The Bruker TOPAS V5 and V6 software packages were used for the quantification of phase compositions.³² For the refinements, crystal structure data from the International Crystal Structure Database (ICSD database, Version 5.2.0, Data release 2024) with the ICSD Collection Codes 61503 (NaI), 165593 (KCl), 181148 (NaCl), and 53843 (KI) were used. In addition to the educts and products, different steel components (balls and walls) were considered in the refinements. The refined parameters were the scaling factors, lattice parameters (to account for violation of the focusing conditions in the volume of the milling vessels), and the peak profiles. Based on the PV_TCHZ peak profile, W, V, and X were refined for high content phases. For small phase fractions, only W and X were refined. Atomic positions as well as Debye Waller factors and microstructure parameters were not refined. For determination of educt and product fractions, their quantitative phase fractions were normalized to the total sum of all four phases (NaI, KCl, KI, and NaCl). There were no further constraints on the contents of the educt and product.

Results and discussion

Mechanochemical ion metathesis

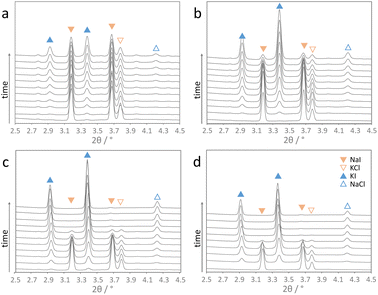
The herein studied mechanochemical ion metathesis proceeds in milling vessels on a shaker mill. Real-time analysis of the transformation in a conventional laboratory environment is quite challenging. Analyzing samples prepared by a mechanochemical process on a laboratory diffractometer is only possible ex situ. Data sampling will be time consuming though and phase compositions may change during the measurement as phase transformations in mechanically activated samples may continue. While the former problem is a mere instrumental limitation, the latter issue can prove significantly troublesome in studying kinetics. Alternatively, respective processes can be studied by in situ diffraction at a synchrotron facility. Reactions proceeding under moderate milling conditions may be investigated in polymer milling vessels. However, reactions proceeding under high energy ball milling conditions cannot be studied in polymer vessels due to insufficient energy transfer. For this reason, we developed steel milling vessels that allow both high energy ball milling and in situ X-ray diffraction experiments (Fig. 1).¹⁸ Examples for time resolved diffraction data acquired during milling with one ball at four shaking frequencies are shown in Fig. 2.

Fig. 2 In situ diffraction data of the ion metathesis reaction obtained at shaking frequencies of (a) 15 Hz, (b) 20 Hz, (c) 25 Hz, and (d) 30 Hz using one steel ball and the high energy extension. Time difference of the scans shown is 1 min (scans were recorded continuously for 15 s, λ = 0.20741 Å).

It is obvious that the progress of the metathesis reaction strongly depends on the applied shaking frequencies. At a frequency of 15 Hz (Fig. 2a), the educts NaI and KCl only slowly transform into the metathesis products NaCl and KI. After 10 min only about 50 mol% of the products are formed. Increasing the frequency to 20 Hz leads to 80 mol% products after 10 min (Fig. 2b). A further increase in the shaking frequencies to 25 and 30 Hz results in complete conversion after only about 7 and 5 min.

The diffraction data were quantitatively evaluated by Rietveld refinements from which concentrations of the substrate (NaI and KCl) and product phases (NaCl and KI) were calculated as shown in Fig. S2.† Milling experiments with the same educt amounts were also performed with two balls but using the low energy extensions. The respective phase compositions with time are shown in Fig. S3.† As no by-phases were formed, the quantitative Rietveld data provide information on time-resolved product formation as shown in Fig. 3. After an induction period with basically no conversion, a more or less linear increase in the conversion with milling time was observed. This behavior was more pronounced for the series with the low energy extension. Deviation from that linear trend was only observed when a major fraction of the educt was converted. Up to a conversion of about 70–80%, a pseudo-zero order kinetics, i.e. linear conversion with time, best describes the experimental data after the induction period (see Fig. S4† for plots assuming first and second order kinetics). As every so often observed for reactions following zero-order kinetics, the reaction order slightly deviates from zero-order when a major fraction of the reactant is consumed. Zero order kinetics are usually an indication that the progress of a reaction is limited by (external) factors. For the salt metathesis reaction, the reaction only proceeds upon impact of the milling balls. The impacts are thus the reaction rate-determining factor in this reaction.

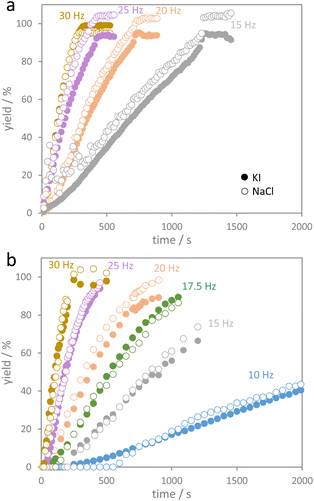Fig. 3 Yields of KI and NaCl as a function of milling time (a) using two balls (low energy extensions) and (b) using one ball (high energy extension) for different shaking frequencies.

Fig. S5† shows the progress of the salt metathesis reaction for four different frequencies using either one ball with the high-energy extensions or two balls with the low energy extensions. For a given shaking frequency, the reactions in both setups indeed proceed at the same rate. The fact that the low energy extensions allow for only half the kinetic energy of the balls (compared to the high energy extension) is apparently compensated for by using two milling balls instead of one. From the slopes of zero-order kinetics plots (Fig. S6†), reaction rate constants k were derived from the changing fractions of the four components NaI, KCl, KI, and NaCl (Table 1). As we are dealing with conversion of pure solids, the reaction rate constants are given as moles of NaI or KCl consumed per second and moles of KI or NaCl formed per second. The reaction rate constants for NaI and KCl then were averaged as average reaction rate constants of educt consumption (k_ave,ed), and accordingly, the reaction rate constants for KI and NaCl formation were averaged as average rate constants of product formation (k_ave,pr). The data show that the average rate of educt consumption (k_ave,ed) is identical to the average rate of product formation (k_ave,pr). Furthermore, the average reaction rate constants observed at the different shaking frequencies in both experiment series (1 ball and 2 balls) are more or less identical for a given frequency.

Table 1 Reaction rate constants k determined for the transformation of NaI and KCl into KI and NaCl at different shaking frequencies using one or two milling balls. k_ave,ed is the average of k_NaI and k_KCl, and k_ave,pr is the average of k_KI and k_NaCl

1 ball^a	10 Hz	15 Hz	17.5 Hz	20 Hz	25 Hz	30 Hz
a High energy extension.b Low energy extension.
kNaI/mol s^−1		−4.04 × 10^−6 ± 4 × 10^−8		−9.25 × 10^−6 ± 9 × 10^−8	−1.507 × 10^−5 ± 1.6 × 10^−7	−2.320 × 10^−5 ± 4.7 × 10^−7
kKCl/mol s^−1		−2.75 × 10^−6 ± 3 × 10^−8		−6.61 × 10^−6 ± 8 × 10^−8	−1.147 × 10^−5 ± 1.9 × 10^−7	−1.794 × 10^−5 ± 3.0 × 10^−7
kave,ed/mol s^−^1		−3.40 × 10^−^6 ± 9.1 × 10^−7		−7.93 × 10^−^6 ± 1.9 × 10^−6	−1.327 × 10^−^5 ± 2.5 × 10^−6	−2.057 × 10^−^5 ± 3.7 × 10^−6
kKI/mol s^−1		3.44 × 10^−6 ± 2 × 10^−8		7.57 × 10^−6 ± 6 × 10^−8	1.224 × 10^−5 ± 1.3 × 10^−7	2.014 × 10^−5 ± 2.5 × 10^−7
KNaCl/mol s^−1		3.30 × 10^−6 ± 6 × 10^−8		8.49 × 10^−6 ± 1.3 × 10^−7	1.430 × 10^−5 ± 2.8 × 10^−7	2.100 × 10^−5 ± 5.6 × 10^−7
kave,pr/mol s^−^1		3.37 × 10^−^6 ± 1.0 × 10^−7		8.03 × 10^−^6 ± 6.5 × 10^−7	1.373 × 10^−^5 ± 1.5 × 10^−6	2.057 × 10^−^5 ± 6.1 × 10^−7

---

2 balls^b	10 Hz	15 Hz	17.5 Hz	20 Hz	25 Hz	30 Hz
kNaI/mol s^−1	−1.14 × 10^−6 ± 2 × 10^−8	−3.05 × 10^−6 ± 1.0 × 10^−7	−4.52 × 10^−6 ± 1.2 × 10^−7	−7.42 × 10^−6 ± 1.3 × 10^−7	−1.386 × 10^−5 ± 1.5 × 10^−7	−2.332 × 10^−5 ± 4.2 × 10^−7
kKCl/mol s^−1	−1.24 × 10^−6 ± 2 × 10^−8	−3.10 × 10^−6 ± 1.2 × 10^−7	−4.39 × 10^−6 ± 8 × 10^−8	−7.26 × 10^−6 ± 1.7 × 10^−7	−1.482 × 10^−5 ± 2.4 × 10^−7	−2.371 × 10^−5 ± 9.4 × 10^−7
kave,ed/mol s^−^1	−1.19 × 10^−^6 ± 7 × 10^−8	−3.08 × 10^−^6 ± 3 × 10^−8	−4.46 × 10^−^6 ± 9 × 10^−8	−7.34 × 10^−^6 ± 1.1 × 10^−7	−1.434 × 10^−^5 ± 6.8 × 10^−7	−2.351 × 10^−^5 ± 2.8 × 10^−7
kKI/mol s^−1	1.08 × 10^−6 ± 4 × 10^−8	2.74 × 10^−6 ± 6 × 10^−8	4.58 × 10^−6 ± 1.0 × 10^−7	6.73 × 10^−6 ± 6 × 10^−8	1.481 × 10^−5 ± 2.5 × 10^−7	2.370 × 10^−5 ± 7.9 × 10^−7
kNaCl/mol s^−1	1.30 × 10^−6 ± 4 × 10^−8	3.41 × 10^−6 ± 6 × 10^−8	4.33 × 10^−6 ± 1.2 × 10^−7	7.95 × 10^−6 ± 1.0 × 10^−7	1.387 × 10^−5 ± 4.4 × 10^−7	2.333 × 10^−5 ± 2.3 × 10^−7
kave,pr/mol s^−^1	1.19 × 10^−^6 ± 1.5 × 10^−7	3.08 × 10^−^6 ± 4.7 × 10^−7	4.46 × 10^−^6 ± 1.8 × 10^−7	7.34 × 10^−^6 ± 8.6 × 10^−7	1.434 × 10^−^5 ± 6.7 × 10^−7	2.352 × 10^−^5 ± 2.6 × 10^−7

---

For the conversion of soft matter via ball-milling, Colacino et al. determined the number of ball impacts as the rate-determining factors next to the duration of milling.³³ If the same does hold for the conversion of the salts investigated here, the reaction rate should scale with the number of impacts per time unit, i.e., with the impact rate. The latter should depend linearly on the shaking frequency, i.e., doubling the frequency should double the impact rate. As shown in Fig. S7a,† the reaction rate constants correlate with the impact rate but not linearly. Thus, additional factors must play a role as well. Different shaking frequencies also imply different kinetic energies of the milling balls. The velocity at which the balls are moving depends on the velocity of the milling vessels and the latter depends on the shaking frequency. Unfortunately, the exact velocities of the balls under milling conditions are unknown. However, one can consider the average velocity of the balls as the product of a given scaling factor, f_s, and the velocity at which the vessel moves. The latter is known from the shaking frequency and moving distance of the vessels. Considering the scaling factor, f_sc, to be constant in a first approximation, one can estimate the ball velocity, v_ball, with the velocity of the vessel, v_ves, simply as

v_{ball =} f_scv_ves

The correct kinetic energy of the ball then can be approximated as

Neglecting f_sc, one will not get correct energies but energies that deviate from the correct values by a factor f_sc². The latter is unknown but induces a constant deviation, which allows for relative comparison of calculated energies, better to be considered as ‘apparent kinetic energies’. Fig. S7b† shows that the reaction rate constants correlate with the apparent kinetic energy, E_kin, of the milling balls but there is also no linear dependence.

The kinetic energy of the ball is likely not transferred quantitatively to the powder as a fraction of the kinetic energy is back-transferred into the rebound of the ball. Thus, one can define an elasticity factor, f_el, which is related to the fraction of energy that is re-transferred to the ball through the rebound. The exact values of f_sc and f_el are again unknown. Consequently, a direct assessment of the kinetic energy, E_kin,i, transferred to the powder by the impact of a ball is not possible. However, assuming that both factors scale linearly, one can use the apparent kinetic energy of a ball to achieve a relative estimate for the kinetic energy transferred to the powder by the impact of a ball, denoted as the apparent kinetic energy transferred, E_kin/i. From the reaction rate constants and the number of impacts per second, as calculated from milling frequency and number of balls (see the ESI†), one gets the fraction of educt that is transformed upon one impact of the ball. A plot of the incremental change in the amounts of educts NaI and KCl per impact (dN_ed,i) versus the apparent kinetic energy transferred per impact shows in fact a linear correlation as shown in Fig. 4. Even more, the data from both experimental series (with one and two balls) fall on the same line. The higher the kinetic energy of the ball, the more educt transforms upon a ball impact. This implies that the reaction rate correlates with the kinetic energy of the balls and the number of impacts per time unit. These two factors also determine the total amount of energy transferred per time unit which has some interesting implications as will be discussed below. The remaining question is now, how does the transferred energy induce the interconversion of the salts? From the fact that the reaction follows pseudo zero-order kinetics, one must assume that the impacts of the balls induce the progress of the reaction. At the impact, the kinetic energy of the balls is transferred to the powder, which could induce various processes. Solid state reactions typically require high temperatures or pressure to overcome the activation barrier for ion diffusion, either via thermal mobilization of ions or generation of defects due to stress and strain by exertion of pressure.^34–38 A certain pressure could be induced by the impact of the milling ball, and theories have been laid out that the impact of the milling balls may induce an extreme increase in temperature if all energy is transferred to a single crystallite (hot spot theory),^13,39–41 and even plasma formation via this process has been considered⁴¹ (magma-plasma theory^42,43). In our experiment, the milling ball does not transfer its kinetic energy to only one crystallite but to an ensemble of crystallites which decorate the surface of the milling vessels as a thin layer. The ball likely transfers its energy to the powder, thus compressing and displacing the crystallites to some extent. A rough estimate on the temperature increase and pressure formation on the sample volume exposed to the impact of one milling ball can be made, assuming that no elastic rebound of the balls from the walls occurs but all energy is transferred to the powder (see the ESI and Table S1†). The powder covers the surface of the endcaps of the milling vessel, where the strongest impact of a milling ball in a shaker mill occurs, as a very thin layer of about 0.2 mm. Depending on the indention depths of the balls into that powder layer, temperature in the sample volume exposed to the impact will increase moderately. The estimated temperature increase will be about 10–30 K (75% to 25% indention into the powder layer at 30 Hz, high energy extension, see Table S1†). The volume fraction of the sample that is affected would be only 0.2% of the total sample volume for 75% indention, a value that goes down to 0.07% of the volume fraction for 25% indention. Thus, only a very small fraction of the sample would potentially heat up by one impact. The absorbed energy in such a case would likely dissipate quickly to the steel walls of the milling vessels. These considerations fit with the fact that only a minute increase in temperature of the milling vessels during a milling experiment is observed. A temperature increase is thus likely not the major driving force for the metathesis reaction. Thermally induced phase transformation is addressed below in some more detail.

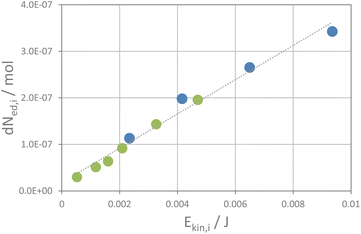Fig. 4 The change in the educt amount per impact of a milling ball plotted versus its apparent kinetic energy per impact.

The calculated local pressure upon impact seems to be more significant (Table S1†). The pressures are not comparable to those of 10 000–50 000 bar in high-pressure metathesis experiments performed in diamond anvil cells.³⁶ For an indention of 25%, a pressure of 374 bar and for an indention of 75% a pressure of 125 bar is calculated (30 Hz, high-energy extension). The pressure reduces at higher indention as the energy is transferred to a larger volume (see impact volume V_i in Table S1†). The investigated metathesis reaction is exothermic with a change in Gibbs free energy of 14 kJ mol⁻¹ and thus proceeds readily when the activation energy for the ion diffusion is overcome. Ion diffusion in alkali halides is considered to proceed mainly via Schottky defects. For NaI, the enthalpy of formation of a Schottky defect is reported to be about 3.63 × 10⁻¹⁹ J (2.27 eV) and for KCl, 3.04 × 10⁻¹⁹ J.^44,45 The apparent energy transferred by one impact at a shaking frequency of 30 Hz using the high-energy extension (9.35 mJ) would be sufficient to generate about 2.8 × 10¹⁶ Schottky defects. Of course, other energy-consuming processes facilitating ion diffusion, such as shear and edge dislocations, also need to be considered. Also, partial amorphization of crystallite surfaces upon ball impact must be taken into account. Thus, the number of Schottky defects is more a hypothetic maximum number rather than an effective number of diffusion-driving defects. In any case, one could expect that the reaction will be driven by defect generation and redistribution of ions within the crystallites. At the end of the reaction, thermodynamically more stable products will have formed. If this hypothesis is correct, the amount of energy required for full conversion should be the same for all milling experiments performed here as then the number of defects generated would be the same as well. Division of the educt concentration by the reaction rate constant gives the total time for full conversion, and multiplying that number with the total number of impacts and the apparent kinetic energy transferred by one impact gives the total apparent energy transferred in the time period from the start of the reaction (after the induction period) to its completion. Fig. 5a and S8† show the total apparent energy transferred for each milling experiment as functions of shaking frequency and milling time required for full conversion. As can be seen, the data accumulate around a value of 102 J (±11 J). Within the precision of the method, the metathesis reaction is accomplished when about 102 J of apparent kinetic energy is transferred. The metathesis reaction is obviously a cumulative process which is driven by processes that require constant energy input, such as, say, defect generation. A rough calculation of the amount of educts converted shows that only a small fraction of the educts is converted by a single impact. This is in line with the data reported by Carta et al. who inspected the effect of single ball drops.⁴⁶

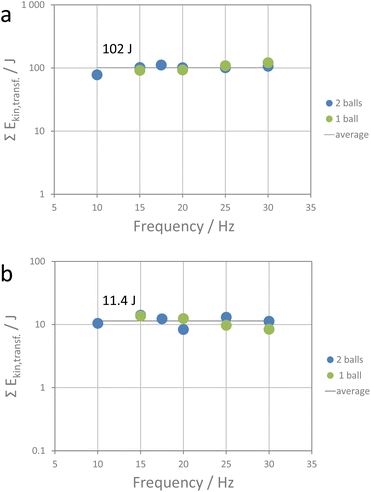Fig. 5 (a) Total apparent energy transferred during the reaction period, and (b) total apparent energy transferred during the induction period for the different metathesis experiments.

As the metathesis reaction investigated here is exothermic, the energy input relates to the activation energy for the metathesis reaction, comprising defect generation and ion migration. Assuming that all transferred energy would be consumed for that process, a nominal apparent activation energy of 22.8 kJ mol⁻¹ (per mol NaI or KCl) results. As mentioned above, this is under the postulate of non-elastic transfer of kinetic energy to the powder, i.e., elastic rebound of the balls can be neglected. Obviously, this value would represent a maximum value. In any case, either a relatively well-defined fraction or the total kinetic energy will be consumed for overcoming the activation barrier for the processes resulting in ion diffusion. If this were not the case, data as consistent as observed here for various experimental setups would be hardly conceivable.

Finally, the induction period requires attention. Intimate mixing and close contact of the educt phases are considered highly beneficial for the metathesis process to proceed.^47,48 Insufficient mixing and contact of particles is likely the reason for the induction period observed in our experiments. The induction time does not correlate linearly with the number of impacts as one could assume if only mixing would be a relevant factor (Fig. S9†). Reduction of crystallite size will increase the specific surface area of the particles and thus allow for a more efficient inter-particle ion transfer as the interface between the phases increases. Crushing (fragmentation) of crystallites thus would allow for a more intimate contact of the phase boundaries. On the other hand, it will consume a major fraction of the energy imposed by the impact of a milling ball during the fragmentation period. Indeed, SEM inspection showed that for example milling the pristine NaI and KCl crystallites with a median crystallite size of 570 μm and 530 μm with one steel ball at a frequency of 15 Hz for 100 s (=end of induction time) resulted in crystallites with sizes of 14 μm (median). After the induction period, the comminution of the crystallites slows down and shortly after the induction period, the crystallites have a median size of 7–8 μm, which then remains constant until completion of the reaction. The mixing during the induction period thus goes clearly along with the major particle size reduction. Energy is consumed for the fragmentation of the crystallites, a process that apparently comes to an end after a while. The energy consumed by the crushing process thus should be also limited. As that energy is also defined, the duration of the induction period should be related to a given energy input. Fig. 5b shows that this assumption is indeed valid as the total amount of apparent energy induced during the induction periods of the different milling experiments accumulates around an average value of 11.4 J (±2 J). As for the apparent activation energy, also this value is under the postulate of completely non-elastic impact events. However, even if only a fraction of energy is transferred, the induction period is a period defined by the time needed to transfer a given energy amount. For completely inelastic energy transfer, the apparent energy would be about 2.6 kJ mol⁻¹ (per mol NaI or KCl). As milling experiments are performed, the latter is likely required for the fragmentation of the crystallites. Once the interface between the educt crystallites is sufficiently large due to crystal fragmentation and intimate mixing, the metathesis reaction proceeds. A similar rationale for an induction period has been proposed by Belenguer et al., Takacs, and Linberg et al.^49–51 In addition to comminution, the formation of a sufficient amount of defects is considered crucial to initiate reactions upon ball milling. For highly exothermic reactions, the energy stored in defects could even initiate self-sustained reactions.^50,52 Activation of a crystalline material via ball milling might also result in partial amorphization. The energy required for the amorphization (surface energy due to particle size reduction and loss of lattice energy due to amorphization) is then considered to be stored in the amorphous fraction of the solid causing its activation for further reaction.⁵³

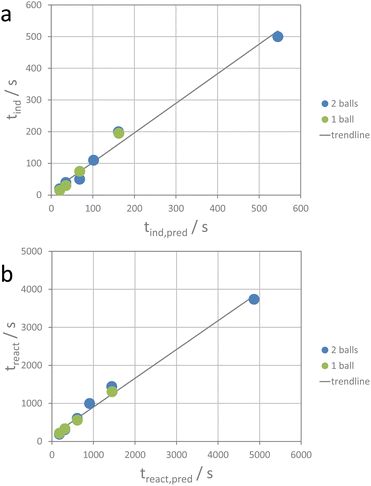
For the ion metathesis reaction, crushing (comminution), mixing, defect generation, and maybe also partial amorphization require a given amount of energy. Using the average value of transferred energy for the induction period and that for the reaction period, the respective time periods can be tentatively predicted (see the ESI†) for a given experimental set-up. Fig. 6 shows the correlation between the observed induction and reaction times and the predicted values.

Fig. 6 Correlation between observed and predicted times for (a) the reaction period and (b) the induction period. Observed times (t_react and t_ind) are plotted on the ordinates and predicted times (t_react,pred and t_ind,pred) on the abscissae.

In summary, the mechanochemical metathesis reaction of NaI and KCl to KI and NaCl proceeds readily after an induction period. The induction period is needed for mixing and crushing the educt crystallites by which a sufficiently large interface for the metathesis reaction is provided. The fragmentation of the crystallites requires a defined amount of energy. Once that energy is incrementally provided by a given number of impacts (the energy per impact depending on the shaking frequency), the fragmentation process ends and the actual metathesis reaction starts. The latter proceeds in incremental steps (per impact) during which the energy for overcoming the activation barrier for ion migration is introduced to the powder. The metathesis reaction follows pseudo-zero order kinetics as impacts of milling balls are required to trigger the progress of the reaction. At each impact, a defined amount of energy is transferred which is consumed for the formation of crystal defects which then facilitate ion diffusion throughout the crystallites. The reaction rate constants depend linearly on the amount of energy transferred per impact and the number of impacts per time unit. A similar relation was observed by Carta et al. and Vugrin et al. in their kinetic studies on the formation of trimeric [Ni(dbm)₂]₃ from planar Ni(dbm)₂ via ball milling.^46,54 Martins et al. report that the volume of the milling balls scales almost linearly with the rate of chemical transformation in a mechanochemically driven N-chlorination reaction.¹⁴ As the volume of balls scales linearly with its mass, this indicates that the reaction kinetics scales linearly with the impact energy, provided that the differently sized balls show identical velocity profiles.

Before discussing the final question, whether a temperature increase or pressure increase upon ball impact are the driving forces for the salt metathesis reaction, humidity of the salt mixture needs to be addressed. As will be seen below, moisture of the salt mixture is a crucial factor in case of thermal salt metathesis. An eminent question is then of course, whether humidity also does affect the mechanochemical salt metathesis process. In the experiments reported above, the salts were not dried prior to the ball milling experiments. Therefore, ex situ ball milling experiments with dried salt mixtures were performed. For this, vessels, milling balls and educts were individually temperature-treated at 100 °C for 2 h. After this, the vessels inside the oven were filled with the educts when hot. The vessels were then closed in the oven and after cooling to room temperature, the milling experiment was started. Successive experiments were performed and the products obtained after different milling times were collected and analyzed (Fig. S10†). After 150 s of ball milling, reflections of KI and NaCl were visible next to ones of NaI and KCl, after 300 s of milling, the majority of the educt was transformed into KI and NaCl, and after 600 s, the metathesis reaction was completed (Fig. S10a†). Further milling did not result in any further change in the composition. Apparently, no major difference is observed if using non-dried or dried salt mixtures for the mechanochemical metathesis reaction. The product formation is completed after about 400 s (Fig. S10b†), which is identical to the time required for non-dried salts as shown in Fig. 3. A slightly hydrated NaI surface apparently has no significant effect on the mechanochemical metathesis reaction, very different to the situation in thermal ion metathesis. The salts used for the mechanochemical metathesis reaction consist of millimeter-sized crystals with very low specific surface area.

Water fixation in a thin NaI·2H₂O layer on the NaI crystals might exist but its presence seems not mandatory. No sodium iodide hydrate was observed in the in situ XRD data measured during the mechanochemical ion metathesis, indicating that water adsorption from the air was not strong.

Tumanov reported inadvertent liquid-assisted processes proceeding by bringing reaction components that form a thermodynamically more stable product into close contact under humid conditions.⁵⁵ The reaction is then mediated by a liquid film on the crystal surfaces and proceeds with time via a dissolution–precipitation process. Our experiments were performed in gas-tight milling vessels with no contact with ambient air. However, to exclude an inadvertent process, we mixed equimolar amounts of non-dried NaI and KCl after milling them separately. Mixing was achieved by shaking the salts in a glass vial (without milling balls). The mixed salts were then transferred into a borosilicate glass capillary where they were gently compacted by dropping the glass capillary repeatedly through a 40 cm glass tube. The capillary then was sealed keeping a gas volume above the salt mix to adopt the situation in gas-tight milling vessels. Then, XRD patterns were repeatedly measured in transmission mode for 50 h (one XRD pattern per hour). No change in the XRD patterns was observed during that time, indicating that under these conditions, no inadvertent ion metathesis occurs.

Thermal ion metathesis

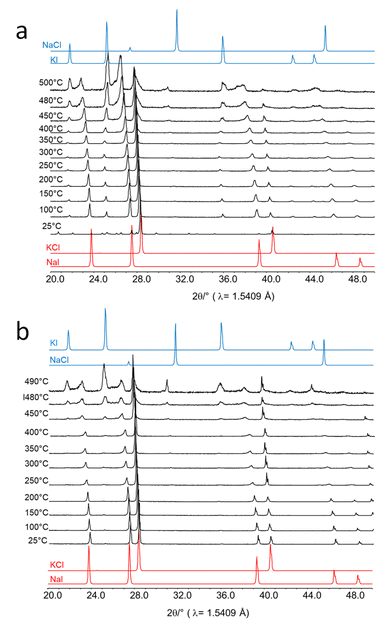
Even though a temperature increase upon impact of the milling balls is likely not responsible for the progress of the metathesis reaction, it seemed appropriate to investigate the effect of temperature on this reaction. NaI is highly hygroscopic and transforms into sodium iodide dihydrate (NaI·2H₂O) when it is in contact with air or humidity at least at its surface. Upon heating, the hydrate releases water and the NaI phase is recovered.

For the first experiment and without any drying of the educts, 400 mg NaI and 200 mg KCl were physically mixed and placed in a calcination crucible (Al₂O₃, ALKASint). The mixture was heated to 100 °C at 5 °C per min and held for 2 h. For one experiment, the crucible was covered, and for the other one it was kept open. After the experiments, glass capillaries were filled with the samples (in air) and XRD patterns were collected (Fig. S11a†). The ex situ XRD patterns show the physical mixture of NaI and KCl before the temperature treatment. A set of very small additional reflections indicate the existence of sodium iodide dihydrate. Heating in an open crucible leads to the partial formation of KI (27 wt%) and some NaCl (13 wt%) beside unreacted NaI (30%) and KCl (30 wt%). The sample which was heated in a closed crucible mainly shows reflections of KI (64 wt%), NaCl (28 wt%), and only small amounts of the educts KCl (6 wt%) and NaI (2 wt%). This simple experiment indicates that the atmosphere over the sample significantly affects the thermal metathesis reaction, and water is the prime suspect for the different reactions.

In a second experiment, 200 mg NaI and 100 mg KCl were first dried separately at 100 °C for 1 h and then the hot salts were mixed by shaking them manually in a sealed glass vial. The mixture was placed in open crucibles into the furnace and heated to 200, 300, 400, and 450 °C. At each temperature, one sample was removed from the oven and kept under a protective atmosphere and loaded into glass capillaries in a glove box. The capillaries were then sealed in the glove box and X-ray data were collected (Fig. S11b†). The salt mixture was now stable upon heating to 200 and 300 °C. After heating to 400 °C, small amounts of KI were formed. Further heating to 450 °C results in increasing amounts of the products. The sample heated to 500 °C appeared as a solidified melt after cooling. The melt was then ground to a powder for XRD measurement. The ex situ XRD pattern of the sample shows that the metathesis reaction proceeded quantitatively. Apparently, the salt mixture forms a melt at 500 °C and the products form, likely during the cooling process.

Next, in situ XRD measurements were performed in a reaction chamber (XRK-900, Anton Paar). For this, equimolar amounts of KCl and NaI were physically mixed and placed onto the sample holder without drying. The sample cell was closed during the measurement but the volume of the sample cell was large and the housing was cooled. Thus, any water vapor evolved from the sample would condense immediately in the housing of the cell. In situ XRD data were collected in the temperature range between room temperature and 500 °C (Fig. 7a). The pattern obtained at room temperature prior to the heating experiment reveals NaI and KCl as major phases and a minor phase of water-containing NaI·2H₂O. At 100 °C all crystal water is released and only reflections of the salt educts, KCl and NaI, are visible. However, fractions of NaCl and KI also did form. Their amount increased with temperature while NaI and KCl were consumed. Above 400 °C a melt started to form before the metathesis was completed.

Fig. 7 In situ XRD patterns recorded during heating of a physical mixture of NaI and KCl (a) not dried prior to the reaction and (b) dried prior to the reaction. As a reference, simulated diffraction patterns of the educts are show in red, and those of the products in blue.

Finally, an equimolar salt mixture was dried at 100 °C and all XRD measurements were performed in a continuous flow of N₂. Under these conditions, no significant metathesis reaction proceeded below 450 °C (Fig. 7b). Above 450 °C, the metathesis reaction started in the dry salt mixtures but melting also proceeded as higher temperatures were applied.

Obviously, thermal salt metathesis is strongly affected by the presence of water. Even a minute amount of moisture may facilitate the thermal metathesis reaction. A tentative explanation could be that a thin water film on the surface of the salt crystallites results in partial dissolution of the salt. The salt solution might then mediate the metathesis reaction.

Pressure-induced ion metathesis

Finally, the effect of applied pressure on the salt metathesis reaction was investigated. The premixed salt mixtures were exposed to loads of 10, 20, and 50 kN, corresponding to pressures of 293, 1466, and 2932 bar, for either 1, 5, or 20 minutes. The XRD data of the pressurized samples in Fig. S12† show no reflections of the educts NaI and KCl but only those of the products KI and NaCl. As the data were measured directly on the pellets, the preferred orientation of the salt crystallites as induced by the pressure treatment results in slightly varying relative intensities of the reflections. However, irrespective of the pressure applied, full conversion was observed at any time of pressure exposure. The load was therefore reduced to the lowest one possible (10 kN) and shorter time intervals were inspected at this pressure. Fig. 8 shows that even after only 5 s of pressure exposure, full interconversion of the salts was achieved. The ion metathesis reaction thus proceeds at tremendous speeds when even a moderate hydrostatic pressure of 293 bar is applied. The reaction rate constant must be at least 8.98 × 10⁻⁴ mol s⁻¹ or higher under these conditions. Shorter time intervals than 5 s could not be accessed as the pressure build-up and stabilization takes about that time.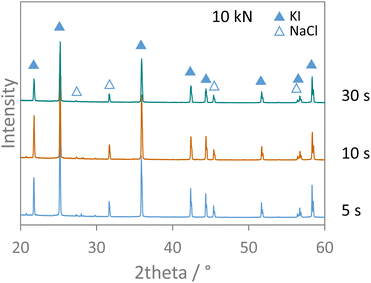

Fig. 8 XRD patterns measured on salt pellets from pressure experiments applying 10 kN for different time intervals. Data were measured with Cu Kα_1,2 radiation.

In any case, the data show that pressure readily facilitates the ion metathesis reaction investigated here. As pressure impulses are repeatedly applied on the salt mixture by the milling balls and pressure is a driving force for the salt metathesis reaction, these pressure pulses can surely trigger the ion metathesis reaction.

Furthermore, the data points in Fig. 4 follow a linear line going more or less through the origin of the graph. Thus, there seems to be no significant threshold energy for the reaction investigated here. Even at very low energy input, the reaction should proceed to some extent. In fact, we observed that even moderate grinding with an agate mortar and pestle induces the metathesis reaction of NaI and KCl to some extent. Intimate mixing of the reaction mixture prior to the experiments by grinding the salts in a mortar was thus not feasible without initiating the metathesis reaction. For the mechanochemical reactions discussed above, the milling vessels were filled with the two salts without preceding mixing. The observed induction period prior to the start of conversion is needed to achieve an intimate mixing of the two phases. The concurrent reduction of crystallites is also beneficial for the metathesis reaction as it increases the specific surface area of the salt particles. As the metathesis reaction most likely proceeds through the phase boundary of two adjacent salt crystallites, intimate surface contact is a decisive factor. Pressure experiments with non-crushed salt crystals resulted in only partial conversion of the educts even at the highest pressure and time applied, which clearly demonstrates the importance of the crystallite size and intimate mixing of the two salts. Once sufficient comminution and mixing is achieved, the pressure exerted on the particles in the compressed powder causes stress and strain in the crystallites, resulting in the formation of defects which can then facilitate ion diffusion in the solid. In a very recent study, pressure has been also considered a crucial factor for the formation of aragonite from calcite upon ball milling.¹⁵ Driscol et al. also identified pressure as the driving force for mechanochemical reactions when milling either Li₂MoO₄ or Nb₂O₃.⁵⁶ As the compressibility of minerals is not very high, a temperature increase as the result of applied pressure is not very pronounced. A pressure of about 250–300 bar is also achieved by the weight of a rock in a mine at a depth of about 1000 m where temperatures of about 35°–45° are observed. This is about the temperature increase that is reported for ball milling experiments by Uzarevich et al.¹² which, however, is not sufficient for initializing the thermal transformation of NaI and KCl into NaCl and KI. In this context, Kulla reported that only a moderate local temperature increase is observed with an IR camera during co-crystal formation upon impact of milling balls.¹³ In contrast, particle–particle interaction of crystallites sliding along each other is discussed to create higher pressure on individual crystal surfaces than that applied to the bulk of the powder. As a consequence, higher local temperatures might also be achievable. However, if salt crystallites glide along each other under pressure, shear dislocation within the crystals will likely consume a major fraction of the energy transferred. This consideration and the work by Uzuarevich or Kulla provide a strong indication that the temperature increase is likely very moderate and not the driving parameter for the salt metathesis.

In order to check whether the concept of only pressure exertion does also work for organic reactions, we loaded an equimolar mixture of o-phenyldiamine and benzil (1,2-diphenylethane-1,2-dione) into the pellet die and exposed it for 10 min to loads of 20, 50, and 100 kN. Julien et al. showed that 2,3-diphenylquinoxaline is formed upon milling this mixture in a ball mill.⁵⁷ In fact 2,3-diphenylquinoxaline also formed in the pellet press as shown in Fig. S13.† However, only about 45% of yield was achieved at all applied pressures whereas the ball milling resulted in full conversion. The reason for the difference in yield might be insufficient mixing under the static conditions in the pellet die. However, this simple experiment shows that organic reactions can also be induced by application of pressure.

Summary and conclusion

The data presented above show that ion metathesis follows certain kinetics and energy that is transferred by the impact of the milling balls into the salt powder facilitates the reaction. Apparently, a given energy amount must be transferred to achieve complete conversion of the reaction educts. Whether that energy amount is achieved by a large number of smaller energy transfers or via a smaller number of higher energy transfers is not decisive as long as the total amount of energy required for full conversion is provided. We would like to emphasize that the apparent energies calculated above likely underestimate the real energies involved as the milling balls may get accelerated by the rebound when colliding with an approaching wall. The balls will then have a substantially higher velocity and will transfer more energy upon impact. Intimate contact of the phase boundaries is a prerequisite for the ion metathesis reaction. Therefore, an induction period is required for crushing and mixing of the crystallites. Once the latter is achieved, the reaction proceeds successively upon the individual impacts of the balls. The kinetic energy of the balls is sufficient to slightly increase the temperature of the powder exposed to the impact and/or to increase the hydrostatic pressure of the powder due to its compression (Table S1†). As the achievable temperature increase is moderate when compared to the temperature required for complete conversion via thermal ion metathesis, the temperature is likely not the decisive factor for the mechanochemical reaction studied here. In contrast, the pressure increase achievable upon ball impact is in the range, which is shown above to facilitate the metathesis reaction at a tremendous rate. Therefore, one must conclude that pressure and not temperature is the decisive factor for the reaction under the mechanochemical conditions applied in this study.

Our observations and considerations laid out above have some interesting implications:

(1) An induction time is needed for crushing (comminution) and intimate mixing of the educts, and once sufficient surface contact of the reacting phases is achieved, the reaction proceeds.

(2) The reaction itself is driven by incremental energy transfer to the powder upon the ball impacts.

(3) The fraction of educt powder that is converted upon one impact scales linearly with the kinetic energy of the ball.

(4) The kinetic energy of the balls depends on their velocity, which is determined by the milling frequency.

(5) The reaction rate scales with the number of impacts per time unit and the kinetic energy transferred upon an impact.

(6) The reaction is driven by pressure pulses rather than the temperature increase upon impact of the balls onto the powder.

Of course we are aware of the fact that other reactions might be driven by different factors. However, for the reaction investigated here, pressure pulses can be identified quite clearly as the main culprit for the reaction progress. We hope that our conclusions will help to shed some light onto the subject of energy transfer during mechanochemical reactions, especially during ball milling.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank W. Kersten and the fine mechanics team at the MPI für Kohlenforschung (KOFO) for great support in constructing and realizing the milling vessels used for the experiments. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III beamline P02.1. Furthermore, we would like to thank O. Vozniuk (KOFO) and J.-C. Tseng (DESY) for their support during the measurement periods at DESY. Finally, financial support by the Max-Planck-Society and the Alexander von Humboldt Foundation is greatly acknowledged.

References

1. B. M. Weckhuysen, Phys. Chem. Chem. Phys., 2003, 5, 4351–4360.
2. D. Mores, J. Kornatowski, U. Olsbye and B. M. Weckhuysen, Chem.–Eur. J., 2011, 17, 2874–2884.
3. S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friscic, F. Grepioni, K. D. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447.
4. I. Halasz, S. A. Kimber, P. J. Beldon, A. M. Belenguer, F. Adams, V. Honkimaki, R. C. Nightingale, R. E. Dinnebier and T. Friscic, Nat. Protoc., 2013, 8, 1718–1729.
5. I. Halasz, A. Puskaric, S. A. Kimber, P. J. Beldon, A. M. Belenguer, F. Adams, V. Honkimaki, R. E. Dinnebier, B. Patel, W. Jones, V. Strukil and T. Friscic, Angew. Chem., Int. Ed. Engl., 2013, 52, 11538–11541.
6. T. Friscic, I. Halasz, P. J. Beldon, A. M. Belenguer, F. Adams, S. A. Kimber, V. Honkimaki and R. E. Dinnebier, Nat. Chem., 2013, 5, 66–73.
7. I. Halasz, T. Friscic, S. A. Kimber, K. Uzarevic, A. Puskaric, C. Mottillo, P. Julien, V. Strukil, V. Honkimaki and R. E. Dinnebier, Faraday Discuss., 2014, 170, 203–221.
8. D. Gracin, V. Strukil, T. Friscic, I. Halasz and K. Uzarevic, Angew. Chem., Int. Ed. Engl., 2014, 53, 6193–6197.
9. A. D. Katsenis, A. Puskaric, V. Strukil, C. Mottillo, P. A. Julien, K. Uzarevic, M. H. Pham, T. O. Do, S. A. Kimber, P. Lazic, O. Magdysyuk, R. E. Dinnebier, I. Halasz and T. Friscic, Nat. Commun., 2015, 6, 6662.
10. K. Uzarevic, I. Halasz and T. Friscic, J. Phys. Chem. Lett., 2015, 6, 4129–4140.
11. P. A. Julien, K. Uzarevic, A. D. Katsenis, S. A. Kimber, T. Wang, O. K. Farha, Y. Zhang, J. Casaban, L. S. Germann, M. Etter, R. E. Dinnebier, S. L. James, I. Halasz and T. Friscic, J. Am. Chem. Soc., 2016, 138, 2929–2932.
12. K. Užarević, V. Štrukil, C. Mottillo, P. A. Julien, A. Puškarić, T. Friščić and I. Halasz, Cryst. Growth Des., 2016, 16, 2342–2347.
13. H. Kulla, M. Wilke, F. Fischer, M. Rollig, C. Maierhofer and F. Emmerling, Chem. Commun., 2017, 53, 1664–1667.
14. I. C. B. Martins, M. Carta, S. Haferkamp, T. Feiler, F. Delogu, E. Colacino and F. Emmerling, ACS Sustain. Chem. Eng., 2021, 9, 12591–12601.
15. K. Kenges, S. Karafiludis, R. Džunda, I. O. Tampubolon, B. Satybaldiyev, F. Emmerling and M. Baláž, Phys. Chem. Chem. Phys., 2024, 26, 24279–24287.
16. F. Fischer, K. J. Wenzel, K. Rademann and F. Emmerling, Phys. Chem. Chem. Phys., 2016, 18, 23320–23325.
17. A. P. Amrute, Z. Lodziana, H. Schreyer, C. Weidenthaler and F. Schuth, Science, 2019, 366, 485–489.
18. T. Rathmann, H. Petersen, S. Reichle, W. Schmidt, A. P. Amrute, M. Etter and C. Weidenthaler, Rev. Sci. Instrum., 2021, 92, 114102.
19. H. Petersen, S. Reichle, S. Leiting, P. Losch, W. Kersten, T. Rathmann, J. Tseng, M. Etter, W. Schmidt and C. Weidenthaler, Chem.–Eur. J, 2021, 27, 12558–12565.
20. G. I. Lampronti, A. A. L. Michalchuk, P. P. Mazzeo, A. M. Belenguer, J. K. M. Sanders, A. Bacchi and F. Emmerling, Nat. Commun., 2021, 12, 6134.
21. V. Ban, Y. Sadikin, M. Lange, N. Tumanov, Y. Filinchuk, R. Černý and N. Casati, Anal. Chem., 2017, 89, 13176–13181.
22. S. Immohr, M. Felderhoff, C. Weidenthaler and F. Schuth, Angew. Chem., Int. Ed. Engl., 2013, 52, 12688–12691.
23. R. Eckert, M. Felderhoff and F. Schuth, Angew. Chem., Int. Ed. Engl., 2017, 56, 2445–2448.
24. H. Schreyer, R. Eckert, S. Immohr, J. de Bellis, M. Felderhoff and F. Schuth, Angew. Chem., Int. Ed. Engl., 2019, 58, 11262–11265.
25. M. Bilke, P. Losch, O. Vozniuk, A. Bodach and F. Schuth, J. Am. Chem. Soc., 2019, 141, 11212–11218.
26. S. Reichle, M. Felderhoff and F. Schüth, Angew. Chem., Int. Ed. Engl., 2021, 60, 26385–26389.
27. S. Reichle, L. Kang, D. Demirbas, C. Weidenthaler, M. Felderhoff, S. DeBeer and F. Schüth, Angew. Chem., Int. Ed. Engl., 2024, 63, e202317038.
28. C. Weidenthaler, A. Pommerin, M. Felderhoff, B. Bogdanovic and F. Schuth, Phys. Chem. Chem. Phys., 2003, 5, 5149–5153.
29. J. M. Bellosta von Colbe, M. Felderhoff, B. Bogdanovic, F. Schuth and C. Weidenthaler, Chem. Commun., 2005, 4732–4734.
30. B. Bogdanović, M. Felderhoff, A. Pommerin, F. Schüth and N. Spielkamp, Adv. Mater., 2006, 18, 1198–1201.
31. J. Ortmeyer, A. Bodach, L. Sandig-Predzymirska, B. Zibrowius, F. Mertens and M. Felderhoff, ChemPhysChem, 2019, 20, 1360–1368.
32. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218.
33. E. Colacino, M. Carta, G. Pia, A. Porcheddu, P. C. Ricci and F. Delogu, ACS Omega, 2018, 3, 9196–9209.
34. K. Gibson, M. Strobele, B. Blaschkowski, J. Glaser, M. Weisser, R. Srinivasan, H. J. Kolb and H. J. Meyer, Z. Anorg. Allg. Chem., 2003, 629, 1863–1870.
35. J. B. Wiley, E. G. Gillan and R. B. Kaner, Mater. Res. Bull., 1993, 28, 893–900.
36. L. Lei and L. L. Zhang, Matter Radiat. Extremes, 2018, 3, 95–103.
37. H. J. Meyer, Dalton Trans., 2010, 39, 5973–5982.
38. R. F. Jarvis, PhD Thesis, University of California, Los Angeles, 1992.
39. A. W. Tricker, G. Samaras, K. L. Hebisch, M. J. Realff and C. Sievers, Chem. Eng. J., 2020, 382, 122954.
40. S. G. Psakhie, K. P. Zol'nikov and D. Y. Saraev, Combust., Explos. Shock Waves, 1997, 33, 246–249.
41. P. Balaz, Mechanochemistry in Nanoscience and Minerals Engineering, Springer-Verlag, Berlin Heidelberg, 2008.
42. F. P. Bowden and A. D. Yoffe, Fast Reactions in Solids, Academic Press, New York, 1958.
43. P. A. Thiessen, K. Meyer and G. Heinicke, Grundlagen der Tribochemie, Akademie-Verlag, 1967.
44. I. M. Hoodless, J. H. Strange and L. E. Wylde, J. Phys. C, 1971, 4, 2737–2741.
45. D. Roy, S. K. Sen and A. Manna, Phys. Status Solidi B, 1974, 61, 723–730.
46. M. Carta, L. Vugrin, G. Miletic, M. J. Kulcsár, P. C. Ricci, I. Halasz and F. Delogu, Angew. Chem., Int. Ed. Engl., 2023, 62, e202308046.
47. G. E. Kamm, G. Huang, S. M. Vornholt, R. D. McAuliffe, G. M. Veith, K. S. Thornton and K. W. Chapman, J. Am. Chem. Soc., 2022, 144, 11975–11979.
48. R. E. Treece, E. G. Gillan and R. B. Kaner, Comments Inorg. Chem., 1995, 16, 313–337.
49. A. M. Belenguer, A. A. L. Michalchuk, G. I. Lampronti and J. K. M. Sanders, Beilstein J. Org. Chem., 2019, 15, 1226–1235.
50. L. Takacs, Prog. Mater. Sci., 2002, 47, 355–414.
51. K. Linberg, P. Szymoniak, A. Schönhals, F. Emmerling and A. A. L. Michalchuk, Chem.–Eur. J., 2023, 29, e202302150.
52. F. Delogu and L. Takacs, J. Mater. Sci., 2018, 53, 13331–13342.
53. K. Tkáčová, H. Heegn and N. Števulová, Int. J. Miner. Process., 1993, 40, 17–31.
54. L. Vugrin, M. Carta, S. Lukin, E. Meštrović, F. Delogu and I. Halasz, Faraday Discuss., 2023, 241, 217–229.
55. I. A. Tumanov, A. A. L. Michalchuk, A. A. Politov, E. V. Boldyreva and V. V. Boldyrev, CrystEngComm, 2017, 19, 2830–2835.
56. L. L. Driscoll, E. H. Driscoll, B. Dong, F. N. Sayed, J. N. Wilson, C. A. O'Keefe, D. J. Gardner, C. P. Grey, P. K. Allan, A. A. L. Michalchuk and P. R. Slater, Energy Environ. Sci., 2023, 16, 5196–5209.
57. P. A. Julien, I. Malvestiti and T. Friščić, Beilstein J. Org. Chem., 2017, 13, 2160–2168.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mr00104d

---