Layer-dependent Schottky contact at TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) van der Waals interfaces

Abstract

The mechanical, thermal and dynamical stabilities, electronic structure, contact type, and height of the barrier at the interface of TaX₂ (X = S, Se, Te) and BY (Y = P, As, Sb) metal–semiconductor (MS) contact are investigated via first principles calculations. Binding energies, mechanical properties, phonon spectra and ab initio molecular dynamics (AIMD) simulations confirm the stabilities of these systems. TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS van der Waals heterostructures (vdWHs) are found to be metal with a Schottky contact at the interface. Formation of the n-type Schottky contact at the interface of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs favors electron conduction over hole conduction. Small (higher) effective mass (carrier mobility) make TaS₂–BSb, TaSe₂–BSb and TaTe₂–BSb MS vdWHs, potential candidates for high speed nanoelectronic applications. Bader charge analysis shows that at the interface of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs, in TaX₂ (BP, BAs) the electrons transfer from the TaX₂ layer to the BP and BAs layer, while in TaX₂ (BSb) the electrons transfer from the BSb layer to TaX₂ layer.

---

1. Introduction

After the successful development of graphene in 2004,¹ researchers isolated and studied more than a dozen 2D materials within less than a decade.² Therefore, the family of 2D materials extended from the carbon materials (graphene) to transition metal dichalcogenides (TMDCs),³ MXene,⁴ layered metal oxides⁵ and many more⁶ with insulating,⁷ semiconducting,⁸ semimetallic,⁹ metallic¹⁰ and superconducting nature.¹¹ The significant interest in 2D materials is attributed to their special physical characteristics that emerge via confinement of the transport of heat and charge to a plane.¹² The unique physical characteristics are expected to make a significant impact across various applications,¹³ spanning from high-performance sensors,¹⁴ storage,¹⁵ catalysis,¹⁶ inert coating,¹⁷ electronic,¹⁸ optoelectronic¹⁹ and spintronic²⁰ devices. In the family of 2D materials, TMDCs with MX₂ (M = transition metal atom, X = chalcogen atom) general formula are of particular importance, where weak van der Waals (vdW) forces hold these layers together, allowing for their easy extraction from the bulk.²¹ The simplicity of their preparation and diverse range of characteristics, make them noteworthy in the realm of 2D materials.²² Similarly, another class of 2D materials based on group III–V semiconductors has been explored both theoretically^23,24 and experimentally.^25,26 The direct band gap and hexagonal lattice structure, identical to graphene, render these materials promising for the next generation of nano²⁷ and optoelectronic device²⁸ applications.

The physical properties of the aforementioned 2D materials come with several key challenges²⁹ such as scalability, the production of high-quality materials with large surface area, and high cost. Current synthesis methods, like chemical vapor deposition (CVD), can be expensive and complex. Stability and durability of some 2D materials can be chemically reactive or sensitive to environmental factors such as air and moisture, which can degrade their properties over time.^30,31 Therefore, controlling the electronic properties and band gap of 2D materials is crucial, while some 2D materials are natural semiconductors, others, like graphene, require engineering to open a band gap for specific applications. Consequently, researchers have focused on the tuning of these materials via several techniques,^32,33 for their useful device applications.¹⁹ In these techniques, stacking of 2D materials in the form of van der Waals heterostructures (vdWHs)³⁴ provides a flexible platform for exploring novel phenomena in the design of nanoelectronic devices.³⁵ Numerous vdWHs, particularly those in the form of semiconductor–semiconductor (SS) contact, have been extensively studied both theoretically^36,37 and experimentally^38,39 for their promising and remarkable applications in the field of optoelectronic devices.⁴⁰ The Schottky barrier (SB) in the metal and semiconductor (MS) vdWHs minimizes resistance at contact, hence tuning (enhancing) the polarity (selectivity) of carriers in the transistor channel (photovoltaic cells), therefore, playing a crucial role in devices.^41,42 These contacts (SS and MS) are fabricated via ultra-thin and flat surfaces without defects and with outstanding chemical (mechanical) stability (flexibility).⁴³

Although, TMDCs have already been used in almost every MS contact,^44–50 a significant gap exists regarding the exploration of 2D TaX₂ (X = S, Se, Te) and BY (Y = P, As, Sb) MS contact. Therefore, in the present work, we have focused on the modelling of TaX₂–BY MS vdWHs. Structural stability, electronic structure, contact type and height of the barrier of the modelled heterostructures are investigated, with the goal of exploring the potential applications of these materials in device fabrications.

2. Computational details

We used density functional theory (DFT) with the PWSCF code⁵¹ with generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) style.⁵² We fixed the convergence criteria for force to 10⁻³ Å⁻¹ and energy to 10⁻⁵ eV for the optimization/relaxation of the lattice constant/atomic positions. We also fixed the cut-off energy to 800 eV and used a 16 × 16 × 1 k-grid for the Brillouin zone integration. To mitigate interactions between neighbouring layers of atoms, we set a vacuum layer with a thickness of 25 Å.

Mechanical stability of these systems are examined using the energy-strain method in the VASPKIT code⁵³ and visualized with the ELATE software.⁵⁴ Thermal (dynamical) stabilities were investigated via AIMD (phonon) simulation (calculations).^55,56 In the case of thermal stability, ab initio molecular dynamics (AIMD) simulations,⁵⁵ through the Nose thermostat algorithm at a temperature of 300 K for a total of 6 ps with a time interval of 1 fs are performed. For dynamical stability, we used a 3 × 3 × 1 supercell consisting of 45 atoms. We have also used density functional perturbation theory (DFPT) with the VASP code⁵⁷ to determine the harmonic second-order interatomic force constants (IFCs). In addition, we employed the PHONOPY code⁵⁸ to calculate the phonon dispersion using the frozen phonon approximation.

Type (height) of the Schottky contact (barrier) is obtained using first principles calculations⁵⁹ using Φ_Bn = E_CBM − E_F and Φ_Bp = E_F − E_VBM, where E_CBM and E_VBM are the energies of the band edges of the semiconducting material and E_F is the Fermi level of the metallic material. Type (n and p) of the Schottky barrier without ΔV were also calculated⁶⁰ using the Schottky–Mott rule; ϕ_Bn = ϕ_{(metallic-monolayer)} − χ_(MS-vdWH) and ϕ_Bp = I_(MS-vdWH) − ϕ_{(metallic-monolayer)}, here ϕ, χ, and I are the work function, electron affinity, and ionization energy, respectively, of the MS vdWHs and corresponding monolayers. Band bending was calculated⁶¹ using Δϕ = ϕ_{(metallic-monolayer)} − ϕ_{(semiconducting-monolayer)}, where ϕ_{(metallic-monolayer)} and ϕ_{(semiconducting-monolayer)} denote the work function of the corresponding metallic and semiconducting monolayers, respectively, in the MS vdWHs.

3. Results and discussion

Although, monolayers of TaX₂ (X = S, Se, Te) and BY (Y = P, As, Sb) have already been investigated in detail in ref. 62 and 63. To verify our present approach, we have further calculated the electronic band structure of TaX₂ (X = S, Se, Te) and BY (Y = P, As, Sb). In agreement with ref. 62 and 63, TaX₂(BY) monolayers exhibit a metallic (direct bandgap semiconducting) nature (see Fig. 1).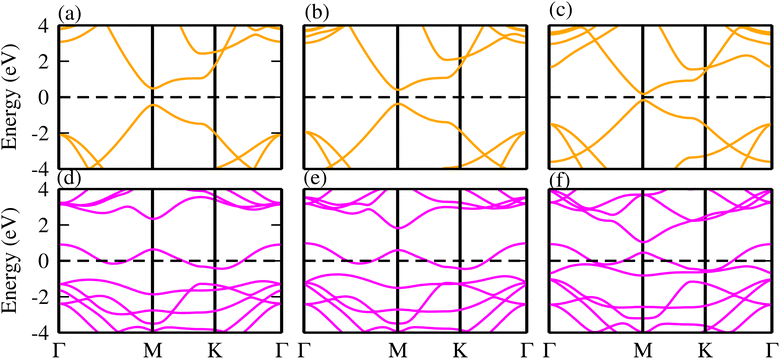

Fig. 1 Electronic band structures of (a) BP, (b) BAs, (c) BSb, (d) TaS₂, (e) TaSe₂ and (f) TaTe₂ monolayers.

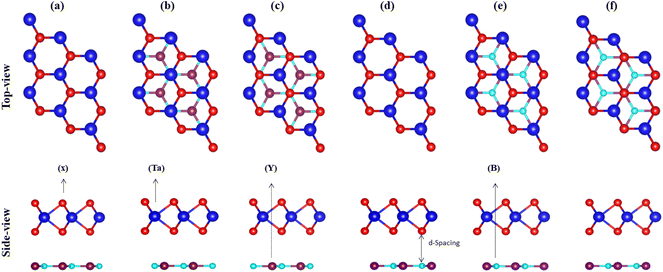
Therefore, using the optimized lattice constant of TaX₂ (X = S, Se, Te)^64,65 and BY (Y = P, As, Sb),^66,67 TaX₂–BY MS contact in six different vdWH stacking configuration patterns are fabricated, see Fig. 2. In (a), the Ta(X) atom of the TaX₂ layer is placed on top of the B(Y) atom of the BY layer. In (b), the Ta atom of the TaX₂ layer is placed on top of the B atom of the BY layer, while the X(Y) atom of the TaX₂(BN) layer is placed on the hexagonal centre. In (c), the X atom of the TaX₂ layer is placed on top of the B atom of the BY layer, while the Ta(Y) atoms of TaX₂(BY) are placed on the hexagonal centre. In (d), the Ta atom of the TaX₂ layer is settled on top of the Y atom of the BY layer. In (e), the Ta atom of the TaX₂ layer is stacked on top of the Y atom of the BY layer, while the X(B) atom of TaX₂(BY) is placed on the hexagonal centre. In (f), the X atom of the TaX₂ is settled on top of the Y atom of BY, while Ta(B) atoms are placed on the hexagonal centre.

Fig. 2 Possible stacking configurations of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs.

Binding energy⁶⁸ and the interlayer distance (d) of all six patterns of TaX₂–BY MS vdWHs are calculated and presented in Table 1. Stacking (b) of TaS₂–BP, (b) of TaS₂–BAs, (b) of TaS₂–BSb, (e) of TaSe₂–BP, (b) of TaSe₂–BAs, (b) of TaSe₂–BSb, (e) of TaTe₂–BP, (e) of TaTe₂–BAs and (d) of TaTe₂–BSb, are found to be the most stable stacking configurations, based on the most smaller (higher) interlayer distance (binding energies),⁶⁸ see Table 1. The variation in stable stacking is due to the induced strain from the distinct chalcogen atoms and the dissimilar interface atoms. The optimized lattice constant and bond length of the most stable stacking configurations are presented in Table 2. Before considering the stable stacking configurations for further investigation, we further confirmed the stability via calculating the mechanical properties of these systems.

Table 1 Binding energy (E_b in eV) and interlayer distance (d in Å) of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs in (a–f) stacking configurations

TaX2–BY		TaS2–BP	TaS2–BAs	TaS2–BSb	TaSe2–BP	TaSe2–BAs	TaSe2–BSb	TaTe2–BP	TaTe2–BAs	TaTe2–BSb
(a)	E b	−0.010	−0.013	−0.025	−0.011	−0.013	−0.019	−0.011	−0.014	−0.019
	d	3.549	3.542	3.062	3.620	3.638	3.574	3.889	3.834	3.811
(b)	E b	−0.016	−0.019	−0.031	−0.017	−0.021	−0.028	−0.018	−0.023	−0.030
	d	3.329	3.327	3.084	3.711	3.406	3.558	3.874	3.880	3.913
(c)	E b	−0.011	−0.014	−0.024	−0.012	−0.015	−0.020	−0.012	−0.015	−0.020
	d	3.378	3.385	3.657	3.444	3.454	3.642	3.626	3.601	3.766
(d)	E b	−0.012	−0.016	−0.025	−0.014	−0.016	−0.021	−0.015	−0.018	−0.049
	d	3.339	3.650	3.639	3.392	3.740	3.606	3.536	3.493	2.293
(e)	E b	−0.015	−0.019	−0.030	−0.018	−0.021	−0.027	−0.019	−0.023	−0.029
	d	3.638	3.661	3.628	3.317	3.765	3.781	3.476	3.486	3.950
(f)	E b	−0.010	−0.013	−0.024	−0.010	−0.013	−0.018	−0.010	−0.012	−0.017
	d	3.576	3.585	3.612	3.738	3.694	3.599	3.934	3.938	3.894

---

Table 2 Lattice constant (a in Å), bond length (in Å), interlayer distance (d in Å), elastic constants (C₁₁ and C₁₂ in N m⁻¹), Young's modulus (E in N m⁻¹), shear modulus (G in N m⁻¹), Poisson's ratio (ν), work function (ϕ in eV), potential (ΔV in eV), effective mass of the carriers , ionization energy (I in eV), electron affinity (χ in eV), and band bending (ΔW in eV) of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs

TaX2–BY	TaS2–BP	TaS2–BAs	TaS2–BSb	TaSe2–BP	TaSe2–BAs	TaSe2–BSb	TaTe2–BP	TaTe2–BAs	TaTe2–BSb
a	3.26	3.35	3.51	3.34	3.43	3.61	3.46	3.54	3.72
M–X	2.46	2.48	2.52	2.58	2.60	2.64	2.79	2.79	2.78
B–N	1.88	1.94	2.08	1.93	1.98	2.10	1.99	2.05	2.32
d	3.33	3.33	3.08	3.32	3.41	3.56	3.48	3.49	2.29
C 11	299.38	282.34	252.80	254.77	252.49	226.39	142.89	156.02	159.40
C 12	84.46	82.65	73.65	79.53	69.60	64.49	62.46	72.88	42.81
E	275.55	258.15	231.34	299.95	233.31	208.02	115.58	121.98	147.90
G	107.46	99.85	89.57	87.62	91.45	80.95	40.21	41.57	58.29
ν	0.282	0.239	0.291	0.312	0.276	0.285	0.437	0.467	0.269
ΔV	4.93	2.22	4.88	7.23	4.41	2.67	4.74	1.64	2.53
ϕ	4.01	3.92	3.65	3.81	3.82	3.63	3.28	3.58	4.01
	0.71	0.61	0.43	0.79	0.68	0.48	0.94	0.79	0.57
	0.66	0.57	0.41	0.75	0.65	0.47	0.91	0.77	0.55
I	4.65	4.59	4.58	4.82	4.79	4.73	5.11	5.05	5.38
χ	4.65	4.58	4.57	4.81	4.79	4.70	5.10	5.04	5.36
ΔW	0.23	0.23	0.23	0.24	0.24	0.24	0.32	0.29	0.24

---

Mechanical stability of the most stable stacking configurations of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWH are assisted via the energy-strain method.^69–71 Using the hexagonal symmetry of TaX₂–BY MS vdWH, two independent elastic constants (C₁₁ and C₁₂), Young's modulus, shear modulus, and Poisson's ratios are calculated and presented in Table 2, that meet the Born criteria: C₁₁ > 0, C₁₂ > 0, and C₁₁ > ∣C₁₂∣.^69–71 Therefore, these findings indicate the high mechanical stability of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWH, in agreement with previous reports.^69–71

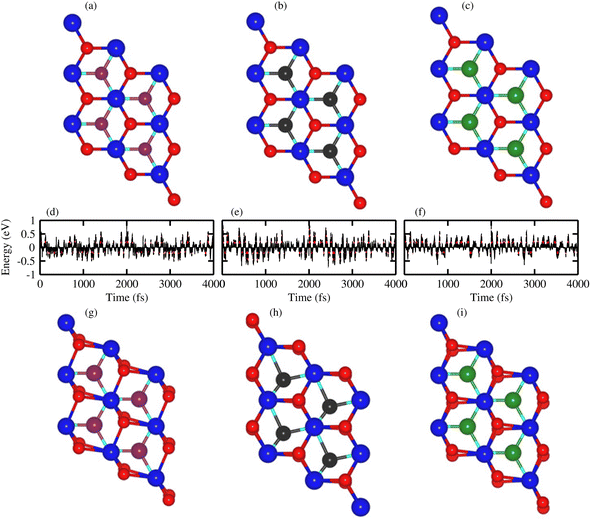
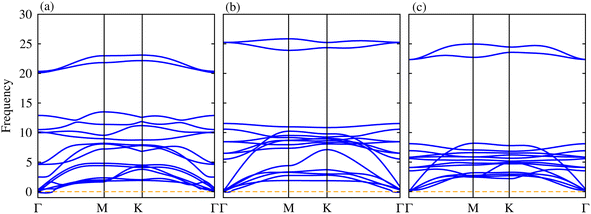
Thermal stability in terms of the fluctuation energy as a function of time, of the energetically most favorable stacking configurations in TaX₂–BY (TaS₂–BP, TaS₂–BAs and TaS₂–BSb), are given in Fig. 3. One can observe that in the case of TaS₂–BP, TaS₂–BAs and TaS₂–BSb, heterostructures after 4 ps, there is no structure distortion. Moreover, through the AIMD simulation, our results demonstrate that the geometrical structure of TaS₂–BP, TaS₂–BAs and TaS₂–BSb is retained after 4000 step simulations and the average value of the total energy remains nearly constant. All these findings demonstrate that TaS₂–BP, TaS₂–BAs and TaS₂–BSb are thermally stable at room temperature.

Fig. 3 Ab initio molecular dynamics simulation of (a, d, and g) TaS₂–BP, (b, e, and h) TaS₂–BAs and (c, f, and i) TaS₂–BSb, van der Waals heterostructures. Geometrical structure (a–c) before heating; (g–i) after heating with (d–f) fluctuating energy.

The phonon dispersion curves in Fig. 4 for the TaS₂–BP, TaS₂–BAs, and TaS₂–BSb MS vdWHs show no imaginary frequencies throughout the Brillouin zone, confirming their dynamic stability. The lack of imaginary modes indicates that the atomic arrangements reside at a local minimum on the potential energy surface, which is a key indicator of structural stability. Using the PBE functional, the electronic band structures are displayed in Fig. 5, where green (red) lines are attributed to the TaX₂(BY) layers in TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs. The electronic band structures in Fig. 5, show that all TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs are metals with type-III band alignment⁷² and look like the sum of band structure of TaX₂ and BY (Y = P, As, Sb) monolayers. The transition of BY (Y = P, As, Sb) to a metal is ascribed to the contribution of metallic states from TaX₂ (X = S, Se, Te) monolayer, enhancing its conductivity and making it suitable for various electronic applications involving Schottky contacts.

Fig. 4 Phonon dispersion curves of (a) TaS₂–BP, (b) TaS₂–BAs and (c) TaS₂–BSb MS vdWHs.

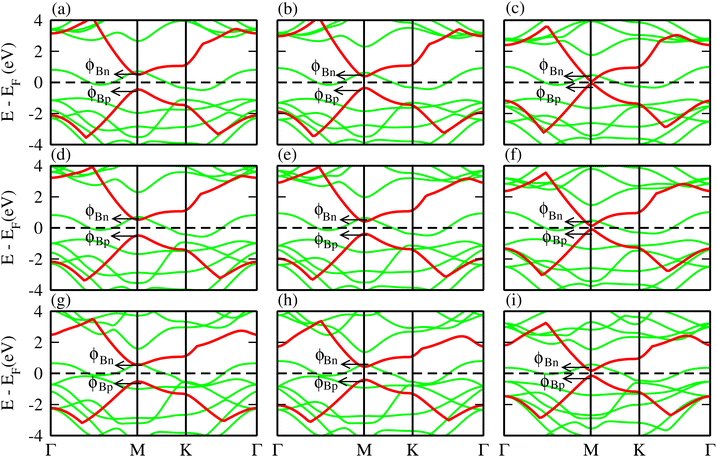Fig. 5 Electronic band structure of (a) TaS₂–BP, (b) TaS₂–BAs, (c) TaS₂–BSb, (d) TaSe₂–BP, (e) TaSe₂–BAs, (f) TaSe₂–BSb, (g) TaTe₂–BP, (h) TaTe₂–BAs and (i) TaTe₂–BSb MS vdWHs.

PDOS of the TaX₂–BY MS vdWHs are presented in Fig. 6, and show that the main contributions at the Fermi level are due to the Ta-d (d_3z²−r², d_xy) and (S, Se, Te)-p orbital of the TaX₂ monolayers (crossing the Fermi level); while both the valence and conduction band without crossing the Fermi level, are due to the B-p_x and (Y = P, As, Sb)-p_z orbitals of the BY monolayer. After stacking, the TaX₂ monolayer shifts the conduction band minimum (CBM) of the BY layer toward the Fermi level due to the difference in electronegativity. The position of these orbitals near to the Fermi level in the valence and conduction bands show that the band structure of BY and TaX₂ monolayers are well preserved in the TaX₂–BY MS vdWHs. The minimum (maximum) of the conduction (valence) band is due to the Ta-d_3z²r² (Ta-d_x²−y², d_xy) orbital with a very small contribution from the Ta-d_x²−y² and d_xy orbitals, see Fig. 6. The B-p_x and p_y orbital dominate the valence band minimum (VBM), with a small contribution from the B-p_z orbitals. Through modelling TaX₂–BY MS vdWHs, we found that strain is induced in the corresponding monolayers due to the lattice mismatch, tuning the coupling between the orbitals of the TMDCs (Ta-d) and chalcogen atoms ((S, Se, Te)-p). Therefore, splitting in the bonding and antibonding states of BY monolayers in TaX₂–BY MS vdWHs fluctuates, and hence the position of the contributing orbital at the Fermi level varies.

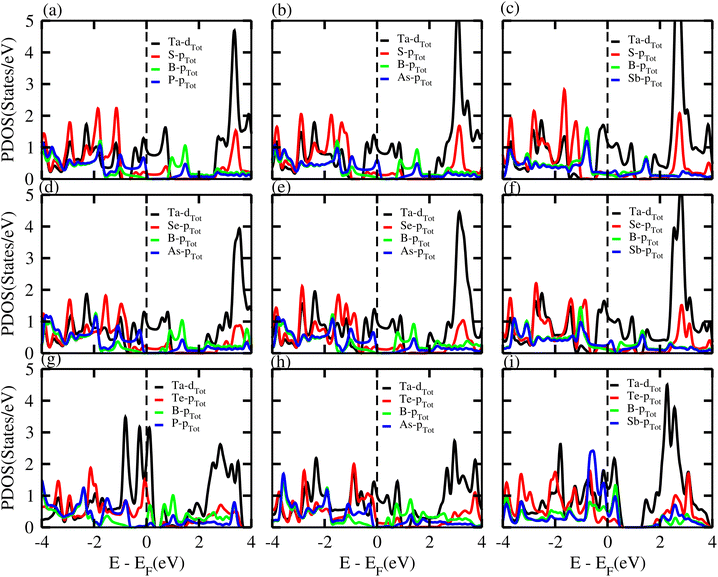Fig. 6 PDOS of (a) TaS₂–BP, (b) TaS₂–BAs, (c) TaS₂–BSb, (d) TaSe₂–BP, (e) TaSe₂–BAs, (f) TaSe₂–BSb, (g) TaTe₂–BP, (h) TaTe₂–BAs and (i) TaTe₂–BSb, vdWHs.

Furthermore, for the use of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs in device applications, effective mass and carrier mobility are investigated and related by μ = eτ/m*.⁷³ Thus, to evaluate the carrier mobility of TaX₂–BY MS vdWHs, effective mass is calculated using⁷⁴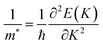 where, ℏ is Planck’s constant and K is the wave vector. Based on the above equation, using the parabolic fitting of the CB and VB of TaX₂–BY MS vdWHs, the calculated effective mass for electrons (holes) are given in Table 2. Quite a small effective mass in the case of TaS₂–BSb, TaSe₂–BSb and TaTe₂–BSb MS vdWHs, exhibit high carrier mobility, and hence show potential for efficient nanoelectronic devices.

Relative locations of the metal (TaX₂) with semiconductor (BY) band edges in TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs establish the Schottky or ohmic junctions across the interface. Tuning the Schottky barrier (SBH) can change the current flow across the interface of the TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs, hence boosting the device performance.^75,76 The band structures in Fig. 5 indicate that the Fermi level of TaX₂ (metal layer) sits in the band edges of BY (semiconductor layer), and hence establish Schottky contacts⁷⁷ at the interface of TaX₂–BY MS vdWHs. The type of Schottky contact (n-type or p-type) is obtained using the Schottky–Mott rule,⁷⁸ see computational details. The calculated values of the Schottky barrier ϕ_Bn and ϕ_Bp using first principles calculations and the Schottky–Mott rule, are given in Fig. 7, which shows that ϕ_Bn of all stacking configurations is smaller than ϕ_Bp, suggesting that they form an n-type Schottky contact. Therefore, the MS vdWHs under consideration favor electron conduction over hole conduction, and hence have significant implications in transistors, sensors, photodetectors, and other electronic components.⁷⁹ It is clearly observed that the SBH increases (decreases) from P to As to Sb in TaS₂–BY (TaTe₂–BY) MS vdWHs. Moreover, the metallic nature of these heterostructures suppress the metal induced gap states (MIGS) in BY (Y = P, As, Sb) monolayers, hence, leading to weak Fermi Level Pinning (FLP). Weak vdW interactions redistribute the charge density at the interface, see Fig. 9 (discussed later on), and hence establish interface dipoles (ID). Therefore, neglecting the metal semiconductor interaction (without considering ΔV) should ideally follow the predictions of the Schottky–Mott rule. Therefore, type (n and p) of the Schottky barrier without ΔV were also calculated⁶⁰ using ϕ_Bn = ϕ_{(metallic-monolayers)} − χ_(vdWH) and ϕ_Bp = I_(vdWH) − ϕ_{(metallic-monolayers)}. These IDs may lead to deviation from the Schottky–Mott limit, due to shifting of the electronic levels and FLP effect at the interface from their original positions.⁸⁰ The band bending of the TaX₂–BY systems reveals the presence of both p-type and n-type Schottky barrier even without the transfer of charge between the corresponding monolayers. When Δϕ are greater than 0 or Δϕ is less than 0, it signifies the formation of n-type and p-type Schottky contacts.⁵⁰ In the TaX₂–BY vdWHs under study, Δϕ is greater than 0, see Table 2. This observation suggests that charge will preferentially flow from metal to semiconductor, indicating n-type contact due to the high values of Δϕ (greater than 0), which demonstrate that holes will flow from TaX₂ to the BY layer. The controllable electronic properties and formation of the Schottky contact in TaX₂–BY MS vdWHs makes it a potential candidate for Schottky nanodevices.⁵⁰

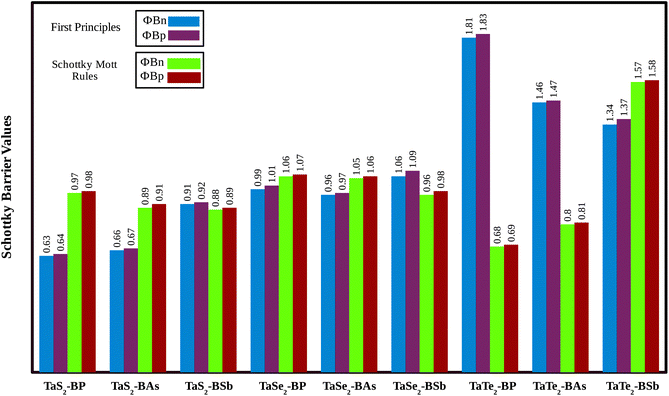Fig. 7 Schottky barrier height calculated using the Schottky–Mott rule and first principles calculation of TaX₂ (X = S, Se, Te)–BY (Y = P, As, Sb) MS vdWHs.

In the case of TaX₂–BY MS vdWHs, the TaX₂ (BP, BAs) layer exhibits shallower (deeper) potential confirming charge transfer from TaX₂ to the BP and BAs layer. On the contrary, in the case of TaX₂ (X = S, Se, Te)–BSb, the TaX₂ (BSb) layer is deeper (shallower), which confirms the transfer of charge from the BSb layer to TaX₂, due to the fact that BSb has a higher work function than TaX₂. The calculated ΔV varies within (1.64 to 7.23 eV) due to the difference in electronegativity among the atoms⁸¹ at the interface. For both TaX₂ and BY monolayers in the form of TaX₂–BY MS vdWHs, the electrostatic potential effectively controls charge movement at the interface, contributing to increased energy conversion efficiency. The work function (ϕ) of TaX₂–BY MS vdWHs – defined as the difference between the vacuum level and Fermi level – was calculated using average electrostatic potential as displayed in Fig. 8. ϕ predominantly depends on the condition of the material surface due to changes in surface electric field settings and electron distribution at the interface. The calculated ϕ for of TaX₂–BY MS vdWHs lies in the range 3.285–4.009 eV, see Table 2, which shows the potential for field effect transistors.⁸²

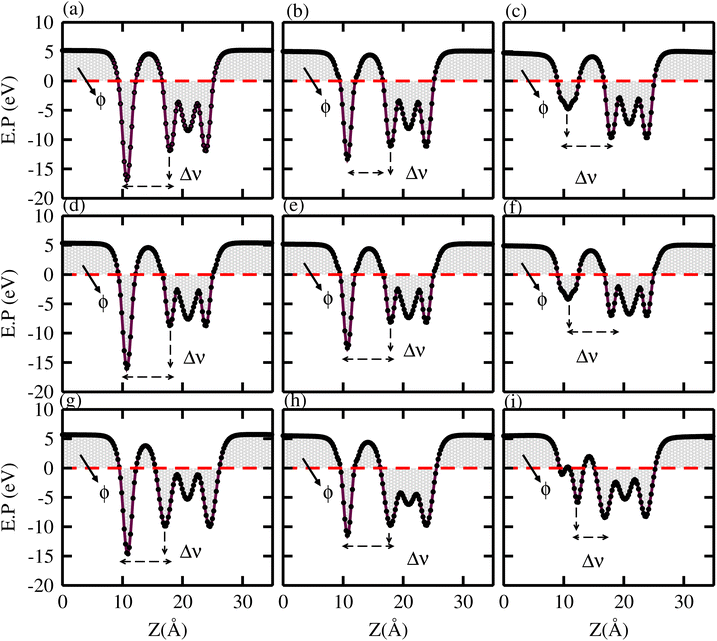Fig. 8 Average electrostatic potential of (a) TaS₂–BP, (b) TaS₂–BAs, (c) TaS₂–BSb, (d) TaSe₂–BP, (e) TaSe₂–BAs, (f) TaSe₂–BSb, (g) TaTe₂–BP, (h) TaTe₂–BAs, and (i) TaTe₂–BSb, MS vdWHs.

To see the contact charge redistribution, we have calculated the charge density difference of the TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs using^83,84 ▽ρ = ρ_MSvdWHs − ρ_monolayer-I − ρ_monolayer-II. In the case of TaX₂–BY (X = S, Se, Te; Y = P, As) MS vdWHs, charge depletion (accumulation) around the TaX₂ (BP) layer indicates loss (gain) of electrons in TaX₂ (BP, BAs). For TaX₂–BSb MS vdWHs, TaX₂ (BSb) gain (loss) of electrons in this region makes an electron (hole)-rich region.⁸⁵ The BSb layer becomes a depletion region with fewer electrons, resulting in a hole-rich environment, while the TaX₂ layer accumulates electrons and becomes electron-rich as shown in Fig. 9. Quantitative behaviour of charge transfer, analysed via Bader charges, show a maximum of 0.065409e and minimum of 0.000399e transferred from TaX₂ to the BY monolayer, see Table 3. The phenomena of the transfer of charge shows a strong interlayer coupling and vdWh interaction established at the interface of TaX₂ and BY monolayers in TaX₂–BN MS vdWHs. A charge transportation built-in-electric field in the interface, creates a region where charges are separated, generating an electric field at the interface⁸⁶ which enhances the carrier mobility along with the number of carriers (holes and electrons). A similar result is also confirmed via experiments in graphene/GaSe ⁸⁷ and graphene/MoS₂.⁸⁸ Ionization potential (I); I = E_vac − E_VBM, for the TaX₂–BY MS contact in Table 2, helps in determining the Schottky barrier height, crucial for understanding the behavior of MS contacts.

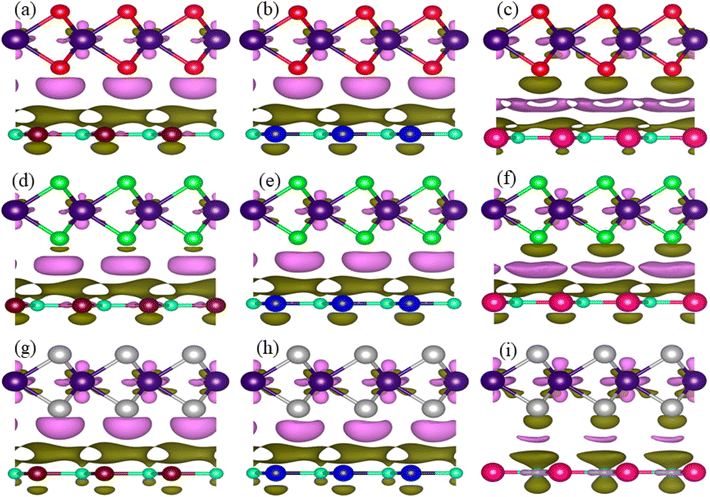Fig. 9 Charge density difference of (a) TaS₂–BP, (b) TaS₂–BAs, (c) TaS₂–BSb, (d) TaSe₂–BP, (e) TaSe₂–BAs, (f) TaSe₂–BSb, (g) TaTe₂–BP, (h) TaTe₂–BAs, and (i) TaTe₂–BSb, MS vdWHs.

Table 3 Charge redistribution at the interface of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs: e⁻ (h⁺) shows transfer of electrons (holes) from one layer to another

TaX2–BY	TaS2–BP	TaS2–BAs	TaS2–BSb	TaSe2–BP	TaSe2–BAs	TaSe2–BSb	TaTe2–BP	TaTe2–BAs	TaTe2–BSb
TaX2	0.026 (h^+)	0.038 (h^+)	0.065 (e^−)	0.013 (h^+)	0.024 (h^+)	0.050 (e^−)	0.001 (h^+)	0.008 (h^+)	0.033 (e^−)
BY	0.027 (e^−)	0.039 (e^−)	0.065 (h^+)	0.012 (e^−)	0.025 (e^−)	0.051 (h^+)	0.001 (e^−)	0.009 (e^−)	0.032 (h^+)

---

4. Conclusion

Using DFT calculations and electronic band structure, the contact (barrier) type (height) at the interface of TaX₂–BY (X = S, Se, Te; Y = P, As, Sb) MS vdWHs are investigated. The stability of these systems are confirmed via binding energies, mechanical (born criteria), properties, AIMD simulation and phonon spectra calculations. Electronic band structures confirm the metallic behaviour of TaX₂–BY MS vdWHs with weak vdW interactions in the corresponding monolayers. The quite small effective mass in the case of TaS₂–BSb, TaSe₂–BSb and TaTe₂–BSb MS vdWHs, exhibit high carrier mobility and hence show potential for high speed nanoelectronic applications. n-type Schottky contact at the interface of TaX₂–BY MS vdWHs favor electron conduction over hole conduction, hence has significant applications in transistors, sensors, photodetectors, and other electronic components. Large potential drop in the case of TaS₂–BP, TaS₂–BSb, TaSe₂–BP, TaSe₂–BAs and TaTe₂–BP of the TaX₂–BY MS vdWHs, suggests a considerable electrostatic field at the interface, which controls the charge transportation and strengthens the power conversion efficiency. Analysis of the Bader charges, show that a maximum (minimum) of 0.065409 (0.000399)e are transferred from the TaX₂(BY) monolayer. The work function for the TaX₂–BY MS contact lies in the 3.285–4.009 eV range, which shows potentiality for FET.

Data availability

The data that support the findings of this study are available on request from the corresponding author.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge Researcher's Supporting Project Number (RSP2024R511), King Saud University, Riyadh, Saudi Arabia. The authors also express their deep gratitude to the Jiangsu University, China, for provision of computational resources.

References

1. H. C. Lee, W. W. Liu, S. P. Chai, A. R. Mohamed, C. W. Lai, C. S. Khe and N. M. S. Hidayah, Procedia Chem., 2016, 19, 916921.
2. D. Geng and H. Y. Yang, Adv. Mater., 2018, 30, 1800865.
3. H. Li, Y. Shi, M. H. Chiu and L. J. Li, Nano Energy, 2015, 18, 293305.
4. J. Fatima, M. B. Tahir, A. Rehman, M. Sagir, M. Rafique, M. A. Assiri and M. Alzaid, Mater. Sci. Eng., B, 2023, 289, 116230.
5. M. E. Landis, B. A. Aufdembrink, P. Chu, I. D. Johnson, G. W. Kirker and M. K. Rubin, J. Am. Chem. Soc., 1991, 113, 3189.
6. K. Khan, A. K. Tareen, M. Aslam, R. Wang, Y. Zhang, A. Mahmood and Z. Guo, J. Mater. Chem. C, 2020, 8, 387440.
7. A. Raza, U. Qumar, J. Hassan, M. Ikram, A. Ul-Hamid, J. Haider and S. Ali, Appl. Nanosci., 2020, 10, 3875.
8. A. Chaves, J. G. Azadani, H. Alsalman, D. R. Da Costa, R. Frisenda, A. J. Chaves and T. Low, npj 2D Mater. Appl., 2020, 4, 29.
9. L. Cao, G. Zhou, Q. Wu, S. A. Yang, H. Y. Yang, Y. S. Ang and L. K. Ang, Phys. Rev. Appl., 2020, 13, 054030.
10. W. Xu, Y. Ke, Z. Wang, W. Zhang and A. T. S. Wee, Surf. Sci. Rep., 2021, 76, 100542.
11. Y. Zhang, M. Xu, Q. Zeng, J. Hao and Y. Li, Mater. Today Electronics, 2023, 5, 100053.
12. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez and J. E. Goldberger, ACS Nano, 2013, 7, 2898.
13. F. R. Fan, R. Wang, H. Zhang and W. Wu, Chem. Soc. Rev., 2021, 50, 10983.
14. S. Mehdi Aghaei, A. Aasi and B. Panchapakesan, ACS Omega, 2021, 6, 2450.
15. B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 17.
16. A. Gupta, T. Sakthivel and S. Seal, Prog. Mater. Sci., 2015, 73, 44126.
17. G. Wang, P. Yang and E. R. Batista, Phys. Rev. Mater., 2020, 4, 024001.
18. N. Izyumskaya, D. O. Demchenko, V. Avrutin, Ü. Özgür and H. Morkoç, Turk. J. Phys., 2014, 38, 478496.
19. S. Kang, D. Lee, J. Kim, A. Capasso, H. S. Kang, J. W. Park and G. H. Lee, 2D Mater., 2020, 7, 022003.
20. Y. P. Feng, L. Shen, M. Yang, A. Wang, M. Zeng, Q. Wu and C. R. Chang, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2017, 7, e1313.
21. M. Zhao, Y. Hao, C. Zhang, R. Zhai, B. Liu, W. Liu and H. Li, Crystals, 2022, 12, 1087.
22. Y. C. Lin, R. Torsi, R. Younas, C. L. Hinkle, A. F. Rigosi, H. M. Hill and J. A. Robinson, ACS Nano, 2023, 17, 9694.
23. M. P. Mikhailova, K. D. Moiseev and Y. P. Yakovlev, Semiconductors, 2019, 53, 273290.
24. H. J. Joyce, Q. Gao, H. H. Tan, C. Jagadish, Y. Kim, J. Zou and M. B. Johnston, Prog. Quantum Electron., 2011, 35, 2375.
25. A. K. Singh, H. L. Zhuang and R. G. Hennig, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 245431.
26. M. Buscema, J. O. Island, D. J. Groenendijk, S. I. Blanter, G. A. Steele, H. S. van der Zant and A. Castellanos-Gomez, Chem. Soc. Rev., 2015, 44, 3691.
27. M. Zeng, Y. Xiao, J. Liu, K. Yang and L. Fu, Chem. Rev., 2018, 118, 6236.
28. C. Lan, Z. Shi, R. Cao, C. Li and H. Zhang, Nanoscale, 2020, 12, 11784.
29. S. Yu, X. Wu, Y. Wang, X. Guo and L. Tong, Adv. Mater., 2017, 29, 1606128.
30. S. K. Chakraborty, B. Kundu, B. Nayak, S. P. Dash and P. K. Sahoo, iScience, 2022, 25, 103942.
31. C.-L. Lo, B. A. Helfrecht, Y. He, D. M. Guzman, N. Onofrio, S. Zhang, D. Weinstein, A. Strachan and Z. Chen, J. Appl. Phys., 2020, 128, 080903.
32. A. J. Watson, W. Lu, M. H. Guimarães and M. Stöhr, 2D Mater., 2021, 8, 032001.
33. X. Wang, Y. Sun and K. Liu, 2D Mater., 2019, 6, 042001.
34. J. Qi, Z. Wu, W. Wang, K. Bao, L. Wang, J. Wu and Q. He, Int. J. Extreme Manuf., 2023, 5, 022007.
35. Z. H. Li, J. N. Han, S. G. Cao and Z. H. Zhang, Appl. Surf. Sci., 2023, 636, 157766.
36. M. K. Mohanta, A. Kishore and A. De Sarkar, Nanotechnology, 2020, 31, 495208.
37. A. Albar and S. A. Aravindh, J. Phys.: Condens. Matter, 2021, 33, 475701.
38. Q. Li, J. Meng and Z. Li, J. Mater. Chem. A, 2022, 10, 8107.
39. Y. Xiong, D. Xu, Y. Feng, G. Zhang, P. Lin and X. Chen, Adv. Mater., 2023, 35, 2206939.
40. T. Su, Y. Li, Q. Wang, W. Zhao, L. Cao and Y. S. Ang, J. Phys. D: Appl. Phys., 2023, 56, 234001.
41. H. S. Nalwa, RSC Adv., 2020, 10, 30529.
42. S. Li, F. Wang, Y. Wang, J. Yang, X. Wang, X. Zhan and Z. Wang, Adv. Mater., 2024, 36, 2301472.
43. R. Yang, J. Fan and M. Sun, Front. Phys., 2022, 17, 43202.
44. C. Kim, I. Moon, D. Lee, M. S. Choi, F. Ahmed, S. Nam, Y. Cho, H.-J. Shin, S. Park and W. J. Yoo, ACS Nano, 2017, 11, 1588.
45. Y. Guo, D. Liu and J. Robertson, ACS Appl. Mater. Interfaces, 2015, 7, 25709.
46. J. Kang, W. Liu, D. Sarkar, D. Jena and K. Banerjee, Phys. Rev. X, 2014, 4, 031005.
47. C. Gong, L. Colombo, R. M. Wallace and K. Cho, Nano Lett., 2014, 14, 1714.
48. H. Khan, M. U. Ashraf, M. Idrees, H. U. Din, C. V. Nguyen and B. Amin, RSC Adv., 2022, 12, 12292.
49. M. U. Ashraf, H. Khan, M. Munawar, H. Ud Din, M. Idrees, M. Bilal, Y. Saeed, M. Shafiq and B. Amin, Mater. Sci. Semicond. Process., 2022, 141, 106424.
50. U. Khan, B. Ali, H. Ullah, M. Idrees, C. Nguyen and B. Amin, Micro Nanostruct., 2024, 187, 207765.
51. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
53. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
54. R. Gaillac, P. Pullumbi and F.-X. Coudert, J. Phys.: Condens. Matter, 2016, 28, 275201.
55. R. Yuan, J. A. Napoli, C. Yan, O. Marsalek, T. E. Markland and M. D. Fayer, ACS Cent. Sci., 2019, 5, 1269.
56. O. I. Malyi, K. V. Sopiha and C. Persson, ACS Appl. Mater. Interfaces, 2019, 11, 24876.
57. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169.
58. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 134106.
59. J. Bardeen, Phys. Rev., 1947, 71, 717.
60. Y. Liu, P. Stradins and S.-H. Wei, Sci. Adv., 2016, 2, e1600069.
61. B. Liu, L. Wu, Y. Q. Zhao, L. Z. Wang and M. Q. Caii, Phys. Chem. Chem. Phys., 2016, 18, 19918.
62. N. Guo, X. Fan, Z. Chen, Z. Luo, Y. Hu, Y. An and S. Ma, Comput. Mater. Sci., 2020, 176, 109540.
63. M. Xie, S. Zhang, B. Cai, Z. Zhu, Y. Zou and H. Zeng, Nanoscale, 2016, 8, 13407.
64. Y. Zhang, Z. Tong, A. Pecchia, C. Yam, T. Dumitric and T. Frauenheim, Nanoscale, 2022, 14, 13053.
65. Y. Ding, Y. Wang, J. Ni, L. Shi, S. Shi and W. Tang, Phys. B, 2011, 406, 2254.
66. B. Onat, L. Hallioglu, S. Ipek and E. Durgun, J. Phys. Chem. C, 2017, 121, 4583.
67. H. Kolavada, D. J. Trivedi, P. N. Gajjar and S. K. Gupta, J. Energy Storage, 2023, 72, 108444.
68. B. Amin, N. Singh and U. Schwingenschlögl, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 075439.
69. G. Barik and S. Pal, Phys. Chem. Chem. Phys., 2020, 22, 1701.
70. X. Zhu, H. Jiang, Y. Zhang, D. Wang, L. Fan, Y. Chen, X. Qu, L. Yang and Y. Liu, Molecules, 2023, 28, 5607.
71. M. U. Ashraf, Y. Xu, M. Yar, X. Ni and F. Tian, Mater. Sci. Semicond. Process., 2024, 183, 108775.
72. C. Lei, Y. Ma, X. Xu, T. Zhang, B. Huang and Y. Dai, J. Phys. Chem. C, 2019, 123, 23089.
73. Z. Hou, Y. Xiao and L. D. Zhao, Nanoscale, 2020, 12, 12741.
74. S. Rezaee, A. Boochani, M. Majidiyan, A. Ghaderi, S. Solaymani and M. Naseri, Rare Met., 2014, 33, 615.
75. X. Zhang, B. Liu, L. Gao, H. Yu, X. Liu, J. Du and Y. Zhang, Nat. Commun., 2021, 12, 1522.
76. R. S. Chen, G. Ding, Y. Zhou and S. T. Han, J. Mater. Chem.C, 2021, 9, 11407.
77. Z. Zhang, Y. Gong, X. Zou, P. Liu, P. Yang, J. Shi and Y. Zhang, ACS Nano, 2018, 13, 885.
78. W. Ai, Y. Shi, X. Hu, J. Yang and L. Sun, ACS Appl. Electron. Mater., 2023, 5, 5606.
79. J. F. Liao, W. Q. Wu, Y. Jiang, J. X. Zhong, L. Wang and D. B. Kuang, Chem. Soc. Rev., 2020, 49, 354.
80. A. Khan, H. U. Din, M. Idrees, F. Khan, T. A. Alrebdi, C. V. Nguyen, M. Shafiq and B. Amin, Phys. Lett. A, 2019, 383, 125867.
81. M. Ahmadi, L. Collins, K. Higgins, D. Kim, E. Lukosi and S. V. Kalinin, ACS Appl. Mater. Interfaces, 2019, 11(44), 41551.
82. C. Liu, Y. Xu and Y. Y. Noh, Mater. Today, 2015, 18, 79.
83. H. T. Nguyen, M. M. Obeid, A. Bafekry, M. Idrees, T. V. Vu, H. V. Phuc and C. V. Nguyen, Phys. Rev. B, 2020, 102, 075414.
84. K. D. Pham, N. N. Hieu, H. V. Phuc, I. A. Fedorov, C. A. Duque, B. Amin and C. V. Nguyen, Appl. Phys. Lett., 2018, 113, 171605.
85. M. Kiguchi, M. Nakayama, K. Fujiwara, K. Ueno, T. Shimada and K. Saiki, Jpn. J. Appl. Phys., 2003, 42, L1408.
86. X. Yue, J. Fan and Q. Xiang, Adv. Funct. Mater., 2022, 32, 2110258.
87. Z. Ben Aziza, H. Henck, D. Pierucci, M. G. Silly, E. Lhuillier, G. Patriarche, F. Sirotti, M. Eddrief and A. Ouerghi, ACS Nano, 2016, 10, 9679.
88. D. Pierucci, H. Henck, J. Avila, A. Balan, C. H. Naylor, G. Patriarche, Y. J. Dappe, M. G. Silly, F. Sirotti, A. C. Johnson, M. C. Asensio and A. Ouerghi, Nano Lett., 2016, 16, 4054.

---