Open Access Article
Open Access ArticleFacile control of giant green-emission in multifunctional ZnO quantum dots produced in a single-step process: femtosecond pulse ablation†
Anubhab
Sahoo
 a,
Tejendra
Dixit
a,
Tejendra
Dixit
 b,
Anshu
Kumari
b,
Anshu
Kumari
 c,
Sharad
Gupta
c,
Sharad
Gupta
 d,
R.
Kothandaraman
d,
R.
Kothandaraman
 e,
P. P.
Rajeev
f,
M. S. Ramachandra
Rao
*ag and
Sivarama
Krishnan
e,
P. P.
Rajeev
f,
M. S. Ramachandra
Rao
*ag and
Sivarama
Krishnan
 *ag
*ag
aDepartment of Physics, Indian Institute of Technology Madras, Chennai-600036, India, +9144 2257 5898. E-mail: srkrishnan@iitm.ac.in
bOptoelectronics and Quantum Devices Group, Department of Electronics and Communication Engineering, Indian Institute of Information Technology Design and Manufacturing Kancheepuram, Chennai-600127, India
cDepartment of Physiology, School of Medicine, University of Maryland, Baltimore-21201, USA
dDisciple of Biosciences and Biomedical Engineering, Indian Institute of Technology Indore, Indore-453552, India
eDepartment of Chemistry, Indian Institute of Technology Madras, Chennai-600036, India
fCentral Laser Facility, STFC Rutherford Appleton Laboratory, Harwell Oxford, Didcot, Oxfordshire OX11 0QX, UK
gQuantum Center of Excellence for Diamond and Emergent Materials (QuCenDiEM) Group, Indian Institute of Technology Madras, Chennai-600036, India
First published on 15th November 2024
Abstract
Controlling both UV and visible emissions in ZnO quantum dots (QDs) poses a significant challenge due to the inherent introduction of defects during the growth process. We have refined the photoluminescence (PL) emission characteristics of ZnO QDs through a single-step, reagent-free femtosecond pulsed laser ablation in liquid (fs-PLAL) technique. The ratio of the near band edge (NBE) to deep-level emission (DLE), which determines the shape of the QDs' optical emission spectrum, is precisely controlled by the ablation laser pulse parameters—namely, pulse energy and temporal duration. Having established our ability to control the optical properties, we have investigated the mechanisms and physics involved in controlling optical emission. The key highlight of the work is that ablation with a fs-pulse induces substantial defect states without altering the particle size, with the extent of the effect being dependent on the pulse energy and pulse duration. The spectroscopic techniques inducing Raman spectroscopy, excitation power dependent PL and transient PL study provided deep insight into the PL emission properties of these similarly sized QDs. The improved DLE in these laser-ablated QDs is explained by a surface-recombination-layer approximation process employing steady-state and transient PL. Moreover, we have demonstrated the applicability of green emission for pH sensing within a linear range of 7–10 and highlight the inherent antibacterial properties of these QDs.
1 Introduction
Multifunctional semiconducting quantum dots (QDs) have attracted remarkable attention as potential materials for application in the field of biotechnology,1,2 sensors,3–5 and optoelectronic devices.6–9 In order to accomplish these applications, materials must have certain crucial features, such as tunable optical properties, photostability, thermal and chemical stability, biocompatibility, and so on. In particular, a photodetector demands high photostability under prolonged light exposure;10,11 photocatalysis requires chemical stability in various pH environments in solution;12–14 and bioimaging necessitates biocompatibility and photo-chemical stability in various solvent media.15,16 Wide bandgap semiconductor ZnO QDs can offer tunable luminescence properties, large exciton binding energy at room temperature, and high linear and nonlinear absorption coefficients17 due to the confinement effect. These naturally biocompatible ZnO QDs can be tuned to have controllable surface defects, hence tuning the luminescence characteristics. This makes ZnO QDs a potential candidate for optoelectronic applications such as UV detectors,18,19 UV emitters,20 active media in solar cells,21,22 photocatalysis,23,24 fluorescent labeling25,26 and biomedical applications such as drug delivery,27 anticancer activity,15 orthodontic adhesives28 as well as bio-imaging.2,29,30 Therefore, it is necessary to synthesize QDs with tunable defect or surface states in order to manipulate the absorption and emission properties by a biocompatible technique. In addition an extensive study is required to understand these optoelectronic properties in the presence of various pH environments.Tunability of photoluminescence (PL) emission in ZnO QDs is one of the key challenges to establish the optoelectronic applications. Both intrinsic and induced defects during pre and post-synthesis can affect the luminescence properties of ZnO in the UV-visible region.31 ZnO displays two distinct peaks in its PL analysis: one corresponding to near band edge emission (NBE), which falls within the UV range, and another corresponding to deep-level emission (DLE), which falls within the visible range. Only a few studies have shown the ability to regulate defect states, namely the NBE/DLE ratio, in pure ZnO QDs. Furthermore, achieving control over the DLE through a single-step synthesis procedure continues to be a challenging task.
The visible emission of the ZnO QDs in the PL spectra is highly influenced by surface states that can be engineered by heat treatment, adsorption of functional groups, etc.32–34 The formation of surface defects usually depends on the synthesis process and the growth environment. Though the shape and size of the QDs influence the DLE,35 the surface defects can selectively control the DLE. There are only a few methods adopted in the past to systematically control the DLE, such as plasma treatment of ZnO QDs by coating Au and Ar–SF6,36,37 doping of rare-earth metals,38–40 and sulfurization and desulfurization followed by annealing of nanostructures.41 Many of these techniques involve multiple steps, typically after introducing materials to the host via doping or gas treatment. This process may either impede the realization of further applications or potentially harm the inherent biocompatibility of ZnO. This motivates the need for a single-step method that is reagent-free and residue-less, which is also capable of controlling and tuning the optical properties of this versatile multi-functional material. Discussing defects in pristine ZnO QDs involves three key aspects: (a) the impact of Urbach energy on DLE, which is limited to NBE for <10 nm QDs, (b) the causes of enhanced DLE emission in QDs of similar size, and (c) selective control of the depletion layer on the surface of QDs and its impact on PL and transient PL. These aspects have been meticulously investigated in this article, and plausible mechanisms have been discussed.
Hence, it is crucial to choose the synthesis process based on physical or chemical properties desired for an application. Interestingly, pulsed laser ablation in liquid (PLAL) creates QDs without residues in a single-step method.42–45 Although most studies on the synthesis of ZnO QDs using PLAL concentrate on laser energy or fluence during the laser ablation process, variation of the pulse-width was not considered for discussion.46–49 For longer pulse regimes, i.e. nanoseconds and picoseconds (>10 ps), several studies demonstrated the preparation of the ZnO QDs from a zinc target (foil)46–48 and ZnO pellet directly,46,50 where the size of nanoparticles was manipulated using pulse energy at a constant pulse-width. The recent work on femtosecond laser ablation in water demonstrated the preparation of ZnO QDs from a zinc plate at different pulse energies at a constant pulse-width of 50 fs, resulting in the variation of the QD size distribution.49 The fixed pulse-width of nanosecond and picosecond laser systems limits the experimental conditions. In contrast, femtosecond pulses, which are sensitive to dispersion, can be easily adjusted over a span of several hundred femtoseconds. Apart from the average pulse power, the nonlinear interactions of pulses are very sensitive to the pulse-width due to the field-dependent avalanche process.51 In such a short pulse regime, ablation pulse intensity matters significantly compared to laser fluence. Despite substantial research, controlled tuning of DLE to NBE in pristine ZnO QDs, notably in the single-step process, has not been anticipated or realized. To our knowledge, for the first time, this article presents the facile control of essential optoelectronic properties in the fs-PLAL process by varying the control parameters including both pulse width and pulse energy.
2 Results and discussion
2.1 Photoluminescence and the fs-PLAL mechanism
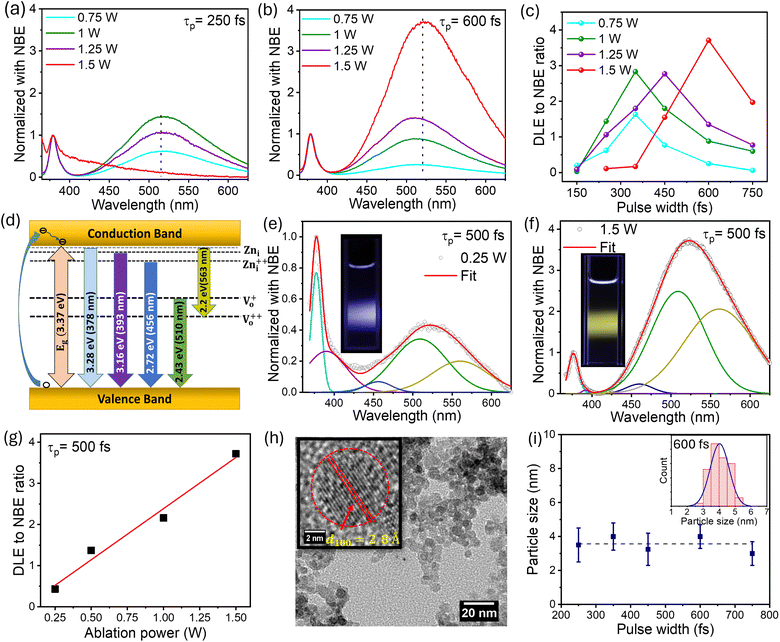
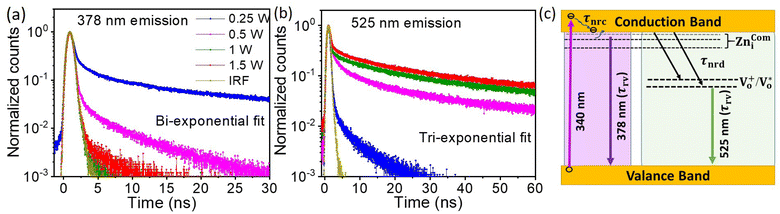
The ZnO QDs synthesized using the fs-PLAL method have been optimized by controlling the process parameters, such as the pulse-width and the average power of the ablation pulses. A detailed explanation of the synthesis of ZnO QDs is provided in Section 1 of the ESI (ESI).† The ZnO QDs were prepared with a wide range of pulse-width variation, starting from 150 fs to 750 fs, and the PL spectra were recorded at 325 nm excitation wavelength. For a clear understanding, the spectra were normalized with respect to the peak intensity of the NBE. Fig. 1 depicts the comparison of two of the PL spectra in panels (a) and (b) for pulse-widths of 250 fs and 750 fs, respectively. A systematic variation in the PL spectra recorded for the samples prepared at 250 fs to 750 fs can be found in ESI (ESI) Fig. S2.† For each pulse-width, we are demonstrating the PL spectra of the samples prepared at different pulse-widths with different ablation powers from 0.75–1.5 W and normalized with respect to the NBE peak. From Fig. 1(c), it is evident that the deep-level emission (DLE) peaked ≈ at 523 nm amplitude increases steadily with increasing pulse-width to a maximum and then starts to decrease for each ablation power. The ratio of DLE to NBE peaks was extracted from these curves to evidence optimal ablation pulse-widths for each ablation power, e.g., pulses with temporal widths between 450 and 600 fs are optimal for maximizing the DLE/NBE ratio (intensity ratio). This clearly demonstrates that the giant-green emission observed in these fs-PLAL synthesized pristine ZnO QDs can be controlled by choosing a suitable pulse-width.The PL measurement is the most straightforward technique for quantifying the defect states present in the material. The NBE peak asymmetry culminated in a sharp peak at 378 nm with a tail state emission at 393 nm.52 The 378 nm emission can be assigned to the band-to-band transition, with a loss of 60 meV due to exciton binding energy.52 The emission tail from 390–410 nm is primarily related to the transitions from the zinc interstitial (Zni) state to the valence band.53,54 Green luminescence (2.4–2.5 eV) is the peak most surveyed in the PL spectra of ZnO; however, the origin of green emission still needs to be better understood. There are two very convenient explanations for the green emission, which are the transition of electrons from singly ionized oxygen vacancies to the valence band Vo52,54,55 while others claim transitions from zinc vacancies VZn as the possible reason.56 Furthermore, the peak centered at around 525 nm can be deconvoluted into two peaks with peak positions at 510 nm and 560 nm, attributed to charged oxygen vacancies present in the ZnO QDs.55 Keeping these spectral positions constant, we have deconvoluted the PL spectra to five Gaussian fits and suggested a possible band diagram for the emission spectra. As shown in Fig. 1(d) and (f), the deconvoluted spectral lines are as follows: (i) the peak at 378 nm corresponds to the band-to-band transition. (ii) The tail emission at 392 nm is attributed to the transition from doubly ionized zinc interstitial (Zni) to the valence band (Zni-VB).54 (iii) A small contribution of blue emission at 456 nm is due to the transition from Zni++ to the valence band (Zni++-VB). (iv) The green emission is accompanied by a donor-level transition from Vo+ to the valence band at 510 nm (Vo+-VB) and the transition from the conduction band to the Vo++ corresponds to the 560 nm emission (CB-Vo++). The schematic for the PL emission is depicted in Fig. 1(d).
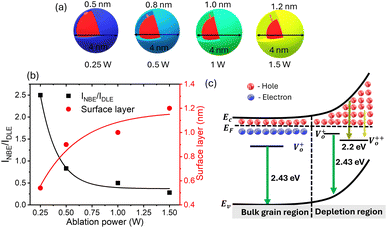
As discussed above, the pulse-width plays a key role in defect-induced green emission. Fig. 1(c) makes it clear that using fs-PLAL, the maximum improvement in green emission can be obtained between 450 and 600 fs. To achieve the systemic enhancement in the green emission, we have selected a 500 fs pulse-width with an extended power variance ranging from 0.25 W to 1.5 W. The PL emission spectra of these QDs are shown in Fig. S2 (ESI).† The deconvoluted emission spectra are shown in Fig. 1(d) and (e) for samples prepared at 0.25 W and 1.5 W, respectively. The emission was controlled from blue to the dominant green emission. The digital images of these samples for real-time fluorescence are shown in the corresponding insets of Fig. 1(d) and (e). Panel (f) depicts the linear enhancement in DLE (green) achieved by varying the ablation power from 0.25 W to 1.5 W. The analysis of the PL spectra can be discussed in two regimes, (a) NBE and (b) DLE. First, the NBE consists of two peaks: a main exciton peak with a shoulder peak at 393 nm. The contribution of this shoulder peak that qualitatively indicates the presence of Zni states is found to be higher at the lowest power, whereas this decreases gradually with an increase in ablation power. Importantly, the key feature of this work lies in the green emission, which increases with ablation power. This evidences that the formation of Vo+ and Vo++ increases with an increase in the ablation power, i.e. higher thermal energy appears to promote the formation of these defects. In the subsequent sections, structural and other optical characteristics are explored in detail in order to explain these fascinating luminescent properties.
While we uncover the reasons underlying this behavior, we note the following in the context of the fs-PLAL synthesis and its impact on the ablation process: ablation pulse-widths, which are employed here, typically less than 1 ps, initiate an ablation of the target, which is a non-equilibrium process. The system cannot attain equilibrium during the interaction of these pulses with matter. Importantly, thermalization occurs much after the ablation pulses are gone, as evidenced in the numerical simulations of Scorticati et al.57 The fs-PLAL plasma responsible for the production of these QDs is unusual and differs significantly from nanosecond or continuous wave laser-produced plumes in typical pulsed laser ablation or deposition processes.58,59 Given that the prevailing model for nanoparticle formation by pulsed laser ablation in liquids is based on the initial extrusion of the material due to photo-absorbed energy and the formation of the plasma plume at the target by interacting laser pulses45 (cf. ESI Section S4†), it is not surprising that the pulse parameters, temporal width, and pulse energy impact the optical properties of these QDs definitively. For longer pulse durations, typically above ∼1 ns, the surrounding solvent significantly influences nucleation and nanoparticle formation, as these processes occur on a similar timescale. This interaction affects the surface characteristics of the QDs. Previous studies on nanosecond-laser ablation in liquids (ns-PLAL) have shown that metal oxide QDs can form when using a metal target for ablation.48 Also they can change the lattice structure due to oxidation and additional phase formation. In contrast, for fs-PLAL, nucleation occurs much later than the pulse duration, minimizing oxidation or other chemical reactions during particle formation. Bond breaking can occur during the early stages of ablation; however, as nucleation progresses, the QDs primarily form in a crystalline structure. Most defects originate from particle collisions within the cavitation bubble, primarily forming as point defects. The identified defect states are atomic vacancies, specifically oxygen vacancies, rather than lattice defects. At higher pulse energies, increased particle collisions during bubble expansion result in a greater formation of defects in the QDs.
2.2 Particle size analysis
We recorded the transmission electron microscope (TEM) images of these ZnO QDs, where one of the TEM micrographs is depicted in Fig. 1(h), for an ablation power of 1.5 W and 600 fs pulse-width. Pulse-width dependent TEM micrographs are depicted in Fig. S4,† showing no change in the particle size distribution. From high-resolution TEM images such as the inset in panel (h) in the same figure, we enunciate the lattice spacing of 2.8 Å indicative of the (100) plane in ZnO.60 The plot of the most probable particle size as a function of pulse-width in Fig. 1(i) demonstrates that the size of these QDs is fairly independent of the temporal pulse duration. Error bars represent the width of the QD size distribution. In panel (i), we plot the particle size from the TEM micrograph with the blue line indicating the size distribution of the QDs at each pulse-width. The XRD study confirmed the formation of a hexagonal wurtzite structure for these QDs cf. Fig. S6(a) in ESI.† The c/a ratio determined from the XRD data is shown in Fig. S6(b).† The c/a ratio remains constant for QDs ablated with increasing average power 0.25–1.5 W while keeping the pulse-width constant. We recall that the green-emission or the DLE/NBE ratio increases with increasing ablation power. The constancy of the c/a ratio over the five-fold increase in the average power of the ablation beam confirms that there is no lattice strain in these QDs. Therefore, the change in PL with the increasing power of the ablation beam can neither be explained by lattice strain nor by a change in particle size.2.3 Raman spectroscopy
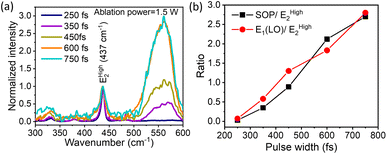
In continuing our exploration of the reasons underlying the variation and control of the optical emission (PL) spectrum with the ablation laser beam parameters, we turn to Raman spectroscopy for further insights. It is well-established that ZnO with a hexagonal wurtzite structure has optical phonon modes, which can be written as γopt = A1 + 2B1 + E1 + 2E2; here, A1 and E1 are the polar modes split into transverse optical (TO) and longitudinal optical (LO) modes, respectively.61 We compared the measured Raman spectra for QDs prepared with increasing temporal widths of the ablation laser pulses for a beam power of 1.5 W, and they fit using this set of well-known peaks. The first of these is the vibration mode EHigh2of the oxygen sub-lattice, known to occur at 437 cm−1,62cf.Fig. 2(a). We deconvoluted the broad peak from 500 cm−1 to 600 cm−1 into the surface optical phonon (SOP) mode at 550 cm−1 and the A1(LO) 570 cm−1 mode.63 These peaks arise from surface defects and oxygen vacancies in the ZnO QDs, which are of particular interest to us. As shown in Fig. 2(b), the ratio of both the SOP mode and the A1(LO) mode with respect to the EHigh2 mode increases steadily with increasing pulse-width for a constant ablation power of 1.5 W. It is pertinent to compare this trend with that of the DLE/NBE ratio in Fig. 1(c) for the same ablation power of 1.5 W (red data points). This leads us to a central message: both the strength of defects and surface peaks follow a very similar trend as a function of the ablation pulse-width to the green emission, characterized by the DLE/NBE ratio. This reveals that the underlying reason for the control of green-emission in these QDs lies in the amount of defects induced by the fs-PLAL process. Both parameters of the ablation pulses, their energy or average beam power, and their temporal duration or pulse-width, systematically induce varying amounts of defects in these pristine single-component QDs. Furthermore, for each ablation power, there is an optimal pulse width at which the green emission is maximized. This is a novel finding, unrealized hitherto, to the best of our knowledge.2.4 UV-visible absorption and Urbach energy
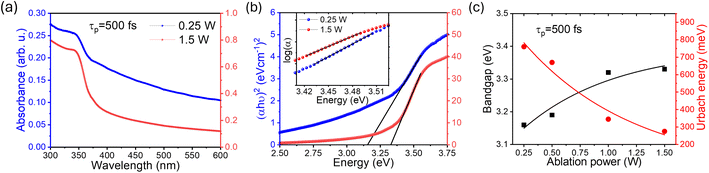
Having established the tuning of deep-level defects by varying both the pulse-width and average power of the pulse, we will continue the discussion on optical properties of the power-dependent QDs synthesized at 500 fs. This will aid in developing a comprehensive understanding of the ablation process by varying power from minimum to maximum for a fixed pulse width where variations in emission properties are noticeable. To correlate band formation with laser power, the UV-visible absorption study was conducted on the colloidal sample using a quartz cuvette. The absorption of the ZnO QDs prepared at 500 fs with variations in average power, i.e. 0.25 W and 1.5 W is shown in Fig. 3(a). To gain a better insight, a comparison of complete UV-visible absorption data for both pulse width and power-dependent synthesized QDs is shown in Fig. S6(a) (ESI).† For all the samples, a strong absorption is observed below 400 nm. However, the edge of the band becomes sharper with an increase in the ablation power. The bandgap of these QDs is quantified using the Tauc plot relation for direct bandgap semiconductors,64 which can be represented as| (αhν)2 = A(hν − Eg) | (1) |
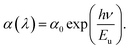 | (2) |
| Iem = η(Iex)α | (3) |
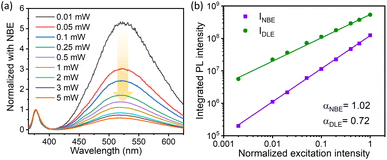
In the above equation, η is the emission efficiency and α is the type of radiative recombination mechanism. As reported, α ≥ 1 is responsible for the exciton transition, and α < 1 is for recombination of electrons with neutral acceptor or donor–acceptor pair (DAP) transitions.72,73 The α value for the NBE and DLE can be determined separately in order to analyze the recombination process.70 The integrated PL intensity was used for the calculation of α where the PL intensity from 365–400 nm and 425–625 nm was integrated to calculate the αNBE and αDLE respectively. Interestingly, for the 1.5 W sample, the measured αNBE value is 1.02 ± 0.01, which represents a pure exciton transition corresponding to NBE. However, the calculated αDLE value for the DLE was found to be 0.7 ± 0.01; this clearly indicates the recombination process of donor–acceptor pairs (DAP) type. A similar study for the sample prepared at 0.5 W ablation power is shown in Fig. S8.† The αNBE and αDLE values are 0.95 ± 0.02 and 0.72 ± 0.01 respectively, which is quite close to the measured value for the 1.5 W sample. In both cases, the α value for the DLE is less than that of NBE, which suggests that the recombination rate for electron–hole is decreasing with excitation power.74 It is important to mention that, at a lower intensity, the concentration of photo-excited holes is negligible compared to shallow-level and deep-level electrons. As the excitation power increases, the photo-excited electrons and holes become dominant over the defect concentration. This favours the linear increase in the NBE intensity with α ≈ 1 and sublinear increase in DLE peak intensity with the α value ranging from 0.5 to 1 (ref. 74).
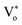 defect levels implicated as the donor level in the emission process account for the major contribution to the green emission at 525 nm. This includes an additional transition of electrons from the conduction band minimum to the donor level (Vo), which introduces an additional nonradiative decay (τnrd) along with the other two decay processes.76 The lifetime for DLE can be denoted as:
defect levels implicated as the donor level in the emission process account for the major contribution to the green emission at 525 nm. This includes an additional transition of electrons from the conduction band minimum to the donor level (Vo), which introduces an additional nonradiative decay (τnrd) along with the other two decay processes.76 The lifetime for DLE can be denoted as: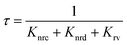 | (4) |
The decay time for this process can be explained using three rate constants, i.e. nonradiative decay to the conduction band minimum (Knr), nonradiative decay to the defect state (Knrd) and radiative decay to the valence band (Krv)76 (c.f.Fig. 5(c)). As the fluorescence intensity for the green emission increases with the ablation power, the effective lifetime is also found to be increased, as shown in Table ST1 (cf. ESI).† The radiative recombination of 525 nm emission depends on the trapped electrons from the oxygen vacancy states with photoexcited holes on the surface of QDs.35 As explained by Longshore,79 the lifetime of a defect-assisted donor–acceptor pair depends on the concentration of the defect level, i.e. Shockley-Read decay and the surface defect layer involved in the emission process. The lifetime due to surface defects depends on the layer thickness (t) and the recombination velocity (S), i.e. τeff = t/2S.79,80 Assuming that the velocity for the same recombination process is constant, the lifetime increases with an increase in the surface layer, which impacts green emission.
As shown in Table ST1 (cf. ESI),† the samples prepared at 0.25 W and 0.5 W, NBE (378 nm) have a relatively long lifetime, 8 ns and 4 ns, respectively. The long lifetime of UV emission is explained as the localization of disorder or defect states associated with the exciton emission.76 A lifetime of less than 0.5 ns can be ignored since the instrument response function (IRF) is of the same order.76 The DLE emission is involved with the Vo defect state, which is an additional state compared to NBE. So, it is reasonable to fit the lifetime of DLE (525 nm) with a tri-exponential function, i.e., 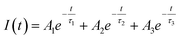 , where Ai is the amplitude and τi is the decay time of the respective process. By maintaining the fast decay time (τnrd) as a constant, we were able to fit the lifetime of the DLE and determine the radiative exciton recombination process. The other two decay times, the nonradiative decay to the defect state (τnrd) and the radiative decay from the defect state (τrv), were fitted independently. The contribution of τnr as well as τrv is increasing with ablation power, as shown in Table ST1.† The slower decay process for the most green-emitting sample indicates the presence of more defect states, which slows down the emission. For UV emission at 378 nm, where the contribution of Urbach energy is more, the lifetime of the corresponding sample is higher. Similarly, the green emission at 525 nm has the highest lifetime for the sample with the most oxygen vacancies. The lifetime of the DLE contributes to the surface layer present in the recombination process. The TRPL analysis infers that the contribution of the defect states associated with an emission process and its decay duration are directly proportional.
, where Ai is the amplitude and τi is the decay time of the respective process. By maintaining the fast decay time (τnrd) as a constant, we were able to fit the lifetime of the DLE and determine the radiative exciton recombination process. The other two decay times, the nonradiative decay to the defect state (τnrd) and the radiative decay from the defect state (τrv), were fitted independently. The contribution of τnr as well as τrv is increasing with ablation power, as shown in Table ST1.† The slower decay process for the most green-emitting sample indicates the presence of more defect states, which slows down the emission. For UV emission at 378 nm, where the contribution of Urbach energy is more, the lifetime of the corresponding sample is higher. Similarly, the green emission at 525 nm has the highest lifetime for the sample with the most oxygen vacancies. The lifetime of the DLE contributes to the surface layer present in the recombination process. The TRPL analysis infers that the contribution of the defect states associated with an emission process and its decay duration are directly proportional.
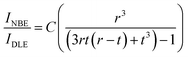 | (5) |
The presence of surface defects leads to the formation of the depletion layer near the surface of QDs.35 The width of the depletion layer depends on the carrier density. The deconvolution of power-dependent PL spectra shown in Fig. S3(c–f)† presents a systematic increase in the green emission that can be attributed to the Vo+ and Vo++ states. The formation of charged oxygen vacancies in pristine ZnO makes it an n-type semiconductor,83 as the redox potential is less than the Fermi energy level. To reach equilibrium, the electrons are transferred to the solvent from the n-type QDs. This subsequently leaves behind a positive charge on the surface of these QDs. Since most of the ionized charge carriers lie in the surface region, a potential barrier is created between the bulk grain region and surface region.84 This forms a depletion layer on the surface, which leads to band bending in the depletion region. In the depletion region, most of the carriers, primarily Vo+ and Vo++ lie above the Fermi level (EF), whereas in the bulk region, carriers Vo+ and 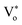 contribute to the DLE emission. The overall charge on these QDs is measured using zeta potential measurement. The zeta potential of the colloidal solution was found to have a positive charge, and it also increases with ablation power. The zeta potential of QDs prepared at different ablation powers is shown on the right axis of Fig. S10 (cf. ESI),† whereas the comparison of the NBE to DLE ratio is shown on the left axis. The maximum zeta potential of 6.7 mV of the QDs with the highest green-emitting sample is indicative of a larger depletion layer with more surface defects.
contribute to the DLE emission. The overall charge on these QDs is measured using zeta potential measurement. The zeta potential of the colloidal solution was found to have a positive charge, and it also increases with ablation power. The zeta potential of QDs prepared at different ablation powers is shown on the right axis of Fig. S10 (cf. ESI),† whereas the comparison of the NBE to DLE ratio is shown on the left axis. The maximum zeta potential of 6.7 mV of the QDs with the highest green-emitting sample is indicative of a larger depletion layer with more surface defects.
3 Applications in pH sensing and anti-microbial action
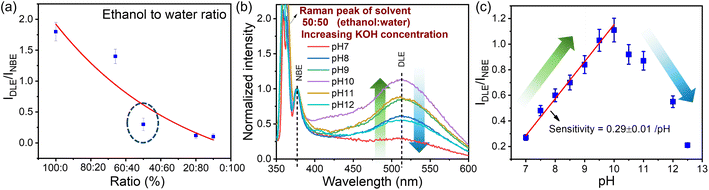
Understanding the influence of solvent on these QDs is crucial in the PL measurement. We have performed two experiments: one in which we introduced water after the solvent had evaporated and another in which we varied the ratio of ethanol to water. At first, the QDs prepared at 1 W were dried, followed by centrifugation at 6000 rpm (rpm) and the evaporation of ethanol by heating at 50 °C. 5 μL of ZnO QDs were then dispersed by sonication in 10 mL of DI water. Interestingly, we observed that the DLE is quenched in PL measurement when exposed to water. Because of the hydrogen bonding network around the water–solid interface, water is proven to be a quenching agent in PL.85,86 The surface defects responsible for the green emission in the QDs of ZnO and the water-adsorbed monolayer on the QDs cause the emission of defects to be quenched.86,87 To further confirm the effect of water on the sample, the water content in the ethanol solution is varied systematically. The sample prepared at 1 W ablation power at a 500 fs pulse-width was used for this study (increasing the percentage (%) of water). As we decrease the ethanol-to-water ratio (ethanol:water), DLE gets quenched, as shown in Fig. 7(a). Since water is more polar as compared to ethanol, OH− interacts with Zn2+ ions, which effectively reduces the DLE.88A detailed study of pH impact analysis was performed by maintaining an equal ratio of ethanol and water (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) at different pH values. As shown in the PL emission spectra in Fig. 7(b), water at normal pH 7 was found to quench the DLE emission intensity from 1.8 to 0.28 compared to the ethanol reference sample. Interestingly, as we made the solution alkaline by adding KOH, there was an enhancement in the DLE emission, which was observed from pH 7–10, and then reduced with a further increase in pH. As discussed by Degen et al., in the aqueous solution of pH 7–12, the hydrated ZnO surface is in equilibrium with differently charged species, i.e. Znaq2+, Zn(OH)aq+, Zn(OH)2(s), Zn(OH)3(aq)− and Zn(OH)4(aq)2−.88 In the pH range of 7–9, Znaq2+and Zn(OH)aq+ are the dominant species in the solution represented in eqn (6). When the pH reaches pH 10, the majority of the species forms stable Zn(OH)2(s) surface hydroxide. The formation of stable zinc hydroxide provides an enhanced green emission compared to other species.89 At higher pH (>10) the ZnO surface hydrolyzes to form zincates, Zn(OH)3(aq)− and Zn(OH)4(aq)2− which effectively reduce the surface charge with a negative zeta potential88 (cf.eqn (8) and (9)). As discussed in the previous section, surface charge plays an important role in DLE quenching.
50) at different pH values. As shown in the PL emission spectra in Fig. 7(b), water at normal pH 7 was found to quench the DLE emission intensity from 1.8 to 0.28 compared to the ethanol reference sample. Interestingly, as we made the solution alkaline by adding KOH, there was an enhancement in the DLE emission, which was observed from pH 7–10, and then reduced with a further increase in pH. As discussed by Degen et al., in the aqueous solution of pH 7–12, the hydrated ZnO surface is in equilibrium with differently charged species, i.e. Znaq2+, Zn(OH)aq+, Zn(OH)2(s), Zn(OH)3(aq)− and Zn(OH)4(aq)2−.88 In the pH range of 7–9, Znaq2+and Zn(OH)aq+ are the dominant species in the solution represented in eqn (6). When the pH reaches pH 10, the majority of the species forms stable Zn(OH)2(s) surface hydroxide. The formation of stable zinc hydroxide provides an enhanced green emission compared to other species.89 At higher pH (>10) the ZnO surface hydrolyzes to form zincates, Zn(OH)3(aq)− and Zn(OH)4(aq)2− which effectively reduce the surface charge with a negative zeta potential88 (cf.eqn (8) and (9)). As discussed in the previous section, surface charge plays an important role in DLE quenching.
| Znaq2+ + OH− ↔ Zn(OH)aq+ | (6) |
| Zn(OH)aq+ + OH− ↔ Zn(OH)2(s) | (7) |
| Zn(OH)2(s) + OH− ↔ Zn(OH)3(aq)− | (8) |
| Zn(OH)2(s) + 2OH− ↔ Zn(OH)4(aq)2− | (9) |
Herein, we suggest that the defect-induced QDs prepared by fs-PLAL in an ethanol medium can be directly used for fluorometric pH sensing application, unlike traditional ZnO-based pH sensors, which utilise ion-sensing membranes made of thin films demonstrated through the electrochemical approach,90,91 surface acoustic wave resonance,92 and extended gate field effect transistor.93 It takes several minutes to find equilibrium for precise measurement. Using the quenching of DLE emission in PL measurement, we show pH sensing applications that take less than a minute. Based on the pH response to PL properties of Ti3C2 MXene,94 cerium activated fluoride nanocrystals,95 polythene protected Cu nanoclusters,96 and Eu3+ metal–organic clusters97 are different materials being demonstrated as ratiometric fluorescence-based pH sensors. To our knowledge, we are demonstrating the ratiometric PL-based pH sensing application utilizing the DLE to NBE ratio of ZnO QDs as the calibration reference for the first time.
As shown in Fig. 7, the sensitivity of this pH sensing will depend on the quenching DLE emission with respect to the reference sample in an ethanol medium. The linear region from pH 7–10 can be used for the pH sensing application, whose sensitivity depends on the percentage of DLE enhancement, which is about 0.28 per pH.
ZnO QDs have been extensively used for antibacterial studies due to the antimicrobial nature of ions and the formation of reactive oxygen species (ROS), which inhibit bacterial growth.2,98 In the present study, the synthesized ZnO QDs by fs-PLAL techniques are also expected to show antibacterial activity. To investigate the potential bactericidal activity of synthesized ZnO QDs against the Gram-negative, rod-shaped Escherichia coli (E. coli) and Gram-positive, Bacillus subtilis (B. subtilis) bacteria, the agar disc diffusion method was used. For the experiment, both E. coli and B. subtilis were cultured separately in a nutrient broth by incubation at 37 °C for 24 hours, followed by agar plate preparation and inoculation with a standardized inoculum of the microbes. Then, Whatman filter papers (5 mm in diameter) containing the samples at the desired concentration are placed on the agar surface. The zones of inhibition were measured after the incubation of the treated Petri dish at 37 °C for 24 hours. The results suggest that the fabricated ZnO QDs were active against both the microbes (both E. coli and B. subtilis) and inhibited bacterial growth in a particular region by creating a zone of inhibition, as shown in Fig. 8. The diameter of the zone of inhibition for E. coli was found to be 10 ± 0.5 mm (Fig. 8(a)), and for B. subtilis, it was 12.5 ± 0.8 mm (Fig. 8(b)) when the 5 (stock concentration 5 μg mL−1) sample was used. Thus, the potential of inactivation of these microbes by inhibiting their growth has been successfully shown. Additionally, this finding confirms that these smaller-sized QDs are highly susceptible to entering the Gram +ve bacteria to inhibit their growth as compared to Gram −ve bacteria, which could be due to variations of cell physiology and the cell wall constitution of these microbes.2
 | ||
| Fig. 8 The figure shows the antibacterial effect by zone inhibition around the filter paper on the (a) Gram −ve bacteria and (b) Gram +ve bacteria. | ||
4 Conclusion
Conclusively, the modification of the pulse-width is crucial in tuning the optoelectronic properties of ZnO QDs, alongside the variation of laser power. The most effective enhancement of PL control, regarding the ratio of deep-level emission (DLE) to near band edge (NBE) emission, is achieved within the range of 450–600 fs. TRPL analysis reveals that for NBE decay at 0.25 W and 0.5 W, the non-radiative decay time (τnrc) remains constant, while the radiative decay time (τrv) peaks for the 0.25 W sample, indicating the presence of donor or trap levels below the conduction band, which prolongs the radiative decay process. However, the decay times for DLE, specifically τnrd and τnv, increase as the ablation power is increased to 1.5 W. Analysis of PL data deconvolution demonstrates a linear increase in oxygen vacancy (Vo) centers with ablation power. Additionally, surface-recombination-layer approximation calculations suggest an increase in the thickness of defect states for the 1.5 W sample, leading to slower recombination compared to the 0.25 W sample. Conversely, NBE emission primarily originates from the bulk, and thus at lower ablation powers where the formation of zinc interstitials (Zni) predominates, shallow-level defects dominate, as evidenced by PL emission and UV-visible absorption spectra.To sum up, the following are the key points of the work: (a) at 500 fs, we achieved a systematic increase in DLE emission as we increased the laser power. Although these QDs have similar size distribution due to surface defects at higher pulse power, green emission is enhanced. (b) Interestingly, the Urbach energy, which also can be tuned systematically in the fs-PLAL process, is independent of deep-level green emission. This only contributes to a shallow donor level in ZnO QDs. (c) The green emission of these QDs is sensitive to the ethanol environment, and it gets quenched when we transfer them from ethanol to water. These QDs having antibacterial properties can be optimized for pH-sensing applications.
Data availability
The data that support the findings of this study are available from the first author and corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support by the Dept. of Science and Technology (DST), Govt. of India, is gratefully acknowledged: A. S. was supported through the DST-INSPIRE scheme and S. K. for research grants through the Technology Development Board, Science and Engineering Research Board, and DST-DAAD bilateral scheme together with the German Academic Exchange Service (DAAD). M. S. R. R. and S. K. gratefully acknowledge the support of the Ministry of Education, Govt. of India, through the Institute of Eminence (IoE) scheme, which funds the Quantum Center of Excellence for Diamond and Emergent Materials (QuCenDiEM); M. S. R. R. acknowledges the support through the DST grant of the “Nano Functional Materials Technology Centre” (Grant: SRNM/NAT/02-2005). S. K. also acknowledges the partial support of the Indo-French Center for Promotion of Academic Research (CEFIPRA). M. S. R. R. acknowledges the Department of Science and Technology (DST) of India for the financial support for the establishment of the Nano Functional Materials Technology Centre (NFMTC) in IIT Madras. The authors thank SAIF, IIT Madras for allowing the use of the TCSPC facility. The authors also thank SAIF, IIT Bombay, Mumbai, India and SIT, Tokyo, Japan for facilitating HR-TEM.Notes and references
- L. Zhang, S. R. Jean, S. Ahmed, P. M. Aldridge, X. Li, F. Fan, E. H. Sargent and S. O. Kelley, Nat. Commun., 2017, 8, 381 CrossRef PubMed.
- A. Sirelkhatim, S. Mahmud, A. Seeni, N. H. M. Kaus, L. C. Ann, S. K. M. Bakhori, H. Hasan and D. Mohamad, Nano-Micro Lett., 2015, 7, 219–242 CrossRef CAS PubMed.
- E. Zor, E. Morales-Narváez, A. Zamora-Gálvez, H. Bingol, M. Ersoz and A. Merkoçi, ACS Appl. Mater. Interfaces, 2015, 7, 20272–20279 CrossRef CAS PubMed.
- Q. Ma and X. Su, Analyst, 2011, 136, 4883–4893 RSC.
- A. Qureshi, T. Shaikh and J. H. Niazi, Analyst, 2023, 148, 1633–1652 RSC.
- C. Buzea, I. I. Pacheco and K. Robbie, Biointerphases, 2007, 2, MR17–MR71 CrossRef PubMed.
- Y. Chen, V. Sai Muthukumar, Y. Wang, C. Li, S. Sivarama Krishnan, S. Siva Sankara Sai, K. Venkataramaniah and S. Mitra, J. Mater. Chem., 2009, 19, 6568–6572 RSC.
- A. P. Litvin, I. V. Martynenko, F. Purcell-Milton, A. V. Baranov, A. V. Fedorov and Y. K. Gun’ko, J. Mater. Chem. A, 2017, 5, 13252–13275 RSC.
- J. Tan, J. Zhang, W. Li, L. Zhang and D. Yue, J. Mater. Chem. C, 2016, 4, 10146–10153 RSC.
- M. Vafaie, J. Z. Fan, A. Morteza Najarian, O. Ouellette, L. K. Sagar, K. Bertens, B. Sun, F. P. García de Arquer and E. H. Sargent, Matter, 2021, 4, 1042–1053 CrossRef CAS.
- L. Chen, J. Liu, P. Liu, S. Lu, Y. Yang, X. Liang, L. Zhang, J. Hu, J. Yang, Y. Liu, W. Ma, X. Zhao, X. Lan, J. Zhang, L. Gao and J. Tang, ACS Photonics, 2023, 10, 2374–2381 CrossRef CAS.
- C. M. Chang, K. L. Orchard, B. C. M. Martindale and E. Reisner, J. Mater. Chem. A, 2016, 4, 2856–2862 RSC.
- G. Ren, H. Han, Y. Wang, S. Liu, J. Zhao, X. Meng and Z. Li, Nanomaterials, 2021, 11, year Search PubMed.
- J. Iyyappan, B. Gaddala, R. Gnanasekaran, M. Gopinath, D. Yuvaraj and V. Kumar, Case Stud. Chem. Environ. Eng., 2024, 9, 100599 CrossRef CAS.
- S. Raha and M. Ahmaruzzaman, Nanoscale Adv., 2022, 4, 1868–1925 RSC.
- T. Kulahava, N. Belko, M. Parkhats, A. Bahdanava, S. Lepeshkevich, V. Chizhevsky and D. Mogilevtsev, J. Photochem. Photobiol., B, 2023, 248, 112800 CrossRef CAS PubMed.
- D. Maikhuri, S. Purohit and K. Mathur, Superlattices Microstruct., 2016, 89, 296–311 CrossRef CAS.
- A. J. Gimenez, J. M. Yáñez-Limón and J. M. Seminario, J. Phys. Chem. C, 2011, 115, 282–287 CrossRef CAS.
- Z. Yuan, W. Wang, H. Wu, F. Nie and J. He, Mater. Lett., 2020, 278, 128413 CrossRef CAS.
- M. Willander, O. Nur, J. R. Sadaf, M. I. Qadir, S. Zaman, A. Zainelabdin, N. Bano and I. Hussain, Materials, 2010, 3, 2643–2667 CrossRef CAS.
- K. Keis, E. Magnusson, H. Lindström, S.-E. Lindquist and A. Hagfeldt, Sol. Energy Mater. Sol. Cells, 2002, 73, 51–58 CrossRef.
- R. Zahoor, A. Jalil, S. Z. Ilyas, S. Ahmed and A. Hassan, Results Surf. Interfaces, 2021, 2, 100003 CrossRef.
- Y. Sun, W. Zhang, Q. Li, H. Liu and X. Wang, Adv. Sens. Energy Mater., 2023, 2, 100069 CrossRef.
- S. de Quadros, D. C. Horst Pereira Metz and L. M. Zimmermann, J. Phys. Chem. Solids, 2023, 181, 111464 CrossRef CAS.
- X. Chen, Q. Wang, X.-J. Wang, J. Li and G.-B. Xu, Sci. Rep., 2021, 11, 5841 CrossRef CAS PubMed.
- Y. Guo, Y. Zhang, T. Li and T. Tao, J. Environ. Chem. Eng., 2021, 9, 106800 CrossRef CAS.
- K. R. Raghupathi, R. T. Koodali and A. C. Manna, Langmuir, 2011, 27, 4020–4028 CrossRef CAS PubMed.
- J. Yan, F. Hua, L. Cao, H. Yang and H. He, Dent. Mater., 2022, 38, 1728–1741 CrossRef CAS PubMed.
- J. Wang, J. S. Lee, D. Kim and L. Zhu, ACS Appl. Mater. Interfaces, 2017, 9, 39971–39984 CrossRef CAS PubMed.
- S. Y. H. Abdalkarim, H.-Y. Yu, C. Wang, L. Yang, Y. Guan, L. Huang and J. Yao, Appl. Bio Mater., 2018, 1, 714–727 CrossRef CAS PubMed.
- A. Janotti and C. G. Van de Walle, Phys. Rev. B, 2007, 76, 165202 CrossRef.
- S. Sakohara, M. Ishida and M. A. Anderson, J. Phys. Chem. B, 1998, 102, 10169–10175 CrossRef CAS.
- H. K. Yadav, K. Sreenivas, V. Gupta, S. Singh and R. Katiyar, J. Mater. Res., 2007, 22, 2404–2409 CrossRef CAS.
- D. Damberga, R. Viter, V. Fedorenko, I. Iatsunskyi, E. Coy, O. Graniel, S. Balme, P. Miele and M. Bechelany, J. Phys. Chem. C, 2020, 124, 9434–9441 CrossRef CAS.
- M. Ghosh and A. K. Raychaudhuri, Nanotechnology, 2008, 19, 445704 CrossRef PubMed.
- N. Gogurla, S. Bayan, P. Chakrabarty and S. Ray, J. Lumin., 2018, 194, 15–21 CrossRef CAS.
- A. Achour, M. Islam, S. Vizireanu, I. Ahmad, M. A. Akram, K. Saeed, G. Dinescu and J.-J. Pireaux, Nanomaterials, 2019, 9, 794 CrossRef CAS PubMed.
- G. Zhang, J. Lang, Q. Zhang, Q. Han, X. Li, J. Wang, J. Wang and J. Yang, J. Mater. Sci.: Mater. Electron., 2018, 29, 16534–16542 CrossRef CAS.
- C. Jayachandraiah, K. S. Kumar, G. Krishnaiah and N. M. Rao, J. Alloys Compd., 2015, 623, 248–254 CrossRef CAS.
- Y.-I. Jung, B.-Y. Noh, Y.-S. Lee, S.-H. Baek, J. H. Kim and I.-K. Park, Nanoscale Res. Lett., 2012, 7, 43 CrossRef PubMed.
- J. Zhou, K. Nomenyo, C. C. Cesar, A. Lusson, A. Schwartzberg, C.-C. Yen, W.-Y. Woon and G. Lerondel, Sci. Rep., 2020, 10, 4237 CrossRef CAS PubMed.
- A. Sahoo, M. Miryala, T. Dixit, A. Klimkowicz, B. Francis, M. Murakami, M. Rao and S. S. R. Krishnan, Nanomaterials, 2020, 10, 1–11 CrossRef PubMed.
- A. Sahoo, T. Dixit, K. V. Anil Kumar, K. Lakshmi Ganapathi, P. K. Nayak, M. S. R. Rao and S. Krishnan, J. Phys. Chem. Lett., 2024, 15, 5586–5593 CrossRef CAS PubMed.
- F. Ye and K. P. Musselman, APL Mater., 2024, 12, 050602 CrossRef CAS.
- T. E. Itina, J. Phys. Chem. C, 2011, 115, 5044–5048 CrossRef CAS.
- A. Said, L. Sajti, S. Giorgio and W. Marine, J. Phys.: Conf. Ser., 2007, 59, 259–265 CrossRef CAS.
- E. Fazio, A. Cacciola, A. Mezzasalma, G. Mondio, F. Neri and R. Saija, J. Quant. Spectrosc. Radiat. Transfer, 2013, 124, 86–93 CrossRef CAS.
- M. Navas, R. Soni, N. Tarasenka and N. Tarasenko, Appl. Surf. Sci., 2017, 414, 413–423 CrossRef CAS.
- P. Camarda, L. Vaccaro, A. Sciortino, F. Messina, G. Buscarino, S. Agnello, F. Gelardi, R. Popescu, R. Schneider, D. Gerthsen and M. Cannas, Appl. Surf. Sci., 2020, 506, 144954 CrossRef CAS.
- C. Sajti, S. Giorgio, V. Khodorkovsky and W. Marine, Appl. Surf. Sci., 2007, 253, 8111–8114 CrossRef CAS.
- P. P. Rajeev, M. Gertsvolf, P. B. Corkum and D. M. Rayner, Phys. Rev. Lett., 2009, 102, 083001 CrossRef CAS PubMed.
- S. Lima, F. Sigoli, M. J. Jafelicci and M. Davolos, Int. J. Inorg. Mater., 2001, 3, 749–754 CrossRef CAS.
- B. Cao, W. Cai and H. Zeng, Appl. Phys. Lett., 2006, 88, 161101 CrossRef.
- C. H. Ahn, Y. Y. Kim, D. C. Kim, S. K. Mohanta and H. K. Cho, J. Appl. Phys., 2009, 105, 013502 CrossRef.
- K. Vanheusden, C. H. Seager, W. L. Warren, D. R. Tallant and J. A. Voigt, Appl. Phys. Lett., 1996, 68, 403–405 CrossRef CAS.
- T. M. Børseth, B. G. Svensson, A. Y. Kuznetsov, P. Klason, Q. X. Zhao and M. Willander, Appl. Phys. Lett., 2006, 89, 262112 CrossRef.
- D. Scorticati, G. R. B. E. Römer, A. J. Huis in’t Veld and D. F. de Lange, J. Heat Transfer, 2015, 138, 031301 CrossRef.
- R. Mannam, S. K. Eswaran, N. DasGupta and M. R. Rao, Appl. Surf. Sci., 2015, 347, 96–100 CrossRef CAS.
- J. Mukherjee, R. Mannam and M. S. R. Rao, Semicond. Sci. Technol., 2017, 32, 045008 CrossRef.
- D. Kuo, S. Kajiyama and T. Kato, CrystEngComm, 2019, 21, 2893–2899 RSC.
- A. Jaramillo, R. Baez-Cruz, L. Montoya, C. Medinam, E. Pérez-Tijerina, F. Salazar, D. Rojas and M. Melendrez, Ceram. Int., 2017, 43, 11838–11847 CrossRef CAS.
- Y. I. A. Özgür, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 041301 CrossRef.
- M. Šćepanović, M. Grujić -Brojčin, K. Vojisavljević, S. Bernik and T. Sreć ković, J. Raman Spectrosc., 2010, 41, 914–921 CrossRef.
- S. Xue, X. Zu, W. Zhou, H. Deng, X. Xiang, L. Zhang and H. Deng, J. Alloys Compd., 2008, 448, 21–26 CrossRef CAS.
- R. Vettumperumal, S. Kalyanaraman, B. Santoshkumar and R. Thangavel, Mater. Res. Bull., 2016, 77, 101–110 CrossRef CAS.
- J. Pankove, Phys. Rev., 1965, 140, A2059–A2065 CrossRef.
- B. Lin, Z. Fu and Y. Jia, Appl. Phys. Lett., 2001, 79, 943–945 CrossRef CAS.
- P. Bindu and S. Thomas, Acta Phys. Pol., A, 2017, 131, 1474–1478 CrossRef CAS.
- B. Goswami and A. Choudhury, J. Exp. Nanosci., 2015, 10, 900–910 CrossRef CAS.
- J. B. Cui and M. A. Thomas, J. Appl. Phys., 2009, 106, 033518 CrossRef.
- L. Bergman, X.-B. Chen, J. L. Morrison, J. Huso and A. P. Purdy, J. Appl. Phys., 2004, 96, 675–682 CrossRef CAS.
- Z. Feng, A. Mascarenhas and W. Choyke, J. Lumin., 1986, 35, 329–341 CrossRef CAS.
- S. Jin, Y. Zheng and A. Li, J. Appl. Phys., 1997, 82, 3870–3873 CrossRef CAS.
- D. Hou, T. Voss, C. Ronning, A. Menzel and M. Zacharias, J. Appl. Phys., 2014, 115, 233516 CrossRef.
- B. Cao, W. Cai, H. Zeng and G. Duan, J. Appl. Phys., 2006, 99, 073516 CrossRef.
- N. S. Han, H. S. Shim, J. H. Seo, S. Y. Kim, S. M. Park and J. K. Song, J. Appl. Phys., 2010, 107, 084306 CrossRef.
- M. H. Huang, S. Mao, H. Feick, H. Yan, Y. Wu, H. Kind, E. Weber, R. Russo and P. Yang, Science, 2001, 292, 1897–1899 CrossRef CAS PubMed.
- C. Li, L. Guo, Z. Wu, L. Ren, X. Ai, J. Zhang, Y. Lv, H. Xu and D. Yu, Solid State Commun., 2006, 139, 355–359 CrossRef CAS.
- R. E. Longshore, Handbook of Infra-red Detection Technologies, Elsevier Science, Amsterdam, 2002, pp. 233 – 267 Search PubMed.
- K. N. Zaunbrecher, D. Kuciauskas, C. H. Swartz, P. Dippo, M. Edirisooriya, O. S. Ogedengbe, S. Sohal, B. L. Hancock, E. G. LeBlanc, P. A. R. D. Jayathilaka, T. M. Barnes and T. H. Myers, Appl. Phys. Lett., 2016, 109, 091904 CrossRef.
- I. Shalish, H. Temkin and V. Narayanamurti, Phys. Rev. B, 2004, 69, 245401 CrossRef.
- A. Makhal, S. Sarkar, T. Bora, S. Baruah, J. Dutta, A. K. Raychaudhuri and S. K. Pal, Nanotechnology, 2010, 21, 265703 CrossRef PubMed.
- L. Liu, Z. Mei, A. Tang, A. Azarov, A. Kuznetsov, Q.-K. Xue and X. Du, Phys. Rev. B, 2016, 93, 235305 CrossRef.
- J. Ye, S. Gu, F. Qin, S. Zhu, S. Liu, X. Zhou, W. Liu, L. Hu, R. Zhang, Y. Shi and Y. Zheng, Appl. Phys. A: Mater. Sci. Process., 2005, 81, 756–762 Search PubMed.
- I. Shahine, N. Beydoun, J. Gaumet, E.-E. Bendeif, H. Rinnert, P. Magri, A. En Naciri, P. Miska, S. Jradi and S. Akil, Catalysts, 2019, 9, 162 CrossRef.
- O. Dulub, B. Meyer and U. Diebold, Phys. Rev. Lett., 2005, 95, 136101 CrossRef PubMed.
- Y.-S. Fu, X.-W. Du, S. A. Kulinich, J.-S. Qiu, W.-J. Qin, R. Li, J. Sun and J. Liu, J. Am. Chem. Soc., 2007, 129, 16029–16033 CrossRef CAS PubMed.
- A. Degen and M. Kosec, J. Eur. Ceram. Soc., 2000, 20, 667–673 CrossRef CAS.
- M. Wang, L. Jiang, E. J. Kim and S. H. Hahn, RSC Adv., 2015, 5, 87496–87503 RSC.
- S.-J. Young and W.-L. Tang, J. Electrochem. Soc., 2019, 166, B3047–B3050 CrossRef CAS.
- A. Fulati, S. Usman Ali, G. Amin, O. Nur and M. Willander, Sensors, 2009, 9, 8911–8923 CrossRef CAS PubMed.
- X. Qiu, R. Tang, S. J. Chen, H. Zhang, W. Pang and H. Yu, Electrochem. Commun., 2011, 13, 488–490 CrossRef CAS.
- P. D. Batista and M. Mulato, Appl. Phys. Lett., 2005, 87, 143508 CrossRef.
- X. Chen, X. Sun, W. Xu, G. Pan, D. Zhou, J. Zhu, H. Wang, X. Bai, B. Dong and H. Song, Nanoscale, 2018, 10, 1111–1118 RSC.
- L. Lei, H. Xia, C.-K. Lim, S. Xu, K. Wang, Y. Du and P. N. Prasad, Chem. Mater., 2019, 31, 8121–8128 CrossRef CAS.
- C. Wang, Y. Yao and Q. Song, Colloids Surf., B, 2016, 140, 373–381 CrossRef CAS PubMed.
- B. Harbuzaru, A. Corma, F. Rey, J. Jordá, D. Ananias, L. Carlos and J. Rocha, Angew. Chem., Int. Ed., 2009, 48, 6476–6479 CrossRef CAS PubMed.
- R. Wahab, M. A. Siddiqui, Q. Saquib, S. Dwivedi, J. Ahmad, J. Musarrat, A. A. Al-Khedhairy and H.-S. Shin, Colloids Surf., B, 2014, 117, 267–276 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00793j |
| This journal is © The Royal Society of Chemistry 2025 |