Open Access Article
Open Access ArticleLeveraging generative neural networks for accurate, diverse, and robust nanoparticle design†
Tanzim
Rahman‡
 a,
Ahnaf
Tahmid‡
a,
Ahnaf
Tahmid‡
 a,
Shifat E.
Arman
b,
Tanvir
Ahmed
c,
Zarin Tasnim
Rakhy
c,
Harinarayan
Das
d,
Mahmudur
Rahman
e,
Abul Kalam
Azad
a,
Md.
Wahadoszamen
c and
Ahsan
Habib
a,
Shifat E.
Arman
b,
Tanvir
Ahmed
c,
Zarin Tasnim
Rakhy
c,
Harinarayan
Das
d,
Mahmudur
Rahman
e,
Abul Kalam
Azad
a,
Md.
Wahadoszamen
c and
Ahsan
Habib
 *a
*a
aDepartment of Electrical and Electronic Engineering, University of Dhaka, Dhaka-1000, Bangladesh. E-mail: mahabib@du.ac.bd
bDepartment of Robotics and Mechatronics Engineering, University of Dhaka, Dhaka-1000, Bangladesh
cDepartment of Physics, University of Dhaka, Dhaka-1000, Bangladesh
dBangladesh Atomic Energy Commission, Dhaka-1000, Bangladesh
eDepartment of Electrical and Electronic Engineering, Dhaka University of Engineering & Technology, Gazipur-1707, Bangladesh
First published on 9th December 2024
Abstract
Tandem neural networks for inverse design can only make single predictions, which limits the diversity of predicted structures. Here, we use conditional variational autoencoder (cVAE) for the inverse design of core–shell nanoparticles. cVAE is a type of generative neural network that generates multiple valid solutions for the same input condition. We generate a dataset from Mie theory simulations, including ten commonly used materials in plasmonic core–shell nanoparticle synthesis. We compare the performance of cVAE with that of the tandem model. Our cVAE model shows higher accuracy with a lower mean absolute error (MAE) of 0.013 compared to 0.046 for the tandem model. Robustness analysis with 100 test spectra confirms the improved reliability and diversity of cVAE. To validate the effectiveness of the cVAE model, we synthesize Au@Ag core–shell nanoparticles. cVAE model offers high accuracy in predicting material composition and spectral features. Our study shows the potential of cVAEs as generative neural networks in producing accurate, diverse, and robust nanoparticle designs.
1 Introduction
Engineered nanoparticles (ENPs) have attracted a lot of attention in fields such as medicine, healthcare,1 neuroengineering,2 environmental remediation,3 and agriculture.4 As a result, there is a substantial need for the design of nanoparticles (NPs) with certain optical properties. Designing NPs with specific size, shape, and material composition is essential for optimizing their properties in targeted applications.5–7 The approach to designing ENPs can typically be framed in two ways.8,9 The first way is as a forward problem, in which the designer sets a target electromagnetic response and iteratively evaluates ENP designs. Forward problems are usually well-posed as they follow J. Hadamard's classical idea that requires the existence, uniqueness, and stability of a solution. The forward problem can be solved using finite-difference time-domain, finite element methods, and Mie theory. The second way is as an inverse problem, which maps a desired electromagnetic response to the ENP design. Inverse problems are often ill-posed because there can be many geometries that correspond to the desired properties of the nanoparticle, violating Hadamard's uniqueness condition.Conventionally, inverse problems are solved using gradient-based techniques such as topology optimization10 and gradient-free methods such as genetic algorithms and particle swarm optimization. Although useful, these methods have drawbacks in nanophotonic inverse designs. For example, gradient-based algorithms often converge to local minima, and gradient-free methods can suffer from slow convergence and high computational costs.11 To solve these inadequacies, there has been a recent emergence in the incorporation of deep learning approaches in the nanophotonic inverse designs.12 In the inverse design model, the electromagnetic (EM) response serves as the input, and the model directly generates the corresponding structure as the output. Two types of deep neural architectures, deterministic and generative networks, can be utilized for nanophotonic inverse design. In nanophotonics, the task of a deterministic network (e.g., basic feed-forward neural network) for inverse design to deduce geometric parameters from optical properties is “ill-posed”. This is because of multiple potential solutions for a given input condition (one-to-many solutions). Consequently, during training, such networks often converge to non-physical averages between different solutions, learning invalid solutions that hurt the network's performance. To address the challenges of inverse networks, researchers use tandem architectures that integrate both an inverse network (mapping optical response to structure) and a forward solver network (mapping structure to optical response).13 Tandem networks are effective in the inverse design of numerous nanophotonic structures.13–15 He et al. utilized a tandem model to predict the structures of multilayered nanoparticles.16 Although tandem networks offer good accuracy, they are limited to providing a single prediction for a specific inverse design task, even if multiple designs can achieve the target. This limitation negatively impacts the diversity of the predicted structures. Diverse designs aid the fabrication process by offering more candidate options, which is especially beneficial for shapes that are challenging to manufacture at the nanoscale. Generative networks, such as generative adversarial networks (GANs) and variational autoencoders (VAEs), can stochastically output multiple different predictions to address this limitation.17,18 These networks can generate numerous optimized solutions based on variations in their latent space which contains an abstraction of learned parameters for diverse generations. VAEs encode input data into a lower-dimensional latent space and then decode it back while creating a compact, continuous, and normally distributed latent space. A conditional variational autoencoder (cVAE) allows further control in such generations by imposing a condition, which is utilized in inverse designing to achieve desired attributes.19,20 This lets the cVAE network explore the latent space and generate multiple valid designs for the same required condition. However, a comprehensive literature search revealed a lack of research focused on the applications of generative neural networks to inverse design ENPs.
Here, we use generative neural network architectures to predict core–shell nanoparticle structures based on specific optical responses. Recent reports indicate that cVAEs are the most efficient generative neural networks for the nanophotonic inverse design task.18 Therefore, we focus on cVAEs for nanoparticle inverse design. We also evaluate the effectiveness of cVAE by comparing results with those obtained from the tandem neural network. For such comparisons, we use evaluation metrics of accuracy, robustness, and diversity. We present a dataset obtained from Mie theory simulations, utilizing the Python module Scattnlay.21 Our results from comparing the input condition spectra with the predicted particle spectra show that the tandem network has a mean absolute error (MAE) of 0.046, while the cVAE has an MAE of 0.013. The lower MAE signifies better accuracy for the cVAE model. Our robustness analysis with 100 test spectra shows that the cVAE has higher robustness compared to the tandem network. Furthermore, the cVAE model exhibits significant diversity, generating multiple valid solutions for the same input condition. To validate the effectiveness of the cVAE model, we synthesize Au@Ag core–shell nanoparticles. Our cVAE model demonstrates high accuracy in ENP inverse design and can correctly predict key plasmonic modes. Our existing dataset, which will be publicly accessible on GitHub for further research, can be extended to accommodate multilayer nanoparticle inverse design.
2 Methodologies
2.1 Dataset generation
Ten materials were selected that are commonly used in the synthesis of plasmonic core–shell nanoparticles: silver (Ag),22 aluminum (Al),23 gold (Au),24 copper (Cu),25 gallium arsenide (GaAs),26 indium arsenide (InAs),27 indium phosphide (InP),28 molybdenum (Mo),29 silicon (Si),30 and silicon dioxide (SiO2).31 Refractive indices for these materials were obtained from various sources32–39 using the online database “RefractiveIndex.INFO”.40 Each material was later assigned an integer ID ranging from 1 to 10 (ESI Table S1†). The material ID for the core and shell layers were indicated as m1 and m2, while the thickness of the core (radius) and shell were indicated as t1 and t2. We used Scattnlay, a Python module for simulating light scattering by multilayered spheres based on Mie theory, to simulate 114![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 samples. Structural parameters (t1, t2) were both uniformly sampled in the ranges of [1, 99] nm, but also ensuring that t1 + t2 does not exceed 100 nm. The absorption cross-section spectrum was computed between the [300, 800] nm wavelength range with a 2.505 nm step size. In both models (i.e., cVAE and tandem neural network), we used 87
750 samples. Structural parameters (t1, t2) were both uniformly sampled in the ranges of [1, 99] nm, but also ensuring that t1 + t2 does not exceed 100 nm. The absorption cross-section spectrum was computed between the [300, 800] nm wavelength range with a 2.505 nm step size. In both models (i.e., cVAE and tandem neural network), we used 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 samples for training, 21
210 samples for training, 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 802 samples for validation, and the rest 5738 samples for testing purposes. The spectra were normalized to values between 0 and 1 for improved training of neural network models. The dataset consisted of 205 columns, where the first two columns represented the material IDs m1 and m2 for the core and shell sections, respectively. The next two columns contained their corresponding thicknesses t1 and t2. The dielectric host medium, either air (0) or water (1), was indicated in the fifth column; only the water medium was considered for this work. The remaining 200 columns contained the absorption cross-section data for each nanosphere.
802 samples for validation, and the rest 5738 samples for testing purposes. The spectra were normalized to values between 0 and 1 for improved training of neural network models. The dataset consisted of 205 columns, where the first two columns represented the material IDs m1 and m2 for the core and shell sections, respectively. The next two columns contained their corresponding thicknesses t1 and t2. The dielectric host medium, either air (0) or water (1), was indicated in the fifth column; only the water medium was considered for this work. The remaining 200 columns contained the absorption cross-section data for each nanosphere.
2.2 Model architecture and training
Two distinct approaches were explored for inverse design: a tandem network and a cVAE (ESI Fig. S1†). Both models used in this work primarily employ a convolutional neural network (CNN) with ResNet architecture.41 In case of the tandem forward model, a resNeXt CNN architecture has been employed. Such resNeXt architecture is a variation on the ResNet architecture that adds an additional dimension (cardinality) to the resnet blocks to achieve higher accuracy using similar model complexity.42 In this case, 1D convolution was performed, and batch normalization has been done on every skip connection. The model utilized nine resNeXt blocks, and up-sampling was done after every 2 blocks. The inverse model was built by directly using a resnet CNN architecture. The model utilized 12 resnet blocks, after which the layers were flattened and 4 branches of dense layers were added. Each branch corresponded to the design properties for the core and shell material and thicknesses. Initially, the forward model was separately trained and the weights and biases were fixed. The forward model was then used for the training of the inverse model within the tandem architecture. Once the training process was completed, the inverse network was saved separately to be used for inverse design predictions.In the case of the cVAE model, both the particle design and optical response (condition) were applied as inputs to the encoder network, which converted these inputs to the latent vector. The decoder network, on the other hand, was given the latent vector and the optical response (condition) as inputs from which it generated the predicted inverse design. In this way, the model can be trained on multiple designs for the same input conditions by changing the latent variables. Hence, exploring different values in the latent space with the same input condition can yield multiple valid designs. The model has a complex architecture that uses resnet CNN branches along with dense layers and uses four additional reconstruction losses for the design parameters of the particle. Categorical cross-entropy was used as a loss function for the core and shell material predictions, and mean squared error (MSE) was used as a loss function for the predicted thickness of the layers. Furthermore, Kullback–Leibler (KL) divergence loss was used for training the encoder to ensure the proper construction of the latent z space.43 The entire model consisting of the encoder and the decoder networks was constructed and trained as a whole, rather than separately, to implement the process. After the completion of training, the decoder section was separated and saved to be used for inverse predictions. All the networks were trained using the AdamW optimizer. Additionally, a callback function that reduces the learning rate once the training loss stops improving was utilized. Furthermore, the batch size was doubled after every 16 epochs. This adaptive batch size technique helps by reducing the training time significantly while minimally affecting the accuracy.44
2.3 Nanoparticle synthesis
After completing the training phase, the performance of the models was evaluated using spectral input from both theoretical and experimental sources. The theoretical assessment involved generating a distinct test set of random nanoparticles via Mie theory. The experimental evaluation of the model performance was conducted with the use of absorbance spectra obtained from UV-vis spectroscopic data of the synthesized Au@Ag core–shell NPs. First, the gold nanoparticles (AuNPs) were prepared by employing a chemical reduction protocol using trisodium citrate (TSC) as a reducing agent.45 In a beaker, approximately 5.2 μL of an aqueous solution of HAuCl4 (approximately 5.0 M) was added to 100 mL of nanopure water. This solution was vigorously stirred at a speed of 1200 rpm while being held on a magnetic hot plate. Once the solution achieved its chilling temperature, a controlled dropwise injection of 1% TSC (4 mL) was started, with a 40 seconds interval between consecutive drops. Subsequently, the mixture was stirred under the same conditions for 30 minutes; at that point, the solution became wine-red, indicating the effective synthesis of AuNPs. The temperature of the nanoparticles was then reduced to room temperature for further use as the seed solution for the synthesis of Au@Ag core–shell nanoparticles.Second, the Au@Ag nanoparticles were prepared by employing a seed-mediated growth chemical reduction protocol.46 To achieve this, 15 mL of AuNPs (seed solution) were placed in a beaker and continuously stirred at room temperature (25 °C) at a speed of approximately 1200 rpm using a magnetic hot plate. After successive additions of 300 μL of TSC (approximately 1%) and 9.0 μL of 100 mM ascorbic acid, the mixture was vigorously stirred for 5 minutes. Then, 90 μL of AgNO3 (approximately 10 mM) solution was added into the mixture at a rate of one drop per 40 seconds. The addition of the specified amount of AgNO3 resulted in a gradual color change of the solution from wine-red to orange-yellow. Color change indicated the successful fabrication of Au@Ag core–shell NPs.
2.4 Nanoparticle characterization
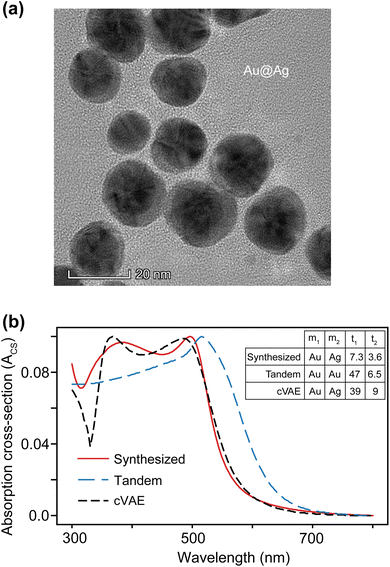
Transmission electron microscopy (TEM) imaging was utilized for particle imagery, enabling the construction of particle size distributions for both the core and shell sections of the nanoparticles. Subsequently, normal distribution curves were overlaid on these distributions, with the maxima of these curves providing the average sizes of the core and shell, approximately 7.3 nm (radius) and 3.6 nm, respectively. Finally, UV-vis spectroscopy was employed to obtain absorbance spectra across the wavelength range of 300 to 800 nm.3 Results & discussion
3.1 Nanoparticle inverse design using tandem neural network
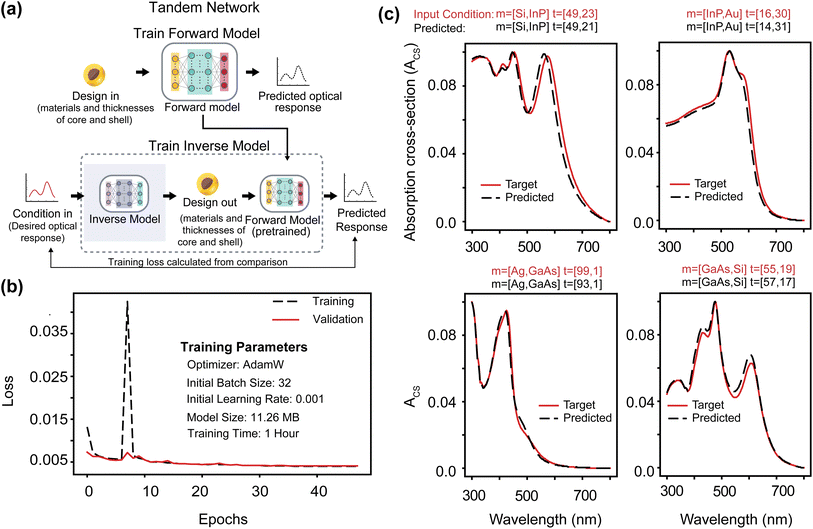
One major challenge in the inverse design of nanophotonic devices is the non-unique mapping between electromagnetic responses and designs when training deep neural networks.13 The tandem network addresses the problem by cascading inverse-design and forward-modeling networks (Fig. 1a). The training process begins with the forward network, which simulates the underlying physics of the system (Fig. 1a-top panel) and predicts the optical response based on design parameters. It is trained using 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 samples. The input parameters include the core material ID (m1), shell material ID (m2), core thickness (t1), and shell thickness (t2). Material IDs range from 1 to 10 (ESI Fig. S1†), corresponding to the following materials: silver (Ag), aluminum (Al), gold (Au), copper (Cu), gallium arsenide (GaAs), indium arsenide (InAs), indium phosphide (InP), molybdenum (Mo), silicon (Si), and silicon dioxide (SiO2). Once the forward network is adequately trained, an inverse network is introduced, and training takes place in tandem (Fig. 1a-bottom panel).11 In the inverse model, the desired optical spectra are provided as conditions to generate the design parameters (m1, m2, t1, t2), which are then fed into the forward network to predict the outcome. As shown in Fig. 1a, the error is calculated by comparing the predicted outcome with the desired outcome. This error is then used to adjust the inverse network (ESI Text 1†). Fig. 1b and S2† show the training loss and validation loss curves during training. In Fig. 1c, we present four random samples where the model-predicted particle designs closely matched the particle designs that produced the input spectra. The optical response is calculated for the predicted inverse design (dashed black line) using Mie theory (Scattnlay) and then compared with the input condition spectra (solid red line). The results in Fig. 1c reveal that the corresponding predicted and target spectra are nearly identical, demonstrating the competence of our model. However, the four solutions predicted by the tandem model for four input conditions may not be the only possible solutions. Therefore, one major disadvantage of the tandem model is that it can only predict one design at a time. As a result, other potential solutions remain unexplored. The lack of diversity represents a significant limitation, particularly during fabrication when multiple designs are required. The use of cVAE addresses this limitation of the tandem network.18
210 samples. The input parameters include the core material ID (m1), shell material ID (m2), core thickness (t1), and shell thickness (t2). Material IDs range from 1 to 10 (ESI Fig. S1†), corresponding to the following materials: silver (Ag), aluminum (Al), gold (Au), copper (Cu), gallium arsenide (GaAs), indium arsenide (InAs), indium phosphide (InP), molybdenum (Mo), silicon (Si), and silicon dioxide (SiO2). Once the forward network is adequately trained, an inverse network is introduced, and training takes place in tandem (Fig. 1a-bottom panel).11 In the inverse model, the desired optical spectra are provided as conditions to generate the design parameters (m1, m2, t1, t2), which are then fed into the forward network to predict the outcome. As shown in Fig. 1a, the error is calculated by comparing the predicted outcome with the desired outcome. This error is then used to adjust the inverse network (ESI Text 1†). Fig. 1b and S2† show the training loss and validation loss curves during training. In Fig. 1c, we present four random samples where the model-predicted particle designs closely matched the particle designs that produced the input spectra. The optical response is calculated for the predicted inverse design (dashed black line) using Mie theory (Scattnlay) and then compared with the input condition spectra (solid red line). The results in Fig. 1c reveal that the corresponding predicted and target spectra are nearly identical, demonstrating the competence of our model. However, the four solutions predicted by the tandem model for four input conditions may not be the only possible solutions. Therefore, one major disadvantage of the tandem model is that it can only predict one design at a time. As a result, other potential solutions remain unexplored. The lack of diversity represents a significant limitation, particularly during fabrication when multiple designs are required. The use of cVAE addresses this limitation of the tandem network.18
3.2 Nanoparticle inverse design using cVAE neural network
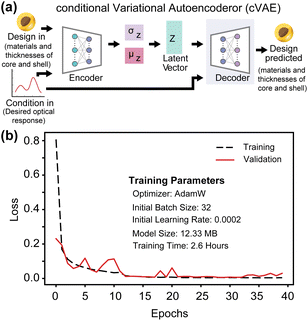
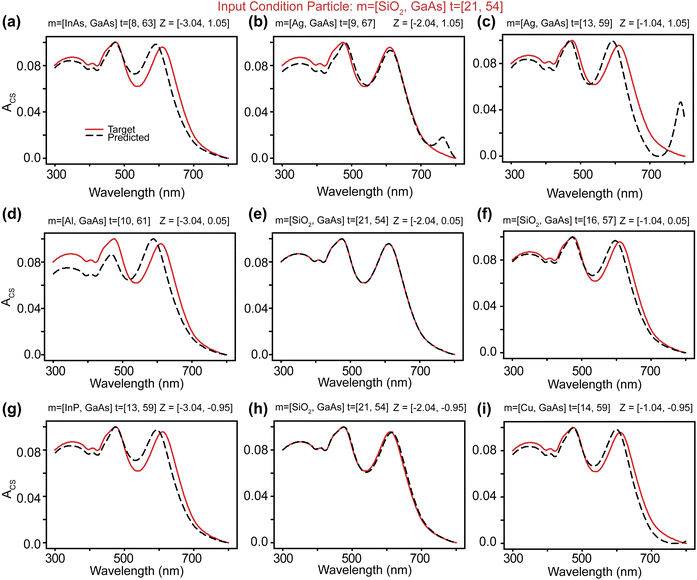
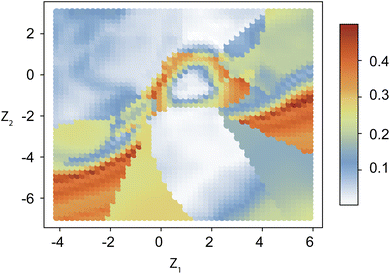
A modification of VAEs, the cVAE defines the latent space using the mean and standard deviation of a normal distribution. It employs latent variables to encode inputs to outputs (Fig. 2a and ESI Text 2†). In cVAE, the VAE architecture, which reproduces designs through an encoder-decoder setup, is extended by an additional input called the design condition. By conditioning designs on their physical properties, such as optical characteristics, a cVAE can be trained as an inverse design network. As illustrated in Fig. 2a, this additional condition is incorporated as input to both the encoder and the decoder. During training, the encoder and decoder are trained together as a unified model. The design parameters (m1, m2, t1, t2) and the corresponding optical response (condition) are provided as inputs to the encoder, which encodes this information into a low-dimensional latent vector, z. This latent vector, along with the same optical response (condition), is then provided as input to the decoder, which predicts the initial design parameters. For any given condition, different values of the latent vector correspond to multiple possible solutions. Fig. 2b shows the learning curve of the network. Once training is complete, only the decoder is utilized for inverse design. This approach allows the exploration of multiple design solutions for a given target condition, enhancing the versatility and robustness of the inverse design process.The capability to identify multiple possible solutions with a cVAE is demonstrated in Fig. 3, S3 and S4.† Different regions of the latent space map to various materials and thickness predictions for the particle. ESI Fig. S5† illustrates how we choose z values. First, we consider a search area centered on the origin (0, 0). Then, we examine a 5 × 5 grid of the latent space within the search area, input them into the cVAE, and compare the spectra of the predicted particles with the input spectrum. The z-value with the lowest MAE is considered the best z-value. The MAE is calculated using the equation: 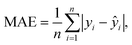 where yi represents the true values, ŷi represents the predicted values, and n is the total number of data points taken on the spectrum. For the next iteration, we regard the best z-value as the new origin (center) and reduce the search area to half of its original size. We repeat the process five times and take the best result at the end as the final model prediction. Fig. 3 represents the z-values found after five iterations. This figure is designed to not only show the prediction results based on the optimal z-values but also to illustrate the impact of slightly different z-values. From left to right, the z1 value changes by 1 in each graph, and from bottom to top, the z2 value changes by 1. Thus, the entire Fig. 3 functions as a larger graph with z1 on the x-axis and z2 on the y-axis. Each sub-figure represents a point on this larger graph, arranged in a 3 × 3 grid for better visibility. This visualization demonstrates how the cVAE model facilitates the exploration of multiple solutions for this inverse design task.
where yi represents the true values, ŷi represents the predicted values, and n is the total number of data points taken on the spectrum. For the next iteration, we regard the best z-value as the new origin (center) and reduce the search area to half of its original size. We repeat the process five times and take the best result at the end as the final model prediction. Fig. 3 represents the z-values found after five iterations. This figure is designed to not only show the prediction results based on the optimal z-values but also to illustrate the impact of slightly different z-values. From left to right, the z1 value changes by 1 in each graph, and from bottom to top, the z2 value changes by 1. Thus, the entire Fig. 3 functions as a larger graph with z1 on the x-axis and z2 on the y-axis. Each sub-figure represents a point on this larger graph, arranged in a 3 × 3 grid for better visibility. This visualization demonstrates how the cVAE model facilitates the exploration of multiple solutions for this inverse design task.
3.3 Performance comparison of cVAE and tandem network in nanoparticle inverse design
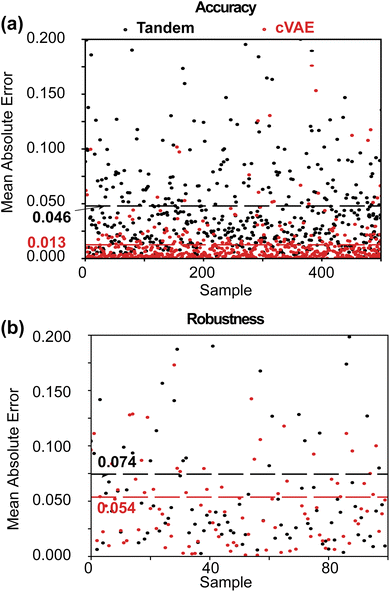
We compare the performance of the two networks in ENP inverse design using accuracy, robustness, and diversity. For this, we create a new test set comprising 500 randomly generated nanospheres and their spectral responses using Mie theory simulations. Both the cVAE and tandem networks are tasked with performing inverse design using these newly generated condition spectra. The spectral response is then calculated for the resultant designs using Mie theory. For the cVAE model, multiple iterations are performed for each condition spectrum to find the optimal value for the input latent variables, predicting the inverse design with the lowest error between the input and predicted spectral responses.We use MAE and root mean squared error (RMSE) to evaluate accuracy, as MAE reflects overall performance, while RMSE highlights the influence of larger errors.18 The RMSE is expressed as 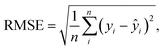 where yi and ŷi refer to the target spectrum values and the spectrum values for the inverse designed structure, respectively, and n is the total number of data points taken across the spectrum. The tandem model gives average MAE and RMSE values of 0.046 and 0.068, respectively, and the cVAE shows average MAE and RMSE of 0.013 and 0.019, respectively (Fig. 4a and S6a†). Both MAE and RMSE measure the differences between the spectral responses of the predicted designs and the input condition spectra. Therefore, lower MAE and RMSE signify better accuracy.
where yi and ŷi refer to the target spectrum values and the spectrum values for the inverse designed structure, respectively, and n is the total number of data points taken across the spectrum. The tandem model gives average MAE and RMSE values of 0.046 and 0.068, respectively, and the cVAE shows average MAE and RMSE of 0.013 and 0.019, respectively (Fig. 4a and S6a†). Both MAE and RMSE measure the differences between the spectral responses of the predicted designs and the input condition spectra. Therefore, lower MAE and RMSE signify better accuracy.
Next, we compare the performance of the two models in terms of their robustness. From the new test set containing 500 samples, we randomly select 100 test targets and obtain the inverse predicted structures. We then vary t1 and t2 randomly in a range of −5% to +5% to create a perturbed set of the predicted designs and simulate the optical response. We again calculate the MAE of the perturbed spectra with respect to the target spectra. Our results show that the cVAE achieves better robustness, with MAE and RMSE values of 0.054 and 0.076, respectively, compared to the tandem model, which suffers from higher MAE and RMSE values of 0.074 and 0.104 (Fig. 4b and S6b†), respectively. This indicates that the optical responses of fabricated structures predicted by the cVAE deviate less from the target responses, demonstrating better fabrication tolerance. Therefore, our results demonstrate that the generative cVAE produces more accurate and robust results in the ENP spectrum inverse design compared to the deterministic tandem model.
Finally, we compare the diversity of predicted structures between the two models. The cVAE generates diverse outputs for the same input condition by sampling from the latent space, introducing variability in the outputs. This feature is beneficial for nanofabrication tasks, as diverse structures aid fabrication by offering more candidate designs for challenging shapes. Conversely, the tandem model provides a single, deterministic output for a given input, limiting its diversity. In accuracy calculations, we select the best solution (the closest match to the desired spectrum) by minimizing MAE. This approach impacts the cVAE's diversity. If researchers prioritize diversity, they can select the top n structures whose spectra best match the desired spectrum instead of just the best one. These top n structures provide a diverse set of solutions close to the target.
To show the diversity of cVAE, we select a test spectrum (target), sample the latent space for potential solutions, and calculate the MAE between each potential solution and the target input. Fig. 5 (ESI Fig. S7†) shows the MAE (RMSE) distributions for a particular test target. The use of cVAE provides multiple diverse nanoparticle structures that match the desired spectrum to varying degrees (Fig. 5). This diversity in predictions offers flexibility in choosing the best structure based on additional criteria like manufacturability or cost. The tandem model, on the other hand, provides a single, highly optimized structure that closely matches the desired spectrum, focusing on precision and suitability when a specific, optimal solution is required.
To further compare the performance of cVAE in ENP spectrum inverse design, we synthesize Au (core)–Ag (shell) nanoparticles. As evident in our TEM image (Fig. 6a), the synthesized nanoparticles are not completely spherical and isotropic in composition; the core and shell thicknesses are not symmetrical throughout the particle. Furthermore, these particles exhibit a wide range of sizes, which affects their absorbance spectra and, in turn, the model predictions. These factors combined hinder the ability of an inverse design network to completely match the synthesized particles. Even so, using the cVAE model, by probing the z-space (ESI Fig. S5†), we find that the most optimized design closely matches the experimental measurements for z = [2.32, – 1.26].
Fig. 6b compares the experimental absorption cross-section given to the models as the input condition (red curve) and the simulated response from the predicted inverse design particles from both the tandem (dashed blue curve) and cVAE (dashed black curve) models. The tandem model essentially predicts a single-layered gold nanoparticle with a radius of 53.5 nm. On the other hand, the cVAE model, due to its advantageous diversity and robustness, shows a close match to the target spectrum, resulting in a low MAE despite the thicknesses being significantly different from the true values (Fig. 6b). ESI Fig. S8† further illustrates that multiple solutions exist where the predicted spectrum closely matches the target spectrum with varied geometrical parameters. The cVAE model predicts the spectral features more correctly. For example, it predicts the ordinary modes47 of plasmon resonance corresponding to field localization at the outer surface of the Ag shell at around 500 nm. It also predicts the extraordinary modes47 of plasmon resonance at around 375 nm, which corresponds to field enhancements at the core–shell interface.
4 Conclusion
We propose a cVAE network for the inverse design of core–shell nanoparticles and compare its performance with that of a tandem neural network. We construct a dataset from Mie theory simulations, which includes ten commonly used materials in plasmonic core–shell nanoparticle synthesis. The cVAE model achieves a lower MAE of 0.013 compared to 0.046 for the tandem model. Lower MAE indicates enhanced accuracy in predicting the desired optical responses. We conduct a robustness analysis using 100 test spectra. The results confirm that the cVAE model is more reliable. If we perturb the structural parameters (thicknesses) and recalculate the spectra, we find that the cVAE offers lower MAE and RMSE values compared to the tandem network. Specifically, the cVAE achieved an MAE of 0.054 and an RMSE of 0.076, while the tandem model recorded an MAE of 0.074 and an RMSE of 0.104. These results show that the cVAE model produces designs more resilient to minor deviations in the manufacturing process. Moreover, with the cVAE model, one can obtain many valid designs corresponding to the same input condition. This diversity allows flexibility in choosing the best structure based on additional criteria like manufacturability or cost. In contrast, the tandem model provides a single, deterministic output, limiting the range of possible solutions. To validate the cVAE model experimentally, we synthesize Au@Ag core–shell nanoparticles. The cVAE model accurately predicts both the material composition and the spectral features of the synthesized nanoparticles. Our findings show the potential of cVAEs as powerful generative neural networks for advancing nanophotonic applications. We will make the dataset used in this study publicly accessible on GitHub to support further research and enable extensions to multilayer nanoparticle inverse design. Future work could improve the model by incorporating additional experimental data on colloidal nanoparticles and accounting for factors like dispersion in solution and nanoparticle agglomeration.Data availability
The datasets generated during the current study are available at GitHub Repository: https://github.com/tanzim-rahman/plasmonics-inverse-design.git.Author contributions
Tanzim Rahman: data curation, formal analysis, software, methodology, validation, writing – original draft, writing – review & editing, visualization. Ahnaf Tahmid: data curation, formal analysis, software, methodology, validation, writing – original draft, writing – review & editing, visualization. Shifat E. Arman: formal analysis, software, methodology, validation, writing – review & editing. Tanvir Ahmed: methodology, writing – review & editing. Zarin Tasnim Rakhy: methodology, writing – review & editing. Harinarayan Das: methodology, writing – review & editing. Mahmudur Rahman: formal analysis, validation. Abul Kalam Azad: formal analysis, validation. Md. Wahadoszamen: formal analysis, validation, writing – review & editing. Ahsan Habib: conceptualization, methodology, writing – original draft, writing – review & editing, visualization, project administration, funding acquisition.Conflicts of interest
The authors declare that there are no conflicts of interest to declare.Acknowledgements
Ahsan Habib acknowledges the funding provided by the Ministry of Science and Technology, Bangladesh (SRG-232417), and the Faculty of Engineering and Technology, University of Dhaka. Mahmudur Rahman acknowledges the University Grants Commission of Bangladesh Research Grant 2024-2025, DUET, Gazipur (CASR No. 79). The authors extend their sincere thanks for the synthesis facilities provided by the Semiconductor Technology Research Centre (STRC) and Centre for Advanced Research in Sciences (CARS). Gratitude is also due to the Bangladesh Atomic Energy Commission (BAEC) for TEM imaging support. The authors acknowledge the assistance of ChatGPT by OpenAI for improving clarity and making grammatical corrections.Notes and references
- Y. Mantri and J. V. Jokerst, ACS Nano, 2020, 14, 9408–9422 CrossRef CAS.
- N. S. S. Mousavi, K. B. Ramadi, Y.-A. Song and S. Kumar, Commun. Mater., 2023, 4, 101 CrossRef.
- P. Babakhani, T. Phenrat, M. Baalousha, K. Soratana, C. L. Peacock, B. S. Twining and M. F. Hochella, Nat. Nanotechnol., 2022, 17, 1342–1351 CrossRef CAS PubMed.
- S. Pradhan and D. R. Mailapalli, J. Agric. Food Chem., 2017, 65, 8279–8294 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, 1998 Search PubMed.
- S. Link and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 4212–4217 CrossRef CAS.
- A. Henglein, J. Phys. Chem., 1993, 97, 5457–5471 CrossRef CAS.
- J. Jiang, M. Chen and J. A. Fan, Nat. Rev. Mater., 2020, 6, 679–700 CrossRef.
- O. Khatib, S. Ren, J. Malof and W. J. Padilla, Adv. Funct. Mater., 2021, 31, 2101748 CrossRef CAS.
- R. E. Christiansen, J. Michon, M. Benzaouia, O. Sigmund and S. G. Johnson, Opt. Express, 2020, 28, 4444 CrossRef PubMed.
- M. M. R. Elsawy, S. Lanteri, R. Duvigneau, J. A. Fan and P. Genevet, Laser Photonics Rev., 2020, 14, 1900445 CrossRef CAS.
- Q. Pan, S. Zhou, S. Chen, C. Yu, Y. Guo and Y. Shuai, Opt. Express, 2023, 31, 23944 CrossRef CAS PubMed.
- D. Liu, Y. Tan, E. Khoram and Z. Yu, ACS Photonics, 2018, 5, 1365–1369 CrossRef CAS.
- X. Xu, C. Sun, Y. Li, J. Zhao, J. Han and W. Huang, Opt. Commun., 2021, 481, 126513 CrossRef CAS.
- T. Jahan, T. Dash, S. E. Arman, R. Inum, S. Islam, L. Jamal, A. A. Yanik and A. Habib, Nanoscale, 2024, 16, 16641–16651 RSC.
- J. He, C. He, C. Zheng, Q. Wang and J. Ye, Nanoscale, 2019, 11, 17444–17459 RSC.
- Z. Liu, D. Zhu, S. P. Rodrigues, K.-T. Lee and W. Cai, Nano Lett., 2018, 18, 6570–6576 CrossRef CAS.
- T. Ma, M. Tobah, H. Wang and L. J. Guo, Opto-Electron. Sci., 2022, 1, 210012 CAS.
- A. Khaireh-Walieh, D. Langevin, P. Bennet, O. Teytaud, A. Moreau and P. R. Wiecha, Nanophotonics, 2023, 12, 4387–4414 CrossRef PubMed.
- Y. Tang, K. Kojima, T. Koike-Akino, Y. Wang, P. Wu, Y. Xie, M. H. Tahersima, D. K. Jha, K. Parsons and M. Qi, Laser Photonics Rev., 2020, 14, 2000287 CrossRef CAS.
- O. Peña and U. Pal, Comput. Phys. Commun., 2009, 180, 2348–2354 CrossRef.
- J.-B. Zeng, Y.-Y. Cao, J.-J. Chen, X.-D. Wang, J.-F. Yu, B.-B. Yu, Z.-F. Yan and X. Chen, Nanoscale, 2014, 6, 9939–9943 RSC.
- G. Maidecchi, C. V. Duc, R. Buzio, A. Gerbi, G. Gemme, M. Canepa and F. Bisio, J. Phys. Chem. C, 2015, 119, 26719–26725 CrossRef CAS.
- A. Loiseau, L. Zhang, D. Hu, M. Salmain, Y. Mazouzi, R. Flack, B. Liedberg and S. Boujday, ACS Appl. Mater. Interfaces, 2019, 11, 46462–46471 CrossRef CAS.
- A. C. Foucher, S. Yang, D. J. Rosen, J. D. Lee, R. Huang, Z. Jiang, F. G. Barrera, K. Chen, G. G. Hollyer, C. M. Friend, R. J. Gorte, C. B. Murray and E. A. Stach, J. Am. Chem. Soc., 2022, 144, 7919–7928 CrossRef CAS PubMed.
- C. Ghosh, S. Pal, B. Goswami and P. Sarkar, J. Phys. Chem. Solids, 2009, 70, 1024–1029 CrossRef CAS.
- D. Franke, D. K. Harris, O. Chen, O. T. Bruns, J. A. Carr, M. W. B. Wilson and M. G. Bawendi, Nat. Commun., 2016, 7, 12749 CrossRef CAS.
- M. Kambayashi, N. Yamauchi, K. Nakashima, M. Hasegawa, Y. Hirayama, T. Suzuki and Y. Kobayashi, SN Appl. Sci., 2019, 1, 1576 CrossRef CAS.
- M. Keerthi, G. Boopathy, S.-M. Chen, T.-W. Chen and B.-S. Lou, Sci. Rep., 2019, 9, 13075 CrossRef PubMed.
- R. Ghosh Chaudhuri, in Metal/semiconductor Core/shell Nanostructures for Environmental Remediation, Elsevier, 2017, pp. 79–98 Search PubMed.
- Y. Lu, Y. Yin, Z.-Y. Li and Y. Xia, Nano Lett., 2002, 2, 785–788 CrossRef CAS.
- K. M. McPeak, S. V. Jayanti, S. J. P. Kress, S. Meyer, S. Iotti, A. Rossinelli and D. J. Norris, ACS Photonics, 2015, 2, 326–333 CrossRef CAS.
- F. Cheng, P.-H. Su, J. Choi, S. Gwo, X. Li and C.-K. Shih, ACS Nano, 2016, 10, 9852–9860 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Phys. Rev. B, 1972, 6, 4370–4379 CrossRef CAS.
- K. Papatryfonos, T. Angelova, A. Brimont, B. Reid, S. Guldin, P. R. Smith, M. Tang, K. Li, A. J. Seeds, H. Liu and D. R. Selviah, AIP Adv., 2021, 11, 025327 CrossRef CAS.
- D. E. Aspnes and A. A. Studna, Phys. Rev. B, 1983, 27, 985–1009 CrossRef CAS.
- W. S. M. Werner, K. Glantschnig and C. Ambrosch-Draxl, J. Phys. Chem. Ref. Data, 2009, 38, 1013–1092 CrossRef CAS.
- I. H. Malitson, J. Opt. Soc. Am., 1965, 55, 1205 CrossRef CAS.
- M. Daimon and A. Masumura, Appl. Opt., 2007, 46, 3811 CrossRef.
- M. N. Polyanskiy, Sci. Data, 2024, 11, 94 CrossRef.
- K. He, X. Zhang, S. Ren and J. Sun, Deep Residual Learning for Image Recognition, 2015, https://arxiv.org/abs/1512.03385 Search PubMed.
- S. Xie, R. Girshick, P. Dollár, Z. Tu and K. He, Aggregated Residual Transformations for Deep Neural Networks, 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 2017, pp. 5987–5995, DOI:10.1109/CVPR.2017.634.
- M. Debbagh, Learning Structured Output Representations from Attributes using Deep Conditional Generative Models, 2023, https://arxiv.org/abs/2305.00980 Search PubMed.
- A. Devarakonda, M. Naumov and M. Garland, arXiv Preprint arXiv:1712.02029, 2017 Search PubMed.
- J. Wang, R. Liu, C. Zhang, G. Han, J. Zhao, B. Liu, C. Jiang and Z. Zhang, RSC Adv., 2015, 5, 86803–86810 RSC.
- K. Wang, D.-W. Sun, H. Pu and Q. Wei, Talanta, 2021, 223, 121782 CrossRef CAS PubMed.
- D. Avşar, H. Ertürk and M. P. Mengüç, J. Quant. Spectrosc. Radiat. Transfer, 2020, 241, 106684 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Text 1: tandem neural network; Text 2: conditional variational autoencoder neural network; Fig. S1: schematic of tandem and cVAE models for inverse design of core–shell nanoparticle; Fig. S2: training and validation loss curves for the forward networks (for tandem) used in the study; Fig. S3: additional examples of the cVAE's capability in predicting varied designs while maintaining accurate optical properties are included; Fig. S4: additional examples of the cVAE's capability in predicting varied designs while maintaining accurate optical properties are included; Fig. S5: illustration of the method for choosing z values; Fig. S6: comparison of root mean squared error (RMSE) between the spectral responses of the predicted designs and the input condition spectra for both the tandem model and the cVAE model; Fig. S7: RMSE distributions in the latent space for a particular test target; Fig. S8: comparison of the experimental absorption cross-section given to the models as the input condition and the simulated response from the predicted inverse design particles from the cVAE models; Table S1: material IDs and sources for refractive indices for the materials used during this work. See DOI: https://doi.org/10.1039/d4na00859f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |