Spintronic devices and applications using noncollinear chiral antiferromagnets†
Ankit
Shukla
 ,
Siyuan
Qian
and
Shaloo
Rakheja
,
Siyuan
Qian
and
Shaloo
Rakheja
 *
*
Electrical and Computer Engineering, The Grainger College of Engineering, University of Illinois Urbana-Champaign, Urbana, USA. E-mail: rakheja@illinois.edu; Tel: +1 217-244-3616
First published on 3rd December 2024
Abstract
Antiferromagnetic materials have several unique properties, such as a vanishingly small net magnetization, which generates weak dipolar fields and makes them robust against perturbation from external magnetic fields and rapid magnetization dynamics, as dictated by the geometric mean of their exchange and anisotropy energies. However, experimental and theoretical techniques to detect and manipulate the antiferromagnetic order in a fully electrical manner must be developed to enable advanced spintronic devices with antiferromagnets as their active spin-dependent elements. Among the various antiferromagnetic materials, conducting antiferromagnets offer high electrical and thermal conductivities and strong electron–spin–phonon interactions. Noncollinear metallic antiferromagnets with negative chirality, including Mn3Sn, Mn3Ge, and Mn3GaN, offer rich physics of spin momentum locking, topologically protected surface states, large spin Hall conductivity, and a magnetic spin Hall effect that arises from their topology. In this review article, we introduce the crystal structure and the physical phenomena, including the anomalous Hall and Nernst effects, spin Hall effect, and magneto-optic Kerr effect, observed in negative chirality antiferromagnets. Experimental advances related to spin–orbit torque-induced dynamics and the impact of the torque on the microscopic spin structure of Mn3Sn are also discussed. Recent experimental demonstrations of a finite room-temperature tunneling magnetoresistance in tunnel junctions with chiral antiferromagnets opens the prospect of developing spintronic devices with fully electrical readout. Applications of chiral antiferromagnets, including non-volatile memory, high-frequency signal generators/detectors, neuro-synaptic emulators, probabilistic bits, thermoelectric devices, and Josephson junctions, are highlighted. We also present analytic models that relate the performance characteristics of the device with its design parameters, thus enabling a rapid technology–device assessment. Effects of Joule heating and thermal noise on the device characteristics are briefly discussed. We close the paper by summarizing the status of research and present our outlook in this rapidly evolving research field.
1 Introduction
The field of spintronics utilizes information stored in the magnetization vector of a magnetically ordered medium. Typical effects, such as spin-transfer torque (STT) and spin–orbit torque (SOT) in conjunction with a magnetic field, are used to switch the magnetic state.1–11 The non-volatility and scalability of spintronic devices can allow us to implement information processing devices with reduced resources (i.e., energy, area, and time). Spintronic devices can complement the functionality of silicon CMOS circuits for beyond von Neumann computing applications including probabilistic and stochastic computing, bio-inspired computing, and Joule heating free transfer of information.12–27Typically, the active element in spintronic devices is a ferromagnet (FM) in which spins on the neighboring ions are aligned in a parallel manner, resulting in a net macroscopic moment. A two-terminal (2T) device composed of thin FM layers separated by a non-magnetic insulating spacer, referred to as the magnetic tunnel junction (MTJ), is considered as the building block in spintronics computing. The net resistance of the MTJ stack depends on the relative magnetic orientation of the two FM leads: a low resistance state is obtained for parallel orientation of the FMs, while a high resistance state is obtained for anti-parallel orientation of the FMs. In a 2T MTJ, STT is used to change the orientation of one of the FMs, referred to as the free layer, while the other FM has a pinned orientation, whose magnetization is unperturbed in the presence of STT. A three-terminal (3T) MTJ in which the SOT is used to control the orientation of the free FM layer offers a higher degree of flexibility and energy efficiency for spintronics computing applications. The on–off ratio, i.e., the difference between the high and low resistance states, of the MTJ is read out via the tunneling magnetoresistance (TMR), which can reach values as high as 631% at room temperature in epitaxial devices employing MgO as the tunneling barrier.28
More recently, antiferromagnetic-based spintronic devices have gained significant attention from the research community. Unlike FMs, antiferromagnets (AFMs) do not have a macroscopic magnetic moment which creates both challenges and opportunities for their future computing paradigms.29–35 For example, the lack of dipolar fields in AFMs can enable their ultra-dense integration in circuits without crosstalk issues and related security vulnerabilities. However, as AFMs lack a macroscopic moment, it is difficult to read their magnetic state in device geometries. In this regard, the octupole moment in chirally ordered noncollinear AFMs (e.g., Mn3Sn, Mn3Ge, Mn3GaN, etc.) can be used as an order parameter in all-AFM MTJs that exhibit finite TMR and have negligible stray fields and the potential for high-speed operation. The octupole moment is a rank-3 multipole moment of Mn atoms averaged over the entire magnetic unit cell.36 The octupole moment has the same irreducible representation as the dipole moment in FMs. Thus, chiral noncollinear AFMs combine the benefits of FMs and other collinear AFMs, setting the stage for advanced information processing devices using the octupole moment as the computational state variable.37,38 Interested readers can refer to ref. 39 for a detailed review on chiral spintronics. Although not the focus of this work, interested readers may also refer to ref. 40–48 for a detailed overview of altermagnetism, which is a newly discovered phase in magnetic materials. Altermagnets are interesting candidates for spintronics research since they share at least two properties in common with chiral AFMs. Firstly, altermagnets exhibit antiferromagnetic properties due to the opposite arrangement of neighboring atomic spins, similar to that in collinear AFMs. Secondly, they exhibit ferromagnetic properties owing to certain broken symmetries (e.g., time-reversal symmetry), which arise due to the alternating variation in the local atomic structure.
In this paper, we review recent experimental and theoretical progress in noncollinear AFMs with negative chirality, in which the octupole moment gives rise to non-degenerate spin-polarized bands at the Fermi level and a finite TMR at room temperature. The octupole moment in these AFMs can be manipulated via SOT from a proximal non-magnetic material such as a heavy metal (e.g., W, Pt, etc.), and high-speed order parameter dynamics including chiral oscillations and switching can be initiated depending on the energy landscape of the AFM and the input SOT and magnetic field. As compared to recent review articles on AFM spintronics that either provide an in-depth picture of a few phenomena49–51 or present brief overviews of various magnetic material systems, phenomena, and applications,35,37,52,53 our work primarily focuses on the recent developments pertaining to detection and manipulation of the magnetic order in the noncollinear chiral AFMs.38 A brief overview of the various possible device applications, driven by chiral AFMs, is also presented in this work.
We present a discussion of the crystal structure and the observed and predicted physical phenomena in chiral AFMs in Section 2. Details regarding order parameter dynamics in six-fold and two-fold symmetric chiral AFMs, particularly in Mn3Sn, are discussed in Section 3. These dynamics along with fully electrical readout of the order parameter, the TMR, form the basis of realizing new types of spintronic devices with chiral AFM serving as the active element. Such devices include high-frequency signal generators and detectors, bio-mimetic neurons, and non-volatile memory. The role of Joule heating and thermal noise in influencing the SOT-driven response of the system is also briefly presented in Section 3. As discussed in Section 4, chiral AFMs can be used in non-volatile memory, artificial synapses, and spiking neurons, and as probabilistic bits, which serve as the building blocks of hardware designed to solve machine learning and hard optimization problems. Additionally, chiral AFMs exhibit the anomalous Nernst effect (ANE), which leads to a voltage signal that is transverse to the thermal gradient and the magnetization of the material. The ANE in chiral AFMs can be exploited for thermoelectric generation, on-chip cooling, and temperature gradient sensor applications. A brief discussion on quantum computing utilizing a chiral AFM-based superconducting Josephson junction is also included. The paper concludes with a summary of key findings and outlooks in the field of condensed matter physics and future chiral AFM spintronic devices.
2 Noncollinear chiral antiferromagnets
2.1 Crystal structure
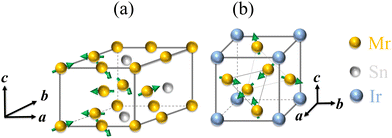
Chiral AFMs are materials with lattice spins oriented in a noncollinear and chiral configuration. In AFMs like Mn3Sn, Mn3Ga and Mn3Ge, the atomic moments are arranged in the basal plane of the hexagonal crystal, while in AFMs like Mn3Ir and Mn3Pt, the atomic spins are in the (111) plane of the face-centered cubic crystal. Fig. 1 shows the crystal and the triangular spin structures of D019-Mn3Sn and L12-ordered Mn3Ir AFMs. The Mn3Sn(Mn3Ir) AFM has negative (positive) chirality: hopping between Mn atoms in a clockwise sense, the atomic moment rotates by 120° in an anticlockwise (a clockwise) sense.The noncollinear moments introduce the Dzyaloshinskii–Moriya interaction (DMI), which stabilizes the triangular spin structure with a given chirality. As the DMI is a super-exchange interaction, it is present in crystal structures with broken inversion symmetry. The DMI introduces a term given as −D12·(S1 × S2) (D12 is the DMI coefficient and S1 and S2 are the atomic spins) in the Hamiltonian and thus favors a certain orientation of S1 with respect to S2. This means that the DMI introduces handedness or chirality to the spin structure of the material. Although Mn3Sn and Mn3Ir are globally centrosymmetric crystals, the noncollinearly arranged moments on Mn atoms break inversion symmetry locally, which introduces DMI in the crystal. Indeed, neutron diffraction measurements carried out on single-crystal Mn3Sn in 1982 revealed weak ferromagnetism54 which was later explained in terms of the DMI mechanism, which leads to canting of moments in the material.55 The chirality of the spin structure breaks the mirror and time-reversal symmetries and lifts degeneracies in the materials’ energy-momentum dispersion, which creates band crossings.
The triangular spin structure in chiral AFMs possess a momentum-space Berry curvature, which can be viewed as an effective magnetic field in the reciprocal space56,57 and is obtained as Ω(k) = ∇k × ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (k), where
(k), where  is the Berry connection. Here, unk is the eigenfunction with wave-vector k and band index n, and the sum extends over all occupied states. Crystal-periodic eigenfunctions from the density functional theory calculations must be used to evaluate the Berry connection. The Berry curvature is then employed to obtain the anomalous Hall conductivity (AHC) as
is the Berry connection. Here, unk is the eigenfunction with wave-vector k and band index n, and the sum extends over all occupied states. Crystal-periodic eigenfunctions from the density functional theory calculations must be used to evaluate the Berry connection. The Berry curvature is then employed to obtain the anomalous Hall conductivity (AHC) as
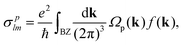 | (1) |
The Berry curvature is concentrated around hot spots in the reciprocal space, while the integral of the Berry curvature over the Brillouin zone modifies the magneto-transport properties of the AFMs.57 The sign of the Berry curvature flips with the chirality of the noncollinear AFM. Thus, the sign of magneto-transport signals that are odd with respect to the Berry curvature also flips in chiral AFMs. Theoretical calculations have shown multiple Weyl points of type II in the bulk bandstructure and Fermi arcs on the surface connecting Weyl points of opposite chirality in Mn3Sn and Mn3Ge.59,60 Weyl points are topological objects that arise when the spin degeneracy of a Dirac point is lifted, and they act as the monopole sources/sinks of the Berry curvature (i.e., a singularity of the Berry curvature).61 Experimental evidence of buried Weyl points in Mn3Sn was presented in ref. 62, where angle-resolved photoemission spectroscopy (ARPES) was used to determine that Mn3Sn is a strongly correlated magnetic material, while the observations of large anomalous Hall effect (AHE), positive longitudinal magnetoconductance, and negative transverse magnetoconductance were utilized to provide evidence for the magnetic Weyl points in the material. Thus, the bandstructure features in chiral AFMs are described as topological in nature and have launched the research field of topological spintronics. Table 1 lists the material properties of various chiral AFMs.
| X | T N (K) | M s (T) | K u (kJ m−3) | J E (MJ m−3) | D M |
|---|---|---|---|---|---|
| Ir63,64 | 960 ± 10 | 1.63 | 3000 | 240 | − |
| Pt63,65 | 473 ± 10 | 1.37 | 10 | 280 | − |
| Rh63,65,66 | 853 ± 10 | 2.00 | 10 | 230 | − |
| Ga63,67–69 | 470 | 0.54 | 100 | 110 | + |
| Sn63,68,70,71 | 420–430 | 0.50 | 110 | 59 | + |
| Ge63,68,69,72 | 365 | 0.28 | 1320 | 77 | + |
| GaN73,74 | 345 | 0.69 | 10 | 280 | − |
| NiN73,74 | 262 | 1.54 | 10 | 177 | − |
2.2 Physical phenomena
Recent magneto-transport measurements have shown the finite AHE,57,58,75,76 the spin Hall effect (SHE),77 ANE,78 and the topological Hall effect (THE) in chiral AFMs. Despite its vanishingly small net magnetic moment of 0.002μB (μB is the Bohr magneton) per Mn atom, large AHC values of 20 (Ω cm)−1 at room temperature and 100 (Ω cm)−1 at low temperatures have been experimentally measured in Mn3Sn.76 Although it is more challenging to observe the AHE in cubic chiral AFMs due to weaker spontaneous ferromagnetism and stronger magnetic anisotropy, uniaxial stress and magnetic field were used in ref. 79 to align the domains in Mn3Pt, leading to a substantial AHC (∼20–30 (Ω cm)−1) in the bulk sample. Similarly, in ref. 80, strain tuning was used to achieve the AHC exceeding 100 (Ω cm)−1, while in ref. 81, epitaxial strain was shown to alter the AHC in Mn3Pt films by more than an order of magnitude. In a chiral AFM, Mn3Ge, anomalous Hall conductivity values of 60 (Ω cm)−1 at room temperature and 380 (Ω cm)−1 at 5 K have been measured, while the AHE was also shown to reverse sign with a rotation of 0.1 T magnetic field.82 Very recently, significantly large anomalous Hall conductivity values of about 150 (Ω cm)−1 at room temperature and 530 (Ω cm)−1 at 10 K have been reported for Mn2.4Ga.83 Similar to other chiral AFMs, the anomalous Hall conductivity in Mn2.4Ga exhibits sign reversal with the rotation of the small external magnetic field.The ANE in which a temperature gradient results in a transverse voltage drop perpendicular to the heat flow and the magnetization is feasible in chiral AFMs. Seebeck coefficient values84 of 0.35 μV K−1 at room temperature and 0.6 μV K−1 at 200 K have been measured for bulk single-crystal Mn3Sn grown via the Bridgman method. Using ab initio calculations, it was shown that the spin Nernst conductivity (SNC) in Mn3Sn and Mn3Ga is about five times larger than that of platinum.85 Moreover, the anomalous Nernst conductivity (ANC) of Mn3Ga at 300 K was found to be 50× that of bcc Fe. The large values of ANC and SNC in noncollinear AFMs are advantageous for implementing thermoelectric and spin caloritronic devices.78
The momentum-dependent spin splitting in Mn3Sn also leads to a magnetic SHE,86 which has an anomalous sign change with the octupole polarity. Novel spin currents in chiral AFMs have also been studied via ab initio methods. In particular, it was shown that spin currents in noncollinear AFMs have both longitudinal and transverse spin polarization components. The longitudinal spin current is similar to the spin-polarized current in FMs. However, the transverse component is odd under time reversal and is thus distinct from the conventional SHE, which is even under time reversal. The first experimental demonstration of the out-of-plane magnetic SHE and the associated out-of-plane field-like torque using spin-torque ferromagnetic resonance (ST-FMR) in single-crystal Mn3Sn/Ni–Fe bilayers was reported in ref. 87. Using macroscopic symmetry analysis and microscopic quantum kinetic theory, Kondou et al. revealed that the origin of the magnetic SHE is likely the momentum-dependent spin splitting in Mn3Sn. In ref. 88, the authors established the relationship between the in-plane polarized spin current in Mn3Sn and its antiferromagnetic order. It was shown that for various thicknesses, in the range of 3–12 nm, of epitaxially grown Mn3Sn on Ru buffered Al2O3, the in-plane polarized spin current was dependent on the AFM order, while the out-of-plane polarized spin current originated from the spin swapping scatterings at the interface between Mn3Sn and Py. These novel spin currents89 can help interpret SOT measurements in noncollinear AFMs, while also being exploited for new spintronics applications.
The electronic bands in Mn3Sn show momentum-dependent spin splitting of the Fermi surface due to the broken time reversal symmetry,90,91 which is postulated to result in the recently reported finite TMR ratio of about 2% at 300 K in experimental Mn3Sn/MgO/Mn3Sn samples91 and about 100% in experimental Mn3Pt/MgO/Mn3Pt samples.92 This is because the TMR values measured in the Mn3Sn/MgO/Mn3Sn tunnel junctions far exceed (by about two orders of magnitude) the TMR ratio theoretically estimated from the anisotropic spin polarization found in Mn3Sn.91 A recent work has suggested that the rather low TMR value measured in Mn3Sn/MgO/Mn3Sn junctions, as compared to that of the Mn3Pt/MgO/Mn3Pt junctions, is likely due to the polycrystalline nature of the top Mn3Sn electrode employed in these samples.51 Another notable recent work has measured an even smaller magnetoresistance (MR) effect of 0.3% at room temperature in granular Mn3Sn–Ag films.93 In the Mn3Sn–Ag composite, the AFM/metal/AFM heterostructure functions as an all-AFM spin valve and thus exhibits a finite MR, which was found to be two orders of magnitude higher compared to the MR measured in Mn3Sn films.
Theoretical estimations presented in ref. 90–92, on the other hand, suggested the possibility of a higher TMR ratio in both Mn3Pt and Mn3Sn tunnel junctions. For example, a theoretical TMR value of 240% was predicted for Mn3Pt/SrTiO3/Mn3Pt in ref. 92. The authors argued that the lower experimental TMR value for all-Mn3Pt junctions with a MgO barrier compared to the theoretically projected TMR value of the junction with a SrTiO3 barrier is a result of grain boundaries and dislocations caused by large lattice mismatch, interfacial roughness, and other defects. In the case of all-Mn3Sn tunnel junctions with vacuum as a barrier, theoretical calculations showed a TMR of 300% while a TMR of 124% was predicted in Mn3Sn junctions with HfO2 as the tunneling barrier. Very recent experimental investigations have provided credibility to such theoretical predictions as a TMR of 110% and resistance-area (RA) product of 1.7 kΩ μm2 at room temperature have been reported for Mn3Pt/Al2O3/Mn3Pt junctions sputter deposited on a thermally oxidized silicon substrate, thus making the process compatible with conventional silicon manufacturing.94 Additional research is needed to understand the reliability of the insulating barrier at high temperatures and current values and enable high-performance AFM-based spintronics applications with fully electrical readout.
Imaging the magnetic domains can provide crucial information regarding the reversal process of the chiral spin structure in a spatially resolved manner. Using the magneto-optic Kerr effect (MOKE) method, Higo et al. measured a large zero-field Kerr rotation angle of 20 mdeg at 300 K in Mn3Sn,95 while a large polar MOKE signal, around 8.2 mdeg, and a large longitudinal MOKE signal, around 5.6 mdeg, have also been measured in Mn3Ge single crystals.96 The Kerr angle value in chiral AFMs is comparable to that found in FMs and is a useful probe to study the dynamics of magnetic domains in chiral AFMs. In this regard, Uchimura et al. measured the Kerr rotation angle in thin films of Mn3+xSn1−x (−0.11 ≤ x ≤ 0.14) and identified that the symmetry requirements of MOKE are the same as those of the AHE.97 Moreover, they showed that the domain reversal process begins by nucleation of reversed domains in the media, followed by domain expansion and preferential propagation along the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction. Uchimura et al. also revealed the size of the nucleated domain to be less than 1 μm, which is much smaller than that observed in the case of bulk samples.95 Studies on current-driven nucleation and displacement of domain walls in chiral AFMs have recently appeared.98,99 Sugimoto et al. identified a sub-micron size Bloch-like domain wall parallel to the Kagome plane in a microfabricated wire of Mn3Sn.99 The nucleation of the domain wall was initiated by current-induced torques in a wedge-shaped device with thickness variation from 500 nm to 1 μm along the [0001] direction. It was found that the current density for the domain-wall nucleation was around 109 A m−2, which was two-to-three orders of magnitude lower than that in the case of ferromagnets. Using MOKE, Wu et al. observed a Néel-like domain wall in Mn3Ge, which could be accelerated up to 750 m s−1 with a current density of 7.56 × 1010 A m−2 without any magnetic fields.98 The results for the imaging, nucleation, and propagation of magnetic-octupole domain walls in microfabricated samples of chiral AFMs are highly significant to drive their new domain-wall-based applications.
0] direction. Uchimura et al. also revealed the size of the nucleated domain to be less than 1 μm, which is much smaller than that observed in the case of bulk samples.95 Studies on current-driven nucleation and displacement of domain walls in chiral AFMs have recently appeared.98,99 Sugimoto et al. identified a sub-micron size Bloch-like domain wall parallel to the Kagome plane in a microfabricated wire of Mn3Sn.99 The nucleation of the domain wall was initiated by current-induced torques in a wedge-shaped device with thickness variation from 500 nm to 1 μm along the [0001] direction. It was found that the current density for the domain-wall nucleation was around 109 A m−2, which was two-to-three orders of magnitude lower than that in the case of ferromagnets. Using MOKE, Wu et al. observed a Néel-like domain wall in Mn3Ge, which could be accelerated up to 750 m s−1 with a current density of 7.56 × 1010 A m−2 without any magnetic fields.98 The results for the imaging, nucleation, and propagation of magnetic-octupole domain walls in microfabricated samples of chiral AFMs are highly significant to drive their new domain-wall-based applications.
Scanning thermal gradient microscopy (STGM) has also been used to image the local magnetic structure of Mn3Sn films. The STGM technique in the presence of magnetic fields can form the basis of writing domain patterns into Mn3Sn as discussed in ref. 100. This work specifically measures the ANE voltage, VANE, for a temperature gradient along the c-axis, which is established with the help of laser illumination. VANE is governed by the average octupole moment of the domains under the illuminated laser spot.
3 Spintronic devices based on chiral AFMs
To realize an energy-efficient spintronic device based on chiral AFMs, it is important to investigate the physics of SOT-driven dynamics of the octupole moment in both bulk and thin film samples of chiral AFMs. On the readout front, although the AHE and anisotropic magnetoresistance can be utilized, the detected signals are generally weak and require amplification adding to the energy consumption and area of the spintronic device. Thus, electrical readout via the TMR is preferred as it provides a more robust signal and is typically compatible with circuit implementations utilizing silicon transistors as the peripherals.A conceptual spintronic device using a chiral AFM is illustrated in Fig. 2. Here, information can be written into the AFM domain via the SOT effect generated in the heavy metal (HM), while TMR can be utilized to transduce the magnetic state into a resistance value. In principle, this device can be used as a high-frequency signal generator/detector, an emulator of a biological neuron, as well as a non-volatile memory element. The specific functionality depends on the device design, including material growth parameters, the presence of strain, and the characteristics of the input stimuli (i.e., pulse width and amplitude of the SOT and the magnetic field). To explore the functionality of the spintronic device, it is important to consider both the order-parameter writing and reading processes and accordingly quantify the limits and challenges of the device for future computing applications.
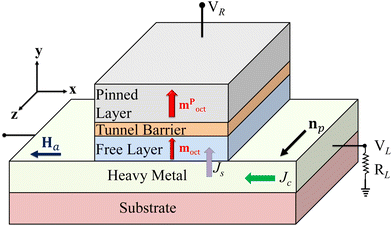 | ||
| Fig. 2 A conceptual three-terminal spintronic device using a negative chirality AFM (e.g., Mn3Sn) as the active element. The AFM serves as both the ‘free layer’ and the ‘pinned layer’. SOT generated in the heavy metal is used to manipulate the octupole moment of the free layer. Jc and Js are the input charge current density and the spin current density, respectively. Js = θSHJc, where θSH is the spin Hall angle of the heavy metal. If needed, Ha is the external magnetic field, applied to aid the deterministic switching of the magnetic octupole, moct – this is useful when the AFM layer is strained resulting in perpendicular magnetic anisotropy. The readout mechanism is via the TMR such that the parallel orientation of the pinned layer (mPoct) and the free layer (moct) results in a lower resistance state, while the anti-parallel configuration of the layers results in a higher resistance state. For a fixed read voltage, VR, and load resistance, RL, the load voltage, VL, has two different values capturing the low and high resistance states of the junction. Previous works have utilized Si/SiO2,70,101–103 sapphire,101,104,105 and MgO106–108 substrates. | ||
In this section, we discuss the control of the octupole moment in negative chirality AFMs via the SOT effect. Progress in SOT manipulation of bulk AFMs with six-fold symmetric energy landscape and thin-film strained AFMs with two-fold symmetric energy landscape is presented. In the case of Mn3Sn, a prototypical negative chirality AFM, the atomic spins are slightly canted toward the in-plane easy axes, resulting in a small net magnetization, which is six-fold degenerate in the Kagome plane.109 In the presence of an in-plane uniaxial strain, the two-fold degeneracy dominates, while the net magnetization, compared to the bulk system, is modified.110 We also analyze the impact of Joule heating, thermal noise, and the limits of electrical readout of the information encoded in the magnetic octupole.
3.1 Current-induced dynamics in six-fold symmetric Mn3Sn
Recent experimental works have extensively investigated the SOT-driven dynamics in polycrystalline films of Mn3Sn, with thicknesses ranging from 8.3 nm to 100 nm, both with and without external magnetic fields.70,101,102,104–106,111–114 These films, owing to their polycrystalline nature, are composed of grains with different orientations of the Kagome plane, and therefore, exhibit different dynamics under the effect of SOT with a fixed spin polarization. In such polycrystalline films, each grain exhibits a six-fold symmetric energy landscape, similar to the case of bulk Mn3Sn. The AHE signal measured in the Hall bar setup is, therefore, an average effect of the final states of all the different grains.To explain the observed Hall measurements, one or all of the three different device configurations shown in Fig. 3 have been explored. In configuration I, the Kagome lattice is perpendicular to the electric current but parallel to the spin polarization direction, p. That is, x‖[0001] (p‖[01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]). In configuration II, the Kagome lattice is parallel to the electric current but perpendicular to p, which corresponds to x‖[01
0]). In configuration II, the Kagome lattice is parallel to the electric current but perpendicular to p, which corresponds to x‖[01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] (p‖[0001]). Finally, in configuration III, both the electric current and p are parallel to the Kagome lattice but perpendicular to each other, or x‖[2
0] (p‖[0001]). Finally, in configuration III, both the electric current and p are parallel to the Kagome lattice but perpendicular to each other, or x‖[2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] (p‖[01
0] (p‖[01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]). In all the three cases, an in-plane symmetry-breaking magnetic field, Hx, is applied parallel to the current. Among the three configurations, II maximizes the initial SOT efficiency, resulting in relatively low switching power consumption.106,107
0]). In all the three cases, an in-plane symmetry-breaking magnetic field, Hx, is applied parallel to the current. Among the three configurations, II maximizes the initial SOT efficiency, resulting in relatively low switching power consumption.106,107
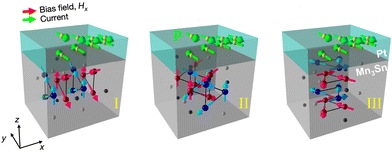 | ||
| Fig. 3 Three different configurations of the Kagome lattice with respect to the input charge current, Iwrite, and spin polarization, p. Magnetic field, Hx, is applied in all three configurations. Reproduced with permission from ref. 70. | ||
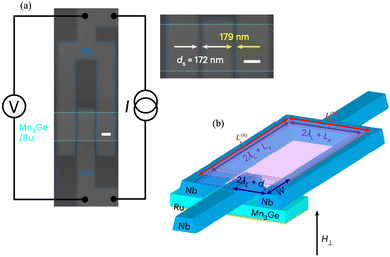
In their seminal experimental work, Tsai et al. demonstrated magnetic field-assisted SOT-driven 60° deterministic switching between two adjacent stable states in the Kagome plane of Mn3Sn.70 To manipulate the order dynamics in Mn3Sn, charge current pulses of duration 100 ms and amplitude (106–107) A cm−2 were applied to a bilayer, which comprises a HM (Pt or W) layer and polycrystalline Mn3Sn film of thickness 40 nm. An optical micrograph of the bilayer device setup to manipulate and detect the magnetic order in Mn3Sn is shown in Fig. 4(a). In this setup, an in-plane external magnetic field, Hx, and a charge current, Iwrite, are both applied along the x-direction while the spin polarization, p, corresponding to the spin current generated in the HM is along the y-direction. Experiments revealed that both the magnitude and the switching direction of the Hall voltage, VH, at fixed Hx, were dependent on the HM layer. This is due to unique positive and negative spin Hall angles in Pt and W, respectively, leading to opposite switching directions in the two cases, as shown in Fig. 4(b). Consequently, the final steady-state of the octupole moment in Mn3Sn is different for Pt and W. The maximum change in VH was measured to be about 30% (25%) of ΔVfieldH (ΔVfieldH = VH(+Hz → 0) − VH(−Hz → 0)) for Pt (W). This was attributed to the polycrystalline nature of the film and the SOT-driven partial 60° switching. For a given HM, the polarity of VH–Iwrite was found to reverse when Hx was reversed, as shown in Fig. 4(c). Furthermore, the change in Hall voltage for the different current directions, i.e., ΔVcurrentH = VH(+Iwrite → 0) − VH(−Iwrite → 0) was found to increase with |Hx|. Finally, no change in VH, due to Iwrite, was observed when the magnetic field was applied along the y- or z-direction.
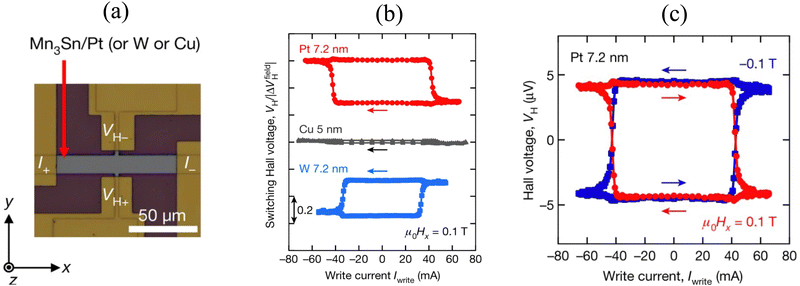 | ||
| Fig. 4 (a) Optical micrograph of the fabricated Mn3Sn/HM bilayer Hall bar devices. Write and read currents are applied along the x direction under magnetic field Hx, Hy or Hz along the x, y or z direction, respectively. (b) Hall voltage, VH, versus write current, Iwrite, for the Mn3Sn/Pt (7.2 nm), Mn3Sn/Cu (5 nm) and Mn3Sn/W (7.2 nm) devices at room temperature. The Hall voltage is normalized by the zero-field Hall voltage, ΔVfieldH, obtained from the magnetic field dependence of each sample. (c) Dependence of VH on Iwrite (VH–Iwrite loops) for the Mn3Sn/Pt (7.2 nm) device under magnetic fields of Hx = +0.1 T (red) and −0.1 T (blue) along the x direction. Reproduced with permission from ref. 70. | ||
To investigate the observed Hall voltage in the bilayer device setup, Tsai et al. numerically explored the SOT-driven dynamics in Mn3Sn with each of the three grain configurations shown in Fig. 3. The numerical simulations revealed that deterministic switching by 60° was possible only in configuration I when a symmetry-breaking magnetic field was applied perpendicular to the Kagome plane. Hx leads to a small out-of-(Kagome)-plane component of the octupole moment of Mn3Sn (i.e., m⊥ along the x-direction). The interplay of m⊥ along with the appropriate magnitude and direction of the injected current lead to deterministic switching. Here, the direction of switching is determined by the vector products (m⊥ × p), or (H × p), which determine the direction of torques. On the other hand, in configuration II, numerical simulations revealed the possibility to generate up to THz oscillations of the order parameter.115,116 Subsequently, probabilistic switching to one of the six-stable states was observed when the current pulse was turned off.115 Configuration III was not studied in detail since it would not contribute to the AHE in the experiments. This is because the octupole moment does not have any out-of-Kagome-plane component for the in-plane magnetic field.
In another work, Takeuchi et al.106 fabricated different epitaxial (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)[0001] Mn3Sn films, with thicknesses ranging from 8.3 nm to 30 nm, on an (110)[001] MgO substrate, and measured the change in the Hall resistance due to both external magnetic fields as well as charge currents within a Hall bar device structure. To investigate charge current-driven SOT dynamics, they considered a device setup, where p‖[0001], similar to configuration II. Using a large magnetic field of |H| = 1 T, the Kagome lattice was initialized in either of the two uniform states, where the uncompensated magnetic moments in all magnetic domains were along the [1
00)[0001] Mn3Sn films, with thicknesses ranging from 8.3 nm to 30 nm, on an (110)[001] MgO substrate, and measured the change in the Hall resistance due to both external magnetic fields as well as charge currents within a Hall bar device structure. To investigate charge current-driven SOT dynamics, they considered a device setup, where p‖[0001], similar to configuration II. Using a large magnetic field of |H| = 1 T, the Kagome lattice was initialized in either of the two uniform states, where the uncompensated magnetic moments in all magnetic domains were along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction. When injected with current pulses of duration 100 ms and amplitude I, in the absence of an external field, the Hall resistance, RH, showed fluctuations for |I| above a certain threshold current, irrespective of the initial state or the direction of current (Fig. 5(a)). The threshold current in this setup was found to be about an order lower than that required in the device setup similar to configuration I, where p‖[11
00] direction. When injected with current pulses of duration 100 ms and amplitude I, in the absence of an external field, the Hall resistance, RH, showed fluctuations for |I| above a certain threshold current, irrespective of the initial state or the direction of current (Fig. 5(a)). The threshold current in this setup was found to be about an order lower than that required in the device setup similar to configuration I, where p‖[11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] (Fig. 5(b)). In the presence of an in-plane external magnetic field, the latter setup demonstrated the expected deterministic switching70 shown in the inset of Fig. 5(b).
0] (Fig. 5(b)). In the presence of an in-plane external magnetic field, the latter setup demonstrated the expected deterministic switching70 shown in the inset of Fig. 5(b).
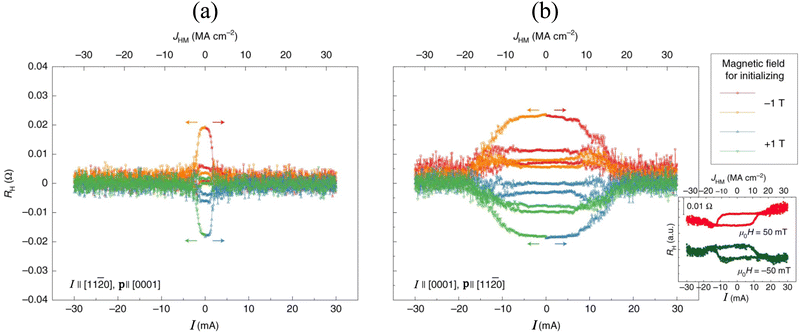 | ||
Fig. 5
R
H–I curves of a fabricated Hall device with tMn3Sn = 8.3 nm for the configurations of (a) I‖[11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] (p‖[0001]) and (b) I‖[0001] (p‖[11 0] (p‖[0001]) and (b) I‖[0001] (p‖[11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0]), respectively. The top axis is the current density JHM corresponding to the electric current I in the bottom axis. The colours represent the initializing magnetic fields (the right panel) and the starting points of the measurements, with the latter indicated by arrows. The inset in (b) shows the bipolar switching under in-plane magnetic field H. Both the electric current I and magnetic field H are applied along the [0001] direction of Mn3Sn. Reproduced with permission from ref. 106. 0]), respectively. The top axis is the current density JHM corresponding to the electric current I in the bottom axis. The colours represent the initializing magnetic fields (the right panel) and the starting points of the measurements, with the latter indicated by arrows. The inset in (b) shows the bipolar switching under in-plane magnetic field H. Both the electric current I and magnetic field H are applied along the [0001] direction of Mn3Sn. Reproduced with permission from ref. 106. | ||
To study the microscopic origin of the observed fluctuations, Takeuchi et al. numerically explored the magnetic field-free SOT-driven dynamics in single-domain Mn3Sn, with six minimum energy states, in both configurations I and II. Firstly, they found that the minimum current required to induce dynamics in configuration II was indeed smaller than that required for configuration I. This is because the antidamping-like (ADL) SOT in configuration II has to overcome the weaker effective in-plane anisotropy. On the other hand, in configuration I, the ADL SOT acts against the stronger exchange interaction. Secondly, above the threshold current, the magnetic octupole demonstrated oscillatory behavior with a non-zero m[0001], which is the out-of-(Kagome)-plane component m⊥. The frequency of these oscillations was shown to be current-tunable in the 100 s of the MHz to GHz range.115,116 When the current pulse was turned off, m[0001] decreased to zero and the magnetic octupole settled to the nearest minimum energy state. This represents a probabilistic, not deterministic, switching behavior since the particular minimum energy state depends on the state of the oscillating magnetization, when the current pulse was turned off. For a fixed pulse duration, therefore, the final state would depend on the pulse magnitude, I. It is likely that the spin state of the single crystal Mn3Sn fabricated by Takeuchi et al. had small non-uniformities between the magnetic domains, which persisted or changed when injected with current above the threshold. Consequently, different domains randomly settled into one of the six degenerate states, leading to the fluctuations in the Hall resistance as the observed ensemble average effect. This theory was supported by the observation of reduced fluctuations in the Hall resistance under the application of an out-of-plane magnetic field. The applied field lifted the degeneracy of the system making one of the states more favorable to the SOT-driven switching. The fluctuations in the Hall resistance were also reduced in a wider device that accommodated more magnetic domains as the non-uniformities were averaged out.
Although the work reported by Takeuchi et al. was significant in understanding oscillatory and switching dynamics in (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)[0001] Mn3Sn thin films, the oscillating signal or its frequency could not be detected experimentally. To address these challenges, Yan et al.101 used a diamond microchip with nitrogen vacancy (NV) centers implanted on the chip's bottom surface. The NV centers are optically active defects in diamond and act as spin sensors, and therefore, enable imaging the effect of charge current on the local spin structure at microscopic length scales. The diamond chip was placed atop a bilayer Hall device comprising HM (Pt or W) and 50 nm thick polycrystalline Mn3Sn. When millisecond charge current pulses of different amplitudes were applied to this device in the absence of an external magnetic field, the Hall resistance demonstrated characteristic fluctuations, similar to those reported by Takeuchi et al., if Iwrite exceeded a certain threshold current. This can be observed from Fig. 6(a) and (b), where the anomalous Hall resistance normalized to the zero-field Hall resistance,
00)[0001] Mn3Sn thin films, the oscillating signal or its frequency could not be detected experimentally. To address these challenges, Yan et al.101 used a diamond microchip with nitrogen vacancy (NV) centers implanted on the chip's bottom surface. The NV centers are optically active defects in diamond and act as spin sensors, and therefore, enable imaging the effect of charge current on the local spin structure at microscopic length scales. The diamond chip was placed atop a bilayer Hall device comprising HM (Pt or W) and 50 nm thick polycrystalline Mn3Sn. When millisecond charge current pulses of different amplitudes were applied to this device in the absence of an external magnetic field, the Hall resistance demonstrated characteristic fluctuations, similar to those reported by Takeuchi et al., if Iwrite exceeded a certain threshold current. This can be observed from Fig. 6(a) and (b), where the anomalous Hall resistance normalized to the zero-field Hall resistance,  , is presented as a function of the write current pulse number N. Enhanced fluctuations can be observed for 44 mA while no such fluctuations are noticed in the case of 2 mA, indicating the existence of a threshold current, which was found to be around 36 MA cm−2. While the polycrystalline Mn3Sn could consist of grains with different configurations, the fluctuations in Fig. 6(a) and (b) are expected to be contributed by grains whose Kagome plane is perpendicular to p (configuration II). This is because the threshold current to induce such fluctuations in grains with configuration I is about an order of magnitude higher106 and no AHE would be contributed by grains with configuration III. Thus, the fluctuations reported in Fig. 6(b) are expected due to the SOT-driven chiral oscillations of the magnetic octupole moment.106
, is presented as a function of the write current pulse number N. Enhanced fluctuations can be observed for 44 mA while no such fluctuations are noticed in the case of 2 mA, indicating the existence of a threshold current, which was found to be around 36 MA cm−2. While the polycrystalline Mn3Sn could consist of grains with different configurations, the fluctuations in Fig. 6(a) and (b) are expected to be contributed by grains whose Kagome plane is perpendicular to p (configuration II). This is because the threshold current to induce such fluctuations in grains with configuration I is about an order of magnitude higher106 and no AHE would be contributed by grains with configuration III. Thus, the fluctuations reported in Fig. 6(b) are expected due to the SOT-driven chiral oscillations of the magnetic octupole moment.106
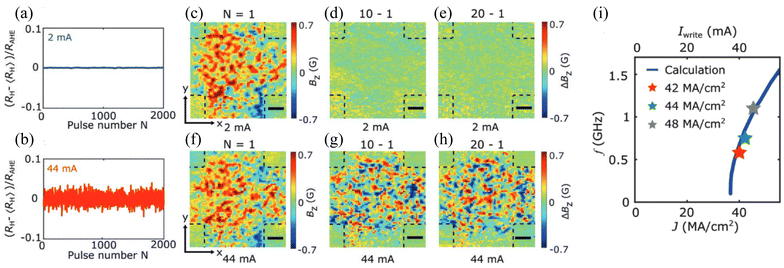 | ||
| Fig. 6 (a) and (b) Measured normalized Hall resistance, (RH − 〈RH〉)/RAHE, as a function of pulse number (N) for write current amplitudes of (c) 2 mA and (d) 44 mA. (c) and (f) 2D images of Bz measured after applying the first current pulse (N = 1) with amplitudes of (e) 2 mA and (h) 44 mA, respectively. (d) and (g) SOT-induced variation of the stray field, ΔBz, recorded after applying a 2 mA current pulse 10 (f) and 20 (g) times. (e) and (h) SOT-induced variation of ΔBz recorded after applying a 44 mA current pulse 10 (i) and 20 (j) times. For (c)–(h) the black dashed lines mark the boundary of the patterned Mn3Sn/Pt Hall cross, and the scale bar is 2.5 μm. (i) Theoretically calculated spin rotation frequency f of Mn3Sn as a function of the electric current density, J, flowing in the Pt layer. The experimentally measured f for J = 42 MA cm−2 (the red marker), 44 MA cm−2 (the green marker), and 48 MA cm−2 (the gray marker) agree with the theoretical calculations. Reproduced with permission from ref. 101. | ||
To establish a real-space correlation between the SOT and the chiral oscillations, Yan et al. performed NV wide-field magnetometry after every write current pulse. Two-dimensional (2D) images of the spatially varying stray field, generated due to the net magnetization exhibited by Mn3Sn, are presented in Fig. 6(c)–(h). The stray field measured after the first write current pulse (N = 1) in the case of both 2 mA and 44 mA demonstrates the multi-domain characteristics of the polycrystalline Mn3Sn film, as shown in Fig. 6(c) and (f). Fig. 6(d) and (e) show that the spatial distribution of the stray field after 10 and 20 current pulses remains largely unchanged for current pulses with an amplitude of 2 mA. On the other hand, for current pulses with an amplitude of 44 mA, the stray field distribution shows a significant change after 10 and 20 current pulses, as shown in Fig. 6(g) and (h). In this case the stray field averaged spatially over the entire Hall cross-region remains constant during the entire measurement sequence. These results corroborate the role of SOT-driven chiral oscillations, followed by probabilistic switching, in multi-domain Mn3Sn used in configuration II. Special care was taken to remove the effects of Joule heating from these results. Furthermore, utilizing NV relaxometry measurements, frequency of the current-driven chiral oscillations for write current pulses above the threshold was also obtained, as shown by symbols in Fig. 6(i). These extracted data point agree well with the numerical calculations based on single-domain coupled Landau–Lifshitz Gilbert (LLG) equations, especially for higher currents. Finally, NV wide-field magnetometry performed in the presence of an in-plane external magnetic field along the direction of current yielded stray field, which averaged spatially over the entire Hall cross demonstrated periodic variations signifying deterministic switching, previously discussed in ref. 70.
To gain further insight into the dependence of the field-free SOT-driven dynamics pertinent to configuration II on the intrinsic energy scale of Mn3Sn and its material parameters, our group has theoretically investigated single-domain Mn3Sn with six stable states.117 On the numerical front, we explored chiral oscillation and probabilistic switching dynamics under the effect of d.c. and pulsed currents, respectively, and found the results to be similar to those presented in ref. 106. Then using a minimal energy landscape model, we obtained an analytic model of the threshold spin current to excite the dynamics as 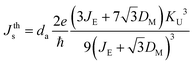 , where e and ħ are the charge of an electron and reduced Planck constant while da, JE, DM, and KU are the thickness, exchange energy constant, DMI constant, and uniaxial energy constant of Mn3Sn, respectively. For d.c. input spin current density Js ≥ Jths, the frequency of oscillation showed a non-linear (linear) behavior with current for small (large) Js. This behavior was accurately captured by the equation
, where e and ħ are the charge of an electron and reduced Planck constant while da, JE, DM, and KU are the thickness, exchange energy constant, DMI constant, and uniaxial energy constant of Mn3Sn, respectively. For d.c. input spin current density Js ≥ Jths, the frequency of oscillation showed a non-linear (linear) behavior with current for small (large) Js. This behavior was accurately captured by the equation
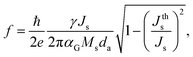 | (2) |
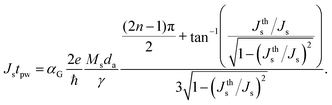 | (3) |
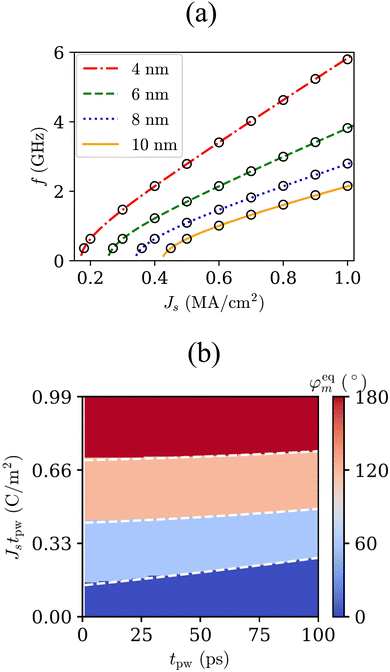 | ||
| Fig. 7 (a) Oscillation frequency as a function of the applied spin current, Js, for different thickness of the Mn3Sn layer. Numerical results from the solution of coupled LLG equations (symbols) agree very well with the analytical results obtained from eqn (2) (lines). (b) The final steady-state of the magnetic octupole as a function of the pulse duration, tpw, and the total injected spin charge density, Jstpw. The overlaid dashed white lines represent the analytic bounds of eqn (3). Here, the thickness of the AFM film is da = 4 nm. Other parameters are JE = 2.4 × 108 J m−3, DM = 2 × 107 J m−3, Ke = 3 × 106 J m−3, and Ms = 1.3 × 106 A m−1. Adapted from ref. 117. | ||
Although the aforementioned investigations attributed the current-induced changes in single crystal as well as polycrystalline Mn3Sn to ADL SOT while neglecting any significant role of Joule heating, Takeuchi et al. evaluated the temperature rise in the case of devices with configuration I to be quite large. In addition, their numerical simulations suggested the threshold current in the case of configuration I to be at least one order of magnitude higher than that observed experimentally. Furthermore, the spin diffusion length in Mn3Sn is only about 1 nm118 but Mn3Sn films used in the experiments were thicker than 8 nm. These peculiarities suggested that in these experiments switching of the octupole moment was caused by another mechanism in addition to SOT. To this end, Pal et al.104 and Krishnaswamy et al.102 independently investigated the current-driven dynamics in a bilayer of HM and polycrystalline Mn3Sn films of thicknesses 30 nm to 100 nm, in the presence of an in-plane external magnetic field collinear with the current pulse. Both these works showed that the demagnetization of the Mn3Sn film, owing to its temperature rise above the Néel temperature, was an important step in the switching process.
In particular, Krishnaswamy et al. showed that the current-induced switching was a function of the pulse fall time, τ. This can be observed from Fig. 8(a) and (b), where bistable switching, typical of configuration I, is possible only for longer fall times, such as τ = 420 ns. On the other hand, shorter fall times (τ < 400 ns) lead to tristable switching, i.e., a third state with small or zero AHE signal is detected in the steady state above the critical voltage, whereas below the critical voltage, two stable states, typical of bistable switching, are obtained. When a current pulse of duration 10 μs is applied, the temperature rises above the Néel temperature, which was found to be 390 K in the 50 nm thick polycrystalline film, in 10 s of ns. When the current is reduced, the Mn3Sn film cools down below its Néel temperature due to the diffusion of heat into the substrate. As depicted in Fig. 8(c), for longer fall times, the current is above a critical value, jc, when the Mn3Sn film cools down below the Néel temperature, resulting in bistable deterministic switching. On the other hand, for τ = 35 ns, the current decreases to values below jc while the temperature of the Mn3Sn film is still above the the Néel temperature, leading to random freeze-out of Mn3Sn grains, resulting in the zero AHE signal. The magnitude and direction of the detected AHE signal was shown to be dependent on the external magnetic field as well as the HM, similar to Fig. 4(b) and (c), thereby making the switching process a function of heat and SOT. The polycrystalline films of Mn3Sn would likely consist of grains representing configuration II; however, no coherent chiral oscillations were observed in experiments, perhaps due to strong damping or heat-induced demagnetization.
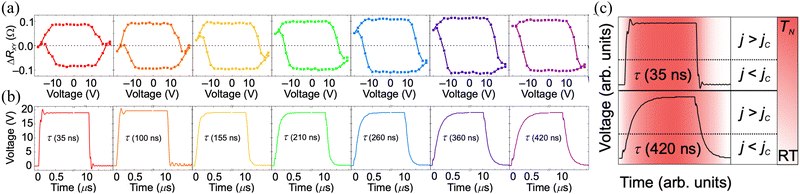 | ||
| Fig. 8 (a) Switching loops of Mn3Sn/Pt as a function of pulse voltage with rise and fall time, τ, increasing from left to right. Short τ such as 35 ns leads to tristable switching whereas a long τ of 420 ns leads to a bistable switching behavior. (b) Corresponding pulse shape. (c) Schematic voltage pulse with temperature profile indicated by the red shading. Reproduced with permission from ref. 102. | ||
On the other hand, Pal et al. proposed seeded SOT as an explanation for the observed field-assisted bistable switching in their 30 nm to 100 nm thick Mn3Sn films. In this mechanism, the current-induced Joule heating randomizes the magnetic domains in Mn3Sn as its temperature rises above the Néel temperature, in the first step. Then the SOT deterministically switches a thin region of Mn3Sn (of the order of the spin diffusion length) near the HM/AFM interface, if the current is above a critical value while the thin region cools down. The interface region then acts as the seed for the deterministic switching of the rest of the AFM as the film cools down. Switching efficiency showed strong dependence on the fall time—longer fall times facilitated deterministic switching—similar to that described in ref. 102. At a fixed pulse duration, the critical current density, Jc, was found to be almost independent of the in-plane magnetic field, Hx, as shown in Fig. 9(a), presenting strong evidence towards the role of heating Mn3Sn above its Néel temperature for deterministic switching. In contrast, the Hall resistance, 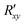 , exhibited a non-monotonic dependence on Hx, as shown in Fig. 9(b). Numerical simulations revealed that the out-of-(Kagome)-plane component of the net magnetization, m⊥, increases with Hx. Pal et al. attributed the initial increase in
, exhibited a non-monotonic dependence on Hx, as shown in Fig. 9(b). Numerical simulations revealed that the out-of-(Kagome)-plane component of the net magnetization, m⊥, increases with Hx. Pal et al. attributed the initial increase in 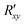 , for Hx ≤ 0.1 T, to the increase in m⊥, whereas they explained the subsequent decrease in
, for Hx ≤ 0.1 T, to the increase in m⊥, whereas they explained the subsequent decrease in 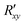 for higher Hx as a consequence of the decreasing energy barrier between the six different minimum energy states. Other evidence for the role of Joule heating in the observed deterministic bistable switching included a decrease in Jc with an increase in the pulse duration (device temperature) at fixed device temperature (pulse duration). Finally, unlike pure SOT, where Jc would increase with thickness of the magnetic layer, here Jc was found to decrease with the thickness of the Mn3Sn layer while the power density remained constant.
for higher Hx as a consequence of the decreasing energy barrier between the six different minimum energy states. Other evidence for the role of Joule heating in the observed deterministic bistable switching included a decrease in Jc with an increase in the pulse duration (device temperature) at fixed device temperature (pulse duration). Finally, unlike pure SOT, where Jc would increase with thickness of the magnetic layer, here Jc was found to decrease with the thickness of the Mn3Sn layer while the power density remained constant.
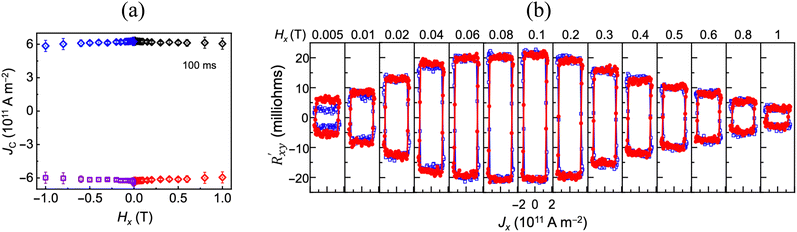 | ||
Fig. 9 (a) Dependence of Jc on Hx for a pulse duration of 100 ms. Black (+Hx, −Jx), red (+Hx, +Jx), purple (−Hx, −Jx), and blue (−Hx, +Jx) show negative and positive current sweep for positive and negative Hx, respectively. (b) Variation of  on Hx during current-induced switching. Reproduced with permission from ref. 104. on Hx during current-induced switching. Reproduced with permission from ref. 104. | ||
A very recent work by Zheng et al. demonstrates the field-assisted current-induced 60° deterministic switching of the AHE signal with current density as low as 1 MA cm−2, due to an efficient charge-to-spin current conversion with assistance of the orbital Hall effect (OHE).114 The OHE refers to the generation of a transverse orbital current (OC) in response to an external electric field. Unlike spin current, OC is an emergent concept and relies on the orbital character of the Bloch states rather than the electronic states of the constituent atoms.119 OC without an accompanying spin current is feasible in many materials,120,121 while in others OC can mediate the spin-Hall122,123 and the valley-Hall effects.124 OC can be used to control the dynamics of proximal magnetic layers. In ref. 114, OC generated in a source layer is first converted into a spin current by means of a heavy metal with a large SOC,125 which enables highly efficient manipulation of the magnetization of Mn3Sn. Towards this, a trilayer device setup comprising polycrystalline Mn3Sn (40 nm)/Pt (0–6 nm)/Mn (0–20 nm)/AlN (5 nm) is deposited on thermally oxidized silicon substrates (SiOx/Si). In this structure, the Mn layer serves as the generator of OC as it is known to possess a gigantic orbital Hall conductivity,126 while Pt with a large SOC is used to convert the OC into a spin current, which induces current-driven switching of Mn3Sn grains in configuration I (i.e., the input current along the [0001] direction is perpendicular to the Kagome plane). As shown in Fig. 10(a), the critical switching current density, Jc, for a thin Pt layer of thickness tPt = 2 nm, is found to decrease monotonically with an increase in the Mn layer thickness, likely due to an increased contribution from orbital-torque (OT). On the other hand, for an Mn layer of thickness tMn = 10 nm, Jc is found to non-monotonically change with tPt (Fig. 10(b)), likely due to a stronger orbital-torque (spin-torque) contribution for a thinner (thicker) Pt layer. Unlike the work reported by Pal et al.,104Jc is found to be almost independent of the pulse duration (Fig. 10(c)), probably due to a smaller or negligible contribution from thermally activated switching mechanisms. However, similar to Fig. 8(a) and 9(b), tristable switching behavior and non-monotonic dependence of the Hall resistance on magnetic field point to a contribution from Joule heating.102 Although the high OT efficiency is promising in the proposed trilayer structure, the observed results warrant further examination of the setup for gaining a better insight into the switching mechanisms at play. Finally, Fig. 10(d) presents stable minor switching loops that are obtained by limiting the maximum current amplitude, Jmax, in the negative direction. These non-volatile intermediate states are current tunable as well as recoverable to the initial state, and therefore raise the possibility of using Mn3Sn-based devices as a memristor.
 | ||
| Fig. 10 (a) Critical switching current density, Jc, as a function of Mn layer thickness, tMn, with a fixed Pt layer thickness of tPt = 2 nm. Jc decreases with tMn as the contribution from OT (red region) increases. (b) Jc as a function of tPt with a fixed Mn thickness (tMn = 10 nm). When tPt ≤ 3 nm, the switching dynamics are dominated by OT (red region) whereas for tPt > 3 nm, spin-torque (blue region) dominates the switching dynamics. The error bars in (a) and (b) are obtained from multiple switching loops for each sample. (c) Anomalous Hall resistance, RAHE, as a function of the amplitude of the applied current pulse, J, for different pulse widths. (d) Minor switching loops obtained by limiting the maximum current value, Jmax, in the negative range. Reproduced with permission from ref. 114. | ||
To further investigate the main mechanism behind the current-driven switching dynamics in a bilayer of polycrystalline Mn3Sn and W, very recently, Yoo et al.103 systematically studied a structure similar to that shown in Fig. 4(a). In particular, they deposited W(7.1 nm)/Mn3Sn(34.4 nm)/MgO(2 nm) films on Si/SiO2 substrates with varying SiO2 thicknesses, hSiO2, ranging from 100 nm to 1 μm, and base temperatures, T0, ranging from 200 K to 400 K. The AHC, σxy, was found to be tunable between about ±30 (Ω cm)−1, when an externally applied out-of-plane magnetic field was tuned between ±2 T, and showed a negligible variation with an increase in hSiO2. However, for T0 > 260 K, σxy and the coercive field reduced with an increase in temperature, likely due to a decrease in the effective magnetic anisotropy. On the other hand, when current pulses of varying magnitudes, j, but a fixed duration of about 105 ms and a fall time of about 150 μs were applied parallel to an in-plane magnetic field of magnitude 0.1 T, σxy exhibited bidirectional switching between about ±10 (Ω cm)−1 for hSiO2 = 100 nm (Fig. 11(a)). When hSiO2 was increased to 1 μm, the range of σxy reduced to about ±7 (Ω cm)−1, with the transition occurring at a lower |j|. This reduction in the switching threshold current with increasing hSiO2 alludes to an important role of the substrate in the switching dynamics, likely via Joule heating. Indeed, further investigations revealed that for a fixed input power, P, which is proportional to the magnitude of the current pulse, the temperature rise, ΔT, was higher for a thicker SiO2 layer. Alternatively, the same temperature rise was obtained at lower P for a thicker SiO2 layer (Fig. 11(b)). Here, the choice of pulse duration was to ensure temperature rise to steady state values for Si/SiO2 substrates while the fall time was chosen to prevent the formation of multi-stable states (Fig. 8). These results provide further evidence and support the claim that current-driven switching in the bilayer of polycrystalline Mn3Sn and HM proceeds via demagnetization above the Néel temperature, followed by a slow cooling down below it.102 Recently, Xu et al.105 utilized current pulses of duration 2 ms but different amplitudes and investigated the dynamics in single crystals of Mn3Sn, in the presence of an in-plane collinear magnetic field. For Mn3Sn in configuration I, they demonstrated a weak dependence of the critical current on Hx while it was found to decrease with an increase in the film thickness, similar to ref. 104. Thus alluding to the role of Joule heating in the bistable deterministic switching dynamics in their devices. They also showed the non-monotonic behavior of the Hall resistance with Hx, suggesting an increase in m⊥ with Hx. Other expected outcomes such as the dependence of the Hall resistance on the magnitude and the direction of Hx were also presented. Unexpectedly, their Mn3Sn device in configuration II showcased deterministic switching, considered to be forbidden by previous works.70,101,102,106 Although they attribute this behavior to imperfect growth of their Mn3Sn crystals, recent numerical works have suggested the possibility of deterministic switching in configuration II, ignoring the effects of Joule heating.127,128 Nevertheless, further experimental investigations are required to evaluate the possibility of chiral oscillation and deterministic switching in configuration II.
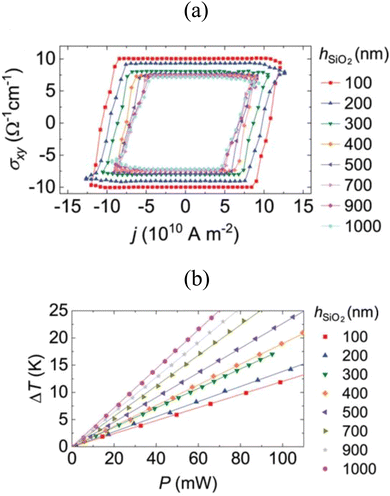 | ||
| Fig. 11 (a) Hysteresis curves obtained for current pulses of different magnitudes, |j|, for different thicknesses of the SiO2 layer, hSiO2. (b) Temperature rise, ΔT, as a function of the input power, P, for different hSiO2. Reproduced with permission from ref. 103. | ||
3.2 SOT-induced dynamics in two-fold symmetric Mn3Sn
Recently, Higo et al. demonstrated that a 30 nm thick film of Mn3Sn, used in a bilayer heterostructure comprising HM and Mn3Sn, grown epitaxially on a (110)[001] MgO substrate, exhibited perpendicular magnetic anisotropy (PMA).107 As shown in Fig. 12(a), the Mn3Sn layer was found to be oriented as MgO (110)[001]‖Mn3Sn (01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)[0001] with a perpendicular magnetic octupole moment along the [01
0)[0001] with a perpendicular magnetic octupole moment along the [01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction. The lattice mismatch between the Mn3Sn layer and the MgO substrate, for a thin HM layer, led to an in-plane tensile strain of about 0.2% in the Kagome plane along the [2
0] direction. The lattice mismatch between the Mn3Sn layer and the MgO substrate, for a thin HM layer, led to an in-plane tensile strain of about 0.2% in the Kagome plane along the [2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction. Consequently, the six degenerate minimum energy states, with the octupole pointing along the six-equivalent 〈2
0] direction. Consequently, the six degenerate minimum energy states, with the octupole pointing along the six-equivalent 〈2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 direction, as shown in Fig. 12(b), reduced to two degenerate minimum energy states shown in Fig. 12(c).
0〉 direction, as shown in Fig. 12(b), reduced to two degenerate minimum energy states shown in Fig. 12(c).
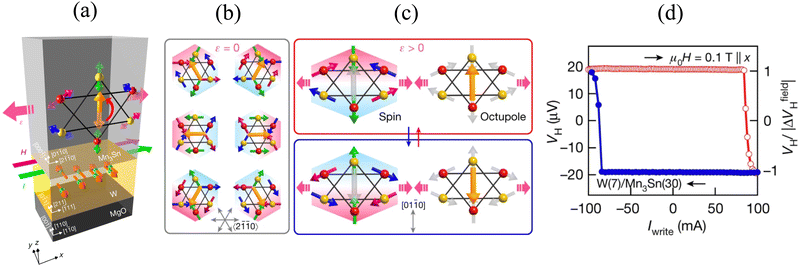 | ||
Fig. 12 (a) Schematic illustrating the bidirectional switching of the perpendicular magnetic octupole (orange arrows) of Mn3Sn by the SOT. The three Mn moments on the Kagome easy plane are shown by arrows with different colours. Red and yellow spheres represent Mn atoms at z = 0 and 1/2, respectively. An electrical current I (green arrow) flowing in the W layer generates a spin current (green spheres) whose polarization vector (red arrow) is perpendicular to the Kagome plane and induces the SOT on the Mn3Sn layer. ε (pink arrows) and H (magenta arrows) schematically show the epitaxial, uniaxial tensile strain and the magnetic field, respectively. (b) Chiral spin structure on the Kagome bilayers with no strain (ε = 0), which has six degenerate states with the octupole pointing along the six-equivalent 〈2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 direction. (c) Chiral PMA binary states on the Kagome bilayers stabilized by the application of the uniaxial tensile strain (ε > 0). (d) The Hall voltage, VH (left) and volume fraction of the current controllable VH/|ΔVfieldH| (right) versus write current Iwrite of the W/Mn3Sn heterostructure at room temperature. The bias magnetic field of 0.1 T is applied along the x direction. Reproduced with permission from ref. 107. 0〉 direction. (c) Chiral PMA binary states on the Kagome bilayers stabilized by the application of the uniaxial tensile strain (ε > 0). (d) The Hall voltage, VH (left) and volume fraction of the current controllable VH/|ΔVfieldH| (right) versus write current Iwrite of the W/Mn3Sn heterostructure at room temperature. The bias magnetic field of 0.1 T is applied along the x direction. Reproduced with permission from ref. 107. | ||
When write current pulses of duration 100 ms and amplitude Iwrite were applied to this bilayer structure, in the presence of a symmetry-breaking magnetic field, Hx, parallel to the current, the Hall voltage, VH, displayed bidirectional deterministic switching behavior above a critical current, as shown in Fig. 12(d) (left axis). The corresponding critical current density was found to be Jwc = 14 MA cm−2. Strikingly, the entire volume of the Mn3Sn film was found to switch due to the applied current pulse, as shown by the ratio on the right axis of Fig. 12(d), where ΔVfieldH is the Hall voltage change due to a magnetic field applied in the out-of-plane direction, Hz. This ratio was limited to only (25–30)% in all previous works.70,101,106 No switching was observed for magnetic fields perpendicular to the Kagome plane, Hy, as it did not break the two-fold symmetry. This, however, changed for devices, where the Kagome plane was rotated from the current direction (x) by an angle. This is because Hy was not perpendicular to the rotated Kagome plane anymore, instead it broke the symmetry, and enabled deterministic switching. Finally, in the absence of any external field, VH showed fluctuations, similar to those described in ref. 106, likely representing probabilistic switching dynamics.
It is well known that in the case of FMs and collinear AFMs the experimentally measurable magnetic order, i.e., the magnetization vector and the Néel vector, respectively, rotate in the same direction as the constituting atomic spins.129,130 Although Higo et al. demonstrated a field-assisted SOT-induced deterministic switching dynamics in PMA Mn3Sn,107 similar to that in FMs, there was no discussion regarding the switching direction of the experimentally measured magnetic octupole. To address this important issue, Yoon and Zhang et al. considered a heterostructure, comprising a HM layer (Pt) and a 8.8 nm thick PMA Mn3Sn film, and applied a symmetry-breaking in-plane magnetic field along a current pulse of duration 100 ms and amplitude I.108 The measured Hall resistance, RH, in configuration II (Fig. 13(a)), showed deterministic switching (Fig. 13(b)), for currents above a certain threshold current (Jco ≈ 15 MA cm−2), similar to ref. 107. However, only 30% of the magnetic domains were found to switch for the SOT-driven dynamics, which is different from the 100% switching shown on the right axis of Fig. 12(d). They attribute the low ratio of switched magnetic domains to possible non-uniform current distribution in the Hall cross device or tilting of the octupole moment from the perpendicular orientation. They observed almost no change in RH for configuration I, even for currents twice as large as that used in configuration II. This observation is similar to that reported in ref. 101 and 106, where the threshold currents for devices in configuration I were found to be about an order higher than those for configuration II (see also Section 3.1). Finally, the temperature rise for 15 MA cm−2 was found to be only about 4 K, thus eliminating any contribution of Joule heating from the switching dynamics, unlike ref. 102 and 104, where the temperature increased by 140 K for a 1 ms long current pulse of magnitude 17 MA cm−2, resulting in deterministic switching (Fig. 9(b)). The small temperature rise could be due to a thinner Mn3Sn layer (8.8 nm) as compared to the 30 nm thick Mn3Sn layer used by Pal et al., where the critical current was found to decrease with the thickness. Another reason for the wide variation in the temperature rise could be the different substrates in the two device setups—sapphire in ref. 104 and (110)MgO in ref. 107 and 108.
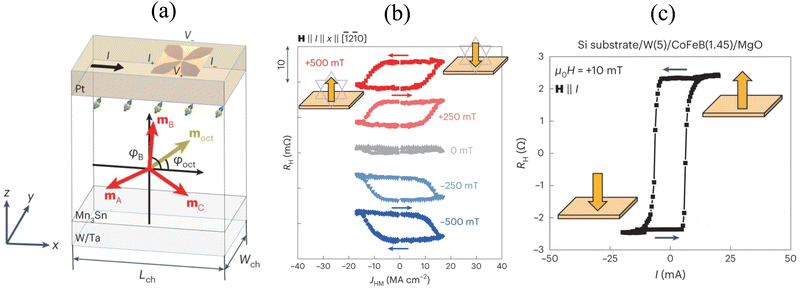 | ||
| Fig. 13 (a) Schematic of the transport measurement reported in ref. 108. The in-plane spins (yellow spheres and green arrows) are injected from Pt to Mn3Sn. The sublattice moments and the octupole moment are defined as m(A,B,C) and moct with angles of φ(A,B,C) and φoct, respectively. An optical micrograph of the fabricated Hall bar with a channel width Wch and a length Lch of 15–30 μm and 90 μm, respectively, is shown on the top of the stacks with the definition of the current and voltage directions. (b) RH−I curves for different magnetic field, applied parallel to the injected current, I, in the x-direction. (c) RH−I curve measured in W(5 nm)/CoFeB(1.45 nm)/MgO stacks deposited on a Si substrate, where the bottom W layer injects spins with the same polarization onto the CoFeB layer as those from the top Pt layer onto the Mn3Sn layer. The schematics in (b) and (c) illustrate the switched magnetic states, represented by the octupole moment and the magnetization vector, respectively, in Mn3Sn and CoFeB, respectively. Reproduced with permission from ref. 108. | ||
To compare the aforementioned switching dynamics in configuration II to that in FMs, Yoon and Zhang et al. measured the field-assisted SOT-driven changes in RH of a W/CoFeB bilayer. As shown in Fig. 13(c), the polarity of the switched magnetization in the CoFeB FM was found to be opposite to that of the octupole moment in Mn3Sn (Fig. 13(b)), for the same polarization of the injected spin current. This surprising observation, pertinent to the opposite rotation of the octupole moment as compared to the direction of rotation of a ferromagnetic moment, was termed as the “handedness anomaly”. Through careful examination of the measurements, they concluded that the effect of the field-like torque on the SOT-induced dynamics in the Mn3Sn film was negligible. Also, owing to the epitaxial nature of the Mn3Sn film, the likelihood of self-generated spin-polarized current131 in Mn3Sn was negligible. Consequently, the observed SOT-driven switching in PMA Mn3Sn could be completely attributed to the ADL torque. This indicates that the direction of the ADL SOT on the magnetic octupole is opposite to its direction on the magnetization of a FM, and therefore, opposite to the direction of the ADL SOT on the constituting sublattice vectors of Mn3Sn.
To gain a deeper insight into the ADL SOT-induced dynamics in PMA Mn3Sn in configuration II, Higo et al. numerically investigated solutions of single-domain coupled LLG equations for a range of input currents and magnetic fields. They showed that, in the steady state, the octupole moment either stayed near the initial minimum energy state or ground state, switched to the other ground state, or exhibited chiral oscillations. The final steady-states were found to be a function of the initial ground state, the direction and magnitude of the input stimuli. Yoon and Zhang et al., on the other hand, developed an effective energy landscape model of the magnetic octupole moment, wherein the in-plane epitaxial tensile strain manifested as perturbations in exchange and uniaxial anisotropy energy interactions. This results in clear two-fold and four-fold effective anisotropies, in addition to the intrinsic six-fold anisotropy. They utilized this model to accurately fit and describe the quasi-static second-harmonic Hall measurements of PMA Mn3Sn, used in configuration II, as a function of the direction of the symmetry-breaking magnetic field and the input current, keeping their respective magnitudes fixed. The dependence of the different steady-states on the intrinsic energy landscape and the material parameters of PMA Mn3Sn, however, was not discussed in either of these works. The time scales associated with switching and oscillation dynamics, and their relation to the material properties as well as the external stimuli, were also not addressed.
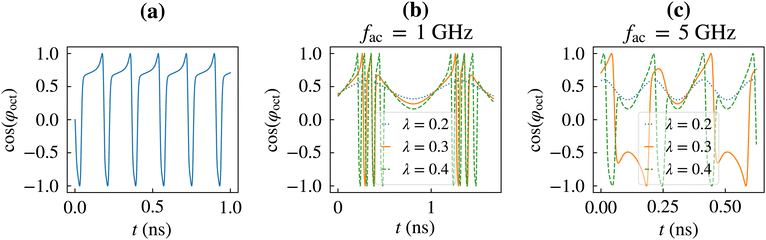
A thorough analysis of the different regimes of operation in strained PMA Mn3Sn films, and their dependence on the material parameters and external stimuli, have been presented in our recent work.127 Our numerical simulations revealed that in the absence of a magnetic field the magnetic octupole either stays in the initial well or oscillates around the spin polarization, depending on the magnitude of applied current. On the other hand, for a non-zero magnetic field, the magnetic octupole can be deterministically switched to the other state, if the injected current satisfies Jth1c < Jc < Jth2c, where Jth1c and Jth2c represent the field-dependent lower and upper current bounds, respectively. For currents above Jth2c, the octupole exhibits chiral oscillations, whose frequency is current tunable. No switching was observed for currents below Jth1c, instead stationary states in the initial ground states are obtained. Our results showed some differences from those reported by Higo et al. To investigate these differences, we utilized an effective energy landscape model of the magnetic octupole moment, which clearly depicts the dependence of the energy barrier separating the two minimum energy states on the in-plane tensile strain.71,108,132 We found that Jth1c and Jth2c were the minimum currents required to overcome the maximum effective in-plane anisotropy in the two energy wells. Since the external magnetic field breaks the symmetry, Jth1c (Jth2c) decreases (increases) with the magnitude of the field. We then derived analytic expressions of the threshold currents, which were found to be independent of the damping constant but linearly proportional to the magnitude of the field, the final stationary steady states as well as the switching time as a function of the input stimuli and the material parameters. Our models show excellent agreement against numerical data, and therefore, provide important insight into the dynamics of the material, which would be useful to experimentalists and designers. Finally, we varied the Gilbert damping constant and found that for damping constants below a certain value (α ≲ 2 × 10−3 for the set of material parameters considered in our work), the dynamics is similar to that reported by Higo et al. For these low values of damping constants, analytic expressions deviate from the numerical results. To resolve these differences, careful analysis involving the exchange interaction due to the out-of-(Kagome)-plane component of magnetic octupole is required.108
3.3 Joule heating in the presence of SOT
As discussed in ref. 102–105, Joule heating likely plays an important role in the current-induced switching dynamics in the bilayer devices, comprising HM and Mn3Sn, especially in configuration I. Temperature rise above the Néel temperature could also be the reason behind the failure in detection of chiral oscillations, in both six-fold and two-fold symmetric Mn3Sn, in configuration II.102 In general, Joule heating induced temperature rise as well as the rate of change of the temperature depend on the properties of the conducting and substrate layers in addition to the input current pulse. In our recent work,117 we considered a one-dimensional (1D) heat flow model133 to investigate the current-induced temperature change in the device setup shown in Fig. 2.Although the current pulse is applied to the HM, a part of the current leaks into the metallic Mn3Sn layer, leading to heat generation in both the layers. To evaluate the current distribution between the two layers a parallel resistor model was employed. According this model, the total generated heat depended on the individual resistivity and dimension of both layers. Both the HM and Mn3Sn were assumed to be at the same temperature and any spatial variation in the temperature was neglected. The generated heat was assumed to flow through the substrate towards the bottom electrode. Consequently, the temperature at the junction between the bilayer and the substrate, Tj, was found to be strongly dependent on the properties of the substrate such as its thermal conductivity (κsub), thickness (dsub), mass density (ρsub), and specific heat capacity (Csub). Therefore, the rise in the junction temperature, ΔTj(t), for the current density pulse of magnitude Jc and duration tpw, was calculated as133
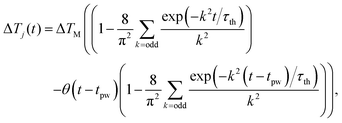 | (4) |
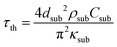 is the thermal rate constant, θ(·) is the Heaviside step function, and
is the thermal rate constant, θ(·) is the Heaviside step function, and | (5) |
Fig. 14 shows ΔTM as a function of dsub and Jc. Here, the thickness of the Mn3Sn (W) film is dMn3Sn = 4 nm (dW = 7 nm)107 and ρMn3Sn = 330 μΩ cm (ρW = 43.8 μΩ cm).107 The substrate is assumed to be MgO and its relevant material parameters134 are κsub = 40 W (m K)−1, ρsub = 3580 kg m−3, and Csub = 930 J (kg K)−1. In Fig. 14, an increase in Jc increases the generated heat in the metallic layers, which in turn, increases ΔTM. On the other hand, an increase in dsub increases the thermal resistance in the direction of heat flow, thereby slowing down the heat removal from the system and increasing ΔTM. The dashed black curve, corresponding to ΔTM = 120 K, represents the maximum temperature rise before Mn3Sn gets demagnetized. Consequently, no chiral oscillations would be observed in the region above the dashed curve. Here, the room temperature and the Néel temperature were assumed to be 300 K and 420 K, respectively. Although not shown here, for a fixed Jc and dsub, ΔTM would increase for thicker dHM or dMn3Sn since the generated heat would increase with the respective thickness. This explains the observed reduction in critical current density with an increase in the AFM thickness.104 The generated heat is expected to be lower if Pt was used as the HM since it has lower resistivity.70 Finally, for the same values of Jc and dsub, ΔTM would be higher in the case of both sapphire and SiO2 substrates. This is due to their lower κsub,135 and therefore, higher thermal resistance (∝ 1/κsub).
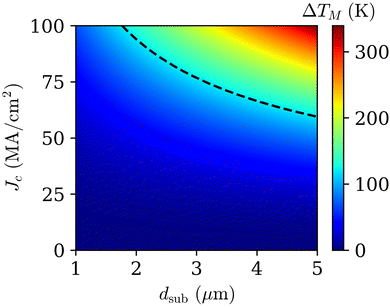 | ||
| Fig. 14 Maximum possible rise in the junction temperature, ΔTM, for different thicknesses of substrate MgO, dsub, and input charge current density, Jc. ΔTM increases with both dsub and Jc, as expected. The dashed black line corresponds to ΔTM = 120 K, which is the maximum temperature rise before the antiferromagnetic order in Mn3Sn changes. Here, the thickness of the AFM film is da = 4 nm. Adapted from ref. 117. | ||
Other factors that affect ΔTj(t) are τth and tpw, which decide the rate of change of the temperature and the total generated heat, respectively. For fixed Jc and dsub, ΔTj(t) reaches to about 95% of the respective ΔTM in t ≈ 3τth; therefore, applying tpw ≪ τth could ensure lower ΔTj(t). In the case of dsub = 3 μm, τth ≈ 304 ns while Jc = 76.8 MA cm−2 leads to ΔTM = 120 K for the MgO substrate. As shown in Fig. 15, ΔTj(t) ≈ 16 K for tpw = 10 ns (≪τth) but increases to about 70 K for tpw = 200 ns. Short input pulses (tpw ≪ τth) could also enable the application of Jc above the limit imposed by the dashed black curve in Fig. 14, and hence facilitate faster switching of the magnetic octupole, if applicable. The heat generated in the bilayer, due to a fixed Jc, would reach the bottom electrode faster for a thinner substrate; therefore, τth decreases with dsub; consequently, ΔTj(t) reaches ΔTM faster for lower dsub. This is expected since the maximum possible ΔTM, at a fixed Jc, is smaller for lower dsub (Fig. 14). Finally, for the same value of dsub, τth would be higher in the case of both sapphire and Si/SiO2 substrates, due to their lower thermal diffusivity 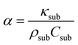 . This slow heat dissipation could be behind the dependence of deterministic switching on the fall time, as reported in ref. 102–104, where either sapphire or Si/SiO2 were used as substrates.
. This slow heat dissipation could be behind the dependence of deterministic switching on the fall time, as reported in ref. 102–104, where either sapphire or Si/SiO2 were used as substrates.
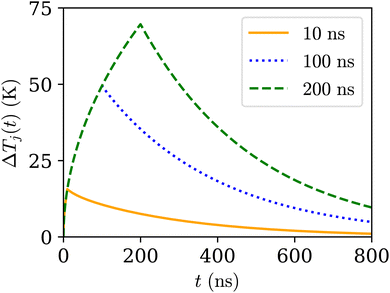 | ||
| Fig. 15 Temperature rise of the HM-Mn3Sn bilayer as a function of time for the charge current pulse of amplitude Jc = 76.8 MA cm−2 but different durations, as indicated in the legend. Here, dsub = 3 μm, τth ≈ 303 ns, and ΔTM = 120 K for the MgO substrate. ΔTj(t) is small if tpw ≪ τth as in the case of 10 ns, and increases with tpw. Here, ΔTj(t) is evaluated using a heat flow model discussed in ref. 133. | ||
3.4 The role of thermal fluctuations in Mn3Sn
Recent experimental70,101,102,104–108 and theoretical works,117,127,128,136 as discussed in Sections 3.1 and 3.2, have made significant progress in elucidating the current-driven dynamics in Mn3Sn with six equivalent minimum energy states as well as in Mn3Sn with PMA, both in the presence and absence of a symmetry breaking magnetic field. The promising results make Mn3Sn a strong candidate for CMOS compatible, compact and low power memory devices as well as GHz–THz signal sources. A practical realization of such devices, however, requires an investigation into the effect of thermal fluctuations, at different temperatures, on the long-term stability of a Mn3Sn memory element and on the linewidth of a coherent signal source. Therefore, a detailed investigation of the thermal stability factor, Δ, which depends on the energy barrier between the stable states, corresponding to thin Mn3Sn films is needed.Towards this, Sato et al., in a very recent work,137 evaluated the thermal stability of 20 nm thick epitaxial films of Mn3Sn of varying diameters D, ranging from 175 nm to 1000 nm, each of which exhibited PMA due to tensile strain from the MgO substrate. They applied magnetic field pulses of duration 1 s but different amplitudes in-the-(Kagome)-plane perpendicular to the interface, and explored the switching probability of the bistable magnetic order. Then using the Néel–Arrhenius thermal activation model and assuming an attempt frequency of 1 GHz, typically used for FMs, they evaluated, from the switching probability curves, the thermal stability factor of the different samples. They found that epitaxial Mn3Sn films, characterized by dominant two-fold and weak six-fold anisotropies, of diameters below ∼300 nm exhibited a single-domain behavior, i.e., Δ ∝ D2. On the other hand, for D ≳ 300 nm, the epitaxial films are expected to be multi-domain in nature since Δ showed a negligible change with D. At D = 300 nm, Δ is evaluated to be in the range of about 100–150. This result, however, is sensitive to the value of the attempt frequency, and needs further analysis for higher attempt frequencies.
Kobayashi et al. investigated the dependence of the critical switching voltage on the duration of the applied pulse, tp, for a bilayer comprising Pt and 40 nm thick Mn3Sn, grown on a Si/SiO2 substrate.138 A symmetry-breaking magnetic field, Hx, was also applied parallel to the current/voltage pulse. The Hall resistance measured as a function of the applied voltage, for tp in the range of 10 μs to 1 ms and different Hx, showed a tristable switching behavior, similar to Fig. 8(a), indicating clearly that Joule heating played a role in switching dynamics.102–105 The voltage at which the Hall resistance changed to zero, Vcritical, was found to decrease monotonically with an increase in tp, as expected.104 Nevertheless, ignoring the effects of Joule heating, and using a switching-time model, pertinent to FMs in the thermally activated regime, given as139
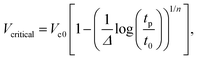 | (6) |
Previous theoretical works involving STT-driven dynamics in single-domain PMA FMs144,145 showed that a careful Fokker–Plank or an ensemble LLG-based approach was required to understand the switching behavior in the long pulse regime. In particular, these works found n to be equal to 2, and discussed the importance of its accuracy for an accurate estimation of Δ. Similarly, solving an ensemble of coupled LLG equations, in the presence of Gaussian random thermal noise,146 could help decipher n in the case of SOT-driven switching dynamics in Mn3Sn nanomagnets with six-fold as well as two-fold symmetry. This would then enable an accurate estimation of Δ, and therefore the long-term retention capability of single-domain Mn3Sn nanodots required for memory elements. Deterministic switching in the case of memory element requires the write error rate (1 − Pswitch, where Pswitch is the switching probability) to be negligible. On the other hand, Pswitch = 0.5 is required to build a true random number generator.24 Increased thermal fluctuations due to an increase in operating temperature due to Joule heating, for example, could change Pswitch, and consequently, the reliability of the device operation.24 An accurate estimation of n in eqn (6) would enable an accurate estimation of the change in Pswitch with temperature, and thus help circuit designers consider the area and energy overhead of spintronics-based probabilistic and neuromorphic computing paradigms.
With the exception of a few studies that focused on thick epitaxial layers, almost all other experimental investigations on field- and current-driven dynamics in noncollinear AFMs have focused on bulk polycrystalline AFM layers with large diameters. Such thick films with large diameters are not compatible with next-generation CMOS technology. Instead, thin epitaxial AFM layers that can be scaled down to 10 s of nanometers are preferable for spintronics applications. However, in ref. 137, Sato et al. predicted that scaling down the diameter below 100 nm could reduce Δ below 20. Furthermore, elevated temperatures likely reduce the effective magnetic anisotropy of the system.103 Consequently, the energy barrier between the bistable states of Mn3Sn nanodots could become comparable to thermal energy, kBT, where kB is the Boltzmann constant while T is the temperature, making the magnetic octupole moment fluctuate between the two states without any external perturbation, similar to the case of FMs147,148 and collinear AFMs.149,150 Such Mn3Sn nanoparticles could find applications in biomedical applications151 as well as spintronics-based probabilistic and neuromorphic computing paradigms.14–16,152–154 Therefore, it is important to theoretically analyze and understand the various thermal and switching properties of such nanodots, similar to the case of ferromagnetic or collinear antiferromagnetic nanoparticles.155–157
3.5 Readout of the order parameter
As discussed in Section 2.2, several methods may be used to detect the state of the octupole moment in Mn3Sn and related chiral AFMs. Of these methods, TMR offers the potential of providing a large readout signal that would be compatible with a CMOS circuitry. In chiral AFMs, the ferroic order of the cluster magnetic octupole breaks the macroscopic time-reversal symmetry leading to a finite TMR.90,91 For the setup shown in Fig. 2, the low and high resistance states correspond to angles 0° and 180° between the magnetic octupoles of the pinned and free Mn3Sn layers, respectively.91 The octupole moment of the pinned layer, mPoct, is fixed and not expected to change for the currents applied to the device. On the other hand, the dynamics of the order parameter of the free layer, moct, depends on the magnitude of Ha and Jc, as described in detail in Sections 3.1 and 3.2. The different steady-state response of moct, with respect to mPoct, is then measured as VL across the resistive load, RL, for a given read voltage, VR. Here, VR is sufficiently small, such that the current due to it does not disturb the steady states of either mPoct or moct.Chen et al. reported a TMR of 2% at room temperature91 in a trilayer device comprising epitaxial Mn3Sn(12 nm)/MgO(3.3 nm)/Mn3Sn(42 nm). The RA product of this device, however, was extremely large on the order of 108 Ω μm2 while the corresponding resistance states were also quite large (about 2 MΩ), making the device CMOS incompatible. Although lowering the RA product reduced the device resistance, it also reduced the already small TMR of the trilayer device. Similarly, reducing the thickness of the tunnel barrier lowers both the resistance and the TMR. Chen et al. found the c-axis of the epitaxial Mn3Sn film to be at an angle of about 30° with the normal direction of the film. Therefore, the current due to VR passed through the trilayer at an angle of about 60° with respect to the Kagome plane. Additional theoretical calculations revealed that with vacuum as the tunnel barrier and current perpendicular (parallel) to the Kagome plane, TMR increased to about 130% (150%) for a barrier thickness of about 0.45 nm (0.65 nm), clearly pointing to the dependence of the TMR on the tunnel barrier and the current direction. In both the cases, the RA product was found to be ≤1 Ω μm2 in the parallel as well as the antiparallel orientations of the two octupole moments. Calculations also suggested that both the TMR and RA products would increase to higher values with the thickness of the barrier, at least for thicknesses smaller than 1.1 nm.
As shown by Dong et al. in their theoretical work,90 a large TMR of about 300% at room temperature, for vacuum as a tunnel barrier (0.6 nm thick) and current perpendicular to the Kagome plane of the AFM tunnel junction, is possible. In this calculation, the RA product increased from approximately 0.05 Ω μm2 in the parallel configuration to 0.2 Ω μm2 in the antiparallel configuration. On the other hand, when moct was at 60° and 120° with respect to mPoct, the RA product was found to be approximately 0.07 Ω μm2 and 0.11 Ω μm2, respectively. Assuming the same values of the RA product for the device setup of Fig. 2, where current is parallel to the Kagome plane, we estimated VL = 91 mV (71 mV) in the parallel (antiparallel) configuration, for VR = 100 mV, RL = 50 Ω and the area of the tunnel barrier ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 100 × 100 nm2. Finally, the relative orientations of 60° (120°) lead to an intermediate value of VL of 88 mV (82 mV). Further improvement in VL could be achieved by increasing VR to a higher value as long as the current flowing through the tunnel junction does not disturb the octupole moments. Improvements in the RA product of the tunnel junction without compromising the TMR could also help enhance the values of VL. Although the TMR of 300% with vacuum as the tunnel barrier, for a fixed RA product, does not necessarily represents the upper limit in chiral AFM tunnel junctions, calculations showed that a more realistic tunnel junction with monolayer hexagonal hafnia, instead of vacuum, reduced the TMR to 124%.90 Finally, in the case of the AHE, the Hall voltage was found to be on the order of a few μV for 10 s of μA of read current,117 which is quite small, making TMR as the better choice for readout.
= 100 × 100 nm2. Finally, the relative orientations of 60° (120°) lead to an intermediate value of VL of 88 mV (82 mV). Further improvement in VL could be achieved by increasing VR to a higher value as long as the current flowing through the tunnel junction does not disturb the octupole moments. Improvements in the RA product of the tunnel junction without compromising the TMR could also help enhance the values of VL. Although the TMR of 300% with vacuum as the tunnel barrier, for a fixed RA product, does not necessarily represents the upper limit in chiral AFM tunnel junctions, calculations showed that a more realistic tunnel junction with monolayer hexagonal hafnia, instead of vacuum, reduced the TMR to 124%.90 Finally, in the case of the AHE, the Hall voltage was found to be on the order of a few μV for 10 s of μA of read current,117 which is quite small, making TMR as the better choice for readout.
4 Applications
Their rich bandstructure physics and the range of dynamical responses in the presence of charge current and magnetic field make Mn3Sn and other negative chirality materials an excellent choice for new spintronic computing applications. Of particular interest in this regard are biologically inspired computing and probabilistic computing paradigms. As we discuss below, the SOT-induced incoherent oscillations of the order parameter in Mn3Sn have striking resemblance to the time-domain response of spiking biological neurons. On the other hand, low-energy barrier Mn3Sn thin films or nanodots can exhibit thermally induced switching which can be used for implementing p-bits, which are an important building block for stochastic computing hardware and Boltzmann machines. Other applications include non-volatile memory devices, high-frequency signal generators/detectors, ANE-based thermoelectric generators and sensors and quantum computing applications.4.1 Neuromorphic computing
Neuromorphic computing leverages the dynamical principles of the brain to implement computing tasks in hardware for AI applications. The basic building blocks of a neuromorphic computer include neurons and synapses. A neuron integrates the membrane potential frequently and fires (i.e., generates a spike) once the integrated potential exceeds a threshold. Synapses capture the strength of the connection between neurons and are associated with learning and memorizing information in the brain. The dynamics of spintronic devices is inherently non-linear, while these devices can also be fabricated at the nanoscale.158 As such, spintronics-based neurons and synapses have been proven to be much more area- and energy-efficient compared to CMOS-only implementations.159 Domain wall motion, skyrmions, spin torque oscillators, and magnetic tunnel junctions have been utilized toward the hardware emulation of neurons and synapses.160 Of these implementations, antiferromagnetic neurons, which can generate voltage spikes when excited by a spin torque above a threshold, can mimic the spiking response of biological neurons.161 Likewise, spintronic synapses utilizing domain-wall motion in magnetic materials can result in nonvolatile multi-state resistance states.162 In the following, we discuss theoretical and experimental advances in utilizing spin-torque driven dynamics in Mn3Sn to emulate neurosynaptic functionality in hardware.In the work reported by Zheng et al.,114 OT generated in a trilayer setup comprising Mn3Sn/Pt/Mn was utilized to switch the AHE signal (Fig. 10). In this work, 120 positive (negative) current pulses of amplitude 4.5 MA cm−2 each, along the [0001] ([000![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]) direction, which is perpendicular to the Kagome plane, were employed to mimic the LTD (LTP) process.114Fig. 16(a) shows the quasi-linear dependence of normalized anomalous Hall resistance, RAHE, on the number of applied pulses. RAHE can be treated as the weight, G, of the artificial synapse in the ANN. The performance of an ANN crossbar array of size 100 × 100 with Mn3Sn-based synapses was also evaluated. An image recognition task, as depicted in Fig. 16(b), was implemented on the ANN crossbar array. As shown in Fig. 16(c), the learning accuracy of the synaptic network comprising OT-driven Mn3Sn devices was found to be approximately 97.5%, which was only slightly lower than that of the ideal device with perfect linearity and significantly higher than that of spin-torque-driven Mn3Sn devices. The lower accuracy of spin-torque Mn3Sn synapses could be due to the inhomogeneous switching of the sample as a result of the higher Joule heating effect.
]) direction, which is perpendicular to the Kagome plane, were employed to mimic the LTD (LTP) process.114Fig. 16(a) shows the quasi-linear dependence of normalized anomalous Hall resistance, RAHE, on the number of applied pulses. RAHE can be treated as the weight, G, of the artificial synapse in the ANN. The performance of an ANN crossbar array of size 100 × 100 with Mn3Sn-based synapses was also evaluated. An image recognition task, as depicted in Fig. 16(b), was implemented on the ANN crossbar array. As shown in Fig. 16(c), the learning accuracy of the synaptic network comprising OT-driven Mn3Sn devices was found to be approximately 97.5%, which was only slightly lower than that of the ideal device with perfect linearity and significantly higher than that of spin-torque-driven Mn3Sn devices. The lower accuracy of spin-torque Mn3Sn synapses could be due to the inhomogeneous switching of the sample as a result of the higher Joule heating effect.
 | ||
| Fig. 16 (a) Long-term depression (LTD) and potentiation (LTP), depicted by the increase and decrease of the AHE resistance, RAHE, for 120 negative and positive current pulses, respectively, is achieved in an OT-driven Mn3Sn/Pt/Mn sample. Here, charge current is converted into orbital current in the Mn layer while the Pt layer assists in orbital-current-to-spin-current conversion. RAHE displays a good linear dependence on the number of current pulses. (b) Schematic of the constructed ANN with 100 × 100 memory cells for image recognition task. (c) Image accuracy rates as a function of learning epochs using three kinds of devices. An ideal device corresponds to one where the non-linearity (NL) index for weight update is set to zero, whereas the NL index for the spin-torque (ST)-driven device, comprising a bilayer of Mn3Sn/Pt, is 0.686 and that of the OT-driven device is only 0.166, which is much closer to that of an ideal device (NL = 0) with linear LTD and LTP. Reproduced with permission from ref. 114. | ||
In a recent work by Wu et al., Néel-like domain wall motion was experimentally probed via MOKE in Mn3Ge and Mn3Sn.98 It was found that current densities as low as 7.5 × 106 A cm−2 could result in a domain-wall velocity of 750 m s−1 in Mn3Ge. Similar to ferromagnets, the motion of the domain wall was found to occur through thermal creep for currents below ∼2.5 × 106 A cm−2 in Mn3Ge. The velocity of Néel-like domain walls was found to be higher than that of Bloch-like domain walls in both Mn3Ge and Mn3Sn. The mobility of domain walls in Mn3Ge and Mn3Sn was extracted to be more than an order of magnitude higher than that in ferromagnetic materials. For a sample size of 6 μm width, 45 μm length, and 800 nm thickness, the energy consumption during the application of nanosecond pulses was estimated to be ∼25 nJ. Thus, for a scaled domain-wall synapse, the energy consumption could be on the order of 100s of fJ. The high domain-wall velocity and mobility at low critical current densities demonstrates the superior potential of chiral AFMs to realize ultra-fast and energy-efficient synaptic devices in a spintronic ANN. Yet, future research must systematically investigate the impact of material properties and device design on the energy consumption and latency of chiral AFM-based synapses.
Several prior works have explored the use of antiferromagnetic materials to implement artificial spiking neurons.116,169–174 For example, Khymyn et al.170 have shown that the thresholding behavior of spin torque induced spiking dynamics can be used in “future neuromorphic signal processing circuits working at clock frequencies of tens of gigahertz.” Likewise, Bradley et al. showed that antiferromagnetic neurons could generate spikes with a duration on the order of picoseconds, while consuming ∼1 fJ per spiking operation.171 Moreover, antiferromagnetic neurons are also shown to possess built-in features, such as response latency, refraction, and inhibition, that resemble the features of biological neurons. More recently, a spiking neural network with antiferromagnetic neurons was designed for pattern recognition using the spike pattern association neuron (SPAN) algorithm. The network was trained under 1 μs for MNIST pattern recognition task, while the energy consumption of the network was estimated to be around 1 pJ during inference.172
Mn3Sn is a promising material for building spiking neurons, owing to a Dirac-comb-like nonlinear dynamics for high damping and currents near the threshold current.116 As illustrated in Fig. 17(a), for a two-fold anisotropy Mn3Sn, when the input spin current density slightly exceeds a critical value, denoted by Jcr1s, the in-plane component of the magnetic octupole measured via the TMR, ∝ cos(φoct), (φoct is the azimuthal angle of the magnetic octupole) demonstrates spiking behavior in the time domain. Moreover, the device automatically resets after the pulsed input current is turned off. In the classic leaky-integrate-and-fire model of spiking neurons, the superposition of current flowing from connected synapses mimics the integration process, while the spiking behavior, when the input exceeds a set threshold value, corresponds to the firing operation of a biological neuron. The activity of the artificial AFM neurons, made using Mn3Sn as the active element, is suppressed for a period of time, known as the refractory period, immediately after a spiking event as depicted in Fig. 17(a), which agrees well with the functionality of biological spiking neurons.
Previous works116,170,175 have shown that the rate of firing of these neurons can be controlled if the d.c. current is superimposed with a small a.c. current such that the net current just exceeds Jcr1s. Furthermore, the co-application of a subthreshold direct current (d.c.) stimulus (e.g., 0.8Jcr1s) with an a.c. component (e.g., λJcr1s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πfact)) can engender a richer spectrum of spiking behaviors. Both the amplitude and the frequency of the a.c. signal can control the nature of the spikes, i.e., it might be possible to generate single spikes as well as bursts of spikes as shown in Fig. 17(b) and (c). Such neuron emulators could then be coupled to each other to get interesting dynamics, where the rate of firing of the second neuron could be controlled by that of the first. If the coupling is bidirectional in nature, unique dynamics, which can then be used for computation, e.g. collective state computing and oscillatory Hopfield network176 is possible.
cos(2πfact)) can engender a richer spectrum of spiking behaviors. Both the amplitude and the frequency of the a.c. signal can control the nature of the spikes, i.e., it might be possible to generate single spikes as well as bursts of spikes as shown in Fig. 17(b) and (c). Such neuron emulators could then be coupled to each other to get interesting dynamics, where the rate of firing of the second neuron could be controlled by that of the first. If the coupling is bidirectional in nature, unique dynamics, which can then be used for computation, e.g. collective state computing and oscillatory Hopfield network176 is possible.
Previous work has benchmarked the performance of a Mn3Sn neuron at the device and system level, by embedding it within an SNN to perform recognition tasks.177,178 It has been shown that an Mn3Sn neuron consumes roughly 12 aJ energy per spike for a time-domain input signal of 90 ps duration. The low energy consumption results from the low critical current required to excite a spiking response in chiral AFMs. In terms of network-level performance, the EDP of spintronics-based SNNs including Mn3Sn-based neurons was found to be as low as 5.30 × 10−20 J s, while that of analog-CMOS-based SNNs was 8.64 × 10−16 J s for a small LeNet workload. The performance of Mn3Sn neurons is significantly better than that of its spintronics counterparts. For example, it was shown in ref. 179 that a stochastic SOT-controlled MTJ consumed 1.16 fJ energy for a 1 ns input current pulse, while a DW-based neuron consumed 0.14 fJ energy for a 2-ns input current pulse.180 A comparison of various neuromorphic device technologies, including resistive, phase-change, ferroelectric, magnetic, and electrochemical RAM, for deep neural networks is presented in a recent article by Lelmini and Ambrogio.181 The authors showed that magnetic, ferroelectric, and Li-ion electrochemical RAM consumed 100 fJ per bit, while magnetic and resistive RAM could operate under 10 ns for training. An SNN based in-memory accelerator with spintronic computational RAM (i.e., STT-MRAM or SOT-MRAM) was shown to reduce the energy consumption by ∼150× compared to a representative application-specific integrated-circuit solution.182 At the element level, it was shown that SOT-based computational RAM used ∼150 fJ energy for spiking at ∼500 ns latency resulting in a spike operation energy-delay product (EDP) of 7.85 × 10−20 J s. Despite the superior performance of Mn3Sn neurons, further research is needed to understand the impact of CMOS peripherals, scalability limits, and mapping of algorithms on to the hardware to harness the full potential of Mn3Sn for neuromorphic computing.
4.2 Probabilistic computing
While traditional computing is characterized by its pursuit of deterministic outputs, probabilistic computing has emerged as a novel paradigm integrating randomness and uncertainty into the computing process. Insights from neuroscience suggest that the human brain optimizes for energy efficiency at the expense of reliability by incorporating stochasticity in computation. This approach proves particularly effective in addressing specific problems such as factorization, satisfiability, and combinatorial optimization.16 In this context, the fundamental computing unit, known as the p-bit, functions akin to a controllable random number generator, with its output being a function of the external input (i.e., SOT).Low barrier MTJs are proposed as viable candidates for p-bits in diverse applications, including invertible logic gates and Boltzmann machines,14 as well as Gaussian random number generators.183 Their suitability arises from the ease of inducing stochastic behaviors with the aid of thermal noise. Although there are no direct experimental reports on p-bits using Mn3Sn, previous studies have evaluated its thermal stability and behavior in the presence of thermal noise. Specifically, the effect of thermal noise during field-driven137 and voltage-driven138 switching has been experimentally investigated in Mn3Sn. To enable p-bit applications with Mn3Sn, such as machine-learning-inspired Bayesian networks, Boltzmann machines, and invertible Boolean logic,154 future work must systematically explore the thermal stability and thermally driven dynamics of the octupole moment, particularly for scaled devices in which the energy barrier separating the stable states is comparable to the thermal energy. This field is rapidly advancing, both experimentally and theoretically, and additional research that provides early insights into the underlying physics of stochastic switching and its application toward probabilistic computing is urgently needed.
4.3 High frequency signal generation and detection
Magnetic materials that can operate at high frequencies are highly desirable for pushing the range and bandwidth of spintronics-based signal generators and detectors. Toward this, antiferromagnetic materials are promising candidates as they can display ultra-fast dynamics resulting from their strong exchange interactions.32,184 While typically ferromagnetic materials have been adopted as GHZ-spin-torque oscillators (STOs),185 microwave and radio frequency signal generators,186 and magneto-optical devices,187 it is expected that AFMs can be used as the active element of similar applications. For these applications, the oscillations in the order parameter can be extracted via the TMR in the device setup of Fig. 2. The TMR is sensitive to the orientation of the order parameter, i.e., the octupole moment in chiral AFMs and the Néel vector in collinear AFMs and can be utilized for the electrical readout. Several proposals for terahertz (THz) signal generation, detection, and signal analysis have appeared in the literature.161,169,188–190 For example, in ref. 191, a nanoscale spectrum analyzer, operational in the THz regime, is conceptualized using a four-layer tunnel junction comprising a lower Pt layer, a conducting AFM, an MgO barrier, and an upper Pt layer. The oscillations in the Néel vector are converted into an electrical signal by means of the tunneling anisotropic magnetoresistance. Output a.c. voltage levels on the order of a milli-volt were shown to be feasible in this structure. Although these prior works are based on collinear AFMs, we also expect high-frequency dynamics in chiral AFMs. Theoretical proposals on electrical control of the THz rotation of the octupole moment in chiral AFMs have recently appeared in the literature.192–194Lund et al.193 theoretically predicted voltage-controlled high-bandwidth oscillations in noncollinear and Kagome AFMs, where the oscillation frequency is continuous from zero up to the THz range, modulated via the SOT. We also theoretically and numerically investigated the spin-current-driven auto oscillations of Mn3Sn and Mn3Ir in the THz regime, revealing the threshold current density and the dependence of oscillation frequency on magnetic parameters.116 Our work also presented several device setups to electrically extract the generated a.c. signal due to the oscillation of the octupole moment. However, we must acknowledge that in the case of current-driven dynamics of the octupole moment, large currents are required to increase the oscillation frequency of the octupole moment, where Joule heating may become prohibitive for practical realization of such high-frequency AFM-based spintronic devices. Nonetheless, the unique spin arrangement and the physics of chiral AFMs permit highly tunable dynamics of the octupole moment, which may eventually be utilized to develop tightly integrated oscillators in a nanoscale platform.
On the experimental front, Miwa et al.140 observed field-induced magnetic octupole order oscillation in Mn3Sn through time-resolved MOKE, with a resonant frequency as high as 0.86 THz under a 2 T external field applied along the [2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction. Ultrafast photocurrents195 have also been generated in an Mn3Sn thin film excited by optical pump-THz emission spectroscopy. The magnitude and direction of these photocurrents could be controlled by the polarization and incidence angle of the optical pump, but the currents remained robust to external field perturbations. THz time-domain spectroscopy has been utilized to determine the dynamical properties of Mn3Sn at ultra-high frequencies in ref. 196, where the authors established that Mn3Sn's room-temperature anomalous Hall conductivity was approximately 20 (Ω cm)−1 for frequencies up to 2 THz. These phenomena collectively highlight the broad potential of chiral AFMs for the generation, manipulation, and sensing of high-frequency signals.
0] direction. Ultrafast photocurrents195 have also been generated in an Mn3Sn thin film excited by optical pump-THz emission spectroscopy. The magnitude and direction of these photocurrents could be controlled by the polarization and incidence angle of the optical pump, but the currents remained robust to external field perturbations. THz time-domain spectroscopy has been utilized to determine the dynamical properties of Mn3Sn at ultra-high frequencies in ref. 196, where the authors established that Mn3Sn's room-temperature anomalous Hall conductivity was approximately 20 (Ω cm)−1 for frequencies up to 2 THz. These phenomena collectively highlight the broad potential of chiral AFMs for the generation, manipulation, and sensing of high-frequency signals.
4.4 Non-volatile memory
Non-volatile memory (NVM) has attracted attention not only for its persistent data storage, but also for in-memory computing197,198 and neuromorphic computing.199,200 Memory devices with faster speed, higher density, lower power consumption, and higher bandwidth are in high demand, and materials, such as ferromagnets, ferroelectrics, and phase change materials, are all candidates for novel memory designs. The large anomalous Hall conductivity and small coercivity of Mn3Sn make it ideally suited for implementing low-power spintronic memory devices. Potentially, the speed of Mn3Sn memory can be much higher than that of ferromagnet-based NVMs, while the lack of stray fields in AFMs can also lead to higher memory density. A qualitative sketch in Fig. 18 highlights the key differences between NVMs implemented using ferromagnet-MTJs versus AFM-MTJs. Yet, there are a few key challenges that must be resolved. For example, although the low coercive field of Mn3Sn promotes energy-efficient write operations, it adversely affects the memory stability to external magnetic fields. To increase the memory density, device miniaturization, while ensuring reliable read and write operations is also essential. An important result in the context of NVMs was reported in 2021 by Tsai et al.111 The authors showed that by optimizing the annealing conditions after the deposition of the heavy metal in Mn3Sn/W, a large Hall resistance of 0.35 Ω and a large read signal of 1 mV could be achieved in the bilayer samples. This is an important step forward for realizing future memory technologies based on Mn3Sn. Recently, Matsuo et al.143 measured anomalous Hall signals in 100-nm-scale Mn3Sn grains in films thinner than 20 nm at room temperature and at zero fields. This result signifies that Mn3Sn samples can retain their topological features at the nanoscale limit, thus paving the path for miniaturized, high density memory applications that utilize AFMs as their key element. On the other hand, the large magnetic spin Hall effect of Mn3Sn can generate a large out-of-plane spin accumulation,87 which may enable the switching of a proximal ferromagnet with perpendicular magnetic anisotropy (PMA) for energy-efficient SOT NVM applications. For example, Hu et al. demonstrated highly efficient, deterministic switching of Ni/Cr multilayers with PMA using the unconventional SOT generated in Mn3Sn.201 A switching current density of 4.6 × 106 A cm−2 was found for Mn3Sn/Cu/Ni–Cr samples, which was less than half of the switching current density of β-Ta/Cu/Ni–Cr samples, highlighting the potential of Mn3Sn as an SOT source wherein an out-of-plane spin current with collinear spin polarization induced by in-plane charge current is feasible. Thus, Mn3Sn and related non-collinear AFMs can also be used as the SOT-generating layer in low-power non-volatile SOT memory devices. | ||
| Fig. 18 An array of MTJs using (a) ferromagnets and (b) antiferromagnets as the active NVM element. Unlike ferromagnet-MTJs, AFM-based MTJs can be more tightly integrated leading to denser memory arrays, while they are also expected to operate at much faster speeds. Taken from ref. 51. | ||
4.5 ANE-based devices
The ANE in Mn3Sn can be used for thermoelectric generation and for on-chip cooling. As a thermoelectric generator, Mn3Sn can convert waste heat into usable electrical power, while it can also harvest heat from integrated circuits to provide localized cooling and thus improve the circuit reliability. Compared to a Seebeck thermopile, which consists of a pillar structure of p- and n-type semiconductors, the ANE-based thermopile has a planar structure and is thus simpler to fabricate. Owing to the lack of stray fields from AFMs, Mn3Sn-based thermopiles can lead to densely integrated thermoelectric modules for providing efficient coverage of the heat source.84 Hideki et al.78 demonstrated the microfabrication of a thermoelectric element comprising Ta/Al2O3/Mn3Sn layered structure, where Ta was used as the heating element, while Al2O3 enabled the diffusion of heat toward Mn3Sn. The anomalous Nernst coefficient of the microfabricted Mn3Sn was extracted to be 0.27 μV K−1, which is similar to the Nernst coefficient of bulk Mn3Sn. This result indicates the potential of developing efficient and dense thermopiles utilizing the topological features of microfabricated Mn3Sn. A planar tilted Nernst thermopile using Mn3Sn as the active element, illustrated in Fig. 19, was demonstrated in ref. 202. In this design, the tilted structure simultaneously acts as the n- and p-legs of a conventional thermopile and thus the need for extrinsic contacts is obviated. Other applications of the ANE in Mn3Sn include logic devices that utilize temperature gradients as the information token, sensor devices based on temperature gradients,203 efficient thermal management and spin current generation via the closely related spin-Seebeck effect,204 and enabling efficient writing of heat-assisted magnetic memory devices. | ||
| Fig. 19 A conceptual thermopile presented in ref. 202, where the transverse magnetization direction is automatically alternated between adjacent elements. A sizeable transverse magnetization results during the domain reversal process in Mn3Sn and thus Mn3Sn can be used as the active element of the thermopile. | ||
4.6 Quantum computing
Quantum computing,205 owing to the superposition of quantum states, is a promising solution for executing certain tasks that are intractable on classical computers. Superconducting qubits, typically implemented using Josephson junctions (JJs),206 are among the most promising candidates for realizing scalable quantum computers. Superconductor/ferromagnet (SC/FM) heterostructures207 are promising platforms for future superconducting spintronics and quantum computation applications because of their unique physical properties, such as spin-triplet superconductivity,208 superconducting order parameter oscillation, and topological superconductivity.209 However, such SC/FM structures require delicate interface engineering, including careful electronic energy band matching and circumventing out-of-plane stray fields.The topological chiral antiferromagnet Mn3Ge210 has been shown to be effective in forming JJs, as well as in further applications in spin-triplet supercurrent spin valves and direct-current superconducting quantum interference devices (d.c. SQUIDs). In ref. 210, a JJ was implemented using a Nb/Mn3Ge/Nb structure and a d.c. SQUID was also fabricated containing two chiral Mn3Ge antiferromagnetic spin-triplet JJs (Fig. 20). An external field perpendicular to the kagome plane changes the associated Berry curvature211 around the Fermi energy and subsequently enables triplet amplitude manipulation through an extremely small magnetic field (<2 mT). These results are the first step toward chiral AFM applications for manipulating spin-triplets and logic circuits, while the lack of stray fields in AFMs can enable highly integrated superconducting spintronic logic circuits.212
5 Conclusions and outlook
Noncollinear AFMs with Kagome lattices exhibit properties such as spin momentum locking, topologically protected surface states, large spin Hall conductivity, and the magnetic spin Hall effect arising from the topology. In particular, research pertaining to the physics and applications of the negative chirality noncollinear AFM, Mn3Sn, have intensified in the last few years. Mn3Sn can only be stabilized in excess of Mn, whereas with a lower Mn concentration the system gets contaminated with Mn2Sn. Below its Neél temperature of 420–430 K, the 120 degree spin structure with negative chirality is stabilized due to the combination of exchange coupling and DM interaction between the Mn moments. With Mn deficiency, a helix phase emerges at intermediate temperatures where Mn moments form a spiral spin structure propagating along its c-axis. At much lower temperatures (≤50 K), a spin glass like texture is also feasible. Due to their many intriguing transport properties including a large spin Hall effect, anomalous Hall effect, and FM-like spin polarized charge current, negative chirality AFM metals can enable the development of AFM spintronic devices and applications along a similar route to their FM counterparts. Furthermore, a comprehensive understanding of these chiral materials can also illuminate the pathways for experimental, theoretical, and applied research and development in the field of altermagnetism.In this paper, we presented recent developments, both on theoretical and experimental fronts, related to understanding Mn3Sn's non-trivial bandstructure properties, which lead to strong magnetotransport signatures in the material. The anomalous Hall effect in Mn3Sn, comparable to that in elemental FMs like Co, Ni, and Fe has been experimentally reported. Magnetic switching of Mn3Sn has been demonstrated in bilayers comprising the AFM and heavy metal and current densities (∼(106–107) A cm−2) comparable to those used for switching FMs in FM/heavy metal bilayers have been obtained. In this structure, readout voltages >1 mV could be detected by optimizing the annealing conditions and the seed layer during the fabrication process. A large magneto-optic Kerr signal, around 20 mdeg at 300 K, has been reported in Mn3Sn. Spin-torque ferromagnetic resonance measurements have been used to quantify the field-like torque due to the magnetic spin Hall effect and values greater than those of conventional heavy metals like Pt, Ta, and W have been found in Mn3Sn. NV relaxometry measurements have been performed to determine the frequency of chiral oscillations of the order parameter in Mn3Sn as a function of the input current. More recently, a finite TMR, around 2% at 300 K, has been experimentally reported in all-AFM MTJs with Mn3Sn electrodes and a MgO tunnel barrier. This discovery sets the stage for developing advanced CMOS-compatible spintronic devices using Mn3Sn as the active magnetic element. Studies of strained Mn3Sn thin films with two fold symmetric energy landscape suggest that they can be used as memory elements or high-frequency signal generators and detectors depending on the magnitude of input spin current and the magnetic field.
Theoretical models of critical input current to induce different dynamics with and without magnetic fields in six-fold and two-fold symmetric Mn3Sn can be valuable to gain physical insight into the effect of material parameters on the order parameter dynamics. Likewise, models of oscillation frequency and switching time versus input current can shed light on the performance metrics and scaling limits of Mn3Sn-based spintronic devices. The effect of Joule heating in Mn3Sn cannot be ignored, especially when the input current significantly exceeds the threshold current for a given dynamical response. However, by employing pulsed SOT in the short pulse regime, the issue of Joule heating can be reduced. Understanding the impact of thermal noise on the order parameter in Mn3Sn is crucial for realizing non-volatile memory as well as p-bits, which serve as the fundamental unit of probabilistic computing hardware. Toward this, thermal stability of Mn3Sn thin films with perpendicular anisotropy has been studied experimentally as well as theoretically by employing the Néel–Arrhenius model. However, further research in this area is needed to quantify Mn3Sn's attempt frequency and the effective temperature in the presence of SOT.
To move the research field further and to develop practical spintronic applications using chiral AFMs, experimental techniques to probe time-domain dynamics without Joule heating are needed. Advances in improving TMR in all-AFM tunnel junctions are also critical for ensuring robust readout signals that are compatible with a CMOS circuitry. Additional work is needed to elucidate the role of thermal noise in Mn3Sn thin films of various dimensions. Theoretical calculations will be indispensable to shed light on the exotic bandstructure physics of these materials and provide a theoretical rigor to experimental investigations. Meanwhile, the state of analytical models must be further advanced to enable technology-device co-design and benchmarking. Development of prototypes of antiferromagnetic spintronic devices that are CMOS-compatible can allow this field to rapidly advance and lead to novel computing paradigms with superior performance compared to that of their ferromagnetic-only counterparts.
Author contributions
Ankit Shukla: methodology, investigation, formal analysis, investigation, data curation, and writing – original draft and review. Siyuan Qian: investigation, data creation, and writing. Shaloo Rakheja: investigation, supervision, conceptualization, methodology, resources, funding acquisition, and writing – review and editing. All authors discussed the results and the implications of this manuscript. All authors have given approval to the final version of the manuscript.Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was partially supported by the NSF through the University of Illinois at Urbana-Champaign Materials Research Science and Engineering Center DMR-1720633. The authors also acknowledge the support of AFRL/AFOSR, under AFRL Contract No. FA8750-21-1-0002.Notes and references
- J. C. Slonczewski, J. Magn. Magn. Mater., 1996, 159, L1–L7 CrossRef CAS.
- L. Berger, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 9353 CrossRef CAS PubMed.
- P. Gambardella and I. M. Miron, Philos. Trans. R. Soc., A, 2011, 369, 3175–3197 CrossRef CAS PubMed.
- A. Brataas, A. D. Kent and H. Ohno, Nat. Mater., 2012, 11, 372–381 CrossRef CAS PubMed.
- J. Sinova, S. O. Valenzuela, J. Wunderlich, C. Back and T. Jungwirth, Rev. Mod. Phys., 2015, 87, 1213 CrossRef.
- A. D. Kent and D. C. Worledge, Nat. Nanotechnol., 2015, 10, 187–191 CrossRef CAS PubMed.
- R. Ramaswamy, J. M. Lee, K. Cai and H. Yang, Appl. Phys. Rev., 2018, 5, 031107 Search PubMed.
- C. Song, R. Zhang, L. Liao, Y. Zhou, X. Zhou, R. Chen, Y. You, X. Chen and F. Pan, Prog. Mater. Sci., 2021, 118, 100761 CrossRef CAS.
- Q. Shao, P. Li, L. Liu, H. Yang, S. Fukami, A. Razavi, H. Wu, K. Wang, F. Freimuth and Y. Mokrousov, et al. , IEEE Trans. Magn., 2021, 57, 1–39 Search PubMed.
- X. Han, X. Wang, C. Wan, G. Yu and X. Lv, Appl. Phys. Lett., 2021, 118, 120502 CrossRef CAS.
- M. Pinarbasi and A. Kent, APL Mater., 2022, 10, 020901 CrossRef CAS.
- X. Fong, Y. Kim, K. Yogendra, D. Fan, A. Sengupta, A. Raghunathan and K. Roy, IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst., 2015, 35, 1–22 Search PubMed.
- X. Fong, Y. Kim, R. Venkatesan, S. H. Choday, A. Raghunathan and K. Roy, Proc. IEEE, 2016, 104, 1449–1488 CAS.
- K. Y. Camsari, R. Faria, B. M. Sutton and S. Datta, Phys. Rev. X, 2017, 7, 031014 Search PubMed.
- K. Y. Camsari, B. M. Sutton and S. Datta, Appl. Phys. Rev., 2019, 6, 011305 Search PubMed.
- W. A. Borders, A. Z. Pervaiz, S. Fukami, K. Y. Camsari, H. Ohno and S. Datta, Nature, 2019, 573, 390–393 CrossRef CAS PubMed.
- V. K. Joshi, P. Barla, S. Bhat and B. K. Kaushik, IEEE Access, 2020, 8, 194105 Search PubMed.
- B. Dieny, I. L. Prejbeanu, K. Garello, P. Gambardella, P. Freitas, R. Lehndorff, W. Raberg, U. Ebels, S. O. Demokritov and J. Akerman, et al. , Nat. Electron., 2020, 3, 446–459 CrossRef.
- J. Grollier, D. Querlioz, K. Camsari, K. Everschor-Sitte, S. Fukami and M. D. Stiles, Nat. Electron., 2020, 3, 360–370 CrossRef PubMed.
- A. Hirohata, K. Yamada, Y. Nakatani, I.-L. Prejbeanu, B. Diény, P. Pirro and B. Hillebrands, J. Magn. Magn. Mater., 2020, 509, 166711 CrossRef CAS.
- Z. Guo, J. Yin, Y. Bai, D. Zhu, K. Shi, G. Wang, K. Cao and W. Zhao, Proc. IEEE, 2021, 109, 1398–1417 CAS.
- A. Houshang, M. Zahedinejad, S. Muralidhar, J. Checiński, R. Khymyn, M. Rajabali, H. Fulara, A. A. Awad, M. Dvornik and J. Åkerman, Phys. Rev. Appl., 2022, 17, 014003 CrossRef CAS.
- S. Misra, L. C. Bland, S. G. Cardwell, J. A. C. Incorvia, C. D. James, A. D. Kent, C. D. Schuman, J. D. Smith and J. B. Aimone, Adv. Mater., 2023, 35, 2204569 CrossRef CAS PubMed.
- A. Shukla, L. Heller, M. G. Morshed, L. Rehm, A. W. Ghosh, A. D. Kent and S. Rakheja, 2023 24th International Symposium on Quality Electronic Design (ISQED), 2023, pp. 1–10.
- A. Litvinenko, R. Khymyn, V. H. González, R. Ovcharov, A. A. Awad, V. Tyberkevych, A. Slavin and J. Åkerman, Commun. Phys., 2023, 6, 227 CrossRef.
- S. Chowdhury, A. Grimaldi, N. A. Aadit, S. Niazi, M. Mohseni, S. Kanai, H. Ohno, S. Fukami, L. Theogarajan, G. Finocchio, S. Datta and K. Y. Camsari, IEEE J. Explor. Solid-State Comput. Devices Circuits, 2023, 9, 1–11 Search PubMed.
- B. Chen, M. Zeng, K. H. Khoo, D. Das, X. Fong, S. Fukami, S. Li, W. Zhao, S. S. Parkin, S. Piramanayagam and S. T. Lim, Mater. Today, 2023, 70, 193–217 CrossRef.
- T. Scheike, Z. Wen, H. Sukegawa and S. Mitani, Appl. Phys. Lett., 2023, 122, 112404 CrossRef CAS.
- E. Gomonay and V. Loktev, Low Temp. Phys., 2014, 40, 17–35 CrossRef CAS.
- T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Nat. Nanotechnol., 2016, 11, 231 CrossRef CAS PubMed.
- O. Gomonay, V. Baltz, A. Brataas and Y. Tserkovnyak, Nat. Phys., 2018, 14, 213–216 Search PubMed.
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono and Y. Tserkovnyak, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- H. Bai, X. Zhou, Y. Zhou, X. Chen, Y. You, F. Pan and C. Song, J. Appl. Phys., 2020, 128, 210901 CrossRef CAS.
- S. A. Siddiqui, J. Sklenar, K. Kang, M. J. Gilbert, A. Schleife, N. Mason and A. Hoffmann, J. Appl. Phys., 2020, 128, 040904 CrossRef CAS.
- D. Xiong, Y. Jiang, K. Shi, A. Du, Y. Yao, Z. Guo, D. Zhu, K. Cao, S. Peng and W. Cai, et al. , Fundam. Res., 2022, 2, 522–534 CrossRef CAS PubMed.
- M.-T. Suzuki, T. Koretsune, M. Ochi and R. Arita, Phys. Rev. B, 2017, 95, 094406 CrossRef.
- T. Higo and S. Nakatsuji, J. Magn. Magn. Mater., 2022, 170176 CrossRef CAS.
- X. Wang, H. Yan, X. Zhou, H. Chen, Z. Feng, P. Qin, Z. Meng, L. Liu and Z. Liu, Mater. Today Phys., 2022, 100878 CrossRef CAS.
- S.-H. Yang, R. Naaman, Y. Paltiel and S. S. Parkin, Nat. Rev. Phys., 2021, 3, 328–343 CrossRef.
- L. Šmejkal, J. Sinova and T. Jungwirth, Phys. Rev. X, 2022, 12, 040501 Search PubMed.
- I. Mazin and P. Editors, Phys. Rev. X, 2022, 12, 040002 CAS.
- I. Mazin, Phys. Rev. B, 2023, 107, L100418 CrossRef CAS.
- S.-W. Cheong and F.-T. Huang, npj Quantum Mater., 2024, 9, 13 CrossRef CAS.
- A. Chakraborty, R. González Hernández, L. Šmejkal and J. Sinova, Phys. Rev. B, 2024, 109, 144421 CrossRef CAS.
- P. A. McClarty and J. G. Rau, Phys. Rev. Lett., 2024, 132, 176702 CrossRef CAS PubMed.
- Z. P. Niu and Y. M. Zhang, Supercond. Sci. Technol., 2024, 37, 055012 CrossRef.
- A. Smolyanyuk, L. Šmejkal and I. I. Mazin, SciPost Phys. Codebases, 2024, 30 DOI:10.21468/SciPostPhysCodeb.30.
- L. Han, X. Fu, W. He, Y. Zhu, J. Dai, W. Yang, W. Zhu, H. Bai, C. Chen, C. Wan, et al., arXiv, 2024, preprint, arXiv:2403.13427 DOI:10.48550/arXiv.2403.13427.
- L. Šmejkal, A. H. MacDonald, J. Sinova, S. Nakatsuji and T. Jungwirth, Nat. Rev. Mater., 2022, 7, 482–496 CrossRef.
- J. Han, R. Cheng, L. Liu, H. Ohno and S. Fukami, Nat. Mater., 2023, 1–12 Search PubMed.
- D.-F. Shao and E. Y. Tsymbal, npj Spintron., 2024, 2, 13 CrossRef.
- P. Khalili Amiri, C. Phatak and G. Finocchio, Annu. Rev. Mater. Res., 2024, 117–142 CrossRef CAS.
- H. Chen, L. Liu, X. Zhou, Z. Meng, X. Wang, Z. Duan, G. Zhao, H. Yan, P. Qin and Z. Liu, Adv. Mater., 2024, 2310379 CrossRef CAS PubMed.
- S. Tomiyoshi and Y. Yamaguchi, J. Phys. Soc. Jpn., 1982, 51, 2478–2486 CrossRef CAS.
- T. Nagamiya, S. Tomiyoshi and Y. Yamaguchi, Solid State Commun., 1982, 42, 385–388 CrossRef CAS.
- B. Gustafsson, H.-O. Kreiss and J. Oliger, Time dependent problems and difference methods, Wiley Online Library, 2013, vol. 2 Search PubMed.
- J. Kübler and C. Felser, Europhys. Lett., 2014, 108, 67001 CrossRef.
- A. K. Nayak, J. E. Fischer, Y. Sun, B. Yan, J. Karel, A. C. Komarek, C. Shekhar, N. Kumar, W. Schnelle and J. Kübler, et al. , Sci. Adv., 2016, 2, e1501870 CrossRef PubMed.
- H. Yang, Y. Sun, Y. Zhang, W.-J. Shi, S. S. Parkin and B. Yan, New J. Phys., 2017, 19, 015008 CrossRef.
- J. Kübler and C. Felser, Europhys. Lett., 2018, 120, 47002 CrossRef.
- C. Shekhar, A. K. Nayak, Y. Sun, M. Schmidt, M. Nicklas, I. Leermakers, U. Zeitler, Y. Skourski, J. Wosnitza and Z. Liu, et al. , Nat. Phys., 2015, 11, 645–649 Search PubMed.
- K. Kuroda, T. Tomita, M.-T. Suzuki, C. Bareille, A. Nugroho, P. Goswami, M. Ochi, M. Ikhlas, M. Nakayama and S. Akebi, et al. , Nat. Mater., 2017, 16, 1090–1095 CrossRef CAS PubMed.
- Y. Zhang, Y. Sun, H. Yang, J. Železný, S. P. Parkin, C. Felser and B. Yan, Phys. Rev. B, 2017, 95, 075128 CrossRef.
- Y. Yamane, O. Gomonay and J. Sinova, Phys. Rev. B, 2019, 100, 054415 CrossRef CAS.
- E. Krén, G. Kádár, L. Pál, J. Sólyom, P. Szabó and T. Tarnóczi, Phys. Rev., 1968, 171, 574 CrossRef.
- W. Feng, G.-Y. Guo, J. Zhou, Y. Yao and Q. Niu, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 144426 CrossRef.
- H. Kurt, K. Rode, M. Venkatesan, P. Stamenov and J. Coey, Phys. Status Solidi B, 2011, 248, 2338–2344 CrossRef CAS.
- B. Nyári, A. Deák and L. Szunyogh, Phys. Rev. B, 2019, 100, 144412 CrossRef.
- J. Seyd, I. Pilottek, N. Schmidt, O. Caha, M. Urbánek and M. Albrecht, J. Phys.: Condens. Matter, 2020, 32, 145801 CrossRef CAS PubMed.
- H. Tsai, T. Higo, K. Kondou, T. Nomoto, A. Sakai, A. Kobayashi, T. Nakano, K. Yakushiji, R. Arita and S. Miwa, et al. , Nature, 2020, 580, 608–613 CrossRef CAS PubMed.
- J. Liu and L. Balents, Phys. Rev. Lett., 2017, 119, 087202 CrossRef PubMed.
- N. Yamada, H. Sakai, H. Mori and T. Ohoyama, Physica B+C, 1988, 149, 311–315 CrossRef CAS.
- G. Gurung, D.-F. Shao and E. Y. Tsymbal, Phys. Rev. B, 2020, 101, 140405(R) CrossRef.
- S. Chen, P. Tong, J. Wu, W.-H. Wang and W. Wang, Comput. Mater. Sci., 2017, 132, 132–136 CrossRef CAS.
- H. Chen, Q. Niu and A. H. MacDonald, Phys. Rev. Lett., 2014, 112, 017205 CrossRef PubMed.
- S. Nakatsuji, N. Kiyohara and T. Higo, Nature, 2015, 527, 212–215 CrossRef CAS PubMed.
- W. Zhang, W. Han, S.-H. Yang, Y. Sun, Y. Zhang, B. Yan and S. S. Parkin, Sci. Adv., 2016, 2, e1600759 CrossRef PubMed.
- H. Narita, M. Ikhlas, M. Kimata, A. A. Nugroho, S. Nakatsuji and Y. Otani, Appl. Phys. Lett., 2017, 111, 202404 CrossRef.
- B. E. Zuniga-Cespedes, K. Manna, H. M. Noad, P.-Y. Yang, M. Nicklas, C. Felser, A. P. Mackenzie and C. W. Hicks, New J. Phys., 2023, 25, 023029 CrossRef.
- Z. Zhao, K. Zhang, Q. Guo and Y. Jiang, Phys. E, 2022, 138, 115141 CrossRef CAS.
- Z. Liu, H. Chen, J. Wang, J. Liu, K. Wang, Z. Feng, H. Yan, X. Wang, C. Jiang and J. Coey, et al. , Nat. Electron., 2018, 1, 172–177 CrossRef CAS.
- N. Kiyohara, T. Tomita and S. Nakatsuji, Phys. Rev. Appl., 2016, 5, 064009 CrossRef.
- L. Song, F. Zhou, H. Li, B. Ding, X. Li, X. Xi, Y. Yao, Y.-C. Lau and W. Wang, Adv. Funct. Mater., 2024, 2316588 CrossRef CAS.
- M. Ikhlas, T. Tomita, T. Koretsune, M.-T. Suzuki, D. Nishio-Hamane, R. Arita, Y. Otani and S. Nakatsuji, Nat. Phys., 2017, 13, 1085–1090 Search PubMed.
- G.-Y. Guo and T.-C. Wang, Phys. Rev. B, 2017, 96, 224415 CrossRef.
- M. Kimata, H. Chen, K. Kondou, S. Sugimoto, P. K. Muduli, M. Ikhlas, Y. Omori, T. Tomita, A. H. MacDonald and S. Nakatsuji, et al. , Nature, 2019, 565, 627–630 CrossRef CAS PubMed.
- K. Kondou, H. Chen, T. Tomita, M. Ikhlas, T. Higo, A. H. MacDonald, S. Nakatsuji and Y. Otani, Nat. Commun., 2021, 12, 6491 CrossRef CAS PubMed.
- B. K. Hazra, B. Pal, J.-C. Jeon, R. R. Neumann, B. Göbel, B. Grover, H. Deniz, A. Styervoyedov, H. Meyerheim and I. Mertig, et al. , Nat. Commun., 2023, 14, 4549 CrossRef CAS PubMed.
- J. Železný, Y. Zhang, C. Felser and B. Yan, Phys. Rev. Lett., 2017, 119, 187204 CrossRef PubMed.
- J. Dong, X. Li, G. Gurung, M. Zhu, P. Zhang, F. Zheng, E. Y. Tsymbal and J. Zhang, Phys. Rev. Lett., 2022, 128, 197201 CrossRef CAS PubMed.
- X. Chen, T. Higo, K. Tanaka, T. Nomoto, H. Tsai, H. Idzuchi, M. Shiga, S. Sakamoto, R. Ando and H. Kosaki, et al. , Nature, 2023, 613, 490–495 CrossRef CAS PubMed.
- P. Qin, H. Yan, X. Wang, H. Chen, Z. Meng, J. Dong, M. Zhu, J. Cai, Z. Feng and X. Zhou, et al. , Nature, 2023, 613, 485–489 CrossRef CAS PubMed.
- X. Wang, H. Chen, H. Yan, P. Qin, X. Zhou, Z. Meng, L. Liu, X. Liu, H. Wang and Z. Liu, Appl. Phys. Lett., 2023, 122, 152403 CrossRef CAS.
- J. Shi, S. Arpaci, V. Lopez-Dominguez, V. K. Sangwan, F. Mahfouzi, J. Kim, J. G. Athas, M. Hamdi, C. Aygen and H. Arava, et al. , Adv. Mater., 2024, 2312008 CrossRef CAS PubMed.
- T. Higo, H. Man, D. B. Gopman, L. Wu, T. Koretsune, O. M. van’t Erve, Y. P. Kabanov, D. Rees, Y. Li and M.-T. Suzuki, et al. , Nat. Photonics, 2018, 12, 73–78 CrossRef CAS PubMed.
- M. Wu, H. Isshiki, T. Chen, T. Higo, S. Nakatsuji and Y. Otani, Appl. Phys. Lett., 2020, 116, 132408 CrossRef CAS.
- T. Uchimura, J.-Y. Yoon, Y. Sato, Y. Takeuchi, S. Kanai, R. Takechi, K. Kishi, Y. Yamane, S. DuttaGupta and J. Ieda, et al. , Appl. Phys. Lett., 2022, 120, 172405 CrossRef CAS.
- M. Wu, T. Chen, T. Nomoto, Y. Tserkovnyak, H. Isshiki, Y. Nakatani, T. Higo, T. Tomita, K. Kondou and R. Arita, et al. , Nat. Commun., 2024, 15, 4305 CrossRef CAS PubMed.
- S. Sugimoto, Y. Nakatani, Y. Yamane, M. Ikhlas, K. Kondou, M. Kimata, T. Tomita, S. Nakatsuji and Y. Otani, Commun. Phys., 2020, 3, 111 CrossRef CAS.
- H. Reichlova, T. Janda, J. Godinho, A. Markou, D. Kriegner, R. Schlitz, J. Zelezny, Z. Soban, M. Bejarano and H. Schultheiss, et al. , Nat. Commun., 2019, 10, 5459 CrossRef PubMed.
- G. Q. Yan, S. Li, H. Lu, M. Huang, Y. Xiao, L. Wernert, J. A. Brock, E. E. Fullerton, H. Chen and H. Wang, et al. , Adv. Mater., 2022, 34, 2200327 CrossRef CAS PubMed.
- G. K. Krishnaswamy, G. Sala, B. Jacot, C.-H. Lambert, R. Schlitz, M. D. Rossell, P. Nöel and P. Gambardella, Phys. Rev. Appl., 2022, 18, 024064 CrossRef CAS.
- M.-W. Yoo, V. O. Lorenz, A. Hoffmann and D. G. Cahill, APL Mater., 2024, 12, 081107 CrossRef CAS.
- B. Pal, B. K. Hazra, B. Göbel, J.-C. Jeon, A. K. Pandeya, A. Chakraborty, O. Busch, A. K. Srivastava, H. Deniz and J. M. Taylor, et al. , Sci. Adv., 2022, 8, eabo5930 CrossRef CAS PubMed.
- T. Xu, H. Bai, Y. Dong, L. Zhao, H.-A. Zhou, J. Zhang, X.-X. Zhang and W. Jiang, APL Mater., 2023, 11, 071116 CrossRef CAS.
- Y. Takeuchi, Y. Yamane, J.-Y. Yoon, R. Itoh, B. Jinnai, S. Kanai, J. Ieda, S. Fukami and H. Ohno, Nat. Mater., 2021, 20, 1364–1370 CrossRef CAS PubMed.
- T. Higo, K. Kondou, T. Nomoto, M. Shiga, S. Sakamoto, X. Chen, D. Nishio-Hamane, R. Arita, Y. Otani and S. Miwa, et al. , Nature, 2022, 607, 474–479 CrossRef CAS PubMed.
- J.-Y. Yoon, P. Zhang, C.-T. Chou, Y. Takeuchi, T. Uchimura, J. T. Hou, J. Han, S. Kanai, H. Ohno and S. Fukami, et al. , Nat. Mater., 2023, 1–8 Search PubMed.
- A. Markou, J. Taylor, A. Kalache, P. Werner, S. Parkin and C. Felser, Phys. Rev. Mater., 2018, 2, 051001 CrossRef CAS.
- M. Ikhlas, S. Dasgupta, F. Theuss, T. Higo, S. Kittaka, B. Ramshaw, O. Tchernyshyov, C. Hicks and S. Nakatsuji, Nat. Phys., 2022, 18, 1086–1093 Search PubMed.
- H. Tsai, T. Higo, K. Kondou, S. Sakamoto, A. Kobayashi, T. Matsuo, S. Miwa, Y. Otani and S. Nakatsuji, Small Sci., 2021, 1, 2000025 Search PubMed.
- H. Tsai, T. Higo, K. Kondou, A. Kobayashi, T. Nakano, K. Yakushiji, S. Miwa, Y. Otani and S. Nakatsuji, AIP Adv., 2021, 11, 045110 Search PubMed.
- Y. Deng, X. Liu, Y. Chen, Z. Du, N. Jiang, C. Shen, E. Zhang, H. Zheng, H.-Z. Lu and K. Wang, Natl. Sci. Rev., 2023, 10, nwac154 Search PubMed.
- Z. Zheng, T. Zeng, T. Zhao, S. Shi, L. Ren, T. Zhang, L. Jia, Y. Gu, R. Xiao and H. Zhou, et al. , Nat. Commun., 2024, 15, 745 Search PubMed.
- H. Fujita, Phys. Status Solidi RRL, 2017, 11, 1600360 Search PubMed.
- A. Shukla and S. Rakheja, Phys. Rev. Appl., 2022, 17, 034037 Search PubMed.
- A. Shukla, S. Qian and S. Rakheja, APL Mater., 2023, 11, 091110 Search PubMed.
- P. Muduli, T. Higo, T. Nishikawa, D. Qu, H. Isshiki, K. Kondou, D. Nishio-Hamane, S. Nakatsuji and Y. Otani, Phys. Rev. B, 2019, 99, 184425 CrossRef CAS.
- D. Go, D. Jo, H.-W. Lee, M. Kläui and Y. Mokrousov, Europhys. Lett., 2021, 135, 37001 CrossRef CAS.
- B. A. Bernevig, T. L. Hughes and S.-C. Zhang, Phys. Rev. Lett., 2005, 95, 066601 CrossRef PubMed.
- V. T. Phong, Z. Addison, S. Ahn, H. Min, R. Agarwal and E. Mele, Phys. Rev. Lett., 2019, 123, 236403 CrossRef CAS PubMed.
- T. Tanaka, H. Kontani, M. Naito, T. Naito, D. S. Hirashima, K. Yamada and J.-I. Inoue, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 165117 CrossRef.
- H. Kontani, T. Tanaka, D. Hirashima, K. Yamada and J. Inoue, Phys. Rev. Lett., 2009, 102, 016601 CrossRef CAS PubMed.
- S. Bhowal and G. Vignale, Phys. Rev. B, 2021, 103, 195309 CrossRef CAS.
- S. Ding, A. Ross, D. Go, L. Baldrati, Z. Ren, F. Freimuth, S. Becker, F. Kammerbauer, J. Yang and G. Jakob, et al. , Phys. Rev. Lett., 2020, 125, 177201 CrossRef CAS PubMed.
- D. Jo, D. Go and H.-W. Lee, Phys. Rev. B, 2018, 98, 214405 CrossRef CAS.
- A. Shukla, S. Qian and S. Rakheja, J. Appl. Phys., 2024, 135, 123903 CrossRef CAS.
- Z. Xu, X. Zhang, Y. Qiao, G. Liang, S. Shi and Z. Zhu, Phys. Rev. B, 2024, 109, 134433 CrossRef CAS.
- L. Liu, T. Moriyama, D. Ralph and R. Buhrman, Phys. Rev. Lett., 2011, 106, 036601 CrossRef PubMed.
- R. Cheng, J. Xiao, Q. Niu and A. Brataas, Phys. Rev. Lett., 2014, 113, 057601 CrossRef CAS PubMed.
- H. Xie, X. Chen, Q. Zhang, Z. Mu, X. Zhang, B. Yan and Y. Wu, Nat. Commun., 2022, 13, 5744 CrossRef CAS PubMed.
- X. Li, S. Jiang, Q. Meng, H. Zuo, Z. Zhu, L. Balents and K. Behnia, Phys. Rev. B, 2022, 106, L020402 CrossRef CAS.
- R. L. Coffie, Characterizing and suppressing DC-to-RF dispersion in aluminum gallium nitride/gallium nitride high electron mobility transistors, University of California, Santa Barbara, 2003 Search PubMed.
- M. Meinert, D. Graulich and T. Matalla-Wagner, Phys. Rev. Appl., 2018, 9, 064040 CrossRef CAS.
- D. G. Cahill, Rev. Sci. Instrum., 1990, 61, 802–808 CrossRef CAS.
- S. Dasgupta and O. A. Tretiakov, Phys. Rev. Res., 2022, 4, L042029 CrossRef CAS.
- Y. Sato, Y. Takeuchi, Y. Yamane, J.-Y. Yoon, S. Kanai, J. Ieda, H. Ohno and S. Fukami, Appl. Phys. Lett., 2023, 122, 122404 CrossRef CAS.
- Y. Kobayashi, Y. Shiota, H. Narita, T. Ono and T. Moriyama, Appl. Phys. Lett., 2023, 122, 122405 CrossRef CAS.
- R. Koch, J. Katine and J. Sun, Phys. Rev. Lett., 2004, 92, 088302 CrossRef CAS PubMed.
- S. Miwa, S. Iihama, T. Nomoto, T. Tomita, T. Higo, M. Ikhlas, S. Sakamoto, Y. Otani, S. Mizukami and R. Arita, et al. , Small Sci., 2021, 1, 2000062 CrossRef CAS.
- G. Vallejo-Fernandez, N. Aley, J. Chapman and K. O’Grady, Appl. Phys. Lett., 2010, 97, 222505 CrossRef.
- S. Jenkins, R. W. Chantrell, T. J. Klemmer and R. F. Evans, Phys. Rev. B, 2019, 100, 220405 CrossRef CAS.
- T. Matsuo, T. Higo, D. Nishio-Hamane and S. Nakatsuji, Appl. Phys. Lett., 2022, 121, 013103 CrossRef CAS.
- T. Taniguchi and H. Imamura, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 054432 CrossRef.
- D. Pinna, A. Mitra, D. L. Stein and A. D. Kent, Appl. Phys. Lett., 2012, 101, 262401 CrossRef.
- D. Go, M. Sallermann, F. R. Lux, S. Blügel, O. Gomonay and Y. Mokrousov, Phys. Rev. Lett., 2022, 129, 097204 CrossRef CAS PubMed.
- C. Bean and U. D. Livingston, J. Appl. Phys., 1959, 30, S120–S129 CrossRef.
- L. Lopez-Diaz, L. Torres and E. Moro, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65, 224406 CrossRef.
- J. Richardson, D. Yiagas, B. Turk, K. Forster and M. Twigg, J. Appl. Phys., 1991, 70, 6977–6982 CrossRef CAS.
- C. Flipse, C. Rouwelaar and F. De Groot, Eur. Phys. J. D, 1999, 9, 479–481 CrossRef CAS.
- K. Wu, D. Su, J. Liu, R. Saha and J.-P. Wang, Nanotechnology, 2019, 30, 502003 CrossRef CAS PubMed.
- D. Vodenicarevic, N. Locatelli, A. Mizrahi, J. S. Friedman, A. F. Vincent, M. Romera, A. Fukushima, K. Yakushiji, H. Kubota and S. Yuasa, et al. , Phys. Rev. Appl., 2017, 8, 054045 CrossRef.
- P. Debashis, R. Faria, K. Y. Camsari and Z. Chen, IEEE Magn. Lett., 2018, 9, 1–5 Search PubMed.
- K. Y. Camsari, P. Debashis, V. Ostwal, A. Z. Pervaiz, T. Shen, Z. Chen, S. Datta and J. Appenzeller, Proc. IEEE, 2020, 108, 1322–1337 CAS.
- W. T. Coffey and Y. P. Kalmykov, J. Appl. Phys., 2012, 112, 121301 CrossRef.
- L. Rózsa, S. Selzer, T. Birk, U. Atxitia and U. Nowak, Phys. Rev. B, 2019, 100, 064422 CrossRef.
- K. Hayakawa, S. Kanai, T. Funatsu, J. Igarashi, B. Jinnai, W. Borders, H. Ohno and S. Fukami, Phys. Rev. Lett., 2021, 126, 117202 CrossRef CAS PubMed.
- J. Zhou and J. Chen, Adv. Electron. Mater., 2021, 7, 2100465 CrossRef CAS.
- D. Kumar, H. J. Chung, J. Chan, T. Jin, S. T. Lim, S. S. Parkin, R. Sbiaa and S. Piramanayagam, ACS Nano, 2023, 17, 6261–6274 CrossRef CAS PubMed.
- S. Fukami and H. Ohno, J. Appl. Phys., 2018, 124, 151904 CrossRef.
- A. Parthasarathy, E. Cogulu, A. D. Kent and S. Rakheja, Phys. Rev. B, 2021, 103, 024450 CrossRef CAS.
- K. Roy, C. Wang, S. Roy, A. Raghunathan, K. Yang and A. Sengupta, Nat. Rev. Electr. Eng., 2024, 1–16 Search PubMed.
- A. Sengupta and K. Roy, Phys. Rev. Appl., 2016, 5, 024012 CrossRef.
- J. Liu, T. Xu, H. Feng, L. Zhao, J. Tang, L. Fang and W. Jiang, Adv. Funct. Mater., 2022, 32, 2107870 CrossRef CAS.
- Y. Park, M.-K. Kim and J.-S. Lee, J. Mater. Chem. C, 2020, 8, 9163–9183 RSC.
- C. Wang, A. Agrawal, E. Yu and K. Roy, Front. Neurosci., 2021, 15, 661667 CrossRef PubMed.
- K. Yamazaki, V.-K. Vo-Ho, D. Bulsara and N. Le, Brain Sci., 2022, 12, 863 CrossRef PubMed.
- D. E. Nikonov and I. A. Young, IEEE J. Explor. Solid-State Comput. Devices Circuits, 2019, 5, 75–84 Search PubMed.
- R. Khymyn, I. Lisenkov, V. Tiberkevich, B. A. Ivanov and A. Slavin, Sci. Rep., 2017, 7, 43705 CrossRef PubMed.
- R. Khymyn, I. Lisenkov, J. Voorheis, O. Sulymenko, O. Prokopenko, V. Tiberkevich, J. Akerman and A. Slavin, Sci. Rep., 2018, 8, 15727 CrossRef PubMed.
- H. Bradley, S. Louis, C. Trevillian, L. Quach, E. Bankowski, A. Slavin and V. Tyberkevych, AIP Adv., 2023, 13, 015206 CrossRef CAS.
- H. Bradley, S. Louis, A. Slavin and V. Tyberkevych, Sci. Rep., 2024, 14, 22373 CrossRef CAS PubMed.
- H. Bradley, L. Quach, S. Louis and V. Tyberkevych, 2023 IEEE International Magnetic Conference-Short Papers (INTERMAG Short Papers), 2023, pp. 1–2.
- H. Bradley, L. Quach, S. Louis and V. Tyberkevych, J. Comput. Neurosci., 2024, 52, 197–206 CrossRef PubMed.
- O. Sulymenko, O. Prokopenko, I. Lisenkov, J. Åkerman, V. Tyberkevych, A. N. Slavin and R. Khymyn, J. Appl. Phys., 2018, 124, 152115 CrossRef.
- G. Csaba and W. Porod, Appl. Phys. Rev., 2020, 7, 011302 CAS.
- E. Cruz-Camacho, S. Qian, A. Shukla, N. McGlohon, S. Rakheja and C. Carothers, ACM Trans. Model. Comput. Simul., 2024 DOI:10.1145/3649464.
- Invited Paper: A materials- and devices-centric approach to neuromorphic computing, 2024.
- G. Srinivasan, A. Sengupta and K. Roy, Design, Automation & Test in Europe Conference & Exhibition (DATE), 2017, 2017, pp. 530–535.
- M.-C. Chen, A. Sengupta and K. Roy, IEEE Trans. Magn., 2018, 54, 1–7 Search PubMed.
- D. Ielmini and S. Ambrogio, Nanotechnology, 2019, 31, 092001 CrossRef PubMed.
- H. Clasun, S. Resch, Z. I. Chowdhury, E. Olson, M. Zabihi, Z. Zhao, T. Peterson, K. K. Parhi, J.-P. Wang and S. S. Sapatnekar, et al. , ACM Trans. Archit. Code Optim., 2021, 18, 1–21 CrossRef.
- P. Debashis, H. Li, D. Nikonov and I. Young, IEEE Magn. Lett., 2022, 13, 1–5 Search PubMed.
- O. Sulymenko, O. Prokopenko, V. Tiberkevich, A. Slavin, B. Ivanov and R. Khymyn, Phys. Rev. Appl., 2017, 8, 064007 CrossRef.
- T. Chen, R. K. Dumas, A. Eklund, P. K. Muduli, A. Houshang, A. A. Awad, P. Dürrenfeld, B. G. Malm, A. Rusu and J. Åkerman, Proc. IEEE, 2016, 104, 1919–1945 Search PubMed.
- Y. He, B. Luo and N.-X. Sun, IEEE J. Microwaves, 2021, 1, 908–929 Search PubMed.
- C. Liu, T. Shen, H.-B. Wu, Y. Feng and J.-J. Chen, Opt. Fiber Technol., 2021, 65, 102634 CrossRef CAS.
- O. R. Sulymenko, O. V. Prokopenko, V. S. Tyberkevych and A. N. Slavin, IEEE Magn. Lett., 2018, 9, 1–5 Search PubMed.
- O. Gomonay, T. Jungwirth and J. Sinova, Phys. Rev. B, 2018, 98, 104430 CrossRef CAS.
- O. Sulymenko and O. Prokopenko, 2018 IEEE 17th International Conference on Mathematical Methods in Electromagnetic Theory (MMET), 2018, pp. 322–325.
- P. Y. Artemchuk, O. Sulymenko, S. Louis, J. Li, R. Khymyn, E. Bankowski, T. Meitzler, V. Tyberkevych, A. Slavin and O. Prokopenko, J. Appl. Phys., 2020, 127, 063905 CrossRef CAS.
- D.-Y. Zhao, P.-B. He and M.-Q. Cai, Phys. Rev. B, 2021, 104, 214423 CrossRef CAS.
- M. A. Lund, D. R. Rodrigues, K. Everschor-Sitte and K. M. Hals, Phys. Rev. Lett., 2023, 131, 156704 CrossRef CAS PubMed.
- S. Hu, C. Zheng, C. Chen, Y. Zhou and Y. Liu, Phys. Rev. B, 2024, 109, 174433 CrossRef CAS.
- D. Hamara, G. F. Lange, F. N. Kholid, A. Markou, C. Felser, R.-J. Slager and C. Ciccarelli, Commun. Phys., 2023, 6, 320 CrossRef CAS.
- T. Matsuda, N. Kanda, T. Higo, N. Armitage, S. Nakatsuji and R. Matsunaga, Nat. Commun., 2020, 11, 909 CrossRef CAS PubMed.
- A. Sebastian, M. Le Gallo, R. Khaddam-Aljameh and E. Eleftheriou, Nat. Nanotechnol., 2020, 15, 529–544 CrossRef CAS PubMed.
- S. Bavikadi, P. R. Sutradhar, K. N. Khasawneh, A. Ganguly and S. M. Pudukotai Dinakarrao, Proceedings of the 2020 on Great Lakes Symposium on VLSI, 2020, pp. 89–94.
- K. Byun, I. Choi, S. Kwon, Y. Kim, D. Kang, Y. W. Cho, S. K. Yoon and S. Kim, Adv. Mater. Technol., 2023, 8, 2200884 CrossRef CAS.
- G. W. Burr, R. M. Shelby, A. Sebastian, S. Kim, S. Kim, S. Sidler, K. Virwani, M. Ishii, P. Narayanan and A. Fumarola, et al. , Adv. Phys.:X, 2017, 2, 89–124 Search PubMed.
- S. Hu, D.-F. Shao, H. Yang, C. Pan, Z. Fu, M. Tang, Y. Yang, W. Fan, S. Zhou and E. Y. Tsymbal, et al. , Nat. Commun., 2022, 13, 4447 CrossRef CAS PubMed.
- X. Li, Z. Zhu and K. Behnia, Adv. Mater., 2021, 33, 2100751 CrossRef CAS PubMed.
- H. Tanaka, T. Higo, R. Uesugi, K. Yamagata, Y. Nakanishi, H. Machinaga and S. Nakatsuji, Adv. Mater., 2023, 35, 2303416 CrossRef CAS PubMed.
- T. Yu, H. Wu, H. He, C. Guo, C. Fang, P. Zhang, K. L. Wong, S. Xu, X. Han and K. L. Wang, APL Mater., 2021, 9, 041111 CrossRef CAS.
- E. Grumbling and M. Horowitz, Quantum Computing: Progress and Prospects, The National Academies Press, Washington, DC, 2019 Search PubMed.
- M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information, Cambridge University Press, 2010 Search PubMed.
- R. Cai, I. Žutić and W. Han, Adv. Quantum Technol., 2023, 6, 2200080 CrossRef CAS.
- F. Bergeret, A. F. Volkov and K. B. Efetov, Rev. Mod. Phys., 2005, 77, 1321 CrossRef CAS.
- I. Lyuksyutov and V. Pokrovsky, Adv. Phys., 2005, 54, 67–136 CrossRef.
- K.-R. Jeon, B. K. Hazra, J.-K. Kim, J.-C. Jeon, H. Han, H. L. Meyerheim, T. Kontos, A. Cottet and S. S. Parkin, Nat. Nanotechnol., 2023, 18, 747–753 CrossRef CAS PubMed.
- D. Xiao, M.-C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959 CrossRef CAS.
- J. Linder and J. W. Robinson, Nat. Phys., 2015, 11, 307–315 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00045e |
| This journal is © The Royal Society of Chemistry 2025 |