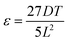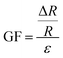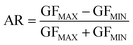Giant anisotropic piezoresponse of layered ZrSe₃

Abstract

We investigated the effect of uniaxial strain on the electrical properties of few-layer ZrSe₃ devices under compressive and tensile strains applied up to ±0.62% along different crystal directions. We observed that the piezoresponse, the change in resistance upon application of strain, of ZrSe₃ strongly depends on both the direction in which electrical transport occurs and the direction in which uniaxial strain is applied. Notably, a remarkably high anisotropy in the gauge factor for a device with the transport occurring along the b-axis of ZrSe₃ with GF = 68 when the strain is applied along the b-axis was obtained, and GF = 4 was achieved when strain is applied along the a-axis. This leads to an anisotropy ratio of almost 90%. Devices whose transport occurs along the a-axis, however, show much lower anisotropy in gauge factors when strain is applied along different directions, leading to an anisotropy ratio of 50%. Furthermore, ab initio calculations of strain dependent change in resistance showed the same trends of the anisotropy ratio as obtained from experimental results for both electrical transport and strain application directions, which were correlated with bandgap changes and different orbital contributions.

---

New concepts

Transition metal trichalcogenides (TMTCs) are among several 2D materials that exhibit a strong in-plane anisotropic structure with quasi-1D electrical and optical properties owing to their reduced in-plane structural symmetry. ZrSe₃ is one of the TMTC representatives recently reported to have a large anisotropy of optical and thermal properties, yet its other properties are only theoretically investigated. Herein, we report the giant anisotropic piezoresponse of ZrSe₃ devices by studying the strain tunable electrical resistance of the fabricated devices under compressive and tensile strains along different crystal directions. We observed that piezoresponse strongly depends on both the direction along which electrical transport occurs and the direction along which uniaxial strain is applied, which was supported by the performed ab initio simulations. The highest anisotropy ratio for a device with transport along the b-axis of ZrSe₃, s gauge factor GF_b-axis of 68 was obtained, while GF_a-axis was 4 when tensile strain was applied along the a-axis. This leads to an exceptionally high AR of ≈90%, which is the highest reported value for electrical properties of 2D materials to the best of our knowledge. Our results emphasize the potential of in-plane anisotropic 2D materials for future flexible electronic devices.

Introduction

Two-dimensional (2D) materials possess intrinsic anisotropy by virtue of their strong in-plane covalent bonds and weak out-of-plane van der Waals interactions.¹ Depending on their crystal structure, some have an additional degree of symmetry, resulting in in-plane anisotropy.² 2D in-plane anisotropic materials exhibit unique physical phenomena such as anisotropic plasmons and linear dichroism, compelling scientific research. The pronounced representatives of anisotropic materials include black phosphorus (BP), ReS₂ and TiS₃.^3–6 Notably, the additional degree of freedom in tailoring the physical properties of anisotropic materials can be utilized to develop selective semiconductor devices. For instance, high mobility transistors can be achieved via reduced backscattering of hot electron inverters.⁷ Furthermore, there have been various reports on exploiting their anisotropy for application in digital inverters and utilization of their anisotropic thermoelectric effects.^8,9 Most interestingly, these materials have great potential in optoelectronic devices such as polarization-sensitive photodetectors and generators of linearly-polarized pulses, which are based on generating or detecting polarized light.^4,10–13

The family of in-plane anisotropic 2D materials consists mainly of layered materials with low-symmetry crystal systems such as orthorhombic, monoclinic, and triclinic structures. These materials can be simple-to-complex structures including BP, transition metal monochalcogenides and trichalcogenides, low-symmetry metal chalcogenides and group IV and V compounds.¹⁴ Among these materials, transition metal trichalcogenides (TMTCs) with the general formula MX₃, where M is the transition metal Ti or Zr and X is S, Se or Te, exhibit a strong in-plane anisotropic structure and thermal conductivity, along with quasi-1D electrical and optical properties, owing to their reduced in-plane structural symmetry.^15,16 MX₃ monolayers exhibit distinct structural and bonding characteristics along the a and b lattice directions. Notably, the valence band maximum (VBM) and conduction band minimum (CBM) of crystal orbitals are oriented spatially in different directions, resulting in highly anisotropic effective masses for both electrons and holes. Based on first-principles calculations, the electron and hole effective masses show entirely different anisotropy, i.e., electrons and holes prefer to be conducted in different directions. As the CBM is located at the B point, triselenides like ZrSe₃ demonstrate a small electron mass perpendicular to the chains of triangular MX₃ prisms, facilitating more accessible electron transport along the a-direction.¹⁵

Our previous work demonstrated high anisotropic strain-tunability of few-layer ZrSe₃ optical properties, investigating the effect of uniaxial strain applied along different crystalline orientations on the micro-reflectance spectra of ZrSe₃. We observed that the strain induced blueshift of the excitonic features strongly depends on the direction of the tension: 60–95 meV %⁻¹ tension along the b-axis and only 0–15 meV %⁻¹ along the a-axis.¹⁷ Moreover, previous reports based on DFT calculations suggested that the indirect bandgaps of ZrSe₃ monolayers increase with the applied tensile strain.¹⁸

Among the array of approaches to tune 2D material properties, applying strain emerges as a promising avenue, as they can withstand substantial deformation without fracturing due to their strong in-plane bonds and small thickness.^19,20 There are many ways to induce strain in 2D materials such as in situ application of strain in the substrate caused by lattice mismatch during growth and external application of the strain after growth.^21–23 Most common straining method in 2D material analysis relies on the mechanical deformation of the flexible substrate upon which the 2D material to be investigated is placed. Here in, the strain in 2D materials can be induced by stretching or bending the substrate, transferring mechanical deformation to the 2D material from its surface.^24,25 Depending on whether the substrate is deformed along one or two axes, uniaxial or biaxial strain is induced in 2D materials, respectively.²⁶

In this work, we have demonstrated a giant strain-tunable anisotropic effect on the piezoresponse, the change of resistance upon strain, of ZrSe₃. A uniaxial tensile and compressive strain was applied along different orientations, which resulted in reversible modification of the ZrSe₃ resistance upon change in strain. The most significant change of the resistance was observed for a device with the electrical transport occurring along the b-axis when the tensile strain was along the b-axis (GF = 68). Remarkably, when the strain was applied along the a-axis on the same device, the GF reached only 4.

Results and discussion

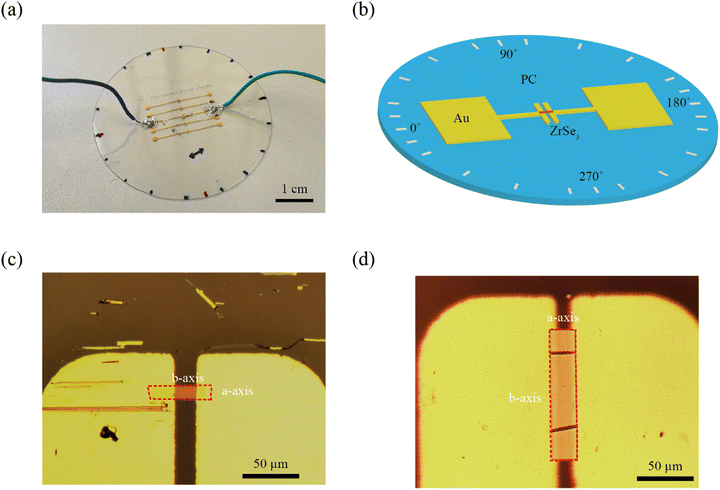
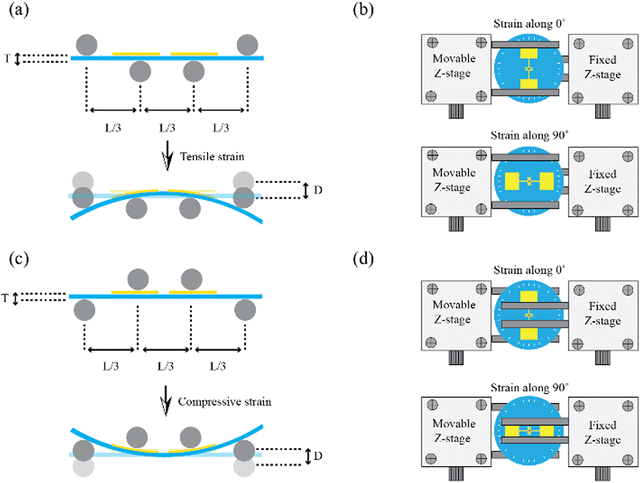
We have designed a specialized apparatus consisting of a four-point bending mechanism for angle-dependent uniaxial strain testing.^17,27 This apparatus allows the application of both tensile and compressive strains on ZrSe₃ device fabricated on top of a flexible polycarbonate (PC) substrate by simply bending the substrate. The fabrication process started with the mechanical exfoliation of a ZrSe₃ bulk crystal (HQ graphene) using Nitto tape SPV 224. The cleaved crystals are then transferred to a Gel-Film WF ×4 6.0 mil (by Gel-Pack) viscoelastic stamp. The surface of the stamp is inspected with transmission mode optical microscopy to select suitable ZrSe₃ flakes based on their high transmittance. Further, Raman spectroscopy was performed to identify the crystalline orientations of the target flake (Fig. S1, ESI†). It could be clearly observed that the characteristic peak A⁶_g (near 230 cm⁻¹) and A⁸_g (near 300 cm⁻¹) reached a maximum when polarized laser aligned perpendicular to the long-cleaved edge of the flake, corresponding to the b-axis crystalline orientation.²⁸ Subsequently, the selected flakes were transferred with a dry transfer method and place them between two electrodes (20 μm channel) pre-patterned onto a PC substrate. A 250 μm thick disk-shaped PC was marked with a permanent marker to indicate different angles for strain application, as shown in Fig. 1(a). First, the strain was applied parallel to the channel conduction direction, which was marked with 0°. Gradually, the disc was rotated and measurements were taken at an interval of 20° rotation along with additional measurements at 10°, 90°, 170°, 190°, 270°, and 350°. Fig. 1(b) depicts a device with ZrSe₃ flake whose b-axis is arranged parallel to the channel conduction direction.

Fig. 1 Sample configuration. (a) A sample photography of a circular PC with patterned pairs of electrodes connected to SMU via macroscopic wires. (b) Illustration of the test sample: a disk-shaped PC substrate is marked at 10° and 20° intervals using a permanent marker, covering angles from 0° to 360°, with 0° (direction parallel to the drain–source electrical transport) indicated by a red line. Following this, an exfoliated ZrSe₃ strip is precisely transferred onto the center of the disk-shaped substrate, positioned between the two Au electrodes, using a dry deterministic placement method. (c) An optical microscopy image of a sample with ZrSe₃b-axis across the channel as indicated with the red-dashed rectangle. (d) An optical microscopy image of a sample with ZrSe₃a-axis across the channel as indicated with the red-dashed rectangle.

As established from our previous work, the ZrSe₃ flakes are highly brittle at the direction perpendicular to the b-axis, making them tend to crack along the a-axis (shorter side of the ribbon-shaped flakes).¹⁷ The present work used flakes around 15 nm thick, with a side along the a-axis (width) around 30 μm and a side along the b-axis (length) above 100 μm, as determined by optical microscopy.¹⁷ The devices were fabricated with b-axis bridging the electrodes, as shown in Fig. 1(c), and a-axis bridging the electrodes, as shown in Fig. 1(d). For both configurations, electrical transport between electrodes with applied uniaxial tensile/compressive strains along different crystal directions were measured.

The developed four-point bending setup is designed with a loading span equal to one-third of the support span, as depicted in Fig. 2(a) and (c), which illustrate the schematic of applying tensile and compressive strains, respectively. Strain (ε) in both cases is calculated using the deflection (D) and thickness (T) of the substrate, following the relation

where the support span (L) is the distance between the two outer pillars.²⁹ In our previous work, we have determined excellent correspondence of the strain values derived from the aforementioned continuum mechanics formula using the values obtained from optical microscopy by measuring strain induced displacement of photoresist micropillars patterned on the PC substrate.²⁷ Thus, by accurately controlling the deflection of the outer pillars, tensile or compressive strain can be induced depending on whether the PC disk-shaped substrate is positioned above or below the inner pillars, as shown in Fig. 2(b) and (d), respectively. In strain-tunable material tests, the gauge factor serves as a metric for assessing how specific properties change under strain. Specifically, resistance gauge factor (GF_R) quantifies the ratio of the relative change in electrical resistance (ΔR) to the 1% of the mechanical strain (ε), expressed as
Here, ΔR refers to the change in strain gauge resistance caused by axial strain.

Fig. 2 Schematics of the strain application. (a) Cross-section illustration of the uniaxial tensile strain application with a four-point bending setup. (b) Top-view illustration of the four-point bending setup used for the tensile strain engineering experiments with a disk-shaped ZrSe₃ flexible device loaded between the pivotal points with configurations of strain applied at 0° (parallel with the drain–source direction) and 90° (perpendicular to the drain–source direction). (c) Cross-section illustration of uniaxial compressive strain application with a four-point bending setup. (d) Top-view illustration of the four-point bending setup used for the compressive strain engineering experiments with a disk-shaped ZrSe₃ flexible device loaded between pivotal points with configurations of strain applied at 0° (parallel with the drain–source direction) and 90° (perpendicular to the drain–source direction).

The effect of uniaxial tensile strain along different directions with the b-axis aligned along the drain–source electrical transport direction for the sample is shown in Fig. 1(c). The current vs. voltage (IVs hereafter) characteristics for different uniaxial strain levels were measured up to 0.62% in the dark (to avoid changes in resistance induced by photocurrent generation). The first set of IVs were acquired while the strain is applied parallel to the drain–source transport direction (labelled as 0°), which in this sample occurs along the b-axis. Fig. 3(a) shows the set of IVs acquired when different uniaxial tension levels are applied along the drain–source direction. The electrical resistance can be readily determined from the slope of the IVs, allowing us to determine the strain-induced change in resistance (i.e. the piezoresponse, ΔR/R₀). Fig. 3(b) summarizes the strain dependent change in resistance when the uniaxial tension is applied along different directions spanning from 0° (parallel to the drain–source and b-axis direction) to 90° (perpendicular to the drain–source direction and parallel to the a-axis). Interestingly, the piezoresponse was observed to strongly depend on the direction along which uniaxial tension is applied. In order to get a better picture of this strong anisotropy, strain tunable IVs for uniaxial tensile strain applied along 24 different directions from 0° to 360° was acquired. Although the measurements were on relatively small strain values, the high number of bending cycles of non-encapsulated samples can lead to strain-induced damage. Considering that, we closely monitored resistance to detect sudden shifts to eliminate material slippage or defects such as cracks and wrinkles. Furthermore, the reproducibility test outcomes from our previous work using reflectance spectroscopy suggested that the strain transfer is adequate and do not induce any critical damage to the ZrSe₃ devices after successive bendings.^17,27Fig. 3(c) shows the dependence of the piezoresponse gauge factor (obtained directly from the slope of the linear relationship between the piezoresponse and the strain, shown in Fig. 3(b)) on the direction of applied uniaxial tension. The strain applied along the b-axis resulted in maximum GF_Tb-axis = 68, while that applied along perpendicular direction resulted in minimum GF_Ta-axis = 4, contributing to a anisotropy ratio AR_T = 89%, calculated with relation

shows subsequently, the compressive uniaxial strain from 0% to −0.62% is applied instead tensile strain on the same device (Fig. 3) and results obtained are shown in ESI,† Fig. S2. In this case, the resistance decreased upon increasing strain, and a maximum GF of GF_Cb-axis = −44 when the strain is applied along the b-axis and minimum of GF_Ca-axis = −10 with the strain along the a-axis. Thus, the anisotropy ratio is obtained to be AR_C = 63%. The applied tensile strain shifts the bandgap to higher energy levels in ZrSe₃, decreasing the conductance. On the other hand, application of compressive strain shifts the bandgap to lower energy levels, thereby enhancing conductance. Thus, the strain-induced anisotropy can be due to the diverse effects of strain on the band structure of ZrSe₃ along different crystalline orientations, resulting in a polarized bandgap tuning.¹⁷ Interestingly, when the experiments shown in Fig. 3 and Fig. S2 (ESI†) are repeated with the device shown in Fig. 1(d) by aligning a-axis parallel to the drain–source electrical transport direction, the observed gauge factors and anisotropy in the piezoresponse gauge factors measured for strain along different directions are sizeably lower (AR ∼ 50%). The results obtained with this configuration are presented in Fig. S3 and S4 (ESI†). Table 1 summarizes the piezoresponse gauge factors and anisotropies obtained in the different configurations. The data reported are measured on two different devices, one with a-axis parallel to drain–source transport and the other with b-axis. In comparison, other 2D materials known for anisotropic properties have notably smaller piezoresponse anisotropy. For instance, BP exhibits almost isotropic piezoresponse while TiS₃ and ReS₂ have opposite piezoresponse with several times smaller absolute values gauge factor ratio than our results.^30–32

Fig. 3 Anisotropic piezoresponse under tensile strain for the b-axis over electrode configuration. (a) IV curves of the ZrSe₃ device under different tensile strains applied along 0°, i.e. the b-axis. The current decreases as the resistance increases on the higher amount of the uniaxial tensile strain. (b) The ratio of the relative change of the resistance vs. applied tensile strain along different directions. The change in electrical resistance is the most significant when the strain is applied along the 0°, i.e. the b-axis and decreases gradually on a minimum value when the strain is applied along 90° – i.e. the a-axis. The gauge factor is represented as the slope of the linear fitted lines. (c) Polar plot of the gauge factor changes as a function of rotating angle from 0° to 360°. 0° means strain parallel to the b-axis, and 90° means strain perpendicular to the b-axis.

Table 1 Summary of the determined gauge factors and anisotropy ratios for different device configurations and types of strain applied

Device configuration	Strain applied	GFMAX	GFMIN	AR (%)
B-axis parallel to drain–source transport (Fig. 3)	Tensile	68	4	89
B-axis parallel to drain–source transport (Fig. S2, ESI)	Compressive	−44	−10	64
A-axis parallel to drain–source transport (Fig. S3, ESI)	Tensile	45	15	50
A-axis parallel to drain–source transport (Fig. S4, ESI)	Compressive	−24	−8	50

---

In addition, Raman spectroscopy was performed with the tensile strain applied along and perpendicular to the b-axis and the results revealed an anisotropic ZrSe₃ nature. As shown in Fig. S5 (ESI†), with increasing strain, the Raman peak of modes A⁵_g, A⁶_g, and A⁸_g exhibit clear red shifts. The shift for all three modes is more pronounced when the strain is applied along the b-axis than that applied perpendicular to the b-axis. These observations are well in agreement with our findings that the strain along the b-axis strongly modulates ZrSe₃ properties, while the strain along the a-axis results in significantly smaller results.

To support the evidence of a strong anisotropy in the GF, ab initio calculations were performed to evaluate the electrical resistance as a function of the applied external strain. In this case, we have used the Boltzmann transport equation in the constant relaxation time approximation (cRTA) to calculate the transport coefficients. Although cRTA might provide inaccurate results, the general trend with the external parameters remains similar to more refined approximations. Additionally, due to the limitation of ab initio methods in evaluating the electronic gap and the electrical resistance, the quantitative agreement cannot be achieved. However, the numerical approach can provide qualitative insight into the behavior of device.^33,34

The ab initio calculations were performed using the Quantum Espresso suite.³⁵ We have built over the calculations performed to evaluate the optical response to strain in the same materials; thus, further details of the numerical parameters can be found there.¹⁷ Once the atomic positions have been defined, the positions were optimized by reducing the relative atomic forces between any atomic pair. The residual forces were found to be below 0.025 eV Å⁻¹ (10⁻³ a.u.). At this stage, residual pressure is reduced to obtain the optimal lattice constants. All calculations were performed using optimized norm conserving Vanderbilt pseudopotentials and a Monkhorst–Pack uniform mesh of 10 × 10 × 10 points with an energy cut-off of 800 eV.³⁶ The Grimme D2 correction was utilized to treat the weak van der Waals force between layers.³⁵ The transport coefficients were evaluated by coupling the BoltzTraP2 code with the output of the Quantum Espresso calculations. The accurate evaluation of the electronic velocities from BoltzTraP2 can be obtained by performing a non-self-consistent calculation with a fine uniform mesh, which was set at 40 × 40 × 40.³⁷ The application of uniaxial strain was either along the a-axis or b-axis. Based on the Poisson effect, the Poisson's coefficient of 0.244 was obtained when the strain is applied along a-axis and 0.017 when applied along b-axis.³⁸

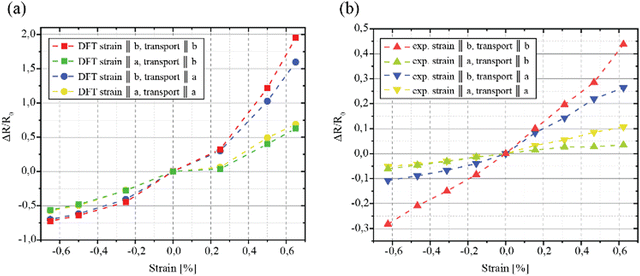
Fig. 4(a) reports the calculation results of the strain dependent change in resistance for uniaxial strain along the a-axis and b-axis, and for both directions of electrical transport. As shown in Fig. 4(b), summarized experimental data shows an excellent qualitative agreement with our results. Firstly, it is evident that the resistance increases with tensile strain, while it reduces with compressive strain. This can be correlated with the change in the (indirect) electronic band gap under strain. The band gap increases with increasing the amount of tensile strain and decreases with increasing compressive strain. Secondly, both experimental calculations of compression and tensile strains show that the piezoresponse is higher when the strain is applied along the b-axis than the a-axis. These observations are in agreement with our previous calculations, see H. Li et al.,¹⁷ where we have analyzed the contribution to the band structure by the different atoms to understand the anisotropic behavior of ZrSe₃. The reports suggested that the Zr d_xy and d_yz orbitals mainly determine conduction bands around its minimum and the Γ point is close to the Fermi energy. Therefore, it clearly indicates that deforming the unit cell along the b-axis might have a more significant impact, since it modifies the bonds containing the d_xy and d_yz orbitals, which contribute to the energy level around the Fermi energy. At the same time, a deformation along a-axis would affect the d_xz orbital, which only contributes at large energy. The same deformation would also deform the d_xy state but this contribution alone seems less efficient in changing the electrical conductance. Although the strain-tuned optical band gap (direct transition) was investigated in previous work, this work is based on electronic band gap (indirect transition) regulation under strain. Therefore, applying the same analogy, the stronger response of ZrSe₃ devices when strain applied along the b-axis can be better understood. Notably, ΔR is also higher for the devices with electrical transport along the b-axis, both in calculations and experimental results. In addition to quantitative difference (GF derived from calculations are almost five times higher), the variations between the experimental calculations upon compressive strain were also investigated. This discrepancy might have roots in the inaccuracy of the cRTA implied in evaluating the resistivity through the solution of the Boltzmann transport equation.

Fig. 4 Comparison of ab initio calculation with experimental piezoresponse results under tension (positive strain) and compression (negative stain). (a) The ab initio calculations on a ratio of the relative change in resistance vs. applied strain. Data expressed with squares represent electrical transport along the b-axis, and circles represent along the a-axis. Red and blue correspond to strain along the b-axis, while green and yellow correspond to strain along the a-axis. (b) Experimental results on a ratio of the relative change in resistance vs. applied strain. Data expressed with up-faced triangles represent electrical transport along the b-axis, and down-faced triangles represent along the a-axis. Red and blue correspond to strain along the b-axis, while green and yellow correspond to strain along the a-axis.

Conclusions

In conclusion, the effect of tensile and compressive uniaxial strain applied along different crystal directions on the electrical resistance (the so-called piezoresistance or piezoresponse) of few-layer ZrSe₃ is reported. A giant anisotropy in the piezoresponse for devices whose b-axis is aligned parallel to the drain–source electrical transport direction was observed. The gauge factor of ∼65 was obtained when tensile strain is also applied along the b-axis and only ∼5 when the strain is applied along the a-axis, yielding an anisotropy ratio of almost 90%. Interestingly, the devices whose transport occurs along the a-axis show lower gauge factors and also lower anisotropy of ∼50%. Further, systematically higher gauge factor values were observed for tensile strain as compared to compressive straining experiments. The ab initio calculations of ZrSe₃ piezoresponse showed excellent qualitative agreement with our experimental data. Conclusively, these results show that ZrSe₃ has a selective reactiveness to the strain, which demonstrates the significant potential of in-plane anisotropic 2D materials for future flexible electronic devices.

Author contributions

They fabricated all devices and measured experimental data while R. D. performed ab initio calculations and A. C.-G. supervised the experiments and secured funds. All authors contributed to the manuscript's writing and the discussion of the results.

Data availability

Results supporting this article have been included as part of the ESI.† Any other data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. C.-G. acknowledges funding the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 101185235, ERC-PoC 2024 project StEnSo) and from the Spanish Ministry of Science, Innovation and Universities (grants: TED2021-132267B-I00, PID2020-115566RB-I00, PDC2023-145920-I00). B. R. acknowledges ERC-CZ program (project LL2101) from the Ministry of Education Youth and Sports (MEYS). R. D'A. acknowledges support from the Grant No. IT1453-22 “GruposConsolidados UPV/EHU del Gobierno Vasco” funded by Eusko Jaurlaritza (Basque Government) and Grant PID2020-112811GB-I00 funded by MCIN/AEI/10.13039/501100011033. H. L. acknowledges the Young Scientists Fund of the National Natural Science Foundation of China Grant 12404042.

References

1. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453.
2. S. Zhao, B. Dong, H. Wang, H. Wang, Y. Zhang, Z. V. Han and H. Zhang, Nanoscale Adv., 2020, 2, 109–139.
3. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 95, 372–377.
4. L. Cao, Q. Chen, Y. Zhu, K. Tong, W. Li, J. Ma, M. Jalali, Z. Huang, J. Wu and Y. Zhai, ACS Appl. Mater. Interfaces, 2024, 16(15), 19764–19770.
5. D. A. Chenet, O. B. Aslan, P. Y. Huang, C. Fan, A. M. Van Der Zande, T. F. Heinz and J. C. Hone, Nano Lett., 2015, 15, 5667–5672.
6. B. K. Choi, S. Ulstrup, S. M. Gunasekera, J. Kim, S. Y. Lim, L. Moreschini, J. S. Oh, S. H. Chun, C. Jozwiak, A. Bostwick, E. Rotenberg, H. Cheong, I. W. Lyo, M. Mucha-Kruczynski and Y. J. Chang, ACS Nano, 2020, 14, 7880–7891.
7. A. Abudukelimu, K. Kakushima, P. Ahmet, M. Genic, K. Tsutsui, A. Nishiyama, N. Sugii, K. Natori, T. Hattori and H. Iwai, in ICSICT-2010-2010 10th IEEE International Conference on Solid-State and Integrated Circuit Technology, Proceedings, 2010, pp. 1247–1249.
8. E. Liu, Y. Fu, Y. Wang, Y. Feng, H. Liu, X. Wan, W. Zhou, B. Wang, L. Shao, C. H. Ho, Y. S. Huang, Z. Cao, L. Wang, A. Li, J. Zeng, F. Song, X. Wang, Y. Shi, H. Yuan, H. Y. Hwang, Y. Cui, F. Miao and D. Xing, Nat. Commun., 2015, 6, 1–7.
9. Z. Zhou, H. Liu, D. Fan, G. Cao and C. Sheng, ACS Appl. Mater. Interfaces, 2018, 10, 37031–37037.
10. M. Chen, L. Li, M. Xu, W. Li, L. Zheng and X. Wang, Research, 2023, 6, 0066.
11. H. Yuan, X. Liu, F. Afshinmanesh, W. Li, G. Xu, J. Sun, B. Lian, A. G. Curto, G. Ye, Y. Hikita, Z. Shen, S. C. Zhang, X. Chen, M. Brongersma, H. Y. Hwang and Y. Cui, Nat. Nanotechnol., 2015, 10, 707–713.
12. E. Zhang, P. Wang, Z. Li, H. Wang, C. Song, C. Huang, Z. G. Chen, L. Yang, K. Zhang, S. Lu, W. Wang, S. Liu, H. Fang, X. Zhou, H. Yan, J. Zou, X. Wan, P. Zhou, W. Hu and F. Xiu, ACS Nano, 2016, 10, 8067–8077.
13. H. Yang, H. Jussila, A. Autere, H. P. Komsa, G. Ye, X. Chen, T. Hasan and Z. Sun, ACS Photonics, 2017, 4, 3023–3030.
14. L. Li, W. Han, L. Pi, P. Niu, J. Han, C. Wang, B. Su, H. Li, J. Xiong, Y. Bando and T. Zhai, InfoMat, 2019, 1, 54–73.
15. Y. Jin, X. Li and J. Yang, Phys. Chem. Chem. Phys., 2015, 17, 18665–18669.
16. H. Liu, X. Yu, K. Wu, Y. Gao, S. Tongay, A. Javey, L. Chen, J. Hong and J. Wu, Nano Lett., 2020, 20, 5221–5227.
17. H. Li, G. Sanchez-Santolino, S. Puebla, R. Frisenda, A. M. Al-Enizi, A. Nafady, R. D’Agosta and A. Castellanos-Gomez, Adv. Mater., 2022, 34, 2103571.
18. M. Li, J. Dai and X. C. Zeng, Nanoscale, 2015, 7, 15385–15391.
19. S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703–9709.
20. S. Manzeli, A. Allain, A. Ghadimi and A. Kis, Nano Lett., 2015, 15, 5330–5335.
21. C. Si, Z. Sun and F. Liu, Nanoscale, 2016, 8, 3207–3217.
22. G. H. Ahn, M. Amani, H. Rasool, D. H. Lien, J. P. Mastandrea, J. W. Ager, M. Dubey, D. C. Chrzan, A. M. Minor and A. Javey, Nat. Commun., 2017, 8, 1–8.
23. R. Yang, J. Lee, S. Ghosh, H. Tang, R. M. Sankaran, C. A. Zorman and P. X. L. Feng, Nano Lett., 2017, 17, 4568–4575.
24. F. Carrascoso, H. Li, R. Frisenda and A. Castellanos-Gomez, Nano Res., 2021, 14, 1698–1703.
25. R. Roldán, A. Castellanos-Gomez, E. Cappelluti and F. Guinea, J. Phys.: Condens. Matter, 2015, 27, 313201.
26. F. Carrascoso, R. Frisenda and A. Castellanos-Gomez, Nano Mater. Sci., 2022, 4, 44–51.
27. H. Li, F. Carrascoso, A. Borrás, G. P. Moreno, F. J. Aparicio, Á. Barranco and A. C. Gómez, Nano Res., 2024, 1–8.
28. K. Osada, S. Bae, M. Tanaka, H. Raebiger, K. Shudo and T. Suzuki, J. Phys. Chem. C, 2016, 120, 4653–4659.
29. P. Costa, A. Ferreira, V. Sencadas, J. C. Viana and S. Lanceros-Méndez, Sens. Actuators, A, 2013, 201, 458–467.
30. J. K. Qin, H. L. Sun, T. Su, W. Zhao, L. Zhen, Y. Chai and C. Y. Xu, Appl. Phys. Lett., 2021, 119, 201903.
31. Z. Zhang, L. Li, J. Horng, N. Z. Wang, F. Yang, Y. Yu, Y. Zhang, G. Chen, K. Watanabe, T. Taniguchi, X. H. Chen, F. Wang and Y. Zhang, Nano Lett., 2017, 17, 6097–6103.
32. C. An, Z. Xu, W. Shen, R. Zhang, Z. Sun, S. Tang, Y. F. Xiao, D. Zhang, D. Sun, X. Hu, C. Hu, L. Yang and J. Liu, ACS Nano, 2019, 13, 3310–3319.
33. J. O. Island, A. J. Molina-Mendoza, M. Barawi, R. Biele, E. Flores, J. M. Clamagirand, J. R. Ares, C. Sánchez, H. S. J. Van Der Zant, R. D’Agosta, I. J. Ferrer and A. Castellanos-Gomez, 2D Mater., 2017, 4, 022003.
34. R. Biele, E. Flores, J. R. Ares, C. Sanchez, I. J. Ferrer, G. Rubio-Bollinger, A. C. Gomez and R. D’Agosta, Nano Res., 2018, 11, 225–232.
35. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
36. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
37. G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145.
38. M. De Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. K. Ande, S. Van Der Zwaag, J. J. Plata, C. Toher, S. Curtarolo, G. Ceder, K. A. Persson and M. Asta, Sci. Data, 2015, 2, 1–13.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00539b

‡ Both B. R. and H. L. contributed equally to this work.

---