Tunable magnetoelectricity and polarity in van der Waals antiferromagnetic CuCr_1−xFe_xP₂S₆

Abstract

The coexistence of electric and magnetic orders with intrinsic coupling, referred to as magnetoelectric coupling in multiferroics, has been extensively studied in oxide materials but remains relatively unexplored in van der Waals materials. Among these, CuCrP₂S₆ (CCPS) is notable for its emergent antiferromagnetic (AFM) and antiferroelectric (AFE) characteristics. However, investigations into magnetoelectric coupling in CCPS are limited, and the effects of dopants on its magnetic properties have yet to be fully addressed. In this study, we synthesized CuCr_1−xFe_xP₂S₆ (CCFPS) samples using the chemical vapor transport (CVT) method to investigate the influence of iron doping on the magnetic and nonlinear optical properties of the CCFPS system. Our results indicate that the AFM state is preserved, while the Néel temperature (T_N) varies with the doping concentration. First-principles calculations were employed to assess the exchange interactions among magnetic atoms. Notably, for samples with doping concentrations x < 0.5, we observed both magnetic-dielectric coupling and second harmonic generation (SHG) effects. However, these effects were absent at higher doping levels. Furthermore, our analysis revealed a distinct odd–even dependence of SHG, suggesting the presence of interlayer symmetry-breaking coupling. These findings advance our understanding of two-dimensional (2D) multiferroic materials and lay the groundwork for designing and optimizing magnetoelectric coupling materials with enhanced performance.

---

New concepts

While extensive research has focused on magnetoelectric coupling in multiferroic oxides with strongly coupled magnetic and electric orders, such coupling remains largely unexplored in van der Waals materials. CuCrP₂S₆, a two-dimensional multiferroic compound, offers a promising platform for investigating magnetoelectric coupling and its modulation. In this study, we investigate the effects of iron (Fe) doping on the magnetic properties and symmetry-breaking behavior of CCFPS, revealing significant remanent magnetism and intrinsic polarity. Moreover, first-principles calculations were performed to examine the interactions between different magnetic atoms, providing deeper insights into their magnetic properties.

Introduction

The interplay between magnetic and electric long-range order parameters in materials is essential for achieving magnetoelectric coupling, which includes phenomena such as magnetically induced ferroelectricity and vice versa.^1,2 This phenomenon is currently a major focus of research within the realm of correlated oxides, due to their rich and complex physics and their potential for enabling novel device functionalities. However, such magnetoelectric effects have remained largely elusive in van der Waals systems, primarily because of the absence of simultaneous intrinsic remanent magnetism and polarization.^3–5 Recently, significant attention has been directed toward metal phosphorus trichalcogenides (MPX₃) as promising candidates within the family of layered van der Waals materials.^6–8 This family can be divided into two main groups, M^IIPX₃ (M^II = Fe, Ni, Mn, Cu, Co, Zn) and M^IM^IIIP₂X₆ (M^I = Ag, Cu, M^III = V, Cr, In, Sc), encompassing a diverse array of transition metal phases.^9–13

Among the M^IM^IIIP₂X₆ compounds, CuInP₂S₆ has attracted significant attention due to its robust room-temperature ferroelectricity, which persists even at the monolayer level.^14–16 This pronounced ferroelectric behavior manifests in anomalous polarization switching phenomena, such as the manipulation of in-plane Cu-ion orientations to facilitate out-of-plane domain inversion.^17–19 However, in the absence of magnetic atoms, layered CuInP₂S₆ does not exhibit ferromagnetic (FM) ordering. A key advancement in this field involves the substitution of In³⁺ with magnetic Cr³⁺, leading to the emergence of the 2D multiferroic material CCPS. Multiferroic materials are characterized by the simultaneous breaking of both spatial inversion and time-reversal symmetries.^20,21 CCPS exemplifies this by exhibiting coexisting AFM and AFE phases below the Néel temperature (32 K). Given the escalating demand for functional, integrated, and miniaturized electronic components, van der Waals multiferroics have garnered substantial attention due to their high compatibility with modern device architectures.^22,23

CCPS exhibits A-type AFM order below the Néel temperature T_N ∼ 32 K,²⁴ corresponding to intralayer FM and interlayer AFM arrangement. In CCPS, the Cu¹⁺ within the sulfur octahedron undergoes positional shifts in response to temperature changes. Above 190 K (T_C1), the Cu¹⁺ arrangement becomes disordered, leading to the formation of a paraelectric phase with space group C2/c. Below 150 K (T_C2), Cu¹⁺ assumes a fixed position either above or below the layer, resulting in a corresponding alteration in electric dipoles and the onset of an AFE phase with Pc space group.^25–27 Between 150 K and 190 K, a quasi-antipolar state exists. Recent studies have focused on the multiferroic properties of CCPS, with reports showing that CCPS nanosheets exhibit ferromagnetism (FM) and driven ferroelectricity,²⁸ and spin-induced ferroelectricity has also been observed.²⁹ Notably, CCPS also demonstrates voltage-driven Cu displacement, inducing a ferroelectric flip–flop behavior despite its centrosymmetric space group at room temperature. The ability to incorporate various functional transition metal ions in the CCPS structure provides opportunities to tailor its properties for a wide range of applications.³⁰

Herein, we employed magnetic dopants as a strategy to modulate the properties of metal phosphorus trichalcogenides CCFPS single crystals, which were grown via CVT with varying levels of Fe doping. Our investigation elucidated the magnetic mechanisms in the doped samples. Notably, the multiferroic nature of CCPS remains intact after doping, with a magnetic–dielectric coupling observed in samples with Fe concentrations below x = 0.5. We further probed the nonlinear optical properties using the SHG technique, revealing a multiplicative optical response in samples with x < 0.5, indicative of symmetry breaking crucial for polarity. Furthermore, the SHG signal exhibits an alternating pattern between odd and even layers, further supporting the presence of symmetry-related effects. This study highlights the potential of phosphorus–sulfur compounds as promising candidates for the development of quasi-2D electronic devices with multifunctional capabilities.

Results and discussion

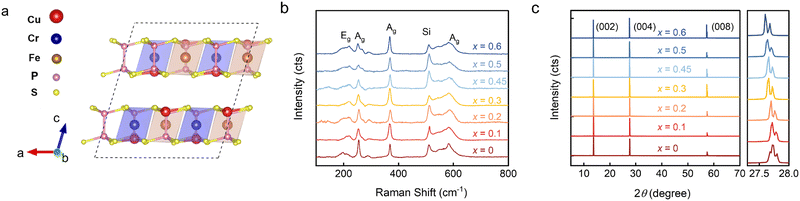
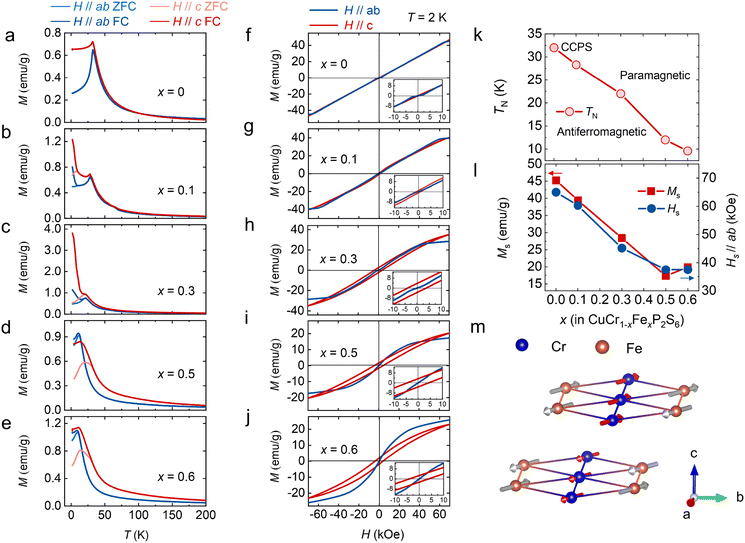
The atomic structure of CuCr_0.5Fe_0.5P₂S₆ is illustrated in Fig. 1a. In this structure, sulfur (S) atoms form a layered framework of cages, with iron (Fe) atoms partially substituting for chromium (Cr) atoms at specific sites and stabilizing within the voids of the sulfur octahedron. Phosphorus bonds (P–P) are integrated into this framework, contributing to its overall structure.^10,11 Notably, the mobility of copper (Cu) ions, which reside in the upper or lower layers of the unit cell below the Curie temperature (T_C), plays a crucial role in facilitating the emergence of ferroelectricity. To assess the structural integrity of CCFPS, spectroscopic measurements were performed. Fig. 1b presents the Raman spectra of CCFPS flakes (∼100 nm) with varying compositions at room temperature. The E_g peak corresponds to rotation (R′) of the PS₃ group within the [P₂S₆]⁴⁻ ethane-like building blocks of the anion sublattice.^31–33 No significant shifts or intensity variations are observed in the Raman spectra of the doped samples, indicating minimal structural perturbations due to doping. Furthermore, Fig. 1c shows the X-ray diffraction (XRD) pattern of CCFPS single crystals, with an expanded view of the (004) plane provided in the right panel. The XRD pattern reveals three prominent peaks at 13.72°, 27.72°, and 57.40°, corresponding to the (002), (004), and (008) planes, respectively. The observed shift of the (004) peak to a lower diffraction angle suggests the successful incorporation of Fe atoms, which leads to an expansion of the interlayer spacing. To further evaluate the elemental valence states after doping, high-resolution X-ray photoelectron spectroscopy (XPS) spectra were performed on the CuCr_0.55Fe_0.45P₂S₆ sample, covering the Cu 2p, Cr 2p, Fe 2p, P 2p, and S 2p binding energy regions. The split-peak fitting for various elements in Fig. S1 (ESI†) reveals that Fe³⁺ substitutes for Cr³⁺. Furthermore, detailed elemental ratios were obtained using an energy dispersive spectrometer (EDS), as shown in Table S1 (ESI†).

Fig. 1 (a) The structure of CuCr_0.5Fe_0.5P₂S₆ at low temperatures. The Fe atom, which replaces the Cr atom, is situated at the center of the octahedral sulfur cage, while the Cu atoms occupy the uppermost or lowermost positions of each atomic layer. (b) Raman spectra of samples with different compositions, measured at room temperature. Vibrational modes are identified near the corresponding peaks, with the Si peak observed at 520 cm⁻¹. (c) XRD patterns of CCFPS with varying Fe-doping ratios. The right panel shows the enlarged view of the peak of the (004) plane, indicating an increase in interlayer spacing with higher Fe doping.

To investigate the effect of Fe doping on the magnetic properties of the CCPS sample, the magnetization of both CCPS and CCFPS was measured under applied magnetic fields along two directions: parallel to the ab-plane (H//ab) and parallel to the c-axis (H//c), as depicted in Fig. 2. The M–H and M–T curves for compositions x = 0.2 and x = 0.45 are presented in Fig. S2, ESI.† Fig. 2a–e illustrate the temperature dependence of out-of-plane and in-plane magnetization under zero-field cooled (ZFC) and field-cooled (FC) conditions at H = 1 kOe for different compositions. As illustrated in Fig. 2a, the undoped CCPS (x = 0) exhibits a typical A-type AFM configuration below 32 K, with M–T curves decreasing below the T_N.^26,34 Partial substitution of Cr with an Fe atom maintains the AFM state while lowering the magnetic transition temperature T_N. Additionally, the ZFC and FC curves exhibit an irreversible bifurcation at a temperature known as T_irr, a characteristic behavior in many magnetic materials. This bifurcation is commonly associated with changes in magnetic ordering, such as the onset of superparamagnetism, and spin glass behavior. Notably, the a.c.-magnetic susceptibility data exhibit no frequency dependence, ruling out spin glass behavior, as shown in Fig. S3, ESI.† The bifurcation is likely caused by the competition among magnetic moments, resulting in a canted AFM structure.

Fig. 2 (a)–(e) Temperature dependence of magnetization under a magnetic field of H = 1 kOe for different doping concentrations (x = 0.1, 0.2, 0.3, 0.5, 0.6). (f)–(j) Magnetic field dependence of magnetization measured at T = 2 K, both parallel to the ab-plane and the c-axis. Insets show magnified views of the magnetization from −10 kOe to 10 kOe. (k) Variation of the Néel temperature (T_N) with doping ratio. (l) The saturation magnetization (M_s) and corresponding saturation magnetic field (H_s) were obtained from magnetization measurements for different compositions. (m) Schematic of the hypothetical spin arrangement of the CuCr_0.5Fe_0.5P₂S₆ bilayer.

The magnetic field-dependent magnetization (M–H) curves for CCFPS are shown in Fig. 2f–j. At 2 K, the samples exhibit saturation along the ab-plane, whereas no saturation is observed along the c-axis, indicating that the easy axis of magnetization lies within the ab-plane. For example, in the case of CuCr_0.5Fe_0.5P₂S₆, the easy magnetization directions were calculated by comparing the energies of different spin alignments, including spin-orbital coupling (SOC). When the spins are aligned perpendicular to the ab-plane, the energy is 17.5 μeV f.u.⁻¹ and 22.5 μeV f.u.⁻¹ higher compared to the alignment along the a and b axes, respectively. Fig. 2 provides an enlarged view of the M–H curves at low magnetic fields, which display an “S”-shaped curve when H//ab. This phenomenon indicates an in-plane spin reorientation transition, corresponding to a spin-flop transition, with the transformed magnetic field is H_SF.³⁵ A slight energy difference between the a axis and b axis leads to competition between magnetic dipoles. When the magnetic field reaches a critical value (H_SF), the antiferromagnetic spins no longer remain strictly antiparallel but instead undergo a flop or form an angle, thus minimizing the total system energy. This magnetic anisotropy is responsible for the spin-flop transition and plays a crucial role in enabling ultrafast spin transfer and optimizing spin-wave excitation.^36,37

The magnetic parameters, including the Néel temperature (T_N), saturation magnetization (M_s), and saturation magnetic field (H_s), obtained from the magnetization measurements, are plotted in Fig. 2k–l as a function of Fe concentration (x). To further investigate the underlying magnetic mechanisms, first-principles calculations were performed using the structure of CuCr_0.5Fe_0.5P₂S₆ to evaluate the magnetic exchange interactions, the detailed calculations are presented in Fig. S4, ESI.† The calculations assess the energies associated with seven distinct magnetic orders to characterize all first-nearest Cr–Cr, Fe–Fe, and Cr–Fe interactions, including both interlayer and intralayer interactions. The schematic in Fig. 2m reveals a schematic of the hypothetical spin arrangement of the CuCr_0.5Fe_0.5P₂S₆ bilayer. Within each layer, the Cr–Cr interactions are FM, while the Fe–Fe and Cr–Fe interactions are AFM. For the interlayer interactions, both the first nearest Cr–Cr and Fe–Fe interactions are AFM. The overall sample exhibits AFM; however, due to the randomness of doping, and the canting of magnetic moments resulting from magnetic frustration, a net magnetic moment is observed in the M–H curve.

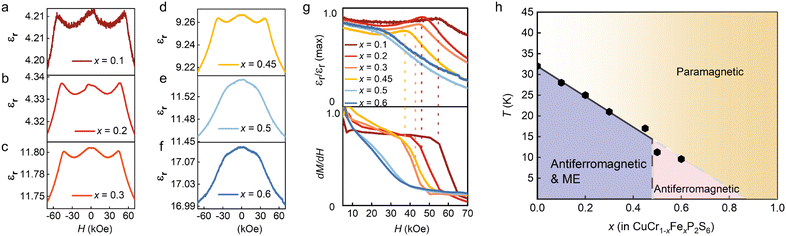
We further investigated the impact of magnetoelectric properties on the magnetodielectric response in this promising multiferroic phase. The magnetodielectric effect was characterized by measuring the magnetic field-dependent dielectric constants ε_r(H) at 4 K for various doping concentrations, as shown in Fig. S5, ESI†. For doping concentrations x < 0.5, as illustrated in Fig. 3a–d, we observed symmetric peaks with a characteristic ‘w’-shaped dielectric response. As the doping concentration increased, there was a noticeable reduction in the dielectric response, culminating in the complete disappearance of the dielectric peaks at x = 0.5 and x = 0.6, as shown in Fig. 3e and f. The upper section of Fig. 3g presents the normalized magnetodielectric results from Fig. 3a–f, while the lower section displays dM/dH results from Fig. 2f–j. For doping ratios x < 0.5, variations in magnetic field-dependent polarization were observed at the saturation points of the magnetization, indicating that the applied magnetic field influences dipole flipping and demonstrates magnetoelectric coupling. Utilizing the measured magnetic data, a magnetic phase diagram was constructed, as demonstrated in Fig. 3h. The purple region in the diagram indicates where the magnetoelectric coupling is favored, occurring when the doping ratio is below x = 0.5. This suggests a modulation of magnetic properties and an enhancement of magneto-electric coupling at lower doping levels. When the Fe substitution ratio exceeds 50%, AFM interactions between iron atoms become dominant, leading to changes in the crystalline structure of the material and the subsequent disappearance of the magnetodielectric response.

Fig. 3 (a)–(f) Magnetodielectric behaviors were measured by sweeping the magnetic field from −7 kOe to 7 kOe for samples with doping concentrations x = 0.1, 0.2, 0.3, 0.45, 0.5, and 0.6, with the magnetic field applied along the H//ab-plane. (g) The upper panel shows the normalized magnetodielectric response at 4 K, while the lower panel displays the first-order derivative of the M–H curves. The color scheme corresponds to the dielectric curves. (h) Magnetic phase diagrams of CCFPS, with the black hexagonal points representing the T_N extracted from M–T curves along the H//ab-plane. Arrows indicate the asymmetric arrangement of magnetic moments.

We employed SHG to investigate symmetry breaking and emergent polarization at room temperature in samples with varying doping concentrations. SHG is a nonlinear optical process in which an incident light field of frequency ω induces a dipole response, resulting in the emission of light at frequency 2ω. For effective SHG, both a non-centrosymmetric sample structure and phase-matching conditions must be satisfied.³⁸ Our experiments on a thin-layer sample with a doping ratio of x = 0.45 revealed layer-dependent SHG effects. Fig. 4a shows an optical microscope image of CuCr_0.55Fe_0.45P₂S₆, highlighting the characteristic triangular shape of the sample. Fig. 4b shows topographical data obtained from the atomic force microscope, illustrating stepwise thickness variations and the number of layers (Fig. S6, ESI†). The SHG mapping of the triangular sample in Fig. 4c shows a distinct layer-dependent pattern, with pronounced SHG signals in odd layers and the absence of SHG signals in even layers.^39–43 To facilitate clear observation, ultrathin monolayer and few-layer samples were exfoliated onto SiO₂ substrates. An optical microscope image of CuCr_0.55Fe_0.45P₂S₆ flakes is shown in Fig. 4d, and the corresponding atomic force microscopic morphology is displayed in Fig. 4e, providing additional thickness details, with further thickness profiles shown in Fig. S7, ESI.† The corresponding SHG mapping underscores a distinct, homogeneous signal in the monolayer sample, which is absent in the bilayer. Furthermore, parity number-dependent behavior was observed in few-layer CuCr_0.55Fe_0.45P₂S₆ nanosheets, as shown in Fig. S8 (ESI†).

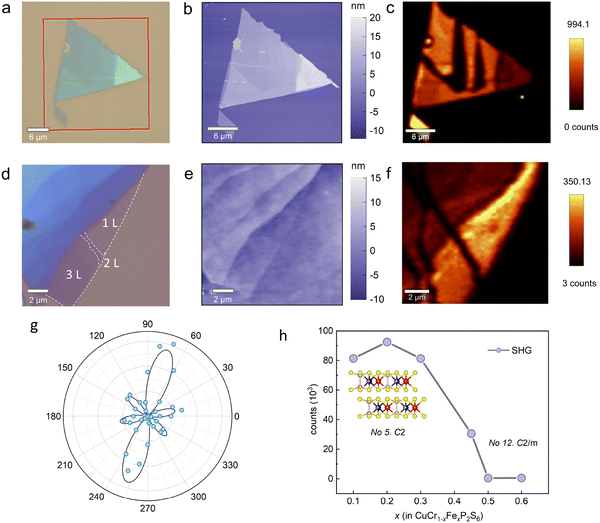Fig. 4 (a) Optical micrograph of a mechanically exfoliated CuCr_0.55Fe_0.45P₂S₆ flake on a SiO₂ substrate. (b) Atomic force microscopic image of the flakes indicated by the red rectangle in (a). (c) Corresponding SHG mapping of the flakes. Brighter regions indicate a strong SHG signal, while darker areas correspond to weak SHG intensity. (d) Optical micrograph of a CuCr_0.55Fe_0.45P₂S₆ flake featuring 1L, 2L, and 3L structures. Detailed thickness data is shown in Fig S5 (ESI†). (e) Corresponding atomic force microscopic image of the flake in (d). (f) SHG mapping image of the flakes in (e). (g) Polar plots of the SHG results captured from a few-layer CuCr_0.55Fe_0.45P₂S₆ with parallel polarization. The blue dots represent the experimental data, and the black line shows the fitting result. (h) Doping ratio dependence of SHG behavior, with the signal becoming negligible for x > 0.5. The inset shows the atomic structures and space groups corresponding to doping ratios below 0.5.

The angle dependence of CuCr_0.55Fe_0.45P₂S₆ SHG intensity (Fig. 4g) reveals a six-lobe pattern, which is indicative of the crystal's two-fold rotational symmetry. Polarization-resolved SHG measurements provide further insight into the lattice symmetry of the crystal. The relationship between the SHG intensity and the crystal lattice is governed by the second-order nonlinear susceptibility tensor (see ESI†).^44,45 The fitted polar plots reflect their C2 symmetry, in agreement with the experimental results.

The doping ratio-dependent SHG intensity revealed a threshold at x = 0.5 (Fig. 4h), with pronounced SHG detected for x < 0.5. However, as the doping concentration exceeded this threshold, the SHG intensity decreased. Single crystal XRD results support these findings, demonstrating that doping alters the space group of the crystal. At lower doping ratios, the introduction of impurities can break the system symmetry, thereby enhancing the SHG signal. Furthermore, the migration of metastable Cu sites within the van der Waals gap may induce dipole polarization, leading to the emergence of interlayer AFE.

Conclusions

In summary, this study expands the range of metal elements incorporated into metal phosphorus trichalcogenides. Using CVT techniques, we successfully synthesized a series of CCFPS samples, which represent a promising 2D multiferroic material. This compound exhibits an AFM state coupled with magnetic dielectric properties. Room-temperature polarity characterization via SHG demonstrates layer-dependent nonlinear optical behavior, suggesting potential applications in optical storage for 2D materials. However, the confirmation of room-temperature ferroelectricity in CCFPS requires further experimental investigation. This research offers valuable insights into the development of 2D multiferroic materials and enhances the potential for utilizing metal phosphorus trichalcogenides in optical modulation applications.

Experimental

Sample synthesis

A series of single crystals CuCr_1−xFe_xP₂S₆ (0 ≤ x ≤0.6) were synthesized by the CVT method. Stoichiometric amounts of high purity Cu (Aladdin, 99.99%), Cr (Aladdin, 99.9%), Fe (Aladdin, 99.95%), P (Aladdin, 99.9%), and S (Aladdin, 99.95%) were precisely weighed and sealed in an evacuated quartz ampoule along with iodine as the transport agent. The sealed ampoules were placed in a two-zone furnace, with the hot and cold zones set to 700 °C and 650 °C, respectively. After a seven-day growth period, single crystals with typical dimensions of 3 mm × 3 mm × 40 μm were obtained from the cold side of the furnace.

Structural and magnetic measurements

The crystal structure of the bulk samples was analyzed using an X-ray diffractometer (SmartLab-3, Rigaku Corp.). The chemical composition of the single crystals was analyzed using a scanning electron microscope (FEI, Inspect F50). Raman spectroscopy was performed using a 532 nm laser on a LabRAM HR UV-visible system. Elemental valence analysis was carried out using X-ray photoelectron spectroscopy (XPS, PreVac/XPS-2). Temperature- and field-dependent magnetization measurements were carried out using a Quantum Design PPMS equipped with a vibrating sample magnetometer (VSM) option. Magnetic-dielectric measurements were performed in a Teslatron PT magnet (Oxford Instruments) coupled with a 6517B test system.

SHG characterization

The SHG spectra were performed using a WITec alpha 300RA microscope. SHG measurements were performed with a 1064 nm laser, featuring a pulse width of approximately 15 picoseconds and a repetition rate of 80 MHz for excitation. For angle-dependent SHG tests, the relative angle between the incident polarized laser and the collected polarized light was varied. The reflective SHG signals were detected using a UHTS spectrometer system and detected by a CCD camera.

Density functional theory (DFT)

First-principles calculations are performed based on projector augmented pseudopotentials, as implemented in the Vienna ab initio Simulation Package (VASP).⁴⁶ A plane-wave cutoff energy of 500 eV and 5 × 3 × 3 k-point meshes was used. The lattice constants and the atomic positions were fully relaxed with the convergence criteria of 10⁻⁵ eV and 0.01 V Å⁻¹ for energy and force, respectively. The Perdew–Burke–Ernzerhof exchange–correlation functional and generalized gradient approximation plus U (GGA+U) are adopted.⁴⁷ The effective Hubbard U parameters are 5 eV and 3 eV for the Fe and Cr 3d orbitals,⁴⁸ respectively. D3 Grimme correction is used for the consideration of van der Waals (vdW) interaction.^49,50

Author contributions

Y. X. and L. L. conceived the study. Y. X. performed the structural, Raman, magnetic, and dielectric measurements with the help of L. M. and X. Li. H. S. Y. conducted first-principles calculations. Y. X. and G. D. performed the SHG test with the help of Y. Y. J. Z. and X. Luo. participated in the collection of XPS and AFM data. X. C., H. R. Y., and A. S. helped to analyze and discuss the experimental phenomena. Y. X. and L. L. wrote the paper with suggestions from Z. W., and S. D. All authors discussed the results and commented on the manuscript.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support from the National Natural Science Foundation of China (No. 12204096 and No. 12274069), the Natural Science Foundation of Jiangsu Province (BK20220797), and the Fundamental Research Funds for the Central Universities. This research is also supported by the Open Research Fund Program of Beijing National Laboratory for Condensed Matter Physics (2024BNLCMPKF019) and the open research fund of the Key Laboratory of Quantum Materials and Devices (Southeast University), Ministry of Education. Most calculations were done on the Big Data Computing Center of Southeast University.

Notes and references

1. N. A. Spaldin and R. Ramesh, Nat. Mater., 2019, 18, 203–212.
2. M. Fiebig, T. Lottermoser, D. Meier and M. Trassin, Nat. Rev. Mater., 2016, 1, 16046.
3. Y. Gao, M. Gao and Y. Lu, Nanoscale, 2021, 13, 19324–19340.
4. Q. Song, C. A. Occhialini, E. Ergecen, B. Ilyas, D. Amoroso, P. Barone, J. Kapeghian, K. Watanabe, T. Taniguchi, A. S. Botana, S. Picozzi, N. Gedik and R. Comin, Nature, 2022, 602, 601–605.
5. C. Gong, E. M. Kim, Y. Wang, G. Lee and X. Zhang, Nat. Commun., 2019, 10, 2657.
6. X. Li, T. Cao, Q. Niu, J. R. Shi and J. Feng, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3738–3742.
7. R. Samal, G. Sanyal, B. Chakraborty and C. S. Rout, J. Mater. Chem. A, 2021, 9, 2560–2591.
8. J. Qi, H. Wang, X. Chen and X. Qian, Appl. Phys. Lett., 2018, 113, 043102.
9. M. J. Swamynadhan and S. Ghosh, Phys. Rev. Mater., 2021, 5, 054409.
10. F. Wang, T. A. Shifa, P. Yu, P. He, Y. Liu, F. Wang, Z. Wang, X. Zhan, X. Lou, F. Xia and J. He, Adv. Funct. Mater., 2018, 28, 1802151.
11. M. A. Susner, M. Chyasnavichyus, M. A. McGuire, P. Ganesh and P. Maksymovych, Adv. Mater., 2017, 29, 1602852.
12. Y. Zhang, W. Wang, M. Huang, P. Liu, G. Hu, C. Feng, X. Lei, M. Gu, H. Yang, K. Liu, B. Xiang and Y. Lu, Nanoscale, 2020, 12, 23266–23273.
13. R. Basnet and J. Hu, Nanoscale, 2024, 16, 15851–15883.
14. F. Liu, L. You, K. L. Seyler, X. Li, P. Yu, J. Lin, X. Wang, J. Zhou, H. Wang, H. He, S. T. Pantelides, W. Zhou, P. Sharma, X. Xu, P. M. Ajayan, J. Wang and Z. Liu, Nat. Commun., 2016, 7, 12357.
15. X. Jiang, X. Zhang, R. Niu, Q. Ren, X. Chen, G. Du, Y. Chen, X. Wang, G. Tang, J. Lu, X. Wang and J. Hong, Adv. Funct. Mater., 2023, 33, 2213561.
16. Y. Zhang, J. Mao, R. K. Zheng, J. Zhang, Y. Wu, X. Wang, K. Miao, H. Yao, L. Yang and H. Zheng, Adv. Funct. Mater., 2023, 33, 2214745.
17. S. Zhou, L. You, H. Zhou, Y. Pu, Z. Gui and J. Wang, Front. Phys., 2020, 16, 13301.
18. D. Zhang, Z. D. Luo, Y. Yao, P. Schoenherr, C. H. Sha, Y. Pan, P. Sharma, M. Alexe and J. Seidel, Nano Lett., 2021, 21, 995–1002.
19. S. Zhou, L. You, A. Chaturvedi, S. A. Morris, J. S. Herrin, N. Zhang, A. Abdelsamie, Y. Hu, J. Chen, Y. Zhou, S. Dong and J. Wang, Mater. Horiz., 2020, 7, 263–274.
20. S. Dong, J.-M. Liu, S.-W. Cheong and Z. Ren, Adv. Phys., 2015, 64, 519–626.
21. S. Dong, H. Xiang and E. Dagotto, Natl. Sci. Rev., 2019, 6, 629–641.
22. J. J. Zhang, L. Lin, Y. Zhang, M. Wu, B. I. Yakobson and S. Dong, J. Am. Chem. Soc., 2018, 140, 9768–9773.
23. B. Behera, B. C. Sutar and N. R. Pradhan, Emergent Mater., 2021, 4, 847–863.
24. V. C. a C. P. V. Maisonneuve, Chem. Mater., 1993, 5, 758–760.
25. A. L. P. Colombet, M. Danot and J. Rouxel, J. Solid State Chem., 1982, 174–184.
26. V. Maisonneuve, C. Payen and V. B. Cajipe, J. Solid State Chem., 1995, 116, 208–210.
27. V. B. Cajipea, J. Ravez, V. Maisonneuve, A. Simon, C. Payen, R. Von Der Muhll and J. E. Fischer, Ferroelectrics, 1996, 185, 135–138.
28. Y. Lai, Z. Song, Y. Wan, M. Xue, C. Wang, Y. Ye, L. Dai, Z. Zhang, W. Yang, H. Du and J. Yang, Nanoscale, 2019, 11, 5163–5170.
29. C. B. Park, A. Shahee, K. T. Kim, D. R. Patil, S. A. Guda, N. Ter-Oganessian and K. H. Kim, Adv. Electron. Mater., 2022, 8, 2101072.
30. W. F. Io, S. Pang, L. W. Wong, Y. Zhao, R. Ding, J. Mao, Y. Zhao, F. Guo, S. Yuan, J. Zhao, J. Yi and J. Hao, Nat. Commun., 2023, 14, 7304.
31. M. A. Susner, R. Rao, A. T. Pelton, M. V. McLeod and B. Maruyama, Phys. Rev. Mater., 2020, 4, 104003.
32. C. S. O. Poizat, J. Solid State Chem., 1985, 59, 371–378.
33. J. P. F. C. Sourisseau and Y. Mathey, J. Solid State Chem., 1983, 49, 134–149.
34. M. E. V. Maisonneuve, C. Payen, V. Cajipe and P. Molinie, J. Alloys Compd., 1995, 218, 157–164.
35. X. Wang, Z. Shang, C. Zhang, J. Kang, T. Liu, X. Wang, S. Chen, H. Liu, W. Tang, Y. J. Zeng, J. Guo, Z. Cheng, L. Liu, D. Pan, S. Tong, B. Wu, Y. Xie, G. Wang, J. Deng, T. Zhai, H. X. Deng, J. Hong and J. Zhao, Nat. Commun., 2023, 14, 840.
36. T. M. J. Cham, S. Karimeddiny, A. H. Dismukes, X. Roy, D. C. Ralph and Y. K. Luo, Nano Lett., 2022, 22, 6716–6723.
37. S. Y. Bodnar, L. Šmejkal, I. Turek, T. Jungwirth, O. Gomonay, J. Sinova, A. A. Sapozhnik, H. J. Elmers, M. Kläui and M. Jourdan, Nat. Commun., 2018, 9, 348.
38. S. A. Denev, T. T. A. Lummen, E. Barnes, A. Kumar, V. Gopalan and D. J. Green, J. Am. Ceram. Soc., 2011, 94, 2699–2727.
39. Y. Li, Y. Rao, K. F. Mak, Y. You, S. Wang, C. R. Dean and T. F. Heinz, Nano Lett., 2013, 13, 3329–3333.
40. R. Beams, L. G. Cancado, S. Krylyuk, I. Kalish, B. Kalanyan, A. K. Singh, K. Choudhary, A. Bruma, P. M. Vora, F. Tavazza, A. V. Davydov and S. J. Stranick, ACS Nano, 2016, 10, 9626–9636.
41. D. L. Zhang, Z. X. S. Zeng, Q. J. Tong, Y. Jiang, S. L. Chen, B. Y. Zheng, J. Y. Qu, F. Li, W. H. Zheng, F. Jiang, H. P. Zhao, L. Y. Huang, K. Braun, A. J. Meixner, X. Wang and A. L. Pan, Adv. Mater., 2020, 32, 1908061.
42. X. Wang, K. Du, W. Liu, P. Hu, X. Lu, W. Xu, C. Kloc and Q. Xiong, Appl. Phys. Lett., 2016, 109, 123103.
43. K. L. Seyler, J. R. Schaibley, P. Gong, P. Rivera, A. M. Jones, S. F. Wu, J. Q. Yan, D. G. Mandrus, W. Yao and X. D. Xu, Nat. Nanotechnol., 2015, 10, 407–411.
44. N. Higashitarumizu, H. Kawamoto, C. J. Lee, B. H. Lin, F. H. Chu, I. Yonemori, T. Nishimura, K. Wakabayashi, W. H. Chang and K. Nagashio, Nat. Commun., 2020, 11, 2428.
45. H. Wang and X. Qian, Nano Lett., 2017, 17, 5027–5034.
46. G. Kresse and J. Furthmuller, Phys. Rev. B, 1996, 54, 11169–11186.
47. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505.
48. J. Chen, C. Gui and S. Dong, Phys. Rev. B, 2024, 110, L060406.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
50. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 15.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00620h

‡ These authors contributed equally to this work.

---