Nanoparticle characterisation via 2D classification using single particle averaging

Abstract

Characterising the size and morphology of nanoparticles (NPs), especially in complex systems like core–shell particles and nanocapsules, remains a significant challenge due to limitations in resolution and applicability of traditional methods. Here, we explore a novel approach to image-based NP characterisation using 2D class averaging (2D-CA) techniques used in single particle analysis. By leveraging well-established software originally developed in structural biology, our method provides detailed size distribution analysis for diverse NP systems, including bimodal particle size distributions, nanocapsules and nanorods. To validate the efficacy and accuracy of this technique, we conduct a comparative study against established characterisation methods, highlighting the potential of 2D-CA to enhance the analysis of challenging NP systems that are otherwise inaccessible using conventional methods, such as highly agglomerated NPs. Our results indicate that single particle averaging techniques offer a sound statistical basis for NP size distribution determination, coupled with a streamlined workflow that utilises established software. This method facilitates the processing of large numbers of micrographs, yielding statistically robust results with minimal human bias through automated particle identification.

---

New concepts

This work introduces a new conceptual use of cryo-EM image classification tools, typically confined to structural biology, for broader image analysis challenges in nanoscience. By applying 2D classification protocols outside their original context, we demonstrate how methods developed for single-particle protein reconstruction can be reframed as general-purpose tools for signal enhancement and feature extraction in electron microscopy datasets. The novelty lies not only in the specific application to nanoparticle sizing, but in showing that the underlying principles of classification and averaging are transferable across disciplines. This cross-disciplinary approach encourages rethinking established cryo-EM workflows as adaptable frameworks, rather than fixed pipelines. The method allows researchers in other fields to leverage powerful EM-based image processing techniques—potentially for enhancing high-resolution imaging, improving signal-to-noise in low-contrast datasets, or tackling other challenges where image quality limits analysis. By repositioning an existing method in a new scientific setting, this work illustrates how concepts from structural biology can be repurposed to support progress in physical chemistry, materials science, and beyond.

1. Introduction

NPs are used in various fields, ranging from self-healing anticorrosion materials¹ to biomedical applications like drug delivery to the cell,² to name a few. Their functional efficacy critically depends on their shape and size distribution,³ which are pivotal for the reproducibility and advancement of nanotechnological applications.^4,5 Even small differences in NP size, as little as 10–20 nm, can significantly impact biological applications. For instance, gold NPs around 50 nm show the highest cellular uptake, while smaller or larger particles are less efficiently internalised, as well as size affecting circulation time and clearance route.^6–8 Beyond biological systems, nanoparticle size and morphology also critically influence catalysis, where they govern surface reactivity and selectivity,⁹ and in polymer nanospheres, mechanical properties have been shown to vary significantly with particle diameter, demonstrating that size effects can also manifest in passive material performance.¹⁰ Additionally, recent developments in machine learning-assisted synthesis highlight that such predictive approaches are only as effective as the accuracy of the underlying structural data, underlining the importance of detailed characterisation.¹¹

NP characterisation is a well-established field with many techniques available,¹² with both general and sample-specific comparisons being made.¹³ The most commonly used techniques include scattering methods like dynamic light scattering (DLS),¹⁴ small-angle X-ray scattering (SAXS),¹⁵ or neutron scattering; imaging methods like electron microscopy (EM),^16,17 and dark field microscopy;¹⁸ and more specialised methods such as the use of nanopores for size and shape studies¹⁹ and centrifugation for density and size measurements.²⁰ While these classical methods form the cornerstone of NP analysis, they come with inherent challenges.²¹

DLS, for instance, is favoured for being non-destructive and fast, providing hydrodynamic radius distributions.¹⁴ However, it requires special caution when carrying out the measurements, as even small amounts of aggregates or larger particles can skew the measurement results.²² This highlights the need for complementary single-particle detection methods that can provide a direct measurement of the particle size distribution. However, such methods require large datasets and robust algorithms to detect individual particles.

Imaging methods, especially EM, offer direct visualisation of the NPs, yielding their size and providing morphological features. This can be vital for detailed NP analysis, but EM can suffer from poor statistics due to a limited field of view and possible artefacts in the image. Larger areas can be imaged to improve sampling, but this increases the analysis workload.²³ This underscores the need to examine a large number of particles over larger areas. To overcome the limited field of view and mitigate preparation artefacts, multiple images need to be taken over a larger area, allowing more particles to be captured but adding to the tedious task of analysis. Software such as ImageJ²⁴ with its associated plugins can improve this, such as with automated circle detection or thresholding measurements. Recent developments in EM NP characterisation include using machine learning to extract morphological statistics.¹³

Despite the valuable insights provided by ensemble- and image-based methods, their limitations necessitate a thoughtful approach to experimental design and data interpretation. Given these challenges, we propose the use of 2D Class Averages (2D-CA), a step within Single Particle Analysis workflow to automate and facilitate image-based NP characterisation in order to catch up with the ensemble measurement capabilities of DLS, aiming to enhance the precision and reliability of challenging NP systems.

Single particle analysis software such as CryoSPARC,²⁵ available for free for non-profit research and RELION,²⁶ a license-free, open-sourced software, are designed for molecular reconstruction by averaging numerous images of individual particles to enhance the signal-to-noise ratio.²⁷ Importantly, the alignment process in 2D-CA methods often employs fast Fourier transforms (FFTs) and cross-correlation to accurately align and group individual particle images into coherent 2D classes.^28,29 By aligning and averaging large datasets of particle images, 2D-CA techniques improve the resolution of structural features that are otherwise obscured by noise in individual images.³⁰ These tools, however, also allow for the precise determination of particle size, shape, and distribution, addressing the limitations of traditional techniques by providing high-resolution insights with ensemble-like measurements.³¹ By integrating 2D-CA into NP characterisation workflows, we are able to automate complex image analyses, reduce human error, and achieve reproducible and accurate results, thereby enhancing the precision and reliability of NP characterisation. In this study, we apply a 2D-CA workflow (Fig. 1) to NP systems, demonstrating the method's effectiveness across different types of particles and complexities. In addition, we perform the established size characterisation methods on these systems to evaluate the performance the 2D-CA based approach of image-based NP size distribution measurement.

Fig. 1 Schematic representation of the 2D-CA process, 2D classes have been inverted for better visual continuity: (a) Acquiring the TEM data set, (b) several manually selected particles are chosen to form an initial template, this template is then used to select all matching particles in the data set. Once checked, these individual particles are cut out of the corresponding micrograph with a constant box size. (c) The ensemble of particles is then classified into a set number of possible classes. This is done using an optimisation algorithm in which the individual micrograph cut-outs are rotated and shifted in order to achieve an optimum match with the class average. As a result, all structures in the vicinity of the central particle are averaged out. (d) The diameter of the particles in the respective class can then be used for characterisation. Together with the population of the respective class, i.e. the number of particles in the class, a particle size distribution can then be plotted.

2. Experimental section

2.1 NP systems

This study investigates several NP systems. Two polystyrene NPs (PS100 and PS50), silica nanocapsules (Si70), and ultrasmall silica nanocapsules (Si10). Both the PS100 and PS50 polystyrene NPs were synthesised via polymerisation in miniemulsion.³² Both silica nanocapsules were produced using the miniemulsion technique with tetraethoxysilane (TEOS) as the primary silica precursor.³³ The gold NPs (Au10) were obtained commercially (Thermo Scientific, catalogue J67188), supplied in 0.1 mg mL⁻¹ sodium citrate with a stabiliser, and exhibited a core diameter of 10 ± 2 nm according to the suppliers certification. Finally, to demonstrate the capability to extract morphological features, we investigated a non-spherical system, e.g. Au nanorods. These systems provided a diverse range of particle sizes and morphologies, suitable for evaluating the robustness and accuracy of single-particle averaging techniques. Further details regarding the synthesis and characterisation of these particles can be found in the ESI.†

2.2 Conventional characterisation methods

To obtain a sufficiently comprehensive representation of the particle size distribution, we used a variety of conventional methods, particularly for the PS100 model system. In DLS, the hydrodynamic radius is determined via diffusion constants extracted from a correlation function. However, the hydrodynamic radius determined this way is subject to a volume basis, as a so-called z-average. This volume-weighted calculation means that large particles or agglomerates contribute significantly more to the measured mean value. Like all scattering-based methods, DLS does not provide ground truth information about the actual size distribution, as the shape (e.g. Gaussian) is inferred from the fitted correlation function rather than directly measured. Here, the DLS measurements for PS100 were performed with a commercial device at 90° (Nicomp) and additionally on a multi-angle set-up. Details of the experimental parameters can be found in the ESI.† In addition, static light scattering (SLS) measurements have been carried out. Here, the scattering intensity versus angle is fitted to a model to yield the particle diameter as the radius of gyration (R_g). We also used fluorescence correlation spectroscopy (FCS) as an additional ensemble-based method. Here, we took advantage of the fact that the PS100 particles are labelled with a fluorescent dye (Bodipy). FCS, like DLS, determines diffusion constants via a correlation function and returns a z-average diameter. Lastly, NP tracking (NPT) serves as a hybrid method, combining image-based and diffusion-based approaches. Particles in dispersion are tracked using optical microscopy, either by fluorescence or light scattering. From the trajectories, diffusion constants and particle sizes are derived. However, only a small number of particles are typically visible in each field of view, reducing the statistical confidence in the results.

On the other hand, we have the image-based characterisation methods. Here, we need to distinguish between image generation and evaluation. For NPs, i.e. objects smaller than the resolution limit of an optical microscope, an electron microscope is primarily used, i.e. either a transmission (TEM) or a scanning electron microscope (SEM). In principle, it is of minor relevance which of the two devices takes the images. The decisive factor is that the particles in the image generate sufficient contrast so that the individual particles can be easily identified with the analysis software used. In general, recording the images is unproblematic, besides sample behaviour on the respective grids. It is only important that the particles can be easily separated from the background to allow a software-based identification of individual particles. In contrast, the analysis software plays a much more important role in the evaluation. Here, the individual particles must be recognised in a secure and consistent manner, and there are a variety of analysis algorithms for image-based evaluation of the particle size distribution. The particles can still be measured by hand, i.e. by measuring the diameter of each particle. However, this method is very time-consuming and not very efficient. For round particles, an algorithm based on the Hough transformation can be used, which can identify round objects in an image. This method is available under the name “DetectCircles” as a plug-in for the image processing software ImageJ.²⁴ This tool is particularly suitable if the particles overlap in the image. Pixel-based methods would identify one single particle from several overlapping particles, whereas the Hough transform is sensitive to round objects and thus detects the individual particle sizes. However, this method is limited to perfectly spherical particles. In addition, there are many other image analysis methods that all work more or less according to the same principle. Depending on the grey value of the image pixels, they are discriminated into background and particles. The contiguous pixels of the particles are then measured according to size. This basic principle has been refined further and further throughout development. One example of this is the interactive learning and segmentation toolkit Ilastik.³⁴ Here, the user interactively trains the software to distinguish particles from background, followed by object classification to exclude false positives based on features such as shape, holes, or aspect ratio. This approach allows image analysis to be tailored to varying particle shapes and raw data quality.

2.3 NP 2D classification

With 2D-CA, we take a completely different approach and no longer use pixel discrimination in particles and background. Instead, the entire particle, including its environment, is examined. In the first step, the software is interactively trained to identify the desired particles and then divide them into different classes using Bayesian classification. Here, 2D classification refers to the process of averaging together similar particle images to enhance signal and reduce noise, helping to group particles with shared orientations or features. 2D-CA analysis was performed using CryoSPARC, a widely used molecular reconstruction and particle analysis software suite. CryoSPARC is designed with a user-friendly web-based UI, making it easier for first-time users, particularly in tasks such as particle picking and template matching for large-scale automated particle picking. Although both CryoSPARC and RELION offer guides and tutorials, we found CryoSPARC's resources to be more accessible and easier to follow, especially for users new to particle analysis workflows. For compatibility, all images were acquired automatically via SerialEM³⁵ at the same magnification and within a defocus range of −2 to −6 μm for lower magnifications and −2 to −4 μm for higher magnifications. The number of micrographs varied depending on particle density; fewer images were required for monodisperse samples, while more extensive datasets were necessary for polydisperse or sparse samples. Images were pre-processed using standard steps in CryoSPARC (Fig. 2), including motion correction if images are collected as frames and Correlation Transfer Function (CTF) estimation. Representative particles were manually picked to create initial templates, with box sizes adjusted to accommodate the largest particles plus ∼20% for variations. This initial step typically requires 30–80 particles, depending on sample diversity. These templates were then refined using 2D classification to identify homogeneous groups of particles, ensuring high-quality starting points for automated particle picking. Automated template picking was applied to the entire dataset, leveraging the refined templates. Parameters such as box size and particle size were based on the manually picked dataset, with an NCC (Normalised Cross-Correlation) score threshold optimised to balance false positives and negatives. An NCC threshold of 0.4 provided a reliable balance across most data sets. Automated picks were then reviewed and refined in subsequent rounds of 2D classification, where poorly defined or overlapping classes were iteratively removed. The process was repeated until clearly defined particle classes were obtained. Final particle class images are saved and used to calculate particle diameters. These diameters were measured directly in software like ImageJ, allowing for precise size distributions based on class averages.

Fig. 2 2D-CA Image Analysis Workflow: After import (1) and, if necessary, drift and CTF correction (2), a small subset of NPs are manually picked to train the software (3). This manual particle picking yields a set of template images (4), which is used for the subsequent automated NP picking (5). Here, almost all particles are identified in the first step, followed by several cleaning steps in which the NCC score is set to an optimum limit value. The selected particles are then cut out of the image with a fixed box size and then subjected to several 2D classifications (6). It can be seen from the images of the class averages that the central particle is aligned by rotating and moving the box so that it is aligned with the class average. The surroundings of the particle are also included so that some of the neighbouring particles can also be recognised. Finally, after several classification runs in which “bad” classes are eliminated, the unambiguous classes are selected and used to determine the size distribution (7).

3. Results

3.1 2D-CA of polystyrene NP model system and commercial gold NPs

To evaluate the performance of 2D-CA, we characterised the PS100 colloid system using DLS, SLS, SEM, and TEM (Fig. S1–S11, ESI†) summarised in Table 1. A clear trend can be seen here that the ensemble-based measurements (DLS, FCS) and also the NPT provide a slightly higher mean value compared to the image-based methods. This reflects the fundamentally different quantities being measured. Scattering-based methods determine the diffusion coefficient of particles by analysing their autocorrelation function. The former determines the diffusion coefficient via the autocorrelation function, from which the hydrodynamic radius (R_h) is derived using the Stokes–Einstein equation. This value includes the hydration shell and thus cannot be directly compared with physical particle diameter. Ensemble methods measure the whole population, producing a mean R_h and polydispersity index (PDI), and benefit from excellent statistics due to the high number of particles sampled over time. The discrepancy in mean values also stems from how each technique averages data. DLS and FCS report a z-average (D_z ≈ Σd⁶/Σd⁵), which is weighted towards larger particles, whereas image-based methods give a number average (D_num = Σd/N), reflecting the number average mean. While z-averages can be estimated from image datasets, the reverse is difficult, complicating direct comparison.

Table 1 Comparison of mean particle diameters for PS100 as determined by the various methods. In order to compare the results of the ensemble and image-based measurements, the z-average was calculated for the latter measurements as well. A closer comparison shows that the ensemble-based methods tend to yield a slightly larger particle diameter measurement, which might be attributed to the different physical quantities measured by the different methods, e.g. R_h and diameter of the solid particle. The analysis by means of 2D-CA delivers rather clearly the same results for the number average as the other, image-based evaluation methods. For the z-average, however, the 2D-CA comes somewhat closer to the measured quantities of the scattering-based characterisation methods. This makes 2D-CA based analysis a suitable method for determining particle size

Method	Number average Dnum_avg = Σd^1/N [nm]	z-Average DDLS ≈ Σd^6/Σd^5 [nm]	Distribution stdev/mean σ/μ
a Using a multi angle setup. b Image analysis done with DetectCircles. c Manual image analysis. d PDI in DLS measurements is defined as PDIDLS = (σ/μ)^2. e Definition of z-average differs between DLS data (Rh) and SLS evaluation (Rg). f Algorithm for particle tracking includes weighting according to track length. Therefore, the diameter is actually not just a true number average. g The highly asymmetric shape of the distribution is improperly characterised by the parameters of a Gaussian distribution.
DLS (Nicomp)	81	117	0.25^d
DLS (Rh)^a		133	0.14^d
SLS (Rg)		120^e
FCS		118
NPT	158^f		(0.87)^g
CryoTEM^b	104	113	0.12
TEM^b	109	112	0.08
TEM^c	110	114	0.09
SEM^b	109	164	0.15
2D-CA	110	121	0.05

---

Despite good overall agreement, ensemble-based methods consistently measured slightly larger sizes, as shown in Table 1. This is expected, since DLS measures the hydrodynamic radius and gives an intensity-weighted average that can be skewed by a few larger particles. In systems with polydispersity or aggregates, this can lead to misleading results. Each technique addresses outliers differently: DLS may use cut-offs during cumulant analysis, image-based methods set size thresholds, and 2D-CA involves manual or automated particle selection. These cut-offs significantly affect the final z-average, and outliers are not always obvious in graphical outputs. Nevertheless, the results in Table 1 are largely consistent and collectively give a reliable estimate of PS100 particle size. The DetectCircles plugin used the same, giving a number average of 109 ± 10 nm. Due to the overlapping of the NPs, thresholding methods in Ilastik did not provide usable data.

In contrast to the other methods, 2D-CA is an image-based method which is designed to automatically measure millions of particles from thousands of micrographs due to its origin from the 3D electron microscopy reconstruction of biostructures. Therefore, we would consider the 2D-CA to be an image-based ensemble measurement, which combines excellent statistics with the advantages of image-based data. For the 2D-CA measurement given in Table 1, 2372 potential particles were initially picked from only seven micrographs (Fig. 3(A) and Fig. S28, ESI†) in the first run. After reviewing and refining the selections, primarily by adjusting the normalised cross-correlation (NCC) score threshold in the software to 0.4, we reduced the dataset to a final of 1044 particles. While manual selection might suppress very rare outliers due to selection bias, the large dataset helps to minimise this effect. The final 2D-CA analysis produced 11 distinct 2D classes (Fig. 3(B) and Fig. S29, ESI†), comprising 1043 particles, with an average diameter of 110 ± 6 nm. The corresponding 2D-CA workflow in cryoSPARC is shown in Fig. S39 (ESI†). The 2D-CA approach yielded number-based diameters that closely matched those derived from conventional analysis via TEM and SEM using DetectCircles or manual analysis, confirming its efficacy in characterising single particles (Fig. 3(C)). Unlike traditional methods, 2D-CA offers a semi-automated, high-throughput workflow that balances speed, image quality, and robust statistics. While it enables automated particle selection and high-resolution imaging, the resulting 2D classes are not size-controllable and must be binned into histograms to produce a particle size distribution (Fig. S26 and Fig. S27, ESI†).

Fig. 3 2D-CA of PS100 polystyrene NPs: (A) example of a raw micrograph used for analysis (B) example of the resulting 2D classes including the class population numbers. (C) Histogram showing the size distribution as reconstructed from 11 class averages, yielding a number average of 110 nm for the PS100 NPs. Histogram binning is 4 nm. Scale bars (A) 500 nm and (B) 100 nm.

In addition to the PS100 system, we applied 2D-CA to the commercial Au10 particles. These particles come with a certificate of analysis with a size of 10 ± 2 nm. For 2D-CA, from 5 micrographs, a total of 75 NPs were manually picked, creating 6 classes, which were used for template picking. Automated picking identified 3072 NPs, of which 2857 were used in the first round of classification. The excluded particles were mainly those at the edges of micrographs or overlapping picks with conflicting radii. After 2 rounds of 2D classifications, removing any classes not displaying a clear NP, a total of 2587 particles were used to create 18 classes for measurement, with an average of 9.9 ± 1 nm. For manual measurement, the average of the TEM image over 200 particles, the average was 9.5 ± 1.7 nm (Fig. S36–S38), ESI.†

3.2 2D-CA of bimodal polystyrene NP

We next tested the 2D-CA method on a bimodal system to evaluate its ability to distinguish and classify two differently sized particle populations from a single dataset. For this, a mixture of PS100 and PS50 polystyrene NPs (67 nm hydrodynamic diameter) was used. Particles in the TEM micrographs often appear agglomerated or overlapping (Fig. 4(A)), making automated detection with tools like Ilastik and DetectCircles challenging. For example, only 44% of DetectCircles’ selections matched were manually assessed to be correct (see ESI,† Fig. S13–S15).

Fig. 4 PS Mixed system (A) raw example micrograph, scale bar 500 nm (B) example 2D classes including the class population numbers, scale bar 100 nm (C) histogram of class average sizes when analysing both large and small systems together with a histogram class binning of 4 nm (D) histogram of class average sizes of PS50 NPs from the same mixed system, histogram class binning of 4 nm.

From 10 micrographs, 32 NPs (both large and small) were manually selected to generate six templates (two large, four small). Template picking identified 4156 particles, reduced to 3925 after initial inspection (Fig. S30 and S31, ESI†). Following two rounds of 2D classification, 3669 particles remained. The larger PS100 particles formed three classes (1790 particles) with an average size of 111 ± 5 nm, while the smaller PS50 particles formed three classes (1865 particles), averaging 57 ± 5 nm (Fig. 4). For comparison, all particles were also forced into just two classes, yielding single-class averages of 110 nm and 56 nm. Further subclassification of the 56 nm group into 50 classes revealed that 26 classes contained usable particles, with only 4% being unmeasurable and 3.5% incorrectly picked. The remaining particles averaged 55.5 nm, consistent with previous values.

3.3 2D-CA of silica nanocapsules

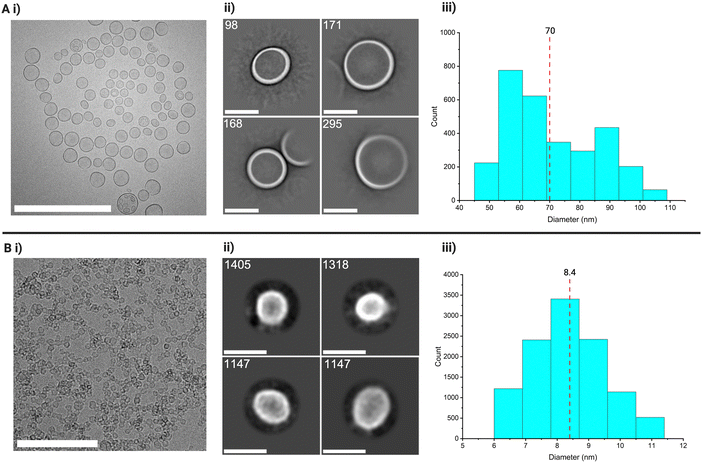
Having established the quality of the 2D-CA method for NPs, we now move to hollow NPs/nanocapsules (NCs). These present a greater challenge due to their internal contrast profile, spherical variation, and aspect ratio, all of which can influence the FFT used during particle alignment and potentially lead to misalignment in the averaging process. In projection, capsule-like particles typically appear as hollow circles in cryo-TEM imaging. To evaluate the performance of 2D-CA on such systems, we studied two types of NCs: larger silica nanocapsules (Si70 ∼70 nm) and ultrasmall silica nanocapsules (Si10, ∼5–10 nm). The larger NCs, Si70, were selected to assess the method for skewed morphologies, while the ultrasmall Si10 NCs served as a more challenging test case due to their low contrast and strong tendency to aggregate. For imaging, we used cryo-TEM, primarily to exclude drying artefacts.

For the Si70 system, from 27 collected micrographs, 87 particles were manually selected to generate initial templates. Eight template classes (69 particles) were created, leading to 16 433 picked particles, reduced to 5023 after inspection (Fig. S32, ESI†). Multiple rounds of 2D classification removed artefacts and overlaps, resulting in 20 final classes containing 2972 particles with an average size of 70 ± 15 nm (Fig. 5(A)). Ilastik detected particles with an average size of 70 ± 9 nm, though the narrow SD indicated underrepresentation of smaller/larger species. DetectCircles showed 52% accuracy and a number average of 75 ± 20 nm. DLS, as expected, skewed to larger sizes with a z-average of 146 ± 107 nm (Fig. S16–S22 ESI†). Neither Ilastik nor DetectCircles could reliably detect or quantify particles for this system.

Fig. 5 (A) 2D-CA of Si70: (i) raw micrograph, scale bar 200 nm (ii) Example 2D classes with corresponding number of particles in class, scale bar 50 nm (iii) histogram of 20 class average sizes with histogram class binning of 8 nm. (B) 2D-CA of Si10: (i) raw TEM micrograph, scale bar 50 nm (ii) Example 2D classes with corresponding number of particles in class, scale bar 10 nm (iii) histogram of 15 class average sizes with histogram class binning of 0.9 nm.

We then applied the method to Si10 ultrasmall nanocapsules, which are difficult to characterise due to low contrast and aggregation. DLS showed a hydrodynamic diameter of 294 nm, reflecting clusters rather than individual particles (Fig. S23 and S24 ESI†). Aggregation also affected cryo-EM image quality (Fig. 5(A)), making this a challenging yet ideal test for single particle analysis, which can, in some cases, resolve overlapping borders. Here, 29 micrographs were collected, and 36 particles were manually selected. Three classes (15 particles) were used for template picking, yielding 42 752 particles, reduced to 39 742 after inspection (Fig. S33 ESI†). 2D classification produced 15 final classes with 11 220 particles, averaging 8.4 ± 0.5 nm (Fig. 5(B)-iii).

3.3 2D-CA of gold nanorods

Finally, we applied the 2D-CA approach to a non-spherical system, gold nanorods (Fig. 6(A) and Fig. S34, S35, ESI†). From 21 micrographs, 39 nanorods were manually selected, creating 2 classes for picking. From the template picking, a total of 9937 particles were extracted for the first 2D classification. From here, only classes with clear single nanorods, ie not multiple rods in a single class, were selected. After 2 rounds of 2D classification, 9 classes containing a total of 2432 particles were measured (Fig. 6(B)). The measured classes gave an average length of 39 ± 2 nm and a width of 11.5 ± 1 nm (Fig. 6(C)). This aligns with the manual measurements over 200 particles with a measured length of 39 ± 7 nm and a width of 12 ± 2 nm. As shown in Fig. 6(B), the class averages display a slight broadening at the axial ends compared to the width, suggesting that the variation in particle length is somewhat greater than the variation in width within each class. This averaged visualisation of morphological variability could serve as a useful descriptor in future analyses, although a more detailed investigation was beyond the scope of this study.

Fig. 6 Au Nanorod system (A) raw example micrograph, scale bar 250 nm (B) example 2D classes including the class population numbers, scale bar 40 nm (C) histogram of class average sizes when analysing both width and length of the nanorods with a histogram class binning of 1 nm.

4. Discussion

A major issue for conventional, automated image analysis is the overlapping of primary particles in the acquired micrographs. This results in merged particles being misidentified as larger single ones, similar to agglomeration issues in scattering. This effect can already be observed in the analysis of the PS100 NPs. In Fig. 2(A) most of the NPs are in contact with their neighbours; some are overlapping. The Hough transform-based algorithm of DetectCircles can still provide good results here due to the perfectly round particles (Fig. S7, S8 and S10, ESI†), but it fails with the bimodal mixture (Fig. S14, ESI†) due to too many false positives identified particles and also with the cryo-TEM images of the NC of Si70 the success rate is too low for a reliable, automated measurement (Fig. S17, ESI†).

A similar scenario can be seen for image analysis with the Ilastik software package. Here, it is already the case that touching particles can no longer be separated and thus also lead to digital agglomeration, as can already be seen from the segmentation results of the images from PS100. Occasionally, isolated particles yield useful results, as in the analysis of Si70, and then also lead to a sufficiently useful particle size distribution, as shown in Fig. S18–S22 (ESI†). However, the efficiency, i.e. the ratio of detected to non-detected particles, is very low in this case. Also, for the bimodal model system and in particular for the Si10 it is shown that an evaluation by means of pixel and subsequent object classification by the Ilastik software is doomed to failure (Fig. S15 and S25, ESI†). In addition, this system is also not accessible for characterisation using DLS, as the primary particles are highly agglomerated and thus an average agglomerate size is measured, as shown in Table 2. Overall, Table 2 summarises that the 2D-CA evaluation in all four examined systems corresponds very well with the manual image analyses. Manual analysis remains most reliable for complex images, despite bias and limited statistics. 2D-CA, in contrast, overcomes these challenges by enabling the analysis of thousands of individual particles, providing a robust statistical foundation and reducing operator bias through automated particle identification and classification. 2D-CA closely matches hand-measured data, but with the addition of larger datasets due to the automation of particle picking.

Table 2 Comparison of particle diameter between methods. Manual measurement made over 200 particles

NP	DLS Z average (nm) [SD]	TEM manual measurement number average (nm) [SD]	2D-CA number average (nm) [SD]	SPA total number of particles [micrographs collected]
a Particle size as certified by the supplier. b DLS is not an appropriate measurement method for this system (Si10) due to clustering of the particles (Fig. S25, ESI).
Polystyrene (PS100)	133 [18]	110 [9]	110 [6]	1043 [7]
Polystyrene (PS50)	67 [18]	51 [10]	56 [5]	1675 [10]
Gold NPs (Au10)^a	N/A	9.5 [1.7]	9.9 [1]	2587 [5]
Silica NCs (Si70)	146 [68]	67 [20]	70 [15]	2970 [214]
Ultra small silica NCs (Si10)	294 [178]^b	7.6 [1.4]	8.4 [0.5]	11 120 [29]
Gold nanorods (AuNR) length, width	N/A	39, 12 [7, 2]	40, 11.5 [2, 1]	2432 [7]

---

For PS100 NPs, 2D-CA produced results consistent with conventional imaging but with enhanced throughput and reduced variability. It also demonstrated superior accuracy in handling bimodal systems, as shown by the clear separation of mixed particle populations in the dual-sized polystyrene system. Beyond standard NPs, 2D-CA performed well with challenging systems like silica nanocapsules. For large silica nanocapsules, 2D-CA provided detailed size distributions, addressing variability less apparent in DLS or image-based thresholding. For ultrasmall silica nanocapsules, where traditional methods struggle with low contrast and clustering, 2D-CA distinguished individual particles, enabling precise measurements of sub-10 nm features. The iterative classification process in 2D-CA was particularly beneficial for these complex systems. While initial classifications may misrepresent outliers, multiple refinement steps ensured accurate final size distributions. Additionally, 2D-CA optimised the analysis of small datasets, as in the case of PS100, where only seven micrographs were analysed, by efficiently using all available particles rather than discarding suitable ones or misclassifying them.

However, A notable limitation of 2D-CA is the lack of flexibility in selecting the size of bins in the 2D classification results. The classes are determined by the software's internal optimisation algorithm, and the resulting particle sizes across classes are not equidistant. While this may limit visual uniformity in some cases, it reflects the natural size variation in the data and avoids user bias. This was demonstrated in the PS50/PS100 bimodal system, where 2D-CA accurately identified over 3600 particles and resolved two distinct size populations (111 ± 5 nm and 57 ± 5 nm), despite significant overlap. If needed, exported data can still be rebinned in post-processing for uniform presentation. With these considerations, 2D-CA is ultimately a robust technique when handling challenging raw image data, including low-contrast images, aggregated particles, and datasets with overlapping structures, providing reliable characterisation where conventional image analysis methods often fall short. Furthermore, as we move from relatively simple systems, such as polystyrene NPs, to more complex systems like ultrasmall, highly agglomerated silica nanocapsules, the range of available characterisation methods significantly diminishes. Traditional techniques often struggle with low signal-to-noise ratios, clustering effects, or artefacts, especially when dealing with highly polydisperse or ultrasmall particles. In contrast, 2D-CA demonstrates remarkable versatility across these systems, providing size distributions and morphological insights where other methods fail. This gain in morphological detail can be seen very clearly in the NC systems. For example, not only the particle size but also the thickness of the capsule shell could be determined from the averaged classes. Moreover, 2D-CA is not limited to spherical particles. Its classification approach can also accommodate anisotropic shapes, such as nanorods, allowing the extraction of both length and width from distinct class averages. This broadens its applicability to a wider range of NP morphologies beyond conventional spheres.

5. Conclusion

The integration of 2D-CA tools into NP characterisation workflows presents a significant opportunity for the nanomaterial field. By combining the high-resolution capabilities of electron microscopy with the large-scale ensemble analysis of 2D-CA, we can provide a more comprehensive and accurate characterisation of NPs with a robust statistical basis. This approach enhances the precision and reliability of NP studies and simplifies the analysis process, making it more accessible and efficient for researchers. Crucially, 2D-CA demonstrates versatility across different NP systems, overcoming the limitations of methods like thresholding, constrained by strict requirements and lacking adaptability. The successful application of 2D-CA to various NP systems in this study underscores its potential to streamline and simplify characterisation while also being able to visualise the variations in the system made visible by 2D classification. Furthermore, we can also envision that 2D classification and the associated averaging process can also be used in other areas of image analysis. Especially for radiation-sensitive samples, which have a certain self-similarity, the signal-to-noise ratio can be significantly improved using 2D-CA. This is already used in the original application of SPA, i.e. the atomic reconstruction of proteins, to increase the signal-to-noise ratio via averaging. Further application examples might include cryo-EM imaging of lipid double membranes or the averaging of high-resolution lattice planes of polymer crystals, which are extremely radiation-sensitive. However, 2D-CA is not restricted to EM data at all, but can be used in any field where images of self-similar objects need to be analysed.

Author contributions

Iain Harley – conceptualisation, methodology, investigation, formal analysis, data curation, manuscript writing. Anke Kaltbeitzel – data analysis, formal analysis, data curation. Francesca Mazzotta – data analysis, formal analysis, manuscript writing. Kaloian Koynov – FCS measurements and analysis. Sarah S. Lembke – particle synthesis and DLS analysis. Thao P. Doan-Nguyen – particle synthesis and DLS characterisation. Katharina Landfester – supervision, funding acquisition, writing the manuscript. Ingo Lieberwirth – conceptualisation, project administration, supervision, manuscript writing.

Data availability

Data for this article have been included as part of the ESI.† Raw data have been deposited to a repository and will be made available via a DOI.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors wish to acknowledge Katja Klein for her synthesis of the NPs used in this project and Kween Saimuang for their synthesis of the gold nanorods. Christine Rosenauer for the DLS advice and measurements, and Gunnar Glasser and Katrin Kirchhoff for their help in electron microscopy characterisation. This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement SuperCol (no. 860914). Open Access funding provided by the Max Planck Society.

References

1. C. I. Idumah, C. M. Obele, E. O. Emmanuel and A. Hassan, Recently Emerging Nanotechnological Advancements in Polymer Nanocomposite Coatings for Anti-Corrosion, Anti-Fouling and Self-Healing, Surf. Interfaces, 2020, 21, 100734,  DOI:10.1016/j.surfin.2020.100734.
2. L. Shang, K. Nienhaus, X. Jiang, L. Yang, K. Landfester, V. Mailänder, T. Simmet and G. U. Nienhaus, Nanoparticle Interactions with Live Cells: Quantitative Fluorescence Microscopy of Nanoparticle Size Effects, Beilstein J. Nanotechnol., 2014, 5(1), 2388–2397,  DOI:10.3762/BJNANO.5.248.
3. I. Montes-Burgos, D. Walczyk, P. Hole, J. Smith, I. Lynch and K. Dawson, Characterisation of Nanoparticle Size and State Prior to Nanotoxicological Studies, J. Nanoparticle Res., 2010, 12(1), 47–53,  DOI:10.1007/S11051-009-9774-Z/FIGURES/6.
4. C. N. R. Rao and K. Biswas, Characterization of Nanomaterials by Physical Methods, Annu. Rev. Anal. Chem., 2009, 2, 435–462,  DOI:10.1146/annurev-anchem-060908-155236.
5. S. Jiang, M. Mottola, S. Han, R. Thiramanas, R. Graf, I. Lieberwirth, V. Mailänder, D. Crespy and K. Landfester, Versatile Preparation of Silica Nanocapsules for Biomedical Applications, Part. Part. Syst. Charact., 2020, 37, 1900484,  DOI:10.1002/ppsc.201900484.
6. N. Hoshyar, S. Gray, H. Han and G. Bao, The Effect of Nanoparticle Size on In Vivo Pharmacokinetics and Cellular Interaction, Nanomedicine, 2016, 11(6), 673–692,  DOI:10.2217/nnm.16.5.
7. A. Zhang, K. Meng, Y. Liu, Y. Pan, W. Qu, D. Chen and S. Xie, Absorption, Distribution, Metabolism, and Excretion of Nanocarriers in Vivo and Their Influences, Adv. Colloid Interface Sci., 2020, 284, 102261,  DOI:10.1016/j.cis.2020.102261.
8. S. A. Kulkarni and S.-S. Feng, Effects of Particle Size and Surface Modification on Cellular Uptake and Biodistribution of Polymeric Nanoparticles for Drug Delivery, Pharm. Res., 2013, 30(10), 2512–2522,  DOI:10.1007/s11095-012-0958-3.
9. K. Loza, M. Heggen and M. Epple, Synthesis, Structure, Properties, and Applications of Bimetallic Nanoparticles of Noble Metals, Adv. Funct. Mater., 2020, 30(21), 1909260,  DOI:10.1002/adfm.201909260.
10. P. Huang, L. Zhang, Q. Yan, D. Guo and G. Xie, Size Dependent Mechanical Properties of Monolayer Densely Arranged Polystyrene Nanospheres, Langmuir, 2016, 32(49), 13187–13192,  DOI:10.1021/acs.langmuir.6b03481.
11. H. Tao, T. Wu, M. Aldeghi, T. C. Wu, A. Aspuru-Guzik and E. Kumacheva, Nanoparticle Synthesis Assisted by Machine Learning, Nat. Rev. Mater., 2021, 6(8), 701–716,  DOI:10.1038/s41578-021-00337-5.
12. S. Mourdikoudis, R. M. Pallares and N. T. K. Thanh, Characterization Techniques for Nanoparticles: Comparison and Complementarity upon Studying Nanoparticle Properties, Nanoscale, 2018, 10(27), 12871–12934,  10.1039/C8NR02278J.
13. M. M. Modena, B. Rühle, T. P. Burg and S. Wuttke, Nanoparticle Characterization: What to Measure, Adv. Mater., 2019, 31(32), 1901556,  DOI:10.1002/ADMA.201901556.
14. N. Farkas and J. A. Kramar, Dynamic Light Scattering Distributions by Any Means, J. Nanoparticle Res., 2021, 23(5), 1–11,  DOI:10.1007/S11051-021-05220-6/FIGURES/4.
15. T. Li, A. J. Senesi and B. Lee, Small Angle X-Ray Scattering for Nanoparticle Research, Chem. Rev., 2016, 116(18), 11128–11180,  DOI:10.1021/acs.chemrev.5b00690.
16. W. D. Pyrz and D. J. Buttrey, Particle Size Determination Using TEM: A Discussion of Image Acquisition and Analysis for the Novice Microscopist, Langmuir, 2008, 24(20), 11350–11360,  DOI:10.1021/LA801367J/ASSET/IMAGES/LARGE/LA-2008-01367J_0012.JPEG.
17. R. Fisker, J. M. Carstensen, M. F. Hansen, F. Bødker and S. Mørup, Estimation of Nanoparticle Size Distributions by Image Analysis, J. Nanoparticle Res., 2000, 2(3), 267–277,  DOI:10.1023/A:1010023316775/METRICS.
18. T. Wagner, H. G. Lipinski and M. Wiemann, Dark Field Nanoparticle Tracking Analysis for Size Characterization of Plasmonic and Non-Plasmonic Particles, J. Nanoparticle Res., 2014, 16(5), 2419,  DOI:10.1007/S11051-014-2419-X.
19. R. Maugi, P. Hauer, J. Bowen, E. Ashman, E. Hunsicker and M. Platt, A Methodology for Characterising Nanoparticle Size and Shape Using Nanopores, Nanoscale, 2019, 12(1), 262–270,  10.1039/C9NR09100A.
20. R. P. Carney, J. Y. Kim, H. Qian, R. Jin, H. Mehenni, F. Stellacci and O. M. Bakr, Determination of Nanoparticle Size Distribution Together with Density or Molecular Weight by 2D Analytical Ultracentrifugation, Nat. Commun., 2011, 2(1), 335,  DOI:10.1038/ncomms1338.
21. E. J. Cho, H. Holback, K. C. Liu, S. A. Abouelmagd, J. Park and Y. Yeo, Nanoparticle Characterization: State of the Art, Challenges, and Emerging Technologies, Mol. Pharmaceutics, 2013, 10(6), 2093–2110,  DOI:10.1021/mp300697h.
22. W. Schärtl, Light Scattering from Polymer Solutions and Nanoparticle Dispersions, Springer Laboratory, Springer, Berlin, Heidelberg, 2007.
23. B. Michen, C. Geers, D. Vanhecke, C. Endes, B. Rothen-Rutishauser, S. Balog and A. Petri-Fink, Avoiding Drying-Artifacts in Transmission Electron Microscopy: Characterizing the Size and Colloidal State of Nanoparticles, Sci. Rep., 2015, 5(1), 9793,  DOI:10.1038/srep09793.
24. T. J. Collins, ImageJ for Microscopy, Biotechniques, 2007, 43(1 Suppl), 25–30,  DOI:10.2144/000112517.
25. A. Punjani, J. L. Rubinstein, D. J. Fleet and M. A. Brubaker, cryoSPARC: Algorithms for Rapid Unsupervised Cryo-EM Structure Determination, Nat. Methods, 2017, 14(3), 290–296,  DOI:10.1038/nmeth.4169.
26. S. H. W. Scheres, RELION: Implementation of a Bayesian Approach to Cryo-EM Structure Determination, J. Struct. Biol., 2012, 180(3), 519–530,  DOI:10.1016/j.jsb.2012.09.006.
27. J. L. Vilas, J. M. Carazo and C. O. S. Sorzano, Emerging Themes in CryoEM—Single Particle Analysis Image Processing, Chem. Rev., 2022, 122(17), 13915–13951,  DOI:10.1021/acs.chemrev.1c00850.
28. Z. Yang, J. Fang, J. Chittuluru, F. J. Asturias and P. A. Penczek, Iterative Stable Alignment and Clustering of 2D Transmission Electron Microscope Images, Structure, 2012, 20(2), 237–247,  DOI:10.1016/j.str.2011.12.007.
29. C. O. S. Sorzano, J. R. Bilbao-Castro, Y. Shkolnisky, M. Alcorlo, R. Melero, G. Caffarena-Fernández, M. Li, G. Xu, R. Marabini and J. M. Carazo, A Clustering Approach to Multireference Alignment of Single-Particle Projections in Electron Microscopy, J. Struct. Biol., 2010, 171(2), 197–206,  DOI:10.1016/j.jsb.2010.03.011.
30. C. O. S. Sorzano, J. R. Bilbao-Castro, Y. Shkolnisky, M. Alcorlo, R. Melero, G. Caffarena-Fernández, M. Li, G. Xu, R. Marabini and J. M. Carazo, A Clustering Approach to Multireference Alignment of Single-Particle Projections in Electron Microscopy, J. Struct. Biol., 2010, 171(2), 197–206,  DOI:10.1016/j.jsb.2010.03.011.
31. M. van Heel and J. Frank, Use of Multivariates Statistics in Analysing the Images of Biological Macromolecules, Ultramicroscopy, 1981, 6(1), 187–194,  DOI:10.1016/S0304-3991(81)80197-0.
32. K. Landfester, Polyreactions in Miniemulsions, Macromol. Rapid Commun., 2001, 22(12), 896–936,  DOI:10.1002/1521-3927(20010801)22:12<896::AID-MARC896>3.0.CO;2-R.
33. S. Jiang, K. Landfester and D. Crespy, Control of the Release of Functional Payloads from Redox-Responsive Nanocapsules, RSC Adv., 2016, 6(106), 104330,  10.1039/C6RA22733C.
34. S. Berg, D. Kutra, T. Kroeger, C. N. Straehle, B. X. Kausler, C. Haubold, M. Schiegg, J. Ales, T. Beier, M. Rudy, K. Eren, J. I. Cervantes, B. Xu, F. Beuttenmueller, A. Wolny, C. Zhang, U. Koethe, F. A. Hamprecht and A. Kreshuk, Ilastik: Interactive Machine Learning for (Bio)Image Analysis, Nat. Methods, 2019, 16(12), 1226–1232,  DOI:10.1038/s41592-019-0582-9.
35. M. Schorb, I. Haberbosch, W. J. H. Hagen, Y. Schwab and D. N. Mastronarde, Software Tools for Automated Transmission Electron Microscopy, Nat. Methods, 2019, 16(6), 471–477,  DOI:10.1038/s41592-019-0396-9.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00094g

---