Probing the spin spiral in Fe chains on Ir(001) using magnetic exchange force microscopy

Abstract

The collective motion of spin textures in atomic-scale one-dimensional systems enables information transmission with low electrical current at the nanometer scale. While reading such spin textures with current-free methods is essential for miniaturized spin-based schemes, directly probing them without relying on electrical techniques remains a significant challenge. In this study, we probed the spin texture in one-dimensional Fe chains on Ir(001) using magnetic exchange force microscopy. At large tip-sample distances, we found that ferromagnetic coupling with the tip apex magnetic atoms enables the readout of the spin texture in the Fe chain. At small tip-sample distances, we found that the spin texture in the Fe chain remained robust against chemical interactions within our measurement regime. Our ability to locally detect spins in a one-dimensional structure may pave the way for examining spin information as it propagates between the input and output of miniaturized spin logic devices.

---

New concepts

Spintronics, or spin-transport electronics, utilizes the spin degrees of freedom in condensed matter systems to improve information-processing technology, which has traditionally relied on electric charge. In this work, we introduce a new concept for reading spin states by demonstrating magnetic exchange force microscopy as a method to read out spin information in a finite one-dimensional Fe chain through ferromagnetic coupling between the Fe tip and the Fe chain. This approach differs from existing methods by providing a charge-independent means of accessing spin states at atomic resolution, making it fundamentally distinct from conventional spintronic readout techniques that often rely on optical methods at the macroscopic scale. Moreover, we find that the detected spin information remains robust against chemical interactions with the Fe tip, highlighting the viability of this technique as a nonintrusive spin readout tool. This finding offers additional insights for developing purely spin-based information technologies, thereby advancing the frontiers of nanoscience and nanotechnology.

1. Introduction

Magnetism in atomic-scale one-dimensional systems is a rapidly growing research field, offering exciting opportunities ranging from technological applications to the exploration of novel quantum phases.^1–8 In spintronics, atomic-scale one-dimensional systems contribute to the realization of miniaturized spin devices, where the collective motion of spin textures often serves as a connection between inputs and outputs in logic devices, enabling information transport without significant dissipative currents associated with electronic charge.^1,3,9 While spin textures have been probed using current-free methods on the macroscopic scale, direct experimental probing of spin textures in atomic-scale one-dimensional structures without relying on an electric current remains largely unexplored.^10–12

Magnetic exchange force microscopy (MExFM) is one of the fascinating tools for studying magnetic interactions at the atomic scale using a magnetic tip.^13–22 This method provides information on magnetic interactions that are commonly interpreted as direct exchange interactions (JS₁·S₂), where J is the coupling constant between two spins S₁ and S₂.^23–26 This coupling constant J determines the preferred alignment between the magnetic moments, whether they are parallel (ferromagnetic) or antiparallel (antiferromagnetic).^26–28 However, MExFM has only been applied to a limited number of surfaces, including antiferromagnetic structures (Fe/W and NiO),^13–18 and spiral structures (magnetic skyrmions and Mn/W).^19–22

To demonstrate the ability to read the spin information in a one-dimensional structure with less electric current, in this study, we perform simultaneous MExFM and spin-polarized scanning tunneling microscopy (SP-STM) imaging on the spin spiral in the one-dimensional biatomic Fe chain on Ir(001).^3,29–31 We employ a Fe tip fabricated by picking up several Fe atoms from the surface. This approach results in a weaker stray field compared to using Fe-coated tips.^13,32 By directly comparing the magnetic contrast in MExFM to that of SP-STM, at large tip-sample distances, we determine the ferromagnetic interaction between the Fe tip and the Fe chain spins.

At small tip-sample distances, the frequency shift contrast reveals chemical interactions, while the tunneling current signal distinctly displays magnetic contrasts, indicating that Fe spins remain robust against chemical interactions. Such robustness implies that the spin spiral can transfer information from one end of the chain to the other, even when the Fe tip is in chemical contact with the Fe chain. To the best of our knowledge, MExFM has not been reported on one-dimensional nanostructures thus far.

2. Results

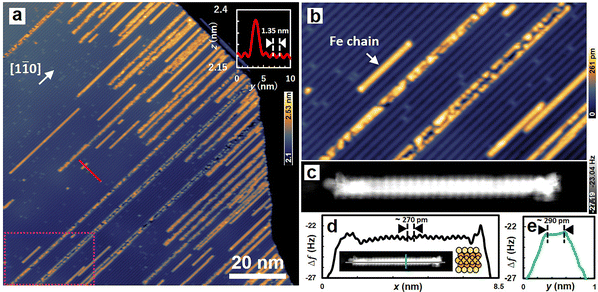
Fig. 1a presents a large-area STM topography image of Fe chains on Ir(001), obtained using a W tip. A large terrace (width ∼100 nm) features a regular arrangement of parallel trenches running along the [11̄0] direction. The distance between two adjacent trenches is approximately 1.35 nm (see inset in Fig. 1a), consistent with previous studies.^3,31 Due to these trenches, the reconstructed Ir(001) surface is an ideal template for growing self-organized one-dimensional nanostructures. As shown in previous results, the small coverage (less than 20–25% of atomic layer) of Fe results in growth solely in the trenches, forming bi-atomic chains.³³ Fig. 1b illustrates the area highlighted by the pink dashed line in Fig. 1a. To investigate the atomic structure of the Fe chain, we conducted dynamic force microscopy (DFM) imaging. The W tip was carefully approached above the Fe chain, and a DFM image was acquired in constant-height mode in a repulsive regime. Fig. 1c displays a frequency-shift (Δf) image. The bright contrast of the Fe chain relative to the Ir substrate indicates that the Fe chain protrudes from the surface. In Fig. 1c, for the first time, we experimentally achieved atomic resolution of the Fe chain on Ir(001) using DFM. Fig. 1d and e show line profiles derived from the Δf image. As seen in Fig. 1d and e, the distance between Fe atoms along the Fe chain axis is 270 pm, and that across the chain is 290 pm.

Fig. 1 (a) STM topography image of Fe chains on Ir(001), which forms on the (5 × 1) – reconstructed Ir(001) surface. Note that incomplete/discontinuous Fe chains are the surface alloy. Imaging condition: constant-current mode. I = 0.1 nA, V = +600 mV, T = 4.5 K and B = +3.0 T. Inset: Line profile measured above the Ir(001) across the Fe chain as indicated by red color. (b) Enlarged STM topography image of Fe chain within the pink dashed box in (a). (c) High-resolution DFM image of the bi-atomic Fe chain obtained by the W tip. Imaging condition: constant-height mode. V = +1.0 mV, T = 4.5 K and B = +2.0 T. (d) and (e) Line profiles obtained from the Δf image in (c). The positions of the profiles are shown in the inset by (d) gray and (e) green with a ball model of a bi-atomic Fe chain.

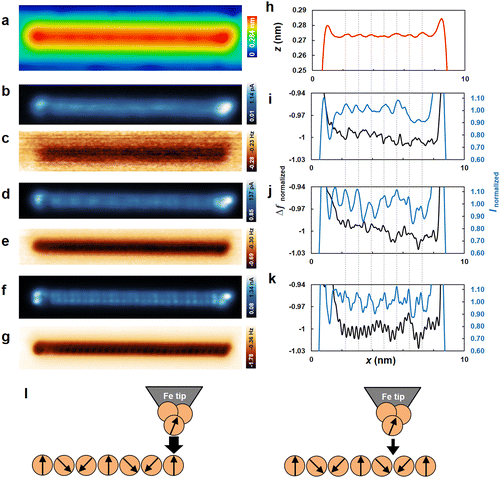
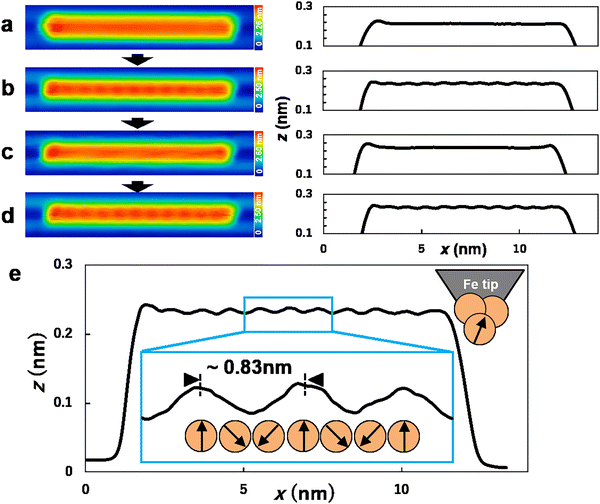
Next, we present the SP-STM images obtained by picking up several Fe atoms from the surface to the tip apex (see ESI†).^13,32 A similar method has been employed in previous SP-STM experiments.^4,13,32,34 Fig. 2a shows the STM image of the target Fe chain acquired using a W tip. This same Fe chain was subsequently scanned using the Fe tip (Fig. 2b). The magnetization of the Fe tip aligns with an external magnetic field in an upward direction due to the superparamagnetic nature of the Fe cluster.³² Fig. 2e presents an enlarged image of the topographic height shown in Fig. 2b. In Fig. 2e, a periodic structure with a length of three atomic distances of Fe atoms (∼0.83 nm ≃ 0.27 nm × 3) is observed in the Fe chain. This periodicity corresponds well with the magnetic structure of the spin spiral reported in previous SP-STM studies conducted with W tips coated with thin Fe films.^3,31 The reproducibility of SP-STM using different tips and various Fe chains is illustrated in Fig. S1 and S2 (ESI†). Hence, we conclude that the spin spiral in the Fe chain was successfully observed using the stable magnetic tip fabricated by picking up Fe atoms. It is important to note that Fig. 2e was obtained in constant-current mode under an upward external magnetic field of 3.0 T. Thus, the maxima and minima along the chain axis in the topographic height indicate positions where the magnetization components point up and down relative to the external magnetic field, respectively (see Fig. S2 and S3, ESI,† for the chain length and bias voltage dependence of magnetic contrast). When the external magnetic field was ramped to 0.0 T (3.0 T → 0.0 T), the periodic structure was barely visible, as shown in Fig. 2c (see Fig. S4 (ESI†) for the dependence of magnetic contrast on external magnetic fields). In previous experiments, these observations were attributed to fast thermal switching in the orientation of the spin spiral, which cannot be captured by the slow scan of STM.^3,31 After ramping the external magnetic field back to 3.0 T (0.0 T → 3.0 T), the magnetic contrast reappeared, as shown in Fig. 2d. In Fig. 2d, the lateral positions of the maxima and minima along the chain axis in the topographic height are qualitatively similar to those in Fig. 2b.

Fig. 2 (a)–(d) Consecutive STM topography image and the corresponding line profile of Fe chain on Ir(001). Imaging condition: constant-current mode. I = +3.0 nA, V = +600 mV, T = 4.5 K, (a) B = +3.0 T; (b) B = +3.0 T; (c) B = 0.0 T; (d) B = +3.0 T. Note that (a) and (b) were both obtained at +3.0 T, but with different tip conditions: (a) was acquired using a W tip, while (b) was acquired using an Fe tip, resulting in different tip states. (b)–(d), on the other hand, were obtained using the same Fe tip condition, with the magnetic field varied as +3.0 T, +0.0 T, and +3.0 T, respectively. (e) Enlarged image of z(x) in (b) with a schematic of the spin spiral in the Fe chain and the Fe tip. The schematics of the spin spiral are validated under similar experimental conditions, as reported in ref. 3 and 31.

Before discussing the distance dependence of the tunneling current and frequency-shift images of SP-STM and MExFM shown in Fig. 4, we present, in Fig. 3, the distance dependence of the tunneling current and frequency-shift signals, which were simultaneously obtained on top of the Fe chain by oscillating the tip. Note that we define the distance at the point conductance G₀ = 7.748 × 10⁻⁵ S as z_d = 0 nm throughout Fig. 3 and 4 (z_d = 0 nm is the lowest turnaround point of the tip oscillation cycle; see the ESI,† for the definition of z_d). Fig. 3a presents the tunneling current at the lowest turnaround point of the tip oscillation cycle versus distance curves (I_deconvolved(z_d)) obtained on top of the Fe chain. I_deconvolved(z_d) is derived from the deconvolution of the time-averaged tip oscillation of I(z_d).^35,36 In Fig. 3a, an exponential dependence is observed in I_deconvolved(z_d). Fig. 3b displays Δf_Fechain(z_d) simultaneously recorded with I(z_d) in Fig. 3a, and Δf_Ir(z_d) obtained on the Ir surface. In previous research on antiferromagnetic or spin spiral surfaces, subtracting the long-range components from Δf(z) might be challenging because the first layer of the surface is thoroughly covered with Fe or Mn atoms.^19,21 However, in this study, the dark contrast of the Fe chain is identifiable in the DFM image (see inset in Fig. 3a), which allows us to obtain Δf_SR(z_d) by subtracting Δf_Ir(z_d) from Δf_Fechain(z_d) (see Fig. S5, ESI†). Fig. 3c shows the short-range force F_SR (z_d) deduced from Δf_SR (z_d) (Δf_SR(z_d) = Δf_Fechain(z_d) − Δf_Ir(z_d)) using the Sader formula³⁷ (see Fig. S5, ESI†). The potential energy U(z_d), shown in Fig. 3d, is further deduced by integrating F_SR(z_d) in the z_d direction. In Fig. 3c and d, we observe that F_SR(z_d) and U(z_d) monotonically decrease as the tip approaches the surface, clarifying the attractive interaction.

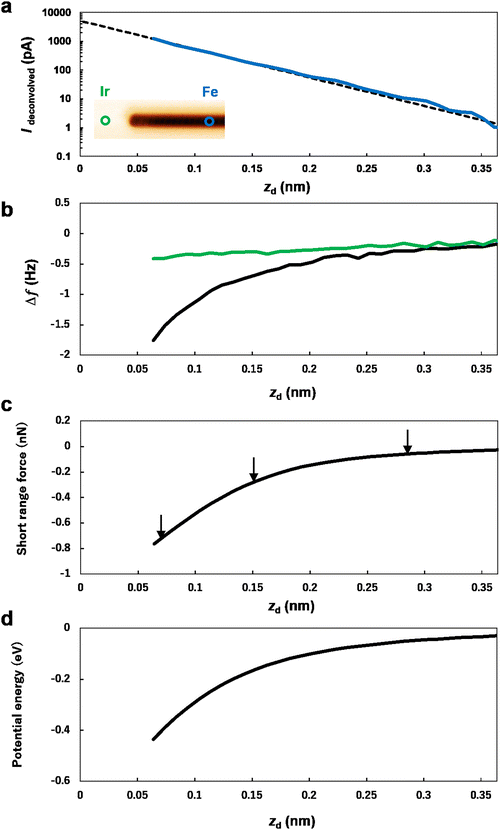Fig. 3 (a) Tunneling current I_deconvolved(z_d) after deconvolution of the tip oscillation from I(z_d). The black dotted line indicates exponential fitting. (b) Δf_Fechain(z_d) simultaneously recorded with (a) (black solid curve). Δf_Ir(z_d) obtained on top of the Ir surface (green solid curve). Tip position is indicated by circles with green (Ir surface) and blue (Fe chain) in the inset image in (a). (a) and (b) are obtained by the Fe tip at V = +65 μV, T = 4.5 K and B = +3.0 T. (c) Short-range force F_SR(z_d) obtained on top of the Fe chain. The arrows indicate the height where Fig. 4(b)–(g) were obtained. (d) Potential energy U(z_d) obtained on top of the Fe chain.

Now, we present the simultaneous observation of MExFM and SP-STM images of the Fe chain;^19,21 see full data sets in Fig. S6 (ESI†). Note that Fig. 4 was obtained using the same tip as shown in Fig. 3. First, we confirm the Fe chain using constant-current mode SP-STM without oscillating the magnetic tip, as shown in Fig. 4a. The image was obtained under an upward external magnetic field of 3.0 T, where maxima and minima along the chain axis indicate positions with magnetization components pointing up and down relative to the surface, respectively (see Fig. 4h). The same Fe chain was then imaged by oscillating the magnetic tip in constant-height mode at large tip-sample distance (z_d = 0.284 nm), medium tip-sample distance (z_d = 0.149 nm), and small tip-sample distance (z_d = 0.069 nm), with the tunneling current (I) and the Δf signals recorded simultaneously, as shown in Fig. 4b, c, d, e, f and g, respectively. The black arrows in Fig. 3c indicate the tip height at which Fig. 4b–g were obtained. To qualitatively assess the dominant effects in the signals, we normalized the I and Δf signals as I_normalized and Δf_normalized in Fig. 4(i–k) (the definitions of I_normalized and Δf_normalized are provided in the ESI†).

Fig. 4 (a) SP-STM topography image of Fe chain on Ir(001). Imaging condition: constant-current mode. V = +600 mV, I = +1.5 nA, T = 4.5 K, B = +3.0 T. (b)–(g), consecutive SP-STM (b), (d) and (f) and MExFM images (c), (e) and (g) of Fe chain on Ir(001). Imaging condition: constant-height mode, V = +65 μV, T = 4.5 K and B = +3.0 T, (b) and (c) z_d = 0.284 nm; (d) and (e) z_d = 0.149 nm; (f) and (g) z_d = 0.069 nm. (h)–(k) Line profiles obtained along the chain axis shown in (a)–(g). The dashed lines across the line profiles are the guide for the lateral positions of the local maxima of the magnetic contrast in (h). (l) A schematic diagram that visually explains the interpretation. The left panel illustrates the case of strong ferromagnetic coupling, while the right panel shows the case of weak ferromagnetic coupling.

Considering the large tip-sample distance in Fig. 4i, the maxima and minima of the I_normalized signal (blue curve in Fig. 4i) along the chain axis indicate the magnetization components pointing up and down, respectively, in agreement with their apparent height in the constant-current SP-STM image in Fig. 4a (see also Fig. 4h). On the other hand, we observe small corrugation in Δf_normalized(x) along the Fe chain (black curve in Fig. 4i). The lateral positions of the minima and maxima of the corrugation in Δf_normalized(x) agree well with the lateral positions of the maxima and minima in I_normalized(x). Moreover, the large tip-sample distance (z_d = 0.284 nm) corresponds to the attractive force regime (see Fig. 3c). Thus, the Δf_normalized contrast suggests ferromagnetic coupling, which increases with the alignment of spins at the tip apex and those at the Fe chain (Fig. 4(l)). Furthermore, we demonstrate the observation of ferromagnetic coupling using different tips on different Fe chains, as shown in Fig. S7 (ESI†).

Now, we focus on the medium and small tip-sample distances to discuss the effect of the chemical interaction between the Fe tip and the Fe chain. The tip height was decreased until individual Fe atoms were seen in the Δf image (Fig. 4d–g). Focusing on the I_normalized signals (blue curves in Fig. 4j–k), the magnetic contrast is observed at the medium tip-sample distances (blue curve in Fig. 4j), while both chemical and magnetic contrasts are evident at the small tip-sample distance (blue curve in Fig. 4k). In contrast, in the Δf_normalized signal, the chemical contrast dominates rather than the magnetic contrast as the tip-sample distance decreases (black curve in Fig. 4i–k). Individual surface atoms were imaged in the Δf signal by detecting the short-range forces associated with the onset of the chemical bond between the foremost tip atom and the surface atoms.^38,39 We identified 19 atoms from the leftmost dotted line to the rightmost dotted line, corresponding to 6 spin periods in Fig. 4k. Hence, we conclude that the magnetic structure and atomic lattices are incommensurate. Such an incommensurate Fe chain is in good agreement with previous results.²⁹

Upon comparing Fig. 3c and d and the constant-height images in Fig. 4b–g, we find ferromagnetic coupling at F_SR (z_d = 0.284 nm) ≃ −0.09 nN, and the atomic contrast at F_SR (z_d = 0.069 nm) ≃ −0.75 nN. The short-range force value of F_SR ≃ −0.75 nN at z_d = 0.069 nm is comparable to those measured in previous results on metallic surfaces using a metal tip.⁴⁰

For the potential energy, ferromagnetic coupling is observed at U (z_d = 0.284 nm) ≃ −0.05 eV, and the atomic contrast at U (z_d = 0.069 nm) ≃ −0.44 eV. The simultaneous observation of the chemical contrast in Δf_normalized and the magnetic contrast in I_normalized in Fig. 4k (at z_d = 0.069 nm) suggests that the Fe spins are robust against chemical interactions within our measurement regime. Therefore, the potential energy of U ≃ −0.44 eV at z_d ∼0.069 nm indicates that the spin spiral is robust under such strong chemical interaction. Such robustness demonstrates that the spin spiral can transport information from one end of the chain to the other, even when the Fe tip is in chemical interaction with the Fe chain. This property is important for applications as it prevents unintended changes in the information being transferred.

3. Discussion

Here, we discuss several possible mechanisms for interpreting the ferromagnetic coupling between the Fe tip and the Fe chain spins. The first interpretation is that the direct exchange interaction occurs between Fe atoms in the Fe tip S_Fe tip and in the Fe chain S_Fe chain, where S_Fe tip is the spin in the Fe tip and S_Fe chain is the spin in the Fe chain (JS_Fe tip·S_Fi chain). The Bethe–Slater curve indicates that ferromagnetic interaction is favored for a large atomic spacing, while antiferromagnetic interaction is stabilized at smaller atomic spacing.^24,26,27 In Fig. 3 and 4, we found ferromagnetic coupling at z_d = 0.284 nm (Fig. 4(l)). Accordingly, the ratio of atomic separation to the diameter of the 3d orbital in our experiment (0.284 nm + d_Fe)/d_Fe ∼2.8 (assuming the Fe diameter as d_Fe = 0.158 nm) is sufficiently larger than the distance of the antiferromagnetic coupling in the Bethe–Slater curve.²⁶

It can be interpreted that there is an indirect interaction between two neighboring Fe atoms with unpaired 3d electrons via 4s conduction electrons. Such an interaction has been theoretically studied by K. Tao et al. for an STM with a Cr tip positioned above a magnetic atom protruding from the surface.⁴¹ At large tip-sample distances, ferromagnetic indirect coupling increases; however, at small tip-sample distances, d–d covalent admixture leads to antiferromagnetic interaction.^41–43 This interpretation is consistent with the ferromagnetic coupling observed by MExFM at large tip-sample distances in our experiment. We found ferromagnetic coupling at z_d ≃ 0.284 nm. Accordingly, the atomic separation of 0.284 nm + d_Fe = 0.442 nm in our experiment is comparable to the tip-sample distance of ferromagnetic coupling observed with the Cr tip. Performing DFT calculations that consider the Fe tip, Fe chain, and Ir surface may facilitate a more detailed quantitative comparison with experimental results. However, we tentatively interpret our experimental results as including both direct exchange interactions and indirect interactions. Moreover, the quantitative evaluation of the magnetic interactions with the distance, as performed in previous works,^15,19,21 allows us to determine the magnetic exchange force between an Fe tip and an Fe chain. Magnetic exchange forces can be extracted from the frequency shift curves as a function of the tip-surface distance, recorded at the maxima and minima of the magnetic contrast in MExFM images of the Fe chain. Such a study could expand our understanding of the interaction between an Fe chain and an Fe tip. However, the observed frequency shift contrasts at large tip-sample distances in Fig. 4(c) and Fig. S7(b) (ESI†) still directly indicate that the interaction between the Fe tip and the Fe chain is due to ferromagnetic coupling. Thus, we conclude that ferromagnetic coupling at large tip-sample distances plays a key role in reading the spin information of Fe chains on Ir(001).

4. Conclusions

In summary, we probed the spin information using MExFM on one-dimensional Fe chains on Ir(001). Our results demonstrate ferromagnetic interaction at a large tip-sample distance and chemical interaction at a small tip-sample distance. Such ferromagnetic interaction enables us to read out the spin information in the Fe chain. Looking ahead, we believe that MExFM can be utilized to read spin information in a one-dimensional structure with controlled input, potentially extending its application to new magnetic devices.

Author contributions

Conceptualization: Y. S., Y. Y., Y. A. AFM, and STM observation: Y. A., A. I., W. K., R. N. Writing original draft: Y. A. Writing review and editing: Y. A., Y. Y., Y. S.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank T. Ozaki and M. Fukuda for the discussions. This work was supported by JST FOREST Program Grant Number JPMJFR203J and JSPS KAKENHI Grants No. 25K17946, No. 25K17933, No. JP24H01175, No. JP23K13656, No. JP22H04496, No. JP20H05849, No. JP21K18867, and No. JP22H01950. Y. S. acknowledges the support of the Asahi Glass Foundation and the Murata Science Foundation. Y. A. acknowledges the support of the Iketani Science and Technology Foundation.

References

1. A. A. Khajetoorians, J. Wiebe, B. Chilian and R. Wiesendanger, Science, 2011, 332, 1062–1064.
2. R. Elbertse, D. Coffey, J. Gobeil and A. Otte, Commun. Phys., 2020, 3, 94.
3. M. Menzel, Y. Mokrousov, R. Wieser, J. E. Bickel, E. Vedmedenko, S. Blügel, S. Heinze, K. von Bergmann, A. Kubetzka and R. Wiesendanger, Phys. Rev. Lett., 2012, 108, 197204.
4. S. Loth, S. Baumann, C. P. Lutz, D. Eigler and A. J. Heinrich, Science, 2012, 335, 196–199.
5. R. Pawlak, M. Kisiel, J. Klinovaja, T. Meier, S. Kawai, T. Glatzel, D. Loss and E. Meyer, npj Quantum Inf., 2016, 2, 1–5.
6. H. Kim, A. Palacio-Morales, T. Posske, L. Rózsa, K. Palotás, L. Szunyogh, M. Thorwart and R. Wiesendanger, Sci. Adv., 2018, 4, eaar5251.
7. A. Kamlapure, L. Cornils, J. Wiebe and R. Wiesendanger, Nat. Commun., 2018, 9, 3253.
8. L. Schneider, S. Brinker, M. Steinbrecher, J. Hermenau, T. Posske, M. dos Santos Dias, S. Lounis, R. Wiesendanger and J. Wiebe, Nat. Commun., 2020, 11, 4707.
9. E. Vedmedenko and D. Altwein, Phys. Rev. Lett., 2014, 112, 017206.
10. G. Yu, P. Upadhyaya, K. L. Wong, W. Jiang, J. G. Alzate, J. Tang, P. K. Amiri and K. L. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 104421.
11. M. Wu, T. Chen, T. Nomoto, Y. Tserkovnyak, H. Isshiki, Y. Nakatani, T. Higo, T. Tomita, K. Kondou and R. Arita, et al., Nat. Commun., 2024, 15, 4305.
12. Z. Luo, A. Hrabec, T. P. Dao, G. Sala, S. Finizio, J. Feng, S. Mayr, J. Raabe, P. Gambardella and L. J. Heyderman, Nature, 2020, 579, 214–218.
13. R. Wiesendanger, Rev. Mod. Phys., 2009, 81, 1495.
14. U. Kaiser, A. Schwarz and R. Wiesendanger, Nature, 2007, 446, 522–525.
15. F. Pielmeier and F. J. Giessibl, Phys. Rev. Lett., 2013, 110, 266101.
16. R. Schmidt, C. Lazo, H. Holscher, U. Pi, V. Caciuc, A. Schwarz, R. Wiesendanger and S. Heinze, Nano Lett., 2009, 9, 200–204.
17. R. Schmidt, C. Lazo, U. Kaiser, A. Schwarz, S. Heinze and R. Wiesendanger, Phys. Rev. Lett., 2011, 106, 257202.
18. C. Lazo, V. Caciuc, H. Hölscher and S. Heinze, Phys. Rev. B, 2008, 78, 214416.
19. N. Hauptmann, J. W. Gerritsen, D. Wegner and A. A. Khajetoorians, Nano Lett., 2017, 17, 5660–5665.
20. J. Grenz, A. Köhler, A. Schwarz and R. Wiesendanger, Phys. Rev. Lett., 2017, 119, 047205.
21. N. Hauptmann, S. Haldar, T.-C. Hung, W. Jolie, M. Gutzeit, D. Wegner, S. Heinze and A. A. Khajetoorians, Nat. Commun., 2020, 11, 1197.
22. N. Hauptmann, M. Dupé, T.-C. Hung, A. K. Lemmens, D. Wegner, B. Dupé and A. A. Khajetoorians, Phys. Rev. B, 2018, 97, 100401.
23. I. M. Billas, A. Chatelain and W. A. de Heer, Science, 1994, 265, 1682–1684.
24. H. J. Terunobu Miyazaki, The Physics of Ferromagnetism, Springer, 2012.
25. S. Blundell, Magnetism in condensed matter, OUP, Oxford, 2001.
26. C.-W. Chen, Magnetism and metallurgy of soft magnetic materials, Courier Corporation, 2013.
27. J. C. Slater, Phys. Rev., 1930, 36, 57.
28. T. Moriya, Prog. Theor. Phys., 1965, 33, 157–183.
29. M. Menzel, A. Kubetzka, K. von Bergmann and R. Wiesendanger, Phys. Rev. Lett., 2014, 112, 047204.
30. R. Mazzarello and E. Tosatti, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 134402.
31. M. Menzel, PhD thesis, University of Hamburg, 2011.
32. J. Yu, C. Urdaniz, Y. Namgoong and C. Wolf, New J. Phys., 2023, 25, 113035.
33. L. Hammer, W. Meier, A. Schmidt and K. Heinz, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125422.
34. S. Yan, D.-J. Choi, J. A. Burgess, S. Rolf-Pissarczyk and S. Loth, Nat. Nanotechnol., 2015, 10, 40–45.
35. Y. Sugimoto, K. Ueda, M. Abe and S. Morita, J. Phys.: Condens. Matter, 2012, 24, 084008.
36. J. E. Sader and Y. Sugimoto, Appl. Phys. Lett., 2010, 97, 043502.
37. J. E. Sader and S. P. Jarvis, Appl. Phys. Lett., 2004, 84, 1801–1803.
38. Y. Sugimoto, P. Pou, M. Abe, P. Jelinek, R. Pérez, S. Morita and O. Custance, Nature, 2007, 446, 64–67.
39. M. Lantz, H.-J. Hug, R. Hoffmann, P. Van Schendel, P. Kappenberger, S. Martin, A. Baratoff and H.-J. Guntherodt, Science, 2001, 291, 2580–2583.
40. M. Ternes, C. González, C. P. Lutz, P. Hapala, F. J. Giessibl, P. Jelnek and A. J. Heinrich, Phys. Rev. Lett., 2011, 106, 016802.
41. K. Tao, V. S. Stepanyuk, W. Hergert, I. Rungger, S. Sanvito and P. Bruno, Phys. Rev. Lett., 2009, 103, 057202.
42. C. Zener, Phys. Rev., 1951, 81, 440.
43. C. Zener, Phys. Rev., 1951, 82, 403.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00162e

---