Strong electric field enhancement near an amorphous silicon metasurface with non-vertical symmetry†
Zi-Jian
Qu
 ac,
Wen-Juan
Shi
ac,
Zhao-Lu
Wang
a,
Cong-Fu
Zhang
ac,
Wen-Juan
Shi
ac,
Zhao-Lu
Wang
a,
Cong-Fu
Zhang
 ac and
Hong-Jun
Liu
*ab
ac and
Hong-Jun
Liu
*ab
aState Key Laboratory of Ultrafast Optical Science and Technology, Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an 710119, China. E-mail: liuhongjun@opt.ac.cn
bCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China
cUniversity of Chinese Academy of Sciences, Beijing 100084, China
First published on 11th June 2025
Abstract
In this work, we propose a novel method to our knowledge for realizing a leakage mode with a super flat band through the modulation of two Friedrich–Wintgen bound states in the continuum (FW BICs) of a non-vertical symmetry metasurface. This unique mode is formed by partially breaking the BIC generated from the first excited collective magnetic dipole (MD) resonance in a sub-diffraction periodic system, which exhibits a low group velocity of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731 m s−1, while its quality factor (Q factor) is 217. We calculate that the near electric field enhancement reached 808 times at an incident angle θ of 9°22′. Our findings provide unique opportunities for realizing strong-enhanced nonlinear effects in metasurfaces.
731 m s−1, while its quality factor (Q factor) is 217. We calculate that the near electric field enhancement reached 808 times at an incident angle θ of 9°22′. Our findings provide unique opportunities for realizing strong-enhanced nonlinear effects in metasurfaces.
New conceptsConfining light near metasurfaces enhances various nonlinear optical effects. The key lies in how to achieve a significant near electric field enhancement. We present a novel method for the modulation of two Friedrich–Wintgen bound states in the continuum (FW BICs) in the dispersion relation diagram, achieving a significant slow light effect with a super flat band. This state, namely, the hybrid magnetic dipole mode, lies between two BICs in the dispersion relation diagram, resulting in a large and stable quality factor. Due to the ultrathin characteristics of the metasurface, the nonlinear effects require extremely high incident light intensities, reaching levels on the order of 1 GW cm−2. We have achieved a significant near field enhancement through the slow light effect, reducing the requirement for incident light intensity by at least 2 orders of magnitude, while maintaining high efficiency of third harmonic generation. Our findings provide a unique opportunity to achieve strong near-field enhancement and nonlinear effects at the nanoscale, paving the way for the development of novel nonlinear photonic devices with diverse functionalities. |
Introduction
Confining light near nonlinear optical metasurfaces enhances various nonlinear optical effects such as frequency conversion, harmonic generation, optical mixing, and all-optical switching.1–8 The fundamental principle of these metasurfaces is to control light through optical resonant metasurfaces made of resonant structures and highly nonlinear materials.9 Initially, researchers aimed to enhance nonlinearity by leveraging the strong field confinement resulting from surface plasmon resonance effects in metallic metasurfaces. However, their performance is significantly limited by high ohmic losses, small mode volumes, and low laser damage thresholds. All-dielectric metasurfaces made from high-refractive-index materials can effectively replace metallic metasurfaces due to their low loss, large mode volume, and high laser damage threshold, facilitated by Mie resonances.10 However, all-dielectric metasurfaces still face challenges in fully confining light, resulting in some unavoidable leakage.In traditional viewpoints, the resonant states present in the radiation continuum are associated with the outward radiation of light, whereas perfect bound states exist only outside the radiation continuum. Introducing states that couple to bound states within the radiation continuum inevitably leads to energy leakage.11–17 However, the discovery of bound state in the continuum (BIC) has broken this paradigm. BIC represents a unique optical phenomenon that does not radiate any light outward, making it a perfect bound state.18–23 A special case of a symmetry-protected BIC exists at the Γ point of periodic structures in metasurfaces.24 Nevertheless, accidental BICs originate from the destructive interference between radiation channels of the system.25–28 Due to the infinitesimally small bandwidth of BICs, experimental instruments are often unable to detect it. In designs, asymmetric parameters are typically introduced intentionally to transform a BIC into quasi-bound states in the continuum (QBICs) with a finite bandwidth and Q factors. Generally, the Q factor of a QBIC is inversely proportional to the square of the asymmetric parameters.24 Therefore, the Q factor of the quasi-BIC can be flexibly adjusted by manipulating these asymmetric parameters. Compared to a BIC, a QBIC is more practical for applications. In 2016, Arseniy proposed that dielectric particles exhibit strong scattering resonances for incident light, with four main resonant modes: magnetic dipole, electric dipole, magnetic quadrupole, and electric quadrupole.29 These modes can be utilized to control the enhancement of electric and magnetic fields. In addition, all-dielectric metasurfaces can also support light-induced magnetic resonances, which effectively enhance the electric nonlinearity commonly used in nonlinear optics. The MD mode has a larger mode volume compared to other magnetic multipole modes and is renowned for its ability to facilitate nonlinear effects. As a result, it is widely employed in metasurfaces to achieve nonlinear enhancements.6,30,31 Moreover, achieving a flat band on metasurfaces, such as electromagnetic induced transparency (EIT),32 can reduce group velocity to induce slow light effects. This, in turn, enhances the interaction between light and matter, resulting in a greater nonlinear enhancement.
In this work, we design a non-vertically symmetric silicon metasurface and investigate the movement of two Friedrich–Wintgen (FW) BICs in the dispersion relation diagram as the filling factor f changes. It is found that the hybrid MD mode ultimately forms a super flat band at the filling factor f = 0.53. On the one hand, this mode exhibits a high and stable Q factor due to the combined effects of two BICs. On the other hand, it features a low group velocity, resulting in a pronounced slow light effect in metasurfaces. We calculate that the near electric field enhancement reached 808 times at an incident angle θ of 9°22′. Our findings provide a unique opportunity for constructing nonlinear optical effects, paving the way for the development of novel nonlinear photonic devices with diverse functionalities.
Results and discussion
Analysis of modes and structural parameter settings
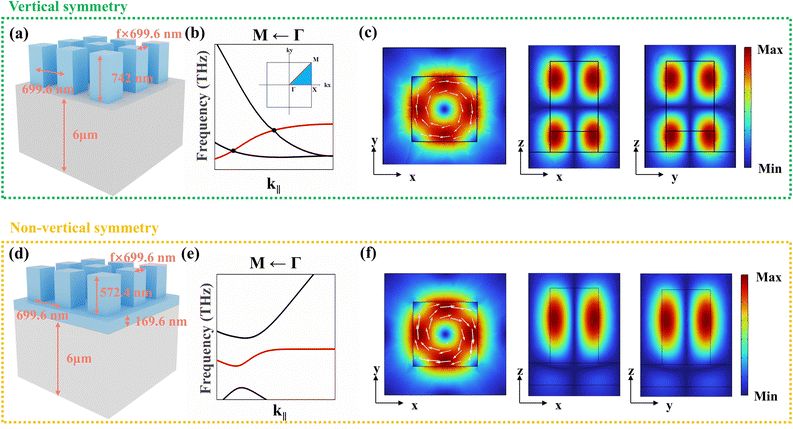
Although the MD mode can effectively enhance the electric field near the metasurfaces and nonlinear effects, it is a lowest-order fundamental mode that does not intersect with any higher-order modes. Consequently, it is not possible to form multiple BICs on a single band in the dispersion relations through symmetry breaking. In this study, we use the first excited MD mode which transitions into a hybrid MD mode, allowing for the achievement of multiple BICs on a single band by breaking the vertical symmetry.We first consider a metasurface with vertical symmetry, composed of a periodic array of silicon nanocuboids, as shown in Fig. 1(a). The substrate is made of 6 μm thick fused quartz. The illustration in Fig. 1(b) reveals the first Brillouin zone of this metasurface, which corresponds to the reciprocal lattice of a two-dimensional square lattice because of its symmetry. Thus, we can employ the analytical methods used for two-dimensional square lattice band structures, specifically by analyzing along the high symmetry path (M ← Γ → X) near the Γ point in the irreducible Brillouin zone. The analytical methods utilized to calculate dispersion relations and mode properties are discussed in Section S1 of the ESI.† Using this method, we calculate the dispersion relations of the first excited MD mode and its nearby modes, with the red curve representing the dispersion curve of the first excited MD mode, as shown in Fig. 1(b). The normalized electric field distribution of this mode is illustrated in Fig. 1(c). When the vertical symmetry of the metasurface is preserved, the intersection points on the dispersion band of this mode do not exhibit coupling. Thus, there is only a symmetry-protected BIC at the Γ point.
Next, we break the vertical symmetry of the metasurface by introducing a homogeneous silicon slab, as shown in Fig. 1(d). It is well known that characteristic modes in a vertical symmetry metasurface can be classified into transverse-electric (TE) polarized modes and transverse-magnetic (TM) polarized modes. However, breaking this vertical symmetry causes the characteristic modes to transition into hybrid modes which have non-zero electric and magnetic fields in the three orthogonal directions. We calculate the dispersion relations of the hybrid MD mode and its nearby modes, discovering that the original intersection points on the dispersion band are opened, indicating that coupling has occurred. Our calculations reveal the generation of a FW BIC off the Γ point, which will be discussed later in this study. Moreover, it is enthralling that hybrid modes also exhibit Mie resonance characteristics like those of TE and TM modes. Therefore, the spectral position of the hybrid MD mode can be controlled by changing the aspect ratio of the metasurface, which makes it possible to shrink the size of the hybrid MD resonator to subwavelength dimensions while maintaining strong hybrid MD resonances.29,31 In the following, we focus our working wavelength on 1550 nm and fix the period and thickness of the metasurface to be 699.6 nm and 742 nm (top: 572.4 nm, bottom: 169.6 nm), respectively. The normalized electric field distributions of the hybrid MD mode are presented in Fig. 1(f). It can be observed that the field intensity of the designed hybrid MD state is confined within the nanocuboids, making it an excellent candidate for enhancing optical nonlinear effects.
Because this metasurface is invariant under symmetry operations from the C4v point group which includes six types of eigenmodes: two doubly degenerate modes and four non-degenerate modes, the only radiating states are the normal plane waves which correspond to doubly degenerate mode for frequencies below the diffraction limit at the Γ point. Thus, the hybrid MD mode as shown in Fig. 1(f), with the electric field vector being even under C2 symmetry, becomes perfectly confined and no longer couples to the free-space radiation channel. The top view of the electric field reveals the in-plane circulating displacement currents, which is a hallmark of the MD mode and confined within the nanocuboids. Additionally, the side view of the electric field's nodal lines further confirms that this mode represents the first excited state. This type of BIC associated with the symmetry of metasurfaces is referred to as symmetry-protected BIC. As shown in Fig. 2(a)–(d), a symmetry-protected BIC is formed at the Γ point of the hybrid MD mode. In addition to the symmetry-protected BIC at the Γ point, accidental BICs are also generated off the Γ point for the hybrid MD mode. One of them, the FW BIC is an excellent choice for achieving a super flat band by modulating the dispersion relations.
Formation of the super flat band through the movement of two FW BICs
From Mie theory, the spectral positions of characteristic modes correspond to a fixed ratio of the wavelength, λ, to its optical path length, n × L.29 As the filling factor f varies, the optical path length is modified due to changes in the proportions of the dielectric material regions and air regions, which causes a shift in the position of the dispersion relations in turn. Thus, the position of the FW BIC on the dispersion band can be adjusted by tuning the filling factor f. Furthermore, it can even merge with the symmetry-protected BIC at the Γ point.33 In this study, we have an exciting discovery of a novel dispersion band variation rule that leads to a super flat band of hybrid MD mode. This hybrid MD mode enables significant slow light effects and holds great promise as a strong candidate for achieving enhanced nonlinear effect interactions in metasurfaces.Fig. 2(a)–(d) show the dispersion band variation. The red band represents the dispersion band of the hybrid MD mode, while the blue and green bands represent the dispersion bands of the higher-order and lower-order modes, respectively. The breaking of the vertical symmetry of the metasurface leads to coupling at the intersection points of the two modes, resulting in accidental BICs. Later, we will demonstrate that these accidental BICs are FW BICs. As the filling factor f increases, the position of the FW BIC of higher-order mode shifts to the left, while the position of the accidental BIC of the hybrid MD mode moves upward, relative to the position of the symmetry-protected BIC. Ultimately, this results in the formation of a super flat band for the hybrid MD mode.
The equation ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) = ω + iγ describes a complex frequency, where the real part ω denotes the characteristic frequency of the mode and the imaginary part ω indicates the leakage rate of the mode, reflecting the energy loss. In this study, γ consists of two components: the losses caused by the coupling of hybrid MD mode and higher-order mode due to symmetry matching and the losses arising from the breaking of vertical symmetry. Through the coupling of the two modes and their radiation channels, when the Friedrich–Wintgen condition for destructive interference is satisfied:
= ω + iγ describes a complex frequency, where the real part ω denotes the characteristic frequency of the mode and the imaginary part ω indicates the leakage rate of the mode, reflecting the energy loss. In this study, γ consists of two components: the losses caused by the coupling of hybrid MD mode and higher-order mode due to symmetry matching and the losses arising from the breaking of vertical symmetry. Through the coupling of the two modes and their radiation channels, when the Friedrich–Wintgen condition for destructive interference is satisfied:  ,34 we can obtain a mode with increased losses and a lossless mode which is a FW BIC. In Fig. 3, we present the γ values for the two modes, and we can see that both BICs occur at a position where the γ of one mode is approximately 0, while the other mode has a maximum γ value. This is a typical characteristic of FW BICs.
,34 we can obtain a mode with increased losses and a lossless mode which is a FW BIC. In Fig. 3, we present the γ values for the two modes, and we can see that both BICs occur at a position where the γ of one mode is approximately 0, while the other mode has a maximum γ value. This is a typical characteristic of FW BICs.
We calculate the dispersion relations and Q factors of the hybrid MD mode as f varied from 0.52 to 0.54. Fig. 4(b) shows that there is a symmetry-protected BIC at the Γ point with the Q factor exceeding 109 and a FW BIC off the Γ point with the Q factor exceeding 103, while the metasurface is placed on a 6 μm fused quartz substrate. Furthermore, the disappearing linewidth is also noted in the reflection spectrum presented in Fig. 4(e). In this study, we utilize oblique incidence to break the symmetry of the metasurface, allowing for straightforward control of the Q factor. Fig. 4(e) reveals that the resonance bandwidth of the hybrid MD mode gradually increases with changes in the incident angle. Notably, a FW BIC appears on the band of the hybrid MD mode when the incident angle θ is 37°54′. The results illustrate that a super flat band of the hybrid MD mode is achieved through the modulation of two FW BICs when the filling factor f = 0.53. The hybrid MD mode has multiple BICs on the band, which can achieve high Q factors in a large range of incident angles.
Achieving strong electric field enhancement near the silicon metasurface through a slow light effect
The group velocity vg of the hybrid MD mode is defined as the derivative of frequency with respect to the wave vector direction. The wave vector can be decomposed into in-plane k‖ and out-of-plane kz, allowing the group velocity to be expressed as | (1) |
 | (2) |
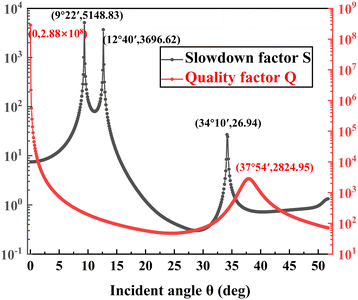
 | (3) |
Fig. 5 shows that the slow light effect is characterized by three peaks in the slowdown factor. We find that the near electric field enhancement is maximized at an incident angle of 9°22′ by comparing the Q factors at the three peak positions. The Q factor is 217, while the S factor is 5149. Fig. 6 shows the electric field distribution and enhancement with the slow light effect. The maximum total electric field enhancement is 808 times. The in-plane circulating displacement currents observed in the top view of the electric field, along with the nodal lines seen in the side view, confirm that this mode represents the first excited hybrid MD state under oblique incidence. Additionally, the region lies between two BICs, which causes the Q factor to be influenced by both BICs, resulting in a higher and more stable Q factor with the minimum being greater than 47. This hybrid MD mode, based on the slow light effect, has the advantages of a large mode volume and a significant near electric field enhancement, making it an excellent candidate for nonlinear effects. Due to the ultrathin characteristics of the metasurface, the nonlinear effects require extremely high incident light intensities, reaching levels on the order of 1 GW cm−2. However, this hybrid MD mode essentially relaxes the requirements for the incident light intensity. For the calculation of the third harmonic conversion efficiency, we provide detailed explanations below.
First, we calculate the complex amplitude of the polarization intensity for the third harmonic:
| P3ω = ε0χ(3)⋮E(ω)·E(ω)·E(ω) | (4) |
Next, we substitute it into the wave equation:
| ∇×(∇×E(3ω)) − (3ω)2μ0ε(3ω)E(3ω) = μ0(3ω)2P3ω | (5) |
Conclusions
In summary, we present an innovative approach to create a new photonic state, namely, the hybrid MD mode with a super flat band and a high Q factor in a silicon metasurface. By breaking the vertical symmetry of the metasurface, we achieve coupling at the intersection points of two modes, resulting in the formation of two FW BICs. We find that as the filling factor f varies, the two FW BICs shift left and upward in the dispersion relation diagram, respectively, achieving a super flat band ultimately. Notably, this hybrid MD mode exhibits a low group velocity of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731 m s−1, while the quality factor (Q factor) is 217, making it an excellent mode for enhancing nonlinear effects in the metasurface. We calculate that the near electric field enhancement reached 808 times at an incident angle θ of 9°22′. The slow light effect significantly relaxes the requirements for pump power density. Due to the strong light confinement within the nano-resonators caused by the characteristics of the hybrid MD mode, we demonstrate that this hybrid MD mode can significantly enhance nonlinear effects. We calculate the third harmonic conversion efficiency of 10−4 at a peak pump density of 10 MW cm−2. Our findings provide unique opportunities for realizing the near electric field enhancement and nonlinear effects in silicon metasurfaces, with broad applications including harmonics generation, frequency conversion, wavefront control, lowering laser thresholds, and sensing.
731 m s−1, while the quality factor (Q factor) is 217, making it an excellent mode for enhancing nonlinear effects in the metasurface. We calculate that the near electric field enhancement reached 808 times at an incident angle θ of 9°22′. The slow light effect significantly relaxes the requirements for pump power density. Due to the strong light confinement within the nano-resonators caused by the characteristics of the hybrid MD mode, we demonstrate that this hybrid MD mode can significantly enhance nonlinear effects. We calculate the third harmonic conversion efficiency of 10−4 at a peak pump density of 10 MW cm−2. Our findings provide unique opportunities for realizing the near electric field enhancement and nonlinear effects in silicon metasurfaces, with broad applications including harmonics generation, frequency conversion, wavefront control, lowering laser thresholds, and sensing.
Author contributions
Zi-Jian Qu: investigation, conceptualization, data curation, formal analysis, methodology, software, validation, visualization and writing – original draft; Wen-Juan Shi: methodology, validation and editing; Zhao-Lu Wang: validation and editing; Cong-Fu Zhang: methodology, validation and editing; Hong-Jun Liu: funding acquisition, supervision, project administration, validation and editing. All authors reviewed the manuscript.Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the National Natural Science Foundation of China (61975232).References
- I. S. Sinev, K. Koshelev, Z. Liu, A. Rudenko, K. Ladutenko, A. Shcherbakov, Z. Sadrieva, M. Baranov, T. Itina, J. Liu, A. A. Bogdanov and Y. Kivshar, Nano Lett., 2021, 21, 8848–8855 CrossRef CAS PubMed.
- A. P. Anthur, H. Zhang, R. Paniagua-Dominguez, D. A. Kalashnikov, S. T. Ha, T. W. W. Mass, A. I. Kuznetsov and L. Krivitsky, Nano Lett., 2020, 20, 8745–8751 Search PubMed.
- B. Reineke Matsudo, B. Sain, L. Carletti, X. Zhang, W. Gao, C. de Angelis, L. Huang and T. Zentgraf, Adv. Sci., 2022, 9, e2104508 CrossRef PubMed.
- Z. Liu, Y. Xu, Y. Lin, J. Xiang, T. Feng, Q. Cao, J. Li, S. Lan and J. Liu, Phys. Rev. Lett., 2019, 123, 253901 CrossRef CAS PubMed.
- R. Camacho-Morales, L. Xu, N. Dimitrov, L. Stoyanov, Z. Ma, A. A. Dreischuh, H. H. H. Tan, C. De Angelis, C. Jagadish, A. E. Miroshnichenko, D. Rocco, V. F. Gili, A. Komar, M. Lysevych, F. Karouta, G. Leo, M. Rahmani and D. N. Neshev, Adv. Photonics, 2021, 3, 036002 CAS.
- G. Yang, S. U. Dev, M. S. Allen, J. W. Allen and H. Harutyunyan, Nano Lett., 2022, 22, 2001–2008 CrossRef CAS PubMed.
- N. Bernhardt, K. Koshelev, S. J. U. White, K. W. C. Meng, J. E. Froch, S. Kim, T. T. Tran, D. Y. Choi, Y. Kivshar and A. S. Solntsev, Nano Lett., 2020, 20, 5309–5314 CrossRef CAS PubMed.
- S. Xiao, M. Qin, J. Duan and T. Liu, Opt. Express, 2022, 30, 32590–32599 CrossRef CAS.
- T. Pertsch and Y. Kivshar, MRS Bull., 2020, 45, 210–220 CrossRef.
- J. A. Schuller and M. L. Brongersma, Opt. Express, 2009, 17, 24084–24095 CrossRef PubMed.
- A. E. Miroshnichenko, A. B. Evlyukhin, Y. F. Yu, R. M. Bakker, A. Chipouline, A. I. Kuznetsov, B. Luk'yanchuk, B. N. Chichkov and Y. S. Kivshar, Nat. Commun., 2015, 6, 8069 CrossRef CAS PubMed.
- B.-S. Song, S. Noda, T. Asano and Y. Akahane, Nat. Mater., 2005, 4, 207–210 CrossRef CAS.
- J. Tian, Q. Li, P. A. Belov, R. K. Sinha, W. Qian and M. Qiu, ACS Photonics, 2020, 7, 1436–1443 CrossRef CAS.
- S. Jahani and Z. Jacob, Nat. Nanotechnol., 2016, 11, 23–36 CrossRef CAS.
- M. F. Limonov, M. V. Rybin, A. N. Poddubny and Y. S. Kivshar, Nat. Photonics, 2017, 11, 543–554 CrossRef CAS.
- I. Staude and J. Schilling, Nat. Photonics, 2017, 11, 274–284 CrossRef CAS.
- W. Zhou, D. Zhao, Y.-C. Shuai, H. Yang, S. Chuwongin, A. Chadha, J.-H. Seo, K. X. Wang, V. Liu, Z. Ma and S. Fan, Prog. Quantum Electron., 2014, 38, 1–74 CrossRef.
- K. Koshelev, G. Favraud, A. Bogdanov, Y. Kivshar and A. Fratalocchi, Nanophotonics, 2019, 8, 725–745 CrossRef.
- K. Koshelev, S. Kruk, E. Melik-Gaykazyan, J.-H. Choi, A. Bogdanov, H.-G. Park and Y. Kivshar, Science, 2020, 367, 288–292 CrossRef CAS PubMed.
- M. Luo, Y. Zhou, X. Zhao, Z. Guo, Y. Li, Q. Wang, J. Liu, W. Luo, Y. Shi, A. Q. Liu and X. Wu, ACS Nano, 2024, 18, 6477–6486 CrossRef CAS PubMed.
- W. Wang, Y. K. Srivastava, T. C. Tan, Z. Wang and R. Singh, Nat. Commun., 2023, 14, 2811 CrossRef CAS PubMed.
- S. You, M. Zhou, L. Xu, D. Chen, M. Fan, J. Huang, W. Ma, S. Luo, M. Rahmani, C. Zhou, A. E. Miroshnichenko and L. Huang, Nanophotonics, 2023, 12, 2051–2060 CrossRef CAS PubMed.
- R. Jin, L. Huang, C. Zhou, J. Guo, Z. Fu, J. Chen, J. Wang, X. Li, F. Yu, J. Chen, Z. Zhao, X. Chen, W. Lu and G. Li, Nano Lett., 2023, 23, 9105–9113 CrossRef CAS PubMed.
- K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov and Y. Kivshar, Phys. Rev. Lett., 2018, 121, 193903 CrossRef PubMed.
- P. Hu, J. Wang, Q. Jiang, J. Wang, L. Shi, D. Han, Z. Q. Zhang, C. T. Chan and J. Zi, Optica, 2022, 9, 1353–1361 CrossRef.
- M. Kang, L. Mao, S. Zhang, M. Xiao, H. Xu and C. T. Chan, Light: Sci. Appl., 2022, 11, 228 CrossRef CAS PubMed.
- D. R. Abujetas, J. Olmos-Trigo and J. A. Sánchez-Gil, Adv. Opt. Mater., 2022, 10, 2200301 CrossRef CAS.
- Z. Li, L. Zhou, Z. Liu, M. Panmai, S. Li, J. Liu and S. Lan, ACS Photonics, 2022, 10, 206–216 CrossRef.
- A. I. Kuznetsov, A. E. Miroshnichenko, M. L. Brongersma, Y. S. Kivshar and B. Luk’yanchuk, Science, 2016, 354, aag2472 CrossRef.
- Z. Han, F. Ding, Y. Cai and U. Levy, Nanophotonics, 2021, 10, 1189–1196 CrossRef.
- L. Xu, K. Zangeneh Kamali, L. Huang, M. Rahmani, A. Smirnov, R. Camacho-Morales, Y. Ma, G. Zhang, M. Woolley, D. Neshev and A. E. Miroshnichenko, Adv. Sci., 2019, 6, 1802119 CrossRef.
- K. M. Devi, A. Jana, A. Punjal, N. Acharyya, S. S. Prabhu and D. Roy Chowdhury, New J. Phys., 2022, 24, 093004 CrossRef.
- J. Jin, X. Yin, L. Ni, M. Soljacic, B. Zhen and C. Peng, Nature, 2019, 574, 501–504 CrossRef CAS.
- H. Friedrich and D. Wintgen, Phys. Rev. A, 1985, 32, 3231–3242 CrossRef CAS PubMed.
- K. Narayanan and S. F. Preble, Opt. Express, 2010, 18, 8998–9005 CrossRef CAS PubMed.
- M. R. Shcherbakov, D. N. Neshev, B. Hopkins, A. S. Shorokhov, I. Staude, E. V. Melik-Gaykazyan, M. Decker, A. A. Ezhov, A. E. Miroshnichenko, I. Brener, A. A. Fedyanin and Y. S. Kivshar, Nano Lett., 2014, 14, 6488–6492 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00225g |
| This journal is © The Royal Society of Chemistry 2025 |