Differential Mg2+ deposition on DNA Holliday Junctions dictates the rate and stability of conformational exchange†
Pratibha
Agarwala
 a,
Arumay
Pal‡
a,
Arumay
Pal‡
 b,
Milan Kumar
Hazra
b,
Milan Kumar
Hazra
 *a and
Dibyendu K.
Sasmal
*a and
Dibyendu K.
Sasmal
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Jodhpur, Rajasthan 342037, India. E-mail: sasmal@iitj.ac.in; milanhazra@iitj.ac.in; Tel: (+91)-291-280-1314 Tel: (+91)-291-280-1308 Web: https://www.sasmallab.org Web: https://sites.google.com/view/msb-lab-iit-jodhpur/home
bSchool of Biosciences, Engineering and Technology, Vellore Institute of Technology Bhopal, India
First published on 5th November 2024
Abstract
DNA Holliday junctions (HJs) are crucial intermediates in genetic recombination and genome repair processes, characterized by a dynamic nature and transitioning among multiple conformations on the timescale ranging from sub-milliseconds to seconds. Although the influence of ions on HJ dynamics has been extensively studied, precise quantification of the thermodynamic feasibility of transitions and detailed kinetic cooperativity remain unexplored. Understanding the heterogeneity of stochastic gene recombination using ensemble-averaged experimental techniques is extremely difficult because of its lack of ability to differentiate dynamics and function in a high spatiotemporal resolution. Herein, we developed a new technique that combines single-molecule fluorescence resonance energy transfer (smFRET) experiments and molecular simulation to investigate the kinetic choreography and preferential stability of HJ conformations under ionic conditions that closely mimic the physiological environment relevant to cellular biology. Our findings predict the prevalence of three distinct conformational macrostates in HJ dynamics. At low ion concentrations, HJs transition rapidly among three thermodynamically stable conformational macrostates. However, in a physiological ionic environment, the open conformation becomes predominant. Using a kinetic network model based on the multi-order time correlation function (TCF), we delineated thermodynamic parameters that govern heterogeneous dynamics as a function of divalent ion concentration. Stabilization of conformations due to an ionic environment and activation barriers concertedly affect transition rates between open and closed conformations. Furthermore, we observed a significant enhancement of Mg2+ condensation in the central region of HJs rather than branch ends, leading to a plausible conclusion that the differential stability of conformational states may be governed by the junction region of HJs rather than duplex branches. This study gives a new insight into the complex interplay between the ionic environment and HJ dynamics, offering a comprehensive understanding of their behavior under conditions relevant to cellular biology and roles in key biological processes for creating a heterogeneous nature of life.
Introduction
Helical poly-nucleotide junctions are essential components of bio-molecular regulation, playing a critical role in maintaining the integrity, functionality and diversity of genetic materials.1–5 These junctions are involved in various fundamental biological processes, including DNA replication, repair and recombination. By facilitating the correct alignment and interaction of DNA strands, the helical polynucleotide junction ensures accurate genetic information transfer and prevents harmful mutations. Their dynamic nature allows them to adapt to different cellular conditions, making them versatile elements in the orchestration of complex cellular mechanisms. Therefore, understanding their structure and behavior is pivotal for the advancement of genetic engineering, molecular biology and therapeutic interventions targeting genetic disorders. Among such examples, DNA Holliday junctions (HJs) are crucial intermediates in genetic information processing through homologous recombination, a process that is vital for repairing double-stranded DNA breaks across all forms of life.6–13 HJs form junction points where duplex poly-nucleotide segments intersect with discontinuities.14 Once formed, HJs undergo spontaneous or protein-facilitated movement, which involves stepwise exchange of base-pairing partners to locate sequence homology, a process known as branch migration that stabilizes the intermediate junction phase.14–16 Finally, as a result of homologous recombination, strands are exchanged between intersecting DNA duplexes to facilitate cross-over and non-crossover products.17,18The structure of HJ, initially proposed by Professor Robin Holliday, is remarkably intriguing.8 It can be best described as a stacked form where four DNA duplexes create two pairs, each pair of which is stacked coaxially, with two strands crossing between the stacked pairs aligned parallelly in a 5′–3′ orientation.19 However, these junctions are dynamic, as observed in previous single molecule studies, and are influenced by various proteins during later steps of recombination.20,21 Previous studies suggest that the dynamic nature of HJ is effectively utilized for resolution by junction-resolving enzymes.22–25 Resolvases, for instance, tend to bias HJ toward open-X conformation, accelerating the genetic recombination process by dictating the orientation and resolution of the junction.24 Interconversion between the isomeric forms of DNA holidays junction occurs through an open-X planar structure.26,27
Junction-resolving enzyme GEN1 (human) in its monomeric form binds to an intact HJ, leading to an undesirable cleavage at the junction point before dimer formation through a partial dissociative step.20,23 The rebinding of the enzyme requires the opening of the DNA structure at the junction point.20,23,28 Tetrameric motor proteins also bind to the open planar structure of HJ with some degree of sequence specificity.26,29 Bacterial resolvases, such as RuvC, first bind to the stacked X isomers of HJ and then undergo a transition to an open planar structure in their dimer form.30 It has been reported that the proteins such as RecU, RuvC, and CCE1, which dimerize, bind to an X-stacked isomer and induce structural changes in HJ by opening the junction center to make a stabilized transition state, allowing the junction to migrate.22,31 Structural dynamics of HJ in the presence of enzyme occur either by conformation exchange between two isomers or branch migration with a partial dissociation state.24,32,33 It has also been found that the monovalent or divalent cation concentration increases the frequency of the partial dissociation state.32 In the absence of protein or enzyme, the junction is crystallized in a stacked X conformation, while in the presence of an enzyme-HJ complex, it can exist as an open conformation or other hybrid structures.26,34 Crystal structure investigations showing phosphate groups at the point of strand exchange are influential contributors to electrostatic interaction.35 Methylation in DNA HJ strands leads to significant deformability as observed in the neutralized phase.36
The stability of the HJ also depends on the sequence and the length of the base pair. It has been observed that the 24 base pair long DNA HJ can be formed at a low ion concentration, (0.1 M NaCl at 5 μM strand concentration), but an 18 base pair long sequence is less stable, and a 12 base pair long sequence cannot be formed using the same ionic concentration. Another study investigated that if the core region of HJ is homologous, then the structure becomes more resistant to thermal denaturation. The divalent cation also increased the melting temperature of the DNA HJ. NMR studies also reported that the Holliday junction cannot be viewed as a static structure; instead, it can be observed as an equilibrium mixture of two crossover isomers.37
DNA supercoiling is a critical factor for the structural bias in the cruciform, as observed in atomic force microscopy experiments, which is a general model for the DNA Holliday junction. It was shown that the cruciform structure can adopt a parallel configuration even in the absence of any divalent cation due to the supercoiling effect.38 A specific trinucleotide core at the junction ACC plays a pivotal role in the stability of DNA HJ in the solution phase, and the general rule of the sequence is that the core must have pupyC nucleotides, where pu refers to the purine and py refers to the pyridine moiety proven by the atomic force microscopy study. The interduplex angle of the junction having the core is ∼30° to ∼40°, while without this core, the structure has a ∼60° interduplex angle, which suggests that the ACC core pulls the arms of the HJ closer to each other.38
Further investigation suggested that crossing strands are often antiparallelly oriented and topologically lock the HJ.39 To possess branch migration ability, the HJ must adopt an open-X conformation in which the four strands are distant from each other. At sufficiently low concentrations of ions, HJ adopts the open conformation to reduce the inter strand repulsions due to unshielded phosphate charges.40 Although branch migration imparts stability to the stacked conformation, all HJs experience occasional switching behaviours toward an open X state even at high ion concentrations. At sufficiently low concentrations of ions, HJ adopts the open conformation to reduce the inter strand repulsions due to unshielded phosphate charges.40 While branch migration imparts stability to the stacked conformation, all HJs experience an occasional switching behaviour toward an open X state even at high ion concentrations.
Not only the monovalent and divalent cations but it was also observed that uranyl ion (UO22+) also induces folding of the junction point into an X-stacked conformation, which increases stacking interaction along the junction, as observed by gel mobility assay.41 The Osmium tetraoxide (OsO4) assays with the nucleotide thymine proved that the binding of divalent cation occurs at the junction point of DNA HJ.42 Uranyl photo probing study reflects the binding of the ions in the junction point, which influences the conformational heterogeneity. As ion concentration increases, the inter-strand repulsions are reduced by masking phosphates with counter-ion condensation, and the junction conformations are easily inter-convertible. The conformational heterogeneity of the junction is highly influenced by the sequence at or near the junction point and specific base pairing.11,43,44
The open planar structure of the Holliday Junction accelerates the branch migration and resolvase activities and also helps in exchanging genetic material.45–47 Not only the stacked conformation but also the open state conformation may be populated even at high ion concentrations, and while the transition from two stacked conformations occurs.48 The open state dynamics play a pivotal role in the resolution of HJ through the enzyme recognition process, and it is also a crucial intermediate in the branch migration process for the mobile HJ.49,50 A clear understanding of the intrinsic conformation properties of HJ is crucial for cellular processing. This information has paramount importance in terms of homologous recombination in the genetic reshuffling process because it exploits the dynamic nature of Holliday Junction.51
The present study aims to address the coordinated thermodynamic and kinetic choreography of conformational transitions in a specific sequence of HJ using smFRET and molecular dynamics (MD) simulations at different ionic concentrations. More importantly, we aim to decode the effect of near-physiological divalent ion concentration on HJ dynamics. A three-state kinetic model ensures the best fit for the conformational exchange mechanism. We obtained newer kinetic information by employing a multi-order time-correlation approach blended with a kinetic network model to decode the transition rates and mapped the same on the free-energy landscape obtained from smFRET trajectories. Coarse-grained MD simulations predict differential counter-ion condensation at the junction center and strand regimes of HJ and may dictate or bias conformational exchange.
Results and discussion
Single-molecule FRET from DNA HJ shows real-time dynamic transition of states in millisecond time-scale
Mg2+ ion plays a critical role in the dynamic conformational change in DNA HJ, which is a key intermediate structure during DNA recombination and repair processes.48 HJs are formed during genetic recombination when two DNA duplexes exchange strands. The four arms of the junction can adopt several conformations, including stacked-X, and open-X structures.52 Mg2+ ions are essential for stabilizing the HJ structure by coordinating and neutralizing the negative charges in phosphate ions in the DNA backbone, which helps in counteracting the repulsion between the negatively charged DNA strands. This stabilization is particularly important during the transition between the different conformations of the HJ. Furthermore, Mg2+ ions facilitate dynamic conformational changes in HJs by promoting strand exchange reactions. During recombination, the junction undergoes structural transitions, including branch migration and resolution, where Mg2+ ions help in facilitating the movement of DNA strands and resolving the junction into two separate duplex molecules.48,53 Moreover, Mg2+ ions can influence the specificity and efficiency of recombination reactions by affecting the kinetics and thermodynamics of the strand exchange process. They can also mediate the interactions between the proteins involved in recombination, such as recombinases and resolvases, and the DNA substrate. Thus, it is essential to understand the Mg2+ dependence on the dynamics and kinetics of the DNA conformational changes in states in real time. To do this, we applied state-of-the-art prism-type TIRF microscopy to calculate the efficiency of single-molecule fluorescence resonance energy transfer in real time. FRET efficiency is inversely proportional to the 6th power of the distance between the donor and acceptor molecules (ESI eqn (1)†). Therefore, when there is a high FRET efficiency, we can consider that the two arms of the Holliday junction are close to each other, forming a stacked conformation.The dynamic nature of conformational change is evident from the fluctuations in FRET efficiency, as shown in Fig. 1, which is derived from the anti-correlated signal fluctuation of the donor (Cy3) and acceptor (Cy5) present in a single HJ molecule.
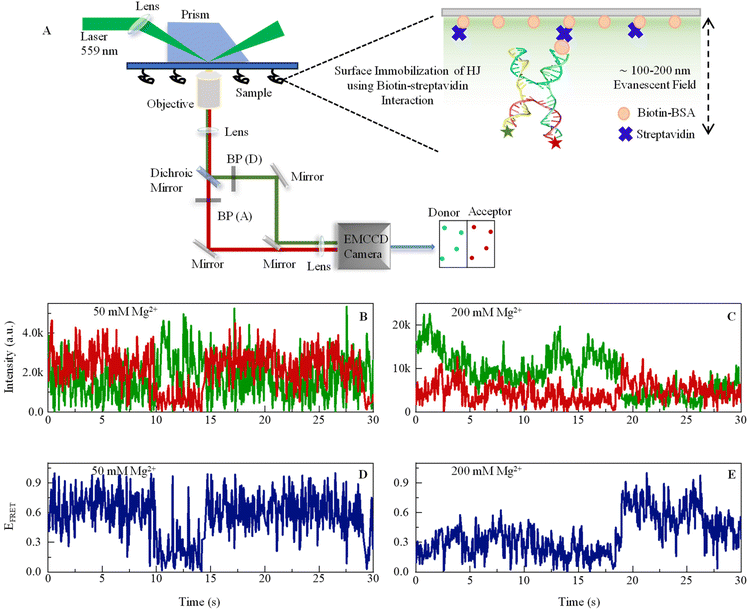 | ||
| Fig. 1 (A) Schematic representation of a custom-built prism-based total internal reflection fluorescence (TIRF) microscope to study smFRET. An excitation beam of a 559 nm laser enters the prism through a biconvex lens of a 200 mm focal length. When the beam approaches the interface of the quartz slide and aqueous sample at the incident angle higher than the critical angle, this results in total internal reflection, which creates an evanescent field of 100–200 nm depth into the sample. The emission signal passes through a 100× objective and enters Optosplit-II, where a dichroic mirror (Chroma: ZT633rdc-UF2) was used to separate signals, and then bandpass filters (BP) – ET585/65m and ET706/95m were used to cleanup signals for the donor and acceptor, respectively. The right-hand side shows a large version of the sample chamber showing how an HJ is immobilized on the glass surface by Biotin-BSA and streptavidin. Sequences of DNA oligos are given in ESI.† (B and C) Representative single-molecule fluorescence intensity time-trajectories of Cy3 (donor, green) and Cy5 (acceptor, red) recorded from one single DNA Holliday junction in the presence of 50 mM and 200 mM Mg2+ ions. The anticorrelated pattern of the two signals is a clear signature of smFRET. (D and E) FRET efficiency fluctuation (blue line) calculated from the respective data shown in B and C. See ESI for details.† | ||
The rationale for selecting Cy3 because of its exceptional photostability, broad absorption cross sections, and high fluorescence efficiencies Cy3 is compatible with common lasers and single photon counting detectors, and it can be used to covalently label proteins and nucleic acids.54 Although as per reported literature, Cy3 may demonstrate mild electrostatic and hydrophobic interactions with DNA.55 However, the crucial factor here is that the interaction is not so strong that it can substantially affect the DNA's structure or function. Several studies have successfully used Cy3-labeled DNA and have not found any dye-induced changes that could impact the biological or biophysical properties of the system under study. Numerous scientists have effectively employed the Cy3–Cy5 FRET pair in their protein or nucleic acid systems.24,32 Despite this, in our investigation, Cy3 and Cy5 were affixed at the 5′ terminal of DNA, which are areas less likely to influence DNA functionality. The terminal attachment also ensures the diminishing of any potential steric or electrical interactions between the dye and the DNA backbone. According to the literature, the relative error in FRET distance measurement using Atto and Alexa dyes is within 2.8 percent.56
This experiment was performed with a 50 ms camera exposure time, which is in the same order of conformational exchange time as its sub-states or intermediate states. The reason for performing experiments with two different Mg2+ ion concentrations is that taking an in situ concentration of 50 mM gives a pattern of dynamics near or below physiological concentration, while 200 mM gives a dynamics pattern in a high abundance of ionic spheres. However, many studies have demonstrated the long-range presence of Mg2+ ions in the cellular environment. It is believed to be essentially a tough experiment to determine Mg2+ considering all physiological environments under artificial conditions. Here, we show conformational fluctuation in real time in the presence of both concentrations. The donor and acceptor fluctuating in the anticorrelated pattern reveals that the fluctuations in the intensity trajectory are due to the energy transfer from the donor to the acceptor molecule, indicating a dynamic conformational change. HJ shows a much more dynamic pattern of conformational dynamics in the presence of 50 mM of Mg2+ (Fig. 1B) compared to the 200 mM Mg2+(Fig. 1D), which is due to more stable DNA HJ phosphate backbone in the presence of a higher concentration of positive ion that neutralizes the negatively charged phosphate ions. The change in ion concentration leads to the different dynamic aspects of HJ in stacked and unstacked conformations, which we investigate in the next section. However, the dynamics leading to various conformational states, including intermediate states and exchange rates with thermodynamic parameters, are revealed from further stational data analysis.
3-State conformation transition dynamics in DNA HJ revealed by smFRET experiment and time-correlation function analysis, molecular simulation for exact quantification of thermodynamic feasibility
HJ undergoes multiple short-lived conformational states (macro-state), including intermediate states, during the conformational interchange dynamic cycle, which ultimately determines and selects the route for DNA recombination and repair processes. Thus, it is important to know the thermodynamically stable conformational states under different cellular conditions, namely ionic environment or temperature, which is extremely difficult to determine by applying conventional ensemble-averaged optical methods. Here, we applied statistical calculation methods to the FRET efficiency time trajectories to determine the most stable thermodynamic structures, which is again supported by molecular simulation. Previously, there are various reports on the number of states present during the dynamics of HJ. Considering that an HJ can go through N number of conformational states at a constant temperature of T, the probability of occurrence of the ith conformation is given by the Boltzmann distribution, as follows:| pi = (1/Z)e−Gi/kBT, | (1) |
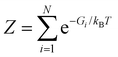 , which is the partition function. In addition, the probability is unity under normalized conditions. The individual HJ conformational state (Fig. 2A) is expected to have a lifetime as well as interconvert in tens of milli-second timescale, which is much above our resolution of the smFRET experiment. This means that the observed fluorescence signal from the donor and acceptor is a time-averaged signature from the microstate that occurs during a particular time t in the framerate. We can also consider that a specific conformational state of HJ (macro-states) is an ensemble of several high-energy quasi-degenerate conformations (micro-state) of HJ. Thus, the signals generated from FRET dyes are an ensemble average of microstates that lie within the time-space boundary of the specific macro-state conformation of HJ.
, which is the partition function. In addition, the probability is unity under normalized conditions. The individual HJ conformational state (Fig. 2A) is expected to have a lifetime as well as interconvert in tens of milli-second timescale, which is much above our resolution of the smFRET experiment. This means that the observed fluorescence signal from the donor and acceptor is a time-averaged signature from the microstate that occurs during a particular time t in the framerate. We can also consider that a specific conformational state of HJ (macro-states) is an ensemble of several high-energy quasi-degenerate conformations (micro-state) of HJ. Thus, the signals generated from FRET dyes are an ensemble average of microstates that lie within the time-space boundary of the specific macro-state conformation of HJ.
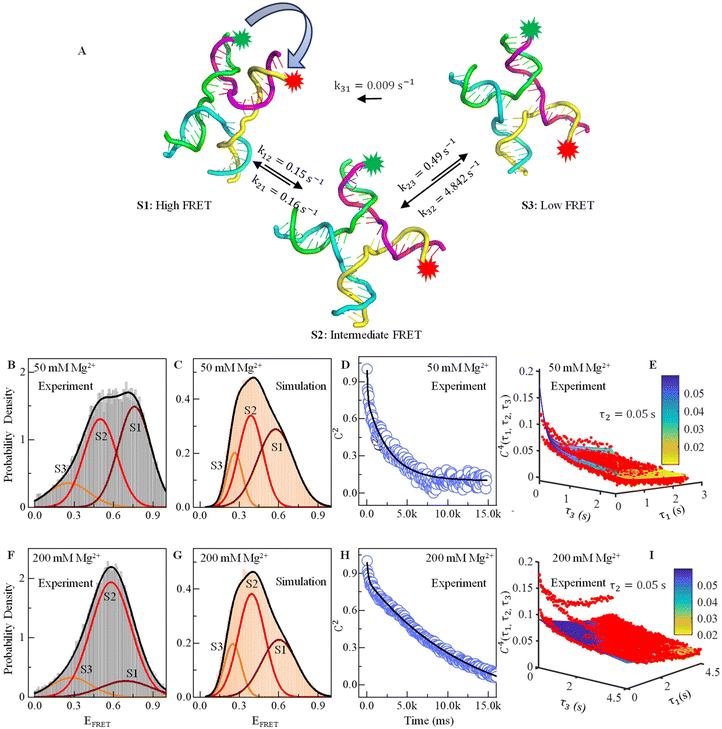 | ||
| Fig. 2 Effect of Mg2+ ions on FRET efficiency and conformational dynamics. (A) Three conformational structures of the HJ captured in MD simulations: one with high FRET, one with low FRET and another with intermediate FRET. (B) Relative probability of the experimental FRET efficiency histogram shows three prominent states at EFRET = 0.25 (S3, orange), 0.5 (S2, red), and 0.76 (S1, maroon) in the presence of 50 mM Mg2+. (C) Similarly, the probability density of MD simulated the time trajectories showing three conformational states in the presence of 50 mM Mg2+. (D) Two-point or 2nd order time correlation function (TCF) fitted with two exponential decay equations (black line) showing two decay constants in the presence of 50 mM Mg2+. (E) Three-dimensional plot of four-point or 4th order time correlation function at τ2 = 0.05 s with fitting lines in the presence of 50 mM Mg2+. (F–I) Similar to B to E, the relative probability density plot of experimental and simulated FRET efficiency, decay of two-point time correlation function and four-point time correlation in the presence of 200 mM Mg2+ are shown. See the ESI table and figures for more details.† | ||
We calculate the normalized probability density function (PDF) of FRET efficiency (Fig. 2B and D), which gives the nature of the subset that is independent of both sample size and bin size in a histogram using the following equation:
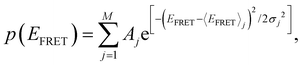 | (2) |
Time correlation function (TCF) formalism describes the rates and time scale of the conformational exchange in the 3-state model of Holliday Junction
Dynamics and kinetic information of the transitional exchange of HJ are characterized by time correlation function (TCF) analysis of EFRET time-trajectories. Two-point TCF are calculated from real-time smFRET fluctuation data using the following equation:57| C(τ) = 〈∂EFRET(0)∂EFRET(τ)〉. | (3) |
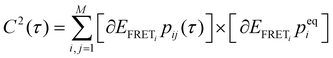 , where peqi is the probability of the presence of ith macrostate present at equilibrium, pij(τ) is the conditional probability that HJ undergoes a transition from ith macrostate to jth. As shown in Fig. 2D and H, the decay of the TCF of HJ in the presence of 50 and 200 mM Mg2+ ions is exponential. However, TCF for 50 mM Mg2+ shows much faster decay at early interval times compared to the same for 200 mM Mg2+ presumably because of less electrostatic interaction in the solution. The decay of TCF is bi-exponential with a longer time of 3.8 s, which is a major component with an amplitude of 64%, and a faster time component of 0.07 s, which is a minor component with an amplitude of 36%. Importantly, the number of the exponential term in TCF dictates the minimum number of macrostates present in the transitional exchange dynamics of HJ, which is 2 + 1 = 3, which is alternative proof of the presence of three macrostates in conformation dynamics in addition to the three-component PDF discussed in Fig. 2B. We assign a 0.07 seconds component as local chain dynamics and a longer time of 3.8 seconds as macrostate interconversion time.
, where peqi is the probability of the presence of ith macrostate present at equilibrium, pij(τ) is the conditional probability that HJ undergoes a transition from ith macrostate to jth. As shown in Fig. 2D and H, the decay of the TCF of HJ in the presence of 50 and 200 mM Mg2+ ions is exponential. However, TCF for 50 mM Mg2+ shows much faster decay at early interval times compared to the same for 200 mM Mg2+ presumably because of less electrostatic interaction in the solution. The decay of TCF is bi-exponential with a longer time of 3.8 s, which is a major component with an amplitude of 64%, and a faster time component of 0.07 s, which is a minor component with an amplitude of 36%. Importantly, the number of the exponential term in TCF dictates the minimum number of macrostates present in the transitional exchange dynamics of HJ, which is 2 + 1 = 3, which is alternative proof of the presence of three macrostates in conformation dynamics in addition to the three-component PDF discussed in Fig. 2B. We assign a 0.07 seconds component as local chain dynamics and a longer time of 3.8 seconds as macrostate interconversion time.
4th-order TCF can give us information about the role of intermediate conformation in the kinetic pathway of the Holiday junction.57Fig. 2E and I show the three-dimensional plot of the 4th order correlation function decay when four successive data points separated by the interval τ1, τ2, and τ3 of time average product, calculated using the following equation:
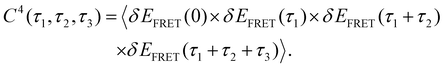 | (4) |
We find that the conformational dynamics of HJ go through a couple of interesting points described here for 50 mM Mg2+. First, the HJ goes through a high-FRET state (S1) to a low-FRET state through an intermediate state (S2). Conversion of high-FRET state to low FRET state (S3) through intermediate state is reversible, but the conversion of low FRET to high FRET state is not reversible (Fig. 2A). The rate constant for the conversion of the high FRET state to intermediate state k12 and reverse transition k21 is almost equal, which is around 0.15 s−1 (Table 2). However, the conversion of the intermediate state to low FRET state k23 is more than three times faster than the same for a high-FRET state to an intermediate state. The HJ conformation returns to the intermediate state with a much higher rate constant of 4.84 s−1 rather than direct interconversion to a high FRET state (S1), which has a much lower rate constant of 0.009 s−1.
| Ion | A 1 | 〈EFRET〉1 | σ 1 | A 2 | 〈EFRET〉2 | σ 2 | A 3 | 〈EFRET〉3 | σ 3 |
|---|---|---|---|---|---|---|---|---|---|
| 50 mM | 0.46 ± 0.05 | 0.76 ± 0.01 | 0.12 ± 0.007 | 0.41 ± 0.002 | 0.50 ± 0.02 | 0.12 ± 0.007 | 0.13 ± 0.05 | 0.26 ± 0.06 | 0.15 ± 0.04 |
| 200 mM | 0.13 ± 0.02 | 0.69 | 0.19 ± 0.01 | 0.75 ± 0.02 | 0.58 | 0.16 ± 0.002 | 0.12 ± 0.007 | 0.28 | 0.16 ± 0.009 |
| Ion | k 12 (s−1) | k 21 (s−1) | k 13 (s−1) | k 31 (s−1) | k 23 (s−1) | k 32 (s−1) |
|---|---|---|---|---|---|---|
| 50 mM | 0.15 | 0.16 | — | 0.009 | 0.43 | 4.84 |
| 200 mM | 0.16 | 0.02 | 0.003 | 0.014 | 0.02 | 0.09 |
For 200 mM Mg2+, the fastest interconversion occurring from the macrostate S1 to S2 is 0.16 s−1, while the backward transition from S2 to S1 has a rate constant of 0.02 s−1. The interconversion from the S2 to S3 states is also the same as the that of the S2 to S1 state at 0.02 s−1, while the backward transition has a rate constant of 0.09 s−1. The slowest interconversion process from the S1 to S3 macrostate has a rate constant of 0.003 s−1; the reverse transition has a rate constant of 0.014 s−1. Overall, HJ conformation transition dynamics go through several structures, and inter-conversion has a complex kinetic network model.
Free-energy landscape of the conformational state determining the transition barrier
Considering the sum of all probabilities of unity, the free energy (in kBT) of HJ's specific conformation, j, can be written as a function of EFRET:58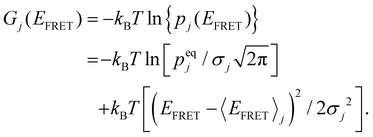 | (5) |
The total free energy of all conformers is calculated from the sum of all macro-state or HJ conformations using the following equation: 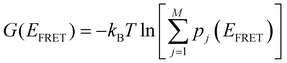 . From the optimized rate constants described in the previous section, the free energy of activation is calculated using the Arrhenius equation:58
. From the optimized rate constants described in the previous section, the free energy of activation is calculated using the Arrhenius equation:58
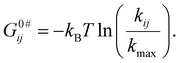 | (6) |
According to the Arrhenius equation kij = kmaxe−Gi/kBT, the pre-exponential factor in the equation is considered to be kmax. The fastest rate conversion in the HJ conformational transition between macrostates corresponds to k32 = 4.84 s−1. For the purine–pyrimidine (G–C) nucleotides, the activation barrier is ∼2 kcal mol−1, which is equivalent to 3.4 kBT.59 Therefore, the corrected pre-exponential factor kmax = k32 × e3.4 = 4.84 × 30 = 145 s−1. All other activation barrier values are calculated based on this value because any interconversion between the three macrostates involves either the formation or disruption of the secondary structure of DNA HJ that can lead to the formation of many other macrostates or intermediate states, which does not support our 3-state model mechanism.
Fig. 3A and C show the individual contribution of macrostate conformation to the free energy surface of DNA HJ, which is shown in three different colors (S1, Maroon; S2, Red; and S3, Orange). The sum or overall free-energy contribution is shown in a black line. The individual contribution to the free energy of each conformation is shown in a parabola in the presence of both 50 mM and 200 mM Mg2+ starting with Gn = 0 (ground state), where n = 1 − 3. In the presence of 50 mM Mg2+, G01 = 0kBT, G02 = 0.119kBT and G03 = 1.44kBT, where superscript ‘0’ represents that we have taken the minimum of macrostate S1 as a reference to all other energies. Each macrostate/conformation also shows a parabolic nature of energy change with respect to EFRET because we considered the Gaussian distribution of the distance from one arm to another arm of the HJ. This also describes the approximate relative probabilities for the occurrence of HJ configuration or macrostate that deviates from the mean values. Thus, an entropic contribution is associated with the conformational change. The Gaussian shape of free energy accurately describes the nature of the conformational dynamics of HJ because of the branch shape and many probabilities of conformational states even with the same FRET efficiency value. However, the non-zero Gaussian shape for both cases of 50 mM and 200 mM may be attributed to the stronger interaction and conformational state changes through specific macrostates over time. The presence of three macrostates for each case is likely due to the presence of distinctly different distances between the two HJ arms, contributing to the existence of chain configurations, the presence of different local arms flexibility, etc., in the presence of positive ions.
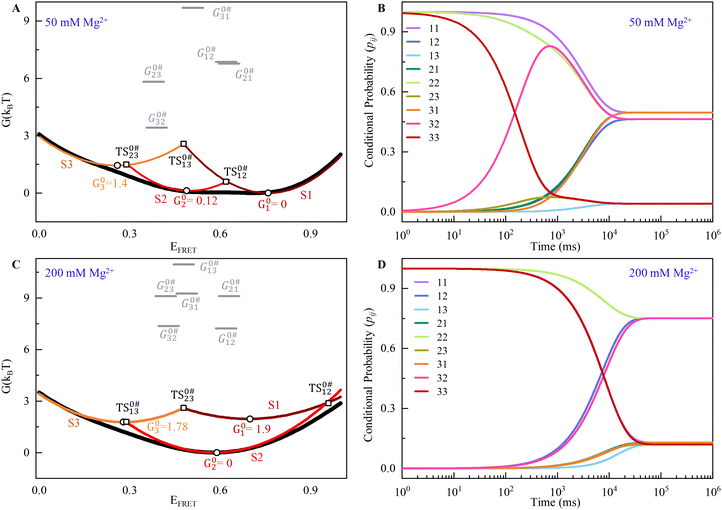 | ||
| Fig. 3 (A) Free energy G(kBT) landscape for the DNA HJ in the presence of 50 mM Mg2+. (B) Time-dependent conditional probabilities, pij, which indicate the likelihood of the system in the presence of 50 mM Mg2+. (C and D) Similar to A and B, the free energy G(kBT) landscape and the time-dependent conditional probabilities of 200 mM Mg2+ are shown. See ESI for more details.† | ||
To find out the activation energy and enthalpic contribution (Table 3), we use the kinetic rate model and Arrhenius equation, and the S1 → S2 state has very high activation energy, G0#12 = 6.86kBT, and for the backward reaction, S2 ← S1 has a similar energy G0#21 = 6.78kBT for the transition in the presence of 50 mM Mg2+ ion. The most favorable transition found for the S3 → S2 state with a low activation energy is 3.40kBT, and the transition from S2 → S3 is 5.82kBT energy, as required. The transition from S3 → S1 requires a very high activation energy (9.7kBT), indicating a less favorable transition. The enthalpic contribution for the S2 → S3 state is 4.35kBT for the transition barrier (G0#23 − G02 = 5.72kBT), and for the backward process, it has 1.92kBT (G0#32 − G03 = 2.04kBT), which is the most favourable one. Similarly, the activation energy for the conformational transition in the presence of 200 mM Mg2+ ion is in the range of approximately 7–11kBT.
| Concentration of Mg2+ | G 0#12 (kBT) | G 0#21 (kBT) | G 0#13 (kBT) | G 0#31 (kBT) | G 0#23 (kBT) | G 0#32 (kBT) | H 0#12 (kBT) | H 0#21 (kBT) | H 0#13 (kBT) | H 0#31 (kBT) | H 0#23 (kBT) | H 0#32 (kBT) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 mM | 6.86 | 6.78 | — | 9.69 | 5.82 | 3.40 | 6.25 | 6.17 | — | 7.13 | 4.35 | 1.92 |
| 200 mM | 7.23 | 9.11 | 10.97 | 9.26 | 9.11 | 7.36 | 6.45 | 8.33 | 8.40 | 6.69 | 7.63 | 5.88 |
The transition barrier for the S1 → S2 states, G0#12 − G01, is 6.81kBT, and the enthalpic contribution for the same state is 6.25kBT. The backward transition for the same states required a 6.17kBT enthalpic contribution higher by G0#21 − G02 = 6.66kBT. The transition barrier of S3 → S1 states is also comparable with the S1–S2 states; it has an enthalpic contribution of 7.13kBT.
To estimate ensemble average quantities, it is necessary to compute the equilibrium probability distribution of individual macrostates and conditional probabilities (pij) that determine the possibility of transition from state i to state j for our proposed three-state kinetic network model.58 Probabilities can be obtained by solving the following master equation that includes a set of coupled 1st order ordinary differential equations depicting time-dependent macrostate probabilities:
| ṗ(t) = kp(t), | (7) |
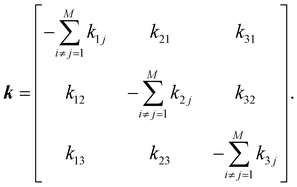 | (8) |
Off-diagonal elements in the rate matrix satisfy kij = kji, which means that the gain in population in macrostate j due to the transition from i to j should be equal to the loss due to the transition in state i. Diagonal elements are depicted as the sum of all reactions that diminish the population of the ith macrostate. To have such a master equation, time-dependent xmacrostate probabilities must show completeness 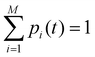 and detailed balance peqikij = peqjkji. Rate matrix k also satisfies a symmetry property that the summation of each column of the rate matrix leads to zero, which leads to the first eigenvalue (λ0) to be also 0 and the remaining ones are negative.
and detailed balance peqikij = peqjkji. Rate matrix k also satisfies a symmetry property that the summation of each column of the rate matrix leads to zero, which leads to the first eigenvalue (λ0) to be also 0 and the remaining ones are negative.
Given a particular set of rate constants, one can solve the master equation by obtaining eigenvalues and eigenvectors for each macrostate that satisfies kνi = λiνi. Eigenvalues for a system denote the characteristic relaxation rates of the coupled equations, and eigenvectors are the linear combination of elementary transitions depicting a collective mode. We obtain the eigenvalues by fitting a two-point correlation function with bi-exponential as C2(τ) = a1eλ1t + a2eλ2t when the general solution of the master equation has the form p(t) = peq + c1v1eλ1t + c2v2eλ2t. Thereafter, we optimize the rate matrix to achieve equilibrium probability in each macrostate and the corresponding eigenvalues obtained for the system of interest with the Nelder–Mead optimization algorithm. Fig. 3(B) and (C) plot time-dependent conditional probabilities obtained from the optimized rate and optimized solution to the master equation, which eventually converges at t → ∝ to equilibrium population (see Table 1; A1, A2 and A3) in macrostates for the ionic environment 50 mM and 200 mM respectively.
Conditional probabilities represent the likelihood of transition from state i to state j if the previous state at t = 0 is state i. We obtain the equilibrium population in the macrostates in 10–100 s timescale.
Differential Mg2+ absorbance dictate conformational exchange and stability in Holliday Junction
To elucidate the temperature-dependent local ionic environment around DNA HJ, we turned toward appropriately calibrated (see ESI Methods and Fig. S1†) structure-based coarse-grained simulations, aiming to quantify the absorbance of positively charged Mg2+ ions on the DNA HJ backbone. In our structure-based CG model, the temperature range 0.5–0.6 in reduced units matches the simulated RMS fluctuations to experimental B-factors at room temperature.60,61 This suggests that the temperature range 0.42–0.5ε/kB is equivalent to room temperature and essentially corresponds to 50–60 K in Gromacs62 units.Mg2+ absorbance on the DNA HJ surface is quantified by the scheme described in Fig. 4A. A cylindrical structure is considered along each DNA duplex strand, while the axis of the cylinder is placed at the line containing the center of masses of complementary backbone nucleotides in the duplex strands. The absorbance of Mg2+ ions is quantified up to a distance of 1 nm in contrast to 6–7 Å, in which the all-atom explicit solvent model predicts counter ion absorption. The ionic environment along HJ and its correlation to the microstate stability is probed for Gromacs temperature (60–90 K). Fig. 4(A–C) plots the simulated probability density of FRET efficiency between a virtual donor and acceptor tagged at chain C and chain D ends, respectively, for temperatures 60 K, 75 K, and 90 K, respectively, at 50 mM explicit Mg2+. At such a moderate ion concentration, significant repulsion between negatively charged HJ strands at conformational states aligns with the effect of temperature to facilitate conformational exchange between macrostates. Although S1 and S2 are fairly populated than S3 at T* = 60 K, the relative population of S1 in comparison to S2 and S3 enhances at higher temperatures (B–C). As temperature increases, a shoulder is prominent in a high-FRET regime. In addition, the gradual broadening of S1 is observed, indicating enhanced conformational freedom in the macrostate due to the temperature rise.
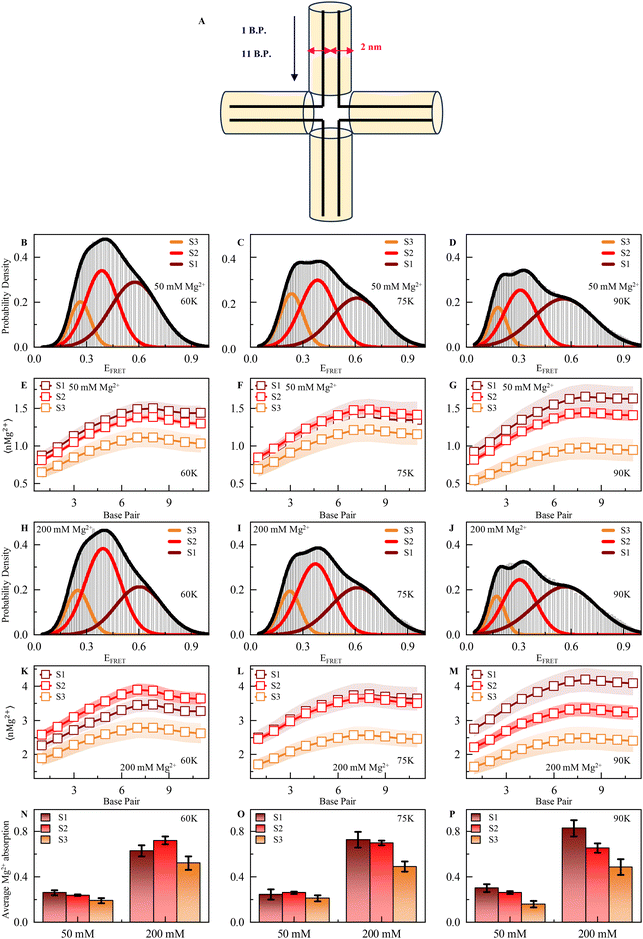 | ||
| Fig. 4 (A) Schematic representation of Mg2+ deposition along the chain in a 1 nm cylinder around each double strand. B.P. means base pair. (B–D) Probability density of FRET efficiency calculated from the MD simulation trajectory shows three prominent states corresponding to EFRET in the presence of 50 mM Mg2+ ions at 60 K (in our structure-based CG model, 60 K represents experimental room temperature), 75 K and 90 K, respectively. (E–G) Number of Mg2+ along the chain in a 1 nm cylinder around each double strand of HJ at 60 K, 75 K and 90 K, respectively, in either state 1 (high FRET), 2 (intermediate FRET) or 3 (low FRET) in the presence of 50 mM ion concentration. (H–J) Probability density of FRET efficiency calculated from the MD simulation trajectory shows three prominent states corresponding to EFRET at in the presence of 200 mM Mg2+ ion 60 K, 75 K and 90 K, respectively. (K–M) Number of Mg2+ ions along the chain in 1 nm cylinder around each double strand of HJ at 60 K, 75 K and 90 K, respectively, in either state 1 (high FRET), 2 (intermediate FRET) or 3 (low FRET) in the presence of 200 mM ion concentration. (N–P) Average Mg2+ absorption (50 and 200 mM Mg2+) for each double strand in each state 60 K, 75 K and 90 K, respectively. See ESI for more details.† | ||
To understand the correlation between the stability of individual macrostates and their local ionic environment, we compute the average number of Mg2+ (nMg2+) along the scheme detailed above at 50 mM divalent MgCl2 (Fig. 4(E–G)). We observe significant spatial heterogeneity in Mg2+-DNA phosphate backbone interaction at the HJ surface. As one moves toward the junction center from strand ends, each nucleotide pair seems to interact with a larger number of Mg2+ ions, and absorbance is maximum at the junction center due to the very high charge density (Fig. 4E–G). Relative absorption at different macrostates (shown with Gaussians in Fig. 4B–D) is quantified from the structural parameters and well correlates with the populations at such moderate ion concentration. Macrostates S1 and S2 have significantly higher Mg2+ counts on the DNA surface at all the temperatures than S3 and conform with the population distribution, as shown in Fig. 4(B–D). At such a moderate ion concentration, due to the enhanced interaction with Mg2+, the conformational ensemble of S1 gains stability due to the reduction of inter-strand repulsion interactions. At near physiological ion concentration (200 mM), conformational state S2 with an unstacked conformation is the predominant one at low temperature (T* = 60 K) due to excessive counter-ion condensation on the DNA surface that switches the negatively charged DNA inter-strand repulsion to a counter-ion-mediated positively charged strand repulsion in the stacked S1 state (Fig. 4H and K–M at different temperatures, namely 60 K, 75 K and 90 K). Such positive counterion condensation-mediated inter-strand repulsion is highest in S3 and S1 due to stacked conformation. Hence, S2 is the most probable conformation with the lowest such inter-strand repulsions with significantly high Mg2+ absorption. At significantly higher temperatures, the enhancement of population in conformational state S1 appears because increased fluctuations can overcome such a barrier of conformational exchange due to repulsion between S2 and S3 (Fig. 4H–J). The average absorbance of Mg2+ per nucleotide in different conformational states at 50 and 200 mM is shown in Fig. 4(N–P) at different temperatures. At a higher ionic strength, the absorbance of Mg2+ on DNA HJ nucleotides is enhanced by a factor of 2, leading to counter-ion-mediated repulsions.
Here, we summarize our discussion and interpretation based on observations from the experimental data. The interpretation of the data in terms of the 3-state model is primarily based on the time constants in the time correlation function analysis and three Gaussian functions in the overall probability density function. As a macrostate is composed of multiple microstates and macrostates are formed based on the energy distributions among microstates, we can assume that this three-state model is the interpretation of the data acquired using our microscope with limited resolution. Therefore, we can state that the dynamics interconversion may go through multiple numbers of intermediate states possibly with high energy. An experiment and interpretation of the data from the single molecule intensity time-trajectories always have a limitation based on the experimental setup. The interconversion rate and dynamics acquired by our setup have a time resolution of 50 ms. However, the dynamic change or interconversion of DNA HJ can go through multiple states and multiple intermediate states, which are beyond the resolution of our setup. The exact characterization of thermodynamic parameters for existing microstates of DNA HJ and the role of Mg2+ are key questions in our study, which give an interpretation that Mg2+ concentration gradually increases towards the center of the junction. This observation opens up various follow-up questions in relation to the exact mapping of Mg2+ ion with the oppositely charged phosphate backbone of DNA, and the relation of charge density with thermodynamically stable macrostate.
Conclusion
In conclusion, our study elucidates the intricate dynamics of DNA Holliday Junction and the critical role of ionic environments in modulating their conformational that are extremely difficult to characterize using ensemble-averaged experimental techniques. By combining sophisticated optical methods of smFRET with molecular dynamics simulations, we identified three distinct thermodynamically stable conformational macrostates and demonstrated that the transition rates between these states are significantly influenced by the divalent ion concentration. The predominance of an open conformational state under physiological conditions highlights the importance of ionic stabilization in HJ dynamics. Additionally, our observation of differential divalent ion concentration in the central region of HJ underscores the junction point's pivotal role in governing conformational stability and genetic recombination. In the future, further study on other biologically relevant ions and DNA repair processes could help understand the molecular mechanism of regulatory processes and provide more comprehensive knowledge of the relationship between structure–function dynamics. In addition, our observation is specific to one sequence of DNA HJ, and future exploration of various sequences of HJ may provide a more general conclusion. Ultimately, our study will contribute to a more detailed understanding of heterogeneous genome maintenance, which is a key feature of nature as well as the genome repair process, potentially informing the development of therapeutic strategies targeting genetic disorders. This may also give us an indication with evidence from experimental and molecular simulations of how life is created with so much genetic diversity.Author contributions
The manuscript was written with contributions from all authors. All authors have given approval to the final version of the manuscript. PA performed the smFRET experiment. PA and MKH performed statistical analysis of smFRET data. MKH de-signed, performed, and analyzed coarse-grained simulations. AP designed, performed, and validated atomistic simulations. PA, MKH, and DKS wrote the manuscript. Both DKS and MKH supervised the progress of the project. DKS conceived, directed, and secured funds for the project.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
Authors declare no conflict of interest.Acknowledgements
DKS thank SERB, Department of Science and Technology for Start-up Research Grant (Grant number – SRG/2020/001730) and Ministry of Education for STARS Grant (STARS2/2023-0473). DKS and MKH would also like to thank IIT Jodhpur for SEED Grant. DKS thank Dr Rajeev Yadav (Michigan State University) for valuable suggestions to develop pTIRF microscope. PA thank IIT Jodhpur for fellowship. Authors sincerely acknowledge help from Prof. Santanu Chaudhury (Former Director, IITJ) and Ann Wheeler (University of Edinburgh) for help and support to develop the microscope setup. This article is dedicated to Professor Kankan Bhattacharyya.References
- A. C. Payne, Z. D. Chiang, P. L. Reginato, S. M. Mangiameli, E. M. Murray, C.-C. Yao, S. Markoulaki, A. S. Earl, A. S. Labade and R. Jaenisch, Science, 2021, 371, eaay3446 CrossRef CAS PubMed.
- B. Schumacher, J. Pothof, J. Vijg and J. H. Hoeijmakers, Nature, 2021, 592, 695–703 CrossRef CAS.
- Y. Dong, C. Yao, Y. Zhu, L. Yang, D. Luo and D. Yang, Chem. Rev., 2020, 120, 9420–9481 CrossRef CAS PubMed.
- J. Elzanowska, C. Semira and B. Costa-Silva, Mol. Oncol., 2021, 15, 1701–1714 CrossRef CAS.
- A. Basu, D. G. Bobrovnikov and T. Ha, J. Mol. Biol., 2021, 433, 166861 CrossRef CAS.
- M. Bzymek, N. H. Thayer, S. D. Oh, N. Kleckner and N. Hunter, Nature, 2010, 464, 937–941 CrossRef CAS PubMed.
- D. R. Duckett, A. I. Murchie, S. Diekmann, E. von Kitzing, B. Kemper and D. M. Lilley, Cell, 1988, 55, 79–89 CrossRef CAS PubMed.
- Q. Song, Y. Hu, A. Yin, H. Wang and Q. Yin, Int. J. Mol. Sci., 2022, 23, 9730 CrossRef CAS PubMed.
- S. Sarbajna and S. C. West, Trends Biochem. Sci., 2014, 39, 409–419 CrossRef CAS PubMed.
- G. Laxmikanthan, C. Xu, A. F. Brilot, D. Warren, L. Steele, N. Seah, W. Tong, N. Grigorieff, A. Landy and G. D. Van Duyne, eLife, 2016, 5, e14313 CrossRef PubMed.
- C. R. Simmons, T. MacCulloch, M. Krepl, M. Matthies, A. Buchberger, I. Crawford, J. Šponer, P. Šulc, N. Stephanopoulos and H. Yan, Nat. Commun., 2022, 13, 3112 CrossRef CAS PubMed.
- C. Hodson, J. K. Low, S. van Twest, S. E. Jones, P. Swuec, V. Murphy, K. Tsukada, M. Fawkes, R. Bythell-Douglas and A. Davies, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2109093119 CrossRef CAS.
- P. S. Ho, Biochem. Soc. Trans., 2017, 45, 1149–1158 CrossRef CAS.
- W. D. Wright, S. S. Shah and W.-D. Heyer, J. Biol. Chem., 2018, 293, 10524–10535 CrossRef CAS.
- B. F. Eichman, J. M. Vargason, B. H. Mooers and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 3971–3976 CrossRef CAS PubMed.
- J. Yu, T. Ha and K. Schulten, Nucleic Acids Res., 2004, 32, 6683–6695 CrossRef CAS.
- H. N. Ho and S. C. West, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2123420119 CrossRef CAS PubMed.
- S. Ray, N. Pal and N. G. Walter, Nucleic Acids Res., 2021, 49, 2803–2815 CrossRef CAS PubMed.
- Y. Liu and S. C. West, Nat. Rev. Mol. Cell Biol., 2004, 5, 937–944 CrossRef CAS.
- Y. Liu, A. D. Freeman, A.-C. Declais, T. J. Wilson, A. Gartner and D. M. Lilley, Cell Rep., 2015, 13, 2565–2575 CrossRef CAS.
- M. A. Karymov, M. Chinnaraj, A. Bogdanov, A. R. Srinivasan, G. Zheng, W. K. Olson and Y. L. Lyubchenko, Biophys. J., 2008, 95, 4372–4383 CrossRef CAS PubMed.
- K. M. Górecka, M. Krepl, A. Szlachcic, J. Poznański, J. Šponer and M. Nowotny, Nat. Commun., 2019, 10, 4102 CrossRef PubMed.
- U. Rass, S. A. Compton, J. Matos, M. R. Singleton, S. C. Ip, M. G. Blanco, J. D. Griffith and S. C. West, Genes Dev., 2010, 24, 1559–1569 CrossRef CAS.
- M. A. Sobhy, A. Bralić, V.-S. Raducanu, M. Takahashi, M. Tehseen, F. Rashid, M. S. Zaher and S. M. Hamdan, Nucleic Acids Res., 2019, 47, 1935–1949 CrossRef CAS PubMed.
- D. M. Lilley, FEBS Lett., 2017, 591, 1073–1082 CrossRef CAS.
- P. A. Khuu, A. R. Voth, F. A. Hays and P. S. Ho, J. Mol. Recognit., 2006, 19, 234–242 CrossRef CAS.
- S. Hohng, R. Zhou, M. K. Nahas, J. Yu, K. Schulten, D. M. Lilley and T. Ha, Science, 2007, 318, 279–283 CrossRef CAS PubMed.
- H. D. Wyatt and S. C. West, Cold Spring Harbor Perspect. Biol., 2014, 6, a023192 CrossRef.
- P. Agarwal, S. H. Kabir and N. Pal, Chem. Phys. Impact., 2023, 7, 100322 CrossRef.
- J. M. Fogg, M. Kvaratskhelia, M. F. White and D. M. Lilley, J. Mol. Biol., 2001, 313, 751–764 CrossRef CAS PubMed.
- G. J. Sharples, Mol. Microbiol., 2001, 39, 823–834 CrossRef CAS PubMed.
- R. Zhou, O. Yang, A.-C. Déclais, H. Jin, G. H. Gwon, A. D. Freeman, Y. Cho, D. M. Lilley and T. Ha, Nat. Chem. Biol., 2019, 15, 269–275 CrossRef CAS PubMed.
- J. Yan, S. Hong, Z. Guan, W. He, D. Zhang and P. Yin, Nat. Commun., 2020, 11, 1417 CrossRef CAS PubMed.
- F. A. Hays, J. Watson and P. S. Ho, J. Biol. Chem., 2003, 278, 49663–49666 CrossRef CAS.
- J. Liu, A.-C. Déclais and D. M. Lilley, J. Mol. Biol., 2004, 343, 851–864 CrossRef CAS PubMed.
- J. K. Strauss and L. J. Maher III, Science, 1994, 266, 1829–1834 CrossRef CAS PubMed.
- S. M. Miick, R. S. Fee, D. P. Millar and W. J. Chazin, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 9080–9084 CrossRef CAS.
- A. L. Mikheikin, A. Y. Lushnikov and Y. L. Lyubchenko, Biochemistry, 2006, 45, 12998–13006 CrossRef CAS PubMed.
- J. Matos and S. C. West, DNA Repair, 2014, 19, 176–181 CrossRef CAS.
- S. A. McKinney, A.-C. Déclais, D. M. Lilley and T. Ha, Nat. Struct. Biol., 2003, 10, 93–97 CrossRef CAS PubMed.
- N. Møllegaard, A. Murchie, D. Lilley and P. Nielsen, EMBO J., 1994, 13, 1508–1513 CrossRef.
- D. R. Duckett, A. Murchie and D. Lilley, EMBO J., 1990, 9, 583–590 CrossRef CAS PubMed.
- W. Wang, L. M. Nocka, B. Z. Wiemann, D. M. Hinckley, I. Mukerji and F. W. Starr, Sci. Rep., 2016, 6, 22863 CrossRef CAS.
- G. Carlström and W. J. Chazin, Biochemistry, 1996, 35, 3534–3544 CrossRef PubMed.
- M. Karymov, D. Daniel, O. F. Sankey and Y. L. Lyubchenko, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 8186–8191 CrossRef CAS.
- J. L. Litke, Y. Li, L. M. Nocka and I. Mukerji, Int. J. Mol. Sci., 2016, 17, 366 CrossRef.
- T. Zettl, X. Shi, S. Bonilla, S. M. Sedlak, J. Lipfert and D. Herschlag, Nucleic Acids Res., 2020, 48, 8090–8098 CrossRef CAS PubMed.
- C. Joo, S. A. McKinney, D. M. Lilley and T. Ha, J. Mol. Biol., 2004, 341, 739–751 CrossRef CAS PubMed.
- Z. Zhang, J. Sponer, G. Bussi, V. Mlynsky, P. Sulc, C. R. Simmons, N. Stephanopoulos and M. Krepl, J. Chem. Inf. Model., 2023, 63, 2794–2809 CrossRef CAS PubMed.
- A. Y. Lushnikov, A. Bogdanov and Y. L. Lyubchenko, J. Biol. Chem., 2003, 278, 43130–43134 CrossRef CAS.
- S. H. Lin, D. Zhao, V. Deng, V. K. Birdsall, S. Ho, O. Buzovetsky, C. M. Etson and I. Mukerji, Int. J. Mol. Sci., 2022, 24, 580 CrossRef PubMed.
- A. Nautiyal and M. Thakur, ACS Omega, 2024, 9, 12515–12538 CAS.
- I. G. Panyutin, I. Biswas and P. Hsieh, EMBO J., 1995, 14, 1819–1826 CrossRef CAS.
- M. Levitus and S. Ranjit, Q. Rev. Biophys., 2011, 44, 123–151 CrossRef CAS.
- J. Spiriti, J. K. Binder, M. Levitus and A. Van Der Vaart, Biophys. J., 2011, 100, 1049–1057 CrossRef CAS PubMed.
- B. Hellenkamp, S. Schmid, O. Doroshenko, O. Opanasyuk, R. Kühnemuth, S. Rezaei Adariani, B. Ambrose, M. Aznauryan, A. Barth and V. Birkedal, Nat. Methods, 2018, 15, 669–676 CrossRef CAS PubMed.
- C. Phelps, B. Israels, D. Jose, M. C. Marsh, P. H. von Hippel and A. H. Marcus, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3612–E3621 CrossRef CAS.
- B. Israels, C. S. Albrecht, A. Dang, M. Barney, P. H. von Hippel and A. H. Marcus, J. Phys. Chem. B, 2021, 125, 9426–9440 CrossRef CAS PubMed.
- S. Jafilan, L. Klein, C. Hyun and J. Florián, J. Phys. Chem. B, 2012, 116, 3613–3618 CrossRef CAS PubMed.
- A. E. García, J. A. Krumhansl and H. Frauenfelder, Proteins: Struct., Funct., Bioinf., 1997, 29, 153–160 CrossRef.
- P. C. Whitford, P. Geggier, R. B. Altman, S. C. Blanchard, J. N. Onuchic and K. Y. Sanbonmatsu, RNA, 2010, 16, 1196–1204 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson and D. Van Der Spoel, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials and methods, experimental details, numerical procedure for calculation solving the three state kinetic network model, molecular dynamic simulation procedure, 4th order TCF of different waiting time, comparison of probability density function obtained from molecular dynamic simulation. See DOI: https://doi.org/10.1039/d4nr02411g |
| ‡ Present address: Department of Pharmaceutical Sciences, University of Illinois at Chicago, Illinois 60607, USA. |
| This journal is © The Royal Society of Chemistry 2025 |
