Quantifying the polar skyrmion motion barrier in an oxide heterostructure

Abstract

Exotic polar topologies such as polar skyrmions have been widely observed in ferroelectric superlattice systems. The dynamic motion of polar skyrmions under external forces holds promise for applications in advanced electronic devices such as race-track memory. Meanwhile, the polar skyrmion motion has proven to be challenging due to the strong skyrmion–skyrmion interaction and a lack of a mechanism similar to the spin-transfer torque. In this study, we have developed a nudged elastic band (NEB) method to quantify the polar skyrmion motion barrier along a specific trajectory. It is indicated that the skyrmion motion barrier can be significantly reduced with the reduction of the periodicity to 8 uc, due to the large reduction of the skyrmion size. Moreover, this barrier can also be greatly reduced with a small external electric potential. Following the analysis, we further performed phase-field simulation to verify the collective motion of the polar skyrmion. We have demonstrated the collective skyrmion motion by applying a 5 μN mechanical force using a blade-shaped indenter with a periodicity of 8 unit cells, under an external applied voltage of 1.5 V. This study further paves the way for the design of polar skyrmion-based electronic devices.

---

Introduction

Topological phases and phase transitions are a fertile field of study in condensed matter physics and materials science, and have attracted wide attention in various fields including liquid crystals,¹ superconductors,² optical materials,³ and ferromagnetic^4,5 and ferroelectric materials.⁶ For instance, in ferroelectric heterostructures, numerous exotic polar topologies have been discovered, such as flux closure,⁷ vortexes,^8–10 skyrmions,^11–13 merons,^14,15etc. These topological structures exhibit emergent phenomena, intriguing physical properties, and wide potential applications.^8,16–20 In particular, polar skyrmions,¹³ with whirl-like spatially non-uniform polarization distributions, show characteristics such as small size,^11,13 chirality,^13,15,21 negative permittivity,¹⁸ and enhanced second harmonic generations,²² making them a promising candidate for applications in memory devices, transistors, and optical switches.

To date, various device applications have been proposed for ferromagnetic skyrmions,^23–26 based on the race track memory concept. In this concept, a narrow wire is designed for the skyrmions to pass through, while the creation and motion of the skyrmions (or antiskyrmions) are driven by an external electric current.^27,28 A skyrmion counter is then placed in the middle of the wire to record the information. The physical mechanism that drives the collective motion of skyrmions in ferromagnetic materials is the spin-transfer torque.^23,29 In ferroelectrics, although the controlled switching and topological phase transitions have been widely investigated for polar skyrmions, it has long been believed that the skyrmions are difficult to move due to the lack of a mechanism similar to the spin transfer torque. Additionally, the strong pinning effect between the skyrmions could further hinder their motion.

Recently, it has been demonstrated that under a combination of mechanical, electrical, and thermal stimuli, the dynamic motion of skyrmions in PbTiO₃/SrTiO₃ (denoted as PTO/STO) superlattices can be achieved.³⁰ The collective motion of polar skyrmions raises hope for the development of polar-skyrmion-based race track memory, where the polar skyrmions are used as bits for data storage and processing, akin to their ferromagnetic counterparts. However, a systematic understanding of the motion of polar skyrmions, in particular, the skyrmion motion barrier that hinders the skyrmion motion is still lacking. Also, the practical methods to lower this barrier have not been investigated yet. Herein, phase-field simulation is performed to quantify the skyrmion motion barrier under different conditions, hoping to find ways to enable the collective movement of polar skyrmions.

Main

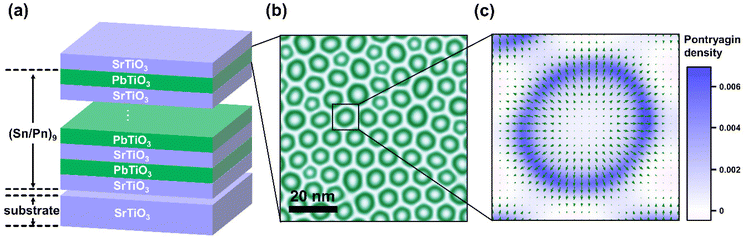
The (PTO)_n/(STO)_n superlattice (n = 6–24) grown on a (001)-STO substrate was chosen as the model system, where polar skyrmions have been widely observed recently.³¹ The initial configuration of the simulation system is given in Fig. 1. The phase-field simulations were performed by solving the time-dependent Ginzburg–Landau equation: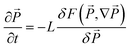 , where 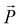is the spontaneous polarization vector, t is the evolution time, and L is the kinetic coefficient which is related to the domain wall mobility. The total free energy F can be written as the volume integration of the Landau chemical, mechanical, electrostatic, and polarization gradient energy densities: 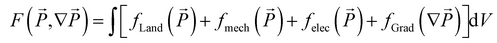. Details of how to solve the phase-field equations, the physical parameters, and the boundary conditions are given in the Methods section and previous reports.^10,12,32 To determine the substrate strain for each layer, the pseudocubic lattice parameters of PTO and STO were set as 3.957 Å and 3.905 Å, respectively.

Fig. 1 Initial setups for the simulation systems. (a) Schematics of the PTO/STO superlattice system with different periodicities n. (b) Planar view of the in-plane polarization distribution on the top PTO layer. (c) Magnified view of the Pontryagin density of the selected bubble, overlaid with the in-plane polar vector.

The calculated polarization distribution of the top PTO layer for (PTO)₁₂/(STO)₁₂ is plotted in Fig. 1(b). The bubble-like polarization structures can be seen in the PTO layer, consistent with a previous report.³¹ The Pontryagin density q was calculated by using the formula 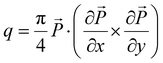,^11,33 and the topological charge Q could then be obtained by calculating the surface integral of the Pontryagin density: Q = ∫qdxdy. The Pontryagin density of the bubble state is shown in Fig. S1,† the magnified view of the in-plane polarization vector and the Pontryagin density of the chosen bubble are shown in Fig. 1(c). A circular-like Pontryagin density distribution could be observed for each bubble, with a topological charge of +1, confirming that it is a polar skyrmion.

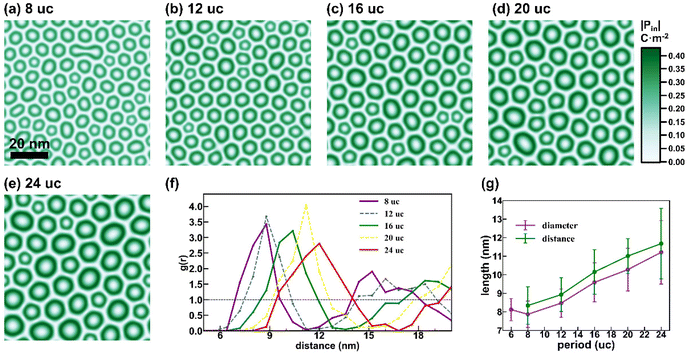
Then, a series of superlattice systems with different periodicities (n = 6, 8, 12, 16, 20, and 24 unit cells, denoted as uc) were simulated (Fig. 2). With a periodicity of 6, mixtures of skyrmions and stripes could be observed in the PTO layer (Fig. S2†), while increasing the periodicity to 8 could reduce the population of the stripes. This can be attributed to the fact that decreasing periodicity increases the depolarization strength, leading to the formation of more stripes instead of bubbles. The polar structures for n > 6 are shown in Fig. 2(a)–(e), where polar skyrmions with different sizes can be seen. Generally, the larger the periodicity, the larger the average skyrmion size and the lower the skyrmion density. The Radial Distribution Function (RDF) of the skyrmions in each system was analyzed and is depicted in Fig. 2(f) to quantitatively measure the neighboring distances of the skyrmions. The first peak in the RDF image can be used to determine the distance between the nearest neighbors. It can be seen in Fig. 2(f) and (g) that the distance between neighbor skyrmions increases with increasing periodicity of the superlattice. The diameter of skyrmions with different periodicities was further measured and plotted by taking 3/8 of the maximum in-plane polarization in as the skyrmion boundary in each system in Fig. 2(g). When the periodicity is larger than 12, the diameter of the polar skyrmions tends to obey the Kittel's law,^34,35 which scales linearly with the periodicity. However, for the system with a shorter periodicity (i.e. n < 8), the diameter of the skyrmions is almost constant. This phenomenon is consistent with previous reports, showing the intrinsic size limit of the polar skyrmions.³¹

Fig. 2 Initial states of different systems at 300 K. (a–e) The patterns of different polar structures of the superlattice with different periodicities, at 300 K, respectively. (f) The Radial Distribution Function (RDF) of the skyrmions in each system. (g) The variation of the distance and diameter with respect to the periodicity.

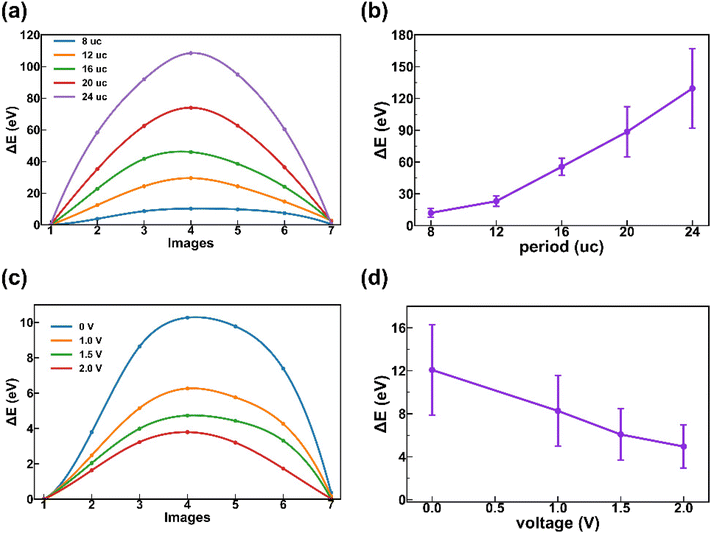
Next, we employed a nudged elastic band (NEB) method to calculate the skyrmion motion barrier with a vacancy diffusion mechanism, similar to a previous report³⁰ (Fig. 3). The NEB method is commonly used in density functional theory (DFT) calculations to determine the diffusion and reaction barrier. A superlattice with a periodicity of n = 12 was used as an example. Initially, a skyrmion vacancy was created in the system by manually switch a skyrmion to a pure c-domain (Fig. 3a, marked as Image 1). Subsequently, we identified a trajectory along which a selected skyrmion near the vacancy could migrate towards the vacancy site, as shown in Fig. 3(b)–(g), marked as Image 2–7. Taking Image 1 as the reference state, the energy for each image along the transition path was then calculated and is plotted in Fig. 3(h). It is evident that the maximum energy occurs in the middle of the migration route as expected (e.g., Image 4), and the energy path is almost symmetric. When the skyrmion passes through the middle part of the path, it experiences a certain degree of deformation due to the interactions with skyrmions on both sides (Fig. 3c–e). Meanwhile, the skyrmion structure is robust with a topological charge of +1 as shown in Fig. S3.† The migration barrier of the chosen skyrmion is approximately 30 eV, which is remarkably high and significantly hinders the skyrmion's motion. The high migration barrier can be understood since it involves the simultaneous motion of polarization for over 2000 unit cells.

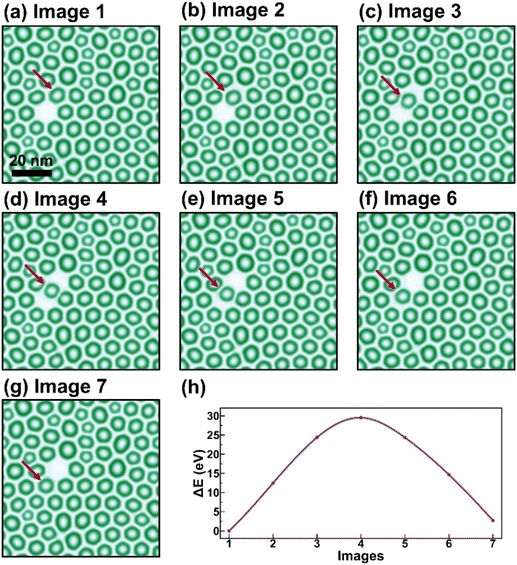Fig. 3 Quantifying the skyrmion migration barrier through a vacancy mechanism. (a–g) The migration pathway. (h) The energy landscape of the designed migration path.

Then, we proceeded to quantify the influence of periodicity and voltage on the skyrmion motion barrier, as shown in Fig. 4, using a similar NEB method with the vacancy migration mechanism as described above. The skyrmion motion for different periodicities at room temperature was investigated. The details of the motion process for different superlattice systems (8, 16, 20, and 24 uc) are plotted in Fig. S4;† a skyrmion vacancy was created, and a trajectory was designed for the chosen skyrmion to migrate towards the vacancy. A symmetric transition energy path was observed for all the periodicities, due to the symmetric nature of the transition pathway. The energy barrier can be deduced from the energy curve, and is plotted in Fig. 4(b). The average energy barrier for a single skyrmion to move through a vacancy mechanism decreases monotonically and linearly as the periodicity decreases from 24 uc to 12 uc, and decreases slightly from 12 uc to 8 uc. The skyrmion motion barrier in the superlattice with a periodicity of 24 uc is approximately 130 eV, while it is only approximately 12 eV with a periodicity of 8 uc, indicating that reducing the periodicity is an effective way to reduce the polar skyrmion motion barrier. This can be understood since the larger the periodicity, the larger the skyrmion size, and higher energy is required to trigger the collective motion.

Fig. 4 The influencing factor of the motion barrier. (a) The energy landscape of the skyrmion in systems with different periodicities. (b) The curve of the average motion barriers with the periodicity. (c) The energy landscape of the same skyrmion under different applied voltages. (d) The curve of the average motion barriers with respect to the voltage.

The voltage applied on the superlattice is another factor that could affect the skyrmion motion barrier. Taking the superlattice with a periodicity of 8 as an example, three different voltages were studied, e.g., 1.0 V, 1.5 V, and 2.0 V, and compared with the case without the applied voltage shown above. The polar patterns and the corresponding Pontryagin density distributions for the top PTO layer after applying different electric fields are given in Fig. S5.† It can be seen that the volume of the skyrmion shrinks continuously upon the application of the external electric bias. This can be understood since the polarization inside the skyrmion is unfavored with a negative applied electric field. It can be seen that the topological charge for each skyrmion is conserved (+1), although the volume of the skyrmion shrinks under higher voltages (from 0 V–2 V). Notably, a stripe decomposes to two skyrmions with an applied potential of 1.5 V, leading to an increase in the total topological charge from +1 to +2. The skyrmion motion barriers were calculated using a similar NEB method, and the energy landscape for the vacancy mechanism is plotted in Fig. 4(c), with the energy barrier deduced and plotted in Fig. 4(d). It can be seen that increasing the applied voltage can reduce the skyrmion motion barrier, due to the increased distance between skyrmions and weakening of the skyrmion–skyrmion pinning effect. The skyrmion barrier can be reduced from 12 eV to 4 eV when the applied voltage increases to 2.0 V for n = 8. This indicates that an applied voltage is another effective way to trigger the skyrmion motion by reducing the skyrmion motion barrier.

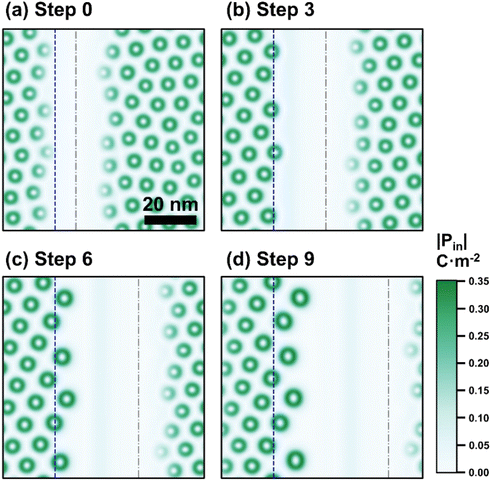
It should be noted that although the collective motion of the skyrmions has been achieved in the previous report,³⁰ the skyrmion motion condition given in that report is difficult to realize experimentally. Based on the above analysis, we performed phase-field simulation to show the dynamic motion of the skyrmion with only two external stimuli (e.g., mechanical and electrical forces) by decreasing the superlattice periodicity. The superlattice with a periodicity of 8 unit cells was used, under an applied voltage of 1.5 V. With a blade-shaped indenter to apply an external force of 5 μN, the collective motion of the skyrmions is demonstrated (Fig. 5). The application of this external force will give rise to a compressive stress of ∼2.5 GPa, which is sufficient to mechanically switch the skyrmions to a single domain state,³⁰ which will leave space for the skyrmions to move freely without the pinning from neighboring skyrmions. Initially, a blade-shaped indenter is used to apply a 5 μN force, with its center located at the grey dash-dot line at step 0 as shown in Fig. 5(a). When the system reaches equilibrium, the skyrmions underneath the indenter disappear and a single c-domain region forms. The blue dashed line indicates the left boundary of the c-domain region and the skyrmions. Next, the indenter is moved rightward, at a speed of 4 nm per step (each step takes 10 000 timesteps). The polar morphologies after 3, 6, and 9 steps are given in Fig. 5(b–d). As the indenter moves rightward, the skyrmions in the vicinity of the indenter also move. After 3 steps, the skyrmions can move by a distance of half a skyrmion. After 6 steps, three skyrmions pass the blue dashed line, which indicates that the skyrmions have moved at least 8 nm, whereas after 9 moves, all the skyrmions in the first line behind the blade move across the blue dashed line, with a distance of ∼15 nm. This indicates that the dynamic motion can be achieved with a simpler condition as compared to our previous report, shedding light for the experimental realization of the skyrmion motion. Moreover, the skyrmion motion speed is also ∼5 m s⁻¹, consistent with the previous report.³⁰ We also calculated the distribution of the Pontryagin density of the system during the skyrmion motion process, as shown in Fig. S6.† For the skyrmions near the blade-shaped indenter, the polarization and Pontryagin density both become asymmetric, but the topological charge of those skyrmions remains +1.

Fig. 5 Dynamic motion of the skyrmions with a moving indenter under an applied voltage of 1.5 V. (a) The initial configuration, step 0, (b) after three moves, (c) after 6 moves, (d) after 9 moves. The collective motion of the polar skyrmions can be clearly seen.

Methods

Phase-field simulations: the ferroelectric system was simulated utilizing phase-field simulations. The order parameter selected was the polarization vector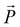 . The temporal evolution of the polarization can be obtained by solving the time-dependent Ginzburg–Landau (TDGL) equation:^36,37

The total free energy 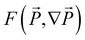can be obtained by the volume integration of four contributions – Landau chemical, mechanical, electrostatic, and polarization gradient energy densities:

Detailed expressions of the free energies and the simulation parameters can be found in the previous literature.^10,37,38

A three-dimensional mesh of 192 × 192 × nz (nz = 164, 200, 278, 350, 422, and 494 when the periodicity is 6, 8, 12, 16, 20, and 24 uc, respectively) discrete grid points was used as the simulation system, with each grid point representing 0.4 nm. The periodic boundary condition was applied in the in-plane dimensions and the superposition method was applied in the out-of-plane direction. Along the out-of-plane direction, the thickness of the STO substrate was assumed to be 12 nm, and 8 nm of air, while the thickness of (PTO)_n/(STO)_n was determined by the periodicity n of the system. The normalized timestep was set to be 0.01.

Conclusions

In conclusion, we have developed a nudged elastic band (NEB) method to quantify the dynamic motion barrier for polar skyrmions in a ferroelectric superlattice system. It is shown that the skyrmion motion barrier can be reduced from 130 eV to 12 eV with the reduction of superlattice periodicity from 24 u.c. to 8 u.c., due to the monotonic reduction of the skyrmion size from 12 nm to 8 nm. Furthermore, the application of an external electric potential could also reduce the skyrmion motion barrier, due to the reduced skyrmion size and skyrmion–skyrmion interaction. The skyrmion motion barrier can be reduced to 4 eV (n = 8 u.c.) after the application of an external potential of 2 V. Based on the above understanding, we performed phase-field simulation to verify the dynamic motion of the skyrmions with a smaller periodicity, and with two external stimuli (mechanical and electrical). It is demonstrated that the collective skyrmion motion can be achieved by applying a mechanical force of 5 μN via a blade-shaped indenter on a superlattice film with a periodicity of 8 u.c., under an applied potential of 1.5 V. Notably, the skyrmion motion condition in this study is much simpler as compared to a previous report, shedding light for further experimental verification. Moreover, the external mechanical force may be replaced by a moving PFM or AFM³⁹ tip by the careful design of materials system and temperature conditions, thus achieving a full electric-driven motion of polar skyrmions towards the design of a race-track memory system. We hope to spur further experimental and theoretical efforts on the dynamic motion of polar skyrmions and the design of polar-skyrmion-based electronic devices.

Author contributions

L. H.: data curation, investigation, visualization, methodology, writing – original draft, and writing – review and editing; Y. H.: formal analysis, supervision, and writing – review and editing; Y. W.: formal analysis, funding acquisition, supervision, methodology, writing – original draft, and writing – review and editing; Z. H.: conceptualization, data curation, investigation, formal analysis, funding acquisition, supervision, methodology, writing – original draft, and writing – review and editing.

Data availability

The data supporting this article have been included as part of the ESI.† Further information can be acquired from the corresponding authors upon reasonable request.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The financial support from the National Natural Science Foundation of China (grant no. 92166104, ZH) and the Joint Funds of the National Natural Science Foundation of China (grant no. U21A2067, YW) is acknowledged. YW is supported by the Natural Science Foundation of Zhejiang Province (LD24E020003). ZH also acknowledges a start-up grant from Zhejiang University and the Fundamental Research Funds for the Central Universities (2023QZJH13). The phase-field simulation was performed using the Mu-PRO software package (https://muprosoftware.com) on the MoFang III cluster at the Shanghai Supercomputing Center (SSC).

References

1. X. Wang, et al., Moiré effect enables versatile design of topological defects in nematic liquid crystals, Nat. Commun., 2024, 15, 1655.
2. L. Hu and R. Zhang, Topological superconducting vortex from trivial electronic bands, Nat. Commun., 2023, 14, 640.
3. Y. Shen, et al., Optical skyrmions and other topological quasiparticles of light, Nat. Photonics, 2024, 18, 15.
4. A. Fert, N. Reyren and V. Cros, Magnetic, skyrmions: advances in physics and potential application, Nat. Rev. Mater., 2017, 2, 17031.
5. J. Sahoo, et al., Role of competing magnetic anisotropies in deriving topologically nontrivial spin textures in oxide heterostructures, Phys. Rev. B, 2024, 110, 104422.
6. X. Guo, et al., Theoretical Understanding of Polar Topological Phase Transitions in Functional Oxide Heterostructures: A review, Small Methods, 2022, 6, 2200486.
7. Y. Tang, et al., Observation of a periodic array of flux-closure quadrants in strained ferroelectric PbTiO3 films, Science, 2015, 348, 547–551.
8. I. Naumov, L. Bellaiche and H. Fu, Unusual phase transitions in ferroelectric nanodisks and nanorods, Nature, 2024, 432, 737–740.
9. A. Yadav, et al., Observation of polar vortices in oxide superlattices, Nature, 2016, 530, 198–201.
10. Z. Hong, et al., Stability of Polar Vortex Lattice in Ferroelectric Superlattices, Nano Lett., 2017, 17, 2246–2252.
11. Y. Nahas, et al., Discovery of stable skyrmionic state in ferroelectric nanocomposites, Nat. Commun., 2015, 6, 8542.
12. Z. Hong and L. Chen, Blowing polar skyrmion bubbles in oxide superlattices, Acta Mater., 2018, 152, 155–161.
13. S. Das, et al., Observation of room-temperature polar skyrmions, Nature, 2019, 568, 368–372.
14. Y. Wang, et al., Polar meron lattice in strained oxide ferroelectrics, Nature, 2020, 19, 881–886.
15. Y. Shao, et al., Emergent chirality in a polar meron to skyrmion phase transition, Nat. Commun., 2023, 14, 1355.
16. P. Shafer, et al., Emergent chirality in the electric polarization texture of titanate superlattices, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 915–920.
17. A. Yadav, et al., Spatially resolved steady-state negative capacitance, Nature, 2019, 565, 468–471.
18. S. Das, et al., Local negative permittivity and topological phase transition in polar skyrmions, Nat. Mater., 2021, 20, 194–201.
19. E. Yang, et al., Nonvolatile Ferroelectric-Domain-Wall Memory Embedded in a Complex Topological Domain Structure, Adv. Mater., 2022, 34, 2107711.
20. J. Seidel, Nanoelectronics based on topological structures, Nat. Mater., 2019, 18, 188–190.
21. W. Zhang, et al., Chiral Skyrmions Interacting with Chiral Flowers, Nano Lett., 2023, 23, 11793–11801.
22. X. Wang, et al., Giant electric field-induced second harmonic generation in polar skyrmions, Nat. Commun., 2024, 15, 1374.
23. F. Büttner, et al., Field-free deterministic ultrafast creation of magnetic skyrmions by spin–orbit torques, Nat. Nanotechnol., 2017, 12, 1040–1044.
24. V. Pham, et al., Fast current-induced skyrmion motion in synthetic antiferromagnets, Science, 2024, 384, 307–312.
25. S. Chen, et al., All-electrical skyrmionic magnetic tunnel junction, Nature, 2024, 627, 522–527.
26. H. Zhang, et al., Magnetic skyrmions: materials, manipulation, detection, and applications in spintronic devices, Mater. Futures, 2023, 2, 032201.
27. S. Woo, et al., Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets, Nat. Mater., 2016, 15, 501–506.
28. S. Vélez, et al., Current-driven dynamics and ratchet effect of skyrmion bubbles in a ferrimagnetic insulator, Nat. Nanotechnol., 2022, 17, 834–841.
29. C. Sarmiento and A. Guimarães, Analysis of stability and transition dynamics of skyrmions and skyrmioniums in ferromagnetic nanodisks: A micromagnetic study at finite temperature, Phys. Rev. B, 2024, 110, 064437.
30. L. Hu, et al., Dynamic Motion of Polar Skyrmions in Oxide Heterostructures, Nano Lett., 2023, 23, 11353–11359.
31. F. Gong, et al., Absence of critical thickness for polar skyrmions with breaking the Kittel's law, Nat. Commun., 2023, 14, 3376.
32. L. Zhou, et al., Local manipulation and topological phase transitions of polar skyrmions, Matter, 2022, 5, 1031–1041.
33. Y. Zhou and M. Ezawa, A reversible conversion between a skyrmion and a domain-wall pair in a junction geometry, Nat. Commun., 2014, 5, 4652.
34. C. Kittel, Theory of the structure of ferromagnetic domains in films and small particles, Phys. Rev., 1946, 70, 965–971.
35. G. Catalan, et al., Domain wall nanoelectronics, Rev. Mod. Phys., 2012, 84, 119–156.
36. L. Chen, Phase-Field Method of Phase Transitions/Domain Structures in Ferroelectric Thin Film: A Review, J. Am. Ceram. Soc., 2008, 91, 1835–1844.
37. Y. Li, et al., Effect of substrate constraint on the stability and evolution of ferroelectric domain structures in thin films, Acta Mater., 2002, 50, 395–411.
38. Y. Li, et al., Effect of electrical boundary conditions on ferroelectric domain structures in thin films, Appl. Phys. Lett., 2022, 81, 427.
39. R. Xu, et al., Advanced atomic force microscopies and their applications in two-dimensional materials: a review, Mater. Futures, 2022, 3, 032302.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03686g

---