Open Access Article
Open Access ArticleAsymmetric [Dy2] molecules deposited into micro-SQUID susceptometers: in situ characterization of their magnetic integrity†
Ana
Repollés‡
a,
María Carmen
Pallarés‡
ab,
David
Aguilà
 cd,
Olivier
Roubeau
cd,
Olivier
Roubeau
 a,
Verónica
Velasco
cd,
Diego
Gella
a,
Leoní A.
Barrios
a,
Verónica
Velasco
cd,
Diego
Gella
a,
Leoní A.
Barrios
 cd,
María José
Martínez-Pérez
cd,
María José
Martínez-Pérez
 a,
Javier
Sesé
a,
Javier
Sesé
 a,
Dietmar
Drung
e,
Jesús Ignacio
Martínez
a,
Dietmar
Drung
e,
Jesús Ignacio
Martínez
 a,
Thomas
Schurig
e,
Boris
Le Guennic
a,
Thomas
Schurig
e,
Boris
Le Guennic
 f,
Anabel
Lostao
f,
Anabel
Lostao
 abg,
Guillem
Aromí
abg,
Guillem
Aromí
 *cd and
Fernando
Luis
*cd and
Fernando
Luis
 *a
*a
aInstituto de Nanociencia y Materiales de Aragón (INMA), CSIC and Universidad de Zaragoza, Plaza San Francisco s/n, 50009 Zaragoza, Spain. E-mail: fluis@unizar.es
bLaboratorio de Microscopias Avanzadas (LMA), Universidad de Zaragoza, 50018 Zaragoza, Spain
cDepartament de Química Inorgànica i Orgànica, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain. E-mail: aromi@ub.edu
dInstitut of Nanoscience and Nanotechnology of the University of Barcelona (IN2UB), Barcelona, Spain
ePhysikalisch-Technische Bundesanstalt (PTB), Abbestraße 2-12, D-10587 Berlin, Germany
fUniv Rennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes) - UMR 6226, F-35000 Rennes, France
gFundación ARAID, 50018 Zaragoza, Spain
First published on 23rd October 2024
Abstract
The controlled integration of magnetic molecules into superconducting circuits is key to developing hybrid quantum devices. Herein, we study [Dy2] molecular dimers deposited into micro-SQUID susceptometers. The results of magnetic, heat capacity and magnetic resonance experiments, backed by theoretical calculations, show that each [Dy2] dimer fulfills the main requisites to encode a two-spin quantum processor. Arrays of between 2 × 108 and 7 × 109[Dy2] molecules were optimally integrated under ambient conditions inside the 20 μm wide loops of micro-SQUID sensors by means of dip-pen nanolithography. Equilibrium magnetic susceptibility and phonon-assisted spin tunneling dynamics measured in situ substantiate that these molecules preserve spin ground states, magnetic interactions and magnetic asymmetry that characterize them in bulk. These results show that it is possible to interface multi-qubit molecular complexes with on-chip superconducting circuits without disturbing their relevant properties and suggest the potential of soft nanolithography techniques to achieve this goal.
Introduction
Molecular nanomagnets are considered good candidates for serving as basic units of future quantum devices.1 The ability to tune their properties by exploiting chemical synthesis has led to major improvements in spin coherence times, even at relatively high temperatures,2–5 that put them on a par with other spin and charge solid-state qubits. Chemical design can also be exploited to scale up quantum resources.6 Molecular and supramolecular structures that encode multiple qubits or, in general, d-dimensional qudits in their electronic7–9 or nuclear10 spin states, or in a combination of both,11 have been reported. Embedding nontrivial quantum operations in each repetitive unit, in this case, a molecule, is seen as one of the main competitive advantages of this approach over other quantum computing platforms as it simplifies the implementation of certain algorithms, in particular quantum error correction.12,13However, achieving full scalability remains challenging because it necessarily involves the ability to control and connect many individual molecules.
A promising idea is to bring concepts and technologies developed for superconducting quantum circuits to the realm of molecules.14–16 The operation of such a hybrid platform sets stringent conditions for the accurate positioning of molecules, ideally under ambient conditions, in suitable locations of a superconducting device.17,18 A second necessary requisite is that relevant molecular properties be retained under such conditions, which might conflict with the need for maximizing their coupling to the circuit.19 While the main concern in the case of individual qubits is that the spin coherence time remains sufficiently long, in the case of molecular structures, hosting multiple spins, even the mere definition of the qubit states, can be strongly affected by the environment. These states and, especially, the ability to address each of them arise from a subtle combination of suitable individual spin states, magnetic asymmetry and intramolecular spin–spin couplings, which critically depend on the composition of the molecular core and molecular structure.7–9 Both aspects can be affected by the loss of crystalline order and interactions with the chip surface that accompany the integration into realistic devices. It is this fundamental aspect that we address in our work.
To this end, we explore molecular complexes hosting two non-equivalent lanthanide ions. The synthesis exploits a protocol that enables selectively obtaining pure homo-7a,c,20,21 or heterometallic7b,22,23 species with chemical formula (Hpy)[LnLn′(HL)3(X)(py)n(H2O)m] (py = pyridine, H3L = 6-(3-oxo-3-(2-hydroxyphenyl)propenol)-pyridine-2-carboxylic acid, X = Cl− or NO3−, n + m = 2), termed here [LnLn′] or [Ln2]. By direct deposition with dip-pen nanolithography, based on AFM, arrays of [Dy2] lanthanide dimers were patterned onto selected areas of suitably designed micro-SQUID superconducting sensors.24,25 The superconducting device allows characterizing in situ their linear magnetic response down to very low temperatures. The ac susceptibility provides information not only on the magnetic moments of the lanthanide ions present in each molecule but also on their mutual interactions and dynamics. The comparison with data measured on the bulk material allows us to critically ascertain whether these molecules retain the ability to encode two addressable spin qubits.
Results and discussion
In previous reports, we have shown that the different coordination environments of the two metal ions in (Hpy)[Tb2(HL)3(Cl)(py)2] and (Hpy)[Gd2(HL)3(NO3)(py)(H2O)], combined with their mutual weak interaction are critical in turning these molecular systems into appropriate prototypes for two- and six-qubit quantum processors, respectively.1c,7a,c In order to probe such properties in a related two-spin system upon deposition onto a superconducting circuit, we synthesized a [Dy2] analogue. On account of the large J = 15/2 angular momentum of free Dy(III), this complex is expected to display a stronger magnetic response, convenient for the detection of signals from thin layers. The compound crystallizes from pyridine/Et2O following the reaction between DyCl3 and H3L. The structure of [Dy2], shown in Fig. 1 and Fig. S1 of the ESI,† exhibits two Dy(III) ions bridged and chelated by three μ:η4−(HL)2− ligands, each via one tri- and one didentate pocket and disposed in a head-to-head-to-tail fashion. The nine-coordination is completed by two py ligands on one metal and by one Cl− donor on the other. This complex forms an H-bond via two COO− moieties with an Hpy+ cation, thus compensating its negative charge. For comparison purposes, a related [LaDy] compound was obtained with the same procedure, using equimolar amounts of Dy(NO3)3 and La(NO3)3 for the reaction. The different coordination sites in the complex allow to selectively discriminate the position of each metal within the molecule selectively based on the ionic radii.7b,21 The structure of [LaDy] (Fig. S2†) is analogous to that of [Dy2] with one Dy(III) substituted by La(III), now coordinated by didentate NO3− (instead of Cl−) and exhibiting coordination number (CN) of 10. The terminal ligands of Dy(III) are here one py and one H2O. The stability of both compounds in solution as well as the heterometallic nature of [LaDy] were shown through mass spectrometry (Fig. S3†).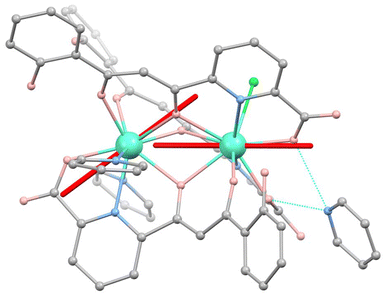 | ||
Fig. 1 Molecular structure of [Dy2]. Turquoise is Dy, grey is C, salmon is O, blue is N and green is Cl. Hydrogen atoms are omitted. Hydrogen bonds between Hpy+ and the complex are in dashed blue lines. Orientations of the magnetic easy axes 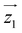 and and 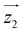 of the two Dy(III) ions, determined via ab initio calculations (see text and ESI†), are shown as red sticks. of the two Dy(III) ions, determined via ab initio calculations (see text and ESI†), are shown as red sticks. | ||
We have tested that [Dy2] fulfils the conditions to encode two addressable spin qubits via a combination of magnetic susceptibility, heat capacity and electron paramagnetic resonance (EPR) experiments on bulk samples, whose results are shown in Fig. 2a, b and c, respectively.
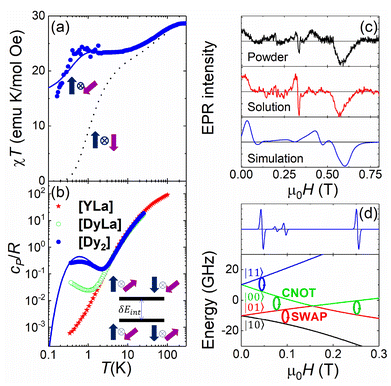 | ||
Fig. 2 Characterization of [Dy2] as a two-qubit system. (a) Plot of χT vs. T between 300 and 0.15 K (dots). The dotted (solid) lines are theoretical predictions for collinear (tilted) magnetic easy axes. They were calculated with χT ≃ χS=1/2T[C0 + C1(2kBT/Δ)tanh(Δ/2kBT) + C2tanh(Δ/2kBT)].7b,26 Here, χS=1/2 is the low temperature susceptibility limit, based on the effective spin Hamiltonian (2), Δ/kB = 1.3(2) × 102 K is the energy gap between the first excited and ground elctronic doublets of each Dy ion, and C0, C1 and C2 are fitting coefficients that depend on the wave functions describing these two doublets. The coupling constant J12/kB was fixed to −0.023 K (−0.014 K) for tilted (collinear) axes, which accounts for the low-T specific heat data. (b) Molar specific heat of [Dy2], [LaDy] and [LaY] at zero magnetic field. The solid line is a calculation that includes the magnetic contribution derived from eqn (2) plus the lattice contribution obtained from the [LaY] data. (c) Continuous wave X-band EPR spectra of [Dy2] at 6 K in bulk powder form (top) and in solution (middle). The bottom panel shows a simulation based on eqn (2) with the same parameters used to calculate the magnetic susceptibility and the specific heat. (d) Bottom: scheme of the 4 lowest lying spin levels of a [Dy2] molecule, calculated with eqn (2) for a magnetic field forming 55 degrees with 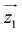 . The magnetic asymmetry and spin–spin coupling lead to unequally spaced levels. Different transitions, shown in the EPR simulation (top), can then be addressed by microwave resonant pulses. This allows encoding two addressable spin qubits and performing conditional quantum operations. . The magnetic asymmetry and spin–spin coupling lead to unequally spaced levels. Different transitions, shown in the EPR simulation (top), can then be addressed by microwave resonant pulses. This allows encoding two addressable spin qubits and performing conditional quantum operations. | ||
The molar magnetic susceptibility χ measured at sufficiently low frequency (1.7 Hz in Fig. 2a) shows the characteristic equilibrium paramagnetic behavior from room temperature down to very low temperatures (T > 0.15 K in Fig. 2a). The χT product provides direct information on the effective magnetic moments μeff of the two Dy ions and their interactions through the Curie–Weiss law
| χT ≃ 2NAμ2eff[T/3kB(T − θ)] | (1) |
The second drop in χT observed below 1 K indicates a weak antiferromagnetic coupling between the two Dy ions. This interaction splits the energies of different mutual spin orientations. The splitting δEint can be detected, even at zero magnetic fields, by means of heat capacity experiments. Fig. 2b and S9† compare the molar specific heat cP of [Dy2] with that measured on the [LaDy] “monomer”. At low temperatures, where the contributions of magnetic excitations overcome those associated with molecular vibrations (estimated from the results obtained for the diamagnetic complex [LaY]),7bcP of [Dy2] shows a Schottky-like anomaly that is clearly absent for [LaDy]. It is then natural to associate this contribution with the energy splitting between the antiparallel and parallel spin orientations in [Dy2]. The temperature of the specific heat maximum Tmax allows estimating δEint ≃ kBTmax/0.42 = 1.50(5) K.
On the basis of the above considerations, it follows that the low-T magnetic behavior of [Dy2] can be understood within a model of two weakly coupled effective S = ½ spins, described by the following spin Hamiltonian7b
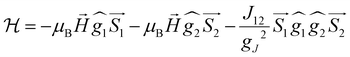 | (2) |
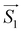 and
and 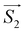 with the magnetic field
with the magnetic field 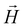 and a spin–spin coupling, where J12 is the coupling constant and gJ = 4/3 is the Landé factor of free Dy(III). It is possible to use eqn (2) to simulate both χT and cP/R. The results, shown in Fig. 2a and b, reveal the need to introduce an asymmetry between the Zeeman interactions of the two ions. As Fig. 2a shows, if the principal values and the axes of
and a spin–spin coupling, where J12 is the coupling constant and gJ = 4/3 is the Landé factor of free Dy(III). It is possible to use eqn (2) to simulate both χT and cP/R. The results, shown in Fig. 2a and b, reveal the need to introduce an asymmetry between the Zeeman interactions of the two ions. As Fig. 2a shows, if the principal values and the axes of 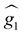 and
and 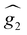 were the same, the cancellation of the two magnetic moments in the ground state would lead to a rapid decrease of χT towards zero (dotted line in Fig. 2a) that is not observed experimentally.
were the same, the cancellation of the two magnetic moments in the ground state would lead to a rapid decrease of χT towards zero (dotted line in Fig. 2a) that is not observed experimentally.
For simplicity, we have accounted for the asymmetry by introducing a tilt between the easy magnetization axes of the two ions, which we take along the 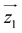 and
and 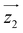 principal axes (see Fig. 1). The experimental χT and cP/R data are compatible with a rotation of
principal axes (see Fig. 1). The experimental χT and cP/R data are compatible with a rotation of 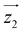 (and
(and 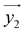 ) around
) around 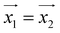 by δ = 52 degrees. Besides, they suggest that gx and gy ≪ gz, thus in the calculations shown in Fig. 2a and b, we have made both of them equal to zero and set g1z = g2z = 19.1, in order to reduce the number of parameters. These assumptions are supported by the ab initio calculations, which give gz = 18.2–19.5 and gx,y/gz ≲ 0.01 for both Dy(III) ions (see Tables S5 and S6†). Besides, they predict that
by δ = 52 degrees. Besides, they suggest that gx and gy ≪ gz, thus in the calculations shown in Fig. 2a and b, we have made both of them equal to zero and set g1z = g2z = 19.1, in order to reduce the number of parameters. These assumptions are supported by the ab initio calculations, which give gz = 18.2–19.5 and gx,y/gz ≲ 0.01 for both Dy(III) ions (see Tables S5 and S6†). Besides, they predict that 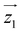 and
and 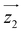 are tilted by about 72 degrees, in fair agreement with the estimate obtained from cP/R and χT (Fig. 1 and S12†).
are tilted by about 72 degrees, in fair agreement with the estimate obtained from cP/R and χT (Fig. 1 and S12†).
In spite of its simplifications, the two-spin model (eqn (2)) has the advantage of accounting well for the main features of the magnetic susceptibility and specific heat results. It also accounts for the low-T EPR spectra, shown in Fig. 2c, with the same parameters, provided that gx and gy are non-strictly zero but still gx,y/gy ≲ 0.01. Besides, it grasps the essential aspects that determine the potential of [Dy2] to encode two spin qubits. In particular, any magnetic field makes the two Dy ions within [Dy2] magnetically inequivalent (i.e. it induces a different Zeeman splitting on each of them). The 4 lowest lying spin energy levels of [Dy2] become then unequally spaced at any magnetic field H > 0. This level of anharmonicity, which ensues from the combination of distinct local coordination sites and a weak spin–spin coupling, constitutes the key ingredient that allows spectroscopically addressing each resonant spin transition. For instance, Fig. 2d shows how a CNOT conditional gate can be implemented via the application of a single resonant pulse. The nonzero, albeit small, transverse gx and gy factors (Tables S4 and S5†), combined with the off-diagonal spin–spin interaction terms and with the non-collinear axes guarantee that these operations are not forbidden,27 which is indeed confirmed by the EPR results and simulations shown in Fig. 2 and S11.†
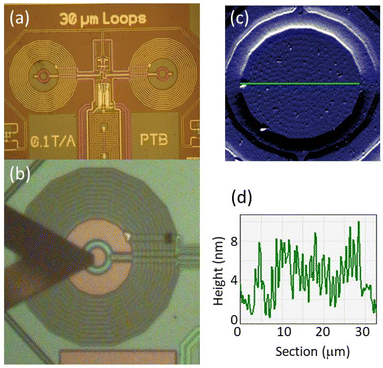
In what follows, we consider to what extent these properties are preserved when the molecules are integrated from solution into a superconducting device. The device was a micro-SQUID ac susceptometer, shown in Fig. 3a, specifically designed to achieve the sensitivity needed to detect the minute linear response of a few molecular layers.25 Arrays of [Dy2] molecular deposits were patterned, under ambient conditions and without any intermediate functionalization, by traversing the AFM tip of a Dip Pen Nanolithography (DPN) system,18,24b,25,28,29 coated with the molecular “ink”, over the surface and contacting it in the form of a predefined pattern, as shown in Fig. 3b. The stability of [Dy2] in the solution was tested by EPR (Fig. 2c) and by UV-Vis spectrophotometry (Fig. S4†). The spatial resolution of AFM allows generating patterns that match the 20 μm wide micro-SQUID pick-up coils (see Fig. S5 and S6†). This allows optimizing the flux coupling between the sample and the micro-SQUID, thus the sensitivity to the magnetic response of the molecules.
Once dried under vacuum, the deposits were analyzed by optical and AFM imaging. In order to accurately determine the amount of [Dy2] transferred into the chip, control deposits of the solvent and glycerol that form part of the ink were also prepared under the same conditions (Fig. S5†). Topographic images and profiles of one of the arrays are shown in Fig. 3c and d, respectively. Repeating successive tip coating and deposition steps gives rise to arrays with an increasing number of molecular dots and with larger thicknesses. Three of them, with 3, 8 and 34 molecular layers, were characterized magnetically down to very low temperatures. We refer to them as [Dy2]DPN1, [Dy2]DPN2 and [Dy2]DPN3, respectively (see Fig. S6†).
With its gradiometric design (Fig. 3a), the micro-SQUID acts as the pick-up loop of an ac susceptometer. The response of the molecular spins to the ac magnetic field 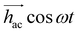 generated by the excitation coils (Fig. 3b) creates a net flux proportional to hacχ, which the micro-SQUID converts into a voltage read-out by a lock-in detection system.
generated by the excitation coils (Fig. 3b) creates a net flux proportional to hacχ, which the micro-SQUID converts into a voltage read-out by a lock-in detection system.
Fig. 4 shows results, in terms of net magnetic flux per magnetic field, measured on bulk [Dy2] and on the [Dy2]DPN3, [Dy2]DPN2 and [Dy2]DPN1 deposits. These data show the ability of the device to detect the minute signal generated by the linear magnetic response of the [Dy2] spins. Besides, the susceptibility of the deposits shows qualitatively similar dependences on temperature and frequency as the bulk material. Numerical simulations of the flux coupled to the SQUID were performed by a finite elements method that uses the susceptibility found for the bulk sample, the spatial dependence of hac and the sample geometry to determine the contribution of each molecular dot. Details are given in the ESI.† They give results, shown in the bottom panels of Fig. 4, quite comparable to those found experimentally, thus suggesting that the spin states are preserved.
 | ||
| Fig. 4 In situ determination of the magnetic susceptibility of [Dy2] deposits. Frequency-dependent flux coupled to the micro-SQUID by the bulk [Dy2] sample (a) and [Dy2]DPN3 (b), [Dy2]DPN2 (c) and [Dy2]DPN1 (d) deposits, normalized by the amplitude hac (= 0.011, 0.5, 0.25 and 0.05 Oe, respectively) of the ac magnetic excitation field at the SQUID centre. (e) Image of the simulated flux sensitivity factor, in units of magnetic flux coupled to the sensor per unit of magnetic moment induced on the sample, calculated for [Dy2]DPN3 and superimposed onto an image of the micro-SQUID loop. These simulations give predictions for the magnetic susceptibility (panels (f–h)), which can be compared to experimental results without any fitting parameters. (i) χT products derived from the low-frequency, equilibrium limit of the same data, scaled at T = 1 K. The lines show the predictions that follow from eqn (2) for collinear easy axes (black, dotted line) with J12/kB = −0.014 K, and for easy axes tilted by either 44 degrees (red, solid line) or 52 degrees (blue, solid line), with J12/kB = −0.023 K. | ||
Since the magnetic behaviour remains paramagnetic for all samples, we can again use the χT product to obtain more precise information on the magnetic moments present in each molecule and on its mutual interactions. As with the bulk sample, we consider first the temperature dependence of the equilibrium susceptibility, obtained at sufficiently low ω (1.7 Hz) and sufficiently high T (≳0.15 K). The experimental χT curves were scaled to molar units using data measured at T = 1 K. They are plotted in Fig. 4i. For all [Dy2] arrays, χT shows a drop below 1 K that resembles, within the experimental uncertainties, that found for the bulk material. Besides, it remains, at any temperature, much higher than the prediction (dotted line in Fig. 4i) for perfectly compensated spins. These results show: (1) that the molecular cores transferred to the chips retain two mutually interacting Dy ions and (2) that the two Dy ions remain magnetically inequivalent.
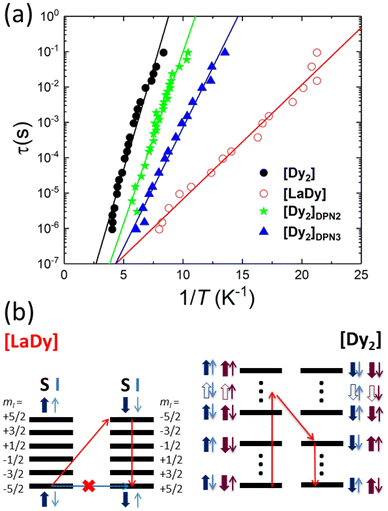
The frequency dependence of the ac susceptibility reveals the existence of spin relaxation processes with time scales ≳1/ω. Besides, the linear susceptibility acquires an out-of-phase component χ′′ that reaches its maximum when the typical spin relaxation time τ becomes equal to 1/ω.30 Using the data measured at different frequencies, shown in Fig. S10,† we have estimated the temperature dependence of τ for [LaDy] and for all [Dy2] samples but one, [Dy2]DPN1, whose χ′′ signal was below the sensitivity of micro-SQUID. The results are shown in Fig. 5a.
The spin relaxation times of [Dy2] and of [LaDy] follow the Arrhenius law τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(U/kBT) that characterizes a thermally activated process (Fig. 5). The low activation energy values, U/kB = 2.2(1) K and 0.8(5) K for bulk [Dy2] and [LaDy], respectively, show that the relaxation processes involve only states belonging to the ground electronic states of the Dy ions since the excited levels lie more than 100 K above them (Fig. 2a). This result confirms that direct transitions between the 4 lowest-lying electronic spin states are not forbidden, as already shown by EPR data. Besides, the fact that the activation energy of the [Dy2] dimer is nearly three times larger than that found for [LaDy] suggests that the spin–spin interaction leaves an imprint on the spin dynamics.
exp(U/kBT) that characterizes a thermally activated process (Fig. 5). The low activation energy values, U/kB = 2.2(1) K and 0.8(5) K for bulk [Dy2] and [LaDy], respectively, show that the relaxation processes involve only states belonging to the ground electronic states of the Dy ions since the excited levels lie more than 100 K above them (Fig. 2a). This result confirms that direct transitions between the 4 lowest-lying electronic spin states are not forbidden, as already shown by EPR data. Besides, the fact that the activation energy of the [Dy2] dimer is nearly three times larger than that found for [LaDy] suggests that the spin–spin interaction leaves an imprint on the spin dynamics.
The physical nature of the relaxation mechanism can be qualitatively understood by considering how hyperfine and spin–spin couplings hinder the reversal of each Dy spin. The basic ideas are illustrated schematically in Fig. 5b. About 44% of the naturally occurring Dy isotopes (161Dy and 163Dy) carry an I = 5/2 nuclear spin. Their electronic spin ground state doublet is then split by the hyperfine interaction, which can be described by introducing an additional term  to the effective spin Hamiltonian (2), where  is the effective hyperfine tensor. Because of the strong anisotropy of the electronic spin, this term mainly introduces a zero-field splitting AzmSmI. The energy detuning between up and down electronic spin states having the same nuclear spin projection effectively suppresses direct spin tunnelling processes and forces the system to “borrow” energy from lattice vibrations.31–33 A similar effect is caused by the interactions between electronic spins, either located in different molecules (like in [LaDy]) or within each of them (in [Dy2]). Irrespective of the specific, and complex, details of the resulting dominant relaxation paths, it then follows that the intra-molecular spin–spin interaction always adds an additional hurdle for the relaxation of the Dy electronic spins (Fig. 5b). The fact that the difference between the activation energies found for [Dy2] and [LaDy] approximately matches δEint provides support for this interpretation.
to the effective spin Hamiltonian (2), where  is the effective hyperfine tensor. Because of the strong anisotropy of the electronic spin, this term mainly introduces a zero-field splitting AzmSmI. The energy detuning between up and down electronic spin states having the same nuclear spin projection effectively suppresses direct spin tunnelling processes and forces the system to “borrow” energy from lattice vibrations.31–33 A similar effect is caused by the interactions between electronic spins, either located in different molecules (like in [LaDy]) or within each of them (in [Dy2]). Irrespective of the specific, and complex, details of the resulting dominant relaxation paths, it then follows that the intra-molecular spin–spin interaction always adds an additional hurdle for the relaxation of the Dy electronic spins (Fig. 5b). The fact that the difference between the activation energies found for [Dy2] and [LaDy] approximately matches δEint provides support for this interpretation.
This also means that the experimental U can be used to characterize spin–spin interactions in [Dy2] molecules patterned onto devices. The relaxation times of [Dy2]DPN2 and [Dy2]DPN3, also shown in Fig. 5, follow Arrhenius laws with activation energies U/kB = 2.4(2) and 1.6(2) K, respectively, which are significantly larger than the value measured for [LaDy]. This confirms that the intramolecular spin–spin coupling is preserved within each of them and, therefore, the composition of the molecular cores remains also intact. Also, they suggest that transitions between different spin states remain as allowed as they are in bulk. Notice that τ measured at the zero magnetic field is independent of the molecular orientation. Therefore, the differences in U observed between different deposits and with respect to the bulk must arise from modifications in the spin–spin interactions that determine the dominant spin relaxation paths (see Fig. 5). Diverse effects can play roles when molecules are patterned onto a device. On the one hand, the molecular packing differs from that in the crystal, and this directly influences intermolecular dipolar interactions. On the other hand, the same effect combined with the coupling of the bottom molecular layers to the chip substrate, can introduce some strain25 and thus generate molecular distortions. The experimental χT data, shown in Fig. 4i, suggest that such modifications cannot be large. Yet, changes in the mutual orientations of the two Dy(III) easy axes of the order of 5 degrees could still be compatible with these results, taking into account the experimental uncertainties, and they could affect U via the modification of the intra-molecular spin–spin couplings.
Conclusions
In summary, we have found that [Dy2] molecules fulfil all requisites to embody two spin qubits and that they can be delivered with high precision and under ambient conditions into specific areas of a superconducting circuit. Thanks to the high sensitivity of this micro-SQUID device, we have been able to detect in situ the linear magnetic response of [Dy2] dot arrays consisting of 34, 8 and 3 molecular layers and show that they largely retain their equilibrium and dynamical magnetic behaviour in spite of the lost crystallinity and the increasing effect of the interface with the substrate. In particular, the experiments confirm that the magnetic asymmetry and the spin–spin coupling remain close to those found for the crystalline material.It is worth emphasizing that chemical design and DPN can be jointly exploited to deliver suitable doses of the functional molecules, e.g. by starting from the right solution with a majority of diamagnetic equivalents, such as [YLa]. Besides, the spin relaxation time, which ultimately limits the spin coherence for quasi-isolated molecules, is found to reach values as long as 100 ms both in bulk and in the molecular arrays. In conclusion, the results of this work support molecular complexes hosting multiple spin centres as promising building blocks for a hybrid quantum computing architecture and provide useful techniques for testing and realizing it with practical devices.
Materials and methods
Materials synthesis
All reactions were performed under aerobic conditions, using the reagents as received. The ligand 6-(3-oxo-3-(2-hydroxyphenyl)propionyl)pyridine-2-carboxylic acid (H3L) was synthesized as previously described.20Patterning of [Dy2] deposits via Dip-Pen nanolithography
Dip Pen Nanolithography (DPN) was carried out using a high-performance DPN5000 AFM-based system (NanoInk Inc., USA). Silicon nitride triangular DPN single probes (Advanced Creative Solutions Technology, USA) were used for the patterning experiments. The molecular “ink” was prepared by dissolving 30 mg mL−1 of [Dy2] in a 90/10 v/v DMSO/glycerol mixture. Glycerol was added to increase the viscosity and slow down ink evaporation.29 The integrity of the molecular complex in solution and their stability over time were checked for different solvents by UV-visible spectrophotometry (Fig. S4†). Prior to the DPN deposition, the sensor was cleaned with ultra-pure ethanol and acetone, and dried by blowing nitrogen gas. The tip coating procedure first involved leaving a drop of the ink into one of the reservoirs of a microfluidic inkwell delivery chip-based system (Advanced Creative Solutions Technology, USA) using a micropipette. Afterwards, the ink was transferred to a microwell through a microchannel, where the DPN tip was dipped and coated with minute amounts of the ink. DPN experiments were carried out under constant conditions at 26 °C and 40% relative humidity using an integrated environmental chamber. The molecular microdeposits were generated by traversing the tip over the surface in the form of the desired pattern, which was previously designed and calibrated using the InkCad software (NanoInk, Inc., USA).Different patterns were fabricated to check the ability to deposit nanostructures of different forms and layer thicknesses adapted to the inner susceptometer circle, which has an approximate radius of 10 μm (see Fig. 3 and Fig. S5 and S6†). Arrays formed by circular patterns of hundreds to thousands of identical dots were deposited inside the pickup coil and, in parallel, on silicon substrates under the same experimental conditions. The latter facilitates a more precise determination of the pattern's dimensions and thicknesses.
Three samples gave a detectable magnetic response. These were arrays of circular molecular deposits made of approximately 3, 8 and 34 [Dy2] molecular layers, which we labelled as [Dy2]DPN1, [Dy2]DPN2 and [Dy2]DPN3, respectively. They are shown in Fig. S6.† The layers were organized by successive coating and deposition steps. The bigger sample was prepared after three successive deposition steps. In [Dy2]DPN2 and [Dy2]DPN3, the circular dots merge to form quasi-continuous films (see Fig. S6†). The solvent and glycerol that form a part of the ink were also deposited under the same conditions as the control. The patterns geometries and topographies were characterized by optical and AFM imaging once dried under a vacuum. The number of molecular layers was estimated using an average diameter of approximately 1.2 nm for each [Dy2] molecule, derived from the crystallographic data.
Physical characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as the eluent (200 μL min−1). As observed previously for related clusters, the ionization caused the removal of terminal nitrate, pyridine and water ligands from the complexes. Moieties related almost exclusively to the expected [LaDy] metal composition were observed (see Fig. S3†), with only minimal signals from homometallic moieties detected, thus evidencing not only the realization of the heterometallic compound but also its robustness and exclusiveness in solution.
1) as the eluent (200 μL min−1). As observed previously for related clusters, the ionization caused the removal of terminal nitrate, pyridine and water ligands from the complexes. Moieties related almost exclusively to the expected [LaDy] metal composition were observed (see Fig. S3†), with only minimal signals from homometallic moieties detected, thus evidencing not only the realization of the heterometallic compound but also its robustness and exclusiveness in solution.
Electron paramagnetic resonance experiments
Continuous wave Electron Paramagnetic Resonance (EPR) experiments were performed with a commercial Elexsys E-580 system by Bruker, operating in the X-band. The spectrometer consists of a resonant cavity, in which the paramagnetic sample was placed and located at the centre of a 1.4 T electromagnet. An rf modulation field generated by a set of small coils results in a derivative-like detection of each absorption resonance. A gas-flow Helium cryostat was used to reach and control temperature in the vicinity of 6 K. EPR measurements were performed on the polycrystalline powder (9.483 GHz) and a frozen solution (9.475 GHz) placed in quartz tubes. The solution was obtained by dissolving 2.40 mg of polycrystalline [Dy2] in 2 drops of d6-DMSO and a mixture of 500 μL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 μL d6-EtOH
500 μL d6-EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d4-MeOH, for a concentration of ca. 1.42 mM. No spin-echo could be detected.
d4-MeOH, for a concentration of ca. 1.42 mM. No spin-echo could be detected.
Simulations were done with Easyspin41 and the spin Hamiltonian described in the main text, fixing gx = gy = 0.1 and gz = 19.1 for both Dy sites, an angle between their z-axis of 53° and J12/kB = −0.023 K.
Very low temperature ac susceptibility measurements
These were performed with integrated micro-SQUID susceptometers developed at the Physikalisch-Technische Bundesanstalt. They are made of Nb deposited on Si/SiO2 wafers and are fabricated by optical lithography. Experiments on bulk [Dy2] and [LaDy] samples were performed using susceptometers made of ≃800 × 400 μm2 banana-shaped excitation and pick-up coils coupled to a micro-SQUID sensor, as described in ref. 42 and 43. Fig. S7† shows an image of one of these devices. A different circuit design25,44 was applied to the detection of the minute signals associated with the linear response of the molecular deposits. In this case, the micro-SQUID sensor itself, with a gradiometric design, acts as the pick-up loop of the ac magnetic susceptometer. The coupling between the sample and the sensor is favoured by the reduced diameter (30 μm) of its two circular loops. Two identical ac excitation coils allow the application of ac magnetic fields with amplitudes of up to 3 Oe. The output signal when no sample is present is minimized by the close-to-perfect reflection symmetry of the setup. Its frequency and temperature dependences were characterized on a bare circuit and then subtracted from the experimental results. This instrument exhibits a white flux noise of 1.3μΦ0 Hz−1/2. All chips were installed inside the mixing chamber of a 3He–4He dilution refrigerator, which allows performing experiments at very low temperatures, between 0.013 K and 2 K.Theoretical methods
Author contributions
VV, DA, LAB and GA synthesized the molecular samples. OR performed and analysed the X-ray diffraction experiments. OR, DG and FL performed and analysed the magnetic and thermal characterization measurements. OR and JIM performed and analysed the EPR experiments. DD and TS designed and fabricated the micro-SQUID sensors. MCP and AL patterned the molecules by DPN and characterized the deposits via AFM and other techniques. AR, DG, JS and FL carried out the micro-SQUID experiments and analysed the results. MJMP performed the simulations of the flux coupled to the micro-SQUIDs. BLG performed the ab initio numerical calculations. GA and FL wrote the manuscript with contributions from all co-authors.Data availability
Crystallographic data can be found in CCDC 2310387 ([Dy2]) and 2310388 ([LaDy]).†Data shown in the main text figures are deposited at the FATMOLS community in the ZENODO repository: https://zenodo.org/communities/fatmols-fet-open-862893/records?q=&l=list&p=1&s=10&sort=newest.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from grants PID2022-140923NB-C21, PID2020-118329RB-I00 and PID2022-137764OB-I00, funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”, from grants TED2021-131447B-C21, TED2021-129214B-I00 and PDC2022-133184-I00, funded by MCIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR, from “Plan Complementario en Comunicación Cuántica” (PRTR-C17.I1) and “Plan Complementario en Materiales Avanzados”, funded by Generalitat de Catalunya, Gobierno de Aragón and the European Union NextGenerationEU/PRTR, from the Gobierno de Aragón (DGA consolidated groups QMAD E09-23R and PLATON E31-23R), and from the CSIC Quantum Technology Platform PT-001. B. L. G. thanks the French GENCI/IDRIS-CINES centers for high-performance computing resources.References
- (a) M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789 CrossRef CAS PubMed; (b) F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119 RSC; (c) G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Soc. Rev., 2012, 41, 537 RSC; (d) A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301 CrossRef PubMed; (e) M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS; (f) M. R. Wasielewski, et al. , Nat. Rev. Chem., 2020, 4, 490 CrossRef CAS PubMed.
- (a) A. Ardavan, O. Rival, J. Morton, S. Blundell, A. Tyryshkin, G. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed; (b) C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef CAS PubMed.
- (a) J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS PubMed; (b) C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678 CrossRef CAS.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234 CrossRef CAS PubMed.
- S. Carretta, D. Zueco, A. Chiesa, Á. Gómez-León and F. Luis, Appl. Phys. Lett., 2021, 118, 240501 CrossRef CAS.
- (a) F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, J. Sesé, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef CAS PubMed; (b) D. Aguilà, D. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215 Search PubMed; (c) F. Luis, P. J. Alonso, O. Roubeau, V. Velasco, D. Zueco, D. Aguilà, J. I. Martínez, L. A. Barrios and G. Aromí, Commun. Chem., 2020, 3, 176 CrossRef CAS; (d) E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, J. I. Martínez, L. A. Barrios, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337 RSC.
- (a) A. Ardavan, A. M. Bowen, A. Fernández, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. Timco, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Inf., 2015, 1, 15012 CrossRef; (b) J. Ferrando-Soria, E. Moreno-Pineda, A. Chiesa, A. Fernández, S. A. Magee, S. Carretta, P. Santini, I. Vitorica-Yrezabal, F. Tuna, G. Timco, E. J. L. McInness and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed; (c) A. Fernández, J. Ferrando-Soria, E. Moreno-Pineda, F. Tuna, I. J. Vitorica-Yrezabal, C. Knappke, J. Ujma, C. A. Muryn, G. A. Timco, P. E. Barran, A. Ardavan and R. E. P. Winpenny, Nat. Commun., 2016, 7, 10240 Search PubMed.
- M. D. Jenkins, Y. Duan, B. Diosdado, J. J. García-Ripoll, A. Gaita-Ariño, C. Giménez-Saiz, P. J. Alonso, E. Coronado and F. Luis, Phys. Rev. B, 2017, 95, 064423 CrossRef.
- (a) E. Moreno-Pineda, M. Damjanovic, O. Fuhr, W. Wernsdorfer and M. Ruben, Angew. Chem., Int. Ed., 2017, 56, 9915 CAS; (b) E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501 Search PubMed; (c) C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 Search PubMed.
- (a) R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814 CrossRef CAS PubMed; (b) I. Gimeno, A. Urtizberea, J. Román-Roche, D. Zueco, A. Camón, P. J. Alonso, O. Roubeau and F. Luis, Chem. Sci., 2021, 12, 5621 RSC; (c) S. Chicco, A. Chiesa, G. Allodi, E. Garlatti, M. Atzori, L. Sorace, R. De Renzi, R. Sessoli and S. Carretta, Chem. Sci., 2021, 12, 12046 RSC.
- B. P. Lanyon, M. Barbieri, M. P. Alemida, T. Jenewein, T. C. Ralph, K. J. Resch, G. J. Pryde, J. L. O'Brien, A. Gilchrist and A. G. White, Nat. Phys., 2009, 5, 134 Search PubMed.
- A. Chiesa, E. Macaluso, F. Petiziol, S. Wimberger, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2020, 11, 8610 CrossRef CAS.
- M. D. Jenkins, T. Hümmer, M. J. Martínez-Pérez, J. J. García-Ripoll, D. Zueco and F. Luis, New J. Phys., 2013, 15, 095007 CrossRef.
- M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682 RSC.
- A. Chiesa, S. Roca, S. Chicco, M. de Ory, A. Gómez-León, A. Gomez, D. Zueco, F. Luis and S. Carretta, Phys. Rev. Appl., 2023, 19, 064060 CrossRef CAS.
- A. Urtizberea, E. Natividad, P. J. Alonso, L. Pérez-Martínez, M. A. Andrés, I. Gascón, I. Gimeno, F. Luis and O. Roubeau, Mater. Horiz., 2020, 7, 885 RSC.
- I. Gimeno, W. Kersten, M. C. Pallarés, P. Hermosilla, M. J. Martínez-Pérez, M. D. Jenkins, A. Angerer, C. Sánchez-Azqueta, D. Zueco, J. Majer, A. Lostao and F. Luis, ACS Nano, 2020, 14, 8707 CrossRef CAS PubMed.
- L. Malavolti, M. Briganti, M. Hänze, G. Serrano, I. Cimatti, G. McMurtrie, E. Otero, P. Ohresser, F. Totti, M. Mannini, R. Sessoli and S. Loth, Nano Lett., 2018, 18(12), 7955 CrossRef CAS.
- D. Aguilà, L. A. Barrios, F. Luis, A. Repollés, O. Roubeau, S. J. Teat and G. Aromí, Inorg. Chem., 2010, 49, 6784 CrossRef PubMed.
- D. Aguilà, L. A. Barrios, V. Velasco, L. Arnedo, N. Aliaga-Alcalde, M. Menelaou, S. J. Teat, O. Roubeau, F. Luis and G. Aromí, Chem. – Eur. J., 2013, 19, 5881 CrossRef.
- J. Gónzalez-Fabra, N. A. G. Bandeira, V. Velasco, L. A. Barrios, D. Aguilà, S. J. Teat, O. Roubeau, C. Bo and G. Aromí, Chem. – Eur. J., 2017, 23, 5117 CrossRef.
- D. Aguilà, V. Velasco, L. A. Barrios, J. González-Fabra, C. Bo, S. J. Teat, O. Roubeau and G. Aromí, Inorg. Chem., 2018, 57, 8429 CrossRef PubMed.
- (a) M. J. Martínez-Pérez, J. Sesé, F. Luis, D. Drung and T. Schurig, Rev. Sci. Instrum., 2010, 81, 016108 CrossRef; (b) M. J. Martínez-Pérez, E. Bellido, R. de Miguel, J. Sesé, A. Lostao, C. Gómez-Moreno, D. Drung, T. Schurig, D. Ruiz-Molina and F. Luis, Appl. Phys. Lett., 2011, 99, 032504 CrossRef.
- E. Bellido, P. González-Monje, A. Repollés, M. D. Jenkins, J. Sesé, D. Drung, T. Schurig, K. Awaga, F. Luis and D. Ruiz-Molina, Nanoscale, 2013, 5, 12565 RSC.
- E. Bartolomé, P. J. Alonso, A. Arauzo, J. Luzón, J. Bartolomé, C. Racles and C. Turta, Dalton Trans., 2012, 41, 10382 RSC.
- E. Moreno-Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed.
- R. D. Piner, J. Zhu, F. Xu, S. Hong and C. A. Mirkin, Science, 1999, 283, 661 CrossRef CAS PubMed.
- E. Bellido, R. de Miguel, D. Ruiz-Molina, A. Lostao and D. Maspoch, Adv. Mater., 2010, 22, 352 CAS.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS.
- N. V. Prokof'ev and P. C. E. Stamp, Phys. Rev. Lett., 1998, 80, 5794 CrossRef.
- J. F. Fernández, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 064423 CrossRef.
- F. Luis, M. J. Martínez-Pérez, O. Montero, E. Coronado, S. Cardona-Serra, C. Martí-Gastaldo, J. M. Clemente-Juan, J. Sesé, D. Drung and T. Schurig, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 060403(R) CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18 CrossRef CAS PubMed.
- A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18 CrossRef CAS.
- I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baró, Rev. Sci. Instrum., 2007, 78, 013705 CrossRef CAS PubMed.
- R. Bachmann, F. J. DiSalvo Jr., T. H. Geballe, R. L. Greene, R. E. Howard, C. N. King, H. C. Kirsch, K. N. Lee, R. E. Schwall, H.-U. Thomas and R. B. Zubeck, Rev. Sci. Instrum., 1972, 43, 205 CrossRef CAS.
- M. Evangelisti, F. Luis, L. J. de Jongh and M. Affronte, J. Mater. Chem., 2006, 16, 2534–2549 RSC.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CAS.
- M. J. Martínez-Pérez, J. Sesé, F. Luis, D. Drung and T. Schurig, Rev. Sci. Instrum., 2010, 81, 016108 Search PubMed.
- M. J. Martínez-Pérez, J. Sesé, F. Luis, R. Córdoba, D. Drung, T. Schurig, E. Bellido, R. de Miguel, C. Gómez-Moreno, A. Lostao and D. Ruiz-Molina, IEEE Trans. Appl. Supercond., 2011, 21, 345 Search PubMed.
- D. Drung, J.-H. Storm, F. Ruede, A. Kirste, M. Regin, T. Schurig, A. M. Repollés, J. Sesé and F. Luis, IEEE Trans. Appl. Supercond., 2014, 24, 1 Search PubMed.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.-A. Malmqvist, P. Neogrady, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224 CAS.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P.Å Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925 CrossRef PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157 CAS.
- (a) P. A. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CAS; (b) P.-A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189 CAS.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365 CrossRef.
- (a) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS; (b) L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126 CrossRef CAS PubMed.
- F. Aquilante, P. A. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694 CrossRef CAS PubMed.
- (a) B. O. Roos, R. Lindh, P. A. Malmqvist, V. Veryazov and P. O. Widmark, J. Phys. Chem. A, 2004, 108, 2851 CrossRef CAS; (b) B. O. Roos, R. Lindh, P. A. Malmqvist, V. Veryazov, P. O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed; (b) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1993, 85, 441 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2310387 and 2310388. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4nr03484h |
| ‡ These two authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |