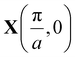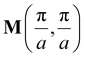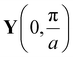Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
One-dimensional Lieb superlattices: from the discrete to the continuum limit†
Dylan
Jones
a,
Marcin
Mucha-Kruczynski
 a,
Adelina
Ilie
a,
Adelina
Ilie
 *a and
Lucian
Covaci
*a and
Lucian
Covaci
 *bc
*bc
aDepartment of Physics, University of Bath, Bath, UK. E-mail: a.ilie@bath.ac.uk
bDepartment of Physics, University of Antwerp, Antwerp, Belgium. E-mail: lucian.covaci@uantwerpen.be
cNANOlight Center of Excellence, University of Antwerp, Antwerp, Belgium
First published on 27th January 2025
Abstract
The Lieb lattice is one of the simplest lattices that exhibits both linear Dirac-like and flat topological electronic bands. We propose to further tailor its electronic properties through periodic 1D electrostatic superlattices (SLs), which, in the long wavelength limit, were predicted to give rise to novel transport signatures, such as the omnidirectional super-Klein tunnelling (SKT). By numerically modelling the electronic structure at tight-binding level, we uncover the evolution of the Lieb SL band structure from the discrete all the way to the continuum regime and build a comprehensive picture of the Lieb lattice under 1D potentials. This approach allows us to also take into consideration the discrete lattice symmetry-breaking that occurs at the well/barrier interfaces created by the 1D SL, whose consequences cannot be explored using the previous low energy and long wavelength approaches. We find novel features in the band structure, among which are intersections of quadratic and flat bands, tilted Dirac cones, or series of additional anisotropic Dirac cones at energies where the SKT is predicted. Our results show that the universal SKT is absent when the lattice details are considered. Such features are relevant to experimental realizations of electronic transport in Lieb 1D SL realized in artificial lattices or in real material systems like 2D covalent organic/metal–organic frameworks and inorganic 2D solids.
1 Introduction
Systems that exhibit non-trivial band topology and flat bands have become the focus of intense recent research. One such system is the Lieb lattice, a two-dimensional (2D) depleted-square lattice that supports a graphene-like conical dispersion intersected by a flat band at zero energy. Although models exhibiting flat bands were originally seen as theoretical toy models, recent experimental developments in ultra cold gases,1 photonics2–4 or artificial lattices5,6 make them a reality. Associated with a large enhancement of the density of states due to quenching of the kinetic energy, flat bands in the Lieb lattice are expected to host many-body phenomena such as superconductivity,7 ferromagnetism8 and topologically non-trivial states.9 A well known example is the “magic” angle twisted bilayer graphene, which showcases the importance of band flatness and its topology in the appearance of correlated states.10 Similarly, it was shown that the flat band realised in the Lieb lattice can sustain robust superconductivity due to its non-trivial quantum metric.7,11Experimental and theoretical works have shown that the electronic properties of electronic systems can be tailored by the application of periodic potentials. For example, when a one-dimensional periodic (1D) potential is applied to graphene, additional Dirac cones are created, flattened in the direction perpendicular to the direction of the applied potential, enabling tunable anisotropy of the group velocity.12–14 Such periodic potentials can be applied through top-down patterned gating, with wavelength as low as 50 nm (ref. 14 and 15) or through bottom-up self-assembly of macromolecules on top of van der Waals materials, with wavelengths as low as 3–5 nm.16–18
Analytical models predict the existence of super-Klein tunnelling (SKT) phenomena in the Lieb lattice (and other pseudospin-1 systems) under a 1D periodic potential.19–21 Different to the Klein tunneling in the graphene lattice (pseudospin-1/2),22 the SKT state manifests as unity transmission probability irrespective of the angle of incidence.23–26 This was recently claimed to be demonstrated in a triangular phononic crystal27 by investigating transport across a singular potential barrier. However, these predictions came with two important caveats: (i) the potential's lengthscale is very large compared to the lattice constant (i.e. the long wavelength or the continuum limit), and (ii) these systems do not require beyond nearest-neighbour interactions to be described accurately. This limits the applicability of the analytical predictions to a wider range of experimentally realisable systems.
The simplest approach towards describing the peculiar electronic properties of the Lieb lattice is based on a tight-binding model with only nearest-neighbour site interactions. However, both in artificial lattices and in a newer class of materials that can possess a Lieb lattice structure, such as recently proposed covalent–organic and metal–organic frameworks (COFs and MOFs)9,28,29 or metal-inorganic frameworks,30–32 the presence of additional next-nearest neighbour (NNN) hoppings disperses the flat band and lattice distortions can easily give rise to band gaps. Additionally, a finite spin–orbit interaction, introduced by the presence of metallic atoms will give rise to topological gaps in the band structure, resulting in topological spin-Hall edge states that are protected from back-scattering.33It is expected that these additional effects will strongly influence many-body correlations predicted for the Lieb lattice flat bands.
In light of growing interest in experimental realizations of the Lieb lattice, further tunability through (1D) periodic potentials will become possible in the near future. Nevertheless, a general description of the electronic properties of the Lieb lattice under a periodic potential landscape is lacking. Important aspects related to the lattice discreteness, band dispersion and distortion-induced gaps remain largely unexplored. Questions whether the universal nature of the SKT survives arise when the discreteness of the lattice has to be taken into account.
Here, we numerically model the electronic structure of a Lieb lattice under a 1D periodic potential (1D Lieb superlattice). This approach is general, applicable to the description of a range of systems from trapped cold atoms and artificial Lieb lattices to solid-state realisations like recently synthesised (M-)COFs, from the discrete (where the potential periodicity is on the order of the lattice constant) to the continuum limit. Using a tight-binding (TB) model permits the inclusion of next-nearest neighbour interactions, an effective mass term, and spin–orbit coupling, required to describe experimentally relevant realisations of the Lieb lattice. Additionally, a tight-binding description provides insights into discrete lattice symmetry-breaking effects at the well/barrier interfaces imposed by the periodic potential and allows the identification of non-trivial topological properties of the system.
We find that in both limits, i.e. the discrete (L ∼ a) and the continuum (L ≫ a) limits, where L is the superlattice wavelength and a is the Lieb lattice constant, the discreteness of the lattice plays an important role in the resulting energy dispersion of the Lieb 1D superlattice. For example, tilted Dirac cones, intersections of quadratic and flat bands and new Dirac cones are found in the discrete limit. In the continuum limit, when comparing to low-energy and long-wavelength approximations near the Dirac cone, although propagating states are recovered, the SKT state is absent in the tight-binding simulations. Instead, we uncover a sequence of anisotropic Dirac cones, reminiscent of the behaviour of graphene under a periodic 1D potential landscape showing a sequence of Dirac cones with frequency dependent on the ratio L/a. Furthermore, we find that a smooth interface gives rise to further localized states that interfere with the propagating states, while the SKT states are still absent, replaced by dispersive anisotropic Dirac cones. We give a special attention to more complex Lieb lattice models that take into account next-nearest neighbour (leading to dispersive bands), imbalance in the on-site energies in the unit cell (leading to band gap opening at the Dirac point) and spin–orbit coupling terms (leading to topological band gaps). With the addition of these terms, corresponding to realistic and experimentally relevant realizations of the Lieb lattice, we provide a comprehensive picture on their effect on the electronic properties of realistic 1D Lieb superlattices.
2 The discrete limit
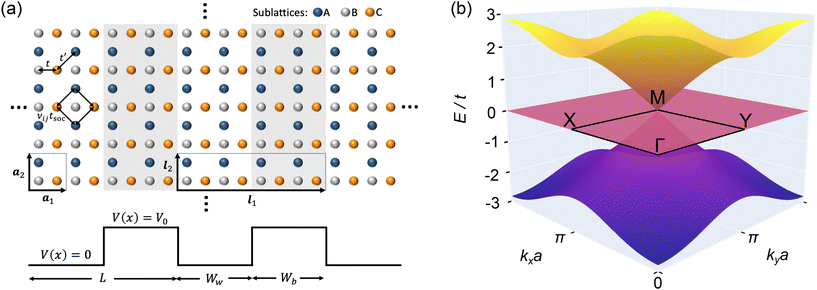
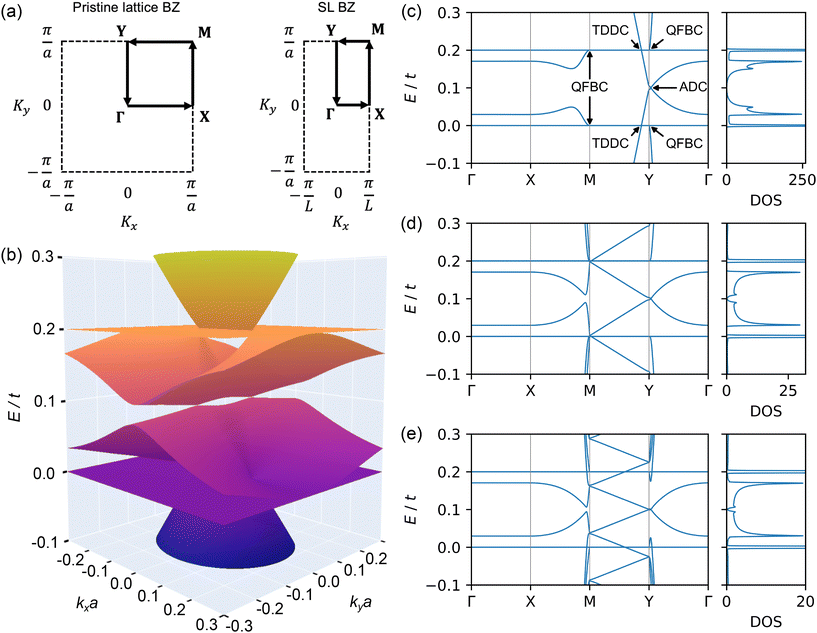
Fig. 1a shows how we construct the tight-binding (TB) model of the Lieb superlattice (SL). In this section we include nearest-neighbour (NN) site interactions only and implement a numerically sharp potential profile.The pristine lattice unit cell is spanned by a1 and a2. In each superlattice unit cell defined by the vectors l2 = a2 and l1 = Na1, we set the onsite energies of L/2 pristine lattice unit cells to zero, and the next L/2 cells to V0, as shown in Fig. 1a. Here, L = Na is the wavelength of the 1D superlattice. We restrict ourselves to the study of symmetric potentials, such that the width of the well and barrier regions are Ww = Wb = L/2. This forms the SL unit cell; we then apply periodic boundary conditions. The used Lieb lattice TB model is shown explicitly in Methods. Fig. 1b shows the band structure of the pristine Lieb lattice, which features the intersection of a perfectly flat band with the Dirac-like cone at the high-symmetry M point. One requirement of this intersection is the C4 rotational symmetry of the system. This is reduced to a C2 symmetry following the application of the periodic potential as outlined in Fig. 1a, which destroys this intersection. However, it also introduces additional features to the band structure, which we discuss now.
We show in Fig. 2a the pristine and SL first Brillouin zones (BZs). The Y point located at (0, π/a) remains a high-symmetry point, while the M and X points shift due to the SL periodicity. This results in the folding of the pristine bands, which contributes with new states at the Y point. Fig. 2b shows the low energy bands of the Lieb SL near the Y point for L = 4a and V0 = 0.2t.
In Fig. 2(c–e) we plot the band structures and BZ-integrated density of states (DOS) for L = 4a, 32a and 50a respectively. A continuous evolution of the band structures from L = 2a to L = 400a is shown in the ESI Video 1.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 There are now two flat bands (FBs) at E = 0 and E = V0 (i.e. E/t = 0.2 in Fig. 2). These arise from the destructive interference of wave functions in the well and barrier regions and manifest as large peaks in the DOS. The FBs are degenerate, with the total number,
34 There are now two flat bands (FBs) at E = 0 and E = V0 (i.e. E/t = 0.2 in Fig. 2). These arise from the destructive interference of wave functions in the well and barrier regions and manifest as large peaks in the DOS. The FBs are degenerate, with the total number, 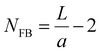 , equal to the number of boundaries between unit cells with the same potential energy (for L = 2a there are no perfect flat bands that extend throughout the whole BZ). Consequently, the height of the FB-related DOS peaks relative to all other features in the BZ-integrated DOS increases with increasing SL periodicity.
, equal to the number of boundaries between unit cells with the same potential energy (for L = 2a there are no perfect flat bands that extend throughout the whole BZ). Consequently, the height of the FB-related DOS peaks relative to all other features in the BZ-integrated DOS increases with increasing SL periodicity.
Breaking the C4 rotational symmetry results in highly anisotropic states that intersect the FBs at E = 0 and E = V0. Marked in Fig. 2c are triply-degenerate Dirac cones (TDDCs) and quadratic flat band crossings (QFBCs), with the former arising from the folding of the pristine lattice cone along YM. The triple-degeneracy becomes apparent in Fig. S1,† where we plot cuts of the band structure around the crossing point for different cut angles ϕq (where |q| is measured from the crossing and ϕq = 0 is defined along YM). Technically, the degeneracy of the TDDC will increase with L, as the number of FBs increases. However, the TDDC will be comprised of two dispersing states and the FBs regardless of the value of L.
Additionally, there are two sets of QFBCs. The first is at Y, where the original linear crossing point is split, and the maximum (minimum) of the quadratic bands touches the flat bands at E = 0 (V0), shown in Fig. S2.† The second set is at M, where the maximum (minimum) cross the FBs at E = 0 (V0), shown in Fig. S3.† It has been shown theoretically that QBCPs can support non-trivial interacting states such as ground-state or nematic ferromagnetism,35 owing to the high density of states which is enhanced here due to the crossing with degenerate flat bands. In these studies, however, the quadratic band is fully symmetric around the crossing point. Here, the bands are only quadratic along ky, potentially opening up the study of directionally dependent interacting phases in the Lieb SL. In Fig. 2(c–e) (and ESI Video 1†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34) we show the effect of varying the potential periodicity L on the band structure due to band folding. From L = 4a to L = 32a, the bands fold down where an additional two quadratic bands cross the flat bands at M. Here, the locations of previously described QFBCs switch between M and Y.
34) we show the effect of varying the potential periodicity L on the band structure due to band folding. From L = 4a to L = 32a, the bands fold down where an additional two quadratic bands cross the flat bands at M. Here, the locations of previously described QFBCs switch between M and Y.
Finally, the bands that are flat along ΓX disperse along ΓY and cross at 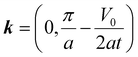 and energy E = V0/2, forming an anisotropic Dirac cone, marked as ADC in Fig. 2c. The band anisotropy around the ADC is shown in Fig. S4.† The ADC is not predicted to exist by previous analytical calculations using a continuum long wavelength model.19 This is because the details of the atomic structure and the left-right discrete lattice symmetry breaking across the well-barrier interface are lost when performing long-wavelength approximation calculations. We have found that the ADC crossing is a result of a specific order of coupling between the sites in the SL cell, valid for all values of L. In the nth unit cell (n = 1, 2, …, N), the A and B sites couple anti-symmetrically (symmetrically) in the well (barrier) regions, and the C sites then couple anti-symmetrically in consecutive unit cells. We give more details on this in the ESI,† and show how an effective description of the bands in the vicinity of the crossing can be derived following a unitary transformation of the original TB Hamiltonian.
and energy E = V0/2, forming an anisotropic Dirac cone, marked as ADC in Fig. 2c. The band anisotropy around the ADC is shown in Fig. S4.† The ADC is not predicted to exist by previous analytical calculations using a continuum long wavelength model.19 This is because the details of the atomic structure and the left-right discrete lattice symmetry breaking across the well-barrier interface are lost when performing long-wavelength approximation calculations. We have found that the ADC crossing is a result of a specific order of coupling between the sites in the SL cell, valid for all values of L. In the nth unit cell (n = 1, 2, …, N), the A and B sites couple anti-symmetrically (symmetrically) in the well (barrier) regions, and the C sites then couple anti-symmetrically in consecutive unit cells. We give more details on this in the ESI,† and show how an effective description of the bands in the vicinity of the crossing can be derived following a unitary transformation of the original TB Hamiltonian.
3 The continuum limit
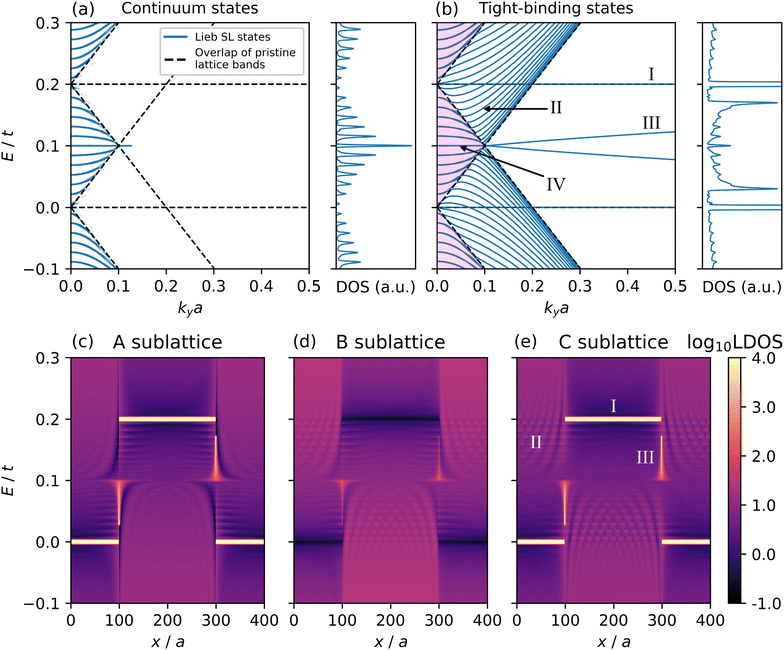
We now discuss the electronic states of the Lieb SL in the continuum limit, i.e. when L ≫ a, and show that the full tight-binding (TB) description differs from previous analytical predictions.19 Numerically, we implemented the sharp step potential described in Methods, while the continuum low-energy long-wavelength calculation is done within the transfer matrix (TM) formalism following the methodology presented in ref. 20 (details in ESI†). Note that none of the discrepancies we show are due to numerically resolving scattering between inequivalent valleys (like in the case of graphene) since all high-symmetry points in the Lieb SL BZ can be connected by reciprocal lattice vectors. In Fig. 3(a and b), we compare the analytical and TB band structures for ky near the Y point and kx = 0. Firstly, we note that the analytical and TB descriptions agree near the Y point where the shifted pristine lattice dispersions overlap (shown by the dashed black lines and the pink shaded regions); here lie extended propagating states. In Fig. S5,† we show that by superposing the band structures for multiple kx values as in,19,20 the bands shift in energy and one sees a continuum of states. For this reason, we refer to this as the ‘continuum region’.There the similarities end.
The analytical dispersion relation for the SL is the following in the continuum limit:20
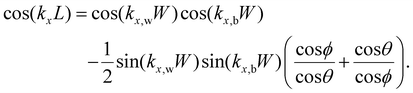 | (1) |
Here, kx,w, kx,b and ϕ, θ are the kx components and propagation direction in the well and barrier respectively. Explicit definitions and a derivation of eqn (1) are given in the ESI.†
The analytical calculation does not contain the flat bands, labelled I in Fig. 3b. The dispersion relation, (1), can only be derived from the low-energy conical eigenstates of the pristine lattice band structure. If one tries to derive an equivalent dispersion relation using the pristine lattice flat band eigenstates, the inverse of eqn (S.7)† diverges, as the band index α = 0. This can also be argued physically since the states derived from a TM calculation are those which propagate through the SL, while the flat bands are not propagating states, but are rather localised at the A and C sublattices. They are the result of destructive interference of the Bloch states on the B sublattice. This is seen in Fig. 3(c–e), where the large primary peaks in the DOS at E = 0 and E = V0 due to the localisation of the wave function in the well and barrier regions on the A and C sublattices are missing for the B sublattice.
The states labelled II in Fig. 3b, which are quantised states confined to the well/barrier regions, are also missing from the analytical continuum calculation. In this region of the band structure, the wavevectors kx,w and kx,b become imaginary, depending on whether states are allowed in the barrier or well at the respective energies in the pristine dispersions. The solution of the long wavelength model becomes numerically unstable and diverges, such that resolving these states is computationally unfeasible. These quantised states do not shift as kx is varied, unlike the states in the continuum region indicated with the pink shading in Fig. 3, meaning they do not propagate along the a1 direction. This can be also visualised in Fig. S5b,† where the dispersion is plotted for a range of kx.
As in Fig. 2(c–e), the states labelled III are the interface states generated by the discrete lattice symmetry breaking (DLSB) of the system at the well/barrier interface. The BZ-integrated LDOS shows that these interface states are asymmetric with respect to the SL unit cell, and highly localised to the well-barrier interface, with the left-right localisation asymmetry a consequence of the reduction from C4 to C2 rotational symmetry. A choice of superlattice cell shifted by a/2 flips the energies of these interface states. As before, the secondary peaks in the DOS are a signature of these dispersing states and the partial flat bands along ΓX.
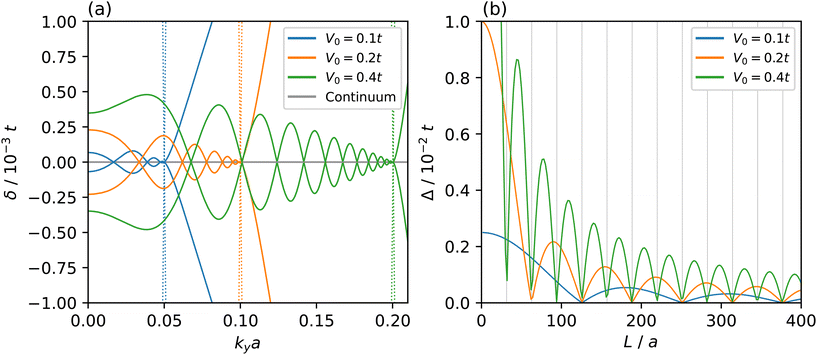
A further discrepancy is the predicted nature of the states at E = V0/2, marked IV in Fig. 3b. Analytical continuum limit calculations of pseudospin-1 particles tunnelling through a single potential barrier predict T = 1 transmission for all incidence angles, coined super-Klein tunnelling (SKT). The band structure of the Lieb SL, i.e. the limit of many barriers, should then feature these states. For kx = 0 and E = V0/2, eqn (1) becomes 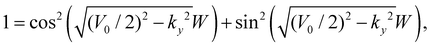 which is satisfied for arbitrary ky. This means, as shown in Fig. 3a, the SKT state manifests as a flat band in the continuum model. However, this is not predicted by the TB calculation. Plotting states IV for small energies δ about E = V0/2 in Fig. 4a shows that the SKT state is described in fact by two bands which braid to form multiple anisotropic Dirac cones, reminiscent of those found in graphene SLs. In fact, the location of these additional crossings follows the same scaling law as found in graphene lattices,
which is satisfied for arbitrary ky. This means, as shown in Fig. 3a, the SKT state manifests as a flat band in the continuum model. However, this is not predicted by the TB calculation. Plotting states IV for small energies δ about E = V0/2 in Fig. 4a shows that the SKT state is described in fact by two bands which braid to form multiple anisotropic Dirac cones, reminiscent of those found in graphene SLs. In fact, the location of these additional crossings follows the same scaling law as found in graphene lattices, 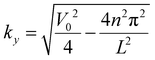 .13 Therefore, at E = V0/2, we expect the transport properties of the Lieb SL to not resemble SKT, but instead that of graphene under a 1D periodic potential. We argue that this is a further consequence of resolving the discrete symmetry broken states (labelled III in Fig. 3b) at the well-barrier interface, and that the connecting of the two-band crossings to these states results in a pseudospin-1/2 symmetry, not pseudospin-1. Additionally, Fig. 4b shows the additional crossings are sourced by the gap closing at Y, a result of the band folding along YM that we can resolve using the full TB description of the system. Finally, we note that the minima (maxima) of Δ in Fig. 4b coincide with the folding of the TDDP onto the Y (M) point shown in Fig. 2(c–e) and ESI Video 1.†
.13 Therefore, at E = V0/2, we expect the transport properties of the Lieb SL to not resemble SKT, but instead that of graphene under a 1D periodic potential. We argue that this is a further consequence of resolving the discrete symmetry broken states (labelled III in Fig. 3b) at the well-barrier interface, and that the connecting of the two-band crossings to these states results in a pseudospin-1/2 symmetry, not pseudospin-1. Additionally, Fig. 4b shows the additional crossings are sourced by the gap closing at Y, a result of the band folding along YM that we can resolve using the full TB description of the system. Finally, we note that the minima (maxima) of Δ in Fig. 4b coincide with the folding of the TDDP onto the Y (M) point shown in Fig. 2(c–e) and ESI Video 1.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 This in turn coincides with the switching of the curvature of the QFBCs at Y and M discussed in the previous section.
34 This in turn coincides with the switching of the curvature of the QFBCs at Y and M discussed in the previous section.
4 Smoothing the potential
The sharp potential profile, i.e. where the potential change occurs over a distance smaller than the lattice constant as depicted in Fig. 1(a), should accurately describe photonic and artificial Lieb SLs.1–5 However, for those realised using optical potentials or in solid-state systems (through electrostatic gating or dielectric patterning of a substrate), it is unlikely this step change will occur over such a small distance. To approximate this, we applied a smoothing of the potential using the sigmoid-like smoothstep function to interpolate the potential in each unit cell n = (1, ⋯N) between V(x, α) = 0 and V(x, α) = V0 for a smoothness parameter value α. Details of the exact numerical implementation are given in the Methods section. Smoothing the potential profile does not change the C2 rotational symmetry of the system, hence the symmetry-protected crossings (TDDCs, QFBCs and ADC) remain. However, we show here that it reduces the degeneracy of the flat bands and induces further discrete translational symmetry breaking at the well-barrier interface, giving rise to localised states in the barrier at intermediate energy range 0 < E < V0.
Fig. 5(a and b) show the band structures near the Y point for two values of the smoothness parameter α, while Fig. 5c shows the LDOS spectra across the superlattice unit cell for sublattice type C, similar to Fig. 3e but for a smoothing parameter α = 10−2. The flat band degeneracy lifting shown in Fig. 5(a and b) can be seen as a consequence of assigning a different on-site energy to the nth unit cell over which the potential change occurs. While for a sharp potential the degeneracy of a flat band is given by 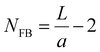 , the smoothing of the potential over several unit cells makes it that a new Vn (x) potential will be assigned to every unit cell n, which shifts the on-site energy and reduces the flat band degeneracy and its contribution to the DOS. However, this feature shows not only as a simple shift of flat bands to new energies, intersecting the extended and evanescent states for each different Vn (x). Instead, as shown in Fig. 5c, multiple tunnelling steps at smaller energy scales appear at the boundary between the nth and n + 1th cells, generating additional pairs of discrete symmetry broken states similar in nature to states of type III introduced in the previous section. These interact and are hybridised with both the evanescent and extended states. The dispersion of the former is altered, evidenced by the smearing of the quantised states in the LDOS spectra shown in Fig. 5c and in Fig. S6(a–c)† where the LDOS is shown separately for all three sublattices. Additionally, the dispersion and braiding behaviour of the extended states also changes, shifting the locations of the band crossings, with the effect being more pronounced for smoother SL potentials.
, the smoothing of the potential over several unit cells makes it that a new Vn (x) potential will be assigned to every unit cell n, which shifts the on-site energy and reduces the flat band degeneracy and its contribution to the DOS. However, this feature shows not only as a simple shift of flat bands to new energies, intersecting the extended and evanescent states for each different Vn (x). Instead, as shown in Fig. 5c, multiple tunnelling steps at smaller energy scales appear at the boundary between the nth and n + 1th cells, generating additional pairs of discrete symmetry broken states similar in nature to states of type III introduced in the previous section. These interact and are hybridised with both the evanescent and extended states. The dispersion of the former is altered, evidenced by the smearing of the quantised states in the LDOS spectra shown in Fig. 5c and in Fig. S6(a–c)† where the LDOS is shown separately for all three sublattices. Additionally, the dispersion and braiding behaviour of the extended states also changes, shifting the locations of the band crossings, with the effect being more pronounced for smoother SL potentials.
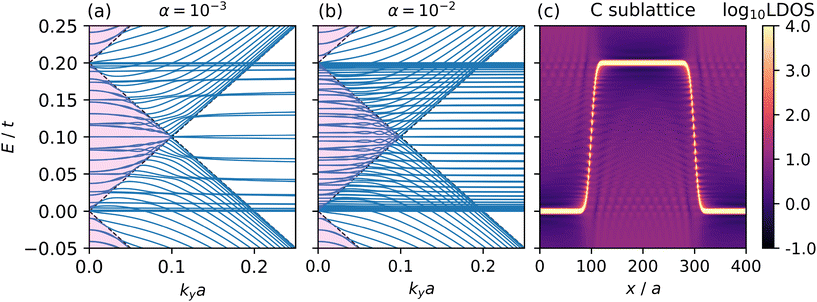 | ||
| Fig. 5 Smoothing the potential profile. The SL parameters are L = 400a and V0 = 0.2t. Low-energy band structures along ky measured from the Y point and at kx = 0, for smoothness parameters (a) α = 10−3 and (b) α = 10−2. When compared with Fig. 3(b) it is clear that smoother potentials lift the degeneracy of the flat bands. As shown in (b) relative to (a), smoother potential steps give rise to more non-degenerate states. The LDOS(x, E) spectra on the C sublattice corresponding to α = 10−2 is shown in (c), indicating the localization of these new states and their interaction with the extended and confined states. The pink shaded area indicates regions where extended states are allowed in both regions and are defined by the overlap between conical dispersion of the pristine lattice in the well and barrier regions shown by the black dashed lines. | ||
The smoothing of the potential also alters the band structure along ΓX and MY, as shown in Fig. S7(a–c).† Each additional pair of discrete symmetry broken state connects to two partial flat bands along ΓX that reconnect forming doubly degenerate partial flat bands along MY. These intersect along MY the linear folded bands, the gradient of which and hence associated group velocity remains unchanged compared to the sharp potential case, forming additional TDDCs between 0 < E < V0; smoother potentials generate a greater number of TDDCs.
Finally, we note further changes to the “SKT” state, shown in Fig. S8(a–c),† as compared to the sharp potential case described in Fig. 4. Smoothing the potential will shift the locations of the ADC towards the Y point: the scaling relation that governs the number and locations of the cones in the sharp potential case is no longer valid and larger values of α suppress the closing of the gap at E = V0/2 that generates them. The dispersion around the ADCs is also affected, leading to larger Fermi velocities at larger ky when compared to the sharp potential case. At the same time the dispersion near the Y point becomes flatter.
5 Including additional parameters
To extend the applicability of our model to solid-state systems, we now include three additional terms in the TB Hamiltonian: (i) a next-nearest neighbour (NNN) interaction term t′, to account for non-zero hopping between A/C site orbitals; (ii) an effective mass term U, to approximate the chemical potential difference between corner (B) and centre-edge (A/C) sites; and (iii) a spin–orbit coupling (SOC) term tSOC, to extend the model for Lieb lattices hosting metallic elements with high-energy electrons. In both Fig. 6 and ESI Videos (2–4)†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 we show how these parameters individually affect the band structure from the discrete to the continuum limit.
34 we show how these parameters individually affect the band structure from the discrete to the continuum limit.
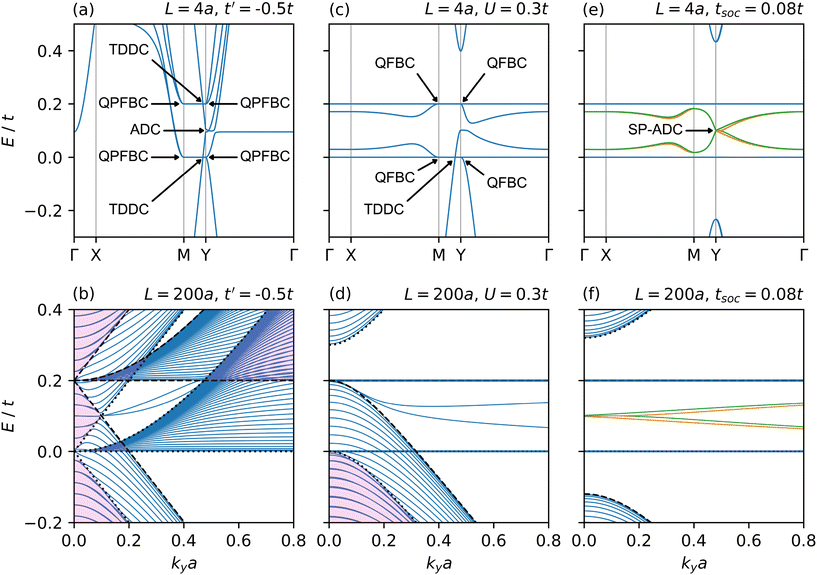 | ||
| Fig. 6 Including additional model parameters. (Top row) Band structure along the high-symmetry path shown in Fig. 2b for L = 4a (discrete limit) and (a) t' = −0.5t, (c) U = 0.3t and (e) tSOC = 0.08t. (Bottom row) Band structure near the Y point for L = 200a (continuum limit) and (b) t' = −0.5t, (d) U = 0.3t and (f) tSOC = 0.08t. The potential height V0 = 0.2t. From left to right the next-nearest neighbour (NNN) hoppings t′, an effective mass term U, and an intrinsic spin–orbit coupling (SOC) term tSOC are individually added to the Lieb SL Hamiltonian. The black dotted (dashed) lines represent the pristine lattice dispersions at kxa = 0 and kxa = π in the well (barrier) regions, given the corresponding t′, U and tSOC. The shaded pink regions show where electronic states are allowed in both well and barrier regions according to their respective pristine dispersions. In panels (e) and (f) the green (spin up) and orange (spin down) bands show the spin polarisation of the discrete lattice symmetry broken states in the presence of a SOC term. | ||
5.1. Next-nearest neighbour hopping, t′
First, we address the effect of including a NNN hopping interaction (t′ = −0.5t), likely to be present in all Lieb lattice systems, both artificial and solid state. As for the pristine lattice case seen in Fig S9a,† the presence of the NNN term disperses the original flat bands, which occurs for all wave vectors except along the MY direction. Consequently, in the SL there is a significant reduction to the DOS at E = 0(V0), further compounded by the band folding which reduces the distances ΓX and MY by a factor of L/a. However, the flat band degeneracy along MY scales linearly with L/a. As a result, in the discrete limit the contribution to the DOS from the partial flat bands at E = 0 (V0) will remain constant for different SL periodicities. Furthermore, as seen in Fig. 6b and ESI Video 2,†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 the uneven dispersion of the original degenerate flat bands for L > 4a means that in the continuum limit the flat bands at E = 0 (V0) are recovered, further enhancing the DOS at these energies.
34 the uneven dispersion of the original degenerate flat bands for L > 4a means that in the continuum limit the flat bands at E = 0 (V0) are recovered, further enhancing the DOS at these energies.
Even though the original flat band now becomes partially flat in the full BZ, the TDDCs and QFBCs are preserved. We relabel the latter as quadratic partial flat band crossings (QPFBCs) owing to the fact that the dispersion of the original flat bands adds further anisotropy to the bands around both the M and Y points, as shown in Fig. 6a and S10–S12.† Generally, a larger t′ yields greater dispersion and therefore larger modification to the electronic transport when compared to the NN case. This is true except at E = 0 (V0) since the band folding along MY remains unchanged and these energies correspond to the extremal points of the now dispersing flat bands. It is important to note that in the discrete limit, only transport experiments that probe around E = 0 will isolate the dynamics of the charge-carriers around the TDDCs and QFBCs, in addition to the presence of any possible strongly correlated phenomena driven by the partial flat band along MY. In the continuum limit, shown in Fig. 6b, the picture is more complicated. Compared to the NN case, regions where extended states in the SL are allowed (depicted in Fig. 6b as pink shaded areas) become more complex due to the unevenly dispersing original flat bands. This can be seen in more detail in Fig. S14 and S15† where the dispersion is shown for different values of L and for a range of kx.
The discrete symmetry broken states, labeled as type III in Fig. 3b, that cross to form the ADC, also disperse strongly upon the addition of the NNN term. Consequently, the ADC becomes tilted, as shown in detail in Fig. S13.† However, this does not affect the identified scaling relation in the NN case that generates additional cones in the SL since the band folding along MY remains unchanged. Instead, all the SL induced ADCs are also tilted and shifted to energies E ≠ V0/2. This is shown in Fig. S16† and compared to the “SKT” states obtained when only NN hoppings are considered. As a result, it should not be expected that the electron transport through the Lieb SL with a non-zero NNN interaction at E = V0/2 would resemble SKT, or that of graphene under a 1D periodic potential.
5.2. Mass term, U
The inclusion of a positive (negative) mass term U to the pristine Lieb lattice will open a gap above (below) the flat band, while the original linear dispersion of the bands becomes quadratic, see Fig S9b.† For the Lieb SL, the value of U needed to open a gap depends on the SL periodicity: in the discrete and continuum limits these conditions are |U| > V0/2 and |U| > V0 respectively, shown in Fig. S17.† A positive (negative) U satisfying these conditions will open a gap above (below) the top (bottom) flat bands, preserving the set of TDDCs and QFBCs at E = 0(V0), shown for U = 0.3t in the discrete limit in Fig. 6c. Additionally, any |U| > 0 destroys the ADC, as the broken sublattice symmetry prevents the Bloch states on the A and B sublattice combining within the coupling conditions required to generate it.The additional ADCs generated in the continuum limit are also affected. Whilst their location in energy E = (V0 + U)/2 agrees with the analytically predicted SKT state for massive charge-carriers,21 Fig. S18† shows fewer ADCs as the NN only case for the same SL periodicity and height. This is because for finite U, the width (in ky) of the overlapping pristine conduction/valence bands from the well/barrier regions shrinks, reducing the number of available wave vectors that can host them. Also, the mass term increases the size of the gap at Y which must close to generate additional ADCs, thus a larger L is required to do so for a given V0. This deviation from the SKT prediction is greater in this case than when only NN hoppings are included: we do not expect SKT of massive particles in a Lieb SL.
As for previous cases, the band folding along MY is affected by the inclusion of the mass term as the SL periodicity is increased towards the continuum limit: the gaps between consecutive states fold towards E = 0 and are flattened (Fig. S19 and ESI Video 3†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34). The slope of these flattened bands is also correlated to the dispersion in the kx direction, as shown in Fig. S20† where the dispersion is plotted for a range of kx.
34). The slope of these flattened bands is also correlated to the dispersion in the kx direction, as shown in Fig. S20† where the dispersion is plotted for a range of kx.
This effectively represents the probability of charge carriers tunnelling through the SL. Therefore, if these states do not disperse in the kx direction, e.g. at E = 0.05t for L = 50a, or 0 < E < V0 for L = 200a, this will give rise to super-collimation along |a2| within the barrier. Effectively, electrons are allowed to move only in the y direction. Such configurations can be readily obtained in the limit V0 < 2Δ, where Δ is the mass term induced gap of the pristine Lieb lattice.
5.3. Spin–orbit coupling term, tSOC
In the case of the pristine Lieb lattice, it is well known that the application of a SOC term opens topological gaps (with Chern number C = ±1) above and below the flat bands.28,33 This can be also seen in the pristine Lieb lattice dispersion in the presence of SOC, shown in Fig. S9c.† In the case of the SL, this modification destroys the TDDCs and QFBCs, as shown in Fig. 6(e). However, the presence of discrete lattice symmetry breaking in the SL induces spin-polarisation along XM and YΓ which splits the ADC into two, forming a spin-polarised ADC (SP-ADC). This is shown for the green (spin-up) and orange (spin-down) spin-split interface bands in Fig. 6e and in more detail in Fig. S21 and S22,† where the splitting becomes visible. As the SL periodicity is increased towards the continuum limit the two quadratic higher-energy bands shift towards the flat bands, eventually converging to the pristine lattice dispersions obtained for tSOC = 0.08t, shown by the black dashed (well) and dotted (barrier) lines in Fig. 6f. However, unlike the NN and NNN case, increasing the SL periodicity towards the continuum limit does not generate additional ADCs since there are no available extended states to fold at E = V0/2. In fact, the SP-ADCs remain stationary as L is varied, as shown in Fig. S22.†5.4. All terms included
A realistic and experimentally relevant description of a solid-state Lieb SL system requires at minimum a NNN hopping interaction t′ and an effective mass term U, simultaneously included. The inclusion of a SOC term tSOC is also required if metallic elements are present. The resulting band structure in the pristine lattice is shown in Fig. S9d.† In Fig. 7 we show the full band structures for L = (4, 50, 200)a and the states near the Y point for t′ = −0.5t, U = 0.3t without and with an SOC interaction tSOC = 0.08t. We also provide a data file containing full band structures for a range of SL parameters which can be visualised using the accompanying Python script.34 We observe that in the absence of SOC (Fig. 7a), the band dispersions inherit features from configurations with NNN or mass term considered separately, i.e. original flat bands of the Lieb lattice become dispersive except along MY (NNN), the original linear bands become quadratic and gaps are introduced in the spectrum (mass term). As such, we see the appearance of four QPFBCs and a bottom (top) TDDC for a positive (negative) mass term, together with the disappearance of the ADC at E = V0/2.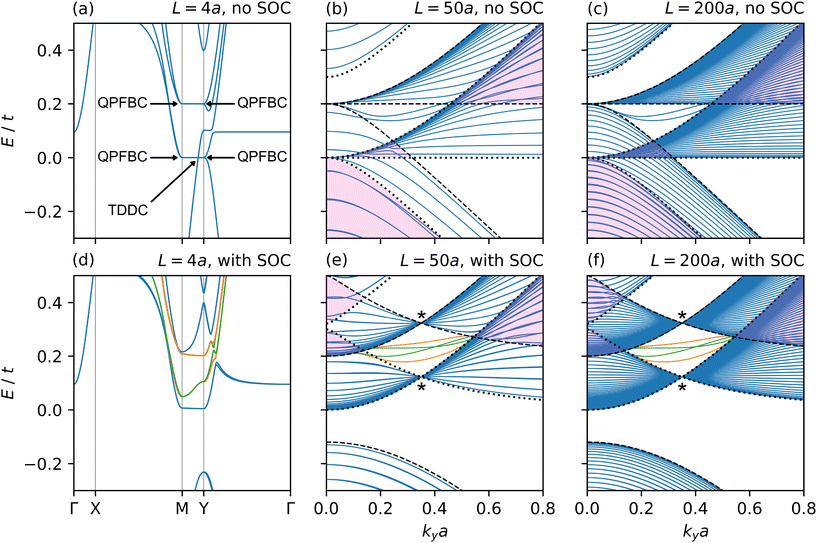 | ||
| Fig. 7 Describing realistic solid-state Lieb SLs without and with spin–orbit coupling. Top row shows (a) the full band structure for L = 4a (discrete limit) and (b and c) the band structure near the Y point for L = 50a and L = 200a and a solid-state system without SOC. Bottom row (d–f) shows the band structure for the same SL wavelength but including a SOC term. The parameters are t′ = −0.5t, U = 0.3t, and tSOC = 0.08t. In panels (e) and (f) the green (spin up) and orange (spin down) bands show the spin polarisation of the discrete lattice symmetry broken states. Same as Fig. 6, the black dotted (dashed) lines are the pristine lattice dispersions at kxa = 0 and kxa = π in the well (barrier) regions given the corresponding t′, U and tSOC parameters. The shaded pink regions show where electronic states are allowed in both well and barrier regions according to their respective pristine dispersions. | ||
A non-zero SOC interaction will gap these crossings, disperse the partial flat bands along MY, and induce a small spin-splitting of the bands along XM and YΓ, most apparent in the well-barrier interface bands in Fig. 7d, shown as orange/green bands for spin-down/up components. However, given that these spin-split bands disperse and overlap with other non-spin polarized bands, these cannot be individually detected in spin-sensitive transport experiments.
The SOC interaction can also open a band gap, the nature of which is set by the sign of the mass term: the system is a topological (trivial) insulator for a positive (negative) mass term. The topological gap hosts a quantum spin-Hall edge-state corresponding to spin-Chern numbers C↑↓ = ±1.
As the SL periodicity is increased towards the continuum limit, shown in Fig. 7(b, c) and (e, f), the band structures for either cases without and with SOC become increasingly complex, owing to the existence of continua of extended propagating states (shaded pink areas), the well/barrier localised states (type II), the interface states (type III) and the uneven dispersion of original degenerate flat bands induced by the NNN term. However, there are general features, including band-flattening and the isolation of localised states that arise for broad ranges of Lieb SL parameters in the continuum limit, which we point out here. Without SOC, flat bands that span the whole BZ at E = 0 (V0) are recovered in the continuum limit (Fig. 7c and S23†) and the presence of the TDDC at E = 0 is tuneable with the SL periodicity (see also ESI Video 5†).34 With the inclusion of the SOC term, this band flattening at E = 0 is not perfect, but the presence of the topological edge state is expected to impact the nature of many-body correlations present in the nearly-flat bands. We also note that increasing the SL periodicity has no effect on the number of topological edge-states. This can be understood intuitively: since the topological gap does not close or reopen as the SL periodicity varies, the number of edge states remains unchanged, with C↑↓ = ±1. This has been confirmed through ribbon band structure calculations, as illustrated in Fig. S27,† which shows the band structure of a ribbon with a width of W = 40a for various SL periodicities. The primary effect of the SL periodicity on the topological edge states is to fold their dispersion within the corresponding first Brillouin zone.
ESI Video 6†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 shows that the spin-up interface states (green bands in Fig. 7(e and f)) form a tilted cone at approximately L = 38a for the given SL parameters. But, for larger SL periodicities, spin-sensitive transport experiments will show even smaller discrepancies than the discrete limit case given the greater number of dispersive states that can contribute to transport. Fig. 7(e, f) and ESI Video 6†
34 shows that the spin-up interface states (green bands in Fig. 7(e and f)) form a tilted cone at approximately L = 38a for the given SL parameters. But, for larger SL periodicities, spin-sensitive transport experiments will show even smaller discrepancies than the discrete limit case given the greater number of dispersive states that can contribute to transport. Fig. 7(e, f) and ESI Video 6†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 also show the formation of two highly-degenerate crossing points (marked *), with the bottom (top) crossing formed from converging well (barrier) localised states. The degeneracy of these crossings is
34 also show the formation of two highly-degenerate crossing points (marked *), with the bottom (top) crossing formed from converging well (barrier) localised states. The degeneracy of these crossings is 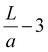 and is formed due to the folding of the band structure through a constant energy contour of the pristine lattice band structure. Plotting a cut of the band structure along kx through this crossing shows no dispersion. This is another feature where dispersive and flat bands occur at the same energies in the band structure. Importantly, these crossings are a result of band folding, a universal feature of all periodic potentials, not a sensitive symmetry constraint of the system.
and is formed due to the folding of the band structure through a constant energy contour of the pristine lattice band structure. Plotting a cut of the band structure along kx through this crossing shows no dispersion. This is another feature where dispersive and flat bands occur at the same energies in the band structure. Importantly, these crossings are a result of band folding, a universal feature of all periodic potentials, not a sensitive symmetry constraint of the system.
Finally we note general features relevant to all Lieb SLs in the continuum limit, without and with SOC. We expect super-collimation of charge carriers along the |a2| direction to be measurable in transport experiments due to both the isolation of the localised states from the continua and the corresponding band flatness along MY. This would occur, for example, at energies E = 0.1t in Fig. 7(c and f). Additionally, for systems with a negative mass term, insulating band gaps can be opened below E = 0 permitting switchable on/off transport measurements. The near-flatness of the dispersing flat bands shown in Fig. S23–S26† will enhance the DOS as energies E > 0 for these super-collimated states and those within the continuum (shaded pink regions), possibly leading to the emergence of strongly correlated phases.
6 Discussion
In the following we summarize the results presented in the previous sections. These can be categorized broadly according to the length scale of the SL, e.g. discrete versus continuum limit, or to the addition of relevant new terms to the Lieb lattice Hamiltonian, e.g. next-nearest neighbour hopping term, imbalance in the on-site potential – mass term, or the presence of SOC interactions.In the discrete limit, i.e. L ∼ a, the electronic dispersion of the Lieb SL presents a range of unexpected features, such as tilted Dirac cones, intersections between quadratic and (partial) flat bands, or spin-polarized states in the presence of SOC. On the other hand, by exploring the continuum limit, i.e. L ≫ a, we compare with previous simulations performed within the continuum limit at low energies and long wavelengths near the Dirac cone. Several features compare well with previous calculations, e.g. the nature of the extended states in the SL and the appearance of confined states that are allowed only in well or barrier regions, depending on the energy. At the same time, we observe new phenomena due to the discreteness of the Lieb lattice and the symmetry breaking induced by the SL. For example, localised states at the well/barrier interface give rise to a series of anisotropic Dirac cones at E = V0/2, the number of which depend on the L/a ratio, reminiscent of periodicity-induced extra Dirac cones in graphene. These states replace the SKT states predicted by the continuum approach when lattice details are ignored in the long-wavelenth limit, but the asymptotic limit L/a → ∞ is non-trivially approached due to the existence of Dirac cones, albeit with increasing frequency and decreasing Fermi velocity or flattening. Furthermore, we show that in the realistic case, where the well/barrier interface becomes smooth, additional flat interface states appear in the energy range 0 < E < V0/2 and eventually hybridize with both the extended and localized states. The interface smoothing also affects the previously predicted SKT states and the newly discovered ADCs.
Adding additional terms to the Hamiltonian strongly affects the electronic states in the SL. For example, the next-nearest neighbour hopping disperses the original flat bands in the BZ, except along the MY direction. This gives rise to additional regions in the BZ where extended states are allowed and induces a larger number of localized states in the well/barrier regions. Furthermore, the SKT states around E = V0/2 become dispersive, resulting in further deviation from the original SKT states.
A mass term gives rise to gapped regions in the spectrum and completely erases the SKT states when V0 is smaller than the pristine gap. We again find regions in the BZ where extended states are possible. Additionally, we find cases showing only localized states within a certain energy range, when no states are allowed in one of the well or barrier regions. Since these do not disperse in the kx direction, they would give rise to super-collimation resulting in pure propagation only along the ky direction.
The SOC term gives rise to topological gaps that survive in the SL, and we find spin-polarized interface states that propagate only along the ky direction.
When all the different terms are combined the band structure becomes complex with shared features resulting from the individual terms: original flat bands become dispersive, (topological) gaps can appear, regions where extended states are allowed shift around the BZ and in energy, well/barrier localized states are ubiquitous and can be isolated within some energy ranges and spin-polarized states can be localized at the well/barrier interfaces.
7 Conclusion
In conclusion, our results reveal a complex picture regarding the effect of 1D periodic potentials on the electronic properties of Lieb lattices. By considering a TB approach we were able to smoothly transition from the discrete to the continuum regimes, with relevance to possible experimental realizations of the SL periodicities. Furthermore, the TB approach allowed us to include terms in the Hamiltonian that describe experimentally relevant effects. These are related to longer range hoppings, distortions or imbalances in the sublattices or the presence of spin–orbit interactions. These terms give rise to rich features observed in the band structure and predict the absence of the universal SKT previously associated with Lieb lattices. All these features are relevant to future experiments in artificial Lieb lattices or newly proposed 2D covalent organic/metal–organic frameworks and inorganic 2D solids.8 Methods
8.1 Tight-binding Hamiltonian
Using the Python-based Pybinding package,36 we build a tight binding model with a single orbital per site to study the electronic states of a single-layer Lieb lattice under an electrostatic potential applied along the a1 direction forming a superlattice (see Fig. 1a). The Hamiltonian of the system is H = H0 + V(x), where the pristine lattice Hamiltonian H0 is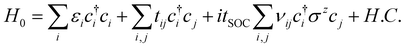 | (2) |
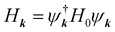 and fully-diagonalised. The resulting band structure for the pristine system can be visualised in Fig. 1b and Fig. S9(a–d).†
and fully-diagonalised. The resulting band structure for the pristine system can be visualised in Fig. 1b and Fig. S9(a–d).†
8.2 Numerical implementation of sharp and smooth potentials
We investigate two forms of periodic potential: an atomically sharp step-like potential where the potential change occurs instantaneously, and a potential with a finite smoothness. These are referred to as ‘step’ and ‘smooth’ periodic potentials in the main text. Application of the step periodic potential Vstep (x) is achieved using the Heaviside step function Θ(x) such that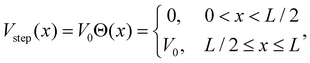 | (3) |
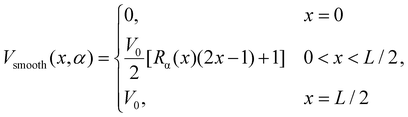 | (4) |
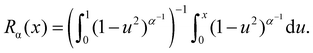 | (5) |
The odd-symmetry of Rα (x) is then used to build the full potential between x = 0 and x = L.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dylan Jones was supported by a Mirai PhD Scholarship in Quantum Phenomena in 2D Materials through the Advancement Office at the University of Bath. Lucian Covaci acknowledges support from Research Foundation-Flanders (FWO) and from the University of Antwerp Research Fund (BOF).References
- S. Taie, H. Ozawa, T. Ichinose, T. Nishio, S. Nakajima and Y. Takahashi, Sci. Adv., 2015, 1, e1500854 CrossRef PubMed.
- R. A. Vicencio, C. Cantillano, L. Morales-Inostroza, B. Real, C. Mejía-Cortés, S. Weimann, A. Szameit and M. I. Molina, Phys. Rev. Lett., 2015, 114, 245503 CrossRef PubMed.
- X. Huang, Y. Lai, Z. H. Hang, H. Zheng and C. T. Chan, Nat. Mater., 2011, 10, 582–586 CrossRef CAS PubMed.
- D. Guzmán-Silva, C. Mejía-Cortés, M. Bandres, M. Rechtsman, S. Weimann, S. Nolte, M. Segev, A. Szameit and R. Vicencio, New J. Phys., 2014, 16, 063061 CrossRef.
- P. Moitra, Y. Yang, Z. Anderson, I. I. Kravchenko, D. P. Briggs and J. Valentine, Nat. Photonics, 2013, 7, 791–795 CrossRef CAS.
- M. R. Slot, T. S. Gardenier, P. H. Jacobse, G. C. P. Van Miert, S. N. Kempkes, S. J. M. Zevenhuizen, C. M. Smith, D. Vanmaekelbergh and I. Swart, Nat. Phys., 2017, 13, 672–676 Search PubMed.
- K.-E. Huhtinen, J. Herzog-Arbeitman, A. Chew, B. A. Bernevig and P. Törmä, Phys. Rev. B, 2022, 106, 014518 CrossRef CAS.
- W. Jiang, H. Huang and F. Liu, Nat. Commun., 2019, 10, 2207 CrossRef PubMed.
- W. Jiang, S. Zhang, Z. Wang, F. Liu and T. Low, Nano Lett., 2020, 20, 1959–1966 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50 CrossRef CAS PubMed.
- A. Julku, S. Peotta, T. I. Vanhala, D.-H. Kim and P. Törmä, Phys. Rev. Lett., 2016, 117, 045303 CrossRef PubMed.
- C.-H. Park, L. Yang, Y.-W. Son, M. L. Cohen and S. G. Louie, Nat. Phys., 2008, 4, 213–217 Search PubMed.
- M. Barbier, P. Vasilopoulos and F. Peeters, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 075438 CrossRef.
- Y. Li, S. Dietrich, C. Forsythe, T. Taniguchi, K. Watanabe, P. Moon and C. R. Dean, Nat. Nanotechnol., 2021, 16, 525–530 CrossRef CAS PubMed.
- T. Li, H. Chen, K. Wang, Y. Hao, L. Zhang, K. Watanabe, T. Taniguchi and X. Hong, Phys. Rev. Lett., 2024, 132, 056204 CrossRef CAS PubMed.
- M. Gobbi, S. Bonacchi, J. X. Lian, Y. Liu, X.-Y. Wang, M.-A. Stoeckel, M. A. Squillaci, G. D′avino, A. Narita and K. Müllen, et al. , Nat. Commun., 2017, 8, 14767 CrossRef CAS PubMed.
- H.-Z. Tsai, J. Lischner, A. A. Omrani, F. Liou, A. S. Aikawa, C. Karrasch, S. Wickenburg, A. Riss, K. C. Natividad and J. Chen, et al. , Nat. Electron., 2020, 3, 598–603 CrossRef CAS.
- M. Gobbi, S. Bonacchi, J. X. Lian, A. Vercouter, S. Bertolazzi, B. Zyska, M. Timpel, R. Tatti, Y. Olivier and S. Hecht, et al. , Nat. Commun., 2018, 9, 2661 CrossRef PubMed.
- Y. Xu and G. Jin, Phys. Lett. A, 2014, 378, 3554–3560 CrossRef CAS.
- S. M. Cunha, D. R. da Costa, J. Milton Pereira Jr., R. N. Costa Filho, B. Van Duppen and F. M. Peeters, Phys. Rev. B, 2021, 104, 115409 CrossRef CAS.
- Y. Betancur-Ocampo, G. Cordourier-Maruri, V. Gupta and R. De Coss, Phys. Rev. B, 2017, 96, 024304 CrossRef.
- M. I. Katsnelson, K. S. Novoselov and A. K. Geim, Nat. Phys., 2006, 2, 620–625 Search PubMed.
- D. F. Urban, D. Bercioux, M. Wimmer and W. Häusler, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 115136 CrossRef.
- E. Illes and E. Nicol, Phys. Rev. B, 2017, 95, 235432 CrossRef.
- A. Fang, Z. Q. Zhang, S. G. Louie and C. T. Chan, Phys. Rev. B, 2016, 93, 035422 CrossRef.
- R. Shen, L. B. Shao, B. Wang and D. Y. Xing, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 041410 CrossRef.
- Y. Zhu, A. Merkel, L. Cao, Y. Zeng, S. Wan, T. Guo, Z. Su, S. Gao, H. Zeng and H. Zhang, et al. , Appl. Phys. Lett., 2023, 122, 211701 CrossRef CAS.
- M. A. Springer, T.-J. Liu, A. Kuc and T. Heine, Chem. Soc. Rev., 2020, 49, 2007–2019 RSC.
- E. Jin, M. Asada, Q. Xu, S. Dalapati, M. A. Addicoat, M. A. Brady, H. Xu, T. Nakamura, T. Heine and Q. Chen, et al. , Science, 2017, 357, 673–676 CrossRef CAS PubMed.
- T. Yang, Y. Z. Luo, Z. Wang, T. Zhu, H. Pan, S. Wang, S. P. Lau, Y. P. Feng and M. Yang, Nanoscale, 2021, 13, 14008–14015 RSC.
- H. Feng, C. Liu, S. Zhou, N. Gao, Q. Gao, J. Zhuang, X. Xu, Z. Hu, J. Wang, L. Chen, J. Zhao, S. X. Dou and Y. Du, Nano Lett., 2020, 20, 2537–2543 CrossRef CAS PubMed.
- W. Wu, S. Sun, C. S. Tang, J. Wu, Y. Ma, L. Zhang, C. Cai, J. Zhong, M. V. Milošević, A. T. S. Wee and X. Yin, Adv. Mater., 2024, 2405615 CrossRef CAS PubMed.
- N. Goldman, D. F. Urban and D. Bercioux, Phys. Rev. A, 2011, 83, 063601 CrossRef.
- The ESI Videos 1–6† and a Python script plotting the data can be access as a Figshare entry, DOI: 10.6084/m9.figshare.25305913.
- W.-F. Tsai, C. Fang, H. Yao and J. Hu, New J. Phys., 2015, 17, 055016 CrossRef.
- D. Moldovan, M. Andelković and F. Peeters, Pybinding v0.9.5: a Python package for tight- binding calculations, 2020, DOI:10.5281/zenodo.594754.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03549f |
| This journal is © The Royal Society of Chemistry 2025 |