Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Landé g-factors of electrons and holes strongly confined in CsPbI3 perovskite nanocrystals in glass
Sergey R.
Meliakov
 *a,
Evgeny A.
Zhukov
*a,
Evgeny A.
Zhukov
 ab,
Vasilii V.
Belykh
ab,
Vasilii V.
Belykh
 b,
Mikhail O.
Nestoklon
b,
Mikhail O.
Nestoklon
 b,
Elena V.
Kolobkova
b,
Elena V.
Kolobkova
 cd,
Maria S.
Kuznetsova
cd,
Maria S.
Kuznetsova
 e,
Manfred
Bayer
e,
Manfred
Bayer
 bf and
Dmitri R.
Yakovlev
bf and
Dmitri R.
Yakovlev
 *ab
*ab
aP.N. Lebedev Physical Institute of the Russian Academy of Sciences, 119991 Moscow, Russia. E-mail: melyakovs@lebedev.ru
bExperimentelle Physik 2, Technische Universität Dortmund, 44227 Dortmund, Germany. E-mail: dmitri.yakovlev@tu-dortmund.de
cITMO University, 199034 St. Petersburg, Russia
dSt. Petersburg State Institute of Technology, 190013 St. Petersburg, Russia
eSpin Optics Laboratory, St. Petersburg State University, 198504 St. Petersburg, Russia
fResearch Center FEMS, Technische Universität Dortmund, 44227 Dortmund, Germany
First published on 13th February 2025
Abstract
The Landé g-factor of charge carriers is a key parameter in spin physics controlling spin polarization and spin dynamics. In turn, it delivers information about the electronic band structure in the vicinity of the band gap and its modification in nanocrystals provided by strong carrier confinement. The coherent spin dynamics of electrons and holes are investigated in CsPbI3 perovskite nanocrystals with sizes varied from 4 to 16 nm by means of time-resolved Faraday ellipticity at the temperature of 6 K. The Landé g-factors of the charge carriers are evaluated through the Larmor spin precession in magnetic fields up to 430 mT across the spectral range from 1.69 to 2.25 eV, provided by variation of the nanocrystal size. The spectral dependence of the electron g-factor follows the model predictions when accounting for the mixing of the electronic bands with increasing confinement resulting from a decrease of the nanocrystal size. The spectral dependence of the hole g-factor, changing from −0.19 to +1.69, is considerably stronger than expected from the model. We analyze several mechanisms and conclude that none of them can be responsible for this difference. The renormalizations of the electron and hole g-factors roughly compensate each other, providing spectral independence for the bright exciton g-factor with a value of about +2.2.
I. Introduction
Colloidal nanocrystals (NCs) made of lead halide perovskite semiconductors provide attractiveness for applications in photovoltaics, optoelectronics, electronics, and beyond.1–5 They are commonly synthesized by colloidal chemistry in solution and can be composed of hybrid organic–inorganic or fully-inorganic materials. The fully-inorganic NCs made, e.g., of CsPbI3, CsPbBr3, or CsPbCl3, show considerably higher stability in ambient conditions compared with the materials containing organic components. Encapsulation of the NCs allows one to further enhance their stability. One of the successful approaches in this respect is to synthesize the perovskite NCs in a glass matrix from a melt.6–11 The surface of such NCs is free from organic ligands that are typical for the growth in solution. Also, the glass samples can be easily polished to get surfaces of optical quality, which facilitates their optoelectronic application.The electronic band structure of lead halide perovskite NCs considerably differs from common III–V and II–VI semiconductor NCs and quantum dots.12–14 Most importantly, the band gap is formed by conduction band and valence band states with a simple structure with spin 1/2, which results in different spin level structure of the bright and dark exciton states, as compared with III–V and II–VI NCs.11 An in-depth understanding of the physical properties of perovskite NCs calls for a comprehensive study by various techniques, among which optical techniques are particularly favorable and informative.
Spin-dependent phenomena typically are helpful, as they deliver information on the charge carriers interacting with each other, with the crystal lattice, and with the nuclear spin system.15 The spin polarization and spin dynamics are sensitive to the details of the band structure and crystal symmetry. The spin properties of perovskite NCs have been addressed by several optical and magneto-optical techniques, namely, optical orientation and optical alignment,16 polarized emission in magnetic field,17 time-resolved Faraday/Kerr rotation,18–22 time-resolved differential transmission,23–25 and optically-detected nuclear magnetic resonance.22 Among them, time-resolved Faraday/Kerr rotation is particularly informative, as it provides data on the electron and hole Landé g-factors, spin coherence, spin dephasing, and longitudinal spin relaxation. Carrier spin coherence up to room temperature has been reported in CsPbBr3 NCs18,21 and its optical manipulation has been demonstrated.20,26
The Landé g-factor of charge carriers and excitons determines their Zeeman splitting in a magnetic field and thus is a key parameter in spin physics. We found recently that in bulk lead halide perovskites the electron and hole as well as exciton g-factors follow universal dependences on the band gap energy.13,27 In NCs, the carrier confinement induces mixing of the electronic ground states with higher bands, which results in a considerable renormalization of the electron g-factor (ge), as predicted theoretically and found experimentally in CsPbI3 NCs in glass.14,28 For the hole g-factor (gh) the predicted renormalization is small, which is in line with the experimental data for relatively large NCs with sizes of 8–16 nm.14 To complete the picture, it is important to study the g-factors in smaller NCs with strong geometric confinement of the carriers. Especially, recently an unusually strong spectral dependence of gh in CsPbBr3 NCs, which considerably exceeds the model expectations, was found.29
In this paper, we study the coherent spin dynamics of electrons and holes in CsPbI3 NCs with sizes in the range 4–16 nm, embedded in a glass matrix, by time-resolved Faraday ellipticity. The spectral dependences of the electron and hole g-factors are measured in the large range of exciton energies of 1.69–2.25 eV accessible by varying carrier confinement. Both g-factors become considerably renormalized with increasing carrier confinement (i.e., decreasing NC size). The changes of the electron g-factor are in line with model predictions, while the hole g-factor demonstrates a much larger renormalization, the mechanism of which needs to be understood.
II. Experimental results
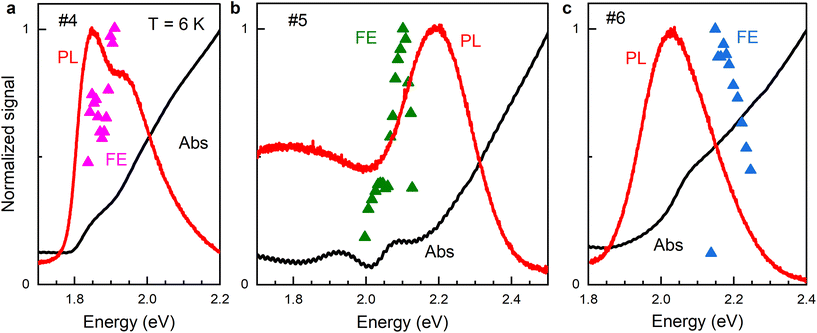
We study experimentally a set of CsPbI3 NCs embedded in a fluorophosphate glass matrix, namely, six samples with different NC sizes covering the range of 4–16 nm. They are labeled as samples #1, #2, #3, #4, #5, and #6 with decreasing NC size with increasing sample number. The samples show inhomogeneous broadening of their optical properties, provided by the considerable dispersion of NC size within one sample. Therefore, in our study we rely on the energy of exciton resonance as a characteristic of the carrier confinement energy. In the studied set of NCs the exciton energy covers the range of 1.69–2.25 eV. Detailed information on the optical properties and carrier g-factors for the larger NCs (samples #1, #2 and #3 with sizes in range of 8–16 nm) can be found in ref. 14 and 28.Fig. 1 shows absorption and photoluminescence (PL) spectra measured at the temperature of T = 6 K for the samples #4, #5, and #6 in the size range of 4–8 nm. The PL lines have a typical half width at half maximum of about 200 meV. In the time-resolved Faraday ellipticity (TRFE) experiments, the laser is tuned spectrally, which allows us to address NCs with a specific exciton transition energy corresponding to a specific NC size. For that, spectrally narrow laser pulses with 1 meV width and 1.5 ps duration are used. The corresponding amplitude of the TRFE signals is shown in Fig. 1 by the symbols.
TRFE is used to measure the coherent dynamics of the electron and hole spins in a magnetic field. This pump–probe-based technique exploits polarized laser pulses:30,31 spin-oriented carriers are photogenerated by the circularly-polarized pump pulses and the dynamics of their spin polarization are detected through the change of the ellipticity of the linearly polarized probe pulses.32,33 We perform these experiments at the temperature of T = 6 K in magnetic fields, B, up to 430 mT, applied in the Voigt geometry, i.e., perpendicular to the light wave vector.
The TRFE dynamics measured in the samples #3, #4, #5, and #6 at B = 430 mT are shown in Fig. 2a. The spin dynamics demonstrate oscillating signals due to the Larmor spin precession of carrier spins about external magnetic field.19,28 The Larmor precession frequency, ωL, is determined by the g-factor and scales with the magnetic field B according to:
| ωL = |g|μBB/ħ | (1) |
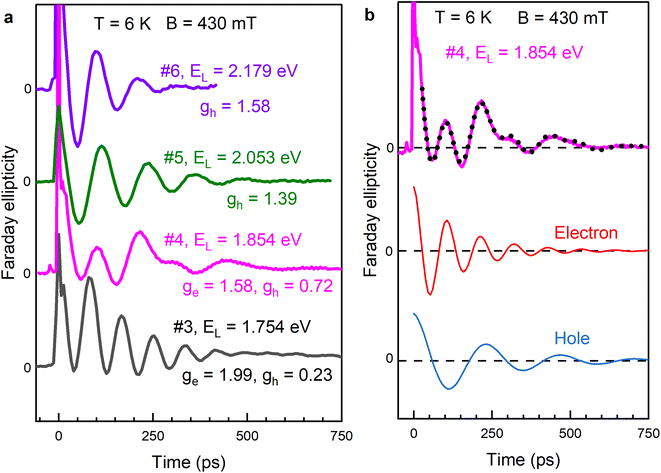 | ||
Fig. 2 (a) Spin dynamics in the CsPbI3 NCs (samples #3, #4, #5 and #6) in 430 mT magnetic field. (b) The upper graph shows the FE dynamics in sample #4. Black dotted line is a fit with eqn (2). The two lower graphs show the oscillatory components in the spin dynamics, corresponding to the electron (red line, |ge| = 1.58 and 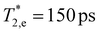 ) and the hole (blue line, |gh| = 0.72 and ) and the hole (blue line, |gh| = 0.72 and 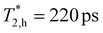 ). ). | ||
Here μB is the Bohr magneton and ħ is the reduced Planck constant. The decay of the oscillations is described by the spin dephasing time 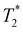 , which at low temperatures mainly reflects the inhomogeneous spread of the Larmor precession frequencies provided by the spread of g-factors, Δg. At weak magnetic fields down to zero field strength, the hyperfine interaction of carriers with the nuclear spin fluctuations also contributes to the carrier spin dephasing.29
, which at low temperatures mainly reflects the inhomogeneous spread of the Larmor precession frequencies provided by the spread of g-factors, Δg. At weak magnetic fields down to zero field strength, the hyperfine interaction of carriers with the nuclear spin fluctuations also contributes to the carrier spin dephasing.29
One can see in Fig. 2a that the spin dynamics in samples #3 and #4 have two oscillating components. To identify them and to extract their parameters we fit the dynamics with the following function:
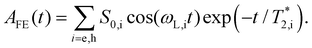 | (2) |
Here, S0,e and S0,h are the initial light-induced spin polarizations of electrons and holes, respectively. 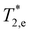 and
and 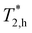 are the electron and hole spin dephasing times. An example of such a fit is shown by the dotted line in Fig. 2b for the sample #4. There, also the separate components of the electron and hole to the spin dynamics are given. According to ref. 14, the oscillations with larger (ωL,e = 58.5 rad ns−1) and smaller (ωL,h = 26.5 rad ns−1) Larmor frequencies correspond to the electron and hole spin precession, respectively. The extracted spin dephasing times at B = 430 mT are
are the electron and hole spin dephasing times. An example of such a fit is shown by the dotted line in Fig. 2b for the sample #4. There, also the separate components of the electron and hole to the spin dynamics are given. According to ref. 14, the oscillations with larger (ωL,e = 58.5 rad ns−1) and smaller (ωL,h = 26.5 rad ns−1) Larmor frequencies correspond to the electron and hole spin precession, respectively. The extracted spin dephasing times at B = 430 mT are 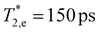 and
and 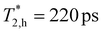 . A similar phenomenology is observed for the sample #3. The electron and hole contributions could be also isolated in the spin dynamics of samples #1, #2 and #3, see ref. 14 and 28. For the samples #5 and #6, only one oscillating component can be detected, which we assign to the holes based on its spectral dependence, as discussed below. We suggest that for NCs in glass matrix a photocharging involving Auger escape of one of the carrier (electron or hole) in matrix is the mechanism that provides singly-charged NCs. Observation of only hole spin precession in small CsPbI3 NCs means that the escape of the electrons dominates over the hole one. Note, that in our recent study on CsPbBr3 NCs in glass we also found dominance of the hole signal.29
. A similar phenomenology is observed for the sample #3. The electron and hole contributions could be also isolated in the spin dynamics of samples #1, #2 and #3, see ref. 14 and 28. For the samples #5 and #6, only one oscillating component can be detected, which we assign to the holes based on its spectral dependence, as discussed below. We suggest that for NCs in glass matrix a photocharging involving Auger escape of one of the carrier (electron or hole) in matrix is the mechanism that provides singly-charged NCs. Observation of only hole spin precession in small CsPbI3 NCs means that the escape of the electrons dominates over the hole one. Note, that in our recent study on CsPbBr3 NCs in glass we also found dominance of the hole signal.29
We measure the spin dynamics for all samples in various magnetic fields. An example of the sample #4, measured at the energy of 1.911 eV, is shown in Fig. 3a. At zero magnetic field, the decay is close to single exponential with the decay time of 230 ps. With increasing magnetic field, the Larmor spin precession signal becomes pronounced. The magnetic field dependences of the Larmor precession frequencies are shown in Fig. 3b. As expected, they scale linearly with the magnetic field strength and show no offset when extrapolated to zero field. This confirms that the spin signals originate from resident carriers, i.e., from NCs charged either by an electron or by a hole,19 rather than from excitons. In the latter case electron–hole exchange interaction would lead to exciton spin beats even at zero magnetic field.24–26 The resident carriers in the NCs can appear from long-living photocharging, where either the electron or the hole from a photogenerated electron–hole pair escapes from the NC. As a result, a fraction of NCs in the ensemble is charged with electrons, another fraction of NCs is charged with holes, while the rest NCs remain neutral. According to eqn (1), the slopes of the dependences in Fig. 3(b) correspond to the absolute values of the electron and hole g-factors: |ge| = 1.41 and |gh| = 0.91. It was shown in ref. 14 and 28 that in CsPbI3 NCs the electron and hole g-factors are positive in this energy range. Worthwhile to note, that in zero and weak magnetic fields additional spin splitting for electrons and holes can be induced due to their hyperfine interaction with nuclear spin fluctuations. We recently found such contribution in CsPbBr3 NCs in glass, where the effective Overhauser field for holes reaches 50 mT.29 It results in deviation of the ωL(B) dependence from linearity for magnetic fields smaller that 100 mT. But it does not contribute to it at larger fields, which we use for evaluation of the carrier g-factors, see Fig. 3b.
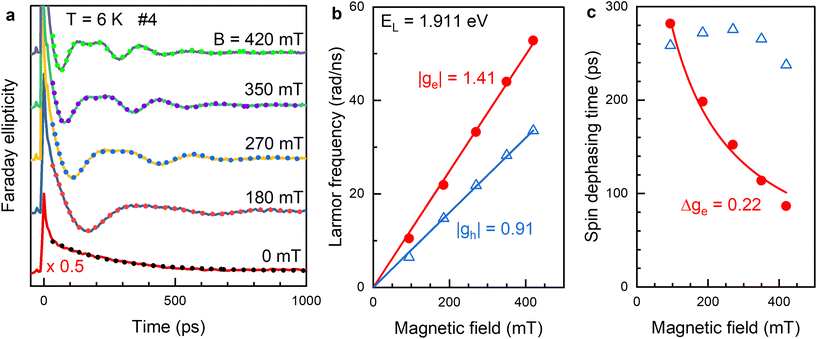 | ||
Fig. 3 Magnetic field dependence of the spin dynamics in CsPbI3 NCs of sample #4, measured at EL = 1.911 eV. (a) TRFE dynamics in various Voigt magnetic fields. Dotted lines show fits to the experimental data using eqn (2). (b) Magnetic field dependences of the electron (red circles) and hole (blue triangles) Larmor precession frequencies. Lines show linear fits using eqn (1). (c) Magnetic field dependences of the electron (red circles) and hole (blue triangles) spin dephasing time 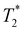 . Red line shows fit using eqn (3). . Red line shows fit using eqn (3). | ||
The magnetic field dependences of the spin dephasing times of electrons (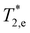 ) and holes (
) and holes (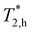 ) are shown in Fig. 3c. The spin dephasing time
) are shown in Fig. 3c. The spin dephasing time 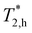 barely depends on magnetic field amounting to about 260 ps, while
barely depends on magnetic field amounting to about 260 ps, while 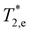 decreases from 280 ps to 90 ps with the magnetic field growing from 90 mT to 420 mT. This behavior is typical for inhomogeneous spin ensembles with a finite g-factor spread Δg and can be described by the following expression:30
decreases from 280 ps to 90 ps with the magnetic field growing from 90 mT to 420 mT. This behavior is typical for inhomogeneous spin ensembles with a finite g-factor spread Δg and can be described by the following expression:30
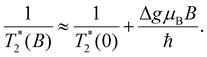 | (3) |
Here,  is the spin dephasing time at zero magnetic field. Fitting the experimental data with eqn (3), yields Δge = 0.22 for the electrons (the relative spread is Δge/ge = 16%). In ref. 28 we reported Δge = 0.25 for the electrons and Δgh = 0.07 for the holes in sample #1.
is the spin dephasing time at zero magnetic field. Fitting the experimental data with eqn (3), yields Δge = 0.22 for the electrons (the relative spread is Δge/ge = 16%). In ref. 28 we reported Δge = 0.25 for the electrons and Δgh = 0.07 for the holes in sample #1.
The spectral dependences of the electron and hole g-factors for the studied CsPbI3 NCs are shown in Fig. 4. The electron g-factors are measured for samples #1 to #4. They decrease from +2.3 to +1.4 with energy increasing from 1.69 eV to 1.91 eV. This dependence closely follows the theory predictions shown by the red line, where the used model accounts for mixing of the electron ground states with higher bands when the confinement energy increases. The situation is different for the hole g-factor. It changes from −0.19 to +1.69 for the energy increasing from 1.69 eV to 2.25 eV. The renormalization of the g-factor is much stronger than the model predictions shown by the blue line in Fig. 4. The difference between experimental and theoretical g-factors reaches 0.8 for the smallest NCs. In fact, the model considerations reported in ref. 14 conclude on a rather weak effect of the hole quantum confinement on its g-factor, and the blue line in Fig. 4 is close to the band gap dependence of gh in bulk crystals, see ref. 13.
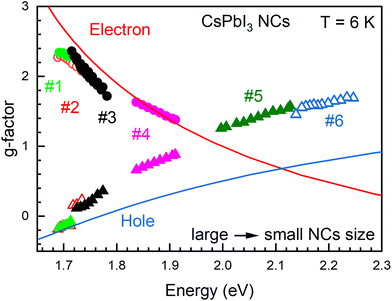 | ||
| Fig. 4 Spectral dependences of the electron (circles) and hole (triangles) g-factors in CsPbI3 NCs in glass: samples #1 (light green symbols), #2 (red), #3 (black), #4 (pink), #5 (dark green), and #6 (blue). Solid lines give the calculations for CsPbI3 NCs from ref. 14. | ||
It is instructive to analyze the spectral dependence of the bright exciton g-factor, which is composed of the electron and the hole g-factor. In lead halide perovskite NCs the bright exciton g-factor is given by gBX = ge + gh. We plot it in Fig. 5 by taking the experimental data from Fig. 4. For the samples #5 and #6, for which experimental results for ge are not available, we take the modeled values from ref. 14, which are shown by the red line in Fig. 4. One can see in Fig. 5 that, surprisingly, gBX is almost independent of energy in the whole range of 1.69–2.25 eV, amounting to gBX ≈ +2.2. Note that in bulk crystals of the lead halide perovskites with different compositions the bright exciton g-factor is also rather constant as it remains in the range of +2.3 to +2.7 for variation of the band gap from 1.5 to 3.2 eV.27 Recently, the exciton g-factor value of |gBX| = 2.29 was reported for CsPbI3 NCs grown in solution.25 It was measured at T = 200 K for NC size of about 7.2 nm (at energy of 1.812 eV) from the exciton spin beats in time-resolved differential absorption. This value is in a very good agreement with our results for CsPbI3 NCs in glass shown in Fig. 5.
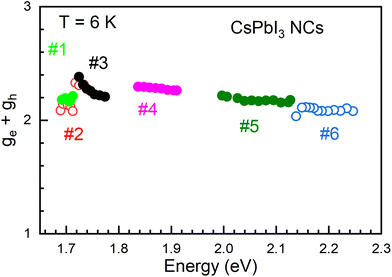 | ||
| Fig. 5 Spectral dependence of the bright exciton g-factor in CsPbI3 NCs, calculated from the electron and hole g-factors as gBX = ge + gh. For the samples #1 to #4, the experimental values for ge and gh are taken. For the samples #5 and #6, we take the experimental values of gh and the modeled values of ge from ref. 14. | ||
III. Discussion
Let us analyze the factors that contribute to the spectral dependence of the electron and hole g-factors in CsPbI3 NCs. As a starting point we take the universal dependence of the carrier g-factors on the band gap found experimentally for cryogenic temperatures and confirmed theoretically for lead halide perovskite bulk crystals.13 These studies were recently extended to address the role of quantum confinement of charge carriers in NCs on the g-factors.14In the atomistic calculations using the empirical tight-binding method (ETB) based on density functional theory (DFT) calculations,34 the hole g-factor as function of energy is expected to follow the bulk trend, while for electrons the situation is more complicated.14 The electron g-factor demonstrates a strong effect of the quantum confinement, decreasing significantly with an increase of the effective band gap (a decrease of the NC size) and even changing sign from positive to negative. The calculations may be explained qualitatively in the framework of the k·p model13 extended to account for the geometric confinement.14 The strong renormalization of the electron g-factor originates from the mixing of the bottom conduction band with the spin–orbit split electron states due to this confinement. In ref. 14 the experimental data were limited, but the expected trend for the electron g-factor was quite pronounced. In the present paper, the experimental results cover a broader energy range. As seen from Fig. 4, the experimentally measured electron g-factors perfectly agree with the theoretical predictions.
In contrast, the hole g-factors measured across the wide energy range deviate significantly from the atomistic calculations and the k·p analysis. While the qualitative trend is in agreement with the predictions, for large quantum confinement energies the experimental data almost twice exceed the predicted values, see Fig. 4. Let us discuss the possible sources of this discrepancy.
One of the complications in comparing theory with experiment is the uncertainty in NC quantum confinement. On the theory side, the transition energy is the difference between the energies of the first quantum confined levels of the electron in the conduction band and the hole in the valence band. On the experimental side, the transition energy is the photon energy of the laser exciting the TRFE signal. The difference between these energies for the same size NCs (due to the exciton binding energy, dielectric screening, etc.) is expected to be small but not zero and, more importantly, may change with the NC size. However, the difference for the hole g-factors in Fig. 4 cannot be explained by this effect: the g-factor is not sensitive enough to energy, and to explain the observed difference an unrealistic renormalization of the energy scale would have to be assumed.
A second possible source of the deviation is the non-parabolicity of the hole energy dispersion, which could result in an overestimated hole quantum confinement energy in theory. We believe that this also cannot explain the observed difference as the non-parabolicity of the dispersion (both for electron and hole) is carefully taken into account in the ETB calculations. The electron and hole energy dispersions in the ETB accurately reproduce the DFT results, see the ESI of ref. 14, and the results qualitatively agree with the k·p calculations. This means that even if non-parabolicity is seriously underestimated in theory, its correct consideration will hardly compensate for the difference between experiment and theory.
The probable cause of the discrepancy is the mixing of the upper valence band with halide bands lying approximately 1.5 eV below the top of valence band. This mixing is underestimated in the ETB consideration. The nearest-neighbor empirical tight-binding calculations allow one to describe the upper valence and three lowest electron bands with meV precision.34 However, the correct dispersion in the lower valence bands formed from the p-orbitals of halide atoms demands for accounting the second-neighbor interaction,35 which is missing in the scheme used in ref. 14. If the admixture of the lower valence band and/or the effect of the spin–orbit interaction on its dispersion is underestimated, the renormalization of the hole g-factor due to quantum confinement may also be significantly underestimated. An additional analysis of the theoretical description, which goes beyond the present study, is needed to reveal whether this factor can close the gap between theory and experiment.
IV. Conclusions
We have measured the coherent spin dynamics of electrons and holes in CsPbI3 perovskite nanocrystals with sizes varying from 4 to 16 nm by time-resolved Faraday ellipticity. We evaluate the Landé g-factors of charge carriers in the regime of strong quantum confinement providing a spectral shift of exciton resonance from 1.69 to 2.25 eV. The electron g-factor demonstrates a strong renormalization caused by the admixture of the upper conduction band to the ground state, in agreement with theoretical predictions. The spectral dependence of hole g-factor qualitatively follows the trend expected for bulk crystals, but also demonstrates a significant renormalization by a value similar to the changes of the electron g-factor, which cannot be explained by the theory. Interestingly, the renormalization of the electron and hole g-factors almost compensate each other, almost canceling the spectral dependence of the bright exciton g-factor leading to an almost constant value of +2.2. Understanding the details of the responsible mechanisms for this behavior would allow one to accurately refine the band parameters for the lead halide perovskites and their NCs.V. Experimental section
Samples
The studied CsPbI3 nanocrystals embedded in fluorophosphate Ba(PO3)2–AlF3 glass were synthesized by rapid cooling of a glass melt enriched with the components needed for the perovskite crystallization. Details of the method are given in ref. 10 and 22. The samples of fluorophosphate (FP) glass with the composition 35P2O5–35BaO–5AlF3–10Ga2O3–10PbF2–5Cs2O (mol%) doped with BaI2 were synthesized using the melt-quench technique. The glass synthesis was performed in a closed glassy carbon crucible at the temperature of T = 1050 °C.Six samples are investigated in this paper, which we label #1, #2, #3, #4, #5, and #6. Their technology codes are EK31, EK7, EK8, EK201, EK205 and EK203, respectively. Note that the first three samples (same codes and synthesis) were investigated in ref. 14 and 28. About 50 g (for samples #1, #2, #3) and 25 g (for samples #4, #5, #6) of the batch were melted in the crucible for 20–30 minutes, then the glass melt was cast on a glassy carbon plate, and pressed to form a plate with a thickness of about 2 mm. Samples with a diameter of 5 cm were annealed at the temperature of 50 °C below Tg = 400 °C to remove residual stresses. The CsPbI3 perovskite NCs were formed from the glass melt during the quenching. The glasses obtained in this way are doped with CsPbI3 NCs. The NC sizes in the initial glass were regulated by the concentration of iodide and the rate of cooling of the melt without heat treatment above Tg. They differ in the NC sizes, which is reflected by the relative spectral shifts of their optical spectra. The change of the NC size was achieved by changing the concentration of iodine in the melt. Due to the high volatility of iodine compounds and the low viscosity of the glass-forming fluorophosphate melt at elevated temperatures, an increase in the synthesis time leads to a gradual decrease of the iodine concentration in the equilibrium melt. Thus, it is possible to completely preserve the original composition and change only the concentration of iodine by means of a smooth change of the synthesis duration.
Time-resolved Faraday ellipticity
To study the coherent spin dynamics of carriers we use a time-resolved pump–probe technique with detection of the Faraday ellipticity (TRFE).30,33 Spin oriented electrons and holes are generated by circularly polarized pump pulses. The used laser system (Light Conversion) generates pulses of 1.5 ps duration with a spectral width of about 1 meV at the repetition rate of 25 kHz (repetition period 40 μs). The laser photon energy is tuned in the spectral range of 1.65–2.30 eV in order to resonantly excite NCs of various sizes. The laser beam is split into the pump and probe beams having the same photon energies. The time delay between the pump and probe pulses is controlled by a mechanical delay line. The pump beam is modulated with an electro-optical modulator between σ+ and σ− circular polarization at the frequency of 26 kHz. The probe beam is linearly polarized. The Faraday ellipticity of the probe beam, which is proportional to the carrier spin polarization, is measured as function of the delay between the pump and probe pulses using a balanced photodetector, connected to a lock-in amplifier that is synchronized with the modulator. Both pump and probe beams have the power of 0.5 mW with spot sizes of about 100 μm. For the time-resolved measurements the samples are placed in a helium-flow optical cryostat at 6 K temperature. Magnetic fields up to 430 mT are applied perpendicular to the laser beam (Voigt geometry, B⊥k) using an electromagnet.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors are thankful to M. M. Glazov for fruitful discussions. Research performed at the P. N. Lebedev Physical Institute was financially supported by the Ministry of Science and Higher Education of the Russian Federation, Contract No. 075-15-2021-598. E. V. K. and M. S. K. acknowledge the Saint-Petersburg State University (Grant No. 1024022800259-7).References
- M. V. Kovalenko, L. Protesescu and M. I. Bondarchuk, Properties and potential optoelectronic applications of lead halide perovskite nanocrystals, Science, 2017, 358, 745–750 CrossRef CAS.
- J. Shamsi, A. S. Urban, M. Imran, L. De Trizio and L. Manna, Metal halide perovskite nanocrystals: synthesis, post-synthesis modifications, and their optical properties, Chem. Rev., 2019, 119, 3296–3348 CrossRef CAS PubMed.
- A. Dey, J. Ye, A. De, E. Debroye and S. K. Ha, et al., State of the art and prospects for halide perovskite nanocrystals, ACS Nano, 2021, 15, 10775–10981 CrossRef CAS.
- Y. Mu, Z. He, K. Wang, X. Pi and S. Zhou, Recent progress and future prospects on halide perovskite nanocrystals for optoelectronics and beyond, iScience, 2023, 25, 105371 CrossRef PubMed.
- C.-Y. Huang, H. Li, Y. Wu, C.-H. Lin, X. Guan, L. Hu, J. Kim, X. Zhu, H. Zeng and T. Wu, Inorganic halide perovskite quantum dots: A versatile nanomaterial platform for electronic applications, Nano-Micro Lett., 2023, 15, 16 CrossRef CAS PubMed.
- P. Li, C. Hu, L. Zhou, J. Jiang, Y. Cheng, M. He, X. Liang and W. Xiang, Novel synthesis and optical characterization of CsPb2Br5 quantum dots in borosilicate glasses, Mater. Lett., 2017, 209, 483–485 CrossRef CAS.
- S. Liu, Y. Luo, M. He, X. Liang and W. Xiang, Novel CsPbI3 QDs glass with chemical stability and optical properties, J. Eur. Ceram. Soc., 2018, 38, 1998–2004 CrossRef CAS.
- S. Liu, M. He, X. Di, P. Li, W. Xiang and X. Liang, Precipitation and tunable emission of cesium lead halide perovskites (CsPbX3, X = Br, I) QDs in borosilicate glass, Ceram. Int., 2018, 44, 4496–4499 CrossRef CAS.
- Y. Ye, W. Zhang, Z. Zhao, J. Wang, C. Liu, Z. Deng, X. Zhao and J. Han, Highly luminescent cesium lead halide perovskite nanocrystals stabilized in glasses for light-emitting applications, Adv. Opt. Mater., 2019, 7, 1801663 CrossRef.
- E. V. Kolobkova, M. S. Kuznetsova and N. V. Nikonorov, Perovskite CsPbX3 (X = Cl, Br, I) nanocrystals in fluorophosphate glasses, J. Non-Cryst. Solids, 2021, 563, 120811 CrossRef CAS.
- V. V. Belykh, M. L. Skorikov, E. V. Kulebyakina, E. V. Kolobkova, M. S. Kuznetsova, M. M. Glazov and D. R. Yakovlev, Submillisecond spin relaxation in CsPb(Cl,Br)3 perovskite nanocrystals in a glass matrix, Nano Lett., 2022, 22, 4583–4588 CrossRef CAS.
- Al. L. Efros and L. E. Brus, Nanocrystal quantum dots: From discovery to modern development, ACS Nano, 2021, 15, 6192–6210 CrossRef CAS PubMed.
- E. Kirstein, D. R. Yakovlev, M. M. Glazov, E. A. Zhukov, D. Kudlacik, I. V. Kalitukha, V. F. Sapega, G. S. Dimitriev, M. A. Semina, M. O. Nestoklon, E. L. Ivchenko, N. E. Kopteva, D. N. Dirin, O. Nazarenko, M. V. Kovalenko, A. Baumann, J. Höcker, V. Dyakonov and M. Bayer, The Landé factors of electrons and holes in lead halide perovskites: universal dependence on the band gap, Nat. Commun., 2022, 13, 3062 CrossRef CAS PubMed.
- M. O. Nestoklon, E. Kirstein, D. R. Yakovlev, E. A. Zhukov, M. M. Glazov, M. A. Semina, E. L. Ivchenko, E. V. Kolobkova, M. S. Kuznetsova and M. Bayer, Tailoring the electron and hole Landé factors in lead halide perovskite nanocrystals by quantum confinement and halide exchange, Nano Lett., 2023, 23, 8218–8224 CrossRef CAS PubMed.
- Spin Response of Hybrid Organic Inorganic Perovskites, in Hybrid Organic Inorganic Perovskites: Physical Properties and Applications, ed. Z. V. Vardeny and M. C. Beard, World Scientific, 2022, vol. 3 Search PubMed.
- M. O. Nestoklon, S. V. Goupalov, R. I. Dzhioev, O. S. Ken, V. L. Korenev, Yu. G. Kusrayev, V. F. Sapega, C. de Weerd, L. Gomez, T. Gregorkiewicz, J. Lin, K. Suenaga, Y. Fujiwara, L. B. Matyushkin and I. N. Yassievich, Optical orientation and alignment of excitons in ensembles of inorganic perovskite nanocrystals, Phys. Rev. B, 2018, 97, 235304 CrossRef CAS.
- D. Canneson, E. V. Shornikova, D. R. Yakovlev, T. Rogge, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, E. Lhuillier, M. Bayer and L. Biadala, Negatively charged and dark excitons in CsPbBr3 perovskite nanocrystals revealed by high magnetic fields, Nano Lett., 2017, 17, 6177–6183 CrossRef CAS PubMed.
- M. J. Crane, L. M. Jacoby, T. A. Cohen, Y. Huang, C. K. Luscombe and D. R. Gamelin, Coherent spin precession and lifetime-limited spin dephasing in CsPbBr3 perovskite nanocrystals, Nano Lett., 2020, 20, 8626–8633 CrossRef CAS PubMed.
- P. S. Grigoryev, V. V. Belykh, D. R. Yakovlev, E. Lhuillier and M. Bayer, Coherent spin dynamics of electrons and holes in CsPbBr3 colloidal nanocrystals, Nano Lett., 2021, 21, 8481–8487 CrossRef CAS PubMed.
- X. Lin, Y. Han, J. Zhu and K. Wu, Room-temperature coherent optical manipulation of hole spins in solution-grown perovskite quantum dots, Nat. Nanotechnol., 2022, 18, 124 Search PubMed.
- S. R. Meliakov, E. A. Zhukov, E. V. Kulebyakina, V. V. Belykh and D. R. Yakovlev, Coherent spin dynamics of electrons in CsPbBr3 perovskite nanocrystals at room temperature, Nanomaterials, 2023, 13, 2454 Search PubMed.
- E. Kirstein, N. E. Kopteva, D. R. Yakovlev, E. A. Zhukov, E. V. Kolobkova, M. S. Kuznetsova, V. V. Belykh, I. A. Yugova, M. M. Glazov, M. Bayer and A. Greilich, Mode locking of hole spin coherences in CsPb(Cl,Br)3 perovskite nanocrystals, Nat. Commun., 2023, 14, 699 CrossRef CAS PubMed.
- S. Strohmair, A. Dey, Y. Tong, L. Polavarapu, B. J. Bohn and J. Feldmann, Spin polarization dynamics of free charge carriers in CsPbI3 nanocrystals, Nano Lett., 2020, 20, 4724–4730 CrossRef CAS PubMed.
- Y. Han, W. Liang, X. Lin, Y. Li, F. Sun, F. Zhang, P. C. Sercel and K. Wu, Lattice distortion inducing exciton splitting and coherent quantum beating in CsPbI3 perovskite quantum dots, Nat. Mater., 2022, 21, 1282–1289 CrossRef CAS.
- K. Gao, Y. Li, Y. Yang, Y. Liu, M. Liu, W. Liang, B. Zhang, L. Wang, J. Zhu and K. Wu, Manipulating coherent exciton dynamics in CsPbI3 perovskite quantum dots using magnetic field, Adv. Mater., 2024, 36, 2309420 CrossRef CAS.
- J. Zhu, Y. Li, X. Lin, Y. Han and K. Wu, Coherent phenomena and dynamics of lead halide perovskite nanocrystals for quantum information technologies, Nat. Mater., 2024, 23, 1027–1040 CrossRef CAS.
- N. E. Kopteva, D. R. Yakovlev, E. Kirstein, E. A. Zhukov, D. Kudlacik, I. V. Kalitukha, V. F. Sapega, D. N. Dirin, M. V. Kovalenko, A. Baumann, J. Höcker, V. Dyakonov, S. A. Crooker and M. Bayer, Weak dispersion of exciton Landé factor with band gap energy in lead halide perovskites: Approximate compensation of the electron and hole dependences, Small, 2023, 2300935 Search PubMed.
- S. R. Meliakov, E. A. Zhukov, V. V. Belykh, M. O. Nestoklon, E. V. Kolobkova, M. S. Kuznetsova, M. Bayer and D. R. Yakovlev, Temperature dependence of the electron and hole Landé g-factors in CsPbI3 nanocrystals embedded in a glass matrix, Nanoscale, 2024, 16, 21496 RSC.
- S. R. Meliakov, V. V. Belykh, E. A. Zhukov, E. V. Kolobkova, M. S. Kuznetsova, M. Bayer and D. R. Yakovlev, Hole spin precession and dephasing induced by nuclear hyperfine fields in CsPbBr3 and CsPb(Cl,Br)3 nanocrystals in a glass matrix, Phys. Rev. B, 2024, 110, 235301 CrossRef CAS.
- D. R. Yakovlev and M. Bayer, Coherent spin dynamics of carriers, in Spin Physics in Semiconductors, ed. M. I. Dyakonov, Springer International Publishing AG, 2017, ch. 6, pp. 155–206 Search PubMed.
- V. V. Belykh, D. R. Yakovlev, M. M. Glazov, P. S. Grigoryev, M. Hussain, J. Rautert, D. N. Dirin, M. V. Kovalenko and M. Bayer, Coherent spin dynamics of electrons and holes in CsPbBr3 perovskite crystals, Nat. Commun., 2019, 10, 673 CrossRef CAS.
- I. A. Yugova, M. M. Glazov, E. L. Ivchenko and Al. L. Efros, Pump-probe Faraday rotation and ellipticity in an ensemble of singly charged quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 104436 Search PubMed.
- M. M. Glazov, I. A. Yugova, S. Spatzek, A. Schwan, S. Varwig, D. R. Yakovlev, D. Reuter, A. D. Wieck and M. Bayer, Effect of pump-probe detuning on the Faraday rotation and ellipticity signals of mode-locked spins in (In,Ga)As/GaAs quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155325 CrossRef.
- M. O. Nestoklon, Tight-binding description of inorganic lead halide perovskites in cubic phase, Comput. Mater. Sci., 2021, 196, 110535 Search PubMed.
- R. Kashikar, B. Khamari and B. R. K. Nanda, Second-neighbor electron hopping and pressure induced topological quantum phase transition in insulating cubic perovskites, Phys. Rev. Mater., 2018, 2, 124204 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |