Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spectral and dynamical properties of multiexcitons in semiconductor nanorods†
Krishan
Kumar‡
 *ab and
Maria
Wächtler§
*ab and
Maria
Wächtler§
 *b
*b
aDepartment Functional Interfaces, Leibniz Institute of Photonic Technology Jena, Albert-Einstein-Straße 9, 07745 Jena, Germany. E-mail: krishan.kumar@uni-oldenburg.de; waechtler@phc.uni-kiel.de
bChemistry Department and State Research Center OPTIMAS, RPTU Kaiserslautern-Landau, Erwin-Schrödinger-Str. 52, 67663 Kaiserslautern, Germany
First published on 20th February 2025
Abstract
Multiple exciton dynamics in semiconductor nanocrystals is usually characterized by the observation of changes in the fast multiexponential kinetics at the band edge transition position in transient absorption spectroscopy at varying excitation intensities. However, analysis of this complex decay dynamics is not straightforward and complicated by varying initial distributions of multiple excitons of increasing order with increasing excitation intensity and the superposition of contributions from multiexciton processes and charge carrier trapping, which need to be distinguished. In this study, we not only analyse kinetics but also transient absorption spectra to identify characteristic spectroscopic signatures for the presence of multiple excitons of varying orders beyond biexcitons in seeded and non-seeded CdS nanorods. Applying an MCMC (Markov Chain Monte Carlo) sampling approach for global target analysis enables us to determine the contributions of multiple exciton decay via Auger recombination and the contribution of a potential population of surface exciton states to the observed decay dynamics.
Introduction
Semiconductor nanocrystals have gained significant attention due to their tuneable optoelectronic properties.1–3 Besides their applications as emitters in sensing and imaging,4,5 in displays,6 as laser media,7 and in quantum computation and communication,8 nanocrystals have shown potential in light-harvesting applications, i.e., photovoltaics9 and photocatalysis for solar-to-fuel conversion as a clean source of energy.10 A highly interesting property of semiconductor nanocrystals is the formation of multiexcitons, e.g., via the consecutive absorption of multiple photons or by multiexciton generation (MEG), whereby multiexcitons are generated by splitting of a high energy single exciton to two or more low energy excitons.11,12 Multiexcitons are of interest in optical amplification13 and could also be beneficial for charge carrier generation in photovoltaics14 and photocatalytic processes involving multielectron reactions.15,16 Unfortunately, the lifetime of multiple excitons is limited through annihilation via Auger recombination, which occurs with rates on the timescale of 10 s to 100 s of ps in semiconductor nanocrystals.12,15,17 Auger recombination rates have been shown to be tuneable via structural parameters such as the size and shape of nanocrystals. The Auger recombination lifetime scales with the volume of the nanocrystal.18 In heterostructures, band alignment and wavefunction engineering impact Auger recombination rates by controlling the overlap between hole and electron wavefunctions.15,19,20 To be able to exploit the relations between structure and dynamics for the design of particles optimized for a certain application, it is crucial to determine multiexciton dynamics reliably.The standard approach to investigate dynamics involving multiple excitons is to perform transient absorption (TA) spectroscopy with increasing pump intensity, observing the decay dynamics of the band-edge bleach feature of the lowest excitonic transition.15,21,22 The observed additional fast decaying components in band-edge kinetics appearing with increasing pump intensity are usually assigned to Auger recombination and are used to determine the lifetimes of multiple excitons. However, the single probe wavelength analysis limited to following only bleach decay kinetics could be misleading as the observed dynamics can contain not only contributions from biexcitons but also higher-order excitonic states.18,23 Furthermore, such results need to be evaluated carefully because the multiexponential behaviour in the bleach decay signatures on the timescale can also arise from processes leading to population of surface exciton states, i.e., trapping of charge carriers.18,24,25 To facilitate the discrimination between multiexciton states of varying orders and populations of surface states, differences in the spectral signatures should be evaluated. For this, global analysis of spectrally resolved datasets recorded at varying excitation intensities needs to be performed to extract the kinetic and spectral information of the contributing species. Only a few reports exist on efforts to determine both dynamical and spectral properties, and so far have mainly focused on biexcitons.26–28 The complexity of the datasets caused by the need to fit kinetics for a large number of wavelengths and varying excitation intensities presents a challenge for data evaluation. Additionally, the spectra for the involved species are broad with complex line shapes and are expected to strongly overlap, which complicates the model selection and the evaluation of the quality of the fit. One approach relies on the standard global analysis of datasets at single pump intensities.16,26 By applying this approach, the species spectra and decay kinetics for single and biexcitons in CdSe quantum dots have been determined. As the contributing species spectra and rates are expected not to vary with excitation intensity, simultaneous analysis of varying intensities could improve the quality of the time constants and species spectra obtained. This has been realized by applying a Markov Chain Monte Carlo (MCMC) sampling approach for global target analysis of the TA spectra of CsPbBr3 and CdSe nanocrystals.27–29 To the best of our knowledge, there have been no attempts to analyse the spectral and dynamical properties of multiexcitons of higher order by applying TA spectroscopy, also considering interferences caused by the population of surface exciton states of nanocrystals.
In this work, we explore the dynamics and spectral properties of multiexcitons in CdSe@CdS nanorods via transient absorption spectroscopy. The complex pump intensity-dependent datasets are globally analysed by applying the MCMC sampling approach for global target analysis. We show in this contribution that this approach allows for determining the spectral and dynamical properties of up to tri-exciton species in cadmium-based nanorods. The sampling of the target kinetic model based on an Auger recombination process revealed the presence of two different monoexcitons dominant in the low or high pump intensity range, respectively. Using a series of experiments on CdS nanorods, MUA-capped CdSe@CdS nanorods and natively capped pre-illuminated nanorods, we assigned the presence of the second monoexciton species to surface trapping-related monoexciton formation which can only be populated via multiexciton excitation.
Experimental
All chemicals and solvents used were purchased from Sigma-Aldrich (Merck KGaA, Darmstadt, Germany), except for octadecyl phosphonic acid (ODPA), which was purchased from Carl Roth GmbH + Co. KG (Karlsruhe, Germany), and used without further purification. All solvents were of spectroscopic grade, dried and deoxygenated.Synthesis of CdSe@CdS nanorods
CdSe seeds were synthesized using a protocol developed by Carbone et al.30 CdO (61.1 mg), ODPA (∼0.29 g) and trioctylphosphine oxide (TOPO, 3 g) were heated in a three-neck flask under constant stirring to 150 °C and evacuated for 30 min. After evacuation, the flask was filled with nitrogen and heated to 340 °C until the brown reaction mixture turns colourless. The reaction mixture was cooled down to 120 °C and evacuated for at least 2 hours to remove water formed as a byproduct of Cd–ODPA complexation. After evacuation, the mixture was reheated to 370 °C. 0.4359 g of 1.7 M Se dissolved in trioctylphosphine (TOP) and 1.56 g of TOP were injected and the reaction stopped immediately by removing the heating mantle and decreasing the temperature. 5 mL of toluene was added when the temperature of the reaction mixture reached below 90 °C. The CdSe seeds were precipitated by adding 5 ml of methanol and centrifuged at 4000 rpm for 5 min. The pellet was redispersed in 5 ml of toluene and the procedure was repeated three times. For the synthesis of CdSe@CdS nanorods, the protocol established by Amirav et al. was applied.31 CdO (0.2097 g), ODPA (1.13 g), n-propylphosphonic acid (PPA, 65.75 mg) and TOPO (3.33 g) were added to a three-neck flask and heated under constant stirring to 120 °C and evacuated for 30 min. Then the flask was flushed with N2 and heated to 340 °C. At this temperature, 1.5 g of TOP and 0.05 g of sulfur dissolved in 0.60 g of TOP were injected, and after 20 s, 2 mg of CdSe seeds dissolved in 0.5 g of TOP was injected. The reaction mixture was kept at this temperature for 10 min until the colour of the solution turned from red to orange. After 10 min, the heating mantle was removed and the reaction mixture was cooled down. 5 mL of toluene was added once the temperature reached below 90 °C. 5 ml of methanol was added to precipitate the nanorods and the mixture was centrifuged at 4000 rpm for 10 min. The precipitate was redispersed in hexane, 2 mL of nonanoic acid and 2 mL of octylamine and precipitated by addition of methanol multiple times. For a size exclusion step, the precipitate was redispersed in 10 mL of toluene and 6 mL of isopropyl alcohol and centrifuged at 4000 rpm for 30 min two times. Finally, the nanorods were redispersed in toluene.Synthesis of CdS nanorods
CdS nanorods were synthesized following the seeded synthesis approach.16,32 To first synthesize CdS seeds, CdO (0.1102 g), oleic acid (OA, 2.19 g) and 1-octadecene (ODE, 15 mL) were mixed in a three-neck flask and heated to 100 °C under vacuum for 1 hour with constant stirring. After evacuation, the flask was filled with nitrogen and heated to 260 °C to dissolve CdO and form a colourless solution. S (0.017 g) dissolved in 7 mL of ODE was injected and the reaction mixture was kept at this temperature for 90 s. The reaction was stopped by removing the heating mantle and 10 mL of toluene was added when the temperature of the reaction mixture reached 90 °C. The product was cleaned by precipitating it with methanol and centrifugation and redispersed in toluene five times. For the synthesis of rods, CdO (0.12 g), ODPA (0.7 g), PPA (0.034) and TOPO (6.2 g) were mixed in a three-neck flask and heated to 100 °C under vacuum for 1 hour with constant stirring. The flask was then filled with nitrogen and heated to 350 °C to dissolve CdO. At this temperature, 1.5 mL of TOP was injected into the hot solution and the solution was further heated to 365 °C. Next, 1.6 mL of sulfur in TOP (0.079 g mL−1) and CdS seeds (∼3 × 10−8 mol) dispersed in toluol were quickly injected into the reaction mixture. The reaction was stopped by removing the heating mantle after 9 min and 10 mL of toluene was added when the temperature of the reaction mixture reached 90 °C. The product was precipitated by adding methanol, centrifuged at 4000 rpm for five minutes and redispersed in toluene. This precipitation cycle was repeated five times. For size selection, the product was mixed with 2 mL of nonaoic acid and 2 mL of oleylamine. The obtained clear mixture was precipitated using methanol and centrifuged at 4000 rpm for five minutes. The precipitation step was repeated 3 times. Finally, the CdS nanorods thus obtained were re-dispersed in toluene.Ligand exchange with 11-mercaptoundecanoic acid (MUA) was performed following a literature procedure.33 238 mg of MUA was dissolved in 10 mL of methanol and mixed with 121 mg of tetramethylammonium hydroxide pentahydrate. 12 mg of CdSe@CdS nanorods were dried under vacuum, mixed with 6 mL of the above solution and stirred for 3 h until the CdSe@CdS nanorods were fully dispersed. Plenty of toluene was added as a non-solvent to precipitate the ligand exchange nanorods. The mixture was centrifuged at 6000 rpm for 20 min, the supernatant was discarded, and the precipitate was re-dispersed in methanol.
Basic sample characterization
Steady-state UV/vis absorption spectra were recorded using a JASCO V780 UV/vis/NIR spectrophotometer (JASCO GmbH, Pfungstadt, Germany). All measurements were performed in 1 cm quartz cuvettes. Photoluminescence spectra were recorded using an FLS980 photoluminescence spectrometer (Edinburgh Instruments Ltd, Livingston, UK). An excitation wavelength of 400 nm was used. FTIR spectra were recorded using a Bruker INVENIO R spectrometer equipped with an ATR (Platinum ATR, Bruker) accessory. Background correction was performed by recording the air spectrum. IR spectra of dried thin films on a CaF2 substrate were recorded. Transmission Electron Microscopy (TEM) images were recorded in bright field (BF) using a Hitachi HT7820 operating at 100 kV acceleration voltage in high-resolution mode.Femtosecond-TA measurements
Femtosecond-TA measurements were performed using a home-built transient absorption setup with a detection system from Pascher Instruments AB. A regenerative Ti:sapphire amplifier (Astrella, Coherent, USA) delivering pulses centred at 800 nm with ∼100 fs full width at half maxima, 5 mJ pulse energy, and 1 kHz pulse repetition rate was used to generate excitation and probe pulses. The output fundamental is split into several beams. One part is travelling over a 2 ns delay line and is focused onto a rotating CaF2 window to generate a broadband white light continuum (300–700 nm). The continuum is split into a probe, which is focused on the sample and a reference beam. To generate the excitation pulses, 2 mJ of the fundamental output of the amplifier pumps an optical parametric amplifier (TOPAS, Light conversion, Lithuania) to produce tuneable pump pulses. For our experiments, pump pulses with a central wavelength of 400 nm were generated. The relative polarization of the pump and probe is set to a magic angle of 54.7°. A mechanical chopper reduces the repetition rate of the pump pulses to 500 Hz and the pump is focused to the sample (beam diameter 400 μm). The spectra of probe and reference pulses are recorded using CCD array detectors after passing a Czerny–Turner spectrograph with a 150 mm focal length (SP2150, Princeton Instruments). The obtained TA data were chirp corrected using a Python-based package KiMoPack.34 The intensity-dependent TA data in the time range of 2–1000 ps were fitted using a script published for target model sampling using the Markov Chain Monte Carlo method.27 The script was modified to adapt our target model, as described in the ESI.† All nanorod samples were prepared and measured under an inert atmosphere in a home-built sealed and air-tight 1 mm cuvette.Results and discussion
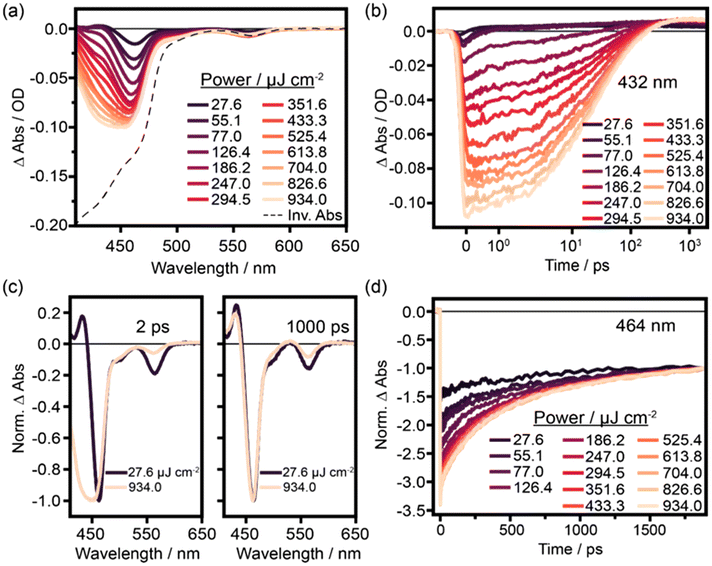
For our study, we chose to investigate the multiexciton dynamics in CdSe@CdS nanorods with quasi-type II band alignment. In these heterostructures, the holes tend to localize to CdSe seed and electrons are delocalized over the entire nanorod, resulting in prolonged multiexciton lifetimes.20,35–37 Due to the extended multiexciton lifetimes, these structures can act as a model system to study multiexcitons beyond biexcitons in semiconductor nanostructures. For this purpose, CdSe@CdS nanorods (length 20.1 ± 1.6 nm, width 4.7 ± 0.7 nm, and seed size 2.3 nm, see Fig. S1–S3† for sample characterization) capped with a mixture of surface ligands such as octadecylphosphonic acid (ODPA), n-propylphosphonic acid (PPA), trioctylphosphine (TOP), and trioctylphosphine oxide (TOPO) were synthesized following the well-established seeded-growth approach.31 These nanorods will be called in short TOPO-capped nanorods even though being well aware that there is a mixture of surface ligands at the surface, but TOPO is often considered to be the major part.38,39 TA spectroscopy was performed by exciting the nanorods dispersed in toluene with pulses having a central wavelength of 400 nm and a pulse duration of 100 fs of varying intensities between ∼28 and 934 μJ cm−2 in an oxygen-free air-tight sealed 1 mm cuvette. In Fig. 1a, transient spectra recorded at a delay time of 2 ps are presented. The TA spectra show the characteristic negative features at 464 nm and 566 nm corresponding to a bleach of the lowest excitonic transitions localized in the CdS and CdSe domains in the seeded nanorods caused by conduction band state population.15,37 In the quasi type-II heterostructures, these transitions correspond to the transitions between the highest VB hole level 1σh (for the CdS rod) or 1Sh (for the CdSe seed), respectively, to the lowest energy CB electron level 1σe.15,37 The CdS rod bleach signal is more intense than the CdSe seed bleach signal due to the larger volume of the CdS rod-shaped shell compared to the CdSe seed. Additionally, at low excitation intensities, a photoinduced absorption (PA) band caused by the biexciton effect is present at 432 nm.21 After the formation of monoexcitons upon interaction with the pump pulse, a second transition to the lowest excitonic CB levels is in principle possible upon interaction with probe light, but appears at a shifted position with modified transition oscillator strength caused by Coulomb multiparticle interactions in the double excited nanoparticle formed upon probe interaction, resulting in negative bleach signatures at the position of the excitonic transitions and the appearance of positive features either red- or blue-shifted depending on the type of interaction (binding or repulsive in the generated multiple excited particles).26,40,41 Increasing pump fluence leads to an increase in intensity and broadening of the band-edge bleach features while the PA band disappears, i.e., the positive signature in the spectral region around 432 nm turns into a negative signal. Similar spectral changes with increasing pump fluence have been observed before for CdSe,26 CdSe@CdS42 quantum dots and CdS nanorods16,41 and were attributed to a changing initial population of monoexcitons and multiexcitons with increasing pump intensity. In the biexcitonic state, the lowest CB electron level is completely populated, and for higher excitonic states, the CB πe levels are populated additionally. This leads to the observed disappearance of the PA band and the broadening of the bleach signal with increasing excitation intensity is directly associated with the presence of higher-order excitons initially generated upon excitation with sufficient intensity. Accordingly, at low pump fluences, when only monoexcitons are generated, the formation of an immediate positive signal is observed, which slowly decays on the ns timescale (Fig. 1b).At high pump fluences, the initial signal after excitation is negative and decays on a few 100 ps timescale to form the positive PA signal, which is in the typical range of Auger recombination times for rod-shaped semiconductor nanocrystals.16,35,43 Hence, the PA signal (432 nm) sensitively reports on the presence and temporal development of multiple excitons and this transition from the negative signal to the positive signal indicates the decay of multiexcitons to monoexcitons. Interestingly, differences in the TA data can be observed not only at early timescales depending on pump fluence, but also at long delay times beyond 1500 ps. In the normalized transient spectra at long delay times, slight differences in low and high excitation intensity data are visible (Fig. 1c). Taken together with slight differences in the long-term decay dynamics for low and high excitation intensities (Fig. 1d), this might be an indication that additional states, which are accessible via multiexcitons, might play a role.
From these qualitative considerations, we can conclude that we observe an increasing initial population of multiexciton states, but we cannot derive any statement on the order of the multiexcitonic states contributing to the data, nor their exact lifetimes. To retrieve quantitative information on the multiexciton decay and to extract timescales and spectral information on the contributing species, the data need to be modelled. The non-radiative annihilation of multiexcitons via Auger recombination occurs according to the established quantized Auger recombination model in a sequential cascade mechanism.18,44 The initially generated multiexciton of the Nth order (N being the number of excitons generated in one particle) decays to form an (N − 1)th order multiexciton, which decays to an (N − 2)th order multiexciton and so on. The initial population of the multiexcitons in an ensemble of nanorods generated by the absorption of light follows a Poisson distribution:
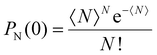 | (1) |
The average number 〈N〉 of excitons per nanorod depends on the excitation intensity and can be estimated from the average energy density (J) and an absorption cross-section scaled with the pump power density (σ):
| 〈N〉 = J × σ | (2) |
Hence, using eqn (1) and (2), the excitation intensity-dependent starting concentrations cN (t = 0, J) can be described. Assuming that the component spectra for the contributing species sN(λ) are not changing with time or excitation intensity and that the observed decay kinetics solely is influenced by dynamics changing the population of the contributing states, i.e. cN(t), the TA data can be simulated by:
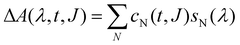 | (3) |
For modelling the excitation intensity-dependent dataset for all intensities simultaneously, the parameters to be determined are the time constants τN representing the lifetime of the Nth order exciton, the absorption cross-section parameter σ, and the component spectra sN(λ) of the species, adding up to a large number of unknown variables (order of magnitude 1000). For such problems, the MCMC sampling method for target analysis can be applied to extract time constants and species spectra and also delivers measures to evaluate the quality of the chosen kinetic model and the uncertainty of the determined parameters in the form of posterior probability distributions.27
We applied this method to analyse the intensity-dependent data in the time range of 2–1000 ps to focus on contributions from Auger recombination-connected population dynamics and exclude contributions from hot carrier thermalization on the sub-ps timescale contributing with constantly changing spectra of non-thermalized states, and contributions from hole localization and trapping.18,26,27 The simple quantized Auger recombination model was unable to describe either the entire dataset at once or datasets for individually chosen intensities satisfactorily, even if ever increasing numbers of components are added to the consecutive cascade Auger recombination scheme (see the kinetic modelling section in the ESI†). This could be related to our qualitative observation of deviations in the decay kinetics and spectra at late delay times depending on excitation fluence, indicating contributions of more than one long-lived species populated depending on the excitation intensity (Fig. S4†). To allow for such a scenario, we modified the standard quantized Auger recombination model by introducing two distinct biexciton decay pathways: one via a monoexciton species (X) with the initial concentration given by the Poisson distribution, i.e. which is accessible by direct optical excitation, and an additional species (XS) formed with no initial concentration but accessible from higher-order multiexcitons within the Auger recombination decay process.
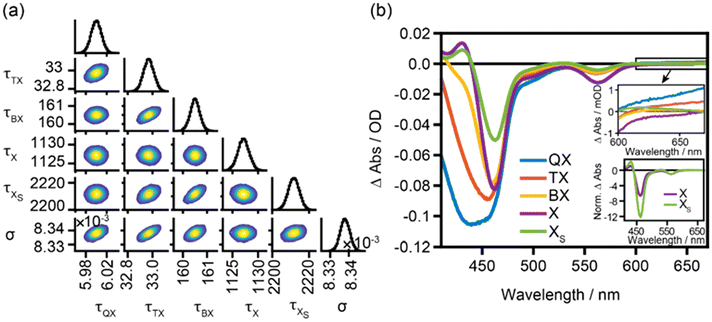
The simplest final kinetic model, which could describe our dataset, is depicted in Scheme 1. It includes five species, i.e., tetra-, tri-, bi- and two monoexciton states X and XS. The fitting results are presented in Fig. 2; for kinetic fits and concentration profiles, see Fig. S5 and S6.† The values of the fitted parameters are summarized in Table 1. The splitting parameter ϕ describing the weight of the two monoexcitons was found to tend to zero, showing that higher-order excitons decay to form only XS. Hence, X is only formed directly via initial excitation of the monoexciton state with a concentration given by the Poisson distribution and all multiexcitons decay via XS. The diagonal plots in the corner plot of the posterior probability distributions (Fig. 2a) display the distribution of the determined lifetimes of the five species and the absorption cross-section parameter. The off-diagonal plots show the two-dimensional projections of the posterior probability distribution sampled by the MCMC method. The round shape of the contour diagrams indicates the absence of severe cross-correlations between parameter pairs, indicating that all the parameters are adequately independent of each other and no redundant parameter is used in the kinetic model. The biexciton lifetime obtained from the fit of 161 ps is consistent with reports for Cd-based nanorods.16,35,45 The ratio of the lifetimes of multiexcitons QX![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TX
TX![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BX is 0.04
BX is 0.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20
0.20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is very close to the statistical ratio 0.08
1, which is very close to the statistical ratio 0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.22
0.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 predicted for 1D nanorods.15,44 The absorption cross-section parameter (σ) found by our model is 8.338 × 10–3 cm2 μJ−1 and corresponds to an absorption cross-section area of 4.14 × 10–15 cm2, in good agreement with the estimated value of 8.9 × 10–15 cm2 at 400 nm for similar-sized CdSe@CdS nanorods.37 The lifetimes of the long-lived monoexciton species X and XS are longer than the timeframe modelled. Hence, the values determined are only estimates with high inaccuracy; nevertheless their spectra can be determined reliably.
1 predicted for 1D nanorods.15,44 The absorption cross-section parameter (σ) found by our model is 8.338 × 10–3 cm2 μJ−1 and corresponds to an absorption cross-section area of 4.14 × 10–15 cm2, in good agreement with the estimated value of 8.9 × 10–15 cm2 at 400 nm for similar-sized CdSe@CdS nanorods.37 The lifetimes of the long-lived monoexciton species X and XS are longer than the timeframe modelled. Hence, the values determined are only estimates with high inaccuracy; nevertheless their spectra can be determined reliably.
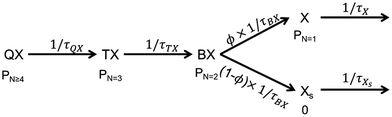 | ||
Scheme 1 Modified quantized Auger recombination model applied in the target analysis of the intensity-dependent TA data in this study: QX, TX, BX, X, and XS stand for tetra-, tri-, bi- and monoexcitons, respectively. PN represents the initial relative concentration of the respective species given by the Poisson distribution as presented in ESI Tables S1–3.† The initial QX population sums over the probability of four or more excitation per nanorod 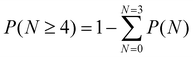 . Such higher excitation will only have small contributions due to decay on the sub 1 ps timescale, and QX is the highest-order exciton expected to contribute significantly to our dataset. The splitting parameter ϕ describes the weight of both processes in the multiexciton decay channel. . Such higher excitation will only have small contributions due to decay on the sub 1 ps timescale, and QX is the highest-order exciton expected to contribute significantly to our dataset. The splitting parameter ϕ describes the weight of both processes in the multiexciton decay channel. | ||
| Parameter name | TOPO-capped CdSe@CdS | MUA-capped CdSe@CdS | TOPO-capped CdS nanorods |
|---|---|---|---|
| a Errors given are the modelling uncertainties, but due to the limited delay time window considered, these values are affected by a large experimental additional inaccuracy. | |||
| τ tetraexciton/ps | 6.006.025.98 | 7.307.317.28 | 7.057.077.04 |
| τ triexciton/ps | 32.9733.0532.89 | 37.6337.6737.59 | 30.0630.1030.02 |
| τ biexciton/ps | 160.5160.9160.1 | 171.7171.8171.5 | 118.1118.3117.9 |
τ
monoexciton/ps![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
112711291125 | 152915311528 | 112611281125 |
τ
surface exciton/ps![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
221122182206 | 224422462241 | 299630072985 |
| Absorption cross-section (σ)/cm2 μJ−1 |
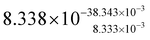
|
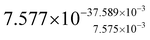
|
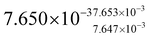
|
The modelled component spectra are depicted in Fig. 2b. It has to be noted that the tetra-exciton spectrum (Fig. 2b, blue trace) contains contributions from QX and higher-order excitons, since the initial concentration is modelled to contain contributions of excitons of the order four and higher 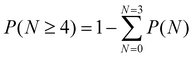 (Scheme 1), and should only be considered with care and will not be discussed in detail. Earlier studies on CdSe nanocrystals have been terminated at triexciton species already. This is due to the shorter higher-order exciton lifetimes of spherical-shaped particles and due to lower maximum pump intensities used compared to our study on rod-shaped heterostructures presented here.28
(Scheme 1), and should only be considered with care and will not be discussed in detail. Earlier studies on CdSe nanocrystals have been terminated at triexciton species already. This is due to the shorter higher-order exciton lifetimes of spherical-shaped particles and due to lower maximum pump intensities used compared to our study on rod-shaped heterostructures presented here.28
On comparing first the spectra of the two long-lived monoexcitonic species, it is noted that the ratio of the CdS and CdSe bleach features differs significantly. The XS species, dominating long delay time decay at high pump intensities, shows stronger relative CdS bleach contributions compared to X (Fig. 2b inset), which could be an indication of different localizations of these two states, with XS being strongly localized in the CdS domain compared to X. Furthermore, a broad PA band is present in the sub-bandgap region above 600 nm in the species spectrum of XS, which is usually assigned to signals from trapped holes or surface-related trap states in general.46–48 This feature is absent for the monoexcitonic state X, which dominates the long-time decay in the range of low pump fluences. This leads us to assign species X to the emitting CdSe seed-localized exciton formed in the seeded nanorods after the excitation of states mainly localized in the CdS rod part with 400 nm centered pulses followed by fast hole localization-driven exciton localization (on a few ps timescales) efficiently competing with hole trapping at the surface in these types of nanorods.33,49 XS on the other hand shows spectral characteristics which relate it to a surface-related trapped state, hence strongly localized in the CdS domain. The CdSe-localized exciton X leads due to the quasi type-II band-alignment to bleach signatures in both the CdS and CdSe domains; the negative contribution in the CdSe bleach region is further increased by stimulated emission, while a surface localized exciton is expected to show stronger impact on the signal in the CdS domain and additional trap state signatures. This is in agreement with the lower CdS/CdSe bleach ratio and dominates the negative bleach signal in the whole spectral range for X compared to the XS spectrum. For XS, the decreased overall bleach intensity compared to the X state and the increased ratio of CdS and CdSe bleach intensities, together with a broad PA sub-band gap PA signature, may indicate an increased localization in the CdS domain and involvements of trapped charge carriers. The potential nature of this species will be discussed below in detail.
On comparing the obtained component spectra of the long-lived monoexcitonic species X and XS with the spectrum of the biexciton BX, it is found that the PA at 432 nm caused by the biexciton effect shifting the position of the excitonic transition disappears in BX due to complete filling of the band edge level leaving the system nearly transparent to the probe pulse at the respective wavelength. Interestingly, in the species spectra of X and BX, almost no change in CdS band-edge bleach is observed and additionally X shows an even stronger bleach signal compared to BX in the region of the CdSe-localized excitonic transition. Recently, for CdSe nanocrystals, BX![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X bleach ratios smaller than 2
X bleach ratios smaller than 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 have been reported; however, an almost similar band edge bleach to that observed in our case for the CdS transition for the X and BX states has not been reported before. Only for CsPbBr3 perovskites, similar band edge bleach contributions to biexciton and monoexciton spectra have been observed and are explained by a pronounced shift of the band-edge transition through biexciton repulsion, resulting in spectral differences only in the PA region.50 For II–IV nanocrystals, such strong exciton–exciton repulsion seems an unlikely explanation. An alternative explanation, which could also explain the behaviour of the bleach intensity of the CdSe excitonic transition, relates again to the localization of these states within the different domains of the nanostructure. Under the assumption that the BX state already contains contributions of charge carriers trapped in surface states inducing the localization of BX at the surface of the CdS rod-shaped shell domain, the missing increase of the CdS band-edge transition and the decreased CdSe excitonic bleach compared to X seem reasonable. Under this assumption, the comparison of the BX spectrum with the XS spectrum is better justified, and indeed for these nanorods, we find that the expected trend for the CdS band-edge bleach is more intense for BX than for XS. A close relationship between BX and XS both involving trapped charge carriers also seems feasible from the fit results, showing that BX solely relaxes forming the XS monoexcitonic state but not the monoexcitonic X state excited in the low excitation intensity regime.
1 have been reported; however, an almost similar band edge bleach to that observed in our case for the CdS transition for the X and BX states has not been reported before. Only for CsPbBr3 perovskites, similar band edge bleach contributions to biexciton and monoexciton spectra have been observed and are explained by a pronounced shift of the band-edge transition through biexciton repulsion, resulting in spectral differences only in the PA region.50 For II–IV nanocrystals, such strong exciton–exciton repulsion seems an unlikely explanation. An alternative explanation, which could also explain the behaviour of the bleach intensity of the CdSe excitonic transition, relates again to the localization of these states within the different domains of the nanostructure. Under the assumption that the BX state already contains contributions of charge carriers trapped in surface states inducing the localization of BX at the surface of the CdS rod-shaped shell domain, the missing increase of the CdS band-edge transition and the decreased CdSe excitonic bleach compared to X seem reasonable. Under this assumption, the comparison of the BX spectrum with the XS spectrum is better justified, and indeed for these nanorods, we find that the expected trend for the CdS band-edge bleach is more intense for BX than for XS. A close relationship between BX and XS both involving trapped charge carriers also seems feasible from the fit results, showing that BX solely relaxes forming the XS monoexcitonic state but not the monoexcitonic X state excited in the low excitation intensity regime.
Finally, the spectra of higher-order multiexcitons, i.e. TX (and QX), show increasing CdS bleach and broadening of the bleach features for higher-order multiexcitons, which agrees well with the discussion above and is due to the filling up of higher conduction band level states, resulting in bleach of the respective higher excitonic transitions as well. Furthermore, the higher-order multiexciton formation does not significantly change the bleach of the excitonic transition of the CdSe domain. This can be regarded as an indication that already these states are strongly localized in the CdS domain induced by the population of surface trap sites.
To summarize the results so far, trapping-induced localization and formation of higher-order excitonic states could explain the extracted spectral signatures and the presence of two long-lived monoexciton species, one dominating in the low pump intensity regime, while the other appears via the decay of multiexcitonic states. This indicates that trapping involves trap states which can only be accessed from higher-order multiexcitonic states with a large amount of excess energy. In principle, an increasing population of trapping sites caused by temperature increase under the high intensity excitation of the sample could be a possibility, but in the case of a significant local increase in temperature, additionally a red-shift in the band edge transition caused by narrowing of the band gap is expected.47,51 No such shifts in the lowest excitonic transitions are observed and significant temperature-induced effects can be disregarded. The nature of the traps, which means where the traps are located in the nanostructures and which charge carriers, electrons or holes are trapped, still needs to be determined. For the nature of the traps involved, in general, two possibilities have to be considered: trapping at the CdSe/CdS interface or on surface sites. Though the discussion above provides an indication that more likely surface trap states are involved, we performed additional experiments to collect further proof.
(I) Trapping in states at the CdSe/CdS interface: the first possibility is a potential trapping in states at the CdSe/CdS interface, which may only be accessible from states with a large amount of excess energy, i.e., from high-lying excitonic states or multiexcitonic states. Such states could result from lattice mismatch and can influence the transient absorption dynamics as observed, e.g., for CdTe/CdS interfaces.52,53 However, lattice mismatch is considered small (∼4%) between CdS and CdSe domains. Another source of trapping sites at the interface is fast anisotropic growth which is reported to induce stacking faults.54–56
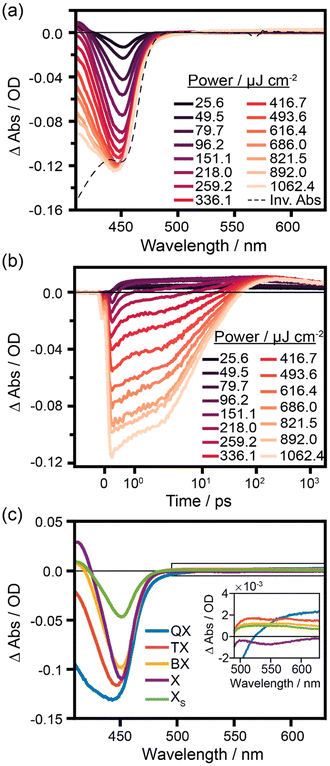
To test the effects connected to the CdSe/CdS interface, we additionally investigated the multiexciton spectral signatures and dynamics of the CdS nanorods without the CdSe seed (length 18.7 ± 4.7 nm, width 3.6 ± 0.7 nm). The TA spectra at 2 ps delay time (Fig. 3a) show a negative feature at 453 nm, which can be attributed to the bleach of the lowest excitonic transition, which is in agreement with the absorption spectrum about 10 nm blue-shifted compared to the CdSe@CdS nanorods caused by a stronger confinement effect in the CdS nanorods which possess a smaller diameter as the seeded rods in our study. At low pump intensities, a positive PA band is present at 413 nm, which disappears with increasing pump pulse intensity, similar to the observations in the seeded nanorods.41 In the pump fluence-dependent kinetic traces for CdS nanorods at a probe wavelength of 413 nm (Fig. 3b), similar to the seeded system, at high pump fluences when multiexciton formation is to be expected, the initial signal after excitation is negative and decays to form a positive signal of the monoexciton on a few 100 ps timescale. The same kinetic model as for the CdSe@CdS nanorods was necessary to explain the experimental data using the MCMC target analysis (Fig. S7–S9†). The lifetimes of higher-order excitons (QX and TX) are similar compared to the lifetimes determined for CdSe@CdS nanorods, while the biexciton lifetime in the non-seeded nanorods is reduced to 118 ps (Table 1), which is reasonably close to the literature-reported biexciton lifetime of 180 ps for slightly longer CdS nanorods.16 The PA feature at 413 nm is only present in the monoexcitonic species spectrum and disappears for the multiexcitons similar to CdSe@CdS nanorods. Also, for the CdS nanorods, a second long-lived species, XS, is present, which shows similar spectral distinction compared to X, i.e., the band-edge bleach of XS is lower than that of X. Higher-order excitons and XS show a positive PA sub-bandgap feature in line with our observation for CdSe@CdS seeded nanorods. From this, we can conclude that the appearance of XS is most probably not related to the presence of the CdSe/CdS interface, which is absent in the pure CdS nanorods.
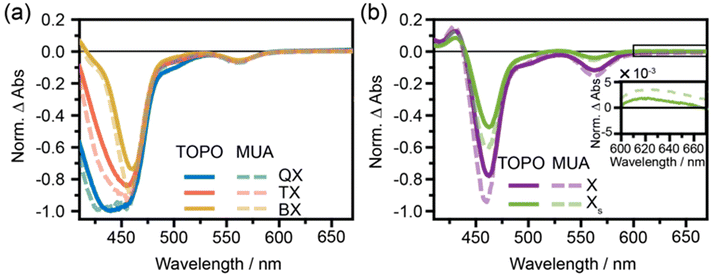
(II) Trapping and formation of surface exciton states: trapping sites that only can be populated from multiexcitons and hot monoexcitons appearing during the cascade-like multiexciton annihilation process have already been reported.13,24 For example, for polyethyleneimine-coated CdS nanocrystals, fast barrierless trapping of hot excitons formed from higher-order multiexciton states resulting in increasing cooling rates with increasing pump intensity, has been reported.57 Though dissipation of excess energy is fast, trap states that are not accessible from the lowest band edge monoexcitonic states can be populated efficiently via this route. Similar observations have been made for CdSe and CdTe nanocrystals.58,59 The presence of an activation energy barrier for trapping has been shown for cadmium-based nanocrystals using temperature-dependent time-resolved photoluminescence measurements60 and state-resolved transient absorption spectroscopy.61 Furthermore, the decrease of the PL quantum yields of Cd-based nanocrystals with increasing pump intensity and energy also hints towards the accelerated charge trapping process from higher energetic states in these systems.62,63 In these studies, contributions from both hole and electron trapping are discussed, which are not easy to discriminate from each other and the nature of the involved trap states is often not defined beyond any doubt. For our data, the comparison of the spectral shape of the two monoexcitonic species in our data, see the discussion above, supports the claim of surface excitonic species XS. The different relative bleach contributions of CdSe and CdS domains in the spectra of these monoexciton species are in agreement with an XS being related to a surface state showing stronger relative CdS bleach contributions due to localization in the CdS domain at the surface of the nanorods. One alternative explanation could relate XS to the formation of charged monoexcitons (trions).64,65 However, the reported lifetimes of charged trions in these types of nanorods are ≪1 ns.64 The lifetimes of X and XS species observed in our experiment are (though the values determined are of limited accuracy due to the limited time window of delay times evaluated) significantly longer. To collect further data for the nature of the trap, the influence of surface chemistry was studied. Therefore, the original surface ligands were exchanged with MUA ligands to modify the densities of the available hole trap states.33 Ligand exchange with MUA was performed according to literature reports and the nanorods were redispersed in methanol (see Fig. S1–S3† for the details on sample characterization).31,33,66 The MUA-capped CdSe@CdS nanorods show similar spectral features and dynamic behaviour to those observed for TOPO-capped nanorods. By applying the kinetic model described above, the lifetimes and species spectra extracted differ only marginally (Table 1 and Fig. S10–S12†). To directly compare the influence of ligand exchange on the spectra of each excitonic species, we normalized the modelled species spectra of TOPO- and MUA-capped nanorods to their maximum bleach, i.e., to the respective tetra-exciton bleach (Fig. 4). XS in MUA-capped nanorods shows increased sub-band edge PA after ligand exchange, which might indicate increased hole-trapping contributions. Furthermore, though the TA bleach signal in II–VI materials is widely thought be independent of hole contributions, new reports suggest a ∼30–33% hole contribution, which is suppressed in the presence of hole traps that can be populated, and the removal of hole traps by surface passivation or shell formation can influence the hole signal contribution.67–69 So, the decreased XS bleach signal compared to X could be caused by the hole trapping process. On the other hand, the decreased bleach of the CdS band edge transition in XS compared to X could also be explained by the electron trap nature of XS, leading to depopulation of the conduction band edge states. This might also explain the low sensitivity of the observed dynamics to the exchange with a strong hole trapping ligand. Hence there are arguments for both electron and hole trap states, and similar to earlier studies, here too the nature of the trapping site cannot be determined beyond any doubt at the current state of research.
A final aspect to consider is the possibility that the surface trap states can also appear during the measurement by illumination-induced changes in the surface chemistry, e.g., by ligand dissociation70,71 or lattice distortions,72 and hence influence the formation of surface localized excitons by reversible and non-reversible effects. A comparison with the datasets of the pre-illuminated TOPO-capped nanorods shows qualitatively and quantitatively similar behaviour with increasing pump pulse intensity compared to the non-illuminated samples (Fig. S13–S23 and Table S4†). This indicates that either illumination-induced changes are not playing a role or are appearing very fast during the first few scans during the measurements.
Conclusions
To summarize, in this work the spectral and dynamical properties of multiexcitons in CdSe@CdS seeded nanorods were investigated. Evaluating the excitation intensity-dependent TA data by applying an MCMC sampling method for target analysis enables us to extract species spectra up to triexcitons. Furthermore, we show that the holistic view of the entire intensity-dependent TA data can help us to detect the decay pathways via surface excitons, which are hard to discriminate while analysing single wavelength kinetics or single power TA data. Thus, the analysis established in this work delivers an important contribution to distinguishing and entangling the decay dynamics of multiexcitons and surface excitons and understanding the details of dynamics observed in the multiexciton regime.Author contributions
The manuscript was written through the contributions of both authors. KK: conceptualization, methodology, data analysis, and writing – original draft. MW: conceptualization, resources, investigation, supervision, funding acquisition, and writing – original draft. Both authors have given approval to the final version of the manuscript.Data availability
The data supporting this article are included in the article itself or as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the German Research Foundation (DFG) for supporting this work under project number 364549901 – TRR234 CATALIGHT, TP B04 and project number 468735112 – KU 4220/1-1. We thank Jan Dellith and Andrea Dellith for acquiring TEM images. We gratefully acknowledge discussions with Mathias Micheel and Raktim Baruah. KK is thankful to Tara Chand for fruitful discussions on the modelling routine.References
- D. V. Talapin, J. S. Lee, M. V. Kovalenko and E. V. Shevchenko, Chem. Rev., 2010, 110, 389–458 CrossRef CAS PubMed.
- F. P. García de Arquer, D. V. Talapin, V. I. Klimov, Y. Arakawa, M. Bayer and E. H. Sargent, Science, 2021, 373, eaaz8541 CrossRef PubMed.
- A. M. Smith and S. Nie, Acc. Chem. Res., 2010, 43, 190–200 CrossRef CAS PubMed.
- J. Zhou, Y. Liu, J. Tang and W. Tang, Mater. Today, 2017, 20, 360–376 CrossRef CAS.
- S. Silvi and A. Credi, Chem. Soc. Rev., 2015, 44, 4275–4289 RSC.
- Y. E. Panfil, M. Oded and U. Banin, Angew. Chem., Int. Ed., 2018, 57, 4274–4295 CrossRef CAS PubMed.
- Y.-S. Park, J. Roh, B. T. Diroll, R. D. Schaller and V. I. Klimov, Nat. Rev. Mater., 2021, 6, 382–401 CrossRef CAS.
- C. R. Kagan, L. C. Bassett, C. B. Murray and S. M. Thompson, Chem. Rev., 2021, 121, 3186–3233 CrossRef CAS PubMed.
- A. R. Kirmani, J. M. Luther, M. Abolhasani and A. Amassian, ACS Energy Lett., 2020, 5, 3069–3100 CrossRef CAS.
- K. Wu and T. Lian, Chem. Soc. Rev., 2016, 45, 3781–3810 RSC.
- M. C. Beard, J. Phys. Chem. Lett., 2011, 2, 1282–1288 CrossRef CAS PubMed.
- V. I. Klimov, J. Phys. Chem. B, 2006, 110, 16827–16845 CrossRef CAS PubMed.
- N. Ahn, C. Livache, V. Pinchetti and V. I. Klimov, Chem. Rev., 2023, 123, 8251–8296 CrossRef CAS PubMed.
- M. C. Beard, J. M. Luther, O. E. Semonin and A. J. Nozik, Acc. Chem. Res., 2013, 46, 1252–1260 CrossRef CAS PubMed.
- H. Zhu, Y. Yang and T. Lian, Acc. Chem. Res., 2013, 46, 1270–1279 CrossRef CAS PubMed.
- Y. Ben-Shahar, J. P. Philbin, F. Scotognella, L. Ganzer, G. Cerullo, E. Rabani and U. Banin, Nano Lett., 2018, 18, 5211–5216 CrossRef CAS PubMed.
- C. Melnychuk and P. Guyot-Sionnest, Chem. Rev., 2021, 121, 2325–2372 CrossRef CAS PubMed.
- V. I. Klimov, A. A. Mikhailovsky, D. W. McBranch, C. A. Leatherdale and M. G. Bawendi, Science, 2000, 287, 1011–1013 CrossRef CAS PubMed.
- F. García-Santamaría, Y. Chen, J. Vela, R. D. Schaller, J. A. Hollingsworth and V. I. Klimov, Nano Lett., 2009, 9, 3482–3488 CrossRef PubMed.
- D. Kong, Y. Jia, Y. Ren, Z. Xie, K. Wu and T. Lian, J. Phys. Chem. C, 2018, 122, 14091–14098 CrossRef CAS.
- V. I. Klimov, Annu. Rev. Phys. Chem., 2007, 58, 635–673 CrossRef CAS PubMed.
- K. Kumar and M. Wächtler, Nanomaterials, 2023, 13, 1579 CrossRef CAS PubMed.
- D. P. Strandell, A. Ghosh, D. Zenatti, P. Nagpal and P. Kambhampati, J. Phys. Chem. Lett., 2023, 14, 6904–6911 CrossRef CAS PubMed.
- P. Tyagi and P. Kambhampati, J. Chem. Phys., 2011, 134, 094706 CrossRef PubMed.
- A. V. Malko, A. A. Mikhailovsky, M. A. Petruska, J. A. Hollingsworth and V. I. Klimov, J. Phys. Chem. B, 2004, 108, 5250–5255 CrossRef CAS.
- T. Labrador and G. Dukovic, J. Phys. Chem. C, 2020, 124, 8439–8447 CrossRef CAS.
- M. N. Ashner, S. W. Winslow, J. W. Swan and W. A. Tisdale, J. Phys. Chem. A, 2019, 123, 3893–3902 CrossRef CAS PubMed.
- K. E. Shulenberger, S. J. Sherman, M. R. Jilek, H. R. Keller, L. M. Pellows and G. Dukovic, J. Chem. Phys., 2024, 160, 014708014708 CrossRef PubMed.
- M. N. Ashner, K. E. Shulenberger, F. Krieg, E. R. Powers, M. V. Kovalenko, M. G. Bawendi and W. A. Tisdale, ACS Energy Lett., 2019, 4, 2639–2645 CrossRef CAS.
- L. Carbone, C. Nobile, M. De Giorgi, F. D. Sala, G. Morello, P. Pompa, M. Hytch, E. Snoeck, A. Fiore, I. R. Franchini, M. Nadasan, A. F. Silvestre, L. Chiodo, S. Kudera, R. Cingolani, R. Krahne and L. Manna, Nano Lett., 2007, 7, 2942–2950 CrossRef CAS PubMed.
- L. Amirav and A. P. Alivisatos, J. Phys. Chem. Lett., 2010, 1, 1051–1054 CrossRef CAS.
- W. W. Yu and X. Peng, Angew. Chem., Int. Ed., 2002, 41, 2368–2371 CrossRef CAS PubMed.
- M. Micheel, B. Liu and M. Wächtler, Catalysts, 2020, 10, 1143 CrossRef CAS.
- C. Müller, T. Pascher, A. Eriksson, P. Chabera and J. Uhlig, J. Phys. Chem. A, 2022, 126, 4087–4099 CrossRef PubMed.
- H. Htoon, J. A. Hollingsworth, R. Dickerson and V. I. Klimov, Phys. Rev. Lett., 2003, 91, 227401 CrossRef CAS PubMed.
- H. Htoon, J. A. Hollingworth, A. V. Malko, R. Dickerson and V. I. Klimov, Appl. Phys. Lett., 2003, 82, 4776–4778 CrossRef CAS.
- K. F. Wu, W. E. Rodriguez-Cordoba, Z. Liu, H. M. Zhu and T. Q. Lian, ACS Nano, 2013, 7, 7173–7185 CrossRef CAS PubMed.
- K. Kuroi, M. Yamada, I. Kawamura, M. Jung, C.-G. Pack and F. Fujii, Phys. Chem. Chem. Phys., 2022, 24, 13356–13364 RSC.
- A. Persano, M. De Giorgi, A. Fiore, R. Cingolani, L. Manna, A. Cola and R. Krahne, ACS Nano, 2010, 4, 1646–1652 CrossRef CAS PubMed.
- V. I. Klimov, J. Phys. Chem. B, 2000, 104, 6112–6123 CrossRef CAS.
- Y. Liu, D. A. Cullen and T. Lian, J. Am. Chem. Soc., 2021, 143, 20264–20273 CrossRef CAS PubMed.
- H. Zhu, N. Song, W. Rodríguez-Córdoba and T. Lian, J. Am. Chem. Soc., 2012, 134, 4250–4257 CrossRef CAS PubMed.
- S. Taguchi, M. Saruyama, T. Teranishi and Y. Kanemitsu, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 155324 CrossRef.
- V. I. Klimov, J. A. McGuire, R. D. Schaller and V. I. Rupasov, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 195324 CrossRef.
- H. Zhu and T. Lian, J. Am. Chem. Soc., 2012, 134, 11289–11297 CrossRef CAS PubMed.
- A. N. Grennell, J. K. Utterback, O. M. Pearce, M. B. Wilker and G. Dukovic, Nano Lett., 2017, 17, 3764–3774 CrossRef CAS PubMed.
- J. K. Utterback, J. L. Ruzicka, H. Hamby, J. D. Eaves and G. Dukovic, J. Phys. Chem. Lett., 2019, 10, 2782–2787 CrossRef CAS PubMed.
- D. Jasrasaria, J. P. Philbin, C. Yan, D. Weinberg, A. P. Alivisatos and E. Rabani, J. Phys. Chem. C, 2020, 124, 17372–17378 CrossRef CAS.
- K. Wu, L. J. Hill, J. Chen, J. R. McBride, N. G. Pavlopolous, N. E. Richey, J. Pyun and T. Lian, ACS Nano, 2015, 9, 4591–4599 CrossRef CAS PubMed.
- J. Dana, T. Binyamin, L. Etgar and S. Ruhman, ACS Nano, 2021, 15, 9039–9047 CrossRef CAS PubMed.
- G. Rainò, T. Stöferle, I. Moreels, R. Gomes, J. S. Kamal, Z. Hens and R. F. Mahrt, ACS Nano, 2011, 5, 4031–4036 CrossRef PubMed.
- F. Enders, A. Budweg, P. Zeng, J. Lauth, T. A. Smith, D. Brida and K. Boldt, Nanoscale, 2018, 10, 22362–22373 RSC.
- R. Bozio, M. Righetto and A. Minotto, Effects of surface and interface traps on exciton and multi-exciton dynamics in core/shell quantum dots, SPIE, 2017 Search PubMed.
- J. Llusar, J. Planelles and J. I. Climente, J. Phys. Chem. C, 2019, 123, 21299–21306 CrossRef CAS.
- A. Demortière, D. N. Leonard, V. Petkov, K. Chapman, S. Chattopadhyay, C. She, D. A. Cullen, T. Shibata, M. Pelton and E. V. Shevchenko, J. Phys. Chem. Lett., 2018, 9, 1900–1906 CrossRef PubMed.
- E. M. Thomas, N. Pradhan and K. G. Thomas, ACS Energy Lett., 2022, 7, 2856–2863 CrossRef CAS.
- S. Das, S. Rakshit and A. Datta, J. Phys. Chem. C, 2020, 124, 28313–28322 CrossRef CAS.
- J. I. Saari, E. A. Dias, D. Reifsnyder, M. M. Krause, B. R. Walsh, C. B. Murray and P. Kambhampati, J. Phys. Chem. B, 2013, 117, 4412–4421 CrossRef CAS PubMed.
- N. Lenngren, M. A. Abdellah, K. Zheng, M. J. Al-Marri, D. Zigmantas, K. Žídek and T. Pullerits, Phys. Chem. Chem. Phys., 2016, 18, 26199–26204 RSC.
- M. Jones, S. S. Lo and G. D. Scholes, J. Phys. Chem. C, 2009, 113, 18632–18642 CrossRef CAS.
- S. L. Sewall, R. R. Cooney, K. E. H. Anderson, E. A. Dias, D. M. Sagar and P. Kambhampati, J. Chem. Phys., 2008, 129, 084701 CrossRef PubMed.
- S. Ghosh, U. Ross, A. M. Chizhik, Y. Kuo, B. G. Jeong, W. K. Bae, K. Park, J. Li, D. Oron, S. Weiss, J. Enderlein and A. I. Chizhik, J. Phys. Chem. Lett., 2023, 14, 2702–2707 CrossRef CAS PubMed.
- D. Roy, A. Das, C. K. De, S. Mandal, P. R. Bangal and P. K. Mandal, J. Phys. Chem. C, 2019, 123, 6922–6933 CrossRef CAS.
- J. Wang, T. Ding and K. Wu, J. Am. Chem. Soc., 2020, 142, 13934–13940 CrossRef CAS PubMed.
- Y.-S. Park, W. K. Bae, J. M. Pietryga and V. I. Klimov, ACS Nano, 2014, 8, 7288–7296 CrossRef CAS PubMed.
- D. V. Talapin, J. H. Nelson, E. V. Shevchenko, S. Aloni, B. Sadtler and A. P. Alivisatos, Nano Lett., 2007, 7, 2951–2959 CrossRef CAS PubMed.
- G. Grimaldi, J. J. Geuchies, W. van der Stam, I. du Fossé, B. Brynjarsson, N. Kirkwood, S. Kinge, L. D. A. Siebbeles and A. J. Houtepen, Nano Lett., 2019, 19, 3002–3010 CrossRef CAS PubMed.
- M. M. Taheri, K. C. Elbert, S. Yang, B. T. Diroll, J. Park, C. B. Murray and J. B. Baxter, J. Phys. Chem. C, 2021, 125, 31–41 CrossRef CAS.
- Z. Huang, S. Wang, Y. Ren and Y. Wang, ACS Photonics, 2023, 10, 639–646 CrossRef CAS.
- K. E. Shulenberger, H. R. Keller, L. M. Pellows, N. L. Brown and G. Dukovic, J. Phys. Chem. C, 2021, 125, 22650–22659 CrossRef CAS.
- S. M. Harvey, J. H. Olshansky, A. Li, S. Panuganti, M. G. Kanatzidis, J. T. Hupp, M. R. Wasielewski and R. D. Schaller, J. Am. Chem. Soc., 2024, 146, 3732–3741 CrossRef CAS PubMed.
- B. Guzelturk, B. L. Cotts, D. Jasrasaria, J. P. Philbin, D. A. Hanifi, B. A. Koscher, A. D. Balan, E. Curling, M. Zajac, S. Park, N. Yazdani, C. Nyby, V. Kamysbayev, S. Fischer, Z. Nett, X. Shen, M. E. Kozina, M.-F. Lin, A. H. Reid, S. P. Weathersby, R. D. Schaller, V. Wood, X. Wang, J. A. Dionne, D. V. Talapin, A. P. Alivisatos, A. Salleo, E. Rabani and A. M. Lindenberg, Nat. Commun., 2021, 12, 1860 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details on nanoparticle synthesis and characterization, experimental details on transient absorption spectroscopy and data evaluation, TEM images, MCMC fits and concentration profiles. See DOI: https://doi.org/10.1039/d4nr04692g |
| ‡ Current address: Institut für Physik, Carl von Ossietzky Universität Oldenburg, 26129 Oldenburg, Germany. |
| § Current address: Institute of Physical Chemistry and Kiel Nano, Surface and Interface Science (KiNSIS), Kiel University, Max-Eyth-Straße 1, 24118, Kiel, Germany. |
| This journal is © The Royal Society of Chemistry 2025 |