Pentagonal-bipyramidal dysprosium(III) complexes with two apical phosphine oxide ligands and equatorial pentadentate N₃O₂ Schiff-base ligands: breakdown of the apical magnetic axiality by a strong equatorial crystal field

Abstract

A series of three new seven-coordinate pentagonal-bipyramidal (PBPY-7) Dy(III) complexes, [Dy(L^CH₃)(Cy₃PO)₂]ClO₄·CH₃CN (1), [Dy(L^2(t-Bu))(Ph₃PO)₂]ClO₄·0.63C₂H₅OH (2), and [Dy(L^OCH₃)(Ph₃PO)₂]ClO₄·2H₂O (3), including various chelating pentadentate ligands with [N₃O₂]²⁻ binding node in the equatorial plane, L^CH₃ = [2,6-diacetylpyridine bis(acetylhydrazone)]²⁻, L^2(t-Bu) = [2,6-diacetylpyridine bis(3,5di-tert-butylbenzoylhydrazone)]²⁻, and L^CH₃ = [2,6-diacetylpyridine bis(4-methoxybenzoylhydrazone)]²⁻, and two apical ligands Cy₃PO and Ph₃PO were synthesized and characterized structurally and magnetically. The ac magnetic measurements indicated the single-molecule-magnet (SMM) behavior of 1–3 with energy barriers of U_eff ≈ 318–350 K. Ab initio calculations and crystal-field (CF) analysis showed that the ground states of 1–3 were a nearly pure Ising type Kramers doublet (KD₀) |±15/2〉_eq with the long magnetic axis lying in the equatorial plane of N₃O₂, which was the opposite of high-performance PBPY-7 Dy(III) SMMs (U_eff > 1000 K), where the long magnetic axis of KD₀ |±15/2〉 invariably pointed toward apical ligands. This difference is due to competition between the apical and equatorial CFs, which have been quantitatively examined with CF calculations. We show that the turning of the long magnetic axis (g_z ∼ 19.6) from apical ligands (z) to the equatorial plane (xy) is due to crossover between the oblate |±15/2〉 and prolate |±1/2〉 ground states of the Dy(III) ion, which occurs at the negative ratio of B₂₀/B₄₀ < −0.07 of the two axial CF parameters B₂₀ and B₄₀. Complexes 1–3 correspond to this case due to the strong equatorial CF of the negatively charged chelate node of [N₃O₂]²⁻ producing a large positive CF parameter B₄₀ and negative B₂₀. In this case, the SMM properties of 1–3 arise from distortions of the PBPY-7 complex (namely, from a large O1–Dy–O2 bond angle of ∼100° in the N₃O₂ pentagon of 1–3) that mix the lowest |±1/2〉 state and low-lying low-m_J states to produce the equatorial KD₀ |±15/2〉_eq. This highlights a breakdown of the apical magnetic axiality, since the SMM performances of 1–3 are governed by a strong equatorial CF and distortions rather than by high D_5h symmetry and strong apical ligands. Some ways to improve the SMM efficiency of 1–3 and related PBPY-7 Dy(III) complexes are discussed.

---

1. Introduction

Mononuclear lanthanide complexes have been extensively explored as high-performance single-molecule magnets (SMMs) in the past few decades,^1–10 since the discovery of slow magnetic relaxation with a high spin-reversal barrier in double decker lanthanide complexes [LnPc₂]⁻ (Ln³⁺ = Tb, Dy, and Ho; Pc = phthalocyanine derivatives) in 2003.¹ Because of the unique electronic structure of lanthanide ions with an open 4f^N electronic shell possessing a large unquenched orbital moment and high magnetic anisotropy, Ln-SMMs have great prospects in emerging advanced technologies such as high-density data storage, quantum computing, and molecular spintronics.^11–16 Presently, myriads of lanthanide SMMs with a wide variety of structures and magnetic properties have been synthesized and characterized.^1–10 In this research field, major efforts have been focused on monometallic lanthanide-based SMMs (termed single-ion magnets, Ln-SIMs), with which incredible progress has been made to increase the effective spin-reversal barrier (U_eff) and blocking temperature (T_B), particularly in Dy(III) complexes, up to U_eff ∼ 1500 cm⁻¹ and T_B = 60–80 K.^17–19 In monometallic Ln-SIMs comprising single magnetic Ln³⁺ ions, the barrier U_eff is controlled solely by the crystal-field (CF) splitting of the ground (2J + 1) multiplet of the open 4f^N shell, without the engagement of spin coupling with other magnetic centers. The characteristic CF splitting pattern is specified by the type and symmetry of the coordination environment and by the nature of the lanthanide ion.⁷

In general, two conditions are essential to obtain the highest SMM performance of mononuclear Ln-based complexes, namely, maximal total CF splitting energy (ΔE_CF) of the ground J-multiplet and perfect axiality of the CF potential of 4f-electrons.^7,20–22 In terms of CF theory, this implies that the axial CF parameters B_k0 (k = 2, 4, 6) should be as large as possible with vanishing non-axial parameters B_kq = 0, |q| > 0. The axial CF suppresses the quantum tunneling of magnetization (QTM) and spin–phonon relaxation processes, and thus leads to higher U_eff and T_B values.⁷ These conditions are best met for an axially compressed coordination geometry of the Dy³⁺ ion having an oblate-shaped 4f-electron density.^5–10,23 In fact, there are only three groups of Dy(III) complexes with the highest U_eff barriers, the quasi-linear sandwich metallocene complexes^17–19,24 (and some low-coordinate complexes²⁵), the pentagonal-bipyramidal (PBPY-7) complexes with D_5h symmetry^26–29 and hexagonal-bipyramidal complexes.^30–32 Formally, despite the exceptionally high SMM performance of some hexagonal-bipyramidal Dy(III) complexes,^30–32 they do not ensure perfect axiality of the crystal field (even at the regular D_6h symmetry) due to the presence of the non-axial CF terms B_6±6, in contrast to linear (D_∞h) and PBPY-7 (D_5h) complexes providing perfect axiality of the CF potential. However, this interesting topic is beyond the scope of our paper, which focuses on PBPY-7 Dy(III) complexes.

The first group of complexes holds the current record for the barrier U_eff and blocking temperature T_B.^17–19 However, even if the maximum SMM performance of PBPY-7 Dy complexes is lower than that in record-holding bis-cyclopentadienyl compounds, they show more diverse structures and magnetic properties with the barrier U_eff up to 1469 cm⁻¹.^26–28 An advantage of the PBPY-7 lanthanide complexes is that they are much more readily available synthetically using a variety of monodentate or polydentate ligands in the apical and equatorial positions.²⁹ This enables efficient control and fine tuning of the apical and equatorial components of the CF potential. Particularly, adopting ligands with short Dy–O bonds in the apical positions (such as Cy₃PO, Ph₃PO, MeO⁻, Me₃SiO⁻) produces a strong apical CF, resulting in an exceptionally high CF splitting energy (ΔE_CF > 1000 cm⁻¹) and nearly pure Ising KDs with minimal mixing of ±m_J states.^26–29

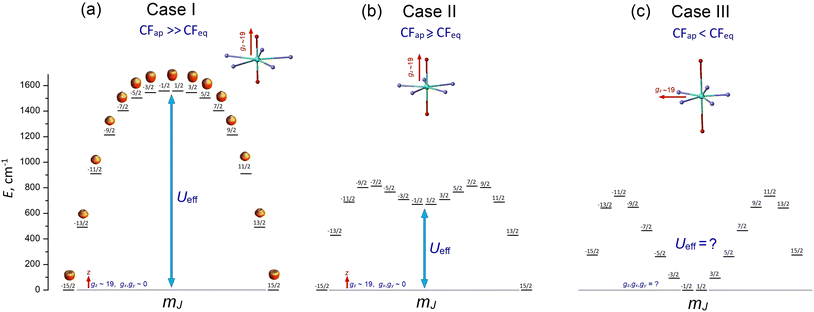
These remarkable properties have attracted great interest in lanthanide PBPY-7 complexes, which have become a popular research field. To date, numerous PBPY-7 Dy(III) complexes have been reported, including those with high energy barriers (U_eff > 1000 cm⁻¹) and blocking temperatures (T_B ∼ 10–20 K).²⁹ However, as noted by many researchers, the SMM performance of these complexes is highly sensitive to the ratio between the CF components originating from the apical and equatorial ligands.^26–29 The apical and equatorial CF components act in opposite ways for the oblate dysprosium ion. More specifically, the electron density distribution of Dy³⁺ has an oblate shape for the m_J = ±15/2 state, but as m_J decreases, the shape gradually transforms from oblate to prolate for the m_J = ±1/2 state.²³ As a result, apical ligands minimize the energy of the highest-m_J state of |±15/2〉 and maximize the energy of the lowest-m_J state of |±1/2〉, resulting in a parabolic profile of the E vs. m_J diagram with the |±15/2〉 ground state and |±1/2〉 top state (Fig. S1a, ESI†). This corresponds to the easy axis magnetic anisotropy of the PBPY-7 Dy complex. In contrast, the CF of equatorial ligands stabilizes the prolate m_J = ±1/2 state and maximizes the energy of the oblate m_J = ±15/2 state (Fig. S1b, ESI†); this corresponds to easy plane magnetic anisotropy. In line with this, competition between the apical (CF_ap) and equatorial (CF_eq) crystal field components leads to considerable changes in the pattern of the spin energy diagram and in the effective energy barrier, U_eff, as the equatorial CF increases due to shorter metal–ligand distances in the equatorial plane of the PBPY-7 complex. Accordingly, there are three cases of E vs. m_J diagrams, resulting in different magnetic behavior and SMM characteristics of the PBPY-7 Dy complexes.

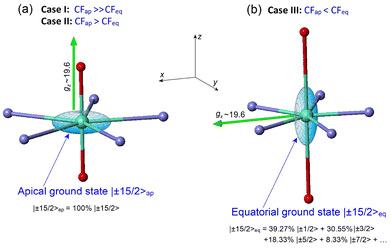
1.1 Case I: dominant apical CF (CF_ap ≫ CF_eq)

This case concerns a family of PBPY-7 complexes with short apical bonds (∼2.1 Å) and long equatorial bonds (>2.5 Å), where the apical crystal field, CF_ap, is much stronger than the equatorial crystal field, CF_eq, CF_ap ≫ CF_eq. The strongest apical field, CF_ap, is generated by negatively charged apical ligands with a short Dy–O bond (2.05–2.15 Å), such as BuO⁻, PhO⁻, Me₃SiO⁻ and MeO⁻, while a weak equatorial CF is formed by five neutral pyridine molecules with long Dy–N distances in the equatorial plane, 2.5–2.6 Å. These complexes exhibit the highest barrier (U_eff > 1000 K) and blocking temperature, [Dy(^t-BuO)₂(py)₅]BPh₄ (U_eff = 1815 K, T_B = 14 K),²⁶ [Dy(Me₃SiO)₂(py)₅]BPh₄ (U_eff = 1596 K, T_B = 15 K),³³ [Dy(CH₃CH(C₆F₅)O)₂(THF)₅]BPh₄·2THF (U_eff = 2113 K, T_B = 22 K),²⁷ and [Dy(PhO)₂(py)₅]BPh₄ (U_eff = 1302 K, T_B = 13 K).³³ The E vs. m_J diagram has a parabolic profile with the lowest |±15/2〉 and top |±1/2〉 states (Fig. 1a). The ground-state Kramers doublet KD₀ |±15/2〉 has nearly perfect axiality, as quantified by the Ising g-tensor with g_z ∼ 19.8 and vanishingly small transverse components, g_x, g_y (<10⁻²).^26,28,33 A strong apical CF also retains the magnetic axiality of several excited KDs (up to KD_4–5), which have nearly pure |±m_J〉 character. In this case, spin relaxation occurs through highly excited |±m_J〉 states close to the upper KD₇ |±1/2〉 (Fig. 1a), thereby pushing up the barrier U_eff toward to the top KD₇ with m_J = ±1/2.^7,26–28,33 In concert with the large total CF splitting energy of the ⁶H_15/2 multiplet of the Dy³⁺ ion, this results in a very high barrier U_eff. Indeed, experimental data and theoretical calculations show that U_eff approximately corresponds to the energy position of the top |±1/2〉 state. The long magnetic axis of the |±15/2〉 ground state is parallel to the apical C₅ axis, and the overall magnetic anisotropy has a distinct easy-axis characteristic.^26–29,33

Fig. 1 Evolution of the E vs. M_J diagram of PBPY-7 Dy(III) complexes with decreasing ratio between the apical crystal field component, CF_ap, and the equatorial crystal field component, CF_eq, (a) CF_ap ≫ CF_eq, (b) CF_ap > CF_eq, (c) CF_ap < CF_eq.

1.2 Case II: moderately strong apical CF (CF_ap > CF_eq)

This group includes numerous PBPY-7 Dy(III) complexes in which the apical CF component still prevails, but the balance between the apical CF_ap and equatorial CF_eq components of the CF is less marked than in Case I. The decrease in the CF_ap/CF_eq ratio may be caused by the enhancement of the equatorial crystal field, CF_eq, due to shorter equatorial metal–ligand distances (2.3–2.4 Å), which occurs in PBPY-7 complexes [DyL₂X₅] with X = THF, H₂O ([Dy(Cy₃PO)₂(H₂O)₅]³⁺,^34,35 [Dy(CyPh₂PO)₂(H₂O)₅]³⁺,³⁶ and [Dy(pz)₂(THF)₅]⁺),³⁷ or with mixed axial ligands Y₁, Y₂ (one strong, one weak) in [Dy(Y₁Y₂)X₅] complexes with Y₁/Y₂ = –OCMe₃, –OSiMe₃, –OPh, Cl⁻ or Br⁻; X = THF, Py.^33,38 A number of PBPY-7 complexes [Dy(Y₁Y₂)L] with polydentate equatorial ligands L can also be attributed to this group.^39–41 In this group of PBPY-7 complexes, the ground state remains KD₀ |±15/2〉, but the non-axial |±1/2〉 state (with g_z = 1.32, g_x = g_y = 10.59) is no longer the highest in energy among the |±m_J〉 states due to the sagging of the top of the E vs. m_J diagram caused by a stronger equatorial field (Fig. 1b). As a result, the total CF splitting energy, ΔE_CF, of the ⁶H_15/2 multiplet decreases significantly (ΔE_CF < 800 cm⁻¹) and the effective barrier, U_eff, is further reduced, in accordance with a lower energy of the non-axial |±1/2〉 state (Fig. 1b). In fact, U_eff typically ranges between 400 and 1000 K.^34–41 The ground state KD₀ |±15/2〉 and a few excited states (|±13/2〉, |±11/2〉) retain high axiality, although their transverse components, g_x and g_y, may be more pronounced compared to Case I due to the reduced overall axiality of the CF. Case II complexes exhibit easy axis magnetic anisotropy parallel to the polar C₅ axis of the bipyramid. As in Case I, the energy barrier, U_eff, is close to the energy of the non-axial |±1/2〉 state.^33–35

1.3. Case III: the apical field is weaker than the equatorial field (CF_ap < CF_eq)

This group comprises PBPY-7 complexes with weak apical ligands (such as Cl, Br)^33,42,43 and rather numerous Dy(III) complexes with polydentate ligands.^43,44 Of special note are PBPY-7 complexes with the strongest equatorial CF comprising pentadentate Schiff-base ligands based on 2,6-diacetylpyridine^45–48 (see below). Complexes of this type reveal low barriers (U_eff < 300 K, in most cases <100 K) as well as overall low CF splitting energies (600–700 cm⁻¹ or lower).^33,42–48 In this group, the magnetic properties change drastically due to crossover between the |±1/2〉 and |±15/2〉 ground states in the E vs. m_J diagram (Fig. 1c). More specifically, under the strong equatorial field, the prolate |±1/2〉 state drops in energy and goes to the ground state, while the |±15/2〉 state with the oblate electron cloud becomes an excited state due to enhanced repulsion from the strong equatorial ligands. As a result, the overall magnetic anisotropy of the PBPY-7 Dy(III) complex transforms from negative (easy-axis) to positive (easy-plane). Accordingly, in Case III PBPY-7 Dy complexes, the driving force behind barrier formation and SMM behavior differs considerably from that in Cases I and II.

As in the high-performance PBPY-7 Dy-SIMs with a strong axial CF, distinct SMM behavior in Case III complexes occurs only when the ground-state KD₀ has a dominant |±15/2〉 character and nearly perfect Ising g-tensor with g_z ∼ 19 and very small g_x, g_y components. However, now the orientation of the long magnetic z axis (which, according to ab initio software, is taken to be the common spin quantization axis)²² turns from the apical C₅ axis to the equatorial plane. In other words, the nature of the equatorial KD₀ |±15/2〉_eq in Case III complexes differs drastically from that for the axial KD₀ |±15/2〉 in Case I and II complexes. This is evident from the fact that with the old spin quantization z axis parallel to the polar C₅ axis, the ground equatorial KD₀ |±15/2〉_eq is mainly composed of the |±1/2〉, |±3/2〉 and |±5/2〉 states, which are all low-lying in the E vs. m_J diagram in Case III (Fig. 1c), which is opposite to Cases I and II, where |±15/2〉 is the lowest state (Fig. 1a and b). Importantly, the formation of the highly anisotropic equatorial Ising-type ground state, |±15/2〉_eq, is now governed not by the strength of the axial ligands (measured by the axial CF parameters B_k0), but by the non-axial CF parameters B_kq, q ≠ 0, which mix the low-lying states, |±1/2〉, |±3/2〉, |±5/2〉, …, to produce the equatorial KD₀ |±15/2〉_eq. Below, we show that this mixing is mainly due to the asymmetry of the equatorial pentagon formed by monodentate or polydentate equatorial ligands (see section 3.5 for details).

In this paper, we report the syntheses, characterization, and magnetic properties of three new seven-coordinate pentagonal-bipyramidal Dy(III) complexes, [Dy(L^CH₃)(Cy₃PO)₂]ClO₄·CH₃CN (1), [Dy(L^2(t-Bu))(Ph₃PO)₂]ClO₄ 0.63C₂H₅OH (2), and [Dy(L^OCH₃)(Ph₃PO)₂]ClO₄·2H₂O (3), including various chelating pentadentate ligands with [N₃O₂]²⁻ binding node in the equatorial plane, L^CH₃ = [2,6-diacetylpyridine bis(acetylhydrazone)]²⁻, L^2(t-Bu) = [2,6-diacetylpyridine bis(3,5di-tert-butylbenzoylhydrazone)]²⁻, and L^CH₃ = [2,6-diacetylpyridine bis(4-methoxybenzoylhydrazone)]²⁻, and OPCy₃ or OPPh₃ in the apical positions. As in our previous works,^49,50 as well as in ref. 45–48, we took advantage of pentadentate chelating L^R ligands based on 2,6-diacetylpyridine, which provided a rigid pentagonal equatorial plane around the Ln(III) ions in the heptacoordinated complexes and left the axial positions free, thereby enabling us to use various axial ligands (Fig. 2).

Fig. 2 2,6-Diacetylpyridine-based acyclic ligands used in this work: R = CH₃ (2,6-diacetylpyridine bis(acetylhydrazone), H₂L^CH₃), R = 4-OCH₃C₆H₄ (2,6-diacetylpyridine bis(4-methoxybenzoylhydrazone), H₂L^OCH₃), R = 3,5-di-tBuC₆H₃ (2,6-diacetylpyridine bis(3,5 di-tert-butylbenzoylhydrazone), H₂L^2(t-Bu)).

Originally, the objective of this work was to investigate the impact of the apical ligands Ph₃PO and Cy₃PO on the SMM characteristics, as well as to compare our results with those of previously reported related complexes with similar equatorial ligands and different combinations of axial ligands.^46–49 In the present study, we show that, like in the PBPY-7 Dy complexes reported in ref. 45–48, the ground state of complexes 1–3 is KD₀ |±15/2〉_eq (g_x ∼ 19.6, g_y, g_z ∼ 0) with the long magnetic axis lying in the equatorial xy plane; therefore, all of these complexes fall under Case III (Fig. 1c). Then, after closer inspection of the magneto-structural correlations in numerous PBPY-7 Dy complexes from Cases I, II and III reported in the literature,²⁹ we have concluded that a more in-depth analysis of the origin of SMM behavior in Case III complexes is highly advisable.

Following the above considerations, herein we report the magnetic properties of complexes 1–3 and provide a detailed theoretical study of the origin of the spin-reversal barrier, U_eff, in Case III complexes in terms of CF theory for lanthanide ions. We show that in Case III complexes, a strong equatorial CF results in a completely different scenario for the origin of SMM behavior, in which distortions of the PBPY-7 geometry (especially the asymmetry of the coordination pentagon in the equatorial plane) are more important than the CF strength of the apical ligands, which is opposite to Cases I and II, in which distorted PBPY-7 geometry is highly undesirable since it tends to decrease U_eff and T_B due to the departure from perfect magnetic axiality. Therefore, these results indicate that Case III complexes, including our complexes 1–3, experience a breakdown of the strong apical magnetic axiality, which is crucial for reaching the highest U_eff and T_B values, as occurs in the record PBPY-7 Dy(III) complexes, [Dy(^t-BuO)₂(py)₅]BPh₄ (U_eff = 1815 K, T_B = 14 K),²⁶ and [Dy(CH₃CH(C₆F₅)O)₂(THF)₅]BPh₄·2THF (U_eff = 2113 K, T_B = 22 K).²⁸ From a wider point of view, this refers to the fact that the oblate Dy³⁺ ion prefers a strong apical CF and a weak equatorial CF to have maximal U_eff and T_B values, while in Case III dysprosium complexes the situation is just the opposite. As a result, the PBPY-7 Dy(III) complexes with the long magnetic axis lying equatorially have little chance of being high-performance SMMs. Even though the negative impact of a strong equatorial CF on the SMM performance of PBPY-7 Dy complexes is currently well-recognized,^5–10 the specific mechanism behind the origin of the pure Ising-type ground state KD₀ |±15/2〉_eq in the equatorial plane of Case III complexes (i.e., with CF_eq > CF_ap) is explored for the first time in this paper. To the best of our knowledge, this issue has not been previously addressed in the literature, despite much research activity in the field of PBPY-7 Ln-SMMs.

2. Experimental section

2.1 Materials and methods

2,6-Diacetylpyridine, Et₃N, Dy(ClO₄)₃·6H₂O, 3,5-di-tert-butylbenzoic acid, 4-methoxybenzoic acid, thionyl chloride, hydrazine hydrate solution (50–60% N₂H₄), acetic hydrazide, tricyclohexylphosphine oxide (Cy₃PO), and triphenylphosphine oxide (Ph₃PO) were purchased from commercial sources and used without further purification. Methanol was dried upon refluxing with magnesium methoxide, followed by distillation. Acetonitrile was distilled over calcium hydride. Diethyl ether was distilled over LiAlH₄. All the solvents were purged with argon and stored over 3 Å molecular sieves prior to use.

IR spectra of solid samples were recorded with a PerkinElmer SPECTRUM TWO FT-IR spectrometer in the range of 4000–600 cm⁻¹. Elemental analyses were performed by the Analytical Department service at the Federal Research Center of Problems of Chemical Physics and Medicinal Chemistry RAS using a Vario MICRO Cube analyzer.

2.2 Synthetic procedures

Methyl-3,5-di-tert-butylbenzoate was prepared from 3,5-di-tert-butylbenzoic acid, methanol and thionyl chloride according to a previously published procedure.⁵¹ 3,5-Di-tert-butylbenzoic acid hydrazide was synthesized from methyl-3,5-di-tert-butylbenzoate and hydrazine hydrate in refluxing methanol.⁵² The 4-methoxybenzoic acid hydrazide was in a similar manner.

The ligands 2,6-diacetylpyridine bis(acetylhydrazone), H₂L^CH₃, 2,6-diacetylpyridine bis(3,5 di-tert-butylbenzoylhydrazone), H₂L^2(t-Bu), and 2,6-diacetylpyridine bis(4-methoxy-benzoylhydrazone), H₂L^OCH_\3, were prepared through a ketone–hydrazine condensation reaction between 1 equiv. of 2,6-diacetylpyridine and 2 equiv. of acetic hydrazide, 3,5-di-tert-butylbenzoic acid hydrazide or 4-methoxybenzoic acid hydrazide, respectively, in 96% ethanol, according to procedures in the literature with minor modification.⁵³ The yield was over 90% for all three ligands.

H ₂ L ^2(t-Bu) found: C, 75.57; H, 8.55; N, 11.04%. Calc. for C₃₉H₅₃N₅O₂: C, 75.12; H, 8.5; N, 11.23%. FT-IR ν_max/cm⁻¹: 3170m, 2959s, 2929m, 1658vs, 1593m, 1529s, 1449s, 1362s, 1312m, 1244vs, 1156s, 1121m, 1077m, 860m, 814m, 738m, 707vs.

H ₂ L ^{OCH ₃} found: C, 65.62; H, 5.71; N, 15.35%. Calc. for C₂₅H₂₅N₅O₄: C, 65.35; H, 5.48; N, 15.24%. FT-IR ν_max/cm⁻¹: 3411m, 3218m, 2296m, 1646s, 1606s, 1580m, 1547s, 1502vs, 1455m, 1365m, 1285s, 1250vs, 1176vs, 1145m, 1120m, 1025s, 919m, 834vs, 758m.

2.2.1 [Dy(L^CH₃)(Cy₃PO)₂]ClO₄·CH₃CN (1). The organic ligand H₂L^CH₃ (47.6 mg, 0.173 mmol) was suspended in 10 mL CH₃CN. To the stirred suspension were added slowly 5 mL CH₃CN solution of Dy(ClO₄)₃·6H₂O (98.5 mg, 0.173 mmol) and 5 mL CH₃CN solution of Cy₃PO (102.5 mg, 0.346 mmol). The whole reaction mixture was refluxed for 1 h under stirring followed by cooling down to room temperature. Afterwards, 0.048 mL (0.346 mmol) of Et₃N was added slowly to the stirred reaction mixture to obtain a transparent, yellow solution, which was stirred further at room temperature for 10 min before it was filtered. The filtrate was left undisturbed at room temperature for one week to produce yellow single crystals suitable for X-ray analysis. The crystals were collected by suction filtration, washed with diethyl ether, and air-dried. Yield: 132 mg, 65%.

Anal. found: C, 52.35; H, 7.32; N, 6.87%. Calc. for DyC₅₁H₈₆N₆O₈P₂Cl (Mm 1171.18 g mol⁻¹): C, 52.25; H, 7.34; N, 7.17%.

FT-IR ν_max/cm⁻¹: 2928s, 2853m, 1579m, 1515s, 1446m, 1388vs, 1333m, 1321m, 1083vs, 892m, 853m, 675m, 622vs (Fig. S2, ESI†).

2.2.2 [Dy(L^2(t-Bu))(Ph₃PO)₂]ClO₄·0.63C₂H₅OH (2). To a suspension of H₂L^2(t-Bu) (0.26 mmol, 0.163 g) and OPPh₃ (0.52 mmol, 0.145 g) in CH₃CN (6 mL), a solution of Dy(ClO₄)₃ 6H₂O in ethanol (0.25 mmol, 144 mg in 6 mL C₂H₅OH) was added at room temperature using a dropping funnel. The white suspension turned yellow immediately, and the white precipitate started to dissolve. The reaction mixture was stirred at 60 °C for 1 h. After that, the reaction mixture was cooled to room temperature and triethylamine (0.072 mL, 0.52 mmol) was adding under stirring. The solution became a more saturated bright yellow. The reaction mixture was stirred at 60 °C for another 15 min and then cooled to room temperature. The solution was filtered and left to slowly evaporate at room temperature. The formation of crystals suitable for XRD analysis was observed in 2 weeks with significant evaporation of the solution. The mother liquor was decanted from the crystals, which were washed with diethyl ether (2 × 3 mL) and dried in vacuo affording 0.25 g of product 2. Yield 67%. Anal. found: C, 62.48; H, 5.804; N, 4.77%. Calc. for C₇₅H₈₁DyN₅ O₄P₂ClO₄·0.63C₂H₆O (Mm 1469.5 g mol⁻¹): C, 62.28; H, 5.77; N, 4.76%.

FT-IR ν_max/cm⁻¹: 2962m, 1557m, 1504s, 1438s, 1407m, 1368vs, 1275s, 1140vs, 1119s, 1075vs, 997m, 890m, 820m, 762m, 726vs, 706s, 692vs, 622vs, 538vs (Fig. S3, ESI†).

2.2.3 [Dy(L^OCH₃)(Ph₃PO)₂]ClO₄·2H₂O (3). The synthesis of complex 3 was similar to that used for the preparation of 2, but methanol was used as a solvent instead of acetonitrile with ethanol. The yield of the crystalline product 3 was 75%.

Anal. found: C, 56.31; H, 4.17; N, 5.41%. Calc. for C₆₁H₅₇ClDyN₅O₁₂P₂, (Mm 1312 g mol⁻¹): C, 55.79; H, 4.34; N, 5.34%.

FT-IR ν_max/cm⁻¹: 3032w, 1586m, 1494s, 1438s, 1362vs, 1352m, 1249s, 1164s, 1140vs, 1083vs, 1040vs, 998s, 765s, 724vs, 684vs, 618vs, 538vs (Fig. S4, ESI†).

2.3 X-ray data collection, structure solution, and refinement

Single-crystal X-ray data for complexes 1 and 2 were collected using a Bruker D8 Venture Photon single-crystal diffractometer equipped with an Incoatec IμS 3.0 microfocus sealed tube (Mo K_α radiation, λ = 0.71073 Å), and for compound 3 using a Bruker SMART APEX II instrument (Mo K_α radiation, λ = 0.71073 Å) in φ- and ω-scan mode at the Center for Collective Use of the Kurnakov Institute RAS (Moscow, Russia). The raw data for 1–3 were treated with APEX3 software;⁵⁴ experimental intensities were corrected for absorption effects using SADABS.⁵⁵ The crystal structures of 1–3 were solved by direct methods⁵⁶ and refined by full-matrix least-squares on F² using the OLEX2 structural data visualization⁵⁷ and analysis program suite.⁵⁸ Non-hydrogen atoms were refined with anisotropic thermal parameters (except disordered methyl and tert-butyl groups in structures 2 and 3 with low occupancies of disordered atom positions, which were refined using isotropical approximations). Geometrical restraints (SADI, DFIX) and restraints on atomic displacement parameters (SIMU, RIGU, ISOR, DELU, EADP) were also applied on disordered atoms of structures 2 and 3. All hydrogen atoms were placed in the calculated positions and refined using the riding model with dependent isotropic thermal parameters with U_iso(H) = 1.5U_eq(C) for the methyl or hydroxyl groups and with U_iso(H) = 1.2U_eq(C) for other hydrogen atoms. Table S1 in the ESI† summarizes crystal data and structure refinement details for 1–3. Full crystallographic data for the crystal structures of 1–3 are given in CCDC deposition numbers 2239615–2239617, respectively.†

The powder XRD patterns for the complexes were recorded at room temperature on an Aeris diffractometer (Malvern PANalytical B.V., Netherlands). The powder XRD measurements showed that polycrystalline samples of the complexes were monophase crystalline materials corresponding to single crystal data (Figs. S5–S7, ESI†).

2.4 Magnetic measurements

The dc and ac magnetic properties were measured by using the Quantum Design PPMS-9 physical property measuring system (complexes 1, 2) and the vibrating-sample magnetometer of a Cryogen Free Measurement System (CFMS, Cryogenic Ltd, UK) in the case of 3. The temperature dependence of the magnetic moment, M(T), was measured at T = 2–300 K in a dc magnetic field of B = 0.5 T. The field dependences of the magnetic moment, M(H), were obtained at temperatures of 2, 3 and 5 or 6 K in the dc magnetic field range of 0–5 T. The ac magnetic behavior of the complexes was studied within the frequency range of 10–10 000 Hz in the absence and under the application of a dc magnetic field. The measurements were carried out on polycrystalline samples moistened with mineral oil (Fomblin YR 1800) to prevent orientation of the crystals in a dc magnetic field. The prepared samples were sealed in plastic bags. The experimental data were corrected for the sample holder and mineral oil. The diamagnetic contribution from the substance was calculated using Pascal's constants.

2.5 Computational details

Ab initio calculations were performed using the OpenMolcas program.⁵⁹ The [.ANO-RCC…8s7p5d3f2g1h.] basis set for the Dy atom, [.ANO-RCC…5s4p2d1f.] for the P atom, [.ANO-RCC…4s3p2d1f] for the N and O atoms, [.ANO-RCC…2s1p.] for C atoms and [.ANO-RCC…1s.] for H atoms were employed. The ground state f-electron configuration for Dy(III) is 4f⁹ with the ⁶H_15/2 multiplet as the ground state. Initially, we generated the guess orbitals and from there the seven Dy(III) based starting orbitals were selected to perform the CASSCF calculations, where 9 electrons were in the 7 active orbitals with an active space of CAS (9,7). Using this active space, 21 sextets were computed using the configuration interaction (CI) procedure. After that, all 21 sextets were mixed using the RASSI-SO module to compute the spin–orbit states. After computing these spin–orbit states, using the SINGLE_ANISO code^60a the corresponding g-tensors and CF parameters for the eight low-lying Kramers doublets (KDs) were extracted. The Cholesky decomposition for two electron integrals was employed throughout the calculations to reduce the disk space. Crystal-field calculations were performed in terms of conventional CF theory using the Wybourne notation for the CF parameters B_kq, as described elsewhere.^60b

3 Results and discussion

3.1 Synthesis

Most of the seven-coordinate high-barrier Dy(III) SMMs described to date contain five neutral weak-field ligands as equatorial ligands and two anionic or neutral strong-field ligands at the axial positions. There are not many 4f element complexes with D_5h symmetry containing chelating pentadentate ligands in the equatorial plane.^45–48,61 In contrast to 3d transition-metal ions, PBPY-7 coordination geometry is rare among 4f complexes with pentadentate acyclic ligands because rare Earth ions prefer large coordination numbers (8–10) and variable coordination geometries. The composition and structures of compounds formed by the interaction of dysprosium salts with planar pentadentate ligands strongly depend on the reaction conditions, and it is possible to obtain 10-, 9-, 8- and 7-coordinate complexes.^45–50,62 To obtain the dysprosium seven-coordinate complex in a targeted manner, it is necessary to strictly control the synthesis conditions, in particular the ratio of reagents, the order of base addition, and the type of anion of the initial dysprosium salt.

In this work, Dy(ClO₄)₃ 6H₂O was used as the starting dysprosium salt. During the synthesis, the ratio of the reaction components, Dy(ClO₄)₃ : H₂L : OPPh₃ : Et₃N = 1 : 1 : 2 : 2, was strictly enforced, and the deprotonating Et₃N base was added to the reaction medium approximately 1 h after the addition of the dysprosium salt to the ligand mixture. The point is that we have previously shown that preliminary deprotonation of the H₂L ligand by adding Et₃N to the ligand before the dysprosium salt leads to the formation of a stable and well crystallized charge-neutral mononuclear complex, [Dy(HL)(L)], in the reaction medium as the main product, in which the Ln³⁺ ion binds two charged pentadentate ligands.⁶² To avoid the formation of such complexes, it is highly desirable not to exceed the ratio of H₂L/Dy(ClO₄)₃ = 1 during synthesis, and also to introduce Et₃N after adding the metal salt to the mixture of H₂L and OPPh₃ ligands.

Following these general rules, we have synthesized a series of three new heptacoordinated mononuclear Dy PBPY-7 complexes, including various pentadentate ligands with [N₃O₂]²⁻ binding node in the equatorial plane, H₂L^CH₃, H₂L^OCH₃, and H₂L^2(t-Bu), and OPPh₃ or OPCy₃ in the apical positions. All the complexes are characterized by elemental analysis, infrared spectroscopy, magnetic measurements and X-ray crystallography. Single crystals of compounds 1–3 are obtained by slow evaporation of the filtered mother liquors. The yields are quite high for the lanthanide complexes (65–75%). Elemental analyses of the complexes were consistent with the composition of [Dy(L)(OPPh₃)₂(ClO₄)]·solv, where L denotes a dideprotonated ligand molecule. All the complexes are air-stable in the crystalline state. The phase purity of the samples of complexes used for magnetic measurements was confirmed by the X-ray powder diffraction data (Figs. S5–S7, ESI†).

Pentadentate ligands with the binding units N₃O₂, H₂L^CH₃, H₂L^OCH₃, and H₂L^2(t-Bu) used in this work differ in that different substituents are introduced into the phenyl groups of the H₂L^OCH₃ and H₂L^2(t-Bu) ligands, which affect the electronic and steric properties of the resulting ligand. The use of slightly different pentadentate ligands with the same binding site allows us to determine whether the peculiarities of the equatorial ligand structure affect the properties of this series of complexes as monomolecular magnets.

All pentadentate ligands used in this work were obtained by the standard condensation reaction of 2,6-diacetylpyridine with two equivalents of the corresponding hydrazide. Hydrazides for the synthesis of H₂L^OCH₃ and H₂L^2(t-Bu) ligands were synthesized beforehand from commercially available substituted phenylcarboxylic acids. The phenylcarboxylic acids were converted into the corresponding methyl esters, which were then converted into hydrazides by treatment with hydrazine hydrate in alcohol medium under heating. The ketone–hydrazine condensation with 2,6-diacetylpyridine yielded the final ligands. The synthesized hydrazides and ligands were characterized by elemental analysis, NMR, and IR spectra (Figs. S8–S10, ESI†).

3.2 Crystal structure descriptions

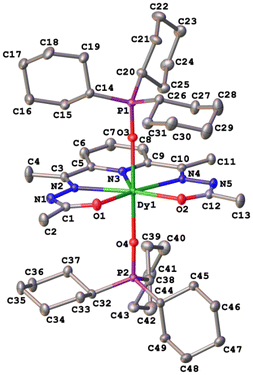
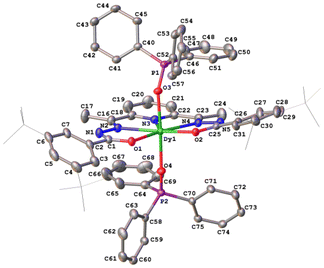
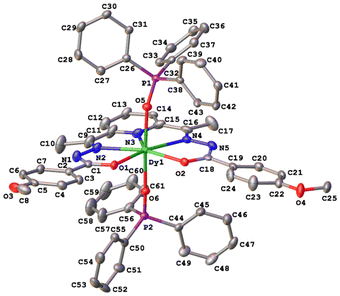
The crystal structures of compounds 1–3 were established by the single crystal X-ray diffraction technique. According to X-ray diffraction data, compounds 1 [Dy(L^CH₃)(Cy₃PO)₂](ClO₄)·CH₃CN (Fig. 3), 2 [Dy(L^2(t-Bu))(Ph₃PO)₂](ClO₄)·0.63C₂H₅OH (Fig. 4), and 3 [Dy(L^OCH₃)(Ph₃PO)₂]ClO₄·2H₂O (Fig. 5) crystallize in three different space groups, P2₁/n, P2₁/c, and P1̄, respectively, with two independent molecular units in 1 (1a, 1b) and 2 (2a, 2b) and one in 3, see Table 1 and Fig. 6.

Fig. 3 Crystal structure and atom numbering scheme of the cationic part of complex 1. ClO₄⁻ anions and hydrogen atoms are omitted for clarity. Atomic displacement parameters are shown at the 50% probability level.

Fig. 4 Crystal structure and atom numbering scheme of the cationic part of complex 2. ClO₄⁻ anions, ethanol molecules, disordering and hydrogen atoms are omitted for clarity. Bulky tert-butyl groups are shown schematically. Atomic displacement parameters are given at the 35% probability level.

Fig. 5 Crystal structure and atom numbering scheme of the cationic part of complex 3. ClO₄⁻ anions, disordering of one methoxy group and hydrogen atoms are omitted for clarity. Atomic displacement parameters are given at the 35% probability level.

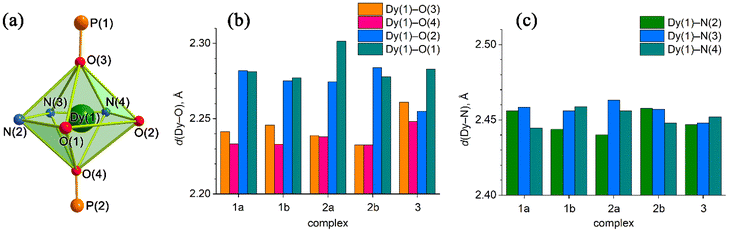Fig. 6 (a) Coordination polyhedron of Dy(III) with atom numbering. (b) Axial Dy(1)–O(3)/O(4) for 1a, 1b, 2a, and 2b and Dy(1)-O(5)/O(6) for 3 (Fig. 5), as well as equatorial Dy(1)–O(1)/O(2) distances. (c) Equatorial Dy–N distances.

Table 1 Selected bond lengths (Å) for complexes 1–3

Bond length	1 (1a, 1b)	2 (2a, 2b)	3, Fig. 6
Dy(1)–O(1)	1a, 2.2813(11)	2a, 2.3013(17)	2.283(3)
Dy(2)–O(1A)	1b, 2.2770(11)	2b, 2.2779(15)
Dy(1)–O(2)	1a, 2.2819(11)	2a, 2.2746(17)	2.255(3)
Dy(2)–O(2A)	1b, 2.2750(11)	2b, 2.2839(15)
Dy(1)–O(3)	1a, 2.2415(12)	2a, 2.2379(17)	2.261(3) [Dy(1)−O(5)]
Dy(2)–O(3A)	1b, 2.2458(11)	2b, 2.2325(15)
Dy(1)–O(4)	1a, 2.2334(11)	2a, 2.2388(17)	2.248(3) [Dy(1)−O(6)]
Dy(2)–O(4A)	1b, 2.2331(11)	2b, 2.2326(15)
Dy(1)–N(2)	1a, 2.4561(13)	2a, 2.440(2)	2.447(3)
Dy(2)–N(2A)	1b, 2.4437(14)	2b, 2.4578(18)
Dy(1)–N(3)	1a, 2.4584(13)	2a, 2.463(2)	2.448(3)
Dy(2)–N(3A)	1b, 2.4560(13)	2b, 2.4571(18)
Dy(1)–N(4)	1a, 2.4446(14)	2a, 2.456(2)	2.452(3)
Dy(2)–N(4A)	1b, 2.4588(14)	2b, 2.4478(18)

---

Each structure could be described by the general formula [Dy(L)(OPR₃)₂](ClO₄), thus being a cation–anion complex with different solvent molecules but the same coordination environment around the central dysprosium atoms. Dysprosium atoms are surrounded by two oxygen atoms and three nitrogen atoms of the pentadentate ligand in the equatorial plane and by two oxygen atoms of the R₃PO ligand, which complete coordination number seven (Figs. 3–5).

Continuous shape measure analysis (CShM) was performed for complexes 1–3 to elucidate the real geometry of the hepta-coordinate environment around the Dy(III) ion.⁶³ The analysis showed that the local geometry of the Dy(III) ions in the complexes was pentagonal bipyramidal with pseudo-D_5h symmetry for the [DyN₃O₄] core (Table S2, ESI† and Fig. 6). Deviations from pentagonal-bipyramidal geometry are between 1.154 and 1.569 (Table S2, ESI†).

The two non-equivalent types of oxygen atoms, which are bonded to Dy, form two different types of Dy–O bonds, as illustrated in Table 1 and Fig. 6: Dy–O(ap) distances are somewhat shorter than those of the Dy–O(eq).

The interatomic bond lengths of Dy with the polydentate equatorial ligand (Dy–N (2.440(2)–2.4588(14) Å) and Dy–O (2.255(3)–2.3013(17) Å)) for complexes 1–3 are close to the values found in previously described Dy complexes with the dianionic form of pentadentate N₃O₂-type Schiff base ligands.^45,46,50 However, it should be noted that these Dy–O(eq) distances for complexes 1–3 are noticeably shorter than those in pentagonal-bipyramidal Dy complexes with magnetization barriers extending to 1000 K and even higher, which contain monodentate weak-field ligands (water, tetrahydrofuran (Dy–O 2.327(5)–2.453(3)), pyridine, pentaazomacrocycles) in the equatorial plane and strong-field ligands in the axial positions (phosphine/silano oxides, acyl/aryl alkoxides, aryl/acyl phosphonamides).^{26,28,33,34,64} At the same time, the Dy–O(ap) bond lengths in 1–3 (Table 1) are comparable to the Dy–O(ap) distances in the previously described seven-coordinate dysprosium complexes with O=PR₃ ligands in axial positions.^34,46

Crystal structure 1 contains two crystallographically independent molecules, but they are almost identical. In complex 2, the independent molecules differ. In particular, the axial angles are different. For complex 1, the O_ap–Dy–O_ap bond angle between oxygen atoms of the axial ligands is 170.91(4)–171.49(4)°; for 2 and 3 it is 169.96(6)–176.71(6)° and 174.43(10)°, respectively (Tables S3–S5, ESI†).

The crystal packing of compounds 1 and 2 does not contain any obvious intermolecular interactions or π-stacked moieties due to high steric hindrance of the axial ligands. In contrast, a single π–π stacking interaction between the phenyl groups of neighboring cations of [Dy(L^OCH₃)(Ph₃PO)₂]⁺ (symmetry code: 2 − x, 1 − y, 1 − z) with a centroid-to-centroid distance of 3.742 Å was detected in 3 (Fig. S11, ESI†). It should be noted that the minimum distances between the dysprosium ions in the crystal structures of 1–3 are 10.949, 10.328 and 10.429 Å, respectively, i.e., the dysprosium ions are well separated in the crystal structures.

3.3 Static magnetic properties

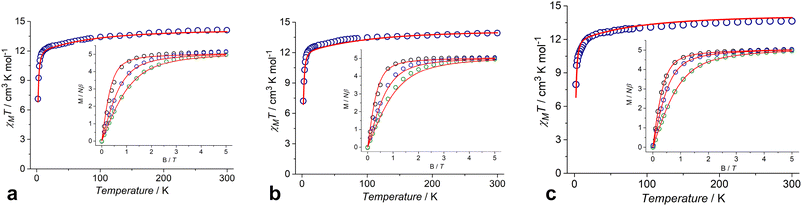
The dc magnetic susceptibility data for complexes 1–3 were measured in the temperature range of 2.0–300 K under an applied field of 5000 Oe (Fig. 7). The χ_MT values at 300 K are 14.11, 13.92 and 13.64 cm³ K mol⁻¹ for 1, 2 and 3, respectively, which are in agreement with the expected value of 14.17 cm³ K mol⁻¹ for an isolated Dy(III) ion (⁶H_15/2, g = 4/3). The χ_MT values decrease gradually upon cooling from room temperature to ∼10 K, and then decrease abruptly, reaching 7.13, 7.22 and 7.96 cm³ K mol⁻¹ at 2 K for 1, 2 and 3, respectively (Fig. 7). Magnetization (M) versus field curves for 1, 2 and 3 at different temperatures are shown in the insets of Fig. 7. All complexes have the same behavior of M(H) dependences with similar values of 5.16N_Aμ_B, 5.05N_Aμ_B and 5.04N_Aμ_B for 1, 2 and 3, respectively, at 2 K and 5 T.

Fig. 7 Temperature dependences of χ_MT for 1 (a), 2 (b) and 3 (c). Insets: Magnetization vs. field plots at different temperatures (2, 4, 6 K for 1, 2 and 2, 3, 5 K for 3). The red solid lines show the corresponding results of the SA-CASSCF/SO-RASSI/SINGLE_ANISO calculations.

Magnetic hysteresis cycles at different temperatures and different magnetic field sweep rates have been studied using complex 3 as an example. At 2 K and a sweep rate of 50 Oe s⁻¹, complex 3 exhibits a tight-waist hysteresis loop (S12, ESI†) with small coercivity and remanence values of 40 Oe and 0.05μ_B, respectively, indicating the occurrence of an effective QTM. As expected for SMM behavior, the hysteresis and remanent magnetization become larger (260 Oe and 0.25μ_B, respectively) when the sweep rate is increased to 150 Oe s⁻¹ at the same 2 K temperature (S12, ESI†). In addition, the loop width (coercive field) and remanence values decrease significantly with increasing temperature from 2 K to 5 K for both 50 Oe s⁻¹ and 150 Oe s⁻¹ sweep rates (S13, ESI†), which is also characteristic of SMMs.

3.4 Dynamic magnetic properties

Complexes 1–3 reveal dynamic magnetic behavior at zero dc field (Fig. 8 and S14, ESI†). For complexes 1 and 2, the maximum frequency dependences of the out-of-phase ac susceptibility are characterized by an asymmetric broadening with a “tail” in the high-frequency region. This kind of broadening cannot be described by the α parameter in the generalized Debye model,⁶⁵ so the two-component model has to be used to fit the experimental data with good quality. For complex 3, the generalized Debye model is sufficient. Best fit parameters are shown in Tables S6–S8, ESI.†

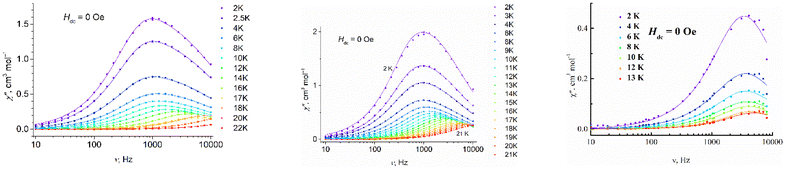Fig. 8 Frequency dependence of the out-of-phase magnetic susceptibility 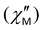for 1–3 at different temperatures at zero dc field. The solid lines are the best fits (see text).

The difference in the magnetic behavior of the complexes could be attributed to differences in their crystal structures. The asymmetric unit contains two crystallographically independent molecules for complexes 1 and 2, and only one independent molecule for complex 3. However, some of the pentagonal- and hexagonal-bipyramidal complexes described containing two independent molecules per asymmetric unit cell showed no asymmetric broadening of the maximum frequency dependences.^66,67

It was already noted earlier that asymmetric broadening arose only when QTM dominated over other relaxation processes.^66,68–71 According to ref. 72, even in the case where only one peak was observable, the second underlying relaxation time could be extracted with the two-component Debye model. A single peak is observed for a small separation between τ₁ and τ₂ and high values of distribution parameter α. The separation is 0.2 ms for both 1 and 2 at 2 K (Fig. S15, ESI†); as the temperature rises, it sharply decreases. The distribution for the first relaxation time, τ₁, is narrow (parameter α₁ < 0.09), while α₂ for the second relaxation time, τ₂, is about twice as high (Tables S6 and S7, ESI†). We consider τ₂ as a satellite of τ₁, therefore, only the first relaxation time, τ₁, is analyzed further in the text.

For complexes 1–3, the position of the maximum remains constant over the temperature range of 2–10 K (Fig. 8), which is characteristic for QTM. Above 10 K, temperature-dependent processes dominate, while the width of the maximum frequency dependence of 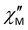decreases.

The contribution of QTM can be reduced by applying a static field; the frequency dependences of the in-phase 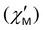and out-of-phase ac susceptibility 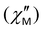over the field range of 0–5000 Oe at a temperature of 10 K for 1 and 3, and 8 K for 2 are shown in Figs. S16–S18 and Tables S9–S11, ESI.† Two relaxation times for 1 and 2 are observed only at low fields. In fields of 1000 Oe for 1 and 500 Oe for 2, the broadening is almost absent and the experimental data are fitted by using the generalized Debye model.

For complexes 1–3, the optimum applied field was estimated at H_dc = 1000 Oe. In the dc field, the QTM process is almost suppressed; the relaxation time is increased at low temperatures (Figs. 9 and S19 and Tables S12–S14, ESI†).

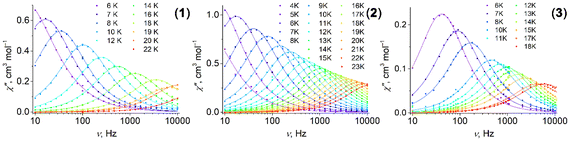Fig. 9 Frequency dependences of the out-of-phase magnetic susceptibility for 1–3 at different temperatures at a dc field of 1000 Oe. The solid lines are the best fits (see text).

The dependences of relaxation time τ on the inverse temperature and the field for complex 1 are shown in Fig. 10a (Fig. S20, ESI† for 2 and 3) and Fig. 10b (Figs. S17d and S18b, ESI† for 2 and 3), respectively. Fitting of the data at zero field (Fig. 10a, black line) was performed according to eqn (1),⁷³ which included one temperature-independent QTM process, and two temperature-dependent Raman and Orbach processes. Best-fit parameters are shown in Table 2.

τ⁻¹ = τ₀⁻¹ exp(−U_eff/k_BT) + CTⁿ + τ_QTM⁻¹ (1)

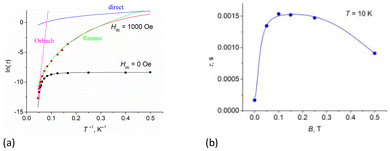Fig. 10 The inverse temperature (a) and field (b) dependences of the relaxation time, τ, for complex 1.

Table 2 Best-fit parameters for the temperature dependences of relaxation time, τ, at zero and 1000 Oe dc field for complexes 1–3

	1		2		3
a The Adirect parameters were fixed to the values defined in Table 3.
H dc, Oe	0	1000	0	1000	0	1000
U eff, K	318	351	323	334	319	325
τ 0, s	3.6 × 10^−13	3.7 × 10^−13	2.9 × 10^−11	2.9 × 10^−11	4.7 × 10^−12	6.9 × 10^−12
C Raman, s^−1 K^−n	0.66	0.0022	1.0	0.08	0.58	0.11
n Raman	3.5	5.4	3.57	4.27	3.73	4.37
τ QTM, s	2.4 × 10^−4	—	2.73 × 10^−4	—	4 × 10^−5	—
A direct, K^−1 T^−4 s^−1	—	919^a	—	536^a	—	780^a

---

The field dependence of τ (Fig. 10b) was fitted by eqn (2), which included two field-dependent processes, QTM and a direct one-phonon process. Best-fit parameters are shown in Table 3. Constant τ_Raman+Orbach implies the sum of Orbach and Raman contributions, because according to eqn (1) they are both field-independent. As follows from the values in Table 2, the main contribution to the τ_Raman+Orbach parameter is the Raman process.

τ⁻¹ = ATH⁴ + B₁/(1 + B₂H²) + τ_Raman+Orbach⁻¹ (2)

Table 3 Best-fit parameters for the field dependences of relaxation time, τ, for complexes 1–3

	1	2	3
T, K	10	8	10
A direct, K^−1 T^−4 s^−1	919	536	780
B 1, s^−1	5358	3585	3655
B 2, T^−2	20.6 × 10^3	44.0 × 10^3	18 × 10^3
τ Raman+Orbach ^−1, s^−1	639	497	415

---

At a dc field of 1000 Oe, the relaxation time is the longest (Fig. 10b). The temperature dependence of the relaxation time at 1000 Oe (Fig. 10a, red line) was fitted with eqn (3), which included Orbach, Raman, and direct one-phonon processes. Best-fit parameters are shown in Table 2.

τ⁻¹ = τ₀⁻¹ exp(−U_eff/k_BT) + CTⁿ + ATH⁴ (3)

In eqn (3), the parameter A_direct was fixed at the value determined from eqn (2) (Table 3). The blue line in Fig. 10a shows that the direct process makes a contribution only at low temperatures, so its inclusion in eqn (3) does not affect the fitting parameters of the Orbach and Raman processes.

The Raman process follows the τ⁻¹ = CTⁿ law, so the Raman process is considered to be field independent. However, as can be seen in Table 2, both C_Raman and n_Raman parameters differ in the zero and applied fields. Parameter C_Raman is noticeably lower in the applied field (0.0022–0.11 s⁻¹ K⁻ⁿ) compared to the zero field values (0.58–1.0 s⁻¹ K⁻ⁿ). The degree, n_Raman, varies over the range of 3.5–3.73 for the zero field and 4.27–5.4 for the dc field. The values of C_Raman and n_Raman are within the range commonly observed for the Raman process for Dy^III SMMs.

Spin reversal energy barriers, U_eff = 318–351 K, are rather high for complexes 1–3. Unlike the Raman process, the fitting parameters for the Orbach process show field independence (Table 2). In Fig. 10a, the green line shows that the Raman process operates over almost the entire temperature range; U_eff observed is only relevant for magnetic relaxation at high temperatures (Fig. 10a, magenta line). This can potentially lead to misdetermination of the Orbach relaxation parameters if only zero-field measurements are used; therefore, dc-field measurements help to verify the fits. Correctly performed fits should give values of U_eff and τ₀ parameters that are almost unaffected by whether a dc field is applied.³⁴ For complexes 1–3, high-frequency ac magnetic measurements (up to 10 000 Hz) made it possible to measure relaxation times up to 20 K and thus obtain accurate data for the Orbach relaxation process. Notably, the effective energy barriers (U_eff) in zero dc field for complexes 1–3 (Table 1), obtained from fitting with eqn (1), are close to the first excited Kramers doublets, as estimated from ab initio calculations (see section 3.5.1). For all three complexes, the magnetization barrier values in zero field and in the presence of a constant magnetic field are similar and over 320–350 K, indicating that the electronic effects associated with the nature of the substituents in the equatorial pentadentate ligands have almost no effect on the magnetic behavior of these mononuclear SMMs. Their magnetic properties are determined primarily by the geometry of the coordination environment of the Dy ions and the nature of the axial and equatorial ligands. The presence of two strong Cy₃PO or Ph₃PO donor ligands in the apical positions of complexes 1–3 leads to a slow relaxation of magnetization in the zero dc field and an increase in the magnetization barriers compared to similar PBPY-7 complexes containing two Cl⁻ or Cl(Cy₃PO/Ph₃PO) in the axial positions.^45,46 However, it should be noted that at the time this work was being prepared for publication, Sutter's group had published a PBPY-7 complex, [Dy(dapbh)(Cy₃PO)₂]BPh₄ ⁴⁷ (where dapbh = 2,6-diacetylpyridine bis-benzoylhydrazone, R = C₆H₅, Fig. 1), similar to our complexes 1–3. Unlike 1–3, this complex showed a low value of magnetization barrier in a field of 750 Oe (U_eff = 51 K). Although the authors observed the signal at 1000 Hz in the absence of a constant magnetic field, no data on the frequency or temperature dependence of 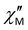at zero field are given in the article; it is noted only that at zero field there is rapid relaxation due to QTM. It can be assumed that the difference in ac magnetic properties between our data for complexes 1–3 and this compound is due to the fact that the ac properties of [Dy(dapbh)(Cy₃PO)₂]BPh₄ are studied over a narrow frequency range to 1500 Hz, whereas our study is conducted up to 10 000 Hz. It should also be noted that the complex obtained by Sutter's group and our compounds 1–3 contain different counterions (BPh₄vs. ClO₄). The influence of the counterion and second coordination sphere on U_eff in the PBPY-7 complexes of Dy was observed in ref. 75.

Although complexes 1–3 have rather high magnetization barriers, the height of these barriers is much lower than those for PBPY-7 Dy complexes containing monodentate weakly coordinating ligands (H₂O, THF, pyridine) or macrocyclic neutral N₅ ligands in the equatorial positions, and strong donor ligands (acyl/aryl alkoxides, aryl/acyl/phosphonamides, and silano/phosphine oxides) in the axial positions. Such a coordination environment of Dy ions, which have an oblate 4f electron density, provides strong apical and weak equatorial CF components, resulting in high values of U_eff extending to 1000 K and beyond.^{26–28,39,68,69,74} The lower values of magnetization barriers for complexes 1–3 compared to the PBPY-7 Dy complexes considered above are explained by the fact that in 1–3 the equatorial plane is formed by negatively charged pentadentate chelating ligands [N₃O₂]²⁻, which create a strong equatorial field competing with the apical crystal field (see the next sections for more detail). The difference in equatorial and apical Dy–O bond lengths in complexes 1–3 is approximately an order of magnitude smaller (0.02–04 Å, Fig. 6 and Table 1) compared to the same difference in the PBPY-7 Dy complexes with a homogeneous fully oxygen coordinated environment in the equatorial plane, [Dy(H₂O)₅(Cy₃PO)₂](Hal)₃ (0.1 Å).³⁴ The strong interaction in the equatorial plane between Dy and two O carrying negative charges leads to significant transverse anisotropy in complexes 1–3; the main magnetic axis in 1–3 is located in the equatorial plane, despite the presence of two strong axial ligands, whereas in all known PBPY-7 Dy complexes with weak monodentate equatorial ligands and strong apical ligands it is directed along the apical axis. A detailed theoretical analysis of the influence of different strengths of equatorial ligands and strong apical ligands on the electronic structure and SMM properties of PBPY-7 Dy complexes is presented below.

3.5 Computational study

3.5.1 Analysis of dc and ac magnetic properties. Ab initio quantum chemical calculations were performed on the electronic structure of isolated Dy(III) complexes with X-ray geometry using OpenMolcas.⁶⁰ X-ray analysis revealed that compounds 1 and 2 consisted of two crystallographically non-equivalent molecules in the asymmetric unit, and our calculations showed that the results did not significantly depend on this (Tables S15 and S16, ESI†), so we present the data and analyze only one molecule for each of these complexes. The theoretical dependences of molar susceptibility and magnetization at different temperatures obtained on the basis of quantum-chemical calculations are in good agreement with experimental data (Fig. 7), which enables a more detailed examination of the features of the electronic structure of the complexes under consideration.

The eight lowest Kramers doublets (KDs) and the g-tensors for 1–3 calculated using the SA-CASSCF/SO-RASSI/SINGLE_ANISO approach have been summarized in Table 4. The main magnetic anisotropy axes (g_z) of ground KDs also lie on the equatorial plane due to the strong crystal field generated by the pentadentate ligand (Fig. S21, ESI†) as in recently studied Dy(III) complexes with the N₃O₂ equatorial ligand.^46–48

Table 4 Ab initio computed energy levels (E, cm⁻¹) with g-tensors of the eight lowest KDs for 1, 2 and 3

	1				2				3
KD	E	g x	g y	g z	E	g x	g y	g z	E	g x	g y	g z
0	0.0	0.026	0.073	19.610	0.0	0.030	0.064	19.691	0.0	0.046	0.098	19.599
1	162.9	1.834	2.844	12.024	187.8	1.125	2.514	14.534	164.2	1.375	3.591	13.334
2	191.5	1.882	2.618	15.032	241.8	0.824	1.087	12.646	218.5	0.265	2.702	11.527
3	227.8	0.115	1.794	6.850	282.3	0.067	1.262	13.344	274.7	0.943	1.315	16.246
4	387.5	1.949	4.848	11.858	395.9	2.181	3.458	14.455	395.2	1.635	4.203	12.866
5	420.7	1.022	3.420	15.062	488.3	9.407	5.338	0.727	466.8	0.058	5.054	11.892
6	510.9	2.289	2.796	12.286	586.8	2.384	5.431	10.339	541.8	2.015	4.344	11.288
7	650.1	0.314	0.816	17.496	721.1	0.331	1.257	17.175	675.9	0.240	1.018	17.436

---

The calculated effective g_zz components of g-tensors are 19.610, 19.691 and 19.599 for the ground KDs of 1, 2 and 3, respectively, which are close to the Ising-limit value of 20 for a pure M_J = 15/2 ground state, thus, all complexes have significant axial anisotropy for Dy(III) centers. The ground state wave functions of complexes 1 (95% |±15/2〉), 2 (96% |±15/2〉) and 3 (95% |±15/2〉) show the dominant contributions of the uniaxial magnetic anisotropy of the Dy(III) ions (Table 5).

Table 5 SINGLE_ANISO computed wave function decomposition analysis for the lowest KDs of Dy(III) ions for 1–3. Only the main (>10%) contributions are shown

	1	2	3
KD0	0.948 |±15/2〉	0.962 |±15/2〉	0.948 |±15/2〉
KD1	0.409 |±13/2〉 + 0.327 |±9/2〉 + 0.195 |±5/2〉	0.499 |±13/2〉 + 0.346 |±9/2〉	0.460 |±13/2〉 + 0.382 |±9/2〉
KD2	0.301 |±7/2〉 + 0.245 |±1/2〉 + 0.149 |±3/2〉	0.425 |±7/2〉 + 0.292 |±11/2〉 + 0.112 |±5/2〉	0.463 |±7/2〉 + 0.412 |±11/2〉
KD3	0.383 |±11/2〉 + 0.212 |±7/2〉 + 0.149 |±3/2〉	0.284 |±3/2〉 + 0.201 |±1/2〉 + 0.199 |±11/2〉 + 0.175 |±5/2〉	0.334 |±3/2〉 + 0.261 |±5/2〉 + 0.258 |±1/2〉
KD4	0.454 |±13/2〉 + 0.313 |±9/2〉 + 0.123 |±5/2〉	0.355 |±13/2〉 + 0.321 |±9/2〉 + 0.138 |±7/2〉	0.413 |±13/2〉 + 0.309 |±9/2〉
KD5	0.290 |±11/2〉 + 0.273 |±7/2〉 + 0.189 |±5/2〉+ 0.163 |±9/2〉	0.254 |±5/2〉 + 0.202 |±11/2〉 + 0.180 |±7/2〉+ 0.123 |±9/2〉	0.277 |±11/2〉 + 0.263 |±7/2〉 + 0.196 |±5/2〉+ 0.129 |±9/2〉
KD6	0.347 |±3/2〉 + 0.287 |±5/2〉 + 0.155 |±11/2〉 + 0.143 |±7/2〉	0.316 |±3/2〉 + 0.251 |±5/2〉 + 0.157 |±7/2〉 + 0.147 |±11/2〉	0.338 |±3/2〉 + 0.265 |±5/2〉 + 0.135 |±11/2〉 + 0.112 |±7/2〉
KD7	0.636 |±1/2〉 + 0.262 |±3/2〉	0.611 |±1/2〉 + 0.259 |±3/2〉	0.601 |±1/2〉 + 0.251 |±3/2〉

---

Strong mixing of the |±13/2〉 and |±9/2〉 (and |±5/2〉 for 1) wave functions (Table 5 and Fig. S22, ESI†) in the first excited KD1 leads to very large thermally assisted quantum tunneling (TA-QTM) values of 0.78, 0.63 and 0.84μ_B; as a result, all complexes have to relax via this state. Moreover, the first excited states, KD1, of all complexes show significant transverse anisotropy (g_x,y are in the range of 1.1–3.6), suggesting that a significant QTM is operational at the first excited state.

It should be noted that the calculated energies of the first excited Kramers doublets, 234.6, 270.4 and 236.4 K, which in the cases under consideration correspond to the ab initio computed energy barriers for magnetization reversal, are slightly higher than those for similar systems with nonequivalent axial ligands.⁴⁶ These values agree satisfactorily with the U_eff values obtained from the analysis of the temperature dependences of relaxation. Some discrepancies may be related to the influence of other relaxation mechanisms (Raman, QTM) on the accuracy of the approximation, since we observe a non-pure Orbach process for these systems.

Thus, replacing the second Cl⁻ ion in the axial position by the neutral R₃PO (R = Cy or Ph) ligand does not significantly affect the values of the spin-reversal barrier (U_eff). Since the main magnetic axis lies in the equatorial plane, the ligand field generated from the equatorial ligands mainly determines the properties of the complexes under consideration; the small differences in the energy spectrum, apparently, depend on the structure of the N₃O₂ ligands (see the next section for more details).

In order to analyze in more detail the reason for the strong influence of the ligand field of equatorial ligands, a LoProp charge analysis was carried out. The total charge on donor atoms in the equatorial plane is higher and it is unevenly distributed (Table 6). Previously,²⁶ for D_5h symmetric Dy(III) complexes, it was shown that, with a decrease in the negative charge on donor atoms in the equatorial plane and their equalization in absolute value upon transition to a homogeneous completely oxygen or nitrogen coordination environment, the U_eff values increased and the properties of such SIMs improved.

Table 6 LoProp charge analysis of the Dy center and donor atoms in complexes 1–3

Atom	1	2	3
Dy	2.5288	2.5084	2.5307
Oax	−1.1225/−1.1229	−1.1019/−1.1067	−1.1073/−1.1086
Oeq	−0.8358/−0.8443	−0.8532/−0.8339	−0.8334/−0.8429
NPy	−0.4141	−0.3979	−0.4190
N	−0.2771/−0.2814	−0.2722/−0.2749	−0.2759/−0.2788

---

The CF parameters of all complexes was estimated using the Stevens formalism, 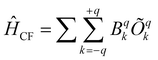, where B^q_k and Õ^q_k are the calculated CF parameter and extended Stevens operator, as defined in ref. 76, respectively, as implemented in the SINGLE_ANISO code.^60a The axial CF parameter B⁰₂ is found to be the largest in absolute value for all complexes (Table S17, ESI†). However, some B^q₂ values are found to be comparable; as a result, it can lead to a loss of expected axiality.

3.5.2. Origin of the m_J = |±15/2〉_eq ground state for Case III PBPY-7 Dy(III) complexes: the key role of distortions in the equatorial plane.
3.5.2.a General remarks. As pointed out above, Dy(III) PBPY-7 complexes with a strong equatorial CF (Case III, Fig. 1c, which involves our complexes 1–3 and similar Dy(III) complexes reported in ref. 45–48) can exhibit SMM behavior when the ground state has a dominant m_J = |±15/2〉 character with the long magnetic axis (g_x ∼ 19.6) located in the equatorial xy plane; this state is referred to as |±15/2〉_eq. From the point of view of the electron density, the equatorial |±15/2〉_eq state (with g_x ∼ 19.6, g_y, g_z ∼ 0) in Case III Dy(III) PBPY-7 complexes has the same oblate shaped electronic cloud as the axial |±15/2〉_ap ground state (with g_x, g_y ∼ 0, g_z ∼ 19.6) in Case I and II complexes differing only in the orientation of the cloud (Fig. 11a and b). However, there is a seminal difference between the equatorial |±15/2〉_eq and apical |±15/2〉_ap states concerning their m_J composition: namely, with a common spin quantization z axis directed along the pentagonal C₅ axis of the bipyramid, KD₀ |±15/2〉_ap is a pure |±15/2〉 state (Fig. 11a), while KD₀ |±15/2〉_eq is a mixture of low-m_J states, |±15/2〉_eq = 39.27% |±1/2〉 + 30.55% |±3/2〉 + 18.33% |±5/2〉 + 8.33% |±7/2〉 + … (Fig. 11b). At this point, it is important to note that this fact in itself highlights a drastic change in the origin of the |±15/2〉 ground state upon passing from Cases I and II to Case III Dy(III) PBPY-7 complexes. The key point is that the pure apical KD₀ |±15/2〉_ap arises with the perfect D_5h symmetry of the PBPY-7 complex (Fig. 11a), whereas equatorial KD₀ |±15/2〉_eq results from some m_J mixing caused by non-axial CF terms B_kq, q ≠ 0, which can appear only in a distorted PBPY-7 geometry (Fig. 11b). Indeed, in the absence of non-axial CF terms B_kq (i.e., at perfect D_5h symmetry), the ground state KD₀ of the Case III complex has pure |±1/2〉 character with g_z = 1.32, g_x = g_y = 10.59, which features positive (in-plane) magnetic anisotropy with no magnetic axiality (Fig. 1c). It is therefore an objective to establish the specific distortions of the PBPY-7 geometry that produce the equatorial KD₀ |±15/2〉_eq ground state in Case III complexes. Below in this section we examine this issue using several model approaches based on CF theory.

Fig. 11 Difference between the nature of the |±15/2〉 ground state in Dy(III) PBPY-7 complexes for Cases I–III. (a) Cases I and II: KD₀ |±15/2〉_ap has pure |±15/2〉 character with the long magnetic axis (g_z ∼ 19.6) pointing to the apical ligands, (b) Case III: KD₀ |±15/2〉_eq is a mixture of several low-m_J states with the long magnetic axis (g_z ∼ 19.6) lying in the equatorial plane. In both cases, the electron density of KD₀ |±15/2〉 has the same oblate shaped electronic cloud that differs only in orientation.

3.5.2.b Simple CF model based on Bleaney's theory of magnetic anisotropy. A primary insight into the specific mechanism of the origin of the equatorial KD₀ |±15/2〉_eq due to the mixing of low-m_J states by the non-axial CF terms can be obtained with a simple CF model considering only the rank-2 CF parameters, B_2q. In fact, this approach is closely related to Bleaney's theory,⁷⁷ according to which the magnetic anisotropy of the lanthanide ion is determined by only two rank-2 CF parameters, the axial parameter B₂₀ and the rhombic parameter B₂₂, while higher-order CF parameters B_kq (k = 4 and 6) can be neglected.⁷⁷

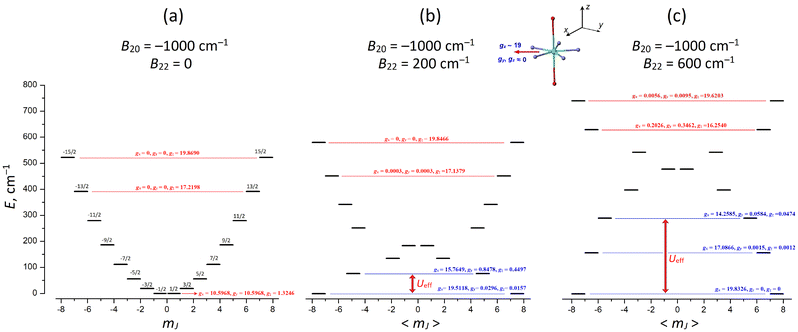
In the frame of this model, we consider the Dy(III) PBPY-7 complex with overall positive (in-plane) magnetic anisotropy, which is described by the negative axial CF parameter B₂₀ < 0 (in the Wybourne notation) and we explore the evolution of the ground and excited CF electronic states with increasing rhombic CF parameter B₂₂, the magnitude of which formally corresponds to the degree of distortion of the PBPY-7 complex in the equatorial plane (see the next section for more detail). For this, we perform comparative CF calculations at a fixed axial CF parameter of B₂₀ = −1000 cm⁻¹ and rhombic parameter B₂₂ increasing from 0 to 600 cm⁻¹ (Table 7 and Fig. 12).

Fig. 12 Formation of the equatorial KD₀ |±15/2〉_eq and the effective energy barrier, U_eff, for Case III PBPY-7 Dy(III) complexes upon increasing the rhombic CF parameter, B₂₂ (which originates from distortions in the equatorial plane of the PBPY-7 complex). (a) Regular D_5h PBPY-7 complex with the m_J = ±1/2 ground state; (b) moderately distorted complex, B₂₂ = 200 cm⁻¹; (c) strongly distorted PBPY-7 complex, B₂₂ = 600 cm⁻¹. At B₂₂ > 200 cm⁻¹, the low-m_J states are mixed by B₂₂ more efficiently to produce the lowest purely Ising equatorial KD₀ |±15/2〉_eq with g_x ≈ 19.8, g_y, g_z ≈ 0 (marked in blue). In all cases, the upper KDs (their g-tensors are marked in red) are rather insensitive to distortions, retaining their Ising-type nature with the long magnetic z axis parallel to the pentagonal C₅ axis of the PBPY-7 complex. Effective energy barrier, U_eff, is indicated by the red arrow. CF calculations are performed with fixed axial CF parameter, B₂₀ = −1000 cm⁻¹, and varied B₂₂ parameter (from 0 to 600 cm⁻¹).

Table 7 Evolution of energies (E, cm⁻¹) and g-tensors of the ground KD₀ and excited KD_1–7 in a Case III PBPY-7 Dy(III) complex with positive magnetic anisotropy (B₂₀ = −1000 cm⁻¹) upon increasing rhombic CF parameter B₂₂

	B 22, cm^−1
	0	20	50	100	200	400	600
State	E, cm^−1, gx,y,z
KD0	0	0	0	0	0	0	0
	g x = 10.5968	g x = 15.1092	g x = 17.8625	g x = 18.9831	g x = 19.5118	g x = 19.7635	g x = 19.8326
	g y = 10.5968	g y = 5.5499	g y = 1.8156	g y = 0.3641	g y = 0.0296	g y = 0.0006	g y = 0
	g z = 1.3246	g z = 1.0670	g z = 0.5110	g z = 0.1415	g z = 0.0157	g z = 0.0004	g z = 0
KD1	18.6	21.1	30.6	48.5	76.9	120.0	157.0
	g x = 0	g x = 4.7982	g x = 8.8665	g x = 12.8251	g x = 15.7649	g x = 16.8278	g x = 17.0866
	g y = 0	g y = 4.7457	g y = 6.9517	g y = 4.4883	g y = 0.8478	g y = 0.0332	g y = 0.0015
	g z = 3.9738	g z = 3.6894	g z = 2.9572	g z = 1.8423	g z = 0.4497	g z = 0.0233	g z = 0.0012
KD2	55.9	57.8	65.6	85.9	135.2	219.9	290.4
	g x = 0	g x = 0.2910	g x = 1.6794	g x = 5.0088	g x = 9.8966	g x = 13.5787	g x = 14.2585
	g y = 0	g y = 0.2958	g y = 1.7443	g y = 5.0717	g y = 5.4227	g y = 0 055	g y = 0.0584
	g z = 6.6230	g z = 6.5893	g z = 6.3757	g z = 5.4758	g z = 3.2450	g z = 0.4954	g z = 0.0474
KD3	111.9	113.6	120.6	138.1	184.0	296.1	398.8
	g x = 0	g x = 0.0053	g x = 0.0802	g x = 0.5945	g x = 3.3895	g x = 8.8745	g x = 11.1474
	g y = 0	g y = 0.0054	g y = 0.0836	g y = 0.6450	g y = 3.8569	g y = 4.8268	g y = 1.0299
	g z = 9.2722	g z = 9.2626	g z = 9.2107	g z = 9.0035	g z = 7.7977	g z = 3.6740	g z = 0.8364
KD4	186.5	188.1	194.9	211.3	252.3	355.8	478.4
	g x = 0	g x = 0	g x = 0.0016	g x = 0.0250	g x = 0.3576	g x = 3.3510	g x = 6.7213
	g y = 0	g y = 0	g y = 0.0017	g y = 0.0272	g y = 0.4216	g y = 4.4267	g y = 5.5485
	g z = 11.9214	g z = 11.9175	g z = 11.8965	g z = 11.8201	g z = 11.4793	g z = 9.1921	g z = 5.1388
KD5	279.7	281.3	287.9	303.7	342.2	434.1	543.4
	g x = 0	g x = 0	g x = 0	g x = 0.0005	g x = 0.0152	g x = 0.4121	g x = 2.1786
	g y = 0	g y = 0	g y = 0	g y = 0.0005	g y = 0.0179	g y = 0.5782	g y = 3.6028
	g z = 14.5706	g z = 14.5688	g z = 14.5592	g z = 14.5246	g z = 14.3808	g z = 13.6771	g z = 11.5791
KD6	391.6	393.1	399.6	415.0	451.7	535.9	630.6
	g x = 0	g x = 0	g x = 0	g x = 0	g x = 0.0003	g x = 0.0183	g x = 0.2026
	g y = 0	g y = 0	g y = 0	g y = 0	g y = 0.0003	g y = 0.0256	g y = 0.3462
	g z = 17.2198	g z = 17.2190	g z = 17.2148	g z = 17.1998	g z = 17.1379	g z = 16.8622	g z = 16.2540
KD7	522.1	523.6	530.0	545.0	580.1	657.9	740.9
	g x = 0	g x = 0	g x = 0	g x = 0	g x = 0	g x = 0.0003	g x = 0.0056
	g y = 0	g y = 0	g y = 0	g y = 0	g y = 0	g y = 0.0004	g y = 0.0095
	g z = 19.8690	g z = 19.8688	g z = 19.8677	g z = 19.8635	g z = 19.8466	g z = 19.7726	g z = 19.6203

---

In the regular D_5h PBPY-7 complex (B₂₂ = 0), the E vs. m_J energy diagram has a perfect parabolic profile with the lowest m_J = ±1/2 state and the upper m_J = ±15/2 state (Fig. 12a). As the rhombic CF parameter B₂₂ increases, the easy-plane character of the ground-state g-tensor (KD₀, g_z = 1.32, g_x = g_y = 10.59 at B₂₂ = 0) is transformed into a nearly perfect Ising one (g_x = 19.80, g_y, g_y ∼ 0 at B₂₂ = 500 cm⁻¹) with the long magnetic x axis lying in the equatorial plane (Fig. 12b and c). Also note that with increasing rhombic parameter B₂₂, the most drastic changes in g-tensors occur in the ground state KD₀ and low-lying excited CF states (KD_1–4), while the upper CF states (KD₆ and KD₇) change insignificantly (Table 7; in Fig. 12 their g-tensors are marked in red).

It is also important that the energy gap, ΔE₀₁, between the ground KD₀ and first excited KD₁ increases with increasing B₂₂, thereby enhancing the effective energy barrier, U_eff, and SMM performance. At strong distortions (B₂₂ > 400 cm⁻¹), not only the ground KD₀ but also low-lying KDs acquire Ising character (Fig. 12c and Table 7); this implies that U_eff may increase beyond the ΔE₀₁ energy gap due to suppression of thermally induced QTM processes in the excited KDs (Fig. 12c).

These results clearly show that in Case III PBPY-7 Dy(III) complexes with overall positive magnetic anisotropy, distortions in the equatorial plane lead to a larger effective barrier, U_eff, and improved SMM characteristics. However, this only occurs when the in-plane distortions are strong enough to efficiently mix the low-m_J states near the bottom of the parabolic E vs. m_J profile to form the equatorial KD₀ |±15/2〉_eq = 39.27% |±1/2〉 + 30.55% |±3/2〉 + 18.33% |±5/2〉 + 8.33% |±7/2〉 + … (Fig. 12 and Table 7).

3.5.2.c CF analysis of in-plane distortions resulting in the equatorial KD₀ |±15/2〉_eq ground state. In this section, we examine specific distortions of the PBPY-7 coordination sphere of the Dy(III) ion leading to a large rhombic parameter B₂₂, which causes formation of the magnetically axial equatorial KD₀ |±15/2〉_eq ground state (Fig. 12 and Table 7). The impact of distortions on the CF energy spectra and SMM characteristics is analyzed with the superposition CF model,^78,79 which relates the ‘global’ B_kq CF parameters to the actual coordination geometry of the metal ion in terms of ‘intrinsic’ CF parameters b_k describing local metal–ligand interactions,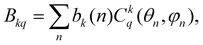where index n runs over metal–ligand pairs involved in the coordination polyhedron of the Ln³⁺ ion, b_k(n) are the three (k = 2, 4, 6) intrinsic CF parameters, C^k_q(θ_n, φ_n) are spherical tensor operators, and (θ_n, φ_n) are the angular coordinates of the nth ligand atom. The foundations of the superposition CF model and its applications are well documented in the literature.^78,79

In these CF calculations, we used an idealized structure of the [DyN₃O₄] core, in which the apical O3–Dy–O4 group is strictly linear and the N₃O₂ pentagon (involving the equatorial atoms O1, O2, N2, N3 and N4) is planar. All atomic distances are set to the averaged experimental values for each group of atoms, namely 2.25 Å for apical O atoms, 2.45 Å for N atoms and 2.28 Å for the equatorial O atoms; the N–Dy–N bond angles are fixed at 72°, while the O1–Dy–O2 bond angle (φ) is variable (Fig. 13a). The intrinsic CF parameters b_k for the equatorial N atoms are set to b₂(N) = 1000, b₄(N) = 300 and b₆(N) = 50 cm⁻¹. For the oxygen atoms, b_k are set to b₂(O) = 1200, b₄(O) = 500 and b₆(O) = 100 cm⁻¹ at a reference distance of R₀ = 2.26 Å; the radial dependence of the b_k(O) parameters for the apical (O3, O4, R = 2.25 Å) and equatorial (O1, O2, R = 2.28 Å) oxygen atoms is described by b_k(R) = b_k(R₀)(R₀/R)^t(k), where t(2) = 6, t(4) = 8 and t(6) = 11.^78,79

Fig. 13 (a) Idealized structure of the DyN₃O₄ core of complexes 1–3 employed in CF calculations; all atomic distances are given in Å, (b) dependence of the rhombic CF parameter B₂₂ on φ, the O1–Dy–O2 bond angle, (c) variation of the energy separation, ΔE₀₁, of the first excited KD₁ with increasing angle φ.

Comparative CF calculations for various types of distortions showed that the strongest impact on the formation of the Ising equatorial KD₀ |±15/2〉_eq ground state was due to in-plane (xy) distortions of the equatorial N₃O₂ pentagon, which led to a large rhombic CF term B₂₂. In this respect, it has also been found that angular in-plane distortions are more important than radial distortions. On the other hand, other types of distortion, including bending distortions of the apical O3–Dy–O4 group and out-of-plane (z) displacements of the equatorial O and N atoms are much less important. In particular, out-of-plane distortions in the N₃O₂ pentagon result mainly in the non-axial rank-2 CF parameters B_2±1, which have a minor effect on the magnetic anisotropy compared to that of B₂₂.

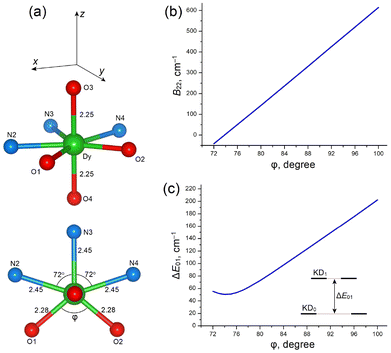
CF analysis indicates that the O1–Dy–O2 bond angle (φ) in the equatorial plane is a key structural parameter (Fig. 13a). We studied the influence of angle φ on the rhombic CF parameter B₂₂, g-tensors of the ground and excited KDs, and the CF splitting energy patterns (Table 8 and Fig. 13). Increasing angle φ from 72° to 100° results in rapid linear growth of the rhombic parameter B₂₂ from almost zero to about 600 cm⁻¹ (Fig. 13b), which is followed by the formation of the equatorial KD₀ |±15/2〉_eq ground state with g_x ≈ 19.6 (lying in the equatorial xy plane, Fig. 13a and Table 8). An increase of φ is also accompanied by nearly linear growth of the energy gap, ΔE₀₁, between the ground KD₀ and the first excited KD₁, from ∼50 to ∼200 cm⁻¹ (Fig. 13c and Table 8). The total CF splitting energy, ΔECF, also increases considerably, from 368 to 645 cm⁻¹ (Table 8).

Table 8 The influence of the O1–Dy–O2 bond angle (φ) on the rhombic CF parameter B₂₂, g-tensors of KD₀ and KD₁, energy gap ΔE₀₁ between KD₀ and KD₁ and the total CF splitting energy ΔE_CF of the ⁶H_15/2 multiplet of the Dy(III) ion in the idealized DyN₃O₄ core (Fig. 13a)

		KD0				KD1
φ	B 22, cm^−1	g x	g y	g z	ΔE01, cm^−1	g x	g y	g z	ΔECF, cm^−1
72°	−41	6.388	14.367	1.129	55.5	1.003	6.759	3.592	368.4
80°	143	17.309	2.356	0.601	72.7	11.067	2.413	3.474	391.7
88°	331	18.903	0.346	0.133	123.3	14.512	1.546	1.613	470.6
92°	426	19.204	0.153	0.067	149.3	15.511	0.974	0.801	523.1
96°	520	19.404	0.073	0.035	175.6	16.067	0.599	0.429	582.2
100°	614	19.542	0.037	0.019	202.2	16.407	0.381	0.268	645.3

---

At a large angle φ, close to the experimental value of ≈100° in complexes 1–3 (Tables S3–S5 ESI†), the ground-state g-tensor has almost pure Ising-type character (g_x ≈ 19.6, g_y, g_z ≈ 0.02–0.03), which is inherent to the |±15/2〉 state. Note also that at φ ≈ 100° the energy gap is ΔE₀₁ = 202 cm⁻¹ and the overall CF energy is ΔE_CF = 645 cm⁻¹, which are reasonably consistent with the results of ab initio calculations for 1–3 (Table 4). In contrast, at a small O1–Dy–O2 bond angle (φ < 80°), CF calculations reveal the poor axiality of KD₀ (due to a large transverse component, g_y, g_z) and small energy separation, ΔE₀₁, of the first excited KD₁ (∼100 cm⁻¹ or less, Table 8), which together lead to a degradation or even complete absence of SMM properties in PBPY-7 complexes with a more symmetric DyN₃O₄ core.

Similar CF calculations for analogous complexes with weaker apical ligands (Cl₂, Cl/Ph₃PO or Cl/Cy₃PO)^45,46 show fairly similar results. This indicates that in Case III PBPY-7 complexes, the SMM characteristics are rather insensitive to the nature of the apical ligands, as they are mainly governed by angular distortions in the equatorial plane. However, a detailed discussion of these issues is quite lengthy and thus it is beyond the scope of this article.

3.5.2.d Relationship between the axial CF parameters B₂₀, B₄₀ and B₆₀ in Case I–III Dy(III) PBPY-7 complexes. Although the above model provides basic insights into the origin of the equatorial KD₀ |±15/2〉_eq due to mixing of low-m_J states by non-axial CF components, it does not describe the actual energy spectrum of KDs of PBPY-7 Dy(III) complexes due to the absence of higher-order CF terms, B_4q and B_6q. This is especially true for Case III PBPY-7 complexes, where the profile of the spin energy diagram is far from being parabolic due to the presence of large rank-4 CF parameters (Fig. 1c).^49,80

In this section, we consider a more realistic CF model for Case III complexes involving the full set of B_kq CF parameters (k = 2, 4, 6). The key point is that in the regular D_5h PBPY-7 complex, the CF Hamiltonian comprises only the axial CF terms, B₂₀, B₄₀ and B₆₀; all non-axial terms, B_kq, are strictly zero under the symmetry conditions. Therefore, it is important to establish general relationships between B₂₀, B₄₀ and B₆₀ when passing sequentially from Case I to Case II and III PBPY-7 Dy(III) complexes. To this end, we take advantage of the superposition CF model^78,79 described in the previous section.

In a regular D_5h PBPY-7 complex, there are two groups of intrinsic CF parameters related to the apical and equatorial ligands, b_k(ap) and b_k(eq) (k = 2, 4, 6). According to eqn (4), in the PBPY-7 Dy(III) complex, their contributions to the global CF parameters B_kq are given by

B₂₀ = 2b₂(ap) − 2.5 b₂(eq), (5a)

B₄₀ = 2b₄(ap) + 1.875 b₄(eq), (5b)

B₆₀ = 2b₆(ap) − 1.5625 b₆(eq). (5c)

It is important to note here that the contributions to the axial CF parameter B₄₀ from the apical and equatorial ligands are summed, while those in parameters B₂₀ and B₆₀ are subtracted. This implies that B₄₀ increases as the strength of the equatorial ligands increases, while B₂₀ and B₆₀ decrease, and at a certain point they change sign from positive to negative. In particular, in a perfectly symmetric PBPY-7 complex with equal metal–ligand distances (i.e., where b_k(ap) = b_k(eq) = b_k for all metal–ligand pairs), the axial CF parameters B_k0 are expressed by B₂₀ = −0.5b₂, B₄₀ = +3.875b₄, and B₆₀ = +0.4375b₆. CF calculations show that this complex exhibits positive magnetic anisotropy due to the m_J = ±1/2 ground state and thus it falls under Case III (Fig. 1c). Therefore, in Case III, the axial CF parameter B₄₀ > 0 is always positive and it dominates due to its far larger factor, eqn (5b). This is supported by experimental data for PBPY-7 lanthanide complexes with an equatorial ligand of DAPSC type, indicating B₄₀ ∼ +1500 cm⁻¹.⁸⁰ In addition, these results show that the B₆₀ parameter is of minor importance in Case III PBPY-7 complexes, both due to the small factor (0.4375) and because of the typical relationship of b₆ < b₂, b₄ for the intrinsic CF parameters.⁷⁹ Therefore, below in our model CF analysis of PBPY-7 Dy(III) complexes, the rank k = 6 B₆₀ parameter can safely be neglected.

Thus, since only two CF parameters (B₂₀ and B₄₀) are active in symmetric D_5h PBPY-7 complexes, the nature of the energy spectrum is determined only by their ratio, B₂₀/B₄₀. It is therefore important to find specific values for the B₂₀/B₄₀ ratio that define the boundaries between Cases I, II and III.

The Case I PBPY-7 complex has a parabolic profile of spin energy levels with the lowest KD₀ |±15/2〉 and KD₇ |±1/2〉 at the top of the parabola (Fig. 14a). The lower boundary of Case I is the point below which KD |±1/2〉 ceases to be the upper level. Calculations show that this occurs at B₂₀/B₄₀ = 1.35. On the other hand, the lower boundary of Case II corresponds to equal energies of KD |±15/2〉 and KD |±1/2〉. This point is reached at B₂₀/B₄₀ ≈ −0.07. Thus, these results quantify the limiting points of the realization of Cases I, II and III for PBPY-7 Dy(III) complexes in terms of CF parameters (Fig. 14):

Case I: B₂₀/B₄₀ > 1.35, (6a)

Case II: 1.35 ≥ B₂₀/B₄₀ ≥ −0.07, (6b)

Case III: B₂₀/B₄₀ < −0.07. (6c)

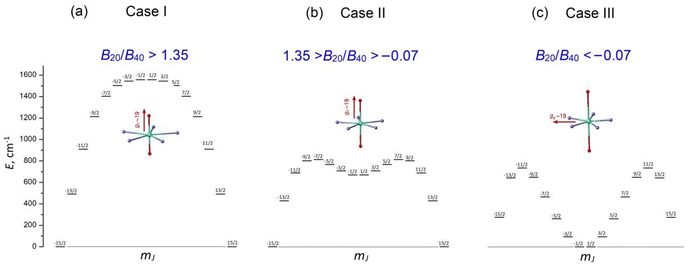Fig. 14 Criterion for the realization of Cases I, II and III of regular D_5h PBPY-7 Dy(III) complexes in terms of CF theory. (a) Case I, B₂₀/B₄₀ > 1.35, (b) Case II, 1.35 > B₂₀/B₄₀ > −0.07, (c) Case III, B₂₀/B₄₀ < −0.07. In Case III, distortions in the equatorial plane (which operate through the rhombic CF parameter B₂₂) mix the low-m_J states near the parabolic bottom of the E vs. m_J profile to produce the lowest equatorial KD₀ |±15/2〉_eq = 39.27% |±1/2〉 + 30.55% |±3/2〉 + 18.33% |±5/2〉 + 8.33% |±7/2〉 + … with g_x ≈ 19.8, g_y ≈ 0, g_z ≈ 0 (see Table 7 and Fig. 12).

In terms of intrinsic CF parameters b_k, the PBPY-7 complex falls under Case III at 2b₂(ap) − 2.5 b₂(eq) < 0 (eqn (5a)), which corresponds to the ratio of b₂(eq)/b₂(ap) > 0.8. Hence, already with equal strengths of apical and equatorial ligands (b₂(eq) = b₂(ap)), the PBPY-7 complex definitely belongs to Case III.

According to eqn (6a–c), in the complexes of Cases I and II, the CF strength of the apical ligands should be significantly larger than that of the equatorial ligands. In particular, for this, the PBPY-7 complex must have short metal–ligand distances in the apical positions and long distances in the equatorial plane.

PBPY-7 complexes where the strength of the apical ligands is comparable to or weaker than that of equatorial ligands fall under Case III (Fig. 14c). Our complexes 1–3 and similar PBPY-7 Dy(III) complexes reported in ref. 45–48 certainly fall under Case III. Note that for Case III (Fig. 14c), the specific mechanism of formation of the equatorial KD₀ |±15/2〉_eq (Fig. 11b) remains essentially the same as in the case of the simplified model discussed above (Table 7 and Fig. 12). The reason is that the local energy structure of low-m_J states near the bottom of the diagram (Fig. 14c) is very close to that of the parabolic profile shown in Fig. 12a. Our CF calculations support this conclusion.

4. Conclusions

In summary, we report the syntheses, structures, and magnetic properties of three new Dy complexes obtained by the reactions of dysprosium perchlorate with mixed ligands, rigid pentadentate 2,6-diacetylpyridine bis(R-hydrazones) and monodentate tricyclohexylphosphine oxide (Cy₃PO) or triphenylphosphine oxide (Ph₃PO), in the presence of Et₃N as a deprotonating base: [Dy(L^CH₃)(Cy₃PO)₂]ClO₄·CH₃CN (1), [Dy(L^2(t-Bu))(Ph₃PO)₂]ClO₄·0.63C₂H₅OH (2), and [Dy(L^OCH₃)(Ph₃PO)₂]ClO₄·2H₂O (3), where L^CH₃ = [2,6-diacetylpyridine bis(acetylhydrazone)]²⁻, L^2(t-Bu) = [2,6-diacetylpyridine bis(3,5di-tert-butylbenzoylhydrazone)]²⁻, and L^CH₃ = [2,6-diacetylpyridine bis(4-methoxybenzoylhydrazone)]²⁻. The central Dy³⁺ ion is seven-coordinated by three N and two O atoms in the equatorial plane of the chelating pentadentate ligands and two O atoms of the apical ligands in all the structures. The CShM analysis showed that the local geometry of the Dy(III) ions in the complexes was PBPY-7 with pseudo-D_5h symmetry for the [DyN₃O₄] core. For all three complexes, the magnetization barrier values in zero dc field and in the presence of a constant magnetic field are similar and are around 320–350 K, indicating that the nature of the substituents in the equatorial pentadentate ligands have almost no effect on the magnetic behavior of these mononuclear SMMs.

The presence of two strong apical donor ligands, Cy₃PO or Ph₃PO, improves the SMM characteristics of 1–3 compared to similar PBPY-7 complexes containing two Cl⁻ or Cl(Cy₃PO/Ph₃PO) in the apical positions,^45,46 as it leads to a slow relaxation of magnetization in zero dc field and larger magnetization barriers. The ground states of 1–3 are almost pure Ising-type KD₀ |±15/2〉 with very small transverse components (g_x, g_y ∼ 0, g_z ∼ 19.6), which suppress the ground-state QTM processes. However, the first excited KD₁ loses magnetic axiality (Table 4), which causes fast thermally assisted quantum tunneling of magnetization. As a result, the effective energy barriers (U_eff) for complexes 1–3 are close to the energy of the first excited Kramers doublets, KD₁, as estimated from ab initio calculations.

Although complexes 1–3 have rather high magnetization barriers, U_eff, their heights are much lower than those of the record PBPY-7 Dy SMM complexes^26–29,33 as well as other PBPY-7 Dy complexes containing monodentate weakly coordinating ligands with long Dy–O(N) distances (H₂O, THF, pyridine) at the equatorial positions and strong donor ligands (acyl/aryl alkoxides, aryl/acyl/phosphonamides, silane/phosphine oxides) at the apical positions.^34–41 It is also crucial that in all high-performance PBPY-7 Dy SMMs the long magnetic z axis invariably points to the apical ligands, whereas in PBPY-7 complexes with an equatorial ligand based on 2,6-diacetylpyridine (our complexes 1–3 and similar complexes reported in ref. 45–48), the long magnetic axis lies in the equatorial xy plane of the pentadentate L^R ligand (Fig. 11b and Fig. S21, ESI†).

To elucidate the origin of these differences, we have examined in detail the influence of the competition between the CF strength of the apical and equatorial ligands in PBPY-7 Dy complexes on the CF splitting pattern and energy barrier, U_eff, in terms of CF theory. Depending on the ratio between the apical and equatorial CF components, PBPY-7 Dy complexes fall into three groups (shown as Cases I, II, and III in Fig. 1). In terms of the CF parameters B_kq, the ranges of Cases I–III are largely quantified by the ratio of the two axial CF parameters B₂₀ and B₄₀: B₂₀/B₄₀ > 1.35 (Case I, Fig. 14a), 1.35 > B₂₀/B₄₀ > −0.07 (Case II, Fig. 14b) and B₂₀/B₄₀ < −0.07 (Case III, Fig. 14c).

In Cases I and II, where the apical field prevails over the equatorial field (CF_ap ≫ CF_eq, and CF_ap > CF_eq, Fig. 1a and b, respectively), the ground state is the ‘apical’ Kramers doublet KD₀ |±15/2〉_ap with a long magnetic z axis directed toward the apical ligands. The maximum SMM performance in Cases I and II is reached at the ideal D_5h symmetry of the PBPY-7 complex, which ensures perfect magnetic axiality of the ground KD₀ |±15/2〉 and excited KDs |±m_J〉. However, in Case III (CF_ap < CF_eq), a fundamentally different situation arises because the oblate |±15/2〉 ground state turns into the prolate |±1/2〉 ground state (Fig. 1c). As a result, the overall magnetic anisotropy of the complex switches from the easy-axis (z) to the easy-plane (xy) regime and the double-well potential turns into a single-well potential (Fig. 1c). This implies that the regular (D_5h) PBPY-7 Dy complex from Case III is no longer a SMM (Fig. 1c). Therefore, in Case III, the necessary prerequisites for SMM behavior (i.e., double-well potential and barrier U_eff) can only arise due to distortions of the PBPY-7 structure of the complex; our complexes 1–3 definitely refer to Case III.

We have explored the specific mechanism of the origin of this ‘equatorial’ KD₀ |±15/2〉_eq (Fig. 11b) in the frame of CF theory. With the spin quantization z axis parallel to the apical axis, the ‘equatorial’ KD₀ |±15/2〉_eq (with g_x ∼ 19.6 and g_y, g_z ∼ 0) is a mixture of low-m_J states (Fig. 11b). This mixing is mainly caused by the rhombic CF parameter B₂₂ arising from distortions in the N₃O₂ equatorial plane, the most important of which is the deviation of the O1–Dy–O2 bond angle from 72° (Fig. 13). As B₂₂ increases, the ground KD₀ |±1/2〉 with easy-plane anisotropy (g_x = g_y = 10.59, g_z = 1.32) progressively transforms into an ‘equatorial’ KD₀ |±15/2〉_eq with easy-axis anisotropy (with g_x ∼ 19.6, g_y, g_z ∼ 0), in which the long magnetic x axis lies in the equatorial xy plane (Table 7 and Fig. 12). This occurs at large values of the rhombic parameter, B₂₂ > 500 cm⁻¹ (Table 7). In complexes 1–3 such values of B₂₂ are reached due to the large O1–Dy–O2 bond angle, about 100° (Table 8 and Fig. 13b). Therefore, apart from the strong equatorial CF of the negatively charged (N₃O₂)²⁻ chelate node of L^R ligands, the large O1–Dy–O2 bond angle in the equatorial plane is the direct cause of the pronounced SMM behavior of 1–3.

Thus, the attribution of PBPY-7 complexes 1–3 and similar complexes^45–48 to Case III highlights a breakdown of apical magnetic axiality, which plays a key role in the high SMM performance in Case I and II PBPY-7 Dy complexes. In other words, the main advantage of PBPY-7 complexes providing a strictly axial CF potential (i.e., with zero non-axial CF parameters B_kq, q ≠ 0) in the regular D_5h geometry is completely lost in Case III, since here the SMM performance is governed by distortions in the N₃O₂ equatorial plane rather than by high D_5h symmetry and strong apical ligands. As a result, Case III complexes can hardly be competitive with Case I and II complexes in terms of SMM performance due to the lower total CF splitting energy of the ⁶H_15/2 multiplet and also because of the absence of magnetic axiality in the excited KDs.

It is also important to point out that the apical KD₀ |±15/2〉_ap and equatorial KD₀ |±15/2〉_eq have the same oblate shaped electron clouds, which differ only in orientation (Fig. 11), but have quite different origins. Turning the apical KD₀ |±15/2〉_ap into the equatorial KD₀ |±15/2〉_eq is a key trigger that switches between high SMM performance (Cases I and II) and low SMM performance (Case III) for PBPY-7 Dy(III) complexes.

In light of the above, when assessing the prospects of complexes 1–3 and other related complexes^45–48 as performable SMMs, it should be emphasized that there is a general crucial problem concerning the rigid [N₃O₂]²⁻-type negatively charged ligands in the equatorial plane, which produce a strong equatorial CF exceeding the CF of apical ligands. Obviously, such a situation is extremely unfavorable because the oblate Dy³⁺ ion prefers a strong apical CF and weak equatorial CF to attain a maximal energy barrier, U_eff, and blocking temperature, T_B.

In this work, we aimed to improve the SMM characteristics of the PBPY-7 Dy complexes with rigid N₃O₂-type Schiff-base ligands by enhancing the apical CF using strong neutral Cy₃PO and Ph₃PO donor ligands in the apical positions. However, despite some improvement in the SMM performance of 1–3, this was insufficient to change the overall positive (easy plane) magnetic anisotropy into a negative one (easy axis), since the long magnetic axis with g_x ∼ 19.6 still lay in the equatorial xy plane of complexes 1–3 (Fig. S21, ESI†). Evidence for the dominance of the equatorial CF over the apical CF is the similarity of the Dy–O bond lengths in the equatorial plane of N₃O₂, 2.25–2.30 Å, to the distances to the apical ligands (Dy–O, 2.23–2.26 Å).

The unfavorable balance between the apical CF and equatorial CF can be improved by further enhancing the apical CF through the use of the strongest negatively charged donor ligands with the shortest Dy–X apical bonds (∼2.05–2.10 Å) occupying two apical positions, such as BuO⁻, PhO⁻, Me₃SiO⁻, MeO⁻ and AdO⁻. The only known example is the recently reported PBPY-7 anion complex, [Dy(L_N3O2)(L_ADTP)₂]⁻ (H₂L_N3O2 = 2,6-diformylpyridine bis(4-phenylsemicarbazone), HL_ADTP = 4-(anthracen-9-yl)-2-(1,3-dithiolan-2-yl)phenol), which reveals a negative (easy-axis) magnetic anisotropy and ‘true’ m_J = ±15/2 ground state with the long g_z axis pointing to the apical ligands.⁸¹

Alternatively, improved balance between the equatorial and apical CFs may be obtained by weakening the equatorial CF through the use of substituents with longer Dy–X bonds in the N₃X₂ chelate ring of the 2,6-diacetylpyridine-based ligand, such as L_N5 in [Dy(L_N5)(Ph₃SiO)₂]²⁷ or L_N3S2 in [Dy(L_N3S2)(L_ADTP)₂]⁻ (H₂L_N3S2 = 2,6-diformylpyridine bis(4-phenylthiosemicarbazone)).⁸¹ The SMM characteristics of these complexes are much higher than those of 1–3 (U_eff > 1000 K vs. ∼350 K) and their long magnetic axes are oriented toward the apical ligands. The CF splitting patterns of these complexes suggest that they belong to Case II.

One more way to take advantage of the rigid structure of equatorial pentadentate ligands like N₃O₂ is to reduce the negative electric charge in the equatorial plane through the use of weaker neutral protonated ligands, H₂N₃O₂. So far, no PBPY-7 Dy complexes with rigid neutral pentadentate H₂N₃O₂ equatorial ligands have been described in the literature. Our further studies are aimed at realizing this approach.

Author contributions

Conceptualization, E. B. Y., V. S. M.; synthesis and characterization of the materials, T. A. B., V. A. K.; X-ray crystallography, formal analysis, I. A. Y.; measurement of dc and ac magnetic properties, formal analysis, M. V. Z., A. I. D., N. N. E., K. A. B.; ab initio calculations, analysis of dc properties, D. V. K.; analysis of the dynamic magnetic properties, E. A. Y.; crystal-field calculations, analysis single-ion magnet behavior of Dy PBPY-7 complexes, V. S. M.; writing–original draft preparation, T. A. B., I. A. Y., A. I. D., D. V. K., E. A. Y., V. S. M., E. B. Y.; writing–review and editing, V. S. M., E. B. Y.; supervision, project administration, E. B. Y. All authors have read and agreed to the published version of the manuscript.

Data availability

The authors confirm that the data supporting the findings of this study are available within the main text of paper and its ESI.† Crystal-field calculations were performed using V. S. M.'s 4f-shell program suite described in V. S. Mironov and L. E. Li, J. Alloys Compd., 1998, 279, 83–92. More detailed data are available on request from the corresponding author, upon reasonable request. Crystallographic details are available in the ESI in CIF format. CCDC numbers 2239615, 2239616, and 2239617.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Ministry of Science and Higher Education within the state assignment for FRC PCP MC RAS, state registration numbers: 124013100858-3 (FFSG-2024-0009) and 124020200104-8 (FFSG-2024-0004). The work was partially performed using equipment of the Computational and Analytical Center of Collective Use of the FRC PCP MC RAS. The work was carried out within the state assignment of NRC ‘Kurchatov institute’.

References

1. N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level, J. Am. Chem. Soc., 2003, 125, 8694–8695.
2. L. Sorace, C. Benelli and D. Gatteschi, Lanthanides in molecular magnetism: old tools in a new field, Chem. Soc. Rev., 2011, 40, 3092–3104.
3. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide single-molecule magnets, Chem. Rev., 2013, 113, 5110–5148.
4. R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley, Hoboken, 2015.
5. S. T. Liddle and J. Van Slageren, Improving f-Element Single Molecule Magnets, Chem. Soc. Rev., 2015, 44, 6655–6669.
6. K. L. M. Harriman and M. Murugesu, An Organolanthanide Building Block Approach to Single-Molecule Magnets, Acc. Chem. Res., 2016, 49, 1158–1167.
7. J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry Strategies for High Performance Lanthanide-Based Single-Molecule Magnets, Chem. Soc. Rev., 2018, 47, 2431–2453.
8. M. Feng and M.-L. Tong, Single Ion Magnets from 3d to 5f: Developments and Strategies, Chem. – Eur. J., 2018, 24, 7574–7594.
9. Z. Zhu, M. Guo, X.-L. Li and J. Tang, Molecular Magnetism of Lanthanide: Advances and Perspectives, Coord. Chem. Rev., 2019, 378, 350–364.
10. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-Molecule Magnets: From Mn₁₂-Ac to Dysprosium Metallocenes, a Travel in Time, Coord. Chem. Rev., 2021, 441, 213984.
11. (a) F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Reading and writing single-atom magnets, Nature, 2017, 543, 226–228; (b) R. Sessoli, Single-atom data storage, Nature, 2017, 543, 189–190.
12. (a) L. Bogani and W. Wernsdorfer, Molecular spintronics using single-molecule magnets, Nat. Mater., 2008, 7, 179–186; (b) S. Sanvito, Molecular spintronics, Chem. Soc. Rev., 2011, 40, 3336–3355.
13. (a) M. N. Leuenberger and D. Loss, Quantum computing in molecular magnets, Nature, 2001, 410, 789–793; (b) A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Molecular spins for quantum computation, Nat. Chem., 2019, 11, 301–309.
14. M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352.
15. E. Coronado, Molecular Magnetism: From Chemical Design to Spin Control in Molecules, Materials and Devices, Nat. Rev. Mater., 2020, 5, 87–104.
16. E. Moreno-Pineda and W. Wernsdorfer, Measuring Molecular Magnets for Quantum Technologies, Nat. Rev. Phys., 2021, 3, 645–659.
17. T. Pugh, N. F. Chilton and R. A. Layfield, A Low-Symmetry Dysprosium Metallocene Single-Molecule Magnet with a High Anisotropy Barrier, Angew. Chem., Int. Ed., 2016, 55, 11082–11085.
18. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442.
19. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403.
20. L. Ungur and L. F. Chibotaru, Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets, Inorg. Chem., 2016, 55, 10043–10056.
21. A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Low-coordinate mononuclear lanthanide complexes as molecular nanomagnets, Coord. Chem. Rev., 2018, 367, 163–216.
22. L. Ungur and L. F. Chibotaru, Magnetic anisotropy in the excited states of low symmetry lanthanide complexes, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090.
23. S.-D. Jiang and S.-X. Qinc, Prediction of the Quantized Axis of Rare-Earth Ions: the Electrostatic Model with Displaced Point Charges, Inorg. Chem. Front., 2015, 2, 613–619.
24. B. M. Day, F.-S. Guo and R. A. Layfield, Cyclopentadienyl Ligands in Lanthanide Single-Molecule Magnets: One Ring To Rule Them, All?, Acc. Chem. Res., 2018, 51, 1880–1889.
25. R. Sun, C. Wang, B. W. Wang, Z. M. Wang, Y. F. Chen and S. Gao, Low-coordinate bis(imidazolin-2-iminato) dysprosium(III) single-molecule magnets, Inorg. Chem. Front., 2023, 10, 485–492.
26. Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet, Angew. Chem., Int. Ed., 2016, 55, 16071–16074.
27. A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Engineering macrocyclic high performance pentagonal bipyramidal Dy(III) single-ion magnets, Chem. Commun., 2020, 56, 12037–12040.
28. J. Long, A. O. Tolpygin, D. M. Lyubov, N. Y. Rad'kova, A. V. Cherkasov, Y. V. Nelyubina, Y. Guari, J. Larionova and A. A. Trifonov, High magnetization reversal barriers in luminescent dysprosium octahedral and pentagonal bipyramidal single-molecule magnets based on fluorinated alkoxide ligands, Dalton Trans., 2021, 50, 8487–8496.
29. J.-P. Sutter, V. Béreau, V. Jubault, K. Bretosh, C. Pichon and C. Duhayon, Magnetic anisotropy of transition metal and lanthanide ions in pentagonal bipyramidal geometry, Chem. Soc. Rev., 2022, 51, 3280–3313.
30. Z. Zhu, C. Zhao, T. Feng, X. Liu, X. Ying, X. L. Li, Y. Q. Zhang and J. Tang, Air-Stable Chiral Single-Molecule Magnets with Record Anisotropy Barrier Exceeding 1800 K, J. Am. Chem. Soc., 2021, 143, 10077–10082.
31. W. J. Xu, Q. C. Luo, Z. H. Li, Y. Q. Zhai and Y. Z. Zheng, Bis-Alkoxide Dysprosium(III) Crown Ether Complexes Exhibit Tunable Air Stability and Record Energy Barrier, Adv. Sci., 2024, 11, 2308548.
32. J. Corredoira-Vazquez, C. Gonzalez-Barreira, P. Oreiro-Martínez, A. M. García-Deibe, J. Sanmartín-Matalobos and M. Fondo, Synthesis and applications of lanthanoid complexes of pentadentate and hexadentate N₅ and N₆ macrocycles: A review, J. Rare Earths, 2024, 42, 1–15.
33. Y.-S. Ding, T. Han, Y.-Q. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, A Study of Magnetic Relaxation in Dysprosium(III) Single-Molecule Magnets, Chem. – Eur. J., 2020, 26, 5893–5902.
34. Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, J. Am. Chem. Soc., 2016, 138, 2829–2837.
35. I. F. Dıáz-Ortega, J. M. Herrera, S. Dey, H. Nojiri, G. Rajaraman and E. Colacio, The effect of the electronic structure and flexibility of the counteranions on magnetization relaxation in [Dy(L)₂(H₂O)₅]³⁺ (L = phosphine oxide derivative) pentagonal bipyramidal SIMs, Inorg. Chem. Front., 2020, 7, 689–699.
36. Y.-C. Chen, J.-L. Liu, Y. Lan, Z.-Q. Zhong, A. Mansikkamäki, L. Ungur, Q.-W. Li, J.-H. Jia, L. F. Chibotaru, J.-B. Han, W. Wernsdorfer, X.-M. Chen and M.-L. Tong, Dynamic Magnetic and Optical Insight into a High Performance Pentagonal Bipyramidal Dy^III Single-Ion Magnet, Chem. – Eur. J., 2017, 23, 5708–5715.
37. Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Q.-C. Luo, T. Han and Y.-Z. Zheng, Breaking the axiality of pentagonal-bipyramidal dysprosium(III) single-molecule magnets with pyrazolate ligands, Inorg. Chem. Front., 2020, 7, 4367–4376.
38. Y.-S. Ding, K.-X. Yu, D. Reta, F. Ortu, R. E. P. Winpenny, Y.-Z. Zheng and N. F. Chilton, Field- and temperature-dependent quantum tunnelling of the magnetisation in a large barrier single-molecule magnet, Nat. Commun., 2018, 9, 3134–3144.
39. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441–5450.
40. Z. Jiang, L. Sun, Q. Yang, B. Yin, H. Ke, J. Han, Q. Wei, G. Xie and S. Chen, Excess axial electrostatic repulsion as a criterion for pentagonal bipyramidal Dy^III single-ion magnets with high U_eff and T_B, J. Mater. Chem. C, 2018, 6, 4273–4280.
41. Y. Dong, L. Zhu, B. Yin, X. Zhu and D. Li, Regulating the magnetic properties of seven-coordinated Dy(III) single-ion magnets through the effect of positional isomers on axial crystal-field, Dalton Trans., 2021, 50, 17328–17337.
42. J. Long, A. N. Selikhov, E. Mamontova, K. A. Lyssenko, Y. Guari, J. Larionova and A. A. Trifonov, Single-molecule magnet behaviour in a Dy(III) pentagonal bipyramidal complex with a quasi-linear Cl-Dy-Cl sequence, Dalton Trans., 2019, 48, 35–39.
43. M. Li, H. Wu, Q. Yang, H. Ke, B. Yin, Q. Shi, W. Wang, Q. Wei, G. Xie and S. Chen, Experimental and Theoretical Interpretation on the Magnetic Behavior in a Series of Pentagonal-Bipyramidal Dy^III Single-Ion Magnets, Chem. – Eur. J., 2017, 23, 17775–17787.
44. H. Wu, M. Li, B. Yin, Z. Xia, H. Ke, Q. Wei, G. Xie, S. Chen and S. Gao, Fine-tuning the type of equatorial donor atom in pentagonal bipyramidal Dy(III) complexes to enhance single-molecule magnet properties, Dalton Trans., 2019, 48, 16384–16394.
45. A. K. Bar, P. Kalita, J.-P. Sutter and V. Chandrasekhar, Pentagonal-bipyramid Ln(III) complexes exhibiting single-ion-magnet behavior: A rational synthetic approach for a rigid equatorial plane, Inorg. Chem., 2018, 57, 2398–2401.
46. P. Kalita, N. Ahmed, A. K. Bar, S. Dey, A. Jana, G. Rajaraman, J.-P. Sutter and V. Chandrasekhar, Pentagonal bipyramidal Ln(III) complexes containing an axial phosphine oxide ligand: Field-induced single-ion magnetism behavior of the Dy(III) analogues, Inorg. Chem., 2020, 59, 6603–6612.
47. P. Kalita, N. Ahmed, S. Moorthy, V. Béreau, A. Kumar Bar, P. Kumar, P. Nayak, J.-P. Sutter, S. K. Singh and V. Chandrasekhar, Slow magnetic relaxation in a homoaxially phosphine oxide coordinated pentagonal bipyramidal Dy(III) complex, Dalton Trans., 2023, 52, 2804–2815.
48. V. Singh, D. Das, S. Anga, J.-P. Sutter, V. Chandrasekhar and A. K. Bar, Rigid N₃O₂-Pentadentate Ligand-Assisted Octacoordinate Mononuclear Ln(III) Complexes: Syntheses, Characterization, and Slow Magnetization Relaxation, ACS Omega, 2022, 7, 25881–25890.
49. V. D. Sasnovskaya, V. A. Kopotkov, A. V. Kazakova, A. D. Talantsev, R. B. Morgunov, S. V. Simonov, L. V. Zorina, V. S. Mironov and E. B. Yagubskii, Slow magnetic relaxation in mononuclear complexes of Tb, Dy, Ho and Er with the pentadentate (N₃O₂) Schiff-base dapsc ligand, New J. Chem., 2018, 42, 14883–14893.
50. T. A. Bazhenova, V. S. Mironov, I. A. Yakushev, R. D. Svetogorov, O. V. Maximova, Y. V. Manakin, A. B. Kornev, A. N. Vasiliev and E. B. Yagubskii, End-to-End Azido-Bridged Lanthanide Chain Complexes (Dy, Er, Gd, and Y) with a Pentadentate Schiff-Base [N₃O₂] Ligand: Synthesis, Structure, and Magnetism, Inorg. Chem., 2020, 59, 563–578.
51. G. Zhang, Y. Yu, Y. Zhao, X. Xie and C. Ding, Iron(III)/TEMPO-Catalyzed Synthesis of 2,5-Disubstituted 1,3,4-Oxadiazoles by Oxidative Cyclization under Mild Conditions, Synlett, 2017, 1373–1377.
52. M. S. R. Murty, R. Penthala, S. Polepalli and N. Jain, Synthesis and biological evaluation of novel resveratrol-oxadiazole hybrid heterocycles as potential antiproliferative agents, Med. Chem. Res., 2016, 25, 627–643.
53. T. J. Giordano, G. J. Palenik, R. C. Palenik and D. A. Sullivan, Pentagonal-bipyramidal complexes. Synthesis and characterization of aqua(nitrato)[2,6-diacetylpyridine bis(benzoyl hydrazone)]cobalt(II) nitrate and diaqua[2,6-diacetylpyridine bis(benzoyl hydrazone)]nickel(II) nitrate dehydrate, Inorg. Chem., 1979, 18, 2445–2450.
54. APEX3, SAINT and SADABS, Bruker AXS Inc., Madison, WI, USA, 2016.
55. L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination, J. Appl. Crystallogr., 2015, 48, 3–10.
56. G. M. Sheldrick, SHELXT-Integrated Space-Group and Crystal Structure Determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
57. G. M. Sheldrick, Crystal Structure Refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
58. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341.
59. (a) I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. L. Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From Source Code to Insight, J. Chem. Theory Comput., 2019, 15, 5925–5964; (b) F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. A. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, Modern quantum chemistry with [Open]Molcas, J. Chem. Phys., 2020, 152, 214117.
60. (a) L. F. Chibotaru and L. Ungur, Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation, J. Chem. Phys., 2012, 137, 064112; (b) B. G. Wybourne, Spectroscopic Properties of Rare Earths, John Wiley, New York, 1965.
61. T. A. Bazhenova, V. A. Kopotkov, D. V. Korchagin, Y. N. Manakin, L. V. Zorina, S. V. Simonov, I. A. Yakushev, V. S. Mironov, A. N. Vasiliev, O. V. Maximova and E. B. Yagubskii, A Series of Novel Pentagonal-Bipyramidal Erbium(III) Complexes with Acyclic Chelating N₃O₂ Schiff-Base Ligands: Synthesis, Structure, and Magnetism, Molecules, 2021, 26, 6908.
62. T. A. Bazhenova, I. A. Yakushev, K. A. Lyssenko, O. V. Maximova, V. S. Mironov, Y. N. Manakin, A. B. Kornev, A. N. Vasiliev and E. B. Yagubskii, Ten-Coordinate Lanthanide [Ln(HL)(L)] Complexes (Ln = Dy, Ho, Er, Tb) with Pentadentate N₃O₂-Type Schiff-Base Ligands: Synthesis, Structure and Magnetism, Magnetochemistry, 2020, 6, 60.
63. M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE Program, version 2.1, Universitat de Barcelona, 2013.
64. P. Kalita, J. Acharyab and V. Chandrasekh, Mononuclear pentagonal bipyramidal Ln(III) complexes: Syntheses and magnetic properties, J. Magn. Magn. Mater., 2020, 498, 166098.
65. K. S. Cole and R. H. Cole, Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics, J. Chem. Phys., 1941, 9, 341–351.
66. Y. Ma, Y.-Q. Zhai, Y.-S. Ding, T. Han and Y.-Z. Zheng, Understanding a pentagonal-bipyramidal holmium(III) complex with a record energy barrier for magnetisation reversal, Chem. Commun., 2020, 56, 3979–3982.
67. Y.-S. Ding, W. J. A. Blackmore, Y.-Q. Zhai, M. J. Giansiracusa, D. Reta, I. Vitorica-Yrezabal, R. E. P. Winpenny, N. F. Chilton and Y.-Z. Zheng, Studies of the Temperature Dependence of the Structure and Magnetism of a Hexagonal-Bipyramidal Dysprosium(III) Single-Molecule Magnet, Inorg. Chem., 2022, 61, 227–235.
68. B. Zhang, X. Guo, P. Tan, W. Lv, X. Bai, Y. Zhou, A. Yuan, L. Chen, D. Liu, H.-H. Cui, R. Wang and X.-T. Chen, Axial Ligand as a Critical Factor for High-Performance Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, Inorg. Chem., 2022, 61, 19726–19734.
69. S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, An air-stable Dy(III) single-ion magnet with high anisotropy barrier and blocking temperature, Chem. Sci., 2016, 7, 5181–5191.
70. E. V. Gorshkov, D. V. Korchagin, E. A. Yureva, G. V. Shilov, M. V. Zhidkov, A. I. Dmitriev, N. N. Efimov, A. V. Palii and S. M. Aldoshin, Effect of Ligand Substitution on Zero-Field Slow Magnetic Relaxation in Mononuclear Dy(III) β-Diketonate Complexes with Phenanthroline-Based Ligands, Magnetochemistry, 2022, 8, 151.
71. A. V. Gavrikov, P. S. Koroteev, N. N. Efimov, Z. V. Dobrokhotov, A. B. Ilyukhin, A. K. Kostopoulos, A.-M. Ariciu and V. M. Novotortsev, Novel mononuclear and 1D-polymeric derivatives of lanthanides and (η⁶-benzoic acid)tricarbonylchromium: synthesis, structure and magnetism, Dalton Trans., 2017, 46, 3369–3380.
72. D. Reta and N. F. Chilton, Extraction of “hidden” relaxation times from AC susceptibility data, Chem. Sq., 2020, 4, 3.
73. K. N. Shrivastava, Theory of Spin-Lattice Relaxation, Phys. Status Solidi B, 1983, 117, 437–458.
74. V. S. Parmar, D. P. Mills and R. E. P. Winpenny, Mononuclear Dysprosium Alkoxide and Aryloxide Single-Molecule Magnets, Chem. – Eur. J., 2021, 27, 7625–7645.
75. S. K. Gupta, S. Dey, Th. Rajeshkumar, G. Rajaraman and R. Murugavel, Deciphering the Role of Anions and Secondary Coordination Sphere in Tuning Anisotropy in Dy(III) Air-Stable D_5h SIMs, Chem. – Eur. J., 2022, 28, e202103585.
76. C. Rudowicz, Transformation relations for the conventional O_k^q and normalised O’_k^q Stevens operator equivalents with k = 1 to 6 and −k ≤ q ≤ k, J. Phys. C: Solid State Phys., 1985, 18, 1415–1430.
77. B. Bleaney, Nuclear magnetic resonance shifts in solution due to lanthanide ions, J. Magn. Reson., 1972, 8, 91–100.
78. D. J. Newman, The orbit-lattice interaction for lanthanide ions. I. determination of empirical parameters, Aust. J. Phys., 1978, 31, 79–94.
79. D. J. Newman and B. Ng, The superposition model of crystal fields, Rep. Prog. Phys., 1989, 52, 699–762.
80. L. Spillecke, C. Koo, O. Maximova, V. S. Mironov, V. A. Kopotkov, D. V. Korchagin, A. N. Vasiliev, E. B. Yagubskii and R. Klingeler, Magnetic behavior of the novel pentagonal-bipyramidal erbium(III) complex (Et₃NH)[Er(H₂DAPS)Cl₂]: high-frequency EPR study and crystal-field analysis, Dalton Trans., 2021, 50, 18143–18154.
81. W. Deng, Y.-Q. Zhou, S.-N. Du, Z.-Y. Ruan, S.-G. Wu, J.-L. Liu and M.-L. Tong, From geometric to charge-distribution symmetry: deeper insights into lifting the performance of dysprosium single-ion magnets, Sci. China: Chem., 2023, 66, 1989–1996.

---

Footnote

† Electronic supplementary information (ESI) available: Additional structural, magnetic and ab initio calculation data. CCDC 2239615 (1), 2239616 (2) and 2239617 (3). For ESI and crystallographic data in CIF or other electronic formats, see DOI: https://doi.org/10.1039/d4qi02262a

---