Intercluster charge ordering in monoclinic and triclinic Ba–Mo-based hollandite phases†
Eslam M.
Elbakry
 and
Jared M.
Allred
and
Jared M.
Allred
 *
*
Department of Chemistry and Biochemistry, The University of Alabama, Tuscaloosa, Alabama 35487, USA. E-mail: jmallred@ua.edu
First published on 16th October 2024
Abstract
Reproducible solid-state synthesis methods are presented for the preparation of tetragonal Ba1.1Mo8O16, monoclinic Na0.325(5)Ba1.006(18)Mo8O16, and triclinic Ba1.12(3)Mo8O16 hollandite phases, with complete, high-resolution crystal structures of the monoclinic and triclinic phases reported for the first time. The similar synthetic conditions allow direct comparisons between phases; differences between structures are shown to be correlated to subtle changes in the metal–metal bonding of the Mo4 cluster motif that is unique to the Mo-based hollandites. The trends in the local Mo valence, stoichiometry, and key Mo–Mo bond lengths of these and other reported Mo-based hollandite phases together support an interchain charge ordering model for this family of compounds, which has been previously suggested for the case of K2Mo8O16. An alternate model, where Mott physics dominate the electronic structure near the Fermi level, is not supported by temperature-dependent magnetic susceptibility measurements, which are reported down to 2 K. The incorporation and homogeneity of Na in the monoclinic phase is verified using atom probe tomography.
Introduction
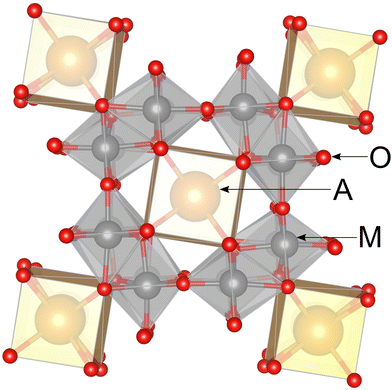
Metal–metal bonding motifs are of interest as functional structural subunits of metal–organic frameworks, molecular-scale conductors, photosensitizers, catalysts, and so on.1 The metallic ions of d1, d2, and d3 configurations such as Nb(IV), Mo(IV), and Re(IV), naturally favour the formation of metal–metal bonds. Molybdenum oxides in particular stand out for the delicate balance between different and sometimes coexisting oxidation states. For example, Mo(IV), Mo(V), and Mo(VI) can coexist within the same structural motif, as in La3Mo4(Al0.67Mo0.33)O14.2In compounds containing chain-like units of edge-sharing metal–oxygen octahedra, the metal–metal bond formation often becomes energetically favored.3 The hollandite structure type, AxM8O16, is one such family of compounds, which has garnered much interest due to the possibility of one-dimensional ionic conductivity through the tunnels located between cages of metal–oxygen octahedra, Fig. 1.4 There is substantial current interest in hollandite compounds for their potential as solid-state battery cathodes5,6 in addition to their potential as molecular sieves7 and for trapping hazardous elements such as radioactive wastes.8
The strong metal–metal bond motifs that are characteristic of molybdenum-based hollandites provide a unique opportunity to explore the interplay between the oxidation state of Mo, patterns of Mo-clustering, electronic properties of A-cations, and presence of vacant sites within the hollandite channels. For instance, La1.16Mo8O16, R1.33Mo8O16 (R = Pr, Nd), and Rb1.5Mo8O16 all have tetragonal symmetry, whereas K2Mo8O16 is monoclinic,9–12 which breaks the usual trend in hollandite crystal symmetry.13 In Rb1.5Mo8O16 and K2Mo8O16 compounds, Mo4 rhombohedral clusters form cage-like channels, inside which larger cations are trapped, while Mo3 triangular clusters exist as either isolated units or within infinite chains in La1.16Mo8O16 and R1.33Mo8O16 (R = Pr, Nd).9–11 Recent electronic structure calculations showed that the monoclinic distortion in K2Mo8O16 can be driven electronically: either by charge ordering between Mo4 clusters that breaks tetragonal symmetry or via strong electronic correlations via a Mott mechanism.14
Patterns of Mo-clustering are not the same in Mo-hollandites that have Ba in their channels. There are two reported ternary Ba–Mo-hollandites, tetragonal Ba1.14Mo8O16 and triclinic Ba1.13Mo8O16, the latter of which being the first and only example of a triclinic distortion of the hollandite structure to our knowledge. The tetragonal form was synthesized electrochemically from a molten mixture of barium and caesium molybdates.15 It contains Mo3 triangles and Mo4 rhomboidal clusters alternating in equal proportions, described by a crystallographic modulation q ≈ 4/7 c*. The triclinic phase only contains Mo4 clusters, though it this information is only derived from a multiphase product and the complete structural details have not been reported.16 Further complicating the picture is a provisional report of a monoclinic form of the Ba–Mo hollandite stabilized by the addition of sodium and lithium (nominally reported as Na0.35BaMo8O16 and Li0.34BaMo8O16),17 which were respectively indexed and solved in the monoclinic cell as K2Mo8O16 and the tetragonal cell of K2Cr8O16, respectively.
Despite the unique diversity of observed crystal symmetries and structural motifs, the origin of the distinct Ba–Mo-containing hollandite polymorphs remains unknown, perhaps due to the difficulties in reproducibly synthesizing them at high phase purities. Alkali salts have previously been used as mineralizers to improve the phase purity of undoped Ba-based hollandites, such as KCl with Ba1.1Mn8O1618 which makes the role of the Na+ and Cs+ alkali ions in the above examples unclear. The Na atoms in the crystallographic model for monoclinic Na0.35BaMo8O16 are only four coordinate with exceptionally short Na–O bonds (2.20 Å) in a square planar geometry,17 which is unusual enough to require revisiting and validation. The effects of stoichiometry and temperature on phase stability are also essentially unexplored.
The lack of validated phase data also impacts broader materials science activities. The reported Ba–Mo–O phase equilibria diagrams lacked critical information regarding the formation of Ba–Mo-containing hollandite phases.19
In this work, we investigate the role of reaction conditions on the polymorph and stoichiometry of Ba–Mo-based hollandites. We develop a consistent and reproducible solid-state synthesis technique for producing high phase-purity Ba–Mo-hollandite compounds separately in all three known crystal systems: triclinic (TRI) phase Ba1.12(3)Mo8O16, tetragonal (TET) Ba1.0+xMo8O16 phase(s), and a monoclinic (MON) Na0.325(5)Ba1.006(18)Mo8O16 (or Na1/3BaMo8O16) phase. The findings support treating TRI and MON as essentially line compounds with fixed stoichiometry, while TET is found to form as a series of at least five distinct modulated structures, only of which has been previously reported. Extensive optimization in reactant choice, presence and type of mineralizer, and quenching rate reveal what factors control the polymorph type. Atom probe tomography (APT) reveals that the monoclinic symmetry is correlated to the presence of Na+ ions in the channels.
High-resolution crystal structure solutions of TRI and MON compounds are also reported. The resulting trends show trends in the metal–metal bonding and local metal atom valence that support an electronically driven charge-ordering model for the structural distortion in MON, TRI, and K2Mo8O16 by extension.
Experimental
Materials
Starting materials include powders of BaCO3 (strem chemicals, 99.9%), Na2CO3 (VWR, 99.9%), K2CO3 (Sigma Aldrich, 99.0%), CaMoO4, BaMoO4, Na2MoO4 (Beantown chemical, 99.9%), MoO2 powder (Prochem Inc., 99.95%), MoO3 (Alfa Aesar, 99.95%), elemental Mo, NaCl (Beantown chemical, 99.0%), NaI, KI (Alfa Aesar, 99.0%) and MoCl3 (Alfa Aesar, 99.5%). Carbonates were dried in air at 250 °C overnight and MoO2 was further purified by sequential washing with 1 M hydrochloric acid and potassium hydroxide solutions to remove other molybdenum oxide phases present.CaMoO4 and BaMoO4 were prepared by solid-state reaction between MoO3 and CaCO3 or BaCO3, respectively, at 800 °C for 24 h. Elemental Mo was obtained via the reduction of MoO2 using 5% H2/Ar gas, at 900 °C, for 48 h. The purity of all reagents was confirmed using powder X-ray diffraction (PXRD) with no impurities detectable above a 2% threshold.
Prior to use, copper tubes (McMaster Carr, Super-conductive 101 copper) were heated to 900 °C under 5% H2/Ar flowing gas to remove the oxide surface.
Synthetic procedures
Starting materials in amounts of 0.250 mmol (about 300 mg) were finely ground using an agate mortar and pestle. Unless otherwise stated, the mixture was placed in a cylindrical copper tube with 0.08 cm thick walls and having the approximate dimensions of 2 cm length and 0.79 cm inner diameter. The copper tubes were sealed under a partial atmosphere of 50 kPa flowing Ar using an electric arc welder, which was then sealed inside of an evacuated quartz ampoule prior to reaction. Since the melting point of copper is 1085 °C, samples (re)fired at temperatures higher than 1000 °C were wrapped in nickel foil. Niobium tubes resulted in the formation of niobium oxides and Mo metal, so they were not used.Unless otherwise specified, reaction vessels were heated at a rate 83 °C h−1 up to 1000 °C and fired for 4 days. Cooling rates were varied between reactions. Rapid quenching steps were performed by moving the reaction vessel from the furnace at 1000 °C directly to a water bath at room temperature.
X-ray diffraction
Samples were ground to powder to carry out PXRD. The PXRD patterns were measured on a Bruker D2-Phaser diffractometer equipped with a Cu-Kα source and a Lynx-Eye detector. The lattice parameters were determined for each composition by fitting the hollandite crystallographic models to the PXRD patterns in the Rietveld method implemented through GSAS II.20,21Single crystal diffraction experiments were performed using a Rigaku Synergy-DW, equipped with a HyPix detector and operated in the Mo-Kα mode. The refinement, absorption correction, and data reduction of the Bragg peak intensity data obtained from single crystal X-ray diffraction were performed using CrysAlisPro software and the crystal structures were refined using SHELX, WinGX, and OLEX2 programs.22–24 Visualizations of crystal structures were carried out with VESTA.25
Bond valence sum parameters for Mo were taken from Chen and coworkers.26 These values provide the most accurate description of extended molybdenum oxide solids such as MoO2, which is the closest binary to the studied hollandite compounds in terms of both structure and stoichiometry.
Atom probe tomography
A three-dimensional compositional map for the Na-doped sample was constructed by atom probe tomography (APT) technique. This was performed on a LEAP 6000 XR operated in laser mode with a wavelength of 267 nm. Prior to sample preparation, the sample was washed with dilute HCl to remove Na-containing impurities. Atom probe samples were prepared as needle-shaped specimens using a Tescan Lyra FIB-FESEM instrument. Dual-beam FIB protocol was applied.27 FIB technique was utilized to prepare sample needles, where the needle direction was perpendicular to the z-direction of the sample crystals, at a shank angle ranging from 3° to 5°. 16 million ions were detected, using pulse rate and energy at 67 kHz and 30 PJ, respectively. The direct current (DC) voltage varied freely to maintain a stable detection rate. Data analysis was performed using the IVAS 6.3 software. Spatial distribution maps (SDM) were constructed by combining two radial distribution functions: one represents the distribution of inter-atomic separations in the z-direction and the other is a 2D map describing the atomic positions in the corresponding x–y lateral plane.28 The composition of the MON specimen was studied down to about 500 nm deep, and the top 50 nm was excluded since the sample surface appears to be oxidized.Magnetization measurements
The temperature-dependent magnetization measurements were performed using a quantum design dynacool physical property measurement system (PPMS) equipped with a 9 Tesla magnet. A group of randomly oriented single crystals of the same batch with a total mass of 10–25 mg was wrapped together in a plastic film and confined in a plastic straw.Electron microscopy, thermogravimetric analysis, and atomic emission spectroscopy
Scanning electron microscope (SEM) images was collected using an Apreo FE SEM at an energy of 20.0 kV. Thermogravimetric analysis was performed using a Simultaneous Thermal Analyzer 8000 (PerkinElmer Inc.). Heating was carried out from 30 to 800 °C in the N2 atmosphere, at a 20 °C min−1 heating rate. Stoichiometries of the synthesized compounds were determined by inductively coupled plasma optical emission spectroscopy (ICP-OES) technique, using the Agilent 5800 ICP-OES instrument.Results
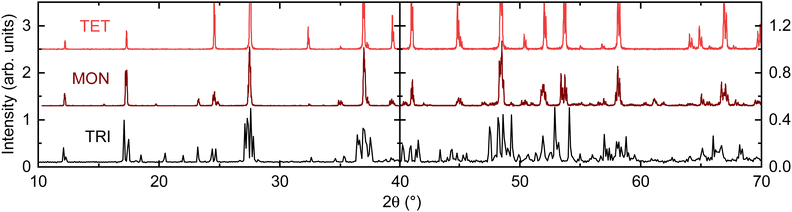
In this work, compounds are only referred to by their specific stoichiometries when measured experimentally here or when referencing a reported phase from prior work. This is done to avoid confusion between nominal and actual stoichiometry and further conflation between different crystallographic phases with similar stoichiometry.Each individual hollandite phase synthesized is referenced by the crystal system that it belongs to, with the terms TET, MON, and TRI each denoting a compound with the previously referenced tetragonal, monoclinic, and triclinic structure types. The crystal system is chosen for convenience because the PXRD patterns are easily distinguished from each phase. This is illustrated in Fig. 2, which shows simulated PXRD patterns for each compound derived from the single crystal diffraction results of TRI and MON reported in Section 3.3, and of TET as reported by Barrier.15 Single crystal diffraction experiments were used to confirm the crystal system of specimens as well.
General synthetic observations
Alternatives to sealed ampoule synthesis methods generally failed in this study. For example, open alumina crucibles under flowing inert gases did not react at 600 °C. At 800 °C, volatile MoO3 crystals form under inert gas flow while reducing conditions tend to reduce Mo past the range needed here.Hollandite phases are successfully prepared when the reaction mixture was sealed in copper tubes and heated at 1000 °C, in keeping with prior literature to prepare molybdenum hollandites.17 Refiring the product at a higher temperature, up to 1150 °C, increases impurity fractions and does not enhance the crystallinity of the target phase(s).
The purity and form of reaction products were found to be strongly affected by the identity of reactant species. MoO2 is a common ingredient in all cases, since it gave a higher yield of products, compared to MoO3 + Mo as precursor compounds. Elemental Mo is required to balance the metal–oxygen stoichiometry, i.e., as the main reducing agent for Mo(IV) and (VI) oxides. Thus, to prepare the Ba–Mo-hollandite phases, MoO2 and Mo were mixed with BaCO3 or BaMoO4, as a reaction mixture. The reduced molybdenum oxide phases Ba0.62Mo4O6, Ba3Mo18O28 and BaMo6O10 could not be distinguished from each other as minority phases, and so they are collectively referred to as BaMo6O10 throughout.29–31
The ensuing synthetic results focus on clearly showing what conditions stabilize each of the three known structure types of Ba–Mo-based hollandites. The section is organized to describe the four major factors found to affect the outcome of the reaction: (1) the effects of metal source type (e.g. BaMoO4vs. BaCO3), (2) input stoichiometry, (3) quenching rate, and (4) whether and how a mineralizer is used. Finally, the synthetic conditions specifically resulting in the MON phase formation are described last as it builds on findings from the other steps.
In these sections, the results of each reaction are discussed with regards to the hollandite phase's crystal size and morphology, diffracted crystal symmetry, yield, and type of impurities present. More detailed characterizations of selected products including specimen stoichiometry, crystal structure determination, and atomic-scale microscopy, are reported in their respective sections below.
Effects of Ba-source without a mineralizer
The first set of reactions reported are for those with no kind of mineralizer or dopant is added, which nearly always produce small single crystals of TRI phase, though TET phases are sometimes observed as a secondary phase.Trials using BaMoO4 and BaCO3 as a Ba source distinguish between the different effects introduced by a carbonate reactant and 42 °C h−1 cooling rate. Generally, BaCO3 was found to give a purer phase when used as a Ba source, instead of BaMoO4. When BaMoO4 is used, split peaks characteristic of phase TRI, appear as a single broad peak, indicating that other hollandite phases, probably of TET form, exist as a major species, Fig. S1 (ESI†).
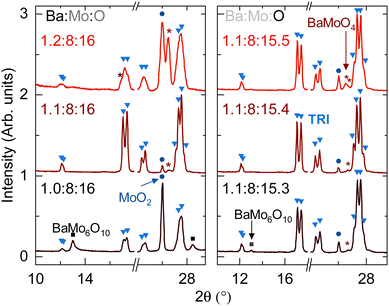
Fig. 3 summarizes the effects of changing input Ba:Mo stoichiometry and Mo:O stoichiometry. The right panel shows mixtures of BaCO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MoO2, and Mo molar ratio was varied as x: 7.15
MoO2, and Mo molar ratio was varied as x: 7.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85, where x ranges from 0.9 to 1.3. The referenced oxygen stoichiometry assumes that BaCO3 is effectively BaO and that the resulting CO2 is inert. However, tubes are not pressurized after the reaction is complete, which implies that either the carbon dioxide is reduced to carbon or that the CO2 intercalated into the hollandite channels. Most of the evidence supports the former scenario, with additional details summarized as ESI.†
0.85, where x ranges from 0.9 to 1.3. The referenced oxygen stoichiometry assumes that BaCO3 is effectively BaO and that the resulting CO2 is inert. However, tubes are not pressurized after the reaction is complete, which implies that either the carbon dioxide is reduced to carbon or that the CO2 intercalated into the hollandite channels. Most of the evidence supports the former scenario, with additional details summarized as ESI.†
Multiple iterations of this study give the optimal target stoichiometry of Ba1.12Mo8O15.44 to synthesize compound TRI. The fact that the purity of TRI is extremely sensitive to conditions and that the lattice parameters do not vary together suggest that TRI is a line compound of approximate stoichiometry Ba1.12Mo8O16.
Effects of mineralizers
A systematic study into the effects of different salts added to the reaction mixture is summarized in Table 1. Compounds such as KCl have previously been successfully added as mineralizers in, for example, Ba1.2Mn8O16,18 to suppress intermediate phase formation. In the present system, the study is complicated by the fact that Na and Li have previously been reported to substitute into the channels, yielding the MON form. Thus, one primary goal of this work is to differentiate between reactive vs. mineralizing salts.| Salt/mineralizera | Ba source | Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mo Mo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O (mol) O (mol) |
Cool rate | Hollandite product | Comments; impurities |
|---|---|---|---|---|---|
| a Unless otherwise stated, 5 to 10 mg of mineralizer is added to 0.25 mmol reactant mixture. Impurities and crystallinity are mentioned when excessively present, or being different relative to best results obtained, respectively. b Optimal yield and crystallinity conditions for this polymorph. | |||||
| None | BaCO3 | 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
50 °C h−1 | TRI | Highest TRI yieldb |
| None | BaCO3 | 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
Quenched | TET (trace TRI) | Poor cryst; MoO2, BaMoO4 |
| None | BaMoO4 | 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
Quenched | TET | Poor cryst.; MoO2, BaMoO4 |
| None | BaMoO4 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
42 °C h−1 | TET + TRI | Very poor cryst; |
| MgO | BaCO3 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
10 °C h−1 | TRI | Mg2Mo3O8, MoO2, BaMoO4 |
| KI | BaMoO4 | 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | TRI | MoO2 |
| K2CO3 | BaCO3 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
10 °C h−1 | TRI | Poor cryst.; MoO2 |
| K2CO3 | BaMoO4 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | TRI | Poor cryst.; BaMo6O10, MoO2 |
| CaCO3 | BaCO3 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
10 °C h−1 | TRI | Poor cryst.; MoO2, BaMoO4 |
| Na2MoO4 | BaCO3 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | TRI | MoO2 |
| Na2MoO4 (excess) | BaCO3 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | MON | MoO2, BaMoO4 |
| Na2MoO4 | BaMoO4 | 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | MON | highest MON yieldb |
| Na2CO3 | BaMoO4 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | MON | MoO2, BaMoO4 |
| NaI | BaMoO4 | 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
83 °C h−1 | TET | highest TET yieldb |
| NaI | BaMoO4 | 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
Quenched | TET | Large cryst.; MoO2, BaMoO4 |
| NaI | BaCO3 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
83 °C h−1 | TET | Poor cryst.; MoO2, BaMoO4 |
| CaMoO4 | BaMoO4 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | TET (tr. TRI) | MoO2 |
| NaCl | BaMoO4 | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
33 °C h−1 | TET (tr. TRI) | MoO2/BaMoO4 |
The preparation of AxMo8O6 hollandite phases, where A = K, Ca or Sr, and x ranges from 0 to 2 was attempted using the compounds K2CO3, CaCO3, CaMoO4, SrCO3 and SrMoO4 as starting materials and with no BaCO3 or BaMoO4 present. No hollandite phases were identified across the range of conditions attempted: cooling rates between 21 °C h−1 and 167 °C h−1 and annealing temperatures from 540 °C to 1150 °C.
Attempts to create mixed cation phases of the form AxBayMo8O16 with y ranges from 1.0 to 1.2 also showed no signs of changes in the crystal system or lattice parameters compared to the Ba-only experiments. The hollandite phases produced with or without adding these salts to the recipe were indistinguishable. These salts were found to be detrimental to purity and crystallinity of the Ba–Mo–O hollandite phase(s) formed, and thus their utilization as mineralizers was also further excluded.
Halide salts were also investigated as potential mineralizers, including NaCl, KCl, NaI, and KI, with the iodides serving the double purpose of being mild reducing agents as well. While most choices suppressed phase purity and crystallinity, the addition of NaI to the reaction mixture was found to favour the formation of TET phases in the form of relatively large, well-faceted single crystals. In this case, using BaMoO4 yields >98% pure TET, based on Rietveld refinement, whereas using BaCO3 yields hollandite as a minority phase. The reaction in the presence of NaI was additionally found to be much less sensitive to oxidative effects and that a slight excess of BaMoO4 further suppresses impurities. The remaining BaMoO4 impurities were then leached out by washing the product with dilute HCl. The change in cooling rate affected the crystals’ morphology and product yield, as rapid quenching yielded larger, often intertwined crystals, accompanied by a higher fraction of impurities, Fig. S4 (ESI†).
The stronger dependence of TET phase formation on cooling rate compared to TRI suggests that TET is thermally unstable at lower temperatures.
MON phase formation
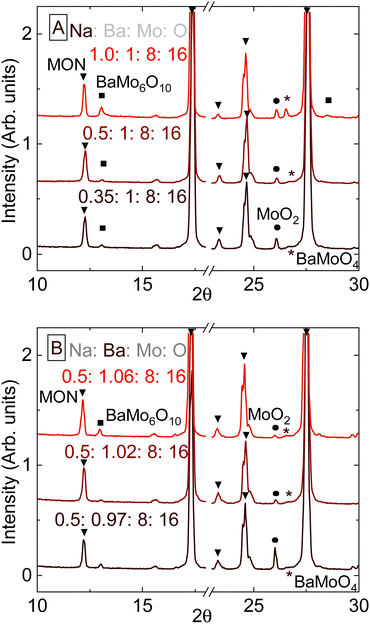
The previous section illustrates the need to better understand the role of Na in the formation of hollandite phases. Trials were carried out using combinations of either BaMoO4 or BaCO3 as Ba sources and either Na2CO3 or Na2MoO4 as a Na source at 1000 °C and an 83 °C h−1 cooling rate. For this compound, MON, BaMoO4 and Na2MoO4 are added instead of BaCO3 and Na2CO3, since adding any of the latter reagents to the recipe gave a higher fraction of MoO2 and BaMoO4 impurities.
Fig. 4 summarizes the results of this series of experiments. The delicate balance between stoichiometry and the redox environment was again not subjected to simple lever-rule laws. Either MoO2 or a combination of BaMoO4 and BaMo6O10 are produced when there either is deficiency or surplus in Ba content, respectively. Na2MoO4 was added in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 to BaMo8O16, to make the stoichiometry of input reactants in the form NaxBaMo8O16, where x ranges between 0.35 to 1 (Fig. 4(A)). Impurities are minimized with the input stoichiometry Na0.5BaMo8O16, in accordance with prior work by Lii.17 Input Ba content was then varied from nominally Na0.5Ba0.97Mo8O16 to Na0.5Ba1.1Mo8O16, where adding 1.02 Ba atoms per Mo8O6 was found to give the highest purity product, Fig. 4(B).
4 to BaMo8O16, to make the stoichiometry of input reactants in the form NaxBaMo8O16, where x ranges between 0.35 to 1 (Fig. 4(A)). Impurities are minimized with the input stoichiometry Na0.5BaMo8O16, in accordance with prior work by Lii.17 Input Ba content was then varied from nominally Na0.5Ba0.97Mo8O16 to Na0.5Ba1.1Mo8O16, where adding 1.02 Ba atoms per Mo8O6 was found to give the highest purity product, Fig. 4(B).
Either modifying cooling rates or the input Mo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O molar ratio (from to 8
O molar ratio (from to 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15.3 to 16
15.3 to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) made minor difference to the phase purity or crystallinity of products, and so those results are not shown. No significant effect on product yield was found upon changing the cooling rate, and thus the cooling rate of 33 °C h−1 used in initial trials was not further adjusted.
8) made minor difference to the phase purity or crystallinity of products, and so those results are not shown. No significant effect on product yield was found upon changing the cooling rate, and thus the cooling rate of 33 °C h−1 used in initial trials was not further adjusted.
In summary, the MON phase wase prepared in optimal form by adding Na2MoO4, BaMoO4, MoO2, and Mo, in a molar ratio of 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.02
1.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.46
5.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.27, respectively. This is equivalent to a Na
1.27, respectively. This is equivalent to a Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba
Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mo
Mo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O molar ratio of 0.5
O molar ratio of 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.02
1.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16.
16.
Spectroscopic stoichiometry determination
Output stoichiometry was determined by ICP-OES analysis for selected hollandite samples. The Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mo ratio for phases TRI and MON was found to be 1.036(3) and 1.083(3) Ba per 8 Mo atoms, respectively. The average Ba
Mo ratio for phases TRI and MON was found to be 1.036(3) and 1.083(3) Ba per 8 Mo atoms, respectively. The average Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mo ratio ranges between 1.15–1.18 Ba per 8 Mo atoms, in TET phase. These stoichiometries are slightly different from those obtained by XRD and APT techniques, because of the presence of MoO2 and BaMo6O10 impurities. Additionally, Mo ions have been reported to be somewhat unstable in aqueous solutions over time, unlike Ba ions.32 Rietveld analysis of the PXRD patterns of the respective optimal synthetic conditions indicates that TRI and MON are ≥98% of the crystalline phases present by mass, with MoO2 being the main impurity in both products, followed by BaMo6O10. No impurity phases were observable in the TET PXRD patterns. An illustration of the experimental PXRD patterns with main peak indices is shown in Fig. S6 of the ESI.† These observations are reproducible across multiple reactions under the same conditions.
Mo ratio ranges between 1.15–1.18 Ba per 8 Mo atoms, in TET phase. These stoichiometries are slightly different from those obtained by XRD and APT techniques, because of the presence of MoO2 and BaMo6O10 impurities. Additionally, Mo ions have been reported to be somewhat unstable in aqueous solutions over time, unlike Ba ions.32 Rietveld analysis of the PXRD patterns of the respective optimal synthetic conditions indicates that TRI and MON are ≥98% of the crystalline phases present by mass, with MoO2 being the main impurity in both products, followed by BaMo6O10. No impurity phases were observable in the TET PXRD patterns. An illustration of the experimental PXRD patterns with main peak indices is shown in Fig. S6 of the ESI.† These observations are reproducible across multiple reactions under the same conditions.
The three-dimensional APT maps were used to determine the stoichiometry and sub-nanometre homogeneity of a specimen derived from a selected MON crystal, Fig. S7 (ESI†). The stoichiometry of atomic interplanar spacings in the APT measurements is consistent with the X-ray diffraction measurements for the monoclinic unit cell. The chemical formula Na0.35(2)Ba1.08(3)Mo8O16, was determined using the ratio of Na, Ba, and Mo atoms in the 15 million ions detected. No significant spatial systematic variance was observed in chemical composition. Fig. S8 (ESI†) shows a 3D reconstruction of the specimen.
Single crystal structure solutions
Fig. 5 shows SEM images of selected TRI, TET, and MON crystals recovered from their sealed copper tubes after heating. Their crystal habits are consistent with their assigned crystal classes, which implies that the phases observed at room temperature remain in the same structure type as when they formed at elevated temperature.For MON and TRI crystals, there were no significant differences in the measured crystallographic parameters between crystals of the same type made using different reaction conditions. The results reported below are from the batches that had undergone optimal preparation conditions as mentioned earlier. The absence of satellite peaks indicates that MON and TRI compounds do not exhibit long-range structural modulations. MON specimens typically exhibit twinning that mimics the primitive tetragonal cell of Rb1.5Mo8O16, but close inspection of the diffraction peaks finds that a monoclinic distortion is present that is consistent with the original preliminary report of nominal Na0.35BaMo8O16 (comparison shown in Table S1, ESI†). TRI crystals also exhibit twinning, but they mimic the higher symmetry body-centred tetragonal cell of K2Cr8O16. In most batches containing TRI, this twinning precluded reliable structure solutions. We were only able to identify suitable crystals in the nearly optimized synthesis batches. Nevertheless, the unit cells and provisional structural models on the lower quality crystals are consistent with the optimal ones reported below. As above, the cell determined here is consistent with the nominal Ba1.13Mo8O16 phase reported in the literature.16 A comparison is shown in Table S1 (ESI†).
Isolated TET crystals are unambiguously of tetragonal metric symmetry, and, unlike MON and TRI crystals, all TET specimens show satellite peaks that are indicative of incommensurate modulated structures. The observations hold true for synthesis methods containing NaI and those without, implying that these exist as ternary Ba–Mo–O phases.
Crystals exhibiting four different q modulation vectors, ranging from 0.533 to 0.554 c*, can be isolated from the same reaction product. These are different lengths than the 0.571 (4/7) c* one that was previously reported in Ba8/7Mo8O16. Assuming a similar modulation model as the latter compound implies a precise composition of BaxMo8O16, where x = 2q with q in reciprocal lattice units. The observed TET phases can thus be assigned nominal compositions ranging in discrete steps from Ba1.067Mo8O16 to Ba1.108Mo8O16. Due to the complexity of solving and describing modulated structures, however, the full structure solutions of all four new TET phases are the subject of a separate article that is in preparation.33
The experimental conditions and model parameters for the complete structural models of TRI and MON are given in in Table 2, which have the refined stoichiometries Ba1.12(3)Mo8O16 and Na0.325(5)Ba1.006(18)Mo8O16, respectively. In both cases, Mo and O positions and anisotropic thermal parameters were freely refined, but the treatment of A-site cations in the channels differs. The atomic positions in the TRI and MON crystallographic models are given in Tables 3 and 4, respectively. The process for choosing and refining crystallographic models for each crystal structures is described as follows.
| MON | TRI | |
|---|---|---|
| Refined formula | Na0.305(8)Ba0.94(2)Mo8O16 | Ba1.12(3)Mo8O16 |
| Space group type | P2/n |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Z | 2 | 1 |
| a | 10.22775(19) Å | 5.73179(12) Å |
| b | 5.73224(12) Å | 7.31811(17) Å |
| c | 10.2849(2) Å | 7.45804(14) Å |
| α | 90° | 89.2492(17)° |
| β | 90.2821(18)° | 78.4863(17)° |
| γ | 90° | 80.4477(18)° |
| V | 602.98(2) Å3 | 302.224(11) Å3 |
| Temp. | 299.4(6) K | 301.15(10) K |
| Size | 63 × 59 × 32 μm | 79 × 24 × 20 μm |
| λ | 0.71073 Å | 0.71073 Å |
| μ | 11.169 mm−1 | 11.689 mm−1 |
| Abs corr | Multi-scan | Multi-scan |
| T min, Tmax | 0.589, 0.750 | 0.508, 0.840 |
| Scan mode | ω-scans | ω-scans |
| θ max, dmin | 42.980°, 0.521 Å | 44.876°, 0.504 Å |
| (h k l)max | (19 10 19) | (11 14 14) |
| Unique ref. | 4294 | 4985 |
| Completness | 97.4% | 99.9% |
| R int, Rσ | 0.0247, 0.0260 | 0.0264, 0.0285 |
| F 000 | 1041 | 527 |
| R 1(all) | 0.0286 | 0.0416 |
| R 1(Fo > 4σFo) | 0.0245 | 0.0339 |
| wR2 (all) | 0.0634 | 0.0576 |
| Max. diff. peaks | 8.02, −1.98 (e− Å−3) | 1.52, −2.03 (e− Å−3) |
| CSD code | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 927 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 928 |
| Atom | x | y | z | U 11·102 | U 22·102 | U 33·102 | U 23·102 | U 13·102 | U 12·102 | Occ. |
|---|---|---|---|---|---|---|---|---|---|---|
| Ba1A | 1 | 0 | 0 | 1.69(17) | 1.08(3) | 0.068(2) | 0.168(18) | 0.21(5) | 0.51(7) | 0.74(2) |
| Ba1B | 1.071(3) | 0.0187(9) | 0.0139(8) | 0.2(2) | 0.85(10) | 0.090(10) | −0.17(8) | −0.20(10) | 0.02(10) | 0.066(10) |
| Ba2 | 0.5923(2) | −0.02740(17) | −0.01957(16) | 1.29(5) | 0.90(5) | 0.067(4) | 0.16(3) | −0.37(3) | −0.45(4) | 0.1240(10) |
| Mo1 | 0.35067(3) | 0.15006(3) | 0.48775(3) | 0.280(6) | 0.488(7) | 0.0380(6) | 0.021(5) | −0.052(5) | 0.021(5) | 1 |
| Mo2 | 0.79853(3) | 0.17005(3) | 0.47590(3) | 0.293(6) | 0.512(7) | 0.0444(6) | 0.014(5) | −0.065(5) | −0.006(5) | 1 |
| Mo3 | 0.44095(3) | 0.49163(3) | 0.84392(3) | 0.341(7) | 0.509(7) | 0.0393(6) | 0.014(5) | −0.108(5) | 0.017(5) | 1 |
| Mo4 | 0.89350(3) | 0.48111(3) | 0.81555(3) | 0.342(7) | 0.551(7) | 0.0442(6) | 0.058(5) | −0.109(5) | −0.020(5) | 1 |
| O1 | 0.6461(3) | 0.0304(3) | 0.2992(2) | 0.55(6) | 0.91(6) | 0.039(5) | 0.00(5) | −0.06(5) | 0.06(5) | 1 |
| O2 | 0.8610(3) | −0.0352(2) | 0.6563(2) | 0.46(6) | 0.68(6) | 0.062(6) | 0.04(5) | −0.05(5) | −0.13(5) | 1 |
| O3 | 0.6680(3) | 0.6436(3) | 0.7007(2) | 0.41(6) | 0.76(6) | 0.066(6) | 0.30(5) | −0.08(5) | −0.01(5) | 1 |
| O4 | 0.8351(3) | 0.3668(3) | 0.2848(2) | 0.50(6) | 0.76(6) | 0.067(6) | 0.29(5) | −0.23(5) | −0.08(5) | 1 |
| O5 | 0.6745(3) | 0.3045(2) | 0.9576(2) | 0.49(6) | 0.65(6) | 0.061(6) | 0.12(5) | −0.06(5) | −0.01(5) | 1 |
| O6 | 0.8376(3) | 0.6453(3) | 1.0448(2) | 0.39(6) | 0.81(6) | 0.067(6) | 0.13(5) | −0.13(5) | −0.08(5) | 1 |
| O7 | 1.0123(3) | 0.2978(3) | 0.6272(2) | 0.34(6) | 0.89(7) | 0.072(6) | −0.19(5) | −0.08(5) | 0.10(5) | 1 |
| O8 | 0.5144(3) | 0.3083(3) | 0.6303(2) | 0.43(6) | 0.77(6) | 0.057(6) | −0.23(5) | −0.15(5) | 0.16(5) | 1 |
| Atom | x | y | z | U 11 102 | U 22 102 | U 33 102 | U 13 102 | Ba occ. | Na occ. |
|---|---|---|---|---|---|---|---|---|---|
| a U ij constrained to zero by symmetry are not included. | |||||||||
| Ba/Na1A | 1/4 | −0.0430(9) | 3/4 | 0.63(3) | 0.61(10) | 0.59(3) | 0.05(2) | 0.146(12) | 0.047(4) |
| Ba/Na1B | 1/4 | −0.1008(11) | 3/4 | 0.60(2) | 3.25(16) | 0.64(2) | 0.028(15) | 0.381(13) | 0.124(4) |
| Ba/Na2A | 1/4 | 0.2721(8) | 3/4 | 0.63(3) | 0.61(10) | 0.59(3) | 0.05(2) | 0.185(11) | 0.060(4) |
| Ba/Na2B | 1/4 | 0.3239(18) | 3/4 | 0.60(2) | 3.25(16) | 0.64(2) | 0.028(15) | 0.231(11) | 0.075(3) |
| Atom | x | y | z | U 11 102 | U 22 102 | U 33 102 | U 23 102 | U 13 102 | U 12 102 |
| Mo1 | 0.43134(2) | 0.61618(3) | 0.42042(2) | 0.267(6) | 0.218(6) | 0.345(6) | 0.048(4) | −0.006(5) | 0.031(4) |
| Mo2 | 0.42496(2) | 0.16683(3) | 0.40104(2) | 0.314(6) | 0.293(7) | 0.388(6) | 0.002(4) | 0.004(5) | 0.001(4) |
| Mo3 | 0.41723(2) | 0.40093(3) | 0.07320(2) | 0.371(6) | 0.277(7) | 0.304(6) | 0.044(4) | −0.043(5) | −0.047(4) |
| Mo4 | 0.39595(2) | 0.84549(3) | 0.08001(2) | 0.392(6) | 0.314(6) | 0.342(6) | 0.021(4) | −0.021(5) | −0.038(5) |
| O1 | 0.41767(16) | 0.6064(3) | 0.61926(17) | 0.52(5) | 0.46(6) | 0.54(5) | −0.05(4) | 0.06(4) | 0.10(4) |
| O2 | 0.44024(16) | 0.1098(3) | 0.59622(16) | 0.53(5) | 0.33(6) | 0.49(5) | 0.05(4) | 0.02(4) | −0.01(4) |
| O3 | 0.41906(17) | 0.6272(3) | 0.22081(16) | 0.88(6) | 0.40(6) | 0.33(5) | 0.09(4) | −0.01(4) | 0.04(4) |
| O4 | 0.41867(17) | 0.1244(3) | 0.20812(16) | 0.81(6) | 0.47(6) | 0.35(5) | 0.01(4) | −0.01(4) | −0.07(4) |
| O5 | 0.61745(17) | 0.3767(3) | 0.07986(16) | 0.66(6) | 0.54(6) | 0.42(5) | 0.03(4) | 0.00(4) | 0.16(4) |
| O6 | 0.59344(16) | 0.8777(3) | 0.05329(16) | 0.52(5) | 0.35(6) | 0.58(6) | 0.02(4) | 0.07(4) | 0.02(4) |
| O7 | 0.28124(16) | 0.3839(3) | 0.41589(17) | 0.24(5) | 0.48(6) | 0.80(6) | −0.07(4) | 0.01(4) | −0.02(4) |
| O8 | 0.21132(16) | 0.8831(3) | 0.08279(17) | 0.28(5) | 0.47(6) | 0.80(6) | −0.01(4) | 0.01(4) | 0.02(4) |
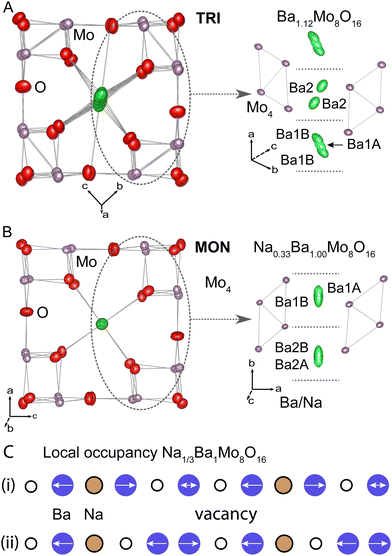
In TRI structure, there are two unique channel sites, which can be seen in the right panel of Fig. 6(A). The cation centred at the unit cell origin requires two inequivalent Ba sites, one (Ba1A) of about 0.62 occupancy on the inversion centre and a second split site (Ba1B) about 0.4 Å away of about 0.125 occupancy each. This gives the cell origin channel site a nearly full combined occupancy of about 0.87. The other cation channel cage only has one inequivalent site (Ba2) that is essentially the same relative position and occupancy as the Ba1B site. This means that the second cage in the model has a much lower average occupancy of 0.25. The overall stoichiometry refines to Ba1.12(3)Mo8O16, which the same as the ideal input stoichiometry within error. The stoichiometry implies that an extra 1 Ba site per 8 vacancies, on average, which also seems to correlate with the approximate occupancies of the three A-sites. An alternate model that uses only one site in the Ba1 cage, which is only stable on the inversion centre, leads to significantly worse overall agreement factor of wR2 = 0.0710, rather than 0.0576 for two Ba sites. In the preferred model, the Ba1B site was constrained to have the same thermal parameters as the Ba1A site, as the freely refined model did not improve agreement with the data despite having more refinement parameters.
The model for MON is shown in Fig. 6(B). In this case, Ba and Na atoms are both present in the channels and the model requires two inequivalent channel cation sites per cage, about 0.30 Å apart, giving a total of four inequivalent channel cation sites in the model. Unlike the TRI structure, there is no special site along the channel to generate extra disorder nor are there any atomic positions on the cage centres. Like the TRI structure, attempts to combine neighbouring partially occupied sites gave many problems. The numerical label refers to the inequivalent cages 1 and 2, with A and B denoting comparable sites for each cage. In this case, the Ba1A and Ba2A sites are the ones farther from their respective cage centres, and they are of slightly lower occupancy. This is shown in the right panel of Fig. 6(B).
All four Ba sites are treated as a disordered mixture of Na and Ba at a ratio fixed to the APT experimental results (0.35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.08 or 0.24
1.08 or 0.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.76), with the total occupancy of each site being freely refined as a single parameter per site. The 1A and 2A site pair and 1B and 2B pair were respectively constrained to have equivalent thermal parameters. More details about these choices are available in the ESI.†
0.76), with the total occupancy of each site being freely refined as a single parameter per site. The 1A and 2A site pair and 1B and 2B pair were respectively constrained to have equivalent thermal parameters. More details about these choices are available in the ESI.†
A final complication in the MON structural model is the observation of excess electron density in the unoccupied part of the hollandite channel (between the 1B and 2B sites in Fig. 6(B)), which is most likely a manifestation of additional local ordering correlations that are not accounted in the model. Attempts to include the residual density as an additional site show that it accounts for about 5% of the total A-site electron density. These attempts required placing the A-site exactly between two cages with an extremely anisotropic thermal parameter. This happens to be the location of the Na-site in the prior report of the same compound.17 However, the resulting A–O bond lengths are around 2.1 Å, which is much too short even for Na and the observations contraindicate fractional O-site distortions nearby.
It is our view that there are significant local structure correlations that preclude choosing a single crystallographic model that best explains all features. Instead, specific parameters should be drawn from the model that they are tailored for. We conclude that the approximate A-site coordination is best described by the four-site model described above and that the fifth A-site between cages does not correspond to an actual crystallographic site. On the other hand, the overall occupation of the hollandite channels is better described by modelling the electron density, which does require using a fifth site. This model yields the final stoichiometry Na0.325(5)Ba1.006(18)Mo8O16, which is a closer match to the mass spectrometry results and within error of the fractional stoichiometry Na1/3BaMo8O16. Though the latter point may be a mere coincidence, we have provided a simple schematic showing the two simplest local vacancy filling models at the determined ratio in Fig. 6(C).
Magnetic properties
The magnetization of TRI and MON phases is overall quite low, as shown in Fig. 7, with each having similar temperature-independent components, χo = 4.50 × 10−5 and 7.20 × 10−5 emu molMo−1. The fitted Curie constants are 1.238(3) × 10−2 and 2.235(7) × 10−3 emu K molMo−1, for TRI and MON species, respectively, which correspond to effective magnetic moments of 0.315 and 0.137μB in the Curie–Weiss model. Along with a larger spin density, the TRI sample also exhibits a larger magnitude Curie–Weiss constant of −12.75(6) K. It also shows a small deviation from Curie Weiss behaviour below 10 K, which is consistent with weak antiferromagnetic correlations. The fitted θW in MON, 1.1(2) K, is effectively zero and is consistent with a very dilute magnetic impurity.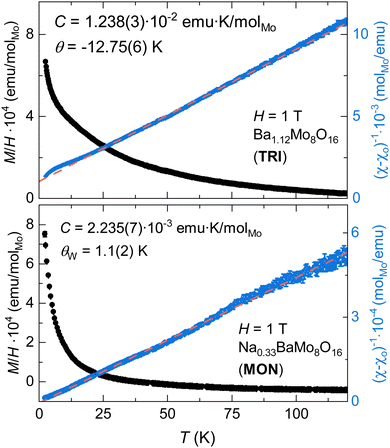 | ||
| Fig. 7 Temperature dependence of M/H of TRI (top) and MON (bottom) phases measured using an applied field of 1 T. | ||
Discussion
A goal of this work is to understand the nature of the observed Mo–Mo bonding motifs, with a particular focus on the relationships between electron count, A-site steric interactions, and thermodynamic stability. Since the A-site filling is equivalent to adding/removing electrons from the chains of [Mo4O8]n− clusters, the synthetic portion of the study provides the foundational details.We found that both TRI and MON phase purity are extremely sensitive to input stoichiometry, requiring greater precision in composition than the sensitivity of these experiments, meaning they can be treated as compounds with fixed stoichiometries at about Ba1.12(3)Mo8O16 and Na0.325(5)Ba1.006(18)Mo8O16.
The TRI phase Ba-site occupancy is also crystallographically disordered, which implies that overall having 56% Ba and 44% vacancies strikes the optimal balance between [Mo4O8]n− reduction and Ba–Ba inter-site repulsion. The present results also favour treating the (as of now) five known TET phases as fixed stoichiometries that are derived from modulated A-site occupancies ranging from 1.067 to 1.143 Ba per 8 Mo. This implies that conditions favouring long-range ordering provide additional stabilization concerns. We speculate that the TRI phase could be the kinetic product that is metastable with respect to the ordered TET phases, but more work is required.
Since there is only one stable composition of Na–Ba–Mo–O hollandite, it is apparently best to treat MON as a unique quaternary phase and not “Na-substituted BaxMo8O16”. The determined stoichiometry's proximity to small rational numbers might be coincidental, as we found no evidence for additional crystallographic order in the dozens of single-crystal diffraction experiments we performed using a high flux rotating anode source and low-background detector.
While this rules out long-range crystallographic ordering as stabilizing the specific stoichiometry, short-range ordering is still expected. A simple interpretation is that a lattice of alternating Ba2+ ions and vacancies can accommodate one Na+ ion per six vacancies without disrupting the Ba occupancies. Fig. 6(C) shows two local structures that are consistent with this scenario. Both local structures appear susceptible to disordered atomic displacements, especially when mixed. We note that this filling of A-sites donates 2.33 e− per formula unit (f.u.), which is higher than any of the ternary Ba–Mo–O phases. It thus appears that thermodynamic stability of MON is driven by the reduction of the [Mo4O8]n− sublattice, which is enabled by the lower electrostatic repulsion of the Na+ ion compared to the Ba2+ ion.
Analysis of crystal symmetries
The above analysis helps explain the compositions to a certain degree, but they do not explain the origin of the different structure types. To do this, one must consider trends in the crystal structures of these and related compounds. In the general case, the symmetry of hollandite compounds is known to correlate to the ionic size of A-cations. If the cation is small enough, the octahedral walls undergo twisting distortions to accommodate minimum energy cation positions closer to the coordinating O atoms and monoclinic symmetry will be favoured.13 Otherwise, a tetragonal symmetry is maintained when larger A-cations occupy tunnels within the hollandite structure.34While the above works well for many hollandites, the opposite trend is seen in Rb1.5Mo8O16 and K2Mo8O16, which are tetragonal and monoclinic at room temperature, though Rb+ is the larger ion. It thus seems likely that there is an electronic component in the case of Mo-based hollandites, with the electron configuration of the Mo clusters playing a major role.35
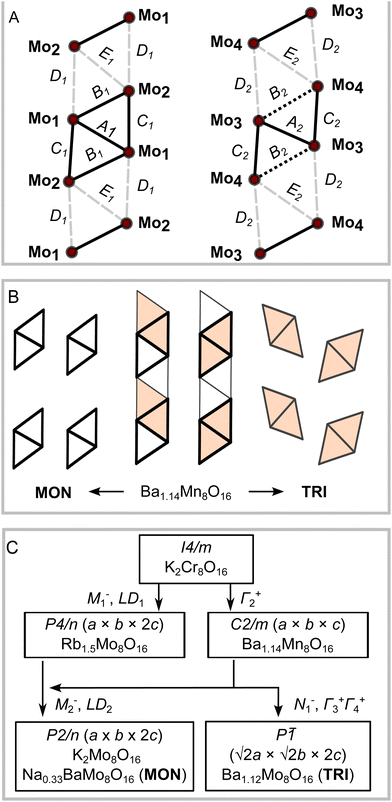
It is necessary to look more closely at the Mo4 clusters to uncover the primary driver of the different structural orderings. Despite the different symmetries and stoichiometries, the main Mo4 cluster motif in MON and TRI is very similar. In both determined crystal structures, the Mo atoms form strong Mo–Mo bonds that are reminiscent of molybdenum oxide clusters embedded in the hollandite chains. The intra-cluster Mo–Mo bonds range from 2.50 A to 2.90 Å, while the distance between two adjacent Mo atoms in different clusters is 3.18–3.20 Å. There are also two distinct types of chains in each compound, shown in Fig. 8(A) as cluster 1 on left and cluster 2 on right. One chain is composed of regular rhombohedra Mo4 clusters, where the five Mo–Mo bonds are nearly equal. The other chain has clusters that have three short Mo–Mo bonds (bonds A and C in Fig. 8(A)) and two long bonds on the outer edges of the rhombus (bond B in Fig. 8(A)). The intercluster distances are also shown in Fig. 8(A) as pale dashes and labelled as D and E.
Table 5 summarizes the bond lengths of both cluster types for the compounds Ba1.12Mo8O16 (TRI), Na1/3BaMo8O16 (MON), and K2Mo8O16 using the prior reported crystallographic data.12 There are evidently only subtle differences between compounds when comparing equivalent bonds, suggesting that such differences are not relevant to the relative stability of triclinic and monoclinic structural forms. The trends in bond lengths are discussed in detail in the electronic structure section below.
| Bond (Å) | TRI | MON | K2Mo8O16 |
|---|---|---|---|
| A1 (Mo1–Mo1) | 2.5797(5) Å | 2.5308(4) | 2.551(3) |
| B1 (Mo1–Mo2) | 2.6170(4) Å | 2.6562(3) | 2.6966(17) |
| C1 (Mo1–Mo2) | 2.5794(4) | 2.5842(3) | 2.5965(17) |
| D1 (Mo1–Mo2) | 3.1626(4) | 3.1634(3) | 3.1765(18) |
| E1 (Mo2–Mo2) | 3.1716(5) | 3.1827(4) | 3.199(3) |
| A2 (Mo3–Mo3) | 2.5605(5) | 2.5392(5) | 2.527(3) |
| B2 (Mo3–Mo4) | 2.8473(3) | 2.8558(3) | 2.8371(17) |
| C2 (Mo3–Mo4) | 2.5483(4) | 2.5585(3) | 2.5653(17) |
| D2 (Mo3–Mo4) | 3.2005(4) | 3.1922(3) | 3.2085(18) |
| E2 (Mo4–Mo4) | 3.2570(5) | 3.2264(4) | 3.195(3) |
Fig. 8(B) compares the pattern of Mo4 clusters in MON and TRI phases. The triclinic distortion in TRI is a result of a unique set of displacement distortions affecting both Ba2+ ions and Mo–O octahedra that results in a staggered tiling pattern. This differs from the other Mo-based hollandites, Na1/3BaMo8O16 (MON) and K2Mo8O16, where both chains of clusters are lined up along the channel axis. The different Mo4 cluster packing in TRI apparently induces shifts in the oxygen sublattice that can be associated with the distinctive Ba-site displacements away from the central channel axis. This might also allow the unusually high Ba occupancy at the cage centre for the remaining site that we observe in the triclinic form.
Fig. 8(C) illustrates the triclinic distortion pathway determined using the Isodistort software suite.36,37 Starting from hollandites of higher symmetry, the highest symmetrical hollandite structure is represented by the space group type I4/m and the compound K2Cr8O16. The distortion complexity is the same in TRI and MON compounds (index 8), and they are both subgroups of the monoclinic Ba1.14Mn8O16 structural type, of space group type C2/m. The latter is the type of monoclinic distortion found in ordinary hollandites that was mentioned above, and it is active on the Γ2+ irrep.
Considering the active mode populations, we find that the orthorhombic strain magnitude, (a − b)/(a + b), in both MON and K2Mo8O16 is less than a quarter of the magnitude observed in Ba1.14Mn8O16, suggesting that the connection may only be circumstantial. The P2/n distortion is also a subgroup of the tetragonal P4/n phase unique to Rb1.5Mo8O16, which is a more descriptive pathway. First, the M1− and LD1 irreps are together responsible for the cluster formation in Rb1.5Mo8O16, yielding crystallographically equivalent chains. The chain degeneracy is then broken by introducing the M2− and LD2 irreps, resulting in the P2/n structures. In other words, the Γ2+ irrep is not needed to understand the primary cluster distortion, though it does contribute as a secondary irrep. Symmetry allows the distortion from P4/n to P2/n to be continuous.
The TRI phase is not a subgroup of Rb1.5Mo8O16 due to the different tiling of clusters. The N1− irrep simultaneously yields the triclinic-type cluster tiling and breaks the chain degeneracy. In other words, only inversion symmetry is compatible with the triclinic-type cluster tiling. We also note that the Γ2+ type orthorhombic distortion magnitude is nearly equivalent in C2/m type Ba1.14Mn8O16 and Ba1.12Mo8O16 (TRI). We suggest the possibility that the different cluster tiling between MON and TRI is linked to the same steric considerations that drive the I4/m to C2/m distortion in ordinary hollandite phases.
Trends in Mo–Mo bonding
Having laid out the symmetry considerations above, this section considers viable electronic models for the origin of the structural distortions in the various Mo-based hollandites. The prior computational study by Toriyama et al. of K2Mo8O16 is a useful framework for the discussion.14In that work, density functional theory (DFT) calculations found a number of flat bands around the Fermi level that are mostly localized to the Mo4 clusters’ d orbitals. They interpreted the bands as corresponding to quasi-molecular Mo–Mo orbitals: four bonding orbitals per cluster, 4 non-bonding orbitals per cluster, and 4 anti-bonding orbitals per cluster. The clusters in K2Mo8O16 are formally [Mo4O8]− if treated as equivalent, meaning there are 9 d electrons per cluster and the Fermi level lies in the middle of the lowest energy non-bonding band (dyz in their nomenclature). In other words, a chain would have a half-filled highest occupied molecular orbital (HOMO), and the configuration might be written dyz1. If both chains are equivalent, there would be a degenerate pair of said orbitals. Two models were then provided under this approach for interpreting the electronic environment of the Mo4 clusters and their effect on the structure and properties of K2Mo8O16.
The first model interpreted K2Mo8O16 as a band insulator, with symmetry-breaking modifications relieving chain degeneracy and opening a band gap of about 80 meV (when using GGA).14 The broken degeneracy yields a fully occupied HOMO that is primarily on chain 1 (in our nomenclature) and lowest unoccupied molecular orbital (LUMO) that is primarily on chain 2. In other words, the chains 1 and 2 might be thought of respectively as dyz2 and dyz0. This is the same as saying there is a net charge transfer that yields one chain with closer to 10 electrons per cluster and the other chain with 8 electrons per cluster.
The second model provided by Toriyama et al. applied Mott physics to the system and found that a Hubbard Ueff ≥ 0.3 eV is sufficient to break the dyz1 orbital degeneracy, driving the formation of an antiferromagnetic insulating (AFI) phase.14 In this model, a single spin-polarized state is filled on each cluster, giving S = ½ per cluster in K2Mo8O16. Notably, the antiferromagnetic exchange interactions in this model were found to lead to geometric frustrations of the spins, which was used to explain the lack of observed long-range magnetic ordering.14
These two models have very different predictions about the relationship between electron count per Mo4 cluster and electronic properties. We show below that the band insulator model provides a good description of the observed compounds with only a minor change in interpretation, while we are unable to understand our observations within the Mott insulator model.
Mott-type model
We consider the utility of the Mott-type model first. The model assumes each cluster has a net S = ½ for the special case of 2 A-site electrons per formula unit (as in K2Mo8O16 = [K+]2[Mo4O8−]2). It is not easy to reconcile this idea with the experimental susceptibilities normally observed in Mo-containing hollandite compounds, which is generally small and more reminiscent of dilute impurity spins. K2Mo8O16, for example, shows one spin per 12 Mo atom,35 meaning 2 out of every 3 clusters are missing the spins predicted by the Mott-like model.The formula of MON indicates 2.33 e− donated per formula unit, which the Mott model would predict leads to a modest change in the number of spins: [Na+]1/3[Ba2+][Mo4O8−]1.67[Mo4O82−]0.33, with the [Mo4O82−] clusters being diamagnetic S = 0. Yet, we found that an effective magnetic moment of 0.137μB per Mo in the MON phase. Treating this as an impurity spin of J = ½ would imply 1 defect per 160 Mo atoms. In contrast with expectation, there are almost no free spins available.
Applying the same arguments to TRI gives a nearly equivalent electron donation count (here, 2.24 e− f.u.−1) as MON. The experimental effective magnetic moment is 0.315μB per f.u in TRI, implying one free spin per 30 Mo atoms, or about one per eight Mo4 clusters.
In summary, the magnetic properties appear to be dominated by defects. We see no obvious way to reconcile the observations with the Mott-like model and so it is not discussed further.
Band insulator model
While Toriyama et al. identified the resulting HOMO and LUMO bands as being essentially non-bonding,14 we argue that the broken-degeneracy HOMO shows clear evidence of bonding character that is mostly localized on the outer Mo–Mo bonds (B1 in Fig. 8(A)). This implies a net increase in bond order along the same bond whenever the state is filled, which indeed matches observation: the B1 orbital is much shorter than B2 in all compounds with broken chain degeneracy, as shown in Table 5. There are also subtle differences between compounds in the relative B1 and B2 bond lengths, which can be understood as arising from different populations of the relevant states in each cluster type. That is, the band character of the states is non-negligible and so there is non-integer electrons per cluster.This interpretation predicts that the bond-lengths should be correlated to the net valence of the Mo atoms in the cluster, since the states at the Fermi level are primarily Mo character. This is tested by applying the bond valence sum (BVS) analysis to the experimental crystal structures of TRI, MON, K2Mo8O16, and room-temperature Rb1.5Mo8O16,38 the results of which are shown in Table 6. The overall BVS of a compound decreases as the A-site electron count increases, as expected, and each of the monoclinic and triclinic phases show a significant difference in overall bond valence between clusters. The P4/n symmetry of Rb1.5Mo8O16 causes the two clusters to be symmetry equivalent, so both chains are approximately equivalent to chain 1 in the other compounds. This is consistent with electron transfer between chains being a significant part of the symmetry-breaking interactions.
| Bond valence | ||||
|---|---|---|---|---|
| TRI | MON | K2Mo8O16 | Rb1.5Mo8O16 | |
| Mo1 | 3.44 | 3.47 | 3.49 | 3.48 |
| Mo2 | 3.59 | 3.61 | 3.67 | 3.61 |
| Mo3 | 3.57 | 3.55 | 3.49 | — |
| Mo4 | 3.91 | 3.90 | 3.89 | — |
The final test of the model is shown in Fig. 9(A), which shows the difference in total valence per Mo4 cluster plotted against the difference in the B Mo–Mo bond lengths from the same clusters. A direct relationship is observed, meaning a net increase in electrons in cluster 1 does in fact correlate to a net decrease in bond length (increase in bond order). This model is depicted schematically in Fig. 9(B), which also considers the different number of electrons donated by the A-site.
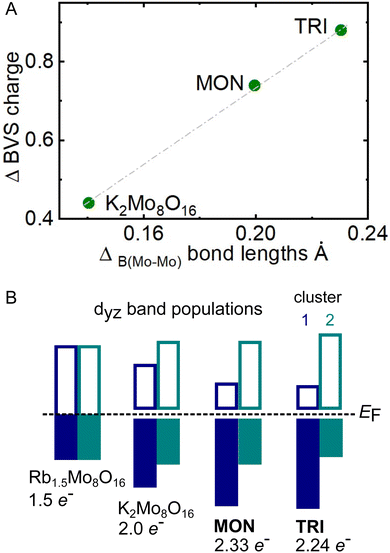 | ||
| Fig. 9 (A) Change in BVS charge per cluster plotted against difference in bond length B for TRI, MON, and K2Mo8O16. (B) Schematic showing the interpretation of panel A using the band insulator model. The electron number refers to the total band population across both clusters, which is calculated from the stoichiometry. The cluster filling ratios are taken from Table 6. | ||
In summary, the band insulator model adapted from Toriyama et al. provides a helpful framework for understanding the subtle difference in molybdenum cluster formation between hollandites. The fact that the per cluster electron populations can be continuously varied (i.e. non-integer) delocalized, at least within the same chain. Similar effects have been observed in the vanadium-based Magnéli phases V8O15 and V9O17,39 which each exhibit a metal-to-insulator transition (MIT) and also show evidence of electron delocalization between local metal–metal bonded motifs.
Further, our group isotropy analysis is also consistent with charge ordering driving the observed electrostructural transition in Rb1.5Mo8O16 at 208 K. Though the low-temperature structure has not yet been proven to be the same as K2Mo8O16, the transition is apparently of second order, which is allowed by symmetry. We also speculate that the K2Mo8O16 and Na1/3BaMo8O16 (MON) may be induced to transform into the tetragonal P4/n structure either above room temperature or under uniaxial strain.
Conclusions
Distinct solid-state synthesis pathways were determined for the closely related triclinic Ba1.12Mo8O16 (TRI), tetragonal Ba1+xMo8O16 (TET), and monoclinic Na1/3BaMo8O16 (MON) hollandites. TRI is optimally synthesized using BaCO3 as the Ba source in the Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mo
Mo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O molar ratio 1.12
O molar ratio 1.12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15.44 and an optimal cooling rate around 50 °C h−1. The reducing conditions seem to be necessary due to the potential for carbothermal oxidation of Mo from the evolved CO2. No evidence was found to suggest there is compositional variance in the Ba occupancy in TRI, and the sensitivity of phase stability to reaction conditions suggests that TRI may be metastable with respect to modulated tetragonal phase formation. The addition of NaI to the reaction mixture enhances crystal quality while simultaneously stabilizing various modulated TET phases not previously reported. Further work is required to fully characterize the complex structure of the modulated structures.
15.44 and an optimal cooling rate around 50 °C h−1. The reducing conditions seem to be necessary due to the potential for carbothermal oxidation of Mo from the evolved CO2. No evidence was found to suggest there is compositional variance in the Ba occupancy in TRI, and the sensitivity of phase stability to reaction conditions suggests that TRI may be metastable with respect to modulated tetragonal phase formation. The addition of NaI to the reaction mixture enhances crystal quality while simultaneously stabilizing various modulated TET phases not previously reported. Further work is required to fully characterize the complex structure of the modulated structures.
The addition of Na2MoO4 instead of NaI results in the formation of the sodium barium molybdate MON, which is also apparently a line compound with the refined formula Na0.325Ba1.005Mo8O16. BaMoO4 is the optimal Ba source and Na2MoO4 should be added in excess, using the Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba
Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mo
Mo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O molar ratio 0.5
O molar ratio 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.02
1.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, which is in accordance with prior work. Atom probe tomography confirms the presence and homogeneous distribution of Na atoms within the hollandite channels of the monoclinic compound.
16, which is in accordance with prior work. Atom probe tomography confirms the presence and homogeneous distribution of Na atoms within the hollandite channels of the monoclinic compound.
Detailed analysis of Mo–O and Mo–Mo bond lengths reveal clear evidence of intercluster charge transfer. This observation supports the charge ordering model proposed by Toriyama et al. for the related K2Mo8O16, indicating that broken symmetry is electronically driven. The effects of electron doping imply that the Mo states near the Fermi level remain at least partially delocalized in the low symmetry form, which highlights the complexity of metal–metal bonding in early transition metal oxides. Additional characterization of the Mo-based hollandites is required to determine the detailed relationship between metal bonding, charge ordering, and the electronic properties.
Author contributions
Eslam Elbakry: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review and editing. Jared M. Allred: conceptualization, data curation, formal analysis, funding acquisition, methodology, project administration, resources, software, supervision, validation, visualization, writing – review and editing.Data availability
CIF files containing crystallographic data and observed structure factors are included as part of the ESI.† They have also been deposited with the Inorganic Crystal Structure Database (ICSD) and Cambridge Crystal Structure Database (CCSD) under deposition numbers 2371927 and 2371928. Other data presented in the manuscript will be made available upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under award DE-SC0018174. Diffraction experiments using the Rigaku Synergy-R DW were made possible with the support of the U.S. National Science Foundation, Division of Chemistry under award NSF CHE MRI 1828078 and the University of Alabama. The authors thank Dr Sanghamitra Deb and Professor Gregory Thompson for their advice and assistance in APT data acquisition and interpretation. We also thank Monir Hossain and Professor Ruigang Wang for their assistance in the thermogravimetric analysis. We are thankful to the AARC at UA for hosting facilities for SEM, APT, and ICP-OES analyses. The authors also gratefully acknowledge the University of Alabama College of Engineering and College of Arts and Sciences shared analytical facility for providing use of the ICP-OES.References
- J. F. Berry and C. C. Lu, Metal–metal bonds: from fundamentals to applications, Inorg. Chem., 2017, 56, 7577–7581 CrossRef CAS PubMed.
- W. McCarroll, K. Podejko, A. Cheetham, D. Thomas and F. DiSalvo, The crystal structure of La3Mo4.33Al0. 67O14 and the electronic structure of La3Mo4XO14 (X = Si; Mo13Al23; Al12V12), J. Solid State Chem., 1986, 62, 241–252 CrossRef CAS.
- T. Hughbanks and R. Hoffmann, Chains of trans-edge-sharing molybdenum octahedra: metal–metal bonding in extended systems, J. Am. Chem. Soc., 1983, 105, 3528–3537 CrossRef CAS.
- S. Yoshikado, Y. Michiue, Y. Onoda and M. Watanabe, Ion conduction in single crystals of the hollandite-type one-dimensional superionic conductor NaxCrxTi8−xO16 (x = 1.7), Solid State Ionics, 2000, 136, 371–374 CrossRef.
- G. Zhao, G. Wan, Y. Tang, X. Xu, X. Zhou, M. Zhou, Z. Deng, S. Lin and G. Wang, Hollandite-type β-FeOOH(Cl) as a new cathode material for chloride ion batteries, Chem. Commun., 2020, 56, 12435–12438 RSC.
- J. H. Jo, H. J. Kim, N. Yaqoob, K. Ihm, O. Guillon, K.-S. Sohn, N. Lee, P. Kaghazchi and S.-T. Myung, Hollandite-type potassium titanium oxide with exceptionally stable cycling performance as a new cathode material for potassium-ion batteries, Energy Storage Mater., 2023, 54, 680–688 CrossRef.
- S. L. Suib, Structure, porosity, and redox in porous manganese oxide octahedral layer and molecular sieve materials, J. Mater. Chem., 2008, 18, 1623–1631 RSC.
- R. Grote, T. Hong, L. Shuller-Nickles, J. Amoroso, M. Tang and K. Brinkman, Radiation tolerant ceramics for nuclear waste immobilization: Structure and stability of cesium containing hollandite of the form (Ba, Cs)1.33(Zn, Ti)8O16 and (Ba, Cs)1.33(Ga, Ti)8O16, J. Nucl. Mater., 2019, 518, 166–176 CrossRef CAS.
- H. Leligny, P. Labbe, M. Ledesert, B. Raveau, C. Valdez and W. McCarroll, La1.16Mo8O16: a hollandite-related compound with an incommensurate modulated structure, Acta Crystallogr., Sect. B: Struct. Sci., 1992, 48, 134–144 CrossRef.
- N. Barrier, J. Tortelier and P. Gougeon, A new reduced molybdenum oxide with a hollandite-type structure, PrMo6O12, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2001, 57, i3–i5 CrossRef CAS.
- J. Tortelier, W. McCarroll and P. Gougeon, Synthesis, crystal structure, and characterization of the new ordered hollandite-type NdMo6O12, J. Solid State Chem., 1998, 136, 87–92 CrossRef CAS.
- C. C. Torardi and J. C. Calabrese, Hydrothermal synthesis of a new molybdenum hollandite containing tetranuclear metal-atom clusters. X-ray crystal structure of K2Mo8O16, Inorg. Chem., 1984, 23, 3281–3284 CrossRef CAS.
- J. E. Post, R. B. Von Dreele and P. R. Buseck, Symmetry and cation displacements in hollandites: structure refinements of hollandite, cryptomelane and priderite, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 1056–1065 CrossRef.
- T. Toriyama, M. Watanabe, T. Konishi and Y. Ohta, Superatomic crystal emerging in transition-metal oxides: Molybdenum hollandite K2Mo8O16, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 235116 CrossRef.
- N. Barrier, P. Gougeon and R. Retoux, Synthesis, crystal structure and TEM study of the new hollandite-type Ba∼8/7Mo8O16, J. Alloys Compd., 2001, 317, 120–126 CrossRef.
- C. Torardi and R. McCarley, Some reduced ternary and quaternary oxides of molybdenum. A family of compounds with strong metal–metal bonds, J. Solid State Chem., 1981, 37, 393–397 CrossRef CAS.
- K.-H. Lii, Synthesis and characterization of some reduced ternary and quaternary molybdenum oxide phases with strong metal–metal bonds, Iowa State University, 1985 Search PubMed.
- S. Ishiwata, J. Bos, Q. Huang and R. J. Cava, Structure and magnetic properties of hollandite Ba1.2Mn8O16, J. Phys.: Condens. Matter, 2006, 18, 3745 CrossRef CAS.
- A. Smith, M. Rutten, L. Herrmann, E. Epifano, R. Konings, E. Colineau, J.-C. Griveau, C. Guéneau and N. Dupin, Experimental studies and thermodynamic assessment of the Ba–Mo–O system by the CALPHAD method, J. Eur. Ceram. Soc., 2021, 41, 3664–3686 CrossRef CAS.
- B. H. Toby and R. B. Von Dreele, GSAS-II: the genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- B. H. Toby and R. B. Von Dreele, What's new in GSAS-II, Powder Diffr., 2014, 29, S2–S6 CrossRef CAS.
- G. Sheldrick, C. Gilmore, H. Hauptman, C. Weeks, R. Miller and I. Usón, Shelx, 2012 Search PubMed.
- L. J. Farrugia, WinGX and ORTEP for Windows: an update, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M. Chen, Z. Zhou and S. Hu, Bond valence parameters linearly dependent on the molybdenum oxidation states, Chin. Sci. Bull., 2002, 47, 978–981 CAS.
- M. K. Miller, K. F. Russell, K. Thompson, R. Alvis and D. J. Larson, Review of atom probe FIB-based specimen preparation methods, Microsc. Microanal., 2007, 13, 428–436 CrossRef CAS PubMed.
- B. P. Geiser, T. F. Kelly, D. J. Larson, J. Schneir and J. P. Roberts, Spatial distribution maps for atom probe tomography, Microsc. Microanal., 2007, 13, 437–447 CrossRef CAS PubMed.
- C. Torardi and R. E. McCARLEY, Synthesis and structure of Ba5(Mo4O6)8: A compound having the NaMo4O6 structure type and superlattice ordering of barium ions, J. Less-Common Met., 1986, 116, 169–186 CrossRef CAS.
- G. L. Schimek, D. A. Nagaki and R. E. McCarley, Synthesis and characterization of Ba3Mo18O28: a metal–metal-bonded oligomer containing four trans edge-shared molybdenum octahedra, Inorg. Chem., 1994, 33, 1259–1265 CrossRef CAS.
- K. Lii, C. Wang and S. Wang, Zigzag octahedral cluster chains in BaMo6O10, J. Solid State Chem., 1988, 77, 407–411 CrossRef CAS.
- G. Hall, C. Jefferson and F. Michel, Determination of W and Mo in natural spring waters by ICP-AES (inductively coupled plasma atomic emission spectrometry) and ICP-MS (inductively coupled plasma mass spectrometry): application to South Nahanni river area, NWT, Canada, J. Geochem. Explor., 1988, 30, 63–84 CrossRef CAS.
- E. Elbakry and J. Allred, Synthesis and structural investigation of novel barium molybdenum hollandite structures, Acta Crystallogr., Sect. A: Found. Crystallogr., 2022, 79, a8–a8 Search PubMed.
- J. Zhang and C. W. Burnham, Hollandite-type phases: geometric consideration of unit-cell size and symmetry, Am. Mineral., 1994, 79, 168–174 CAS.
- T. Ozawa, I. Suzuki and H. Sato, Structural, magnetic and electronic transport properties of novel Hollandite-type molybdenum oxide, Rb1.5Mo8O16, J. Phys. Soc. Jpn., 2006, 75, 014802 CrossRef.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, ISODISPLACE: a web-based tool for exploring structural distortions, J. Appl. Crystallogr., 2006, 39, 607–614 CrossRef CAS.
- H. T. Stokes, D. M. Hatch and B. J. Campbell, ISODISTORT, ISOTROPY Software Suite, https://iso.byu.edu.
- I. D. Brown, Bond valences—A simple structural model for inorganic chemistry, Chem. Soc. Rev., 1978, 7, 359–376 RSC.
- J. M. Allred and R. J. Cava, Crystal structures of the high temperature forms of V8O15 and V9O17 and structural trends in the VnO2n−1 Magnéli series, J. Solid State Chem., 2013, 198, 10–17 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4qm00622d |
| This journal is © the Partner Organisations 2025 |