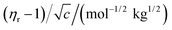Open Access Article
Open Access ArticleInterference of potassium chloride and diammonium hydrogen phosphate on volumetric, viscometric and spectroscopic properties of aqueous nicotinamide†
Prachiprava Mohapatra,
Siddhartha Panda,
Dwitikrishna Mishra ,
Sulochana Singh* and
Malabika Talukdar
,
Sulochana Singh* and
Malabika Talukdar *
*
Department of Chemistry, Siksha O Anusandhan Deemed to be University, Bhubaneswar-751030, Odisha, India. E-mail: sulochanasingh@soa.ac.in; malabikatalukdar@soa.ac.in
First published on 21st January 2025
Abstract
Understanding how vitamins and fertilizers interact in aquatic environments is crucial for managing water quality, protecting aquatic life, and promoting sustainable agricultural practices. The molecular interactions between nicotinamide (NA) and two fertilizers, potassium chloride (KCl) and diammonium hydrogen phosphate (DAP), were examined by density (ρ) and viscosity (η) measurements in order to investigate and analyze the solvation behavior that occurs in the ternary solutions (NA + KCl/DAP + water). All of these investigations were conducted at temperatures ranging from 293.15 to 313.15 K and experimental pressures P = 101 kPa. The volumetric characteristics such as apparent molar volume (Vϕ), partial molar volume (V0ϕ) and partial molar expansibility (E0ϕ) were analyzed. The Jones–Dole equation was used to link experimentally observed viscosity values with solution molarity, yielding viscosity coefficients AF and BJ, temperature derivatives of E0ϕ (∂E0ϕ/∂T)P and BJ (∂BJ/∂T) have been used to determine the structure-building/breaking properties of the solute. The free energy of activation for viscous flow per mole of solvent (Δμ0#1) and per mole of solute (Δμ0#2), as well as the entropy and enthalpy of activation per mole of solvent (ΔS0#2 and ΔH0#2 respectively) were also evaluated. The results show that ion–ion and ion–hydrophilic interactions are dominant in the systems under investigation. The novelty of studying vitamins and fertilizers in aquatic environments lies in the potential to uncover new interactions and mechanisms, leading to more effective environmental management strategies, innovative agricultural practices, and improved understanding of aquatic ecosystem dynamics.
1. Introduction
The relationship between humans and fertilizers is one that has evolved over millennia, shaping agriculture, nutrition, and public health. While the positive impacts of fertilizers on crop yields and food security are undeniable, concerns about their potential negative effects on human health have also been raised. This article explores the future scope of study on the interactions of fertilizers with human beings, considering the complex interplay of factors that influence these interactions. Chemical fertilizers are purposefully modified chemicals containing known proportions of three macroelements, namely nitrogen, potassium, and phosphorous (NPK). The continuous and excessive utilization of chemical fertilizers plays a major role, directly and/or indirectly on human health and in changing environmental conditions. The food crops grown using chemical fertilizers aren't as nutrient-dense as they should be. Because artificial fertilizers sacrifice a plant's health for rapid growth, the outcome is less nutritious produce. Current research on fertilizer–human interactions focuses on impact of fertilizer runoff on water bodies,1 uptake of fertilizers by plants and the subsequent transfer of contaminants to consumers,2 and impact of fertilizer-related emissions on air quality and respiratory health.3 Diammonium hydrogen phosphate (DAP) is an inorganic phosphate, widely used as fertilizer. It is made from two common macronutrients phosphate (P) and nitrogen (N). The pH of the soil is temporarily raised by DAP treatment, but eventually the treated ground becomes more acidic due to the nitrification of the ammonium.4 Another most widely used fertilizer is potassium chloride (KCl), also known as muriate of potash. It provides crops with two nutrients K+ and Cl−1, necessary for both plants and animals.5Maintaining a healthy metabolism is facilitated by a healthy lifestyle that includes consuming a balanced diet and engaging in physical activity. Vitamins are micronutrients necessary for many body processes, including hormone regulation, wound healing, infection prevention, and strong bones. In addition, vitamins aid in proper growth and development as well as the functionality of cells and organs. Vitamins are organic compounds found in trace levels in natural foodstuffs. Having too little or too high of any particular vitamin may increase the risk of developing certain health issues.
Nicotinamide/niacinamide (naturally non-synthesized vitamin), is a water-soluble form of vitamin B3, found in many foods, including meat, fish, milk, eggs, vegetables, and cereals. The body needs nicotinamide to function properly, as well as to maintain healthy cells and fats and sugars. When niacin (C5H4N–COOH) is consumed in excess of what the body requires, it is transformed into nicotinamide.6 Nicotinamide (C5H4N–CONH2) is used by people to avoid vitamin B3 deficiency and associated illnesses like pellagra.7 Along with many other ailments, it is also utilized for acne, diabetes, cancer, osteoarthritis, aging skin, and skin discolouration.6 Now-a-days farmers are using excessive amount of fertilizers for faster plant growth. The long-term accumulation of fertilizers in soil, due to either frequent applications or high-density use, has multiple implications across agricultural ecosystems, impacting human health, biodiversity, food nutrition, and broader ecological balance. When excessive amount of chemical fertilizer is absorbed by the plants they can “withstand” it through increased protein synthesis. The extra nitrogen is stored mostly in the plant's green, leafy sections as nitrate and enabling toxins to enter the food chain through cereals, vegetables, and water. This causes health effects to rise and spread quickly, which can lead to haemoglobin disorders and human health hazards.8 Also excessive use of these fertilizers can adversely affect various physiological processes in aquatic organisms. Some studies shows that DAP caused decreases in the haemoglobin, haematocrit, red blood cell and total leukocyte counts in the freshwater fish.9
For many in the food, chemical, and pharmaceutical industries, it is essential to comprehend thermo-physical properties. The characterization or performance of solute–solvent and solute–solute interactions in diverse dissociation or association processes can be taught using this kind of information. Understanding solute–solvent interactions requires a reasonable understanding of both thermophysical and transport aspects. Several molecular interaction types and their implications on solubility, solute–solvent interaction, and phase behaviour in solution are investigated in this study.9 Understanding how environmental factors and nutrient availability influence metabolic pathways is essential for optimizing plant health. Fertilizers, such as KCl and DAP, are commonly applied in agricultural practices to enhance nutrient availability, particularly potassium and phosphorus. However, the specific interactions between these fertilizers and NA, particularly in an aqueous medium, remain largely unexplored. This study aims to explore the interactions between KCl and DAP with NA in an aqueous medium, focusing on: volumetric and viscometric characteristics of NA in aqueous medium in the absence and presence of fertilizers. Study on the interactions between NA and fertilizers will provide new insights into how fertilizers can be used not just to supply essential nutrients but also to fine-tune plant metabolic pathways for improved growth, stress tolerance, and overall agricultural productivity. By focusing on nutrient efficiency, metabolic regulation, and sustainability, it connects the specific research to practical outcomes in agriculture.
Researchers employ a range of instruments and techniques to characterize the volumetric, viscometric, acoustic, and conductometric properties of solutions.10–13 We have reported the studies on physicochemical properties on different electrolytes and nonelectrolytes in aqueous systems.14–19 This article is the continuation of our recent publication, where we have explored the volumetric and acoustic properties of aqueous L-ascorbic acid in aqueous solutions of potassium chloride and diammonium hydrogen phosphate.19 In the present article we investigated the volumetric and viscometric behaviours of NA in aqueous medium in the presence of KCl/DAP at different temperatures. These studies have yielded valuable information that is applicable to many fields, such as agricultural science, chemistry, and pharmaceutical sciences. A review of the literature on the physicochemical characteristics of vitamin aqueous solutions with or without co-solutes reveals a small number of publications where these characteristics are analyzed in the light of vitamin–water or vitamin–water–co-solute interactions. S. S. Dhondge et al. have investigated volumetric and viscometric properties of binary mixture of nicotinamide in water at different temperature (T = 275.15, 277.15 and 279.15 K).10 They have concluded that nicotinamide acts as a structure maker when it is dissolved in water at the temperature of maximum density i.e. at 277.15 K, due to the presence of –CONH2 group. They also have observed that hydrophobic interactions are predominant in binary (nicotinamide + water) systems. They have shown that the viscosity A-coefficient is small and positive for (nicotinamide + water), indicating the presence of weak ion–ion interactions and the positive value of B-coefficient indicating the presence of strong solute–solvent interactions at all temperatures.
By studying the physicochemical properties of NA with KCl/DAP in aqueous medium and understanding how nicotinamide interacts with water and fertilizer components, we can gain insights into the ecological relevance of these solutions, particularly in terms of nutrient retention, soil health, and the potential impact on aquatic ecosystems.
2. Experimental
2.1 Materials
The manufacturers' local vendors provide the AnalR grade reagents. Due to their high purity, the chemicals were used without further purification except drying in a vacuum desiccator over anhydrous CaCl2 for a minimum of 48 hours before use (Table 1).| Name and CAS no. of chemicals | Molecular formula & molar mass (kg mol−1) | Molecular structure | Manufacturers | Percent puritya | Purification method |
|---|---|---|---|---|---|
| a As proclaimed by the manufacturer. | |||||
| Nicotinamide | C6H6N2O (0.12212) | 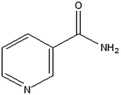 |
Loba Chemie Pvt. Ltd, Mumbai, India | >99% | Drying over anhydrous CaCl2 |
| Diammonium hydrogen phosphate 7783-28-0 | (NH4)2HPO4 (0.13212) | 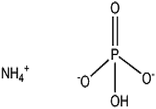 |
Merck Life Science Pvt. Ltd, Mumbai, India | >99% | Drying over anhydrous CaCl2 |
| Potassium chloride 7447-40-7 | KCL (0.0745) |  |
Merck Life Science Pvt. Ltd, Mumbai, India | >99% | Drying over anhydrous CaCl2 |
2.2 Preparation of solutions
Binary solutions (i.e. aqueous NA/KCl/DAP) were prepared by dissolving a carefully weighed amount of solute in 1 kg of water (density of water is 0.998 kg L−1). For weighing purpose a digital balance from Citizen-Synchronics Electronics Pvt. Ltd was used with a precision of ±0.01 mg. The triply distilled degassed water with conductivity less than 1.0 × 10−6 Sm−1 was procured from a Millipore, Milli-Q Academic water purification system and was used for preparation of solutions. The ternary solutions of nicotinamide (i.e. NA/KCl/DAP + water) were prepared by maintaining concentrations in the range (0.01–0.15) mol kg−1 in aqueous (0.5, 0.75, 1.0) mol kg−1 DAP/KCl. The combined standard Uncertainty in the concentration of solutions is found to be within 1 × 10−3 mol kg−1. The solutions were prepared at room temperature (298.15 K) and atmospheric pressure (101 kPa) and stored in polypropylene airtight storage bottles to minimize the assimilation of moisture and to avert the contamination by microbes.2.3 Methods
| ρ2 = ρ1w2/w1 | (1) |
| η0/η1 = (ρ0t0)/(ρ1t1) | (2) |
3. Results and discussion
3.1 Volumetric study
A comprehensive understanding of the physicochemical properties of NA solutions through volumetric study in aqueous medium is essential for various fields including pharmaceuticals, cosmetics, and food science, where NA finds important applications. The solution behaviour of aqueous NA in different electrolytes and nonelectrolytes has been studied by researchers. A. Kundu et al. conducted research on the apparent molar volumes and apparent molar heat capacities of aqueous NA at various temperatures.20 S. S. Dhondge et al. explored the density and viscosity of NA and nicotinic acid in diluted aqueous solutions at and around the temperature of the maximum density of water.10 The molecular interactions of NA in aqueous citric acid monohydrate solutions were studied by M. N. Roy et al. in relation to measurements of viscosity B-coefficient and partial molar volume manifestation.11 The apparent molar volumes and viscosity B-coefficients of NA in aqueous tetrabutylammonium bromide solutions at T = (298.15, 308.15, and 318.15) K were investigated by B. Sinha et al.21 For the present article, the density of aqueous NA are measured and compared with the literature data. SF Fig. 1 provides a graphic representation of comparison of the experimental density data for aqueous NA with the corresponding literature values21,22 and is found to be in well accordance with each other.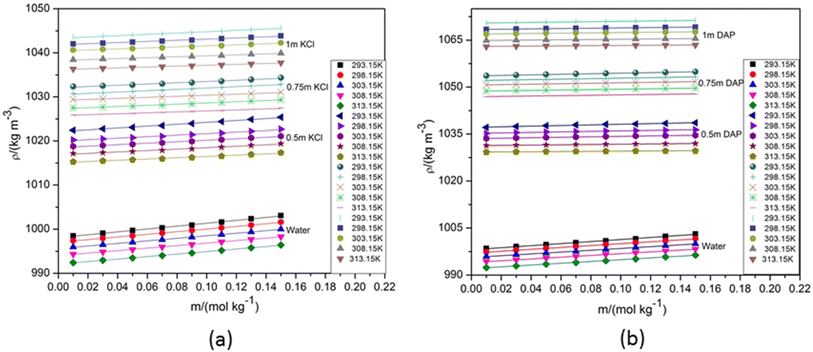 | ||
| Fig. 1 Density (ρ) versus molality (m) of aqueous NA in (a) water and aqueous KCl of varying compositions and (b) water and aqueous DAP of varying compositions. | ||
SF Table 1 enlists the experimental density values of NA measured at various temperatures in water, aqueous KCl and aqueous DAP with varying compositions. The corresponding graphs in Fig. 1 demonstrate how an increase in solute and cosolute molality leads to an increase in density because of closer packing of particles, occurrence of stronger intermolecular interactions and increase in mass per unit volume. Higher temperature boosts the particles' kinetic energy which results in volume expansion of the solution and the consequent decline in density.
| Vϕ = (ρ0 − ρ)(mρρ0)−1 + Mρ−1 | (3) |
The conventional symbols for density of solvent, density of solution, molality of solution, and molar mass of solute are ρ0, ρ, m and M, respectively. The following expression (eqn (4)) is used to calculate the uncertainty for apparent molar volume, ∂Vϕ, taking into account the effects of m, M, ρ0 and ρ.12
| ∂Vϕ = [(M/ρ − Vϕ)2(∂m/m)2 + (Vϕ + 1/mρ0)2(∂ρ/ρ)2]1/2 | (4) |
Since the uncertainty in molality is small in this calculation, only the uncertainty in density (∂ρ) is included when calculating the uncertainty in apparent molar volume, which at low molality ranges is approximated as ±0.2 × 10−6 m3 mol−1.
When a solute is added to a solvent, the solvent molecules must adjust to accommodate the solute particles, which can lead to changes in the volume occupied by a given number of moles of the solvent. In some cases, the molar volume of the solution might decrease due to interactions between the solute and solvent molecules, leading to a decrease in the overall volume occupied by the solution compared to the pure solvent. Conversely, in other cases, the molar volume might increase, especially if the solute–solvent interactions result in the formation of new molecular arrangements that occupy more space. Overall changes in molar volume upon adding a solute depend on factors such as the nature of the solute and solvent, their concentrations, and the specific interactions between them. For the present study, Table 2 displays the Vϕ values for NA in water and in aqueous KCl and DAP as functions of temperature and molality of NA/KCl/DAP.
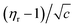 of NA in water, (water + KCl) and (water + DAP) at different temperatures and experimental pressure, P = 101 kPaa
of NA in water, (water + KCl) and (water + DAP) at different temperatures and experimental pressure, P = 101 kPaa
| mA/mol kg−1 | Vϕ × 105/m3 mol−1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 293.15 K | 298.15 K | 303.15 K | 308.15 K | 313.15 K | 293.15 K | 298.15 K | 303.15 K | 308.15 K | 313.15 K | |
| a Standard uncertainty in molality u(m) = 0.001 mol kg−1, in pressure u(p) = 0.01 × 106 Pa, in temperature u(T) = 0.01 K, in density u(ρ) = 0.5 kg m−3, in viscosity u(η) = 0.02 mPa s. | ||||||||||
| NA + water | ||||||||||
| 0.000 | 9.32 | 9.63 | 9.65 | 9.65 | 9.77 | |||||
| 0.009 | 9.25 | 9.52 | 9.62 | 9.63 | 9.69 | 0.070 | 0.179 | 0.176 | 0.166 | 0.169 |
| 0.029 | 9.23 | 9.48 | 9.57 | 9.60 | 9.65 | 0.108 | 0.185 | 0.204 | 0.234 | 0.188 |
| 0.051 | 9.20 | 9.40 | 9.52 | 9.55 | 9.61 | 0.127 | 0.212 | 0.220 | 0.252 | 0.223 |
| 0.069 | 9.18 | 9.35 | 9.45 | 9.50 | 9.55 | 0.152 | 0.236 | 0.238 | 0.235 | 0.242 |
| 0.089 | 9.11 | 9.32 | 9.40 | 9.46 | 9.51 | 0.163 | 0.259 | 0.260 | 0.268 | 0.267 |
| 0.111 | 8.98 | 9.30 | 9.38 | 9.45 | 9.46 | 0.182 | 0.283 | 0.286 | 0.290 | 0.286 |
| 0.129 | 8.92 | 9.21 | 9.34 | 9.40 | 9.41 | 0.202 | 0.303 | 0.309 | 0.315 | 0.304 |
| 0.149 | 9.32 | 9.63 | 9.65 | 9.65 | 9.77 | 0.225 | 0.318 | 0.327 | 0.366 | 0.323 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| NA + 0.501 mol kg−1KCl | ||||||||||
| 0.000 | 10.69 | 11.19 | 11.33 | 11.38 | 11.54 | |||||
| 0.009 | 10.51 | 11.00 | 11.09 | 11.15 | 11.22 | 0.252 | 0.282 | 0.311 | 0.346 | 0.379 |
| 0.029 | 10.40 | 10.85 | 10.96 | 11.02 | 11.10 | 0.268 | 0.294 | 0.331 | 0.352 | 0.394 |
| 0.049 | 10.31 | 10.75 | 10.81 | 10.89 | 11.03 | 0.276 | 0.309 | 0.351 | 0.378 | 0.408 |
| 0.069 | 10.19 | 10.62 | 10.71 | 10.81 | 10.95 | 0.287 | 0.326 | 0.378 | 0.399 | 0.425 |
| 0.089 | 10.11 | 10.54 | 10.59 | 10.67 | 10.86 | 0.321 | 0.340 | 0.389 | 0.408 | 0.442 |
| 0.109 | 10.02 | 10.46 | 10.50 | 10.57 | 10.76 | 0.324 | 0.353 | 0.396 | 0.428 | 0.460 |
| 0.129 | 9.94 | 10.34 | 10.44 | 10.50 | 10.65 | 0.338 | 0.375 | 0.408 | 0.436 | 0.478 |
| 0.151 | 10.69 | 11.19 | 11.33 | 11.38 | 11.54 | 0.352 | 0.388 | 0.421 | 0.461 | 0.497 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| NA + 0.749 mol kg−1KCl | ||||||||||
| 0.000 | 11.02 | 11.16 | 11.33 | 11.38 | 11.52 | |||||
| 0.009 | 10.89 | 11.05 | 11.08 | 11.25 | 11.32 | 0.281 | 0.315 | 0.374 | 0.427 | 0.452 |
| 0.029 | 10.79 | 10.91 | 10.98 | 11.12 | 11.20 | 0.315 | 0.377 | 0.408 | 0.430 | 0.506 |
| 0.049 | 10.62 | 10.83 | 10.90 | 11.06 | 11.11 | 0.333 | 0.393 | 0.444 | 0.465 | 0.523 |
| 0.069 | 10.56 | 10.70 | 10.86 | 10.93 | 11.07 | 0.354 | 0.413 | 0.474 | 0.491 | 0.543 |
| 0.089 | 10.48 | 10.62 | 10.80 | 10.82 | 11.01 | 0.384 | 0.425 | 0.489 | 0.507 | 0.561 |
| 0.109 | 10.40 | 10.54 | 10.70 | 10.71 | 10.95 | 0.395 | 0.443 | 0.499 | 0.538 | 0.585 |
| 0.129 | 10.31 | 10.46 | 10.64 | 10.67 | 10.88 | 0.405 | 0.455 | 0.511 | 0.561 | 0.602 |
| 0.151 | 1.14 | 1.04 | 0.96 | 0.88 | 0.81 | 0.423 | 0.476 | 0.525 | 0.573 | 0.624 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| NA + 1.001 mol kg−1KCl | ||||||||||
| 0.000 | 2.80 | 2.83 | 2.82 | 2.88 | 2.91 | |||||
| 0.009 | 11.15 | 11.20 | 11.27 | 11.33 | 11.38 | 0.300 | 0.346 | 0.357 | 0.382 | 0.503 |
| 0.031 | 10.94 | 11.07 | 11.12 | 11.17 | 11.21 | 0.318 | 0.362 | 0.370 | 0.418 | 0.546 |
| 0.049 | 10.81 | 10.93 | 11.02 | 11.08 | 11.13 | 0.358 | 0.391 | 0.403 | 0.453 | 0.558 |
| 0.071 | 10.67 | 10.84 | 10.98 | 10.99 | 11.03 | 0.393 | 0.428 | 0.434 | 0.482 | 0.598 |
| 0.089 | 10.60 | 10.79 | 10.91 | 10.95 | 10.99 | 0.414 | 0.460 | 0.466 | 0.508 | 0.658 |
| 0.109 | 10.52 | 10.68 | 10.85 | 10.91 | 10.97 | 0.436 | 0.485 | 0.493 | 0.538 | 0.705 |
| 0.129 | 10.45 | 10.63 | 10.78 | 10.84 | 10.92 | 0.458 | 0.502 | 0.519 | 0.561 | 0.691 |
| 0.149 | 10.37 | 10.56 | 10.67 | 10.80 | 10.88 | 0.474 | 0.518 | 0.538 | 0.583 | 0.679 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| NA + 0.499 mol kg−1DAP | ||||||||||
| 0.000 | 5.32 | 5.46 | 5.51 | 5.61 | 5.65 | |||||
| 0.009 | 10.02 | 10.34 | 10.58 | 10.79 | 10.92 | 0.149 | 0.193 | 0.219 | 0.257 | 0.304 |
| 0.029 | 10.28 | 10.56 | 10.84 | 11.14 | 11.28 | 0.193 | 0.243 | 0.276 | 0.305 | 0.327 |
| 0.049 | 10.43 | 10.68 | 10.93 | 11.24 | 11.36 | 0.214 | 0.264 | 0.298 | 0.335 | 0.371 |
| 0.069 | 10.49 | 10.81 | 10.99 | 11.24 | 11.41 | 0.238 | 0.280 | 0.316 | 0.353 | 0.400 |
| 0.089 | 10.56 | 10.86 | 11.00 | 11.29 | 11.43 | 0.257 | 0.300 | 0.337 | 0.375 | 0.415 |
| 0.109 | 10.68 | 10.92 | 11.02 | 11.32 | 11.46 | 0.275 | 0.323 | 0.357 | 0.394 | 0.435 |
| 0.131 | 10.71 | 10.94 | 11.06 | 11.34 | 11.51 | 0.291 | 0.347 | 0.377 | 0.414 | 0.450 |
| 0.149 | 10.74 | 10.96 | 11.09 | 11.36 | 11.54 | 0.311 | 0.368 | 0.397 | 0.431 | 0.471 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| NA + 0.749 mol kg−1DAP | ||||||||||
| 0.000 | 7.33 | 7.37 | 7.38 | 7.41 | 7.41 | |||||
| 0.009 | 10.53 | 10.65 | 10.71 | 10.75 | 10.79 | 0.100 | 0.165 | 0.197 | 0.226 | 0.246 |
| 0.031 | 10.61 | 10.68 | 10.77 | 10.88 | 10.92 | 0.170 | 0.203 | 0.233 | 0.271 | 0.314 |
| 0.049 | 10.65 | 10.75 | 10.82 | 10.93 | 11.01 | 0.194 | 0.227 | 0.268 | 0.305 | 0.333 |
| 0.071 | 10.68 | 10.78 | 10.84 | 10.95 | 11.02 | 0.214 | 0.265 | 0.290 | 0.328 | 0.352 |
| 0.089 | 10.70 | 10.81 | 10.87 | 10.98 | 11.04 | 0.232 | 0.286 | 0.315 | 0.345 | 0.376 |
| 0.109 | 10.73 | 10.82 | 10.88 | 11.00 | 11.05 | 0.250 | 0.301 | 0.333 | 0.363 | 0.390 |
| 0.129 | 10.75 | 10.84 | 10.90 | 11.02 | 11.06 | 0.279 | 0.325 | 0.355 | 0.386 | 0.408 |
| 0.149 | 10.76 | 10.84 | 10.92 | 11.02 | 11.07 | 0.294 | 0.341 | 0.373 | 0.404 | 0.428 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| NA + 1.001 mol kg−1DAP | ||||||||||
| 0.000 | 5.64 | 5.73 | 5.73 | 5.77 | 5.78 | |||||
| 0.009 | 10.69 | 10.73 | 10.78 | 10.83 | 10.92 | 0.108 | 0.116 | 0.149 | 0.181 | 0.213 |
| 0.029 | 10.71 | 10.77 | 10.83 | 10.91 | 10.99 | 0.150 | 0.202 | 0.229 | 0.259 | 0.288 |
| 0.049 | 10.74 | 10.81 | 10.87 | 10.96 | 11.03 | 0.182 | 0.224 | 0.249 | 0.279 | 0.309 |
| 0.069 | 10.78 | 10.85 | 10.90 | 10.97 | 11.09 | 0.209 | 0.243 | 0.269 | 0.299 | 0.329 |
| 0.089 | 10.80 | 10.86 | 10.92 | 11.00 | 11.10 | 0.234 | 0.263 | 0.290 | 0.319 | 0.349 |
| 0.109 | 10.81 | 10.90 | 10.95 | 11.02 | 11.13 | 0.256 | 0.283 | 0.309 | 0.339 | 0.369 |
| 0.129 | 10.84 | 10.93 | 10.97 | 11.05 | 11.14 | 0.286 | 0.302 | 0.329 | 0.359 | 0.389 |
| 0.151 | 10.85 | 10.93 | 10.99 | 11.06 | 11.16 | 0.296 | 0.323 | 0.349 | 0.379 | 0.408 |
A perusal of Table 2 shows that the values of Vϕ for NA are higher in aqueous KCl/DAP than in water. NA (C5H4N–CONH2) is produced by substituting the carboxylic group (–COOH) in niacin (C5H4N–COOH) with an amide (–CONH2) group. The NA molecule has an electrical dipole moment of 3.315 debye.23 It has many protonation sites (see Table 1) connected to the moieties of pyridine (C5H5N) and amide (–CONH2). Since pyridine is a potent nucleophile, there is a significant electron density at this location on the NA molecule. When a co-solute (KCl/DAP) is present in the aqueous solution of NA, the cations (K+ and NH4+) interact strongly with the high electron dense moieties of NA. NA can also gain a proton from water or NH4+ ion of DAP and appears in a salt form (C5H4N–CONH2·HCl). Thus, Vϕ values are higher in ternary solutions of NA (NA + KCl/DAP + water) than the binary solution (NA + water).
It can also be seen from Table 2 that at each experimental temperature the values of Vϕ for NA in aqueous DAP are increased with concentration of NA whereas in aqueous KCl the values are in decreasing trend (Fig. 2). It can also be observed that Vϕ values are higher in aqueous KCl than in aqueous DAP. As stated earlier the nature of the solute and solvent, their concentrations and compositions, and the particular interactions between them are some of the variables that affect changes in molar volume with the addition of a solute. NA molecules are relatively large and hydrophobic in nature. The electrostatic interactions between ions and their surrounding water molecules influence the volumetric properties. KCl is a simple ionic compound with high solubility in water as compared to DAP. Besides, KCl has a high degree of symmetry and packing efficiency. KCl dissociates completely into potassium (K+) and chloride (Cl−) ions in aqueous solution. Due to its complete dissociation and smaller ion sizes, K+ and chloride Cl− interact more efficiently with NA in water. The dissociation of KCl into K+ and Cl− ions results in simple ion–water interactions. K+ ions have a relatively high charge density for a monovalent ion, meaning they attract water molecules more strongly, forming a stable hydration shell around the ion. This structuring of water molecules around K+ can significantly influence the volumetric properties, making the solution denser. DAP undergoes partial dissociation into ammonium (NH4+) and hydrogen phosphate (HPO42−) ions in water. While NH4+ interacts with water in a similar way to K+, HPO42− have a much more complex hydration structure due to their higher charge and larger size. The phosphate anion can form strong hydrogen bonds with water molecules, creating a more organized hydration shell around the ion. These interactions tend to increase the viscosity of the solution but may not affect the density as dramatically as KCl because phosphate ions do not lead to the same level of ion pairing or simple solvation effects as potassium ions.
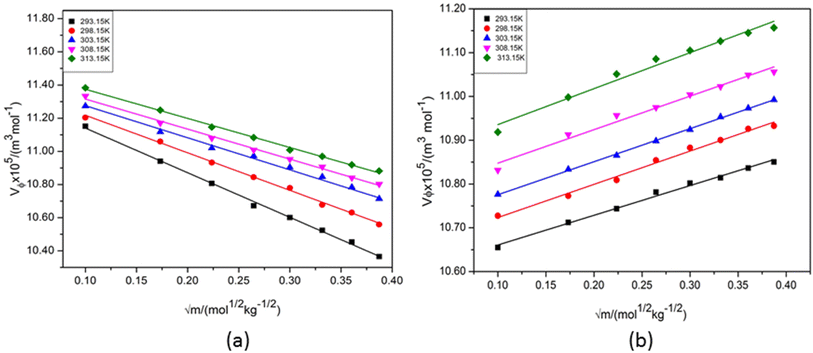 | ||
| Fig. 2 Apparent molar volume (Vϕ) versus (√m) plots of aqueous nicotinamide in (a) 1 mol kg−1 KCl and (b) 1 mol kg−1 DAP at different temperatures. | ||
Also, ion-pair formation influence the volumetric properties. KCl solutions often form ion pairs (K+ and Cl−) in certain concentrations. The formation of these ion pairs reduces the effective number of free ions in solution and results in a lower effective volume. However, at certain concentrations, the overall solution volume can expand due to the combined effects of hydration and electrostatic interactions between ions. This effect is typically more pronounced in solutions of simple salts like KCl. In DAP solutions, while ion pairing between NH4+ and HPO42− is less likely due to the significant difference in charge, stronger interactions between the phosphate anion and water molecules may lead to a more stable, structured solvation environment. This structured solvation can result in a lower expansion of the solution's volume, especially compared to the effect seen in KCl solutions. The hydration of the HPO42− ions in DAP solutions leads to more ordered water structures that don't necessarily result in as much volume expansion. When NA is added to the aqueous solution of DAP, it can disrupt the structure of the water molecules surrounding the ions of DAP influencing the hydration shells around DAP ions. This disruption can lead to an increase in the volume occupied by the solvent molecules, resulting in an apparent increase in molar volume. Hence, the values of Vϕ for NA in aqueous KCl is higher than aqueous DAP.
Apparent molar volume at infinite dilution, i.e. limiting apparent molar volume (V0ϕ) of NA (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte) was derived from Redlich, Rosenfield, and Mayer (RRM) eqn (5),
1 electrolyte) was derived from Redlich, Rosenfield, and Mayer (RRM) eqn (5),
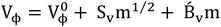 | (5) |
| Sv = kw3/2 | (6) |
The limiting slope k can be solved by the following polynomial eqn (7) developed by Redlich–Meyer,
| k = 1.4447 + 1.6799 × 10−2t − 8.4055 × 10−6t2 + 5.5153 × 10−7t3 | (7) |
w is the valency factor and can be evaluated by the following eqn (8),
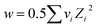 | (8) |
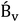 is the RRM empirical coefficient that describes deviation from Debye–Hückel limiting law (DHLL), which can be understood in terms of interactions among ion solvation shells. Because of the lack of necessary data for calculating DHLL slopes at temperatures other than 298.15 K, V0ϕ is calculated from the intercept of the straight line obtained from the Masson-type relation (eq. (6)).
is the RRM empirical coefficient that describes deviation from Debye–Hückel limiting law (DHLL), which can be understood in terms of interactions among ion solvation shells. Because of the lack of necessary data for calculating DHLL slopes at temperatures other than 298.15 K, V0ϕ is calculated from the intercept of the straight line obtained from the Masson-type relation (eq. (6)).
Additionally, we can also ascertain V0ϕ using Masson's eqn (9) to determine the linear regression of Vϕ versus m1/2 plots,
| Vϕ = V0ϕ + Sexpvm1/2 | (9) |
| Temperature | RRM coefficients | Masson coefficients | ||
|---|---|---|---|---|
| V0ϕ × 106/m3 mol−1 | Sv × 105/m3 mol−2 kg | V0ϕ × 106/m3 mol−1 | Sexpv × 105/m3 mol−2 kg | |
| a Standard uncertainty in molality u(m) = 0.001 mol kg−1, in pressure u(p) = 0.01 × 106 Pa, in temperature u(T) = 0.01 K, in density u(ρ) = 0.5 kg m−3. | ||||
| NA + H2O | ||||
| 293.15 (K) | 93.63 ± 0.28 | −2.68 ± 0.31 | 94.93 ± 0.63 | −1.29 ± 0.22 |
| 298.15 (K) | 96.20 ± 0.18 | −2.75 ± 0.20 | 97.72 ± 0.18 | −1.39 ± 0.06 |
| 303.15 (K) | 96.78 ± 0.10 | −2.33 ± 0.11 | 97.99 ± 0.27 | −1.15 ± 0.09 |
| 308.15 (K) | 96.79 ± 0.09 | −1.88 ± 0.10 | 98.38 ± 0.25 | −0.92 ± 0.09 |
| 313.15 (K) | 97.79 ± 0.05 | −2.47 ± 0.05 | 99.09 ± 0.20 | −1.22 ± 0.07 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NA + 0.501 mol kg−1KCl | ||||
| 293.15 (K) | 106.85 ± 0.24 | −5.19 ± 0.26 | 113.05 ± 0.31 | −2.61 ± 0.07 |
| 298.15 (K) | 111.79 ± 0.31 | −5.79 ± 0.33 | 114.98 ± 0.18 | −2.92 ± 0.06 |
| 303.15 (K) | 113.01 ± 0.41 | −6.23 ± 0.44 | 116.49 ± 0.15 | −3.15 ± 0.05 |
| 308.15 (K) | 113.58 ± 0.33 | −6.08 ± 0.36 | 116.93 ± 0.21 | −3.06 ± 0.07 |
| 313.15 (K) | 114.59 ± 0.53 | −5.60 ± 0.58 | 117.78 ± 0.45 | −2.86 ± 0.16 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NA + 0.749 mol kg−1KCl | ||||
| 293.15 (K) | 110.32 ± 0.26 | −5.01 ± 0.28 | 113.05 ± 0.31 | −2.51 ± 0.11 |
| 298.15 (K) | 111.89 ± 0.16 | −5.08 ± 0.18 | 114.61 ± 0.33 | −2.53 ± 0.12 |
| 303.15 (K) | 112.59 ± 0.44 | −4.36 ± 0.47 | 115.09 ± 0.33 | −2.23 ± 0.12 |
| 308.15 (K) | 114.07 ± 0.18 | −5.20 ± 0.19 | 116.84 ± 0.41 | −2.58 ± 0.14 |
| 313.15 (K) | 114.63 ± 0.42 | −4.13 ± 0.45 | 117.02 ± 0.27 | −2.12 ± 0.10 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NA + 1.001 mol kg−1KCl | ||||
| 293.15 (K) | 111.10 ± 0.41 | −5.28 ± 0.44 | 114.09 ± 0.14 | −2.69 ± 0.05 |
| 298.15 (K) | 111.96 ± 0.26 | −4.49 ± 0.28 | 114.44 ± 0.17 | −2.26 ± 0.06 |
| 303.15 (K) | 112.59 ± 0.23 | −3.86 ± 0.25 | 114.69 ± 0.30 | −1.93 ± 0.11 |
| 308.15 (K) | 112.90 ± 0.33 | −3.54 ± 0.36 | 114.94 ± 0.19 | −1.81 ± 0.07 |
| 313.15 (K) | 113.24 ± 0.39 | −3.27 ± 0.42 | 115.18 ± 0.28 | −1.69 ± 0.10 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NA + 0.499 mol kg−1DAP | ||||
| 293.15 (K) | 101.06 ± 0.56 | 4.77 ± 0.61 | 98.25 ± 0.41 | 2.48 ± 0.15 |
| 298.15 (K) | 104.22 ± 0.59 | 4.19 ± 0.63 | 101.69 ± 0.48 | 2.20 ± 0.17 |
| 303.15 (K) | 106.99 ± 0.61 | 2.97 ± 0.66 | 104.64 ± 0.51 | 1.87 ± 0.18 |
| 308.15 (K) | 109.77 ± 0.72 | 3.00 ± 0.78 | 107.20 ± 0.50 | 1.50 ± 0.18 |
| 313.15 (K) | 111.71 ± 0.36 | 2.68 ± 0.39 | 108.11 ± 0.30 | 1.41 ± 0.11 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NA + 0.749 mol kg−1DAP | ||||
| 293.15 (K) | 99.36 ± 0.57 | −9.58 ± 0.62 | 104.68 ± 0.09 | 0.78 ± 0.03 |
| 298.15 (K) | 100.10 ± 0.64 | −10.25 ± 0.69 | 105.81 ± 0.14 | 0.71 ± 0.05 |
| 303.15 (K) | 100.49 ± 0.67 | −10.81 ± 0.72 | 106.49 ± 0.06 | 0.72 ± 0.02 |
| 308.15 (K) | 101.26 ± 0.52 | −10.51 ± 0.57 | 107.27 ± 0.19 | 0.81 ± 0.07 |
| 313.15 (K) | 101.47 ± 0.47 | −11.05 ± 0.51 | 108.48 ± 0.18 | 0.64 ± 0.06 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NA + 1.001 mol kg−1DAP | ||||
| 293.15 (K) | 100.64 ± 0.68 | −9.91 ± 0.74 | 105.98 ± 0.06 | 0.68 ± 0.02 |
| 298.15 (K) | 100.79 ± 0.68 | −10.15 ± 0.73 | 106.48 ± 0.08 | 0.76 ± 0.03 |
| 303.15 (K) | 101.02 ± 0.70 | −10.69 ± 0.76 | 107.00 ± 0.03 | 0.75 ± 0.01 |
| 308.15 (K) | 101.77 ± 0.63 | −10.70 ± 0.69 | 107.71 ± 0.12 | 0.77 ± 0.04 |
| 313.15 (K) | 102.26 ± 0.67 | −11.10 ± 0.73 | 108.54 ± 0.14 | 0.82 ± 0.05 |
Molecular structure of NA contains a hydrophobic aromatic ring attached to hydrophilic sites, i.e. amide (–CONH2) and hydroxyl group (–OH). NA's structure strikes a balance between hydrophilic and hydrophobic properties, which is crucial for its biological roles. The hydrophilic amide group allows NA to participate in enzymatic catalysed reactions and metabolic processes where interaction with water is possible. For the present experiment, as the concentration of NA increases, these hydrophilic regions can interact more powerfully with each other and with smaller ions of KCl than the bigger ions of DAP. This results in an increase in the limiting apparent molar volume in KCl. All positive V0ϕ values increase as temperature rises. At higher temperature, since the degree of hydrogen bonding between solvent molecules decreases more monomeric water molecules are available for the solvation of electrolytic ions. At all experimental temperatures, positive values of V0ϕ indicate significant ion–solvent interactions. As the molal composition of KCl/DAP increases, so does V0ϕ. Due to stronger forces of attraction between KCl/DAP's polar groups and those of NA, water molecules in the loosely held secondary solvation layers should become less electrostricted and be released into the bulk. Larger values of V0ϕ are resulted from volume expansion of the solution.
The experimental slope values (Sexpv) offer valuable insights into the interactions between solute particles in a solution.25 Positive sign of Sexpv suggests that even at infinite dilution there are reasonable amount of solute–solute interactions in the system, whereas its negative sign suggests that solute–solute interactions are negligible.13 A significant solute–solute interaction for NA with DAP is indicated by positive values of Sexpv, whereas a prevalent solute–solvent interaction with KCl is shown by negative values of Sv. H. Kumar et al. found a potent solute–solvent interaction of L-serine and L-leucine13 and a significant solute–solute interaction of D(+)-glucose and D(−)-fructose26 in aqueous DAP. Larger NH4+ and HPO42− ions in DAP hinders hydrophilic cosphere overlapping between ionic and hydrophilic parts of NA and DAP. In contrast, stronger solute–solvent interaction is revealed in aqueous KCl where the ions are smaller and favour hydrophilic cosphere overlapping.
| ΔtrV0ϕ = V0ϕ(in aqueous KCl/DAP) − V0ϕ(in water) | (10) |
Table 4 shows that the values of ΔtrV0ϕ are positive at all experimental temperatures. The concept of overlapping of hydration co-spheres can be used to explain the concentration-dependent thermodynamic characteristics of the solutes in aqueous solutions. The co-sphere model, created by Friedman and Krishnan,27 states that the overlap of hydration co-spheres of hydrophobic groups causes a net volume loss. This means that the effect of hydration co-sphere overlap is detrimental. Conversely, the volume of the solution increases when the hydrophilic hydration cospheres overlap. The overall effect of the overlap of the hydration co-spheres of NA and KCl/DAP reduces the effect of water electrostriction by NA molecules The effect of hydration cosphere overlap increases with the molarity of KCl/DAP in the ternary mixtures. In the current study, ion–hydrophilic and hydrophilic–hydrophilic group interactions are predominate over ion–hydrophobic, hydrophobic–hydrophobic, and hydrophilic-hydrophobic contacts, as suggested by positive values of ΔtrV0ϕ.
| Property | T/K | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| a Standard uncertainty in molality u(m) = 0.001 mol kg−1, in pressure u(p) = 0.01 × 106 Pa, in temperature u(T) = 0.01 K, in density u(ρ) = 0.5 kg m−3. | |||||
| NA + H2O | |||||
| E0ϕ × 107/m3 mol−1 K−1 | 3.50 | 2.75 | 1.99 | 1.24 | 0.49 |
| σ × 101 | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.501 mol kg−1KCl | |||||
| E0ϕ × 107/m3 mol−1 K−1 | 9.31 | 6.47 | 3.63 | 0.78 | −2.06 |
| σ × 101 | 0.26 | 0.36 | 0.27 | 0.21 | 0.31 |
| ΔtrV0ϕ × 105/m3 mol−1 | 1.48 | 1.73 | 1.85 | 1.86 | 1.87 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.749 mol kg−1KCl | |||||
| E0ϕ × 107/m3 mol−1 K−1 | 2.89 | 2.46 | 2.03 | 1.61 | 1.18 |
| σ × 101 | 0.00 | 0.02 | −0.04 | 0.03 | −0.01 |
| ΔtrV0ϕ × 105/m3 mol−1 | 1.81 | 1.69 | 1.71 | 1.85 | 1.79 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 1.001 mol kg−1KCl | |||||
| E0ϕ × 107/m3 mol−1 K−1 | 0.66 | 0.59 | 0.53 | 0.47 | 0.41 |
| σ × 101 | −0.23 | −0.46 | −0.61 | −0.77 | −0.86 |
| ΔtrV0ϕ × 105/m3 mol−1 | 1.92 | 1.67 | 1.67 | 1.66 | 1.61 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.499 mol kg−1DAP | |||||
| E0ϕ × 107/m3 mol−1 K−1 | 7.45 | 6.75 | 6.05 | 5.34 | 4.64 |
| σ × 101 | 0.00 | 0.00 | −0.04 | 0.04 | 0.00 |
| ΔtrV0ϕ × 105/m3 mol−1 | 5.56 | 4.43 | 3.59 | 3.02 | 2.67 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.749 mol DAP | |||||
| E0ϕ × 107/m3 mol−1 K−1 | 1.66 | 1.73 | 1.81 | 1.88 | 1.96 |
| σ × 101 | 0.00 | 0.00 | 0.00 | 0.02 | 0.09 |
| ΔtrV0ϕ × 105/m3 mol−1 | 6.20 | 4.84 | 3.78 | 2.93 | 2.51 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 1.001 mol kg−1DAP | |||||
| E0ϕ × 107/m3 mol−1 K−1 | 0.93 | 1.11 | 1.29 | 1.47 | 1.65 |
| σ × 101 | −0.02 | 0.00 | 0.00 | 0.00 | 0.01 |
| ΔtrV0ϕ × 105/m3 mol−1 | 6.33 | 4.91 | 3.83 | 2.98 | 2.52 |
Furthermore, a basic model has also been used to describe conventional partial molar quantities of the solute,28,29 i.e.
| V0ϕ = Vvw + Vvoid − Vshrinkage | (11) |
The interactions between NA, KCl/DAP and water in ternary solutions can be summarized as,
(i) Ion–hydrophilic interactions between ionic of NA and KCl/DAP with polar end of water
(ii) Ion–hydrophobic interactions of the ions of KCl/DAP with the non-polar hydrocarbon structure of NA
(iii) Ion–ion interactions between charged end group of NA and ions of KCl/DAP (K+, Cl−/NH4+, PO43−)
(iv) Hydrogen bonding of water with the N-atom in the heterocyclic ring and the N and O-atoms in the amide group of NA.
A rise in V0ϕ values and all the above stated interactions determine the overall state of the solution.
| V0ϕ = a + bT + cT2 | (12) |
Table 5 shows the values for the empirical constants a, b, and c. T represents the experimental temperature. Putting the values of a, b, and c in eqn (12), theoretical values of V0ϕ can be evaluated. The formula given in eqn (13) can determine the values of average relative deviations (ARD) σ, from which we can compare the effectiveness of the polynomial eqn (12). Small ARD values, as seen in Table 4, suggests that the experimentally obtained V0ϕ values show minimum divergence from the theoretically derived values, and the aforementioned polynomial eqn (12) fits well in the current volumetric investigation. Furthermore, the values of empirical constants a, b, and c are thus useful in determining other two volumetric parameters i.e. apparent molar expansibility and Hepler's constant which are discussed in Section 3.1.4.
| σ = (1/n)∑√[(V0ϕ(experimental) − V0ϕ(calculated))/V0ϕ(experimental)] | (13) |
| mB/mol−1 kg−1−1 | a × 104/m3 mol−1 | b × 106/m3 mol−1 K−1 | c × 108/m3 mol−1 K−2 | (∂E0∅/∂T)P × 108/m3 mol−1 K−2 |
|---|---|---|---|---|
| a Standard uncertainty in molality u(m) = 0.001 mol kg−1, in pressure u(p) = 0.01 × 106 Pa, in temperature u(T) = 0.01 K, in density u(ρ) = 0.5 kg m−3. | ||||
| Nicotinamide in (water + KCl) | ||||
| 0.000 | −6.54 ± 1.87 | 4.76 ± 1.24 | −0.75 ± 0.20 | −1.50 |
| 0.501 | −26.10 ± 9.26 | 17.60 ± 6.11 | −2.84 ± 1.01 | −5.69 |
| 0.749 | −3.39 ± 4.42 | 2.80 ± 2.92 | −0.43 ± 0.48 | −0.86 |
| 1.001 | 0.41 ± 0.23 | 0.43 ± 0.15 | −0.06 ± 0.02 | −0.13 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Nicotinamide in (water + DAP) | ||||
| 0.499 | −7.25 ± 3.79 | 4.87 ± 2.50 | −0.70 ± 0.41 | −1.41 |
| 0.749 | 1.20 ± 1.96 | −0.27 ± 1.30 | 0.07 ± 0.21 | 0.15 |
| 1.001 | 2.33 ± 0.39 | −0.96 ± 0.25 | 0.18 ± 0.04 | 0.36 |
| E0ϕ = (∂V0ϕ/∂T)P = b + 2cT | (14) |
The values of E0ϕ are useful to understand the solvation behaviour of the solvent and the consequent changes in solvent structure. Hepler31 developed the thermodynamic eqn (15) to determine the solute's ability to reform or deform the hydrogen bonded structure of water in the solvation spheres.
As observed from Table 4, the values of E0ϕ are positive and reveals that in an aqueous solution, ions of NA interact with solvated KCl/DAP ions, indicating solute–solvent interactions. A similar result was also reported by Harsh Kumar et al.13 from the thermophysical studies of zwitterions of amino acids L-serine and L-leucine in aqueous solutions of DAP.
Additionally, positive E0ϕ values may indicate packing or caging effects of water due to the interaction between NA and KCl/DAP ions.32 The positive E0ϕ values demonstrates efficient ion-hydrophilic and hydrophilic–hydrophilic interactions between NA and KCl/DAP ions, as well as hydrophobic solvation of the solute.33
To determine if NA functions as a water structure-building or structure-deforming agent, the temperature derivative of E0ϕ was determined using the following thermodynamic expression (eqn (15)):
| (∂E0ϕ/∂T)P = (∂2V0ϕ/∂T2)P = 2c | (15) |
The equation above yields a temperature-independent constant term (2c) called Hepler's constant after L. G. Hepler. This Hepler's constant is a term which provides a way to characterize how the apparent molar expansibility of a solute changes with temperature. The sign of (∂E0ϕ/∂T)P indicates whether a dissolved solute is a structure maker or breaker in a solvent.34 Positive and small negative (∂Eϕ/∂T)P values (tending to zero) indicate structure making capacity, while negative (∂E0ϕ/∂T)P values indicate structure breaking. There is an existence of dynamic equilibrium between a highly structured 3D network of bulk and single water molecules. If adding a solute promotes the structured form of water, the solute is referred to as a structure creator. In contrast, if the hydrogen-bonded 3D network of water is damaged, the solute will be identified as a structural breaker.
The Hepler constant values for NA in aqueous DAP at 0.75 mol kg−1 and 1.0 mol kg−1 concentrations are positive, The values in 0.75 mol kg−1 and 1.0 mol kg−1 KCl though are negative but very close to zero. That indicates that NA in higher concentration of aqueous KCl/DAP has a structure-making nature, whereas it functions as a structure breaker at lower concentrations of aqueous KCl/DAP. The structure-forming tendency of NA in aqueous DAP demonstrates that hydrophobic hydration prevails over electrostriction of water molecules near solutes which may be due to the presence of amide (–CONH2) and hydroxyl group (–OH) in the molecular structure of NA. The structure-making property, i.e., hydrogen bond strengthening capacity of NA aids in solvation and transport of nutrients. This directly benefits nutrient availability, solvent uptake efficiency, hence crop health and yield.
The findings here are similar with previous investigations on amino acids L-serine and L-leucine13 and D(+)-glucose and D(−)-fructose26 in aqueous DAP.
The limiting apparent molar volume of transfer can be represented as follows (eqn (16)) to find ion pair (VAB) and triplet (VABB) volumetric interaction coefficients,
| ΔtrV0ϕ = 2VABmB + 3VABBmB2… | (16) |
| Solvent | VAB × 105 (m3 kg mol−2) | VABB × 105 (m3 kg2) mol−3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 293.15 (K) | 298.15 (K) | 303.15 (K) | 308.15 (K) | 313.15 (K) | 293.15 (K) | 298.15 (K) | 303.15 (K) | 308.15 (K) | 313.15 (K) | |
| Aqueous KCl | 1.98 | 2.56 | 2.80 | 3.00 | 2.89 | −0.68 | −1.19 | −1.35 | −1.48 | −1.42 |
| Aqueous DAP | 0.18 | 0.40 | 0.88 | 1.36 | 1.31 | 0.29 | 0.05 | −0.29 | −0.60 | −0.57 |
Table 6 documents the values of VAB and VABB. The positive values of pair interaction coefficient, VAB for volumetric measurements signify that pair wise interactions are dominating in the (NA + KCl/DAP + water) mixtures than triplet interactions. Pair wise interaction in the ternary solutions of NA in aqueous KCl leading over aqueous DAP solutions is observed from higher positive VAB values in KCl. Close proximity of smaller ions favours overlapping of hydration cospheres and promote subsequent pairwise interactions between NA and KCl. The negative sign of VABB states that in DAP medium triplet formation is as plausible as pair formation at lower temperatures. However, triplet formation is subdued at higher temperatures in DAP medium and at all temperatures in KCl. At higher temperatures, higher kinetic energy of the ions prevents them to approach each other and triplet formation is unlikely to take place.
3.2 Viscometric study
Transport properties describe how energy, particles, or momentum move through a material or fluid/liquid. These properties are critical in various fields, including solution chemistry, materials science, physics, and engineering. The main transport properties are: thermal conductivity, electrical conductivity, diffusion coefficient and viscosity. Viscosity, specifically characterizes a fluid's resistance to deformation or flow. Viscosity depends on various factors like temperature, pressure, chemical composition, shear rate, presence of solutes or additives, etc. A deeper understanding of the molecular basis of viscosity changes in fertilizer solutions, and how these changes affect nutrient uptake in plants, is crucial for optimizing agricultural practices. The relationship between viscosity, nutrient delivery, and the physical properties of fertilizers can have significant practical implications for crop productivity and fertilizer efficiency. The molecular interactions in fertilizer solutions that determine viscosity play a significant role in how nutrients are delivered and absorbed by plants. High-viscosity solutions can impede the efficient movement of nutrients through soil and reduce nutrient uptake, while low-viscosity solutions generally facilitate better delivery and absorption. For the present investigation, using eqn (2) the dynamic viscosities of NA in water and aqueous KCl/DAP were evaluated by measuring the density and flow time of the solutions at various temperatures. The experimentally determined viscosity values of aqueous NA are compared to the reported data in the literature.22 SF Fig. 2 shows that the experimental values are consistent with the data given in the literature at all temperatures tested.SF Table 1 specifies the viscosity values of the solutions (NA + water) and (NA + water + KCl/DAP), which are visually depicted as functions of the solutions' molality and temperature in Fig. 3. From SF Table 1 it also can be seen that the viscosity increases with increase in concentration of NA in aqueous and aqueous KCl/DAP solutions.
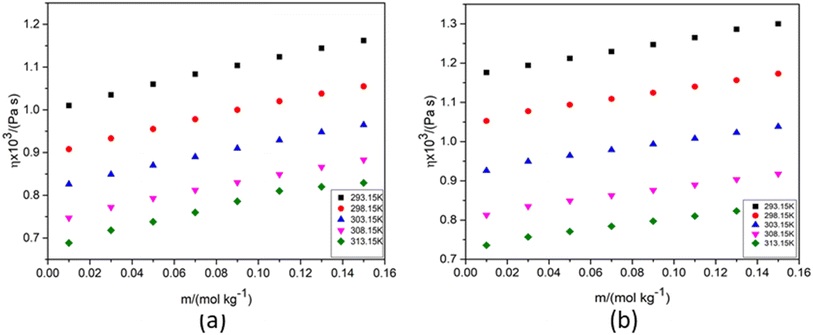 | ||
| Fig. 3 Viscosity (η) versus molality (m) of NA in (a) 1 mol kg−1 aqueous KCl and (b) 1 mol kg−1 aqueous DAP. | ||
The ascending trend of viscosity of the binary and ternary solutions of NA with the molality of NA and compositions of KCl/DAP in aqueous solutions support the fact of increased cohesive interactions between the liquid layers of the solution at higher concentrations. In contrast, at higher temperatures, the liquid layers overcome the cohesive forces to some extent due to the particles' enhanced thermal and kinetic energy. As a result, the solution's viscosity reduces with increasing temperature. Furthermore, the NA structure (Table l) suggests that self-association could occur by intermolecular stacking of pyridine rings, hydrogen bonding through proton-bearing amide groups, or interaction between amide protons and the nitrogen atom of the pyridine ring. The possible relevance of these interactions in the self-association process was evaluated by measuring concentration-dependent 1H and 13C chemical shift shifts, and the role of interamide hydrogen bonding was further investigated by studying the self-association potential of two substituted amide analogues.37 A rise in viscosity is observed because of the self-association or solute–solute interactions of NA as well as different ion association or solute–solvent interactions among NA, KCl/DAP and water in solutions (possible interactions are discussed in Section 3.1.2). The nature of the solvent affects the extent of self-association. Since KCl/DAP are polar solvents, they might facilitate hydrogen bonding and other intermolecular interactions, along with more significant self-association through ion–ion, ion-dipole, ion-hydrophilic/hydrophobic interactions resulting in increase in viscosity.
The Jones–Dole21 relation (eqn (17)) was used to investigate the viscosity of (NA + water) and (NA + KCl/DAP + water).
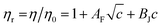 | (17) |
Molal concentration (m/mol kg−1) is converted to molar concentration (c/mol dm−3) using the standard concentration relationship and taking the density (ρ) of the solution and molar mass (M) of the solute into consideration. The relative viscosity (ηr) is the ratio between the viscosities of the solution (η) and the corresponding solvent (η0). The viscosity coefficients AF and BJ are also known as Falkenhagen and Jones–Dole coefficients (A-coefficient and B-coefficient, respectively). In order to give a straight line form to the above eqn (17) it can be rewritten as follows (eqn (18)),
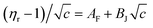 | (18) |
The intercept and slope of (ηr − 1)/c versus c plots can be used to compute the viscosity coefficients (AF and BJ). The constants AF and BJ are computed using this least-squares approach and are shown in Table 7. AF characterizes the extent of solute–solute or ion–ion interactions. Table 7 indicates that the AF coefficients are consistently positive for all investigated solutions at all experimental temperatures which indicates an active solute–solute or ion–ion interactions in the solution.
| Parameters | Temperature (K) | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
a Standard uncertainty in molality u(m) = 0.001 mol kg−1, in pressure u(p) = 0.01 × 106 Pa, in temperature u(T) = 0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, in density u(ρ) = 0.5 kg m−3, in viscosity u(η) = 0.02 mPa s. K, in density u(ρ) = 0.5 kg m−3, in viscosity u(η) = 0.02 mPa s. |
|||||
| NA + water | |||||
| AF × 102 (mol−1/2 dm3/2) | 10.47 ± 0.64 | 10.56 ± 1.39 | 11.04 ± 1.17 | 11.09 ± 2.43 | 10.08 ± 0.84 |
| BJ × 102 (mol−1 dm3) | 52.19 ± 2.28 | 53.15 ± 4.96 | 53.52 ± 4.19 | 54.15 ± 8.69 | 56.36 ± 3.01 |
| Δμ0#1 × 10−1 (kJ mol−1) | 2.61 | 2.63 | 2.65 | 2.67 | 2.69 |
| Δμ0#2 × 10−1 (kJ mol−1) | 10.00 | 10.47 | 10.82 | 11.17 | 11.71 |
| TΔS0#2 × 10−2 (kJ mol−1) | −2.42 | −2.46 | −2.50 | −2.54 | −2.58 |
| ΔH0#2 × 10−2 (kJ mol−1) | −1.42 | −1.41 | −1.42 | −1.42 | −1.41 |
| Sn | 12.23 | 9.26 | 7.79 | 6.95 | 6.76 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.501 mol kg−1KCl | |||||
| AF × 102/mol−1/2 dm3/2 | 20.61 ± 1.03 | 23.21 ± 0.97 | 26.75 ± 0.48 | 29.17 ± 0.99 | 32.44 ± 1.07 |
| BJ × 102/mol−1 dm3 | 36.13 ± 3.64 | 37.98 ± 3.45 | 39.62 ± 1.69 | 41.07 ± 3.54 | 41.75 ± 3.83 |
| Δμ0#1 × 10−1/kJ mol−1 | 3.06 | 3.09 | 3.12 | 3.15 | 3.19 |
| Δμ0#2 × 10−1 kJ mol−1 | 9.41 | 9.61 | 9.99 | 10.33 | 10.57 |
| TΔS0#2 × 10−2/kJ mol−1 | −1.78 | −1.83 | −1.86 | −1.89 | −1.92 |
| ΔH0#2 × 10−2/kJ mol−1 | 2.72 | 2.79 | 2.86 | 2.93 | 2.98 |
| Sn | 3.29 | 3.30 | 3.40 | 3.51 | 3.54 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.749mol kg−1KCl | |||||
| AF×102/mol−1/2 dm3/2 | 22.62 ± 0.56 | 27.33 ± 0.86 | 32.08 ± 0.68 | 35.34 ± 1.26 | 39.70 ± 0.67 |
| BJ × 102/mol−1 dm3 | 49.79 ± 1.97 | 51.35 ± 3.00 | 53.53 ± 2.38 | 54.71 ± 4.41 | 56.62 ± 2.34 |
| Δμ0#1 × 10−1/kJ mol−1 | 3.06 | 3.09 | 3.07 | 3.05 | 3.03 |
| Δμ0#2 × 10−1 kJ mol−1 | 10.80 | 11.18 | 11.43 | 11.57 | 11.79 |
| TΔS0#2 × 10−2/kJ mol−1 | −1.40 | −1.42 | −1.44 | −1.47 | −1.49 |
| ΔH0#2 × 10−2/kJ mol−1 | 2.48 | 2.54 | 2.59 | 2.63 | 2.67 |
| Sn | 4.54 | 4.47 | 4.60 | 4.68 | 4.81 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 1.001 mol kg−1KCl | |||||
| AF × 102/mol−1/2 dm3/2 | 21.99 ± 1.02 | 26.06 ± 1.41 | 26.50 ± 1.60 | 29.89 ± 0.85 | 21.74 ± 2.75 |
| BJ × 102/mol−1 dm3 | 65.10 ± 3.62 | 65.94 ± 4.99 | 68.41 ± 5.70 | 72.01 ± 3.03 | 75.26 ± 9.78 |
| Δμ0#1 × 10−1/kJ mol−1 | 3.12 | 3.10 | 3.08 | 3.06 | 3.05 |
| Δμ0#2 × 10−1 kJ mol−1 | 12.95 | 13.05 | 13.37 | 13.82 | 14.23 |
| TΔS0#2 × 10−2/kJ mol−1 | −1.95 | −1.98 | −2.02 | −2.05 | −2.08 |
| ΔH0#2 × 10−2/kJ mol−1 | 3.25 | 3.29 | 3.35 | 3.43 | 3.51 |
| Sn | 5.71 | 5.76 | 5.97 | 6.26 | 6.53 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.499 mol kg−1DAP | |||||
| AF × 102/mol−1/2 dm3/2 | 9.31 ± 0.34 | 13.34 ± 0.78 | 16.35 ± 0.61 | 19.87 ± 0.32 | 23.14 ± 0.64 |
| BJ × 102/mol−1 dm3 | 54.56 ± 1.18 | 57.72 ± 2.73 | 58.59 ± 2.13 | 59.01 ± 1.11 | 61.00 ± 2.23 |
| Δμ0#1 × 10−1/kJ mol−1 | 2.64 | 2.66 | 2.63 | 2.69 | 2.70 |
| Δμ0#2 × 10−1 kJ mol−1 | 11.38 | 11.58 | 11.69 | 12.14 | 12.60 |
| TΔS0#2 × 10−2/kJ mol−1 | −1.75 | −1.78 | −1.81 | −1.84 | −1.87 |
| ΔH0#2 × 10−2/kJ mol−1 | −0.61 | −0.62 | −0.64 | −0.63 | −0.61 |
| Sn | 5.55 | 5.68 | 5.60 | 5.50 | 5.64 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 0.749mol kg−1DAP | |||||
| AF × 102/mol−1/2 dm3/2 | 4.53 ± 0.88 | 9.58 ± 0.61 | 12.93 ± 0.38 | 16.47 ± 0.32 | 19.58 ± 0.83 |
| BJ × 102/mol−1 dm3 | 62.72 ± 3.04 | 61.68 ± 2.10 | 60.94 ± 1.33 | 60.05 ± 1.12 | 58.76 ± 2.87 |
| Δμ0#1 × 10−1/kJ mol−1 | 2.65 | 2.67 | 2.68 | 2.69 | 2.71 |
| Δμ0#2 × 10−1 kJ mol−1 | 12.05 | 12.09 | 12.15 | 12.19 | 12.18 |
| TΔS0#2 × 10−2/kJ mol−1 | −0.21 | −0.22 | −0.22 | −0.23 | −0.23 |
| ΔH0#2 × 10−2/kJ mol−1 | 0.98 | 0.99 | 1.00 | 1.00 | 0.99 |
| Sn | 5.99 | 5.83 | 5.72 | 5.60 | 5.42 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| NA + 1.001mol kg−1DAP | |||||
| AF × 102/mol−1/2 dm3/2 | 3.38 ± 0.57 | 6.74 ± 1.27 | 9.84 ± 1.10 | 13.00 ± 1.06 | 16.16 ± 0.95 |
| BJ × 102/mol−1 dm3 | 65.92 ± 1.95 | 64.35 ± 4.39 | 63.05 ± 3.80 | 62.50 ± 3.66 | 61.95 ± 3.28 |
| Δμ0#1 × 10−1/kJ mol−1 | 2.63 | 2.68 | 2.69 | 2.70 | 2.72 |
| Δμ0#2 × 10−1 kJ mol−1 | 12.37 | 12.36 | 12.35 | 12.44 | 12.53 |
| TΔS0#2 × 10−2/kJ mol−1 | −0.23 | −0.24 | −0.24 | −0.24 | −0.25 |
| ΔH0#2 × 10−2/kJ mol−1 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 |
| Sn | 6.22 | 6.04 | 5.89 | 5.80 | 5.71 |
The viscosity BJ-coefficient21 measures the impact of solute–solvent interactions on solution viscosity. Table 7 shows that the viscosity BJ coefficient for NA in the examined solvent systems is positive, indicating significant solute–solvent/ion–solvent interaction. This sort of interaction is reinforced with an increase in both temperature and composition of KCl/DAP in water. Positive BJ-coefficients are also reported by M. N. Roy et al. in investigating molecular interactions of NA in aqueous citric acid monohydrate solutions. Table 7 shows that the viscosity BJ coefficient is positive for both binary systems at all the experimental temperatures indicating substantial interactions between the solute and the solvent.
Table 7 shows an increasing trend of BJ values with molality of KCl/DAP, indicating stronger ion–solvent interactions at higher electrolyte concentrations in the solution. At increased temperatures, the pattern reverses. These variation patterns are significant for understanding the changes in the solvent structure caused by solute solvation and can be analysed in terms of ion–ion and ion–hydrophilic interactions, which are expected to increase with electrolyte concentration.
The temperature derivative of the B-coefficient (∂BJ/∂T)P provides more information on a solute's role in forming and breaking structures in solvent media than the B-coefficient itself. Structure-making (kosmotropic) solutes have a negative (∂BJ/∂T)P, while structure-breaking (chaotropic) solutes have a positive value.38 A kosmotropic (order promoting) electrolyte enhances the order and structure of the solvent, affecting the behaviour of solutes and influencing various chemical and biochemical processes. For the present study, a negative (∂BJ/∂T)P suggests that the vitamin NA exhibits kosmotropic behaviour. This means that it contributes to ordering the water molecules around it, stabilizing the hydrogen-bonded network in the solution. It contributes to the stabilization and strengthening of the hydrogen-bonded network of water molecules around it, reflecting its role in enhancing the ordering of the solvent and potentially affecting the properties of the solution in the presence of KCl/DAP. Making a connection between these results and agricultural settings, where viscosity might affect the delivery of nutrients, could significantly increase their practical significance. A thorough understanding of these molecular and physical properties along with the practical considerations for agricultural environments can help optimize fertilizer formulations and application methods, leading to more efficient and sustainable farming practices.
| Sn = BJ/V0ϕ | (19) |
If the solvation number ranges between 0 and 2.5, we can consider the solute ions to be improperly solvated, which implies they remain as unsolvated spherical species dispersed in the solvent. In contrast, a value greater than 2.5 indicates the production of solvated spherical species.40
Table 7 enlists Sn values for NA in various solvent compositions and temperatures. As shown in the table, the Sn values for all solutions are greater than 2.5, implying that the investigated vitamin is soluble in water as well as KCl and DAP aqueous solutions at all temperatures. Higher values of Sn in binary and ternary solutions of NA at different experimental temperatures indicates several important factors about the solute–solvent interaction and the nature of the solution, such as (i) presence of more number of ionic species in the solution, (ii) more solvent molecules (aqueous KCl/DAP and water) are closely associated with each solute (NA) molecule. This often leads to a more significant solvation shell around NA, (iii) greater solubility of NA in the solvent, (iv) stronger or more favorable interactions between NA, KCl/DAP and water molecules. This can be due to stronger hydrogen bonding, ion–dipole interactions, or other types of intermolecular forces, (v) presence of large or highly polar hydrophilic molecules. However, it may be inferred that in aqueous NA, due to the stronger ion-hydrophilic attraction, more water molecules are present in the hydration shell, and the hydration number increases with temperature.
To initiate viscous flow in a solution, particles must overcome an energy barrier to transit from a lower-energy state to a higher-energy state. This energy barrier is known as the free energy of activation. Δμ0#1 and Δμ0#2 are the average free energy of activation per mole of solvent and that of solute, respectively, can be computed by following the theory proposed by Feakin41 later modified by Eyring42 as the following eqn (20) and (21),
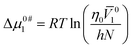 | (20) |
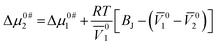 | (21) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 10 and
10 and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 20 indicates the limiting apparent molar volumes of aqueous KCl/DAP (solvent) and NA (solute), respectively, η0 is the viscosity of aqueous KCl/DAP, h is the Planck constant and N is the Avogadro's number. The calculated values of Δμ0#1 and Δμ0#2 are documented in Table 7. Δμ0#2 values are dependent on viscosity BJ-coefficient and (
20 indicates the limiting apparent molar volumes of aqueous KCl/DAP (solvent) and NA (solute), respectively, η0 is the viscosity of aqueous KCl/DAP, h is the Planck constant and N is the Avogadro's number. The calculated values of Δμ0#1 and Δμ0#2 are documented in Table 7. Δμ0#2 values are dependent on viscosity BJ-coefficient and (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 01 −
01 − ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 02). The activation energy (Δμ0#1 and Δμ0#2) values for viscous flow being positive (Table 7) suggest that strong interactions exist between solute and solvent molecules in the ground state, which contributes to the difficulty of flow.43 Feakins et al.44 found that solutes with Δμ0#2 > Δμ0#1 having positive viscosity B-coefficients have stronger ion–solvent interactions, indicating the formation of a transition state with rupture and distortion of intermolecular forces in solvent structures.45 In the presence of the vitamin, NA the creation of a transition state is inhibited, and the viscous flow of solutions is nonspontaneous.
02). The activation energy (Δμ0#1 and Δμ0#2) values for viscous flow being positive (Table 7) suggest that strong interactions exist between solute and solvent molecules in the ground state, which contributes to the difficulty of flow.43 Feakins et al.44 found that solutes with Δμ0#2 > Δμ0#1 having positive viscosity B-coefficients have stronger ion–solvent interactions, indicating the formation of a transition state with rupture and distortion of intermolecular forces in solvent structures.45 In the presence of the vitamin, NA the creation of a transition state is inhibited, and the viscous flow of solutions is nonspontaneous.
The other two thermodynamic functions, activation entropy (ΔS0#2) and enthalpy (ΔH0#2), support this interpretation for the viscous flow of vitamin in aqueous solution. To evaluate the values of (ΔS0#2) and (ΔH0#2), the following eqn (22) and (23) are used.
| (∂Δμ0#2/∂T) = −ΔS0#2 | (22) |
| ΔH0#2 = Δμ0#2 + TΔS0#2 | (23) |
The negative values of ΔS0#2 for all experimental solutions at all temperatures indicate that the transition state is related with bond formation and as a more ordered transition state is formed entropy of the solution lowers during activation.
Negative ΔH0#2 values in water and aqueous 0.5 mol kg−1 DAP indicate a loss in order caused by solute–solvent interactions and an exothermic viscous flow for NA. Positive values of ΔH0#2 in aqueous KCl of all compositions, 0.75 mol kg−1 and 1 mol kg−1 DAP suggest the viscous flow is endothermic in nature. ΔS0#2 and ΔH0#2 values are presented in Table 7.
3.3 FTIR analysis
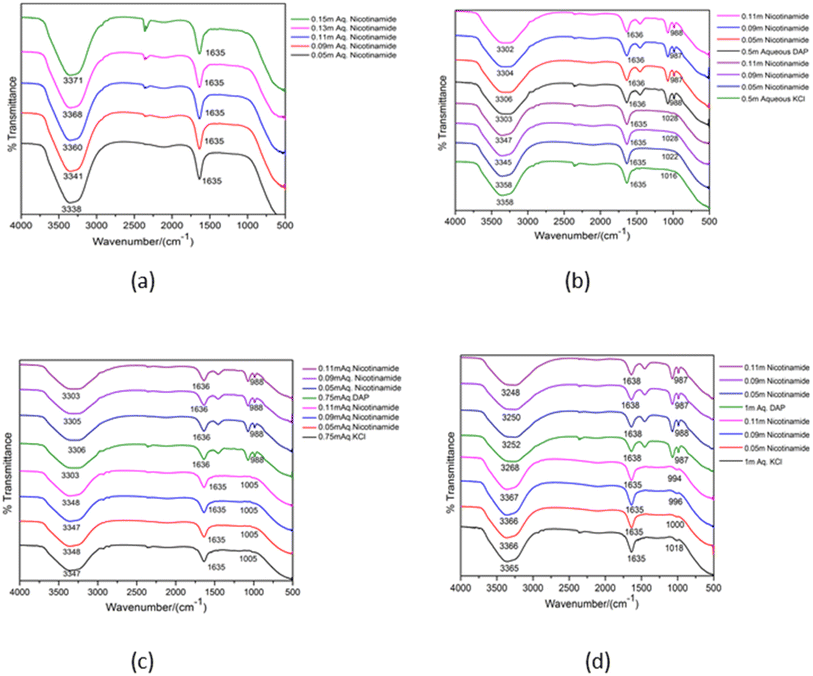
For Structural elucidation and study of interactions between molecules FTIR provides vital information about the varieties of functional groups as well as different types of vibrations associated within the molecules. Such technique is not only restricted to solid compounds but also liquids and suspensions. This spectroscopic method is based on the vibrational frequency of the bonds present in a molecule. As the infrared radiation is passed through the sample by the FTIR instrument, the absorbed radiation energy causing electronic transition in the molecule get dissipated as vibrational energy from the sample, and ultimately a spectra is obtained.In the present work FTIR analysis of aqueous NA having 0.05, 0.09, 0.11 molal concentration with 0.5, 0.75 and 1 molal concentrations of aqueous DAP as well as KCl have been done within a range of 4000–500 cm−1. In Fig. 4 the broad peak around 3300–3380 cm−1 in the FTIR spectra of NA in various solvent systems represents the evidence of intermolecular hydrogen bonding which is appearing due to O–H (νO−H) as well as N–H (νN–H) stretching vibrations possessed by the interaction between the water molecule and the –NH2 group present on NA.46 These spectra are strongly influenced by H-bonding. In the said figures it is apparent that the band associated with OH stretching absorbs at lower wave numbers in ternary solutions than in aqueous NA. As hydrogen bonding leads to a weakening of the OH band47 we can infer that stronger H-bonding is taking place between NA and water in presence of DAP than in KCl. Strengthening of H-bonding in presence of DAP is also reinforced by its positive Hepler's constant values. Another absorption band is noticed at the region of ∼2104 cm−1 in aqueous NA. In the literature it is said that this band is associated with bending of H–O–H bond and confirms the existence of strong hydrogen bonding.48 However, the absorption at this wave number range is barely visible in the ternary solutions (NA + KCl + water) and (NA + DAP + water). The peak around ∼1635 cm−1 shows the characteristics peak of carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) stretching frequency present on amide group of NA. A sharp band can be observed around ∼1000 cm−1 due to C–N stretching in amide bond which is very prominently visible in (NA + DAP + water). This absorption band is not visible in aqueous NA and in (NA + KCl + water). This peak may be the result of involvement of nitrogen atom present on the amide group in hydrogen bonding with water49 in presence of DAP.
O) stretching frequency present on amide group of NA. A sharp band can be observed around ∼1000 cm−1 due to C–N stretching in amide bond which is very prominently visible in (NA + DAP + water). This absorption band is not visible in aqueous NA and in (NA + KCl + water). This peak may be the result of involvement of nitrogen atom present on the amide group in hydrogen bonding with water49 in presence of DAP.
4. Conclusion
The present investigation were examined on volumetric and viscometric analysis for the binary and ternary solutions of NA in (0.0, 0.05, 0.75 and 0.1) mol. kg−1 aqueous KCl/DAP solutions at different temperature and atmospheric pressure. Several thermodynamic factors were investigated and examined in order to anticipate the types and extent of interactions between the solute (NA) and co-solute (KCl/DAP). Positive apparent molar volume of solutions at varying concentrations and infinite dilution (Vϕ and V0ϕ) indicates considerable solute–solvent interaction across all experimental temperatures. An increase in V0ϕ values results in positive transfer values, indicating solute–cosolute interactions and reduced electrostriction in ternary solution. NA was discovered to act as a structure builder except in water and 0.5 m aqueous DAP. The solution's viscosity reduces as the temperature rises. The positive values of AF and BJ imply the presence of ion–ion and ion–solvent interactions in the solutions, with larger BJ values indicating a predominance of ion–solvent contact. Strong solute–solvent interactions in the ground state impede solution movement, as indicated by a positive free energy of activation for both solvent and solute viscous flow. The examined vitamin is soluble in water, KCl, and DAP aqueous solutions at all temperatures, as indicated by the Sn values which are larger than 2.5 for all solutions. However, in aqueous NA, the Sn values rises with temperature because of the higher ion-hydrophilic attraction, which results in a greater concentration of water molecules in the hydration shell. Greater values of Δμ0#2 relative to Δμ0#1 indicate that the presence of the vitamin inhibits the creation of a transition state and nonspontaneous viscous flow of solutions. The broad peak around 3300–3380 cm−1 represents the evidence of presence of intermolecular hydrogen bonding in binary and ternary solutions. Strengthening of H-bonding in the presence of KCl/DAP in aqueous medium is apparent from the shifting of peak to lower frequency. In summary, studying the molecular interactions of vitamin, NA with fertilizers (KCl/DAP) in aqueous media at different temperatures is crucial for its wide application in optimizing fertilizer performance, ensuring environmental sustainability, and improving agricultural outcomes. This research supports the development of effective and stable fertilizer products and helps in adhering to regulatory standards. The future of research on fertilizer–human interactions may focus on long-term health effects of fertilizer exposure, sustainable fertilizer management practices and studies on the effectiveness of existing regulations and the need for new policies.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
P. M. and S. P: investigation and experimental work, data curation and graphics and writing original draft. D. M: software, validation, Formal analysis, S. S. and M. T.: conceptualization, supervision, data curation, formal analysis, writing review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Authors express their heartfelt gratitude to the management of Siksha O Anusandhan Deemed to be University, Bhubaneswar, Odisha, India for providing them all the facilities required to carry out this investigation.References
- E. Priya, S. Sarkar and P. K. Maji, J. Environ. Chem. Eng., 2024, 12, 113211, DOI:10.1016/j.jece.2024.113211.
- M. K. Mosharaf, R. L. Gomes, S. Cook, M. S. Alam and A. Rasmussen, Chemosphere, 2024, 364, 143055, DOI:10.1016/j.chemosphere.2024.143055.
- Z. Wang, X. Ma, H. Pan, X. Yang, X. Zhang, Y. Lyu, W. Liao, W. Shui, J. Wu, M. Xu, Y. Zhang, S. Zhang, Y. Xiao and H. Luo, J. Cleaner Prod., 2023, 409, 137248, DOI:10.1016/j.jclepro.2023.137248.
- S. NAarajan and S. Sukumaran, Controlled Release Fertilizers for Sustainable Agriculture, 2021, pp. 195–229, DOI:10.1016/B978-0-12-819555-0.00012-1.
- H. W. Scherer, Encyclopedia of Soils in the Environment, 2005, pp. 20–26, DOI:10.1016/B0-12-348530-4/00229-0.
- R. M. Ayling and C. Biochem, Metabolic and Clinical Aspects, 3rd edn, 2014, pp. 180–199, DOI:10.1016/B978-0-7020-5140-1.00010-9.
- L. J. Kinsella and D. E. Riley, Textbook of Clinical Neurology, 3rd edn, 2007, pp. 897–917, DOI:10.1016/B978-141603618-0.10040-2.
- A. Mozafar, J. Plant Nutr., 2008, 16(12), 2479–2506, DOI:10.1080/01904169309364698.
- S. P. Trivedi, P. Singh, N. Sethi and R. K. Singh, Ecotoxicol. Environ. Saf., 1990, 19, 135–142, DOI:10.1016/0147-6513(90)90062-A.
- S. S. Dhondge, P. N. Dahasahasra, L. J. Paliwal and D. W. Deshmukh, J. Chem. Thermodyn., 2014, 76, 16–23, DOI:10.1016/j.jct.2014.02.024.
- M. N. Roy, A. Bhattacharjee and P. Chakraborti, Thermochim. Acta, 2010, 507–508, 135–141, DOI:10.1016/j.tca.2010.05.014.
- P. Rajput, H. Singh and A. Kumar, J. Chem. Thermodyn., 2022, 171, 106805, DOI:10.1016/j.jct.2022.106805.
- H. Kumar, V. Kumar, S. Sharma, A. A. Ghfar, A. Katal, M. Singla and K. Girdhar, J. Mol. Liq., 2021, 344, 117780, DOI:10.1016/j.molliq.2021.117780.
- K. Dhal, P. Das, S. Singh and M. Talukdar, J. Mol. Liq., 2023, 376, 121413, DOI:10.1016/j.molliq.2023.121413.
- K. Dhal, S. Singh and M. Talukdar, J. Mol. Liq., 2022, 368, 120761, DOI:10.1016/j.molliq.2022.120761.
- M. Talukdar, S. Singh and S. K. Dehury, Biointerface Res. Appl. Chem., 2020, 10(2), 5332–5337, DOI:10.33263/BRIAC102.332337.
- S. Singh and U. N. Dash, Biointerface Res. Appl. Chem., 2020, 10(2), 5061–5067, DOI:10.33263/BRIAC101.061067.
- S. Singh and U. N. Dash, Int. J. Pharm. Sci. Rev. Res., 2015, 35(1), 25–29 CAS.
- P. Mohapatra, S. Singh and M. Talukdar, J. Chem. Eng. Data, 2024, 69, 3805–3818, DOI:10.1021/acs.jced.4c00350.
- A. Kundu and N. Kishore, J. Sol. Chem., 2003, 32(8), 703–717, DOI:10.1023/B:JOSL.0000002990.73945.c9.
- B. Sinha, B. K. Sarkar and M. N. Roy, J. Chem. Thermodyn., 2008, 40(3), 394–400, DOI:10.1016/j.jct.2007.09.012.
- S. B. Ingole, S. G. Shankarwar and A. G. Shankarwar, International Journal of Universal Print, 2018, 4(7), 427–432 Search PubMed.
- M. Paluch and P. Dynarowicz, Colloid Polym. Sci., 1988, 266, 180–183, DOI:10.1007/BF01452816.
- S. Li, X. Hu, R. Lin, W. Sang and W. Fang, J. Solution Chem., 2001, 30, 365–373 CrossRef CAS , https://www.link.springer.com/article/10.1023/A:1010379223751.
- S. S. Dhondge, S. P. Zodape and D. V. Parwate, J. Chem. Thermodyn., 2012, 48, 207–212, DOI:10.1016/j.jct.2011.12.022.
- H. Kumar, S. Kaur, V. Kumar, A. A. Ghfar, A. Katal, M. Sharma, M. Singla and Khyati, J. Chem. Thermodyn., 2022, 172, 106793, DOI:10.1016/j.jct.2022.106793.
- Viscometric Studies of Some Amino Acids/Peptides in Aqueous K2SO4/KNO3 Solutions at Different Temperatures, ed. H. L. Friedman, C. V. Krishnan and F. Franks, Plenum Press, New York, 1973, ch. 1, vol. 3, pp. 1–118, DOI:10.1007/978-1-4684-2955-8.
- R. K. Wadi and P. Ramasami, J. Chem. Soc. Faraday Trans., 1997, 93, 243–247, 10.1039/A604650I.
- R. Bhat and J. C. Ahluwalia, J. Phys. Chem., 1985, 89, 1099–1105 CrossRef CAS , https://www.pubs.acs.org/doi/pdf/10.1021/j100253a011.
- A. K. Mishra and J. C. Ahluwalia, J. Chem. Soc., Faraday Trans. 1, 1981, 77, 1469–1483 RSC.
- L. G. Hepler, Can. J. Chem., 1969, 47, 4613–4617, DOI:10.1139/v69-762.
- P. R. Misra, B. Das, M. L. Parmar and D. S. Banyal, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 2005, 44, 1582–1588 Search PubMed.
- H. Kumar, V. Kumar, S. Sharma, A. Katal and A. A. Alothman, J. Chem. Thermodyn., 2021, 155, 106350, DOI:10.1016/j.jct.2020.106350.
- B. K. Pandit, A. Sarkar and B. Sinha, J. Chem. Thermodyn., 2016, 98, 193–199, DOI:10.1016/j.jct.2016.03.010.
- W. G. Mcmillan and J. E. Mayer, J. Chem. Phys., 1945, 13, 276–305, DOI:10.1063/1.1724036.
- C. V. Krishnan and H. L. Friedman, J. Solution Chem., 1973, 2, 37–51, DOI:10.1007/BF00645870.
- W. N. Charman, C. S. C. Lai, D. J. Craik, B. C. Finnin and B. L. Reed, Aust. J. Chem., 1993, 46, 377–385 CrossRef.
- S. K. Lomesh, M. Bala and V. Nathan, J. Mol. Liq., 2024, 404(15), 124997, DOI:10.1016/j.molliq.2024.124997.
- T. S. Banipal, H. Singh, P. K. Banipal and V. Singh, Thermochim. Acta, 2013, 553, 31–39, DOI:10.1016/j.tca.2012.10.017.
- H. Zhao, Biophys. Chem., 2006, 122, 157–183, DOI:10.1016/j.bpc.2006.03.008.
- R. Rani, A. Kumar and R. K. Bamezai, J. Mol. Liq., 2016, 224, 1142–1153, DOI:10.1016/j.molliq.2016.10.063.
- A. Feakins, D. Freemantle and K. G. Lawrence, J. Chem. Soc., Faraday Trans., 1974, 70, 795–806, 10.1039/F19747000795.
- K. J. Laidler and J. H. Meiser, Physical Chemistry (Benjamin/Cummings), 1982, vol. 269, ISBN no 0-8053-5682-7 Search PubMed.
- D. Feakins, D. J. Freemantle and K. G. Lawrence, J. Chem. Soc., Faraday Trans., 1974, 70, 795–806, 10.1039/F19747000795.
- H. Kumar, G. Singh, R. Kataria and S. K. Sharma, J. Mol. Liq., 2020, 303, 112592, DOI:10.1016/j.molliq.2020.112592.
- S. S. Pattanaik, B. Nanda, S. R. Panda, B. Dalai and B. B. Nanda, J. Mol. Liq., 2022, 351, 167–7322, DOI:10.1016/j.molliq.2022.118644.
- P. Krishnamurthi, H. B. Ramalingam and K. Raju, Adv. Appl. Sci. Res., 2015, 6(12), 44–52 CAS.
- K. Dhal, S. Singh and M. Talukdar, J. Mol. Liq., 2022, 352, 118659, DOI:10.1016/j.molliq.2022.118644.
- H. Kumar and A. Katal, J. Chem. Thermodyn., 2018, 116, 85–96, DOI:10.1016/j.jct.2017.08.025.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra06869f |
| This journal is © The Royal Society of Chemistry 2025 |