Red-shifted optical absorption induced by donor–acceptor–donor π-extended dibenzalacetone derivatives

Abstract

Chalcones demonstrate significant absorption in the near ultraviolet-visible spectrum, making them valuable for applications such as solar cells, light-emitting diodes, and nonlinear optics. This study investigates four dibenzalacetone derivatives (DBAd), DBA, DBC, DEP, and DMA, examining the impact of electron-donating and electron-withdrawing groups and conjugation elongation on their electronic structure in solvents of varying polarities. Using the Polarizable Continuum Model (PCM) and time-dependent density functional theory (TD-DFT), we characterized the excited states of these compounds. Our results reveal a consistent red-shift in the absorption spectrum, with electron-donating groups like ethoxy inducing a more pronounced red-shift than chlorine. Extending conjugation in DMA further shifted the absorption band to lower energy. Solvatochromism influenced the absorption intensities, underscoring the importance of evaluating parameters beyond λ_max. Although our methodologies provided a satisfactory correlation between theoretical and experimental data, they also indicate the need for further theoretical models to accurately capture solute–solvent interactions and describe charge-separated states. The results indicated that dibenzalacetone derivatives have potential as alternative materials for development of organic solar cells.

---

1 Introduction

Photophysical properties of small organic molecules have received significant attention due to their potential in optoelectronic, electrochemical, and biological applications.^1–4 However, the optical properties of these compounds are extensively modified through changes in their molecular structure, such as increased conjugation and replacement by specific functional groups.^5,6 Furthermore, when in solution, solvents can influence the electronic structure of the organic molecules. Therefore, predictive tools that accurately estimate these modifications in solvated compounds are essential for advancing our understanding in this field.^7,8

Among these materials, chalcones are generally non-luminescent due to quenching processes caused by intramolecular twisting motions and isomerization of the α, β-unsaturated ketone fragment.⁹ Howeverm, their derivatives exhibit a wide range of absorption energies in the ultraviolet–visible light spectrum and extensive π-electron delocalization. This results from the reaction of a diketone with two equivalents of an aromatic aldehyde or, alternatively, a dialdehyde reacting with two equivalents of an aromatic ketone.^10–14 In this case, the “chalcone” term is used to designate the core molecular fragment of a variety of relevant natural compounds that have two aromatic rings in conjugation with an electrophilic α,β-unsaturated carbonyl system, denoted as 1,3-diaryl-2-propen-1-one.¹⁵ In addition, they comprise a class of compounds that are efficiently synthesized with high yields and isomeric selectivity.¹⁶

For this reason, chalcones and their derivatives have been extensively studied for their biological properties as anti-inflammatory agents,¹⁷ antibacterial agents,¹⁸ anticancer agents,¹⁹ antituberculosis agents,²⁰ and antileishmanial agents.²¹ Moreover, chalcones and their associated compounds have gained recognition as π-conjugated organic dyes with significant potential in various photovoltaic applications, such as solar cells, photodetectors, and light-emitting diodes.²² Additionally, they present applications in nonlinear optics, optical limiting, and electrochemical sensing.^23,24 Also, they can be employed as precursors in synthesizing advanced polymer materials²⁵ and act as effective corrosion inhibitors for carbon steel.²⁶

However, solvation also plays a significant role in the electronic properties of chalcone derivatives. Specifically, polar solvents can enhance the red-shift effect by interacting with electron donor and acceptor groups, reducing the energy of the excited state.^27,28 Due to the above, we were motivated to investigate four dibenzalacetone derivatives (DBAd): (i) DBA [molecular formula C₁₇H₁₄O, (1E,4E)-1,5-diphenylpenta-1,4-dien-3-one, PubChem CID 640180];²⁹ (ii) DBC [molecular formula C₁₇H₁₂Cl₂O, (1E,4E)-1,5-bis(4-chlorophenyl)penta-1,4-dien-3-one, PubChem CID 5378584];³⁰ (iii) DEP [molecular formula C₂₁H₂₂O₃, (1E,4E)-1,5-bis(4-ethoxyphenyl)penta-1,4-dien-3-one, PubChem CID 668155];³¹ and (iv) DMA [molecular formula C₂₁H₁₈O, (1E,3E,6E,8E)-1,9-diphenylnono-1,3,6,8-tetraen-5-one, PubChem CID 5378259].³² Their chemical structures are presented in Fig. 1. Although these compounds are known and their crystal structures have been solved, to the best of our knowledge, there has not yet been a complete characterization of the low-energy excited states in solvents with varying polarities.

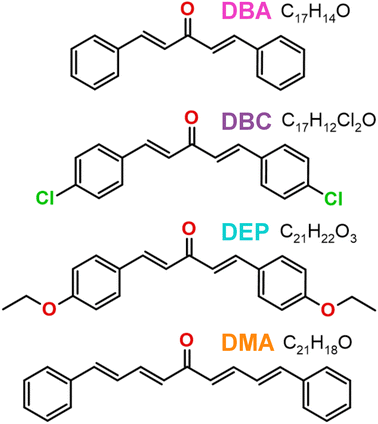Fig. 1 Two-dimensional chemical structures of the four dibenzalacetone derivatives (DBAd): DBA (C₁₇H₁₄O), DBC (C₁₇H₁₂Cl₂O), DEP (C₂₁H₂₂O₃), and DMA (C₂₁H₁₈O). Carbons and hydrogens are not explicitly shown. Non-carbon and non-hydrogen atoms are colored by atom type (oxygen in red, chloride in green). The figure was drawn using ChemCraft³³ program (graphical software for visualization of quantum chemistry computations https://www.chemcraftprog.com).

In the present study, we address experimentally and computationally the impact of the modification of dibenzalacetone derivatives (DBAd), substituted with electron-donating and electron-withdrawing groups in the aromatic rings and with elongation of the conjugated chain, in a series of solvents with increasing order of dielectric constants. We used the Polarizable Continuum Model (PCM) with the variant of the integral equation formalism of the polarizable continuum model (IEFPCM) for density functional theory (DFT)^34–36 and time-dependent density functional theory (TD-DFT)³⁷ to determine the electronic structure of DBAd in their ground and excited states. This research provides insights into the molecular architecture and solvatochromism that drive the functionality of these compounds in advanced technological applications.

2 Materials and methods

2.1 Sample preparation and measurements

The powder samples of dibenzalacetone derivatives (DBAd), Fig. 1, were kindly provided by the Department of Chemistry, Universidade Estadual Vale do Acaraú (UVA), located in Sobral (CE), Brazil, and probed using nuclear magnetic resonance (NMR) spectroscopy (data not shown here). Fourier transform infrared (FT-IR) spectroscopy experimental spectra for solid-state samples were measured at room temperature using a Shimadzu IRTracer-100 model, and measurements on a KBr wafer in the transmittance and scanning mode of 400–4000 cm⁻¹ with 4.0 cm⁻¹ resolution. For this purpose, the solid samples were initially macerated in an agate mortar and subjected to a pressure of 80 kN in a hydraulic press. The experimental UV-vis spectra obtained in toluene (TOL, known as methylbenzene, with molecular formula C₆H₅CH₃, often abbreviated as PhCH₃),³⁸ dichloromethane (DCM, known as methylene chloride, with molecular formula CH₂Cl₂),³⁹ and acetonitrile (ACN, known as methyl cyanide, with molecular formula CH₃CN)⁴⁰ solvents were measured with a Shimadzu UV-1800 spectrophotometer. The absorption measurement was carried out at room temperature of 25 °C in quartz cuvettes with a 10 mm optical path and a range of 180–460 nm. Spectral data are plotted as molar absorptivity (L mol⁻¹ cm⁻¹) versus wavelength (nm).

Initially, stock solutions with concentrations on the order of 10⁻³ mol L⁻¹ were prepared for each dibenzalacetone derivative – as detailed in Table S1 of the ESI.† These solutions were homogenized in an ultrasonic bath for 5 minutes. Optical absorption spectra measurements of each DBAd with each of the three solvents were taken for five distinct concentrations in the range from an initial low concentration (LC, 0.5 × 10⁻⁵ mol L⁻¹) to high concentration (HC, 3.5 × 10⁻⁵ mol L⁻¹), obtained from the stock solution. According to the Beer–Lambert law, the molar absorption coefficient of DBAd was calculated via linear regression analysis of the experimental data in the graph of maximum absorption as a function of concentration. The result is expressed as 1 × 10⁵ L mol⁻¹ cm⁻¹. The y-axis of the graph containing the optical absorption spectra, which are usually acquired in arbitrary units, was corrected to L mol⁻¹ cm⁻¹; see obtained coefficients in Table S2 of the ESI.† Fig. 2 summarizes the experimental and computational protocol.

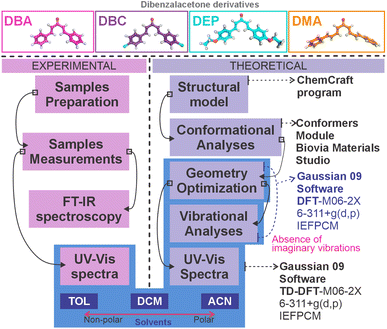Fig. 2 The experimental and computational protocol employed to obtain the UV-vis spectra and electronic properties of the four dibenzalacetone derivatives (DBAd) – DBA, DBC, DEP, and DMA – (presented in Fig. 1) in the toluene (TOL), dichloromethane (DCM), and acetonitrile (ACN) solvents. The experimental protocol (left side) is pink, and the theoretical protocol (right) is purple. Solvents (bottom) are represented in blue, and methods that used solvents are shaded in light blue.

2.2 Theoretical calculations

Initially, input coordinates of the structural model were constructed using the ChemCraft³³ program for the four dibenzalacetone derivatives (DBAd) DBA, DBC, DEP, and DMA presented in Fig. 1. How the atoms of a molecule are distributed in space can result in different properties despite having the same chemical formula. Therefore, for 3D models to be obtained, it is essential to obtain the conformers and determine the best three-dimensional atomic arrangement for each of the four DBAd under study. After that, we used the Conformers Module from the Biovia Materials Studio⁴¹ package, using the classical methodology with the Universal Force Field (UFF)⁴² parameter set and the systematic grid scanning method, for a systematic search in conformational analysis across the potential energy surface of the DBAd, which is fundamental to knowing the relationships between the properties and geometries of the molecules and, thus, obtaining the lowest-energy conformations for geometry optimization. Subsequently, for each of the most stable DBAd, density functional theory (DFT)^34–36 calculations were performed with functional M06-2X, a meta-hybrid exchange-correlation functional,⁴³ and the basis set 6-311+G(d,p) with the implicit solvent method (sometimes termed continuum solvation), the polarizable continuum model (PCM), through the integral equation formalism variant (IEFPCM)⁴⁴ as default self-consistent reaction field (SCRF) theory using three different solvents: toluene (κ_TOL = 2.37), dichloromethane (κ_DCM = 8.93), and acetonitrile (κ_ACN = 35.67), where κ is the dielectric constant of the solvent, in the Gaussian 09 (ref. 45) program.

Geometry optimizations with no constraints were performed using the gradient method, with the final maximum force below 7 × 10⁻⁵ Ha Bohr⁻¹ and the RMS force less than 1 × 10⁻⁵ Ha Bohr⁻¹, producing geometries accurate to 0.001 Å. The harmonic vibrational frequencies of the ground state were obtained using analytical derivatives within the harmonic approximation in the Gaussian 09 (ref. 45) program at the same theory level (M06-2X/6-311+G(d,p)) used for geometry optimizations. These frequencies (ω) do not include anharmonic corrections due to the lack of scaling factors for this specific combination of functional and basis set in the Computational Chemistry Comparison and Benchmark Database (CCCBDB).⁴⁶ All optimized structures for each dibenzalacetone derivative (DBAd) were considered absolute minima due to the absence of an imaginary mode in the vibrational analysis calculations. Finally, for the four DBAd as the optimized geometry fundamental state, we use the time-dependent density functional theory (TD-DFT) method based on the Runge–Gross theory and the time-dependent Kohn–Sham formulation^47–49 to determine the 50 lowest-energy singlet–singlet vertical electronic transitions using the same functional and base optimization parameters, also with the implicit solvent method (IEFPCM) using the same three solvents in the geometry optimization calculations (TOL, DCM, and ACN) chosen to evaluate the influence of solvatochromism on the electronic properties of the four DBAd. Finally, the theoretical UV-vis absorption spectra were obtained using Gaussian functions centered on the vertical excitation energy (σ = 0.283 eV and the half width at half height (HWHH) = 0.333 eV or 2685.830 cm⁻¹). The band’s intensity is proportional to the strength of the oscillator, which is related to the probability of the transition between states.

The M06-2X functional⁴³ is known for its precision in handling noncovalent interactions, long-range charge transfer, and electronic excitations. The 6-311+G(d,p) basis set was chosen for its ability to accurately model electronic and optical properties, and it complements M06-2X, providing a good correlation between theoretical results, such as optimized geometries and electronic transitions, and experimental observations.

3 Results and discussion

3.1 Molecular geometry optimization

The fundamental step of an ab initio computational calculation is determining the geometric parameters corresponding to the molecule’s ground state,⁵⁰ as these parameters directly influence its electronic and vibrational properties. In this work, the bond lengths and angles calculated by the DFT/PCM/M06-2X/6-311+G(d,p) methodology for the four dibenzalacetone derivatives (DBAd) – DBA, DBC, DEP, and DMA – are listed, respectively, in Tables S3 and S4 of the ESI† and organized according to the labeling scheme for the atoms, indicated in Fig. 3. The geometry optimization indicated that the four DBAd correspond to minima in the potential energy surface due to the absence of imaginary vibrational frequencies.⁵²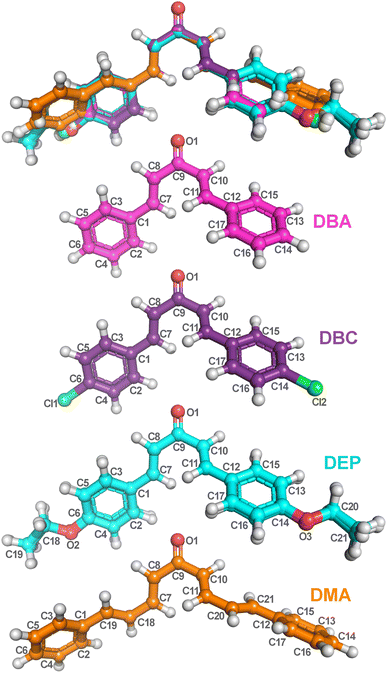

Fig. 3 Optimized dibenzalacetone derivatives (DBAd) using the DFT method with functional M06-2X and 6-311+G(d,p) basis sets. Superposition image of ball and stick representations of all four DBAd (top), followed by representations of DBA (C₁₇H₁₄O), DBC (C₁₇H₁₂Cl₂O), DEP (C₂₁H₂₂O₃), and DMA (C₂₁H₁₈O) with atom labels. The carbons of each of the DBAd are colored differently (DBA in pink balls, DBC in purple balls, DEP in cyan balls, and DMA in orange balls), while non-carbon atoms are colored by atom type (oxygen in red, chloride in green, and hydrogen in light grey). The atom labels referring to hydrogen atoms were suppressed. The figure was drawn using PyMOL⁵¹ (PyMOL Molecular Graphics System; http://www.pymol.org).

Furthermore, calculations show that the bond lengths and angles are slightly perturbed due to the electronic effects of the substituents.¹¹ This difference arises because the DFT/PCM calculations considered a single molecule was considered in a continuous dielectric medium, whereas the experimental measurements accounted for closely packed molecules in a condensed phase.^53,54 Additionally, the four dibenzalacetone derivatives (DBAd) adopt a quasi-planar s-trans configuration across the enone fragment O₁=C₉–C₁₀=C₁₁, causing lower steric repulsion between the aryl and carbonyl groups and favoring π-extended conjugation throughout the molecule.^55,56 The crystallographic parameters for the DBAd have been deposited at the Cambridge Crystallographic Data Centre (CCDC). They can be consulted using the reference number 187856 for DBA,⁵⁷ 608330 for DBC,⁵⁸ 1015509 for DEP,⁵⁹ and 1563359 for DMA.⁶⁰

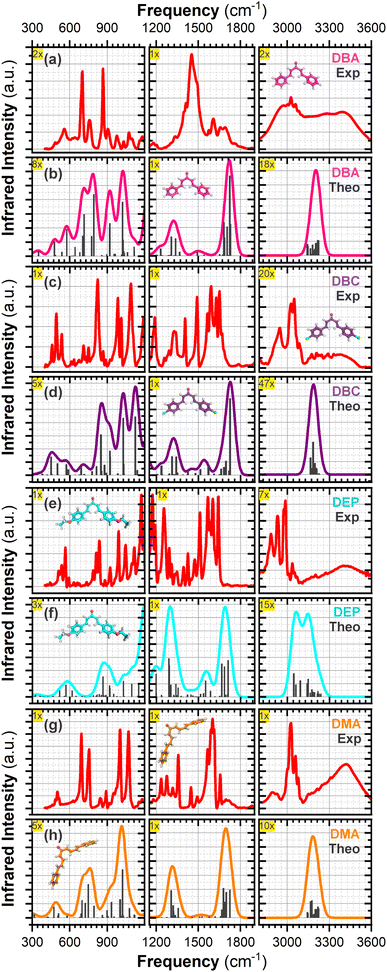
3.2 Vibrational analysis

This section shows the experimental and theoretical FT-IR spectra in Fig. 4 for comparative purposes, presented in order of increasing energy. In Table 1, vibrational signatures for some main modes of the infrared bands of four dibenzalacetone derivatives (DBAd) in the solid state for experimental measurements, and in toluene (TOL), dichloromethane (DCM), and acetonitrile (ACN) solvents for theoretical results, are presented. The four DBAd – DBA, DBC, DEP, and DMA – are angular geometry molecules with 32 (90), 32 (90), 46 (132), and 40 (114) atoms – normal modes of vibration in parentheses, respectively. Therefore, these are classified according to the spatial groups C2/c (15) for DBA,⁵⁷ P2₁2₁2 (18) for DBC,⁵⁸ P2₁/c (14) for DEP,⁵⁹ and F2dd (43) for DMA⁶⁰ (space group number in parentheses). Here, we will discuss only a few characteristic vibration modes in DBAd.

Fig. 4 Experimental FT-IR vibrational spectra and theoretical spectra were calculated using the DFT methodology with M06-2X/6-311+G(d,p) in dichloromethane (DCM) using the IEFPCM implicit solvent method. Experimental spectra (red line) are shown for (a) DBA, (c) DBC, (e) DEP, and (g) DMA. Gaussian fits were applied to the theoretical spectra (colored lines) for (b) DBA (pink line), (d) DBC (purple line), (f) DEP (light blue line), and (h) DMA (orange line). IR modes are presented in the spectral ranges of 300–1199 (left), 1150–1900 (middle), and 2800–3600 cm⁻¹ (right). Infrared intensity is presented in arbitrary units (a.u.).

Table 1 Experimental and theoretical main vibrations modes for the four dibenzalacetone derivatives (DBAd): DBA (C₁₇H₁₄O), DBC (C₁₇H₁₂Cl₂O), DEP (C₂₁H₂₂O₃), and DMA (C₂₁H₁₈O). Experimental measurements were obtained from solid samples, while theoretical results were obtained using PCM solvation with DFT/M06-2X/6-311+G(d,p)

	Experimental frequency^a (cm^−1)				Theoretical frequency^b (cm^−1)
DBAd	DBA	DBC	DEP	DMA	DBA			DBC			DEP			DMA
A^c/solvent^d	Solid	Solid	Solid	Solid	TOL	DCM	ACN	TOL	DCM	ACN	TOL	DCM	ACN	TOL	DCM	ACN
a Frequencies were determined using a second-derivative-based method.b ω harmonic vibrational frequencies calculated using the M06-2X/6-311+G(d,p) DFT method.c Assignment.d TOL, toluene (κTOL = 2.37); DCM, dichloromethane (κDCM = 8.93); ACN, acetonitrile (κACN = 35.67); where κ is the dielectric constant for the solvent.e ν: stretching modes.
ν(C–H)sp^2^e	3375	3036	3036	3028	3200	3206	3206	3054	3053	3056	3153	3147	3146	3172	3174	3190
ν(C–H)sp^3	—	—	2883	—	—	—	—	—	—	—	3054	3053	3059	—	—	—
ν(C=O)^e	1690	1650	1640	1654	1747	1720	1714	1750	1729	1719	1684	1685	1680	1688	1692	1685
ν(C=C)^e	1450	1587	1568	1446	1500	1494	1493	1542	1541	1541	1561	1560	1560	1538	1536	1536
ν(C–C)^e	1448	1323	1255	1357	1317	1321	1323	1319	1321	1323	1298	1295	1291	1312	1312	1312
ν(C–O)^e	—	—	1167	—	—	—	—	—	—	—	1198	1196	1200	—	—	—
ν(CCl)^e	—	565	—	—	—	—	—	446	448	447	—	—	—	—	—	—

---

In α,β-unsaturated ketones, the strong coupling between the C=C bond and the adjacent carbonyl group causes the delocalization of the π electrons due to the conjugation effect.⁶¹ This delocalization causes the C=O and C=C bonds to exhibit characteristics that are intermediate between those of single and double bonds (and decreases the localized electron density at a specific bond), thereby lowering their force constants and resulting in decreased frequency vibrations of the carbonyl and double bonds.⁶² Therefore, the formation of chalcones can be strongly indicated by the presence of bands with values between 1650 to 1780 cm⁻¹ for C=O, 1550 to 1650 cm⁻¹ for C=C, and 800 to 1200 cm⁻¹ for C–C in the IR spectra.

In the theoretical results, the IR frequency of the C=O group agrees with typical values for α,β-unsaturated ketones.⁶³ The values calculated in TOL, DCM, and ACN are, respectively, 1747, 1720, and 1714 cm⁻¹ for DBA, 1750, 1729, and 1719 cm⁻¹ for DBC, 1684, 1685, and 1680 cm⁻¹ for DEP, and 1688, 1692, and 1685 cm⁻¹ for DMA (see Table 1), subtly shifted to lower frequencies due to the increased conjugation effect along the enone fragment (C=C–C=O) and the nature of the substituents on the aromatic rings. That is, electron-donating substituents such as the ethoxy group in the DEP dibenzalacetone derivative and excellent conjugation such as in DMA increase electronic delocalization by the conjugation effect, reducing the force constant of the C=O bond and lowering the vibrational frequency.⁶⁴

In contrast, electronegative substituents that withdraw electrons through inductive effects, such as chlorine atoms in DBC, exhibit the opposite behavior to DEP and DMA. Although they exert an electron-donating effect through their lone pairs (also known as a positive mesomeric effect), the electron-withdrawing inductive effect predominates, leading to a subtle increase in vibrational frequency due to the increase in electronic coupling. Moreover, polarized solvents stabilize the carbonyl dipole moment, further influencing these frequencies.⁶⁵ In general, for the four dibenzalacetone derivatives (DBAd), the carbonyl stretching frequencies subtly decrease as the solvent polarity increases (TOL > DCM > ACN), consistent with stabilizing the carbonyl dipole through dipole–dipole interactions – see Table 1.

The C=C stretch typically occurs at 1650 cm⁻¹, but conjugation moves it to lower frequencies and increases the intensity.^65,66 In addition, the presence of the electron donor and acceptor also changes the vibration of the C=C aliphatic and aromatic groups. In the calculated results for DEP and DBC, the presence of substituents in the para-position of the aromatic rings, in addition to shifting the IR to frequencies of approximately 1540 and 1560 cm⁻¹, respectively, increased the absorption intensity of C=C compared to DMA and DBA due to conjugation and inductive effects that modify the force constants, despite the inertial mass of the ethoxy group and chlorine atoms. Furthermore, in the ground state, the substitutions in DEP and DBC appear to remove the electron density of the aromatic rings instead of interacting by resonance,^66,67 which could justify the frequency values being slightly higher than 1495 cm⁻¹ for DBA and 1536 cm⁻¹ for para-DMA.

In general, the C–H stretching peaks for the sp² carbon appear at values greater than 3100 cm⁻¹ for the four dibenzalacetone derivatives (DBAd) in the results calculated by DFT/PCM. However, since the C–H stretching for both aliphatic and aromatic chain alkenes appears in the same range,⁶⁶ it is not easy to use the C–H bands to differentiate between both types of contribution. For simplicity, we do not distinguish the contributions of the aliphatic and aromatic chains to the C–H vibrations. In the DEP exception, the calculated C–H stretching peaks for the sp² carbon in TOL, DCM, and ACN occur at 3153, 3147, and 3146 cm⁻¹, respectively, and the C–H peaks for the sp³ carbon atoms appear below these values (at 3054, 3054, and 3059 cm⁻¹, respectively). C–H out-of-plane bending bands occur in the range of 650 to 1000 cm⁻¹, but these will not be assigned here.

The vibrations for C–C, C–O and C–Cl occur in the range of 600 to 1550 cm⁻¹,⁶⁸ so that the greater the inertial mass, the lower the vibrational frequency. In the theoretical results, the observed vibrational frequencies for DBA demonstrate vibrations around 800 to 1200 cm⁻¹, corresponding to C–C stretching modes and C–H out-of-plane bending. For DBC, in addition to the C–C stretching modes, vibrations around 440 to 780 cm⁻¹ indicate the presence of C–Cl stretching. For DEP, the presence of C–O stretching is evident in the range of 1000 to 1300 cm⁻¹ along with C–C stretching modes, and the results for DMA are similar to those for DBA.

The experimental IR spectra of dibenzalacetone derivatives show similarities (see Fig. 4). However, we initially noticed that the DBA derivative exhibited an extensive band around 3400 cm⁻¹ associated with forming a hydrated precipitate or adsorbed water.¹¹ A strong C=O stretching mode appeared at 1690, 1650, 1640, and 1654 cm⁻¹ for DBA, DBC, DEP, and DMA, respectively, associated with enone (O₁=C₉–C₁₀=C₁₁) stretching. The C=C stretching modes of the aromatic rings and the aliphatic chain appeared at 1604 cm⁻¹ for DBA, 1591 cm⁻¹ for DBC, 1600 cm⁻¹ for DEP, and 1600 cm⁻¹ for DMA. Below 1500 cm⁻¹, the modes were mainly attributed to C–C stretching, C–C=C and O–C=C bending, and out-of-plane torsions.^11,66 The region between 3000 and 3200 cm⁻¹ was attributed to stretching of the C–H bond of the sp² carbon of the aromatic rings and aliphatic chain. Furthermore, for DEP, we attribute the mode at 2880 cm⁻¹ to the stretching of C–H sp³ due to ethoxy groups.

The DFT/PCM-calculated vibrational frequencies (unscaled) were systematically overestimated relative to the experimental values. The reason for this disagreement between calculated and observed vibrational wavenumbers is that the calculations were made for a free-solvated molecule,⁶⁹ while experiments were performed for a crystalline conformation of the solid sample. The reason is also partly due to the anharmonicity and the approximate nature of the quantum mechanical methods.⁷⁰

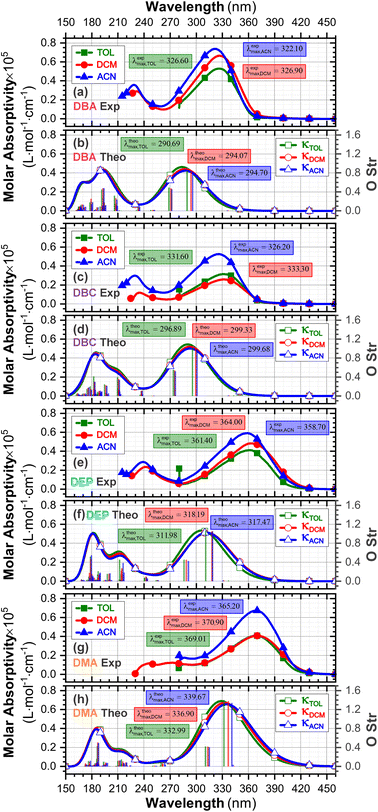
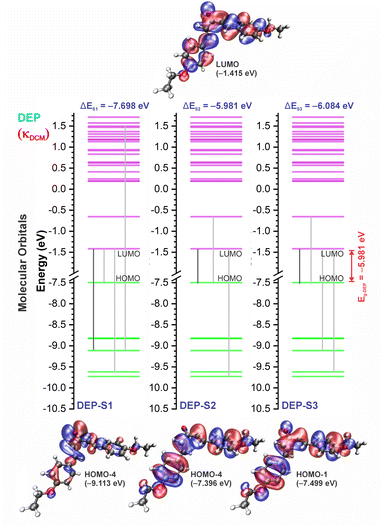
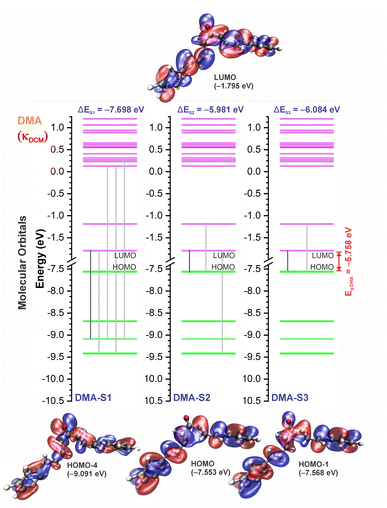
3.3 UV-vis spectra and HOMO–LUMO analysis

The experimental and theoretical UV-vis absorption spectra for the dibenzalacetone derivatives (DBAd) – see Fig. 3 – in toluene (methylbenzene, TOL, κ_TOL = 2.37), dichloromethane (methylene chloride, DCM, κ_DCM = 8.93), and acetonitrile (methyl cyanide, ACN, κ_ACN = 35.67) solvents are shown in Fig. 5. The spectra are plotted as a function of molar absorptivity (L mol⁻¹ cm⁻¹) vs. wavelength (nm) across a range of 150 to 460 nm. These solvents when employed in organic electronics^71,72 (the reason we chose them) have high dielectric constants and dipole moments (increasing in the order TOL < DCM < ACN) and are utilized here to evaluate the influence of solvatochromism on the electronic properties of the DBAd.

Fig. 5 Experimental (a, c, e and g) and theoretical (b, d, f and h) UV-vis absorption spectra of DBA, DBC, DEP, and DMA, respectively, across a range of wavelengths from 150 to 460 nm, and oscillator force (right axis), using the DFT methodology with the M06-2X functional, 6-311+G(d,p) basis set, and three solvents, toluene (κ_TOL = 2.37), dichloromethane (κ_DCM = 8.93) and acetonitrile (κ_ACN = 35.67) with the implicit solvent method IEFPCM. The vertical lines represent the oscillator strengths, indicating the relative probability of the leading electronic transitions (singlet–singlet) for the lowest-energy excited states.

Initially, the optical absorption spectra were collected in arbitrary units by default by the equipment. However, to standardize the interpretation with the theoretical results, the absorbance in arbitrary units was converted to molar absorption coefficient values. We used the linear regression technique on the absorbance values at the maximum wavelength (λ_max) for different concentrations of each DBAd in TOL, DCM, and ACN, according to the Beer–Lambert law.^73,74 The regression plots are shown in Fig. 6(a) for DBA, Fig. 6(c) for DBC, Fig. 6(e) for DEP, and Fig. 6(g) for DMA. The TD-DFT calculations were performed as function of the oscillator strength, vertical excitation energies (E in eV), and probability of an electronic transition between orbital types (%); see Fig. 6(b) for DBA, Fig. 6(d) for DBC, Fig. 6(f) for DEP, and Fig. 6(h) for DMA. Table 2 shows the first six main electronic transitions of the DBAd in the employed solvents, calculated using the TD-DFT/PCM/M06-2X/6-311+G(d,p) methodology.

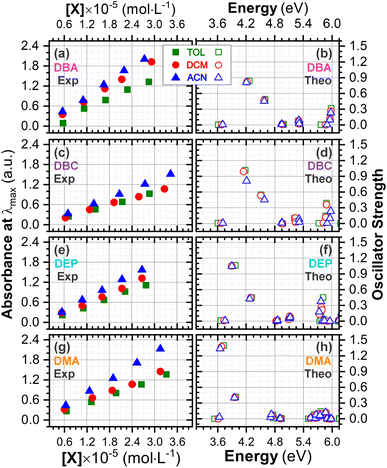Fig. 6 Determination of molar absorption coefficients for DBA (a), DBC (c), DEP (e) and DMA (g) in toluene (κ_TOL = 2.37), dichloromethane (κ_DMC = 8.93) and acetonitrile (κ_ACN = 35.67) by linear regression analysis of the experimental data of maximum absorption as a function of molar concentration, according to the Beer–Lambert law. The results on the y-axis, initially described in arbitrary units, were corrected to mole per L per cm⁻¹ to standardize the interpretation with the theoretical results and can be found in Table S2 in the ESI.† Theoretical oscillator strengths as a function of photon energy (in eV) for DBA (b), DBC (d), DEP (f) and DMA (h) in TOL, DCM, and ACN.

Table 2 Excited states (ES) and energy of excited state (E^the_opt in eV) obtained for six excited states with the oscillator strength (O Str), which indicates the electronic transitions energies and probability (%) for DBA, DBC, DMA, and DEP dibenzalacetone derivatives (DBAd) calculated at TD-DFT M06-2X/6-311+G(d,p) level in toluene (TOL), dichloromethane (DCM) and acetonitrile (ACN) solvents

DBAd	ES	Toluene (κTOL^a = 2.37)				Dichloromethane (κDCM = 8.93)				Acetonitrile (κACN = 35.67)
		E (eV)	O Str^c	Electronic transition	(%)^d	E (eV)	O Str^c	Electronic transition	(%)^d	E (eV)	O Str^c	Electronic transition	(%)^d
a κ is the dielectric constant for the solvent.b H = HOMO, L = LUMO.c O Str, oscillator strength.d Probability.
DBA	1	3.61	0.006	H−4 → L^b	76.3	3.68	0.007	H−4 → L	77.1	3.71	0.007	H−4 → L	77.3
	2	4.27	0.839	H → L	87.5	4.22	0.824	H → L	88.8	4.21	0.810	H → L	89.3
	3	4.59	0.490	H−1 → L	87.2	4.58	0.474	H−1 → L	88.1	4.58	0.454	H−1 → L	88.6
	4	4.98	0.014	H−3 → L	27.5	4.96	0.019	H−2 → L	32.9	4.95	0.019	H−3 → L	26.8
	5	4.98	0.011	H−2 → L	27.4	4.96	0.012	H−3 → L	33.1	4.95	0.013	H−2 → L	26.6
	6	5.30	0.077	H−1 → L+1	79.3	5.30	0.084	H−1 → L+1	81.4	5.31	0.086	H−1 → L+1	81.5
DBC	1	3.60	0.007	H−4 → L	74.0	3.67	0.008	H−4 → L	74.7	3.69	0.008	H−4 → L	74.8
	2	4.18	1.014	H → L	85.0	4.14	0.992	H → L	86.4	4.13	0.975	H → L	87.0
	3	4.51	0.549	H−1 → L	83.8	4.50	0.534	H−1 → L	85.1	4.51	0.514	H−1 → L	85.8
	4	4.96	0.000	H−2 → L	19.4	4.95	0.002	H−2 → L	26.3	4.95	0.003	H−2 → L	27.5
	5	4.96	0.001	H → L+3	21.1	4.96	0.002	H−3 → L	26.8	4.96	0.002	H−3 → L	28.1
	6	5.21	0.100	H−1 → L+1	70.4	5.23	0.110	H−1 → L+1	72.5	5.23	0.035	H → L+1	71.1
DEP	1	3.67	0.011	H−4 → L	72.7	3.74	0.016	H−4 → L	73.5	3.76	0.011	H−4 → L	74.0
	2	3.97	1.065	H → L	85.8	3.90	1.053	H → L	87.2	3.91	1.048	H → L	87.2
	3	4.32	0.451	H−1 → L	82.7	4.30	0.449	H−1 → L	82.0	4.28	0.424	H−1 → L	85.5
	4	4.85	0.013	H → L+1	23.7	4.83	0.005	H → L+1	35.5	4.85	0.002	H → L+1	30.7
	5	4.86	0.015	H → L+3	24.6	4.85	0.018	H → L+2	27.7	4.86	0.017	H → L+2	27.2
	6	5.12	0.073	H−1 → L+1	30.1	5.09	0.038	H → L+1	46.3	5.11	0.055	H → L+1	41.2
DMA	1	3.53	0.002	H−4 → L	63.5	3.61	0.003	H−4 → L	57.4	3.64	0.034	H−4 → L	54.0
	2	3.72	1.397	H−1 → L	77.6	3.68	1.376	H → L	79.6	3.65	1.336	H → L	75.7
	3	3.98	0.418	H → L	81.1	3.96	0.413	H−1 → L	82.4	3.95	0.402	H−1 → L	79.4
	4	4.76	0.078	H → L+1	70.7	4.74	0.049	H → L+1	48.1	4.71	0.032	H → L+1	54.4
	5	4.77	0.014	H−1 → L+1	71.7	4.75	0.063	H−1 → L+1	47.5	4.72	0.088	H−1 → L+1	53.4
	6	4.93	0.011	H−3 → L	23.6	4.92	0.011	H−3 → L	24.5	4.90	0.009	H−3 → L	40.1

---

According to the Franck–Condon principle, the maximum absorption peaks in a UV-vis spectrum correspond to a vertical excitation from the ground (S₀) to excited (S_n) electronic states.^75,76 In the theoretical spectra, three absorption bands located at 170 to 187 nm, 192 to 214 nm, and 284 to 336 nm were observed for the four dibenzalacetone derivatives (DBAd) in the employed solvents, relating to π–π* and n–π* electronic transitions originating from the aromatic rings and α,β-unsaturated ketone fragment. In DMA, an additional absorption band with weak intensity was observed at about 260, 261, and 263 nm (approximately 4.77, 4.75, and 4.71 eV) for TOL, DCM, and ACN, respectively, due to increased oscillator strength in this region. This band corresponds to the HOMO−1 to LUMO+1 and HOMO to LUMO+1 electronic transitions; see Table 2.

However, due to the inherent limitations of experimental measurements, constrained by the equipment setup, source limitations, optical components, atmospheric absorption, quartz cuvette absorption, and solvent absorption, only the lowest energy band was reported in the DBAd experimental UV-vis spectra with the cutoff point being above 285 nm for toluene, 235 nm for dichloromethane, and 190 nm for acetonitrile; see Fig. 5. In some cases, it is possible to observe two experimental bands. The main bands characterized by absorption at a maximum wavelength (λ^exp_max) of 327.0, 326.5, and 322.5 nm for DBA, 331.0, 332.0, and 326.0 nm for DBC, 361.5, 364.0, and 359.0 nm for DEP, and 369.0, 370.5, and 369.0 nm for DMA in the solvents TOL, DCM, and ACN, respectively, are in good approximation to the calculated λ^the_max values. These values are shown in Table 3.

Table 3 Comparative analysis of experimental and theoretical maximum wavelengths (λ_max) and molar absorption coefficients (ε_max) for the four dibenzalacetone derivatives (DBAd): DBA (C₁₇H₁₄O), DBC (C₁₇H₁₂Cl₂O), DEP (C₂₁H₂₂O₃) and DMA (C₂₁H₁₈O) in toluene (TOL), dichloromethane (DCM), and acetonitrile (ACN). Table includes calculated percentage errors (%) between experimental (λ^exp_max) and theoretical (λ^the_max) values

DBAd	Solvent	Experimental^a		Theoretical^b					Error%
		λ^expmax (nm)	ε^expmax (10^5 mol L^−1 cm^−1)	E^expopt^g (eV)	λ^theomax (nm)	ε^theomax (10^5 mol L^−1 cm^−1)	E^theopt^h (eV)	O Str^f
a Experimental peak maxima and molar absorption coefficients determined using a second-derivative-based method.b Theoretical values calculated using M06-2X/6-311+G(d,p).c TOL, toluene (κTOL = 2.37).d DCM, dichloromethane (κDCM = 8.93).e ACN, acetonitrile (κACN = 35.67); where κ is the dielectric constant for the solvent.f O Str, oscillator strength.g Experimental optical gap (E^expopt) determined using the Tauc plot method,^77 which involves plotting (absorption coefficient × photon energy)^n in (eV cm^−1)^n against photon energy (in eV) to extrapolate the linear portion to the energy axis. Adopted n = 2 considering indirect allowed transitions. Data expressed with one decimal place due to the resolution of the spectrophotometer.h Theoretical optical gap (E^theopt) obtained from the second excited state (S2) and selected due to its higher oscillator strength and HOMO → LUMO transition probability, which indicates allowed electronic transitions;^78 ↓ increases the value in this direction; ↑ decreases the value in this direction.
DBA	TOL^c	327.0↑	0.471↓	3.50↑	290.69↓	0.463↑	4.27↑	0.839↑	12
	DCM^d	326.5↑	0.659↓	3.49↑	294.07↓	0.441↑	4.22↑	0.824↑	17
	ACN^e	322.5↑	0.744↓	3.54↓	294.70↓	0.425↑	4.21↑	0.810↑	18
DBC	TOL^c	331.0↓	0.324↓	3.42↑	296.89↓	0.544↑	4.18↑	1.014↑	12
	DCM^d	332.0↓	0.327↓	3.42↑	299.33↓	0.520↑	4.14↑	0.992↑	11
	ACN^e	326.0↑	0.444↓	3.48↓	299.68↓	0.501↑	4.13↑	0.975↑	9
DEP	TOL^c	361.5↓	0.405↓	3.15↑	311.98↓	0.535↑	3.97↑	1.065↑	16
	DMC^d	364.0↓	0.483↓	3.10↑	318.19↓	0.511↑	3.90↑	1.053↑	14
	ACN^e	359.0↑	0.596↓	3.15↓	317.47↑	0.512↓	3.91↓	1.048↑	13
DMA	TOL^c	369.0↓	0.409↓	3.07↑	332.99↓	0.689↑	3.72↑	1.397↑	11
	DMC^d	370.5↓	0.463↓	3.05↑	336.90↓	0.671↑	3.68↑	1.376↑	10
	ACN^e	369.0↑	0.675↓	3.07↓	339.67↓	0.656↑	3.65↑	1.336↑	8

---

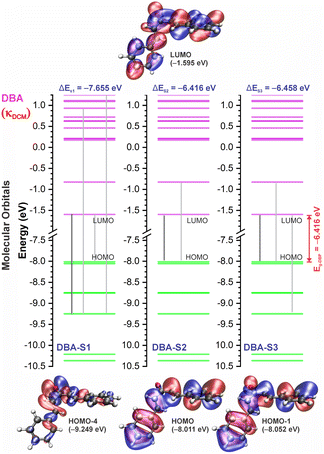
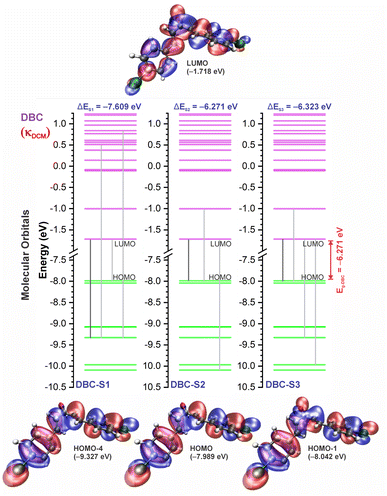
In good agreement with λ^exp_max, the TD-DFT calculations predict the occurrence of a higher probability electronic transition (allowed) at 290.69, 294.07, and 294.70 nm (4.26, 4.22, and 4.21 eV) for DBA, 296.89, 299.33, and 299.68 nm (4.18, 4.14, and 4.13 eV) for DBC, 311.98, 318.19, and 317.47 nm (3.97, 3.90, and 3.90 eV) for DEP, and 322.99, 336.90, and 339.67 nm (3.72, 3.68, and 3.65 eV) for DMA in TOL, DCM, and ACN, respectively, due to the highest calculated value of the oscillator strength in this vertical transition. These absorption maxima correspond mainly to the electronic excitation from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO); this transition between frontier orbitals corresponds to the energy of the second excited state, as seen in Table 2. Fig. 7–10 illustrate the symmetry of the molecular orbitals involved in the main electronic transitions of the first three lowest-energy excited states that compose the band centered at λ^the_max.

Fig. 7 Molecular orbital diagram for the excited states (S₁, S₂, and S₃) and frontier orbital isosurfaces for DBA in dichloromethane (κ_DCM = 8.93). The isosurfaces are displayed with contour values of +0.015 (blue) and −0.015 (red). The solvents toluene (κ_TOL = 2.37) and acetonitrile (κ_ACN = 35.67) involve very similar frontier orbitals, which are not repeated here. κ is the dielectric constant of the solvent.

Fig. 8 Molecular orbital diagram for the excited states (S₁, S₂, and S₃) and frontier orbital isosurfaces for DBC in dichloromethane (κ_DCM = 8.93). The isosurfaces are displayed with contour values of +0.015 (blue) and −0.015 (red). The solvents toluene (κ_TOL = 2.37) and acetonitrile (κ_ACN = 35.67) involve very similar frontier orbitals, which are not repeated here. κ is the dielectric constant of the solvent.

Fig. 9 Molecular orbital diagram for the excited states (S₁, S₂, and S₃) and frontier orbital isosurfaces for DEP in dichloromethane (κ_DCM = 8.93). The isosurfaces are displayed with contour values of +0.015 (blue) and −0.015 (red). The solvents toluene (κ_TOL = 2.37) and acetonitrile (κ_ACN = 35.67) involve the very similar frontier orbitals, which are not repeated here. κ is the dielectric constant of the solvent.

Fig. 10 Molecular orbital diagram for the excited states (S₁, S₂, and S₃) and frontier orbital isosurfaces for DMA in dichloromethane (κ_DCM = 8.93). The isosurfaces are displayed with contour values of +0.015 (blue) and −0.015 (red). The solvents toluene (κ_TOL = 2.37) and acetonitrile (κ_ACN = 35.67) involve the very similar frontier orbitals, which are not repeated here. κ is the dielectric constant of the solvent.

For qualitative analysis of the experimental (E^exp_opt) and theoretical (E^the_opt) optical gap values, we used the Tauc method⁷⁷ to determine E^exp_opt and the energy of the second excited state (S₂) to quantify E^the_opt, because the optical gap corresponds to the energy of the lowest electronic transition that is accessed through the absorption of a photon.⁷⁸ Here, we consider that the first excited state (S₁) for DBAd may be optically forbidden due to the symmetry of the orbitals, justifying the low values of oscillator strength; see excited state (S₁) for DBAd in Fig. 7–10. In general, E^exp_opt decreases in the order DBA > DBC > DEP > DMA and from TOL to DCM, while acetonitrile increases the optical gap energy. Similarly, E^the_opt decreases from DBA to DMA (with DEP in ACN as an exception) and decreases with solvent polarity. These occur because in α,β-unsaturated ketones, the π–π* and n–π* electronic transitions are shifted to longer wavelengths due to the conjugation effect causing increased proximity of the electronic levels of the chromophores that form molecular orbitals with lower electronic excitation energy.^66,79

In addition, auxochromes with unpaired electrons also cause shifts in the absorption bands to longer wavelengths since the unbonded electrons enhance the delocalization due to the conjugation effect with the π system.⁸⁰ So, the more n electrons interacting with unsaturated bonds, the greater the bathochromic shifts.⁸¹ Therefore, the presence of a para-position substitution group at the aromatic rings justifies shifting the π–π* and n–π* transitions in compounds DBC and DEP to a lower energy region (a longer wavelength) relative to non-substituted DBA. Despite the electron-withdrawing inductive effect of chlorine atoms – chlorine atoms withdraw electrons by induction but can donate one electron by conjugation when in aromatic rings⁸² – when substituted in aromatic rings, they weaken the bond order of C=C and C=O due to increased electronic delocalization.

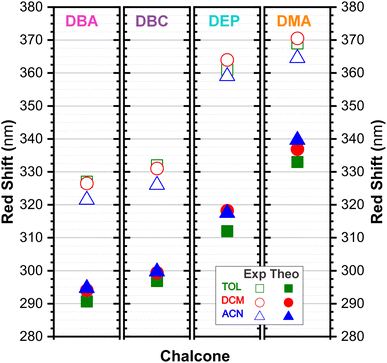
In DEP, in addition to the conjugation effect by unpaired electron-donation from the oxygen at the ethoxy group, the overlap of the C–H bonding orbitals of the alkyl group with the π system results in an extension of the conjugation. This type of interaction is often called hyperconjugation;⁸³ see Fig. 9, which shows the electron density arising from the alkyl group. In DMA, the increase in the α,δ-unsaturated chain promoted the largest red-shift due to the increased interaction between the π orbitals that promoted the increase in electronic delocalization. Therefore, the red-shift of λ^exp_max and λ^the_max in DMA > DEP > DBC > DBA is justified by the donor–acceptor–donor structural modification in DBAd. Fig. 11 shows the experimental and calculated red-shift by the TD-DFT/PCM/M06-2X/6-311+G(d,p) methodology.

Fig. 11 Dibenzalacetone derivatives experimental red-shift in TOL (open green squares) DCM (open red circles), and ACN (open blue triangles) with theoretical red-shift, using the TD-DFT methodology and M06-2X functional, and the 6-311+G(d,p) basis set with the implicit solvent method (IEFPCM) in TOL (solid green squares, κ_TOL = 2.37), DCM (solid red circles, κ_DCM = 8.93) and ACN (solid blue triangles, κ_ACN = 35.67).

The excitation of n electrons in the π-extended chromophore renders the excited atom partially electron-deficient, while the π system acquires an electron in the π* antibonding orbital.⁸⁴ This state causes charge separation in the molecule, and is called the charge-transfer excited state,⁸⁵ which solvents also influence. In general, a very low red-shift observed in the λ^the_max of the DBAd (with the exception of DEP) upon going from TOL to DCM and DCM to ACN solvents suggests a low increase in the molecular dipole moment in the excited state with solvent polarity. However, the acetonitrile solvent practically promoted a hypsochromic shift in λ^exp_max by obliterating the absorption peak due to the dipole–dipole interaction with the solute molecules (or due to the effect not being captured by the theoretical methodology); see Fig. 5 and Table 3 for comparison of the variation in λ^exp_max and λ^the_max values.

In summary, DBC induced a red-shift in the optical absorption spectra, with λ^exp_max increasing by approximately 4.00, 5.50, and 3.50 nm compared to DBA in the solvents toluene (TOL), dichloromethane (DCM), and acetonitrile (ACN), respectively. In contrast, DEP and DMA induced the largest shifts of 34.50, 37.50, and 36.50 nm for DEP, and 42.00, 44.00, and 46.50 nm for DMA compared to DBA. In the theoretical results, the red-shift of λ^the_max in the absorption spectra corresponded to 6.20, 5.26, and 4.98 nm for DBC compared to DBA in the solvents TOL, DCM, and ACN, respectively. For DEP, the shifts were 21.29, 24.12, and 22.77 nm compared to DBA, while for DMA they were 42.30, 42.83, and 44.97 nm compared to DBA; see comparative values of λ^exp_max and λ^theo_max in Table 3. The similar trend observed in the theoretical and experimental results corroborates the accuracy and sensitivity of the study.

Our results demonstrate a satisfactory match between λ^exp_max and λ^theo_max for the dibenzalacetone derivatives (DBAd), with a theoretical–experimental difference that is between 8% and 18% (see Table 3). DMA in acetonitrile (ACN) showed the highest accuracy with an 8% discrepancy, indicating good predictive reliability of the theoretical models employed. In contrast, DBA in ACN presented the most significant discrepancy at 18%. These findings underscore the impact of molecular structure and solvatochromism on the absorption characteristics of these compounds. Although the methodologies employed produced a satisfactory correlation, they also demonstrate the need to evaluate other theoretical models.

3.4 Exciton binding energy

The exciton binding energy (E_B) is a fundamental parameter in the efficiency of optoelectronic materials. In π-conjugated systems, the E_B arises from the difference between the fundamental gap (EF), determined by the ionization potential (IP) and electron affinity (EA), and the optical gap (E_opt), which corresponds to the energy difference between the ground and lowest excited state. Typically, the optical gap is smaller than the fundamental gap because the electron remains electrostatically bound to the hole in the excited state, unlike in the ionized state, where a free charge carrier is generated in the material.

According to Koopmans’ theorem,⁸⁶ we calculated the global chemical reactivity descriptors from the theoretical results obtained using the DFT/TD-DFT/PCM/M06-2X/6-311+G(d,p) methodology. The results in Table S5 of the ESI† show that the exciton binding energy decreases with increasing π-conjugation and solvent polarity. The trend observed for the derivatives follows the order: DMA < DEP < DBC < DBA, with E_B values in toluene (TOL), dichloromethane (DCM), and acetonitrile (ACN) of 2.29, 2.15, and 2.07 eV for DMA, 2.41, 2.24, and 2.21 eV for DEP, 2.71, 2.60, and 2.56 eV for DBC, and 2.86, 2.73, and 2.69 eV for DBA.

Reducing the exciton binding energy by modifying the donor–acceptor–donor structure in dibenzalacetone derivatives (DBAd) tends to improve the exciton dissociation efficiency in charge-transfer significantly states,⁸⁷ especially in interactions with electron-acceptor materials such as fullerene and its derivatives. This results in an effective minimization of energy losses in high-efficiency organic devices. Therefore, the reported results suggest that DBAd have promising potential for both biological applications and optoelectronic devices, significantly expanding their field of utilization.

4 Conclusions

One strategy to improve the performance of optoelectronic devices, such as organic solar cells (OSCs), is to increase the orbital overlap and intermolecular interactions between conjugated molecules. These molecules should promote strong light absorption through π–π* transitions, facilitate charge transport due to π-electron delocalization, and minimize nonradiative relaxation mechanisms, which result in excited state deactivation and reduced fluorescence quantum efficiency. In this context, dibenzalacetone (DBAd) derivatives have the potential to optimize these characteristics, mainly due to their relatively simple synthesis and functionalization capacity. In this study, a consistent red-shift in the absorption spectrum was observed, both in theoretical calculations and experimental measurements, which validates the reasonable ability of the methodology to predict changes in electronic properties despite the theoretical–experimental error variations between 8% and 18%, induced by different substituents and higher conjugation. Notably, electron-donating auxochromes with additional hyperconjugation effects, such as the ethoxy group in the DEP compound, induced a more pronounced red-shift compared to substituents that donate electrons by conjugation and withdraw them by induction, like the chlorine halogen in the DBC compound. This greater delocalization in DEP, relative to DBC, is also due to the symmetry of the orbitals involved. Furthermore, the extension of the δ, γ-unsaturation in the DMA compound shifted the absorption band to lower energies due to the increased electronic delocalization without large twists in the molecule. Despite the minimal changes of the wavelength at the maximum absorption (λ_max), solvatochromism also influenced the absorption intensities, highlighting the importance of evaluating other parameters besides λ_max. Although the methodologies employed yielded a satisfactory correlation between theoretical and experimental data, they also highlight the need to evaluate other theoretical models to accurately capture solute–solvent interactions and describe charge-separate states. Future research should also investigate the light-emitting properties of these dibenzalacetone derivatives, which could open up opportunities in certain applications, including their potential use as more sustainable and low-cost alternative materials in organic solar cells.

Data availability

The data that support the findings of this study are available from the corresponding author, E. M. B., upon reasonable request.

Author contributions

V. M. R. V., R. F. C., and E. M. B. proposed the idea, contributed to the conception and design of the study, and planned and carried out the simulations. B. B. P., V. M. R. V., H. S. S., F. F. M. C., and I. F. V. planned, carried out, and discussed the experimental results, provided critical feedback, and co-wrote and finalized the manuscript. V. N. F.: provision of the computer simulation laboratory and software license. C. A. J., and C. P.: analysis and discussion of the results, provided critical feedback, and co-wrote and finalized the manuscript. All authors contributed to the manuscript revision and approved the submitted version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the Brazilian research foment agencies: Coordenação de Aperfeiçoamento de Pessoal de Nivel Superior (CAPES), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Fundação Cearense de Apoio ao Desenvolvimento Científico e Tecnológico (FUNCAP), and Instituto Nacional de Ciência e Tecnologia em Eletrônica Orgânica (INCT/INEO) for financial support. R. F. C. received financial support from CNPq project 102541/2024-8. E. M. B. received financial support from FAPERN/CAPES. H. S. S. acknowledges financial support from CNPq-PQ (Grant 306008/2022-0) and FUNCAP-UNIVERSAL (Grant UNI-0210-00337.01.00/23). C. A. J. acknowledges financial support from CNPq under grant numbers 402536/2021-5 and 304422/2021-5, as well as by the National Institute of Surface Engineering under grant number CNPq 465423/2014-0.

References

1. O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412.
2. N. A. Kukhta and M. R. Bryce, Mater. Horiz., 2021, 8, 33–55.
3. A. Hirono, H. Sakai, S. Kochi, T. Sato and T. Hasobe, J. Phys. Chem. B, 2020, 124, 9921–9930.
4. M. Mellado, R. Sariego-Kluge, F. Valdés-Navarro, C. González, R. Sánchez-González, N. Pizarro, J. Villena, C. Jara-Gutierrez, C. Cordova and M. A. Bravo, et al., Spectrochim. Acta, Part A, 2023, 291, 122332.
5. I. Shafiq, M. Khalid, M. Muneer, M. A. Asghar, R. Baby, S. Ahmed, T. Ahamad, S. F. de Alcântara Morais and A. A. Braga, Mater. Chem. Phys., 2023, 308, 128154.
6. M. Y. Mehboob, R. Hussain, M. Adnan, Z. Irshad and M. Khalid, Phys. B, 2022, 625, 413465.
7. C. F. Poole and S. N. Atapattu, J. Chromatogr. A, 2023, 1687, 463682.
8. B. Mennucci, Int. J. Quantum Chem., 2015, 115, 1202–1208.
9. C. I. C. Esteves, L. F. B. Fontes, A. F. N. Borges, J. Rocha, A. M. S. Silva and S. Guieu, Dyes Pigm., 2022, 202, 110275.
10. M. G. Tay, M. H. Tiong, Y. Y. Chia, S. H. C. Kuan and Z.-Q. Liu, J. Chem., 2016, 2016, 3608137.
11. M. M. de Oliveira, C. E. Nogueira, F. W. Q. Almeida-Neto, H. S. Santos, A. M. Teixeira, P. de Lima-Neto, E. S. Marinho, M. O. de Moraes, C. Pessoa and F. W. A. Barros-Nepomuceno, J. Mol. Struct., 2021, 1231, 129670.
12. K. Mezgebe, Y. Melaku and E. Mulugeta, ACS Omega, 2023, 8, 19194–19211.
13. R. Pereira, A. M. Silva, D. Ribeiro, V. L. Silva and E. Fernandes, Eur. J. Med. Chem., 2023, 252, 115280.
14. A. A. da Silva, P. I. da Silva Maia, C. D. Lopes, S. de Albuquerque and M. S. Valle, J. Mol. Struct., 2021, 1232, 130014.
15. E. M. Lima, L. M. Fernando, L. P. Felix, A. A. de Oliveira Filho, A. N. Carneiro Neto, R. T. Moura Jr and Y. C. Teles, Nat. Prod. Res., 2022, 36, 419–423.
16. C. Zhuang, W. Zhang, C. Sheng, W. Zhang, C. Xing and Z. Miao, Chem. Rev., 2017, 117, 7762–7810.
17. S. H. Emam, A. Sonousi, E. O. Osman, D. Hwang, G.-D. Kim and R. A. Hassan, Bioorg. Chem., 2021, 107, 104630.
18. S. Wang, C. Li, L. Zhang, B. Sun, Y. Cui and F. Sang, Bioorg. Med. Chem., 2023, 93, 117454.
19. Y. Ouyang, J. Li, X. Chen, X. Fu, S. Sun and Q. Wu, Biomolecules, 2021, 11, 894.
20. D. Ramesh, A. Joji, B. G. Vijayakumar, A. Sethumadhavan, M. Mani and T. Kannan, Eur. J. Med. Chem., 2020, 198, 112358.
21. A. R. Garcia, D. M. Oliveira, J. B. Jesus, A. M. Souza, A. C. R. Sodero, A. B. Vermelho, I. C. Leal, R. O. M. Souza, L. S. Miranda and A. S. Pinheiro, et al., Front. Chem., 2021, 8, 624678.
22. S. N. A. Mohd Nizar, S. N. F. Ab Rahman, M. F. Zaini, A. H. Anizaim, I. Abdul Razak and S. Arshad, Crystals, 2021, 11, 1357.
23. A. M. Asiri, H. M. Marwani, K. A. Alamry, M. S. Al-Amoudi, S. A. Khan and S. A. El-Daly, Int. J. Electrochem. Sci., 2014, 9, 799–809.
24. Z. Sun, S. Li, S. Zhang, F. Deng, M. Hong and J. Luo, Adv. Opt. Mater., 2014, 2, 1199–1205.
25. E. M. Sharshira, A. A. Ataalla, M. Hagar, M. Salah, M. Jaremko and N. Shehata, Molecules, 2022, 27, 5409.
26. Z. Ait El Caid, D. Benmessaoud Left, A. Thoume, R. Kellal and M. Zertoubi, J. Bio- Tribo-Corros., 2024, 10, 9.
27. H. S. Abbo, C. H. Lai and S. J. Titinchi, Spectrochim. Acta, Part A, 2023, 303, 123180.
28. E. Mathew and I. H. Joe, J. Mol. Liq., 2023, 392, 123415.
29. (1E,4E)-1,5-diphenylpenta-1,4-dien-3-one, https://pubchem.ncbi.nlm.nih.gov/compound/640180, accessed: 15th July 2024.
30. (1E,4E)-1,5-bis(4-chlorophenyl)penta-1,4-dien-3-one, https://pubchem.ncbi.nlm.nih.gov/compound/5378584, accessed: 15th July 2024.
31. (1E,4E)-1,5-bis(4-ethoxyphenyl)penta-1,4-dien-3-one, https://pubchem.ncbi.nlm.nih.gov/compound/668155, accessed: 15th July 2024.
32. (1E,3E,6E,8E)-1,9-diphenylnono-1,3,6,8-tetraen-5-one, https://pubchem.ncbi.nlm.nih.gov/compound/5378259, accessed: 15th July 2024.
33. Chemcraft, Graphical Software for Visualization of Quantum Chemistry Computations, Version 1.8, Build 682, 2022, https://www.chemcraftprog.com.
34. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
35. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
36. R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1995.
37. A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039.
38. PubChem Compound Summary for CID 1140, Toluene, 2024, https://pubchem.ncbi.nlm.nih.gov/compound/Toluene.
39. PubChem Compound Summary for CID 6344, Methylene Chloride, 2024, https://pubchem.ncbi.nlm.nih.gov/compound/Methylene-Chloride.
40. PubChem Compound Summary for CID 6342, Acetonitrile, 2024, https://pubchem.ncbi.nlm.nih.gov/compound/Acetonitrile.
41. D. S. Biovia, R2, Dassault Systèmes BIOVIA, San Diego, 2017.
42. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. I. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
43. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
44. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
45. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian ∼09 Revision A.01, Gaussian Inc., Wallingford CT, 2009.
46. N. I. of Standards and T. (NIST), Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, 2023, https://cccbdb.nist.gov, release 23, accessed December 5, 2024.
47. E. Gross, J. Dobson and M. Petersilka, Density Functional Theory II: Relativistic and Time Dependent Extensions, 2005, pp. 81–172.
48. J. M. Herbert, Theoretical and Computational Photochemistry, Elsevier, 2023, pp. 69–118.
49. T. Tsuneda and T. Tsuneda, Density Functional Theory in Quantum Chemistry, 2014, pp. 79–99.
50. M. Vonci, M. J. Giansiracusa, R. W. Gable, W. Van den Heuvel, K. Latham, B. Moubaraki, K. S. Murray, D. Yu, R. A. Mole and A. Soncini, et al., Chem. Commun., 2016, 52, 2091–2094.
51. L. Schrödinger and W. DeLano, PyMOL, http://www.pymol.org/pymol.
52. I. Pallikara, P. Kayastha, J. M. Skelton and L. D. Whalley, Electron. Struct., 2022, 4, 033002.
53. A. Stanger and E. Tkachenko, J. Comput. Chem., 2001, 22, 1377–1386.
54. N. Kalaiarasi and S. Manivarman, Orient. J. Chem., 2017, 33, 304.
55. J. Dabrowski and K. Kamienska-Trela, J. Am. Chem. Soc., 1976, 98, 2826–2834.
56. B. E. Aksöz and R. Ertan, FABAD J. Pharm. Sci., 2012, 37, 205–216.
57. I. Turowska-Tyrk, Chem. Phys., 2003, 288, 241–247.
58. R. J. Butcher, H. Yathirajan, B. Sarojini, B. Narayana and K. Vijaya Raj, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2006, 62, o1973–o1975.
59. S. Chantrapromma, P. Ruanwas, N. Boonnak, K. Chantrapromma and H.-K. Fun, Crystallogr. Rep., 2016, 61, 1081–1085.
60. P. S. P. da Silva, P. Martín-Ramos, S. R. Domingos, M. d. C. Bota de Sousa, C. T. Arranja, A. J. Sobral and M. Ramos Silva, ChemPhysChem, 2018, 19, 82–92.
61. P. Costa, R. Pilli, S. Pinheiro and P. Bakuzis, The Chemistry of Carbonyl Compounds and Derivatives, Royal Society of Chemistry, 2022.
62. G. M. Barrow, J. Chem. Phys., 1953, 21, 2008–2011.
63. C. Foster and P. Mackie, Comprehensive Organic Functional Group Transformations II, 2005, pp. 215–266.
64. Y.-H. Wang, J.-W. Zou, B. Zhang, Y.-X. Lu, H.-X. Jin and Q.-S. Yu, J. Mol. Struct.:THEOCHEM, 2005, 755, 31–37.
65. S. I. Vdovenko, I. I. Gerus, Y. I. Zhuk, V. P. Kukhar, M. Pagacz-Kostrzewa, M. Wierzejewska and C.-G. Daniliuc, J. Mol. Struct., 2017, 1128, 741–753.
66. D. L. Pavia, G. M. Lampman, G. S. Kriz and J. R. Vyvyan, Introduction to Spectroscopy, Cengage Learning, Mason, Ohio, USA, 5th edn, 2015.
67. C. Laurence and M. Berthelot, J. Chem. Soc., Perkin Trans. 2, 1979, 98–102.
68. P. Larkin, Infrared and Raman Spectroscopy: Principles and Spectral Interpretation, Elsevier, 2017.
69. S. Y. Haoyu, L. J. Fiedler, I. Alecu and D. G. Truhlar, Comput. Phys. Commun., 2017, 210, 132–138.
70. Y. Cornaton, M. Ringholm, O. Louant and K. Ruud, Phys. Chem. Chem. Phys., 2016, 18, 4201–4215.
71. J. A. Del-Oso, B. A. Frontana-Uribe, J.-L. Maldonado, M. Rivera, M. Tapia-Tapia and G. Roa-Morales, J. Solid State Electrochem., 2018, 22, 2025–2037.
72. P. Zarzycki, M. Zarzycka, M. Ślączka and V. Clifton, Anal. Bioanal. Chem., 2010, 397, 905–908.
73. J. H. Lambert, Lamberts Photometrie (Photometria sive de mensura et gradibus luminis, colorum et umbrae, Sumptibus viduae Eberhardi Klett, typis Christophori Petri Detleffsen) (1760), Wentworth Press, Germany, 2018.
74. Beer, Ann. Phys., 1852, 162, 78–88.
75. V. V. Rybkin, J. Phys. Chem. A, 2017, 121, 5758–5762.
76. A. Hazra, H. H. Chang and M. Nooijen, J. Chem. Phys., 2004, 121, 2125–2136.
77. J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637.
78. J.-L. Bredas, Mater. Horiz., 2014, 1, 17–19.
79. R. B. Woodward, J. Am. Chem. Soc., 1941, 63, 1123–1126.
80. Y. A. Mikheev, L. Guseva and Y. A. Ershov, Russ. J. Phys. Chem. A, 2015, 89, 2036–2050.
81. J. Mizuguchi and G. Wooden, Ber. Bunsenges. Phys. Chem., 1991, 95, 1264–1274.
82. J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, USA, 2012.
83. C. G. Pitt, J. Organomet. Chem., 1973, 61, 49–70.
84. T. Wolf, R. H. Myhre, J. Cryan, S. Coriani, R. Squibb, A. Battistoni, N. Berrah, C. Bostedt, P. Bucksbaum and G. Coslovich, et al., Nat. Commun., 2017, 8, 29.
85. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4032.
86. T. Koopmans, Physica, 1934, 1, 104–113.
87. J. Zhao, C. Yao, M. U. Ali, J. Miao and H. Meng, Mater. Chem. Front., 2020, 4, 3487–3504.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07256a

---