Open Access Article
Open Access ArticleThe scavenging mechanism of hydrazone compounds towards HOO˙ and CH3OO˙ radicals: a computational mechanistic and kinetic study†
Chhinderpal Kaur and
Debasish Mandal *
*
Department of Chemistry and Biochemistry, Thapar Institute of Engineering and Technology, Patiala-147004, Punjab, India. E-mail: debasish.mandal@thapar.edu
First published on 3rd January 2025
Abstract
In this study, a detailed DFT investigation was conducted to systematically analyze the scavenging activity of six hydrazone compounds (1–6) against HOO˙ and CH3OO˙ radicals. Three mechanistic pathways were explored: hydrogen atom transfer (HAT), single electron transfer followed by proton transfer (SETPT), and sequential proton loss electron transfer (SPLET). These mechanisms were evaluated based on thermodynamic parameters, including bond dissociation enthalpy (BDE), ionization potential (IP), proton dissociation enthalpy (PDE), proton affinity (PA), and electron transfer enthalpy (ETE) in the gas phase, water, and pentyl ethanoate. HAT was identified as the most favorable mechanism in the gas phase, while SPLET was preferred in water. Among the studied compounds, compound 2 showed the highest rate constants for HOO˙ scavenging following the HAT mechanism in the gas phase observed at the O2′–H bond with a kEck value of 6.02 × 104 M−1 s−1. For CH3OO˙ scavenging, the same compound exhibited the highest rate constants at the N8–H (9.03 × 104 M−1 s−1) and O2′–H (7.22 × 104 M−1 s−1) sites. The calculated overall rate constant values of compound 2 are koverall (HOO˙) = 6.86 × 104 M−1 s−1 and koverall (CH3OO˙) = 1.63 × 105 M−1 s−1. These results suggest that compound 2 exhibits antioxidant activities comparable to butylated hydroxyanisole (BHA), consistent with experimental findings, indicating its potential as an effective scavenger of hydroperoxyl and methoxy peroxyl radicals. In aqueous solution, the anionic form of compound 2 showed the greatest HOO˙ and CH3OO˙ radical scavenging activity among all of the studied compounds with rate constants of kapp = 1.8 × 107 M−1 s−1 and kapp = 3.3 × 106 M−1 s−1, respectively. Compared with some typical antioxidants such as rubiadin, natural fraxin, and natural anthraquinones, compound 2 showed higher HOO˙ and CH3OO˙ radical scavenging activity in water. Thus, compound 2 is a promising antioxidant in aqueous physiological environments.
Introduction
Oxidative stress, which results from an imbalance between the production and consumption of reactive oxygen species (ROS) in biological systems, has become a critical health concern.1 Excessive ROS generation contributes significantly to the development of chronic and degenerative diseases, including cancer, heart failure, cardiovascular disorders, autoimmune conditions, arthritis, and Alzheimer's disease.2,3 ROS, such as hydroxyl radicals (HO˙), peroxyl radicals (ROO˙), superoxide anions (O2˙−), and non-free-radical species like singlet oxygen (1O2), are continuously produced in the body through various cellular metabolic processes, including NADPH oxidase reactions, cellular respiration, and electron transfer via cytochrome P450 systems, as well as from exposure to UV radiation.4–6 Among these, peroxyl radicals (ROO˙) are particularly toxic due to their selective attack on biological molecules like proteins, DNA, and lipids.7,8 However, these harmful effects can be mitigated by antioxidants, which neutralize free radicals by converting them into stable products.9 Antioxidants prevent the initiation and propagation of radical reactions, ultimately slowing the oxidation process.10 Numerous studies have explored effective antioxidants and their mechanisms of action.11,12 Both synthetic and natural antioxidants demonstrate the ability to prevent cellular damage by scavenging ROS.13–15Hydrazones are an important class of organic compounds that have garnered significant attention in medicinal chemistry due to their wide range of pharmacological properties, which can be harnessed to prevent and treat diseases associated with oxidative stress.16 Hydrazones containing the azomethine group (–NH–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–) form a hydrazide-like moiety (–C(
CH–) form a hydrazide-like moiety (–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–NH–N
O)–NH–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–) when linked to a carbonyl group.17 This structure exhibits high reactivity due to the nucleophilic nature of the nitrogen atoms and the combined electrophilic and nucleophilic character of the carbon atom.18 These hydrazone derivatives have demonstrated various biological activities, including anticancer,19 antioxidant,20–24 antidepressant,25 antitubercular,26 anti-inflammatory,27 and anti-Alzheimer's effects.28 Additionally, they have also demonstrated potent antioxidant properties, which are largely attributed to the presence of the crucial N–H bond.17,29
CH–) when linked to a carbonyl group.17 This structure exhibits high reactivity due to the nucleophilic nature of the nitrogen atoms and the combined electrophilic and nucleophilic character of the carbon atom.18 These hydrazone derivatives have demonstrated various biological activities, including anticancer,19 antioxidant,20–24 antidepressant,25 antitubercular,26 anti-inflammatory,27 and anti-Alzheimer's effects.28 Additionally, they have also demonstrated potent antioxidant properties, which are largely attributed to the presence of the crucial N–H bond.17,29
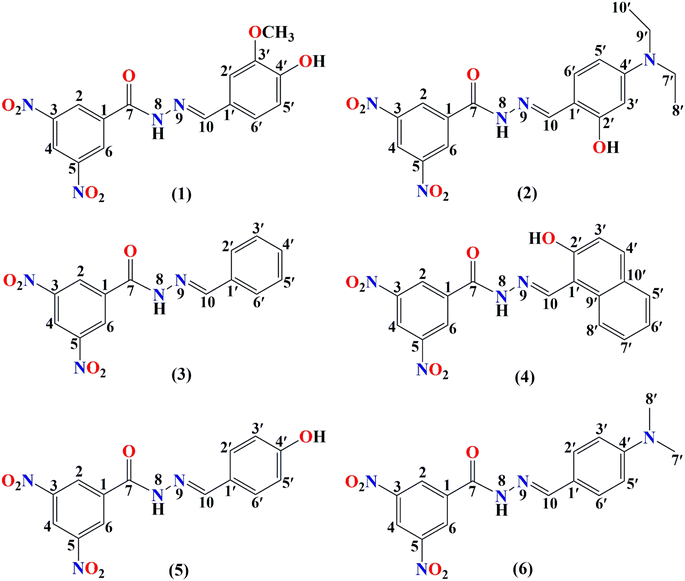
In this study, we have focused on the scavenging mechanism and kinetics of six promising heterocyclic hydrazone derivatives, which are presented in Fig. 1.
Başaran et al. synthesized the aforementioned hydrazone derivatives and assessed their antioxidant activity experimentally.28 They demonstrated that these synthesized compounds have promising properties as antioxidant agents. The authors determined that compound 2 has better antioxidant activity than BHA among the studied compounds, whereas compounds 1 and 4 exhibited antioxidant activity close to that of BHA. Previous studies successfully used computational approaches to explore structure–activity relationships and guide the development of more potent antioxidants.15,30,31 The experimental findings showed promising activity, prompting a yet-to-be-conducted theoretical investigation.
Herein, a systematic DFT study of the radical scavenging mechanism of hydrazone compounds (1–6), focusing on frontier molecular orbitals, molecular descriptors, and key thermodynamic parameters, has been presented. Solvent effects in polar (water) and nonpolar (pentyl ethanoate) media were also considered. Thermodynamic and kinetic analyses of the reactions with HOO˙ and CH3OO˙ radicals were investigated using potential energy surfaces.
Computational details
All calculations were performed using the Gaussian 16 program suite.32 Geometry optimizations were carried out with the DFT-M06-2X functional33 and 6-311+G(d,p) basis set, which is a reliable method for studying radical thermodynamics and kinetics.34–38 Harmonic vibrational frequencies were calculated to confirm minima and transition states, with local minima showing all real frequencies and transition states having one imaginary frequency. IRC calculations ensured correct connectivity between reactants and products.39 The influence of solvents (water and pentyl ethanoate) was computed with Truhlar's Solvation Model Density (SMD)40 using the Self-consistent reaction field (SCRF) method. Water (ε = 78.33) and pentyl ethanoate (ε = 4.73) were chosen as they are highly recommended standard solvents in the literature to mimic the polar and lipid environments in the human body.41–43Three potential mechanisms, namely, HAT, SETPT, and SPLET (as discussed below) have been considered here to explain the antioxidant activity of the hydrazone derivatives.42,44
(i) Hydrogen atom transfer (HAT)
| A − H + R˙ → A˙ + RH | (1) |
(ii) Single electron transfer followed by proton transfer (SETPT)
| A − H + R˙ → AH˙+ + R− → A˙ + RH | (2) |
(iii) Sequential proton loss electron transfer (SPLET)
| A − H + R˙ → A− + H+; A− + R˙ → A˙ + RH | (3) |
These mechanisms were defined by intrinsic thermodynamic descriptors, including bond dissociation enthalpy (BDE), ionization energy (IE), proton dissociation enthalpy (PDE), proton affinity (PA), and electron transfer enthalpy (ETE). These values were computed in the gas phase, water, and pentyl ethanoate at 298.15 K and 1 atm using the following expressions:45
| BDE = H(A˙) + H(H˙) − H(A–H) | (4) |
| IE = H(AH˙+) + H(e−) − H(A–H) | (5) |
| PDE = H(A˙) + H(H+) − H(AH˙+) | (6) |
| PA = H(A−) + H(H+) − H(A–H) | (7) |
| ETE = H(A˙) + H(e−) − H(A−) | (8) |
In this work, the kinetics calculations for the hydroperoxyl and methylperoxyl radical scavenging of hydrazones in the gas phase and water solvent were carried out using the quantum-mechanics-based test for overall free radical scavenging activity (QM-ORSA) protocol. In brief, this methodology separately quantifies the scavenging mechanisms and antioxidant efficiency in both polar (aqueous) and nonpolar (lipid) media, using overall rate coefficients.41,42 The rate constant (k) for the hydrogen atom transfer reactions was computed in the gas phase using conventional transition state theory (eqn (1))49,50 (at 298.15 K, 1 M standard state) according to eqn (9) using the Eyringpy program.51,52
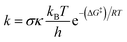 | (9) |
The Marcus theory was used to estimate the energy barriers of single electron transfer (SET) reactions.55,56 Eqn (10) and (11) were employed to compute the activation barrier (ΔG‡SET) of SET, which comprises the nuclear reorganization energy (λ) and Gibbs energy of reaction (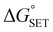 ) parameter.
) parameter.
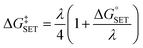 | (10) |
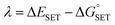 | (11) |
A correction was applied to rate constants that were close to the diffusion limit in order to obtain realistic results. The apparent rate constants (kapp) were determined using the Collins–Kimball theory58 in solvents at 298.15 K; the steady-state Smoluchowski rate constant (kD) for an irreversible biomolecular diffusion-controlled reaction was estimated using the literature corresponding to eqn (12) and (13).59
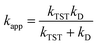 | (12) |
| kD = 4πRABDABNA | (13) |
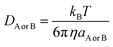 | (14) |
The solvent cage effects were incorporated according to the correction proposed by Okuno,63 taking into account the free volume theory following the Benson correction, which was also applied to reduce over-penalizing entropy losses in solution.41,64,65
Molecular descriptors such as electronegativity (χ), hardness (η), softness (S), and the electrophilicity index (ω) were calculated using eqn (15)–(18).66–69
| Electronegativity (χ) = −μ ≈ (IP + EA)/2 | (15) |
| Hardness (η) ≈ (IP − EA)/2 | (16) |
| Softness (S) ≈ 1/2η | (17) |
| Electrophilicity index (ω) = μ2/2η | (18) |
The molar fractions of neutral and ionic species for all compounds was obtained by adapting the simple Henderson–Hasselbalch equation into eqn (19) and (20) outlined below.70
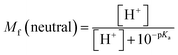 | (19) |
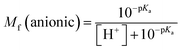 | (20) |
| HA + H2O → A− + H3O+ | (21) |
| ΔGsol = ΔGg + ΔGsolv(A−) + ΔGsolv(H3O+) − ΔGsolv(HA) − ΔGsolv(H2O) | (22) |
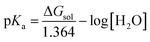 | (23) |
| pKa (corrected) = pKa (calculated) − 4.54 | (24) |
Results and discussion
Physicochemical descriptors analysis
Molecular descriptors such as electronegativity (χ), hardness (η), softness (S), and the electrophilicity index (ω) can be employed to examine the electron-donating abilities of hydrazone compounds.66,74 The computed molecular descriptors have been presented in Table 1.| Medium | Comp. | Electronegativity (χ) | Hardness (η) | Softness (S) | Electrophilicity index (ω) |
|---|---|---|---|---|---|
| Gas phase | 1 | 4.94 | 3.40 | 0.15 | 3.59 |
| 2 | 4.37 | 2.99 | 0.17 | 3.20 | |
| 3 | 5.20 | 3.61 | 0.14 | 3.73 | |
| 4 | 4.98 | 3.07 | 0.16 | 4.04 | |
| 5 | 4.97 | 3.43 | 0.15 | 3.60 | |
| 6 | 4.43 | 2.99 | 0.17 | 3.28 | |
| Water | 1 | 4.74 | 1.54 | 0.32 | 7.31 |
| 2 | 4.30 | 1.10 | 0.45 | 8.37 | |
| 3 | 4.93 | 1.73 | 0.29 | 7.04 | |
| 4 | 4.64 | 1.43 | 0.35 | 7.54 | |
| 5 | 4.73 | 1.53 | 0.33 | 7.32 | |
| 6 | 4.34 | 1.14 | 0.44 | 8.25 | |
| Pentyl ethanoate | 1 | 4.65 | 2.02 | 0.25 | 5.35 |
| 2 | 4.16 | 1.58 | 0.32 | 5.46 | |
| 3 | 4.84 | 2.20 | 0.23 | 5.33 | |
| 4 | 4.67 | 1.74 | 0.29 | 6.26 | |
| 5 | 4.65 | 2.02 | 0.25 | 5.34 | |
| 6 | 4.15 | 1.55 | 0.32 | 5.53 |
As can be seen in Table 1, all the investigated hydrazones have relatively comparable values of χ, η, S, and ω in the range of 4.15–5.20, 1.10–3.61, 0.14–0.45, and 3.20–8.37, respectively. These results clearly indicate that in all the studied mediums, hydrazone compounds (1–6) prefer to act as electron donors rather than electron acceptors, which is an indication of their radical scavenging activity.74
Frontiers molecular orbital (FMO) analysis
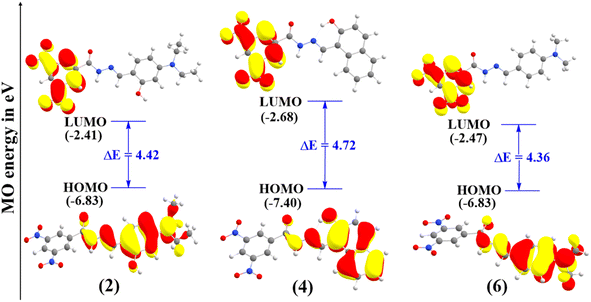
The HOMO energy reflects a molecule's electron-donating ability; while its distribution indicates potential sites for free radical attack.38 The HOMO–LUMO energy gaps for compounds 2, 4, and 6 are presented in Fig. 2, while other compounds with high energy gaps are shown in Fig. S2 in the ESI.†As shown in Fig. 2, all the FMOs show the typical π-type molecular orbital characteristics. The HOMO of all the hydrazone compounds is distributed mainly on the hydrazone moiety and substituted benzene ring, and LUMO orbitals are primarily distributed over the 3,5-dinitrobenzohydrazide ring. The calculated HOMO–LUMO energy gaps follow the order of 6 (4.36 eV) < 2 (4.42 eV) < 4 (4.72 eV) < 1 (5.12 eV) < 5 (5.15 eV) < 3 (5.54 eV). Compounds 6 and 2 exhibit the lowest energy gaps among the compounds, and their values are nearly identical. Therefore, we can conclude that they have comparable reactivity.
Mechanistic study
| Comp. | Site | BDE | ||
|---|---|---|---|---|
| Gas phase | Water | Pentyl ethanoate | ||
| 1 | N8–H | 87.9 | 94.8 | 91.4 |
| O4′–H | 81.2 | 86.5 | 82.0 | |
| 2 | N8–H | 84.7 | 85.0 | 83.9 |
| O2′–H | 84.8 | 86.0 | 84.6 | |
| C7′–H | 88.5 | 90.4 | 88.9 | |
| 3 | N8–H | 89.4 | 96.6 | 93.1 |
| 4 | N8–H | 83.3 | 91.9 | 87.4 |
| 5 | N8–H | 87.9 | 94.2 | 91.0 |
| O4′–H | 87.1 | 88.4 | 86.3 | |
| 6 | N8–H | 84.8 | 87.8 | 86.1 |
Table 2 shows the BDEs of the molecules (1–6) in the range of 81.2–96.6 kcal mol−1 in the gas phase and solvents. The lowest BDE values were obtained at the O4′–H (Comp. 1), N8–H (Comp. 4, 2 and 6), and O2′–H (Comp. 2) positions with values ranging from 81.2 to 91.9 kcal mol−1 in all phases. The O2′–H BDE of compound 4 is significantly higher (96.6 kcal mol−1) compared to those of other O–H groups (Table S2†), reducing its reactivity. This result can be attributed to an intra-molecular hydrogen bond with the imine nitrogen atom, which elevates the BDE value and is consistent with previous studies.16 The C–H BDEs are high, ranging from 90.0 to 134.8 kcal mol−1, except for that of the C7′–H bond of compound 2 (88.5 kcal mol−1). This suggests they have a minimal impact on free radical scavenging activity, so all except the C7′–H bond of compound 2 were excluded from further calculations.
Compounds 1 and 2 possess electron-donating –OCH3 and N–(CH2CH3)2 groups on the aromatic ring, which stabilizes the phenoxide radical.17 Compound 4 has only a hydroxyl group on the naphthalene ring, which may result in hydrogen bonding with the hydrazone moiety. The lowest BDE values of O4′–H (81.2 kcal mol−1), O2′–H (84.8 kcal mol−1), and N8–H (83.3, 84.7 and 84.8 kcal mol−1) in the gas phase of compounds 1, 2, 4 and 6 were comparable with the BDE values of other well-known antioxidants such as resveratrol (83.9 kcal mol−1),75 vanillic acid (85.2 kcal mol−1),76 puerarin (87.3 kcal mol−1),77 magnolol (83.1 kcal mol−1),78 BHA (81.2 kcal mol−1) and other antioxidant polyphenols.74
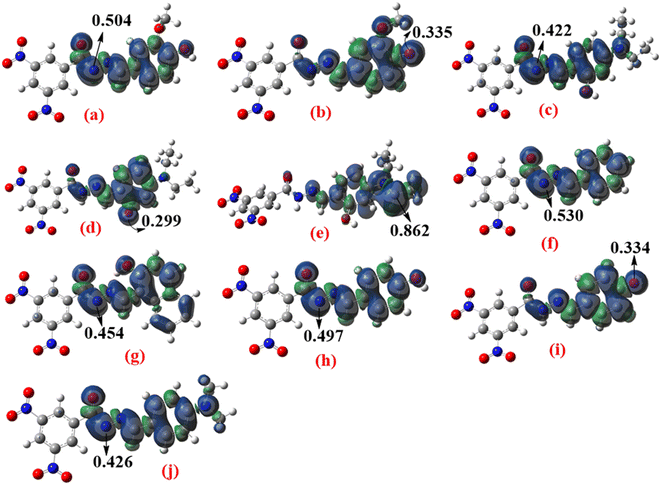
The spin density distributions of the radical forms (Fig. 3) were calculated in the gas phase to explain the BDE differences. Greater spin delocalization corresponds to easier antioxidant radical formation and lower BDEs. As shown in Fig. 3, the spin density after H-abstraction from O–H bonds is lower than that for N–H bonds, consistent with the BDE values. The most localized radicals were formed after H-abstraction from the C7′–H (Comp. 2) and N8–H (Comp. 3) bonds, aligning with the BDE results.
| Compound | IP | PDE | |||||
|---|---|---|---|---|---|---|---|
| Gas phase | Water | Pentyl ethanoate | Site | Gas phase | Water | Pentyl ethanoate | |
| 1 | 183.5 | 113.2 | 131.6 | N8–H | 217.7 | 13.9 | 11.8 |
| O4′–H | 211.0 | 5.6 | 2.4 | ||||
| 2 | 161.9 | 94.0 | 111.7 | N8–H | 236.1 | 23.3 | 24.2 |
| O2′–H | 236.2 | 24.3 | 24.9 | ||||
| 3 | 195.0 | 121.6 | 140.1 | N8–H | 207.8 | 7.3 | 5.0 |
| 4 | 180.2 | 111.0 | 128.6 | N8–H | 216.5 | 13.1 | 10.7 |
| O2′–H | 229.7 | 13.0 | 17.3 | ||||
| 5 | 186.0 | 113.4 | 132.3 | N8–H | 215.2 | 13.1 | 10.7 |
| O4′–H | 214.4 | 7.3 | 6.0 | ||||
| 6 | 166.9 | 96.1 | 113.6 | N8–H | 231.3 | 24.1 | 24.5 |
Compounds 2 and 6 exhibit better electron-donor abilities than the others, as predicted by the FMO calculations. Table 3 shows that the IP values in solution are lower than those in the gas phase, following the trend gas phase > pentyl ethanoate > water, likely due to higher electron solvation enthalpies.74 This suggests that a polar medium enhances electron transfer, promoting free radical scavenging, which is consistent with previous studies.38
The lowest PDE values were observed for O4′–H of compound 1 (2.4–211.0 kcal mol−1) and N8–H of compound 3 (5.0–207.8 kcal mol−1) across all media. Compared to those in the gas phase, the PDE values in pentyl ethanoate and water dropped significantly by an average of 207.8 and 207.1 kcal mol−1, respectively, due to the high solvation enthalpy of protons in solution, which is consistent with previous studies.79
The performance of different mechanisms is generally governed by the enthalpy of the first step. Since the BDE is lower than the IP values, this suggests that the HAT mechanism is thermodynamically more favourable than the SETPT mechanism.
| Comp. | Site | PA | ETE | ||||
|---|---|---|---|---|---|---|---|
| Gas phase | Water | Pentyl ethanoate | Gas phase | Water | Pentyl ethanoate | ||
| 1 | N8–H | 318.4 | 32.8 | 51.8 | 82.9 | 94.3 | 91.5 |
| O4′–H | 323.0 | 30.4 | 53.6 | 71.5 | 88.3 | 80.4 | |
| 2 | N8–H | 323.8 | 32.8 | 54.5 | 74.3 | 83.7 | 81.4 |
| O2′–H | 326.5 | 30.4 | 56.1 | 71.6 | 85.5 | 80.5 | |
| 3 | N8–H | 317.4 | 32.2 | 50.8 | 85.4 | 96.7 | 94.4 |
| 4 | N8–H | 309.7 | 29.1 | 45.3 | 87.0 | 95.1 | 94.1 |
| O2′–H | 335.4 | 36.0 | 63.1 | 74.5 | 88.0 | 82.8 | |
| 5 | N8–H | 318.6 | 32.7 | 51.6 | 82.6 | 93.8 | 91.4 |
| O4′–H | 325.9 | 32.2 | 55.0 | 74.5 | 88.5 | 83.2 | |
| 6 | N8–H | 321.7 | 33.2 | 52.7 | 76.5 | 86.9 | 85.4 |
Table 4 demonstrates that compound 4 has the lowest PA value at the N8–H position, with PAs of 309.7 (gas phase), 29.1 (water), and 45.3 (pentyl ethanoate), showing that the proton at this position may be readily deprotonated. In the solution phase, all PA values are significantly lower than in the gas phase, likely due to the large solvation enthalpy of protons. The ETE values of the O4′–H (1) and O2′–H (2) bonds are smaller than those of other bonds in the gas phase and lipid media. In polar solvent, the N8–H and O2′–H bonds of compound 2 have the smallest ETE values. This may be due to the easy movement of electrons from the unstable ions resulting from these bonds. It is also important to note that all of the ETE values are much lower than the corresponding IP values in the examined medium, implying that the anionic forms of hydrazone compounds (1–6) have better electron-donating capacity than the neutral forms. These findings are consistent with previous studies.44,75
Upon comparing the values of PA, IP, and BDE in Tables 2–4, it is evident that the PA values are lower in water solvent. Hence, it can be concluded that the SPLET mechanism is the thermodynamically dominant mechanism in water.
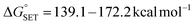 ,
, 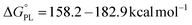 ). Therefore, the HAT mechanism is anticipated to be the primary radical trapping pathway of hydrazone compounds in the gas phase, and thus, this mechanism should be modeled for the kinetic study.
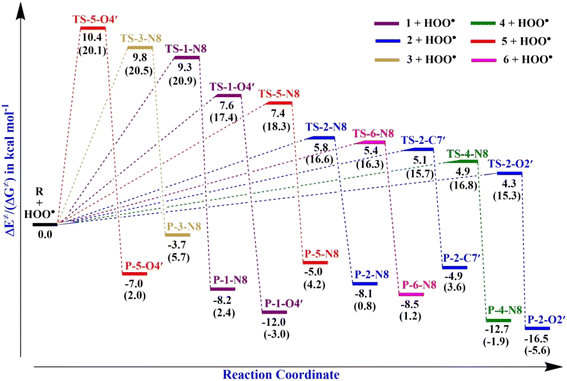
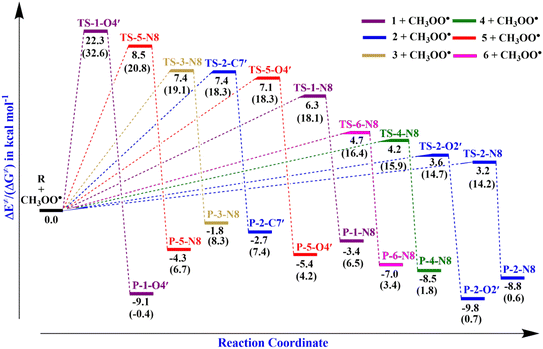
). Therefore, the HAT mechanism is anticipated to be the primary radical trapping pathway of hydrazone compounds in the gas phase, and thus, this mechanism should be modeled for the kinetic study.The computed energy barriers of all the reactions were in the range of 4.3 to 10.4 kcal mol−1. The lowest energy barriers were observed at TS-2-O2′ and TS-4-N8 at 4.3 and 4.9 kcal mol−1, respectively. This observation aligns with the lowest computed BDE values at 2-O2′–H (84.8 kcal mol−1) and 4-N8–H (83.3 kcal mol−1). This suggests that the H-abstractions of the HOO˙ radical at O2′ of compound 2 and N8 of compound 4 play a fundamental role in the hydroperoxyl radical scavenging activity.
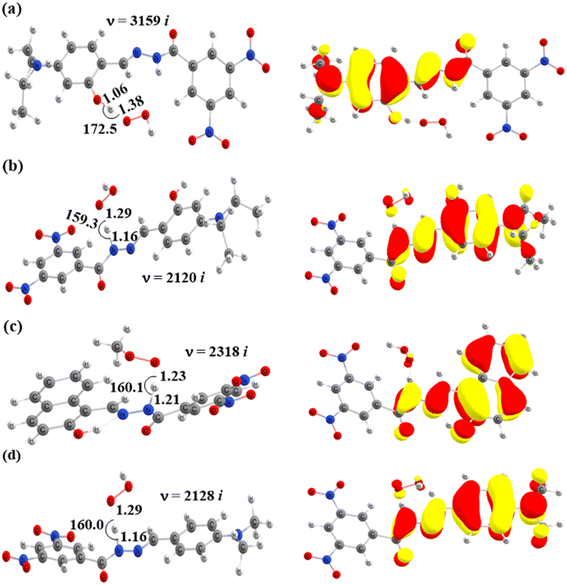
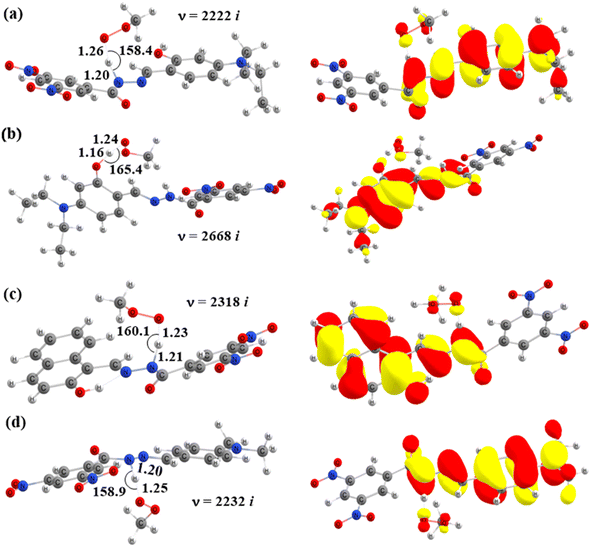
In addition, the SOMOs of the TSs were examined (Fig. 5 and S3†), in which the atomic orbital aligns with the direction of H-atom transfer, and the electron density appears localized on the donor and acceptor sites.
TS-2-N8 (3.2 kcal mol−1), TS-2-O2′, (3.6 kcal mol−1) and TS-4-N84.2 (4.2 kcal mol−1) possess very low barriers, as expected based on the BDE results, which indicates that the compounds 2 and 4 have high CH3OO˙ scavenging activity compared to the others. The breaking bond distances at the TSs are around 1.16–1.41 Å, and the distances for forming bonds (H⋯OOH) are around 1.03–1.33 Å. The C/N/O⋯H⋯O bond angles vary in the range of 154.5 to 170.4°, which indicates the linear arrangements of the atoms around the transferred hydrogen atom. The relative energies of the products were more negative than those of the reactants by about −1.8 to −9.8 kcal mol−1.
Finally, the SOMO density (presented in Fig. 7 and S4†) distributed along the donor–H–acceptor transition vectors confirm the occurrence of the HAT mechanism.
Kinetic study
This section employed the QM-ORSA protocol41,42 to analyse the kinetics of hydroperoxyl and methylperoxyl radical scavenging of the studied compounds in the gas phase following the HAT mechanism. The data presented in Table 5 indicate that the rate constant values for reactions involving the HOO˙ radical fall between 6.02 × 101 to 6.02 × 104 M−1 s−1, whereas the ΔG‡ values range from 15.3 to 20.9 kcal mol−1. The tunnelling corrections (κ) vary from 3.9 to 3334.5, significantly impacting the rate constant. The highest rate constant was observed for the H-abstraction at O2′–H (2) with a kEck value of 6.02 × 104 M−1 s−1 (ΔG‡ = 15.3 kcal mol−1). Nevertheless, the values for compounds 6 and 2 were 6.02 × 103 M−1 s−1 (N8–H, ΔG‡ = 16.3 kcal mol−1 6), 4.70 × 103 M−1 s−1 (N8–H, ΔG‡ = 16.2 kcal mol−1 2), and 3.67 × 103 M−1 s−1 (C7′–H, ΔG‡ = 15.7 kcal mol−1 2), which are lower than those for compound 4 (kEck = 7.83 × 103 M−1 s−1), even though the reaction barrier for the 4-N8–H + HOO˙ reaction (ΔG‡ = 16.8 kcal mol−1) is higher than that of these reactions. This apparent disparity can be elucidated by the tunneling correction for the H-abstraction at the N8–H (4) bond (κ = 101.8) in comparison to those for the N8–H (6) (κ = 38.0), N8–H (2) (κ = 43.3), and C7′–H (2) bonds (κ = 3.9).| Comp. | Position | HOO˙ | koverall | CH3OO˙ | koverall | ||||
|---|---|---|---|---|---|---|---|---|---|
| ΔG‡ | κ | kEck | ΔG‡ | κ | kEck | ||||
| 1 | N8–H | 20.9 | 1974.3 | 1.51 × 102 | 4.85 × 103 | 18.1 | 63.6 | 5.24 × 102 | 5.24 × 102 |
| O4′–H | 17.4 | 178.8 | 4.70 × 103 | 32.6 | 4.4 | 8.43 × 10−10 | |||
| 2 | N8–H | 16.6 | 43.3 | 4.70 × 103 | 6.86 × 104 | 14.2 | 14.5 | 9.03 × 104 | 1.63 × 105 |
| O2′–H | 15.3 | 69.5 | 6.02 × 104 | 14.7 | 29.3 | 7.22 × 104 | |||
| C7′–H | 15.7 | 3.9 | 3.67 × 103 | 18.3 | 10.7 | 1.20 × 102 | |||
| 3 | N8–H | 20.5 | 417.5 | 6.02 × 101 | 6.02 × 101 | 19.1 | 83.6 | 1.26 × 102 | 1.26 × 102 |
| 4 | N8–H | 16.8 | 101.8 | 7.83 × 103 | 7.83 × 103 | 15.9 | 29.0 | 1.08 × 104 | 1.08 × 104 |
| 5 | N8–H | 18.3 | 90.1 | 5.24 × 102 | 1.49 × 103 | 20.8 | 596.1 | 5.54 × 101 | 1.02 × 103 |
| O4′–H | 20.1 | 3334.5 | 9.63 × 102 | 18.3 | 158.9 | 9.63 × 102 | |||
| 6 | N8–H | 16.3 | 38.0 | 6.02 × 103 | 6.02 × 103 | 16.4 | 34.7 | 5.24 × 103 | 5.24 × 103 |
| BHA | O–H | 12.9 | 4.7 | 2.41 × 105 | 2.41 × 105 | 15.7 | 146.1 | 6.62 × 104 | 6.62 × 104 |
Conversely, the H-abstractions involving the CH3OO˙ radical exhibited the highest rate constants on the N8–H (2, 4) and O2′–H (2) bonds with kEck values of 9.03 × 104 M−1 s−1 (ΔG‡ = 14.2 kcal mol−1, 2), 1.08 × 104 M−1 s−1 (ΔG‡ = 15.9 kcal mol−1, 2) and 7.22 × 104 M−1 s−1 (ΔG‡ = 14.7 kcal mol−1, 4), respectively. The overall rate constants for the reactions of compounds 2 and 4 with CH3OO˙ are often higher than those with the HOO˙ radical. This is owing to a smaller reaction energy barrier for reactions via the CH3OO˙ radical than via HOO˙. Based on the computed data, compounds 2 and 4 have faster HOO˙ and CH3OO˙ radical scavenging activity in the gas phase than typical antioxidants like umbelliferone (4.57 × 101 M−1 s−1),81 artepillin C (3.49 × 102 M−1 s−1),82 3-pyrroline-2-ones (5.48 × 101 M−1 s−1)83 and natural depsidones (1.37 M−1 s−1).84
Furthermore, Başaran et al.28 performed experimental investigations and discovered that compound 2 exhibited better antioxidant activity compared to BHA, followed by that of compound 4. As per the aforementioned discussion, our results are in excellent agreement with these findings.
Radical scavenging activity of hydrazones in aqueous solutions
| Comp. | Position | pKa | Mf (AH) | Mf (A−) |
|---|---|---|---|---|
| 1 | O4′–H | 5.64 | 0.017 | 0.983 |
| 2 | O2′–H | 7.41 | 0.506 | 0.494 |
| 3 | N8–H | 6.95 | 0.262 | 0.738 |
| 4 | N8–H | 4.66 | 0.002 | 0.998 |
| 5 | O4′–H | 6.96 | 0.266 | 0.734 |
| 6 | N8–H | 7.71 | 0.671 | 0.329 |
The SET mechanism in its neutral form is non-spontaneous, showing a significantly positive reaction free energy (ΔG°) (Table S4†). For the anionic forms, although ΔG° remains slightly positive rather than negative, this could still contribute to the radical scavenging activity, as suggested by previous reports.15
Marcus' theory was used to evaluate the kinetic parameters such as ΔG≠SET (activation barrier), λ (nuclear reorganization energy) and rate constants (kapp, kf) of the reaction between anions of the studied compounds with the typical radicals HOO˙ and CH3OO˙ following the SET mechanism. As shown in Table 7, the hydroperoxyl and methoxy peroxyl radical scavenging activity is greatest for the anion of compound 2 with kapp = 1.8 × 107 M−1 s−1 (ΔG≠SET = 7.6 kcal mol−1) and kapp = 3.3 × 106 M−1 s−1 (ΔG≠SET = 8.6 kcal mol−1), respectively. Compounds 1, 4, 5, and 6 exhibited moderate radical scavenging behaviour following the SET mechanism (kapp = 102–106 M−1 s−1). Conversely, compound 3 shows very low antioxidant activity (kapp = 101 M−1 s−1). Based on the calculated data, we can conclude that compound 2 showed better HOO˙ and CH3OO˙ radical scavenging activity compared to some typical antioxidants such as rubiadin [1.50 (HOO˙), 4.5 × 10−2 M−1 s−1 (CH3OO˙) ],30 natural fraxin [(HOO˙) 6.7 × 103, 4.2 × 102 M−1 s−1 (CH3OO˙)],86 and natural anthraquinones [2.10 × 102 M−1 s−1(CH3OO˙)]87 in water at pH = 7.4.
| Radical | Comp. | Position | ΔG≠SET | λ | kapp | Mf | kf |
|---|---|---|---|---|---|---|---|
| HOO˙ | 1 | O4′–H | 8.2 | 15.2 | 6.3 × 106 | 0.983 | 6.2 × 106 |
| 2 | O2′–H | 7.6 | 21.2 | 1.8 × 107 | 0.494 | 8.9 × 106 | |
| 3 | N8–H | 15.1 | 20.4 | 5.0 × 101 | 0.738 | 3.7 × 101 | |
| 4 | N8–H | 14.3 | 20.0 | 2.1 × 102 | 0.998 | 2.1 × 102 | |
| 5 | O4′–H | 9.6 | 20.3 | 5.7 × 105 | 0.734 | 4.2 × 105 | |
| 6 | N8–H | 8.8 | 21.5 | 2.3 × 106 | 0.329 | 7.6 × 105 | |
| CH3OO˙ | 1 | O4′–H | 9.5 | 14.7 | 7.2 × 105 | 0.983 | 7.1 × 105 |
| 2 | O2′–H | 8.6 | 20.7 | 3.3 × 106 | 0.494 | 1.6 × 106 | |
| 3 | N8–H | 16.7 | 19.9 | 3.7 × 100 | 0.738 | 2.7 × 100 | |
| 4 | N8–H | 15.8 | 19.5 | 1.7 × 101 | 0.998 | 1.7 × 101 | |
| 5 | O4′–H | 10.8 | 19.9 | 7.9 × 104 | 0.734 | 5.8 × 104 | |
| 6 | N8–H | 9.9 | 21.0 | 3.7 × 105 | 0.329 | 1.2 × 105 |
Conclusion
In this work, a systematic DFT investigation of the HOO˙ and CH3OO˙ radical scavenging activity of six hydrazone compounds has been reported. The mechanism has been studied based on a thermodynamic perspective utilizing three distinct pathways: HAT, SETPT, and SPLET, alongside their corresponding molecular descriptors, including BDE, IP, PDE, PA, and ETE. The results show that HAT is most favorable in the gas phase, while SPLET is preferred in a polar medium. The O2′–H and N8–H bonds play a decisive role in the radical scavenging of compound 2. Among the studied compounds, compound 2 showed the highest rate constants for HOO˙ scavenging via the HAT mechanism in the gas phase at the O2′–H site (k = 6.02 × 104 M−1 s−1). For CH3OO˙ scavenging, it achieved peak rates at the N8–H (9.03 × 104 M−1 s−1) and O2′–H (7.22 × 104 M−1 s−1) sites. The calculated overall rate constant values for the HOO˙ and CH3OO˙ radical scavenging of compound 2 are 6.86 × 104 M−1 s−1 and 1.63 × 105 M−1 s−1, respectively. These findings, which are consistent with the experimental data, suggest antioxidant activity comparable to that of butylated hydroxyanisole (BHA). In aqueous solution, the anionic form of compound 2 displayed the highest radical scavenging rates among the tested compounds, with kapp values of 1.8 × 107 M−1 s−1 for HOO˙ and 3.3 × 106 M−1 s−1 for CH3OO˙, outperforming antioxidants like rubiadin and natural anthraquinones. Thus, compound 2 shows promise as an effective antioxidant in aqueous physiological environments.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.References
- A. M. Pisoschi and A. Pop, Eur. J. Med. Chem., 2015, 97, 55–74 CrossRef CAS PubMed
.
- V. Lobo, A. Patil, A. Phatak and N. Chandra, Pharmacogn. Rev., 2010, 4, 118–126 CrossRef CAS PubMed
.
- L. A. Pham-Huy, H. He and C. Pham-Huy, Int. J. Biomed. Sci., 2008, 4, 89–96 CrossRef CAS PubMed
.
- S. K. Bardaweel, M. Gul, M. Alzweiri, A. Ishaqat, H. A. Alsalamat and R. M. Bashatwah, Eurasian J. Med., 2018, 50, 193–201 CrossRef CAS PubMed
.
- F. Magnani and A. Mattevi, Curr. Opin. Struct. Biol., 2019, 59, 91–97 CrossRef CAS PubMed
.
- M. Hayyan, M. A. Hashim and I. M. Alnashef, Chem. Rev., 2016, 116, 3029–3085 CrossRef CAS PubMed
.
- Q. V. Vo, P. C. Nam, M. V. Bay, N. M. Thong, L. T. Hieu and A. Mechler, RSC Adv., 2019, 9, 42020–42028 RSC
.
- C. Iuga, J. R. Alvarez-Idaboy and N. Russo, J. Org. Chem., 2012, 77, 3868–3877 CrossRef CAS PubMed
.
- H. Jabeen, S. Saleemi, H. Razzaq, A. Yaqub, S. Shakoor and R. Qureshi, J. Photochem. Photobiol., B, 2018, 180, 268–275 CrossRef CAS PubMed
.
- I. Gülçin, J. Med. Food, 2011, 14, 975–985 CrossRef PubMed
.
- M. V. Bay, N. M. Thong, P. C. Nam, A. Mechler, N. T. Hoa and Q. V. Vo, Chem. Phys. Lett., 2023, 832, 140867 CrossRef
.
- N. M. Thong, Q. V. Vo, T. L. Huyen, M. V. Bay, D. Tuan and P. C. Nam, ACS Omega, 2019, 4, 14996–15003 CrossRef PubMed
.
- T. D. Ngoc, T. N. Le, T. V. A. Nguyen, A. Mechler, N. T. Hoa, N. L. Nam and Q. V. Vo, J. Phys. Chem. B, 2022, 126, 702–707 CrossRef CAS PubMed
.
- C. Kaur and D. Mandal, Comput. Theor. Chem., 2023, 1219, 113973 CrossRef CAS
.
- M. K. Georgieva, N. Anastassova, D. Stefanova and D. Yancheva, J. Phys. Chem. B, 2023, 127, 4364–4373 CrossRef CAS PubMed
.
- N. G. Hristova-Avakumova, E. P. Valcheva, N. O. Anastassova, B. I. Nikolova-Mladenova, L. A. Atanasova, S. E. Angelova and D. Y. Yancheva, J. Mol. Struct., 2021, 1245, 131021 CrossRef CAS
.
- H. S. Kareem, A. Ariffin, N. Nordin, T. Heidelberg, A. Abdul-Aziz, K. W. Kong and W. A. Yehye, Eur. J. Med. Chem., 2015, 103, 497–505 CrossRef CAS PubMed
.
- N. O. Can, D. Osmaniye, S. Levent, B. N. Saǧlik, B. Inci, S. Ilgin, Y. Özkay and Z. A. Kaplancikli, Molecules, 2017, 22, 1381–1400 CrossRef PubMed
.
- I. F. Nassar, A. F. EI Farargy, F. M. Abdelrazek and Z. Hamza, Nucleosides, Nucleotides Nucleic Acids, 2020, 39, 991–1010 CrossRef CAS PubMed
.
- Z. Peng, G. Wang, Q. H. Zeng, Y. Li, Y. Wu, H. Liu, J. J. Wang and Y. Zhao, Food Chem., 2021, 341, 128265 CrossRef CAS PubMed
.
- B. B. Kashid, J. T. Kilbile, K. D. Wani, S. M. Pawar, V. M. Khedkar and A. A. Ghanwat, Comb. Chem. High Throughput Screen., 2020, 25, 274–283 CrossRef PubMed
.
- A. Baier, A. Kokel, W. Horton, E. Gizińska, G. Pandey, R. Szyszka, B. Török and M. Török, ChemMedChem, 2021, 16, 1927–1932 CrossRef CAS PubMed
.
- S. A. Aly and S. K. Fathalla, Arab. J. Chem., 2020, 13, 3735–3750 CrossRef CAS
.
- E. Bozkurt, Y. Sıcak, E. E. Oruç-Emre, A. K. Iyidoğan and M. Öztürk, Russ. J. Bioorg. Chem., 2020, 46, 702–714 CrossRef CAS
.
- N. Afriana, N. Frimayanti, A. Zamri and J. Jasril, J. Phys.:Conf. Ser., 2020, 1655, 012036 CrossRef CAS
.
- B. R. Thorat, A. Gurav, B. Dalvi, A. Sawant, V. Lokhande and S. N. Mali, Curr. Chin. Chem., 2020, 1, 30–46 CrossRef
.
- N. A. Alsaif, M. A. Bhat, M. A. Al-Omar, H. M. Al-Tuwajiri, A. M. Naglah and A. Al-Dhfyan, J. Chem., 2020, 2020, 4916726 Search PubMed
.
- E. Başaran, N. Haşimi, R. Çakmak and E. Çınar, Russ. J. Bioorg. Chem., 2022, 48, 143–152 CrossRef
.
- I. A. Khodja, C. Bensouici and H. Boulebd, J. Mol. Struct., 2020, 1221, 128858 CrossRef
.
- L. T. Hieu, N. T. Hoa, A. Mechler and Q. V. Vo, J. Phys. Chem. B, 2023, 127, 11045–11053 CrossRef CAS PubMed
.
- L. T. Hieu, M. Van Bay, N. T. Hoa, A. Mechler and Q. V. Vo, RSC Adv., 2022, 12, 32693–32699 RSC
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, G. Z. J. Bloino, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
- H. Boulebd, I. A. Khodja, M. V. Bay, N. T. Hoa, A. Mechler and Q. V. Vo, J. Phys. Chem. B, 2020, 124, 4123–4131 CrossRef CAS PubMed
.
- H. Boulebd, A. Mechler, N. T. Hoa and Q. V. Vo, New J. Chem., 2020, 44, 9863 RSC
.
- L. T. Hieu, M. V. Bay, N. T. Hoa, A. Mechler and Q. V. Vo, RSC Adv., 2022, 12, 32693 RSC
.
- D. Mandal, C. Sahu, S. Bagchi and A. K. Das, J. Phys. Chem. A, 2013, 117, 3739–3750 CrossRef CAS PubMed
.
- C. Kaur and D. Mandal, Theor. Chem. Acc., 2024, 143, 28 Search PubMed
.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1991, 95, 5853–5860 CrossRef CAS
.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed
.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed
.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef
.
- D. Q. Dao, T. T. T. Phan, T. L. A. Nguyen, P. T. H. Trinh, T. T. Van Tran, J. S. Lee, H. J. Shin and B.-K. Choi, J. Chem. Inf. Model., 2020, 60, 1329–1351 CrossRef CAS PubMed
.
- C. Kaur and D. Mandal, Struct. Chem., 2024, 1–11 Search PubMed
.
- Y. Shang, H. Zhou, X. Li, J. Zhou and K. Chen, New J. Chem., 2019, 43, 15736–15742 RSC
.
- J. J. Fifen, J. Chem. Theory Comput., 2013, 9, 3165–3169 CrossRef CAS PubMed
.
- J. J. Fifen, Z. Dhaouadi and M. Nsangou, J. Phys. Chem. A, 2014, 118, 11090–11097 CrossRef CAS PubMed
.
- Z. Marković, J. Tošović, D. Milenković and S. Marković, Comput. Theor. Chem., 2016, 1077, 11–17 CrossRef
.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC
.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS
.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef
.
- E. Dzib, A. Quintal, F. Ortiz-Chi and G. Merino, Eyringpy 2.0, Cinvestav, Merida, Yucatan, 2021 Search PubMed
.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS
.
- R. Jaglan and D. Mandal, Comput. Theor. Chem., 2020, 1187, 112920 CrossRef CAS
.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS
.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS
.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682 CrossRef CAS
.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425–437 CrossRef CAS
.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS
.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS
.
- G. G. Stokes, Mathematical and Physical Papers, University Press, Cambridge, 1905 Search PubMed
.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS
.
- Y. Okuno, Chem.–Eur. J., 1997, 3, 212–218 CrossRef CAS PubMed
.
- S. Benson, The Foundations of Chemical Kinetics, Malabar, Florida, 1982 Search PubMed
.
- J. R. Alvarez-Idaboy, L. Reyes and N. Mora-Diez, Org. Biomol. Chem., 2007, 5, 3682–3689 RSC
.
- R. G. Parr, L. V. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS
.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS
.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS
.
- P. K. Chattaraj, H. Lee and R. G. Parr, J. Am. Chem. Soc., 1991, 113, 1855–1856 CrossRef CAS
.
- R. A. Rusdipoetra, H. Suwito, N. N. T. Puspaningsih and K. U. Haq, RSC Adv., 2024, 14, 6310–6323 RSC
.
- S. A. McKee and T. V. Pogorelov, Gaussian 09, University of Illinois, Urbana-Champaign, 2019 Search PubMed
.
- J. R. Pliego Jr and J. M. Riveros, Phys. Chem. Chem. Phys., 2002, 4, 1622–1627 RSC
.
- J. R. Pliego Jr, Chem. Phys. Lett., 2003, 367, 145–149 CrossRef
.
- Y. Z. Zheng, G. Deng, Q. Liang, D.-F. Chen, R. Guo and R.-C. Lai, Sci. Rep., 2017, 7, 7543 CrossRef PubMed
.
- Y. Shanga, H. Zhoua, X. Li, J. Zhoua and K. Chen, New J. Chem., 2019, 43, 15736–15742 RSC
.
- C.-H. Hsu, Y. M. Hung, K.-A. Chu, C.-F. Chen, C.-H. Yin and C.-C. Lee, Sci. Rep., 2020, 10, 1–10 CrossRef PubMed
.
- H. Zhou, X. Li, Y. Shang and K. Chen, Antioxidants, 2019, 8, 590 CrossRef CAS PubMed
.
- J. Sharanya, A. Purushothaman, D. Janardanan and K. Koley, Comput. Theor. Chem., 2024, 1232, 114460 CrossRef CAS
.
- M. Spiegel, J. Phys. Chem. B, 2023, 127, 8769–8779 CrossRef CAS PubMed
.
- L. T. Hieu, M. V. Bay, N. T. Hoa, A. Mechler and Q. V. Vo, RSC Adv., 2022, 22, 32693–32699 RSC
.
- H. Boulebd, Phytochemistry, 2021, 184, 112670 CrossRef CAS PubMed
.
- H. Boulebd, A. Mechler, N. T. Hoa, P. C. Nam, D. T. Quang and Q. V. Vo, New J. Chem., 2021, 45, 7774–7780 RSC
.
- N. T. Nguyen, V. V. Dai, A. Mechler, N. T. Hoa and Q. V. Vo, RSC Adv., 2022, 12, 24579–24588 RSC
.
- M. Van Bay, P. C. Nam, D. T. Quang, A. Mechler, N. K. Hien, N. T. Hoa and Q. V. Vo, ACS Omega, 2020, 5, 7895–7902 CrossRef PubMed
.
- N. M. Tam, N. M. Thong, T. Le Huyen, L. P. Hoang, A. Mechler and Q. V. Vo, J. Mol. Graphics Modell., 2021, 105, 107892 CrossRef CAS PubMed
.
- P. C. Nam, N. M. Thong, N. T. Hoa, D. T. Quang, L. P. Hoang, A. Mechler and Q. V. Vo, RSC Adv., 2021, 11, 14269–14275 RSC
.
- N. Q. Trung, N. M. Thong, D. H. Cuong, T. D. Manh, L. P. Hoang, N. K. Hien, P. C. Nam, D. T. Quang, A. Mechler and Q. V. Vo, ACS Omega, 2021, 6, 13391–13397 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07625g |
| This journal is © The Royal Society of Chemistry 2025 |