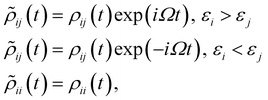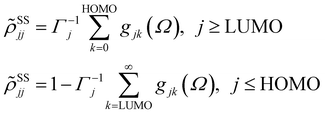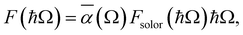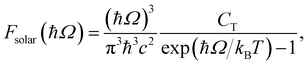Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Functionalization of zeolite-encapsulated Cu5 clusters as visible-light photoactive sub-nanomaterials†
Katarzyna M. Krupka ,
Lenard L. Carroll
,
Lenard L. Carroll and
María Pilar de Lara-Castells
and
María Pilar de Lara-Castells *
*
Institute of Fundamental Physics (AbinitSim Unit, ABINITFOT Group), Consejo Superior de Investigaciones Científicas (CSIC), E-28006 Madrid, Spain. E-mail: Pilar.deLara.Castells@csic.es
First published on 22nd January 2025
Abstract
The unique structural properties of zeolites make them ideal environments for encapsulating subnanometric metal clusters on their microporous channels and cavities, showing an enhanced catalytic performance. As a first step towards the functionalization of these clusters as photocatalysts as well, this work addresses the optical properties of zeolite-encapsulated Cu5–TiO2 nanoparticles as well as their application in the photo-induced activation of CO2 by sunlight. Model density functional theory (DFT) calculations indicate the stability of the Cu5 cluster adsorbed on the TiO2 nanoparticles filling the pores of a model zeolite structure. Second, it is shown that while TiO2 nanoparticles absorb in the UV, the photo-absorption spectrum of the Cu5–TiO2 nanoparticle composite is peaked at the visible region, where the sun has its maximum energy input, also allowing for the photo-induced activation of CO2 adsorbed onto the Cu5 cluster.
1 Introduction
With the advent of the subnanometer scale as a critical feature size, our chemical and physical insight into the structure of matter is deepening almost exponentially.1 One of the key aspects driving this transformation in materials science is the emergence of highly selective experimental techniques allowing for the synthesis of monodisperse atomically precise metal clusters (referred to as AMCs), composed of just one to tens of atoms.2 Exhibiting strong quantum confinement effects, AMCs are attracting significant interest in various fields due to their unexpected stability and unique properties with potential applications in catalysis,3–10 photocatalysis,11–14 luminescence,15 therapeutics,16 bioimaging,17,18 and sensing,19 bridging fundamental science and the world of nanotechnology (see, e.g., ref. 20 for a recent perspective).Featuring molecular-like structures and discrete energy levels,21–25 AMCs, typically smaller than 1 nm in size, differ markedly from larger nanoparticles and isolated metal cations in their catalytic behaviors. These differences are strongly influenced by low coordination numbers, high surface-to-volume ratios, and structural fluxionality, which arises from dynamical fluctuations in their atomic arrangements.12,13,20,26–33 As a result, subnanometric metal clusters provide a plethora of dynamically inter-connected active sites, and offer significantly higher reactivity compared to larger nanoparticles.34–36
For instance, copper pentamer clusters exhibit novel and remarkable properties, including exceptional thermodynamical and chemical stability in solution across the entire pH range (1–14),37 an unexpected resistivity to deep irreversible oxidation despite their tiny size,32,38–40 an applicability to different catalytic reactions,12,41,42 and their capability to improve the optoelectronic and (photo)catalytic properties of photo-absorbers such as titanium dioxide.11,43
The encapsulation of subnanometric metal clusters in porous materials such as zeolites,25 carbon nanotubes,44–46 and metal–organic frameworks47,48 (MOFs) is an effective strategy for stabilizing and controlling their reactivity, offering enhanced catalytic performance and selectivity. By tuning the pore size, shape, and surface chemistry of these materials, AMCs can be effectively immobilized, preventing their aggregation. Furthermore, the high surface area and porosity of zeolites and MOFs facilitate efficient mass transfer and substrate accessibility.49–51 For instance, a recent study has demonstrated that heteroatom-doped Ag25 clusters encapsulated in MOFs drive photocatalytic hydrogen production.47 Moreover, the versatile applications of porphyrin-based metal–organic frameworks (PMOFs) as photocatalysts in aqueous environments have been recently reviewed,52 with a specific focus on solar fuel production and pollutants degradation. The use of metal–organic framework heterojunctions for photocatalysis has been also summarized53 alongside the application of MOFs as solid catalysts for liquid-phase reactions, including synthesis by design, high porosity in the micro-mesoporous range, and a high density of unsaturated transition-metal ions.54 Likewise, it has been shown that the encapsulation of AMCs within carbon nanotubes enhance the catalytic activities of AMCs in various reactions, including Fischer–Tropsch synthesis,44 syngas-to-ethanol transformations,45 and ester hydrogenation reactions.55 Additionally, AMCs are less prone to oxidation.46
Zeolites, crystalline aluminosilicates known for their well-defined pore structures, high thermal stability, and tunable acidity and basicity,56 are excellent candidates for hosting subnanometric metal clusters.57,58 The spatial confinement within the microporous channels and cavities of zeolites stabilizes them, hindering their escape.59,60 This stabilization helps in suppressing the migration and aggregation of the metal clusters, as demonstrated in high-temperature oxidation and reduction treatments.36 Moreover, as recently reviewed in ref. 25, zeolite-encapsulated AMCs exhibit higher catalytic efficiencies than their non-encapsulated counterparts in various reactions, such as propane dehydrogenation, formic acid decomposition, ammonia borane hydrolysis, cyclohexane oxidation, the water–gas shift reaction, and hydrogenation. These encapsulated clusters also demonstrated higher hydrogen evolution rates.61 Remarkably, the encapsulation of AMCs in zeolites has also made it possible to achieve one of the highest turnover frequency values for heterogeneously catalyzed formic acid decomposition.62
Naturally, experimental capabilities for synthesizing and characterizing zeolite-encapsulated AMCs have advanced hand-in-hand with those allowing their theoretical underpinnings such as state-of-the-art (single-reference) dispersion-corrected density functional theory (DFT)-based modelling. These developments have enabled the investigation of the catalytic behaviour of subnanometric copper clusters in the methane to methanol (MTM) reaction supported in zeolites and zeotypes using O2 as oxidant without water molecules assisting the process.63–66 Notably, studies have demonstrated that the selective oxidation of methane to methanol can be achieved with Cu5 clusters encapsulated in zeolite structures.64 However, while these studies have primarily focused on electronic ground-state properties, there remains a lack of theoretical investigations exploring the excited states and, in particular, the optical properties of these encapsulated systems.
Our work addresses this significant research gap by using advanced methods to investigate the encapsulation of Cu5 clusters supported on a TiO2 nanoparticle within the micropores of a zeolite structure. This approach allows us to explore not only the fundamental electronic structure but also the photo-absorption spectra in great detail. Our study is motivated by the joint experimental–theoretical demonstration that the deposition of a single monolayer of Cu5 on a TiO2 surface markedly enhances its optical properties, making it a visible-light photoactive material (see, e.g., ref. 11). As a result, much more energy can be harvested from sunlight, with the coated titanium dioxide temporally storing this energy as charge pairs (i.e., electrons and holes), an ideal prerequisite for follow-up chemistry. Notably, a later study12 demonstrated the photoinduced activation of CO2 physisorbed on TiO2-modified Cu5 clusters under visible light. Our work is further inspired by a recent study67 that highlighted the successful use of TiO2 nanoparticles within MOF mesopores for CO2 photoreduction under UV light.68 By modeling the same process using Cu5-modified TiO2 nanoparticles instead, the photoreduction could potentially extend into the visible light spectrum, enhancing its applicability and efficiency.68
Applying density functional theory (DFT) and a combined approach that integrates DFT with reduced density matrix theory, we investigate the optical response of the system under solar irradiation. Thus, in Section 2, the computational approach and the details of our calculations are presented. Section 3 focuses on the analysis of the photo-absorption spectra of non-encapsulated and zeolite-encapsulated Cu5–TiO2 composite nanoparticles, including their potential for physisorbed CO2 photo-reduction. Finally, Section 4 closes with the concluding remarks.
2 Computational–theoretical methods
2.1 Structural models
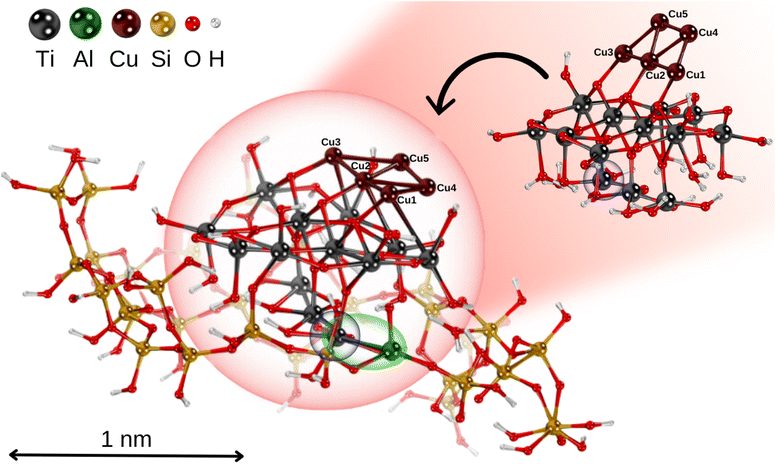
Following ref. 69, a hydrogen-saturated cluster of stoichiometry Ti9O25H14 has been used as a model for a TiO2 nanoparticle based on the experimental geometry of the TiO2(110)-(1 × 1) surface.70 The structure of the TiO2 units within the nanoparticle remains unchanged from the original surface, ensuring it accurately represents the properties of bulk TiO2 in nanoparticulate form. The planar trapezoidal two-dimensional (2D) Cu5 structure has been selected as the initial configuration (referred to as Cu5-2D).The TiO2 nanoparticle was inserted into a zeolite pore model based on the extra-large-pore zeolite structure UTD-1 from ref. 71, which is constructed from typical tetrahedral SiO4 units forming oxygen 4-, 5- and 6-membered rings.72 The resulting microporous structure has a diameter close to the size of the TiO2 nanoparticle (see Fig. 1). To achieve charge balance and enhance the interaction capabilities, one silicon atom in the zeolite framework was substituted with an aluminum atom, resulting in Si–O–Al linkages that generated a net negative charge in the system.64,72 As shown in Fig. 1, the TiO2 nanoparticle adheres to the microporous structure of the zeolite framework via a Ti–Al bond.
2.2 Computational details
Periodic electronic structure calculations were performed using spin-polarized DFT + U as implemented in the Vienna Ab initio Simulation Package (VASP 5.4.4).73,74 The Perdew–Burke–Ernzerhof (PBE) functional was used to approximate the exchange correlation potential.75 Geometries were relaxed using the conjugate gradient method, with dispersion corrections applied using the DFT-D3 approach76,77 with Becke–Johnson damping. Dipole corrections were incorporated along the z-direction in the simulation cell, and particle occupancies were handled using a Gaussian smearing scheme with a smearing factor 0.05 eV. Hubbard U parameters of 4.2 eV for Ti and 5.2 eV for Cu were adopted, consistent with a prior study of the Cu5–TiO2(110) system.11 Electron–ion interactions were described by the projector augmented-wave (PAW) method,78,79 using PAW-PBE pseudopotentials (PP) as implemented in VASP. Electrons of O 2s2p, Al 2s2p, Si 2s2p and Cu 3d4s orbitals were explicitly treated as valence electrons. For Ti atoms, two calculations sets were considered: one treating 3d4s and another treating 3s3p3d4s as valence electrons, referred to as 3d4s + PP and 3s3p3d4s + PP. A plane-wave basis set with a kinetic energy cutoff of 400 eV was used, while a cut-off energy of 605.392 eV for the plane wave representation of the augmentation charges was chosen. The Brillouin zone was sampled at the Γ point, to minimize computational cost. The convergence threshold criterion was set to 10−4 eV for the self-consistent electronic minimization. Geometries were relaxed with a force threshold of 0.02 eV Å−1. We selected a cell volume for Cu5–TiO2@zeolite of 5 × 5 × 5 nm3, avoiding the interaction between periodic replicas.As a complement to the periodic DFT-based study, all-electron cluster model calculations were carried out using the same DFT-D3 (BJ) scheme with the ORCA80 suite of programs (versions 5.0.4 and 6.0.0). For this purpose, the atom-centered (augmented) polarized correlation-consistent triple-ζ (aug-cc-pVTZ) basis of Woon and Dunning Jr,81 as reported in ref. 69 was used for oxygen and titanium atoms.
The Cu5–TiO2 and Cu5–TiO2@zeolite interaction energies (Eint) were calculated as,
| Eint(Cu5–TiO2) = ECu5–TiO2 − ECu5 − ETiO2 |
| Eint(Cu5–TiO2@zeolite) = ECu5–TiO2@zeolite − ECu5 − ETiO2@zeolite |
Calculations of the interaction potentials between a single Cu atom and a TiO5H6 nanoparticle were carried out at the DFT-D3 and Møller–Plesset second-order perturbation theory (UMP2) levels using the aug-cc-pVTZ basis set with the ORCA code.80 Uncoupled, open-shell Hartree–Fock and coupled dispersion energy contributions were independently obtained in Symmetry-Adapted Perturbation Theory (SAPT) calculations using the Psi4 and Psi4NumPy software packages.82–85 For details on the methodology, see ref. 86.
2.3 Reduced density matrix treatment
In order to obtain the photo-absorption spectra, we have applied the Reduced Density Matrix (RDM) approach in the Redfield approximation,87 using the orbitals obtained in periodic calculations with the HSE06 approach. This RDM-DFT approach was proposed by Micha and collaborators.88–90 It has been successfully applied to AMCs adsorbed on semiconductor rutile TiO2(110) (see ref. 13 and references cited therein) and silicon surfaces.91–94 The performance of the RDM-DFT scheme has been directly evaluated by comparing the absorbance of TiO2 and Cu5–TiO2 interfaces with the experimentally determined one (via diffuse reflectance spectroscopy) in ref. 11.For the sake of completeness, we briefly overview the main equations applied within the RDM-DFT framework (see, e.g., ref. 88 for a detailed description). When the surface of the material is exposed to a monochromatic electromagnetic field 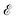 of frequency Ω, the evolution equation for the RDM, referred to as ρ, can be expressed as,
of frequency Ω, the evolution equation for the RDM, referred to as ρ, can be expressed as,
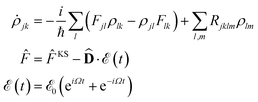 | (1) |
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) KS is the Kohn–Sham (KS) Hamiltonian, which is represented in the basis set of KS orbitals. In eqn (1),
KS is the Kohn–Sham (KS) Hamiltonian, which is represented in the basis set of KS orbitals. In eqn (1), ![[D with combining circumflex]](https://www.rsc.org/images/entities/b_char_0044_0302.gif) is the electric dipole moment operator. Finally. Rjklm are the Redfield coefficients (i.e., the KS component of the relaxation tensor, see ref. 87 and 88 for details). Next, in order to account for the electromagnetic field oscillations, a coordinate transformation is carried out into a rotating frame as,
is the electric dipole moment operator. Finally. Rjklm are the Redfield coefficients (i.e., the KS component of the relaxation tensor, see ref. 87 and 88 for details). Next, in order to account for the electromagnetic field oscillations, a coordinate transformation is carried out into a rotating frame as,where εi is the energy of the ith Kohn–Sham orbital. An average over time of the fast terms in the equations of motion of the RDM yields88,93
with HOMO (LUMO) denoting the highest-energy occupied (lowest-energy unoccupied) orbitals, Γj standing for the depopulation rate. The terms gjk are expressed through the equation
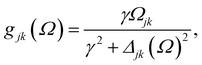 | (2) |
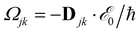 , and Δjk(Ω) = Ω − (εj − εk). The population relaxation rate ℏΓ and the decoherence rate ℏγ are kept fixed to known rates in the target semiconductor (e.g., 27 ps and 27 fs for TiO2 surfaces from ref. 95).
, and Δjk(Ω) = Ω − (εj − εk). The population relaxation rate ℏΓ and the decoherence rate ℏγ are kept fixed to known rates in the target semiconductor (e.g., 27 ps and 27 fs for TiO2 surfaces from ref. 95).
The absorbance can be expressed in terms of the stationary populations as11,92,93,96,97
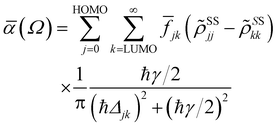 | (3) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) jk is an oscillator strength per active electron.
jk is an oscillator strength per active electron.
To investigate the practical applications of materials upon sunlight exposition, the absorbance from eqn (3) is weighted with the absorption of solar energy88 (referred to as ‘solar flux’). The solar flux absorption spectrum (i.e., the absorbed flux of light energy) is given as:92
with CT as the flux normalization constant. Hence, the incident photon energy flux is simply Fsolar(ℏΩ)ℏΩ.
2.4 Computational protocol
The procedure followed in the VASP calculations is briefly outlined as follows: (1) structural optimizations are initially carried out with the DFT-D3 scheme;98,99 (2) in the next step, the obtained structures are re-optimized applying the Hubbard DFT + U term,100 with the spin-polarization accounted for; (3) the optimized structures at DFT + U/D3 level are then used in subsequent calculations with the HSE06 hybrid functional of Heyd, Scuseria and Ernzerhof;101,102 (4) finally, the orbitals obtained at HSE06 level are utilized for the calculations of the photo-absorption spectra. The HSE06 functional is particularly suitable as it provides values for the band-gap and mid-gap states of semiconductors that agree with experimental observations. For example, it estimates the band-gap of rutile TiO2(110) at 3.3 eV, which is consistent with the experimental value of 3.3 ± 0.5 eV (ref. 103).3 Results and discussion
3.1 Optical properties of non-encapsulated Cu5–TiO2 nanoparticles
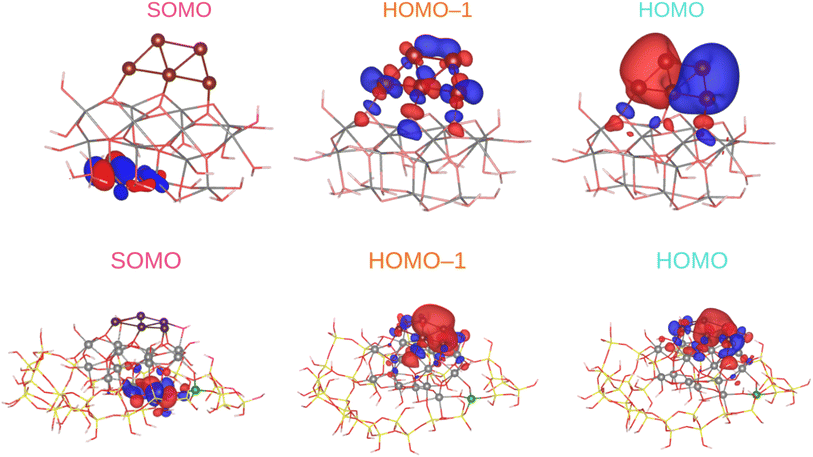
We begin by discussing the optical properties of Cu5-decorated TiO2 nanoparticles. To characterize the main features of Cu5 adsorption onto the TiO2 nanoparticle in the electronic ground state, Fig. 2 presents the frontier orbitals of the structure pictured in Fig. 1 (see also Fig. S1 of the ESI†). The photo-absorption spectra and the projected density of states are displayed in Fig. 3 instead.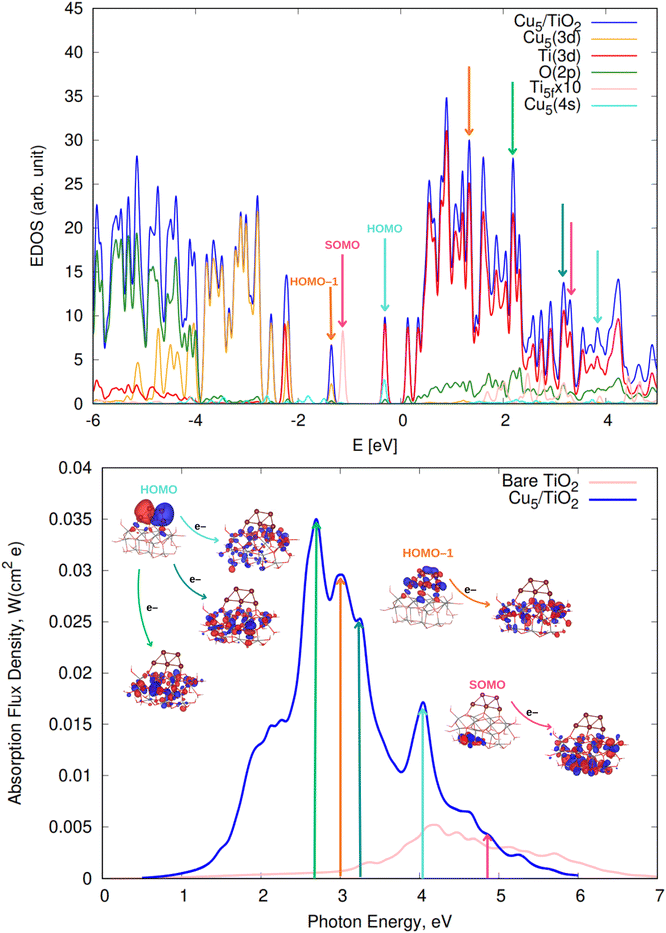 | ||
| Fig. 3 (Upper panel) Electronic density of states (EDOS) of non-encapsulated Cu5–TiO2 nanoparticles. The projected density of states onto atomic Ti(3d) and O(2p) orbitals as well as the sum of projections of Cu(3d) and Cu(4s) orbitals are also shown along with the projection onto the 3d orbital of the Ti atom hosting the small polaron-like state (i.e., the SOMO state). The arrows indicate the positions of the orbitals responsible for the most intense photo-absorption peaks. (Bottom panel) Photo-absorption spectra of non-encapsulated Cu5–TiO2 nanoparticles and bare TiO2 rutile (110) from ref. 11. The positions of the most intense peaks is also indicated. The insets present the orbitals involved in the photo-excitation processes. The zero of energy is set to the energy of the lowest unoccupied molecular orbital (LUMO). | ||
The estimate of the interaction energy at the DFT + U/D3 level (ca. −3.8 eV, see Table 1) indicates a high stability of the Cu5 cluster on the small TiO2 structure. This value is comparable to the interaction energy reported for the Cu5–TiO2(110) system (ca. −3.5 eV in ref. 11). A recent study involving the open-shell Cu3 cluster interacting with a molecular graphene model (coronene) highlighted that the Grimme D3 correction overestimates the dispersion contribution to the cluster–support interaction energy (see ref. 86 for details). However, the DFT-D3 scheme has also been shown to deliver sensible results for van-der-Waals-dominated interactions, such as the interaction of the closed-shell Ag2 cluster with graphene105 and rutile TiO2 (110) surfaces.96 The results were consistent with those obtained using, e.g., symmetry adapted perturbation theory (SAPT) with a DFT description of the monomers (i.e., the SAPT(DFT) approach106,107) as well as the domain-based local pair natural orbital DLPNO-CCSD(T) method (agreeing to within 10%). Benchmarking the intermolecular Cu5–TiO2 interaction could benefit from applying the open-shell coupled UMP2 (UMP2C) theory proposed in ref. 86 for transition metal oxides. This approach replaces the uncoupled Hartree–Fock dispersion energy with a coupled dispersion contribution from frequency-integrated linear-response functions in time-dependent unrestricted Hartree–Fock theory. In this work, its application to the interaction potential between a single Cu atom and a TiO5H6 cluster (see Fig. S2 and Table S4 of the ESI†) shows that the DFT-D3 approach overestimates the interaction energy at the potential minimum by 0.2 eV (ca. −0.8 vs. −0.6, see Table S4†) and predicts an optimized Cu–TiO5H6 distance approximately 10% shorter than the UMP2C estimate. Once again, however, as can be observed in Table S2 of the ESI,† the interatomic Cu–Cu distances for the free Cu5–TiO2 nanoparticle differ minimally from those reported using high level ab initio theory in ref. 104. In contrast, the range of inter-atomic Cu–O distances aligns well with those reported in DFT studies on the structural and magnetic properties of low-index Cu2O surfaces.108
| DFT-D3//all-electron | DFT + U/D3//3d4s + PP | |
|---|---|---|
| Cu5–TiO2 | −3.26 | −3.79 |
| Cu5–TiO2@zeolite | −3.51 | −3.93 |
As shown in the middle panel of Fig. 2, the HOMO-1 features a clear hybridization between Cu(3d) orbitals and O(2p) orbitals of the nearest bridging oxygen atoms (see also Fig. S1 of the ESI†), indicating a covalent nature of the Cu5–TiO2 bonding. The energy of the HOMO-1 in the free Cu5 cluster is very close to the HOMO energy of the free TiO2 nanoparticle, facilitating the mixing of Cu(3d) and O(2p) contributions. In contrast, the HOMO, which is single occupied and dominated by 4s contributions from all Cu atoms in the free cluster, becomes double occupied and dominated by 4s contributions localized on the two terminal apical Cu atoms of the trapezoidal structure. This outcome suggests an internal charge transfer from the basal Cu atoms to the apical ones, leading to a polarization of the electronic charge within the trapezoidal structure. This polarization tilts the structure toward an uncoordinated five-fold (5f) Ti atom on the surface of the TiO2 nanoparticle. As shown in the projected density of states (Fig. 3), this orbital also presents Ti(3d) contributions.
Interestingly, in all-electron (non-periodic) calculations excluding the DFT + U Hubbard term (see Fig. S1 of the ESI†), the frontier orbitals are very similar to those obtained in periodic calculations. In both cases, the Cu5 cluster loses its magnetic moment in favor of the SOMO which characterizes the localization of its unpaired electron in the 3d orbital of a Ti atom. A comparison of periodic calculations using large (4-valence electrons 3d4s) and small (12-valence electrons 3s3p3d4s) pseudopotentials for Ti atoms also indicates a modest impact on the frontier orbitals. Both total and average Bader charges on Cu atoms (see Table S1 of the ESI†) differ only slightly (to within 0.1 and 0.02|e|). Larger variations are observed in the Bader charges of the Ti atoms and O–H species of the TiO2 nanoparticle (e.g., up to 24% for Ti atoms). Appealing, Mulliken analysis109 indicates that the Cu5 cluster becomes slightly negatively charged (by −0.2|e| in contrast to the Bader analysis, which assigns a total charge of 0.8|e|). Such discrepancies between Mulliken and Bader charges for transition metal atoms have been previously observed.110 This outcome indicates the high degree of covalent character in the Cu5–TiO2 chemical bonding and suggests a charge-transfer mechanism where the TiO2 nanoparticle supplies charge to Cu5 through the Cu–O bonds. Additionally, there is also back transfer of charge from the TiO2 nanoparticle to the d-type orbitals centered on the Cu atoms, which in turn, become mixed with (primarily) O(2p) orbitals. This mechanism also explains why the total Bader charge of Cu5 (−0.8|e|) is less than unity. Similarly, when charges are estimated based on projections of one-electron-wavefunctions from VASP calculations onto spherical harmonics centered on Cu atoms, the Cu atoms are predicted to be slightly, yet negatively, charged. However, unlike the Bader charges, these projected charges show a significant dependence on the pseudopotential used for the Ti atoms.
There is also photo-induced electron transfer from the (SOMO) polaron-like state (indicated with a pink arrow in Fig. 3) but the associated absorption peak is much less intense and located in the short-wave UV region (ca. 4.9 eV). As shown in Fig. 3, the photo-excitation leads to the delocalization of the polaronic charge across all Ti atoms of the nanoparticle. In contrast, for Cu5-modified TiO2(110) surfaces,11 surface polarons are formed. Upon photo-excitation with visible light, these polarons become delocalized over all surface Ti atoms (i.e., indicating the photo-induced conversion of a small localized polaron into a large delocalized polaron2,111,112). Moreover, for Cu5-decorated TiO2 nanoparticles, the spectra clearly peak at the visible region whereas for the extended Cu5-modified TiO2(110) system,11 the peak at the UV region is still the most intense. As discussed in ref. 11, Cu5 clusters enhance the absorption in the UV region through a mechanism involving electron transfer from surface and subsurface O anions to surface and subsurface Ti atoms. The number of Ti atoms and O anions in the unit cell for the TiO2 nanoparticle is much lower than for the extended TiO2(110) surface, explaining why the UV peak is not the more intense for the nanoparticle.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds compared to those featured by the neutral CO2 counterpart, facilitating its cleavage and dissociation. Otherwise, the physisorption of the CO2 molecule on top of the Cu5 cluster modifies the spectrum profile of the bare Cu5–TiO2 nanoparticle only slightly. Once again, the major modification is observed at about 1.9 eV (blue and green arrows in Fig. 4), with the transition responsible for the two additional peaks involving the electron “jump” from the HOMO to final states characterized as the CO2˙− attached to the Cu5–TiO2 nanoparticle.
O bonds compared to those featured by the neutral CO2 counterpart, facilitating its cleavage and dissociation. Otherwise, the physisorption of the CO2 molecule on top of the Cu5 cluster modifies the spectrum profile of the bare Cu5–TiO2 nanoparticle only slightly. Once again, the major modification is observed at about 1.9 eV (blue and green arrows in Fig. 4), with the transition responsible for the two additional peaks involving the electron “jump” from the HOMO to final states characterized as the CO2˙− attached to the Cu5–TiO2 nanoparticle.
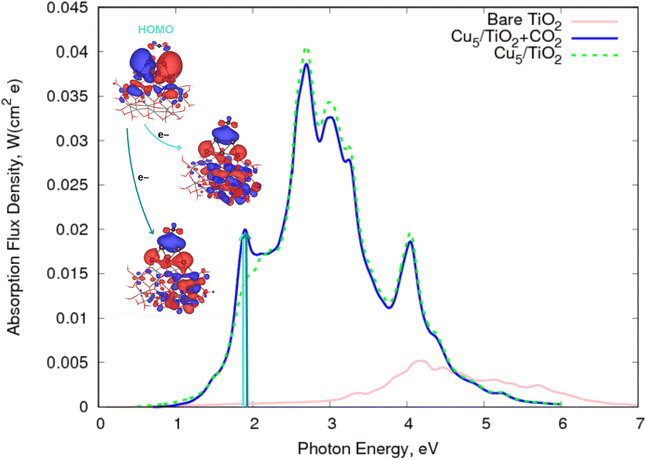 | ||
| Fig. 4 Photo-absorption spectra of non-encapsulated Cu5–TiO2 nanoparticles (with and without CO2 adsorbed) and bare TiO2 rutile (110) from ref. 11. | ||
3.2 Optical properties of zeolite-encapsulated Cu5–TiO2 nanoparticles
In the first part of this section, the geometries and the electronic structure of free and zeolite-encapsulated Cu5–TiO2 nanoparticles are compared, as obtained using the DFT + U/D3 approach. In the second section, the frontier orbitals and the photo-absorption spectrum of the zeolite-encapsulated Cu5–TiO2 nanoparticle are analyzed based on final HSE06 calculations.As illustrated in Fig. 2 (bottom panel), the electronic structure of the composite Cu5–TiO2 nanoparticle undergoes modification upon encapsulation, accompanied by aforementioned structural changes. The polaron-like electron relocates to a Ti atom covalently bonded to an Al atom within the zeolite framework. The SOMO, which exhibits polaron-like characteristics, becomes the highest occupied molecular orbital, in contrast to its position as the second-highest orbital in the non-encapsulated system. The doubly-occupied HOMO involves s-type orbitals from the Cu cluster and p-type orbitals from the oxygen atoms, including those from the additional OH groups of TiO2. The next frontier orbital, HOMO-1, remains localized at the nanoparticle, specifically at the bonding site with the Al atom. HOMO-1 features Cu d-type orbitals and O p-type orbitals but also includes Cu s-type orbitals.
Our conclusions align closely with those reported in a DFT-based study investigating the influence of zeolite supports on the catalytic properties of Cu5 clusters.64 In that study, it was observed that substituting a single Si atom with Al in the CHA zeolite generates a net negative charge, which is compensated by the appearance of a positive Bader charge (ca. 0.8|e|) on the Cu5 clusters. This charge redistribution leads to a reduction in the shortest Cu–O distances to 1.974 Å. This value is comparable to those obtained for Cu5–TiO2 within the zeolite cavity (see Table S2 of the ESI†). Similarly, the planar Cu5 cluster undergoes structural distortion within the micropores of the CHA zeolite,64 with the shortest Cu–O distance being comparable to that observed in the zeolite@TiO2 system (1.9 vs. 2.0 Å, see Table S1 of the ESI† and ref. 64).
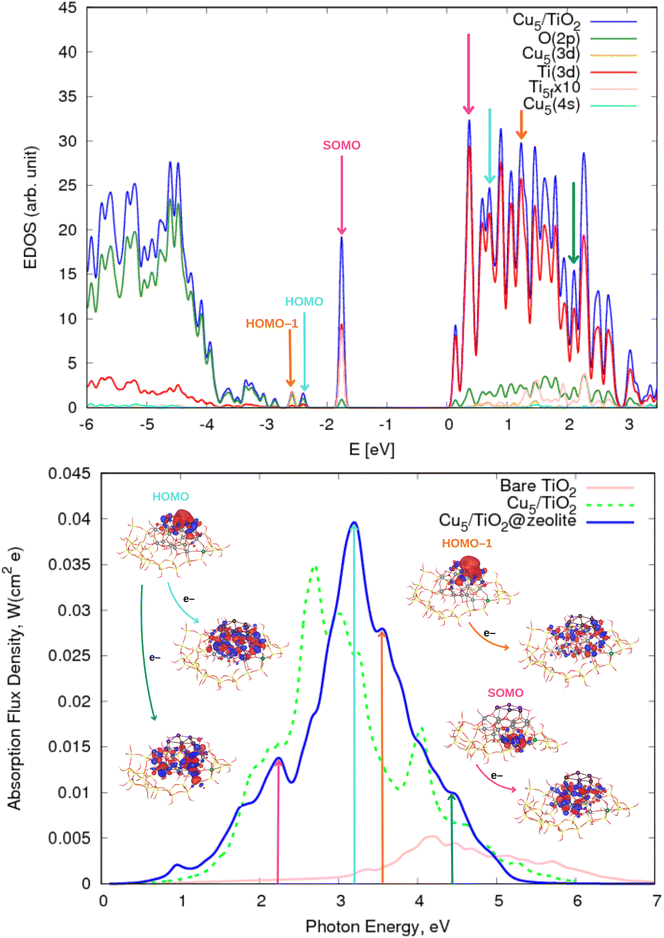 | ||
| Fig. 5 (Upper panel) Electronic density of states (EDOS) of the zeolite-encapsulated Cu5–TiO2 nanoparticle shown in Fig. 1. The projected density of states onto atomic Ti(3d) and O(2p) orbitals as well as the sum of projections of Cu(3d) and Cu(4s) orbitals are also shown along with the projection onto the 3d orbital of the Ti atom hosting the small polaron-like state (i.e., the SOMO state). The arrows indicate the positions of the orbitals responsible of the most intense photo-absorption peaks. (Bottom panel) Photo-absorption spectra of zeolite-encapsulated and non-encapsulated Cu5–TiO2 nanoparticles and bare TiO2 rutile (110) from ref. 11. The positions of the most intense peaks is also indicated. The insets present the orbitals involved in the photo-excitation processes. The zero of energy is set to the energy of the lowest unoccupied molecular orbital (LUMO). | ||
The most pronounced difference between the spectra of non-encapsulated and encapsulated nanoparticles, however, lies in the photo-excitation of the SOMO, i.e., the polaron-like state with an electron localized in a Ti(3d) orbital. In the encapsulated nanoparticle, the SOMO is the highest-energy occupied orbital, and the corresponding transition peak is significantly more intense and shifted from the UV region to the long-wave visible region (ca. 2.3 eV). The acceptor state is a delocalized polaron-like state involving primarily Ti d- and O p-orbitals from the upper layer of the encapsulated TiO2 nanoparticle at the bottom of the conduction band while, for the non-encapsulated system, the accepting state involves Ti(3d) orbitals from the inner layer. On the one hand, as shown in previous works on Ag5-decorated TiO2 surfaces,2,111,112 the photo-excitation of a small electron polaron leads to a large delocalized electron polaron, highlighting its dual nature. On the other hand, the shifting of the delocalized polaron-like state from bottom to top layers upon encapsulation can be explained by considering the net generated charge caused by the substitution of a Si atom by Al in the zeolite structure.
The main findings regarding the photo-absorption spectra can likely be generalized to other zeolite structures with cavities hosting TiO2 nanoparticles of appropriate size. As previously discussed for Cu5@zeolite composites,64 the structure adopted by Cu5 clusters may depend on the number of Si atoms replaced by Al ones. However, the photo-absorption spectra are still expected to exhibit the high absorption peaks in the visible region. Notably, both zeolite-encapsulated and non-encapsulated systems demonstrate absorption peaks in the visible range regardless of the specific structure adopted by the Cu5 cluster. Further investigation is required to explore the interaction of smaller nanoparticles that can fit into different pore sizes and to examine the influence of multiple aluminum atoms on the physicochemical properties of the cluster-decorated TiO2 nanoparticles. The effects of multiple aluminum atoms in zeolite frameworks on bare subnanometric metal clusters have been previously analyzed (see, e.g., ref. 64). Extending these studies to cluster-decorated TiO2 nanoparticles could offer new perspectives on their photoactivity and functional properties.
4 Conclusions
The transition to a green economy necessitates advancement of industrial chemistry, the reduction of greenhouse gases in the atmosphere and the generation and storage of environmentally clean energy. Theoretical and experimental results have demonstrated how Cu5 clusters significantly improve the catalytic, photocatalytic and solar energy conversion properties of titanium dioxide, one of the most widely used materials for this type of process (see, e.g., ref. 20 as a recent perspective). These findings are not only relevant to industrial chemistry or clean energy generation, but also to reducing atmospheric carbon dioxide. In this work, we take a step forward by exploring the possibility of using small TiO2 nanoparticles embedded within the micropores of a zeolite structure as a cost-effective alternative to TiO2 surfaces or large TiO2 nanoparticles for these applications. Moreover, spatial confinement within the zeolites microporous materials allows for the stabilization of Cu5 clusters, suppressing their aggregation. Remarkably, we point out three important findings: (1) the high stability of the Cu5 clusters on TiO2@zeolite structures; (2) the activation of the small TiO2 nanoparticles as visible-light photoactive through the adsorption of the Cu5 clusters; (3) their applicability in trapping CO2 molecules from the atmosphere which, when irradiated with visible light, are transformed into CO2˙− radicals. These radicals represent a precursor state for dissociation due to their weakened C–O bonds.Interestingly, while the photo-absorption spectrum of the Cu5–TiO2(110) interface11 exhibited peaks in both the visible and the UV regions, the zeolite-encapsulated Cu5–TiO2 nanoparticle shows a pronounced peak in the visible region. This outcome suggests that the zeolite structure not only serves to stabilize the Cu5 clusters but also to improve the optical response of TiO2 in the visible region as compared to Cu5-decorated rutile TiO2(110).11 Moreover, natural zeolite has been proven to be a good supporting material for TiO2 nanoparticles in photo-catalytic reactions due to its high specific surface area, adsorption capacity, stability, hydrophobicity, crystal size, optical absorption properties, lifetime of charge carriers, unique uniform pores and channel sizes, etc. (see, e.g., ref. 115–120), with the applications including water waste treatment.121,122 Our findings also suggest the possibility of shifting experimentally demonstrated photocatalytic reactions such as oxidation of propene and CO2 photo-reduction with TiO2 nanoparticles filling the zeolite cavities117 and metal–organic framework mesospores123 with UV light towards the visible via their decoration with Cu5 clusters.
Data availability
The data supporting the findings of this study are available in the ESI of this article.†Author contributions
Conceptualization: M. P. d. L.-C.; investigation: K. M. K, L. L. C., and M. P. d. L.-C.; methodology: K. M. K. and M. P. d. L.-C.; data analysis: K. M. K. and M. P. d. L.-C.; data curation: K. M. K. and M. P. d. L.-C.; visualization: K. M. K. and M. P. d. L.-C.; supervision: M. P. d. L.-C.; project administration: M. P. d. L.-C.; funding acquisition: M. P. d. L.-C.; software: K. M. K., L. L. C., and M. P. d. L.-C.; writing: K. M. K and M. P. d. L.-C.; revision and editing: K. M. K., L. L. C., and M. P. d. L.-C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been partially supported by the Spanish Agencia Estatal de Investigación (AEI) under Grant No. PID2020-117605GB-I00/AEI/10.13039/501100011033 and the EU Doctoral Network PHYMOL 101073474 (project call reference HORIZON-MSCA-2021-DN-01). This publication is also based upon the work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). The CESGA supercomputer center (Spain) and the Secretaria Adjunta de Informática (SGAI) at CSIC are acknowledged for providing the computational resources.Notes and references
- Memorandum of Understanding of the COST Action CA21101 – Confined Molecular Systems: from a New Generation of Materials to the Stars (COSY), 2022, https://www.cost.eu/actions/CA21101 Search PubMed.
- M. P. de Lara-Castells and S. Miret-Artés, Europhys. News, 2022, 53, 7–9 CrossRef.
- L. Liu and A. Corma, Nat. Mater., 2018, 118, 4981–5079 CAS.
- A. Halder, C. Lenardi, J. Timoshenko, A. Mravak, B. Yang, L. K. Kolipaka, C. Piazzoni, S. Seifert, V. Bonačić-Koutecký, A. I. Frenkel, P. Milani and S. Vajda, ACS Catal., 2021, 11, 6210–6224 CrossRef CAS.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef CAS.
- R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088 CrossRef CAS PubMed.
- L. Vega, H. A. Aleksandrov, R. Farris, A. Bruix, F. Viñes and K. M. Neyman, Mater. Adv., 2021, 2, 6589–6602 RSC.
- E. Fernández and M. Boronat, J. Phys.: Condens. Matter, 2019, 31, 013002 CrossRef PubMed.
- S. Sharma and A. Ansari, Results Chem., 2023, 5, 100982 CrossRef CAS.
- Z. Luo and A. Shehzad, ChemPhysChem, 2024, e202300715 CrossRef CAS PubMed.
- M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500 RSC.
- P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074 CrossRef PubMed.
- M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759 CrossRef CAS PubMed.
- J. Juraj, A. Fortunelli and S. Vajda, Phys. Chem. Chem. Phys., 2022, 24, 12083–12115 RSC.
- H.-T. Sun and Y. Sakka, Sci. Technol. Adv. Mater., 2014, 15, 014205 CrossRef CAS PubMed.
- V. Porto, E. Borrajo, D. Buceta, C. Carneiro, S. Huseyinova, B. Domínguez, K. J. E. Borgman, M. Lakadamyali, M. F. Garcia-Parajo and J. Neissa, Adv. Mater., 2018, 30, 1801317 CrossRef PubMed.
- V. Bonačić-Koutecký and R. Antoine, Nanoscale, 2019, 11, 12436–12448 RSC.
- M. V. Romeo, E. López-Martínez, J. Berganza-Granda, F. Goñi-de Cerio and A. L. Cortajarena, Nanoscale Adv., 2021, 3, 1331–1341 RSC.
- L. Zhang and E. Wang, Nano Today, 2014, 9, 132–157 CrossRef CAS.
- M. P. de Lara-Castells, Small Struct., 2024, 2400147 CrossRef CAS.
- B. Ni, Y. Shi and X. Wang, Adv. Mater., 2018, 30, 1802031 CrossRef PubMed.
- M. Flytzani-Stephanopoulos and B. Gates, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 545–574 CrossRef CAS PubMed.
- M. Boronat, A. Leyva-Pérez and A. Corma, Acc. Chem. Res., 2014, 47, 834–844 CrossRef CAS PubMed.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- Z. Ou, Y. Li, W. Wu, Y. Bi, E. Xing, T. Yu and Q. Chen, J. Chem. Eng., 2022, 40, 132925 CrossRef.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef CAS.
- Q.-Y. Fan, Y. Wang and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 3891–3897 CrossRef CAS PubMed.
- Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458 CrossRef CAS PubMed.
- U. Mondal and P. Ghosh, Catal. Today, 2021, 370, 93–103 CrossRef CAS.
- P. López-Caballero, R. Garsed and M. P. de Lara-Castells, ACS Omega, 2021, 6, 16165–16175 CrossRef PubMed.
- A. O. Mitrushchenkov, A. Zanchet, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. A, 2021, 125, 9143–9150 CrossRef CAS PubMed.
- D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. López-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. J. Calvino, M. López-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, Chem.–Eur. J., 2023, 29, e202301517 CrossRef CAS PubMed.
- K. M. Krupka and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2024, 26, 28349–28360 RSC.
- M. Peng, C. Dong, R. Gao, D. Xiao, H. Liu and D. Ma, ACS Cent. Sci., 2021, 7, 262–273 CrossRef CAS PubMed.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- K. Zhang, X. Dou, H. Hou, Z. Zhou, M. Lopes-Haro, D. M. Meira, P. Liu, P. He and L. Liu, JACS Au, 2023, 3, 3213–3226 CrossRef CAS PubMed.
- S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908 CrossRef CAS.
- P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568 CrossRef.
- A. Zanchet, P. López-Caballero, A. O. Mitrushchenkov, D. Buceta, M. A. López-Quintela, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 27064–27072 CrossRef CAS PubMed.
- J. Garrido-Aldea and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 24810–24822 RSC.
- E. Fernández, M. Boronat and A. Corma, J. Phys. Chem. C, 2020, 124, 21549–21558 CrossRef.
- M. Gallego, A. Corma and M. Boronat, J. Phys. Chem. A, 2022, 126, 4941–4951 CrossRef CAS PubMed.
- A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901 CrossRef PubMed.
- X. Pan and X. Bao, Acc. Chem. Res., 2011, 44(8), 553–562 CrossRef CAS PubMed.
- X. Pan, Z. Fan, W. Chen, Y. Ding, H. Luo and X. Bao, Nat. Mater., 2007, 6, 507–511 CrossRef CAS PubMed.
- F. Zhang, F. Jiao, X. Pan, K. Gao, J. Xiao, S. Zhang and X. Bao, ACS Catal., 2015, 5, 1381–1385 CrossRef CAS.
- H. Wang, X. Zhang, W. Zhang, M. Zhou and H.-L. Jiang, Angew. Chem., 2024, e202401443 CAS.
- Y. Li, D. Shi, J. Yuan, R. Zuo, H. Yang, J. Hu, S. Hu, H. Sheng and M. Zhu, Adv. Mat., 2025, 37, 2412768 CrossRef CAS PubMed.
- S. Subudhi, S. P. Tripathy and K. Parida, Inorg. Chem. Front., 2021, 8, 1619–1636 RSC.
- J. Mann, V. Y. Doluda, C. Leonard, Y. B. Losovyj, D. G. Morgan, S. S. Bukalov, Z. Shifrina, B. D. Stein, N. Cherkasov, E. V. Rebrov, Z. D. Harms, M. Pink, E. M. Sulman and L. Bronstein, RSC Adv., 2016, 6, 75166–75177 RSC.
- L.-Q. Wang, H.-J. Li, J.-Q. Diao, D.-D. Hou, M.-M. Qiang and L.-J. Chen, Inorg. Chem. Commun., 2022, 140, 109425 CrossRef CAS.
- F. Liu, I. Rincón, H. G. Baldoví, A. Dhakshinamoorthy, P. Horcajada, S. Rojas, S. Navalón and A. Fateeva, Inorg. Chem. Front., 2024, 11, 2212–2245 RSC.
- A. Dhakshinamoorthy, Z. Li, S. Yang and H. Garcia, Chem. Soc. Rev., 2024, 53, 3002–3035 RSC.
- A. Dhakshinamoorthy, A. M. Asiri and H. García, Trends Chem., 2020, 2, 454–466 CrossRef CAS.
- D. Wang, G. Yang, Q. Ma, M. Wu, Y. Tan and Y. Yoneyama, ACS Catal., 2012, 2, 1958–1966 CrossRef CAS.
- V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044–7111 RSC.
- D. Farrusseng and A. Tuel, New J. Chem., 2016, 40, 3933 RSC.
- G. Riahi, D. Guillemot, M. Polisset-Thfoin, A. A. Khodadadi and J. Fraissard, Catal. Today, 2002, 72, 115 CrossRef CAS.
- L. Liu, U. Diaz, R. Arenal, G. Agostini, P. Concepcion and A. Corma, Nat. Mater., 2017, 16, 132–138 CrossRef CAS PubMed.
- L. Liu, M. Lopez-Haro, C. W. Lopes, C. Li, P. Concepcion, L. Simonelli, J. J. Calvino and A. Corma, Nat. Mater., 2019, 18, 866–873 CrossRef CAS PubMed.
- Z. Zhao, T. Zhang, Y. Feng, N. Wang and Q. Sun, J. Chem. Eng., 2024, 496, 154194 CrossRef CAS.
- N. Wang, Q. Sun, R. Bai, X. Li, G. Guo and J. Yu, J. Am. Chem. Soc., 2016, 138, 7484–7487 CrossRef CAS PubMed.
- M. Gallego, A. Corma and M. Boronat, J. Phys. Chem. A, 2022, 126, 4941–4951 CrossRef CAS PubMed.
- M. Gallego, A. Corma and M. Boronat, Phys. Chem. Chem. Phys., 2022, 24, 30044–30050 RSC.
- M. Gallego, A. Corma and M. Boronat, Phys. Chem. Chem. Phys., 2024, 26, 5914–5921 RSC.
- M. Gallego Rodríguez, Selective Oxidation of Methane into Methanol Using Sub-nanometre Copper Clusters: A Computational Study, 2024, DOI:10.4995/Thesis/10251/207338.
- Z. Jiang, X. Xu, Y. Ma, H. S. Cho, D. Ding, C. Wang, J. Wu, P. Oleynikov, M. Jia, J. Cheng and Y. Zhou, Nature, 2020, 586, 549 CrossRef CAS PubMed.
- M. P. de Lara-Castells, Small Struct., 2024, 5, 2400147 CrossRef CAS.
- M. P. de Lara-Castells, H. Stoll and A. O. Mitrushchenkov, J. Phys. Chem. A, 2014, 118, 6367–6384 CrossRef CAS PubMed.
- W. Busayaporn, X. Torrelles, A. Wander, S. Tomić, A. Ernst, B. Montanari, N. M. Harrison, O. Bikondoa, I. Joumard, J. Zegenhagen, G. Cabailh, G. Thornton and R. Lindsay, Phys. Rev. B, 2010, 81, 153404 CrossRef.
- R. F. Lobo, M. Tsapatsis, C. C. Freyhardt, S. Khodabandeh, P. Wagner, C.-Y. Chen, K. J. Balkus, S. I. Zones and M. E. Davis, J. Am. Chem. Soc., 1997, 119, 8474–8484 CrossRef CAS.
- D. Breck, Zeolite Molecular Sieves: Structure, Chemistry, and Use, Wiley, 1973 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1116 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- D. G. A. Smith, L. A. Burns, D. A. Sirianni, D. R. Nascimento, A. Kumar, A. M. James, J. B. Schriber, T. Zhang, B. Zhang, A. S. Abbott, E. J. Berquist, M. H. Lechner, L. A. Cunha, A. G. Heide, J. M. Waldrop, T. Y. Takeshita, A. Alenaizan, D. Neuhauser, R. A. King, A. C. Simmonett, J. M. Turney, H. F. Schaefer, F. A. Evangelista, A. E. DePrince, T. D. Crawford, K. Patkowski and C. D. Sherrill, J. Chem. Theory Comput., 2018, 14, 3504–3511 CrossRef CAS PubMed.
- K. Madajczyk, P. S. Żuchowski, F. Brzęk, L. Rajchel, D. Kędziera, M. Modrzejewski and M. Hapka, J. Chem. Phys., 2021, 154, 134106 CrossRef CAS PubMed.
- M. Hapka, P. S. Zuchowski, M. M. Szczęśniak and G. Chałasiński, J. Chem. Phys., 2012, 137, 164104 CrossRef PubMed.
- K. M. Krupka, A. Krzemińska and M. P. de Lara-Castells, RSC Adv., 2024, 14, 31348–31359 RSC.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH, 2011 Search PubMed.
- D. S. Kilin and D. A. Micha, J. Phys. Chem. C, 2009, 113, 3530–3542 CrossRef CAS.
- D. A. Micha, Adv. Quantum Chem., 2015, 71, 195–220 CrossRef CAS.
- D. A. Micha, Molecular Interactions: Concepts and Methods, Wiley, 2019, pp. 1–400 Search PubMed.
- D. S. Kilin and D. A. Micha, J. Phys. Chem. Lett., 2010, 1, 1073–1077 CrossRef CAS.
- T. Vazhappilly, D. S. Kilin and D. A. Micha, J. Phys. Chem. C, 2012, 116, 25525–25536 CrossRef CAS.
- R. H. Hembree, T. Vazhappilly and D. A. Micha, J. Chem. Phys., 2017, 147, 224703 CrossRef PubMed.
- T. Vazhappilly, D. S. Kilin and D. A. Micha, Phys. Chem. Chem. Phys., 2023, 25, 14757–14765 RSC.
- K. Ozawa, S. Yamamoto, R. Yukawa, R.-Y. Liu, N. Terashima, Y. Natsui, H. Kato, K. Mase and I. Matsuda, J. Phys. Chem. C, 2018, 122, 9562–9569 CrossRef CAS.
- M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119 RSC.
- T. Vazhappilly and D. A. Micha, J. Phys. Chem. C, 2014, 118, 4429–4436 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- Y. Tezuka, S. Shin, T. Ishii, T. Ejima, S. Suzuki and S. Sato, J. Phys. Soc. Jpn., 1994, 63, 347–357 CrossRef CAS.
- A. O. Mitrushchenkov and M. P. de Lara-Castells, ChemPhysChem, 2023, 24, e202300317 CrossRef CAS PubMed.
- M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804 CrossRef PubMed.
- A. J. Misquitta, R. Podeszwa, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2005, 123, 214103 CrossRef PubMed.
- A. Heßelmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 014103 CrossRef PubMed.
- S. E. Bogenrieder, J. Beßner, A. K. Engstfeld and T. Jacob, J. Phys. Chem. C, 2024, 128, 9693–9704 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1962, 36, 3428–3439 CrossRef CAS.
- C. Fonseca Guerra, J. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2003, 25, 189–210 CrossRef PubMed.
- P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853 RSC.
- P. López-Caballero, S. Miret-Artés, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Chem. Phys., 2020, 153, 164702 CrossRef PubMed.
- A. Jafarzadeh, K. M. Bal, A. Bogaerts and E. C. Neyts, J. Phys. Chem. C, 2019, 123, 6516–6525 CrossRef CAS.
- S. N. Mohammad, Nanotechnology, 2012, 23, 1–13 Search PubMed.
- M. Takeuchi, T. Kimura, M. Hidaka, D. Rakhmawaty and M. Anpo, J. Catal., 2007, 246, 235–240 CrossRef CAS.
- M. Takeuchi, M. Hidaka and M. Anpo, J. Hazard. Mater., 2012, 237–238, 133–139 CrossRef CAS PubMed.
- J. Fernández-Catalá, M. Sánchez-Rubio, M. Navlani-García, Á. Berenguer-Murcia and D. Cazorla-Amorós, ACS Omega, 2020, 5, 31323–31331 CrossRef PubMed.
- R. Sasikala, A. Shirole, V. Sudarsan, V. Kamble, C. Sudakar, R. Naik, R. Rao and S. Bharadwaj, Appl. Catal., A, 2010, 390, 245–252 CrossRef CAS.
- G. Liao, W. He and Y. He, Catalysts, 2019, 9, 502 CrossRef CAS.
- S. Anandan and M. Yoon, J. Photochem. Photobiol., C, 2003, 4, 5–18 CrossRef CAS.
- S. Liu, M. Lim and R. Amal, Chem. Eng. Sci., 2014, 105, 46–52 CrossRef CAS.
- M. N. Chong, Z. Y. Tneu, P. E. Poh, B. Jin and R. Aryal, J. Taiwan Inst. Chem. Eng., 2015, 50, 288–296 CrossRef CAS.
- Z. Jiang, X. Xu, Y. Ma, H. S. Cho, D. Ding, C. Wang, J. Wu, P. Oleynikov, M. Jia, J. Cheng, Y. Zhou, O. Terasaki, T. Peng, L. Zan and H. Deng, Nature, 2020, 586, 549–554 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Isosurfaces of the frontier orbitals in non-encapsulated Cu5–TiO2 nanoparticles at all computational levels, Bader charges, Cu–Cu and Cu–O distances, Cu–TiO5H6 complex used for a benchmark study, numerical values of Cu–TiO5H6 interaction energies at DFT-D3 and UMP2C levels, dipole moment vectors, orbital projection charge color plot in zeolite-encapsulated Cu5–TiO2 nanoparticles. See DOI: https://doi.org/10.1039/d4ra08633c |
| This journal is © The Royal Society of Chemistry 2025 |