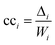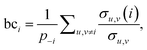Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Identify structures underlying out-of-equilibrium reaction networks with random graph analysis†
Éverton F.
da Cunha‡
ab,
Yanna J.
Kraakman‡
 c,
Dmitrii V.
Kriukov
c,
Dmitrii V.
Kriukov
 ab,
Thomas
van Poppel
a,
Clara
Stegehuis
ab,
Thomas
van Poppel
a,
Clara
Stegehuis
 *c and
Albert S. Y.
Wong
*c and
Albert S. Y.
Wong
 *ab
*ab
aDepartment of Molecules and Materials, Faculty of Science and Technology, University of Twente, Drienerlolaan 5, Enschede, 7522 NH, The Netherlands
bMESA+ Institute and BRAINS (Center for Brain-inspired Nano Systems), University of Twente, Drienerlolaan 5, Enschede, 7522 NH, The Netherlands
cDepartment of Mathematical Operation Research, Faculty of Electrical Engineering, Mathematics and Computer Science, University of Twente, Drienerlolaan 5, Enschede, 7522 NH, The Netherlands. E-mail: c.stegehuis@utwente.nl
First published on 8th January 2025
Abstract
Network measures have proven very successful in identifying structural patterns in complex systems (e.g., a living cell, a neural network, the Internet). How such measures can be applied to understand the rational and experimental design of chemical reaction networks (CRNs) is unknown. Here, we develop a procedure to model CRNs as a mathematical graph on which network measures and a random graph analysis can be applied. We used an enzymatic CRN (for which a mass-action model was previously developed) to show that the procedure provides insights into its network structure and properties. Temporal analyses, in particular, revealed when feedback interactions emerge in such a network, indicating that CRNs comprise various reactions that are being added and removed over time. We envision that the procedure, including the temporal network analysis method, could be broadly applied in chemistry to characterize the network properties of many other CRNs, promising data-driven analysis of future molecular systems of ever greater complexity.
Introduction
Complex networks describe the interactions between a vast number of components and are the foundation of many natural, societal, and technological phenomena.1 At the molecular level, interactions take place in networks based on DNA, proteins, or metabolites.2 The discovery of recurrent patterns in biochemical networks (i.e., network motifs),3 in particular, has sparked chemists to translate theoretical design principles that use feedback loops4,5 into practical molecular methods that enable the synthesis of out-of-equilibrium chemical reaction networks (CRNs).6,7 Despite significant progress, expanding the complexity in CRNs in a modular, theory-based way remains scarce.8One of the main difficulties in the synthesis of CRNs resides in the requirement of the integral approach, involving organic synthesis and mathematical modelling.9 Advances in systems chemistry—a subdiscipline at the interface of systems biology and supramolecular chemistry8—demonstrate that CRNs can be experimentally designed, rationalizing behaviour ubiquitous for living systems e.g., bistability,10–12 oscillations,13,14 and other transient behaviours.15–17 In all examples, mass-action models18 are used to support and validate their observed dynamics, demonstrating the need for mathematical modelling to guide the design of CRNs.19 Experimentally-designed CRNs (or, more generally, CRNs designed artificially by chemists), however, cannot always be accurately modelled using mass-action kinetics due to complexity of the reaction mechanisms involved as well as limitations in the determination of rate constants thereof.20 The experimental framework for CRNs with more complex behaviour21–23 is gaining ground rapidly, and novel approaches that can capture their dynamics are needed.
Alternatively, mass-action models can be represented by a bipartite graph with nodes representing chemical species and reactions. The mathematical foundation for so-called species–reaction graphs was introduced in the early 1970’s,24 and gained significant attention after Feinberg demonstrated that abstract graph theory can be applied to study interconnected chemical reactions.25,26 Bipartite graphs are commonly applied to represent CRNs,27,28 or to detect the lowest-energy paths in molecular transformations (wherein reaction mechanisms are treated as CRNs).29–31 In all examples, paths are used as network properties. Other network statistics (such as centrality, clustering and motifs) have been used to analyse CRNs that are large. In this context, biochemical networks32–34 and combustion networks35 are similar because they both comprise many intermediates, each with numerous reaction paths. When analysing network statistics, random graphs can provide a benchmark to filter out effects that are created by randomness. Overall, mathematical properties of the solutions of mass-action systems are strongly related to key properties of the CRNs that generate them, including their feedback interactions.36
Despite the advances in CRN theory, analyses of species–reaction graphs that are sufficiently informative to guide the design of CRNs for the synthesis-oriented chemist are scarce. An important distinction between the out-of-equilibrium reaction networks of interest to the systems chemist8–17 and the aforementioned networks, wherein reaction mechanisms are treated as CRNs,27–31,35 is that the first type of CRNs use intermediates that are stable and separable compounds whereas the second type of CRNs use intermediates that are short lived and cannot be separated as individual compounds. That is, while theory can take the perspective that thousands of reactions can be treated as similar, in practice, each class of reactions can have its own chemical rules.37,38 We need new methods to represent, collect and extract information to predict structures and functions of CRNs that are synthetically feasible. This is a non-trivial task as the design of CRNs requires expertise in chemical synthesis and graph analysis to create a foundation that takes into account the chemical and mathematical perspectives on how reactions become networks.
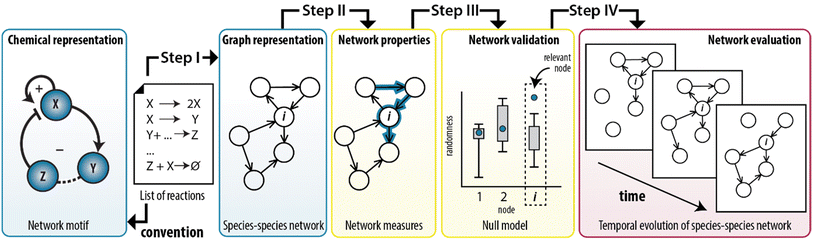
In this work, we show that we can combine the temporal dynamics of the CRN with the information provided by the graph to analyse the temporal behaviour of the network statistics. We developed a method that integrates the representation of CRNs as graphs with the application of network measures to model experimentally-designed CRNs (Fig. 1). Briefly, any chemical system can be described by a set of elementary reactions but to create insights into the system, chemists typically use conceptual models to visualize the interactions as positive and a negative feedback loops (Fig. 1, left panel). To illustrate, ESI, Fig. S1† shows a previously developed enzymatically-driven CRN for which a mass-action model was developed.13 Building on this foundation, we designed a procedure (illustrated in Fig. 1 as steps I–IV) that could translate the reactions in this model into a species–species network comprising of nodes and edges. This procedure not only allows for an explicit illustration of the relationships among the nodes, but also for the application of network measures commonly employed in network science. We show that measures for clustering and centrality could reveal the underlying network statistics important for the temporal existence of feedback loops. To the best of our knowledge, this is the first work that combines random graph theory with dynamics of out-of-equilibrium reaction networks.
Results and discussion
From elementary reactions to structure (step I)
The first step in the procedure encodes the enzymatic oscillator as a species–species network (ESI, S2†). In here, each edge represents a unique chemical conversion from one species to another represented by nodes. Our procedure transforms the set of elementary reactions into a network. The species are labeled as reactants, intermediates and products resulting in a total of 10 nodes; three reactants (Tg, Ap, Pro-I), six intermediates (Tr, Int-I, I, Tr·Tg, Tr·Pro-I, Ap·Int-I), and one product (P) that summarizes the species that do not contribute to the overall dynamics (the inhibited trypsin complex and hydrolysed inhibitors). Subsequently, we assigned a directed edge for each pair of species in an elementary reaction, with the direction of the edge indicating whether the species was consumed or produced. We note that multiple chemical conversions could take place between the same pair of species.39 To account for this multiplicity, we defined weights based on the number of edges assigned to each pair of species. ESI, Table S1† show the outputs of the algorithm applied on the enzymatic oscillator, where the final column (a so-called edge list) defines the species–species network: a graph with 10 nodes and 19 weighted edges (G1).Network properties of the enzymatic oscillator (step II)
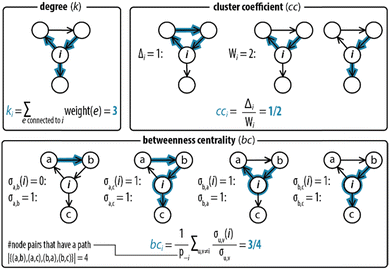
Next, step II in the procedure is to choose and adapt the network measure of interest. To illustrate, we chose three network measures2,40 (degree, clustering coefficient, and betweenness centrality, Fig. 2) commonly applied in network science. To account for the directed and weighted nature of the edges in our species–species network, we adapted these measures slightly.41,42 To be precise, the first measure, degree (ki), computes the sum of the weights of the edges connected to each node:ki = ∑e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) connectedto connectedto![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) iweight(e) iweight(e) |
The second measure, clustering coefficient (cci), investigates paths that form cycles between triples of nodes i, j and k. Such paths are called ‘feedback triangles’, and they are of the form i → j → k →i. The clustering coefficient computes the fraction of feedback triangles formed by the node with its neighbours. In particular,
The third measure, betweenness centrality (bci), computes the centrality of a node based on the shortest paths in the network: for every pair of nodes, node i may lie on the path with the least number of steps between these nodes. The bci outputs the fraction of nodes for which this is true. In particular,
Having established the foundation for the three network measures, we then applied the measures to characterize the species–species network (ESI, S3.1†). Crucially, the oscillator can only exist when the network is maintained under out-of-equilibrium conditions. Therefore, we introduced two nodes (source, S, and waste, W) to take the inflow of the reactants and the outflow of the products of the network into account. Fig. 3a shows that the graph for the CRN out-of-equilibrium (G2) comprises more nodes (12 instead of 10) and more weighted edges (32 instead of 19) than the graph for the CRN in equilibrium (G1). Details of the graphs are appended to ESI, Tables S1 and S2.†
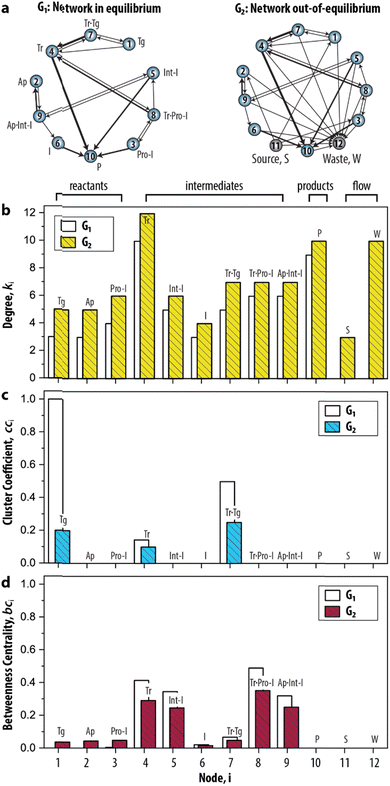 | ||
| Fig. 3 Static analysis of the species–species network of the enzymatic oscillator using network measures. (a) Graph-based models, or species–species networks, of the enzymatic oscillator in- and out-of-equilibrium. G, abbreviates graph. Source, S, is the node that accounts for the inflow of the reactants, and waste, W, is the node that accounts for the outflow of the products of the network. (b–d) Network measures applied on the enzymatic oscillator. Data are reported in ESI, Table S3.† | ||
In this CRN, the intermediates are nodes that on average have a higher contribution than other species to the connectivities in the graph, given that their degree (![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 4–9 = 7.1) is higher in comparison to the degree of the reactants (
4–9 = 7.1) is higher in comparison to the degree of the reactants (![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1–3 = 5.3) (Fig. 3b). The node 10 has an artificially high value (k10 = 10) because it summarizes several species as products. The degree for nodes 11 and 12 that represent the flow components, S (k11 = 3) and W (k12 = 10), reflects the inflow of the three reactants and outflow of ten species. That the node for Tr (i = 4) has the highest degree (k4 = 12) reflects the fact that the design of the CRN is built around the key enzyme Tr (see conceptual model in ESI, Fig. S1†).13
1–3 = 5.3) (Fig. 3b). The node 10 has an artificially high value (k10 = 10) because it summarizes several species as products. The degree for nodes 11 and 12 that represent the flow components, S (k11 = 3) and W (k12 = 10), reflects the inflow of the three reactants and outflow of ten species. That the node for Tr (i = 4) has the highest degree (k4 = 12) reflects the fact that the design of the CRN is built around the key enzyme Tr (see conceptual model in ESI, Fig. S1†).13
A different pattern emerges when we considered the cci (Fig. 3c). On the node for Tg (i = 1), for instance, cc1 = 0.2 as 1/5 of the wedges can create the feedback triangle representing the conversion of Tg into Tr (via the auto-activation, Tg → Tr, and autocatalytic steps, Tg + Tr = Tr·Tg → 2 Tr). For Tr·Tg, node 7, cc7 = 1/4 is slightly higher because it has the same number of triangles but one less wedge. The cci for 4, species Tr, is significantly lower (cc4 = 1/10) as this node has neighbours that are not shared with 1 and 7. Overall, we observed two distinct responses: a cci for any node is (i) non-zero for species that are involved in the positive feedback loop (Tg, Tr, and Tr·Tg), and (ii) zero for species that are not involved in the positive feedback loop. Notably, the auto-activation step was included as a side reaction in the mass-action model of the enzymatic oscillator as it was required to provide the initial activation of Tr.13 In this case, the auto-activation, plays a critical role as well, because it is required to complete the feedback triangle between 1, 4 and 7, making the numerator of cci non-zero.
The bci (Fig. 3d) shows that nodes 4 and 5 have the highest betweenness centrality value. This underscores the importance of the species Tr and Int-I to act as the key intermediates of the network. Surprisingly, the nodes 8, and 9—nodes for species which role in the oscillator is often neglected in the mass-action model, Tr·Pro-I and Ap·Int-I—also appear to share a similar high occurrence with which the species act as an intermediate between network connections. In contrast, species I (bc6 = 0.05) appears to have a less important role to sustain the network connectivity than anticipated in previous work.13 Other nodes with low values for bci are 1–3, and 7. The nodes for the reactants (i = 1–3) only appear on shortest paths that direct from an inflow (S). The node for Tr·Tg (i = 7) only lies on the shortest path corresponding to when Tg converts into Tr, explaining its similarly low betweenness value. Finally, the three nodes, i = 10–12, do not lie on any shortest path. bc10 is zero and validates that 10 summarizes species that do not contribute to the overall dynamics. bc11 and bc12 are zero is because edges are either directing from 11 (the source) or directing to 12 (the waste). Overall, that similar patterns for ki, cci, and bci were observed for G1 shows that the introduction of the nodes to account for the continuous inflow of reactants and outflow of products does not significantly alter the structural properties of the CRN.
The significance of network measures applied on the enzymatic oscillator (step III)
In step III of the procedure, the significance of the network measures is assessed by a random graph null model. This is important, as often the measured values depend, in unknown ways, on the CRN size, its edge density and other intrinsic system properties.43 For this reason, it is common in network science to compare statistics on a given network to randomized versions of the same network, to see whether they stand out, i.e., are significant.43 This approach has proven extremely successful in e.g., metabolic, genetic and protein networks,2 and we propose it can be applied to out-of-equilibrium networks relevant to systems chemistry. We developed a random graph null model to compare the statistics of G2 to randomized versions of the same species–species network. The procedure generates 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 randomized configurations of G2, under the condition that the degrees are fixed but connections are randomized. Subsequently, the cci and bci are applied to these randomized networks to determine the range of values that these measures can take (ESI, S3.2†). In other words, we provide a negative control for the measures applied on G2 (a so-called null hypothesis). In this way, we can identify which nodes show features that may be used to characterize the trypsin oscillator.
000 randomized configurations of G2, under the condition that the degrees are fixed but connections are randomized. Subsequently, the cci and bci are applied to these randomized networks to determine the range of values that these measures can take (ESI, S3.2†). In other words, we provide a negative control for the measures applied on G2 (a so-called null hypothesis). In this way, we can identify which nodes show features that may be used to characterize the trypsin oscillator.
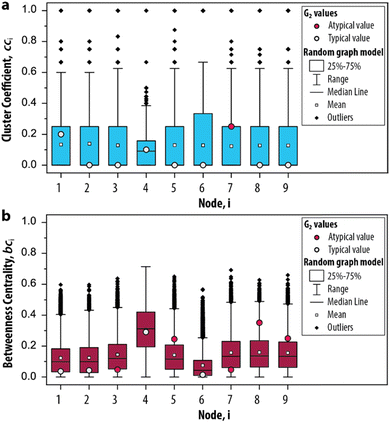
The possible values that the measures can take, given random conditions, are summarized as boxplots in Fig. 4a and b. The distributions for cci and bci based on the null model are compared with the values obtained for G2 to determine if its node occurs within the 25–75th percentile of the randomized networks (i.e., a typical value, depicted as a grey circle). A typical value indicates that the properties of the node would also appear if the CRN was driven by random processes. On the other hand, a node that is not within the 25–75th percentile (i.e., an atypical value, depicted as a red circle) indicates that their properties are different from an otherwise randomly assembled CRN. For the clustering coefficient, we found that only 7 appears to be atypical (Fig. 4a) and for the betweenness centrality, 3, 5, 7, 8 and 9 all appear atypical (Fig. 4b). The nodes 10–12 are excluded from this analysis as they did not contribute to the overall dynamics of the system. Hence, we identified the relevant set of nodes for the graph-based analysis of the enzymatic oscillator under out-of-equilibrium conditions. That is, for further analysis of the cluster coefficient there is only one relevant node (7) and for the betweenness centrality there are five nodes from which we can choose (3, 5, 7, 8 and 9).
Network measures applied on temporal behaviour (step IV)
Finally, in step IV of the procedure, the time-dependent dynamics of the network measures is analysed. This is done, since reactions take place all the time but at specific moments during the reaction trajectory certain ones are more prevalent (depending on the change in the concentration of the species involved in the reaction). Therefore, we simulated the CRN using the model described by ODEs. Fig. 5a shows the characteristic behaviour of the oscillator in time, wherein the concentration of key intermediates Tr, [Tr], and Int-I, [Int-I], oscillate with the same frequency. The simulated time series are used as input to represent the temporal evolution of the species to determine the addition or removal of edges in G2. Briefly, we considered that an outgoing edge can only exist when the associated node is present, and used a threshold to determine the presence of the nodes at each time interval (for details, see ESI S3.2†). To ensure that the sustained oscillations had established, our analysis starts from 50 h onwards.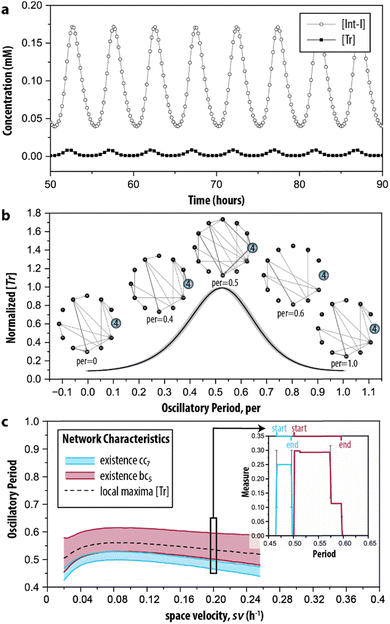 | ||
| Fig. 5 Time-dependent graph-based analysis. (a) Simulated time series of the enzymatic CRN wherein oscillations of key intermediates (Tr and Int-I) are sustained. See ESI, S3† for initial conditions. (b) The evolution of network G2 during the time required for completing a single oscillation (oscillatory period). The normalized [Tr] is determined by averaging five consecutive oscillations in (a). (c) The emergence of the cluster coefficient (cci) and betweenness centrality (bci) as a function of space velocity (sv), the parameter that determines the inflow and outflow of species. The insert shows the appearance of cc7 and bc5 during the oscillatory period under the conditions depicted in (b) (sv = 0.2 h−1). Extended materials include animated image sequence used in (b), and (c). | ||
During the development of each oscillation, different subgraphs of G2 were identified. Fig. 5b shows the behaviour of the CRN as a single oscillation with the oscillatory period ranging from 0 to 1. The inserts highlight the node for Tr (i = 4). At the local minima of the oscillation (per = 0 and per = 1) the node is only connected with one edge in the graph, whereas at the local maxima (per = 0.5), the node is connected with many edges. When transitioning from a minimum to a maximum (e.g., per = 0.4), edges are formed, but they disappear during the transition from a maximum to a minimum. Particularly, at per = 0.6 the node becomes disconnected from the graph. The extended set of ‘snapshots’ is appended to ESI, Fig. S4,† which shows that the discussed transitions are rather abrupt and that, remarkably, new edges are often being formed, even during per between 0.5 and 1. Hence, the network with all chemical interactions involved does not exist, and moreover, while the trend in the total number of reactions that are active may go up or down, the system still constantly adds and removes individual reactions.
The graph-based analysis was extended by determining when the clustering coefficient of 7 (cc7) and betweenness centrality of 5 (bc5) are non-zero during the oscillatory period. The cci and bci of the discussed example are indicated in the insert of Fig. 5c, which shows that cc7 could yield its maximal value of 1/4 only within per = 0.47–0.49 (thus, before the local maximum of the oscillation). The maximal value of 0.30 for bc5, instead, was found at a different interval, 0.5–0.58 (thus, when the oscillation started to decrease). We note that 7 was the only option for the temporal analysis of cci, and that 5 was chosen arbitrarily for the temporal analysis of bci. The latter can be substituted by any of the other relevant nodes identified in the random null model (3, 7, 8 and 9) without influencing the analysis.
Essentially, the clustering coefficient and betweenness centrality show if (and when) the desired feedback loops are acting on the network. Fig. 5c shows the impact of different initial conditions on network dynamics, measured by the appearance of the network measures cci and bci under a range of space velocities, sv—the parameter that determines the rate of inflow and outflow of species. The cci and bci cannot distinguish oscillations that are sustained or damped (ESI, Fig. S5†). To this end, we determined the intervals for their presence only for sv values within 0.02 h−1 ≤ sv ≤ 0.25 h−1, the conditions wherein oscillations are sustained. We found that the trajectories of cc7 and bc5 follow the pattern of the local maxima of the oscillation in [Tr] (dashed line). Fig. 5c shows the (dis)appearance of the connection with the intermediate inhibitor (i = 5), highlighting the emergence of the reactions important for a short, or efficient, pathway in G2. In this case, the edges that are present when bc5 reached its maximum value indicate that the connections crucial for the negative feedback loop are made. Therefore, bc5 appears when the oscillation decreases. Oppositely, the clustering coefficient allows for examining the existence of the positive feedback. In the case of this CRN, it was built on three species forming a feedback loop, and Fig. 5c indicates that it is present only in a narrow interval.
Conclusions
Graph-based analyses are widely used in literature for basic characterization of networks of any kind but have rarely been applied to experimentally-designed chemical reaction networks (CRNs). We have developed a method to characterize experimentally-designed CRNs, which we demonstrated based on an existing enzymatic network. The method comprises four steps: (I) represent a CRN as a graph to model the interactions as edges. (II) Apply network measures to provide the key characteristics of the structure underlying the CRN. (III) Identify the crucial nodes in the network using a random graph null model. (IV) Perform temporal analysis on the graph to reveal the evolution of the structure over time. This method allows us to analyse systems with out-of-equilibrium behaviour such as oscillations in which the standard CRN theory of does not apply. The integration of the expertises in system chemistry and random graph analysis ensured that the translation from a reaction scheme that defines the CRN into a graph as well as the opposite translation—from network measures into the chemical functioning of the CRN—was executable.The algorithm developed in this work can be used for translating many other synthetically-designed CRNs into species–species networks, providing ample opportunities to extend the analysis beyond the clustering coefficient and betweenness centrality and apply it to a larger set of out-of-equilibrium networks. Most of the current measures are built on the occurrence of specific network patterns of specified sizes,43 while in systems chemistry, similar structures such as feedback loops may result from differently sized network patterns. Characterizing CRNs with more complex feedback loops will require network measures capable of including longer and more diverse cycles. Furthermore, this may require constructing these models on more complex graph-like structures, such as hypergraphs,44,45 where it becomes possible to identify higher-order paths (known as hyperpaths). These hyperpaths provide a more detailed view of the feedback loops in complex interactions, capturing the intricate dependencies within the networked chemical system. Testing newly designed measures would require a broader training set of CRNs to assess their validity, underlining the need for developing such a database.46 We anticipate that our approach forms a foundation that may lead to training algorithms that can go beyond the synthesis of complex molecules47,48 and enable data-driven analysis of complex out-of-equilibrium reaction networks with ever greater complexity.
Methods
Software
NetworkX (an open source Python package for complex networks) was used as the computational data structure to develop the species–species networks and implement the network measures used in this work. Functions were encoded in Python and MATLAB®. The Python file CRN_network_tools.py contains most of the scripts: the CRN2NET algorithm, the measures, the temporal evolution of the measures, and the visualization. The Python files in the null_model folder contain the scripts used to create the null model. All Python scripts developed for this work contain detailed information on the functions in the comments. The Python environment can be setup with CRN_network_tools_env.yml. The MATLAB® files (*.m in enzymatic oscillator.zip) were used separately to simulate the time series of the CRN. A README.txt is included as a user guide to setup the computational environment and how to execute the scripts. A Jupyter Notebook file (Complex Network analysis of oscillatory CRN.ipynb) is provided to allow for an interactive interface for importing, generating and manipulating Python functions and data.Script development
Details on the development of the CRN2NET algorithm and application of the network measures on the enzymatic oscillator are appended to ESI S2 and S3,† respectively. ESI S3† includes the implementation of the network measures, development of the random graph null model, and network measures applied on temporal behaviour.Data availability
The data that support the findings of this study are available in the ESI† of this article. Source codes for the simulated data can be downloaded from https://doi.org/10.4121/ac3c7c42-f367-41d7-bd3b-fa54714b3a1b. The readme file provides instructions to run the codes, and produce the full dataset used in this work.Author contributions
A. S. Y. W. and C. S. conceived and supervised the project. É. F. C. designed and T. P. revised step I of the procedure. Y. J. K. implemented the measures and the null model analysis (step 2 and step 3). É. F. C. implemented and D. V. K. designed the codes for the temporal analysis (step 4). A. S. Y. W., C. S., É. F. C. and Y. J. K. wrote the manuscript. É. F. C. prepared the extended materials. All authors contributed to revising the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The project is supported by the Netherlands Organization for Scientific Research (NWO, OCENW.M20.379).References
- S. H. Strogatz, Exploring complex networks, Nature, 2001, 410, 268–276 CrossRef PubMed.
- A.-L. Barabási and Z. N. Oltvai, Network biology: understanding the cell's functional organization, Nat. Rev. Genet., 2004, 5, 101–113 CrossRef PubMed.
- R. Milo, S. Shen-Orr, S. Itzkovitz, N. Kashtan, D. Chklovskii and U. Alon, Network motifs: simple building blocks of complex networks, Science, 2002, 298, 824–827 CrossRef CAS PubMed.
- B. Novák and J. J. Tyson, Design principles of biochemical oscillators, Nat. Rev. Mol. Cell Biol., 2008, 9, 981–991 CrossRef.
- B. N. Kholodenko, Cell-signalling dynamics in time and space, Nat. Rev. Mol. Cell Biol., 2006, 7, 165–176 CrossRef CAS.
- J. H. van Esch, R. Klajn and S. Otto, Chemical systems out of equilibrium, Chem. Soc. Rev., 2007, 46, 5474–5475 RSC.
- G. Ashkenasy, T. M. Hermans, S. Otto and A. F. Taylor, Systems chemistry, Chem. Soc. Rev., 2017, 46, 2543–2554 RSC.
- Q. Wang, Z. Qi, M. Chen and D. Qu, Out-of-equilibrium supramolecular self-assembling systems driven by chemical fuel, Aggregate, 2021, 2, 1–15 CrossRef.
- A. S. Y. Wong and W. T. S. Huck, Grip on complexity in chemical reaction networks, Beilstein J. Org. Chem., 2017, 13, 1486 CrossRef CAS PubMed.
- S. N. Semenov, L. J. Kraft, A. Ainla, M. Zhao, M. Baghbanzadeh, V. E. Campbell, K. Kang, J. M. Fox and G. M. Whitesides, Autocatalytic, bistable, oscillatory networks of biologically relevant organic reactions, Nature, 2016, 537, 656–660 CrossRef CAS.
- F. Schnitter, B. Rieß, C. Jandl and J. Boekhoven, Memory, switches, and an OR-port through bistability in chemically fueled crystals, Nat. Commun., 2022, 13, 2816 CrossRef CAS PubMed.
- D. V. Kriukov, A. H. Koyuncu and A. S. Y. Wong, History dependence in a chemical reaction network enables dynamic switching, Small, 2022, 18, 2107523 CrossRef CAS PubMed.
- S. N. Semenov, A. S. Y. Wong, R. M. van der Made, S. G. J. Postma, J. Groen, H. W. H. van Roekel, T. F. A. de Greef and W. T. S. Huck, Rational design of functional and tunable oscillating enzymatic networks, Nat. Chem., 2015, 7, 160–165 CrossRef CAS PubMed.
- M. ter Harmsel, O. R. Maguire, S. A. Runikhina, A. S. Y. Wong, W. T. S. Huck and S. R. Harutyunyan, A catalytically active oscillator made from small organic molecules, Nature, 2013, 621, 87–93 CrossRef.
- J. Boekhoven, W. E. Hendriksen, G. J. M. Koper, R. Eelkema and J. H. van Esch, Transient assembly of active materials fueled by a chemical reaction, Science, 2015, 349, 1075–1079 CrossRef CAS.
- C. G. Pappas, I. R. Sasselli and R. V. Ulijn, Biocatalytic pathway selection in transient tripeptide nanostructures, Angew. Chem., Int. Ed., 2015, 127, 8237–8241 CrossRef.
- Q. Wang, H. Xu, Z. Qi, J. Mei, H. Tian and D.-H. Qu, Dynamic near-infrared circularly polarized luminescence encoded by transient supramolecular chiral assemblies, Angew. Chem., Int. Ed., 2024, 63, e202407385 CrossRef CAS PubMed.
- E. O. Voit, H. A. Martens and S. W. Omholt, 150 Years of the mass action law, PLoS Comput. Biol., 2015, 11, e1004012 CrossRef PubMed.
- J. E. Ferrell, T. Y.-C. Tsai and Q. Yang, Modeling the cell cycle: why do certain circuits oscillate?, Cell, 2011, 144, 874–885 CrossRef CAS PubMed.
- R. Bundschuh, F. Hayot and C. Jayaprakash, Fluctuations and slow variables in genetic networks, Biophys. J., 2003, 84, 1606–1615 CrossRef CAS PubMed.
- W. E. Robinson, E. Daines, P. van Duppen, T. de Jong and W. T. S. Huck, Environmental conditions drive self-organization of reaction pathways in a prebiotic reaction network, Nat. Chem., 2022, 14, 623–631 CrossRef CAS.
- B. Bartolec, A. Kiani, M. A. Beatty, M. Altay, G. M. Santiago and S. Otto, Selection of diverse polymorphic structures from a small dynamic molecular network controlled by the environment, Chem. Sci., 2022, 13, 14300–14304 RSC.
- M. G. Howlett, A. H. J. Engwerda, R. J. H. Scanes and S. P. Fletcher, An autonomously oscillating supramolecular self-replicator, Nat. Chem., 2022, 14, 805–810 CrossRef CAS.
- G. Oster and A. Perelson, Chemical reaction networks, IEEE Trans. Circuits Syst., 1974, 21, 709–721 CrossRef.
- M. Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors—I. The deficiency zero and deficiency one theorems, Chem. Eng. Sci., 1987, 42, 2229–2268 CrossRef CAS.
- M. Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors—II. Multiple steady states for networks of deficiency one, Chem. Eng. Sci., 1988, 43, 1–25 Search PubMed.
- P. L. Türtscher and M. Reiher, Pathfinder—navigating and analyzing chemical reaction networks with an efficient graph-based approach, J. Chem. Inf. Model., 2023, 63, 147–160 CrossRef.
- S. Stocker, G. Csányi, K. Reuter and J. T. Margraf, Machine learning in chemical reaction space, Nat. Commun., 2020, 11, 5505 CrossRef CAS PubMed.
- S. M. Blau, H. D. Patel, E. W. C. Spotte-Smith, X. Xie, S. Dwaraknath and K. A. Persson, A chemically consistent graph architecture for massive reaction networks applied to solid-electrolyte interphase formation, Chem. Sci., 2021, 12, 4931–4939 RSC.
- X. Xie, E. W. C. Spotte-Smith, M. Wen, H. D. Patel, S. M. Blau and K. A. Persson, Data-driven prediction of formation mechanisms of lithium ethylene monocarbonate with an automated reaction network, J. Am. Chem. Soc., 2021, 143, 13245–13258 CrossRef PubMed.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction mechanism generator: automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef.
- J. Yoon, A. Blumer and K. Lee, An algorithm for modularity analysis of directed and weighted biological networks based on edge-betweenness centrality, Bioinformatics, 2006, 22, 3106–3108 CrossRef PubMed.
- E.-Y. Kim, D. Ashlock and S. H. Yoon, Identification of critical connectors in the directed reaction-centric graphs of microbial metabolic networks, BMC Bioinform., 2019, 20, 328 CrossRef PubMed.
- E. Ravasz, A. L. Somera, D. A. Mongru, Z. N. Oltvai and A.-L. Barabási, Hierarchical organization of modularity in metabolic networks, Science, 2002, 297, 1551–1555 CrossRef PubMed.
- P. Zhao, S. M. Nackman and C. K. Law, On the application of betweenness centrality in chemical network analysis: computational diagnostics and model reduction, Combust. Flame, 2015, 162, 2991–2998 CrossRef.
- P. Y. Yu and G. Craciun, Mathematical analysis of chemical reaction systems, Isr. J. Chem., 2018, 58, 733–741 CrossRef.
- S. Szymkuć, E. P. Gajewska, T. Klucznik, K. Molga, P. Dittwald, M. Startek, M. Bajczyk and B. A. Grzybowski, Computer-assisted synthetic planning: the end of the beginning, Angew. Chem., Int. Ed., 2016, 55, 5904–5937 CrossRef.
- S. Müller, C. Flamm and P. F. Stadler, What makes a reaction network “chemical”?, J. Cheminform., 2022, 14(63), 1–24 Search PubMed.
- M. E. J. Newman, Networks, Oxford Univ. Press, 2010 Search PubMed.
- D. J. Watts and S. H. Strogatz, Collective dynamics of ‘small-world’ networks, Nature, 1998, 393, 440–442 CrossRef PubMed.
- O. Sinanoglu, Theory of chemical reaction networks. All possible mechanisms or synthetic pathways with given number of reaction steps or species, J. Am. Chem. Soc., 1975, 97, 2309–2320 CrossRef.
- U. Brandes, On variants of shortest-path betweenness centrality and their generic computation, Soc. Netw., 2008, 30, 136–145 CrossRef.
- A. Barrat, M. Barthélemy, R. Pastor-Satorras and A. Vespignani, The architecture of complex weighted networks, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 3747–3752 CrossRef CAS.
- F. Battiston, E. Amico, A. Barrat, G. Bianconi, G. F. de Arruda, G. Franceschiello, I. Iacopini, S. Kéfi, V. Latora, Y. Moreno, M. M. Murray, T. P. Peixoto, F. Vaccarino and G. Petri, The physics of higher-order interactions in complex systems, Nat. Phys., 2021, 17, 1093–1098 Search PubMed.
- Y. J. Kraakman and C. Stegehuis, Configuration models for random directed hypergraphs, arXiv, 2024, preprint, arXiv:2402.06466, DOI:10.48550/arXiv.2402.06466.
- S. Back, A. Aspuru-Guzik, M. Ceriotti, G. Gryn'ova, B. A. Grzybowski, G. H. Gu, J. Hein, K. Hippalgaonkar, R. Hormázabal, Y. Jung, S. Kim, W. Y. Kim, S. M. Moosavi, J. Noh, C. Park, J. Schrier, P. Schwaller, K. Tsuda, T. Vegge, O. A. von Lilienfeld and A. Walsh, Accelerated chemical science with AI, Digital Discovery, 2023, 3, 23–33 RSC.
- B. A. Grzybowski, T. Badowski, K. Molga and S. Szymkuć, Network search algorithms and scoring functions for advanced-level computerized synthesis planning, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2023, 13, 1–22 CrossRef.
- B. Mikulak-Klucznik, P. Gołębiowska, A. A. Bayly, O. Popik, T. Klucznik, S. Szymkuć, E. P. Gajewska, P. Dittwald, O. Staszewska-Krajewska, W. Beker, T. Badowski, K. A. Scheidt, K. Molga, J. Mlynarski, M. Mrksich and B. A. Grzybowski, Computational planning of the synthesis of complex natural products, Nature, 2020, 588, 83–88 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05234j |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |