Open Access Article
Open Access ArticleA machine learned potential for investigating single crystal to single crystal transformations in complex organic molecular systems†
Chengxi
Zhao
 *ab,
Honglai
Liu
a,
Da-Hui
Qu
*ab,
Honglai
Liu
a,
Da-Hui
Qu
 a,
Andrew I.
Cooper
a,
Andrew I.
Cooper
 b and
Linjiang
Chen
*cd
b and
Linjiang
Chen
*cd
aKey Laboratory for Advanced Materials, Joint International Research Laboratory of Precision Chemistry and Molecular Engineering, Feringa Nobel Prize Scientist Joint Research Center, Frontiers Science Center for Materiobiology and Dynamic Chemistry, School of Chemistry and Molecular Engineering, East China University of Science and Technology, Shanghai, China
bLeverhulme Research Centre for Functional Materials Design, Materials Innovation Factory, Department of Chemistry, University of Liverpool, Liverpool, UK. E-mail: chengxi.zhao@liverpool.ac.uk
cKey Laboratory of Precision and Intelligent Chemistry, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: linjiangchen@ustc.edu.cn
dSchool of Chemistry, School of Computer Science, University of Birmingham, Birmingham B15 2TT, UK
First published on 31st December 2024
Abstract
The packing of organic molecular crystals is often dominated by weak non-covalent interactions, making their in situ rearrangement under external stimuli challenging to understand. We investigate a pressure-induced single-crystal-to-single-crystal (SCSC) transformation between two polymorphs of 2,4,5-triiodo-1H-imidazole using machine learning potentials. This process involves the rearrangement of halogen and hydrogen bonds combined with proton transfer within a complex solid-state system. We developed a strategy to progressively approach the transition state along the phase transition path from both ends by using both the α and β crystal phases as initial structures for active learning. This method allowed us to develop a DFT-based machine learning potential that faithfully describes both of the stable phases and the transition processes. Our results demonstrate that these anisotropic interactions are represented accurately during molecular dynamic simulations. Bond breaking and reforming during proton transfer is observed and analysed in detail. This approach holds promise for simulating SCSC transitions in organic molecular crystals involving anisotropic interactions and chemical bond changes.
Introduction
Polymorphism refers to crystals that have identical chemical compositions but different molecular arrangements. Polymorphism is important because the physical and chemical properties of polymorphs can vary, even though the chemical components are the same.1–3 In some cases, transformations between two polymorphs may be triggered by external stimuli such as changes in temperature or pressure,4,5 leading to a rearrangement of the intermolecular interactions as the crystals adapt to new environmental conditions. Analysing and predicting polymorph transformations accurately is important in specific research fields, such as drug design or porous materials.Crystal structure prediction (CSP) has made significant progress in recent years and can be used to discover potentially novel crystalline forms.4,6 CSP serves as a valuable tool for detecting potential transformations and lowering the risk of encountering unknown crystalline forms.6–8 However, understanding polymorph transformations between stable structures in different energy basins is still challenging,9 especially for complex systems. New computational methods are needed here to capture missing details that can occur on femtosecond timescales, and which are largely inaccessible to experiments.
By applying molecular dynamics (MD) methods, researchers can gain a direct view of the dynamic evolution of solid-state transformations. Typically, the forces exerted on each particle—which are crucial for solving Newton's equations and obtaining trajectories of atoms and molecules over time—are given by empirically parameterized force fields. However, for some systems dominated by non-covalent interactions, it is still difficult if not impossible to provide a sufficiently accurate results using classical force fields.10–12
Both hydrogen bonding (HB) and halogen bonding (XB) are directional non-covalent interactions.13,14 For halogen bonds, a positive electrostatic potential exists along the R–X bonds (referred to as a σ-hole15), distinguishing this area from the negative electrostatic regions surrounding the halogen atom. This anisotropic charge distribution around halogen atoms makes it challenging to accurately represent halogen bonds using traditional atomic-point charges in classical force fields, which typically assume a spherical charge distribution. Additionally, accurate interaction calculations are necessary to model systems that containing a balance of hydrogen bonding, halogen bonding, and other weak interactions. It is also important to faithfully represent the potential bond breaking and reforming behaviours in specific systems. For example, crystals with short N–H⋯N distances are favourable for activating proton transfer between H-bonded molecules and can potentially exhibit ferroelectric properties.16Ab initio molecular dynamics (AIMD) based on density functional theory (DFT) can provide the required accuracy to achieve these goals. However, moderately sized simulation boxes containing large numbers of atoms/molecules are needed to simulate the properties of a system and to avoid potential size effects,17 making the time consuming DFT methods a bottleneck in these simulations.
Nowadays, machine learning (ML) has become widely adopted in solving high-dimensional problems. It has been demonstrated that ML can achieve high accuracy in predicting the energy of individual molecules and periodic systems, provided that the training involves a suitably large and accurate database.18–20 This makes the creation of such databases an important step. By using high-dimensional models, ML can address energies and forces without pre-assuming a specific functional form, allowing for calculations with high accuracy while keeping the computational timescale similar to force field levels. This allows ML methods to be applied to MD simulations that contain tens of thousands of atoms.21,22 Without fixed specification of bond types, ML could also handle arbitrary atomic configurations and enables bonds to break and reform during simulations, a feature particularly useful for simulating specific phenomenon like proton transfer. This makes machine learning potentials (MLP) a promising method for simulating systems such as thermal or pressure-induced polymorph transformations in complex systems.
Here, we focus on simulating organic molecular crystal polymorphs formed by 2,4,5-triiodo-1H-imidazole (tIIm) molecule, which can undergo single-crystal-to-single-crystal (SCSC) transformations under external pressure stimulation. The tIIm-β can transform into tIIm-α by decreasing pressure to atmospheric levels, while it reverts back to tIIm-β when the pressure is increased to 2 GPa. This process involves two types of anisotropic interaction—bond breaking and bond reforming—as well as interaction rearrangements, all in the same system. During the setup of the training dataset, we implemented a special active learning method that utilizes both tIIm-α and tIIm-β crystal phases as initial structures. This active learning approach gradually progresses towards the transition state along the transition path from both ends, resembling the construction of a bridge connecting two islands. By constructing an ab initio-based MLP that accurately reproduces energy and atomic forces obtained from DFT calculations, we were able to perform long duration, large-scale molecular dynamic simulations to investigate the thermal fluctuations of these two stable crystals and, hence, investigate the details of the SCSC transformation. This MLP model enabled us to accurately describe directional interactions, such as hydrogen bonding and halogen bonding, and to simulate proton transfer during MD simulations. This elucidated the details of the transformation from tIIm-β to tIIm-α. These results allowed us to use MLP to predict the SCSC transformation of an organic molecular crystal while maintaining accuracy at AIMD level. This opens new possibilities for understanding complex molecular crystal transformations.
Results and discussion
Analyses of tIIm molecule and crystals
The electrostatic potential (ESP) surface for tIIm is shown in Fig. 1a. This molecule contains both N–H and C–I bonds, which are typical HB/XB bonding donors, offering the potential for intermolecular HB/XB interactions in the solid state. As seen in the ESP surface, tIIm exhibits 3 positive regions along the extension of the C–I bonds, indicating the existing of σ-hole areas. The charge accumulation around the frontier atoms23 for these regions, Vs.max, are unequal and show ESP values of 33.09, 34.27 and 23.30 kcal mol−1 respectively. The space around the H atom also exhibits a positive region, with Vs.max = 56.67 kcal mol−1 at the extension of the N–H bond. By contrast, the nitrogen atom with its lone pair electrons shows a negative ESP area with Vs.min = −35.82 kcal mol−1 and can act as an acceptor.The tIIm crystal structures for phase α and β were obtained from the Cambridge Structural Database (tIIm-α: BOWRUC, tIIm-β: BOWRUC02) and geometry optimized. No significant geometry changes were observed during optimization, except for a slight change in the bond length of the N–H bond. Both tIIm-α and tIIm-β have one dimensional HB chains in unit cell that link different molecules. The N–H⋯N non-covalent bonds in these chains are around 1.7 Å in length, which suggests the potential for proton transfer between two adjacent nitrogen atoms.16 Non-covalent I⋯I interactions were also found in both polymorphs. In tIIm-α, both type I halogen⋯halogen interactions (θ1 = θ2) and type II halogen⋯halogen interactions (θ1 ≈ 180° and θ2 ≈ 90°, which is due to halogen bonding because of the σ-hole, Fig. S2†) coexist with the N–H⋯N bonds, which is rare because the weak interactions are not suppressed by the strong ones.14,24Fig. 1b and c shows the optimized crystal structures for tIIm-α and tIIm-β, with representative non-covalent interactions also highlighted using dot lines in the figures. For clarity, only I⋯I short contacts with angles close to the θ1 and θ2 definition are shown in Fig. 1.
Generation of training data and training process
The converged reference set consisted of 7774 periodic structures obtained from DFT calculations. These structures were obtained as follows: initial dataset calculations (iteration 1) were carried out through AIMD simulations at various temperatures (ranging from 300 to 1200 K) and pressures (ranging from 0 to 2 GPa) for both tIIm-α and tIIm-β phases. Supercells were employed, including 2 × 1 × 1 (216 atoms), 2 × 1 × 2 (432 atoms), and 2 × 2 × 1 (432 atoms) unit cells, to mitigate the significant mirror effect present in the original cell while simultaneously considering computational efficiency (see ESI† for further details). None of the original AIMD simulations led to any observable polymorph transformation or molecule disintegration. Subsequently, active learning was used to enhance the MLP model's performance. In each iteration, several MD simulations were performed using the current MLP model with a unit cell containing up to 432 atoms. Additionally, within the same iteration, MD simulations were conducted for both increase the pressure on tIIm-α and reduce the pressure on tIIm-β. Under-predicted images, including structures that were close to disintegration or had high deviations among different model during simulation, were identified and recomputed via DFT. These recalculated structures were then added to the dataset as references for training next iteration of the MLP model. This iterative improvement process (illustrated in Fig. 2, Active learning iteration section) was repeated until the model stabilized, with polymorph transformations were observed and no molecular disintegration was observed during MD simulations. In subsequent iterations (Fig. 2, Reinforcement section), the focus was on adding references primarily from images captured during the polymorph transformation process. We believed that these additional data would further reinforce the accuracy of the phase transition between tIIm-α and tIIm-β. In the final model training procedure, 5% of the reference data was used as a test set to prevent overfitting. The entire training process is illustrated in Fig. 2.Performance of machine learning potential model
The RMSE of the energies in the training set of the final model is 0.95 meV per atom, while that of the test set is 0.77 meV per atom. For the forces, the RMSE of the final model is 58.2 meV Å−1 for the training set and 58.0 meV Å−1 for the test set. These error ranges are comparable to those reported for the MLP models used in MD simulations for MOF-5.21 To assess the coverage of the training data, Fig. 3 displays the RMSE values for energy and force separately, with all reference data binned based on unit cell volume per atom. Across the entire volume per atom range, the RMSE for the energy is less than 1.5 meV per atom, and for force, it remains below 70 meV Å−1. The volume per atom value for the tIIm-α and tIIm-β phases are 25.86 Å3 per atom and 20.68 Å3 per atom, respectively, and these values are highlighted in red within the bar chart. The regions between and outside of the stable phases are all well trained.Various numerical representations are available for encoding structures and properties, enabling the measurement of similarity between crystal structures. These representations can be based on either structure-based descriptors, such as Smooth Overlap of Atomic Positions (SOAP),25 or properties-based descriptors such as pore-descriptors.6 SOAP descriptors encode atomic neighbour environments within a cutoff radius and proved highly effective at capturing the local chemical environment.26 Here we generated SOAP descriptor for all reference data, and employed Uniform Manifold Approximation and Projection (UMAP)27 as dimensionality reduction method to visualize the high-dimensional reference data in a 2D space. Fig. 3d illustrates the resulting mapping of all data after dimensionality reduction, where each point represents a crystal structure, and similar structures are positioned closer together.
The experimental polymorphs tIIm-α and tIIm-β are highlighted with red stars and they are separated on left and right sides of the plot respectively. On the left side an island is observed, consisting of structures with packing similar with tIIm-α, spanning the entire unit cell volume per atom range. This island extends from the bottom left to the top middle of the plot, with the experimental crystal located in the center of it. On the right side of the plot, a cluster with various density is formed by structures similar with tIIm-β. This cluster has a ribbon-like appearance due to the relatively small changes in volume and local atomic environments in the high-pressure structures compared to its low-pressure polymorph. Between these two islands, a bridge is formed by crystal structures undergoing the phase transition, indicating the explored transition structure space between different phases in high-dimensional space. All of these structures (transition structures and those similar to the tIIm-α and tIIm-β polymorphs) collectively form the dimension-reduction figure. The structures display a gradual increase in packing density from tIIm-α to tIIm-β, consistent with the experimental observations.
MD stability of tIIm crystal
We first tried the widely used classical force field Dreiding28 within Materials studio 2022 version29 as a reference method to simulate the experimental crystal structure of tIIm. Atomic charge were calculated using the charge equilibration (QEq) method.30 The results of the MD simulations revealed that the tIIm-α crystal experienced distortion under the classical force field, while the structure of tIIm-β could not remain stable under a pressure of 2 GPa. Additionally, proton transfer between N–H⋯N was impossible, as classical force field do not account for describe bond breaking and reforming. This limitation is critical because bond changes are essential for crystals with N–H⋯N hydrogen bonds, which may play a pivotal role in indicating ferroelectric properties through switchable bond polarization depending on the proton site.31 Fig. S6† illustrates the simulation results using the Dreiding force fields, indicating the need for other method to simulate this system.The stability of final MLP model was tested through a 1 ns NPT MD simulation at 300 K on both tIIm-α and tIIm-β crystal structures using a 2 × 1 × 2 unit cell containing 432 atoms, consistent with most of the system size in reference data. Throughout the simulation, structures of both tIIm-α and tIIm-β phase crystals remain stable apart from the expected thermal fluctuations typically observed. The lattice constants during the MD simulation is in good agreement with the experimental result obtained from single-crystal X-ray diffraction,5 as shown in Fig. 4. Expected HB and XB are maintained stable as their original bonding relationship throughout the simulation.
Next the simulation system was expanded to a 4 × 3 × 3 supercell containing 3888 atoms. The supercell was elongated four times along the A axis, as this direction is much shorter in the original cell compared to the other two axes. This system size is significantly larger than any unit cell sizes used in the reference set, and this stability test was used to demonstrate the scalability of this method. Despite the increased size of the simulation box, both tIIm-α and tIIm-β phase crystals remained stable throughout the simulation. Due to the larger simulation box, the variation in lattice parameters converted to the original cell size, was smaller compared to the 2 × 1 × 2 unit cell. Simulation result for both 2 × 1 × 2 cell and 4 × 3 × 3 large cell were consistent with each other, no significant difference is observed.
Proton transfer in tIIm crystal
In structures containing the imidazole moiety, protons can occupy disordered positions between two nitrogen atoms on different molecules, leading to hydrogen bond (HB) inversion from an N–H⋯N bond to N⋯H–N.32 This process involves rapid bond breaking and reforming, which is difficult to simulate using classical force field, as they preset and fix the bonding relationship for all atoms.We first investigate the proton transfer behaviour in a 2 × 1 × 2 unit cell during simulations. For each hydrogen atom, the difference in distance between hydrogen and its two adjacent nitrogen atoms were calculated over a 1 ns simulation. Proton transfer, including bond breaking and reforming, was observed for most hydrogen atoms during simulation, although most hopping events occurred in isolation and persisted for less than 1 ps before the proton hopping back. Fig. 5a and b shows a representative hydrogen atom exhibiting fast and isolated proton transfer.
The proton transfer behaviour in 4 × 3 × 3 large cell was also analysed. Fig. 5c illustrates one of the representative hydrogen atoms that undergo hopping between two adjacent nitrogen atoms. Trajectory analysis revealed that hydrogen position inversion occurred multiple times during simulation. When inversion involved only one isolated hydrogen atom, it quickly hops back to its original side. In contrast, when proton transfer affects all corresponding hydrogen position within the same N–H⋯N chain, the transfer could stabilize and persist for an extended period (Fig. 5c). The mechanism of concerted proton transfer observed in our simulation involves the simultaneous transfer of multiple protons. As shown in Fig. 5e, within the same HB chain, two nearby hydrogen atoms hop to adjacent nitrogen atoms within a short time frame at the beginning of the process. This configuration is more stable than isolated hydrogen hopping and can persist longer, even though its HB orientation is opposite to other HBs in the same chain. The junction molecules may either reverse their HB orientation or maintain their HB position until the connected HB chain either returns to its original state or the whole HB chain fully reverses. This competition process could last for several ps or even longer (Fig. 5e). Concerted proton hopping along a HB chain is only observed in tIIm-α crystal. We speculate that although the N⋯N distance in tIIm-β is shorter than tIIm-α, the H–N bonds are also shortened, making bond dissociation more difficult. To further study, we wrote a script to modify the initial input structures for both tIIm-α and tIIm-β. In this process, all the heavy atoms were kept at their original positions, while the hydrogen atoms were relocated to random side of adjacent nitrogen atom. In a 1 ns NPT MD simulation at 300 K, we found that in the tIIm-β structure, nearly all hydrogen atoms rearranged back to their original position within 17.5 ps and no concerted proton hopping was observed in the following simulation. In contrast, for tIIm-α, some HB chain become reverse and last for about 343 ps and new concerted proton hopping continuously occurring in the remaining simulation time (Fig. S7 and S8†).
Phase transitions between tIIm polymorph
Next, we simulated the phase transitions between different tIIm crystal phases. For this purpose, NPT MD simulations were performed to reproduce the phase transitions observed experimentally. The efforts to reproduce this process at 300 K failed, owing to the presence of a substantial energy barrier that cannot be easily overcome within ns scales at this temperature. As a result, were-run the simulations at a higher temperature (500 K) to overcome the energy barrier and successfully induce the phase transitions.The tIIm-β crystal with a 4 × 3 × 3 large cell was used as the initial structure, following a short equilibration period of 50 ps. The pressure was then gradually reduced from 2.0 GPa to 1.0 atmosphere over a 1 ns process, and maintained at 1.0 atmosphere for an additional 200 ps. To monitor the phase change, we defined an effective similarity metric to represent the chemical environment and compare the changes in crystal structure. Snapshots of the crystal structures were taken every 1 ps during the simulation. Each structure was encoded using the SOAP descriptor with an outer average kernel first and then normalization by each feature. The chemical environment difference was calculated using the following equation:
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i and
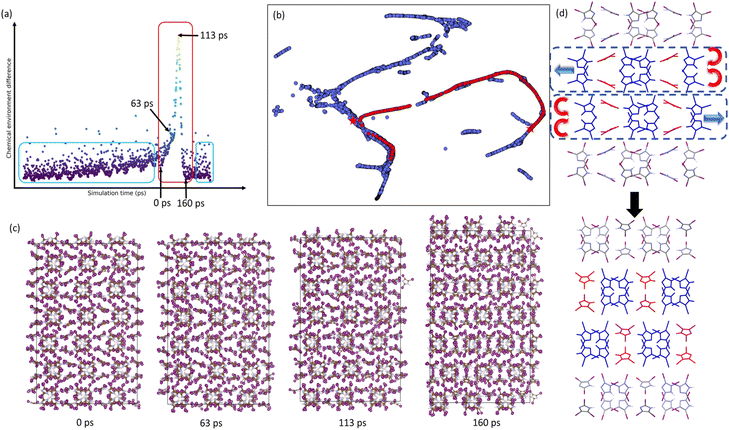
i and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j represent the descriptor of i-th and j-th snapshot respectively, n is a parameter used to control the comparison window of the dissimilarity measure, and n = 25 is used here. This equation provides a metric for measuring the dissimilarity between the i-th configuration and the configurations from i − n to i + n, allowing for a consistent comparison to determine when the structure begins to change. The relationship between chemical environment difference and simulation time is shown in Fig. 6a and S9.† Although the cell volume and non-covalent interaction distance changed due to the pressure reduce, structures within the blue box could be consider as the same phase since their chemical environment difference is rather small compare with adjacent snapshot. Some of the points outside the blue rectangle are attributed to hydrogen atoms shifting to different nitrogen at the specific snapshot. The phase transformation from tIIm-β to tIIm-α was observed (see red rectangle in Fig. 6a) and this was clearly detected by chemical environment difference measurement (Fig. S10† shows the packing similarity result).
j represent the descriptor of i-th and j-th snapshot respectively, n is a parameter used to control the comparison window of the dissimilarity measure, and n = 25 is used here. This equation provides a metric for measuring the dissimilarity between the i-th configuration and the configurations from i − n to i + n, allowing for a consistent comparison to determine when the structure begins to change. The relationship between chemical environment difference and simulation time is shown in Fig. 6a and S9.† Although the cell volume and non-covalent interaction distance changed due to the pressure reduce, structures within the blue box could be consider as the same phase since their chemical environment difference is rather small compare with adjacent snapshot. Some of the points outside the blue rectangle are attributed to hydrogen atoms shifting to different nitrogen at the specific snapshot. The phase transformation from tIIm-β to tIIm-α was observed (see red rectangle in Fig. 6a) and this was clearly detected by chemical environment difference measurement (Fig. S10† shows the packing similarity result).
The phase transition could be described as the following steps: as the pressure decreases, the cell volume of tIIm-β gradually enlarges without significant structural changes. At the beginning of phase transition, there is a sudden enlargement of the b-axis of unit cell (Fig. 6c and S11†). Subsequently, specific tIIm molecules (red molecules in Fig. 6d) rotate to form new non-covalent interaction networks and adjacent layers slip along the c-axis as illustrated in Fig. 6d.
To verify the influence of scale-effect, we performed a similar molecular dynamic process with a larger 8 × 5 × 5 supercell containing 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 atoms and reduced the pressure within 250 ps. The simulation result is consistent with previous results. Due to the larger system size, it was easier to observe that the layer slips occur simultaneously with molecule flips within a very short time (Fig. S12†).
920 atoms and reduced the pressure within 250 ps. The simulation result is consistent with previous results. Due to the larger system size, it was easier to observe that the layer slips occur simultaneously with molecule flips within a very short time (Fig. S12†).
The trajectory of simulation of 4 × 3 × 3 system was extracted every 1 ps, encoded with SOAP descriptors, and mixed with reference data. These were then projected onto a 2D space using UMAP embedding (Fig. 6b). The transformation pathway from tIIm-β to tIIm-α is depicted as a red path formed by scatter points on the plot. Despite the larger simulation unit cell size compared to the reference data, the points along the transition path are closely aligned with the DFT reference data in the SOAP space. Note that the initial structure of this MD simulation is the optimized tIIm-β, so the path starts from tIIm-β. However, tIIm-α is not perfectly along the path due to thermal fluctuations throughout the simulation.
A further test was performed to confirm the accuracy of the transition structures. Ten parallel MD simulations were performed using the transition structures (113 ps in Fig. 6a) as the initial configurations. Five of the simulations were set under the experimental conditions of tIIm-β (2 GPa), and the other five were set under the experimental conditions of tIIm-α. The results showed that, in the five simulations under the experimental conditions of tIIm-β, the transition structures transformed into tIIm-β. Similarly, under the experimental conditions of tIIm-α, the transition structures transformed into tIIm-α. Since the two systems were under different pressures, each transitioned into its respective crystal phase as expected.
Significant effort was dedicated to simulating the phase transition from tIIm-α to tIIm-β, but it was not observed when the pressure was increased to 2 GPa or higher. During the application of pressure, compression of the crystal, primarily along the a-axis, was observed, while the packing of the crystal remained unchanged. This outcome is consistent with the results of a 5 ps AIMD simulation at 2 GPa. We hypothesize that the system is trapped in a state that it is difficult to escape from within a ns timescale.
Conclusions
We used a novel method to construct a machine learning potential for studying transformations between organic molecular crystal systems. These systems, which involve halogen bonding, hydrogen bonding and proton transfer, present challenges that extend beyond traditional frameworks based solely on covalent bonding. By using data exclusively from DFT level calculation as reference, the constructed machine learning potential model successfully simulated the phase transition from tIIm-β crystal structure to tIIm-α. We demonstrated that MLP enables us to simulate and observe detailed aspects of transformation process, which were not captured in experiments, even when whole transition process was not directly observed in the original AIMD simulations. The entire transition process took approximately 160 ps to finish in a simulation involving 3888 atoms, which is unaffordable for traditional AIMD simulations to capture due to computational cost.The analysis of proton transfer demonstrated the bond-breaking and forming capabilities of our model. During the phase transformation, a specific change in halogen bonding from type-II to type-I was observed. This approach differs from traditional virtual site methods, allowing for the simulation of directional XB interactions with accuracy comparable to DFT calculations. Moreover, our model also enhances the simulation of HB interactions, as these are highly directional, and their orientation is critical in this system.
Since the packing in organic molecular crystals is governed by many weak interactions, simulating dynamic processes in such systems is both challenging and promising. Given the importance of these interactions, the ability to simulate experimental phenomena using only crystal structures is appealing when investigating new systems or predicting material structures for applications such as materials and drug design. This work presents a strategy for investigating complex systems involving hydrogen bonding, halogen bonding, and proton transfer. We believe that this approach is not limited to specific systems and could be applied as a more general method for researching solid phase transitions.
Methods
Density functional theory calculations
Periodic DFT calculations were carried out within the plane-wave pseudopotential formalism, using the Vienna ab initio simulation package (VASP) code version 5.4.4.33 Projector augmented-wave (PAW) method was applied to describe the electron–ion interactions.34 Generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional was adopted to treat electron interaction energy.35 Grimme's semi-empirical DFT-D3 scheme with Becke–Johnson damping functions was used here to give a better description of interactions.36–38A kinetic-energy cut-off of 600 eV was used to define the plane-wave basis set. Electronic Brillouin zone was integrated with the smallest allowed spacing between k-points (KSPACING) being 0.3 Å−1 and the generated grid is centred at the Γ-point. Convergence threshold of self-consistency was set to 10−5 eV during total energy and force calculation and the Hellmann–Feynman force convergence criterion on each atom was set to smaller than 0.02 eV Å−1 when geometry optimizations are needed.
Molecular dynamics
MD simulations were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package39 with a timestep of 0.5 fs using the implementation of the deepMD model. The temperature was controlled using a Nose–Hoover40,41 thermostat with a dumping parameters of 100 timesteps and the pressure was controlled using a Nose–Hoover barostat with a dumping parameters of 1000 timesteps.Machine learning model
The MLP models were constructed using DeepMD-kit20 implemented by Python/C++ and TensorFlow framework. In the descriptor part of the model, which maps atomic configuration to a set of symmetry invariant features, a hybrid descriptor was used contain both se_e2_a and se_e3. Both two descriptors are Deep Potential Smooth Edition (DeepPot-SE) type, the se_e2_a descriptor constructed from angular and radical information of atomic configurations and takes the distance between atoms as input, while se_e3 constructed from angular and radical information of atomic configurations too and takes the angles between two neighbouring atoms as input. The hidden layer side of se_e2_a embedding net is [15, 30, 60] with a 10 Å cut-off searching and se_e3 is [6, 12, 24] with a 8 Å cut-off searching. A ResNet is built between each hidden layers of these embedding net. The configuration of fitting net is [240, 240, 240] and a ResNet architecture is built between neighbouring layers. Both energy and force are used during the training.Visualization of the high-dimensional reference data
SOAP descriptor were generated for all atoms in the crystal structures using the DScribe package,42 with an averaging over the power spectrum of different sites. The maximum degree of spherical harmonics, number of radial basis functions and cutoff for local region is set to 6, 8 and 8 Å respectively. Subsequently, the UMAP27 technique was employed as dimensionality reduction algorithm on these numerical descriptors. Its purpose was to preserve the pair-wise distance structure among all data points and to preservation of local distances over global distances for all crystal structures. The Euclidean distances between SOAP vectors were used during the position generating stage of UMAP.Electrostatic potential surface
Geometry of tIIm is optimized by means of the hybrid M06-2X functional.43 For I atom, adjusted effective core potential basis set cc-pVDZ-PP was employed while cc-pVDZ is used for all other atom types.44,45 Grimme's D3 correction for dispersion was used during calculation. All calculation is carried out by Gaussian16 (ref. 46) software, analysed with Multiwfn47 and visualized with VMD.48Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
C. Z. performed the machine learning potential training, DFT calculation, data analyses and script writing. L. C. advised C. Z. on machine learning potential active learning methods. D. Q., A. I. C. and H. L. contributed to the discussions. L. C. conceived and supervised the project. C. Z., A. I. C. and L. C. led the writing of the manuscript with contributions from all co-authors.Conflicts of interest
The authors declare no competing interests.Acknowledgements
C. Z. acknowledges the financial support from the China Scholarship Council (No. 202106745008). H. L. acknowledge the financial support from the National Natural Science Foundation of China (No. 22378112). A. I. C. acknowledges funding from the Engineering and Physical Sciences Research Council (EPSRC; EP/N004884/1) and the Leverhulme Trust via the Leverhulme Research Centre for Functional Materials Design.References
- D. Gentili, M. Gazzano, M. Melucci, D. Jones and M. Cavallini, Polymorphism as an additional functionality of materials for technological applications at surfaces and interfaces, Chem. Soc. Rev., 2019, 48, 2502–2517 RSC.
- C. E. Shields, X. Wang, T. Fellowes, R. Clowes, L. Chen, G. M. Day, A. G. Slater, J. W. Ward, M. A. Little and A. I. Cooper, Experimental Confirmation of a Predicted Porous Hydrogen-Bonded Organic Framework, Angew. Chem., Int. Ed., 2023, e202303167 Search PubMed.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Ritonavir: an extraordinary example of conformational polymorphism, Pharm. Res., 2001, 18, 859–866 CrossRef.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo and C. J. Stackhouse, Functional materials discovery using energy–structure–function maps, Nature, 2017, 543, 657–664 CrossRef.
- K. W. Rajewski, M. Andrzejewski and A. Katrusiak, Competition between halogen and hydrogen bonds in triiodoimidazole polymorphs, Cryst. Growth Des., 2016, 16, 3869–3874 CrossRef.
- C. Zhao, L. Chen, Y. Che, Z. Pang, X. Wu, Y. Lu, H. Liu, G. M. Day and A. I. Cooper, Digital navigation of energy–structure–function maps for hydrogen-bonded porous molecular crystals, Nat. Commun., 2021, 12, 817 CrossRef.
- J. Hoja, H.-Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio Jr and A. Tkatchenko, Reliable and practical computational description of molecular crystal polymorphs, Sci. Adv., 2019, 5, eaau3338 CrossRef PubMed.
- D. McDonagh, C.-K. Skylaris and G. M. Day, Machine-learned fragment-based energies for crystal structure prediction, J. Chem. Theory Comput., 2019, 15, 2743–2758 CrossRef.
- P. W. Butler and G. M. Day, Reducing overprediction of molecular crystal structures via threshold clustering, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2300516120 CrossRef.
- D. Franchini, F. Dapiaggi, S. Pieraccini, A. Forni and M. Sironi, Halogen bonding in the framework of classical force fields: the case of chlorine, Chem. Phys. Lett., 2018, 712, 89–94 CrossRef.
- R. S. Paton and J. M. Goodman, Hydrogen bonding and π-stacking: how reliable are force fields? A critical evaluation of force field descriptions of nonbonded interactions, J. Chem. Inf. Model., 2009, 49, 944–955 CrossRef PubMed.
- J. Behler, First principles neural network potentials for reactive simulations of large molecular and condensed systems, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef PubMed.
- T. Steiner, The hydrogen bond in the solid state, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, The halogen bond, Chem. Rev., 2016, 116, 2478–2601 CrossRef PubMed.
- J. S. Murray, P. Lane, T. Clark and P. Politzer, σ-Hole bonding: molecules containing group VI atoms, J. Mol. Model., 2007, 13, 1033–1038 CrossRef PubMed.
- M. Andrzejewski, J. Marciniak, K. W. Rajewski and A. Katrusiak, Halogen and hydrogen bond architectures in switchable chains of di-and trihaloimidazoles, Cryst. Growth Des., 2015, 15, 1658–1665 CrossRef.
- D. P. Sellan, E. S. Landry, J. Turney, A. J. McGaughey and C. H. Amon, Size effects in molecular dynamics thermal conductivity predictions, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214305 CrossRef.
- A. P. Bartók and G. Csányi, Gaussian approximation potentials: a brief tutorial introduction, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- J. Behler, Constructing high-dimensional neural network potentials: a tutorial review, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef.
- H. Wang, L. Zhang, J. Han and E. Weinan, DeePMD-kit: a deep learning package for many-body potential energy representation and molecular dynamics, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef.
- M. Eckhoff and J. r. Behler, From molecular fragments to the bulk: development of a neural network potential for MOF-5, J. Chem. Theory Comput., 2019, 15, 3793–3809 Search PubMed.
- M. F. C. Andrade, H.-Y. Ko, L. Zhang, R. Car and A. Selloni, Free energy of proton transfer at the water–TiO2 interface from ab initio deep potential molecular dynamics, Chem. Sci., 2020, 11, 2335–2341 RSC.
- S. C. Van Der Lubbe, F. Zaccaria, X. Sun and C. l. Fonseca Guerra, Secondary electrostatic interaction model revised: prediction comes mainly from measuring charge accumulation in hydrogen-bonded monomers, J. Am. Chem. Soc., 2019, 141, 4878–4885 CrossRef PubMed.
- A. Mukherjee, S. Tothadi and G. R. Desiraju, Halogen bonds in crystal engineering: like hydrogen bonds yet different, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Erratum: on representing chemical environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 ( Phys. Rev. B , 2017 , 96 , 019902 ) CrossRef.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Big-data science in porous materials: materials genomics and machine learning, Chem. Rev., 2020, 120, 8066–8129 CrossRef PubMed.
- L. McInnes, J. Healy and J. Melville, Umap: uniform manifold approximation and projection for dimension reduction, arXiv, 2018, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, DREIDING: a generic force field for molecular simulations, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- D. S. Biovia, Material Studio 2022, Dassault Systemes, 2022 Search PubMed.
- A. K. Rappe and W. A. Goddard III, Charge equilibration for molecular dynamics simulations, J. Phys. Chem., 1991, 95, 3358–3363 CrossRef.
- M. Szafrański, A. Katrusiak and G. J. McIntyre, Ferroelectric order of parallel bistable hydrogen bonds, Phys. Rev. Lett., 2002, 89, 215507 CrossRef.
- S. Horiuchi, F. Kagawa, K. Hatahara, K. Kobayashi, R. Kumai, Y. Murakami and Y. Tokura, Above-room-temperature ferroelectricity and antiferroelectricity in benzimidazoles, Nat. Commun., 2012, 3, 1308 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, A density-functional model of the dispersion interaction, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef.
- S. Nosé, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Canonical dynamics: equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- L. Himanen, M. O. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, DScribe: library of descriptors for machine learning in materials science, Comput. Phys. Commun., 2020, 247, 106949 CrossRef.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016, vol. 3 Search PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc06467d |
| This journal is © The Royal Society of Chemistry 2025 |