Open Access Article
Open Access ArticleEffects of benzoheterocyclic annelation on the s-indacene core: a computational analysis†
Gabrielle I.
Warren
 ab,
Katarzyna
Młodzikowska-Pieńko
ab,
Katarzyna
Młodzikowska-Pieńko
 b,
Said
Jalife
b,
Said
Jalife
 c,
Isabella S.
Demachkie
c,
Isabella S.
Demachkie
 a,
Judy I.
Wu
a,
Judy I.
Wu
 c,
Michael M.
Haley
c,
Michael M.
Haley
 a and
Renana
Gershoni-Poranne
a and
Renana
Gershoni-Poranne
 *b
*b
aDepartment of Chemistry & Biochemistry and the Materials Science Institute, University of Oregon, Eugene, Oregon 97403, USA
bSchulich Faculty of Chemistry and the Resnick Sustainability Center for Catalysis, Technion – Israel Institute of Technology, Haifa 32000, Israel. E-mail: rporanne@technion.ac.il
cDepartment of Chemistry, University of Houston, Houston, Texas 77204, USA
First published on 18th November 2024
Abstract
Aromaticity and antiaromaticity are pivotal concepts in chemistry, with significant implications for molecular properties and reactivity. In particular, thanks to their increased conductivity and small HOMO–LUMO energy gaps, antiaromatic molecules are promising for use in organic electronics. The inherent instability of such molecules is often addressed by carbocyclic fusion, which also reduces the antiaromaticity of the core structure. Herein, we have employed a computational approach to explore the effects of heterocyclic fusion on the s-indacene core, focusing on three main aspects: the impact of the heteroatom, the heterocycle, and extended conjugation. We found that the heteroatoms themselves can substantially modulate antiaromaticity, and that the site of substitution plays a large role in the extent of stabilization afforded. Heterocycle fusion further modulates antiaromaticity, though to a lesser extent than the heteroatom effect. This effect diminishes upon benzannelation, highlighting the complexity of aromatic and antiaromatic interplay. Our findings offer a nuanced understanding of the factors affecting antiaromaticity in s-indacene-based polycyclic systems, providing a conceptual framework for predicting and tuning these properties for applications in organic electronics. This work underscores the importance of both substitution position and heterocyclic fusion in designing stable antiaromatic compounds.
Introduction
Aromaticity and its counterpart, antiaromaticity, are concepts that have provided a nonstop conundrum since they were first introduced into the chemical narrative.1,2 In addition to the conceptual interest these terms evoke, they also have practical utility, e.g., in the rationalization of molecular properties and reactivity. For example, the relationship between aromaticity and HOMO–LUMO energy gaps3 and, hence, conductance,4,5 has led to this concept having great importance in the field of organic electronics. In this regard, antiaromatic molecules are of particular interest because antiaromaticity correlates with higher HOMO and lower LUMO energy levels, smaller HOMO–LUMO energy gaps, and increased conductance,6–8 making them attractive targets for use in organic electronics. However, at the same time, antiaromaticity generally imparts instability, which makes these structures elusive or short-lived. As a result, synthetic methods to isolate and tune antiaromaticity remain relatively limited. One common strategy to overcome their inherent instability is to fuse aromatic components onto the antiaromatic cores; therefore, the majority of isolated antiaromatic systems are, in fact, polycyclic hybrids, which makes the characterization of their aromatic/antiaromatic behavior even more challenging.Leveraging this fusion strategy, different groups have explored ways to tune antiaromaticity in fused aromatic/antiaromatic compounds by varying the combinations of aromatic carbocycles or heterocycles and by changing the orientation in which the stabilizing components are fused onto the core.9–14 The Haley group has focused on exploring the antiaromaticity of s-indacene through annulation of additional rings onto the core in multiple orientations through the preparation of sets of structural isomers.15,16 In particular, fusion of various heterocycles has led to increases in the antiaromaticity of the s-indacene core.17,18
Nevertheless, a fundamental understanding of antiaromaticity modulation by heterocycle fusion has proven more elusive because polycyclic hydrocarbons, both aromatic and antiaromatic (PAHs and PAAHs, respectively), are complex cases that challenge our conceptual understanding of aromaticity as well as our tools for quantitative assessment of these properties. These systems are nuanced, often with a combination of local, semi-global, and global trends19 that are difficult to disentangle, especially if the molecules contain a mix of both aromatic and antiaromatic subunits. For example, annulation of aromatic rings to the outside of an antiaromatic system has afforded PAAHs suitable for materials applications,20–23 but these goals were achieved at the cost of significant loss of antiaromaticity in the core system.9,24,25 A better understanding of the interplay between aromatic and antiaromatic subunits is key to tuning the aforementioned properties associated with antiaromaticity.
To address these open questions, we initiated a computational investigation aimed at identifying the fundamental effects of heterocyclic fusion onto an antiaromatic core, using the quintessential s-indacene core as our antiaromatic template. To this end, we assembled a test set of molecules comprising an s-indacene core and various substituents: acyclic heteroatomic groups (‘acyclic’, Fig. 1, left), annelated heterocycles (‘annelated’, Fig. 1, center), and annelated benzoheterocycles (‘benzannelated’, Fig. 1, right). For each of these three types of substituents, we varied the orientation of the heteroatom with respect to the apical carbon of the five-membered ring of the s-indacene, thereby creating anti and syn isomers (Fig. 1, top and bottom, respectively). The dataset was designed to enable us to separate the effects of the heteroatom itself (1a–1f), the heterocycle (2a–2f), and extended conjugation on these scaffolds (3a–3f). In addition, the molecules are separated into anti (a–c derivatives) and syn (d–f derivatives) throughout, which enabled us to study the importance of substitution site. Herein, we present and discuss the different behavior of the molecules in terms of these three aspects and place these findings into a conceptual framework that allows understanding and prediction of such effects.
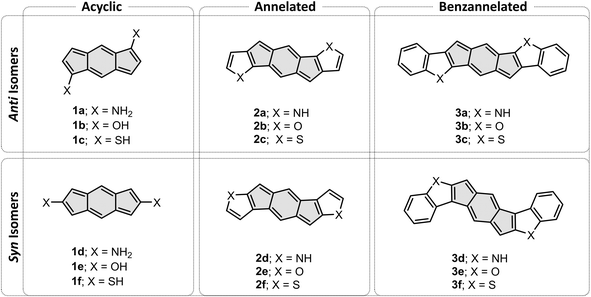 | ||
| Fig. 1 Dataset of acyclic systems (1a–1f), heterocyclic-fused s-indacenes (2a–2f), and benzoheterocycle-annelated s-indacenes (3a–3f). | ||
Computational methods
The geometries of all molecules were optimized at the CAM-B3LYP-26D3BJ27/def2-TZVP28,29 (or UCAM, if the wavefunction showed instability) level of theory using Gaussian 09.E01.30 The CAM-B3LYP functional has been specifically recommended for the study of aromatic and antiaromatic molecules, as its long-range-corrected component of the Hartree–Fock exchange effectively reduces delocalization errors.31 NICS(1)ZZ32–34 values were calculated at 1 Å above the centers of each rings along the Z-axis using the NICS-scan35 procedure, for which input files were generated using the Aroma program19,35,36 and performed with Gaussian using CAM-B3LYP/def2tzvp and the gauge-including atomic orbital (GIAO)37 method. This method is performed after aligning the molecule such that it is lying in the XY plane. In this position, the π-electron currents induced during NMR calculations are above and below this plane, which results in induced magnetic field parallel to the Z axis. Therefore, the ZZ component of the chemical shielding tensor is the most appropriate one to consider. Furthermore, using both the ZZ component and the NICS(1) value reduces inherent σ-contaminations, resulting in more appropriate π-electron currents that are a closer reflection of the magnetic aromaticity of the molecule.34,38,39 Current densities were calculated using SYSMOIC40 and NICS2BC41 plots were generated with BCWizard, using with the settings as described by Paenurk et al.41 for both types of plots (further information and input templates are provided in the ESI†). All π-density calculations were computed using an Extended Hückel population analysis42 as implemented in Gaussian16 version C.01.43Results
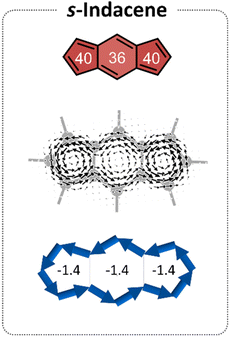
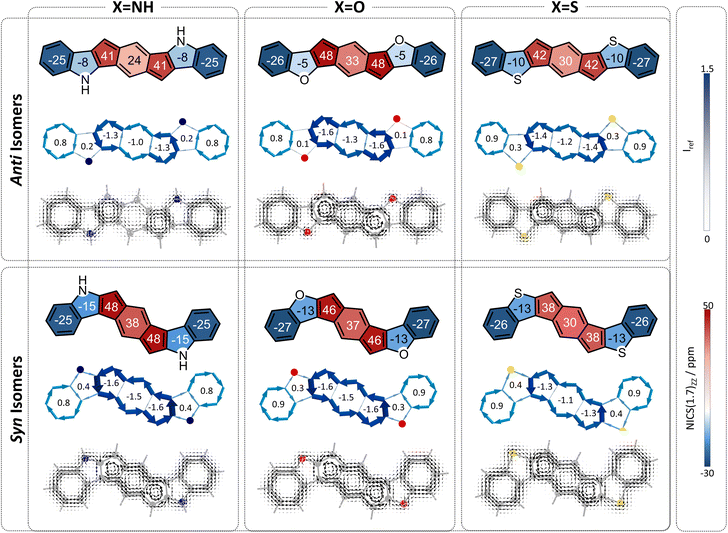
s-Indacene (Fig. 2) comprises a central six-membered ring (6MR) flanked by two 5-membered rings (5 MRs) and contains 12 π-electrons. Its magnetic antiaromatic character can be seen in the strong paratropic (counterclockwise) ring currents in each of the three rings as well as a global current along the periphery (Fig. 2, middle). A more quantitative evaluation and a clearer visualization of this magnetic antiaromatic behavior is provided by NICS(1)ZZ values (NICS(1)ZZ = 36 and 40 ppm, for the 6MR and 5MRs, respectively, compared with NICS(1)ZZ = −30 ppm for benzene, at the same level of theory) and generated NICS2BC plots, which translate the NICS values to bond currents (shown as blue arrows in Fig. 2, bottom). NICS2BC provides an additional quantitative metric, known as the weight, which reports the strength of the current relative to the current of benzene, calculated at the same level of theory. For s-indacene, the weights for all rings are w = −1.4, meaning, a ring current that is opposite in direction and 140% the strength of the ring current in benzene.Extension of the s-indacene core via fusion of additional rings has been shown to influence the core's magnetic behavior.25 When the annelated component is a benzene, it can be assumed that the changes arise from the modification of the π-conjugated system. However, when the annelated component is a heterocycle, it is unclear whether the effect is due to the nature of the heteroatom itself (e.g., its electronegativity), the extension of the π-system, or both. To answer this question, as well as provide further insight into the site-dependency of the effects (i.e., syn vs. anti annelation), we divided our analysis into three subsets, based on the different modifications to the s-indacene core. As shown in Fig. 1 and described above, these are the (a) acyclic, (b) annelated, and (c) benzannelated derivatives. The discussion herein follows the same division. For conciseness and clarity, we use the values of the 6MR of the indacene core in our discussion. The results for all rings are provided in the figures and the 5MRs show similar trends (albeit the NICS(1)ZZ values and weights in the 5MRs are generally larger, most likely due to the smaller radius of these rings).
s-Indacenes with acyclic heteroatomic substitution
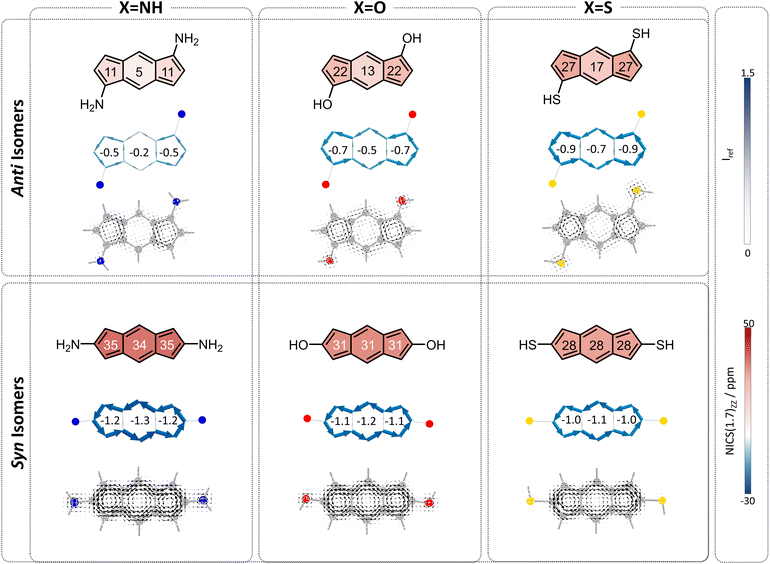
To begin, we computed a set of molecules (1a–1f) that are acyclic analogues of the annelated systems. By design, these systems are devoid of any competing/overriding effect that may come from a fused aromatic ring. In these theoretical systems, substitution at the 1,5-position of the s-indacene core mimics the anti-isomers (1a–1c) whereas substitution at the 2,6-position mimics the fully annelated syn-isomers (1d–1f).NICS(1)ZZ values and NICS2BC weights indicate that all substituted isomers 1a–1f are less antiaromatic than s-indacene. More interestingly, these metrics show that the magnitude of the effect is strongly dependent on the position of the substituent. Specifically, annelation at the 1,5-positions reduces the antiaromaticity of the s-indacene core substantially, from NICS(1)ZZ = 36 ppm to NICS(1)ZZ = 5, 13, 17 ppm and from w = −1.4 to w = −0.2, −0.5, −0.7 for the 6MR in 1a–1c, respectively (Fig. 3, top row). These results are further corroborated by SYSMOIC current density plots, which clearly depict the dramatic weakening of the paratropic current in the anti isomers, particularly within the 6MR. Placing the same groups at the 2,6-positions leads to a much milder reduction of antiaromaticity, to NICS(1)ZZ = 34, 31, 28 ppm and w = −1.3, −1.2, −1.1, respectively, for the 6MR in 1d–1e (Fig. 3, bottom row). Furthermore, the current density plots for these isomers show current patterns that are similar to the parent s-indacene.
Interestingly, for the syn set, the order of NICS(1)ZZ values/weights is S < O < N (i.e., S has the strongest effect on reducing the antiaromaticity of the core and N has the weakest), while for the anti set, the order is reversed: N < O < S, with the amino groups effectively rendering the core non-aromatic. Computed π-densities on the heteroatoms in 1a–1f (Table 1) indicate that the heteroatoms differ slightly between the anti and syn isomers, but the discrepancies do not seem large enough to explain the dramatic difference in the magnetic behavior of the isomers (e.g., the density on the oxygen is 1.87 and 1.90, in the anti and syn, respectively). This led us to hypothesize that the mechanism by which the heteroatom influences the core may be different, e.g., resonative versus inductive effects.
| Acyclic (1a–1f) | Annelated (2a–2f) | Benzannelated (3a–3f) | ||
|---|---|---|---|---|
| anti | X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N N |
1.69 | 1.46 | 1.52 |
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.87 | 1.72 | 1.77 | |
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
1.40 | 1.07 | 1.15 | |
| syn | X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N N |
1.76 | 1.47 | 1.55 |
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.90 | 1.73 | 1.78 | |
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
1.29 | 1.09 | 1.14 | |
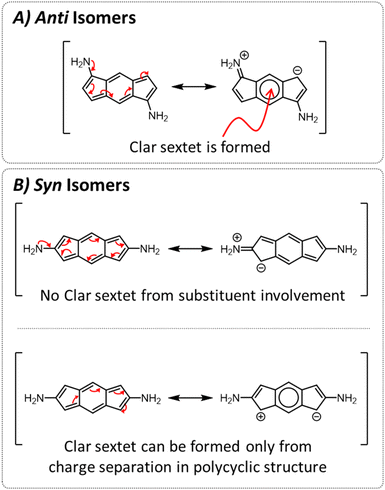
To test this hypothesis, we studied the resonance structures of the two types of species (Fig. 4). We found that for the anti isomers, by pushing electrons from the substituents, it is possible to draw resonance structures with a Clar sextet in the central ring of the s-indacene, which corroborates the sharp decrease in antiaromaticity that is observed most strongly in the 6MR for these systems. From the current density plots, it can be seen that the 5MRs continue to sustain local paratropic currents, but the global paratropic current is lost. This can also rationalize the observed order of N < O < S, as it is in agreement with the respective Hammett σ metrics of these substituents (−0.66, −0.37, 0.15 for NH2, OH, SH, respectively;44 Fig. S3 and S4 in the ESI† display the agreement graphically).
In contrast, for the syn isomers, pushing electrons from the substituent does not lead to the formation of a Clar sextet. In fact, the only way to obtain a Clar sextet in these species is by charge separation within the polycyclic framework, which would lead to an antiaromatic cyclopentadienyl cation that we expect to be highly disfavored. The lack of direct resonative participation of the substituent aligns with our observation that the syn isomers have a weaker attenuation of antiaromaticity and the patterns of current density remain the same as in the parent s-indacene. It may also explain the order of the effect, as the sulfur atoms are the most polarizable, which allows them to participate more effectively in electron delocalization.
Regardless of the underlying reason, the importance of the characterization of these acyclic species is to emphasize the sensitivity of the s-indacene core to substitution with heteroatoms. To the best of our knowledge, previous analyses have only focused on extension of the core via fusion of additional rings. These results now showcase that the heteroatom, by itself, can have a significant impact on the antiaromaticity of the core and that this effect is highly site-dependent.
s-Indacenes with heterocyclic annelation
Following our characterization of the acyclic model systems, we turned to examine the cyclized derivatives, 2a–2f. For these systems, it is necessary to consider two effects: the impact of the heteroatom and the impact of π-system extension. These effects may either contradict or reinforce one another. In our evaluation of the two effects, we rely on the parent s-indacene and the acyclic systems 1a–1f to provide reference points.First, we considered how cyclization may change the effect of the heteroatom on the s-indacene core. As a result of the cyclization, the lone pairs on the heteroatoms become part of the π-system, as is evident from the decrease in π-densities (Table 1). Although the π-densities are very similar for the anti and syn species, we can expect that this reduction will affect the species differently, because of their different mechanisms of stabilization. For the anti species, this should lead to a reduction in the ability of the heteroatom to donate electrons into the core. Consequently, the attenuation of antiaromaticity is expected to decrease and the s-indacene core should display higher positive NICS values. In contrast, for the syn species, the heteroatom effect does not appear to strongly rely on the lone pairs (i.e., π-density). Nevertheless, other effects, such as changing the hybridization from sp3 to sp2, can modulate the electron-withdrawing nature of the atoms, causing a (small) reduction in their impact on the s-indacene core.
Second, we considered the effect of extending the π-system. In this case, the extension is achieved by annelating an additional ring to the core; thus, we use here the term “neighboring ring effect” as shorthand. When two components of opposite aromatic character are fused together, it is often the case that both experience a decrease in their respective behavior. This can be seen, for example, in the case of biphenylene, in which the two benzene rings become essentially non-aromatic and the central cyclobutadiene ring displays substantially reduced antiaromaticity.19 Although the system loses some (or most) of the aromatic stabilization energy afforded by the benzene units, overall it is stabilized by attenuating the antiaromaticity of the cyclobutadiene unit. A similar situation is seen in the case of unsymmetric bis(antiaromatics),45 and it stands to reason that the same holds true when adding a heterocycle to the s-indacene core. The s-indacene core features a paratropic ring current, whereas the heterocycle features a diatropic one. Accordingly, we expected that both the antiaromaticity of the central core and the aromaticity of the heterocycle will be reduced. As opposed to the heteroatom effect, here the specific site of annelation is not of primary importance, meaning that a similar effect is expected for both anti and syn cases.
The overall behavior of each individual system is the sum of these two effects. In all cases, both of the effects serve to attenuate antiaromaticity, and therefore we expect the s-indacene core to display NICS(1)ZZ values and weights that are lower than the parent s-indacene. The difference is in comparison to the respective acyclic cases. The acyclic anti species have a strong heteroatom effect, which is weakened by the cyclization of the substituent. If the neighboring ring effect is strong, it may replace this loss and the low antiaromaticity will be retained; if it is relatively weak, then the result will be intermediate antiaromaticity. The computed NICS values and weights show intermediate values (Fig. 5), indicating that the loss of the heteroatom effect is more costly than the gain of the neighboring ring effect: NICS(1)ZZ = 21, 26, 21 ppm and w = −0.8, −1.0, −0.8 for the 6MR in 2a–2c. Most notably, the N-containing system displays the largest regain of antiaromaticity, which aligns with this heterocycle having the strongest aromaticity of the three. Altogether, the antiaromaticity of the N-containing system is largely restored, after being essentially rendered nonaromatic in the acyclic species, as is corroborated by the current density plots (Fig. 5, top row).
In contrast, the acyclic syn species 1d–1f have a relatively weak heteroatom effect that is not expected to change upon cyclization. Thus, for the cyclized species, the addition of the attenuating neighboring ring effect should lead to further decreased antiaromaticity. Indeed, we calculated NICS(1)ZZ = 26, 29, 22 ppm and w = −1.0, −1.1, and −0.8, for 2d–2f, respectively (Fig. 5, bottom row).
s-Indacenes with benzoheterocyclic annelation
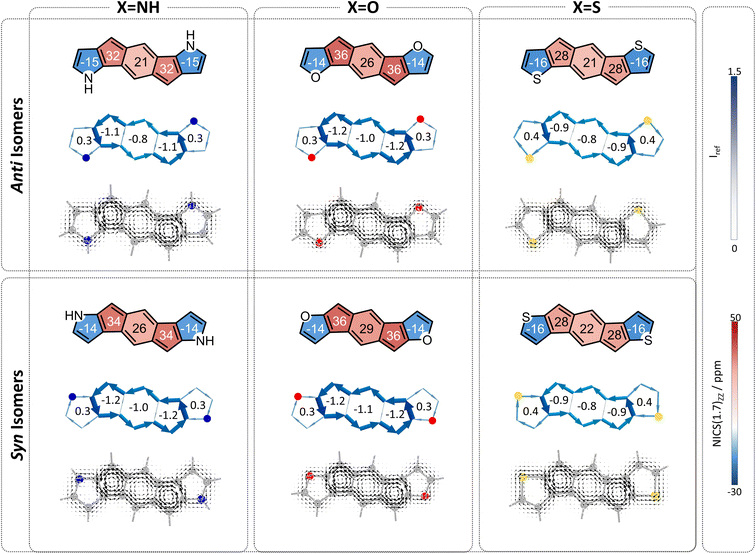
Finally, we turned our attention to the third family of compounds, 3a–3f, which feature further π-conjugation extension in the form of an additional benzene ring annelated to the heterocycle. Once again, we considered the impact of this structural change on both the heteroatom effect and the π-extension effect. Although formally still fully conjugated, the addition of a benzene ring to a heterocycle is known to reduce the delocalization within the five-membered ring.46,47 As Wu and coworkers recently showed using π-densities, the N atom in indole is more amine-like than in pyrrole.14 This is also true for our systems, as shown by the π-densities in Table 1, as well as the NICS(1)ZZ values and SYSMOIC plots (Fig. 6), which indicate a strong diatropic current localized within the benzene unit and a much weaker one sustained in the five-membered ring. The weakening of the ring current in the five-membered ring is expected to impact both the heteroatom effect and the so-called neighboring ring effect.Regarding the behavior of the heteroatom, the decrease in cyclic delocalization causes the heteroatoms to regain some small degree of “acyclic” behavior, as shown by computed π-densities (Table 1); however, they still remain closer in character to the cyclized systems 2a–2f than to the acyclic 1a–1f. In other words, despite the strong impact on the local aromaticity of the heteroatom, benzannelation has a relatively minor impact on the heteroatom effect. While this has a negligible impact on the syn molecules, for the anti molecules this leaves the heteroatoms largely unable to alleviate antiaromaticity. In terms of the delocalization effect, we expect that the weakening of the current will reduce the neighboring ring attenuation, resulting in an increase in the antiaromaticity of the s-indacene core, in both syn and anti species.
Overall, we expect the anti systems to display an increase in antiaromaticity, due to the loss of the neighboring ring effect combined with the loss of the heteroatom effect, both of which serve to alleviate antiaromaticity. Because the heteroatoms regain some degree of acyclic behavior, the antiaromaticity is expected to be somewhat lower than the parent s-indacene. The computed NICS values align with this expectation, NICS(1)ZZ = 24, 33, 30 ppm for 3a–3c, respectively (Fig. 6, top row). The syn systems, which are mostly affected by the loss of the neighboring ring effect, are also expected to show increased antiaromaticity. As demonstrated by the NICS values (NICS(1)ZZ = 38, 37, 30 ppm for 3d–3f, respectively), these systems essentially revert to the antiaromatic character of the parent s-indacene, and in some cases (3d, 3e) even slightly more antiaromatic (Fig. 6, bottom row).
Conclusions
In this work, we explored the impact of benzoheterocycle annelation on an antiaromatic core, by monitoring the magnetic (anti)aromaticity of s-indacene derivatives using the NICS(1)ZZ metric and current density maps. Previous work had shown that extending the π-system of s-indacene through heterocycle or benzoheterocycle annelation leads to modification of the antiaromatic character of the core; however, it had not been established whether this is a result of the π-system extension or the presence of the heteroatom. Our test set of molecules was designed to enable elucidation of the specific effects of the heteroatom and its substitution position, the heterocycle, and the further extension of π-conjugation.First and foremost, we found that the heteroatom itself can have a dramatic effect on the antiaromaticity of the core: placing uncyclized heteroatoms at the 1,5-positions (i.e., the anti isomers) affords the greatest extent of antiaromaticity alleviation, leading in the case of the N-substituted s-indacene 1a to almost complete loss of antiaromatic character. Second, we established that this effect is highly site-specific. Using resonance structures, we were able to rationalize this site-sensitivity by showing that the anti position enables the substituent to resonatively interact with the core while the syn position does not. Third, by comparing the two types of isomers we found that the extension of the π-system by heterocycle annelation does indeed alleviate the antiaromaticity of the core, although it is a weaker effect than the resonative heteroatom effect. Finally, we demonstrated that this effect is dampened by the addition of another (benzene) ring.
Overall, this work has shown that the reduction in antiaromaticity in the anti isomers is primarily a heteroatom effect, which is weakened by cyclization and further benzannelation. In contrast, for the syn isomers, the heteroatom effect is weak and the majority of antiaromaticity alleviation is achieved by the neighboring ring effect. However, further benzannelation cancels this, allowing the s-indacene to regain its full antiaromaticity. Not unexpectedly, the trends in antiaromatic behavior show an agreement with the HOMO–LUMO energy gap, whereby the gap decreases as antiaromaticity increases (see ESI Fig. S1 and S2†), underlining that such analysis may be beneficial in the design of new functional molecules for (opto)electronic uses.
Data availability
The data supporting this article have been included in the main text or as part of the ESI.† All software used in the generation of the data has been specified, and input templates have been provided in the ESI† to facilitate reproduction of any and all computations.Author contributions
RGP and MMH conceived the idea. GIW and KM-P performed the calculations and analyzed the data with RGP. ISD provided scientific input. SJ and JIW performed the π-density computations. RGP and GIW wrote the manuscript and created graphics, with editorial assistance from MMH and KMP.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was generously supported by the National Science Foundation (CHE-2246964 to M. M. H. and CHE-2303851 to J. I. W.). J. I. W. thanks the Alfred P. Sloan Research Foundation (FG-2020-12811) for support and the Research Computing Data Core at the University of Houston for computational resources. This work benefited from access to the University of Oregon high performance computing cluster, Talapas, and the Technion computational clusters, Zeus and Nyx. The authors are deeply indebted to Dr Sabyasachi Chakraborty, Mr Itay Almog, and Dr Alexandra Tsybizova for their help with computations and for fruitful discussions. R. G. P. is a Branco Weiss Fellow and a Horev Fellow. K. M.-P. is an Azrieli postdoctoral fellow supported by the Azrieli Foundation.Notes and references
- M. Solà, Front. Chem., 2017, 5, 22 CrossRef.
- G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569–5576 RSC.
- R. Gershoni-Poranne, A. P. Rahalkar and A. Stanger, Phys. Chem. Chem. Phys., 2018, 20, 14808–14817 RSC.
- W. Chen, H. Li, J. R. Widawsky, C. Appayee, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2014, 136, 918–920 CrossRef PubMed.
- T. Stuyver, M. Perrin, P. Geerlings, F. De Proft and M. Alonso, J. Am. Chem. Soc., 2018, 140, 1313–1326 CrossRef PubMed.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002 CrossRef.
- R. Breslow and F. W. Foss Jr, J. Phys.: Condens. Matter, 2008, 20, 374104 CrossRef.
- R. Breslow, J. Brown and J. J. Gajewski, J. Am. Chem. Soc., 1967, 89, 4383–4390 CrossRef.
- J. Cao, G. London, O. Dumele, M. Von Wantoch Rekowski, N. Trapp, L. Ruhlmann, C. Boudon, A. Stanger and F. Diederich, J. Am. Chem. Soc., 2015, 137, 7178–7188 CrossRef.
- T. Gazdag, P. J. Mayer, P. P. Kalapos, T. Holczbauer, O. El Bakouri and G. London, ACS Omega, 2022, 7, 8336–8349 CrossRef.
- P. K. Sharma, D. Mallick, H. Sharma and S. Das, Org. Lett., 2023, 25, 2201–2206 CrossRef.
- J. Usuba, M. Hayakawa, S. Yamaguchi and A. Fukazawa, Chem.–Eur. J., 2021, 27, 1638–1647 Search PubMed.
- T. Xu, X. Hou, Y. Han, H. Wei, Z. Li and C. Chi, Angew. Chem., Int. Ed., 2023, 62, e202304937 CrossRef PubMed.
- S. Jalife, A. Tsybizova, R. Gershoni-Poranne and J. I. Wu, Org. Lett., 2024, 26, 1293–1298 CrossRef.
- C. K. Frederickson, B. D. Rose and M. M. Haley, Acc. Chem. Res., 2017, 50, 977–987 CrossRef.
- J. L. Marshall, K. Uchida, C. K. Frederickson, C. Schütt, A. M. Zeidell, K. P. Goetz, T. W. Finn, K. Jarolimek, L. N. Zakharov, C. Risko, R. Herges, O. D. Jurchescu and M. M. Haley, Chem. Sci., 2016, 7, 5547–5558 RSC.
- G. I. Warren, J. E. Barker, L. N. Zakharov and M. M. Haley, Org. Lett., 2021, 23, 5012–5017 CrossRef PubMed.
- J. E. Barker, T. W. Price, L. J. Karas, R. Kishi, S. N. MacMillan, L. N. Zakharov, C. J. Gómez-García, J. I. Wu, M. Nakano and M. M. Haley, Angew. Chem., Int. Ed., 2021, 60, 22385–22392 CrossRef PubMed.
- R. Gershoni-Poranne and A. Stanger, Chem.–Eur. J., 2014, 20, 5673–5688 CrossRef PubMed.
- J. Wang, M. Chu, J.-X. Fan, T.-K. Lau, A.-M. Ren, X. Lu and Q. Miao, J. Am. Chem. Soc., 2019, 141, 3589–3596 CrossRef CAS PubMed.
- C. Liu, S. Xu, W. Zhu, X. Zhu, W. Hu, Z. Li and Z. Wang, Chem.–Eur. J., 2015, 21, 17016–17022 CrossRef.
- A. M. Zeidell, L. Jennings, C. K. Frederickson, Q. Ai, J. J. Dressler, L. N. Zakharov, C. Risko, M. M. Haley and O. D. Jurchescu, Chem. Mater., 2019, 31, 6962–6970 CrossRef.
- J. Sprachmann, T. Wachsmuth, M. Bhosale, D. Burmeister, G. J. Smales, M. Schmidt, Z. Kochovski, N. Grabicki, R. Wessling, E. J. W. List-Kratochvil, B. Esser and O. Dumele, J. Am. Chem. Soc., 2023, 145, 2840–2851 CrossRef PubMed.
- S. Hashimoto and K. Tahara, J. Org. Chem., 2019, 84, 9850–9858 CrossRef PubMed.
- C. K. Frederickson, L. N. Zakharov and M. M. Haley, J. Am. Chem. Soc., 2016, 138, 16827–16838 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, J. V. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Going, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, T. Throssell, J. A. Jr. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brother, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision E.01 (version A.1.), 2009 Search PubMed.
- I. Casademont-Reig, E. Ramos-Cordoba, M. Torrent-Sucarrat and E. Matito, Molecules, 2020, 25, 711 CrossRef PubMed.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. Van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef PubMed.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef.
- R. Gershoni-Poranne and A. Stanger, Aromaticity, Elsevier, 2021, pp. 99–154 Search PubMed.
- A. Stanger, J. Org. Chem., 2006, 71, 883–893 CrossRef PubMed.
- A. Stanger, J. Org. Chem., 2010, 75, 2281–2288 CrossRef.
- G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1995, 99, 606–611 CrossRef.
- H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v R. Schleyer, Org. Lett., 2006, 8, 863–866 CrossRef PubMed.
- R. Báez-Grez, L. Ruiz, R. Pino-Rios and W. Tiznado, RSC Adv., 2018, 8, 13446–13453 RSC.
- G. Monaco, F. F. Summa and R. Zanasi, J. Chem. Inf. Model., 2021, 61, 270–283 CrossRef PubMed.
- E. Paenurk and R. Gershoni-Poranne, Phys. Chem. Chem. Phys., 2022, 24, 8631–8644 RSC.
- R. Hoffmann, J. Chem. Phys., 1963, 39, 1397–1412 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, J. V. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Going, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, T. Throssell, J. A. Jr. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark,J. J. Heyd, E. Brother, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016 Search PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef.
- P. J. Mayer, O. El Bakouri, T. Holczbauer, G. F. Samu, C. Janáky, H. Ottosson and G. London, J. Org. Chem., 2020, 85, 5158–5172 CrossRef.
- R. Pino-Rios and M. Solà, J. Phys. Chem. A, 2021, 125, 230–234 CrossRef PubMed.
- M. Zora and İ. Özkan, J. Mol. Struct.: THEOCHEM, 2003, 638, 157–162 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc06812b |
| This journal is © The Royal Society of Chemistry 2025 |