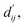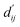Open Access Article
Open Access ArticleRobust protein–ligand interaction modeling through integrating physical laws and geometric knowledge for absolute binding free energy calculation†
Qun
Su‡
,
Jike
Wang‡
,
Qiaolin
Gou‡
,
Renling
Hu
 ,
Linlong
Jiang
,
Hui
Zhang
,
Tianyue
Wang
,
Yifei
Liu
,
Chao
Shen
,
Linlong
Jiang
,
Hui
Zhang
,
Tianyue
Wang
,
Yifei
Liu
,
Chao
Shen
 ,
Yu
Kang
,
Yu
Kang
 ,
Chang-Yu
Hsieh
,
Chang-Yu
Hsieh
 * and
Tingjun
Hou
* and
Tingjun
Hou
 *
*
College of Pharmaceutical Sciences, Zhejiang University, Hangzhou 310058, Zhejiang, China. E-mail: tingjunhou@zju.edu.cn; kimhsieh@zju.edu.cn
First published on 17th February 2025
Abstract
Accurate estimation of protein–ligand (PL) binding free energies is a crucial task in medicinal chemistry and a critical measure of PL interaction modeling effectiveness. However, traditional computational methods are often computationally expensive and prone to errors. Recently, deep learning (DL)-based approaches for predicting PL interactions have gained enormous attention, but their accuracy and generalizability are hindered by data scarcity. In this study, we propose LumiNet, a versatile PL interaction modeling framework that bridges the gap between physics-based models and black-box algorithms. LumiNet utilizes a subgraph transformer to extract multiscale information from molecular graphs and employs geometric neural networks to integrate PL information, mapping atomic pair structures into key physical parameters of non-bonded interactions in classical force fields, thereby enhancing accurate absolute binding free energy (ABFE) calculations. LumiNet is designed to be highly interpretable, offering detailed insights into atomic interactions within protein–ligand complexes, pinpointing relatively important atom pairs or groups. Our semi-supervised learning strategy enables LumiNet to adapt to new targets with fewer data points than other data-driven methods, making it more relevant for real-world drug discovery. Benchmarks show that LumiNet outperforms the current state-of-the-art model by 18.5% on the PDE10A dataset, and rivals the FEP+ method in some tests with a speed improvement of several orders of magnitude. We applied LumiNet in the scaffold hopping process, which accurately guided the discovery of the optimal ligands. Furthermore, we provide a web service for the research community to test LumiNet. The visualization of predicted inter-molecular energy contributions is expected to provide practical value in drug discovery projects.
Introduction
Absolute binding free energy (ABFE) is a pivotal concept in computational biology and medicinal chemistry, providing a rigorous and transparent framework to quantify the PL interactions. The modeling of binding affinity through molecular simulation has been an active research area, aiming to achieve a holy grail in computer chemistry. With recent strides in computational hardware and advanced algorithms, we have witnessed how ABFE calculations are influencing molecular design and screening in drug discovery and beyond.1,2 For instance, in 2022, Wu et al. utilized ABFE calculations to guide scaffold hopping in the design of PDE5 inhibitors,3 ultimately leading to the discovery of the potent lead L12 with an IC50 of 8.3 nmol L−1 and a distinct scaffold compared to the initial compounds. In 2023, Biggin et al. proposed a novel method that integrates ABFE calculations to enhance fragment-based molecular optimization, further highlighting the vast potential of ABFE.2 The prevailing methods for computing ABFE mainly rely on free energy perturbation (FEP) and thermodynamic integration (TI), both of which require extensive sampling in the configurational space.4–6 This, in turn, demands substantial computational resources and time. Alternatively, endpoint methods, such as MM/PBSA or MM/GBSA, can approximate ABFE by calculating the free energy difference between the bound and unbound states of solvated molecules, which significantly reduces computational demands but at the expense of accuracy.7,8 Balancing computational resource consumption and calculation accuracy remains a perennial challenge, significantly limiting the practicality of ABFE calculations.9The recent trend of utilizing deep learning (DL) to predict molecular properties has sparked innovative data-driven approaches,10–15 which may be adapted to estimate ABFE efficiently and accurately. Notable examples of such approaches include IGN,16 OnionNet,17 and GIGN.10 These first-generation DL solutions predominantly rely on learning statistical patterns from training data, often neglecting well-established physical principles. However, the experimental data used for training and testing DL models, compiled from diverse sources, is not ideal. Undocumented or neglected variations in experimental conditions inevitably result in disparities in binding affinity reports for the same compound. Additionally, bias is prevalent in modern scientific data. Despite a wide range of data sources for binding affinity, the chemical space covered remains limited in most cases. These data issues severely impede DL models from accurately capturing the authentic patterns of protein–ligand interactions, making them susceptible to dataset-dependent bias.18,19
A promising approach to address the aforementioned challenge lies in minimizing the dependence of DL models on data volume and exploring interaction patterns grounded in physics.20–25 For instance, in 2022, Moon et al. proposed PIGNET, a physics-inspired DL scoring function,20 which achieved competitive results on the CASF-2016 (ref. 26) benchmark but showed limited improvement in scoring performance. In 2024, the same team proposed an enhanced version, PIGNET2,21 which further incorporated data augmentation for active compounds. This upgraded model notably outperformed those trained solely on PDBbind. However, while PIGNET aims to develop a physics-aware model, its integration of DL and physical principles still have room for improvement. The current methods directly map a high dimensional latent vector (learned by a graph neural network, GNN) to a few physical parameters for scoring, lacking direct feedback on these parameters as in supervised learning. This leads to an ineffective incorporation of domain knowledge, and the model's reliability remains heavily dependent on the quality of training data. In another line of research, PBCNET22 has been proposed to predict the relative binding free energy (RBFE) between a pair of ligands towards the same receptor. By utilizing approximately 0.6 million training samples containing ligand pairs and proteins, PBCNET achieved comparable results to the FEP+ method on both the FEP1 (ref. 27) and FEP2 (ref. 28) tests through active learning. This method focuses on structural variations between ligand pairs, facilitating data-driven learning of possible RBFE values rather than directly modeling protein–ligand interaction patterns. Therefore, in the current scenario with limited labeled data, RBFE methods have a significant advantage in predicting accuracy. However, in practical ABFE prediction, estimating binding free energies through RBFE calculations limits its applicability. Some studies emphasize learning structural information to infer ABFE. For example, DSMbind24 introduced an interesting hypothesis: assuming that the default crystal structure represents the lowest protein–ligand energy state, it employs SE(3) denoising score matching (DSM) to estimate the likelihood of complexes, thereby inferring binding free energy. GenScore,23 on the other hand, initially utilizes a mixture density network (MDN) to fit the distance distribution of residue-atom pairs in protein–ligand complexes, learning more structural information. The model is then fine-tuned with actual binding free energy labels, delivering remarkable results on the FEP2 dataset developed by Schindler.28 While both GenScore and DSMbind exhibit notable statistical correlation between predicted and experimental energies, their actual errors remain substantial for practical applications. For instance, when dealing with specific systems, direct application is challenging and requires a certain number of known ABFE values for correction. In summary, the reliance of current DL-based models on data may introduce biases, thereby limiting their generalizability and practical applications. Additionally, the inherent opacity of machine learning (ML) algorithms contributes to a lack of clear and intuitive physical explanations in existing models. Therefore, there is an urgent need to develop improved ABFE prediction models with robust generalization, wide applicability, and a high level of interpretability.
In this study, we present LumiNet, an innovative approach designed for robust PL interaction modeling and accurate calculation of ABFE. We adopt a ‘divide and conquer’ approach, fully leveraging the powerful structural representation capabilities of deep learning and well-established physical principles. LumiNet transformed the original ABFE estimation task into a process that leverages structural data of protein–ligand complexes to calculate ‘effective’ atomic distances, which are then incorporated into a physics-driven scoring function for ABFE computation. Specifically, in LumiNet, we developed a subgraph transformer to extract multiscale information from molecular graphs to fit distances between PL pairs, providing a comprehensive comprehension of the underlying structural features. Then by fine-tuning the atom pair distance with geometric neural networks, we convert them into key parameters 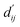 for classical force fields, used to calculate various non-bonded interactions, encompassing van der Waals forces, hydrogen bond interactions, hydrophobic interactions, and metal interactions.29 Furthermore, we introduce Trotor to account for ligand entropy, thereby enhancing the model's generalization ability. These energy terms are computed for each atomic pair and can be visualized through an intuitive web interface. It means we can swiftly locate atom pairs or groups with significant interactions across various interaction types, directly aiding our analysis in drug discovery. The benchmark tests on CASF-2016 resulted in a Pearson correlation coefficient (PCC) of 0.85. When evaluated on the FEP1 and FEP2 holdout sets, the model achieved PCC values of 0.65 and 0.46, respectively. This performance is competitive with all current DL approaches for direct ABFE prediction. The notable strengths of LumiNet in prediction accuracy and computational efficiency were confirmed by the predictions on the SARS-CoV-2 inhibitor dataset30 and the PDE10A inhibitor dataset.31 To improve portability, stability, and performance on target receptors, we adopted a semi-supervised learning approach that promotes structural awareness, yielding more reliable results. On the FEP1 and FEP2 datasets, the average PCC values are 0.696 and 0.534, respectively, demonstrating significant improvement over PIGNET2 on FEP1 (0.64) and GenScore on FEP2 (0.51). Impressively, fine-tuning with only 6 data points in a single iteration achieved a PCC of 0.73 on FEP1, with an RMSE of 0.82 kcal mol−1, closer to the actual experimental values than the FEP+ RMSE of 1.08 kcal mol−1. Moreover, we applied LumiNet in the scaffold hopping process reported by Wu et al.,3 which accurately guided the discovery of the optimal ligands. We provided a web service to compute ABFE and pinpoint key atomic interactions in PL complexes at https://www.ai2physic.top.
for classical force fields, used to calculate various non-bonded interactions, encompassing van der Waals forces, hydrogen bond interactions, hydrophobic interactions, and metal interactions.29 Furthermore, we introduce Trotor to account for ligand entropy, thereby enhancing the model's generalization ability. These energy terms are computed for each atomic pair and can be visualized through an intuitive web interface. It means we can swiftly locate atom pairs or groups with significant interactions across various interaction types, directly aiding our analysis in drug discovery. The benchmark tests on CASF-2016 resulted in a Pearson correlation coefficient (PCC) of 0.85. When evaluated on the FEP1 and FEP2 holdout sets, the model achieved PCC values of 0.65 and 0.46, respectively. This performance is competitive with all current DL approaches for direct ABFE prediction. The notable strengths of LumiNet in prediction accuracy and computational efficiency were confirmed by the predictions on the SARS-CoV-2 inhibitor dataset30 and the PDE10A inhibitor dataset.31 To improve portability, stability, and performance on target receptors, we adopted a semi-supervised learning approach that promotes structural awareness, yielding more reliable results. On the FEP1 and FEP2 datasets, the average PCC values are 0.696 and 0.534, respectively, demonstrating significant improvement over PIGNET2 on FEP1 (0.64) and GenScore on FEP2 (0.51). Impressively, fine-tuning with only 6 data points in a single iteration achieved a PCC of 0.73 on FEP1, with an RMSE of 0.82 kcal mol−1, closer to the actual experimental values than the FEP+ RMSE of 1.08 kcal mol−1. Moreover, we applied LumiNet in the scaffold hopping process reported by Wu et al.,3 which accurately guided the discovery of the optimal ligands. We provided a web service to compute ABFE and pinpoint key atomic interactions in PL complexes at https://www.ai2physic.top.
Results and discussion
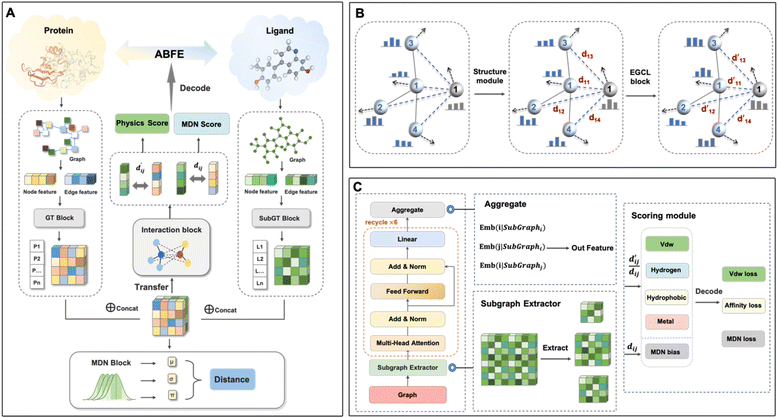
Model architecture
This model consists of two main components: a structure information extraction module (structure module) built on Mixture Density Networks (MDN) and a physics-based scoring module (physics module), as shown in Fig. 1. Distance plays a pivotal role in this integration. When predicting protein–ligand interaction patterns, it is typical to input distances between residue atoms or atom pairs of protein–ligand complexes into the model for learning.12,32 Models that leverage this information tend to show more robust predictive capabilities, as absolute free energy is closely linked to geometric conformations, similar to how bond energy is sensitive to bond length. However, the study of Mastropietro et al.19 suggests that bond information contributes relatively little to the model's prediction process, partly due to challenges in distinguishing between bonds within protein–ligand complexes and internal bonds. Models trained without explicit distance information may rely more on inherent information within protein–ligand complexes. By omitting distance information from the model input and focusing solely on the structural data of proteins and ligands as prediction targets, the model is more prone to learn information relevant to the interaction. This involves inferring the distance distribution of each atom pair between the protein and ligand based on given atomic 2D and 3D information, thus enabling the model to learn the underlying patterns of protein–ligand interactions. In this process, the 3D information is used only to calculate the distance features within the protein and ligand separately and does not directly participate in the inference process. For ABFE prediction, the structure module is employed to infer the distance when the potential energy of interaction between two bodies is the lowest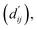 with the bidirectional EGCL modules fine-tuning this information.
with the bidirectional EGCL modules fine-tuning this information. 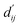 is essential for calculating van der Waals forces, hydrogen bond interactions, etc. The model's design is motivated by the correlation between dij and
is essential for calculating van der Waals forces, hydrogen bond interactions, etc. The model's design is motivated by the correlation between dij and 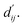 By applying
By applying 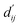 in the computation of physical energy terms through the physical scoring module, it facilitates the mapping from distance to energy. This strategy enables the model to prioritize learning structural information rather than resorting to various methods to fit a more distant target, ABFE.
in the computation of physical energy terms through the physical scoring module, it facilitates the mapping from distance to energy. This strategy enables the model to prioritize learning structural information rather than resorting to various methods to fit a more distant target, ABFE.
The first module in LumiNet incorporates encoding methods for proteins and ligands, accompanied by an MDN designed to fit the distance (dij). This MDN functions as a pre-training model, learning the structural-to-distance mapping. Extracting protein pockets at 5 Å yielded less comprehensive global information than those at 10 Å, but atomic-level features provided more refined insights. We explored using larger fully atomic pockets, but the computational complexity escalates quickly. With a 10 Å pocket, the training time increased by roughly 11-fold. While there was an improvement in prediction accuracy, it didn't justify the steep rise in computational cost. Conversely, using smaller pockets resulted in a significant drop in prediction performance. Ultimately, we found a 5 Å pocket to offer the best trade-off between computational efficiency and predictive accuracy. For protein encoding, a Graph Transformer is employed, whereas ligand encoding utilizes a Subgraph Transformer (SubGT). Their respective coordinates are separately fed into the network. In the SubGT block, ligands are decomposed into substructures and subgraphs, encoded individually, and then aggregated via centroid, subgraph, and context blocks after 6 iterations to derive the feature representation of each atom. These representations are then concatenated with protein–ligand features to fully capture structural information, which the MDN module then uses to fit the distance. The second module incorporates an interaction block and four energy terms for physical scoring, serving to fine-tune the pre-trained model. The information extracted by the pre-trained model, combined with real distance data, is inputted into the bidirectional EGCL module, functioning as an interaction block for additional structural refinement to improve the fit of 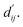 This block determines interaction edges based on protein–ligand atom distances, enabling authentic information exchange. Unlike the pre-training phase that inferred atom pairs information in a result-driven manner, this method directly aggregates information across atom pairs. By integrating these two approaches, the objective of capturing structural information smoothly shifts from dij to
This block determines interaction edges based on protein–ligand atom distances, enabling authentic information exchange. Unlike the pre-training phase that inferred atom pairs information in a result-driven manner, this method directly aggregates information across atom pairs. By integrating these two approaches, the objective of capturing structural information smoothly shifts from dij to 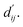 The resultant information is then evaluated by four energy terms and further integrated with the mdn score to compute the final score. A more detailed description of the model's architecture is provided in the Methods section.
The resultant information is then evaluated by four energy terms and further integrated with the mdn score to compute the final score. A more detailed description of the model's architecture is provided in the Methods section.
Pre-train structure module and motivation of physical scoring
We pre-trained the structure module using PDBbind2020,33 excluding 285 data points from CASF-2016. For testing, we utilized the FEP1 set from Merck and FEP2 set from Schrödinger. PDBbind2020 contains 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443 curated co-crystal structures from diverse protein families. However, due to the diversity of sources and assay types, the data inherently contains notable noise. For instance, PDB entry 2w9h reports a dissociation constant (Kd) of 430 nM in PDBbind, whereas BindingDB lists 7 inhibition constant (Ki) values ranging from 1.2 nM to 5.5 μM.31 In cases with abundant data, noise may enhance the model's generalization ability. In 2021, Takashi et al.34 investigated the impact of noise and batch size on prediction accuracy through noise augmentation on real datasets. They found that, within acceptable noise levels, augmentation can effectively bolster a model's generalization. Nevertheless, insufficient data for comprehensive training may introduce unavoidable biases, posing challenges to the model's performance even in similar systems. Therefore, depending solely on the PDBbind dataset to achieve robust generalization in predicting ABFE poses substantial challenges.
443 curated co-crystal structures from diverse protein families. However, due to the diversity of sources and assay types, the data inherently contains notable noise. For instance, PDB entry 2w9h reports a dissociation constant (Kd) of 430 nM in PDBbind, whereas BindingDB lists 7 inhibition constant (Ki) values ranging from 1.2 nM to 5.5 μM.31 In cases with abundant data, noise may enhance the model's generalization ability. In 2021, Takashi et al.34 investigated the impact of noise and batch size on prediction accuracy through noise augmentation on real datasets. They found that, within acceptable noise levels, augmentation can effectively bolster a model's generalization. Nevertheless, insufficient data for comprehensive training may introduce unavoidable biases, posing challenges to the model's performance even in similar systems. Therefore, depending solely on the PDBbind dataset to achieve robust generalization in predicting ABFE poses substantial challenges.
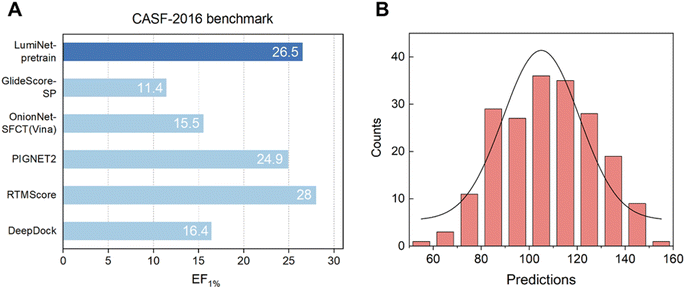
First, we tested our pre-trained model on CASF-2016 to validate its screening power. We found that, through the efficient information extraction of the Subgraph Transformer and the sufficient fitting of the MDN, the enrichment factor for the top 1% of ligands reached a noteworthy value of 26.5, suggesting that the structure module has proficiently learned the structural information of protein–ligand interactions. Next, we fine-tuned our pre-trained model using two distinct loss functions and individually assessed their efficacy in predicting ABFE. Unfortunately, both approaches exhibited significant limitations, rendering them insufficient for achieving high-precision predictions of ABFE.
In the encoding module for small molecules, we used the Subgraph Transformer to enable the model to understand ligand information more deeply. This is logical given that small molecules collectively possess extensive structural diversity, and the model tends to use them to distinguish overall structural states. However, this approach may introduce bias as the model heavily depends on ligands for ABFE prediction. To mitigate this, we effectively convert the structural information of protein–ligand interactions into complex distance distributions, encapsulating the overall structural context despite differing labels. The Subgraph Extractor explores each central atom and its adjacent atoms to construct new subgraphs, which are then aggregated via the GT module. This process surpasses the limitations of the first-order Weisfeiler–Leman (1-WL) isomorphism test,20 which can capture higher-order information and integrate structural information at different levels, resulting in superior expressive ability.
Our investigation revealed that direct fine-tuning substantially improves the scoring performance of the structure module, albeit with limitations. As illustrated in Table S1,† we examined two fine-tuning techniques: one using Mean Squared Error (MSE) as the loss function and the other utilizing the Pearson correlation coefficient. The results indicate that the latter outperforms the former in terms of the Pearson correlation coefficient on the final test set. However, while the Pearson-based method predominantly yields results in the 100–140 range (Fig. 2), the MSE-based method aligns closely with the actual value distribution. This difference mainly stems from the direct mapping of the fitted distance values to ABFE through a simple logarithmic transformation. Notably, using the Pearson correlation coefficient as the loss minimizes trade-offs between fitting distance and scoring tasks due to their inherent correlation. Conversely, with MSE as the loss, balancing both objectives becomes more challenging, resulting in slightly inferior performance. For ranking tasks, the Pearson-based method is preferable for training, whereas the MSE-based method is more suitable for precise ABFE calculations. To meet both requirements, we employ transfer learning on the pre-trained model to fine-tune the parameters of physical energy terms, thereby achieving ABFE prediction results with exceptional generalization and accuracy.
Performance on the FEP dataset
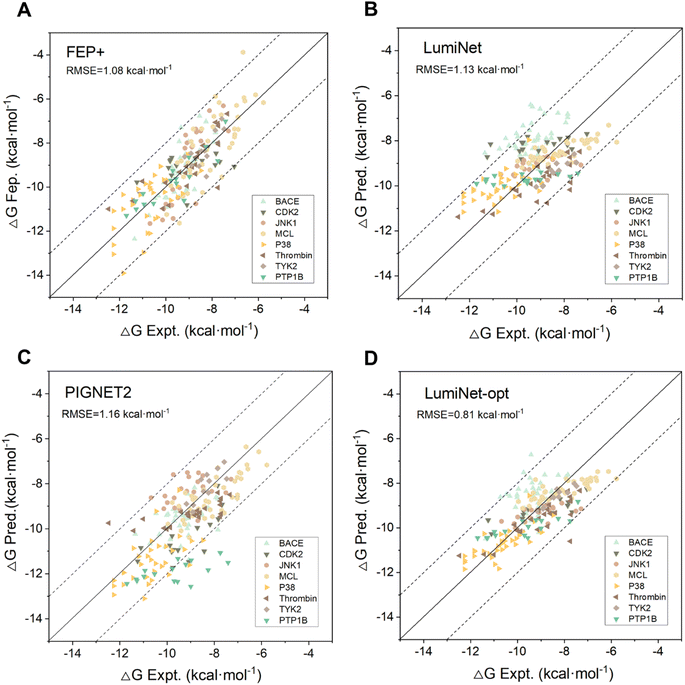
To enhance the model's generalization capability and scoring accuracy, we integrated DL with physical scoring and parameterized structural information derived from the pre-trained model. To assess the integration's effectiveness and its ability to fulfill previous tests, we trained the model using 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158 data points from PDBbind2020. During this process, we kept the weights of the pre-trained model fixed and fine-tuned only the physical scoring component. This step culminated in the successful mapping of structural and distance features to ABFE. We tested our model on the FEP1 and FEP2 datasets against Schrödinger's FEP+, Schrödinger's Glide SP,35 MM/GBSA,7 and two DL-based models, PIGNet2,21 and PBCNET,22 which predict ABFE either directly or indirectly. For PIGNet2, we used the author's original prediction data and calculated the corresponding metrics, while for the other baselines, we referred to their original publications for performance metrics. As detailed in Tables S2 and S3,† the LumiNet method exhibited significant advantages over all baselines, achieving RMSEs of 1.13 kcal mol−1 and 1.32 kcal mol−1 on the respective datasets, compared to 1.08 kcal mol−1 and 1.67 kcal mol−1 for the FEP+ method, with a slight advantage on the FEP2 dataset. Moreover, the correlation coefficients for all targets in FEP1 exceeded 0.4, indicating stable performance. Fig. 3 displays scatter plots of predicted values for PIGNet2, FEP+, LumiNet, and LumiNet-opt. Notably, most LumiNet predictions fell within the ±2 kcal mol−1 range, with only one outlier exceeding ±3 kcal mol−1, similar to the FEP+ method. Additionally, we tested our model on the extended FEP1 dataset provided by Himanshu Goel et al.,36 where the number of ligands was expanded to 407. The average RMSE of LumiNet reached 1.54 kcal mol−1, as shown in Fig. S1.† Furthermore, on the traditional CASF-2016 dataset, the Pearson correlation coefficient reached 0.848, confirming the model's good generalization ability.
158 data points from PDBbind2020. During this process, we kept the weights of the pre-trained model fixed and fine-tuned only the physical scoring component. This step culminated in the successful mapping of structural and distance features to ABFE. We tested our model on the FEP1 and FEP2 datasets against Schrödinger's FEP+, Schrödinger's Glide SP,35 MM/GBSA,7 and two DL-based models, PIGNet2,21 and PBCNET,22 which predict ABFE either directly or indirectly. For PIGNet2, we used the author's original prediction data and calculated the corresponding metrics, while for the other baselines, we referred to their original publications for performance metrics. As detailed in Tables S2 and S3,† the LumiNet method exhibited significant advantages over all baselines, achieving RMSEs of 1.13 kcal mol−1 and 1.32 kcal mol−1 on the respective datasets, compared to 1.08 kcal mol−1 and 1.67 kcal mol−1 for the FEP+ method, with a slight advantage on the FEP2 dataset. Moreover, the correlation coefficients for all targets in FEP1 exceeded 0.4, indicating stable performance. Fig. 3 displays scatter plots of predicted values for PIGNet2, FEP+, LumiNet, and LumiNet-opt. Notably, most LumiNet predictions fell within the ±2 kcal mol−1 range, with only one outlier exceeding ±3 kcal mol−1, similar to the FEP+ method. Additionally, we tested our model on the extended FEP1 dataset provided by Himanshu Goel et al.,36 where the number of ligands was expanded to 407. The average RMSE of LumiNet reached 1.54 kcal mol−1, as shown in Fig. S1.† Furthermore, on the traditional CASF-2016 dataset, the Pearson correlation coefficient reached 0.848, confirming the model's good generalization ability.
Despite the lack of intricate data preprocessing or extensive augmentation, the model still effectively learned the patterns and information governing protein–ligand interactions. This success can be attributed to the fusion of physical scoring and mixed density scoring. We acknowledge that energy-based scoring methods inherently rely on multidimensional approximations, especially for non-bonded interactions where energy terms overlap without clear boundaries. Consequently, we incorporated linear fitting when combining energy terms, enabling the model to independently learn their weight relationships. Furthermore, to bridge the gap between the four energy terms and ABFE, we transformed the mdn score scoring into a bias energy term, thereby enhancing the rationality of each term (as detailed in the Methods section). For feedback propagation, we carefully designed multiple loss functions to ensure the model's interpretability. Although the actual values of individual energy terms were unknown during training, the predicted values proved to be significant. Naturally, if these energy values were derived through high-throughput calculations and integrated into our training model, its performance would undoubtedly be further improved.
However, it is evident that the model's predictive performance has markedly declined across various targets in the FEP2 dataset. In contrast to datasets like FEP1, molecules in FEP2 undergo more transformations, such as changes in net charge and charge distribution, ring openings and core hopping.28 These transformations lead to substantial alterations in solvent interactions. Additionally, the ligand sets display a slightly broader range of structural diversity compared to previous benchmarks. For our model, the influence of solvent interactions is significant. For instance, in the SYK target, a ligand with two aromatic rings extending into the solvent results in a notable discrepancy between predicted and actual values. Similar situations can be observed with small molecules in the PFKFB3 target. Since solvent molecules were not included in the modeling process, the model is less sensitive to changes in this aspect of the energy. Regarding net charge changes, the model can partially distinguish them. For ligands in the c-Met target, which involve six perturbations with a change in net charge, the predictive performance aligns with the average level in the FEP1 dataset. This is attributed to the inclusion of nuclear charge and covalent bonds in the input features. Although charge interactions are not directly included in the energy terms due to the computational complexity of accurately calculating atomic partial charges and discrepancies in semi-empirical charges, the bias term can be learned from embeddings, indirectly compensating for this process. Overall, the results on the FEP1 and FEP2 datasets highlight the model's accuracy and generalization ability for ABFE predictions. This represents a relatively successful attempt at AI scoring based on physics and structure.
Performance on the SARS and PDE10A datasets
The LumiNet model has shown promising performance in the preliminary ABFE tests, but it still experiences fluctuations across diverse datasets, a common challenge for most data-driven models. Here, an important question may be raised: can the model exhibit robust transferability in a new system, and do the structural weight parameters learned from PDBbind remain effective? To answer this question, we first assessed the model on a dataset compiled by Mohammad et al., which contains 16 primary SARS-CoV-2 inhibitors.30 These inhibitors exhibit structural diversity but share similar core scaffolds, with binding free energies (BFEs) ranging over 5 kcal mol−1. Notably, some inhibitors differ structurally by just a halogen atom, posing a challenge to the model's discriminative capacity. Our results indicate that the correlation between experimental and predicted results is on par with the FEP+ method, achieving a Pearson correlation coefficient of 0.73, and an RMSE of 2.61 kcal mol−1 (comparable to FEP+: Pearson correlation coefficient of 0.76, and RMSE of 2.87 kcal mol−1).Moreover, we designed a new test utilizing a dataset curated by Tosstorff et al.31 in 2022, which contains 1162 PDE10A inhibitors. PDE10A, a crucial regulator of the striatal signaling pathway, is a promising target for schizophrenia due to its capacity to ameliorate abnormal striatal conditions. It should be noted that the protein structures in this dataset differ significantly from those in the training set, rendering testing on this practically significant dataset more meaningful and convincing. To ensure experimental fairness, our testing protocol follows the approach outlined in Tosstorff's paper. Furthermore, instead of relying on the models fine-tuned with ABFE labels from PDBbind models, we directly used the protein–ligand structures and ABFE data provided in the article for fine-tuning, exclusively building upon the pre-trained model. We implemented seven different data partitioning techniques, including three rolling temporal splits where the test data is evaluated subsequent to the training data, enabling an assessment of the model's prospective performance. Additionally, we used random splits and three structure-based combination mode splits, wherein the model is trained on the data from two binding mode classes to predict a third, assessing the model's extrapolation capability, akin to a scaffold hop scenario.
During LumiNet training, we also do not update the pre-trained model parameters, instead opting to fine-tune solely the physical scoring component while retaining the original structural parameters. This strategy ensures rapid adaptation to new systems. As shown in Table S4,† we selected several of the best-performing and most classical models reported for this dataset as baselines, including four DL-based models and four classical method-based models. Among them, the 2D3D hybrid model31 combines AttentiveFP37 and RF-PLP,38 while the “extend data” approach signifies the model's utilization of both docked poses and supplementary training with molecules possessing only 2D structures. Moreover, we included the models developed by Isert et al.39 in 2024, who predicted ABFE using electron density-based geometric DL and tested it on PDE10A, as part of our baselines.
The comprehensive results for the other models are shown in Tables 1, S4 and S5,† illustrating that LumiNet achieves a Spearman correlation coefficient higher than 0.5 across various data partitioning scenarios, achieving state-of-the-art results in five partitioning methods. This suggests the robust applicability of the models across different systems, with the structural knowledge gained from pre-training exhibiting significant transferability. However, a notable challenge lies in the models' inconsistency in maintaining stable performance across diverse data partitioning scenarios. Nevertheless, we remain optimistic that with the continual expansion of datasets in this field, this challenge can be overcome. As the model gains a deeper understanding of the interactions between PDE10A and ligands, it is anticipated to perform well even in the presence of temporal and binding mode variations. We eagerly look forward to the practical application of these findings to accelerate research advancements on this target.
| Model | Random | Split 2011 | Split 2012 | Split 2013 | Mode 1 | Mode 2 | Mode 3 | Average |
|---|---|---|---|---|---|---|---|---|
| a The above seven data partitioning methods were used for each model, modes 1, 2, and 3 define different protein–ligand binding modes, all sharing a key feature: a hydrogen bonding acceptor atom of the ligand is in a hydrogen bonding distance with the amino group of the Gln726 sidechain. However, structural variations of ligands lead to different binding configurations. Based on these differences, ligands are classified into three categories: aminohetaryl-C1-amide, C1-hetaryl-alkyl-C2-hetaryl, and aryl-C1-amide-C2-hetaryl.31 The Pearson correlation coefficient was used as an indicator, where bold numbers represent the best results. | ||||||||
| BCP-based graph | 0.525 | 0.246 | −0.009 | 0.480 | 0.207 | 0.064 | 0.139 | 0.236 |
| NCP-based graph | 0.601 | 0.300 | 0.331 | 0.559 | 0.299 | 0.355 | 0.328 | 0.390 |
| 2D3D hybrid | 0.712 | 0.608 | 0.559 | 0.637 | 0.453 | 0.333 | 0.494 | 0.541 |
| LumiNet | 0.799 | 0.587 | 0.736 | 0.687 | 0.564 | 0.640 | 0.490 | 0.643 |
Application of LumiNet in scaffold hopping
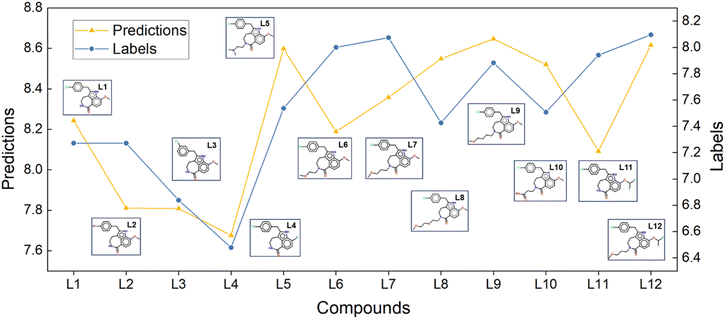
Scaffold hopping, a technique used in drug discovery and development, aims to find new molecules with comparable biological activity by altering the core scaffold of a given molecule. Therefore, identifying privileged scaffolds is crucial for drug molecule design. Currently, the main methods for scaffold hopping include heterocycle replacements, ring opening or closure, topology-based hopping, and computational methods.40–42 Typically, these methods require validation of scaffold hopping rationality through binding free energy calculations. However, few computational methods take this into account largely owing to the high computational cost and challenges in achieving accuracy. When performing binding free energy calculations for scaffold hopping, relying solely on RMSE and correlation coefficients is not sufficient for a thorough evaluation.Recently, the core hopping FEP method has successfully conducted RBFE calculations for minor and limited scaffold hopping cases. However, most scaffold hopping procedures typically involve substantial topology changes of the entire ligand. To accurately predict the binding free energies of ligands following scaffold hopping, it is essential to use ABFE calculations rather than RBFE calculations. In 2022, Wu et al.3 utilized ABFE calculations to guide scaffold hopping in the design of PDE5 inhibitors. Following their reported procedure, we used Glide to dock L1 to the crystal structure of PDE5-tadalafil (PDB ID: 1XOZ) and to dock L2 to L12 to the crystal structure of PDE5-L1 (PDB ID: 7FAQ). The LumiNet model was then used to perform ABFE predictions in a zero-shot setting. Notably, compounds L1 to L12 were designed based on tadalafil and LW1607, with significant structural differences from their initial structures.
L1 to L4 served as the initial structures. The design of L7 primarily aimed to study the structure–activity relationships (SAR) at the 2-position. As shown in Fig. 4, our prediction results were consistent with the bioassay results, indicating that replacing the 2-position with an oxygen-containing alkane chain led to a significant enhancement in inhibitory activity compared to L1 through L4. Based on the design of L7, L5, L6, L8, L9, L10, and L12 the aim was to explore how the length and charge characteristics of the substituents at the 2-position influence activity. Our prediction results remained consistent with the bioassay results, exhibiting comparable trends. Notably, L12, with a moderately long hydrocarbon chain at the 2-position and a difluoromethoxy substituent at the 5-position, was theoretically supported by both prediction results and SAR analysis.
The original article used the FEP-ABFEP calculation method and achieved a Pearson correlation coefficient of 0.72 between the computational results and experimental activity values. Our LumiNet model, evaluated in a zero-shot setting, exhibited a correlation coefficient of 0.67 with the experimental values. Obviously, both the LumiNet method and the original FEP-ABFEP method demonstrated consistency in prediction accuracy and trends related to lead compound optimization. Therefore, our model offers valuable insights for lead compound optimization and remains applicable even in cases where significant structural differences exist between optimized and initial structures.
Application of semi-supervised policies in real-world scenarios
It can be observed that despite the remarkable progress of DL-based ABFE prediction, most models have hit a performance ceiling. This is likely caused by the constraints posed by the currently accessible training data, which may determine the peak performance attainable. Additionally, even with robust models, obtaining reliable predictions for a novel target complex continues to be a formidable challenge.To ensure practicality in real-world scenarios, we designed a semi-supervised workflow that accounts for the scarcity of labels for novel targets and the complexity of ligand molecules. We have tried two strategies. The first strategy involves optimizing the entire test set by leveraging predictions from the previous round as pseudo-labels and incorporating them into the model's training process. This method, which shares the results across all targets using a common checkpoint, yielded promising outcomes, as evidenced by a Pearson correlation coefficient of 0.7 after two iterations as shown in Table S6.† However, it is also evident that the deviation from the true values (RMSE) is gradually increasing, attributed to the uncertainty of pseudo-labels. Although hyperparameter tuning can alleviate this issue, as evidenced by improved LumiNet indicators on the FEP2 dataset in Table S7† the model remains susceptible to fluctuations due to insufficient monitoring. To enhance the workflow's robustness, we implemented the second strategy: randomly selecting data with two or more known true value labels and integrating them into the training set for real-time monitoring. Furthermore, we incorporated the pseudo-labels of these data points during training to further strengthen the model. Training was terminated when the RMSE of the true data points reached a minimum.
To ensure the reproducibility and stability of the second strategy experiment, we assigned five random seeds (0–4) for data extraction. However, this approach poses a challenge of potentially being trapped into a local optimum. As the model tends to prioritize the best checkpoint for a limited dataset, complicating generalization to other candidate molecules for the target. Therefore, it is prone to overfitting, when the monitoring data is scarce, as repeated semi-supervised iterative training can exacerbate this issue. To address these limitations, we incorporated more real value data into training and supervision. As the volume of real-value data increases, the predictive performance of the model across various targets gradually improves. When the number of real values reached six, the performance on the FEP1 dataset matched that of the FEP+ method named LumiNet-opt, as shown in Fig. 3D and Table S8.† The RMSE further confirms that our method yields predictions closer to true values. We did not continue to the next iteration, considering this performance a realistic benchmark for our current modeling approach. Although continued iterations may enhance performance on the current test set, they could introduce significant bias when applied to larger datasets, restricting us to a local optimum within the vast search space. Hence, we view this method as a valuable reference, particularly suitable for specific systems.
Model interpretability
The LumiNet model was developed based on physical energy terms, inherently providing interpretability. The transparency of individual energy terms, their weights, and the core parameter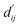 allows for direct quantitative verification of the effectiveness of a system. Adhering to the interpretability principle, each module in the model is designed accordingly. Although the pre-trained model adeptly captures structural information, the BiEGCL layer, a crucial interaction block component of the model, remains indispensable. We aim to refine
allows for direct quantitative verification of the effectiveness of a system. Adhering to the interpretability principle, each module in the model is designed accordingly. Although the pre-trained model adeptly captures structural information, the BiEGCL layer, a crucial interaction block component of the model, remains indispensable. We aim to refine 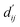 using this method because the pre-training focuses on learning atom pair distance in the current protein–ligand configuration. However,
using this method because the pre-training focuses on learning atom pair distance in the current protein–ligand configuration. However, 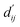 refers to the minimum atom-to-atom distance when energy is minimized. We intend to use prior structural information to make adjustments via the interaction block, achieving a better fitting of
refers to the minimum atom-to-atom distance when energy is minimized. We intend to use prior structural information to make adjustments via the interaction block, achieving a better fitting of 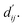 The ablation experiments prove that eliminating the interaction block leads to a performance decline on the FEP1 and FEP2 datasets, particularly on FEP1, where the Pearson correlation coefficient dropped from 0.646 to 0.547. This result also confirms that our pre-trained model has indeed learned current-state distance distributions, evident in the tendency of the
The ablation experiments prove that eliminating the interaction block leads to a performance decline on the FEP1 and FEP2 datasets, particularly on FEP1, where the Pearson correlation coefficient dropped from 0.646 to 0.547. This result also confirms that our pre-trained model has indeed learned current-state distance distributions, evident in the tendency of the 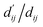 ratios for certain atoms to approach 1, a trend that gradually diminishes as the model iterates. The subsequent energy term calculations demonstrate that the van der Waals interaction and hydrophobic interactions constitute the largest proportion, primarily due to the integration of van der Waals force constraints into the loss function. While this method has its merits and limitations, it adequately satisfies the evaluation requirements for most interactions, albeit with potential deficiencies in specific cases.
ratios for certain atoms to approach 1, a trend that gradually diminishes as the model iterates. The subsequent energy term calculations demonstrate that the van der Waals interaction and hydrophobic interactions constitute the largest proportion, primarily due to the integration of van der Waals force constraints into the loss function. While this method has its merits and limitations, it adequately satisfies the evaluation requirements for most interactions, albeit with potential deficiencies in specific cases.
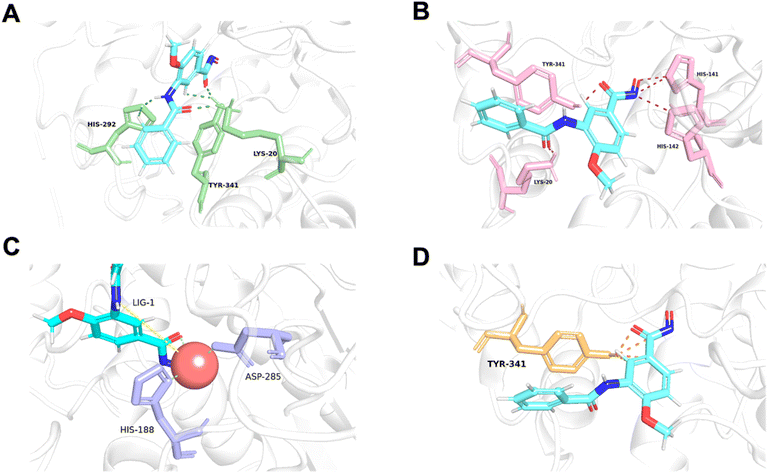
As data volume increases, we can eliminate this constraint while still achieving good results. Our model can quickly predict the energy values for each atom pair and visually demonstrate key protein–ligand interaction. As shown in Fig. 5, we predicted the affinity between the protein 6ht8 and its ligand, using color differentiation to represent the affinity of each atom pair and setting a threshold to highlight significant interactions. Consequently, our model readily unveils the interaction strength between atom pairs, pinpointing relatively important atom pairs or groups. However, due to current data constraints, the detailed energies provided should be considered as references rather than exact predictions. Nevertheless, during training, if accurate labels for each energy component are provided, the model can learn true interactions, thereby improving prediction accuracy. In conclusion, LumiNet undoubtedly offers researchers a straightforward assessment of protein–ligand interactions.
Conclusions
With the advancement of AI technology, a number of models for predicting ABFE have been developed. Nevertheless, there is still room for improvement in terms of both generalization capability and precision. LumiNet stands out by innovatively merging the structure and physics modules, utilizing distance distribution to achieve exceptional performance. Using only 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points from PDBbind, it outperformed baseline models on the FEP dataset and achieved an 18.5% improvement over state-of-the-art results on the PDE10A dataset, demonstrating impressive generalization across multiple key targets. By adopting a semi-supervised approach, further improvement was achieved. With a modest amount of target-specific data, LumiNet can match or even exceed the predictive power of FEP+, holding considerable potential in optimizing lead compounds with notable structural differences. However, it should be noted that such superiority has its limitations. Moreover, we applied LumiNet in the scaffold hopping process, which accurately guided the discovery of the optimal ligands. Although LumiNet demonstrated resilience to data volume dependency and promoted the integration of AI with fundamental physics, it still failed to fully capture the underlying patterns of protein–ligand interactions based on the current dataset, thereby not breaking through the existing bottleneck. LumiNet provides intuitive displays of protein–ligand interactions, allowing us to understand the contribution of different atom pairs to the overall energy and the importance of certain functional groups. Moreover, we aim to expand beyond just protein–ligand interactions in the future. We will augment the training dataset to gain a deeper understanding of non-covalent interactions and target a wider spectrum of dimer types, such as peptide–peptide, and peptide–ligand. This expansion will further enhance the versatility of the models, and potentially result in a qualitative leap in predictive accuracy for various interactions as the data volume increases.
000 data points from PDBbind, it outperformed baseline models on the FEP dataset and achieved an 18.5% improvement over state-of-the-art results on the PDE10A dataset, demonstrating impressive generalization across multiple key targets. By adopting a semi-supervised approach, further improvement was achieved. With a modest amount of target-specific data, LumiNet can match or even exceed the predictive power of FEP+, holding considerable potential in optimizing lead compounds with notable structural differences. However, it should be noted that such superiority has its limitations. Moreover, we applied LumiNet in the scaffold hopping process, which accurately guided the discovery of the optimal ligands. Although LumiNet demonstrated resilience to data volume dependency and promoted the integration of AI with fundamental physics, it still failed to fully capture the underlying patterns of protein–ligand interactions based on the current dataset, thereby not breaking through the existing bottleneck. LumiNet provides intuitive displays of protein–ligand interactions, allowing us to understand the contribution of different atom pairs to the overall energy and the importance of certain functional groups. Moreover, we aim to expand beyond just protein–ligand interactions in the future. We will augment the training dataset to gain a deeper understanding of non-covalent interactions and target a wider spectrum of dimer types, such as peptide–peptide, and peptide–ligand. This expansion will further enhance the versatility of the models, and potentially result in a qualitative leap in predictive accuracy for various interactions as the data volume increases.
Methods
Graph representation
In the study of protein–ligand interactions, ligands are often abstracted into the form of topological graphs. In our model, the ligand is represented as an undirected graph, with atoms as nodes and covalent bonds as edges. It is represented as [Gl = (Hl, El, Xl)], where Hl represents node features, El represents edge features, and Xl represents atomic coordinates.For the protein, it is also abstracted into a topological graph. Unlike many models, we still represent each atom as a node rather than using residues. This is done to facilitate the calculation of atomic pair energy terms in the subsequent steps. Although there are a large number of atoms in proteins, not all of them actively participate in the binding between the protein and ligand. Therefore, a protein pocket is extracted to reduce the computational load. Additionally, in the processing of edges, due to the complex protein structures, using only covalent bonds as edges to describe the connectivity of the entire topological graph may cause information loss. Hence, we consider not only covalent bonds as edges but also atom pairs within a 6 Å distance as connected edges. To differentiate them, we assign a feature value of 1 to covalent bond edges and 0 to non-covalent bond edges. Finally, the protein is represented as [Gp = (Hp, Ep, Xp)], where Hp denotes node features, Ep denotes edge features, and Xp denotes atomic coordinates.
Graph transformer (GT)
The Transformer-based model,43 specifically designed for processing graph data that represent entities and their interactions, has demonstrated remarkable efficacy in studies such as GenScore,23 RTMScore,44 and Karmadock,45 particularly in analyzing protein–ligand interaction graphs. These investigations highlight the exceptional performance of Graph Transformer. By integrating a self-attention mechanism, the model establishes dynamic correlations between nodes, allowing for flexible adjustment of weights based on their relationships. In the input molecular graph [Gp = (Hp, Ep, Xp)], the node features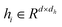 for the i-th node and edge features
for the i-th node and edge features 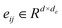 for the edge connecting node i and node j are initialized to h0i and e0ij, respectively, in a d-dimensional space using two linear layers.
for the edge connecting node i and node j are initialized to h0i and e0ij, respectively, in a d-dimensional space using two linear layers.| h0i = W0hhi + b0h; e0ij = W0eeij + b0e | (1) |
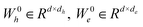 and b0h, b0e ∈ Rd. After passing through the embedding layer, the features are expanded to the same dimension. Then, message passing and aggregation are executed via the convolutional layers. In the Graph Transformer, this operation is primarily achieved by the self-attention mechanism. The model performs six convolutional operations, with the convolution process for the l-th layer expressed by the following equations:
and b0h, b0e ∈ Rd. After passing through the embedding layer, the features are expanded to the same dimension. Then, message passing and aggregation are executed via the convolutional layers. In the Graph Transformer, this operation is primarily achieved by the self-attention mechanism. The model performs six convolutional operations, with the convolution process for the l-th layer expressed by the following equations:| qik,l = WQk,lNorm(hil) | (2) |
| kjk,l = WKk,lNorm(hjl) | (3) |
| vjk,l = WVk,lNorm(hjl) | (4) |
| eijk,l = WEk,lNorm(eijl) | (5) |
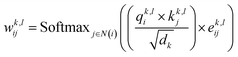 | (6) |
| ĥil+1 = hil + Wh0lDropout(Concatk∈1,…,H(Aggregation_Sumj∈ N(i)(wijk,lvjk,l))) | (7) |
| êijl+1 = eijl + We0lDropout(Concatk∈1,…,H(wijk,l)) | (8) |
| hil+1 = ĥil+1 + Wh2lDropout(SiLU(Wh1lNorm(ĥil+1))) | (9) |
| eijl+1 = êijl+1 + We2lDropout(SiLU(We1lNorm(êijl+1))) | (10) |
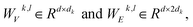
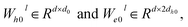
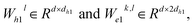
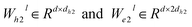 represent learnable parameters derived from linear layers. k ∈ 1, …, H signifies the number of attention heads, while dk represents the dimension of each head, calculated as d divided by H. j ∈ N(i) denotes the neighboring nodes of node i, with Norm indicating batch normalization. Concatenation is denoted by Concat, and Dropout denotes the dropout operation. Activation functions are represented by SiLU. The aggregation of messages on the edges connecting node i and its neighboring nodes j is depicted by Aggregation_Sumj∈N(i), while Softmaxj∈N(i) symbolizes the SoftMax operation applied to the neighboring nodes j.
represent learnable parameters derived from linear layers. k ∈ 1, …, H signifies the number of attention heads, while dk represents the dimension of each head, calculated as d divided by H. j ∈ N(i) denotes the neighboring nodes of node i, with Norm indicating batch normalization. Concatenation is denoted by Concat, and Dropout denotes the dropout operation. Activation functions are represented by SiLU. The aggregation of messages on the edges connecting node i and its neighboring nodes j is depicted by Aggregation_Sumj∈N(i), while Softmaxj∈N(i) symbolizes the SoftMax operation applied to the neighboring nodes j.
SubGraph transformer (SubGT)
Graph neural networks (GNNs) employ a recursive mechanism to continuously gather information from neighboring nodes, drawing considerable attention due to their efficiency and intuitiveness.46,47 However, traditional Message Passing Neural Networks (MPNNs) are unable to approximate all permutation–invariant graph functions, and their expressive ability is limited by the 1st-order Weisfeiler–Leman (1-WL) isomorphism test.48 Importantly, researchers have demonstrated that these 1-WL-equivalent GNNs lack expressive ability and fail to capture fundamental structural concepts, such as counting elementary structures like cycles or triangles,49 which are known to be valuable in bioinformatics and cheminformatics. Despite the Graph Transformer enhancing the effectiveness of graph neural networks to some extent, it has not adequately addressed this issue as it still relies on direct information propagation among neighboring nodes. To overcome these challenges, subgraphs are proposed to enhance receptive fields with a higher structural information perception.For an input graph [G = (H, E, X)], the molecular graph is first split based on the adjacency matrix:
| SubGraphi = {i, j ∈ E|Hi, Hj, Hij, Xi, Xj} | (11) |
For the i-th node, the nodes directly connected to it are identified, and these nodes and edges collectively form SubGraphi. The partitioning continues until the generated subgraphs completely cover the input molecular graph. Each subgraph is then processed through the Graph Transformer. For the i-th convolutional layer, the process is defined as follows:
| hv(l+1) = GT(l)(G(l)[Nk(v)]), l = 0, 1, …, L − 1 | (12) |
| hG = POOL(hv(L)|v ∈ V) | (13) |
This iteration repeats six times until reaching the output layer, where Emb(i|SubGraphi), Emb(j|SubGraphi), and Emb(i|SubGraphj)are computed. These three computations are concatenated, and the linear layer is applied to obtain the feature representation of each node.
BiEGCL
BiEGCL (Bidirectional Equivariant Graph Convolutional Layer) is a key component of the model that handles interactions between proteins and ligands. This module computes the distances between corresponding atoms in proteins and ligands using the input coordinate information. Subsequently, based on predetermined thresholds, it determines which atom pairs are connected by edges, thus forming a directed graph. In the implementation of BiEGCL, the normalized coordinate differences are used instead of raw coordinate differences to better meet the requirements of the model. During the information propagation process, we also employ an attention mechanism module to enhance the attention and processing of the interactions among different atoms.| mij(pl), mji(pl) = φ(Zij, hi(pl), hj(pl), ‖xi(pl) − xj(pl)‖) | (14) |
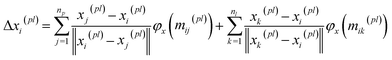 | (15) |
It is noteworthy that the module does not perform any coordinate updating operations during its execution, as equivariance is not necessary to achieve in this way. However, even without coordinate updates, we still need to use distance information to guide subsequent computations to more accurately capture interactions between proteins and ligands.
Mixture density network
The Mixture density network (MDN) is an architecture commonly used in deep learning to model complex probability distributions, which is particularly suitable for handling data with multi-modal distributions, as it introduces the concept of mixture models to flexibly capture multiple modes in the data. The purpose of this module is to effectively select ligand poses and enrich activity by learning the complex probability distribution of protein–ligand interactions. By embedding the encoding nodes of proteins and ligands and processing them through a series of linear, normalization, activation, and dropout layers, the module ultimately utilizes three linear layers to output the mean, standard deviation, and mixture coefficients.| hp,l = Dropout(ELU(BatchNorm(Wp,lConcat(hp, hl) + bp,l))) | (16) |
| μp,l = ELU(Wμhp,l + bμ) + 1 | (17) |
| σp,l = ELU(Wσhp,l + bσ) + 1.1 | (18) |
| πp,l = Softmax(Wπhp,l + bπ) | (19) |
LMDN = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P((dp,c|hp, hc)) P((dp,c|hp, hc)) | (20) |
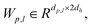 Wμ, Wμ,
Wμ, Wμ, 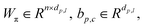 bμ, bσ and bπ ∈ Rn are learnable parameters of linear layers; hp and
bμ, bσ and bπ ∈ Rn are learnable parameters of linear layers; hp and 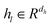 denote the features; Concat, Softmax, and Dropout denote the concatenation, softmax, and dropout operations, respectively. Constructing a mixture density model for encoding distance distributions provides a powerful tool for describing the diversity and uncertainty among protein–ligand node pairs, thereby enhancing the model's performance in complex structures.
denote the features; Concat, Softmax, and Dropout denote the concatenation, softmax, and dropout operations, respectively. Constructing a mixture density model for encoding distance distributions provides a powerful tool for describing the diversity and uncertainty among protein–ligand node pairs, thereby enhancing the model's performance in complex structures.
Calculation of physical energy terms
In order to enhance the generalization ability of the model, we aim to let the model learn which energy terms constitute the binding free energy and how they are calculated. In the model, the knowledge learned by the deep learning network is fitted into the parameters of the formula to perform more universal calculations. This mainly involves van der Waals interactions, hydrogen bonding interactions, hydrophobic interactions, and metal interactions. They are all calculated by dij and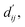 where dij represents the absolute distance between protein–ligand atom pairs, and
where dij represents the absolute distance between protein–ligand atom pairs, and 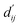 is the corrected sum of van der Waals radii. It is expressed as:
is the corrected sum of van der Waals radii. It is expressed as: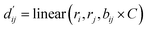 | (21) |
(1) van der Waals interaction: the van der Waals interaction is primarily calculated using the Lennard-Jones potential formula, as shown in the following equation:
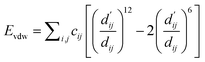 | (22) |
During the data preprocessing stage, we obtained the indices of non-metal atoms, pairing each index of protein atoms with those of ligand atoms to include as many potential pairs of van der Waals interactions as possible. The van der Waals interaction energy is then calculated for each pair. The parameter cij is initialized during preprocessing and updated during model iterations to better approximate the true van der Waals energy values. Finally, the van der Waals interaction energy between the protein and ligand is obtained by summing the energies of all atom pairs.
(2) Hydrogen bond interaction, hydrophobic interaction, and metal interaction: these interactions share the same expression but have different parameters, which need to be learned based on the energy of each interaction type, such as c1, c2 and ω, where eij represents the energy between each atom pair, as shown in the following equation:
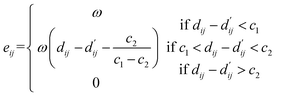 | (23) |
(3) MDN score as a bias term: due to incomplete consideration of energy terms such as charge interactions and overlaps or computational deficiencies among various energy terms, we introduce a bias term for correction. Based on the initial model, we compute the distance distribution outputted by the MDN block against the actual distance and modify it using specified weight values to obtain our energy bias term. It is mainly represented by the following formula:
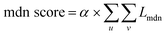 | (24) |
(4) Calculation of absolute binding free energy: the rotation penalty term Trotor aims to consider the entropy loss due to the free rotation of chemical bonds during protein–ligand binding within the binding pocket. We assume that the entropy loss is proportional to the number of rotatable bonds in the ligand molecule. Trotor can be described as follows:
| Trotor = 1 + Crotor + Nrotor | (25) |
The total binding free energy can be described as a linear combination of multiple energy terms. The reason for not directly using summation is that there may exist biases that cannot be calculated well, and this approach can minimize errors as much as possible.
 | (26) |
Dataset and preparation
The PDBBind (Protein Data Bank Binding) dataset is a vital resource in drug research, primarily composed of high-quality protein–ligand (PL) complexes whose structural information is sourced from the Protein Data Bank (PDB). Each complex is experimentally measured under specific conditions and provides binding affinity information, widely used for assessing and training models of drug–target interactions. This dataset offers scientists experimentally validated structural data, supporting them to better understand and predict molecular interactions. In this model, we utilize the latest version of the dataset, PDBBind 2020, as the training set, comprising a total of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443 protein–ligand complexes. As CASF-2016 is used as the test set, 285 data points included in the test set will be excluded during training.
443 protein–ligand complexes. As CASF-2016 is used as the test set, 285 data points included in the test set will be excluded during training.
Given that our work primarily focuses on high-precision prediction of binding free energies, we mainly use FEP1 and FEP2 datasets for testing. The two challenging datasets are widely employed as important benchmarks by models such as GenScore, PBCNet, and PIGNET2. The FEP1 dataset includes eight targets: BACE, CDK2, Jnk1, MCL1, p38, PTP1B, thrombin, and Tyk2, with a total of 199 data points. The FEP2 dataset comprises eight targets: cdk8, cmet, eg5, hif2a, pfkfb3, shp2, syk, and tnks2, with 264 data points. For all proteins, we select the portion where the distance to the ligand atoms is not more than 5 Å as the molecular pocket and compute the distances between atoms within the protein. Atoms with distances less than 6 Å and having a covalent bond are considered to be connected by an edge. Additionally, based on different interaction rules, we extract the corresponding atom indices for each energy term. The atom indices for the ligand atoms are also extracted accordingly.
Model training
Our model is built using PyTorch50 and the data is processed into the PYG51 format. The training process mainly consists of three modules. First is the pre-training module. We utilize the PDBbind2020 database, excluding 285 data points from the coreset. The remaining data is split into a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio for training and validation sets, respectively. During training, the MDN module is employed to fit the distance distribution between PL atom pairs.
1 ratio for training and validation sets, respectively. During training, the MDN module is employed to fit the distance distribution between PL atom pairs.| L = LMDN + 0.001 × Latom + 0.001 × Lbond | (27) |
LMDN = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P((dp,c|hp, hc)) P((dp,c|hp, hc)) | (28) |
Next, fine-tuning the pre-trained model uses the same database, where ABFE is utilized as the label. All data points are used for training, with the coreset serving as the test set and FEP1 and FEP2 as external test sets. The information learned by the SubGT block and GT block is input into the interactive block to transform the distance distribution into the 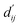 to fit the parameters of the LJ potential formula. Multiple energy terms are linearly regressed to obtain the final ABFE. Three loss functions are involved in the training process.
to fit the parameters of the LJ potential formula. Multiple energy terms are linearly regressed to obtain the final ABFE. Three loss functions are involved in the training process.
| L = Lphysical score + Lmdn score + Lvdw | (29) |
| Lphysical score = MSE(pred, label) | (30) |
| Lmdn score = Pearson(mdn_pred, label) | (31) |
| Lvdw = |MSE(vdwpred, 0.8 × label) − delta| | (32) |
The physical score mainly consists of van der Waals energy terms, hydrogen bond energy terms, hydrophobic interaction energy terms, metal interaction energy terms, and an MDN score term. Among them, the vdw score and MDN score are the most important. To ensure the rationality of each energy term, separate loss functions are applied to enhance the model's interpretability. In the end, several energy terms can be printed out individually for analysis.
Finally, the effectiveness of specific systems is optimized through semi-supervised training. Taking the FEP1 dataset as an example, firstly the fine-tuned scoring model in the previous step is utilized to predict the ABFE of 199 PLs in FEP1 dataset. The predicted values are then treated as pseudo-labels. In semi-supervised training, only the physical scoring component is trained, with gradients retained solely for this part, including 536![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772 parameters. Leading to significantly improved training efficiency. Subsequently, each epoch trains the 199 data points from PDBbind and the 199 data points from FEP1 together. The training is conducted on an RTX Tesla V100 GPU, with a batch size set to 32. On average, each batch iteration requires 0.67 seconds. Consequently, each epoch typically takes approximately 15 seconds to complete. The overall loss function is as follows:
772 parameters. Leading to significantly improved training efficiency. Subsequently, each epoch trains the 199 data points from PDBbind and the 199 data points from FEP1 together. The training is conducted on an RTX Tesla V100 GPU, with a batch size set to 32. On average, each batch iteration requires 0.67 seconds. Consequently, each epoch typically takes approximately 15 seconds to complete. The overall loss function is as follows:
| L = Lreal + α × Lvir | (33) |
Model testing
The testing datasets mainly include CASF-2016, FEP1, FEP2, and PDE10A. In the pre-training phase, torch geometric is utilized to process the decoys screening dataset in CASF-2016. Initially, 57 target pockets were extracted and then scored based on the binding affinities between small molecules and pockets. The model's virtual screening performance on the target pocket is evaluated using enrichment factors (EF_1%), BEROC, etc. The model's ability to predict ABFE was evaluated on the FEP1, FEP2, and PDE10A datasets. The key evaluation metrics include Pearson correlation coefficient (R), Spearman correlation coefficient (ρ), and root mean square error (RMSE).Data availability
The code used in the study is publicly available from the GitHub repository: https://github.com/lingcon01/SuScore.Author contributions
T. J. H., C. Y. H. and Y. K. designed the research study. Q. S. developed the method and wrote the code. J. K. W., R. L. H., L. L. J., H. Z., T. Y. W., and Y. F. L. performed the analysis. Q. S., G. Q. L., Y. K., C. Y. H. and T. J. H. wrote the paper. All authors read and approved the manuscript.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work was financially supported by the National Key R&D Program of China (2024YFA1307501), National Natural Science Foundation of China (92370130, 22373085, 22303083), and China Postdoctoral Science Foundation (2023M733128, 2023TQ0285).References
- Z. Li, Y. Huang, Y. Wu, J. Chen, D. Wu, C.-G. Zhan and H.-B. Luo, J. Med. Chem., 2019, 62, 2099–2111 CrossRef CAS PubMed.
- I. Alibay, A. Magarkar, D. Seeliger and P. C. Biggin, Commun. Chem., 2022, 5, 105 CrossRef.
- D. Wu, X. Zheng, R. Liu, Z. Li, Z. Jiang, Q. Zhou, Y. Huang, X.-N. Wu, C. Zhang, Y.-Y. Huang and H.-B. Luo, Acta Pharm. Sin. B, 2022, 12, 1351–1362 CrossRef CAS PubMed.
- N. Hansen and W. F. van Gunsteren, J. Chem. Theory Comput., 2014, 10, 2632–2647 CrossRef CAS PubMed.
- J. D. Chodera, D. L. Mobley, M. R. Shirts, R. W. Dixon, K. Branson and V. S. Pande, Curr. Opin. Struct. Biol., 2011, 21, 150–160 CrossRef CAS.
- X. He, S. Liu, T.-S. Lee, B. Ji, V. H. Man, D. M. York and J. Wang, ACS Omega, 2020, 5, 4611–4619 CrossRef CAS.
- S. Genheden and U. Ryde, Expert Opin. Drug Discovery, 2015, 10, 449–461 CrossRef CAS.
- Y.-X. Zhu, Y.-J. Sheng, Y.-Q. Ma and H.-M. Ding, J. Phys. Chem. B, 2022, 126, 1700–1708 CrossRef CAS PubMed.
- Z. Cournia, C. Chipot, B. Roux, D. M. York and W. Sherman, in Free Energy Methods in Drug Discovery: Current State and Future Directions, 2021, vol. 1397, pp. 1–38 Search PubMed.
- Z. Yang, W. Zhong, Q. Lv, T. Dong and C. Yu-Chian Chen, J. Phys. Chem. Lett., 2023, 14, 2020–2033 CrossRef CAS PubMed.
- K. Wang, R. Zhou, Y. Li and M. Li, Briefings Bioinf., 2021, 22, bbab072 CrossRef PubMed.
- X. Zhang, H. Gao, H. Wang, Z. Chen, Z. Zhang, X. Chen, Y. Li, Y. Qi and R. Wang, J. Chem. Inf. Model., 2024, 64, 2205–2220 CrossRef CAS PubMed.
- Y. Wang, Z. Wei and L. Xi, BMC Bioinf., 2022, 23, 222 CrossRef CAS PubMed.
- L. Guo, T. Qiu and J. Wang, IEEE Trans. NanoBiosci., 2023, 22, 734–743 CAS.
- J. Jiménez-Luna, L. Pérez-Benito, G. Martínez-Rosell, S. Sciabola, R. Torella, G. Tresadern and G. De Fabritiis, Chem. Sci., 2019, 10, 10911–10918 RSC.
- D. Jiang, C.-Y. Hsieh, Z. Wu, Y. Kang, J. Wang, E. Wang, B. Liao, C. Shen, L. Xu, J. Wu, D. Cao and T. Hou, J. Med. Chem., 2021, 64, 18209–18232 CrossRef CAS.
- Z. Wang, L. Zheng, Y. Liu, Y. Qu, Y.-Q. Li, M. Zhao, Y. Mu and W. Li, Front. Chem., 2021, 9, 7533002 Search PubMed.
- G. Durant, F. Boyles, K. Birchall, B. Marsden and C. M. Deane, bioRxiv, 2023, DOI:10.1101/2023.10.30.564251.
- A. Mastropietro, G. Pasculli and J. Bajorath, Nat. Mach. Intell., 2023, 5, 1427–1436 CrossRef.
- S. Moon, W. Zhung, S. Yang, J. Lim and W. Y. Kim, Chem. Sci., 2022, 13, 3661–3673 RSC.
- S. Moon, S.-Y. Hwang, J. Lim and W. Y. Kim, Digital Discovery, 2024, 3, 287–299 RSC.
- J. Yu, Z. Li, G. Chen, X. Kong, J. Hu, D. Wang, D. Cao, Y. Li, R. Huo, G. Wang, X. Liu, H. Jiang, X. Li, X. Luo and M. Zheng, Nat. Comput. Sci., 2023, 3, 860–872 CrossRef PubMed.
- C. Shen, X. Zhang, C.-Y. Hsieh, Y. Deng, D. Wang, L. Xu, J. Wu, D. Li, Y. Kang, T. Hou and P. Pan, Chem. Sci., 2023, 14, 8129–8146 RSC.
- W. Jin, C. Uhler and N. Hacohen, NeurIPS 2023 Generative AI and Biology (GenBio) Workshop, 2023 Search PubMed.
- I. Yasuda, K. Endo, E. Yamamoto, Y. Hirano and K. Yasuoka, Commun. Biol., 2022, 5, 481 CrossRef CAS.
- M. Su, Q. Yang, Y. Du, G. Feng, Z. Liu, Y. Li and R. Wang, J. Chem. Inf. Model., 2019, 59, 895–913 CrossRef CAS PubMed.
- L. Wang, Y. Wu, Y. Deng, B. Kim, L. Pierce, G. Krilov, D. Lupyan, S. Robinson, M. K. Dahlgren, J. Greenwood, D. L. Romero, C. Masse, J. L. Knight, T. Steinbrecher, T. Beuming, W. Damm, E. Harder, W. Sherman, M. Brewer, R. Wester, M. Murcko, L. Frye, R. Farid, T. Lin, D. L. Mobley, W. L. Jorgensen, B. J. Berne, R. A. Friesner and R. Abel, J. Am. Chem. Soc., 2015, 137, 2695–2703 CrossRef CAS.
- C. E. M. Schindler, H. Baumann, A. Blum, D. Böse, H.-P. Buchstaller, L. Burgdorf, D. Cappel, E. Chekler, P. Czodrowski, D. Dorsch, M. K. I. Eguida, B. Follows, T. Fuchß, U. Grädler, J. Gunera, T. Johnson, C. Jorand Lebrun, S. Karra, M. Klein, T. Knehans, L. Koetzner, M. Krier, M. Leiendecker, B. Leuthner, L. Li, I. Mochalkin, D. Musil, C. Neagu, F. Rippmann, K. Schiemann, R. Schulz, T. Steinbrecher, E.-M. Tanzer, A. Unzue Lopez, A. Viacava Follis, A. Wegener and D. Kuhn, J. Chem. Inf. Model., 2020, 60, 5457–5474 CrossRef CAS.
- R. Meli, G. M. Morris and P. C. Biggin, Frontiers in Bioinformatics, 2022, 2, 885983 CrossRef PubMed.
- M. M. Ghahremanpour, A. Saar, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Inf. Model., 2023, 63, 5309–5318 CrossRef CAS PubMed.
- A. Tosstorff, M. G. Rudolph, J. C. Cole, M. Reutlinger, C. Kramer, H. Schaffhauser, A. Nilly, A. Flohr and B. Kuhn, J. Comput.-Aided Mol. Des., 2022, 36, 753–765 CrossRef CAS.
- W. Lu, Q. Wu, J. Zhang, J. Rao, C. Li and S. Zheng, Adv. Neural Inf. Process. Syst., 2022, 35, 7236–7249 Search PubMed.
- R. Wang, X. Fang, Y. Lu and S. Wang, J. Med. Chem., 2004, 47, 2977–2980 CrossRef CAS.
- T. Mori and M. Ueda, arXiv, 2020, preprint, arXiv:2009.13094, DOI:10.48550/arXiv.2009.13094.
- R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley, J. K. Perry, D. E. Shaw, P. Francis and P. S. Shenkin, J. Med. Chem., 2004, 47, 1739–1749 CrossRef CAS PubMed.
- H. Goel, A. Hazel, V. D. Ustach, S. Jo, W. Yu and A. D. MacKerell, Chem. Sci., 2021, 12, 8844–8858 RSC.
- Z. Xiong, D. Wang, X. Liu, F. Zhong, X. Wan, X. Li, Z. Li, X. Luo, K. Chen, H. Jiang and M. Zheng, J. Med. Chem., 2020, 63, 8749–8760 CrossRef CAS.
- A. Tosstorff, J. C. Cole, R. Bartelt and B. Kuhn, ChemMedChem, 2021, 16, 3428–3438 CrossRef CAS PubMed.
- C. Isert, K. Atz, S. Riniker and G. Schneider, RSC Adv., 2024, 14, 4492–4502 RSC.
- G. Schneider, W. Neidhart, T. Giller and G. Schmid, Angew. Chem., Int. Ed., 1999, 38, 2894–2896 CrossRef CAS.
- H. Sun, G. Tawa and A. Wallqvist, Drug Discovery Today, 2012, 17, 310–324 CrossRef CAS PubMed.
- P. Schneider, Y. Tanrikulu and G. Schneider, Curr. Med. Chem., 2009, 16, 258–266 CrossRef CAS PubMed.
- K. Han, A. Xiao, E. Wu, J. Guo, C. Xu and Y. Wang, Adv. Neural Inf. Process. Syst., 2021, 34, 15908–15919 Search PubMed.
- C. Shen, X. Zhang, Y. Deng, J. Gao, D. Wang, L. Xu, P. Pan, T. Hou and Y. Kang, J. Med. Chem., 2022, 65, 10691–10706 CrossRef CAS.
- X. Zhang, O. Zhang, C. Shen, W. Qu, S. Chen, H. Cao, Y. Kang, Z. Wang, E. Wang, J. Zhang, Y. Deng, F. Liu, T. Wang, H. Du, L. Wang, P. Pan, G. Chen, C.-Y. Hsieh and T. Hou, Nat. Comput. Sci., 2023, 3, 789–804 CrossRef CAS PubMed.
- J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, AI Open, 2020, 1, 57–81 CrossRef.
- C. Zhang, D. Song, C. Huang, A. Swami and N. V. Chawla, Presented in Part at the Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 2019 Search PubMed.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, arXiv, 2018, preprint, arXiv:1810.00826, DOI:10.48550/arXiv.1810.00826.
- Z. Chen, L. Chen, S. Villar and J. Bruna, Adv. Neural Inf. Process. Syst., 2020, 33, 10383–10395 Search PubMed.
- S. Imambi, K. B. Prakash and G. Kanagachidambaresan, Programming with TensorFlow: Solution for Edge Computing Applications, 2021, pp. 87–104 Search PubMed.
- M. Fey and J. E. Lenssen, arXiv, 2019, preprint, arXiv:1903.02428, DOI:10.48550/arXiv.1903.02428.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc07405j |
| ‡ Equivalent authors. |
| This journal is © The Royal Society of Chemistry 2025 |