Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crowding effects on the structure and rheology of ultrasoft PNIPAM–PEGMA copolymer microgels†
Gavino
Bassu
ab,
Jacopo
Vialetto
 ab,
José
Ruiz-Franco
ab,
José
Ruiz-Franco
 cd,
Andrea
Scotti
cd,
Andrea
Scotti
 e,
Judith E.
Houston
f,
Jitendra
Mata
e,
Judith E.
Houston
f,
Jitendra
Mata
 gh,
Emanuela
Zaccarelli
gh,
Emanuela
Zaccarelli
 ij and
Marco
Laurati
ij and
Marco
Laurati
 *ab
*ab
aDipartimento di Chimica “Ugo Schiff”, Università di Firenze, Sesto Fiorentino (FI) 50019, Italy. E-mail: marco.laurati@unifi.it
bConsorzio per lo Sviluppo dei Sistemi a Grande Interfase (CSGI), via della Lastruccia 3, Sesto Fiorentino (FI) 50019, Italy
cDepartment of Condensed Matter Physics, University of Barcelona, 08028 Barcelona, Spain
dInstitute for Complex Systems (UBICS), University of Barcelona, 08028 Barcelona, Spain
eDivision of Physical Chemistry, Lund University, SE-22100 Lund, Sweden
fEuropean Spallation Source ERIC, Box 176, SE-22100 Lund, Sweden
gAustralian Centre for Neutron Scattering (ACNS), Australian Nuclear Science and Technology Organisation (ANSTO), Lucas Height, New South Wales 2234, Australia
hSchool of Chemistry, University of New South Wales, NSW, Australia
iDepartment of Physics, Sapienza University of Rome, Piazzale Aldo Moro 2, 00185 Roma, Italy
jCNR Institute of Complex Systems, Uos Sapienza, Piazzale Aldo Moro 2, 00185 Roma, Italy
First published on 26th November 2024
Abstract
We investigate the link between the internal microstructure of poly(N-isopropylacrylamide)–poly(ethylene glycol) methyl ether methacrylate (PNIPAM–PEGMA) microgels, their bulk moduli and the rheological response and structural arrangement in dense suspensions. The low degree of crosslinking combined with the increased hydrophilicity induced by the presence of PEGMA results in a diffuse, star-like density profile of the particle and very low values of the bulk modulus in dilute conditions, as determined by small angle neutron scattering (SANS). The ultrasoft nature of the particle is reflected in the changes of the structural arrangement in dense suspensions, which evidence a strong deswelling and a sharp rise of the bulk modulus at moderate packing fractions. At larger packings the single particle morphology and softness saturate, and we observe a structural transition from a dispersion-like to a hydrogel-like behavior. The transition is also reflected in the rheological response in the form of a two-step yielding at large packing fractions, characteristic of systems in which a network structure is present. Our results demonstrate that a knowledge of the internal structure and mechanics of individual microgels is needed to determine and tune the properties of dense suspensions, and optimize their response for applications in biomedicine and as filtration systems.
1 Introduction
Microgels are soft colloidal particles formed by cross-linked polymer networks. The properties of the polymers forming the network make them responsive to stimuli like temperature,1 pH,2,3 light,4 among others. This responsiveness is appealing for applications and can be also used to tune their physicochemical properties to address fundamental physics questions. Thermoresponsive microgels composed of poly(N-isopropylacrylamide) (PNIPAM) have been thoroughly studied for several years. They undergo a volume phase transition (VPT) at Tc ≈ 32 °C5,6 from a swollen to a collapsed state, associated with the hydrophilic to hydrophobic transition of PNIPAM.7 This results also in a change in particle softness.8,9 When following a batch precipitation polymerization route their internal microstructure is characterized by a non-uniform density profile, consisting of a denser core and a more diffuse corona10 that contains dangling ends.11,12 This microstructure can be manipulated through the synthetic process,13,14 the degree of crosslinking15,16 and the presence of a copolymer,17,18 resulting in different degrees of heterogeneity and different amounts and distributions of the crosslinkers within the gel network. These changes in turn determine the mechanical response of single particles and also affect the rheological response of suspensions in the linear and non-linear regimes19,20 and the interaction with surfaces and interfaces.21 The individual particle softness can be quantified by measuring the elastic modulus of the microgels using atomic force microscopy22 or micropipette aspiration,23 or the bulk modulus by applying osmotic stress combined with dynamic light scattering24 or small angle neutron scattering (SANS) with contrast variation.25,26 Application of osmotic stresses is obtained by dispersing the microgels in solutions of non-adorbing polymers with different concentrations. Measurement of the microgel size as a function of osmotic pressure through SANS, by contrast matching the scattering contribution of the deuterated polymer, allows to determine the bulk modulus.25,26 Moreover, SANS is particularly suitable for nanometric microgels due to the accessible range of scattering vectors. The microgel internal microstructure is also closely connected to the phase behavior of the corresponding suspensions.27 In particular, recent studies on PNIPAM microgels showed that when the packing fraction exceeds random-close-packing, the core-corona structure of these particles and the presence of dangling ends give rise to different mechanisms by which the microgels can adapt to overpacking, namely deformation and faceting, interpenetration and isotropic compression.28 These variations in the internal microstructure were also linked to the rheological response.29 However, this study was limited to a degree of crosslinking (5 mol%) of PNIPAM microgels, corresponding to relatively stiff particles with an internal microstructure that can be modeled as a fuzzy sphere. Therefore, the interplay between the internal architecture and the softness of the network in determining the phase behavior and rheological properties of microgels is still largely unexplored.In this work, we investigate such interplay for the case of copolymer microgels formed by PNIPAM and poly(ethylene glycol) methyl ether methacrylate (PEGMA). Being non-cytotoxic,30 the presence of PEGMA increases the biocompatibility of thermoresponsive PNIPAM microgels in view of biomedical applications.31–33 The PEGMA used in this work has no measurable low critical solution temperature (LCST)34 due to its large molecular weight (Mn = 950 g mol−1) and is thus non-thermoresponsive. Shorter PEGMA alone or in combination with other copolymers can be also used to form microgels, that for smaller Mn can be thermoresponsive with tunable VPT temperature.35 In a recent work, we showed that for low crosslinking degree (1 mol%) PNIPAM–PEGMA copolymer microgels obtained in one-batch synthesis present a very diffuse, star-like polymer density profile and an inhomogeneous collapse, with the VPT transition shifted to higher temperatures compared to pure PNIPAM microgels.18 Furthermore, the presence of PEGMA modifies the interparticle interactions, in particular above the VPT temperature, and the resulting phase behavior.36 Here, we first link the internal microstructure of PNIPAM–PEGMA microgels to the mechanical properties of the individual particles by measuring the bulk modulus of microgels dispersed in PEG solutions through SANS. We find that the low crosslinking degree and star-like profile result in ultrasoft colloids. We then explore the effects of the internal microstructure and associated softness on the phase behavior of dense packings, analyzing scattering intensities obtained by small angle X-rays scattering (SAXS). We find that particles deswell significantly at moderate packing fractions, even smaller than what previously observed for pure PNIPAM microgels,37 and we link this unusual response to the single particle mechanical properties. When the particles become mechanically harder following deswelling,25 a saturation of the structural changes is instead observed and the structural organization of the system resembles that of a hydrogel network. The structural changes have a signature in the non-linear rheological response of the system, with the appearance of a second yielding process when the structural saturation occurs. Our findings provide evidence of the close connection between internal architecture, individual particle softness and rheological response of dense microgel suspensions, showing how this could be manipulated in view of applications.
2 Materials and methods
2.1 Experimental system
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rcf for 20 minutes in order to remove any residual impurity and were subsequently recovered by freeze-drying. 1H-NMR characterization showed that the effective incorporation of PEGMA corresponded to a weight proportion of 66% PNIPAM and 34% PEGMA.36 The hydrodynamic radius of the microgels was determined by dynamic light scattering, RH ≈ 144 nm in water at low temperature T = 20 °C and decreases to RH ≈ 78 nm at high T = 50 °C, with the VPT occurring at Tc ≈ 36 °C (see Fig. S1 of the ESI† for the entire RHvs. T dependence). The value of the VPT temperature Tc, also later called VPTT, is higher than that of pure PNIPAM microgels in water (Tc ≈ 32 °C).
000 rcf for 20 minutes in order to remove any residual impurity and were subsequently recovered by freeze-drying. 1H-NMR characterization showed that the effective incorporation of PEGMA corresponded to a weight proportion of 66% PNIPAM and 34% PEGMA.36 The hydrodynamic radius of the microgels was determined by dynamic light scattering, RH ≈ 144 nm in water at low temperature T = 20 °C and decreases to RH ≈ 78 nm at high T = 50 °C, with the VPT occurring at Tc ≈ 36 °C (see Fig. S1 of the ESI† for the entire RHvs. T dependence). The value of the VPT temperature Tc, also later called VPTT, is higher than that of pure PNIPAM microgels in water (Tc ≈ 32 °C).
2.2 Small-angle neutron and X-ray scattering (SANS/SAXS)
SAXS measurements for ϕeff = 0.48, 0.61 and 0.95 were performed on a Xeuss 3.0 HR (Xenocs, Grenoble, France) using a 1028 × 1062 pixels (pixel size 75 × 75 μm2) EIGER2R 1 M hybrid pixel photon counting detector (Dectris Ltd, Baden, Switzerland). The wavelength of the X-ray beam was λ = 1.542 Å. The sample chamber was maintained at atmospheric pressure. A sample-to-detector distance of 1800 mm was used to access a Q-range of 0.004 to 0.14 Å−1. Microgel suspensions were contained in 1.5 mm thick borosilicate glass capillaries sealed with glue to avoid evaporation. Absolute scattering intensities in cm−1 were obtained by using glassy carbon as a secondary standard. The 1D azimuthally averaged scattering patterns were reduced by subtracting the scattering intensity from empty holder plus water. Data reduction, normalization, and merging was performed in XSACT (X-ray scattering analysis and calculation tool, Xenocs, France). Additional measurements for ϕeff = 1.22, 1.30, 1.41 and 1.49 were performed at the CoSAXS beamline at the 3 GeV ring of the MAX-IV Laboratory (Lund, Sweden). The Q-range of interest in between 7 × 10−4 and 7 × 10−2 Å−1 was covered on CoSAXS using a sample-to-detector distance of 14.2 m with X-ray beam energy E = 12.4 keV. The instrument is equipped with an Eiger2 4 M SAXS detector with pixel size of 75 × 75 μm2. A python-based code was used to convert the 2D images to 1D profiles.
| I(Q) = ϕV(Δρ)2P(Q)S(Q) + bkg | (1) |
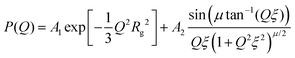 | (2) |
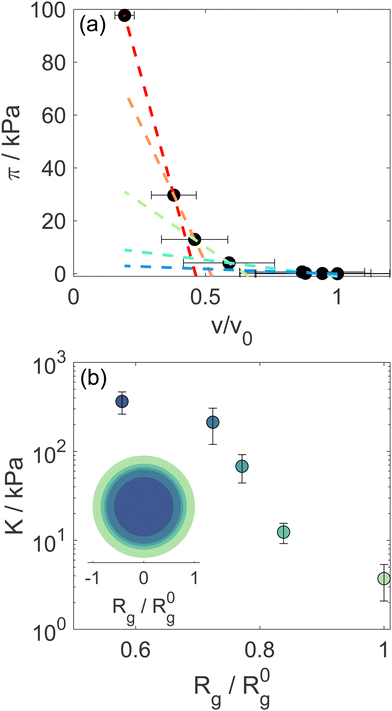
Using Rg we calculate the microgel volume v and we correlate it with the known osmotic pressure π of the d85%PEG solutions. The concentrations of d85%PEG are converted in π using the empirical law from Houston et al.,25 measured using a membrane osmometer, and are chosen in order to cover a range between 0 and ∼100 kPa. The bulk modulus K is then determined from the slope of the π vs. v curves: K = −vdπ/dv.
Following previous studies,36S(Q) was obtained from Langevin dynamics simulations of N = 2000 particles with mass m and polydispersity 0.25. These particles interact by a Hertzian potential, which is expressed as
| V(r) = U(1 − r/σ)5/2θ(σ − r), | (3) |
For ϕeff > 1 an additional term was included in eqn (1) to describe the excess scattering at low Q values. This regime was described with the Debye–Bueche model46 for solid-like heterogeneities of average size a:
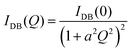 | (4) |
2.3 Rheology
All measurements were performed on a DHR-3 (TA Instruments) stress-controlled rheometer. The eventual presence of wall slip effects was preliminary tested through the measurement of the dependence of the sample viscosity on the gap size obtained with a 20 mm smooth plate-plate geometry. For samples with ϕeff > 0.48 no indications of slip were found and a cone-plate geometry with a 40 mm diameter and a cone angle of 0.5081° was used for all tests. For ϕeff = 0.48 we found indications of wall slip and therefore a crosshatched plate-plate geometry with diameter 40 mm was used instead. Temperature was controlled through a Peltier lower plate and it was fixed to 20 °C. To avoid evaporation, a solvent trap was used.In order to minimize the effects of sample history, a rejuvenation protocol was applied before each measurement. First, an oscillatory dynamic time sweep with a large strain amplitude (100% < γ0 < 700%, depending on sample) was applied for 180 s. This was followed by a dynamic time sweep with a low strain amplitude (0.05% < γ0 < 0.2%, depending on sample) that was stopped when a steady state in the viscoelastic moduli was reached. We found that 180 s were sufficient to reach the steady state for all samples. The frequency used for the two time sweeps was ω = 10 rad s−1.
3 Results and discussion
3.1 Form factor and bulk modulus
The particle form factor of the microgels was determined from the SANS measurement of a dilute suspension and is shown as the bottom curve in Fig. 1. The very smooth Q-dependence of the scattered intensity I(Q), with no clear indication of a minimum, indicates a very diffuse density profile together with significant polydispersity. I(Q) was modeled according to eqn (1) and the star polymer form factor model of eqn (2) (Fig. 1). The fitting leads to a value for the radius of gyration Rg = 900 ± 20 Å and a blob size ξ = 300 ± 10 Å, with ν = 0.66 and a polydispersity of about 25%, in good agreement with previous findings.18 The other curves in Fig. 1 corresponds to the scattered intensities measured for microgel–d85%PEG mixtures used to estimate the bulk modulus of the microgels. The d85%PEG concentration increases from bottom to top and varies between 0.30 and 5.98 wt% (top curve). It can be observed that with increasing d85%PEG amount the Guinier regime of the curves progressively shifts to larger Q values, as an effect of microgel deswelling induced by the increasing osmotic pressure produced by the d85%PEG solution. The curves were modeled also in this case using eqn (1) and (2) and the corresponding fits are shown as solid lines in Fig. 1. | ||
| Fig. 1 SANS scattering intensities I(Q) for mixtures of PNIPAM–PEGMA microgels and d85%PEG with increasing d85%PEG concentration (as indicated). Lines represent fits of the microgel form factor using the star polymer model of eqn (2). | ||
The progressive decrease of the value of Rg obtained from fits as a function of d85%PEG concentration is shown in Fig. S2 of the ESI.† These values were used to determine the particle volume v = 4πRH3/3, that was normalized to the value in the absence of d85%PEG (v0 = 4π(R0H)3/3). Note that in the calculation we ignored the proportionality factor between RH and Rg since the modulus only depends on the slope of the π vs. v/v0 curves. Fig. 2a shows the osmotic pressure as a function of v/v0, the dashed lines are the fits used to determine the bulk modulus K of the microgel in different compression regimes (more details in the Materials and methods section). As it can be seen in Fig. 2b, the value of K in the low compression regime is about 3.7 ± 1.6 kPa, which confirms previous estimates36 and is comparable to that of ultra-low crosslinked microgels.25 As expected and similar to the case of the ultra-low crosslinked microgels, with increasing osmotic pressure and induced deswelling (smaller Rg/R0g), K increases, reaching a value about 2 orders of magnitude larger for the highest applied osmotic pressure (Rg/R0g ≈ 0.58). Interestingly, while the bulk modulus shows the mentioned similarities with ultra-low crosslinked microgels, the deswelling induced by temperature presents differences. Indeed the swelling ratio in response to temperature changes of our star-like microgels is relatively small, SD = RH(T = 20 °C)/RH(T = 50 °C) = 1.77 ± 0.05 (Fig. S1, ESI†), i.e. much lower than that of ultra-low crosslinked microgels, for which SD ≈ 3.2,25 and rather comparable to that of regular microgels synthesized with 5 mol% N,N′-methylenebis(acrylamide) (BIS) crosslinker (SD ≈ 1.8).9 We should consider, however, that the presence of non-thermoresponsive PEGMA within the PNIPAM network hinders the temperature-induced collapse of the microgel, as demonstrated in previous work18 (while PEGMA on the surface does not affect the collapse19), in comparison to ultralow crosslinked microgels or PNIPAM microgels with similar star-like architecture having comparable initial value of the modulus. It is interesting to note that the swelling ratio estimated from the reduction of Rg at the largest measured osmotic pressure seems comparable to that of temperature-induced deswelling. However, the microgels could continue shrinking at higher applied osmotic pressures that could not be achieved in our experiments. Thus a conclusive comparison between temperature-induced and compression-induced deswelling cannot be provided in this work. The coexistence of a low modulus with a moderate swelling ratio indicates once more that the relation between these quantities might be complex, since the crosslinking degree, the internal architecture and the responsiveness of the components of a microgel might play a different role in determining them, as already shown by the case of microgels with a solvent-filled cavity in their center.47
3.2 Structural arrangement for increasing packing fraction
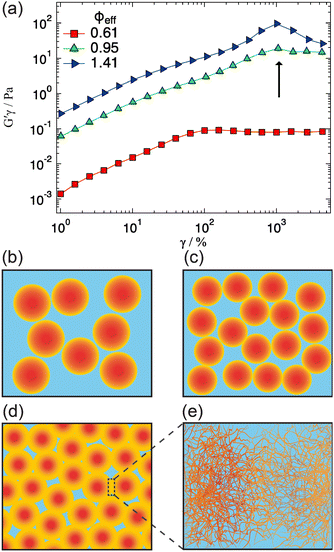
In previous work36 we characterized the structure and interactions of similar suspensions from the relatively dilute case (ϕeff = 0.06) to intermediate concentrations (ϕeff = 0.34), still well below random close packing. We found that even if the explored packing fractions were moderate, and therefore the pressure exerted by neighbors on a single particle should not be large enough to induce particle shrinking, the size of the particles showed a pronounced reduction with increasing ϕeff, indicating strong deswelling. As reported in the literature particles synthesized with ionic initiator are slightly charged and surrounded by counter-ion clouds.48 Once the particle concentration increases these counter-ion clouds percolate the available volume outside the microgels. This induces an unbalance in the osmotic pressure inside and outside the particles leading to deswelling when it becomes comparable or larger than the bulk modulus of the particles.37 As shown in the previous section, we were now able to determine the bulk modulus of the particles that is comparable to the increase in osmotic pressure reported in the literature,37 confirming their very pronounced softness, therefore supporting that charge effects can become relevant at relatively moderate packing fractions due to the suspension osmotic pressure. To address how this influences the structural evolution also at larger ϕeff, where contacts are present and provide an additional contribution to the deformation, interpenetration and deswelling of the particles, we extended our study to cover the interval 0.48 ≤ ϕeff ≤ 1.49.For ϕeff < 1 the SAXS scattering curves in Fig. 3a show clearly the presence of a structure factor peak. Furthermore, with increasing ϕeff the curves progressively shift to larger Q values. Increasing ϕeff from 0.48 to 0.61 the shift involves the entire curve, while further increasing ϕeff to 0.95 the large Q-value part (Q > 0.015 Å−1), where the decay of the form factor is observed, only moves slightly. This indicates that structural changes are significant when increasing effective packing fraction from ϕeff = 0.48 to ϕeff = 0.61, while they are more moderate up to ϕeff = 0.95. For the intermediate Q-value part (0.004 Å−1 ≤ Q ≤ 0.01 Å−1), where the structure factor peak is observed, the shift of the position of the I(Q) (S(Q)) peak (Qp) to larger values (Fig. 3a, inset) means a reduction of the average inter-particle distance. It is interesting to note that, in addition, the I(Qp) peak first increases in height from ϕeff = 0.48 to ϕeff = 0.61, while it decreases for ϕeff = 0.95 (Fig. 3a, inset), in agreement with what previously observed in simulations36 and explained as a combined effect of the large polydispersity of our system and hertzian interactions.
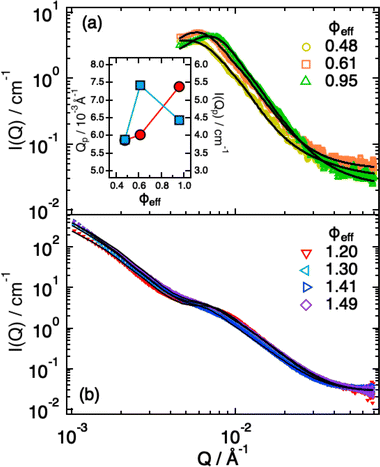 | ||
| Fig. 3 SAXS intensities I(Q) for ϕeff < 1.0 (a) and ϕeff > 1.0 (b). Lines are fits according to eqn (1), in (b) with the addition of the term from eqn (4). Inset: Dependence of the position (red circles) and height (blue squares) of the I(Q) peak as a function of ϕeff. | ||
Modeling of the scattering curves using eqn (1) and (2) and simulated structure factors (lines in Fig. 3a) leads to the determination of the radius of gyration and blob size for the curves in Fig. 3a. The results are reported in Fig. 4a, together with those obtained for larger ϕeff (that will be discussed later). In all cases a polydispersity p ≈ 0.25 was obtained from the fits, in agreement with the one used for calculating S(Q) in simulations. As anticipated from the qualitative analysis of the scattering curves, Rg and ξ (inset of Fig. 4a) decrease slightly when increasing ϕeff. Note that the value of Rg for ϕeff = 0.48 is about a factor 3 smaller than its corresponding value in dilute conditions,36R0g, indicating a very pronounced particle deswelling/compression. Note also that the values of Rg measured for these packing fractions are almost half of the Rg value measured for the largest osmotic pressure reported in Fig. 2, for which Rg/R0g ≈ 0.58. A comparable value of Rg/R0g ≈ 0.58 was obtained for ϕeff = 0.24 in previous work.36 Since the bulk modulus of the particles shows a sharp increase when the particle size decreases from 1 to 0.58 as an effect of the increase in osmotic pressure, reaching a value of 364 ± 102 kPa, it is reasonable to assume that for a crowding induced deswelling corresponding to Rg/R0g ≈ 0.31 at ϕeff = 0.48 the bulk modulus of the particles is K ≳ 350 kPa: the particles are already very stiff, and the size reduction should become very moderate, as indeed observed in our data, where Rg/R0g decreases to Rg/R0g ≈ 0.26 for almost double packing fraction, ϕeff = 0.95. Fig. S3 of the ESI† shows Rg/R0gvs. ϕeff including former data for 0.05 ≤ ϕeff ≤ 0.36, better evidencing the slowdown of the size reduction already at intermediate packing fractions. These results suggest that the structural evolution of single particles in increasingly crowded suspensions can be semi-quantitatively linked to the corresponding evolution of the bulk modulus.
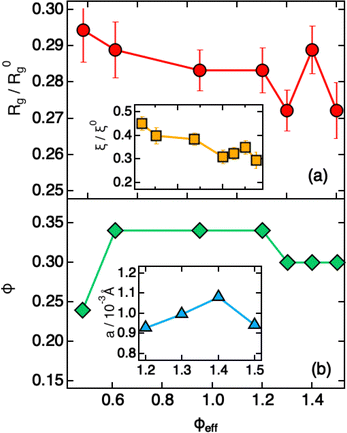 | ||
| Fig. 4 Parameters extracted from fitting SAXS intensities of Fig. 3 using eqn (1), (2) and (4), plotted as a function of ϕeff. (a) Reduced radius of gyration Rg/R0g and (inset, same x-axis as the main plot) reduced blob size ξ/ξ0. R0g and ξ0 are the values measured in dilute conditions. (b) Estimated volume fraction (ϕ) and (inset, x-axis values corresponding to ϕeff) heterogeneity size a. | ||
A qualitative change in the scattering curves is observed for ϕeff ≥ 1.20 (Fig. 3b): the structure factor peak at intermediate Q values is no longer discernible and for Q > 2 × 10−2 Å−1 the curves, including the one for ϕeff = 0.95 (not shown), are closely comparable and only slightly shifted toward larger Q values with increasing packing fraction, as expected since polymer chain scattering is observed in this Q range. This suggests that no further morphological variation of the single particles is observed with increasing ϕeff in this regime. A low Q scattering is observed for all samples, indicating the presence of structural heterogeneities. Modeling of the data with eqn (1) and (2) and with in addition the term in eqn (4) to describe heterogeneities leads to values of Rg and ξ that are closely comparable to those obtained for ϕeff = 0.95 (Fig. 4a). This confirms that no significant structural variation occurs for ϕeff ≥ 0.95, in agreement with the strongly compressed and stiff morphology of the particles. The values of the packing fraction ϕ obtained from the fits are closely comparable for ϕeff ≥ 0.61, suggesting a saturation of the local packing of the particles, which coincided with the saturation of deswelling. The size of heterogeneities a for ϕeff ≥ 1.20 increases from 910 ± 40 to 1080 ± 50 Å up to ϕeff = 1.41, and decreases again to 900 ± 30 Å for the largest effective packing fraction here investigated. These values correspond to 1.5 to 2 particle diameters, i.e. relatively small scale heterogeneities. The small variations of the structural organization of the system for ϕeff > 0.61 suggest the formation of a state that resembles a macroscopic hydrogel at these packing fractions. Indeed the data for ϕeff ≥ 1.20 resemble those measured for such systems and can be also modeled in these terms, as shown in Section SIV and Fig. S4 of the ESI.† The structural changes with increasing ϕeff discussed in this section, namely the strong deswelling at intermediate packing fractions and the formation of a dense, hydrogel-like suspension for ϕeff > 0.61, are sketched in Fig. 5b–e.
3.3 Rheology: signatures of network yielding
We explored possible signatures of the structural transition occurring for ϕeff > 0.61, and sketched in Fig. 5d and e in the rheological response of the system. It has been shown that the non-linear rheological response is especially sensitive to the structural arrangements and interactions of particles in dense suspensions.49–52Fig. 5 shows the results of amplitude sweeps at oscillation frequency ω = 1 rad s−1 measured for ϕeff = 0.61, 0.95 and 1.41. The data are reported as elastic stress G′γ0vs. γ0 (strain amplitude): in this representation the yielding points are clearly evidenced as inflections or maxima.49,53 The sample with ϕeff = 0.61 shows initially a linear increase, corresponding to the linear viscoelastic regime, followed by an inflection for γ0 ≈ 80% and then tends to a plateau, indicating the transition to a fluid-like response after yielding, in agreement with findings on colloidal glasses and gels.49,54,55 With the increasing of ϕeff to 0.95 the first inflection is still visible but in addition a second one appears at larger strains, γ0 ≈ 1000%. Further increasing ϕeff to 1.41 the second inflection becomes a pronounced maximum that is observed at approximately the same strain amplitude as for ϕeff = 0.95. In agreement with previous findings on soft, hairy particles,40 we interpret the first inflection as the initial restructuring of the sample at the level of nearest neighbors, i.e. the breaking of entropic cages.54,56 For ϕeff = 0.61 the restructuring of the local order of the colloidal suspension, corresponding to the coordination represented by the structure factor peak, is sufficient to induce complete yielding and the onset of flow. On the other hand, for ϕeff ≥ 0.95 the additional network structure formation and the presence of heterogeneities and entanglements with significantly long lifetime does not allow the system to flow. Larger strain amplitudes are necessary to disentangle interpenetrated and compressed coronas of local clusters before this becomes possible. It is interesting to note that even for ϕeff ≥ 0.95 the first inflection is present, indicating that, despite the transition to a gel-like structure, individual particles are still present and can displace with respect to each other under shear. Furthermore, the second yielding occurs at comparable strain amplitudes for ϕeff = 0.95 and 1.41, which seems to be consistent with the fact that the Rg and the characteristic size of the heterogeneities are almost independent of ϕeff in the gel-like state.4 Conclusions
We investigated the link between the internal microstructure, the single particle mechanics and the structural arrangement and rheological response of dense suspensions of PNIPAM–PEGMA microgels. The smooth and diffuse star-like density profile of the microgels determined by SANS results in a very low bulk modulus in dilute suspensions, that is comparable to that of ultra-low crosslinked microgels. The large softness of the particles leads to a pronounced reduction of the particle size even at intermediate effective packing fractions. This reduction slows down above ϕeff = 0.48 and stops for ϕeff ≥ 0.95. The slowdown can be linked to the strong rise of the bulk modulus with increasing osmotic pressure. Correspondingly, the structure factor peak that was increasing in height and shifting to larger Q values up to ϕeff = 0.61, indicative of the reduced interparticle distance, starts to decrease until becoming indistinguishable for ϕeff > 1. In this region the scattering curves present a similar shape independent of ϕeff, that can be described alternatively with a polymer gel network model. This is attributed to the interpenetration of increasingly collapsed coronae that form relatively long-lived entanglements and thus an extended polymer network of connected microgels. This scenario is further supported by the non-linear rheological response of samples with ϕeff ≥ 1, in which relaxation of the temporary entanglements leads to a yielding point at large strain amplitudes that, as the gel structure, is almost independent of ϕeff. A yielding point associated with restructuring of entropic cages is however still present. Our results thus indicate that for ultrasoft microgels with a diffuse density profile and dangling ends, the properties of dense suspensions with ϕeff ≥ 1 are strongly influenced by the formation of entanglements between chains and of an extended polymer network. These findings have important implications for applications in which dense suspensions of soft particles are involved, like 3D printing of artificial tissue and the fabrication of anti-fouling surfaces.Data availability
Data for this article, including raw SANS, SAXS and Rheology data are available at Zenodo at DOI: https://doi.org/10.5281/zenodo.13769530.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This manuscript is dedicated to Prof. Stefan U. Egelhaaf, an outstanding scientist, wonderful person and true friend. M. L. and E. Z. acknowledge financial support by the Italian Ministry of University and Research (MUR) under the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender No. 104 published on 2.2.2022 by the Italian Ministry of University and Research (MUR), funded by the European Union – NextGenerationEU – Project Co-MGELS, contract No. 2022PAYLXW. AS acknowledges financial support from the Knut and Alice Wallenberg Foundation (Wallenberg Academy Fellows). We acknowledge MAX IV Laboratory for time at the CoSAXS beamline under Proposals 20231840 and 20231866, and ANSTO for the time at the Quokka beamline under Proposal P16948. We thank Jürgen Allgaier and Lisa Fruhner for the synthesis of d85%PEG. J. V. acknowledges funding from Ministero dell’Università e della Ricerca (D.D. 247 published on 19.08.2022, grant No. MSCA_0000004), funded by European Union – NextGenerationEU – PNRR, Missione 4, Componente 2, Investimento 1.2.Notes and references
- B. Sierra-Martin, J. J. Lietor-Santos, A. Fernandez-Barbero, T. T. Nguyen and A. Fernandez-Nieves, Swelling Thermodynamics of Microgel Particles, John Wiley & Sons, Ltd, 2011, ch. 4, pp. 71–116 Search PubMed.
- B. H. Tan and K. C. Tam, Adv. Colloid Interface Sci., 2008, 136, 25–44 CrossRef CAS.
- V. Nigro, R. Angelini, M. Bertoldo, V. Castelvetro, G. Ruocco and B. Ruzicka, J. Non-Cryst. Solids, 2015, 407, 361–366 CrossRef CAS.
- H.-J. Zhang, Y. Xin, Q. Yan, L.-L. Zhou, L. Peng and J.-Y. Yuan, Macromol. Rapid Commun., 2012, 33, 1952–1957 CrossRef CAS.
- T. T. Nguyen, Microgel Suspensions: Fundamentals and Applications, 2011, vol. 73 Search PubMed.
- F. Scheffold, Nat. Commun., 2020, 11, 1–13 CrossRef.
- L. Tavagnacco, E. Zaccarelli and E. Chiessi, Phys. Chem. Chem. Phys., 2018, 20, 9997–10010 RSC.
- L. Rovigatti, N. Gnan, A. Ninarello and E. Zaccarelli, Macromolecules, 2019, 52, 4895–4906 CrossRef CAS.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS PubMed.
- S. Meyer and W. Richtering, Macromolecules, 2005, 38, 1517–1519 CrossRef CAS.
- N. Dingenouts, C. Norhausen and M. Ballauff, Macromolecules, 1998, 31, 8912–8917 CrossRef CAS.
- N. Boon and P. Schurtenberger, Phys. Chem. Chem. Phys., 2017, 19, 23740–23746 RSC.
- T. Kyrey, J. Witte, A. Feoktystov, V. Pipich, B. Wu, S. Pasini, A. Radulescu, M. U. Witt, M. Kruteva, R. von Klitzing, S. Wellert and O. Holderer, Soft Matter, 2019, 15, 6536–6546 RSC.
- M. U. Witt, S. Hinrichs, N. Möller, S. Backes, B. Fischer and R. von Klitzing, J. Phys. Chem. B, 2019, 123, 2405–2413 CrossRef CAS PubMed.
- I. Varga, T. Gilányi, R. Mészáros, G. Filipcsei and M. Zrnyi, J. Phys. Chem. B, 2001, 105, 9071–9076 CrossRef CAS.
- F. Schneider, A. Balaceanu, A. Feoktystov, V. Pipich, Y. Wu, J. Allgaier, W. Pyckhout-Hintzen, A. Pich and G. J. Schneider, Langmuir, 2014, 30, 15317–15326 CrossRef CAS PubMed.
- Y. Hertle and T. Hellweg, J. Mater. Chem. B, 2013, 1, 5874–5885 RSC.
- R. Rivas-Barbosa, J. Ruiz-Franco, M. A. Lara-Peña, J. Cardellini, A. Licea-Claverie, F. Camerin, E. Zaccarelli and M. Laurati, Macromolecules, 2022, 55, 1834–1843 CrossRef CAS PubMed.
- J. Vialetto, S. N. Ramakrishna, L. Isa and M. Laurati, J. Colloid Interface Sci., 2024, 672, 814–823 CrossRef CAS.
- A. Scotti, M. Brugnoni, C. G. Lopez, S. Bochenek, J. J. Crassous and W. Richtering, Soft Matter, 2020, 16, 668–678 RSC.
- J. Vialetto, S. N. Ramakrishna and L. Isa, Sci. Adv., 2022, 8, eabq2019 CrossRef CAS PubMed.
- S. M. Hashmi and E. R. Dufresne, Soft Matter, 2009, 5, 3682–3688 RSC.
- P. Voudouris, D. Florea, P. van der Schoot and H. M. Wyss, Soft Matter, 2013, 9, 7158–7166 RSC.
- B. Sierra-Martin, J. A. Frederick, Y. Laporte, G. Markou, J. J. Lietor-Santos and A. Fernandez-Nieves, Colloid Polym. Sci., 2011, 289, 721–728 CrossRef CAS.
- J. E. Houston, L. Fruhner, A. de la Cotte, J. R. González, A. V. Petrunin, U. Gasser, R. Schweins, J. Allgaier, W. Richtering, A. Fernandez-Nieves and A. Scotti, Sci. Adv., 2022, 8, eabn6129 CrossRef CAS.
- T. Höfken, U. Gasser, S. Schneider, A. V. Petrunin and A. Scotti, Macromol. Rapid Commun., 2024, 2400043 CrossRef.
- P. S. Mohanty, S. Nöjd, K. van Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1487 CrossRef.
- G. M. Conley, P. Aebischer, S. Nöjd, P. Schurtenberger and F. Scheffold, Sci. Adv., 2017, 3, e1700969 CrossRef PubMed.
- G. M. Conley, C. Zhang, P. Aebischer, J. L. Harden and F. Scheffold, Nat. Commun., 2019, 10, 2436 CrossRef PubMed.
- L. Hartmann, K. Watanabe, L. L. Zheng, C.-Y. Kim, S. E. Beck, P. Huie, J. Noolandi, J. R. Cochran, C. N. Ta and C. W. Frank, J. Biomed. Mater. Res., Part B, 2011, 98, 8–17 CrossRef.
- M. Zhang, X. Li, Y. Gong, N. Zhao and X. Zhang, Biomaterials, 2002, 23, 2641–2648 CrossRef CAS.
- K. Bjugstad, K. Lampe, D. Kern and M. Mahoney, J. Biomed. Mater. Res., Part A, 2010, 95, 79–91 CrossRef CAS.
- L. Luo Zheng, V. Vanchinathan, R. Dalal, J. Noolandi, D. J. Waters, L. Hartmann, J. R. Cochran, C. W. Frank, C. Q. Yu and C. N. Ta, J. Biomed. Mater. Res., Part A, 2015, 103, 3157–3165 CrossRef.
- J.-F. Lutz, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 3459–3470 CrossRef CAS.
- Z. Hu, T. Cai and C. Chi, Soft Matter, 2010, 6, 2115–2123 RSC.
- J. Ruiz-Franco, R. Rivas-Barbosa, M. A. Lara-Peña, J. R. Villanueva-Valencia, A. Licea-Claverie, E. Zaccarelli and M. Laurati, Soft Matter, 2023, 19, 3614–3628 RSC.
- A. Scotti, U. Gasser, E. S. Herman, M. Pelaez-Fernandez, J. Han, A. Menzel, L. A. Lyon and A. Fernández-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5576–5581 CrossRef CAS.
- A. Serrano-Medina, J. Cornejo-Bravo and A. Licea-Claveríe, J. Colloid Interface Sci., 2012, 369, 82–90 CrossRef CAS PubMed.
- X. Di, X. Peng and G. B. McKenna, J. Chem. Phys., 2014, 140, 054903 CrossRef.
- M. Lara-Peña, A. Licea-Claverie, I. Zapata-González and M. Laurati, J. Colloid Interface Sci., 2021, 587, 437–445 CrossRef PubMed.
- K. Wood, J. P. Mata, C. J. Garvey, C.-M. Wu, W. A. Hamilton, P. Abbeywick, D. Bartlett, F. Bartsch, P. Baxter, N. Booth, W. Brown, J. Christoforidis, D. Clowes, T. d’Adam, F. Darmann, M. Deura, S. Harrison, N. Hauser, G. Horton, D. Federici, F. Franceschini, P. Hanson, E. Imamovic, P. Imperia, M. Jones, S. Kennedy, S. Kim, T. Lam, W. T. Lee, M. Lesha, D. Mannicke, T. Noakes, S. R. Olsen, J. C. Osborn, D. Penny, M. Perry, S. A. Pullen, R. A. Robinson, J. C. Schulz, N. Xiong and E. P. Gilbert, J. Appl. Crystallogr., 2018, 51, 294–314 CrossRef CAS.
- S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- J. S. Higgins and H. C. Benoît, Polymers and Neutron Scattering, Clarendon Press, 1st edn, 1997 Search PubMed.
- W. D. Dozier, J. S. Huang and L. J. Fetters, Macromolecules, 1991, 24, 2810–2814 CrossRef CAS.
- J. Clara-Rahola, A. Fernandez-Nieves, B. Sierra-Martin, A. B. South, L. A. Lyon, J. Kohlbrecher and A. Fernandez Barbero, J. Chem. Phys., 2012, 136, 214903 CrossRef CAS PubMed.
- M. Shibayama, Macromol. Chem. Phys., 1998, 199, 1–30 CrossRef CAS.
- A. Scotti, U. Gasser, A. V. Petrunin, L. Fruhner, W. Richtering and J. E. Houston, Soft Matter, 2022, 18, 5750–5758 RSC.
- B. Zhou, U. Gasser and A. Fernandez-Nieves, Nat. Commun., 2023, 14, 3827 CrossRef CAS PubMed.
- M. Laurati, S. U. Egelhaaf and G. Petekidis, J. Rheol., 2011, 55, 673–706 CrossRef CAS.
- N. Koumakis, A. Pamvouxoglou, A. S. Poulos and G. Petekidis, Soft Matter, 2012, 8, 4271–4284 RSC.
- K. van der Vaart, Y. Rahmani, R. Zargar, Z. Hu, D. Bonn and P. Schall, J. Rheol., 2013, 57, 1195–1209 CrossRef CAS.
- A. Ghosh, G. Chaudhary, J. G. Kang, P. V. Braun, R. H. Ewoldt and K. S. Schweizer, Soft Matter, 2019, 15, 1038–1052 RSC.
- J. C. Fernández-Toledano, J. Rodríguez-López, K. Shahrivar, R. Hidalgo-Álvarez, L. Elvira, F. Montero de Espinosa and J. de Vicente, J. Rheol., 2014, 58, 1507–1534 CrossRef.
- K. N. Pham, G. Petekidis, D. Vlassopoulos, S. U. Egelhaaf, W. C. K. Poon and P. N. Pusey, J. Rheol., 2008, 52, 649–676 CrossRef CAS.
- R. G. Joshi and B. V. R. Tata, Colloid Polym. Sci., 2017, 295, 1671–1683 CrossRef CAS.
- C. Pellet and M. Cloitre, Soft Matter, 2016, 12, 3710–3720 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01103a |
| This journal is © The Royal Society of Chemistry 2025 |