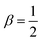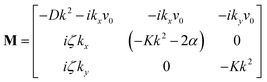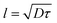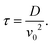Coarsening dynamics of aster defects in model polar active matter†
Soumyadeep
Mondal
 *,
Pankaj
Popli
*,
Pankaj
Popli
 and
Sumantra
Sarkar
and
Sumantra
Sarkar

Centre for Condensed Matter Theory, Indian Institute of Science, Bangalore, Karnataka, India. E-mail: sumantra@iisc.ac.in
First published on 11th November 2024
Abstract
We numerically study the dynamics of topological defects in 2D polar active matter coupled to a conserved density field, which shows anomalous kinetics and defect distribution. The initial many-defect state relaxes by pair-annihilation of defects, which behave like Ostwald ripening on short timescales. However, defect coarsening is arrested at long timescales, and the relaxation kinetics becomes anomalously slow compared to the equilibrium state. Specifically, the number of defects in the active system approaches a steady state, following a power-law dependence in the rate of change of the inverse density. In contrast, in thermal equilibrium, the decay is exponential. Finally, we show that the anomalous coarsening of defects leads to unique patterns in the coupled density field, which is consistent with patterns observed in experiments on the actin cytoskeleton. These patterns can act as cell signaling platforms and may have important biological consequences.
1 Introduction
Active materials consist of particles that stay inherently out of equilibrium by converting supplied energy into work.1,2 Unlike externally-driven non-equilibrium systems, the energy generation and dissipation in active materials happen at the level of individual entities. The interactions among these active particles result in rich, diverse collective behaviors spanning from microscopic scales to kilometers.3,4 For example, the collective movement of bacteria, the arrangement of cytoskeleton filaments within cells, and the flocking behavior of birds etc.2Topological defects are nontrivial configurations allowed by the symmetries of the system and correspond to the discontinuities in the order parameter field, which cannot be annealed out by any smooth deformations of the field. For instance, in a 2D XY model, they manifest as point vortices or saddles.5–7 They are characterized by their topological charge, which is the winding number of the singular order-parameter field at the defect core.
In equilibrium, defects with opposite charges unbind above a nonzero critical temperature, TKT, destroying quasi-long-range order.8 In active systems, in contrast, topological defects unbind even at zero temperature,2 which makes the homogeneous ordered state unstable to fluctuation above a length scale.9 The dynamics of individual active defects also differ significantly from the passive cases. Whereas passive defects move purely through diffusive motion,10 active defects, depending on their symmetries, may also self-propel. For example, in 2D active nematic materials, +1/2 topological defects self-propel, leading to active turbulence.11,12 In 2D active polar materials, the rotational symmetries of ±1 defects prevent any self-propulsion in general, but when the rotational symmetry is broken, self-propulsion is observed.13
Interactions between many topological defects determine the emergent macroscopic properties of active materials.14–20 Understanding the dynamics of many defects has been of recent interest.21–23 In active nematic systems, the defects can lead to the chaotic or polar organization of ±1/2 charges.22 In 2D polar active systems, such as in the actin cytoskeleton (ACS), the interaction and dynamics of multiple defects shape the macroscopic organization of the material, leading to nontrivial dynamic patterns.24–27 In cells, such patterns in the ACS have been hypothesized to control the size24,25 and the lifetime of clusters of membrane proteins.28 In experiments with polar filaments, it has been observed that the coarsening of topological defects is a key driver of pattern formation.29,30 However, the underlying mechanism of coarsening and the resultant patterns are poorly understood. In this paper, we investigate the anomalous coarsening dynamics of topological defects in a model of 2D polar active matter25 in the absence of thermal and active noise.
The rest of the paper is organized as follows: In the next section, we provide a summary of the hydrodynamic equations for polar fluids and examine the effects of various terms. This is followed by Section 3 where we present our results. We begin with a linear stability analysis of the ordered state and identify instabilities that lead to pattern formation. To extend the analysis beyond the linear regime, we numerically integrate the nonlinear hydrodynamic equations for different activity values, with methodologies outlined in the Appendix. In the subsequent subsections, we focus on defect dynamics and its coalescence kinetics. We first observe that defects merge until they reach an activity-dependent threshold density. This threshold density decreases with lower activity, approaching the passive limit at zero activity. This indicates the screening of long-range interactions between topological defects. To better understand the origin of this screening, we study the kinetics of defect coalescence. By investigating the microscopic aspects of the coarsening process (Section 3.3), we show that defect coarsening occurs in a three-step process. In Section 4, we validate our theoretical predictions by comparing them with live-cell measurements of ACS heterogeneity.31 We conclude this paper with a discussion of the implications of our results on the organization of various biological and soft matter systems.
2 Model
We consider a two-dimensional system with active polar particles. The hydrodynamic description of the active fluid is written in terms of two coarse-grained fields: (i) a vector orientation field (p) and (ii) a scalar concentration field (c). The complete dynamics of the two fields are described by the following equations,25,26| ∂tp + λ(p·∇)p = k1∇2p + k2∇(∇·p) + (α − β|p|2)p + ζ∇c + fp | (1) |
| ∂tc = −∇·(ja + jd) = −∇·(v0cp − D∇c) | (2) |
| ∂tp = K∇2p + α(1 − |p|2)p + ζ∇c + fp | (3) |
| ∂tc = −∇·(v0cp − D∇c) | (4) |
The first term on the right side of eqn (3) arises due to the elastic deformation of the p field, the second term ensures the stability of the p-field through the parameter α and β and arises from the functional derivative of the Landau–Ginzburg free energy functional, and the third term is an active term which couples the p-field with the c-field via an active parameter called contractility ζ. Stochasticity, arising from the binding kinetics of myosin with the actin filaments, is represented by the fourth term where fp is a conservative noise in the system with noise strength Ta, called the active temperature. It is delta correlated both in space and time: 〈fp(r,t)fp′(r′,t′)〉 = Taδ(r − r′)δ(t − t′). In eqn (4), the active term couples the two fields through the self-propulsion speed v0, which we take to be 1. This model has been used extensively for investigating biological systems like the actin cytoskeleton.13,24–26,32 Actin filaments, being polar entities, have the capability to interact with active motor proteins, including myosin. Consequently, the system becomes active, with the concentration field coupled with the orientational field. For simplicity, in the main text, we describe results at Ta = 0 and show results at nonzero Ta in the ESI.† We vary the contractility ζ, which can be controlled by, for example, the concentration of myosin in the actomyosin cortex.13
3 Results
3.1 Density of defects
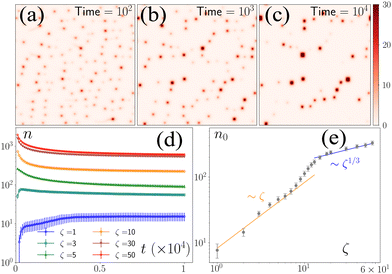
To study the model's behavior, we numerically solved the equations for 107 iterations (dt = 10−3) for different values of ζ, keeping all other parameters fixed. We initialized the equations with p(r) = (1,0) for all r and used a disordered initial condition for c(r) where the number of defects, n0, did not change appreciably over several million iterations (Fig. 1a–d).‡n0 is nonzero for all ζ values. However, the approach to n0 is different above and below ζ = 5 (Fig. 1d and e). Below this threshold, the initial ordered state becomes linearly unstable through laminar structures at wave numbers qd, whose magnitude qd scales as ζ0.5. For ζ > 5, the ordered state transforms to a lattice of asters with each row alternating between inward (in-) and outward (out-) pointing asters. Because of the coupling of the c field with the p field, c is depleted from the out-asters and enhanced at the in-asters (ESI†). Hence, local peaks in c field correspond to the location of the in-asters. After the initial transient, the nonlinear effects become important, which leads to the nucleation of asters followed by their coalescence for ζ ≤ 5, leading to a nonmonotonic evolution of asters towards n0(ζ). For ζ > 5, the number of asters decays to n0(ζ) through the coalescence of smaller asters to larger asters. The zeta-dependence of n0 is nontrivial. For ζ ≤ 5, n0 ∼ ζ1, which agrees with the prediction from the linearized theory, because the nucleation of the defects happens along the laminar structures, implying the scaling n0 ∼ qd2. In contrast, for ζ ≥ 20, n0 ∼ ζ1/3, implying that the minimum separation between the defects scales as ζ1/6 (ESI†). The effect of nonlinearity becomes important for 5 ≤ ζ ≤ 20, where n0 shows a smooth transition between the two regimes. The difference in the steady states in the different regimes is readily observed in the defect arrangements, which organize along 1D channels for ζ ≤ 5 and in liquid-like 2D structures for ζ ≥ 20, showing intermediate arrangements in between (ESI† movies).3.2 Coalescence kinetics
The dynamics of defects is fundamentally different from its equilibrium counterpart. In equilibrium, at zero temperature, all defects are annealed out to lower the free energy.6 The annealing kinetics is slow and shows logarithmic relaxation.10 For example, below TKT, the defect density, n(t), scales as n(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(t) ∼ t−1, which goes to zero as t → ∞.10 The relaxation kinetics of n(t) in our model is clearly different from thermal equilibrium. To make the difference in kinetics evident, we compare how n(t) varies with ϒ(t) = −(n−2dn/dt)−1.10 When the equilibrium kinetics hold, n(t) ∼ e−Aϒ, where A is a system-dependent constant. In contrast, in our model, we find that n(t) − n0 ∼ ϒ−1, which confirms the fundamental difference between the active and the passive cases (Fig. 2).
n(t) ∼ t−1, which goes to zero as t → ∞.10 The relaxation kinetics of n(t) in our model is clearly different from thermal equilibrium. To make the difference in kinetics evident, we compare how n(t) varies with ϒ(t) = −(n−2dn/dt)−1.10 When the equilibrium kinetics hold, n(t) ∼ e−Aϒ, where A is a system-dependent constant. In contrast, in our model, we find that n(t) − n0 ∼ ϒ−1, which confirms the fundamental difference between the active and the passive cases (Fig. 2).
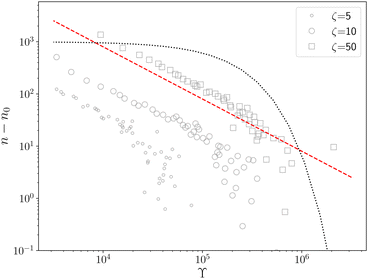 | ||
| Fig. 2 n − n0vs. ϒ for different ζ (legend); n0 is the steady state defect number. In our model n − n0 ∼ ϒ−1 (red dashed line) and not an exponential (black dotted line) as predicted by equilibrium kinetics.10 | ||
3.3 Three-step process
To get a more microscopic understanding of the coarsening kinetics, we studied the coalescence of two in-asters. In between every two asters, there is a saddle point, which carries −1 topological charge (Fig. 3). The saddle point connects two out-asters along a separatrix that separates the basin of attraction of the two in-asters (Fig. 3a). The coalescence is facilitated through a large-scale reorganization of the p field. In the immediate neighborhood of the two in-asters of interest, this reorganization results in the disappearance of the separatrix and the overlap of their basins of attraction (step 1, Fig. 3b). After the overlap, one of the in-asters rapidly annihilates the saddle (step 2, Fig. 3c and d), and the surrounding material relaxes to a rotationally symmetric structure around the remaining defect (step 3, Fig. 3e). What is surprising is that this process does not continue indefinitely. Once the defect density reaches n0, the defects do not coalesce anymore. Our initial hypothesis was that these are kinetically arrested states and would require longer simulations to continue the coalescence. However, even after running the simulation much longer than required to reach the steady state (Fig. 1), we could not observe a single coalescence event. The average aster size also reaches a plateau (ESI†), instead of growing as t1/3, as expected from classical nucleation theory.33 Further support for the arrested state comes from the observation that cyclic annealing of the state reduces the number of defects (Appendix D). Also, for Ta slightly greater than zero, the number of defects tends to decrease to a lower value (ESI†). Therefore, our simulations suggest that the system contains many metastable states where the system can be arrested depending on the initial conditions and its nonequilibrium dynamics.This observation is surprising because, in equilibrium, defects interact with each other through the long-range 2D Coulomb interactions, which implies that at T = 0 the coalescence should continue until no defects are present. This observation, therefore, is consistent with the hypothesis that activity screens the effective interaction between the defects. The screening in the presence of activity is inherently different from that observed for T > TKT in equilibrium, where proliferation of many defects leads to the screening of the interaction and maintenance of the defect plasma.8 In contrast, here, the screening increases with ζ, implying that the non-reciprocity of the active terms may be the origin of the screening, which has also been shown in the absence of number conservation.§ Understanding the active screening process requires the equations of motions of defects in 2D polar active materials, which are currently unavailable. Therefore, we resort to an indirect confirmation of this hypothesis by measuring the aster size distributions.
3.4 Aster size distribution
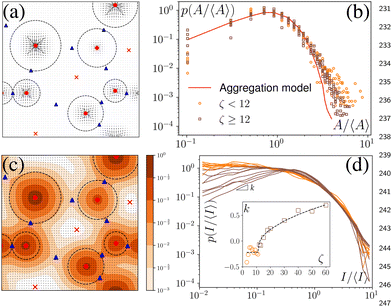
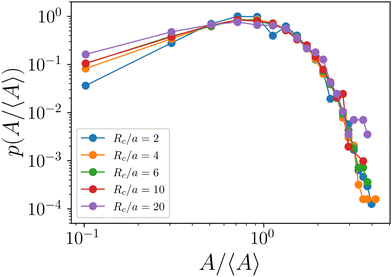
We have defined the size of the basin of attraction (BoA) of an aster as the size of the aster. However, the true BoA is hard to calculate for our system and a simpler approximation must be found to generalize across the different system sizes and the parameters that we explore here. To this end, we have found that a disk centered on the aster core, whose radius is the distance to the nearest saddle, is a good approximation of the BoA and is our measure of the size, A, of the aster (Fig. 4a). The aster size distribution, p(A) shows lognormal tails with power law head (Fig. 4b). We can quantitatively reproduce p(A) from a model of aggregation which only assumes that the aster interactions are screened beyond a cutoff distance Rc and that the asters are immobile (Appendix). An aster increases its size by coalescing with the nearest aster until it exhausts all asters within Rc or gets absorbed into another aster. For a wide range of Rc, the p(A) obtained from the simulation and the model are identical except at the tail (Fig. 4b), which bolsters our hypothesis that the equilibrium long-range interactions between the asters is screened in the presence of activity.3.5 Aster intensity distribution
In experiments, such as those with actomyosin complexes,31 identifying the BoA is difficult, if not impossible. In contrast, the fluorescent intensity of materials around the defects can be easily measured through optical microscopes. The fluorescent intensity is proportional to the total concentration of the tagged material, which, in our model, is proportional to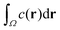 , where Ω is the basin of attraction of a defect. We define the integral as the intensity of asters. Among all the defects considered here, the in-asters are the sinks, whereas the out-asters are the source. Hence, the c-field concentrates around the in-asters. Therefore, by integrating the c field in the disk to measure A, we can calculate the intensity of the in-asters. Because cp vanishes exponentially outside the circle, the quantity of materials present outside the disk is negligible (Fig. 4c). Hence, using our method, we can easily and accurately calculate the aster intensity for various parameters. The mean aster intensity 〈I〉 ∼ n0−1. Surprisingly, the aster intensity distribution, p(I/〈I〉) itself shows a nontrivial transition with ζ (Fig. 4d). For Isc = I/〈I〉 < 1, p(Isc) ∼ Ik(ζ)sc. The power law exponent, k(ζ), interestingly scales as k ∼ (ζ − ζ0)1/2 for ζ > ζ0 ≈ 12, and as (ζ − ζ0)0 for ζ < ζ0.¶ The observed scaling indicates that the power law exponent is the order parameter of some underlying transition, which we cannot ascertain here. The value of ζ0 is also unclear due to noise in the data. A comprehensive investigation of this transition is beyond the scope of this manuscript.
, where Ω is the basin of attraction of a defect. We define the integral as the intensity of asters. Among all the defects considered here, the in-asters are the sinks, whereas the out-asters are the source. Hence, the c-field concentrates around the in-asters. Therefore, by integrating the c field in the disk to measure A, we can calculate the intensity of the in-asters. Because cp vanishes exponentially outside the circle, the quantity of materials present outside the disk is negligible (Fig. 4c). Hence, using our method, we can easily and accurately calculate the aster intensity for various parameters. The mean aster intensity 〈I〉 ∼ n0−1. Surprisingly, the aster intensity distribution, p(I/〈I〉) itself shows a nontrivial transition with ζ (Fig. 4d). For Isc = I/〈I〉 < 1, p(Isc) ∼ Ik(ζ)sc. The power law exponent, k(ζ), interestingly scales as k ∼ (ζ − ζ0)1/2 for ζ > ζ0 ≈ 12, and as (ζ − ζ0)0 for ζ < ζ0.¶ The observed scaling indicates that the power law exponent is the order parameter of some underlying transition, which we cannot ascertain here. The value of ζ0 is also unclear due to noise in the data. A comprehensive investigation of this transition is beyond the scope of this manuscript.
4 Experimental evidence
Experiments on the actin cytoskeleton provide direct experimental confirmation of our results. For example, in vitro experiments on actomyosin complexes show the coalescence of actin asters that are visually similar to our model: asters coalesce rapidly, the smaller asters get absorbed by larger asters, and the asters never coalesce into one single aster.29,30 We expect similar dynamics to be present in live cells also. In fact, measurement of residence times of peripheral membrane proteins on the plasma membrane provides indirect evidence of the heterogeneous distribution of actin asters.28 To make this observation more concrete, we compared the steady state distribution of aster intensities from our model with that obtained from live cell experiments on mouse embryonic stem cells (mESCs).31 To make an exact comparison, we converted the aster densities in our model to experimental units and compared it with the experimental aster densities (Fig. 5a). For untreated cells and for cells treated with the drug cytochalasin D (CytoD) the average density of the asters was approximately 0.2 μm−2. In our model, the aster density at ζ = 60 is comparable to the above experiments, and we found that the aster intensity distribution for this ζ matches almost exactly with the experimental data (Fig. 5b). Treating the mESCs with the drug SMIFH2 reduces the aster density to 0.15 μm−2, which corresponds to ζ between 20 and 30 in our model. We found that p(I) for ζ = 20 matches excellently with the experimental data (Fig. 5c), which predicts that SMIFH2 reduces the density of asters through the reduction of contractility. This observation is surprising because SMIFH2 is an inhibitor of Formin, a catalyst for actin polymerization, whereas contractility arises due to the effect of the motor protein myosin on the ACS. Interestingly, recent experiments suggest that SMIFH2 also inhibits myosin,34 which may explain our observation. Finally, we compared our model with CK666-treated cells, for which ζ = 5 seemed the best match. However, the predicted p(I) distribution did not match well with the experimental data for ζ = 5, but matched well with the distribution for ζ = 30 (Fig. 5d, see ESI† for the comparison). This mismatch suggested that CK666 lowers aster density, not by lowering the contractility of the ACS. Indeed, CK666 is an inhibitor of the actin nucleating protein Arp2/3, which has been shown to regulate the ACS architecture.31 Therefore, our model needs to be modified appropriately to understand the effect of Arp2/3-dependent aster nucleation.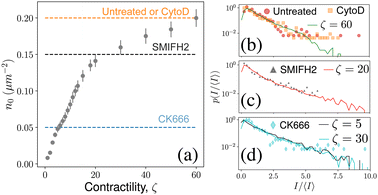 | ||
| Fig. 5 Experimental validation: (a) simulated in-aster density compared with experimental aster density under various drug treatments (dashed lines). (b)–(d) Comparison of aster area distribution from experiments31 (markers) with p(I/〈I〉) distribution from simulations. Error-bar denotes standard deviation. | ||
5 Discussion and conclusion
We have studied a model of polar active matter and have investigated the nucleation and dynamics of topological defects in this system. We have found that the interaction of the topological defects in polar active matter is nontrivial. The defects proliferate rapidly upon a quench to zero noise, and the density concentrates around inward pointing asters due to the coupling between the c and the p fields. The proliferation is followed by a nontrivial ripening process through the coalescence of the defects. The ripening process is similar to Ostwald ripening at short time scales but becomes anomalously slow beyond a certain timescale. The anomalous slow behavior is reminiscent of glassy dynamics and suggests that the coarsening of the topological defects is arrested. This is surprising, as theoretically, it has been suggested that defects should completely anneal out in polar active matter.23The qualitative behavior of the coarsening process remains unchanged for a wide range of parameters and initial conditions (see ESI†). For example, the dynamics of coarsening remains qualitatively unchanged for nonzero λ and k2 values, both of which we set to zero in our model. Nor does it depend on whether we use an ordered or a disordered initial condition. Due to computational challenges, we were able to explore the dependence on λ for only a few parameter values. However, it was shown in ref. 26 that increasing λ or k2 does not change the phenomenology of the model. Also, in an unpublished work, one of us has shown that the screening, which we suspect to be the main reason behind arrested coarsening, does not depend on λ. Therefore, we postulate that the arrested coarsening will persist even when we are able to explore broader ranges of λ. Similarly, below a threshold Ta, the number of defects decrease with time, but above this threshold value, the defects start to proliferate through aster fragmentation. This phenomenon is akin to the Kosterlitz–Thouless transition, where defect pairs unbind above a threshold temperature. The results presented here have weak dependence on the choice of the integration algorithm. At Ta = 0, we compared the evolution of the equations through the Euler–Maruyama and the second-order Runge–Kutta (RK2) methods. While the results match quantitatively at lower ζ values, they differ slightly at higher values of ζ. However, the aster intensity distribution did not change significantly between the two algorithms, which suggests that our observations do not depend strongly on the choice of the integration algorithm. An advantage of the Euler–Maruyama algorithm is that it can be used in the presence of noise (Ta > 0), but RK2 and similar methods cannot be used.
The arrested coarsening of topological defects may have important biological consequences. Prior experimental data30 shows that in in vitro actomyosin systems, the defects never anneal out of the system during the experimental duration, which is orders of magnitude longer than the maximum timescales of our simulations. Hence, the arrest of the defect coarsening is a potential mechanobiological mechanism to facilitate the formation of signaling platforms.28,35,36 The arrested coarsening is also important from the point of view of liquid–liquid phase separation.37 Indeed, it has been suggested that branched actin and associated proteins create phase-separated droplets during signaling.38 The arrested coarsening of the actin defects may be a potential mechanism to nucleate the droplets.
As we pointed out in the results section, we have not proven beyond doubt that the coarsening is arrested in our model. Therefore, there is a possibility that the defects will eventually anneal out of the system or will relax to a steady state with many defects. This conundrum has important repercussions for the stability of polar active matter. It was recently shown that a spontaneous proliferation of defects into a multi-aster state destroys order in a model of 2D polar active fluids.39 If the multi-aster state is an arrested state, we expect the order of the flocking state to be restored after a sufficiently long time. Whereas, if the multi-aster state is a true steady state, then the ordered state is truly metastable. Pragmatically, the distinction between an arrested metastable state and a steady state should be judged based on the relevant timescales of the problem. For a biological system, the important timescales are not the timescale to reach the final state but the timescales of signaling, which are often much shorter than the time to relax to the final state. Similar considerations may apply even when we consider a material made out of active polar filaments, where the timescales of perturbations may be much shorter than the relaxation timescales.
As we have shown, excellent correspondence exists between experiments on the actomyosin cortex and our model. Therefore, various predictions from our model, such as the phase transition in the intensity distribution, can be easily tested in existing experimental systems. The theory itself will be useful to understand general 2D active polar systems. In particular the dynamics of multiple topological defects will prove useful in understanding these materials’ mechanical and rheological properties. These questions will be addressed elsewhere.
The coarsening of topological defects in polar active matter is an interesting physical phenomenon with applications across many fields. The arrest of defect coarsening is reminiscent of glassy dynamics and suggests the presence of some rugged landscape that describes the elastic interaction between the defects. Therefore, studying the dynamics of topological defects in polar active matter is exciting and promises to bring together various branches of nonequilibrium physics.
Data availability
Due to its large size, the analyzed data will not be hosted on any data repository. It will be available upon reasonable request.Conflicts of interest
There are no conflicts to declare.Appendices
In this appendix, we provide details of the hydrodynamic model used to describe the organization of the actin cytoskeleton in a cell. We discuss our numerical analysis along with the linear stability analysis of the coupled partial differential equations. We also discuss the static aggregation model used to rationalize the active screening of defect interaction. The appendix concludes with details about the experimental evidence of our findings.A Linear stability analysis
We perform the linear stability analysis of eqn (3) and (4) with small perturbations in both the p field and c-field as p → p + δp and c → c + δc.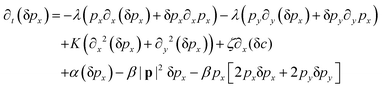 | (5) |
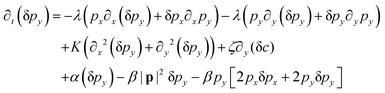 | (6) |
| ∂t(δc) = Df(∂x2 + ∂y2)(δc) − v0[∂x(cδpx + pxδc) + ∂y(cδpy + pyδc)]. | (7) |
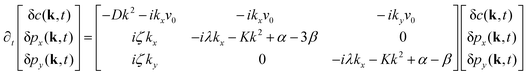 | (8) |
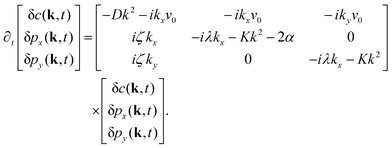 | (9) |
Further, taking λ = 0 we get,
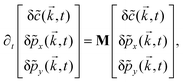 | (10) |
• Case-I, pure splay term (kx = 0)
| Λ1 = 2α − Kky2 | (11) |
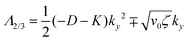 | (12) |
• Case-II, pure bend term (ky = 0)
| Λ1 = −Kkx2 | (13) |
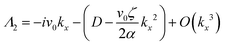 | (14) |
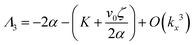 | (15) |
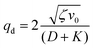 | (16) |
Thus, any positive value of ζ leads to the formation of the patterns in the system.
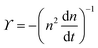 . The simplified form of ϒ is given by,
. The simplified form of ϒ is given by,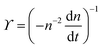 | (17) |
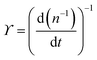 | (18) |
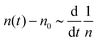 . This relationship shows that the defect number varies with the rate of the inverse of defect density.
. This relationship shows that the defect number varies with the rate of the inverse of defect density.
B Numerical analysis
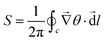 | (19) |
We utilize this mathematical framework to identify and locate defects in the system.
• At each grid point (i,j), we compute the values of pxi,j and pyi,j (x and y component of ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ) and determine the corresponding angle θi,j using the inverse tangent function:
) and determine the corresponding angle θi,j using the inverse tangent function: 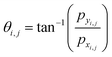 .
.
• We then calculate the angle of the three nearest neighbors of the grid point (i,j). To calculate the 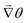 , we take the difference of their angles, which calculates
, we take the difference of their angles, which calculates ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) = 2πS.
= 2πS.
• From ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) , we calculate the winding number S of the defect, which we identify as its topological charge (±1).
, we calculate the winding number S of the defect, which we identify as its topological charge (±1).
Depending on the configuration of the ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) field, we identify two basic types of topological defects with charges of +1 and −1. The +1 charge corresponds to inward and outward pointing asters, while the −1 charge represents a saddle point. We use basic electrostatic principles to distinguish between inward and outward pointing +1 asters. By calculating the flux of the vector field around each +1 point and considering the sign of the flux, we can differentiate between these two configurations. Observing their positions, we integrate the concentration around these +1 inward defects to calculate the intensity of the asters.
field, we identify two basic types of topological defects with charges of +1 and −1. The +1 charge corresponds to inward and outward pointing asters, while the −1 charge represents a saddle point. We use basic electrostatic principles to distinguish between inward and outward pointing +1 asters. By calculating the flux of the vector field around each +1 point and considering the sign of the flux, we can differentiate between these two configurations. Observing their positions, we integrate the concentration around these +1 inward defects to calculate the intensity of the asters.
In our simulation, we take D = 2.5 and v0 = 1, so the value of
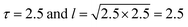 . From the FCS studies24,25 of the living cell, the rotational diffusion constant is given by D = 0.1 μm2 s−1 and
. From the FCS studies24,25 of the living cell, the rotational diffusion constant is given by D = 0.1 μm2 s−1 and 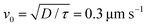 . So, in the physical unit length,
. So, in the physical unit length, 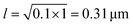 . The distance between two grid points (dx = dy) is given by 0.31/2.5 = 0.12 μm. Also, for timescale, 1 second is equivalent to 2.5, so the physical time scale of each timestep (dt) is 1/2.5 s = 0.4 s. The total simulation time is 10−3 × 107 = 104. So, the timescale in physical units is 104 × 0.4 s ∼ 1 hour and the length scale is 31 × 31 μm2.
. The distance between two grid points (dx = dy) is given by 0.31/2.5 = 0.12 μm. Also, for timescale, 1 second is equivalent to 2.5, so the physical time scale of each timestep (dt) is 1/2.5 s = 0.4 s. The total simulation time is 10−3 × 107 = 104. So, the timescale in physical units is 104 × 0.4 s ∼ 1 hour and the length scale is 31 × 31 μm2.
| Parameter and scaled value | ||
|---|---|---|
| Parameter (dimensions) | Scaled value | Physical value |
| K (l2/t) | 2.5 | 0.1 μm2 s−1 |
| ζ (l3/t) | 0 → 60 | 0 → 1.6 μm3 s−1 |
| α (1/t) | 100 | 100 s−1 |
| β (1/t) | 100 | 100 s−1 |
| v 0 (l/t) | 1 | 0.3 μm s−1 |
| D (l2/t) | 2.5 | 0.1 μm2 s−1 |
These values are chosen to closely align with previous experimental studies, ensuring that all terms are of the same order of magnitude.24
C Time evolution of average aster sizes
To gain insights into how the aster size evolves with time, we calculated the time-evolution of the average aster size. Following an initial growth phase, the aster sizes reach a plateau for all ζ values. We observed a decrease in average aster size with increasing contractility (ζ) Fig. 6.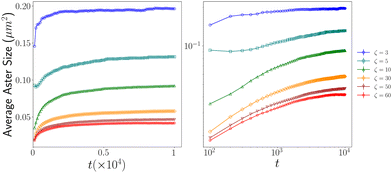 | ||
| Fig. 6 Figure shows how the average aster sizes evolve with time: (left) normal scale; (right) log–log scale. | ||
D Arrested state
In order to investigate whether the final state is an arrested or a steady state, we performed simulated annealing to the final state of the system by cycling through the active temperature by increasing first Ta from 0 to 20 and then decreasing it by 20 to 0 (Fig. 7). For every temperature, we performed the simulation for 1000 simulation timesteps. We observed that when we increased the temperature, the aster fragmented and relaxed to a homogeneous state with no asters. However, when we lowered the temperature and set it back to zero, we observed the system coarsened and again settled down to a finite number of asters (Fig. 7), which did not change after some iterations. From our observation, we can conclude that the final state is an arrested state. We have also calculated the number of topological defects at each cycle (Fig. 7).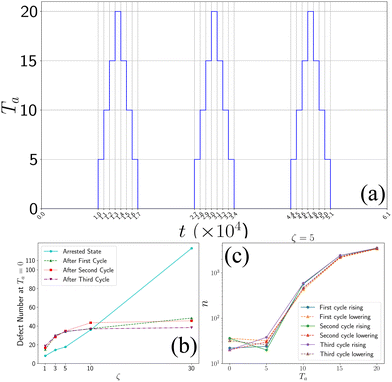 | ||
| Fig. 7 Annealing process: (a) temperature profile of annealing. (b) Number of defects at Ta = 0 after each cycle. (c) Variation of defects throughout the annealing process for ζ = 5. | ||
E Aggregation model for aster size distributions
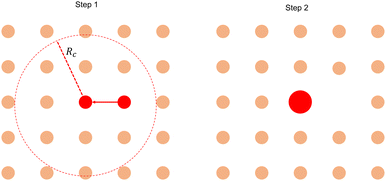
Our analysis focuses on the positive inward defects as the c-field concentrated only around the core of the in-asters. Calculating the size of the basin of attraction (BoA) involves finding the region around the core of an in-aster where the p-field flows towards the core. An approximate method to detect this region is described in the main text. The size obtained from this method is compared with the size obtained from a static aggregation model, which we describe here.(1) We initialize the system with asters placed on a lattice of lattice spacing a. All asters have equal size A = 1, i.e., the probability distribution function P(x = A/〈A〉) = δ(x − 1).
(2) We next perform Monte Carlo (MC) simulations until P(x = A/〈A〉) reached a steady state.
(3) The MC algorithm is as follows:
(a) Pick a random aster with A ≠ 0. Let's denote its area by Ai.
(b) Identify all its neighbors within a radius Rc with nonzero A.
(c) Find the nearest neighbor with A ≠ 0. If there are multiple nearest neighbors, pick one randomly. Let's call its area Aj.
(d) Merge asters i and j with the following criteria:
• If Ai > Aj, j coalesces into i and transfers its area to i, such that Anewj = 0 and Anewi = Ai + Aj. The opposite happens when Ai < Aj. This rule stems from the observation that the smaller asters coalesce with larger asters.
• If Ai = Aj, then pick any one of i or j with equal probability and merge it with the other.
(e) Stop simulation when the surviving asters have exhausted all asters within Rc and P(A/〈A〉) has reached a steady state.
The evolution of the aggregation model from the initial state is shown in Fig. 8. The steady-state probability distribution is shown in Fig. 9.
Acknowledgements
The authors would like to thank Pakorn Kanchanawong for sharing experimental data for Fig. 5. The authors would also like to thank Sriram Ramaswamy, Kripa Gowrishankar, Frank Jullicher, Hugues Chaté, Anubhav A., and Saurav Varma for insightful discussions. SS thanks IISc, Axis Bank Center for Maths and Computing (OD/ACMC-23-0013), and SERB-DST India (SRG/2022/000163) for funding. SM thanks for the support received through the UGC-CSIR fellowship (211610108599) and PMRF fellowship (0203001). PP thanks IISc-IoE fellowship (80008199) for funding.Notes and references
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- J. Toner and Y. Tu, Phys. Rev. Lett., 1995, 75, 4326 CrossRef CAS PubMed.
- J. Toner and Y. Tu, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 4828 CrossRef CAS.
- N. D. Mermin, Rev. Mod. Phys., 1979, 51, 591 CrossRef CAS.
- P. M. Chaikin and T. C. Lubensky, Principles of condensed matter physics, Cambridge University Press, Cambridge, 1995 Search PubMed.
- L. M. Pismen, Vortices in nonlinear Fields, Oxford University Press, USA, 1999 Search PubMed.
- J. M. Kosterlitz and D. J. Thouless, Basic Notions Of Condensed Matter Physics, CRC Press, 2018, pp. 493–515 Search PubMed.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef PubMed.
- B. Yurke, A. Pargellis, T. Kovacs and D. Huse, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 1525 CrossRef PubMed.
- S. Thampi and J. Yeomans, Eur. Phys. J.: Spec. Top., 2016, 225, 651–662 Search PubMed.
- R. Alert, J. Casademunt and J.-F. Joanny, Annu. Rev. Condens. Matter Phys., 2022, 13, 143–170 CrossRef.
- K. Husain and M. Rao, Phys. Rev. Lett., 2017, 118, 078104 CrossRef.
- S. J. DeCamp, G. S. Redner, A. Baskaran, M. F. Hagan and Z. Dogic, Nat. Mater., 2015, 14, 1110–1115 CrossRef CAS.
- B. Lemma, N. P. Mitchell, R. Subramanian, D. J. Needleman and Z. Dogic, Phys. Rev. X, 2022, 12, 031006 CAS.
- A. Chardac, S. Shankar, M. C. Marchetti and D. Bartolo, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018218118 CrossRef CAS.
- A. Chardac, L. A. Hoffmann, Y. Poupart, L. Giomi and D. Bartolo, Phys. Rev. X, 2021, 11, 031069 CAS.
- N. Rana and P. Perlekar, Phys. Rev. E, 2022, 105, L032603 CrossRef CAS.
- N. Rana and P. Perlekar, Phys. Rev. E, 2020, 102, 032617 CrossRef CAS.
- S. Saha, R. Golestanian and S. Ramaswamy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062316 CrossRef.
- S. Shankar, S. Ramaswamy, M. C. Marchetti and M. J. Bowick, Phys. Rev. Lett., 2018, 121, 108002 CrossRef CAS PubMed.
- S. Shankar and M. C. Marchetti, Phys. Rev. X, 2019, 9, 041047 CAS.
- F. Vafa, Soft Matter, 2022, 18, 8087–8097 RSC.
- D. Goswami, K. Gowrishankar, S. Bilgrami, S. Ghosh, R. Raghupathy, R. Chadda, R. Vishwakarma, M. Rao and S. Mayor, Cell, 2008, 135, 1085–1097 CrossRef CAS PubMed.
- K. Gowrishankar, Biophys. J., 2010, 98, 304a–305a CrossRef.
- K. Gowrishankar and M. Rao, Soft Matter, 2016, 12, 2040–2046 RSC.
- K. Kruse, J.-F. Joanny, F. Jülicher, J. Prost and K. Sekimoto, Phys. Rev. Lett., 2004, 92, 078101 CrossRef CAS PubMed.
- S. Sarkar and D. Goswami, Biophys. J., 2023, 122, 290–300 CrossRef CAS PubMed.
- M. Soares e Silva, M. Depken, B. Stuhrmann, M. Korsten, F. C. MacKintosh and G. H. Koenderink, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9408–9413 CrossRef.
- V. Wollrab, J. M. Belmonte, L. Baldauf, M. Leptin, F. Nédeléc and G. H. Koenderink, J. Cell Sci., 2019, 132, jcs219717 CrossRef CAS PubMed.
- S. Xia, Y. B. Lim, Z. Zhang, Y. Wang, S. Zhang, C. T. Lim, E. K. Yim and P. Kanchanawong, Cell Rep., 2019, 28, 1251–1267 CrossRef CAS PubMed.
- G. Kripa, PhD thesis, Raman Research Institute, 2012.
- R. C. Desai and R. Kapral, Dynamics of Self-organized and Self-assembled Structures, Cambridge University Press, 2009 Search PubMed.
- Y. Nishimura, S. Shi, F. Zhang, R. Liu, Y. Takagi, A. D. Bershadsky, V. Viasnoff and J. R. Sellers, J. Cell Sci., 2021, 134, jcs253708 CrossRef CAS PubMed.
- Y. Maroudas-Sacks, L. Garion, L. Shani-Zerbib, A. Livshits, E. Braun and K. Keren, Nat. Phys., 2021, 17, 251–259 Search PubMed.
- H. I. Ingólfsson, C. Neale, T. S. Carpenter, R. Shrestha, C. A. López, T. H. Tran, T. Oppelstrup, H. Bhatia, L. G. Stanton and X. Zhang, et al. , Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2113297119 CrossRef PubMed.
- C. A. Weber, D. Zwicker, F. Jülicher and C. F. Lee, Rep. Prog. Phys., 2019, 82, 064601 CrossRef CAS.
- L. B. Case, X. Zhang, J. A. Ditlev and M. K. Rosen, Science, 2019, 363, 1093–1097 CrossRef CAS PubMed.
- M. Besse, H. Chaté and A. Solon, Phys. Rev. Lett., 2022, 129, 268003 CrossRef CAS.
- W. H. Press, Numerical recipes: The art of scientific computing, Cambridge University Press, 3rd edn, 2007 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00788c |
| ‡ It is unclear whether this final state is a steady state or an arrested state. We perturbed the final, defect-laden state by cycling between Ta = 20 and Ta = 0, which seems to suggest that it is an arrested state, but the evidence is inconclusive. See Appendix C for details. |
| § Unpublished data from Pankaj Popli and Sriram Ramaswamy. |
| ¶ The scaling of k with ζ is suggestive and requires more careful investigation to ascertain the scaling exponent. |
| This journal is © The Royal Society of Chemistry 2025 |