DOI:
10.1039/D4SM01223B
(Paper)
Soft Matter, 2025,
21, 2400-2412
Poroelasticity and permeability of fibrous polymer networks under compression†
Received
17th October 2024
, Accepted 24th January 2025
First published on 11th February 2025
Abstract
Soft biopolymer networks play pivotal roles in governing cellular mechanics, tissue structure, and physiological processes such as blood coagulation. Understanding their permeability and mechanical responses under compression is crucial for elucidating mass transport phenomena and their impact on extra- and intra-cellular behavior as well as processes affecting functionality of blood clots, cartilage and other fibrous tissues. The nonlinear responses of these networks to mechanical stresses prevent application of established linear poro-elasticity models. Despite extensive studies of fibrous network viscoelastic properties under shear deformations, their dynamic responses to compressive deformations remain poorly understood, particularly in physiological contexts of growth and collective migration of solid bodies. Conventional experimental techniques face challenges in accurately evaluating the permeability of these networks, hindering comprehensive understanding of their poromechanical behavior. In this study, we employ a novel poroelastic hybrid approach combining rheometer-based compression rheology with camera-facilitated sample shape detection to directly measure fluid flux and network permeability under controlled compressive strains. Accompanying experimental investigations, a continuum model implemented in finite elements, and an analytical model are developed to interpret the findings. The experimental data align well with the analytical model, revealing the emergence and disappearance of distinct densification regimes within the gel under mechanical stress. This study advances our understanding of the intricate interplay between mechanical forces, fluid flow, and structural properties in soft biopolymer networks, with a specific focus on fibrin- and collagen-based gels which represent the most abundant protein networks in the extracellular environment.
1 Introduction
Soft biopolymer networks are indispensable components of living systems, governing cellular mechanics,1,2 structural properties of tissue,3 and physiological processes such as blood coagulation.4,5 These intra- and extracellular components, characterized by hydraulic permeability and viscoelastic properties,6 regulate cellular shape and dynamics,7 and material transport,8 and provide mechanical support within the extracellular matrix (ECM).9 Understanding their permeability is crucial for unraveling mass transport phenomena in soft tissues and elucidating their impact on cellular behavior and blood clot functionality. Polymer networks have been extensively studied for their behavior under shear deformations.10–12 Along with experimental advances, theoretical frameworks have been developed13 to describe the viscoelastic properties of networks across various phases including the vast phase space of different cross-linker affinities14–16 as well as to explore the impact of molecular interactions between polymers.17,18 Despite advancements in understanding the viscoelastic properties of polymer networks, their dynamic responses to compressive deformations, particularly at timescales related to physiological contexts such as solid tumor growth and collective cell migration, remain poorly understood.6,19,20 However, poroelastic effects, especially in volume-changing deformations, likely modulate the rheological behavior of these networks, contributing to the ECM's stability against compressive loads for instance. Models to describe compressive deformations and fluid permeability are based on the theory of poroelasticity,21,22 developed to apply to polymer based soft materials23 and to account for non-linear deformations, which are physiologically relevant.24 Meanwhile, conventional experimental techniques, including those reliant on microfluidic devices, encounter challenges in accurately assessing the permeability of adhesive biopolymers, or cannot capture fluid flow properties under dynamic compressions.25 This limitation impedes a comprehensive understanding of both their permeability and poromechanical behavior. Combining compression rheology with theoretical modeling offers new insights into the coupling of fluid flow and elasticity in biopolymer networks during compression, but current models rely on model assumptions to determine system parameters.6 To address this experimental challenge, our study employs a novel poroelastic hybrid approach, integrating rheometer-based compression rheology with camera-facilitated sample shape detection. This setup enables direct measurement of fluid flux and network permeability under rate-controlled compressive strains, providing unprecedented insights into the coupling between network stress and fluid pressure dynamics.
We investigated the permeabilities of fibrous polymer gels under stepwise increasing compressive strains. Accompanying the experimental investigations, we employed a continuum theory implemented using the finite element method (FEM)26,27 to interpret our findings. While this approach qualitatively reproduced experimental results regarding trends in Poisson ratios and volume change for both investigated systems, it showed large deviations with regard to stress relaxation, which appeared more pronounced in the experiment particularly for compressive strains in the intermediate strain regime. We attribute this discrepancy to the assumption of the continuum theory, which is based on a homogeneous network with a uniform permeability. Introducing an analytical model instead, which accounts for heterogeneity of deformations,28 we disclosed fluid flow properties in gels under increasing compressive strains. The experimental data on fluid permeation under compressive conditions aligns well with our model, which postulates the coexistence of two compartments within the gel in a distinct compression regime. This compartmentalization has been observed for collagen29 as well as for fibrin gels.27 We show the emergence as well as the disappearance of a rarefied (slightly denser than uncompressed state) and a densified phase (much denser than uncompressed state) within these gels in a distinct compression regime. The densification assumed by the theory and confirmed experimentally extends from the top part of the gel, where the displacement is applied, to the bottom with increasing compressive strain, revealing structural transformations under mechanical stress with implications for fluid flow behavior. The mechanical properties of fibrin and collagen networks, crucial components of blood clots and the ECM, are of particular interest due to their pivotal role in structural integrity of the extracellular space,30 hemostasis31,32 and thrombosis.33 While their response to shear deformation has been extensively studied, the behavior under compression presents new complexities, including phase transitions and foam-like behavior.20,27 Through experimental investigations and theoretical modeling, our study discloses the intricate interplay between mechanical forces, fluid flow and structural properties in soft fluid-enclosing biopolymer networks.
2 Results
Conventional compression rheology has been used in previous studies to compute6,34 the normal stress relaxation behavior of biopolymer networks. Flow defining parameters were calculated by employing theoretical models as they were experimentally difficult to access. To address this experimental challenge, we designed and manufactured a measurement setup to monitor the entire parameter space necessary to determine the fluid flux as a result of applied compressive strains on liquid enclosing gels. The setup specifically designed to investigate poromechanics for small volume samples, illustrated in Fig. 1, consists of a glass plate sitting on top of a camera, which replaces the bottom plate in a conventional rheometer setup. A gel sample, placed between a 20 mm plate and the glass surface, is exposed to compressive strains by lowering the gap size in a strain rate-controlled manner. The normal force during and after compression is monitored as a function of gap size. Assuming a cylindrical sample geometry, the volume can be calculated for every point in time over the entire experiment from the cross-section area, detected by the camera below the glass plate and the gap size, measured by the rheometer.
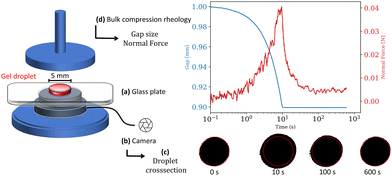 |
| | Fig. 1 The experimental setup combines classic bulk compression rheometry with a camera facilitated shape detection. A gel sample (red) is placed between a transparent glass plate (a), sitting on a camera (b), and the upper geometry plate of the rheometer. The camera monitors the change in the gel droplet's cross-section area (c) during and after compression. (d) The gap change during compression as well as normal force during and after compression are measured with a HR 20 Rheometer (TA Instruments). | |
2.1 Compression rheology
Fibrin gels were polymerized between a stationary bottom glass plate and a movable upper plate at a concentration of 15 mg ml−1. The fibrin gels were stabilized by the addition of 10 mM CaCl2 to activate factor XIII crosslinking and minimize potential contributions such as viscoelastic relaxation due to non-covalent crosslink unbinding to the measured response to compression deformation. The initial height of the gel was set to 1 mm. Using volumes of 22.5 microliter the corresponding initial gel radius was 2.68 mm, assuming a cylindrical volume. To prevent evaporation and potential protein degradation at the air–gel interface the gels were surrounded by 1× Tris buffer after 10 minutes polymerization time. The gels were equilibrated for another 10 minutes until the storage modulus G′ reached a stable value. Prior to the compression tests the sample's average elastic storage modulus was G′ = 1130 (±130) Pa, the average loss modulus G′′ = 93 (±20) Pa, and the corresponding loss factor tan(Φ) = G′′/G′ = 0.08 (±0.015).
Collagen gels were pre-polymerized and subsequently stabilized with glutaraldehyde to a cylindrical shaped disk matching the geometry of the fibrin gels at the same initial volume. After being placed on the bottom glass plate the gels were immersed in 1× PBS buffer and equilibrated for 10 minutes with the upper plate being in contact with the samples at 1 mm gap height. Collagen samples at a concentration of 10 mg ml−1, crosslinked with glutaraldehyde exhibited an average storage modulus of G′ = 5160 (±120) Pa, an average loss modulus G′′ = 395 (±200) Pa, and a corresponding loss factor of tan(Φ) = 0.08 (±0.04). In order to investigate the gels’ mechanical response to compression, gel samples were exposed to stepwise compressive strains between 10% and 80% by lowering the upper plate with a rate of 10 μm s−1. During and after each compression the resulting normal force was measured as a function of time. Representative measurements for fibrin and collagen samples respectively are shown in Fig. 2, where the normal stress σN, calculated from the measured normal force FN and the time-dependent sample cross-section area S(t) according to σN(t) = FN(t)/S(t), are plotted over time. We interpret the normal stress as the sum of a hydraulic pressure and an upward directed normal stress resulting from network deformation that builds up during the compression phase to reach a maximum and subsequently decays. The first 10% strain step induced a maximum pressure of 1.38 (±0.26) kPa for the fibrin gels and 1.05 (±0.25) kPa for collagen gels. The normal stress subsequently relaxes with the values decreasing by half of the maximum stress in less than 10 seconds. With increasing strain, the normal stress response of the sample increases to values exceeding 50 kPa for fibrin and 20 kPa for collagen.
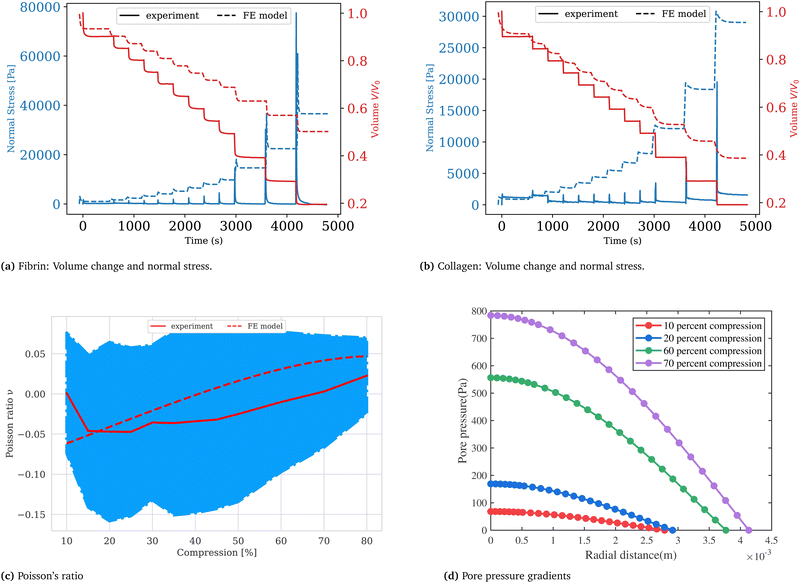 |
| | Fig. 2 Fibrin (a) and collagen (b) gels are stepwise compressed at a rate of 10 μm s−1 to strains between 10% and 80%. The normal stress builds up during compression and subsequently relaxes after the strain step at a constant gap width. Synchronizing rheometer data with image acquisition gives the parameters necessary to calculate the sample volume over time V(t) =π·r(t)2·g(t). (c) The Poisson ratio is calculated according to eqn (15) and plotted as a function of compressive strain for collagen gels. The FEM simulation predicts the same trend as in experiment suggesting that our choice of constitutive parameters is adequate. (d) The pore pressure (chemical potential) shown in this figure corresponds to near the end of the relaxation step when the fluxes are measured to determine the Darcy constant in our experiments. The profile can be approximated as linear in the radial coordinate except near the central region. A plot of the non-uniform void ratio at this stage of the relaxation process is given in the (ESI†). | |
2.2 Fluid flow and permeability
Synchronizing the data collected by the rheometer, particularly the gap size values, with the cross-section area detected by the camera we calculate the volume by assuming a cylindrical sample geometry V = π·r2(t)·g(t), where g(t) is the gap size and r(t) the sample radius at time t. This allows for the monitoring of the samples’ volume during compression as well as relaxation as shown in Fig. 3.
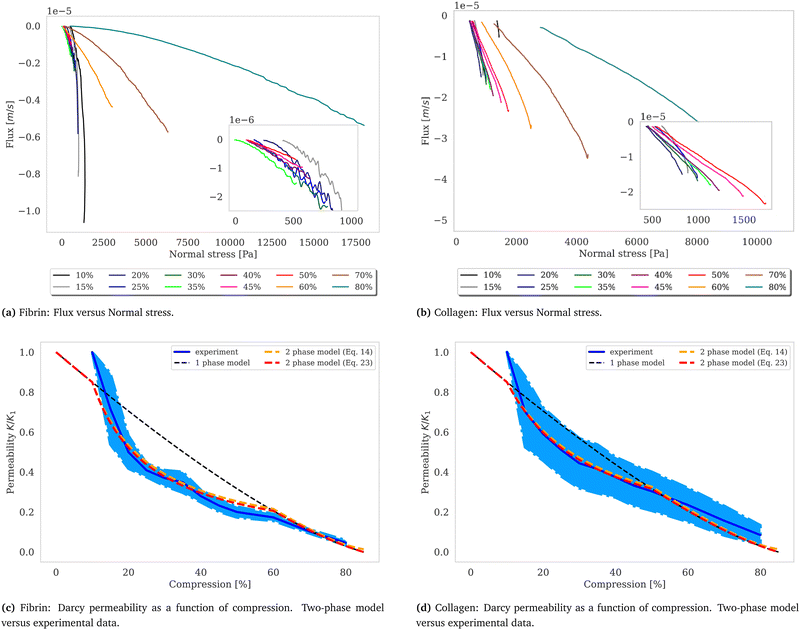 |
| | Fig. 3 Flux and permeability. The volumetric flux, calculated as q = Q/A, with the volumetric flow rate Q (unit: m3 s−1) and the cross-section area A = 2π·r(t)·g(t) (unit: m2), the surface area of a cylinder where g(t) is the gap size and r(t) the gel radius at time t plotted over normal stress for fibrin (a) and collagen (b). Fitting a linear function to the curves, which correspond to the volumetric flux close to where the volume change is negligible, yields the slope α = k/(ηL), considering Darcy's law, 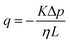 , with the viscosity of water η. The calculated Darcy constants K, divided by K1, the permeability for the first compression step exhibits nonlinear behavior in the intermediate compression strain regime and shows good agreement with the two-phase model shown in red (c) and (d). The dependence of the permeability according to Wufsus et al. which assumes uniform density of the gel is shown by the dashed black curve.35 Plots of the Darcy constant as a function of average concentration appears in the ESI† for fibrin and collagen gels. , with the viscosity of water η. The calculated Darcy constants K, divided by K1, the permeability for the first compression step exhibits nonlinear behavior in the intermediate compression strain regime and shows good agreement with the two-phase model shown in red (c) and (d). The dependence of the permeability according to Wufsus et al. which assumes uniform density of the gel is shown by the dashed black curve.35 Plots of the Darcy constant as a function of average concentration appears in the ESI† for fibrin and collagen gels. | |
Fluid dynamics through confined spaces within soft material is determined by the material's permeability and quantified via the volumetric flux q. The volumetric flux is a measure of flow rate per unit area and is mathematically expressed as 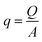 , where Q denotes the volumetric flow rate in units m3 s−1 and A the cross-section area, which represents the effective area available for fluid flow. We assume a cylindrical geometry with A = 2·π·r(t)·g(t), where the sample height equals the gap size g(t) and the sample radius is denoted as r(t). The volumetric flow rate is determined by monitoring the change in volume of the gel as a function of time. In calculating the outward liquid flux in this way we tacitly assume that the liquid phase and solid phase material in the gel are incompressible36,37 so the volume change of the gel is equal to the volume of liquid leaving the gel.
, where Q denotes the volumetric flow rate in units m3 s−1 and A the cross-section area, which represents the effective area available for fluid flow. We assume a cylindrical geometry with A = 2·π·r(t)·g(t), where the sample height equals the gap size g(t) and the sample radius is denoted as r(t). The volumetric flow rate is determined by monitoring the change in volume of the gel as a function of time. In calculating the outward liquid flux in this way we tacitly assume that the liquid phase and solid phase material in the gel are incompressible36,37 so the volume change of the gel is equal to the volume of liquid leaving the gel.
Permeability is a defining attribute that characterizes porous or permeable material regarding its ability to allow a fluid to pass through. The foundational principle, which establishes a relation between volumetric flux q and pressure difference Δp is given by Darcy's law 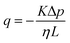 with the viscosity of the permeating fluid η and L, the distance over which the pressure difference Δp is effective and consequently where fluid flow appears. The proportionality constant K, also called the Darcy constant, expressed in units of m2 characterizes the permeability of the material. Previous studies investigated fluid flow at various pressure gradients in setups relying on hydrostatics. Instead, here we apply finite deformations at a fast strain rate and read the materials’ resistance to these compressive strains as an effective pressure. We calculated the flux curves for each compression step as outlined above. For the determination of the Darcy permeability, we consider the part of the curves which represent the relaxation phase after the compression. Representative curves showing the flux over normal stress during compression and relaxation for fibrin and collagen are presented in the ESI.† Fitting a linear function to the curve yields the slope α, and considering the equation for the Darcy permeability we determine K according to
with the viscosity of the permeating fluid η and L, the distance over which the pressure difference Δp is effective and consequently where fluid flow appears. The proportionality constant K, also called the Darcy constant, expressed in units of m2 characterizes the permeability of the material. Previous studies investigated fluid flow at various pressure gradients in setups relying on hydrostatics. Instead, here we apply finite deformations at a fast strain rate and read the materials’ resistance to these compressive strains as an effective pressure. We calculated the flux curves for each compression step as outlined above. For the determination of the Darcy permeability, we consider the part of the curves which represent the relaxation phase after the compression. Representative curves showing the flux over normal stress during compression and relaxation for fibrin and collagen are presented in the ESI.† Fitting a linear function to the curve yields the slope α, and considering the equation for the Darcy permeability we determine K according to 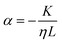 . In the above we take L ≈ r(t) so that the pore pressure gradient is approximated as
. In the above we take L ≈ r(t) so that the pore pressure gradient is approximated as 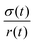 where σ is the average normal Cauchy stress on the top plate. In doing so we follow38 who give a simple expression for fluid flow through compressed open cell foams in terms of the measured compressive stress and dimensions of the foam. We chose the fitting boundaries to capture the last linear part of the curve at the low flux regime for each compression strain step because near the end of the relaxation step the pore pressure gradient in the radial direction can be approximated as linear in agreement with our assumption above. Finite element calculations in Fig. 2 reveal that the order of magnitude of the pore pressure gradient at this stage of relaxation is the same as σ/r for various values of the applied strain. Evaluating the first compression and relaxation we obtained a Darcy constant K1,F = −2.59 × 10−14 (± 7.6 × 10−15) m2 for fibrin and K1,C = −1.7 × 10−13 (± 5.4 × 10−14) m2 for collagen respectively. These values correspond to the range of permeabilities reported in previous studies.25,39–41 The derived Darcy permeabilities show a decrease for increasing compressive strain. Assuming a general increase in protein concentration as a result of fluid outflow explains the apparent decrease in permeability. Previous studies reported a Darcy permeability for small-pored fibrin gels, scaling inverse squared with protein concentration.6 Interestingly, our data shows permeabilities K that match this scaling behavior for 10% compressive strain as well as for compressions exceeding 60% strain for fibrin and 50% strain for collagen, but are distinctly lower for the respective intermediate strain regime (see Fig. 3). This observation highlights the complexity inherent in fluid flow through permeable soft polymer gels such as fibrin and collagen, where changes in structural integrity and pore geometry intricately influence the permeation dynamics. The experimental results align with the analytical model described in Section 2.4. The essential idea of this model is a non-uniform densification of a gel that is subjected to a rapid compressive deformation.
where σ is the average normal Cauchy stress on the top plate. In doing so we follow38 who give a simple expression for fluid flow through compressed open cell foams in terms of the measured compressive stress and dimensions of the foam. We chose the fitting boundaries to capture the last linear part of the curve at the low flux regime for each compression strain step because near the end of the relaxation step the pore pressure gradient in the radial direction can be approximated as linear in agreement with our assumption above. Finite element calculations in Fig. 2 reveal that the order of magnitude of the pore pressure gradient at this stage of relaxation is the same as σ/r for various values of the applied strain. Evaluating the first compression and relaxation we obtained a Darcy constant K1,F = −2.59 × 10−14 (± 7.6 × 10−15) m2 for fibrin and K1,C = −1.7 × 10−13 (± 5.4 × 10−14) m2 for collagen respectively. These values correspond to the range of permeabilities reported in previous studies.25,39–41 The derived Darcy permeabilities show a decrease for increasing compressive strain. Assuming a general increase in protein concentration as a result of fluid outflow explains the apparent decrease in permeability. Previous studies reported a Darcy permeability for small-pored fibrin gels, scaling inverse squared with protein concentration.6 Interestingly, our data shows permeabilities K that match this scaling behavior for 10% compressive strain as well as for compressions exceeding 60% strain for fibrin and 50% strain for collagen, but are distinctly lower for the respective intermediate strain regime (see Fig. 3). This observation highlights the complexity inherent in fluid flow through permeable soft polymer gels such as fibrin and collagen, where changes in structural integrity and pore geometry intricately influence the permeation dynamics. The experimental results align with the analytical model described in Section 2.4. The essential idea of this model is a non-uniform densification of a gel that is subjected to a rapid compressive deformation.
2.3 Finite element method
2.3.1 Kinematics.
Microscopically, collagen and fibrin gels are not homogeneous since the topology of the fibers and the concentration of other solutes in the liquid is not the same everywhere. However, since our interest is in length scales that are much larger than that of the gel micro-structure, we will treat the gel as a homogeneous material. Letting x(X,t) and X denote the current and initial positions of a specific material point, respectively, we can define the deformation gradient tensor and its determinant as:| | 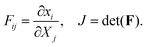 | (1) |
In the treatment that follows the initial (reference) configuration is the swollen state that the fibrous network forms with water at equilibrium. We assume that the network material (dry polymer) and the interstitial liquid are both incompressible and that the volume change of the gel is caused purely by the movement of liquid. Let C(X,t) denote the volume fraction of liquid (in the reference state), then:where ϕrefs denotes the volume fraction of the fibrous polymer in the reference configuration. Now, if we consider a volume V with a normal N(X) and surface S(X) in the reference configuration, then mass balance in the absence of any liquid source can be written as:| |  | (3) |
where Q denotes the liquid flux per unit reference area and ρ denotes the density of the liquid. Utilizing the divergence theorem, we can rewrite this equation in localized form as:| | 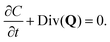 | (4) |
If we consider the loading to be quasi-static, which means that the load is applied slowly, we can write our momentum balance equation expressed in the reference configuration as:where P is the first Piola–Kirchhoff stress tensor. Note that this is a statement of mechanical equilibrium for a representative volume element of the gel that contains both solid and liquid. It is assumed to be valid even when there is relative motion between the solid and fluid in the chemo-elastic formulation36,37 used here. The theory of porous media separately considers the equilibrium and mass balance of the solid and liquid parts of the gel (including the body forces exerted by the solid and liquid on each other), but it has been shown to be equivalent to the chemo-elastic formulation used here by Stracuzzi et al.42 for incompressible fluid and solid material.
2.3.2 Constitutive laws.
Experimental results presented in Section 1 indicate that the viscous effects are negligible in both collagen and fibrin gels. Consequently, both materials are modeled as purely poroelastic. Based on Flory–Rehner theory,43 the total Helmholtz free energy per reference volume of a fibrous network and solvent mixture can be written as a summation of the free energy density due to the deformation of the network Ψnet(F), and the free energy density of (hydrophilic) interaction of two phases Ψint(C):| | | Ψ(F,C) = Ψnet(F) + Ψint(C). | (6) |
Utilizing Legendre transformation, we define a new free energy density as:
| | ![[capital Psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b0.gif) = Ψ(F,C) − μC. = Ψ(F,C) − μC. | (7) |
Here
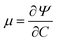
is the chemical potential of the interstitial liquid.
37 Here the units of the chemical potential are J m
−3, same as the units of stress. This is different from the units of chemical potential in standard thermodynamics because in addition to taking the derivative of a free energy with respect to the number of moles of a species (liquid) we are also dividing by the molar volume of the incompressible liquid. Based on standard continuum mechanical derivations that use the dissipation inequality, it can be shown that:
| | 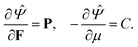 | (8) |
The free energy Ψnet(F) and Ψint(C) used in this work is based on:42,44,45
| | 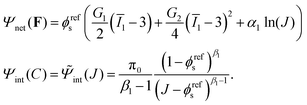 | (9) |
Notice that
C in
eqn (9) is replaced by
J according to
eqn (2). Here
G1 and
G2 are two constants.
G1 the shear modulus for small strain of the dry polymer, while
G2 is related to the shear modulus at large strain of the dry polymer. A two-term polynomial hyper-elastic model is used to characterize the strain-stiffening behaviors of both fibrin and collagen under compression. Such strain stiffening was demonstrated for fibrin networks in Kim
et al.20 and for collagen networks in Novak
et al.29 A ln(
J) term is included in the expression for the free energy density following standard texts in nonlinear elasticity (
e.g., Ogden,
46 Holzapfel
47) and biophysics (
e.g., Boal
48). The ln(
J) term is phenomenological in our description, and it could be replaced by another term such as (
J − 1)
2, but we use it because of analytical convenience (
e.g. in computing
α1, see below).
Ī1 is the modified invariant of the left Cauchy–Green tensor
B. The isochoric part of
I1 is chosen to account for the incompressibility of both liquid and solid phases. π
0 is the initial osmotic pressure, and the value of
α1 is chosen such that the reference state is stress free.
β1 is a power law coefficient, which is slightly larger than 1 in the current formulation. The form of the mixing free energy used here was given by Ehret
et al.30 for collagen gels and shown to agree well with experiments in uniaxial and bi-axial tension. It was also adopted in Garyfallogiannis
et al.49 for fibrin gels and shown to result in excellent agreement of the tensile stress–strain curve and the volumetric shrinkage of cracked specimens. FE computations using free energy density with the usual invariants was also performed, but the relaxation results did not match with experiment well, compared with the free energy density with isochoric invariants. In particular, a higher stress drop during relaxation was observed with isochoric invariants compared to normal invariants
I1 although the stiffness during compression was the same for both choices. This is why isochoric invariants are adopted in the remainder of this work. Utilizing
eqn (9), the Cauchy stress can be calculated as:
| | 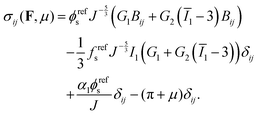 | (10) |
In order to set the value of
α1, we require
σ(
I,0) = 0 at
t = 0, so that:
| | 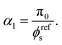 | (11) |
By setting the value of
α1 in this way we have worked differently from the standard Flory–Rehner model. In that model the constitutive properties of the dry polymer would be known; similarly, change in free energy due to mixing of polymer and liquid (which determines the osmotic pressure) would also be known. Then, the minimization of the total free energy by setting
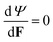
(which leads the requirement of a stress free reference state) would determine the swelling ratio, or
ϕrefs, in terms of the known constitutive parameters in the free energy densities
Ψnet and
Ψint. However, in our experiments the fibrin and collagen gel are naturally in a wet (or swollen) state with known
ϕrefs and it is not clear how to make a dry network whose mechanical behavior can be characterized. Similarly, it is hard to measure and characterize the mixing behavior of the fibrin and collagen with liquid. For these reasons we assume a simple form for the network free energy density and determine the constants (
e.g.,
G1,
G2,
etc.) in it by matching to experiments. In particular, the phenomenological parameter
α1 is determined from the fact that
ϕrefs, or the swelling ratio, in the stress-free reference state is known.
Now imagine a representative volume element (a unit cube) of this gel and apply a small shear strain of magnitude γ on it. A shear is a volume preserving deformation, and we assume the effect of liquid diffusion is negligible so J = 1 everywhere in the gel. Therefore, we can calculate the shear stress using eqn (10) by substituting the corresponding deformation gradient F:
where we have only kept terms up to linear order in
γ. So the small strain shear modulus of the gel is in fact
Ggel =
G1ϕrefs. We have measured the small strain shear modulus of our fibrin and collagen gels in rheometer experiments as discussed in a previous section. Since we know the solid volume fraction of our gels we can set the value of
G1 in our continuum model.
2.3.3 Liquid flux.
In this work, Darcy's law is used for the constitutive behavior of the liquid flux. Further, we assume the material is isotropic so that this relation can be written as:| | 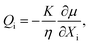 | (13) |
where η is the viscosity of the liquid and K is the permeability, which is a decreasing function of the solid phase volume fraction ϕs. We use a result mentioned by Wufsus et al.:35| | 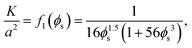 | (14) |
where a is the average radius of the network fibers. When the value of a increases, the pore size will increase if the solid volume fraction is held fixed, which results in a larger permeability. In the finite element simulations that follow the solid phase volume fraction varies temporally and spatially within the gels.
2.3.4 FEM implementation and results.
Cylindrical specimens of height 1 mm and radius 2.68 mm are subjected to displacement-controlled uniaxial compression up to an axial compression of λz = 0.2, with the side surfaces traction free and at zero chemical potential since they are exposed to a bath of pure liquid. The displacement in the z direction of the bottom surface is set to zero, and the top and bottom surfaces are impermeable. Fibrin was polymerized between the plates and it was stuck to both top and bottom plate, therefore, no slip boundary conditions are applied for the fibrin gel at top and bottom surfaces. However, collagen was pre-polymerized and put between the plates afterwards, so there is no bond between gel and rheometer in the case of collagen, and slip boundary conditions are applied. The boundary value problem is solved using finite element software ABAQUS using its soils module26 with the constitutive model described above as a user-defined sub-routine.
For the fibrin gel, we choose: ϕrefs = 0.056,  , G2 = 4000 Pa, π0 = 60
, G2 = 4000 Pa, π0 = 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, β1 = 1.08, then
000 Pa, β1 = 1.08, then 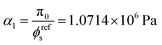 . For the collagen gel, we choose: ϕrefs = 0.03,
. For the collagen gel, we choose: ϕrefs = 0.03, 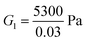 , G2 = 15
, G2 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, π0 = 30
000 Pa, π0 = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, β1 = 1.06, then
000 Pa, β1 = 1.06, then 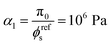 . To understand why G1 is written as above, note that G1 represents the small strain shear modulus of the unswollen dry fiber network, but we measure shear moduli of the swollen fibrin and collagen gels in the reference state which is ϕrefsG1. The value of a is chosen as 56 nm for fibrin and 58 nm for collagen.35
. To understand why G1 is written as above, note that G1 represents the small strain shear modulus of the unswollen dry fiber network, but we measure shear moduli of the swollen fibrin and collagen gels in the reference state which is ϕrefsG1. The value of a is chosen as 56 nm for fibrin and 58 nm for collagen.35
We first look at the Poisson ratio. We performed compression experiments on collagen gels that were not attached to the top and bottom plates of the rheometer. This allowed for slip between the surfaces of the gel and the plates which could approximate a uniaxial state of stress. In our theoretical calculations we modeled the top and bottom surfaces of the collagen gels as shear free so that σx = σy = 0. Then, we find the stretch λx = λy in the lateral direction using eqn (10) with λz specified. We can compute the Poisson ratio according to
| | 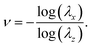 | (15) |
The results are shown in
Fig. 2. The trends are in good agreement with those seen in experiment indicating that our choice of constitutive parameters is good. Similar experiments could not be performed with fibrin gels because they were stuck to the top and bottom plates, thus the surfaces could not be modeled as shear free. As such the state of deformation in the fibrin gels is non-uniform.
Next, we consider compression of the gel samples. As in experiment, height changes ranging from λz = 0.9 to λz = 0.2 are applied by compressing the fibrin gels stepwise at a rate of 10 μm s−1, and the results of engineering stress and volume change are shown in Fig. 2. For fibrin the peak compressive stress achieved after each stepwise increase in applied strain ε = 1 − λz agrees well with the experimental results in the ranges ε ≤ 0.2 and ε ≥ 0.6. The agreement of the experimental peak stress and FE simulations for fibrin in the intermediate range 0.25 ≤ ε < 0.6 is not so good. The FE model consistently underestimates the volume decrease in the fibrin gels over the whole range of applied strains ε. The magnitude of the relaxation in stress is also consistently smaller in the FE simulations than in experiment both for fibrin and collagen gels. For collagen the peak compressive stress achieved after each stepwise increase in applied strain agrees well with experiment only for smaller strains ε ≤ 0.25. The FE model does reasonably well in predicting the volume decrease for ε ≤ 0.25, but it underestimates the volume decrease for larger strains. In spite of these discrepancies, the qualitative trends in the peak stress, volume decrease, and stress relaxations are reasonably captured by the continuum model. Quantitatively, the continuum model performs best for both fibrin and collagen gels for ε ≤ 0.25, and reasonably well for fibrin gels for ε ≥ 0.6.
Could the magnitude of the stress relaxation and the volume of fluid escaping the gel (both underestimated by FE simulations) be related? Likely, yes, since if a large amount of fluid escapes from the gel then the relaxation in stress will be larger after each compression step; the quicker the fluid escapes the quicker will be the relaxation. The motion of fluid in gels depends on the pore size and the chemical potential gradient, which in turn depends on the osmotic pressure gradient. In order to examine the effect of pore size and osmotic pressure on the stress drop during relaxation, we vary the value of a and π0 while keeping the other parameters fixed. The results are shown in Fig. 4. Here we choose ϕrefs = 0.056, 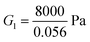 , G2 = 15
, G2 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, β1 = 1.1. Slip between the plates and the top and bottom surfaces of the gels is allowed. The relaxation seen in experiments is rapid suggesting that the pore-sizes are bigger than what is obtained assuming a homogeneously deforming gel. The equilibrium value of the stress after relaxation is lower for a low value of π0. Lower values of π0 imply a lower solid volume fraction than that predicted by a homogeneously deforming gel. In the next section we show that our gels do not deform in a homogeneous manner under compression for intermediate applied strains. Thus, there are regions in the specimen where the pore size is larger and the solid volume fraction is lower which could help explain the discrepancies between experiment and continuum (FE based) simulations for intermediate strains. Good agreement between experiments and FE simulations for small applied strains suggests that gels do deform homogeneously for these strains.
000 Pa, β1 = 1.1. Slip between the plates and the top and bottom surfaces of the gels is allowed. The relaxation seen in experiments is rapid suggesting that the pore-sizes are bigger than what is obtained assuming a homogeneously deforming gel. The equilibrium value of the stress after relaxation is lower for a low value of π0. Lower values of π0 imply a lower solid volume fraction than that predicted by a homogeneously deforming gel. In the next section we show that our gels do not deform in a homogeneous manner under compression for intermediate applied strains. Thus, there are regions in the specimen where the pore size is larger and the solid volume fraction is lower which could help explain the discrepancies between experiment and continuum (FE based) simulations for intermediate strains. Good agreement between experiments and FE simulations for small applied strains suggests that gels do deform homogeneously for these strains.
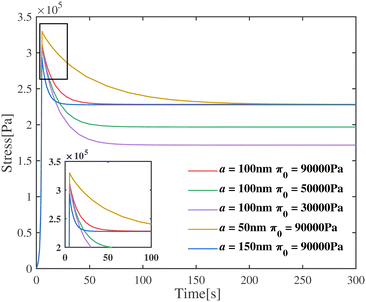 |
| | Fig. 4 Engineering stress of the gel as a function of time for various values of fiber radius and initial osmotic pressure. The permeability affects the peak value of the stress, whereas the initial osmotic pressure mainly affects the value of stress at equilibrium. | |
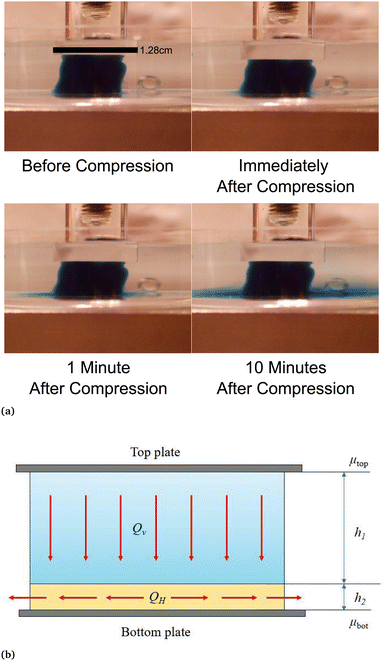 |
| | Fig. 5 (a) Fluid outflow from the sample visualized by colored liquid. A fibrin gel at a concentration of 15 mg ml−1 was polymerized with a blue stained buffer. After compression the colored fluid leaves the sample only from the bottom over a period of minutes. (b) Schematic representation of fluid flow in our compressed gel samples. The flow in the upper layer (height h1) is directed downward, while the flow in the lower layer (height h2) is radial. The chemical potential at the middle of the top plate is denoted by μtop and that at the middle of the bottom plate μbot. The lower layer thickness h2 is significantly smaller than the upper layer thickness h1 (h2 ≪ h1). These two layers are not to be confused with densified and rarefied phases that are formed under compression. | |
2.4 Densification and compartmentalization
To examine the non-uniform densification in compressed gels we suspended fluorescently labeled microspheres in the networks. With an average diameter of 4 μm the spheres are distinctly larger than the networks’ mesh size, which we estimate to be less than 0.5 μm for fibrin networks50 and less than 1 μm for collagen networks,51 hence not able to move through the network under compressive stresses. Counting the number of microspheres per slice in a z-stack with a step size of 10 μm we quantify the local gel density along the height of the gel. The initial height was 0.5 mm for the fibrin gel and 1 mm for collagen respectively. Compressive strains were applied in a strain-rate controlled manner via a piezo driven plate geometry mounted on a microscope to ensure the same conditions as in the rheology experiments. A picture of the compression device is presented in the ESI.† The z-stack measurements were performed after an equilibration phase of 10 minutes after each compression step. Particle counts divided by the number of particles per respective slice for the uncompressed control measurement, plotted as a function of relative height, are shown in Fig. 6. The relative particle count is visualized as a heatmap for each compression step. The black lines indicate the height of the gel, or the position of the compressing plate. Compressing the gel to 10% and equilibrating results in little to no deviation of the particle density of the control measurement. For strains between 20% and 40%, the particle density increases in the top layers of the gel, indicated by darker blue shades near the top of the gel, while the bottom layers remain at a similar particle density. Compressive strain steps exceeding 40% of the initial height of the gel eventually lead to a general increase of particles per slice. The densification reaches the bottom of the gel for strains around 70% for fibrin and 50% for collagen. We attribute the occurrence of finite values above the actual height of the gel sample to errors due to reflections on the plate. The densification reaches the bottom of the gel for strains around 70% for fibrin and 50% for collagen.
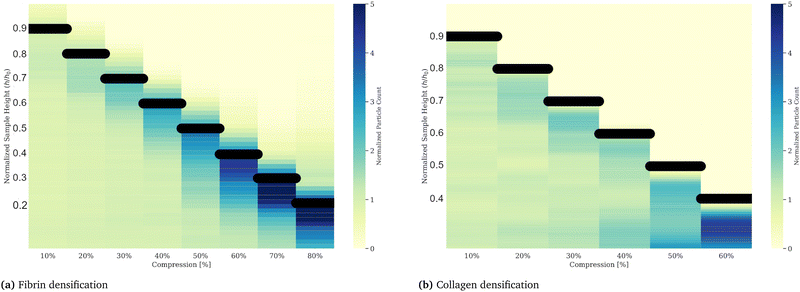 |
| | Fig. 6 Gel densification of fibrin (a) and collagen (b) upon compressive strains plotted as a heatmap. Counted particles, inserted into a gel by co-polymerization, in vertical layers via z-stack imaging, reveal a non-uniform densification of fibrin and collagen gels upon successive compressions. The particle counts are divided by the control measurement, taken after polymerization and in an uncompressed state. Compressive strains, applied at a strain rate of 10 μm s−1, result in a gel densification in the upper layers of the gel, indicated by increased particle densities at the respective upper part of the gel (near the top plate indicated by the black bar), while the lower layers, where the values do not deviate from the control measurement, stay unaffected. An alternative representation for these data is shown in the (ESI†) Fig. 5. From these data we conclude the existence of two compartments on compressed gels. | |
It is evident from Fig. 6 that for small applied strains the deformation of both fibrin and collagen gels is relatively small and homogeneous everywhere, while for large applied strains the gels are densified everywhere. This could be the reason why the continuum model performs well for low applied strains, in addition to the fact that our choice of G1 for both materials is based on the experimentally measured small strain shear modulus. For intermediate applied strains the FE simulation predicts a smoothly varying strain, but experiment shows that the strain profile is heterogeneous with both gels divided into two compartments. The region adjacent to the top plate is densified with a smaller pore size than the initial reference state, while the region adjacent to the bottom plate is rarefied with pore size close to that of the initial reference state. In open cell foams such densification occurs due to progressive buckling of struts leading to the collapse of pores and contact between neighboring buckled struts in the densified phase.28,38 Similar micro-buckling of fibrin fibers in compressed fibrin gels was demonstrated using confocal microscopy in Kim et al.19 which shows that the same physics as in fluid-filled foams is also applicable in fibrous gels. An interface separates the densified and rarefied regions of the gels, and it moves toward the bottom plate as more compression is applied. At the end of each relaxation step when the gel is at equilibrium and the compressive stress is uniform everywhere in the gel there are two different micro-structural states of the fibrin or collagen network that co-exist. The coexistence of phases and a moving interface (or phase boundary) separating them is characteristic of martensitic phase transitions.52 The 3D continuum model described above cannot capture the co-existence of densified and rarefied phases of the fiber network or the moving interface seen in experiment which is why it performs poorly for intermediate applied strains. However, a 1D continuum model based on a multi-well free energy density captures many features in the cyclic stress–strain response (including hysteresis) of fibrin gels as discussed in detail in Liang et al.27 and Sun et al.53 In the following section we show that a model based on the co-existence of phases can also account for the dependence of permeability on the applied compressive strain in our gels.
2.5 Simple model for permeability of heterogeneous fibrous gels under compression
To understand better the flow of fluid in our compressed gels we performed experiments on gels in which the fluid was infused with a blue dye (Fig. 5(a)). The sample was immersed in clear fluid before compressive strain steps were applied so that the blue fluid draining out of the gel could be clearly seen after each strain step. Surprisingly, it was found that after each compression step the blue fluid emerged from the gel through the lateral surface very close to the bottom plate and not over the full height of the cylindrical sample (see bottom panels in Fig. 5(a)). This suggests that after each compression step fluid flows from top to bottom in most of the cylindrical sample and it turns outward and drains from the periphery only when it reaches the impermeable bottom plate. A schematic figure depicting this flow pattern is shown in Fig. 5(b). Fluid flow is downward over current height h1 of the compressed sample, while it is radial over a thin layer of current height h2 of the sample. The vertical fluid flux assumed constant all over the circular cross-section can be approximated as:| | 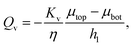 | (16) |
where we assume that the chemical potential is μtop at the center of the top plate and it is μbot at the center of the bottom plate, that the chemical potential gradient is uniform along the radial direction and Kv is a Darcy constant for the vertical direction. The radial outward flux of fluid through the thin layer near the bottom plate can be approximated as:| | 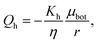 | (17) |
where we have assumed that the chemical potential on the boundary is 0 and Kh is the Darcy constant for radially outward flow. By mass conservation all the fluid that is flowing downward is draining out through the lateral surface so that 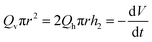 where V(t) is the current volume of the compressed sample. Then, mass conservation gives us the following relation between Kv and Kh:
where V(t) is the current volume of the compressed sample. Then, mass conservation gives us the following relation between Kv and Kh:| | 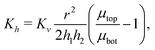 | (18) |
Thus, the experimentally obtained Kh is related to the vertical permeability Kv and both of them depend on the applied compressive strain ε. In what follows we compute Kv(ε); later we will exploit the relation between the measured Kh and the computed Kv to understand the permeability of compressed fibrin and collagen gels.
We showed in the previous section that under compressive loads the gel undergoes a phase transition that leads to the formation of a rarefied and densified phase that co-exist at the same stress. The rarefied phase consists of mostly straight fibers with some contacts while the densified phase consists of bent and buckled fibers with a large number of contacts. The two phases are separated by a relatively sharp interface that nucleates at the top plate and moves toward the bottom plate as more strain is applied. This interface divides the gel into two compartments with the densified phase on top and the rarefied phase on the bottom. The pore size in the densified phase is smaller than that in the rarefied phase. This should result in different permeabilities, or Darcy constants, yet the previous continuum theory could not account for this because the strain varied smoothly from top to bottom in those calculations. The rarefied-to-densified phase transition does not play a role in the permeability expressions of Wufsus et al.,35 either, since they make fibrin gels of different solid volume fraction not by applying compressive load but by changing the initial fibrinogen concentration. Our goal in this section is to present an analytical model to account for the heterogeneity of deformation in our fibrous gel and its effect on the overall permeability.
We have assumed that the fluid flux in most of the gel, especially in the neighborhood of the axis of the cylinder, is downward. We know that the gel is divided into a densified compartment of height hd near the top plate and a rarefied compartment of height hr near the bottom plate. The compressive stress in the gel is the same in the densified and rarefied phases since the major part of the stress is relaxed after a compression step when the flux measurements are made. In the same way, the flux across the cylinder cross-section is the same for the two compartments and is given by Darcy's law. Assuming that the chemical potential gradient in each of the two phases is constant:
| | 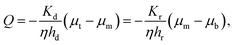 | (19) |
where
μt,
μb and
μm are the liquid chemical potentials at the center of top plate, bottom plate and at the rarefied-densified interface, respectively. Here,
Kd and
Kr are permeabilities in the densified and rarefied phases, respectively. We can eliminate
μm between the two equations for
Q and get
| | 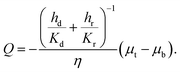 | (20) |
The above equation is in the form of Darcy's law with an effective permeability
Keff given by:
| | 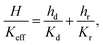 | (21) |
where
H is the undeformed height of the specimen.
K
eff is nothing but Kv(ε), so our goal is to find a simple formula for Keff(ε) where ε is the applied strain. The constants Kd and Kr depend on the average fiber radius a and the solid volume fraction as:
| | | Kr = a2f(ϕr), Kd = a2f(ϕd), | (22) |
where
f(
ϕ) is known from the following expressions given in Wufsus
et al.35 For example,
f(
ϕ) could be
f1(
ϕ) from
eqn (14). We also use
| | 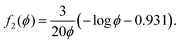 | (23) |
Other expressions for
f(
ϕ) given in Wufsus
et al. also capture the trend in permeability as a function of solid volume fraction quite well. For the solid volume fractions in the densified and rarefied phases, we take (to a first approximation)
| | 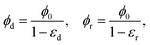 | (24) |
where
εd and
εr are the compressive strains in the densified and rarefied phases, respectively and
ϕ0 is the solid volume fraction in the undeformed configuration of the gel. The expressions above assume that the Poisson effect in the network is negligible so that volume change is dominated by the axial compressive strain. This is certainly true of the collagen gel in our experiments. Assuming that rarefied phase occupies the region 0 ≤
z ≤
s in the undeformed gel and the densified state occupies the region in
s ≤
z ≤
H in the undeformed gel we can write:
| | | H(1 − ε) = hr + hd = s(1 − εr) + (H − s)(1 − εd), | (25) |
where
εr and
εd are strains in the rarefied and densified phase, respectively, corresponding to a stress
σ0 which is the Maxwell stress for the phase transition from rarefied to densified phase of the fibrous network.
Eqn (25) can be solved for
s to give
| |  | (26) |
Using eqn (25) for hr and hd in eqn (21) we get
| | 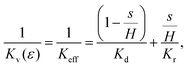 | (27) |
where
s can be computed in terms
ε and
H using
eqn (26). We will take
εr to be the strain at which the phase transition begins and
εd is the strain at which it ends. In other words, the entire fiber network is in the rarefied phase for
ε ≤
εr and the entire network is in the densified phase for
ε ≥
εd. Typically,
εr ≈ 0.05 and
εd ≈ 0.6 for fibrin gels. For
ε <
εr and
ε >
εd the effective permeability is simply given by
Keff(
ε) =
a2f(
ϕ) with
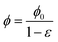
.
In Fig. 3 we plot the experimentally obtained 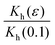 together with the theoretically computed
together with the theoretically computed 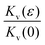 remembering that Kv(0) = Kh(0) due to isotropy. We have used both f1(ϕ) (eqn (14)) and f2(ϕ) (eqn (23)) with very similar results. Remarkably, the two quantities agree with each other suggesting that
remembering that Kv(0) = Kh(0) due to isotropy. We have used both f1(ϕ) (eqn (14)) and f2(ϕ) (eqn (23)) with very similar results. Remarkably, the two quantities agree with each other suggesting that 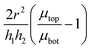 in eqn (18) does not vary much with applied strain.
in eqn (18) does not vary much with applied strain.
3 Discussion
With an experimental setup specifically designed to investigate poroelastic effects in soft biomaterials we revealed complex structural behaviors exhibited by fibrin- and collagen-based gels undergoing compressive deformations. The setup we designed can be transferred to a theoretical model of large deformation poroelasticity through the boundary conditions; we perform finite element calculations based on this model to capture qualitative trends in the stress, volume change and relaxation behavior of the gels. Our setup integrates compression rheology with camera-facilitated shape detection and provides insights into the dynamic responses of fibrin gels to deformations over a broad range of applied compressive strains. We observed a nonlinear behavior of permeability for successively compressed gels, indicative of flow properties governed by the morphology in network structure. Theoretical modeling based on the finite element method (FEM) showed that a homogeneous deformation field captures some but not all observations in our experiments. The deviation of the modeling from experimental data was particularly clear in the intermediate compression regime. The predictions from the finite element calculations agreed well with experiments for strains below 0.25 for both fibrin and collagen gels. For fibrin gels the predictions of peak stress after steps at strains > 0.6 agreed well with experimental measurements. The volume decrease and magnitude of stress relaxation was under-predicted in finite element calculations over most of the applied strains for both gels. This motivated us to assume a heterogeneous deformation field and the emergence and disappearance of distinct densification regimes within the gel to capture the trends in permeability. We confirmed the model assumptions about the coexistence of two phases that differ in density in the intermediate compression regime by means of fluorescence microscopy. Utilizing fluorescent microspheres as tracers, we unveiled densification along the height of the gel. This compartmentalization underscores the heterogeneous nature of mechanical responses within soft biopolymer networks, related to previous rheological measurements of response to compression54,55 and potentially influencing various physiological processes. This result also calls for more sophisticated continuum energy densities and allied computational methods which allow for the coexistence of multiple phases. Unraveling the intricate interplay between mechanical forces, structural properties, and fluid flow behavior in biopolymer networks, particularly fibrin- and collagen-based gels, will enable future experimental advancements to improve mass transport through native and engineered biomaterials.
4 Materials and methods
4.1 Fibrin purification and preparation
Fibrinogen from individual cow plasma was prepared with modifications to the Capet–Antonini method as described by Mosher and Blout.56 Eight parts of cow blood, mixed with 1 part of 0.1 M sodium–EDTA (pH 7.0), underwent two centrifugations at 5000 × g for 20 minutes each to remove cells. Barium sulfate (100 g l−1) and ε-ACA (6.5 g l−1) were added, stirred for 1 hour, and the supernatant collected by centrifugation. Solid ammonium sulfate (129) g l−1 was added at 4 °C, yielding a precipitate collected by centrifugation, washed with 25% saturated ammonium sulfate, and dissolved in 0.05 M sodium phosphate, 0.01 M sodium–EDTA (pH 6.6). A second ammonium sulfate precipitation yielded a white precipitate, dissolved in 0.01 M Tris, 0.1 M sodium chloride (pH 7.4), and dialyzed. After cooling to 0–1 °C, ε-ACA and ethanol were added to solutions of 0.1 M and 7% respectively, and the resulting precipitate dissolved in 0.01 M Tris, 0.01 M sodium–EDTA, 0.1 M sodium chloride (pH 7.4). To separate fibrinogen from fibronectin the solution was applied to a column of Sepharose 4B equilibrated with 0.05 M Tris/HCL pH 7.5, containing 5 mM benzamidine and 0.02% (w/v) sodium azide. After eluting and equilibrating the column with this buffer the gelatin-Sepharose was washed with 1000 ml of the equilibration buffer, 1000 ml of 1 M NaCl in the same buffer and 400 ml, 0.2 M arginine buffered with 0.05 M Tris/HCl, pH 7.5 in this order. The obtained fibrinogen solution was aliquoted and frozen at −80 °C. Fibrinogen was polymerized to fibrin gels by adding 6.4 units per ml thrombin and 10 mM CaCl2.
4.2 Collagen preparation
Collagen type 1 from calf skin was purchased from MP Biomedicals, USA. A stock solution of 15 mg ml−1 was prepared by dissolving lyophilized collagen in 0.02 M acetic acid on a rocker at 4 °C for 48 hours. Collagen samples were prepared to total volumes of 22.5 μl by neutralizing the pH with sodium hydroxide and adjust the buffer conditions to 1× PBS at pH 7.2. Collagen samples were polymerized for 1 hour at 37 °C in a cut syringe with a radius of 2.68 mm to match an initial height of 1 mm at a total sample volume of 22.5 μl. After polymerization, collagen gels were crosslinked with glutaraldehyde by adding 50 μl of 0.5% glutaraldehyde on top of the gel in the syringe and rested for at least 2 hours.
4.3 Rheology and camera-supported flow determination
Compression rheology measurements were performed with a dynamic shear rheometer (Discovery HR20, TA Instruments, USA) and a plate geometry with a diameter of 20 mm. The bottom plate was replaced by a transparent glass surface to enable camera detection as described in Section 2. The initial gap size was set to 1 mm. Fibrin was polymerized between the plates for 30 minutes at room temperature after initiating polymerization by adding thrombin (at a stock concentration of 80 units per ml) to a final concentration of 6 units per ml and 10 mM of CaCl2. Tris buffer was used to get to a final volume of 22.5 μl, which corresponds to an initial gel diameter of 2.68 mm for the respective initial height of 1 mm. After 10 minutes of polymerization, the fibrin gel was surrounded with 1× Tris buffer to prevent interfacial elasticity artefact, prevent evaporation and improve imaging. Polymerization was monitored with a dynamic time sweep with one measurement point every 10 seconds at a frequency of 1 Hz and an applied shear strain of γ = 5%. After the sample was polymerized, a sequence of axial compression strains was applied by lowering the upper plate with a set strain rate of 10 μm s−1 while measuring the normal force response. Between compression steps, a stress relax test was used to monitor the relaxation behavior of the normal force. The relaxation after compression was monitored for 10 minutes after a 10% compression step and 5 minutes after a 5% compression step. During and after compression the sample's cross-section was monitored using a Moticam S20 high resolution camera at a frame rate of ∼5 fps. The change of cross-section area was calculated by transferring the acquired video to a series of binary images and counting the pixels for each frame using ImageJ plugins. A self-written Python script was used to synchronize and process both the data from the rheometer as well as the camera data to determine permeability defining parameters as well as mechanical properties.
4.4 Fluorescence microscopy
Fluorescence microscopy was used to determine the density of microspheres along the vertical axis of the gel sample. Fibrin was polymerized in presence of a 1/1000 solution of 4 μm sized fluorescent labeled sulfate microspheres (Invitrogen FluoSpheres) between a Petri dish sitting on the microscope sample holder and an 8 mm methyl methacrylate plate. To ensure reproducibility and to enable a uniform particle distribution by fast polymerization, the same preparation protocol was used as for the rheology experiment. The plastic plate was mounted on a piezo driven stage to enable rate controlled compressive deformations (see ESI†). Compressive strains were applied in 10% steps at a strain rate of 10 μm s−1 by lowering the piezo stage in fast successive 20 nm steps. After compression and prior to the z-stack measurement, the sample was equilibrated for 10 minutes. A z-stack measurement with a vertical step size of 10 nm was performed to capture the number of microspheres per slice.
Author contributions
P. M., P. K. P., and P. A. J. designed the project. P. M. and J. A. K. performed experiments. P. M. and J. A. K. analyzed data. P. K. P. and Y. R. performed modeling. P. M., P. A. J., K. H. V., Y. R., J. A. K. and P. K. P. wrote the manuscript.
Data availability
Data for this article are available at a repository at https://github.com/PennAverell/Mollenkopf-et-al-Soft-matter-2025.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by grants from the US National Science Foundation (DMR-2309043) and the US National Institute of General Medical Sciences (GM136259). YR was supported by a grant from US National Science Foundation (DMR-2212162). PKP was partially supported by a grant from the National Heart, Lung and Blood Institute (R01 HL 148227).
Notes and references
- D. A. Fletcher and R. D. Mullins, Nature, 2010, 463, 485–492 CrossRef CAS PubMed.
- F. Huber, J. Schnauß, S. Rönicke, P. Rauch, K. Müller, C. Fütterer and J. Käs, Adv. Phys., 2013, 62, 1–112 CrossRef CAS PubMed.
-
P. Fratzl, Collagen: structure and mechanics, Springer, 2008, pp. 1–13 Search PubMed.
- J. C. Chapin and K. A. Hajjar, Blood Rev., 2015, 29, 17–24 CrossRef CAS PubMed.
-
J. W. Weisel and R. I. Litvinov, Fibrous proteins: structures and mechanisms, 2017, pp. 405–456 Search PubMed.
- M. T. Punter, B. E. Vos, B. M. Mulder and G. H. Koenderink, Soft Matter, 2020, 16, 1298–1305 RSC.
- P. A. Janmey, Curr. Opin. Cell Biol., 1991, 3, 4–11 CrossRef CAS PubMed.
- M. A. Swartz and M. E. Fleury, Annu. Rev. Biomed. Eng., 2007, 9, 229–256 CrossRef CAS PubMed.
- C. Frantz, K. M. Stewart and V. M. Weaver, J. Cell Sci., 2010, 123, 4195–4200 CrossRef CAS PubMed.
- C. P. Broedersz and F. C. MacKintosh, Rev. Mod. Phys., 2014, 86, 995–1036 CrossRef CAS.
-
J. D. Ferry, Biological and Synthetic Polymer Networks, Springer, 1988, pp. 41–55 Search PubMed.
- I. K. Piechocka, R. G. Bacabac, M. Potters, F. C. MacKintosh and G. H. Koenderink, Biophys. J., 2010, 98, 2281–2289 CrossRef CAS PubMed.
- D. C. Morse, Macromolecules, 1998, 31, 7044–7067 CrossRef CAS.
- F. MacKintosh, J. Käs and P. Janmey, Phys. Rev. Lett., 1995, 75, 4425 CrossRef CAS PubMed.
- M. Glaser, S. Deb, F. Seier, A. Agrawal, T. Liedl, S. Douglas, M. K. Gupta and D. M. Smith, Molecules, 2021, 26, 2287 CrossRef CAS PubMed.
- J. S. Lorenz, J. Schnauß, M. Glaser, M. Sajfutdinow, C. Schuldt, J. A. Käs and D. M. Smith, Adv. Mater., 2018, 30, e1706092 CrossRef PubMed.
- K. Kroy and J. Glaser, New J. Phys., 2007, 9, 416 CrossRef.
- P. Mollenkopf, D. Prascevic, M. Glaser, D. M. Smith and J. Schnauß, Adv. Mater. Interfaces, 2024, 2300623 CrossRef CAS.
- O. V. Kim, R. I. Litvinov, J. W. Weisel and M. S. Alber, Biomaterials, 2014, 35, 6739–6749 CrossRef CAS PubMed.
- O. V. Kim, X. Liang, R. I. Litvinov, J. W. Weisel, M. S. Alber and P. K. Purohit, Biomech. Model. Mechanobiol., 2016, 15, 213–228 CrossRef PubMed.
-
O. Coussy, Poromechanics, John Wiley & Sons, 2004 Search PubMed.
-
R. De Boer, Theory of porous media: highlights in historical development and current state, Springer Science & Business Media, 2012 Search PubMed.
- M. Doi, J. Phys. Soc. Jpn., 2009, 78, 052001 CrossRef.
- C. W. MacMinn, E. R. Dufresne and J. S. Wettlaufer, Phys. Rev. Appl., 2016, 5, 044020 CrossRef.
- B. Blombäck and M. Okada, Thromb. Res., 1982, 25, 51–70 CrossRef PubMed.
- K. Garyfallogiannis, P. K. Purohit and J. L. Bassani, J. Mech. Phys. Solids, 2022, 167, 105009 CrossRef CAS.
- X. Liang, I. Chernysh, P. K. Purohit and J. W. Weisel, Acta Biomater., 2017, 60, 275–290 CrossRef CAS PubMed.
- R. Lakes, P. Rosakis and A. Ruina, J. Mater. Sci., 1993, 28, 4667–4672 CrossRef CAS.
- T. Novak, B. Seelbinder, C. M. Twitchell, C. C. van Donkelaar, S. L. Voytik-Harbin and C. P. Neu, Adv. Funct. Mater., 2016, 26, 2617–2628 CrossRef CAS PubMed.
- A. E. Ehret, K. Bircher, A. Stracuzzi, V. Marina, M. Zündel and E. Mazza, Nat. Commun., 2017, 8, 1002 CrossRef PubMed.
-
S. P. Magnusson, K. M. Heinemeier and M. Kjaer, Metabolic influences on risk For tendon disorders, 2016, pp. 11–25 Search PubMed.
- M. Pieters and A. S. Wolberg, Res. Pract. Thromb. Haemostasis, 2019, 3, 161–172 CrossRef PubMed.
- S. Kattula, J. R. Byrnes and A. S. Wolberg, Arterioscler., Thromb., Vasc. Biol., 2017, 37, e13–e21 CrossRef CAS PubMed.
- Q.-M. Wang, A. C. Mohan, M. L. Oyen and X.-H. Zhao, Acta Mech. Sin., 2014, 30, 20–27 CrossRef CAS.
- A. R. Wufsus, N. Macera and K. Neeves, Biophys. J., 2013, 104, 1812–1823 CrossRef CAS PubMed.
- S. A. Chester and L. Anand, J. Mech. Phys. Solids, 2010, 58, 1879–1906 CrossRef CAS.
- W. Hong, Z. Liu and Z. Suo, Int. J. Solids Struct., 2009, 46, 3282–3289 CrossRef CAS.
- L. J. Gibson, MRS Bull., 2003, 28, 270–274 CrossRef.
- R. C. Spero, R. K. Sircar, R. Schubert, R. M. Taylor, A. S. Wolberg and R. Superfine, Biophys. J., 2011, 101, 943–950 CrossRef CAS PubMed.
- M. Pieters, A. Undas, R. Marchi, M. De Maat, J. Weisel and R. Ariëns, J. Thromb. Haemostasis, 2012, 10, 2179–2181 CrossRef CAS PubMed.
- V. Serpooshan, T. M. Quinn, N. Muja and S. N. Nazhat, Acta Biomater., 2013, 9, 4673–4680 CrossRef CAS PubMed.
- A. Stracuzzi, E. Mazza and A. E. Ehret, J. Appl. Math. Mech., 2018, 98, 2135–2154 Search PubMed.
- F. T. Borges, G. Papavasiliou and F. Teymour, Biomacromolecules, 2020, 21, 5104–5118 CrossRef CAS PubMed.
- K. Garyfallogiannis, P. K. Purohit and J. L. Bassani, Int. J. Solids Struct., 2024, 286, 112563 CrossRef PubMed.
- J. E. Bischoff, E. M. Arruda and K. Grosh, Rubber Chem. Technol., 2001, 74, 541–559 CrossRef CAS.
-
R. W. Ogden, Non-linear elastic deformations, Courier Corporation, 1997 Search PubMed.
-
G. A. Holzapfel, Nonlinear solid mechanics: a continuum approach for engineering science, 2002 Search PubMed.
-
D. H. Boal, Mechanics of the Cell, Cambridge University Press, 2012 Search PubMed.
- K. Garyfallogiannis, R. K. Ramanujam, R. I. Litvinov, T. Yu, C. Nagaswami, J. L. Bassani, J. W. Weisel, P. K. Purohit and V. Tutwiler, Acta Biomater., 2023, 159, 49–62 CrossRef CAS PubMed.
- H. C. De Cagny, B. E. Vos, M. Vahabi, N. A. Kurniawan, M. Doi, G. H. Koenderink, F. C. MacKintosh and D. Bonn, Phys. Rev. Lett., 2016, 117, 217802 CrossRef PubMed.
- Y.-l Yang, L. M. Leone and L. J. Kaufman, Biophys. J., 2009, 97, 2051–2060 CrossRef CAS PubMed.
-
R. Abeyaratne and J. K. Knowles, Evolution of phase transitions: a continuum theory, Cambridge University Press, 2006 Search PubMed.
- C. Sun, I. N. Chernysh, J. W. Weisel and P. K. Purohit, Proc. R. Soc. A, 2020, 476, 20200643 CrossRef PubMed.
- A. S. Van Oosten, M. Vahabi, A. J. Licup, A. Sharma, P. A. Galie, F. C. MacKintosh and P. A. Janmey, Sci. Rep., 2016, 6, 19270 CrossRef CAS PubMed.
- M. Vahabi, A. Sharma, A. J. Licup, A. S. Van Oosten, P. A. Galie, P. A. Janmey and F. C. MacKintosh, Soft Matter, 2016, 12, 5050–5060 RSC.
- D. F. Mosher and E. R. Blout, J. Biol. Chem., 1973, 248, 6896–6903 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Jakub A.
Kochanowski
a,
Jakub A.
Kochanowski
 a,
Yifei
Ren
a,
Yifei
Ren
 b,
Kyle H.
Vining
b,
Kyle H.
Vining
 c,
Paul A.
Janmey
c,
Paul A.
Janmey
 *ad and
Prashant K.
Purohit
*ad and
Prashant K.
Purohit
 b
b


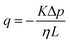 , with the viscosity of water η. The calculated Darcy constants K, divided by K1, the permeability for the first compression step exhibits nonlinear behavior in the intermediate compression strain regime and shows good agreement with the two-phase model shown in red (c) and (d). The dependence of the permeability according to Wufsus et al. which assumes uniform density of the gel is shown by the dashed black curve.35 Plots of the Darcy constant as a function of average concentration appears in the ESI† for fibrin and collagen gels.
, with the viscosity of water η. The calculated Darcy constants K, divided by K1, the permeability for the first compression step exhibits nonlinear behavior in the intermediate compression strain regime and shows good agreement with the two-phase model shown in red (c) and (d). The dependence of the permeability according to Wufsus et al. which assumes uniform density of the gel is shown by the dashed black curve.35 Plots of the Darcy constant as a function of average concentration appears in the ESI† for fibrin and collagen gels.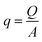 , where Q denotes the volumetric flow rate in units m3 s−1 and A the cross-section area, which represents the effective area available for fluid flow. We assume a cylindrical geometry with A = 2·π·r(t)·g(t), where the sample height equals the gap size g(t) and the sample radius is denoted as r(t). The volumetric flow rate is determined by monitoring the change in volume of the gel as a function of time. In calculating the outward liquid flux in this way we tacitly assume that the liquid phase and solid phase material in the gel are incompressible36,37 so the volume change of the gel is equal to the volume of liquid leaving the gel.
, where Q denotes the volumetric flow rate in units m3 s−1 and A the cross-section area, which represents the effective area available for fluid flow. We assume a cylindrical geometry with A = 2·π·r(t)·g(t), where the sample height equals the gap size g(t) and the sample radius is denoted as r(t). The volumetric flow rate is determined by monitoring the change in volume of the gel as a function of time. In calculating the outward liquid flux in this way we tacitly assume that the liquid phase and solid phase material in the gel are incompressible36,37 so the volume change of the gel is equal to the volume of liquid leaving the gel.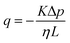 with the viscosity of the permeating fluid η and L, the distance over which the pressure difference Δp is effective and consequently where fluid flow appears. The proportionality constant K, also called the Darcy constant, expressed in units of m2 characterizes the permeability of the material. Previous studies investigated fluid flow at various pressure gradients in setups relying on hydrostatics. Instead, here we apply finite deformations at a fast strain rate and read the materials’ resistance to these compressive strains as an effective pressure. We calculated the flux curves for each compression step as outlined above. For the determination of the Darcy permeability, we consider the part of the curves which represent the relaxation phase after the compression. Representative curves showing the flux over normal stress during compression and relaxation for fibrin and collagen are presented in the ESI.† Fitting a linear function to the curve yields the slope α, and considering the equation for the Darcy permeability we determine K according to
with the viscosity of the permeating fluid η and L, the distance over which the pressure difference Δp is effective and consequently where fluid flow appears. The proportionality constant K, also called the Darcy constant, expressed in units of m2 characterizes the permeability of the material. Previous studies investigated fluid flow at various pressure gradients in setups relying on hydrostatics. Instead, here we apply finite deformations at a fast strain rate and read the materials’ resistance to these compressive strains as an effective pressure. We calculated the flux curves for each compression step as outlined above. For the determination of the Darcy permeability, we consider the part of the curves which represent the relaxation phase after the compression. Representative curves showing the flux over normal stress during compression and relaxation for fibrin and collagen are presented in the ESI.† Fitting a linear function to the curve yields the slope α, and considering the equation for the Darcy permeability we determine K according to 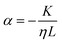 . In the above we take L ≈ r(t) so that the pore pressure gradient is approximated as
. In the above we take L ≈ r(t) so that the pore pressure gradient is approximated as 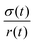 where σ is the average normal Cauchy stress on the top plate. In doing so we follow38 who give a simple expression for fluid flow through compressed open cell foams in terms of the measured compressive stress and dimensions of the foam. We chose the fitting boundaries to capture the last linear part of the curve at the low flux regime for each compression strain step because near the end of the relaxation step the pore pressure gradient in the radial direction can be approximated as linear in agreement with our assumption above. Finite element calculations in Fig. 2 reveal that the order of magnitude of the pore pressure gradient at this stage of relaxation is the same as σ/r for various values of the applied strain. Evaluating the first compression and relaxation we obtained a Darcy constant K1,F = −2.59 × 10−14 (± 7.6 × 10−15) m2 for fibrin and K1,C = −1.7 × 10−13 (± 5.4 × 10−14) m2 for collagen respectively. These values correspond to the range of permeabilities reported in previous studies.25,39–41 The derived Darcy permeabilities show a decrease for increasing compressive strain. Assuming a general increase in protein concentration as a result of fluid outflow explains the apparent decrease in permeability. Previous studies reported a Darcy permeability for small-pored fibrin gels, scaling inverse squared with protein concentration.6 Interestingly, our data shows permeabilities K that match this scaling behavior for 10% compressive strain as well as for compressions exceeding 60% strain for fibrin and 50% strain for collagen, but are distinctly lower for the respective intermediate strain regime (see Fig. 3). This observation highlights the complexity inherent in fluid flow through permeable soft polymer gels such as fibrin and collagen, where changes in structural integrity and pore geometry intricately influence the permeation dynamics. The experimental results align with the analytical model described in Section 2.4. The essential idea of this model is a non-uniform densification of a gel that is subjected to a rapid compressive deformation.
where σ is the average normal Cauchy stress on the top plate. In doing so we follow38 who give a simple expression for fluid flow through compressed open cell foams in terms of the measured compressive stress and dimensions of the foam. We chose the fitting boundaries to capture the last linear part of the curve at the low flux regime for each compression strain step because near the end of the relaxation step the pore pressure gradient in the radial direction can be approximated as linear in agreement with our assumption above. Finite element calculations in Fig. 2 reveal that the order of magnitude of the pore pressure gradient at this stage of relaxation is the same as σ/r for various values of the applied strain. Evaluating the first compression and relaxation we obtained a Darcy constant K1,F = −2.59 × 10−14 (± 7.6 × 10−15) m2 for fibrin and K1,C = −1.7 × 10−13 (± 5.4 × 10−14) m2 for collagen respectively. These values correspond to the range of permeabilities reported in previous studies.25,39–41 The derived Darcy permeabilities show a decrease for increasing compressive strain. Assuming a general increase in protein concentration as a result of fluid outflow explains the apparent decrease in permeability. Previous studies reported a Darcy permeability for small-pored fibrin gels, scaling inverse squared with protein concentration.6 Interestingly, our data shows permeabilities K that match this scaling behavior for 10% compressive strain as well as for compressions exceeding 60% strain for fibrin and 50% strain for collagen, but are distinctly lower for the respective intermediate strain regime (see Fig. 3). This observation highlights the complexity inherent in fluid flow through permeable soft polymer gels such as fibrin and collagen, where changes in structural integrity and pore geometry intricately influence the permeation dynamics. The experimental results align with the analytical model described in Section 2.4. The essential idea of this model is a non-uniform densification of a gel that is subjected to a rapid compressive deformation.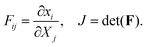

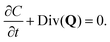
![[capital Psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b0.gif) = Ψ(F,C) − μC.
= Ψ(F,C) − μC.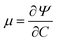 is the chemical potential of the interstitial liquid.37 Here the units of the chemical potential are J m−3, same as the units of stress. This is different from the units of chemical potential in standard thermodynamics because in addition to taking the derivative of a free energy with respect to the number of moles of a species (liquid) we are also dividing by the molar volume of the incompressible liquid. Based on standard continuum mechanical derivations that use the dissipation inequality, it can be shown that:
is the chemical potential of the interstitial liquid.37 Here the units of the chemical potential are J m−3, same as the units of stress. This is different from the units of chemical potential in standard thermodynamics because in addition to taking the derivative of a free energy with respect to the number of moles of a species (liquid) we are also dividing by the molar volume of the incompressible liquid. Based on standard continuum mechanical derivations that use the dissipation inequality, it can be shown that: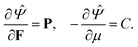
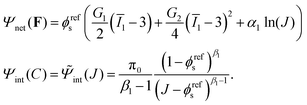
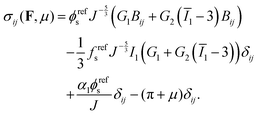
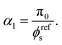
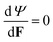 (which leads the requirement of a stress free reference state) would determine the swelling ratio, or ϕrefs, in terms of the known constitutive parameters in the free energy densities Ψnet and Ψint. However, in our experiments the fibrin and collagen gel are naturally in a wet (or swollen) state with known ϕrefs and it is not clear how to make a dry network whose mechanical behavior can be characterized. Similarly, it is hard to measure and characterize the mixing behavior of the fibrin and collagen with liquid. For these reasons we assume a simple form for the network free energy density and determine the constants (e.g., G1, G2, etc.) in it by matching to experiments. In particular, the phenomenological parameter α1 is determined from the fact that ϕrefs, or the swelling ratio, in the stress-free reference state is known.
(which leads the requirement of a stress free reference state) would determine the swelling ratio, or ϕrefs, in terms of the known constitutive parameters in the free energy densities Ψnet and Ψint. However, in our experiments the fibrin and collagen gel are naturally in a wet (or swollen) state with known ϕrefs and it is not clear how to make a dry network whose mechanical behavior can be characterized. Similarly, it is hard to measure and characterize the mixing behavior of the fibrin and collagen with liquid. For these reasons we assume a simple form for the network free energy density and determine the constants (e.g., G1, G2, etc.) in it by matching to experiments. In particular, the phenomenological parameter α1 is determined from the fact that ϕrefs, or the swelling ratio, in the stress-free reference state is known.
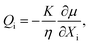
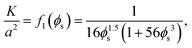
 , G2 = 4000 Pa, π0 = 60
, G2 = 4000 Pa, π0 = 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, β1 = 1.08, then
000 Pa, β1 = 1.08, then 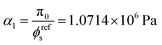 . For the collagen gel, we choose: ϕrefs = 0.03,
. For the collagen gel, we choose: ϕrefs = 0.03, 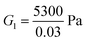 , G2 = 15
, G2 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, π0 = 30
000 Pa, π0 = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, β1 = 1.06, then
000 Pa, β1 = 1.06, then 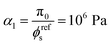 . To understand why G1 is written as above, note that G1 represents the small strain shear modulus of the unswollen dry fiber network, but we measure shear moduli of the swollen fibrin and collagen gels in the reference state which is ϕrefsG1. The value of a is chosen as 56 nm for fibrin and 58 nm for collagen.35
. To understand why G1 is written as above, note that G1 represents the small strain shear modulus of the unswollen dry fiber network, but we measure shear moduli of the swollen fibrin and collagen gels in the reference state which is ϕrefsG1. The value of a is chosen as 56 nm for fibrin and 58 nm for collagen.35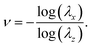
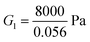 , G2 = 15
, G2 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa, β1 = 1.1. Slip between the plates and the top and bottom surfaces of the gels is allowed. The relaxation seen in experiments is rapid suggesting that the pore-sizes are bigger than what is obtained assuming a homogeneously deforming gel. The equilibrium value of the stress after relaxation is lower for a low value of π0. Lower values of π0 imply a lower solid volume fraction than that predicted by a homogeneously deforming gel. In the next section we show that our gels do not deform in a homogeneous manner under compression for intermediate applied strains. Thus, there are regions in the specimen where the pore size is larger and the solid volume fraction is lower which could help explain the discrepancies between experiment and continuum (FE based) simulations for intermediate strains. Good agreement between experiments and FE simulations for small applied strains suggests that gels do deform homogeneously for these strains.
000 Pa, β1 = 1.1. Slip between the plates and the top and bottom surfaces of the gels is allowed. The relaxation seen in experiments is rapid suggesting that the pore-sizes are bigger than what is obtained assuming a homogeneously deforming gel. The equilibrium value of the stress after relaxation is lower for a low value of π0. Lower values of π0 imply a lower solid volume fraction than that predicted by a homogeneously deforming gel. In the next section we show that our gels do not deform in a homogeneous manner under compression for intermediate applied strains. Thus, there are regions in the specimen where the pore size is larger and the solid volume fraction is lower which could help explain the discrepancies between experiment and continuum (FE based) simulations for intermediate strains. Good agreement between experiments and FE simulations for small applied strains suggests that gels do deform homogeneously for these strains.
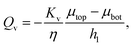
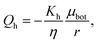
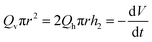 where V(t) is the current volume of the compressed sample. Then, mass conservation gives us the following relation between Kv and Kh:
where V(t) is the current volume of the compressed sample. Then, mass conservation gives us the following relation between Kv and Kh: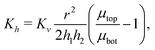
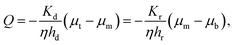
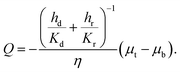
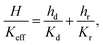
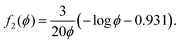
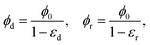

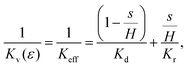
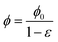 .
.
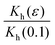 together with the theoretically computed
together with the theoretically computed 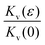 remembering that Kv(0) = Kh(0) due to isotropy. We have used both f1(ϕ) (eqn (14)) and f2(ϕ) (eqn (23)) with very similar results. Remarkably, the two quantities agree with each other suggesting that
remembering that Kv(0) = Kh(0) due to isotropy. We have used both f1(ϕ) (eqn (14)) and f2(ϕ) (eqn (23)) with very similar results. Remarkably, the two quantities agree with each other suggesting that  in eqn (18) does not vary much with applied strain.
in eqn (18) does not vary much with applied strain.


