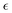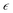Open Access Article
Open Access ArticleCharacterizing dynamic heterogeneities during nanogel degradation†
Zafrin Ferdous
Mira
 ,
Vaibhav
Palkar
,
Vaibhav
Palkar
 and
Olga
Kuksenok
and
Olga
Kuksenok
 *
*
Department of Materials Science and Engineering, Clemson University, Clemson, South Carolina 29634, USA. E-mail: okuksen@clemson.edu
First published on 17th January 2025
Abstract
Understanding photodegradation of nanogels is critical for dynamic control of their properties and functionalities. We focus on nanogels formed by end-linking of four-arm polyethylene glycol precursors with photolabile groups and characterize dynamic heterogeneities in these systems during degradation. We use our recently developed dissipative particle dynamics framework that captures the controlled scission of bonds between the precursors and diffusion of degraded fragments at the mesoscale. To quantify spatiotemporal fluctuations in the local dynamic behavior, we calculate the self-part of the van-Hove correlation function for the reactive beads for nanogels degrading in various environments. We demonstrate strong deviations from the Gaussian behavior during the degradation and quantify variations in the non-Gaussian parameter as a function of the relative extent of degradation. We show that for the nanogels degrading in a good solvent, the peak values in the non-Gaussian parameter are observed significantly earlier than the reverse gel point, and earlier than the peak values in the dispersity of the broken off fragments. Further, our study shows that a systematic decrease in solvent quality significantly affects the behavior of the non-Gaussian parameter as a function of the relative extent of degradation. The findings of this study allow one to quantify the dynamic heterogeneities during degradation in various environments and can potentially provide guidelines for designing controllably degrading nanocarriers.
1. Introduction
Understanding degradation of polymer networks is critical for a range of applications, from drug delivery using hydrogel nanocarriers and tissue engineering1 to diverse applications of hydrogels in agriculture, packaging, and water treatment.2 In many real-world scenarios the hydrogel carriers or the remnants of these carriers need to be removed upon fulfilling the target application, for example upon performing a site-specific delivery, which in turn highlights an importance of understanding the degradation process from the perspective of environmental sustainability.2 Photo-controlled bond scission3–7 is one of the triggers to initiate delivery of a nanocarrier's load to a precise location or to permit dynamic and spatially localized modulation of properties of the degrading network. It is important to characterize the degradation process in various environments and the fate of the remnants of the degraded polymer matrix dependent on the external environment the degradation took place in.As a model system, we consider hydrogels formed by end-linking of four-arm polyethylene glycol precursors,8–11 often referred to as tetra-PEG gel. Tetra-PEG gels originally fabricated by Sakai et al.8 have been shown to form close to ideal, nearly homogeneous network provided that the stoichiometric ratio of two types of precursors is equal to one and overlap concentration is used. Further, the PEG precursors can be readily modified during their synthesis by including photodegradable nitrobenzyl or coumarin functional groups,5,9–11 so that the resulting network can be controllably degraded under external illumination. Coumarin-based hydrogels may offer potential advantages for use in biological applications with respect to nitrobenzyl-based hydrogels, since the byproducts of photodegradation of these networks are biologically inert.11 Of particular interest is design of materials with irreversible photocleavage of covalent bonds,11,12 so that the extent of degradation can be controlled remotely via external light.
Herein, we focus on the tetra-PEG networks functionalized with photolabile functional groups to enable controlled photodegradation and characterize the dynamic heterogeneities as the degradation of nanogels takes place. Dynamic heterogeneity (DH) refers to the existence of localized spatiotemporal fluctuations in the dynamic behavior of complex fluids.13,14 To quantify dynamic heterogeneity in either experimental or theoretical studies, local fluctuations need to be tracked and characterized in addition to the measurements of the ensemble-averaged characteristics. Specifically, characterizing DH allows one to quantify to what extent the properties of the complex fluid of interest differ from the properties of a homogeneous fluid. For example, a deviation of the distribution of particles’ displacements from the Gaussian distribution corresponding to Brownian motion in the homogeneous system can be quantified by the non-Gaussian parameter defined via the ratio of the 4th moment and the 2nd moment squared of the particles displacements distribution function. The non-Gaussian parameter is related to a four-point velocity correlation function, which in turn characterizes mobility fluctuations.15,16
DH is an inherent feature of the glass-forming liquids;13,14,17 characterization of DH informed our fundamental understanding of the relaxation phenomena in these systems. DH in the glass-forming liquids reflects the formation and growth of assemblies of particles of high and low mobilities as the temperature approaches the glass transition temperature.14,17,18 One of the key questions is understanding the correlations between the DH and structural properties;13,19 recently, machine learning approaches were employed to identify structural heterogeneities in supercooled liquids20 and to predict DH in glass-forming liquids at glass transition temperatures.21,22 DH play an important role during gelation in colloidal systems23,24 and during the glass transition in polymers.15,25–27 Interestingly, recent studies showed15,25 that the glassy plateau shear modulus is proportional to the natural logarithm of the non-Gaussian parameter, thereby demonstrating an important correlation between the effective stiffness of the glassy polymer material and DH quantified via the non-Gaussian parameter.
To date the role DH plays in structurally complex reactive systems, such as systems undergoing chemical gelation or degradation, is significantly less understood. In the recent experimental study28 of the gelation process in tetra-PEG gels, DH was characterized via single-particle tracking during gelation of glutarate terminated and amine terminated four arm PEG stars. This study demonstrated non-monotonic behavior of the non-Gaussian parameter during the gelation process. The peak in the non-Gaussian parameter was significantly delayed with respect to the gel point defined from the rheological measurements; these results were attributed to the initial formation of a highly heterogenous structure, which then transitioned into the relatively homogeneous network.28 Nanoparticles with hydrodynamic diameter close to the average mesh size were used in these experiments.28 While particle tracking microrheology is often used to characterize non-Gaussian behavior in various networks,29–37 it is worth emphasizing the importance of the probe particle size with respect to the characteristic length scale of the polymer networks probed. Specifically, while the probe particles significantly larger than the network mesh size allow one to characterize an average elastic response, the probe particles comparable with the characteristic length scale of the network allow one to capture spatial and dynamic heterogeneities.38 It is important to note that the displacements of the probe particle characterize DH of the medium accessible to the particle, hence it is recognized that DH of the particle motion does not necessarily reflect the DH of the entire medium.34
To this end, the DH of the reactive polymer medium can be directly probed in simulations by characterizing displacements of the constitutive components of this medium, such as displacements of the reactive groups or the central crosslinker beads in vitrimers39–43 and displacements of sticky groups or the centers of mass in the associative polymers.44–48 MD simulations of telechelic polymer solutions characterized the relationship between dynamic and structural heterogeneities due to the micelle formation, which in turn resulted in caging of the reactive end groups.45 Specifically, this study showed that the non-Gaussian parameter as a function of a mean squared displacement (MSD) of the reactive end groups attained maximum values at approximately the same values of the MSD for a range of temperatures considered, with the maximum in the non-Gaussian parameter found between the average radius of gyration of micelles and inter-micellar distance.45
Herein, we focus on characterizing DH during the process of controlled degradation of hydrogel particles. Below we first introduce the mesoscale modeling approach used in this work and a framework needed to characterize the dynamic heterogeneities during the degradation process. For all the cases considered, we use our recently developed dissipative particle dynamics approach to capture degradation and erosion in nanogels49–51 and first characterize degradation by tracking the distribution of clusters of all sizes and the fraction of bonds intact as functions of time. In each case, we identify the reverse gel point corresponding to the disappearance of the percolating network. We track the self-part of the van-Hove correlation function, which characterizes the probability distribution of displacements of the reactive beads during the degradation process, with respect to their positions at the onset of degradation. We then systematically characterize the non-Gaussian parameter as a function of the relative extent of the degradation reaction for a range of systems encompassing different initial properties of the nanogels and a range of solvent qualities. Our study shows that a systematic decrease in solvent quality significantly affects the behavior of the non-Gaussian parameter as a function of the relative extent of reaction.
2. Model
We use dissipative particle dynamics (DPD),52,53 which is a computationally efficient mesoscale approach utilizing soft repulsive interactions between the beads representing groups of atoms. This approach was used to model a broad variety of systems on the mesoscale,54–64 including modeling various polymer networks.65–75 The motion of DPD beads is governed by Newton's equations of motion.53 For the non-bonded beads, such as explicit solvent beads in our system, the total pairwise additive force acting between the beads i and j consists of conservative (FCij), dissipative (FDij), and random (FRij) contributions; all three contributions vanish beyond a cutoff radius, rc, which introduces an intrinsic model length scale.53 A typical choice of the conservative force acting between the beads i and j is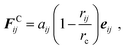 provided that the distance between these beads, rij = |rij|, is below the cutoff distance rc; herein, rij = ri − rj, and
provided that the distance between these beads, rij = |rij|, is below the cutoff distance rc; herein, rij = ri − rj, and 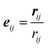 . The dissipative and random contributions FDij and FRij, are provided in Section S1 of ESI.† The repulsion coefficient between the dissimilar beads relates to the Flory–Huggins interaction parameter, χij, as53aij = aii + 3.27χij for the typical choice of the bead number density of three, where aii is the repulsion coefficient between the same type of beads, which is often derived based on the degree of coarse-graining, and herein is chosen as76aii = 78.0 in reduced units of
. The dissipative and random contributions FDij and FRij, are provided in Section S1 of ESI.† The repulsion coefficient between the dissimilar beads relates to the Flory–Huggins interaction parameter, χij, as53aij = aii + 3.27χij for the typical choice of the bead number density of three, where aii is the repulsion coefficient between the same type of beads, which is often derived based on the degree of coarse-graining, and herein is chosen as76aii = 78.0 in reduced units of 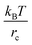 . With this parameterization, three water molecules are coarse-grained into one DPD bead, and the dimensionless cutoff distance rc = 1 is related to the dimensional distance of76
. With this parameterization, three water molecules are coarse-grained into one DPD bead, and the dimensionless cutoff distance rc = 1 is related to the dimensional distance of76![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) c ≈ 0.65 nm. Within the same parameterization, the reduced units of time in DPD can be related to the dimensional time as76τ ≈ 88 ps via matching diffusion coefficient of water beads to diffusion coefficient of water. The repulsion parameter between the polymer and water beads is chosen based on the PEG–water Flory–Huggins interaction parameter at room temperature,77χ = 0.45, as apw = 79.5 in reduced DPD units. Notably, while water is a good solvent for PEG at room temperatures, its solvent quality decreases at significantly higher temperatures.78–82 Further, mixed solvents83,84 notably modify solvent–polymer interactions depending on solvent composition due to the co-nonsolvency effects, while oils are known to be poor solvents76 for PEG. In the study below, we vary solvent quality systematically by increasing apw from the value corresponding to a good solvent as given above to the higher value corresponding to the poor solvent. We recently showed that an increase in apw parameter within the DPD framework with the same parametrization reproduces collapse in polymers with complex architectures upon decrease in solvent quality.58
c ≈ 0.65 nm. Within the same parameterization, the reduced units of time in DPD can be related to the dimensional time as76τ ≈ 88 ps via matching diffusion coefficient of water beads to diffusion coefficient of water. The repulsion parameter between the polymer and water beads is chosen based on the PEG–water Flory–Huggins interaction parameter at room temperature,77χ = 0.45, as apw = 79.5 in reduced DPD units. Notably, while water is a good solvent for PEG at room temperatures, its solvent quality decreases at significantly higher temperatures.78–82 Further, mixed solvents83,84 notably modify solvent–polymer interactions depending on solvent composition due to the co-nonsolvency effects, while oils are known to be poor solvents76 for PEG. In the study below, we vary solvent quality systematically by increasing apw from the value corresponding to a good solvent as given above to the higher value corresponding to the poor solvent. We recently showed that an increase in apw parameter within the DPD framework with the same parametrization reproduces collapse in polymers with complex architectures upon decrease in solvent quality.58
For the bonded beads, such as beads constituting polymer precursors (Fig. 1), in addition to the forces defined above, the bonded interactions are introduced. Herein the bonded beads are taken to interact via harmonic potential 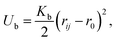 where r0 is an equilibrium bond length, and Kb is a spring constant. To mitigate unphysical crossing of polymer chains, which is a well-known limitation of the standard DPD approach, we adopted modified segmental repulsion potential (mSRP)85 formulation, in which an additional force acting between the centers of the bonds is introduced provided that the distance between the centers of these beads is below a critical mSRP cut-off distance (see Section S1 of ESI,† for details).
where r0 is an equilibrium bond length, and Kb is a spring constant. To mitigate unphysical crossing of polymer chains, which is a well-known limitation of the standard DPD approach, we adopted modified segmental repulsion potential (mSRP)85 formulation, in which an additional force acting between the centers of the bonds is introduced provided that the distance between the centers of these beads is below a critical mSRP cut-off distance (see Section S1 of ESI,† for details).
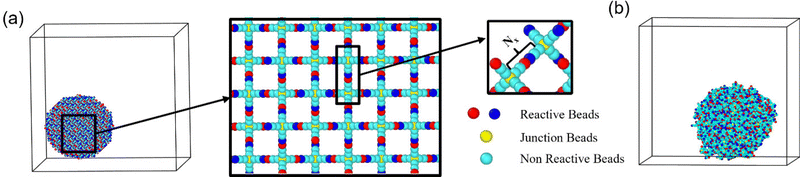 | ||
| Fig. 1 (a) Snapshot of a hydrogel particle made by crosslinking of four-arm precursors prior to equilibration; reactive end beads are shown in red and blue; junction beads are shown in yellow, and remaining polymer beads are shown in cyan, respectively. (b) Simulation snapshot of the hydrogel spherical particle equilibrated in water; parameters correspond to case A (Table S1, ESI†). Water beads are not shown for clarity of representation. | ||
To simulate bond breaking within the nanogel particles, random numbers are generated for each degradable bond at each reaction time step, τr; the bond is broken if the generated random number is lower than the probability of bond breaking, P. We had shown86 that with the proposed approach, the ratio between the number of degradable bonds remaining intact at a given time instant t, and the total number of degradable bonds in the system, or the fraction of bonds intact, p(t), accurately follows first-order degradation kinetics, p = exp(−kt), with the rate constant k = P/τr. For polymer networks undergoing controlled photodegradation, the degradation occurs significantly slower73 than the characteristic diffusion times on the relevant length scales.49,86 Hence, we use a relatively low degradation rate set by the probability of bonds breaking49P = 9 × 10−6 to ensure that our system is in a kinetically limited regime.73,86 Further details of the simulations and all the simulation parameters used in this work are listed in Section S1 of ESI.† In what follows, we provide our simulation results in reduced DPD units of length and time as76![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) c ≈ 0.65 nm, and τ ≈ 88 ps, respectively. The probability of bond breaking P is set constant49 independent of the position of degrading bond within the box, since no light attenuation is expected on the length scale of the simulation box. It is worth noting that light intensity within the degrading hydrogels was shown to notably decrease at depths exceeding a hundred microns,87 which is several orders of magnitude larger than the size of nanogel particles considered here.
c ≈ 0.65 nm, and τ ≈ 88 ps, respectively. The probability of bond breaking P is set constant49 independent of the position of degrading bond within the box, since no light attenuation is expected on the length scale of the simulation box. It is worth noting that light intensity within the degrading hydrogels was shown to notably decrease at depths exceeding a hundred microns,87 which is several orders of magnitude larger than the size of nanogel particles considered here.
The LAMMPS simulation package88,89 along with the mSRP code85 was used to integrate the equations of motion; and Ovito software90 was used to perform visualizations and generate all the simulation snapshots reported in this work. We use our recently implemented modification of the mSRP framework, which allows for the additional mSRP forces to be switched off as the bonds break;49,86 this modification is implemented within the LAMMPS simulation package as pair style srp/react.91 We used the diamond-like lattice49,73,92 as an initial configuration of the nanogel's polymer network (Fig. 1a), since this lattice reflects the initial topology of tetrafunctional polymer network. We follow procedure detailed in our recent work50 to construct a spherical gel particle with the chosen number of beads between the centers of two bonded precursors, Nx, and chosen particle size.
Prior to degradation, all the nanogel particles are equilibrated in solvent. An equilibrated nanogel particle swollen in water is shown in Fig. 1b. PEG beads are shown in cyan, the end groups of two types of precursors are shown in red and blue, respectively, and the solvent beads are not shown for clarity of representation. The degradable bonds in the system are chosen to be the bonds between the end functionalities (Fig. 1a). Three water molecules are represented by a single DPD bead,76 and the number of beads between the centers of two bonded precursors, Nx, is varied as detailed in Table S1 (ESI†). All the simulation parameters are listed in Section S1 of ESI.† The dimensionless box size in the simulation in the reference case in units of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) c defined above is 60 × 60 × 60, and the dimensionless radius of gyration of the spherical nanogel is Rg ≈ 11.99 (Fig. S1 of ESI†), which with the above scaling corresponds to ≈7.8 nm.
c defined above is 60 × 60 × 60, and the dimensionless radius of gyration of the spherical nanogel is Rg ≈ 11.99 (Fig. S1 of ESI†), which with the above scaling corresponds to ≈7.8 nm.
For all the scenarios considered, we first characterize the degradation process by tracking the distribution of clusters of all sizes and the fraction of bonds intact, p, as functions of time from the onset of the degradation process. The reverse gel point, or the loss of the percolating network, corresponds to the peak in the reduced weight average degree of polymerization of clusters (or fragments),49,50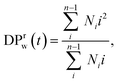 where Ni is the number of fragments with i beads at a time t and the summation is taken over all but the largest cluster. By cluster we refer here to chemically bonded polymer fragment; in addition to this topological cluster, an agglomerate (or distance-based cluster) can also be defined based on the distance criterium.49,50 Notably, a peak position in the reduced z-average degree of polymerization,
where Ni is the number of fragments with i beads at a time t and the summation is taken over all but the largest cluster. By cluster we refer here to chemically bonded polymer fragment; in addition to this topological cluster, an agglomerate (or distance-based cluster) can also be defined based on the distance criterium.49,50 Notably, a peak position in the reduced z-average degree of polymerization, 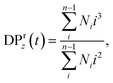 can also be used to identify the reverse gel point.49 This definition of the reverse gel point is based on the characterization of the gel point while modeling gelation process in finite size systems.93–96
can also be used to identify the reverse gel point.49 This definition of the reverse gel point is based on the characterization of the gel point while modeling gelation process in finite size systems.93–96
We previously quantified the reverse gel point during the hydrogel degradation via the fraction of bonds intact, pc, corresponding to the peak in DPrw, and showed that this value scales with the total number of precursors, Np, as50pc = p∞c + cN−0.7p, where p∞c = 0.39 is an analytical estimate for the bond percolation on a diamond lattice.97 This observed increase in pc with the decrease in Np is consistent with analytical theories of gelation reflecting the finite size of the simulated systems compared to the infinite number of precursors postulated in classical percolation theories.97–99 The functional form provided above for the scaling of pc with the number of precursors Np was taken the same as proposed earlier for percolation during gelation process.97,98,100 Notably, the gel point values close to the values for the bond percolation on a diamond lattice97 have been reported in experiments for the gelation of tetra-arm PEG precursors near the overlap concentration.101,102 A delay in the gel point during the gelation process is often attributed to an increased tendency of intramolecular reactions.96,100,103–106
Identifying pc for each simulation run allows one to calculate the relative extent of reaction, 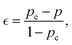 as a function of time. While the specific time instants corresponding to the reverse gel point can differ significantly among the simulation runs with the same parameters but with different initial trajectories due to the stochastic character of the bond breaking, quantifying all the relevant dynamic characteristics as a function of the proximity to the reverse gel point (as a function of
as a function of time. While the specific time instants corresponding to the reverse gel point can differ significantly among the simulation runs with the same parameters but with different initial trajectories due to the stochastic character of the bond breaking, quantifying all the relevant dynamic characteristics as a function of the proximity to the reverse gel point (as a function of 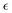 ) allows one to identify major features depending on the relative extent of reaction.
) allows one to identify major features depending on the relative extent of reaction.
To characterize dynamic heterogeneities (DH) in our systems of interest, we track the displacements of the reactive end groups of polymer precursors during the degradation process. Specifically, we calculate the self-part of the van Hove correlation function of precursor end groups as107
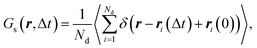 | (1) |
For Brownian motion, eqn (1) is reduced to the Gaussian distribution,
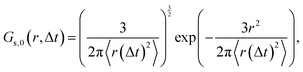 | (2) |
In what follows, we calculate the displacements of the beads representing end groups of precursors (beads shown in red and blue in Fig. 1) during the time Δt since the onset of degradation for various scenarios and plot the probability density of finding these beads at a distance within r to r + dr from its original position, 4πr2Gs(r, Δt), and compare this calculated probability density with the expression corresponding to the Gaussian distribution, 4πr2Gs,0. We also track the non-Gaussian parameter, α2, which is calculated via the ratios of 4th and 2nd squared moments of the bead's displacements, r(Δt), and serves as an important quantitative characteristic of the dynamic heterogeneities, as
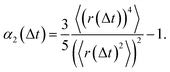 | (3) |
3. Results and discussion
Herein, we systematically characterize DH in simulations of controlled degradation for the range of systems encompassing different initial properties of the hydrogel particle as well as a range of solvent qualities (cases A–G in Table S1, ESI†). The parameters provided for the case A correspond to our reference case scenario. Cases B–D allow us to analyze the effects of decrease in solvent quality with respect to the reference case, while case E corresponds to the same hydrogel particle as in case A but placed into a smaller simulation box. Finally, the sizes of the hydrogel particles in cases F and G are chosen such that the equilibrium radii of gyration in these cases are closely matching that in case A (Fig. S1 of ESI†), while the values of Nx are varied, so that case F corresponds to significantly higher, and case G to significantly lower crosslink density than that in case A.3.1 Characterizing dynamic heterogeneities upon degradation of a hydrogel particle in a good solvent
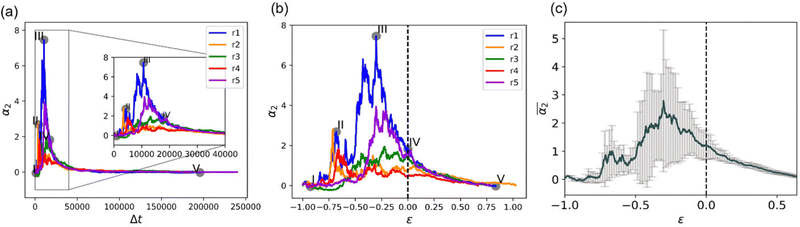
We begin with characterizing DH as a function of the proximity to the reverse gel point in our reference case scenario (case A in Table S1, ESI†). In Fig. 2 (top panel), we plot the MSD of the end groups of polymer precursors as a function of time since the onset of degradation, Δt, and in the insets at selected time instants marked I–V we visualize the placement of the polymer fragments within the simulation box. This plot shows an existence of an approximately plateau region, corresponding to the motion of the end groups effectively “caged” within the polymer network, where the characteristic length scale corresponding to such caged motion, referred to as localization length, can be calculated as a square root of the plateau value.108 A notable increase in MSD (super-diffusive regime) is observed when a sufficiently large fraction of fragments is broken off, with the slope reaching unity corresponding to the diffusive regime upon the degradation of the entire system. The non-Gaussian parameter, α2, (eqn (3)) and the reduced weight average degree of polymerization, DPrw, along with the fraction of bonds intact, p, are shown in the middle and lower panels of Fig. 2, respectively, for the same simulation run. These plots clearly show a distinct non-monotonous increase in α2 as degradation takes place, with the peak in α2 (time instant marked III) observed significantly earlier than the reverse gel point (marked IV). This peak approximately corresponds to the time from the onset of degradation at which the average msd of all the reactive beads is on the scale of![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g2, where
g2, where ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g is the radius of gyration of equilibrated nanogel (see Fig. S2 of ESI†). Our results also show further sharp decrease in α2 immediately after the reverse gel point with essentially Gaussian behavior (α2 ≈ 0) at the late stages of degradation. We note that here and below (unless specified otherwise) we calculate individual displacements of the precursor's end groups and related average characteristics (non-Gaussian parameter and MSD) without accounting for the drift of the center-of-mass of the chosen type of beads. This choice is made since the diffusion of smaller clusters that escaped the remnant hydrogel is largely independent from the position of this remnant particle while – as shown further below – these faster clusters contribute the most to the non-Gaussian dynamics. It is however instructive to compare the calculated values of α2 and MSD provided in Fig. 2 with the same values calculated while accounting for the drift of the center-of-mass subtracted out before the displacement is calculated (Fig. S2 of ESI†). As anticipated, the MSD is somewhat lower, specifically in the caging region, since the drift of the center-of-mass is subtracted out, while the α2 attains higher values, but follows similar trends (Fig. S2, ESI†).
g is the radius of gyration of equilibrated nanogel (see Fig. S2 of ESI†). Our results also show further sharp decrease in α2 immediately after the reverse gel point with essentially Gaussian behavior (α2 ≈ 0) at the late stages of degradation. We note that here and below (unless specified otherwise) we calculate individual displacements of the precursor's end groups and related average characteristics (non-Gaussian parameter and MSD) without accounting for the drift of the center-of-mass of the chosen type of beads. This choice is made since the diffusion of smaller clusters that escaped the remnant hydrogel is largely independent from the position of this remnant particle while – as shown further below – these faster clusters contribute the most to the non-Gaussian dynamics. It is however instructive to compare the calculated values of α2 and MSD provided in Fig. 2 with the same values calculated while accounting for the drift of the center-of-mass subtracted out before the displacement is calculated (Fig. S2 of ESI†). As anticipated, the MSD is somewhat lower, specifically in the caging region, since the drift of the center-of-mass is subtracted out, while the α2 attains higher values, but follows similar trends (Fig. S2, ESI†).
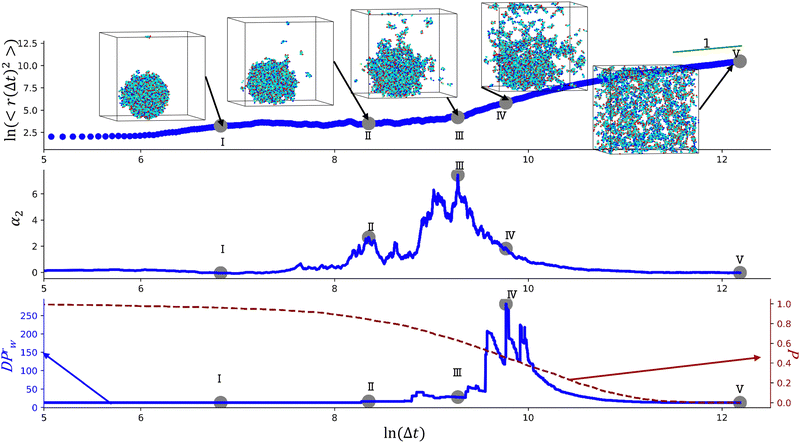 | ||
| Fig. 2 Characterization of the degradation process of a nanogel particle, parameters correspond to case A (Table S1, ESI†). Time evolutions of the mean squared displacement, 〈r(Δt)2〉, non-Gaussian parameter α2, and reduced weight average degree of polymerization, DPrw, are shown in top, middle, and bottom panels, respectively. In the simulation snapshots in the top panel, water beads are not shown for clarity of representation. The fraction of bonds intact, p, is also shown in the bottom panel (red dashed curve, right axes). The time instant marked by a point IV corresponds to the reverse gel point. | ||
To better understand the observed non-Gaussian behavior, in Fig. 3 we plot the heat maps of the end group displacements from the onset of degradation (panel (a)) and the probability density of finding the end group bead i at a time Δt at a distance in the range of r to r + dr from its original position calculated via the self-part of the van Hove correlation function as 4πr2Gs (panel (b)). We consider the following time instants: (I) shortly after the degradation is turned on, (II) when only a small fraction (p ≈ 0.84) of bonds are broken, (III) the time instant corresponding to the peak of α2, (IV) the reverse gel point, and (V) when all the degradable bonds are broken. The corresponding time instants (I–V) are also marked on plots in Fig. 2. We plot the histograms utilizing the Freedman–Diaconis rule,109 which is used to find the optimal number of bins and bin width based on the simulation data to better represent the non-Gaussian behavior of the data. According to the Freedman–Diaconis rule, the number of bins is proportional to 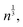 and bin width is equal to109
and bin width is equal to109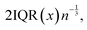 where n is the number of observations and IQR(x) is the interquartile range for an observable variable x.
where n is the number of observations and IQR(x) is the interquartile range for an observable variable x.
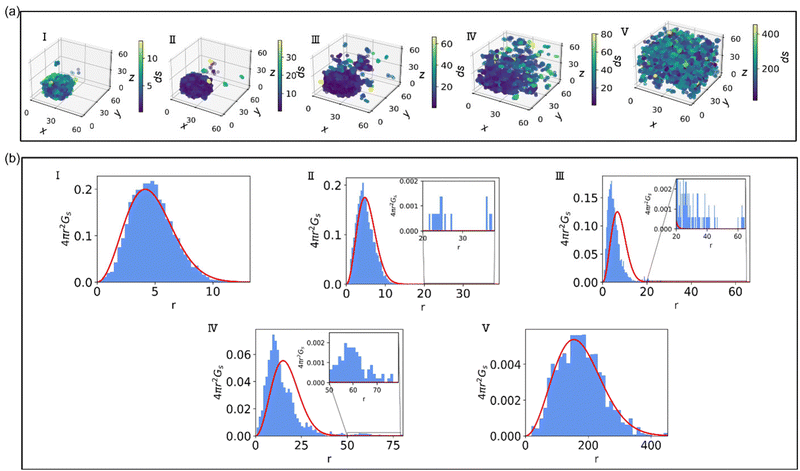 | ||
| Fig. 3 (a) Heat map of displacements (ds) of reactive beads during the degradation of nanogel at the time instants marked (I–V) in Fig. 2. (b) Probability density of the displacements of reactive beads at the same time instants; bar plots in blue represent simulation data, and red curves represent Gaussian distribution. The insets in (II–IV) show close-up of the probability density at higher distances as marked. | ||
These plots demonstrate that at the time instant I, the magnitude of the displacements of reactive beads with respect to their position at the onset of degradation remain low and Gs relatively closely matches the Gaussian distribution (4πr2Gs,0, in red). At the time instant II, a few fragments diffuse relatively far from the original hydrogel particle, while the beads within the largest agglomerate appear to have significantly smaller displacement (see displacements heat map in panel (a)). Note that the largest agglomerate might include some fragments that broke off but remain stuck within this fragment.50 The corresponding plot of 4πr2Gs includes contributions from the slower group of beads (preferentially located within the largest agglomerate) with relatively small deviations from the Gaussian distribution (4πr2Gs,0 in red), and a long tail (primarily corresponding to the contributions from the end groups of precursors within the broken off fragments). For clarity, this tail is shown in the inset of Fig. 3b, time instant II. This tail in Gs distribution contributes the most to a notable increase in α2 at the same time instant. Note that here and in all the subsequent plots based on the self-part of the van Hove distribution function, the maximum distance r these distributions are plotted for corresponds to the non-zero probability of finding an end group bead at this distance; for low probabilities and long tails, the corresponding insets are shown.
At the time instant III, the distribution of slower moving beads exhibits more pronounced deviations from the Gaussian distribution (compare the portion of the bar plot corresponding to the highest peak in Fig. 3b(III) to the red curve corresponding to the Gaussian distribution), and even a longer tail corresponding to the end groups beads belonging to the broken off clusters. This specific time instant corresponds to the peak in α2 for the given simulation run (see middle panel in Fig. 2, time instant III), and exhibits the longest tail in 4πr2Gs (i.e., the overall distribution is strongly skewed to the right). At the reverse gel point (time instant IV), the deviation of the distribution of displacements of the slower beads from the Gaussian behavior is more pronounced, as can be seen from the portion of the bar plot corresponding to the highest peak in Fig. 3b(IV), with the maximum values skewed to the left with respect to the Gaussian distribution (red curve). However, the tail corresponding to the faster end groups becomes relatively shorter compared to the width of Gaussian distribution at the same time instant. The value of α2 at this point remains significantly higher than zero but is also distinctly lower than the peak value at the time instant III, confirming that the broad tail in the self-part of the van Hove distribution contributes the most to the non-Gaussian behavior. Finally, when most of the fragments are broken off, we observe a return to the Gaussian behavior (Fig. 3b, time instant V).
Due to the stochastic character of bond breaking, there is high variability in the system dynamics, from the actual time instant corresponding to the reverse gel point,50 to the maximum observed value of α2 (see Fig. 4a for the time evolution of α2 for five simulation runs for case A). Thereby it is instructive to quantify α2 with respect to its proximity to the reverse gel point, or as a function of 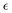 , rather than with respect to the time lag from the onset of degradation. The individual plots
, rather than with respect to the time lag from the onset of degradation. The individual plots 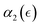 and the non-Gaussian parameter averaged over five trajectories,
and the non-Gaussian parameter averaged over five trajectories, 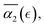 are shown in Fig. 4b and c, respectively. These results show that in all cases, α2 ≈ 0 at the onset of degradation and again approaches zero upon full degradation, while a significant increase in α2 is observed prior to the reverse gel point. Further, examination of the plots of the probability distribution of displacements of reactive beads and respective heat maps for all the remaining individual simulations (Fig. S3, ESI†) confirms that the above trends relating Gs distribution to the increase in α2 hold for all the scenarios. Specifically, in all cases prior to the reverse gel point, 4πr2Gs distributions are skewed to the right, with the longest tails contributing to the highest values of α2 for each individual simulation run. Notably, the same trends in
are shown in Fig. 4b and c, respectively. These results show that in all cases, α2 ≈ 0 at the onset of degradation and again approaches zero upon full degradation, while a significant increase in α2 is observed prior to the reverse gel point. Further, examination of the plots of the probability distribution of displacements of reactive beads and respective heat maps for all the remaining individual simulations (Fig. S3, ESI†) confirms that the above trends relating Gs distribution to the increase in α2 hold for all the scenarios. Specifically, in all cases prior to the reverse gel point, 4πr2Gs distributions are skewed to the right, with the longest tails contributing to the highest values of α2 for each individual simulation run. Notably, the same trends in 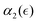 are observed for case E (same gel particle prior to degradation, but smaller simulation box) (Fig. S4 and S5a, ESI†), and for even lower reaction rate with the remaining parameters corresponding to case A (Fig. S5b, ESI†) as long as the degradation process takes place within a good solvent.
are observed for case E (same gel particle prior to degradation, but smaller simulation box) (Fig. S4 and S5a, ESI†), and for even lower reaction rate with the remaining parameters corresponding to case A (Fig. S5b, ESI†) as long as the degradation process takes place within a good solvent.
3.2 Quantifying effects of crosslink density
In the next series of simulations, we quantify the effect of the crosslink density on α2. Herein, we compare the dynamics in reference case A considered above and in cases F and G, which correspond to the higher and lower crosslink densities, respectively. The sizes of the equilibrated hydrogel particles in cases F and G are chosen such that the radii of gyration in these cases closely match that in case A (Fig. S1 of ESI†), while the values of Nx are varied such that Nx = 4 in case F and Nx = 10 in case G. Compared to case A, the number of precursors is approximately twice higher in case F and approximately 2.3 times lower in case G (Table S1 of ESI†). For all three cases considered, the dispersity of the fragments Đ during degradation reaches maximum values at approximately the same value of the relative extent of reaction,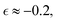 i.e. significantly prior to the reverse gel point, while the peak value of Đ scales with the number of precursors,50 thereby attaining a significantly higher value for case F than that for case D (Fig. 5a). The non-Gaussian parameter in all cases increases significantly before the reverse gel point (Fig. 5b). It is worth noting that the maximum values in
i.e. significantly prior to the reverse gel point, while the peak value of Đ scales with the number of precursors,50 thereby attaining a significantly higher value for case F than that for case D (Fig. 5a). The non-Gaussian parameter in all cases increases significantly before the reverse gel point (Fig. 5b). It is worth noting that the maximum values in 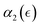 are observed not only significantly earlier than the reverse gel point but also earlier than the peak in Đ. The simulation snapshots at select time instants and the time evolution of the MSD are provided in Fig. S6 (ESI†). Notably, in cases F and G the probability distributions of displacements of reactive beads exhibit the same characteristic features at the time instant corresponding to the maximum in α2 as that in case A, as can be seen by comparing probability densities in Fig. S7 (ESI†) (cases G and F), and the snapshot marked III in Fig. 2 middle row (case A).
are observed not only significantly earlier than the reverse gel point but also earlier than the peak in Đ. The simulation snapshots at select time instants and the time evolution of the MSD are provided in Fig. S6 (ESI†). Notably, in cases F and G the probability distributions of displacements of reactive beads exhibit the same characteristic features at the time instant corresponding to the maximum in α2 as that in case A, as can be seen by comparing probability densities in Fig. S7 (ESI†) (cases G and F), and the snapshot marked III in Fig. 2 middle row (case A).
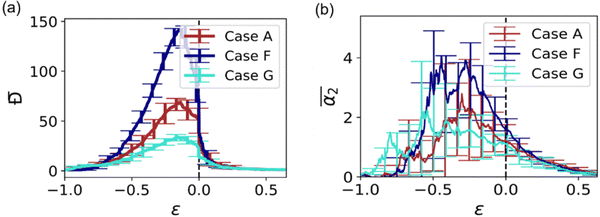 | ||
Fig. 5 (a) Averaged dispersity, Đ, as a function of the relative extent of reaction, 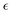 . (b) Averaged non-Gaussian parameter, . (b) Averaged non-Gaussian parameter, 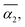 as a function of the relative extent of reaction, as a function of the relative extent of reaction, 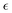 . . | ||
3.3 Quantifying effects of solvent quality
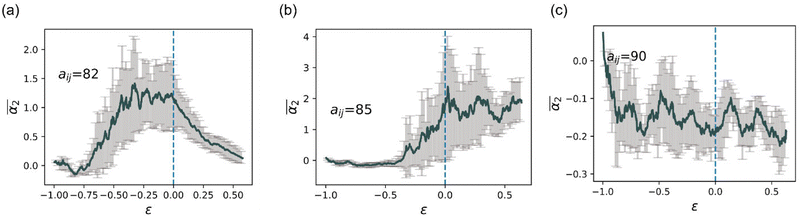
Next, we examine the effects of solvent quality on the non-Gaussian parameter during hydrogel degradation. The solvent quality is progressively decreased in cases B–D with respect to the reference case A via increasing interaction parameter between the polymer and solvent beads to aij = 82 in case B, aij = 85 in case C, and aij = 90 in case D. Time evolution of α2 from the onset of degradation in the representative simulation runs corresponding to all the cases with different solvent qualities are shown in Fig. 6a. This plot clearly illustrates that in case B, α2 for the chosen simulation run increases prior to the reverse gel point similar to that in case A, while in case C, the peak in α2 is observed significantly after the reverse gel point (dark cyan curve). For case D (olive curve), α2 attains small magnitude negative values as discussed further below.The simulation snapshots at the time instants marked I–V for cases B, C, and D are shown in top, middle, and bottom rows in Fig. 6b. The time instant III in all the cases corresponds to the reverse gel point, and the time instant V corresponds to a time close to the fully degraded systems. The characteristic simulation snapshots for case B (Fig. 6b, top row) illustrate visually similar dynamics during degradation to that in case A (insets in Fig. 2 top row); upon full degradation (time instant V), individual precursors appear to be well dispersed in case B similar to that in case A. In case C, the largest agglomerate remains clearly visible even after majority of the bonds are broken (time instant V, middle row in Fig. 6b). Finally, in case D, all the precursors remain within the largest agglomerate, and no diffusion of precursors away from this largest agglomerate is observed even when the system is close to fully degraded as seen in the simulation snapshots in Fig. 6b, bottom row.
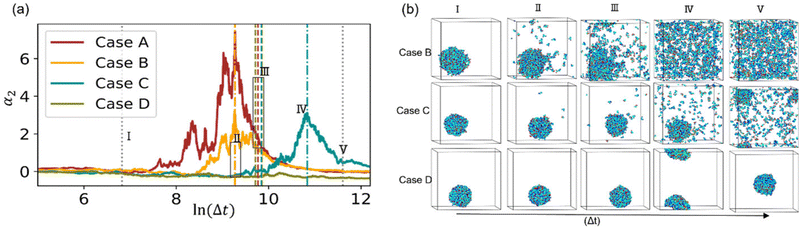
To better understand the effect of solvent quality on the time evolution of α2 during polymer network degradation, in Fig. 7 we plot the probability densities of displacements of reactive end groups for cases B, C, and D at the time instants II–V as marked in Fig. 6a. Note that at the time instant I, the distributions remain nearly Gaussian for all the cases and hence are not shown in Fig. 7. The peak in α2 for case B is observed at the time instant II, correspondingly the distribution is strongly skewed to the right (top row in Fig. 7, image II), and exhibits similar features as the distribution corresponding to the maximum α2 in case A (Fig. 3b, time instant III). At the reverse gel point in case B (top row, time instant III), the tail in the distribution corresponding to the large displacements becomes relatively shorter with respect to the width of the distribution displacements of the slower population of the end groups, while the center of the distribution of slower population is skewed to the left. Again, these features are similar to the features at the reverse gel point in case A (Fig. 3b, time instant IV). Finally, the distribution returns to nearly Gaussian form when all the bonds are broken (time instant V in the top row in Fig. 7).
The time evolution of 4πr2Gs in case C is drastically different from that in Case B (middle row in Fig. 7). At the time instant II, the distribution of slower end groups is significantly narrower than the Gaussian distribution, indicating that a population of slower beads undergoes cooperative motion, resulting in small magnitude negative values of α2 at this time instant as seen in the plots of the non-Gaussian parameter as a function of the relative extent of reaction provided in Fig. S8a (ESI†) for the individual runs. The displacements distribution at the time instant IV, corresponding to the peak in α2 for case C, exhibits similar characteristic features as the distribution in the top panel (case B) at a time instant II, also corresponding to a high value of α2. Finally, we no longer observe a return to the Gaussian distribution upon breaking most the degradable bonds (time instant V); this non-Gaussian behavior is attributed to the existence of a larger agglomerate composed of broken-off precursors due to relatively low affinity between polymer and solvent. Notably, this type of behavior persists in a fully degraded system, as seen in Fig. S9 (ESI†), where the heat maps of displacements and 4πr2Gs distributions of end groups are shown for the cases of various solvent qualities.
Finally, the distribution of displacements of end groups is dramatically different for case D (bottom row in Fig. 7) than that for all the remaining cases. The distribution of displacements of the end groups, in this case, is significantly narrower than the Gaussian distribution, and no long tails are observed during the entire degradation process, indicating that an entire population of end groups undergoes cooperative motion due to poor solvent quality, consistent with the simulation snapshots (Fig. 6b). It is known that the cooperative motion of a population results in the negative values of α2.38,110,111 The values of α2 during the degradation (five individual simulations) are provided in Fig. S8 (ESI†). A similar distribution of displacements of reactive end groups holds for a fully degraded system (case D, Fig. S9, ESI†). Note that at the onset of the degradation process, the motion of the end groups is effectively caged within the polymer network (first plateau in Fig. S10, ESI†), while upon reverse gelation, the precursors are caged within the polymer agglomerate (second plateau in Fig. S10, ESI†). This second plateau corresponds to the dimensional length of ≈11.25, which in turn closely corresponds to the radius of the agglomerate, 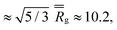 where
where 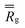 is taken for the case D as given in Fig. S1 (ESI†).
is taken for the case D as given in Fig. S1 (ESI†).
The behavior of the non-Gaussian parameter as a function of the relative extent of reaction, 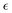 , averaged over five simulation trajectories, is shown in Fig. 8 for the cases B, C and D. In case B (Fig. 8a),
, averaged over five simulation trajectories, is shown in Fig. 8 for the cases B, C and D. In case B (Fig. 8a), 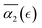 remains low at the initial stages of degradation (approximately for
remains low at the initial stages of degradation (approximately for 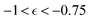 ), then this value increases significantly during the degradation, with the high values observed prior to the reverse gel point (prior to
), then this value increases significantly during the degradation, with the high values observed prior to the reverse gel point (prior to 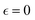 ). Finally, for the fully degraded system, the motion of precursors returns to close to the Gaussian motion with α2 ≈ 0 in each of the individual simulation runs (Fig. S8a, ESI†). This behavior is similar to that for case A (Fig. 4c), since the affinity between the polymer and solvent is only slightly decreased in case B compared to that in case A. A broad distribution in locations of peak α2 for individual simulation runs results in the broadening of
). Finally, for the fully degraded system, the motion of precursors returns to close to the Gaussian motion with α2 ≈ 0 in each of the individual simulation runs (Fig. S8a, ESI†). This behavior is similar to that for case A (Fig. 4c), since the affinity between the polymer and solvent is only slightly decreased in case B compared to that in case A. A broad distribution in locations of peak α2 for individual simulation runs results in the broadening of 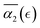 peak.
peak.
Further decrease in solvent quality significantly affects the 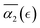 dependence. In case C, the increase in
dependence. In case C, the increase in 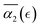 is observed prior to the reverse gel point (approximately for
is observed prior to the reverse gel point (approximately for 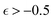 ), however, the peak values in
), however, the peak values in 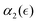 distributions for the individual runs are reached at or after the reverse gel point (Fig. S8(b), ESI†), resulting in a consistent increase in
distributions for the individual runs are reached at or after the reverse gel point (Fig. S8(b), ESI†), resulting in a consistent increase in 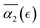 after the reverse gel point. We note that the absolute values of α2 in cases C and B are below the average values observed in the case A. For the case of a poor solvent (case D), α2 attain low negative values for all the individual simulation runs (Fig. S8c, ESI†), in some instances, approaching a limiting value of α2 ≈ −0.4, which in turn corresponds to ideal cooperative motion (i.e., the same displacements of all the beads considered). Case D corresponds to a sufficiently poor solvent so that all the precursors that are broken off remain within the same agglomerate which diffuses as a whole in the solvent.
after the reverse gel point. We note that the absolute values of α2 in cases C and B are below the average values observed in the case A. For the case of a poor solvent (case D), α2 attain low negative values for all the individual simulation runs (Fig. S8c, ESI†), in some instances, approaching a limiting value of α2 ≈ −0.4, which in turn corresponds to ideal cooperative motion (i.e., the same displacements of all the beads considered). Case D corresponds to a sufficiently poor solvent so that all the precursors that are broken off remain within the same agglomerate which diffuses as a whole in the solvent.
4. Conclusions
Herein, we characterized dynamic heterogeneities during controlled degradation of tetra-PEG nanogels and quantified the non-Gaussian behavior of hydrogels degrading in solvents of various quality. We used our recently developed DPD framework that captures the controlled scission of bonds between the precursors and diffusion of degraded fragments at the mesoscale.49,50 We tracked the self-part of the van-Hove correlation function, Gs, which characterizes the probability distribution of displacements of the reactive beads during the degradation process, with respect to their positions at the onset of degradation. We characterized the non-Gaussian parameter, α2, as a function of the relative extent of degradation reaction,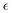 , which indicates the proximity to the reverse gel point. Our results show distinct non-monotonous increase in the non-Gaussian parameter as degradation takes place, with the peak in α2 observed significantly prior to the reverse gel point for our reference case scenario (referred to as case A above). The same trends in
, which indicates the proximity to the reverse gel point. Our results show distinct non-monotonous increase in the non-Gaussian parameter as degradation takes place, with the peak in α2 observed significantly prior to the reverse gel point for our reference case scenario (referred to as case A above). The same trends in 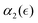 dependence are observed for all the scenarios of nanogels considered herein, including nanogels with different crosslink densities, provided that the degradation takes place in a good solvent. This result is consistent with the recent experimental observations during the gelation of tetra-PEG precursors, which demonstrated non-monotonic behavior of the non-Gaussian parameter as measured by the single particle tracking, with the peak value in α2 significantly delayed with respect to the gel point defined independently in the same experiments.28 While it is recognized that the DH of the tracer particle motion does not necessarily reflect the DH of the medium34 (as discussed in the introduction), the similarity between the trends in the experimental observations of the delayed peak in the non-Gaussian parameter with respect to the gel point28 and observations of the peak in α2 of reactive beads displacements significantly prior to the reverse gel point in simulations points out to comparable trends in quantifying DH either by tracking the motion of the reactive end groups or by the single particle tracking experiments in the respective cases.
dependence are observed for all the scenarios of nanogels considered herein, including nanogels with different crosslink densities, provided that the degradation takes place in a good solvent. This result is consistent with the recent experimental observations during the gelation of tetra-PEG precursors, which demonstrated non-monotonic behavior of the non-Gaussian parameter as measured by the single particle tracking, with the peak value in α2 significantly delayed with respect to the gel point defined independently in the same experiments.28 While it is recognized that the DH of the tracer particle motion does not necessarily reflect the DH of the medium34 (as discussed in the introduction), the similarity between the trends in the experimental observations of the delayed peak in the non-Gaussian parameter with respect to the gel point28 and observations of the peak in α2 of reactive beads displacements significantly prior to the reverse gel point in simulations points out to comparable trends in quantifying DH either by tracking the motion of the reactive end groups or by the single particle tracking experiments in the respective cases.
Note that an increase in α2 for the systems degrading in a good solvent is observed in our simulations not only significantly earlier than the reverse gel point but also notably earlier than the peak value in dispersity, Đ. It is worth noting that the peak in Đ is also observed prior to the reverse gel point (approximately at 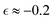 ) for all the crosslink densities considered in this study. Examination of the plots of the probability density of displacements of reactive beads allows one to highlight the following trends relating Gs to an increase in α2 for hydrogels degrading in a good solvent. First, during early stages of degradation, when only a small number of degradable bonds are broken, Gs distribution follows a Gaussian limit, and correspondingly, the values of α2 are close to zero. As the degradation proceeds and a significant fraction of bonds is broken, yet significantly prior to the reverse gel point, 4πr2Gs distributions become skewed to the right, with the long tails contributing to the highest values of α2 for each individual simulation run of nanogels degrading in a good solvent. At the reverse gel point, the deviation of the distribution of displacements of the slower population of beads from the Gaussian behavior is clearly pronounced, with the position corresponding to the maximum 4πr2Gs values skewed to the left with respect to the Gaussian distribution. However, the tail corresponding to the faster beads becomes relatively shorter compared to the width of Gaussian distribution; correspondingly, the value of α2 at the reverse gel point remains significantly higher than zero yet notably lower than the peak value. Finally, when most of the fragments are broken off, we observe a return to the Gaussian behavior, such that Gs distribution follows a Gaussian limit and α2 ≈ 0 in all the cases of nanogels degraded in a good solvent considered herein.
) for all the crosslink densities considered in this study. Examination of the plots of the probability density of displacements of reactive beads allows one to highlight the following trends relating Gs to an increase in α2 for hydrogels degrading in a good solvent. First, during early stages of degradation, when only a small number of degradable bonds are broken, Gs distribution follows a Gaussian limit, and correspondingly, the values of α2 are close to zero. As the degradation proceeds and a significant fraction of bonds is broken, yet significantly prior to the reverse gel point, 4πr2Gs distributions become skewed to the right, with the long tails contributing to the highest values of α2 for each individual simulation run of nanogels degrading in a good solvent. At the reverse gel point, the deviation of the distribution of displacements of the slower population of beads from the Gaussian behavior is clearly pronounced, with the position corresponding to the maximum 4πr2Gs values skewed to the left with respect to the Gaussian distribution. However, the tail corresponding to the faster beads becomes relatively shorter compared to the width of Gaussian distribution; correspondingly, the value of α2 at the reverse gel point remains significantly higher than zero yet notably lower than the peak value. Finally, when most of the fragments are broken off, we observe a return to the Gaussian behavior, such that Gs distribution follows a Gaussian limit and α2 ≈ 0 in all the cases of nanogels degraded in a good solvent considered herein.
Further, our study shows that a systematic decrease in solvent quality significantly affects the behavior of the non-Gaussian parameter as a function of the relative extent of degradation, 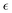 . A small decrease in the affinity between the polymer and solvent beads (case B) results in the non-Gaussian parameter behavior similar to that for case A, with a broader distribution in peak values of α2 for the individual simulation runs resulting in broadening of averaged high values of
. A small decrease in the affinity between the polymer and solvent beads (case B) results in the non-Gaussian parameter behavior similar to that for case A, with a broader distribution in peak values of α2 for the individual simulation runs resulting in broadening of averaged high values of 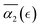 . Further decrease in solvent quality significantly affects the
. Further decrease in solvent quality significantly affects the 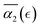 dependence. With further decrease of solvent quality (case C), the peak values in
dependence. With further decrease of solvent quality (case C), the peak values in 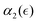 distributions for the individual runs are observed at or after the reverse gel point, resulting in a consistent increase in
distributions for the individual runs are observed at or after the reverse gel point, resulting in a consistent increase in 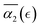 after the reverse gel point. The maximum absolute values of the
after the reverse gel point. The maximum absolute values of the 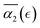 in cases C and B are below the values of
in cases C and B are below the values of 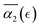 in case A. For the case of a poor solvent (case D), the non-Gaussian parameter attains small negative values for all the individual simulation runs. In this case all the precursors that are broken off remain within the same agglomerate, which diffuses as a whole in a poor solvent resulting in similar displacements of reactive end beads and correspondingly in negative values of α2. The findings of this study allow one to quantify the dynamic heterogeneities during nanogels’ degradation in various environments, and the distribution of the fragments of controllably degrading nanocarriers depending on the relative extent of degradation reaction.
in case A. For the case of a poor solvent (case D), the non-Gaussian parameter attains small negative values for all the individual simulation runs. In this case all the precursors that are broken off remain within the same agglomerate, which diffuses as a whole in a poor solvent resulting in similar displacements of reactive end beads and correspondingly in negative values of α2. The findings of this study allow one to quantify the dynamic heterogeneities during nanogels’ degradation in various environments, and the distribution of the fragments of controllably degrading nanocarriers depending on the relative extent of degradation reaction.
Author contributions
Z. F. M.: formal analysis, software, data curation, investigation, methodology, visualization, validation, writing – original draft, writing – review & editing; V. P.: software, methodology, investigation, writing – review & editing; O. K.: conceptualization, funding acquisition, investigation, supervision, formal analysis, writing – original draft, writing – review & editing.Data availability
The data underlying this study are openly available in the repository: https://zenodo.org/records/13952413.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors thank Rupali Sharma and Arefin Mustafa Anik for useful discussions. This work was supported in part by the National Science Foundation under NSF Award DMR-2110309. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect those of the National Science Foundation. Clemson University is acknowledged for generous allotment of compute time on Palmetto cluster.References
- C.-C. Lin and A. T. Metters, Hydrogels in controlled release formulations: network design and mathematical modeling, Adv. Drug Delivery Rev., 2006, 58(12–13), 1379–1408 CrossRef CAS PubMed.
- B. Hosseinzadeh and M. Ahmadi, Degradable hydrogels: design mechanisms and versatile applications, Mater. Today Sustainability, 2023, 23, 100468 CrossRef.
- A. M. Kloxin, A. M. Kasko, C. N. Salinas and K. S. Anseth, Photodegradable Hydrogels for Dynamic Tuning of Physical and Chemical Properties, Science, 2009, 324(5923), 59–63 CrossRef CAS PubMed.
- D. Y. Wong, D. R. Griffin, J. Reed and A. M. Kasko, Photodegradable Hydrogels to Generate Positive and Negative Features over Multiple Length Scales, Macromolecules, 2010, 43(6), 2824–2831 CrossRef CAS.
- D. R. Griffin and A. M. Kasko, Photoselective Delivery of Model Therapeutics from Hydrogels, ACS Macro Lett., 2012, 1(11), 1330–1334 CrossRef CAS PubMed.
- V. V. Ramanan, J. S. Katz, M. Guvendiren, E. R. Cohen, R. A. Marklein and J. A. Burdick, Photocleavable side groups to spatially alter hydrogel properties and cellular interactions, J. Mater. Chem., 2010, 20(40), 8920–8926 RSC.
- A. M. Kloxin, M. W. Tibbitt, A. M. Kasko, J. A. Fairbairn and K. S. Anseth, Tunable Hydrogels for External Manipulation of Cellular Microenvironments through Controlled Photodegradation, Adv. Mater., 2010, 22(1), 61–66 CrossRef CAS PubMed.
- T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U. I. Chung, Design and fabrication of a high-strength hydrogel with ideally homogeneous network structure from tetrahedron-like macromonomers, Macromolecules, 2008, 41(14), 5379–5384 CrossRef CAS.
- V. X. Truong, F. Y. Li and J. S. Forsythe, Photolabile Hydrogels Responsive to Broad Spectrum Visible Light for Selective Cell Release, ACS Appl. Mater. Interfaces, 2017, 9(38), 32441–32445 CrossRef CAS PubMed.
- M. Villiou, J. I. Paez and A. del Campo, Photodegradable Hydrogels for Cell Encapsulation and Tissue Adhesion, ACS Appl. Mater. Interfaces, 2020, 12(34), 37862–37872 CrossRef CAS PubMed.
- M. A. Azagarsamy, D. D. McKinnon, D. L. Age and K. S. Anseth, Coumarin-Based Photodegradable Hydrogel: Design, Synthesis, Gelation, and Degradation Kinetics, ACS Macro Lett., 2014, 3(6), 515–519 CrossRef CAS PubMed.
- S. Shahi, H. Roghani-Mamaqani, S. Talebi and H. Mardani, Stimuli-responsive destructible polymeric hydrogels based on irreversible covalent bond dissociation, Polym. Chem., 2022, 13(2), 161–192 RSC.
- L. Berthier, Dynamic Heterogeneity in Amorphous Materials, Physics, 2011, 4, 42 CrossRef.
- M. D. Ediger, Spatially heterogeneous dynamics in supercooled liquids, Annu. Rev. Phys. Chem., 2000, 51(1), 99–128 CrossRef CAS PubMed.
- X. Xu, J. F. Douglas and W.-S. Xu, Parallel emergence of rigidity and collective motion in a family of simulated glass-forming polymer fluids, Macromolecules, 2023, 56(13), 4929–4951 CrossRef CAS.
- H. Zhang and J. F. Douglas, Glassy interfacial dynamics of Ni nanoparticles: part I Colored noise, dynamic heterogeneity and collective atomic motion, Soft Matter, 2013, 9(4), 1254–1265 RSC.
- C. Donati, S. C. Glotzer, P. H. Poole, W. Kob and S. J. Plimpton, Spatial correlations of mobility and immobility in a glass-forming Lennard-Jones liquid, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60(3), 3107 CrossRef CAS PubMed.
- W. Kob, C. Donati, S. J. Plimpton, P. H. Poole and S. C. Glotzer, Dynamical heterogeneities in a supercooled Lennard-Jones liquid, Phys. Rev. Lett., 1997, 79(15), 2827 CrossRef CAS.
- C. P. Royall and S. R. Williams, The role of local structure in dynamical arrest, Phys. Rep., 2015, 560, 1–75 CrossRef CAS.
- E. Boattini, S. Marín-Aguilar, S. Mitra, G. Foffi, F. Smallenburg and L. Filion, Autonomously revealing hidden local structures in supercooled liquids, Nat. Commun., 2020, 11(1), 5479 CrossRef CAS PubMed.
- G. Jung, G. Biroli and L. Berthier, Predicting Dynamic Heterogeneity in Glass-Forming Liquids by Physics-Inspired Machine Learning, Phys. Rev. Lett., 2023, 130(23), 238202 CrossRef CAS PubMed.
- G. Jung, G. Biroli and L. Berthier, Dynamic heterogeneity at the experimental glass transition predicted by transferable machine learning, Phys. Rev. B, 2024, 109(6), 064205 CrossRef CAS.
- A. M. Puertas, M. Fuchs and M. E. Cates, Dynamical heterogeneities close to a colloidal gel, J. Chem. Phys., 2004, 121(6), 2813–2822 CrossRef CAS PubMed.
- C. J. Dibble, M. Kogan and M. J. Solomon, Structure and dynamics of colloidal depletion gels: coincidence of transitions and heterogeneity, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74(4), 041403 CrossRef PubMed.
- X. Xu, J. F. Douglas and W.-S. Xu, Thermodynamic–dynamic interrelations in glass-forming polymer fluids, Macromolecules, 2022, 55(19), 8699–8722 CrossRef CAS.
- D. Pan and Z.-Y. Sun, Influence of chain stiffness on the dynamical heterogeneity and fragility of polymer melts, J. Chem. Phys., 2018, 149(23), 234904 CrossRef PubMed.
- M. Asai, M. Shibayama and Y. Koike, Common origin of dynamics heterogeneity and cooperatively rearranging region in polymer melts, Macromolecules, 2011, 44(16), 6615–6624 CrossRef CAS.
- E. Parrish, K. A. Rose, M. Cargnello, C. B. Murray, D. Lee and R. J. Composto, Nanoparticle diffusion during gelation of tetra poly(ethylene glycol) provides insight into nanoscale structural evolution, Soft Matter, 2020, 16(9), 2256–2265 RSC.
- A. Corrigan and A. Donald, Particle tracking microrheology of gel-forming amyloid fibril networks, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 28(4), 457–462 CrossRef CAS PubMed.
- T. Moschakis, Microrheology and particle tracking in food gels and emulsions, Curr. Opin. Colloid Interface Sci., 2013, 18(4), 311–323 CrossRef CAS.
- C. H. Lee, A. J. Crosby, T. Emrick and R. C. Hayward, Characterization of heterogeneous polyacrylamide hydrogels by tracking of single quantum dots, Macromolecules, 2014, 47(2), 741–749 CrossRef CAS.
- E. Parrish, M. A. Caporizzo and R. J. Composto, Network confinement and heterogeneity slows nanoparticle diffusion in polymer gels, J. Chem. Phys., 2017, 146(20), 203318 CrossRef PubMed.
- E. Parrish, S. C. Seeger and R. J. Composto, Temperature-Dependent Nanoparticle Dynamics in Poly(N-isopropylacrylamide) Gels, Macromolecules, 2018, 51(10), 3597–3607 CrossRef CAS.
- W. Hong, G. Xu, X. Ou, W. Sun, T. Wang and Z. Tong, Colloidal probe dynamics in gelatin solution during the sol–gel transition, Soft Matter, 2018, 14(19), 3694–3703 RSC.
- O. Watts Moore, C. Lewis, T. Ross, T. A. Waigh, N. Korabel and C. Mendoza, Extreme heterogeneity in the microrheology of lamellar surfactant gels analyzed with neural networks, Phys. Rev. E, 2024, 110(1), 014603 CrossRef PubMed.
- M. T. Valentine, P. D. Kaplan, D. Thota, J. C. Crocker, T. Gisler, R. K. Prud’homme, M. Beck and D. A. Weitz, Investigating the microenvironments of inhomogeneous soft materials with multiple particle tracking, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64(6), 061506 CrossRef CAS PubMed.
- A. G. Cherstvy, S. Thapa, C. E. Wagner and R. Metzler, Non-Gaussian, non-ergodic, and non-Fickian diffusion of tracers in mucin hydrogels, Soft Matter, 2019, 15(12), 2526–2551 RSC.
- Y. Dai, R. Zhang, W. Sun, T. Wang, Y. Chen and Z. Tong, Dynamical heterogeneity in the gelation process of a polymer solution with a lower critical solution temperature, Soft Matter, 2021, 17(11), 3222–3233 RSC.
- A. Perego, D. Lazarenko, M. Cloitre and F. Khabaz, Microscopic dynamics and viscoelasticity of vitrimers, Macromolecules, 2022, 55(17), 7605–7613 CrossRef CAS.
- J. Xia, J. A. Kalow and M. Olvera de la Cruz, Structure, Dynamics, and Rheology of Vitrimers, Macromolecules, 2023, 56(19), 8080–8093 CrossRef CAS.
- H. Zhao, P. Duan, Z. Li, Q. Chen, T. Yue, L. Zhang, V. Ganesan and J. Liu, Unveiling the Multiscale Dynamics of Polymer Vitrimers Via Molecular Dynamics Simulations, Macromolecules, 2023, 56(23), 9336–9349 CrossRef CAS.
- H. Pandya, A. Perego and F. Khabaz, Stress-induced dynamics of glassy vitrimers with fast bond exchange rate, J. Appl. Polym. Sci., 2024, 141(10), e55039 CrossRef CAS.
- H. Pandya and F. Khabaz, Effect of dynamic bond concentration on the mechanical properties of vitrimers, Chem. Commun., 2024, 60(75), 10354–10357 RSC.
- D. Bedrov, G. Smith and J. F. Douglas, Influence of self-assembly on dynamical and viscoelastic properties of telechelic polymer solutions, Europhys. Lett., 2002, 59(3), 384 CrossRef CAS.
- D. Bedrov, G. Smith and J. F. Douglas, Structural and dynamic heterogeneity in a telechelic polymer solution, Polymer, 2004, 45(11), 3961–3966 CrossRef CAS.
- J. Ramirez, T. J. Dursch and B. D. Olsen, A Molecular Explanation for Anomalous Diffusion in Supramolecular Polymer Networks, Macromolecules, 2018, 51(7), 2517–2525 CrossRef CAS.
- A. Rao, J. Ramírez and B. D. Olsen, Mechanisms of Self-Diffusion of Linear Associative Polymers Studied by Brownian Dynamics Simulation, Macromolecules, 2021, 54(24), 11212–11227 CrossRef CAS.
- S. K. Kumar and J. F. Douglas, Gelation in physically associating polymer solutions, Phys. Rev. Lett., 2001, 87(18), 188301 CrossRef.
- V. Palkar and O. Kuksenok, Controlling Degradation and Erosion of Polymer Networks: Insights from Mesoscale Modeling, J. Phys. Chem. B, 2022, 126(1), 336–346 CrossRef CAS PubMed.
- V. Palkar, D. Thakar and O. Kuksenok, Nanogel degradation at soft interfaces and in bulk: tracking shape changes and interfacial spreading, Macromolecules, 2023, 56(4), 1289–1302 CrossRef CAS.
- V. Palkar, D. Thakar and O. Kuksenok, Data for manuscript: Nanogel degradation at soft interfaces and in bul k: tracking shape changes and interfacial spreading, Zenodo, 2022 Search PubMed.
- P. Espanol and P. Warren, Statistical-Mechanics Of Dissipative Particle Dynamics, Europhys. Lett., 1995, 30(4), 191–196 CrossRef CAS.
- R. D. Groot and P. B. Warren, Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation, J. Chem. Phys., 1997, 107(11), 4423–4435 CrossRef CAS.
- P. Espanol and P. B. Warren, Perspective: Dissipative Particle Dynamics, J. Chem. Phys., 2017, 146(15), 150901 CrossRef PubMed.
- K. P. Santo and A. V. Neimark, Dissipative particle dynamics simulations in colloid and interface science: a review, Adv. Colloid Interface Sci., 2021, 102545 CrossRef CAS PubMed.
- S. Chen, E. Olson, S. Jiang and X. Yong, Nanoparticle assembly modulated by polymer chain conformation in composite materials, Nanoscale, 2020, 12(27), 14560–14572 RSC.
- M. Dutt, O. Kuksenok, M. J. Nayhouse, S. R. Little and A. C. Balazs, Modeling the Self-Assembly of Lipids and Nanotubes in Solution: Forming Vesicles and Bicelles with Transmembrane Nanotube Channels, ACS Nano, 2011, 5(6), 4769–4782 CrossRef CAS PubMed.
- S. Tu, C. K. Choudhury, M. Giltner, I. Luzinov and O. Kuksenok, Mesoscale modeling of agglomeration of molecular bottlebrushes: focus on conformations and clustering criteria, Polymers, 2022, 14(12), 2339 CrossRef CAS PubMed.
- Z. Xu, Y. Yang, G. Zhu, P. Chen, Z. Huang, X. Dai, C. Hou and L. T. Yan, Simulating transport of soft matter in micro/nano channel flows with dissipative particle dynamics, Adv. Theory Simul., 2019, 2(2), 1800160 CrossRef.
- L. Wei, T. D. Caliskan, S. Tu, C. K. Choudhury, O. Kuksenok and I. Luzinov, Highly Oil-Repellent Thermoplastic Boundaries via Surface Delivery of CF3 Groups by Molecular Bottlebrush Additives, ACS Appl. Mater. Interfaces, 2020, 12(34), 38626–38637 CrossRef CAS PubMed.
- M. Dutt, M. J. Nayhouse, O. Kuksenok, S. R. Little and A. C. Balazs, Interactions of end-functionalized nanotubes with lipid vesicles: spontaneous insertion and nanotube self-organization, Curr. Nanosci., 2011, 7(5), 699–715 CrossRef CAS.
- M. Zhang, T. Larison, S. Tu, O. Kuksenok and M. Stefik, Effect of Fluorophobic Character upon Switching Nanoparticles in Polymer Films from Aggregated to Dispersed States Using Immersion Annealing, ACS Appl. Polym. Mater., 2022, 4(10), 7042–7053 CrossRef CAS.
- A. M. Anik, V. Palkar, I. Luzinov and O. Kuksenok, Mesoscale modeling of random chain scission in polyethylene melts, JPhys Mater., 2024, 7(3), 035010 CrossRef CAS.
- S. Shrivastava, A. Upadhyay, S. S. Pradhan, S. Saha and A. Singh, Evolution Kinetics of Stabilizing Pickering Emulsion by Brush-Modified Janus Particles: DPD Simulation and Experimental Insights, Langmuir, 2024, 40(27), 13920–13934 CrossRef CAS PubMed.
- S. Nikolov, A. Fernandez-Nieves and A. Alexeev, Mesoscale modeling of microgel mechanics and kinetics through the swelling transition, J. Appl. Math. Mech., 2018, 39(1), 47–62 CrossRef.
- R. A. Gumerov, A. A. Rudov, W. Richtering, M. Moller and I. I. Potemkin, Amphiphilic Arborescent Copolymers and Microgels: From Unimolecular Micelles in a Selective Solvent to the Stable Monolayers of Variable Density and Nanostructure at a Liquid Interface, ACS Appl. Mater. Interfaces, 2017, 9(37), 31302–31316 CrossRef CAS PubMed.
- X. Yong, O. Kuksenok and A. C. Balazs, Modeling free radical polymerization using dissipative particle dynamics, Polymer, 2015, 72, 217–225 CrossRef CAS.
- A. Singh, O. Kuksenok, J. A. Johnson and A. C. Balazs, Tailoring the structure of polymer networks with iniferter-mediated photo-growth, Polym. Chem., 2016, 7(17), 2955–2964 RSC.
- C. K. Choudhury, V. Palkar and O. Kuksenok, Computational Design of Nanostructured Soft Interfaces: Focus on Shape Changes and Spreading of Cubic Nanogels, Langmuir, 2020, 36(25), 7109–7123 CrossRef CAS PubMed.
- Y. Liu, J. Aizenberg and A. C. Balazs, Using Dissipative Particle Dynamics to Model Effects of Chemical Reactions Occurring within Hydrogels, Nanomaterials, 2021, 11(10), 2764 CrossRef CAS PubMed.
- T. Zhang, S. Biswas, J. Cuthbert, T. Kowalewski, K. Matyjaszewski and A. C. Balazs, Understanding the origin of softness in structurally tailored and engineered macromolecular (STEM) gels: A DPD study, Polymer, 2020, 208, 122909 CrossRef CAS.
- S. I. Zholudev, R. A. Gumerov, A. A. Larina and I. I. Potemkin, Swelling, collapse and ordering of rod-like microgels in solution: computer simulation studies, J. Colloid Interface Sci., 2023, 629, 270–278 CrossRef CAS PubMed.
- X. Yong, O. Kuksenok, K. Matyjaszewski and A. C. Balazs, Harnessing Interfacially-Active Nanorods to Regenerate Severed Polymer Gels, Nano Lett., 2013, 13(12), 6269–6274 CrossRef CAS PubMed.
- Y. Xiong, C. K. Choudhury, V. Palkar, R. Wunderlich, R. K. Bordia and O. Kuksenok, Mesoscale modeling of phase separation controlled by hydrosilylation in polyhydromethylsiloxane (PHMS)-containing blends, Nanomaterials, 2022, 12(18), 3117 CrossRef CAS PubMed.
- Y. Xiong, H. Yuan and M. O. de la Cruz, Janus magnetoelastic membrane swimmers, Soft Matter, 2023, 19(35), 6721–6730 RSC.
- R. D. Groot and K. L. Rabone, Mesoscopic Simulation of Cell Membrane Damage, Morphology Change and Rupture by Nonionic Surfactants, Biophys. J., 2001, 81(2), 725–736 CrossRef CAS PubMed.
- A. Metters and J. Hubbell, Network formation and degradation behavior of hydrogels formed by Michael-type addition reactions, Biomacromolecules, 2005, 6(1), 290–301 CrossRef CAS PubMed.
- N. Kameta, T. Matsuzawa, K. Yaoi and M. Masuda, Short polyethylene glycol chains densely bound to soft nanotube channels for inhibition of protein aggregation, RSC Adv., 2016, 6(43), 36744–36750 RSC.
- S. Saeki, N. Kuwahara, M. Nakata and M. Kaneko, Upper and lower critical solution temperatures in poly(ethylene glycol) solutions, Polymer, 1976, 17(8), 685–689 CrossRef CAS.
- G. D. Smith and D. Bedrov, Roles of Enthalpy, Entropy, and Hydrogen Bonding in the Lower Critical Solution Temperature Behavior of Poly(ethylene oxide)/Water Solutions, J. Phys. Chem. B, 2003, 107(14), 3095–3097 CrossRef CAS.
- R. Chudoba, J. Heyda and J. Dzubiella, Temperature-Dependent Implicit-Solvent Model of Polyethylene Glycol in Aqueous Solution, J. Chem. Theory Comput., 2017, 13(12), 6317–6327 CrossRef CAS PubMed.
- R. Kjellander and E. Florin, Water structure and changes in thermal stability of the system poly(ethylene oxide)–water, J. Chem. Soc., Faraday Trans. 1, 1981, 77(9), 2053–2077 RSC.
- R. Dahanayake, U. Dahal and E. E. Dormidontova, Co-solvent and temperature effect on conformation and hydration of polypropylene and polyethylene oxides in aqueous solutions, J. Mol. Liq., 2022, 362, 119774 CrossRef CAS.
- X. Zheng, M. A. Anisimov, J. V. Sengers and M. He, Mesoscopic diffusion of poly (ethylene oxide) in pure and mixed solvents, J. Phys. Chem. B, 2017, 122(13), 3454–3464 CrossRef PubMed.
- T. W. Sirk, Y. R. Slizoberg, J. K. Brennan, M. Lisal and J. W. Andzelm, An enhanced entangled polymer model for dissipative particle dynamics, J. Chem. Phys., 2012, 136(13), 11 CrossRef PubMed.
- V. Palkar, C. K. Choudhury and O. Kuksenok, Development of Dissipative Particle Dynamics framework for modeling hydrogels with degradable bonds, Mrs Adv., 2020, 5(17), 927–934 CrossRef CAS.
- D. R. Griffin, J. T. Patterson and A. M. Kasko, Photodegradation as a mechanism for controlled drug delivery, Biotechnol. Bioeng., 2010, 107(6), 1012–1019 CrossRef CAS PubMed.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. I. Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18(1), 015012 CrossRef.
- https://docs.lammps.org/pair_srp.html#pair-style-srp-react-command (accessed 11/21/2022).
- P. K. Jha, J. W. Zwanikken, F. A. Detcheverry, J. J. De Pablo and M. O. de la Cruz, Study of volume phase transitions in polymeric nanogels by theoretically informed coarse-grained simulations, Soft Matter, 2011, 7(13), 5965–5975 RSC.
- L. Y. Shy, Y. K. Leung and B. E. Eichinger, Critical Exponents For Off-Lattice Gelation Of Polymer-Chains, Macromolecules, 1985, 18(5), 983–986 CrossRef CAS.
- A. M. Gupta, R. C. Hendrickson and C. W. Macosko, Monte-Carlo Description Of Af Homopolymerization – Diffusional Effects, J. Chem. Phys., 1991, 95(3), 2097–2108 CrossRef CAS.
- J. Somvarsky and K. Dusek, Kinetic Monte-Carlo Simulation Of Network Formation. 2. Effect Of System Size, Polym. Bull., 1994, 33(3), 377–384 CrossRef CAS.
- P. Polanowski, J. K. Jeszka, W. W. Li and K. Matyjaszewski, Effect of dilution on branching and gelation in living copolymerization of monomer and divinyl cross-linker: modeling using dynamic lattice liquid model (DLL) and Flory-Stockmayer (FS) model, Polymer, 2011, 52(22), 5092–5101 CrossRef CAS.
- D. Stauffer and A. Aharony, Introduction To Percolation Theory, Taylor & Francis, 1994 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, OUP, Oxford, 2003 Search PubMed.
- J. Šomvársky and K. Dušek, Kinetic Monte-Carlo simulation of network formation, Polym. Bull., 1994, 33(3), 369–376 CrossRef.
- R. Wang, T. S. Lin, J. A. Johnson and B. D. Olsen, Kinetic Monte Carlo Simulation for Quantification of the Gel Point of Polymer Networks, ACS Macro Lett., 2017, 6(12), 1414–1419 CrossRef CAS PubMed.
- T. Sakai, T. Katashima, T. Matsushita and U. I. Chung, Sol–gel transition behavior near critical concentration and connectivity, Polym. J., 2016, 48(5), 629–634 CrossRef CAS.
- K. Nishi, K. Fujii, U. Chung, M. Shibayama and T. Sakai, Experimental Observation of Two Features Unexpected from the Classical Theories of Rubber Elasticity, Phys. Rev. Lett., 2017, 119(26), 267801 CrossRef PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- S. E. Rankin, L. J. Kasehagen, A. V. McCormick and C. W. Macosko, Dynamic Monte Carlo simulation of gelation with extensive cyclization, Macromolecules, 2000, 33(20), 7639–7648 CrossRef CAS.
- J. L. Spouge, Equilibrium Ring Formation In Polymer-Solutions, J. Stat. Phys., 1986, 43(1–2), 143–196 CrossRef.
- Y. Tanaka, J. L. Stanford and R. Stepto, Interpretation of Gel Points of an Epoxy-Amine System Including Ring Formation and Unequal Reactivity: Measurements of Gel Points and Analyses on Ring Structures, Macromolecules, 2012, 45(17), 7197–7205 CrossRef CAS.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids: with Applications to Soft Matter. Academic Press, San Diego, 2013 Search PubMed.
- V. Sorichetti, A. Ninarello, J. Ruiz-Franco, V. Hugouvieux, E. Zaccarelli, C. Micheletti, W. Kob and L. Rovigatti, Structure and elasticity of model disordered, polydisperse, and defect-free polymer networks, J. Chem. Phys., 2023, 158(7), 074905 CrossRef CAS PubMed.
- D. W. Scott, Multivariate density estimation: theory, practice, and visualization, John Wiley & Sons, 2015 Search PubMed.
- B.-Q. Ai, R.-X. Guo, C.-H. Zeng and Y.-F. He, Rotational inertia-induced glassy transition in chiral particle systems, Phys. Rev. E, 2024, 109(6), 064902 CrossRef CAS PubMed.
- A. Rahman, Correlations in the motion of atoms in liquid argon, Phys. Rev., 1964, 136(2A), A405 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01256a |
| This journal is © The Royal Society of Chemistry 2025 |