Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Network design for soft materials: addressing elasticity and fracture resistance challenges
Yong Eun
Cho†
a,
Sihwan
Lee†
a,
Sang Jun
Ma†
a and
Jeong-Yun
Sun
 *ab
*ab
aDepartmant of Materials Science and Engineering, Seoul National University, Seoul 08826, Republic of Korea. E-mail: lsihwan16@snu.ac.kr; sang219@snu.ac.kr; jysun@snu.ac.kr; whdyddms111@snu.ac.kr
bResearch Institute of Advanced Materials (RIAM), Seoul National University, Seoul 08826, Republic of Korea
First published on 5th February 2025
Abstract
Soft materials, such as elastomers and gels, feature crosslinked polymer chains that provide stretchable and elastic mechanical properties. These properties are derived from entropic elasticity, which limits energy dissipation and makes the material susceptible to fracture. To address this issue, network designs that dissipate energy through the plastic zone have been introduced to enhance toughness; however, this approach compromises elasticity, preventing the material from fully recovering its original shape after deformation. In this review, we describe the trade-off between fracture resistance and elasticity, exploring network designs that overcome this limitation to achieve both high toughness and low hysteresis. The development of soft materials that are both elastic and fracture-resistant holds significant promise for applications in stretchable electronics, soft robotics, and biomedical devices. By analyzing successful network designs, we identify strategies to further improve these materials and discuss potential enhancements based on existing limitations.
1. Introduction
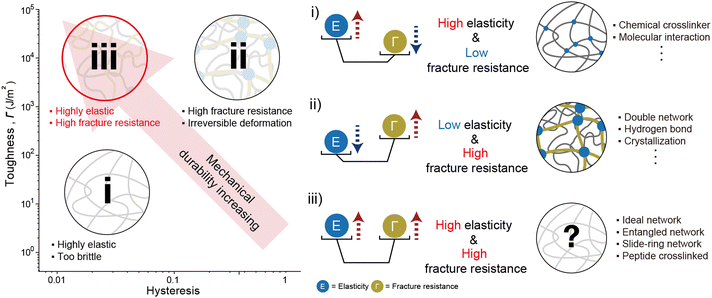
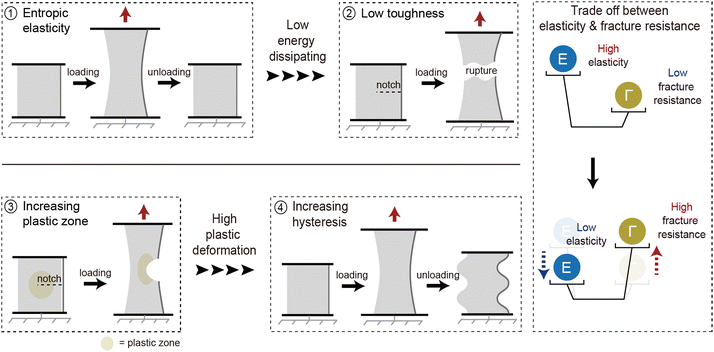
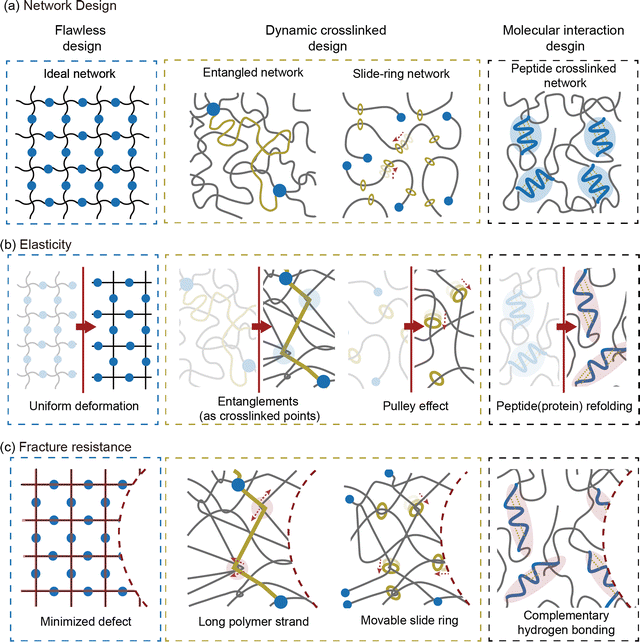
Soft materials such as elastomers and hydrogels, feature a three-dimensional crosslinked polymer network that provides exceptional stretchability and elasticity.1–3 These mechanical properties endow soft materials with capabilities such as energy dissipation,3 adaptability to changing environments,4 biocompatibility,5 and nonlinear mechanical responsiveness.6 Unlike rigid materials, soft materials can undergo extensive deformation while maintaining structural integrity, making them suitable for diverse applications stretchable electronics,7–9 soft robotics,10–13 and biomedical devices.14–18 However, such applications subject soft materials to challenging conditions, including load-bearing conditions,19,20 cyclic loading environments,21 or damage-prone situations.22 To ensure consistent and reliable performance under these conditions, soft materials require enhanced mechanical performance.The mechanical properties of soft materials stem from entropic elasticity, which limits energy dissipation and makes the material vulnerable to fracture.23–25 Researchers have developed network designs that increase the plastic zone size to improve energy dissipation and enhance fracture resistance.26–28 However, this approach inevitably compromises elasticity, limiting the capacity of the material to recover its original state after deformation.3,29 This inherent trade-off between fracture resistance and elasticity presents a significant challenge in developing soft materials that are simultaneously tough and elastic. Addressing this challenge requires a comprehensive understanding of how network design affects the mechanical properties of soft materials (Fig. 1).
The mechanical properties of soft materials are closely related to network design.30–32 Enhancing the mechanical properties requires careful consideration of factors such as the type of polymer backbone,33 the topology of chain connections,34–36 molecular interactions between chains,37 and interactions between polymers and solvents or additives.38,39 To enhance the performance of soft materials, this review addresses network design strategies to resolve the trade-off between fracture resistance and elasticity. We begin by discussing the methods to characterize elasticity and fracture resistance, followed by an analysis of network designs that improve each property individually. The inherent trade-off is examined in detail, highlighting strategies that enable the simultaneous enhancement of toughness and elasticity. By analyzing successful network designs, we outline future directions and potential improvements based on current limitations.
2. Mechanisms and mechanical characterization of elasticity and fracture resistance in soft materials
Soft materials are characterized by their unique ability to undergo substantial deformations, even under small forces. Following such deformations, two key factors must be evaluated: (1) whether the material returns to its original shape upon removal of the external load, and (2) whether cracks propagate during deformation.40 These can be characterized as elasticity and fracture resistance, respectively, and understanding both is crucial when evaluating soft materials.1,40,412.1 Brief overview
Elasticity describes the ability of a material to return to its original shape after being deformed by stress. This property is often evaluated through hysteresis, which quantifies the energy lost during cyclic loading and unloading of the material.42 Materials exhibiting low hysteresis can recover elastically with high efficiency, making them suitable for repeated applications under consistent performance requirements.Fracture resistance indicates the ability of a material to resist crack propagation during deformation. To quantify fracture resistance, toughness (Γ) is introduced, which reflects the material's capacity to dissipate energy and prevent crack growth.43–45 Materials with high toughness can withstand a variety of loads, enabling them to perform reliably across diverse conditions.
2.2 Origins of the elasticity-fracture resistance trade-off in soft materials
The mechanical performance of soft materials is primarily governed by entropic elasticity, which inherently restricts energy dissipation and leaves the material prone to fracture. To increase resistance to fracture, innovative network designs have been developed to expand the plastic deformation zone.3,29,46,47 Energy dissipation in increasing plastic zone enhances fracture resistance significantly. However, indiscriminate increases in the plastic zone within the network have introduced unforeseen challenges, even in the absence of cracks. When strain is applied, internal plastic deformation within the network increases the hysteresis of the material, even before fracture occurs. This relationship is distinctly observed in the Lake–Thomas model, one of the prominent approaches for explaining the fracture resistance of soft materials. An increase in cross-linking density in soft materials reduces fracture toughness. Simultaneously, higher cross-linking density decreases the distance between cross-linking points, resulting in enhanced entropic elasticity. A more detailed explanation of the Lake–Thomas model will be provided in the following section. Balancing these conflicting requirements of toughness and elasticity, as influenced by factors such as cross-linking density and energy dissipation, remains a critical challenge in the development of advanced soft materials (Fig. 2).2.3 Theory of elasticity
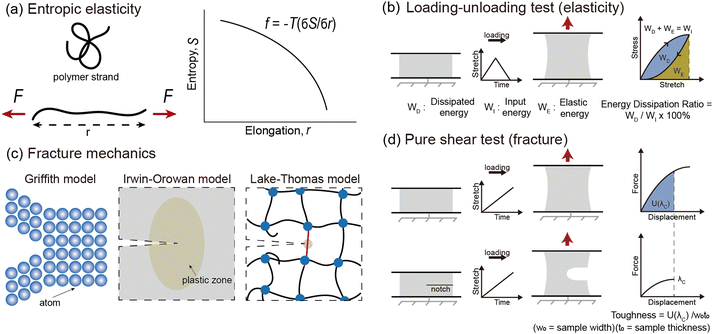
The elasticity of soft materials composed of polymers is influenced by the conformation of polymer chains and molecular interactions. Due to their inherently long and flexible chains, polymers naturally adopt a coiled and disordered structure. This fundamental phenomenon can be explained from an entropic perspective, where entropic elasticity serves as a fundamental concept describing elasticity driven by the entropy of polymer chains.1,48,49 When polymer chains stretched, these chains are forced into a more ordered conformation (low entropy state).1 As soon as the external force is removed, they spontaneously return to their original, high-entropy, disordered state.The number of conformations of the polymer chains, Ω can be expressed as
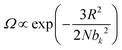 | (1) |
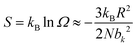 | (2) |
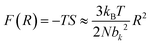 | (3) |
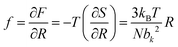 | (4) |
2.4 Testing methods for elasticity
The universal testing machine (UTM) is commonly used to measure the mechanical properties of soft materials, including tensile and compressive tests. To measure hysteresis, a loading–unloading curve is required. The energy applied during the loading process is called input energy (WI). The energy recovered by the material, known as elastic energy (WE), is the area beneath the unloading curve. The unrecovered energy, called dissipated energy (WD), is the area between the loading and unloading curves. These values satisfy the relationship WD + WE = WI, and the energy dissipation ratio, calculated as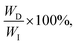 quantifies hysteresis (Fig. 3b). A higher energy dissipation ratio indicates a reduced ability for the material to return to its original state after load removal. However, as soft materials exhibit viscoelastic properties, their behavior is time-dependent, making the loading rate an influential factor. Additionally, soft materials are generally capable of large deformations, meaning the extent of stretching has a considerable impact. Generally, the faster the loading rate and the greater the stretch, the higher the energy dissipation ratio.42 Therefore, conducting experiments under identical conditions is crucial when comparing energy dissipation ratios. Residual stretch is a measure of elasticity, defined as the remaining stretch when the stress returns to zero after a material has been loaded and then unloaded.50 Lower residual stretch values indicate better recovery to the original state, implying greater elasticity. Additionally, changes in the loading–unloading curve over multiple cycles can also be used to assess elasticity.40 If the curve remains consistent across many cycles, the material exhibits high elasticity. These measurements are essential for understanding a material's recovery ability after deformation, which is a critical factor in soft material design.
quantifies hysteresis (Fig. 3b). A higher energy dissipation ratio indicates a reduced ability for the material to return to its original state after load removal. However, as soft materials exhibit viscoelastic properties, their behavior is time-dependent, making the loading rate an influential factor. Additionally, soft materials are generally capable of large deformations, meaning the extent of stretching has a considerable impact. Generally, the faster the loading rate and the greater the stretch, the higher the energy dissipation ratio.42 Therefore, conducting experiments under identical conditions is crucial when comparing energy dissipation ratios. Residual stretch is a measure of elasticity, defined as the remaining stretch when the stress returns to zero after a material has been loaded and then unloaded.50 Lower residual stretch values indicate better recovery to the original state, implying greater elasticity. Additionally, changes in the loading–unloading curve over multiple cycles can also be used to assess elasticity.40 If the curve remains consistent across many cycles, the material exhibits high elasticity. These measurements are essential for understanding a material's recovery ability after deformation, which is a critical factor in soft material design.
2.5 Theory of fracture mechanics
Fracture resistance, the energy required to propagate a crack, plays a pivotal role in determining the lifetime and mechanical durability of materials.40 The ability to resist fracture depends on how effectively materials dissipate energy at both molecular and macroscopic levels. Intrinsically brittle materials, like silica glass, exhibit low fracture energy, as described by the Griffith model.51 Ductile materials such as metals possess higher fracture energy, as explained by the Irwin–Orowan model,52,53 which incorporates energy dissipation through plastic deformation near the crack tip. Crosslinked polymer networks achieve toughness through mechanisms specific to their structure. The Lake–Thomas model describes this toughness by considering energy dissipation along stretched covalent bonds within polymer chains, providing insights into the fracture resistance of polymers41 (Fig. 3c).In fracture mechanics, Griffith introduced a model in 1921 to calculate fracture energy based on the difference in energy before and after fracture.51 According to Griffith, fracture occurs with the formation of two new surfaces; therefore, toughness can be expressed as
| Γ = 2γ | (5) |
In the 1940s, G. Irwin and E. Orowan extended Griffith's model to include plastic deformation for ductile materials.52,53 For such materials, local plasticity around the crack tip requires additional energy for fracture, enhancing fracture resistance. In metals, for example, a plastic zone forms near the crack tip, where atomic bonds release energy through deformation. Thus, considering the plastic zone, toughness can be expressed as
| Γ = 2γ + Wp | (6) |
Following in 1967, Lake and Thomas developed a model specifically for polymer networks, considering that each polymer chain is composed of numerous monomers with chemical energy stored in the C–C bonds.41 In this model, fracture energy is influenced by the number of C–C bonds along stretched polymer chains. At the front of a crack, polymer chains are stretched to the point where all the C–C bonds along the chain approach their breaking threshold. The mechanical energy needed to stretch the chain to this critical state is equal to the total chemical energy stored in its C–C bonds. When the chain finally breaks, this stored mechanical energy is released and dissipated, contributing to fracture resistance. The energy required to reach this breaking point, termed intrinsic fracture energy can be expressed as
| Γ0 = eL | (7) |
| e = bJ | (8) |
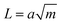 | (9) |
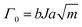 | (10) |
| Γ = Γ0 + ΓD |
2.6 Testing methods for fracture resistance
Fracture, often an undesirable occurrence, can be assessed through various testing methods. These include tearing45 or peeling tests,54 where force and displacement are recorded, as well as puncture55 and impact tests.56 Tearing tests involve applying a tensile force to a pre-cut sample to measure the material's resistance to crack propagation. Peeling tests focus on determining the adhesive strength between two layers by measuring the force needed to peel one layer from another. Puncture tests evaluate the force required to penetrate a material using a sharp probe, simulating real-world puncture scenarios. Impact tests measure the energy absorbed when a material is subjected to sudden, high-speed loading, providing insights into its toughness under dynamic conditions. Among these, the pure shear test is widely used. For this test, two types of samples—unnotched and notched—are required.3,40 Both are stretched using a UTM to obtain a force–displacement curve. For the notched sample, the critical stretch (λc) is determined, which marks the onset of crack propagation. For the unnotched sample, the area under the force–displacement curve up to λc is integrated and divided by the cross-sectional area of the sample to determine toughness (Γ)45 (Fig. 3d). The parameters that influence Γ include the strength of the unnotched sample and the resistance to crack propagation in the notched sample. Since Γ is an intrinsic material property, it is valuable for comparing the fracture characteristics of different materials. However, Γ does not always yield consistent values due to limitations associated with measurement methods. Variations in sample dimensions can affect the measured values of Γ, as they influence the stress distribution within the material. Additionally, for soft materials that exhibit viscoelasticity, differences in strain rate during testing can lead to discrepancies in Γ, as their time-dependent behavior causes the energy dissipation to vary with the rate of deformation. To enable reliable comparisons of Γ across different materials, standardized testing protocols are necessary. Despite these limitations, Γ remains a crucial indicator for assessing whether a material is suitable for specific applications.3. Enhancing elasticity or fracture resistance
3.1 Elastic network design
One of the most critical properties that have enabled the broad application of soft materials across various fields is undoubtedly their elasticity. Materials with high elasticity are particularly important in applications involving repeated loading and unloading or in ensuring long-term durability. Consequently, extensive research has been conducted to enhance the elasticity characteristics of soft materials composed of polymeric springs.57–59 Researchers employ crosslinkers to reinforce the polymer network, leveraging entropic elasticity to enhance its elastic response. Additionally, tailoring molecular interactions within the polymer network utilizes elasticity driven by enthalpic contributions. In the following sections, we outline strategies to enhance elasticity through network topology and molecular interactions.Increasing the crosslinker density reduces the number of segments N between crosslinking points. Consequently, the number of possible conformations decreases, leading to an increased restoring force. This increased restoring force suppress plastic deformation, facilitating the recovery to its original state, thereby enhancing elasticity.62 He et al. demonstrated that optimizing chemical crosslinker density improved elasticity and minimized hysteresis (Fig. 4a).57 This phenomenon can be explained using the standard linear solid model, which is based on Maxwell theory. Higher crosslinking density enhances the elasticity of the spring, effectively reducing creep and making the material more elastic.
 | ||
| Fig. 4 Highly elastic networks. (a) Schematic illustration of a highly crosslinked polyelectrolyte elastomers. The network enhances entropic elasticity through high crosslinking density. Reproduced with permission from ref. 57. Copyright 2024, Springer Nature. (b) Tri-branched hydrogels achieve high elasticity and stretchability through reversible strain-induced crystallization, despite their low crosslinker functionality. Reproduced with permission from ref. 63. Copyright 2022, AAAS. (c) Zwitterionic hydrogel network exhibits strain-stiffening through a dual-network design, which stiffens the network while maintaining high elasticity. Reproduced with permission from ref. 58. Copyright 2021, Springer Nature. (d) Schematic illustration of a pearl-necklace network in polyelectrolyte hydrogels. The network unfolds and refolds under mechanical strain, allowing rapid recovery and hyper elasticity. Reproduced with permission from ref. 59. Copyright 2023, AAAS. | ||
Another approach involves enhancing crosslinker functionality, which refers to the number of polymer chains a single crosslinker can connect.48 High-functionality crosslinkers introduce multiple polymer chains between adjacent crosslinkers, strengthening the elasticity of the network.64–66 However, increasing crosslinker functionality does not always yield beneficial outcomes;63,67,68 in specific polymers, such as poly(ethylene glycol) (PEG), reducing functionality can impart distinctive material properties. For example, Sakai et al. presented a tri-branched network structure that improved elasticity through reversible strain-induced crystallization despite its reduced functionality.63 This finding highlights that lower-functionality crosslinkers can also enhance elasticity when combined with other mechanisms, such as crystallization (Fig. 4b).
Besides covalent crosslinking and their functionality, network defects such as loops and dangling ends also play a crucial role in determining elasticity.39 Loops form when polymer chains react intramolecularly instead of participating in the network structure.32 This reduces the effective number of elastically active chains, leading to diminished elasticity.69 By employing controlled synthesis methods to minimize loop formation, network connectivity can be improved, resulting in enhanced elasticity. Similarly, dangling ends refer to the freely moving chain ends that do not contribute to the network.70,71 These defects increase the elastically inactive regions, further reducing the overall elasticity of the network. Therefore, minimizing network defects is essential for optimizing elasticity in polymer networks.
Zhang et al. reported a skin-like ionic elastomer with a supramolecular zwitterionic network embedded within hydrogen-bonded polycarboxylic acid chains.58 The two networks exhibit varying strengths, enabling sequential debonding during stretching. This unique combination of dynamic interactions enables fast recovery and high performance under cyclic stress (Fig. 4c).
Moreover, Chen et al. increased the elasticity of polyelectrolyte hydrogels by adjusting the water content.59 With the optimal amount of water, the polymer chains form a pearl-necklace chain (PNC) structure, where (1) hydrophobic alkyl chains act as soft beads and (2) hydrophilic ionic groups form the string. Upon external deformation, the optimum amount of water acts as a lubricant, allowing reversible hydrophobic interactions to reform, further enhancing the elasticity of the material (Fig. 4d).
3.2 Fracture resistant network design
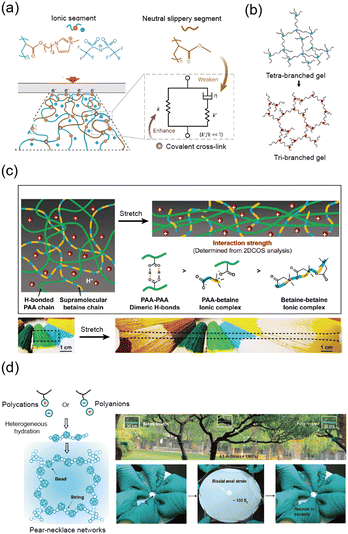
The elasticity of polymer networks relies on the capacity to store energy under stress and release it upon unloading. Although the ability to store and release energy is beneficial for elasticity, effective crack resistance requires energy dissipation rather than energy storage and release.81,82 To make soft materials tougher, researchers have investigated strategies to improve fracture resistance by promoting energy dissipation within the polymer network.83,84 A primary approach involves expanding the plastic zone, a region around a crack tip where energy dissipation can occur more readily. In the following sections, we will explore various network design strategies that aim to increase fracture resistance by expanding the plastic zone size.Gong et al. significantly increased the fracture energy of hydrogels by introducing a double network structure composed of a brittle, energy-dissipating first network and a soft, stretchable second network.46,87 The fracture of the first network dissipates mechanical energy, while the second network maintains the structural integrity of the hydrogel (Fig. 5a). This method of using double networks to enhance fracture resistance has been widely studied, with many researchers focusing on the use of covalent crosslinking.43,88–93
 | ||
| Fig. 5 Highly tough networks. (a) Schematic illustration of a double network (DN) hydrogel composed of a rigid, brittle first network and a soft, stretchable second network. The DN hydrogel exhibits high toughness as the brittle network dissipates energy through sacrificial bond breakage. Reproduced with permission from ref. 46 and 85. Copyright 2014, AAAS, Copyright 2003, Wiley-VCH. (b) Alginate–polyacrylamide hydrogel demonstrates high stretchability and notch insensitivity due to the synergy between crack bridging by covalent crosslinks and energy dissipation through ionic crosslink unzipping. Reproduced with permission from ref. 3. Copyright 2012, Springer Nature. (c) Tough ionogel network formed through in situ phase separation. The polymer-rich domains enhance fracture resistance by dissipating energy, while the solvent-rich domains maintain stretchability. Reproduced with permission from ref. 20. Copyright 2022, Springer Nature. (d) Tough hydrogel formed by the synergy of freeze-casting and salting-out methods, creating a hierarchical structure with aligned nanofibrils, showing notch insensitivity when stretched. Reproduced with permission from ref. 29. Copyright 2021, Springer Nature. | ||
Sun et al. extended this concept by creating a double network of physically crosslinked alginate and covalently crosslinked acrylamide, expanding the plastic zone to achieve even higher fracture energies of ∼9000 J m−2 (Fig. 5b).3 This design introduced ionic interactions that rupture under stress, making the material more stretchable while maintaining toughness.94 They further demonstrated the fracture resistance of the double network hydrogel using various multivalent cations.95
The double network design has also been applied in combination with various other networks, establishing itself as a versatile method for enhancing the mechanical properties of polymer systems.96–99
Phase separation in polymer networks can manifest in two representative forms: polymer–polymer separation and polymer–solvent separation. Each method produces unique network architectures that contribute to the ability of the material to resist fracture.89,118,119
For instance, Fernández-Rico et al. demonstrated polymer–polymer phase separation through microphase separation within an elastomer matrix.120 By supersaturating polydimethylsiloxane (PDMS) with heptafluorobutyl methacrylate (HFBMA), phase separation was induced upon cooling, forming a robust bicontinuous microstructure. This structure enhanced the fracture resistance of the material through strong interactions between similar components.
In another study, Wang et al. demonstrated polymer–solvent separation to create tough and stretchable ionogels through in situ phase separation.20 The ionic liquid was miscible with poly(acrylic acid) (PAA) but immiscible with polyacrylamide (PAAm), leading to the formation of a bicontinuous polymer network. The polymer-rich domain, strengthened by hydrogen bonds, contributed to toughness, while the solvent-rich domain provided stretchability (Fig. 5c).
The type of polymer and the fabrication method are key factors in achieving crystallization within polymers. Certain polymers, such as poly(vinyl alcohol) (PVA), are more prone to crystallization due to their molecular structure.122 Additionally, the way the polymer is processed—through methods like annealing, freeze–thaw cycles, or salting-out—can significantly affect the degree and distribution of crystallinity within the material.
For example, Peppas et al. introduced crystalline domains into poly(vinyl alcohol) (PVA) hydrogels using a freeze–thaw method, which improved the ultimate tensile strength, modulus, and toughness of the hydrogels.123,124 Building on this approach, Hua et al. combined freeze-casting and salting-out methods to create a hierarchical structure with high crystallinity in PVA hydrogels.29 The crystalline regions acted as energy dissipation centers, while well-aligned nanofibrils helped blunt crack propagation (Fig. 5d).
3.3 General relationship between elasticity and fracture resistance
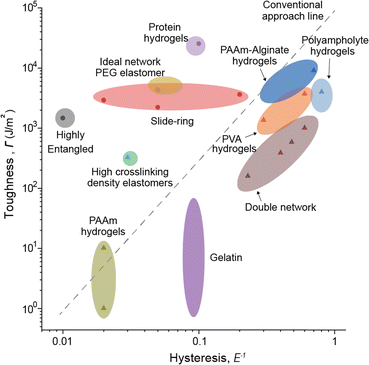
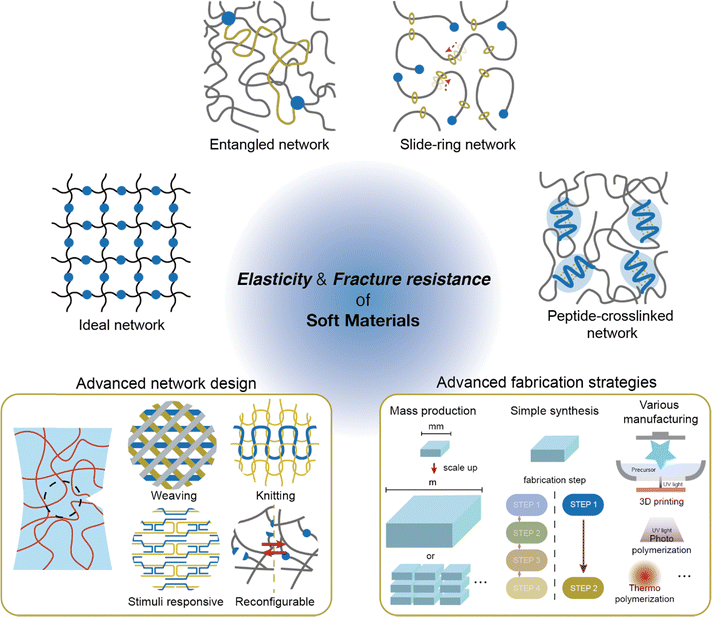
When examining network designs that enhance elasticity and fracture resistance individually, it becomes evident that the factors required to improve each property are fundamentally different. However, it is often overlooked that incorporating these factors into a single network design can negatively impact the opposing property. This trade-off becomes particularly apparent when analyzing network designs through their relationship between elasticity and fracture resistance (Fig. 6). This is because both toughness and hysteresis are generally influenced by the size of the plastic zone, which impacts these properties simultaneously. As a result, most materials fall along a predictable trend line on the Ashby plot. However, certain network designs have successfully achieved both low hysteresis and high toughness. These designs, which deviate from conventional approaches, are referred to as advanced network designs. Such designs are achieved through flawless structures, dynamically moving components during deformation, or harnessing specific molecular interactions. In the following section, we will explore network designs that simultaneously exhibit high elasticity and fracture resistance.4. Improving both elasticity and fracture resistance
Overcoming the traditional trade-off between fracture resistance and elasticity, various network designs have been developed to achieve both high toughness and low hysteresis. The approaches to resolving this trade-off relationship can be broadly categorized into three strategies: increasing elasticity without compromising fracture resistance, enhancing fracture resistance without reducing elasticity, and, finally, improving both properties simultaneously (Fig. 7). Notable examples include ideal networks, highly entangled networks, slide-ring networks, and peptide-crosslinked networks. These designs reduce hysteresis without compromising toughness by minimizing flaws in the network, enhance toughness through dynamic crosslinking, or resolve trade-offs using molecular interactions. The following sections provide an in-depth discussion of the energy dissipation and recovery mechanisms that support these network designs.4.1 Flawless network design
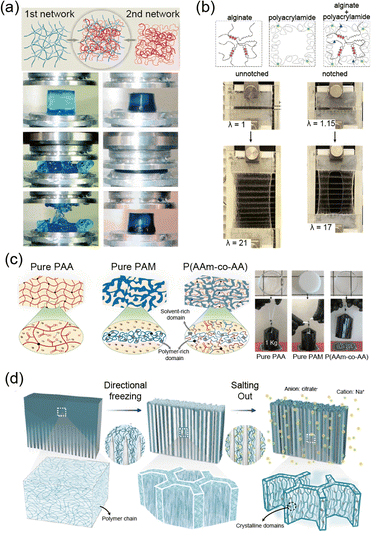
In polymer networks, defects play a critical role in determining the mechanical performance of the material. Common defects include uneven crosslinking, unreacted chains that form dangling ends, and the formation of loops.130 These irregularities act as stress concentration points under load, reducing fracture resistance. Furthermore, they hinder uniform deformation across the network, thereby lowering elasticity. To address these issues, researchers have made efforts to minimize defects and create ideal networks that make soft materials more robust.Kamata et al. developed hydrogels based on defect-free ideal networks, eliminating mechanical hysteresis without compromising fracture resistance (Fig. 8a).141 The hydrogel maintains consistent mechanical properties even after multiple stretches. The synthesis involved end-linking tetra-armed PEG through step-growth polymerization. This design ensures uniform chain distribution within the hydrogel, resolving the trade-off between elasticity fracture resistance. Additionally, the isotropic extension of chains within the ideal network confers a low swellable property. This design is not limited to a single material and can be applied to a wide range of polymer networks.
 | ||
| Fig. 8 Ideal network. (a) Tetra-armed hydrogels, with a well-organized network structure, increase fracture energy without compromising elasticity, maintaining mechanical integrity under repetitive loading. Reproduced with permission from ref. 141. Copyright 2014, AAAS. (b) Elastomer with a highly homogeneous network structure demonstrates both elasticity and notch resistance due to uniform stress distribution. Reproduced with permission from ref. 139. Copyright 2023, Wiley-VCH. (c) An ideal polyethylene glycol (PEG) network with a hierarchical structure of crystalline and amorphous phases shows high toughness and elasticity, attributed to the orderly arrangement of the polymer network. Reproduced with permission from ref. 138. Copyright 2023, AAAS. | ||
The ideal network design can be applied not only to hydrogels but also to elastomers. Nakagawa et al. developed an elastomer with excellent mechanical properties by creating a uniform network structure with long chains (Fig. 8b).139 The ideal network structure enabled uniform stress distribution across the long chains, allowing for high stretchability and toughness without sacrificing elasticity. The structure was achieved through end-linking multi-arm prepolymers, creating a highly uniform network. The uniformity facilitated chain alignment and led to strong strain-stiffening behavior. Typically, strain-stiffening is difficult to achieve due to the challenges of chain alignment after a certain level of deformation, which is often caused by defects in the network. By overcoming these limitations, this design holds potential for applications in fields such as stretchable electronics and soft robotics, where superior mechanical properties are essential.
Incorporating chains capable of SIC into an ideal network can significantly enhance the mechanical performance of elastomers.138–140 SIC allows rapid recovery even after large deformations, ensuring high elasticity (Fig. 8c).138 Additionally, chain alignment during deformation suppresses crack propagation. Therefore, the elastomer maintains high toughness (Γ = 5 kJ m−2) and low hysteresis (<1%) even under significant strain. This design enables the material to undergo repeated deformation and recovery cycles while maintaining high performance across a broad temperature range. As the strain aligns the polymer chains, crystallization occurs, enhancing mechanical properties while also improving thermal conductivity through more efficient stress distribution. These properties make the material adaptable for applications requiring both mechanical resilience and thermal management.
The ideal network design has significant advantages for polymer network modeling, which has led to extensive theoretical studies. When a near-perfect network is achieved, it maintains fracture resistance while significantly enhancing elasticity. Moreover, applying this network design to various polymers can create synergistic effects, enhancing mechanical performance. However, from a material processing standpoint, creating such ideal networks remains challenging. Scaling up production through efficient and simplified processing methods could enable broader industrial applications and enhance their feasibility for diverse fields.
4.2 Dynamic cross-linked network
The mechanical properties of soft materials can vary depending on how the internal network is structured. Typically, chemically crosslinked points remain fixed under stress, whereas crosslinks formed through entanglements or slide-ring mechanisms can move when stress is applied. In this section, we explore network design strategies with dynamic crosslinking that overcome trade-off between fracture resistance and elasticity. We focus on how dynamic crosslinking increases fracture resistance while maintaining elasticity.From eqn (10), the Lake–Thomas model suggests that the energy required to rupture a single polymer strand is directly proportional to the number of monomers in that strand (m). As a result, increasing m can be an effective approach to improving fracture resistance. However, reducing crosslink density to increase m may enhance fracture resistance but does not lead to a decrease in elasticity. A highly entangled network design achieves high fracture toughness while maintaining elasticity (Fig. 7).38,55,97,143–153
Entanglements in polymer networks act as movable crosslinks, playing a crucial role in enhancing both fracture resistance and elasticity in soft materials. Unlike chemical crosslinkers, which are fixed within the network, polymer strands in entanglements are not confined and can move freely. This mobility enables the entanglements to act dynamically, adjusting under load by slipping and effectively increasing the length of the polymer strands experiencing stress (m), which improves the material's ability to resist fracture. Additionally, the stress applied to one polymer strand is dispersed to others through these entanglements, reducing stress concentration across the network and further enhancing fracture resistance.
In terms of elasticity, entanglements also offer distinct characteristics. One of the key requirements for elasticity is that the internal network conformation should remain largely unchanged after the load is applied and then removed. The entangled polymer strands contribute to this by preventing significant alterations in the network's structure under stress. Furthermore, because the network consists of long polymer chains forming these entanglements, chain rupture does not occur before material fracture, ensuring that the network returns to its original conformation after deformation. Therefore, an entanglement-based topology supports the design of materials with elasticity.
Kim et al. and Norioka et al. conducted pioneering work on synthesized soft materials where entanglements greatly outnumber crosslinks, allowing for high fracture resistance and elasticity.145,151 They drastically increased the monomer concentration while adjusting the amounts of water, crosslinker, and initiator during synthesis. They show single network polyacrylamide (PAAm) hydrogels that are and have superior fracture resistance (Γ = 2 kJ m−2) and elasticity (<1%) (Fig. 9a). This entanglements based network design is relatively simple in structure, which has led to its recent application not only in PAAm based hydrogels but also across various polymer chains. For example, Nian et al. developed a method to create highly elastic and tough hydrogels from doughs made of synthetic polymer chains, such as PEG.55 By kneading and annealing the polymer dough, the polymer chains are densely entangled without breaking. This method is compatible with synthetic and natural polymers, opening new possibilities for sustainable, high performance hydrogels (Fig. 9b).
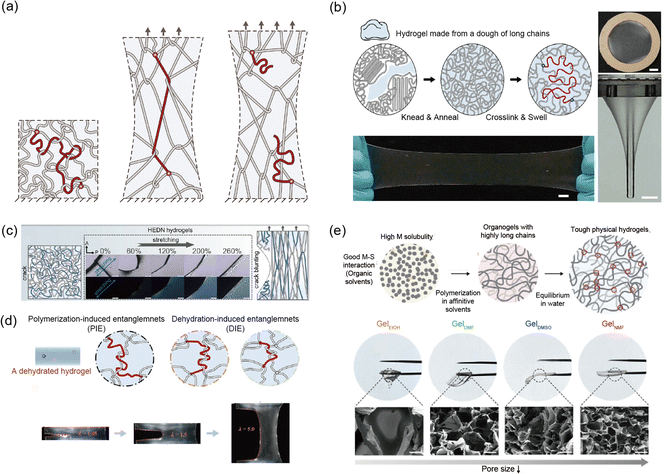 | ||
| Fig. 9 Highly entangled network. (a) Schematic illustration of a highly entangled network. The dense entanglements provide elasticity, while the long chains contribute to enhanced fracture resistance. Reproduced with permission from ref. 145. Copyright 2021, AAAS. (b) A highly entangled polyethylene glycol hydrogel demonstrates resistance to fracture when stretched or pierced with a rod. Reproduced with permission from ref. 55. Copyright 2021, Wiley-VCH. (c) The combination of a highly entangled network and a double network shows both crack blunting and enhanced elasticity when stretched. Reproduced with permission from ref. 97. Copyright 2024, Springer Nature. (d) Additional entanglements formed through dehydration in the highly entangled network enhance both elasticity and prevent crack propagation. Reproduced with permission from ref. 150. Copyright 2024, Springer Nature. (e) A tough thermo-responsive hydrogel made from highly entangled poly(N-isopropylacrylamide) (pNIPAAM) hydrogel via solvent engineering. The type of solvent affects the network formation. Reproduced with permission from ref. 38. Copyright 2024, Wiley-VCH. | ||
Recently, efforts have been made to enhance material properties by incorporating other network designs into entangled network design. Wang et al. developed highly entangled double network (HEDN) hydrogels with superior mechanical properties, including high fracture resistance and elasticity.97 The hydrogels use physical entanglements as effective crosslinking in the first network, leading to a highly uniform orientation under strain. This structure enables the hydrogels to achieve a high tensile strength (σf = 3 MPa), fracture resistance (Γ = 8 kJ m−2), and strain-stiffening behavior. Unlike traditional double-network (TDN) hydrogels, which rely on energy dissipation mechanisms, HEDN hydrogels store energy in oriented polymer chains, providing high reversibility. These properties make HEDN hydrogels promising for high performance applications requiring mechanical durability (Fig. 9c).
Various approaches have been explored in the fabrication of entangled networks. Yang et al. introduced a simple approach by incorporating dehydration into the process.150 They present a strategy for creating tough hydrogels by combining loose crosslinking with dense dehydration induced entanglements, providing a simple yet effective method for designing hydrogels that are highly resilient under stress (Fig. 9d).
In the synthesis of poly(N-isopropylacrylamide) (pNIPAAm) hydrogels, Cho et al. found that the formation of entanglements within the network varies depending on the solvent used during polymerization.38 They found that N-isopropylacrylamide (NIPAAm) exhibits extremely high solubility in N-methyl formamide (NMF). Furthermore, the strong interaction between NIPAAM and NMF significantly increased the polymer's degree of polymerization, resulting in a pNIPAAm network with a high degree of internal entanglement. These hydrogels, made from poly(N-isopropylacrylamide) (pNIPAAm), demonstrate significantly enhanced mechanical properties, including increased elasticity, strength, and toughness, alongside improved actuation without any additional components. The solvent engineering method improves polymer chain growth and entanglement, leading to robust thermo-responsive hydrogels (Fig. 9e).
Based on this network design, research is actively being conducted not only to enhance mechanical properties but also to explore applications of entangled network designs in various fields, such as battery electrolytes,154,155 tire materials,2 actuators,38 and 3D printing.156 However, there are limitations to the versatility of the entangled network design. Polymer entanglement is inherently influenced by the intrinsic properties of each polymer. Polymers with a low entanglement molecular weight (Me) for entanglement tend to form entangled networks more easily, whereas creating entangled networks with polymers of higher Me presents challenges. Therefore, more research is needed on how to design entangled networks using polymers that are not easily entangled. Additionally, the topology of entanglements is difficult to observe directly. Since imaging entanglements is challenging, the analysis of network entanglements is still conducted indirectly through methods such as mechanical properties, swelling ratio, and degree of polymerization. To better understand how entanglements influence the mechanical characteristics of the matrix, further research is needed to develop methods for directly analyzing entanglements.
Slide-ring networks usually incorporate PEG, a polymer known for its crystal forming properties, and various design approaches have utilized this feature in network development. Liu et al. developed a damage less reinforcement strategy for tough hydrogels using SIC.168 This hydrogel structure, based on slide-ring gels, features movable crosslinks of PEG chains. Under deformation, the PEG chains align, and form crystallized structures that melt and reform, allowing for nearly 100% recovery of extension energy and providing excellent toughness. The slide-ring mechanism enables both high fracture toughness (3.6 kJ m−2) and mechanical recoverability, making these hydrogels highly effective in applications requiring resilience under repeated stress (Fig. 10a). Hashimoto et al. also developed a tough slide-ring solid polymer electrolyte (SR-SPE) using SIC and phase separation mechanisms. Here, the slide-ring structure allows polymer chains to align under strain, promoting crystal formation without impairing ionic conductivity (Fig. 10b).167 It is also possible to design networks by incorporating other polymers into the slide-ring network. For example, Bin Imran et al. developed highly stretchable thermosensitive hydrogels by incorporating slide-ring polyrotaxane (PR) crosslinkers, ionic groups, and pNIPAAm into polymer networks.159 The PR crosslinkers, which enable a pulley effect, combined with ionic groups, result in hydrogels with enhanced fracture resistance and elasticity (Fig. 10c).
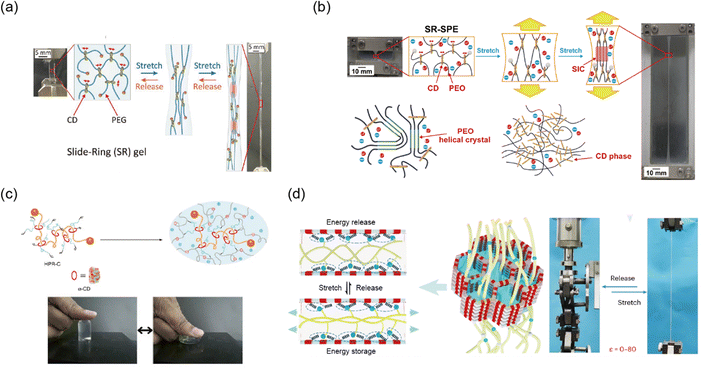 | ||
| Fig. 10 Slide-ring network. (a) An elastic and tough hydrogel was achieved by inserting polyethylene glycol (PEG) chains into hydroxypropyl-α-cyclodextrin (CD) rings, forming movable crosslink points. Reproduced with permission from ref. 168. Copyright 2021, AAAS. (b) The toughness of the elastic hydrogel was enhanced by adding strain-induced crystallization and phase separation to the slide-ring network. Reproduced with permission from ref. 167. Copyright 2023, AAAS. (c) The slide-ring network was applied to poly(N-isopropylacrylamide) (pNIPAM) hydrogels to produce a tough and elastic thermos-responsive hydrogel. Reproduced with permission from ref. 159. Copyright 2014, Springer Nature. (d) A hysteresis-free hydrogel was developed by nanoconfined polymer chains using covalent organic frameworks (COFs) or molecular sieves (MSs). The strong hydrogen bonding interactions with COFs or MSs also impart enhanced fracture resistance. Reproduced with permission from ref. 163. Copyright 2023, Springer Nature. | ||
Recently, Yan et al. introduced a nanoconfined polymerization (NCP) strategy to produce tough, hysteresis free gels with remarkable crack propagation resistance and elasticity.163 By confining polymerization within the nanochannels of covalent organic frameworks (COFs) or molecular sieves (MSs), this method mimics the mechanics of slide-ring structures, where movable crosslinks allow for enhanced toughness while maintaining elasticity. This approach was successfully applied to hydrogels, ionogels, and organogels, offering a versatile strategy for material synthesis (Fig. 10d).
As numerous studies have shown, slide-ring networks exhibit superior mechanical properties in terms of fracture resistance and elasticity. These superior mechanical properties enable slide ring network to various applications, stretchable electronics,98,160,162,169,170 actuators171 and bioelectronics.172 However, the use of polyrotaxane in constructing these networks requires specific combinations of polymers and host molecules, which inevitably limit the choices of materials for soft material fabrication. Moreover, synthesizing polyrotaxanes with low and precise host coverage is complex and challenging. Recent research has focused on developing a variety of polymers and host ring structures to construct slide-ring networks, as well as exploring approaches such as 3D printing173 to facilitate the fabrication of these networks.
4.3 Molecular interaction design
As discussed in Section 3, introducing specific interactions within the network can enhance fracture resistance, while incorporating reversible interactions can improve elasticity. However, the types of interactions required to enhance each mechanical property differ. Thus, achieving simultaneous improvements in both fracture resistance and elasticity through interaction-based designs presents challenges. To increase fracture resistance, strong interactions are necessary within the network to act as sources of energy dissipation. For elasticity, precise, reversible interactions are needed to ensure that the original network conformation remains unchanged before and after load application. A type of interaction that meets both conditions is the complementary hydrogen bonding found in peptides (proteins). The refolding ability of peptides174–176 after stress enhances elasticity, while complementary hydrogen bonds provide strong interactions, which thereby improve fracture resistance.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and amide hydrogens (NH) within the peptide backbone form complementary hydrogen bonds. These complementary hydrogen bonds enable peptides to form specific helical and coiled structures, increasing regularity. These unique structures and hydrogen bonds play a crucial role in the fracture resistance and elasticity of peptide-based networks, significantly influencing their mechanical properties. The numerous complementary hydrogen bonds within peptides can act as energy dissipation sources in the network. In coiled structures, such as helices, peptides unfold under applied load, breaking internal hydrogen bonds and allowing for energy dissipation, which increases fracture resistance. Simultaneously, the unfolded structure refolds rapidly into its original coiled form once the load is removed, restoring the original conformation and contributing to the network's high elasticity.177–182
O) and amide hydrogens (NH) within the peptide backbone form complementary hydrogen bonds. These complementary hydrogen bonds enable peptides to form specific helical and coiled structures, increasing regularity. These unique structures and hydrogen bonds play a crucial role in the fracture resistance and elasticity of peptide-based networks, significantly influencing their mechanical properties. The numerous complementary hydrogen bonds within peptides can act as energy dissipation sources in the network. In coiled structures, such as helices, peptides unfold under applied load, breaking internal hydrogen bonds and allowing for energy dissipation, which increases fracture resistance. Simultaneously, the unfolded structure refolds rapidly into its original coiled form once the load is removed, restoring the original conformation and contributing to the network's high elasticity.177–182
For example, Fu et al. engineered cartilage like protein hydrogels by introducing chain entanglements into folded peptides.177 These hydrogels achieved a balance of high toughness and fast recovery. The design mimics the mechanical properties of cartilage, which relies on an entangled network of collagen and proteoglycans. The study demonstrated that incorporating peptide crosslinkers with chain entanglements serves as a non-covalent stiffening mechanism without compromising toughness, providing a general approach for creating stiff and tough protein-based biomaterials (Fig. 11a). Liu et al. developed a highly entangled polymer network strengthened by poly(L-lysine) based peptide crosslinkers.180 The peptide crosslinked hydrogel exhibit excellent elasticity (<1%) and fracture resistance (Γ = 2100 J m−2). The peptide based crosslinkers introduce a novel energy dissipation mechanism through the breakage of intramolecular hydrogen bonds within α-helical peptide structures (Fig. 11b).
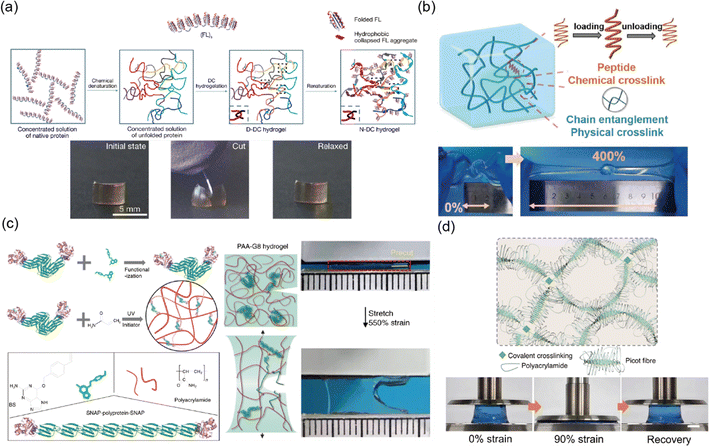 | ||
| Fig. 11 Peptide (protein) crosslinked network. (a) A cartilage-like hydrogel was created by folding proteins into a hydrophobic collapsed state within the protein hydrogel, which increased elasticity. This hydrogel is tough enough to resist cutting even when pressed with a knife. Reproduced with permission from ref. 177. Copyright 2023, Springer Nature. (b) An elastic protein-crosslinked hydrogel resists fracture, even when twisted and knotted. Reproduced with permission from ref. 180. Copyright 2023, Wiley-VCH. (c) Elastic tandem-repeat proteins were used as crosslinkers in poly(acrylic acid) (pAA) hydrogels, preventing crack propagation during stretching. Reproduced with permission from ref. 181. Copyright 2020, Springer Nature. (d) Poly(acrylamide) (pAAm) hydrogels crosslinked with picot peptide fibers exhibit rapid recovery, even after being compressed up to 90% strain. Reproduced with permission from ref. 182. Copyright 2023, Springer Nature. | ||
Efforts have also been made to design networks where peptides (proteins) and other polymers play distinct roles in the fracture resistance and elasticity of soft materials. Lei et al. developed stretchable hydrogels with low hysteresis and high anti-fatigue properties by utilizing polyprotein crosslinkers in combination with randomly coiled polymers.181 Random coiled polymers form a percolating phase within the network, exhibiting high elasticity like highly entangled networks, while polyprotein crosslinkers unfold to prevent crack propagation. This design decouples network elasticity from local mechanical response, resulting in hydrogels with excellent elasticity (<5%) and high fracture resistance (Γ = 900 J m−2) (Fig. 11c).
Introducing ionic coordination bonds within peptides can further enhance their energy dissipation capabilities. Xue et al. developed highly elastic and fatigue resistant hydrogels based on hierarchical structures of picot peptide fibers with metal coordination interaction.182 These hydrogels utilize copper-bound self-assembling peptide strands with zipped flexible hidden lengths that allow for energy dissipation without reducing network connectivity. This design yields hydrogels with impressive mechanical properties, including high toughness (Γ = 25.3 kJ m−2) and excellent elasticity (Fig. 11d).
Peptide crosslinker based network design gained significant research attention due to the distinct advantages of using bio-based materials, which make these networks highly applicable in biomedical fields.183 For example, the high fracture resistance and elasticity of peptide-crosslinked soft materials make them suitable for cartilage replacement.177 Moreover, these materials could serve as matrices for implantable devices,184 such as drug delivery systems.185 Therefore, the precise control of complementary hydrogen bonds in peptides opens possibilities for designing networks with a variety of tailored functions.
5. Conclusion and outlook
Soft materials have shown great promise for a wide range of applications. However, for practical applications, there are still significant mechanical limitations that need to be addressed. Considerable research has been conducted to improve the mechanical properties of soft materials. This review is aimed at exploring various network designs aimed at enhancing both elasticity and fracture resistance.Traditionally, approaches used to improve fracture resistance or elasticity have struggled to achieve simultaneous improvement in both properties. Soft materials possess elasticity due to entropic elasticity, but their low energy dissipation makes them susceptible to fracture. Conversely, increasing fracture resistance by expanding the plastic zone leads to a reduction in elasticity. Recent advances in network design, including ideal networks, highly entangled networks, slide-ring structures, and peptide-crosslinked networks, have shown the potential to enhance both fracture resistance and elasticity.
In ideal networks, defects are minimized, allowing them to behave as nearly perfect structures. This enables uniform deformation and effective stress deconcentration, resulting in high elasticity without compromising fracture resistance. Dynamic crosslinked designs, such as slide-ring and highly entangled networks, have mobile crosslink points that respond to applied stress, dispersing the stress effectively. Slide-ring networks achieve efficient recovery through the pulley effect, while in highly entangled networks, entanglements acting as crosslink points enhance elasticity. Lastly, peptide-crosslinked networks exhibit high elasticity and fracture resistance due to the refolding capability of peptides and complementary hydrogen bonds. These designs overcome the trade-off between fracture resistance and elasticity, achieving exceptional performance without compromise.
5.1 Advances in network design
Beyond the network designs discussed in this review, there is significant potential to develop new structures with superior mechanical properties. While controlling the architecture of polymers at the molecular scale has traditionally been challenging, recent advances in molecular engineering are opening new possibilities (Fig. 12, left).Molecular engineering has enabled the on-demand control of molecular structures at the level of single molecules or oligomers.186–190 Extending this level of molecular control to polymers opens the possibility of manipulating them similarly to textile fibers.191 Applying textile patterns, such as weaving or knitting, to network design is expected to yield superior mechanical properties. Such designs combine the regularity of ideal networks or peptide-crosslinked networks with the mobile crosslink points found in dynamic crosslinked designs, facilitating enhanced elasticity and fracture resistance. A technology that allows polymer chains to be manipulated as freely as textile fibers would have the potential to surpass current network design capabilities.
Applying molecular engineering to soft materials enables both network formation and dynamic tuning of material properties.192,193 By incorporating dynamic covalent bonds,194–197 materials can now be tuned in response to stimuli. For example, soft materials utilizing DNA origami198–200 and peptide-crosslinked networks, with numerous complementary hydrogen bonds, allow for precise control under external stimuli. Additionally, dynamic bonds enable recyclability and self-healing, further enhancing mechanical durability and promoting efficient resource use. Integrating these advanced molecular architectures into molecular-scale networks could unlock unprecedented mechanical properties, pushing the boundaries of soft material design.
5.2 Advances in fabrication strategies
Despite the promise of novel network designs, several challenges remain before soft materials can be widely applied. To be viable for practical use, these materials should be scalable for large-scale production.201 Currently, soft materials are typically fabricated in laboratory settings at sizes ranging from millimeters to centimeters. Although superior mechanical properties are achievable on a small scale, scaling up to industrial production can hinder performance and introduce new manufacturing challenges. Thus, further research is needed to develop methods that ensure uniform mechanical properties at larger scales (Fig. 12, right).Additionally, simplifying the production process for these novel networks is critical.202,203 For example, ideal networks require precisely controlled polymers to achieve a perfect structure. In particular, the synthesis of an ideal PEG network necessitates careful pH control to ensure optimal polymer formation. Similarly, the construction of highly entangled networks and slide-ring networks not only depends on the type of suitable polymers but also involves tedious processing. Highly entangled networks demand extended curing times, and constructing slide-ring networks entails additional steps to incorporate slide rings into the polymer structure. Such long or multi-step processing can limit their practical applications. Therefore, finding ways to simplify these processes is essential to advancing soft materials toward practical use.
Various manufacturing methods are also essential. Soft materials can typically be cured with light or heat, allowing for versatile shaping techniques such as molding and additive manufacturing, including 3D printing,204–206 to easily create various forms. However, network designs that are both elastic and fracture-resistant often require specific conditions, which can limit fabrication options. For instance, highly entangled networks have traditionally required long curing times, posing challenges for additive manufacturing. Recently, Dhand et al. demonstrated that by reducing curing time using both redox and photo-initiators, 3D printing became feasible, allowing for complex shapes and the use of multiple materials.156 As new network designs are developed, processing methods that maintain their unique properties while supporting easy fabrication become essential. Ultimately, achieving simultaneous enhancement in fracture resistance and elasticity in soft materials through advanced network design and facile fabrication strategies pave the way for the next generation of soft materials.
Author contributions
Y. E. Cho, S. Lee, and S. J. Ma contributed equally to this work. Y. E. Cho, S. Lee, and S. J. Ma conceived this work, designed figures, and organized the outline of the manuscript. J.-Y. Sun supervised this work. All authors discussed this work and wrote the manuscript.Data availability
The manuscript entitled ‘Network design for soft materials: addressing elasticity and fracture resistance challenges’ does not include data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Research Foundation of Korea (NRF) grants funded by the Korean Government (RS-2024-00459269 and RS-2021-NR059617). The Institute of Engineering Research at Seoul National University provided research facilities for this work.References
- L. G. Treloar, The physics of rubber elasticity, Oxford Univ. Press, 1975 Search PubMed.
- J. Steck, J. Kim, Y. Kutsovsky and Z. Suo, Nature, 2023, 624, 303–308 CrossRef CAS PubMed.
- J. Y. Sun, X. H. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. G. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- Y. S. Zhang and A. Khademhosseini, Science, 2017, 356, eaaf3627 CrossRef PubMed.
- Y.-W. Kim, J. E. Kim, Y. Jung and J.-Y. Sun, Mater. Sci. Eng., C, 2019, 95, 86–94 CrossRef CAS PubMed.
- L. Rijns, M. G. T. A. Rutten, R. Bellan, H. Yuan, M. L. Mugnai, S. Rocha, E. del Gado, P. H. J. Kouwer and P. Y. W. Dankers, Sci. Adv., 2024, 10, eadr3209 CrossRef CAS PubMed.
- J.-M. Park, J. Park, Y.-H. Kim, H. Zhou, Y. Lee, S. H. Jo, J. Ma, T.-W. Lee and J.-Y. Sun, Nat. Commun., 2020, 11, 4638 CrossRef CAS PubMed.
- C. Keplinger, J.-Y. Sun, C. C. Foo, P. Rothemund, G. M. Whitesides and Z. Suo, Science, 2013, 341, 984–987 CrossRef CAS PubMed.
- C.-C. Kim, H.-H. Lee, K. H. Oh and J.-Y. Sun, Science, 2016, 353, 682–687 CrossRef CAS PubMed.
- X. Liu, J. Liu, S. Lin and X. Zhao, Mater. Today, 2020, 36, 102–124 CrossRef CAS.
- C. S. Park, Y.-W. Kang, H. Na and J.-Y. Sun, Prog. Polym. Sci., 2024, 101791 CrossRef CAS.
- H. Na, Y.-W. Kang, C. S. Park, S. Jung, H.-Y. Kim and J.-Y. Sun, Science, 2022, 376, 301–307 CrossRef CAS PubMed.
- Y. Lee, W. J. Song, Y. Jung, H. Yoo, M.-Y. Kim, H.-Y. Kim and J.-Y. Sun, Sci. Rob., 2020, 5, eaaz5405 CrossRef PubMed.
- S.-H. Jeong, Y. Lee, M.-G. Lee, W. J. Song, J.-U. Park and J.-Y. Sun, Nano Energy, 2021, 79, 105463 CrossRef CAS.
- S.-H. Jeong, M.-G. Lee, C.-C. Kim, J. Park, Y. Baek, B. I. Park, J. Doh and J.-Y. Sun, Mater. Horiz., 2023, 10, 2215–2225 RSC.
- Y. Jiang, A. A. Trotsyuk, S. Niu, D. Henn, K. Chen, C.-C. Shih, M. R. Larson, A. M. Mermin-Bunnell, S. Mittal and J.-C. Lai, Nat. Biotechnol., 2023, 41, 652–662 CrossRef CAS PubMed.
- R. T. Arwani, S. C. L. Tan, A. Sundarapandi, W. P. Goh, Y. Liu, F. Y. Leong, W. Yang, X. T. Zheng, Y. Yu and C. Jiang, Nat. Mater., 2024, 1–8 Search PubMed.
- C. Lim, Y. J. Hong, J. Jung, Y. Shin, S.-H. Sunwoo, S. Baik, O. K. Park, S. H. Choi, T. Hyeon and J. H. Kim, Sci. Adv., 2021, 7, eabd3716 CrossRef CAS PubMed.
- M. Wang, X. Xiao, S. Siddika, M. Shamsi, E. Frey, W. Qian, W. Bai, B. T. O’Connor and M. D. Dickey, Nature, 2024, 1–6 Search PubMed.
- M. X. Wang, P. Y. Zhang, M. Shamsi, J. L. Thelen, W. Qian, V. K. Truong, J. Ma, J. Hu and M. D. Dickey, Nat. Mater., 2022, 21, 359–365 CrossRef CAS PubMed.
- J.-Y. Sun, C. Keplinger, G. M. Whitesides and Z. Suo, Adv. Mater., 2014, 26, 7608–7614 CrossRef CAS PubMed.
- J. Li, Z. Suo and J. J. Vlassak, J. Mater. Chem. B, 2014, 2, 6708–6713 RSC.
- P. J. Flory, Polym. J., 1985, 17, 1–12 CrossRef CAS.
- S. Edwards and T. Vilgis, Polymer, 1986, 27, 483–492 CrossRef CAS.
- S. K. Goswami, C. J. McAdam, L. R. Hanton and S. C. Moratti, Macromol. Rapid Commun., 2017, 38, 1700103 CrossRef PubMed.
- W. Wu, J. Fan, C. Zeng, X. Cheng, X. Liu, S. Guo, R. Sun, L. Ren, Z. Hao and X. Zeng, Adv. Mater., 2024, 36, 2403661 CrossRef CAS PubMed.
- J. Ju, G. E. Sanoja, L. Cipelletti, M. Ciccotti, B. Zhu, T. Narita, C. Yuen Hui and C. Creton, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2410515121 CrossRef CAS PubMed.
- S. T. Lin, C. D. Londono, D. C. Zheng and X. H. Zhao, Soft Matter, 2022, 18, 5742–5749 RSC.
- M. Hua, S. Wu, Y. Ma, Y. Zhao, Z. Chen, I. Frenkel, J. Strzalka, H. Zhou, X. Zhu and X. He, Nature, 2021, 590, 594–599 CrossRef CAS PubMed.
- X. Li and J. P. Gong, Nat. Rev. Mater., 2024, 1–19 Search PubMed.
- A. V. Dobrynin and J. M. Y. Carrillo, Macromolecules, 2011, 44, 140–146 CrossRef CAS.
- M. J. Zhong, R. Wang, K. Kawamoto, B. D. Olsen and J. A. Johnson, Science, 2016, 353, 1264–1268 CrossRef CAS PubMed.
- M. Vatankhah-Varnosfaderani, W. F. M. Daniel, M. H. Everhart, A. A. Pandya, H. Y. Liang, K. Matyjaszewski, A. V. Dobrynin and S. S. Sheiko, Nature, 2017, 549, 497–501 CrossRef PubMed.
- A. V. Dobrynin, Y. Tian, M. Jacobs, E. A. Nikitina, D. A. Ivanov, M. Maw, F. Vashahi and S. S. Sheiko, Nat. Mater., 2023, 22, 1394–1400 CrossRef CAS PubMed.
- K. Urayama, Polym. J., 2008, 40, 669–678 CrossRef CAS.
- B. Deng, S. Wang, C. Hartquist and X. Zhao, Phys. Rev. Lett., 2023, 131, 228102 CrossRef CAS PubMed.
- S. P. O. Danielsen, H. K. Beech, S. Wang, B. M. El-Zaatari, X. D. Wang, L. Sapir, T. Ouchi, Z. Wang, P. N. Johnson, Y. X. Hu, D. J. Lundberg, G. Stoychev, S. L. Craig, J. A. Johnson, J. A. Kalow, B. D. Olsen and M. Rubinstein, Chem. Rev., 2021, 121, 5042–5092 CrossRef CAS PubMed.
- Y. E. Cho, J. M. Park, W. J. Song, M. G. Lee and J. Y. Sun, Adv. Mater., 2024, 36, e2406103 CrossRef PubMed.
- Y. W. Gu, J. L. Zhao and J. A. Johnson, Angew. Chem., Int. Ed., 2020, 59, 5022–5049 CrossRef CAS PubMed.
- X. Zhao, Soft Matter, 2014, 10, 672–687 RSC.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, 300, 108–119 CAS.
- B. Hopkinson and T. G. Williams, Proc. R. Soc. London, Ser. A, 1912, 87, 502–511 Search PubMed.
- Y. Tanaka, R. Kuwabara, Y.-H. Na, T. Kurokawa, J. P. Gong and Y. Osada, J. Phys. Chem. B, 2005, 109, 11559–11562 CrossRef CAS PubMed.
- R. Bai, J. Yang and Z. Suo, Eur. J. Mech. A, 2019, 74, 337–370 CrossRef.
- R. Long and C.-Y. Hui, Soft Matter, 2016, 12, 8069–8086 RSC.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155–1158 CrossRef CAS.
- T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. A. Haque, T. Nakajima and J. P. Gong, Nat. Mater., 2013, 12, 932–937 CrossRef CAS PubMed.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- P. J. Flory and M. Volkenstein, Biopolymers, 1969, 8, 699–700 CrossRef.
- L. Gao, B.-L. Hu, L. Wang, J. Cao, R. He, F. Zhang, Z. Wang, W. Xue, H. Yang and R.-W. Li, Science, 2023, 381, 540–544 CrossRef CAS PubMed.
- A. Griffith, Trans. R. Soc. London, Ser. A, 1920, 221, 163–198 Search PubMed.
- G. R. Irwin, Fracturing of metals, 1947 Search PubMed.
- E. Orowan, Rep. Prog. Phys., 1949, 12, 185 CrossRef.
- Y. Wang, T. Yin and Z. Suo, J. Mech. Phys. Solids, 2021, 150, 104348 CrossRef CAS.
- G. Nian, J. Kim, X. Bao and Z. Suo, Adv. Mater., 2022, 34, e2206577 CrossRef PubMed.
- J. Zhang, Y. Miao, Q. Qin, T. Lu, Y. Ye, H. He, J. Wang and H. Li, Mech. Mater., 2021, 154, 103717 CrossRef.
- Y. He, Y. Cheng, C. Yang and C. F. Guo, Nat. Mater., 2024, 1–8 Search PubMed.
- W. Zhang, B. Wu, S. Sun and P. Wu, Nat. Commun., 2021, 12, 4082 CrossRef CAS PubMed.
- L. Chen, Z. Jin, W. Feng, L. Sun, H. Xu and C. Wang, Science, 2024, 383, 1455–1461 CrossRef CAS PubMed.
- P. J. Flory, Br. Polym. J., 1985, 17, 96–102 CrossRef CAS.
- Y. Gu, J. Zhao and J. A. Johnson, Trends Chem., 2019, 1, 318–334 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- T. Fujiyabu, N. Sakumichi, T. Katashima, C. Liu, K. Mayumi, U.-I. Chung and T. Sakai, Sci. Adv., 2022, 8, eabk0010 CrossRef CAS PubMed.
- Y. Masubuchi, Polym. J., 2024, 56, 163–171 CrossRef CAS.
- C. Zhou and Q. Wu, Colloids Surf., B, 2011, 84, 155–162 CrossRef CAS PubMed.
- K. Hashimoto, T. Enoki, C. Liu, X. Li, T. Sakai and K. Mayumi, Macromolecules, 2024, 57, 1461–1468 CrossRef CAS.
- H. Shi, W. Zhou, Z. Wen, W. Wang, X. Zeng, R. Sun and L. Ren, Mater. Horiz., 2023, 10, 928–937 RSC.
- M. E. Seitz, D. Martina, T. Baumberger, V. R. Krishnan, C.-Y. Hui and K. R. Shull, Soft Matter, 2009, 5, 447–456 RSC.
- Y. Gu, K. Kawamoto, M. Zhong, M. Chen, M. J. Hore, A. M. Jordan, L. T. Korley, B. D. Olsen and J. A. Johnson, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4875–4880 CrossRef CAS PubMed.
- C. Tsenoglou, Macromolecules, 1989, 22, 284–289 CrossRef CAS.
- A. k Zhang, J. Ling, K. Li, G. d Fu, T. Nakajima, T. Nonoyama, T. Kurokawa and J. P. Gong, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1227–1236 CrossRef CAS.
- S. Guan, C. Xu, X. Dong and M. Qi, J. Mater. Chem. A, 2023, 11, 15404–15415 RSC.
- Z. Zhang, L. Qian, J. Cheng, C. Ma and G. Zhang, Adv. Funct. Mater., 2024, 2402115 CrossRef CAS.
- X. Yu, Y. Wang, H. Zhang, Z. Li, Y. Zheng, X. Fan, Y. Lv, X. Zhang and T. Liu, Chem. Mater., 2023, 35, 9287–9298 CrossRef CAS.
- J. Wang, F. Tang, C. Yao and L. Li, Adv. Funct. Mater., 2023, 33, 2214935 CrossRef CAS.
- W. Sun, B. Xue, Q. Fan, R. Tao, C. Wang, X. Wang, Y. Li, M. Qin, W. Wang and B. Chen, Sci. Adv., 2020, 6, eaaz9531 CrossRef CAS PubMed.
- G. Zhang, S. Chen, Z. Peng, W. Shi, Z. Liu, H. Shi, K. Luo, G. Wei, H. Mo and B. Li, ACS Appl. Mater. Interfaces, 2021, 13, 12531–12540 CrossRef CAS PubMed.
- T. Li, X. Li, J. Yang, H. Sun and J. Sun, Adv. Mater., 2023, 35, 2307990 CrossRef CAS PubMed.
- X. Yu, Z. Wang, Z. Li, X. Fan and T. Liu, Chem. Mater., 2024, 36, 9822–9833 CrossRef CAS.
- K. Xu, K. Shen, J. Yu, Y. Yang, Y. Wei, P. Lin, Q. Zhang, C. Xiao, Y. Zhang and Y. Cheng, Chem. Mater., 2022, 34, 3311–3322 CrossRef CAS.
- X. Guo, Y. Dong, J. Qin, Q. Zhang, H. Zhu and S. Zhu, Adv. Mater., 2024, 2312816 Search PubMed.
- C. Yang and Z. Suo, Nat. Rev. Mater., 2018, 3, 125–142 CrossRef CAS.
- E. Zhang, R. Bai, X. P. Morelle and Z. Suo, Soft Matter, 2018, 14, 3563–3571 RSC.
- T. Baumberger, C. Caroli and D. Martina, Nat. Mater., 2006, 5, 552–555 CrossRef CAS PubMed.
- J. P. Gong, Science, 2014, 344, 161–162 CrossRef CAS PubMed.
- T. Nakajima, H. Furukawa, Y. Tanaka, T. Kurokawa, Y. Osada and J. P. Gong, Macromolecules, 2009, 42, 2184–2189 CrossRef CAS.
- J. P. Gong, Soft Matter, 2010, 6, 2583–2590 RSC.
- J. Yang, K. Li, C. Tang, Z. Liu, J. Fan, G. Qin, W. Cui, L. Zhu and Q. Chen, Adv. Funct. Mater., 2022, 32, 2110244 CrossRef CAS.
- Y. Zheng, R. Kiyama, T. Matsuda, K. Cui, X. Li, W. Cui, Y. Guo, T. Nakajima, T. Kurokawa and J. P. Gong, Chem. Mater., 2021, 33, 3321–3334 CrossRef.
- Q. Chen, L. Zhu, C. Zhao, Q. Wang and J. Zheng, Adv. Mater., 2013, 25, 4171–4176 CrossRef CAS PubMed.
- S. Naficy, J. M. Razal, P. G. Whitten, G. G. Wallace and G. M. Spinks, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 423–430 CrossRef CAS.
- T. Matsuda, T. Nakajima and J. P. Gong, Chem. Mater., 2019, 31, 3766–3776 CrossRef CAS.
- J. Murai, T. Nakajima, T. Matsuda, K. Tsunoda, T. Nonoyama, T. Kurokawa and J. P. Gong, Polymer, 2019, 178, 121686 CrossRef.
- C. Jiang, Y. Mai, W. Li and B. Liao, Macromol. Chem. Phys., 2020, 221, 1900516 CrossRef CAS.
- C. H. Yang, M. X. Wang, H. Haider, J. H. Yang, J.-Y. Sun, Y. M. Chen, J. Zhou and Z. Suo, ACS Appl. Mater. Interfaces, 2013, 5, 10418–10422 CrossRef CAS PubMed.
- K. Chen, Y. Feng, Y. Zhang, L. Yu, X. Hao, F. Shao, Z. Dou, C. An, Z. Zhuang and Y. Luo, ACS Appl. Mater. Interfaces, 2019, 11, 36458–36468 CrossRef CAS PubMed.
- R. Zhu, D. Zhu, Z. Zheng and X. Wang, Nat. Commun., 2024, 15, 1344 CrossRef CAS PubMed.
- S. Wang, Y. Chen, Y. Sun, Y. Qin, H. Zhang, X. Yu and Y. Liu, Commun. Mater., 2022, 3, 2 CrossRef CAS.
- Z. J. Wang, J. Jiang, Q. Mu, S. Maeda, T. Nakajima and J. P. Gong, J. Am. Chem. Soc., 2022, 144, 3154–3161 CrossRef CAS PubMed.
- Y. Ren and X. Dong, Prog. Polym. Sci., 2024, 101890 CrossRef CAS.
- Z. Li, Y. L. Zhu, W. Niu, X. Yang, Z. Jiang, Z. Y. Lu, X. Liu and J. Sun, Adv. Mater., 2021, 33, 2101498 CrossRef CAS PubMed.
- H. J. Zhang, L. Wang, X. Wang, Q. Han and X. You, Soft Matter, 2020, 16, 4723–4727 RSC.
- L. Chen, W. You, J. Wang, X. Yang, D. Xiao, H. Zhu, Y. Zhang, G. Li, W. Yu and J. L. Sessler, J. Am. Chem. Soc., 2023, 146, 1109–1121 CrossRef PubMed.
- H. Zhang, W. Niu and S. Zhang, ACS Appl. Mater. Interfaces, 2018, 10, 32640–32648 CrossRef CAS PubMed.
- J. Wu, F. Zeng, Z. Fan, S. Xuan, Z. Hua and G. Liu, Adv. Funct. Mater., 2024, 2410518 CrossRef CAS.
- J. Chen, Y. Gao, L. Shi, W. Yu, Z. Sun, Y. Zhou, S. Liu, H. Mao, D. Zhang and T. Lu, Nat. Commun., 2022, 13, 4868 CrossRef CAS PubMed.
- H. Fan, J. Wang and Z. Jin, Macromolecules, 2018, 51, 1696–1705 CrossRef CAS.
- J.-M. Park, S. Lim and J.-Y. Sun, Soft Matter, 2022, 18, 6487–6510 RSC.
- Y. Huang, L. Xiao, J. Zhou, T. Liu, Y. Yan, S. Long and X. Li, Adv. Funct. Mater., 2021, 31, 2103917 CrossRef CAS.
- G. A. Lawrance, Introduction to coordination chemistry, John Wiley & Sons, 2013 Search PubMed.
- C.-H. Li, C. Wang, C. Keplinger, J.-L. Zuo, L. Jin, Y. Sun, P. Zheng, Y. Cao, F. Lissel and C. Linder, Nat. Chem., 2016, 8, 618–624 CrossRef CAS PubMed.
- H. Park, T. Kang, H. Kim, J.-C. Kim, Z. Bao and J. Kang, Nat. Commun., 2023, 14, 5026 CrossRef CAS PubMed.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. Guan, P. B. Messersmith and N. Holten-Andersen, Nat. Mater., 2015, 14, 1210–1216 CrossRef CAS PubMed.
- J.-C. Lai, X.-Y. Jia, D.-P. Wang, Y.-B. Deng, P. Zheng, C.-H. Li, J.-L. Zuo and Z. Bao, Nat. Commun., 2019, 10, 1164 CrossRef PubMed.
- W. Li, L. Li, Z. Liu, S. Zheng, Q. Li and F. Yan, Adv. Mater., 2023, 35, 2301383 CrossRef CAS PubMed.
- S. Krause, J. Macromol. Sci., Rev. Polym. Technol., 1972, 7, 251–314 CrossRef CAS.
- M. Shaw, J. Appl. Polym. Sci., 1974, 18, 449–472 CrossRef CAS.
- F. Zhu, S. Feng, Z. Wang, Z. Zuo, S. Zhu, W. Yu, Y. N. Ye, M. An, J. Qian and Z. L. Wu, Macromolecules, 2023, 56, 5881–5890 CrossRef CAS.
- L. Wang, L. Guo, K. Zhang, Y. Xia, J. Hao and X. Wang, Angew. Chem., Int. Ed., 2023, 62, e202301762 CrossRef CAS PubMed.
- C. Fernández-Rico, S. Schreiber, H. Oudich, C. Lorenz, A. Sicher, T. Sai, V. Bauernfeind, S. Heyden, P. Carrara and L. D. Lorenzis, Nat. Mater., 2024, 23, 124–130 CrossRef PubMed.
- X. Liang, G. Chen, S. Lin, J. Zhang, L. Wang, P. Zhang, Z. Wang, Z. Wang, Y. Lan and Q. Ge, Adv. Mater., 2021, 33, 2102011 CrossRef CAS PubMed.
- M. Wang, J. Bai, K. Shao, W. Tang, X. Zhao, D. Lin, S. Huang, C. Chen, Z. Ding and J. Ye, Int. J. Polym. Sci., 2021, 2021, 2225426 Search PubMed.
- N. A. Peppas and E. W. Merrill, J. Polym. Sci., Polym. Chem. Ed., 1976, 14, 441–457 CrossRef CAS.
- N. A. Peppas and E. W. Merrill, J. Biomed. Mater. Res., 1977, 11, 423–434 CrossRef CAS PubMed.
- S. Lin, J. Liu, X. Liu and X. Zhao, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 10244–10249 CrossRef CAS PubMed.
- G. Wei, Y. Kudo, T. Matsuda, Z. J. Wang, Q. F. Mu, D. R. King, T. Nakajima and J. P. Gong, Mater. Horiz., 2023, 10, 4882–4891 RSC.
- M. Du, H. A. Houck, Q. Yin, Y. Xu, Y. Huang, Y. Lan, L. Yang, F. E. Du Prez and G. Chang, Nat. Commun., 2022, 13, 3231 CrossRef PubMed.
- Z. Wang, X. Zheng, T. Ouchi, T. B. Kouznetsova, H. K. Beech, S. Av-Ron, T. Matsuda, B. H. Bowser, S. Wang and J. A. Johnson, Science, 2021, 374, 193–196 CrossRef CAS PubMed.
- S. Wang, Y. Hu, T. B. Kouznetsova, L. Sapir, D. Chen, A. Herzog-Arbeitman, J. A. Johnson, M. Rubinstein and S. L. Craig, Science, 2023, 380, 1248–1252 CrossRef CAS PubMed.
- C. Yang, T. Yin and Z. Suo, J. Mech. Phys. Solids, 2019, 131, 43–55 CrossRef CAS.
- Y. Akagi, T. Matsunaga, M. Shibayama, U.-I. Chung and T. Sakai, Macromolecules, 2010, 43, 488–493 CrossRef CAS.
- T. Sakai, Polym. J., 2014, 46, 517–523 CrossRef CAS.
- T. Matsunaga, T. Sakai, Y. Akagi, U.-I. Chung and M. Shibayama, Macromolecules, 2009, 42, 1344–1351 CrossRef CAS.
- K. Fujii, H. Asai, T. Ueki, T. Sakai, S. Imaizumi, U.-I. Chung, M. Watanabe and M. Shibayama, Soft Matter, 2012, 8, 1756–1759 RSC.
- T. Sakai, Y. Akagi, T. Matsunaga, M. Kurakazu, U. I. Chung and M. Shibayama, Macromol. Rapid Commun., 2010, 31, 1954–1959 CrossRef CAS PubMed.
- X. Li, S. Nakagawa, Y. Tsuji, N. Watanabe and M. Shibayama, Sci. Adv., 2019, 5, eaax8647 CrossRef CAS PubMed.
- Y. J. Liu, L. H. Fu, S. Liu, L. Y. Meng, Y. Y. Li and M. G. Ma, J. Mater. Chem. B, 2016, 4, 4847–4854 RSC.
- C. M. Hartquist, S. Lin, J. H. Zhang, S. Wang, M. Rubinstein and X. Zhao, Sci. Adv., 2023, 9, eadj0411 CrossRef CAS PubMed.
- S. Nakagawa, D. Aoki, Y. Asano and N. Yoshie, Adv. Mater., 2023, 35, e2301124 CrossRef PubMed.
- C. M. Hartquist, B. X. Li, J. H. Zhang, Z. H. Yu, G. X. Lv, J. Shin, S. V. Boriskina, G. Chen, X. H. Zhao and S. T. Lin, Nat. Commun., 2024, 15, 5590 CrossRef CAS PubMed.
- H. Kamata, Y. Akagi, Y. Kayasuga-Kariya, U. I. Chung and T. Sakai, Science, 2014, 343, 873–875 CrossRef CAS PubMed.
- S. Schlögl, M.-L. Trutschel, W. Chassé, G. Riess and K. Saalwächter, Macromolecules, 2014, 47, 2759–2773 CrossRef.
- D. Li, W. Zhan, W. Zuo, L. Li, J. Zhang, G. Cai and Y. Tian, Chem. Eng. J., 2022, 450, 138417 CrossRef CAS.
- Y. Feng, S. Wang, Y. Li, W. Ma, G. Zhang, M. Yang, H. Li, Y. Yang and Y. Long, Adv. Funct. Mater., 2023, 33, 2211027 CrossRef CAS.
- J. Kim, G. Zhang, M. Shi and Z. Suo, Science, 2021, 374, 212–216 CrossRef CAS PubMed.
- Y. Li, X. Feng, C. Sui, J. Xu, W. Zhao and S. Yan, Chem. Eng. J., 2024, 479, 147689 CrossRef CAS.
- M. Shi, J. Kim, G. Nian and Z. Suo, Extreme Mech. Lett., 2023, 59, 101953 CrossRef.
- P. Hu, J. Madsen and A. L. Skov, Nat. Commun., 2022, 13, 370 CrossRef CAS PubMed.
- P. Zhou, W. Zhan, S. Shen, H. Zhang, Z. Zou and X. Lyu, Adv. Funct. Mater., 2024, 2402952 CrossRef CAS.
- D. Zhong, Z. Wang, J. Xu, J. Liu, R. Xiao, S. Qu and W. Yang, Nat. Commun., 2024, 15, 5896 CrossRef CAS PubMed.
- C. Norioka, Y. Inamoto, C. Hajime, A. Kawamura and T. Miyata, NPG Asia Mater., 2021, 13, 34 CrossRef CAS.
- Y. Kamiyama, R. Tamate, T. Hiroi, S. Samitsu, K. Fujii and T. Ueki, Sci. Adv., 2022, 8, eadd0226 CrossRef CAS PubMed.
- A. Saruwatari, Y. Kamiyama, A. Kawamura, T. Miyata, R. Tamate and T. Ueki, Soft Matter, 2024, 20, 7566–7572 RSC.
- Q. He, Z. Chang, Y. Zhong, S. Chai, C. Fu, S. Liang, G. Fang and A. Pan, ACS Energy Lett., 2023, 8, 5253–5263 CrossRef CAS.
- Z. Shen, Y. Liu, Z. Li, Z. Tang, J. Pu, L. Luo, Y. Ji, J. Xie, Z. Shu and Y. Yao, Adv. Funct. Mater., 2024, 2406620 CrossRef.
- A. P. Dhand, M. D. Davidson, H. M. Zlotnick, T. J. Kolibaba, J. P. Killgore and J. A. Burdick, Science, 2024, 385, 566–572 CrossRef CAS PubMed.
- Y. Okumura and K. Ito, Adv. Mater., 2001, 13, 485–487 CrossRef CAS.
- T. Karino, Y. Okumura, C. Zhao, T. Kataoka, K. Ito and M. Shibayama, Macromolecules, 2005, 38, 6161–6167 CrossRef CAS.
- A. Bin Imran, K. Esaki, H. Gotoh, T. Seki, K. Ito, Y. Sakai and Y. Takeoka, Nat. Commun., 2014, 5, 5124 CrossRef CAS PubMed.
- L. Feng, S. S. Jia, Y. Chen and Y. Liu, Chem. – Eur. J., 2020, 26, 14080–14084 CrossRef CAS PubMed.
- L. Jiang, C. Liu, K. Mayumi, K. Kato, H. Yokoyama and K. Ito, Chem. Mater., 2018, 30, 5013–5019 CrossRef CAS.
- R. Du, T. Bao, T. Zhu, J. Zhang, X. Huang, Q. Jin, M. Xin, L. Pan, Q. Zhang and X. Jia, Adv. Funct. Mater., 2023, 33, 2212888 CrossRef CAS.
- W. Li, X. Wang, Z. Liu, X. Zou, Z. Shen, D. Liu, L. Li, Y. Guo and F. Yan, Nat. Mater., 2024, 23, 131–138 CrossRef CAS PubMed.
- H. Gotoh, C. Liu, A. B. Imran, M. Hara, T. Seki, K. Mayumi, K. Ito and Y. Takeoka, Sci. Adv., 2018, 4, eaat7629 CrossRef CAS PubMed.
- Z. Xu, J. Lu, D. Lu, Y. Li, H. Lei, B. Chen, W. Li, B. Xue, Y. Cao and W. Wang, Nat. Commun., 2024, 15, 4895 CrossRef CAS PubMed.
- S. Y. Zheng, C. Liu, L. Jiang, J. Lin, J. Qian, K. Mayumi, Z. L. Wu, K. Ito and Q. Zheng, Macromolecules, 2019, 52, 6748–6755 CrossRef CAS.
- K. Hashimoto, T. Shiwaku, H. Aoki, H. Yokoyama, K. Mayumi and K. Ito, Sci. Adv., 2023, 9, eadi8505 CrossRef CAS PubMed.
- C. Liu, N. Morimoto, L. Jiang, S. Kawahara, T. Noritomi, H. Yokoyama, K. Mayumi and K. Ito, Science, 2021, 372, 1078–1081 CrossRef CAS PubMed.
- Z. Zhang, W. Wang, Y. Jiang, Y.-X. Wang, Y. Wu, J.-C. Lai, S. Niu, C. Xu, C.-C. Shih and C. Wang, Nature, 2022, 603, 624–630 CrossRef CAS PubMed.
- Y. Bai, W. Li, Y. Tie, Y. Kou, Y. X. Wang and W. Hu, Adv. Mater., 2023, 35, 2303245 CrossRef CAS PubMed.
- D. Yang, F. Ge, M. Tian, N. Ning, L. Zhang, C. Zhao, K. Ito, T. Nishi, H. Wang and Y. Luan, J. Mater. Chem. A, 2015, 3, 9468–9479 RSC.
- Y. Jiang, Z. Zhang, Y.-X. Wang, D. Li, C.-T. Coen, E. Hwaun, G. Chen, H.-C. Wu, D. Zhong and S. Niu, Science, 2022, 375, 1411–1417 CrossRef CAS PubMed.
- M. Tang, D. Zheng, J. Samanta, E. H. Tsai, H. Qiu, J. A. Read and C. Ke, Chem, 2023, 9, 3515–3531 CAS.
- J. M. Fernandez and H. Li, Science, 2004, 303, 1674–1678 CrossRef CAS PubMed.
- Y. Cao, T. Yoo, S. Zhuang and H. Li, J. Mol. Biol., 2008, 378, 1132–1141 CrossRef CAS PubMed.
- J. Fang, A. Mehlich, N. Koga, J. Huang, R. Koga, X. Gao, C. Hu, C. Jin, M. Rief and J. Kast, Nat. Commun., 2013, 4, 2974 CrossRef PubMed.
- L. Fu, L. Li, Q. Bian, B. Xue, J. Jin, J. Li, Y. Cao, Q. Jiang and H. Li, Nature, 2023, 618, 740–747 CrossRef CAS PubMed.
- L. Zeng, M. Song, J. Gu, Z. Xu, B. Xue, Y. Li and Y. Cao, Biomimetics, 2019, 4, 36 CrossRef CAS PubMed.
- Y. Zhang, Y. Wang, Y. Guan and Y. Zhang, Nat. Commun., 2022, 13, 6671 CrossRef CAS PubMed.
- P. Liu, Y. Zhang, Y. Guan and Y. Zhang, Adv. Mater., 2023, 35, 2210021 CrossRef CAS PubMed.
- H. Lei, L. Dong, Y. Li, J. Zhang, H. Chen, J. Wu, Y. Zhang, Q. Fan, B. Xue and M. Qin, Nat. Commun., 2020, 11, 4032 CrossRef CAS PubMed.
- B. Xue, Z. Bashir, Y. Guo, W. Yu, W. Sun, Y. Li, Y. Zhang, M. Qin, W. Wang and Y. Cao, Nat. Commun., 2023, 14, 2583 CrossRef CAS PubMed.
- T. Wang, Y. Li, J. Wang, Y. Xu, Y. Chen, Z. Lu, W. Wang, B. Xue, Y. Li and Y. Cao, ACS Biomater. Sci. Eng., 2020, 6, 6800–6807 CrossRef CAS PubMed.
- W. Sun, T. Duan, Y. Cao and H. Li, Biomacromolecules, 2019, 20, 4199–4207 CrossRef CAS PubMed.
- B. Xue, M. Qin, T. Wang, J. Wu, D. Luo, Q. Jiang, Y. Li, Y. Cao and W. Wang, Adv. Funct. Mater., 2016, 26, 9053–9062 CrossRef CAS.
- T. J. Hubin and D. H. Busch, Coord. Chem. Rev., 2000, 200, 5–52 CrossRef.
- J.-F. Ayme, J. E. Beves, D. A. Leigh, R. T. McBurney, K. Rissanen and D. Schultz, Nat. Chem., 2012, 4, 15–20 CrossRef CAS PubMed.
- F. B. Cougnon, K. Caprice, M. Pupier, A. Bauzá and A. Frontera, J. Am. Chem. Soc., 2018, 140, 12442–12450 CrossRef CAS PubMed.
- S. D. Fielden, D. A. Leigh and S. L. Woltering, Angew. Chem., Int. Ed., 2017, 56, 11166–11194 CrossRef CAS PubMed.
- D. A. Leigh, J.-F. Lemonnier and S. L. Woltering, Angew. Chem., Int. Ed., 2018, 57, 12212–12214 CrossRef CAS PubMed.
- J.-X. Li, S. Wu, L.-L. Hao, Q.-L. Lei and Y.-Q. Ma, Sci. Adv., 2024, 10, eadr0716 CrossRef CAS PubMed.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707 CrossRef CAS.
- G. A. Parada and X. H. Zhao, Soft Matter, 2018, 14, 5186–5196 RSC.
- Z. Q. Song, Z. J. Wang and S. Q. Cai, Mech. Mater., 2021, 153, 103687 CrossRef.
- J. J. Hernandez, S. P. Keyser, A. L. Dobson, A. S. Kuenstler and C. N. Bowman, Macromolecules, 2024, 57, 1426–1437 CrossRef CAS.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- D. J. Bischoff, T. Lee, K. S. Kang, J. Molineux, W. O. Parker, J. Pyun and M. E. Mackay, Nat. Commun., 2023, 14, 7553 CrossRef CAS PubMed.
- M. Kim, C. Lee, K. Jeon, J. Y. Lee, Y.-J. Kim, J. G. Lee, H. Kim, M. Cho and D.-N. Kim, Nature, 2023, 619, 78–86 CrossRef CAS PubMed.
- B. Saccà and C. M. Niemeyer, Angew. Chem., Int. Ed., 2012, 51, 58–66 CrossRef PubMed.
- A. E. Marras, L. Zhou, H.-J. Su and C. E. Castro, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 713–718 CrossRef CAS PubMed.
- A. C. Yu, H. Chen, D. Chan, G. Agmon, L. M. Stapleton, A. M. Sevit, M. W. Tibbitt, J. D. Acosta, T. Zhang and P. W. Franzia, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14255–14260 CrossRef CAS PubMed.
- J. Cao, X. Zhao and L. Ye, Ind. Eng. Chem. Res., 2020, 59, 10705–10715 CrossRef CAS.
- J. Li, H. Liu, C. Wang and G. Huang, RSC Adv., 2017, 7, 35311–35319 RSC.
- Z. Fang, H. Mu, Z. Sun, K. Zhang, A. Zhang, J. Chen, N. Zheng, Q. Zhao, X. Yang, F. Liu, J. Wu and T. Xie, Nature, 2024, 631, 783–788 CrossRef CAS PubMed.
- X. Kuang, J. T. Wu, K. J. Chen, Z. Zhao, Z. Ding, F. J. Y. Hu, D. N. Fang and H. J. Qi, Sci. Adv., 2019, 5, eaav5790 CrossRef CAS PubMed.
- M. A. Skylar-Scott, J. Mueller, C. W. Visser and J. A. Lewis, Nature, 2019, 575, 330–335 CrossRef CAS PubMed.
Footnote |
| † These authors contribute to this work equally. |
| This journal is © The Royal Society of Chemistry 2025 |