Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Urea and salt induced modulation of protein interactions: implications for crystallization and liquid–liquid phase separation†
M.
Madani
 a,
T.
Hamacher
a and
F.
Platten
a,
T.
Hamacher
a and
F.
Platten
 *ab
*ab
aFaculty of Mathematics and Natural Sciences, Heinrich Heine University Düsseldorf, 40225 Düsseldorf, Germany. E-mail: florian.platten@hhu.de
bInstitute of Biological Information Processing IBI-4, Forschungszentrum Jülich, 52428 Jülich, Germany
First published on 13th February 2025
Abstract
Urea is a well-known protein denaturant if added at high concentrations. The unfolding of proteins induced by urea is typically attributed to specific mechanisms; however, the influence of urea on protein–protein interactions, which can give rise to protein crystallization and liquid–liquid phase separation (LLPS), remains less understood. In this study, we examine the modulation of protein–protein interactions by urea at non-denaturing concentrations, in combination with sodium chloride. The effects of these additives on the state diagram and protein–protein interactions in lysozyme solutions are analyzed using optical microscopy and small-angle X-ray scattering (SAXS), respectively. Our findings indicate that the addition of urea diminishes net protein attractions, while the introduction of salt enhances them, resulting in respective shifts of the state boundaries. Moreover, the protein–protein interactions can be effectively characterized by a Derjaguin–Landau–Verwey–Overbeek (DLVO) potential. The impact of urea on these interactions can thus be explained entirely by alterations in the dielectric properties of the solution.
1 Introduction
Protein condensation is a fundamental process in both biology and materials science,1–6 playing a critical role in various phenomena, including crystallization,7 fibril formation,8,9 and liquid–liquid phase separation (LLPS).10 Condensed protein states are essential not only in biological processes such as protein aggregation, cellular organization, and disease (e.g., Alzheimer's, Parkinson's, and amyloidosis), but also offer significant potential for applications in biotechnology, materials science, and drug discovery. The ability to control and manipulate protein condensation, for example through specific solution conditions11,12 or the application of external fields,13,14 holds promise for designing novel biomaterials, developing protein-based therapeutics, and advancing our understanding of disease-related protein aggregation.Protein crystallization, one of the most well-studied forms of protein condensation,15,16 is a cornerstone technique in structural biology that enables the determination of atomic-level structures of proteins.17 This process requires the precise arrangement of protein molecules into an ordered three-dimensional lattice. Despite its importance, the search for optimal crystallization conditions remains largely a trial-and-error process.18 This challenge arises partly from the complex behaviour of proteins in solution, where intermolecular interactions can vary significantly depending on factors such as protein type, solvent conditions, and the presence of additives. A more comprehensive understanding of the physical principles governing protein crystallization would be very valuable for the optimization of crystallization protocols, thereby reducing the time and resources spent on empirical experimentation.7
To identify conditions that promote crystallization, researchers often modify the solution environment by introducing various solution additives or precipitants.19–21 These additives can affect protein solubility, charge distribution, and intermolecular interactions, which, in turn, may drive the formation of ordered aggregates or crystals. While many additives, including salts, polyethylene glycol (PEG), and organic solvents, have been extensively studied for their impact on protein crystallization, urea has received comparatively less attention in this context.22 Urea, a small organic molecule commonly found in biological systems, is a well-known protein denaturant at high concentrations and has been widely used to study protein folding and unfolding.23–35 Although the precise mechanism remains a subject of ongoing debate, urea is generally thought to disrupt the network of non-covalent interactions – such as hydrogen bonds, hydrophobic forces, and electrostatic interactions – that stabilize protein three-dimensional structure, thereby promoting protein unfolding. Additionally, urea preferentially binds to proteins, altering their solvation properties and hydration shell, which in turn might affect overall protein stability.
The effects of urea at lower, sub-denaturing concentrations are not fully understood. At these concentrations, urea may still significantly modulate protein–protein interactions, potentially affecting processes such as protein aggregation, crystallization, and phase separation. Although the exact mechanisms remain unclear, they may involve changes in protein solubility, modifications to the dielectric properties of the solution, or subtle alterations in hydrophobic and electrostatic interactions.
Urea has been shown to influence adsorbed protein layers by reducing the amount of protein bound to surfaces.36,37 While the bulk concentration of protein solutions adsorbing to an interface is typically low, the adsorbed protein films are effectively two-dimensional and often behave as dense systems with high packing densities, where protein–protein interactions likely play a significant role. For instance, studies have demonstrated that the interfacial affinity of albumins is indicative of the phase behaviour and interactions in bulk solution.38,39 Consequently, the observed reduction in surface excess upon urea addition suggests that urea may modulate protein–protein interactions even in these condensed states. This implies that the effects of urea in bulk solution could parallel those observed in confined systems, where subtle changes in intermolecular forces may influence the onset of crystallization or phase separation.
In this study, we systematically investigate the effects of urea and salt on the state diagram of lysozyme, a well-established model system for studying protein crystallization and phase behaviour.40,41 We identify solution conditions that promote protein crystallization and phase separation, and examine how urea and salt affect the state boundaries. Using small-angle X-ray scattering (SAXS), we analyze the protein–protein interactions that govern the formation of these condensed states. By determining the second virial coefficient (B2), we provide a quantitative measure of protein–protein interactions. This parameter has been used as a predictor for crystallization and LLPS.42,43 Through the combination of the state diagram with SAXS data on protein–protein interactions, we offer a comprehensive picture of the effects of urea and salt on protein phase behaviour. To gain a deeper understanding of how urea influences these interactions, we apply the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory, a well-established model for colloidal interactions. This approach allows us to investigate how urea influences the balance between attractive and repulsive forces between proteins in solution. The B2 values derived from the DLVO potential, accounting for the dielectric properties of the urea–water mixtures and the electrostatic screening effects due to salt, show quantitative agreement with the experimentally observed data. By combining complementary experimental techniques with theoretical calculations, this study provides a detailed understanding of the physical principles underlying protein phase behaviour, enhances the mechanistic understanding of the impact of urea on protein–protein interactions, and contributes to the development of improved strategies for protein crystallization.
The article is organized as follows: Section 2 describes the materials and methods, Section 3 presents and discusses the results, and Section 4 provides a summary of the findings and their implications.
2 Experimental methods
The sample preparation procedure is outlined first (Section 2.1), followed by a description of the method used to investigate the condensed states of the protein solutions by light microscopy (Section 2.2). The instrumental setup for SAXS measurements and the data analysis methodology are presented in Sections 2.3 and 2.4, respectively.2.1 Sample preparation
Lysozyme from Sigma-Aldrich (prod. no. L6876) was used for the light microscopy experiments, while lysozyme from Roche Diagnostics (prod. no. 10837059001) was used in the X-ray scattering experiments, where higher sample purity was required. Previous studies on the state diagram and interactions of lysozyme from different suppliers have yielded consistent results.44,45 Sodium chloride (NaCl; Fisher Scientific, prod. no. S/3160/60), urea (Merck, prod. no. 1.08488; Sigma, prod. no. 33247), and sodium acetate (NaAc; Merck, prod. no. 1.06268) were used as received.Ultrapure water with a resistivity of 18.2 MΩ cm was used to prepare all buffer solutions. Lysozyme powder was solubilized in a 50 mM sodium acetate (NaAc) buffer, and the pH was adjusted to 4.5 by incrementally adding hydrochloric acid. At this pH, lysozyme carries a net positive charge of Z = +11.4 elementary charges. The protein solution, with an initial concentration between c = 50 mg mL−1 and c = 80 mg mL−1, was filtered several times using an Acrodisc syringe filter (Pall, prod. no. 4611) with a pore size of 0.1 μm, designed for minimal protein binding. This filtration step removed impurities and undissolved protein aggregates. In cases requiring a more concentrated stock solution, the protein solution was further concentrated using a stirred ultrafiltration cell (Amicon, Millipore, prod. no. 5121) equipped with an Omega 10 kDa membrane disc filter (Pall, prod. no. OM010025). The resulting retentate was used as the concentrated protein stock solution. The protein concentration in the stock solution after (ultra)filtration was determined using UV/Vis absorption spectroscopy and refractometry, following procedures outlined in previous work.46 The concentrations of salt and urea stock solutions were carefully measured using refractometry and compared with literature data.24,47 Due to the hygroscopic nature of urea, precise measurements were particularly critical when preparing highly concentrated urea stock solutions. Samples were prepared by accurately pipetting defined volumes of buffer, protein, salt, and urea stock solutions. To ensure data reliability and reproducibility, samples were prepared and measured several times under selected solution conditions. All measurements were conducted at ambient temperature, (22 ± 2) °C.
2.2 Determination of the state diagram by optical microscopy and visual inspection
The condensed state of the protein solution is determined based on its microscopic morphology and macroscopic appearance, as in previous studies.48,49The microscopic morphologies were observed using bright-field optical microscopy. Custom-designed microscopy sample cells consisted of a microscope slide and three cover slips, as described previously.50 Two cover slips served as spacers, creating a gap between them, while the third cover slip was positioned on top to form a narrow capillary sample chamber. The sample solution was then introduced into the chamber, and the sample cell was sealed with UV-curing adhesive. The resulting sample cell was mounted onto the stage of a Nikon Eclipse 80i microscope, equipped with a Pixellink PL-B741F camera. The samples were observed for several days after preparation.
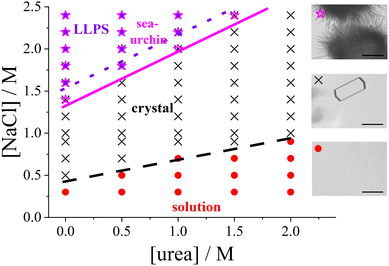
The condensed state of the protein solution is classified as follows: a homogeneous solution was characterized by the absence of micron-sized particles. In contrast, the presence of tetragonal crystals and spherulitic structures, resembling sea urchins, indicated protein crystallization in the presence of sodium chloride (NaCl).51,52 Under the experimental conditions, crystal formation was observed after a period ranging from several minutes to a few days. LLPS was identified through visual inspection, as samples exhibiting LLPS became cloudy immediately after preparation.48,53
2.3 Small-angle X-ray scattering: instrumentation
SAXS was employed to analyze the form factor and structure factor of the samples.54,55 The SAXS experiments were performed at the laboratory facility of the Center for Structural Studies at Heinrich Heine University Düsseldorf, Germany, using a XENOCS 2.0 instrument equipped with a Pilatus3 300 K detector. The protein and buffer solutions were introduced into a thin flow-through capillary cell for measurements. Protein samples were analyzed immediately after preparation. Acquisition times were set to 60 minutes for dilute solutions and 5 minutes for concentrated solutions. To improve statistics, several consecutive measurements recorded before the onset of crystallization were averaged. The obtained data were background-subtracted and normalized to an absolute scale using glassy carbon as a standard reference. The scattered intensity was plotted as a function of the scattering vector magnitude, Q = (4π/λ0)sin(θ), where λ0 = 1.54 Å is the X-ray wavelength, and 2θ is the angle between the incident and scattered X-rays. Calibration of Q was performed using silver behenate. The experimentally accessible Q-range was 0.012 ≤ Q/Å−1 ≤ 0.63.2.4 Small-angle X-ray scattering: data analysis
The data analysis strategy used in this study closely follows the approach outlined in our previous studies.45,56 Protein molecules typically exhibit anisotropic shapes, and X-ray crystallography has shown that lysozyme approximates a prolate ellipsoid. In a monodisperse solution of particles with minimal anisotropy, the interactions can be considered orientation-independent. Consequently, the absolute scattered intensity I(Q) is described using the decoupling approximation:54,57,58| I(Q) = KcMP(Q)Seff(Q), | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 g mol−1, and the contrast factor K, which is proportional to (Δρ)2, where Δρ represents the difference in electron density between the proteins and the solvent.59,60
320 g mol−1, and the contrast factor K, which is proportional to (Δρ)2, where Δρ represents the difference in electron density between the proteins and the solvent.59,60
The Q-dependence of I(Q) arises from both intra-particle and inter-particle interference effects, which are described by the form factor P(Q) and the structure factor S(Q), respectively. The form factor P(Q) is defined as the average of the square of the form factor amplitude A(Q), expressed as P(Q) = 〈A2(Q)〉Ω, where the average is taken over all possible orientations of the particles, indicated by Ω. The effective structure factor is given by the following expression:
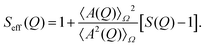 | (2) |
Here, S(Q) represents the structure factor of an effective one-component system.
In very dilute systems, S(Q) ≈ 1, indicating that the Q-dependence of I(Q) is determined by P(Q), which encodes information about the size, shape, and structural characteristics of the individual particles.54 The form factor of folded lysozyme is approximated as a prolate ellipsoid of revolution, defined by its minor and major axes. For the range of urea concentrations studied, the form factor is modelled as an ellipsoid with a semi-minor axis 16.0 Å and an axial ratio of 1.5, consistent with previous reports for the form factor of natively folded lysozyme.45,56 The experimentally determined form factor of proteins in buffer and in 2 M urea is presented in the ESI.†
In concentrated solutions, the structure factor S(Q) reflects the spatial arrangement of particles, providing insights into inter-particle interactions. According to liquid-state theory,61 the interaction potential U(r), where r is the center-to-center distance between particles, is encoded in S(Q). To model experimentally measured S(Q), a theoretical potential is typically assumed, for which an analytical expression for S(Q) is known. The model parameters are determined by fitting the theoretical S(Q) to the experimental data, and once these parameters are obtained, the interaction potential U(r) can be derived.
A common method to quantify the overall effect of the interaction potential is by calculating the second virial coefficient B2. For a spherosymmetric potential U(r), B2 is given by the following integral:
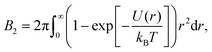 | (3) |
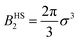 , with σ representing the particle diameter.
, with σ representing the particle diameter.
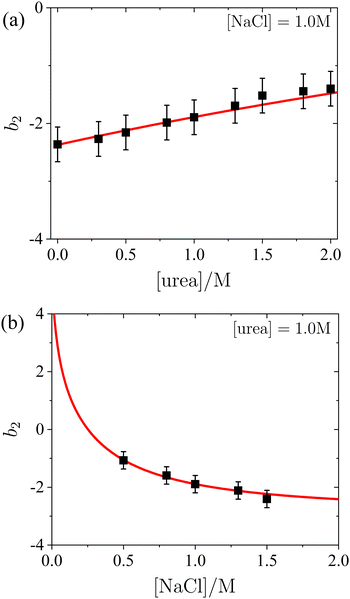
When modeling the structure factor of proteins, protein–protein interactions are often described by a combination of an attractive and a repulsive hard-core Yukawa potential, each with its own range and interaction strength parameters.62–67 However, in protein solutions prone to crystallization, interactions are primarily governed by net attractive forces. In such cases, the simpler adhesive hard-sphere (AHS) model is often preferred, as it allows for a direct determination of b2, depending only on one free parameter (τ) instead of four, as detailed below.
The AHS potential, as proposed by Baxter,68,69 represents a specific limit of the square-well (SW) potential. The SW potential is commonly used to model for systems dominated by short-range attractions.70–73 This potential combines a hard-core repulsion with a range of σ (the particle diameter) and a constant attractive component, which has a depth ε and extends to a distance of λσ from the particle center. In the Baxter limit, the depth ε approaches infinity, and the width (λ − 1)σ becomes infinitesimally small (i.e., λ → 1). This configuration ensures a finite and non-zero contribution to the second virial coefficient B2 (eqn (3)), which is critical for describing inter-particle interactions. The AHS potential is expressed as:
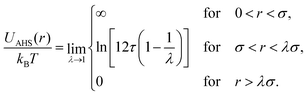 | (4) |
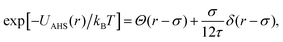 | (5) |
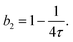 | (6) |
Analytical approximations for the structure factor of adhesive hard spheres, based on the Percus–Yevick closure, have been established in the literature.74–76 These approximations are frequently used to interpret scattering data from systems with short-range attractive interactions,77–79 particularly for proteins.80–82 The AHS structure factor is determined by the effective particle diameter σ, the stickiness parameter τ, and the particle volume fraction ϕ. The effective diameter σ corresponds to the diameter of a sphere that has the same volume as the ellipsoidal particle, as estimated from form-factor modeling in dilute solution. The volume fraction ϕ is directly related to the protein concentration c.46 Therefore, only τ requires fitting to describe the Q-dependence of I(Q).
The scattered intensity I(Q), as described by eqn (1) with a Q-independent prefactor, is analyzed together with a constant scattering background and fitted to the experimentally measured intensity using a least-squares routine. As noted previously,56 background subtraction is particularly sensitive at very low Q-values. At high Q-values, SAXS data become increasingly noisy due to the reduced scattered intensity, resulting in a lower signal-to-noise ratio. Therefore, model fits are systematically compared with experimental data for the range 0.03 ≤ Q/Å−1 ≤ 0.31, ensuring a reliable comparison between the experimental data and model calculations. The choice of the Q-range used in the fits is further justified in the ESI.†
3 Results and discussion
First, we examine the state diagram of lysozyme solutions as a function of urea and salt concentrations (Section 3.1). This is followed by an analysis of SAXS data (Section 3.2), first for constant salt concentration with various urea concentrations, and then for constant urea concentration with various salt concentrations. From the SAXS data, we determine the normalized second virial coefficient b2 as a function of both urea and salt concentrations. Additionally, b2 is calculated using the DLVO theory, incorporating data on the dielectric properties of water–urea solutions, and the calculations are compared with the experimental results (Section 3.3). Finally, we correlate the results for b2 with the state diagram to determine the strength of attractive interactions required for phase transitions such as crystallization or phase separation (Section 3.4).At high molar concentrations, urea is known to denature proteins,23,24,30 but at moderate concentrations, well below the threshold for unfolding, it does not significantly disrupt the native protein structure. In this study, we focus on moderate urea concentrations that do not induce denaturation. The retention of the native protein conformation is supported by two observations, which are further detailed below: first, tetragonal lysozyme crystals formed at all urea concentrations investigated (see Fig. 1), and second, the form factor of the lysozyme solutions was consistently described by the same ellipsoid parameters across all urea concentrations under study (see ESI†). In contrast, denatured proteins are unlikely to form high-quality crystals due to the loss of the specific, stable, and ordered structure necessary for crystallization. The molecular shape of unfolded proteins is expected to resemble a polymeric coil rather than a colloidal particle. At the urea concentrations studied here, we expect that changes in the physicochemical properties of the solvent, which modulate protein–protein interactions, play a more significant role than alterations in protein structures themselves, such as those arising from preferential binding. These solvent-mediated changes are relevant for understanding the protein state diagram and the associated protein–protein interactions.
3.1 Protein state diagram as a function of urea and salt concentrations
Fig. 1 presents the state diagram of lysozyme solutions with a fixed protein concentration of 20 mg mL−1 in an acidic environment (pH 4.5) at room temperature. This protein concentration is moderate, being high enough to promote protein–protein interactions that drive the formation of condensed states, yet not so high as to approach the critical point for phase separation. Therefore, this concentration provides an optimal condition for systematically studying condensation phenomena, such as crystallization. The state diagram is systematically examined as a function of salt and urea concentrations at this fixed protein concentration.Various condensed states are observed, with typical microscope images shown on the right side of Fig. 1. As the salt concentration increases, the solution initially remains homogeneous, followed by the appearance of tetragonal protein crystals coexisting with the solution. At higher salt concentrations, spherulitic (sea urchin-like) crystals emerge, and further increases in salt concentration can induce metastable LLPS, leading to macroscopic turbidity. This topology of the state diagram, which includes a homogeneous solution, a crystal-solution coexistence region, and a metastable LLPS regime, is characteristic of colloidal systems dominated by short-range attractive interactions (e.g., ref. 70,83 or reviews1,7,41).
In the absence of urea, the transition points are consistent with previous studies:48,52,84 tetragonal crystals form at salt concentrations of 0.5 M or higher, spherulitic crystals appear at approximately 1.4 M or higher, and phase separation occurs at salt concentrations of around 1.6 M or higher. This consistency underscores the reproducibility of the salt concentration effect on the formation of the different states.
With the addition of urea, the salt concentration required to induce various phase transitions increases progressively. At 1 M urea, tetragonal crystals form only above 0.9 M NaCl, spherulitic crystals appear at 2.0 M NaCl or higher, and phase separation occurs at 2.2 M or higher. At 2 M urea, crystals form only above 1 M NaCl, and no spherulites or phase separation are observed up to 2.4 M NaCl. The increase in the NaCl concentration required to induce LLPS or spherulite formation is more pronounced than that of the threshold for tetragonal crystal formation.
Interestingly, spherulites are observed under conditions where the solution remains macroscopically transparent. Previous studies (e.g., ref. 51,52) have suggested that spherulites typically form following phase separation. However, other studies (e.g., ref. 85), using specific salts such as nitrate or thiocyanate, have reported that spherulites can also form outside the LLPS region, as observed in this work.
The state boundaries can be interpreted as a measure of the strength of the attractive interactions required to trigger each observed state (see, e.g., ref. 12). As noted previously (e.g., ref. 86,87), the addition of NaCl enhances protein–protein attraction. The increased concentration of NaCl required to induce phase transitions in the presence of urea suggests that urea weakens the net attractive interactions between protein molecules, unlike NaCl. The state diagram suggests that a minimum level of attraction is required for protein crystals to form, with even stronger attractions necessary for the formation of spherulites and LLPS.
3.2 Protein–protein interactions as reflected in scattered X-ray intensity
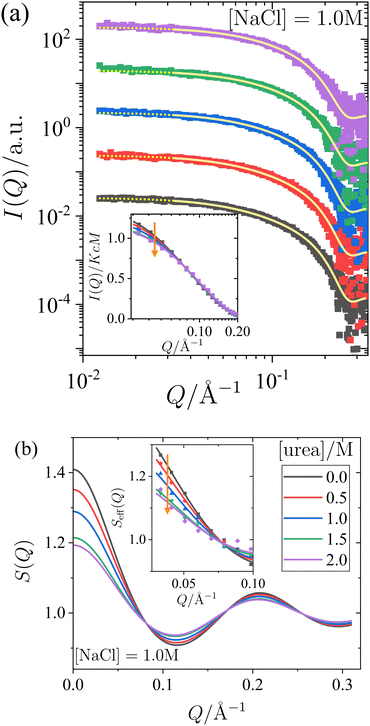
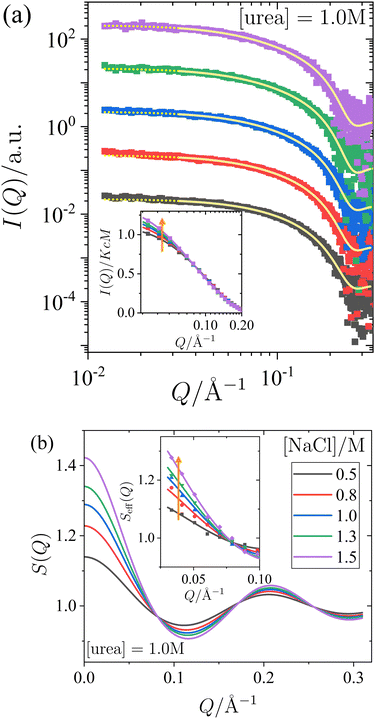
To systematically understand the interactions driving the condensed states observed in the previous section, we present SAXS measurements that provide insights into the structure factor of the solutions under investigation. Two sets of measurements were performed: one with a constant salt concentration of 1.0 M and varying urea concentrations between 0 and 2 M (Fig. 2), and another with a constant urea concentration of 1.0 M and varying salt concentrations between 0.5 M and 1.5 M (Fig. 3). Under most of these conditions, crystallization occurs over time (cf.Fig. 1), but they are far away from the LLPS boundary. The SAXS measurements were performed immediately after sample preparation to ensure that the solutions remained homogeneous throughout the measurement, prior to the onset of crystallization. Since the protein solutions are only moderately concentrated, no significant contributions to the structure factor from off-critical scattering or due to the nonspherical shape of the proteins are expected. Therefore, as confirmed below, it is reasonable to employ approximate analytical models for the structure factor to analyze the scattered intensity under the conditions considered here.In Fig. 2 and 3, panel (a) shows the experimental scattered intensity I(Q) as a function of Q (symbols), along with the corresponding model fits (lines). Panel (b) presents the structure factors S(Q) as a function of Q, derived from the model fits. The I(Q) data presented in Fig. 2a and 3a do not exhibit any distinct features and are very similar, with the primary difference observed in the low-Q behaviour, as particularly evident in the normalized, unshifted I(Q)/KcM data shown in the insets. The differences in the low-Q behaviour are more pronounced in the corresponding structure factors S(Q) shown in Fig. 2b and 3b, and they can be clearly seen in the data expressed as effective structure factors Seff(Q) in the insets. The observation of only small differences in the low-Q part is consistent with expectations for the moderate protein concentration used in this study.
The model fits for I(Q) follow the eqn (1), where the Q-dependence of I(Q) is determined by both the form factor P(Q) and the structure factor S(Q). The parameters of the form factor, modeled as a prolate ellipsoid, are known from measurements of dilute solutions (as detailed in Section 2.4). Therefore, in analyzing the Q-dependence of the SAXS data for concentrated samples, only a single fit parameter, the stickiness parameter τ, needs to be determined. Once the fit is performed and τ is determined, the structure factor (as shown in Fig. 2b and 3b) is calculated analytically for all Q-values based on the fitted model. Although small differences are observed in the data, particularly in the low-Q region, the analysis of the scattered intensity presented in Fig. 2a and 3a remains robust. The model fits adequately describe the data, capturing the low-Q differences, which are reflected in the effective structure factors shown in the insets of Fig. 2b and 3b.
The effects of urea and NaCl on the structure factor S(Q) (Fig. 2b and 3b) are most pronounced at low Q. Under all conditions studied, the proteins exhibit net attractive interactions, as S(Q → 0) > 1 in all cases. An increase in urea concentration leads to a decrease in S(Q) at low Q, corresponding to a reduction in net attractive interactions. In contrast, the addition of NaCl results in an increase in S(Q) at low Q, indicating an enhancement of attractive interactions. These findings are consistent with the interpretation of the effects of urea and salt on the state diagram in Section 3.1, in terms of underlying interactions.
It has been previously noted in studies using X-ray or neutron scattering (e.g., ref. 62,88) that NaCl promotes attractive interactions between proteins, while urea weakens them. However, the combined effects of both additives have as yet not been systematically explored, particularly under the conditions investigated in the state diagram studied in this work. This gap is addressed by the measurements described in this section. Furthermore, as discussed in the next section, model calculations using eqn (6) allow to infer the second virial coefficient b2 for the various solution conditions examined from the SAXS fits.
3.3 The second virial coefficient b2 of proteins as a function of urea and salt concentrations: experimental results and DLVO model description
When the net attractive forces between proteins are sufficiently strong, such as when salt is added, proteins tend to crystallize or undergo phase separation (see Fig. 1). The enhancement of these net attractive forces due to salt is reflected in an increase in the low-Q scattering contribution from the structure factor S(Q), as shown in Fig. 3. Consequently, it is anticipated that the second virial coefficient, b2, will decrease as the salt concentration increases.Conversely, the addition of urea shifts both the crystal-solution and LLPS coexistence curves of lysozyme towards higher salt concentrations (see Fig. 1), indicating a reduction in net attraction. This reduction is further evidenced by a decrease in the low-Q scattering contribution from S(Q), shown in Fig. 2. Therefore, we expect b2 to increase with higher urea concentrations.
To quantitatively assess the relationship between b2 and the concentrations of salt and urea, b2 values were extracted from the SAXS model fits presented in Fig. 2 and 3. The results shown in Fig. 4 indicate a weak, but systematic, increase in b2 with increasing urea content (Fig. 4a, which also includes additional data), alongside a consistent decrease with rising salt concentration (Fig. 4b). These observations are in agreement with the low-Q behaviour of S(Q). The experimental uncertainty in b2 has been previously estimated to be approximately ±0.3 for a similar system.56 The value of b2 in the presence of 1.0 M NaCl but without urea (i.e., the first data point in Fig. 4a) is consistent with previously reported data (e.g., ref. 87 and references therein). A decrease in b2 with increasing salt concentration, similar to the trend in Fig. 4b, has also been observed in earlier studies (e.g., ref. 73,87), though without the presence of urea. Moreover, the ESI† includes an additional SAXS dataset for NaCl alone, without urea (see Fig. S4 of the ESI†). For lysozyme in brine, extensive literature data for b2 are in quantitative agreement with the values obtained from the model fits. This consistency confirms the reliability of the SAXS data and the appropriateness of the analysis approach for inferring b2.
 | ||
| Fig. 4 Normalized second virial coefficient b2 of lysozyme solutions: (a) as a function of urea concentration in the presence of 1.0 M NaCl, and (b) as a function of salt concentration with a fixed urea concentration of 1.0 M. The data (symbols) were obtained from fits shown in Fig. 2 and 3, while the model calculations (lines) are based on DLVO theory, as described in the text. | ||
In order to further understand the mechanisms by which urea and salt modulate the protein–protein interactions, as quantified by b2, the interactions are analyzed using the DLVO model potential. The DLVO theory is widely used to describe the colloidal interactions between charged particles in suspension89 and provides a useful framework for understanding the effective interactions between proteins in solution, particularly in the presence of salt.90–92 However, the presence of urea introduces additional complexities, as urea is known to influence the solvation environment and preferentially bind to proteins. This could alter both the individual proteins and their mutual interactions in ways that are not directly captured by DLVO theory.
The total DLVO potential can be expressed as the sum of three contributions: the hard-sphere potential UHS(r), the screened Coulomb repulsion USC(r), and the attractive van der Waals component UvdW(r):
| UDLVO(r) = UHS(r) + USC(r) + UvdW(r). | (7) |
For r > σp with the particle diameter σp, the screened Coulomb potential USC(r) is defined as described in ref. 86:
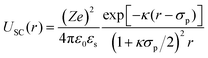 | (8) |
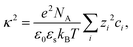 | (9) |
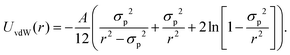 | (10) |
In this equation, A denotes the Hamaker constant, which for two identical particles located within a medium can be estimated using the following equation:89
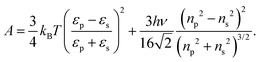 | (11) |
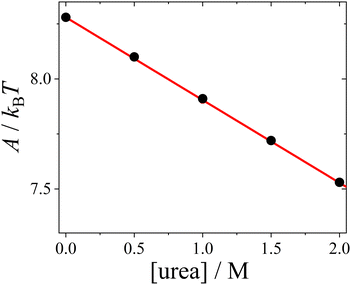 | ||
| Fig. 5 Hamaker constant A (symbols), calculated based on the dielectric solution properties of urea–water mixtures, as a function of urea concentration, with a linear fit (line). | ||
The change in the Hamaker constant A leads to a notable decrease in the magnitude of the attractive van der Waals component UvdW(r) (see ESI† for exemplary plots). Under our conditions, the effect of urea on UvdW(r) is much stronger than its impact on the screened Coulomb repulsion USC(r), which is minimal. The main effect of urea is to shorten the range of the DLVO potential UDLVO(r).
The normalized second virial coefficient, b2, can be calculated using the DLVO potential (eqn (7)) as described in eqn (3). To prevent divergence in the integral, a cut-off length, δ, associated with the Stern layer is employed as the lower limit of integration. This parameter was previously optimized to match light scattering data for b2.97 In the current study, the value of δ was refined by 2% to approximately 0.15 nm, independent of urea and salt concentration. This refinement ensures that the b2 value in the absence of urea, which serves as a reference, is accurately recovered. It is important to note that σp + δ ≈ σ; this indicates that the diameter of the adhesive hard sphere, σ, used in the structure factor modeling is consistent with that of the hard sphere modified by the cut-off layer in the DLVO model. Consequently, the DLVO framework may implicitly incorporate non-DLVO effects98 (e.g., hydration, the hydrophobic effect, and hydrogen bonding) through the choice of δ. The results for b2 derived from the DLVO model are presented in Fig. 4a and b as solid lines. The model predicts that b2 increases monotonically with urea concentration (Fig. 4a) and decreases with salt concentration (Fig. 4b). The model aligns quantitatively with the experimental data represented by symbols. Therefore, the urea-dependent modifications in protein–protein interactions are fully explained by its influence on the dielectric properties of the solution, affecting the Hamaker constant and the screening length, and the effects of salt are contained in κ (eqn (9)).
Although cosolvents can exhibit preferential binding to, or exclusion from, the surface of proteins,99 and the composition of the surface layer can influence protein–protein interactions,100 the DLVO theory successfully predicts the experimental observations of protein–protein interactions in terms of b2 in the presence of both urea and salt. This suggests that electrostatic and van der Waals interactions are the dominant forces governing protein interactions and phase behaviour, and that non-DLVO effects can be effectively accounted for by a constant cut-off length. Consequently, the addition of urea does not significantly alter the overall protein–protein interactions in a way that would require more complex models, such as those accounting for additional interaction forces beyond the simple attractive and repulsive interactions considered in DLVO theory. While it is possible that factors such as preferential binding, patchiness, directionality, asymmetric shapes, charge distributions, or other phenomena have some influence, their impacts are anticipated to be minimal or counterbalancing, as our DLVO model adequately describes the data. Moreover, the addition of glycerol, ethanol, or dimethyl sulfoxide, which also reduces the permittivity of the solution, can be similarly interpreted within the DLVO framework.45,87,96,97 Additionally, according to the extended law of corresponding states,71,73,101–103 the collective behaviour of systems dominated by short-range attractions can be characterized by integral parameters, such as b2, while the specific details of the interaction potential become less significant. This supports the idea that protein–protein interactions can be described by a coarse-grained DLVO model, which relies on macroscopic solution properties despite the underlying complexity of protein interactions.
3.4 Relation between the protein state diagram and the underlying interactions
While the SAXS data (Section 3.2) examine interactions at specific urea and salt concentrations, the DLVO model (Section 3.3) allows for the calculation of b2 across all the solution conditions studied in this work, in particular for all conditions explored in the state diagram (Section 3.1). Consequently, the state diagram (Fig. 1) can be re-plotted as a function of b2. Instead of salt concentration, Fig. 6 now uses b2 as the ordinate to represent the different solution conditions.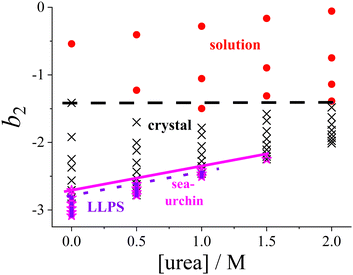 | ||
| Fig. 6 Experimental state diagram of lysozyme solutions (Fig. 1), with the ordinate axis expressed in terms of the normalized second virial coefficient b2 instead of salt concentration. States are indicated as follows: homogeneous solution (red circles), tetragonal crystals (black crosses), spherulitic (sea-urchin) crystals (magenta stars), and liquid–liquid phase separation (LLPS; blue squares). Lines representing the state boundaries are included as guides to the eye. | ||
Since increasing NaCl concentration corresponds to a decreasing (more negative) b2, the order in which the states appear in Fig. 6 is reversed along the ordinate axis as compared with Fig. 1. The lowest salt and urea concentrations studied correspond to b2 values in the range of 0 to −1.5. In this range, the attractive forces are insufficient to allow crystallization to occur spontaneously within the experimentally accessible timescale.
As noted in Section 3.1, a certain minimum level of attraction is required to induce the phase transitions, which can be achieved by the addition of NaCl. It is further noteworthy that the transition between the homogeneous solution and the coexistence region of crystals and solution is now represented by a horizontal line, rather than a line with a specific slope in the state diagram. This indicates that a minimum threshold of net attractive interactions must be present in the system for spontaneous crystallization to occur, regardless of the salt and urea concentrations. This observation supports the concept of a “crystallization slot”, as proposed by George and Wilson.104 The observed value of b2 ≲ −1.5 required for crystallization is consistent with the previously reported typical boundary of the crystallization region.42 Since the crystallization boundary can be interpreted as an estimate of the liquidus line, this finding aligns with the reported correlation between solubility and b2.105,106
Similarly, the boundaries for the regions where spherulites or phase separation occur show only a relatively gentle slope in Fig. 6. Phase separation is encountered if the protein–protein interactions satisfy b2 ≲ −2.6, consistent with previously obtained values for such low volume fractions as considered here.73 With respect to phase separation, this can be interpreted as a further confirmation of the extended law of corresponding states.71,73,103
To our knowledge, no systematic studies have been reported in the literature on the relationship between the appearance of spherulitic crystals and their position in the state diagram as expressed in terms of b2. However, these structures are commonly observed in or near the LLPS region.
4 Conclusion
In this study, we systematically investigated the effects of urea and salt on the phase behaviour and interactions in lysozyme solutions. While urea is well-known as a denaturant at high concentrations, its effects at non-denaturing concentrations, particularly on protein crystallization and LLPS, remain less understood. Our results demonstrate that urea decreases protein–protein attraction, while salt enhances it, resulting in shifts in the lysozyme state diagram. SAXS measurements allowed to quantify the changes in protein–protein interactions in terms of b2. By combining the state diagram with SAXS data, we provide a comprehensive picture of how urea and salt modulate protein phase behaviour. The application of the DLVO theory indicates that electrostatic and van der Waals forces dominate the protein–protein interactions. Our findings suggest that urea alters the dielectric properties of the solution, modifying protein–protein interactions without necessitating more complex models beyond the DLVO framework. Overall, this study provides further insights into the physical principles governing protein condensation and enhances the mechanistic understanding of how urea and salt influence protein–protein interactions. These findings could thus contribute to the development of improved strategies for protein crystallization and phase separation, with implications for both fundamental research and biotechnological applications.Author contributions
MM performed and analyzed the SAXS experiments, TH determined the state diagram. FP conceived and supervised the project. All authors discussed the results and contributed to the writing of the paper.Data availability
The data that support the findings of this study are available within the article and the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We grieve deeply over the untimely passing away of our colleague, mentor and friend Stefan U. Egelhaaf. We have greatly profited from his advice and continuous support. We are thankful for numerous insightful, inspiring and highly beneficial discussions, both in general and particularly in the context of this project. We thank Jan Dhont (Jülich, Germany) for very helpful discussions, and Jens Reiners (Düsseldorf, Germany) for assistance with the SAXS set-up. Financial support by the Deutsche Forschungsgemeinschaft (DFG Grant number 495795796) is gratefully acknowledged. We thank the Center for Structural Studies (CSS) for access to the SAXS instrument. CSS is funded by the Deutsche Forschungsgemeinschaft (DFG Grant numbers 417919780 and INST 208/761-1 FUGG).Notes and references
- J. J. McManus, P. Charbonneau, E. Zaccarelli and N. Asherie, Curr. Opin. Colloid Interface Sci., 2016, 22, 73–79 CrossRef CAS.
- R. Mezzenga and P. Fischer, Rep. Prog. Phys., 2013, 76, 046601 CrossRef PubMed.
- J. D. Gunton, A. Shiryayev and D. L. Pagan, Protein condensation. Kinetic pathways to crystallization and disease, Cambridge University Press, 2007 Search PubMed.
- W. Wang, Int. J. Pharm., 2005, 289, 1–30 CrossRef CAS PubMed.
- Y. Shen, A. Levin, A. Kamada, Z. Toprakcioglu, M. Rodriguez-Garcia, Y. Xu and T. P. J. Knowles, ACS Nano, 2021, 15, 5819–5837 CrossRef CAS PubMed.
- L. R. De Young, A. L. Fink and K. A. Dill, Acc. Chem. Res., 1993, 26, 614–620 CrossRef CAS.
- D. Fusco and P. Charbonneau, Colloids Surf., B, 2016, 137, 22–31 CrossRef CAS PubMed.
- F. Chiti and C. M. Dobson, Ann. Rev. Biochem., 2006, 75, 333–366 CrossRef CAS PubMed.
- A. K. Buell, C. M. Dobson and T. P. Knowles, Essays Biochem., 2014, 56, 11–39 CrossRef PubMed.
- A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58 CrossRef CAS PubMed.
- F. Zhang, F. Roosen-Runge, A. Sauter, M. Wolf, R. M. J. Jacobs and F. Schreiber, Pure Appl. Chem., 2014, 86, 191–202 CrossRef CAS.
- J. Hansen, F. Platten, D. Wagner and S. U. Egelhaaf, Phys. Chem. Chem. Phys., 2016, 18, 10270–10280 RSC.
- B. Smejkal, B. Helk, J.-M. Rondeau, S. Anton, A. Wilke, P. Scheyerer, J. Fries, D. Hekmat and D. Weuster-Botz, Biotechnol. Bioeng., 2013, 110, 1956–1963 CrossRef CAS PubMed.
- K. Kang and F. Platten, Sci. Rep., 2022, 12, 3061 CrossRef CAS PubMed.
- S. D. Durbin and G. Feher, Annu. Rev. Phys. Chem., 1996, 47, 171–204 CrossRef CAS PubMed.
- P. G. Vekilov and A. A. Chernov, Solid State Phys., 2003, 57, 1–147 Search PubMed.
- N. E. Chayen and E. Saridakis, Nat. Methods, 2008, 5, 147–153 CrossRef CAS PubMed.
- A. McPherson and J. A. Gavira, Acta Crystallogr., Sect. F:Struct. Biol. Commun., 2014, 70, 2–20 CrossRef CAS PubMed.
- D. Bolen, Methods, 2004, 34, 312–322 CrossRef CAS PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2007, 7, 2239–2246 CrossRef CAS.
- H. Hamada, T. Arakawa and K. Shiraki, Curr. Pharm. Biotechnol., 2009, 10, 400–407 CAS.
- J. Berthou and P. Jollès, FEBS Lett., 1973, 31, 189–192 CrossRef CAS PubMed.
- Y. Nozaki and C. Tanford, J. Biol. Chem., 1963, 238, 4074–4081 CrossRef CAS PubMed.
- C. Pace, Methods Enzymol., 1986, 131, 266–280 CAS.
- G. I. Makhatadze and P. L. Privalov, J. Mol. Biol., 1992, 226, 491–505 CrossRef CAS PubMed.
- A. Soper, E. Castner and A. Luzar, Biophys. Chem., 2003, 105, 649–666 CrossRef CAS PubMed.
- D. Tobi, R. Elber and D. Thirumalai, Biopolymers, 2003, 68, 359–369 CrossRef CAS PubMed.
- S. N. Timasheff and G. Xie, Biophys. Chem., 2003, 105, 421–448 CrossRef CAS PubMed.
- L. Hua, R. Zhou, D. Thirumalai and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16928–16933 CrossRef CAS PubMed.
- B. J. Bennion and V. Daggett, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5142–5147 CrossRef CAS PubMed.
- L. B. Sagle, Y. Zhang, V. A. Litosh, X. Chen, Y. Cho and P. S. Cremer, J. Am. Chem. Soc., 2009, 131, 9304–9310 CrossRef CAS PubMed.
- D. R. Canchi, D. Paschek and A. E. García, J. Am. Chem. Soc., 2010, 132, 2338–2344 CrossRef CAS PubMed.
- D. R. Canchi and A. E. García, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- Z. Su and C. L. Dias, J. Mol. Liq., 2017, 228, 168–175 CrossRef CAS.
- D. Niether, S. Di Lecce, F. Bresme and S. Wiegand, Phys. Chem. Chem. Phys., 2018, 20, 1012–1020 RSC.
- A. K. Hüsecken, F. Evers, C. Czeslik and M. Tolan, Langmuir, 2010, 26, 13429–13435 CrossRef PubMed.
- F. Evers, R. Steitz, M. Tolan and C. Czeslik, Langmuir, 2011, 27, 6995–7001 CrossRef CAS PubMed.
- M. R. Fries, D. Stopper, M. K. Braun, A. Hinderhofer, F. Zhang, R. M. J. Jacobs, M. W. A. Skoda, H. Hansen-Goos, R. Roth and F. Schreiber, Phys. Rev. Lett., 2017, 119, 228001 CrossRef PubMed.
- R. Maier, M. R. Fries, C. Buchholz, F. Zhang and F. Schreiber, Cryst. Growth Des., 2021, 21, 5451–5459 CrossRef CAS.
- A. C. Dumetz, A. M. Chockla, E. W. Kaler and A. M. Lenhoff, Biophys. J., 2008, 94, 570–583 CrossRef CAS PubMed.
- A. Stradner and P. Schurtenberger, Soft Matter, 2020, 16, 307–323 RSC.
- G. A. Vliegenthart and H. N. W. Lekkerkerker, J. Chem. Phys., 2000, 112, 5364–5369 CrossRef CAS.
- F. Zhang, R. Roth, M. Wolf, F. Roosen-Runge, M. W. A. Skoda, R. M. J. Jacobs, M. Stzucki and F. Schreiber, Soft Matter, 2012, 8, 1313–1316 RSC.
- J. Hansen, C. J. Moll, L. López Flores, R. Castañeda-Priego, M. Medina-Noyola, S. U. Egelhaaf and F. Platten, J. Chem. Phys., 2023, 158, 024904 CrossRef CAS PubMed.
- J. Hansen, R. Uthayakumar, J. S. Pedersen, S. U. Egelhaaf and F. Platten, Phys. Chem. Chem. Phys., 2021, 23, 22384–22394 RSC.
- F. Platten, J. Hansen, J. Milius, D. Wagner and S. U. Egelhaaf, J. Phys. Chem. B, 2015, 119, 14986–14993 CrossRef CAS PubMed.
- J. R. Warren and J. A. Gordon, J. Phys. Chem., 1966, 70, 297–300 CrossRef CAS.
- H. Sedgwick, K. Kroy, A. Salonen, M. B. Robertson, S. U. Egelhaaf and W. C. K. Poon, Eur. Phys. J. E:Soft Matter Biol. Phys., 2005, 16, 77–80 CrossRef CAS PubMed.
- D. Ray, M. Madani, J. K. G. Dhont, F. Platten and K. Kang, J. Phys. Chem. Lett., 2024, 15, 8108–8113 CrossRef CAS PubMed.
- M. C. Jenkins and S. U. Egelhaaf, Adv. Colloid Interface Sci., 2008, 136, 65 CrossRef CAS PubMed.
- M. Muschol and F. Rosenberger, J. Chem. Phys., 1997, 107, 1953–1962 CrossRef CAS.
- Y. Liu, X. Wang and C. B. Ching, Cryst. Growth Des., 2010, 10, 548–558 CrossRef CAS.
- M. L. Broide, T. M. Tominc and M. D. Saxowsky, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 6325–6335 CrossRef CAS PubMed.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171–210 CrossRef CAS.
- C. M. Jeffries, J. Ilavsky, A. Martel, S. Hinrichs, A. Meyer, J. S. Pedersen, A. V. Sokolova and D. I. Svergun, Nat. Rev. Methods Primers, 2021, 1, 70 CrossRef CAS.
- J. Hansen, J. N. Pedersen, J. S. Pedersen, S. U. Egelhaaf and F. Platten, J. Chem. Phys., 2022, 156, 244903 CrossRef CAS PubMed.
- M. Kotlarchyk and S.-H. Chen, J. Chem. Phys., 1983, 79, 2461–2469 CrossRef CAS.
- S. H. Chen, Annu. Rev. Phys. Chem., 1986, 37, 351–399 CrossRef CAS.
- A. E. Whitten, S. Cai and J. Trewhella, J. Appl. Crystallogr., 2008, 41, 222–226 CrossRef CAS.
- K. L. Sarachan, J. E. Curtis and S. Krueger, J. Appl. Crystallogr., 2013, 46, 1889–1893 CrossRef CAS.
- J. P. Hansen and I. McDonald, Theory of Simple Liquids, Academic Press, 3rd edn, 2006 Search PubMed.
- A. Tardieu, A. Le Verge, M. Malfois, F. Bonneté, S. Finet, M. Riès-Kautt and L. Belloni, J. Cryst. Growth, 1999, 196, 193–203 CrossRef CAS.
- S.-H. Chen, M. Broccio, Y. Liu, E. Fratini and P. Baglioni, J. Appl. Crystallogr., 2007, 40, s321–s326 CrossRef CAS.
- N. Javid, K. Vogtt, C. Krywka, M. Tolan and R. Winter, ChemPhysChem, 2007, 8, 679–689 CrossRef CAS PubMed.
- Y. Liu, L. Porcar, J. Chen, W.-R. Chen, P. Falus, A. Faraone, E. Fratini, K. Hong and P. Baglioni, J. Phys. Chem. B, 2011, 115, 7238–7247 CrossRef CAS PubMed.
- A. J. Chinchalikar, V. K. Aswal, J. Kohlbrecher and A. G. Wagh, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062708 CrossRef CAS PubMed.
- S. Kundu, V. Aswal and J. Kohlbrecher, Chem. Phys. Lett., 2016, 657, 90–94 CrossRef CAS.
- R. J. Baxter, J. Chem. Phys., 1968, 49, 2770–2774 CrossRef CAS.
- S.-H. Chen and P. Tartaglia, Scattering Methods in Complex Fluids, Cambridge University Press, 2015 Search PubMed.
- N. Asherie, A. Lomakin and G. B. Benedek, Phys. Rev. Lett., 1996, 77, 4832–4835 CrossRef CAS PubMed.
- M. G. Noro and D. Frenkel, J. Chem. Phys., 2000, 113, 2941–2944 CrossRef CAS.
- N. E. Valadez-Pérez, A. L. Benavides, E. Schöll-Paschinger and R. Castañeda-Priego, J. Chem. Phys., 2012, 137, 084905 CrossRef PubMed.
- F. Platten, N. E. Valadez-Pérez, R. Castañeda Priego and S. U. Egelhaaf, J. Chem. Phys., 2015, 142, 174905 CrossRef PubMed.
- C. Regnaut and J. C. Ravey, J. Chem. Phys., 1989, 91, 1211–1221 CrossRef CAS.
- S. V. G. Menon, C. Manohar and K. S. Rao, J. Chem. Phys., 1991, 95, 9186–9190 CrossRef CAS.
- S. V. G. Menon, V. K. Kelkar and C. Manohar, Phys. Rev. A:At., Mol., Opt. Phys., 1991, 43, 1130–1133 CrossRef CAS PubMed.
- M. Bergström, J. S. Pedersen, P. Schurtenberger and S. U. Egelhaaf, J. Phys. Chem. B, 1999, 103, 9888–9897 CrossRef.
- A. J. Chinchalikar, V. K. Aswal, J. Kohlbrecher and A. G. Wagh, Colloid Polym. Sci., 2010, 288, 1601–1610 CrossRef CAS.
- A. P. R. Eberle, R. Castañeda-Priego, J. M. Kim and N. J. Wagner, Langmuir, 2012, 28, 1866–1878 CrossRef CAS PubMed.
- M. Wolf, F. Roosen-Runge, F. Zhang, R. Roth, M. W. Skoda, R. M. Jacobs, M. Sztucki and F. Schreiber, J. Mol. Liq., 2014, 200, 20–27 CrossRef CAS.
- M. K. Braun, A. Sauter, O. Matsarskaia, M. Wolf, F. Roosen-Runge, M. Sztucki, R. Roth, F. Zhang and F. Schreiber, J. Phys. Chem. B, 2018, 122, 11978–11985 CrossRef CAS PubMed.
- O. Matsarskaia, F. Roosen-Runge, G. Lotze, J. Möller, A. Mariani, F. Zhang and F. Schreiber, Phys. Chem. Chem. Phys., 2018, 20, 27214–27225 RSC.
- D. Rosenbaum, P. C. Zamora and C. F. Zukoski, Phys. Rev. Lett., 1996, 76, 150–153 CrossRef CAS PubMed.
- L. Hentschel, J. Hansen, S. U. Egelhaaf and F. Platten, Phys. Chem. Chem. Phys., 2021, 23, 2686–2696 RSC.
- M. C. R. Heijna, M. J. Theelen, W. J. P. van Enckevort and E. Vlieg, J. Phys. Chem. B, 2007, 111, 1567–1573 CrossRef CAS PubMed.
- W. C. K. Poon, S. U. Egelhaaf, P. A. Beales, A. Salonen and L. Sawyer, J. Phys.: Condens. Matter, 2000, 12, L569 CrossRef CAS.
- H. Sedgwick, J. E. Cameron, W. C. K. Poon and S. U. Egelhaaf, J. Chem. Phys., 2007, 127, 125102 CrossRef CAS PubMed.
- M. G. Ortore, R. Sinibaldi, F. Spinozzi, F. Carsughi, D. Clemens, A. Bonincontro and P. Mariani, J. Phys. Chem. B, 2008, 112, 12881–12887 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press London, San Diego, 2nd edn, 1991 Search PubMed.
- M. Muschol and F. Rosenberger, J. Chem. Phys., 1995, 103, 10424–10432 CrossRef CAS.
- G. Pellicane, J. Phys. Chem. B, 2012, 116, 2114–2120 CrossRef CAS PubMed.
- S. Kumar, I. Yadav, D. Ray, S. Abbas, D. Saha, V. K. Aswal and J. Kohlbrecher, Biomacromolecules, 2019, 20, 2123–2134 CrossRef CAS PubMed.
- C. Wohlfarth, Dielectric constant of the mixture (1) water; (2) urea: Datasheet from Landolt-Börnstein – Group IV Physical Chemistry, Volume 17: “Supplement to IV/6” in SpringerMaterials DOI:10.1007/978-3-540-75506-7_320.
- M. Farnum and C. Zukoski, Biophys. J., 1999, 76, 2716–2726 CrossRef CAS PubMed.
- J. J. Dwyer, A. G. Gittis, D. A. Karp, E. E. Lattman, D. S. Spencer, W. E. Stites and B. García-Moreno E., Biophys. J., 2000, 79, 1610–1620 CrossRef CAS PubMed.
- C. Gögelein, D. Wagner, F. Cardinaux, G. Nägele and S. U. Egelhaaf, J. Chem. Phys., 2012, 136, 015102 CrossRef PubMed.
- F. Platten, J. Hansen, J. Milius, D. Wagner and S. U. Egelhaaf, J. Phys. Chem. Lett., 2016, 7, 4008–4014 CrossRef CAS PubMed.
- G. Pellicane, D. Costa and C. Caccamo, J. Phys. Chem. B, 2004, 108, 7538–7541 CrossRef CAS.
- S. N. Timasheff, Biochemistry, 2002, 41, 13473–13482 CrossRef CAS PubMed.
- I. L. Shulgin and E. Ruckenstein, J. Phys. Chem. B, 2008, 112, 14665–14671 CrossRef CAS PubMed.
- T. Gibaud, F. Cardinaux, J. Bergenholtz, A. Stradner and P. Schurtenberger, Soft Matter, 2011, 7, 857–860 RSC.
- S. Bucciarelli, N. Mahmoudi, L. Casal-Dujat, M. Jehannin, C. Jud and A. Stradner, J. Phys. Chem. Lett., 2016, 7, 1610–1615 CrossRef CAS PubMed.
- J. Hansen, S. U. Egelhaaf and F. Platten, Phys. Chem. Chem. Phys., 2023, 25, 3031–3041 RSC.
- A. George and W. W. Wilson, Acta Crystallogr., Sect. D:Biol. Crystallogr., 1994, 50, 361–365 CrossRef CAS PubMed.
- B. Guo, S. Kao, H. McDonald, A. Asanov, L. Combs and W. W. Wilson, J. Cryst. Growth, 1999, 196, 424–433 CrossRef CAS.
- D. F. Rosenbaum, A. Kulkarni, S. Ramakrishnan and C. F. Zukoski, J. Chem. Phys., 1999, 111, 9882–9890 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Complementary SAXS data, additional details on the SAXS analysis, and further discussion of the DLVO interaction potential. See DOI: https://doi.org/10.1039/d4sm01392a |
| This journal is © The Royal Society of Chemistry 2025 |