 Open Access Article
Open Access ArticleProtein–membrane interactions with a twist†
Jordan
Klein
 a,
Lorène
Schad
a,
Thérèse E.
Malliavin
a,
Lorène
Schad
a,
Thérèse E.
Malliavin
 *ab and
Martin Michael
Müller
*ab and
Martin Michael
Müller
 *a
*a
aUniversité de Lorraine, CNRS, LPCT, 57000 Metz, France. E-mail: Martin-Michael.Mueller@univ-lorraine.fr
bUniversité de Lorraine, CNRS, LPCT, 54000 Nancy, France
First published on 8th April 2025
Abstract
Within a framework of elasticity theory and geometry, the twister mechanism has been proposed some years ago for describing the interaction between a biofilament containing a twisted hydrophobic strip and a lipid membrane: this mechanism is capable of inducing deformations of the membrane, which can lead to its opening. The present work intends to extend this model to the interactions between a membrane and protein regions conserving their folds using coarse-grained molecular dynamics simulations. The protein region is modeled as a cylinder stabilized by a tensegrity scheme, leading to an elasticity similar to that observed in real proteins. Recording molecular dynamics trajectories of this cylinder in the presence of a fluid lipid bilayer membrane allows investigation of the effect of the positions of the hydrophobic parts on the interaction with the membrane. The entire configuration space is explored by systematically varying the hydrophobic strip width, the twisting of the strip as well as the range of hydrophobic interactions between the cylinder and the membrane. Three different states are observed: no interaction between the cylinder and membrane, the cylinder in contact with the membrane surface and the cylinder inserted into the membrane with a variable tilt angle. The variations of the tilt angle are explained using a qualitative model based on the total hydrophobic moment of the cylinder. A deformation pattern of the membrane, previously predicted for the filament–membrane interaction by the twister model, is observed for the state when the cylinder is in contact with the membrane surface, which allows estimation of the applied torques.
I. Introduction
Biological membranes are important players in physiological and pathological processes as they allow the separation of cells into different compartments, the protection of cells from the outside as well as the trafficking of ions, biopolymers and ligands.1 Traffic across the membranes is often mediated by a wide variety of transmembrane proteins or protein complexes.1 In addition, some water-soluble proteins are capable of translocating across the membrane.2Numerous water-soluble proteins interacting with the membrane undergo conformational transitions in order to adapt to the hydrophobic environment of the membrane's interior. The 3D structure of water-soluble proteins is generally built around a hydrophobic core, with hydrophilic sidechains pointing towards the aqueous environment.3,4 A simplistic view of the transition into the membrane would be that the structure switches in order to position the hydrophobic sidechains towards the hydrophobic tails of the lipids. This principle is globally exact, but there are numerous ways to achieve this goal, and no method is universally acknowledged that can predict the conformational transition of a protein in contact with a membrane. In particular, some protein regions may unfold when in contact with a membrane which complicates enormously the description of the transition due to the huge number of conformations populated by the system.
Several α-helical water-soluble proteins interact with membranes, such as the pore-forming proteins,5 the engrailed homeodomain,6 or various toxins7 and anti-microbial peptides.8 Killing target cells using pore-forming toxins (PFTs) is a common virulence mechanism in a wide range of pathogenic bacteria.9 PFTs generally fold into water-soluble, monomeric structures which oligomerize and change their conformation upon binding to specific receptors in the membrane of target cells to form transmembrane pores. The structural biology of PFTs has revealed numerous structures of soluble monomers of such toxins along with the corresponding pore structures (see ref. 9–11 for surveys). Examining these structures, one is struck by the fact that conformational transitions involve only limited parts of the structure. Numerous conformational changes involve rotations of α helices, as for example in the cytolysin A family,12,13 fragaceatoxin,14 and the Yersinia YaxAB system.15 Modeling the interaction of α helices with the membrane would thus be an important step for the understanding of the conformational transitions of soluble α helical proteins during their interaction with the membrane.
Recent numerical studies of peptide–membrane systems have focused on the case of interactions and pore formation by antimicrobial peptides.16–23 These interactions are also studied using coarse-grained molecular dynamics simulations.18,24,25 The simulation of conformational transitions for monomeric toxins to form a pore26 requires the knowledge of the final pore state. Physics-based inverse design27 as well as cross-parametrization of peptide–membrane interactions28 have also been proposed to infer models of interactions from experimental measurements.
In these coarse-grained models, the successive amino-acid residues in the peptides are replaced by a few beads gathering backbone and sidechain atoms. In the case of a protein containing several secondary structure elements, the use of a coarse-grained model requires the application of long-range restraints to keep the tertiary structure of the protein.29 Imposing such tertiary constraints makes it difficult to study the conformational transition of proteins. In the present work, we intend to propose another model in which secondary structure elements are modeled using a tensegrity scheme, allowing reduction of the configuration space of the studied system. We focus on one of the simplest secondary structure elements, the α helix or the α helix bundle.
The distribution of hydrophobic patches on α helix surfaces influences their interactions with membranes. For example, an amphipathic helix displaying hydrophobic residues on one side and hydrophilic residues on the other leads to a large so-called hydrophobic moment,30 and is known to insert itself parallel to the membrane surface.31 Nevertheless, the relative positions of the hydrophobic residues of an α helix are not always ordered in this simple way. A systematic study of the interaction between a membrane and an α helix for any organization of hydrophobic residues is still missing. The mesoscopic twister model32 suggests that an asymmetric distribution of hydrophobic residues in a filament can deform a membrane via the application of torques, leading to the insertion of the filament. This potentially provides a generalization of the amphipathic case. In the present work, we present the results of coarse-grained molecular dynamics (MD) simulations of the α helix-membrane interaction investigating systematically all possible helical distributions of hydrophobic residues. The coarse-grained model of the cylinder is similar to the model in ref. 33 in which pore-forming peptides were studied. The cylinder shape is maintained during the simulation using an original tensegrity scheme. The membrane model is the one proposed by Cooke and Deserno, where each lipid molecule is modeled with three beads.34,35 They showed that lipids with properly tuned pair-wise interactions between their beads spontaneously self-assemble into a fluid membrane without the need of an explicit solvent. This initial work was recently extended to the case of asymmetric membranes.36,37
In the following, we will first present details of the modeling together with the interaction pair potentials and a wide range of distributions of the hydrophobic residues on the cylinder. The analysis of the simulations provides the configuration space of the cylinder–membrane system as a function of the residue distribution as well as the strength of the hydrophobic interactions. The configurations of the cylinder inserted into the membrane are analyzed and related to the hydrophobic moment, and the corresponding membrane deformation is described. In particular, the analysis of systems in which the cylinder interacts only with the membrane surface allows obtaining a surface deformation pattern similar to that previously deduced with the twister model.32
II. Simulation models
II.A Membrane model
The membrane is a fluid bilayer as described by the Cooke model.34,35 Each lipid is represented by three beads: one bead for the hydrophilic head of the lipid and two beads for the hydrophobic tail (Fig. 1) denoted LI1 and LI2 with LI1 located in the middle of the lipid.Next neighbor beads in one lipid are connected with FENE bonds (Fig. 1a, green springs) whose potential depends on the distance r between the beads’ centers:38
 | (1) |
 where
where  and σ are the energy and the length scale, respectively (see below). An additional harmonic bond (Fig. 1a, brown spring) is added between the head bead and bead LI2 to ensure the alignment of the beads within the lipid:
and σ are the energy and the length scale, respectively (see below). An additional harmonic bond (Fig. 1a, brown spring) is added between the head bead and bead LI2 to ensure the alignment of the beads within the lipid: | (2) |
 .
.
To model the repulsion between the head beads and between a head and a tail bead, we apply a Weeks–Chandler–Anderson (WCA) potential (Fig. 1a, orange arrows):
 | (3) |
The interactions between lipid tails are modeled with an attractive potential (Fig. 1a, green arrows) between the beads of the hydrophobic tails:34,35
 | (4) |
![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = wc/σ. For r < rc the potential Vcos
c = wc/σ. For r < rc the potential Vcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2(r) corresponds to a Lennard-Jones potential. Note that σ and ε are nothing but the reduced units of this potential.
2(r) corresponds to a Lennard-Jones potential. Note that σ and ε are nothing but the reduced units of this potential.
Setting ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 1.6, ε = kBT/1.1, and σ = 1 nm results in the spontaneous self-assembly of a fluid membrane with properties that are close to experimental values:35 the thickness of the simulated membrane is about 5 nm, the membrane area per lipid is 1.1 to 1.5 nm2 compared to that of 0.75 nm2 in experiments on fluid membranes. For
c = 1.6, ε = kBT/1.1, and σ = 1 nm results in the spontaneous self-assembly of a fluid membrane with properties that are close to experimental values:35 the thickness of the simulated membrane is about 5 nm, the membrane area per lipid is 1.1 to 1.5 nm2 compared to that of 0.75 nm2 in experiments on fluid membranes. For ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 1.6 and
c = 1.6 and  , the obtained bending rigidity κ of the membrane is κ ≈ 13kBT ≈ 0.56 × 10−19 J with temperature T = 310 K (see Fig. 7 of ref. 35). This value agrees well with the typical bending rigidity of a fluid membrane, which lies between 0.24 and 2.3 × 10−19 J.
, the obtained bending rigidity κ of the membrane is κ ≈ 13kBT ≈ 0.56 × 10−19 J with temperature T = 310 K (see Fig. 7 of ref. 35). This value agrees well with the typical bending rigidity of a fluid membrane, which lies between 0.24 and 2.3 × 10−19 J.
III.B Protein model
The protein is modeled as a cylinder (Fig. 1b) composed of six disks stacked on top of each other.33 Each disk consists of seven beads: one in the center and six peripheral beads arranged on a circle, forming a hexagon. The beads are of two types: hydrophobic beads (Fig. 1, red beads) and non-hydrophobic beads (Fig. 1, gray beads) with a diameter of rc = 0.95σ. The attractive potential of the membrane model, eqn (4), is used to model the interaction between the hydrophobic beads of the cylinder and the hydrophobic tail beads of the lipids (Fig. 1a, green arrows). In the present study, we vary the parameter![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c of this potential used to model the attraction between the cylinder and membrane in the range of 1.00 to 3.25. Moreover, we apply a Weeks–Chandler–Anderson (WCA) potential, eqn (3), between the non-hydrophobic beads of the cylinder and all lipid beads (Fig. 1a, orange arrows).
c of this potential used to model the attraction between the cylinder and membrane in the range of 1.00 to 3.25. Moreover, we apply a Weeks–Chandler–Anderson (WCA) potential, eqn (3), between the non-hydrophobic beads of the cylinder and all lipid beads (Fig. 1a, orange arrows).
The hydrophobic beads are placed on a helical strip of a certain thickness (Fig. 1b). The aim of this work is to study how the relative positions of hydrophobic and non-hydrophobic beads on the cylinder influence cylinder–membrane interactions. Variations in the positions of the hydrophobic beads on the cylinder are described using two parameters: (i) the helicity of the hydrophobic strip of the cylinder, which will be set by the nominal angle α ∈ [0,180°] in steps of 10°, defined as the angle between the vectors connecting the central bead and the peripheral bead in the middle of the hydrophobic strip in two successive disks (Fig. 1c); (ii) the thickness of the hydrophobic strip given by the number d ∈ {1,2,3,4} of hydrophobic beads per disk. At small angles α, this cylinder model allows investigating the membrane–cylinder interaction in the framework of the twister model.32 By contrast, at larger values of α or large strip thickness d, the cylinder model results in a description of the cylinder solubilization within the membrane. Note that high helicities 180° < α < 360° can be mapped to α ∈ [0,180°].
The stability of the cylinder is enforced by the use of tensegrity,39 which does not depend on whether the bead is hydrophobic or not. Due to the hexagonal symmetry of each disc, it is sufficient to consider cylinders with an helicity angle α0 varying between 0 and 30°. This angle is the angle between the vectors connecting beads 0 (central bead) and 1 (peripheral bead) in two successive disks (Fig. 1c, bottom). It is defined in the following way:
| α0 = |β − 30°|, | (5) |
In the tensegrity framework, the beads are connected by harmonic bonds with the corresponding potential:
 | (6) |
 is the spring constant and req is the equilibrium length of the bond. When req is larger than the geometrical distance r0 between the beads at the beginning of the simulation, the bond is compressed (Fig. 1c, magenta bonds), when it is smaller than r0 the bond is stretched, (Fig. 1c, blue bonds) respectively.
is the spring constant and req is the equilibrium length of the bond. When req is larger than the geometrical distance r0 between the beads at the beginning of the simulation, the bond is compressed (Fig. 1c, magenta bonds), when it is smaller than r0 the bond is stretched, (Fig. 1c, blue bonds) respectively.
Stability is ensured by a delicate balance between compressed and stretched bonds (Table 1). Beads of the same disc are connected by compressed harmonic bonds. The state of the bonds between beads located in two adjacent disks depends on the beads' positions. When one bead is at the center and the other is peripheral, the bond is stretched ((1) in Table 1), whereas it is compressed when the beads are both located at the centers ((2) in Table 1).
 ,
,  , and
, and  . Note that R1 = R2 for α0 = 30°
. Note that R1 = R2 for α0 = 30°
For the bonds between two peripheral beads of adjacent discs ((3) in Table 1), the distances between all beads of the two peripheries are calculated and sorted from the smallest to the largest. For α0 ≠ 30° we generate three types of bond (Fig. 1c): when the two beads are first neighbors corresponding to the smallest distance, the bond is compressed. In the case where the distance between the two beads is the second smallest (2nd neighbors) or third smallest (3rd neighbors), the bond is stretched.
The case α0 = 30°, which corresponds to α = 30°, 90° and 150°, is special due to its symmetry: the number of first neighbors doubles and the corresponding bonds are compressed. To ensure cylinder stability, one needs a balance between stretched and compressed bonds. Too many stretched bonds, however, make the construction unstable as well. Several simulations of different configurations showed that it is sufficient to add stretched bonds to half of all possible second neighbors to obtain a stable cylinder (see also Section III.A).
Illya and Deserno33 have used a similar description for the cylinder. However, one should notice that they have restricted themselves to the case of α0 equal to zero, which simplifies the mechanical system and allows to set req = 1.2rc.
For small values of α, the hydrophobic beads are located on the same side of the cylinder and the non-hydrophobic beads on the opposite side (Fig. 1b). This configuration is analogous to the one of amphiphatic α helices of a protein.30 We thus call the corresponding cylinders amphiphatic cylinders.
II.C Molecular dynamics simulations
The coarse-grained MD trajectories were recorded using version 4.1.2 of the software ESPResSo (Extensible Simulation Package for Research on Soft Matter: https://espressomd.org/wordpress)40 with a timestep of 0.005τ, where is the instantaneous timescale.33 The system temperature was controlled using a Langevin thermostat, with a temperature T such that
is the instantaneous timescale.33 The system temperature was controlled using a Langevin thermostat, with a temperature T such that  , and with a friction γ set equal to m/τ.35 We used a modified Andersen barostat,41 with friction γV = 10−4m/τ and the mass of the piston Q = 5 × 10−4 m as in ref. 33. The barostat was applied in the x and y directions parallel to the membrane surface. In this way, the lateral tension of the membrane could be fixed to zero by setting the external pressure to zero. During the MD simulations, the equations of motions were integrated using the Verlet scheme.42,43
, and with a friction γ set equal to m/τ.35 We used a modified Andersen barostat,41 with friction γV = 10−4m/τ and the mass of the piston Q = 5 × 10−4 m as in ref. 33. The barostat was applied in the x and y directions parallel to the membrane surface. In this way, the lateral tension of the membrane could be fixed to zero by setting the external pressure to zero. During the MD simulations, the equations of motions were integrated using the Verlet scheme.42,43
In each simulation, 1498 lipids were positioned in a box of 30 × 30 × 100σ3 with periodic boundary conditions. Additional systems with boxes of 35 × 35 × 100σ3 and 40 × 40 × 100σ3 were built using respectively 2038 and 2664 lipids (see the ESI†). All trajectories were recorded over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, and only one iteration out of 10 was saved, i.e., 2000 iterations were analyzed subsequently. For the box of 30 × 30 × 100σ3, two independent runs were used to obtain the analyzed observables of Section III and the trajectories were recorded for α ∈ [0,180°] in steps of 10°, for d ∈ {1,2,3,4}, and for
000 steps, and only one iteration out of 10 was saved, i.e., 2000 iterations were analyzed subsequently. For the box of 30 × 30 × 100σ3, two independent runs were used to obtain the analyzed observables of Section III and the trajectories were recorded for α ∈ [0,180°] in steps of 10°, for d ∈ {1,2,3,4}, and for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c ∈ [1.00,3.25]. The averages of the analyzed parameters were calculated over the last saved 500 iterations. Most of the analyses used the tools from the MDAnalysis44 and matplotlib45 python libraries.
c ∈ [1.00,3.25]. The averages of the analyzed parameters were calculated over the last saved 500 iterations. Most of the analyses used the tools from the MDAnalysis44 and matplotlib45 python libraries.
Further analysis of the trajectories in which the cylinder was inserted in the membrane required superimposing the cylinder positions along all frames. This was realized by translating the system along the x and y axes in order to place the cylinder's center of mass in the middle of the membrane plane, i.e., at x = y = 0, and by rotating the system such that the long axis of the cylinder was located in the (xz) plane.
III. Results
III.A Torsional rigidity of the cylinder
According to the twister model,32 a cylinder with a helicoidal distribution of hydrophobic regions can apply local torques on the membrane to which it adheres inducing a deformation of the membrane surface. By principle of action and reaction, torques of equal strength but of opposite direction act on the cylinder. The torsional rigidity of the cylinder is thus an important parameter to estimate the ability of the cylinder to keep its structure when interacting with the membrane. In addition, in the perspective of modeling proteins with cylinders, it is necessary to know whether the tensegrity model proposed here in connection to the force field parametrization of Deserno and coworkers33,34 reproduces well the orders of magnitude known for the stiffness of proteins in the framework of mechanical continuous media.To estimate the torsional rigidity of the cylinder, MD trajectories were recorded using EsPreSSO 4.1.2 on an isolated cylinder. The positions of the beads forming the first disk of the cylinder were fixed, whereas a torque τcyl was imposed on the disk located at the other end of the cylinder by applying a tangential force A on each of the six peripheral beads:
| τcyl = 6RcylAε, | (7) |
The induced cylinder deformation was monitored by calculating the rotation between the first and last disks. The resulting torsional angle was determined by measuring the total angle
| αt = 5(α0 + δα) | (8) |
One should notice that the tensegrity model we developed here is different from the one of ref. 33, as it includes a twisted geometry of the relative positions of the disks, described by the specified angle α0 (see eqn (5), Section II.B). Because of this twist, we had to define spring networks which differ for α0 ≠ 30° and α0 = 30°. In addition, the network of the diagonal springs in the twisted geometries is loosing symmetry with respect to the untwisted case (Fig. 1c). During the MD trajectories, the specified geometry of the tensegrity model thus slightly deforms. The resulting configuration exhibits shorter cylinder lengths and slightly larger radii for each disk. But, the δα values observed for a vanishing torque (A = 0) (Table 2) are smaller than 1° for all twisted geometries with a slight improvement for α0 = 30°. Thus, the nominal value of α0 can be used in the following.
| α 0 (deg) | χ (pN nm2) | σ χ (pN nm2) | δα (A = 0) (deg) |
|---|---|---|---|
| 0 | 2939 | 29 | −0.01 |
| 10 | 2980 | 28 | 0.77 |
| 20 | 2956 | 28 | 0.73 |
| 30 | 2431 | 25 | 0.36 |
A closer inspection of Fig. 2 reveals a linearity between the applied torque and the variations of αt. For a perfect elastic cylinder:46
 | (9) |
Van Reenen and Janssen47,48 experimentally measured the torsional rigidity of an IgC immunoglobulin using magnetic particles attached to the protein. They find for the IgC protein a torsional rigidity ranging from 500 to 5000 pN nm2. The torsional rigidity values that we measured here in silico are of the same order of magnitude than experimental data. The cylinder representing the protein has therefore mechanical properties in agreement with the literature.
III.B Configuration space
As described in Section II.C, we recorded 532 trajectories while varying the parameters α, d and wc in order to explore different geometries of hydrophobic strips and different ranges of the hydrophobic attractive potential. We identified three possible final states (Fig. 3): (i) the cylinder does not display a stable state interacting with the membrane; (ii) the cylinder remains on the surface of the membrane; (iii) the cylinder is inserted into the membrane.For each trajectory, the final state was determined by monitoring the minimal distance dM between the cylinder and membrane beads, and the minimal distance dQ between the cylinder beads and the hydrophobic beads LI2 of the lipids (Fig. 1a). These distances were averaged over the last 500 frames of the trajectory. The states were then identified in the following way: no interaction  , cylinder at the surface
, cylinder at the surface 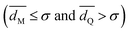 and inserted cylinder
and inserted cylinder  .
.
Fig. 3 shows that the values of d and wc have a strong influence on the final state of the cylinder. A large value of wc facilitates insertion into the membrane. Similarly, a large value of d reduces the value of wc needed for insertion, since the total number of hydrophobic beads is increased. In contrast, the value of α has a lower influence on the insertion.
The transition lines between the different states (Fig. 3) become flatter for increasing values of d. A region of surface states (light grey) of the cylinder is observed for d = 1 only and collapses for larger d. The cylinder with the tiniest hydrophobic strip is thus the one displaying a larger number of surface states, which can be seen as transition states between no interaction and insertion.
Increasing the helicity of the strip, which is equivalent to reducing the cylinder's amphipathicity, reduces the propensity of the cylinder to interact with the membrane. This is reflected by the observation that increasing α at a constant d increases the value of wc at which the transition between the states take place. A system similar to the case where α = 0° and d = 4 was considered by Illya and Deserno,33 where the insertion was observed around ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 1.4. It is interesting to see that the present work qualitatively agrees with their results.
c = 1.4. It is interesting to see that the present work qualitatively agrees with their results.
The internal dynamics of the cylinder has been monitored by calculating the value of α averaged along the trajectories. Averaged and nominal values coincide within the determined errors (Fig. S1, ESI†). The cylinders thus conserve their geometries along the trajectories, which permits to use the nominal values of α in the presentation of the results.
Repeating the simulations produces similar regions of the phase diagram (Fig. 3). Nevertheless, variations are observed at the transition lines for d < 4. The limits between different states are thus prone to various fates depending on the recorded trajectory. This behavior is reminiscent of the transition state ensemble observed in the unfolding of a protein.49
III.C Orientation of inserted cylinders
The position of the cylinder within the membrane was analyzed by monitoring the angle θ between the vector c defining the long axis of the cylinder and the normal vector z of the membrane plane. The vector c connects the centers of mass of the first and last disks of the cylinder and is averaged along the MD trajectory. The coordinates cx, cy and cz of c are averaged to obtain . As the main axis of the cylinder of our model has no specific orientation we restrict ourselves to θ ∈ [0°,90°] by replacing values of θ > 90° by 180° − θ.
. As the main axis of the cylinder of our model has no specific orientation we restrict ourselves to θ ∈ [0°,90°] by replacing values of θ > 90° by 180° − θ.
From the values of θ averaged along the last 500 frames of each trajectory (Fig. 4a and Fig. S2, ESI†), two main sub-states of the inserted state can be inferred: (i) cylinder parallel to the membrane, i.e., the cylinder axis is located in the membrane plane and θ = 90° (Fig. 4c), and (ii) cylinder tilted in the membrane: the axis of the cylinder has a non-zero component along the normal of the membrane (Fig. 4d).
 | ||
Fig. 4 (a) Angle θ between the membrane normal and the cylinder axis plotted for different values of α for the first run of the MD simulations (see Fig. S2 for the second run, ESI†). The four panels correspond to different values of d while the colors correspond to different values of the cohesion parameter ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c. (b) Gibbs free energy G as a function of θ for different values of α for c. (b) Gibbs free energy G as a function of θ for different values of α for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 3 and d = 2. The profiles are colored according to the type of θ distribution (Fig. 5 and Fig. S3, ESI†). Unimodal distributions with a parallel cylinder are colored in black, unimodal distributions with a tilted cylinder in grey and bimodal distributions in red. (c) and (d) Views of the possible inserted states of the trajectories. (c) Cylinder–membrane system with the cylinder in a parallel state (α = 90°, d = 1 and wc = 3.25). (d) Cylinder–membrane system with the cylinder in the tilted state (α = 60°, d = 1 and wc = 3.25). Lipid polar heads are colored blue, hydrophobic tails yellow, hydrophobic cylinder beads red, and non-hydrophobic beads gray. The direction of the hydrophobic moment is drawn in red. c = 3 and d = 2. The profiles are colored according to the type of θ distribution (Fig. 5 and Fig. S3, ESI†). Unimodal distributions with a parallel cylinder are colored in black, unimodal distributions with a tilted cylinder in grey and bimodal distributions in red. (c) and (d) Views of the possible inserted states of the trajectories. (c) Cylinder–membrane system with the cylinder in a parallel state (α = 90°, d = 1 and wc = 3.25). (d) Cylinder–membrane system with the cylinder in the tilted state (α = 60°, d = 1 and wc = 3.25). Lipid polar heads are colored blue, hydrophobic tails yellow, hydrophobic cylinder beads red, and non-hydrophobic beads gray. The direction of the hydrophobic moment is drawn in red. | ||
The angle θ (Fig. 4a and Fig. S2, ESI†) displays two valleys centered around α = 60° and 120°: the cylinder is tilted whatever the values of ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c and d. Around α = 90°, α = 150° and for small values of α, we observe plateaus with maximum values of θ close to 90°. When d or
c and d. Around α = 90°, α = 150° and for small values of α, we observe plateaus with maximum values of θ close to 90°. When d or ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c increases, the hydrophobicity of the cylinder increases and the difference between the two states is reduced. The cylinder in the tilted state tends towards a parallel orientation (θ = 90°), which is reflected in a decrease in the valleys' depths in Fig. 4a.
c increases, the hydrophobicity of the cylinder increases and the difference between the two states is reduced. The cylinder in the tilted state tends towards a parallel orientation (θ = 90°), which is reflected in a decrease in the valleys' depths in Fig. 4a.
Looking more closely at each trajectory, the angle θ displays variations as a function of time. Gibbs free energy profiles were calculated from the logarithm of the density of orientation states. Fig. 4b shows a series of such energy profiles as a function of θ and α for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 3 and d = 2. The energy barriers for bimodal profiles are in the range of
c = 3 and d = 2. The energy barriers for bimodal profiles are in the range of  , where
, where  is the energy scale. The range of values sampled by the Gibbs energy agrees with the fluctuations between metastable states during the timescale of the simulations.
is the energy scale. The range of values sampled by the Gibbs energy agrees with the fluctuations between metastable states during the timescale of the simulations.
The positions of local maxima in the density of θ states corresponding to minima in the profiles of the Gibbs energy, θp, have been determined (Fig. 5 and Fig. S3, ESI†). For the unimodal distributions (Fig. 5a and Fig. S3a, ESI†), the histogram of θp displays two sets of values: θp ∈ (84°–90°) corresponding to an inserted cylinder parallel to the membrane, and θp ∈ (40°–80°) corresponding to a tilted cylinder. These are the two states of orientation observed in Fig. 4c and d. For the bimodal distributions, two maxima are located at θp1 and θp2 with θp1 < θp2. The values of θp1 (Fig. 5b and Fig. S3b, ESI†) range from 33° up to 87°. The histogram of the values of θp2 (Fig. 5c and Fig. S3c, ESI†) displays a peak around 80–90°, which indicates that some of the bimodal distributions are entirely located close to 90°. One observes six values of θp2 < 70° in Fig. 5c and two in Fig. S3c (ESI†), corresponding to cases where the cylinder oscillates around several tilted states.
The two peaks observed for each bimodal distribution in a given trajectories are displayed together with the helicity of the cylinder (Fig. 5d and Fig. S3d, ESI†). In most of the cases, θp2 is located between 80 and 90° (red points), which shows that the parallel position of the cylinder is populated. The cases where the cylinder oscillates between tilted states display isolated red points in the range 50–70°. The corresponding parameter values (α,![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c,d) are (40°,2.5,2), (50°,3.0,2), (60°,2.0,3), (70°,3.25,1), (110°,1.5,4), and (130°,3.0,1) for Fig. 5d and (70°,2.5,2) and (130°,1.75,4) for Fig. S3d (ESI†). These points correspond to helicity angles larger than 30° with either strips wider than 2 or cohesion ranges larger than 3. The corresponding cylinders thus display large surfaces of hydrophobic beads dispersed in all directions: they are not so much amphipathic and display unsurprisingly a tendency to stay away from a horizontal position.
c,d) are (40°,2.5,2), (50°,3.0,2), (60°,2.0,3), (70°,3.25,1), (110°,1.5,4), and (130°,3.0,1) for Fig. 5d and (70°,2.5,2) and (130°,1.75,4) for Fig. S3d (ESI†). These points correspond to helicity angles larger than 30° with either strips wider than 2 or cohesion ranges larger than 3. The corresponding cylinders thus display large surfaces of hydrophobic beads dispersed in all directions: they are not so much amphipathic and display unsurprisingly a tendency to stay away from a horizontal position.
For each trajectory with a bimodal distribution, the positions of the smallest and the largest peak were plotted on a two-dimensional graph (Fig. 5e and Fig. S3e, ESI†). These sets define two lines, one corresponding to cases where the largest peak is located in the 80–90° region, and the other corresponding to the isolated red points quoted above, in which the cylinders sample different tilted states. The slopes of the lines provide a simplified description of the relationship between the position of the two maxima in θ distributions, arising from the underlying coarse-grained scheme used here for describing the membrane–cylinder interaction.
III.D Relationship between cylinder orientation and hydrophobic moment
The orientation of the inserted cylinders described in the previous Section III.C can be investigated by examining the competition between the various hydrophobic interactions between the hydrophobic beads, within the lipids and between the lipids and the cylinder (eqn (4)). The smallest value for which the cylinder inserts into the membrane is![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 1.25 (Fig. 3). A closer look at the phase diagram reveals inserted cylinders for all helicities for
c = 1.25 (Fig. 3). A closer look at the phase diagram reveals inserted cylinders for all helicities for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c ≥ 1.5 at d = 4. At smaller d the cohesion range has to be larger to obtain the same effect. If the cylinder was inserted horizontally (θ = 90°) in the middle of a hypothetical undeformed membrane, the distance between the surface of the cylinder and the polar membrane heads would only be approximately 0.5. This value is smaller than the range of
c ≥ 1.5 at d = 4. At smaller d the cohesion range has to be larger to obtain the same effect. If the cylinder was inserted horizontally (θ = 90°) in the middle of a hypothetical undeformed membrane, the distance between the surface of the cylinder and the polar membrane heads would only be approximately 0.5. This value is smaller than the range of ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c for which the cylinder is inserted in the phase diagram (Fig. 3), which induces a frustration between the various hydrophobic attractions present in the system. This frustration is at the origin of the two cylinder states (i) and (ii) found in the simulations. To go further into the analysis, one identifies two extreme cases of these states: an amphipathic cylinder in which all hydrophobic beads are located on the same side (α = 0°), and a cylinder where the hydrophobic beads are distributed in a balanced way on the surface of the cylinder (in particular for α = 60°, 120° and 180°). In the first case, the cylinder orients itself parallel to the membrane, which allows the hydrophobic tails of the lipids to concentrate on the hydrophobic side of the cylinder (Fig. 4c). In the second case, no direction perpendicular to the axis of the cylinder is preferred. Nevertheless, the cylinder will try to maximize the hydrophobic interactions with the lipid tails. Consequently, the cylinder would prefer to orient itself perpendicular to the membrane surface so that each hydrophobic bead experiences the same environment. However, since the cylinder is longer than the thickness of the hydrophobic part of the membrane, the cylinder tilts to stay inside the membrane (Fig. 4d).
c for which the cylinder is inserted in the phase diagram (Fig. 3), which induces a frustration between the various hydrophobic attractions present in the system. This frustration is at the origin of the two cylinder states (i) and (ii) found in the simulations. To go further into the analysis, one identifies two extreme cases of these states: an amphipathic cylinder in which all hydrophobic beads are located on the same side (α = 0°), and a cylinder where the hydrophobic beads are distributed in a balanced way on the surface of the cylinder (in particular for α = 60°, 120° and 180°). In the first case, the cylinder orients itself parallel to the membrane, which allows the hydrophobic tails of the lipids to concentrate on the hydrophobic side of the cylinder (Fig. 4c). In the second case, no direction perpendicular to the axis of the cylinder is preferred. Nevertheless, the cylinder will try to maximize the hydrophobic interactions with the lipid tails. Consequently, the cylinder would prefer to orient itself perpendicular to the membrane surface so that each hydrophobic bead experiences the same environment. However, since the cylinder is longer than the thickness of the hydrophobic part of the membrane, the cylinder tilts to stay inside the membrane (Fig. 4d).
The presented observations can be correlated with the hydrophobic moment of the cylinder. In analogy to the definition of the hydrophobic moment of protein α helices proposed by Eisenberg,30 the hydrophobicity of each hydrophobic bead is defined as a vector Mi connecting the center of the central bead of the disk and the center of the considered hydrophobic bead i. Contrary to the Eisenberg model, the hydrophobic scale is assumed to be constant for all beads. The total hydrophobic moment M of the cylinder is defined as the sum of the individual hydrophobic moments:
 | (10) |
In the Eisenberg model, a larger norm of the total hydrophobic moment M := |M| corresponds to an α helix with a higher attractive interaction with the membrane. To be generic, we only consider the geometric effect of the arrangement of the hydrophobic beads and not the cohesion parameter ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c.
c.
In an ideal cylinder geometry, the moments of all beads are in the plane (x,y) perpendicular to the cylinder axis. We thus replace the 3D problem by a 2D problem in which the hydrophobic moments of each disk are summed up in the (x,y) plane to obtain the total hydrophobic moment. Fig. 6a shows how the total hydrophobic moment of the cylinder (red arrows) results from a vector sum of the individual moments of each disk (blue arrows) for different values of α. The largest norms are observed for small helicity α. In this case, the geometry of the cylinder is close to an amphipathic geometry; all individual bead moments almost point in the same direction and produce a large resulting vector, as shown for α = 30° (red arrow in Fig. 6a). The norm of the hydrophobic moment is zero for angles α of 60°, 120° and 180° and is maximum for angles α of 0°, 90° and 150°. Even when the hydrophobic moment is close to zero, the individual moments of each disk are not zero (Fig. 6a).
 | ||
| Fig. 6 (a) Hydrophobic moment calculated from the cylinder geometry: in blue the hydrophobic moments of each disk, in red, the total hydrophobic moment. The disk numbers (Fig. 1) are indicated next to the blue arrows. (b) Norm of the hydrophobic moment as a function of the helicity of the cylinder (see eqn (12)). | ||
A geometrical consideration yields an analytical expression for the norm of M. We orient the moment of disk 0 along the x axis. It is the vector sum of all moments of the disk:  . Summing up over the disks we obtain:
. Summing up over the disks we obtain:
 | (11) |
 for d = 2 and 4, whereas μ = 2 for d = 3. For the norm M of M one obtains
for d = 2 and 4, whereas μ = 2 for d = 3. For the norm M of M one obtains | (12) |
This equation was used to generate the plot of Fig. 6b.
Interestingly, the symmetry observed for the norm of the hydrophobic moment (Fig. 6b) is the same as for the orientation of the inserted cylinders (Fig. 4a and Fig. S2, ESI†). When the cylinder is in the parallel state, the norm of the hydrophobic moment displays its maximum values, as predicted by the model described above. Conversely, when the norm becomes smaller, or even zero, the cylinder tilts. In the case of individual moments of constant norm (Fig. 6), the inclination of the cylinder is thus essentially determined by the norm of the total hydrophobic moment.
III.E Membrane deformations
The physical and thermodynamical properties of membranes can be modeled at different scales. The Helfrich model provides a correct description at a scale of around ten nanometers by modeling the membrane as an elastic surface.50,51 To relate the present work to this level of description, we determine the bilayer midplane for the trajectories in which the cylinder is inserted into the membrane. This midplane is defined as the surface separating the two layers of lipids, where the lipids are sorted between the two layers according to their up/down orientation.52 The positions of the central lipid beads LI1 of each monolayer are then interpolated (Fig. 1) using the class SmoothBivariateSpline available in the python library SciPy.53 The resulting two interpolated surfaces are then averaged at each point of the interpolation grid to produce the bilayer midplane surface. To obtain a consistent result for each simulation trajectory, the midplane surfaces are time-averaged using the frames in which the cylinder is displaced in the middle of the simulation box as described at the end of Section II.C.The results obtained for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 3 and d = 2 (Fig. 7) display typical patterns which are encountered for other sets of parameters corresponding to inserted cylinders. The different patterns obtained as a function of the angle α are correlated with the distributions of the angle θ observed in Fig. 4. A very pronounced invagination at the position of the cylinder is observed for small values of α and θ distributions close to 90°. A similar configuration is observed for α equal to 90° and 150° even though the invaginations are shallower. For other values of α, we observe that the surface tends to form an invagination (blue color) on one side of the cylinder and a bump (red-orange color) on the other side.
c = 3 and d = 2 (Fig. 7) display typical patterns which are encountered for other sets of parameters corresponding to inserted cylinders. The different patterns obtained as a function of the angle α are correlated with the distributions of the angle θ observed in Fig. 4. A very pronounced invagination at the position of the cylinder is observed for small values of α and θ distributions close to 90°. A similar configuration is observed for α equal to 90° and 150° even though the invaginations are shallower. For other values of α, we observe that the surface tends to form an invagination (blue color) on one side of the cylinder and a bump (red-orange color) on the other side.
 | ||
Fig. 7 Central parts of the membrane surface (10 × 10 in scaled units) obtained by averaging the interpolated surfaces defined by the LI1 beads of the lipids of each monolayer of the membrane. The surfaces have been determined for the set of trajectories recorded with ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 3 and d = 2. The reference height z = 0 is set to the mean height of the displayed surface. Similar surfaces with the same patterns have been interpolated for simulations recorded with box sizes 35 × 35 × 100σ3 and 40 × 40 × 100σ3 (Fig. S4, ESI†). c = 3 and d = 2. The reference height z = 0 is set to the mean height of the displayed surface. Similar surfaces with the same patterns have been interpolated for simulations recorded with box sizes 35 × 35 × 100σ3 and 40 × 40 × 100σ3 (Fig. S4, ESI†). | ||
The observed deformation patterns (Fig. 7) follow the same symmetry as the orientation of the cylinder. When the cylinder is inserted parallel to the membrane, it imposes an invagination of the membrane's midplane whereas we obtain a midplane which is antisymmetric with respect to the y axis for the tilted cylinder state. Furthermore, in the case where the cylinder is parallel, the depth of the invagination increases with the norm of the hydrophobic moment (Fig. 6). For small values of α, the hydrophobic moment is maximal as well as the invagination depth.
For d = 1 a region of surface states is observed in the configuration space (see Fig. 3). Fig. 8 shows the corresponding midplanes for α = 20°. At ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 2 and 2.25 one observes a two-fold symmetry for the surface states, for which the cylinder is not yet inserted (crosses in Fig. 3). The symmetry reflects the presence of a torque doublet which is due to the mismatch of the orientations of the helicoidal hydrophobic strip and the originally flat membrane. This confirms the predictions of the twister model.32
c = 2 and 2.25 one observes a two-fold symmetry for the surface states, for which the cylinder is not yet inserted (crosses in Fig. 3). The symmetry reflects the presence of a torque doublet which is due to the mismatch of the orientations of the helicoidal hydrophobic strip and the originally flat membrane. This confirms the predictions of the twister model.32
 | ||
| Fig. 8 Central parts of the membrane surface (10 × 10 in scaled units) obtained by averaging the interpolated surfaces defined by the LI1 beads of the lipids of each monolayer of the membrane. The surfaces have been determined for the set of trajectories recorded with α = 20° and d = 1. The reference height z = 0 is set to the mean height of the displayed surface. Similar patterns exhibiting a two-fold symmetry have been observed for simulations recorded with box sizes of 35 × 35 × 100σ3 and 40 × 40 × 100σ3 (Fig. S5, ESI†). | ||
Increasing ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c in Fig. 8 leads to the insertion of the cylinder into the membrane reflected by the formation of an invagination. Note, however, that the two-fold symmetry and thus the torque doublet persists as visible by the higher z values at the lower left and the upper right corners as compared to the other corners. This behavior can also be observed for the surface of α = 30° in Fig. 7, where only inserted states are depicted.
c in Fig. 8 leads to the insertion of the cylinder into the membrane reflected by the formation of an invagination. Note, however, that the two-fold symmetry and thus the torque doublet persists as visible by the higher z values at the lower left and the upper right corners as compared to the other corners. This behavior can also be observed for the surface of α = 30° in Fig. 7, where only inserted states are depicted.
For α ≳ 60° the hydrophobic part of the cylinder is not a strip any more. The membrane cannot adhere to all hydrophobic beads of the cylinder due to the rigidity of the membrane and the torque doublet ceases to exist. For small d and large α the hydrophobic strip even vanishes.
The mechanical properties of the membrane have been investigated by calculating the average scaled hydrophobic thickness of the membrane h (Fig. 9 and Fig. S6, ESI†). The bending rigidity of a uniform membrane is proportional to h2 which implies that membrane thickening leads to more rigid membranes.54
 | ||
Fig. 9 Averaged scaled hydrophobic thickness of the membrane, h, as a function of α for the first run of the MD simulations (see Fig. S6 for the second run, ESI†). The four panels correspond to different values of d while the colors correspond to different values of the cohesion parameter ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c. The thickness was calculated as the difference of time-averaged z coordinates of the interpolated monolayers obtained from the positions of the LI1 beads and spatially averaged over a square of 5 × 5σ2 located at the center of the membrane where the cylinder is situated. c. The thickness was calculated as the difference of time-averaged z coordinates of the interpolated monolayers obtained from the positions of the LI1 beads and spatially averaged over a square of 5 × 5σ2 located at the center of the membrane where the cylinder is situated. | ||
The hydrophobic thickness was calculated from the time-averaged distance between the monolayers averaged spatially over a square of 5 × 5σ2 in the center of the membrane. The scaled thickness values close to 2.6 display very small standard deviations and correspond to membranes not interacting with the cylinder. Unsurprisingly, the standard deviations increase for deformed membranes with a scaled thickness far from 2.6.
Increasing the cohesion parameter ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c at constant number of hydrophobic beads per disc, d, one observes a thinning of the membrane as soon as the cylinder starts to interact. In this case cylinders with a parallel orientation with respect to the membrane are situated at the interface between the hydrophobic and the hydrophilic part of the membrane like in Fig. 4c. For higher values of
c at constant number of hydrophobic beads per disc, d, one observes a thinning of the membrane as soon as the cylinder starts to interact. In this case cylinders with a parallel orientation with respect to the membrane are situated at the interface between the hydrophobic and the hydrophilic part of the membrane like in Fig. 4c. For higher values of ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c the cylinder inserts further inside leading to an increase of the membrane thickness. For d > 2 and large enough
c the cylinder inserts further inside leading to an increase of the membrane thickness. For d > 2 and large enough ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c, it is surrounded by the membrane beads and h lies above the hydrophobic thickness of the undeformed membrane. A similar effect is observed for constant
c, it is surrounded by the membrane beads and h lies above the hydrophobic thickness of the undeformed membrane. A similar effect is observed for constant ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c and increasing d.
c and increasing d.
There is thus a cooperative effect between ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c and d to increase the membrane thickness related to the hydrophobicity of the cylinder. Additionally, one observes minima of the thickness related to the orientation of the cylinder (Fig. 4) for large
c and d to increase the membrane thickness related to the hydrophobicity of the cylinder. Additionally, one observes minima of the thickness related to the orientation of the cylinder (Fig. 4) for large ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c and α ≈ 120° (see Fig. 9 for d = 2 and
c and α ≈ 120° (see Fig. 9 for d = 2 and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 3 as well as for d = 4 and
c = 3 as well as for d = 4 and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 2).
c = 2).
III.F Estimation of the twister
The membrane midplanes allow us to estimate the torque doublet induced by the cylinder at the surface for small values of α. To this end we will exploit the results of ref. 32. However, a word of caution is due here: several approximations and simplifications will have to be done to apply the continuous model used in ref. 32. The varying thickness of the membrane close to the cylinder cannot be taken into account. Furthermore, the interpolation of the midplane surface from the discrete positions of the lipid beads potentially introduces additional errors. Ignoring these shortcomings, we can obtain the torque doublet from the geometric properties of the midplane, i.e., the position of the local minima. This simplifies the necessary treatment considerably. Further interpretation of the simulation results in the framework of Helfrich theory would, however, risk to be too crude.The deviation from a flat plane can be approximated by the superposition of the deformations of two opposite point torques and an invagination caused by the hydrophobic interactions between the cylinder and the lipid tails of the membrane. To estimate the value of the torques, we make the strong assumption that the position of each surface minimum at lowest order is due to a single point torque. For a point torque τ at the origin the scaled height above a flat reference plane is given by:32
 | (13) |
 is the nth Bessel function of the second kind. In our simulations κ ≈ 13kBT (see Section II.A), whereas τ can be inferred from the height and the position of the surface minima.
is the nth Bessel function of the second kind. In our simulations κ ≈ 13kBT (see Section II.A), whereas τ can be inferred from the height and the position of the surface minima.
The extrema of z(x,y) lie at x = 0. The minimum ymin can be found by solving the equation
 | (14) |
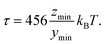 | (15) |
Note that the value of ymin implies that the extrema of the surface are close to the cylinder. Consequently, variations in membrane thickness would have to be taken into account to obtain a more accurate estimate of the torque.
To apply this result on the interpolated midplane surfaces of the previous section, for which the cylinder is at the surface (i.e., ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 2 and
c = 2 and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 2.25 with α = 20° and d = 1, see Fig. 8), one first has to read off the position of the minimum Ymin < 0 and Zmin for each surface and replace
c = 2.25 with α = 20° and d = 1, see Fig. 8), one first has to read off the position of the minimum Ymin < 0 and Zmin for each surface and replace  by
by  in eqn (15). This yields τ = 37kBT for
in eqn (15). This yields τ = 37kBT for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 2 and τ ≈ 46kBT for
c = 2 and τ ≈ 46kBT for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 2.25 when the cylinder is at the surface of the membrane. In the case of insertion (
c = 2.25 when the cylinder is at the surface of the membrane. In the case of insertion (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 2.5), the estimate for τ yields approximately 62kBT. The torque allowing the cylinder to enter in the membrane is thus in-between these two numerical values, at the order of 50kBT. Similar estimations of τ are obtained for box sizes 35 × 35 × 100σ3 and 40 × 40 × 100σ3 (Table S1, ESI†).
c = 2.5), the estimate for τ yields approximately 62kBT. The torque allowing the cylinder to enter in the membrane is thus in-between these two numerical values, at the order of 50kBT. Similar estimations of τ are obtained for box sizes 35 × 35 × 100σ3 and 40 × 40 × 100σ3 (Table S1, ESI†).
A glance at eqn (9) in Section III.A allows us to compare these values with the torque that is necessary to deform the cylinder such that the torsional angle yields 5α = 100°. From eqn (9) one obtains τcyl = 244kBT with L ≈ 5 nm and χ ≈ 3000 pN nm2. The corresponding value of τ is thus 122kBT since the twister contains two opposite torques τ and can be understood as an upper bound for the twister that can be applied by the cylinder with α = 20° and d = 1.
The above calculations should only be taken as a rather crude estimate of the real values given the simplifications that have been made. Nevertheless, they allow us to connect the mesoscopic twister model of ref. 32 with coarse-grained MD simulations of a protein–membrane system.
IV. Discussion
In the present work, a coarse-grained model was used to describe the interaction of a folded α helical structure with a lipid bilayer membrane. In this coarse-grained model, the protein structure is represented by a cylinder, where the configurations of hydrophobic patches are obtained by systematically varying the positions of hydrophobic beads. The coarse-graining proposed here includes an originality in the way the protein is modeled: the rigidity of the cylinder is enforced by a tensegrity framework. A similar framework was previously used in the literature,33 but we significantly extended it by introducing a helicity parameter, which is essential to investigate the asymmetric organization of hydrophobic residues corresponding to non-amphipathic α helices. It should be stressed that the model chosen here for the definition of hydrophobic patches does not describe all possible distributions, but the underlying symmetry of the model allows us to identify some rules in the analysis of the orientation. An extension of the model to further hydrophobic distributions has still to be explored.Another possible extension of the model could include an adapted scale of hydrophobicity for the amino-acid residues. Various scales could be exploited in this respect.31,55 A description at atomic resolution of this interaction would, however, require the development of a related energy function and is beyond the scope of this paper.
The model of Cooke and Deserno34,35 was used here, since we intended to focus on large scale effects of asymmetric hydrophobicity in α helix/membrane interactions. Nevertheless, the Martini force model56,57 is one of the most applied coarse-grained force fields devoted to biological polymers and membranes. One further step of the use of the tensegrity approach in coarse-grained modeling should be the introduction of the Martini 3 model57 to account for the variety of chemical species contained in biological membranes.
By systematically varying the parameters of the cylinder, we were able to determine the configuration space of the system. Three states were identified: (i) a state where the membrane and the cylinder do not interact, (ii) a state where the cylinder is in contact with the membrane surface, (iii) a state where the cylinder is inserted into the membrane with two metastable orientations: either parallel or tilted with respect to the plane of the membrane. Depending on the conditions we recorded unimodal or bimodal distributions of the corresponding tilt angle.
The observed configuration states are similar to observations made previously with coarse-grained Martini models.58–61 But the cylinder model proposed here has the advantage of allowing systematic studies based on the distribution of hydrophobic residues in proteins, which opens the way to comparative studies connecting the atomistic structures of proteins and their behavior in the presence of a membrane.
Moreover, the coarse-grained description allowed identifying a direct correlation between the hydrophobic moment30 and the tilt angle of the cylinder. Since the hydrophobic moments of protein structures can be calculated quickly, this would allow fast bioinformatics processing of a large number of protein structures in order to predict configurations of transmembrane proteins.
Structures of membrane proteins with atomic resolution have long been rare, particularly because of the difficulties in crystallizing membrane samples. However, the experimental problems have been alleviated, as there are now more than 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 membrane protein structures in the Protein Data Bank (https://www.rcsb.org). However, there is little information at atomic resolution on how proteins interact with a membrane during translocation. Studies by solid-state nuclear magnetic resonance have highlighted different tilt angles on small proteins.62–65 Furthermore, the analysis of α amphipathic helices shows configurations where the protein lies on the membrane.66
500 membrane protein structures in the Protein Data Bank (https://www.rcsb.org). However, there is little information at atomic resolution on how proteins interact with a membrane during translocation. Studies by solid-state nuclear magnetic resonance have highlighted different tilt angles on small proteins.62–65 Furthermore, the analysis of α amphipathic helices shows configurations where the protein lies on the membrane.66
Note that the results described here on the membrane thickness display an interesting correlation with NMR experimental observations.67 The authors used the quadrupolar splittings of the 2H solid-state NMR to estimate the membrane thickness in the presence of peptides with various hydrophobicity levels and showed that the increase in peptide hydrophobicity induces thicker membranes.
The model proposed here, which is limited to the case of a stable protein structure should allow us to explain some of these observations and can even be extended to the case of proteins displaying possible structural variability, by simulating several cylinders in interaction with the membrane. Of course, the regions of proteins prone to unfolding should be detected before building the cylinders. In the perspective of an application to biological systems, the balance between the propensity of a protein to unfold when placed in contact with the membrane and the propensity of the protein to deform the membrane due to an asymmetry of its hydrophobic residues, is essential to be estimated.
The application of Helfrich theory68 using the bilayer's midplane allowed us to identify local torques acting on the membrane during the interaction with the cylinder. Cylinders with a helical hydrophobic strip (i.e., small α) at the surface of the membrane induce a two-fold symmetry of the midplane indicating the existence of a torque doublet exactly as predicted by Fierling et al.32 Further simulation studies with multiple cylinders could help in understanding how several of these twisters interact cooperatively. These predictions could allow the recently performed analysis of atomistic MD simulations using the twister model to be extended.69
Data availability
The datasets supporting the conclusions of this article are available at https://www.doi.org/10.5281/zenodo.15102341.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We would like to thank Dr Sam Foley as well as Dr Markus Deserno for providing us with their membrane simulation scripts which were the starting point to set up the cylinder–membrane simulations presented here. The calculation resources were provided by the EXPLOR meso-computing center at the University of Lorraine (Project: 2022CPMXX2687). Drs Fabien Pascale and Mauricio Chagas are acknowledged for installing the EsPreSSo software.References
- T. Pollard, W. Earnshaw, J. Lippincott-Schwartz and G. Johnson, Cell Biology, Elsevier, 2022 Search PubMed.
- M. Dong, G. Masuyer and P. Stenmark, Annu. Rev. Biochem., 2019, 88, 811–837 CrossRef CAS PubMed.
- J. Koop, J. Merz and G. Schembecker, J. Biotechnol., 2021, 334, 11–25 CrossRef CAS PubMed.
- S. Tang, J. Li, G. Huang and L. Yan, Protein Pept. Lett., 2021, 28, 938–944 CAS.
- I. Ilangumaran Ponmalar, N. K. Sarangi, J. K. Basu and K. G. Ayappa, Front. Mol. Biosci., 2021, 8, 737561 CrossRef PubMed.
- L. Carlier, D. Samson, L. Khemtemourian, A. Joliot, P. Fuchs and O. Lequin, Biochim. Biophys. Acta, Biomembr., 2022, 1864, 184030 CrossRef CAS PubMed.
- K. H. Lam, Z. Guo, N. Krez, T. Matsui, K. Perry, J. Weisemann, A. Rummel, M. E. Bowen and R. Jin, Nat. Commun., 2018, 9, 5367 CrossRef CAS PubMed.
- J. Hong, X. Lu, Z. Deng, S. Xiao, B. Yuan and K. Yang, Molecules, 2019, 24, 1775 CrossRef CAS PubMed.
- Y. Li, Y. Li, H. M. Mengist, C. Shi, C. Zhang, B. Wang, T. Li, Y. Huang, Y. Xu and T. Jin, Toxins, 2021, 13, 128 CrossRef CAS PubMed.
- J. S. Wilson, A. M. Churchill-Angus, S. P. Davies, S. E. Sedelnikova, S. B. Tzokov, J. B. Rafferty, P. A. Bullough, C. Bisson and P. J. Baker, Nat. Commun., 2019, 10, 2900 CrossRef PubMed.
- S. Pacheco, J. P. J. Quiliche, I. Gómez, J. Sánchez, M. Soberón and A. Bravo, Toxins, 2020, 12, 647 CrossRef CAS PubMed.
- M. Mueller, U. Grauschopf, T. Maier, R. Glockshuber and N. Ban, Nature, 2009, 459, 726–730 CrossRef CAS PubMed.
- A. M. Churchill-Angus, T. H. B. Schofield, T. R. Marlow, S. E. Sedelnikova, J. S. Wilson, J. B. Rafferty and P. J. Baker, Sci. Rep., 2021, 11, 6447 CrossRef CAS PubMed.
- K. Tanaka, J. M. M. Caaveiro, K. Morante, J. M. González-Mañas and K. Tsumoto, Nat. Commun., 2015, 6, 6337 CrossRef PubMed.
- B. Bräuning, E. Bertosin, F. Praetorius, C. Ihling, A. Schatt, A. Adler, K. Richter, A. Sinz, H. Dietz and M. Groll, Nat. Commun., 2018, 9, 1806 CrossRef PubMed.
- S. A. Kirsch and R. A. Böckmann, Biochim. Biophys. Acta, 2016, 1858, 2266–2277 CrossRef CAS PubMed.
- E. Ermakova and Y. Zuev, J. Membr. Biol., 2017, 250, 205–216 CrossRef CAS PubMed.
- J. Su, S. J. Marrink and M. N. Melo, Front. Cell Dev. Biol., 2020, 8, 350 CrossRef PubMed.
- P. W. Simcock, M. Bublitz, F. Cipcigan, M. G. Ryadnov, J. Crain, P. J. Stansfeld and M. S. P. Sansom, J. Chem. Theory Comput., 2021, 17, 1218–1228 CrossRef CAS PubMed.
- R. Talandashti, F. Mehrnejad, K. Rostamipour, F. Doustdar and A. Lavasanifar, J. Phys. Chem. B, 2021, 125, 7163–7176 CrossRef CAS PubMed.
- L. Sun, S. Wang, F. Tian, H. Zhu and L. Dai, Biophys. J., 2022, 121, 4368–4381 CrossRef CAS PubMed.
- E. N. Frigini, R. D. Porasso, T. Beke-Somfai, J. J. López Cascales, R. D. Enriz and S. Pantano, J. Chem. Inf. Model., 2023, 63, 6877–6889 CrossRef CAS PubMed.
- A. van Teijlingen, M. C. Smith and T. Tuttle, Acc. Chem. Res., 2023, 56, 644–654 CrossRef CAS PubMed.
- S. Kmiecik, D. Gront, M. Kolinski, L. Wieteska, A. E. Dawid and A. Kolinski, Chem. Rev., 2016, 116, 7898–7936 CrossRef CAS PubMed.
- A. Manandhar, M. Kang, K. Chakraborty, P. K. Tang and S. M. Loverde, Org. Biomol. Chem., 2017, 15, 7993–8005 RSC.
- V. V. H. Giri Rao, R. Desikan, K. G. Ayappa and S. Gosavi, J. Phys. Chem. B, 2016, 120, 12064–12078 CrossRef CAS PubMed.
- J. Methorst, N. van Hilten, A. Hoti, K. S. Stroh and H. J. Risselada, J. Chem. Theory Comput., 2024, 20, 1763–1776 CrossRef CAS PubMed.
- T. Bereau, Z.-J. Wang and M. Deserno, J. Chem. Phys., 2014, 140, 115101 CrossRef PubMed.
- Z. Jia and J. Chen, J. Comput. Chem., 2016, 37, 1725–1733 CrossRef CAS PubMed.
- D. Eisenberg, R. M. Weiss and T. T. Terwilliger, Nature, 1982, 299, 371–374 CrossRef CAS PubMed.
- D. Eisenberg and A. D. McLachlan, Nature, 1986, 319, 199–203 CrossRef CAS PubMed.
- J. Fierling, A. Johner, I. M. Kulić, H. Mohrbach and M. M. Müller, Soft Matter, 2016, 12, 5747–5757 RSC.
- G. Illya and M. Deserno, Biophys. J., 2008, 95, 4163–4173 CrossRef CAS PubMed.
- I. R. Cooke, K. Kremer and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011506 CrossRef PubMed.
- I. R. Cooke and M. Deserno, J. Chem. Phys., 2005, 123, 224710 CrossRef PubMed.
- S. L. Foley, M. Varma, A. Hossein and M. Deserno, Emerging Top. Life Sci., 2023, 7, 95–110 CrossRef CAS PubMed.
- S. L. Foley and M. Deserno, J. Chem. Phys., 2024, 160, 064111 CrossRef CAS PubMed.
- S. Jin and L. R. Collins, New J. Phys., 2007, 8, 360 CrossRef.
- R. Connelly and S. D. Guest, Frameworks, Tensegrities, and Symmetry, Cambridge University Press, Cambridge, 2022 Search PubMed.
- F. Weik, R. Weeber, K. Szuttor, K. Breitsprecher, J. de Graaf, M. Kuron, J. Landsgesell, H. Menke, D. Sean and C. Holm, et al. , Eur. Phys. J.: Spec. Top., 2019, 227, 1789–1816 Search PubMed.
- A. Kolb and B. Dünweg, J. Chem. Phys., 1999, 111, 4453–4459 CrossRef CAS.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- N. Meyer, PhD thesis, Université de Lorraine, 2017.
- R. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domański, D. L. Dotson, S. Buchoux, I. M. Kenney and O. Beckstein, Proceedings of the 15th Python in Science Conference, Austin, TX, 2016, vol. 32, pp. 98–105.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- F. P. Beer, E. R. Johnston and J. T. DeWolf, Mechanics of Materials, McGraw-Hill, New York, 2001 Search PubMed.
- A. van Reenen, F. Gutiérrez-Mejía, L. J. van IJzendoorn and M. W. J. Prins, Biophys. J., 2013, 104, 1073–1080 CrossRef CAS PubMed.
- X. J. A. Janssen, J. M. van Noorloos, A. Jacob, L. J. van IJzendoorn, A. M. de Jong and M. W. J. Prins, et al. , Biophys. J., 2011, 100, 2262–2267 CrossRef CAS PubMed.
- C. Royer, Arch. Biochem. Biophys., 2008, 469, 34–45 CrossRef CAS PubMed.
- M. Deserno, Chem. Phys. Lipids, 2015, 185, 11–45 CrossRef CAS PubMed.
- O.-Y. Zhong-can and W. Helfrich, Phys. Rev. Lett., 1987, 59, 2486–2488 CrossRef PubMed.
- X. Wang and M. Deserno, J. Chem. Phys., 2015, 143, 164109 CrossRef PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- H. Bermúdez, D. Hammer and D. Discher, Langmuir, 2004, 20, 540–543 CrossRef PubMed.
- C. T. Mant, J. M. Kovacs, H. M. Kim, D. D. Pollock and R. S. Hodges, Biopolymers, 2009, 92, 573–595 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- P. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grunewald, I. Patmanidis, H. Abdizadeh, B. Bruininks, T. Wassenaar, P. Kroon, J. Melcr, V. Nieto, V. Corradi, H. Khan, J. Domanski, M. Javanainen, H. Martinez-Seara, N. Reuter, R. Best, I. Vattulainen, L. Monticelli, X. Periole, D. Tieleman, A. de Vries and S. Marrink, Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed.
- A. Khalfa, W. Treptow, B. Maigret and M. Tarek, Chem. Phys., 2009, 358, 161–170 CrossRef CAS.
- A. Khalfa and M. Tarek, J. Phys. Chem. B, 2010, 114, 2676–2684 CrossRef CAS PubMed.
- G. Paraskevi and S. Lev, J. Phys. Chem., 2010, 114, 826–839 CrossRef PubMed.
- A. Paulo F, Langmuir, 2023, 39, 10289–10300 CrossRef PubMed.
- V. V. Vostrikov, C. V. Grant, S. J. Opella and R. E. Koeppe 2nd, Biophys. J., 2011, 101, 2939–2947 CrossRef CAS PubMed.
- T. Nagao, D. Mishima, N. Javkhlantugs, J. Wang, D. Ishioka, K. Yokota, K. Norisada, I. Kawamura, K. Ueda and A. Naito, Biochim. Biophys. Acta, 2015, 1848, 2789–2798 CrossRef CAS PubMed.
- A. Marquette and B. Bechinger, Biomolecules, 2018, 8, 18 CrossRef PubMed.
- E. Strandberg, P. Wadhwani, J. Bürck, P. Anders, C. Mink, J. van den Berg, R. A. M. Ciriello, M. N. Melo, M. A. R. B. Castanho, E. Bardají, J. P. Ulmschneider and A. S. Ulrich, ChemBioChem, 2023, 24, e202200602 CrossRef CAS PubMed.
- U. Kaur and J. C. Lee, Acc. Chem. Res., 2021, 54, 302–310 CrossRef CAS PubMed.
- S. Grage, S. Afonin, S. Kara, G. Buth and A. Ulrich, Front. Cell Dev. Biol., 2016, 4, 65 Search PubMed.
- A. Guckenberger and S. Gekle, J. Phys.: Condens. Matter, 2017, 29, 203001 CrossRef PubMed.
- A. Delort, G. Cottone, T. Malliavin and M. Müller, Int. J. Mol. Sci., 2024, 25, 2481 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01494d |
| This journal is © The Royal Society of Chemistry 2025 |















